Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metamagnetic transition and a loss of magnetic hysteresis caused by electron trapping in monolayers of single-molecule magnet Tb2@C79N†
Emmanouil
Koutsouflakis
a,
Denis
Krylov‡
a,
Nicolas
Bachellier
b,
Daria
Sostina§
b,
Vasilii
Dubrovin
 a,
Fupin
Liu
a,
Fupin
Liu
 a,
Lukas
Spree
a,
Lukas
Spree
 a,
Georgios
Velkos
a,
Georgios
Velkos
 a,
Sebastian
Schimmel¶
a,
Yaofeng
Wang
a,
Bernd
Büchner
a,
Rasmus
Westerström
a,
Sebastian
Schimmel¶
a,
Yaofeng
Wang
a,
Bernd
Büchner
a,
Rasmus
Westerström
 cd,
Claudiu
Bulbucan
cd,
Claudiu
Bulbucan
 cd,
Kyle
Kirkpatrick
cd,
Kyle
Kirkpatrick
 e,
Matthias
Muntwiler
e,
Matthias
Muntwiler
 b,
Jan
Dreiser
b,
Jan
Dreiser
 b,
Thomas
Greber
b,
Thomas
Greber
 bf,
Stas M.
Avdoshenko
bf,
Stas M.
Avdoshenko
 a,
Harry
Dorn
a,
Harry
Dorn
 e and
Alexey A.
Popov
e and
Alexey A.
Popov
 *a
*a
aLeibniz Institute for Solid State and Materials Research (IFW Dresden), Helmholtzstraße 20, 01069 Dresden, Germany. E-mail: a.popov@ifw-dresden.de
bSwiss Light Source, Paul Scherrer Institute, CH-5232 Villigen PSI, Switzerland
cThe Division of Synchrotron Radiation Research, Lund University, SE-22100 Lund, Sweden
dNanoLund, Lund University, Box 118, 22100 Lund, Sweden
eDepartment of Chemistry, Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24061, USA
fPhysik-Institut der Universität Zürich, Winterthurerstr. 190, CH-8057 Zürich, Switzerland
First published on 28th June 2022
Abstract
Realization of stable spin states in surface-supported magnetic molecules is crucial for their applications in molecular spintronics, memory storage or quantum information processing. In this work, we studied the surface magnetism of dimetallo-azafullerene Tb2@C79N, showing a broad magnetic hysteresis in a bulk form. Surprisingly, monolayers of Tb2@C79N exhibited a completely different behavior, with the prevalence of a ground state with antiferromagnetic coupling at low magnetic field and a metamagnetic transition in the magnetic field of 2.5–4 T. Monolayers of Tb2@C79N were deposited onto Cu(111) and Au(111) by evaporation in ultra-high vacuum conditions, and their topography and electronic structure were characterized by scanning tunneling microscopy and spectroscopy (STM/STS). X-ray photoelectron spectroscopy (XPS), in combination with DFT studies, revealed that the nitrogen atom of the azafullerene cage tends to avoid metallic surfaces. Magnetic properties of the (sub)monolayers were then studied by X-ray magnetic circular dichroism (XMCD) at the Tb-M4,5 absorption edge. While in bulk powder samples Tb2@C79N behaves as a single-molecule magnet with ferromagnetically coupled magnetic moments and blocking of magnetization at 28 K, its monolayers exhibited a different ground state with antiferromagnetic coupling of Tb magnetic moments. To understand if this unexpected behavior is caused by a strong hybridization of fullerenes with metallic substrates, XMCD measurements were also performed for Tb2@C79N adsorbed on h-BN|Rh(111) and MgO|Ag(100). The co-existence of two forms of Tb2@C79N was found on these substrates as well, but magnetization curves showed narrow magnetic hysteresis detectable up to 25 K. The non-magnetic state of Tb2@C79N in monolayers is assigned to anionic Tb2@C79N− species with doubly-occupied Tb–Tb bonding orbital and antiferromagnetic coupling of the Tb moments. A charge transfer from the substrate or trapping of secondary electrons are discussed as a plausible origin of these species.
Introduction
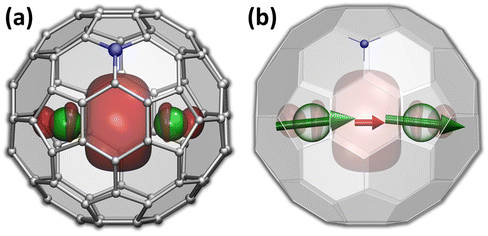
The versatility of carbon cages as robust hosts for various atoms, ions, and more complex endohedral species led to their frequent use in the design of endohedral fullerenes with unusual electronic and magnetic properties.1–10 The fullerene cage itself can be further modified by a substitution of carbon with heteroatoms. When a heteroatom is nitrogen, the substitution products are known as azafullerenes.11,12 As a nitrogen atom has one more electron than carbon, azafullerenes have a different electronic structure when compared to all-carbon fullerenes. For instance, the azafullerene C59N dimerizes spontaneously with the formation of a single interfullerene bond.12,13 Azafullerenes with endohedral metal atoms were discovered in 2008, when Dorn et al. isolated and structurally characterized two M2@C79N compounds with M = Y and Tb.14 Whereas the C80-Ih cage in normal endohedral metallofullerenes is stabilized by a metal-to-fullerene transfer of 6 electrons,15 replacement of one carbon by nitrogen effectively contributes one extra electron to the fullerene π-system. The endohedral unit therefore only has to transfer five electrons to the fullerene cage to stabilize its electronic structure. Thus, the formal charge distribution in dimetallo-azafullerenes is (M2)5+@(C79N)5−. A single valence electron in the endohedral M25+ dimer populates the M–M bonding orbital (Fig. 1a).Dimetallo-azafullerenes form a subclass of rare-earth based dimetallofullerenes featuring a single-electron metal–metal bond.16 These molecules gained particular interest during recent years because of their interesting magnetic properties.17–29 Delocalization of a valence electron between two lanthanide ions results in giant magnetic coupling in the endohedral metal dimer with a formal [M3+–e–M3+] configuration. For metal ions exhibiting axial single-ion magnetic anisotropy in these settings, like Dy and Tb, strong coupling results in robust single-molecule magnetism with enhanced blocking temperature of magnetization and very broad magnetic hysteresis.23–25,30 In particular, ab initio calculations indicated that single-ion quantization axes of Tb3+ ions in Tb2@C79N are almost parallel to the Tb–Tb axis (Fig. 1b).30 The almost collinear arrangement of Tb magnetic moments and the strong ferromagnetic coupling via unpaired electron result in high stability of the giant-spin state and its reluctance to magnetization reversal. As a result, magnetic hysteresis in powder samples of Tb2@C79N was observed up to 27 K, with 100-second blocking temperature of magnetization near 24 K.30 In fact, Tb-based dimetallofullerenes, Tb2@C79N (ref. 30) and Tb2@C80(CH2Ph) (ref. 23), are among the strongest single-molecule magnets (SMMs) second to only some metallocenium-based SMMs,31–34 and show the highest hysteresis temperatures among air-stable SMMs.
An important advantage of metallofullerenes as molecular magnets is the high thermal and chemical stability of fullerene cages. It not only makes dimetallofullerenes air-stable, despite the unconventional oxidation state of endohedral lanthanides, but also allows deposition of metallofullerenes on conducting substrates by sublimation or solution-based self-assembly. Sustained magnetic bistability in a thin film, a monolayer, and eventually a single molecule in contact with a conducting substrate is an important prerequisite for the use of SMMs in nanoscale spintronics. However, a realization of hysteretic behaviour in monolayers is not straightforward and was demonstrated only for a handful of SMMs,35–55 including some metallofullerene-SMMs.56–62 The nitride clusterfullerenes Dy2ScN@C80 and DySc2N@C80 were shown to maintain their SMM properties in monolayers on metallic substrates.56–60 Even more promising are recent studies of Dy2@C80(CH2Ph) deposited onto graphene61 and Tb2@C80(CH2Ph) on graphene and HOPG,62 which demonstrated that dimetallofullerenes with single-electron lanthanide–lanthanide bonds can also sustain their superb SMM performance in monolayers. Magnetic hysteresis in these monolayers was observed at considerably higher temperatures than in all other surface-supported SMMs, reaching 28 K for a self-assembled monolayer of Tb2@C80(CH2Ph) derivative.62 Unlike M2@C80(CH2Ph) derivatives, Tb2@C79N is free from exohedral organic group, which makes it sufficiently thermally stable for the growth of thin films by sublimation in ultrahigh-vacuum conditions. In this work, we report on the deposition of submonolayers of Tb2@C79N onto Au(111) and Cu(111) substrates and the electronic and magnetic properties thereof studied by scanning-tunneling microscopy, DFT calculations, and synchrotron-based X-ray absorption spectroscopy (XAS). The influence of the fullerene–substrate interaction on the electronic and magnetic states is further evaluated by introducing thin layers of insulators, MgO and h-BN, between fullerenes and metallic substrates.
Methods
Tb2@C79N was obtained by arc-discharge evaporation of hollow graphite rods filled with Tb4O7 in nitrogen-containing atmosphere and separated from other Tb-EMFs by HPLC following ref. 14 with modifications introduced in ref. 30.The surfaces of Au(111) and Cu(111) single crystals were prepared by repeated Ar+-sputtering and annealing cycles. An h-BN monolayer on Rh(111) was prepared according to ref. 63 and 64, and before evaporation of fullerenes, the wafer was annealed in UHV at 1100 K for 15 min. The thin film of MgO on Ag(100) was grown by sublimation of Mg in O2 atmosphere (10−6 mbar) while keeping the substrate at 645 K; the film thickness determined by XAS at the Mg-K edge was in the range of 5 monolayers.
For the surface deposition, Tb2@C79N was transferred by drop-casting to a crucible of a custom-made molecular evaporator, whose design allowed reducing the distance to the substrate to 4–5 cm. The samples were degassed for several hours at 400 K under high vacuum to remove the traces of solvent. Evaporation then proceeded at 700–710 K, giving submonolayer coverage after 5 min. During evaporation of fullerenes, all substrates were kept at room temperature.
Low-temperature STM measurements were performed at the PEARL beamline65 (Swiss Light Source, Paul Scherrer Institute) using an Omicron LT-STM microscope with the samples cooled to 4.8 K. Topography and dI/dU maps were measured in constant-current mode, while dI/dU curves were obtained in constant height mode. Spectroscopy data were measured through lock-in detection of the ac tunnel current driven by an 877 Hz, 5 mV rms signal added to the junction bias, produced by a STANFORD SR830 amplifier.
X-ray photoelectron spectroscopy (XPS) measurements were also performed at PEARL for submonolayer and multilayer (ca. 0.3 ML and 3 ML coverage) of Tb2@C79N deposited onto Cu(111), the samples for XPS measurements were cooled to 77 K.
Magnetic properties of Tb2@C79N layers on various substrates were studied by X-ray magnetic circular dichroism (XMCD) with synchrotron radiation at the X-Treme beamline66 (Swiss Light Source, Paul Scherrer Institute). Deposition conditions on Au(111) and Cu(111) substrates were the same as for the experiments at the PEARL beamline, and the formation of submonolayers was confirmed in situ by room-temperature STM measurements shown in ESI.† In XMCD measurements, the magnetic field was collinear with the X-ray beam, and X-ray absorption was measured in the total electron yield mode. The photon flux on the sample was in the range of 0.3–4 × 10−2 photons nm−2 s−1. Each measured spectrum was normalized to the intensity of the pre-edge signal, and then the broad background was subtracted. Thus, the XAS signal intensity reported in the paper corresponds to the normalized increase of the XAS due to the specific absorption at the Tb-M4,5 edge over the background signal. Non-polarized XAS intensity is defined as XAS = (I+ + I−), XMCD intensity is (I− − I+). When XMCD intensities are plotted in %, the XMCD signal is divided by the XAS intensity at its maximum. In the measurement of magnetization curves, I+ or I− intensity during each magnetic field sweep was measured at fixed energies corresponding to the maximum of XMCD signal and to the pre-edge energy. In the magnetic hysteresis and angular dependence plots, the (I− − I+) values are divided by the (I+ + I−) sum, giving normalized XMCD, denoted as XMCD/XAS. Sum rule analysis for estimation of Tb-4f magnetic moments was performed only for Tb2@C79N on Au(111) and MgO|Ag(100) substrates, because the strong non-linear background of Cu(111) prevents an accurate estimation of integral values, whereas on h-BN|Rh(111) the signal-to-noise ratio was too low.
DFT modeling of the Tb2@C79N molecule placed on Au(111), Cu(111), and MgO(100) substrates were performed at the PBE-D level with PAW potentials using the VASP 5.0 code.67–71 The 4f-in-core potentials used for Tb allowed DFT calculation without explicit treatment of 4f electrons. Metallic Cu(111) and Au(111) substrates were modelled as slabs of 6 atomic layers with lateral unit cells of 12.76 Å (Cu) and 14.43 Å (Au). MgO(100) was described by 4 atomic layers with the lateral unit cell of 12.65 Å. At these intermolecular distances, fullerene–fullerene interactions are presumed to be rather weak. In the course of optimization, both the fullerene and the substrate atomic positions were refined; uncertainty of the relative energies with the numerical settings used in the calculations did not exceed 2 meV. Atomic charges were derived from DFT-computed electronic densities using Bader code.72 Simulations of magnetization curves were performed with PHI code.73
Surface deposition and STM characterization of Tb2@C79N on Au(111) and Cu(111)
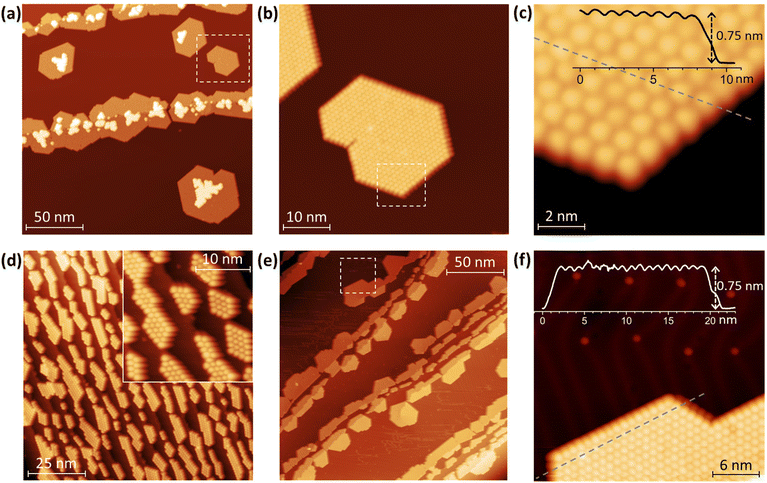
Topographies of Tb2@C79N layers deposited onto Au(111) and Cu(111) are shown in Fig. 2 (see also Fig. S1–S9 in ESI† for additional data). As common for fullerenes on metallic surfaces,74 Tb2@C79N molecules on Cu(111) exhibit sufficiently high mobility on the surface of the room temperature substrate to diffuse over the atomically flat terraces. Step edges of the metal substrate act as preferential starting points for the fullerene island growth, eventually leading to stripes of fullerene islands anchored to the step-edges, although some islands were also found on the substrate terraces. Due to the hcp arrangement of the molecules, a pronounced tendency to hexagonally shaped islands is clearly seen (Fig. 2). An onset of the second layer growth is seen on many of the monolayer islands, even though there is still a large area of bare metallic substrate. This is rather uncommon for fullerenes, which usually preferentially cover the whole metallic surface.On the fragment of the Au(111) crystal with many edge-steps, Tb2@C79N molecules arrange into arrays of narrow aligned stripes (Fig. 2d and Fig. S8†). This indicates that deposition onto vicinal surfaces may be used in future to create aligned fullerene ribbons with controlled width.75 On the larger Au(111) terraces, the morphology of the Tb2@C79N submonolayer is similar to that on Cu(111) except for a much smaller degree of the second layer formation (Fig. 2e and f). Lateral and vertical parameters of the islands on Au(111) are similar to those on Cu(111). The apparent height of fullerene molecules determined from height profiles measured at the bias voltage of +0.8 V is 7.5(1) Å, whereas the lateral size of the hexagonal monolayer lattice is 10.7(3) Å.
Further details of the electronic structure near the Fermi level were studied by scanning tunneling spectroscopy (STS); for technical reasons, the measurements were limited to the ±1 V window. The spectra measured on several Tb2@C79N islands on Cu(111) can be divided into three groups with slightly different position of the HOMO peak varying between −0.58 V and −0.64 V (Fig. 3a and Fig. S5†). In the LUMO range, no well-defined peaks can be seen. Instead, dI/dU grows continuously with the increase of the bias voltage above +0.5 V. The transport gap in the Tb2@C79N monolayer on Cu(111) varies in the range of 1.05–1.12 V. The measurements did not reveal pronounced features near the Fermi level.
Measurements over a double-layer of Tb2@C79N demonstrate a completely different STS profile with the peak at +0.5 V, presumably derived from the LUMO and accompanied by a negative differential conductance feature at the more positive bias (Fig. 3a and Fig. S6†). The transport gap for the double layer is increased beyond 1.5 V, and the HOMO-derived peak cannot be observed in the available voltage window. Both the negative differential conductance and the increase of the gap are consistent with the double-layer structure. Similar phenomena were observed in STM studies of fullerene C60 decoupled from metallic substrates, either in C60 double layers or in C60 deposited on top of other organic molecules.76–79
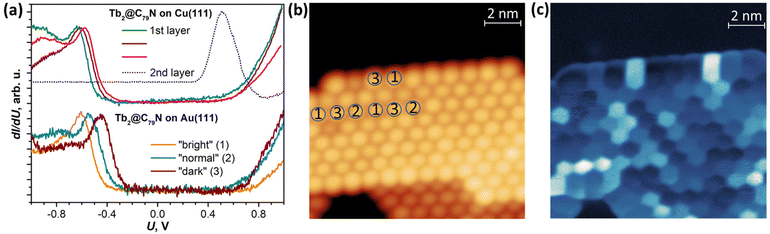
A Tb2@C79N monolayer on Au(111) has a similar STS pattern to that on Cu(111) with a well-defined HOMO peak, a flat region around the Fermi level, and a steady increase of dI/dU above +0.6 V (Fig. 3b and Fig. S9†). For one of the islands, we performed dI/dU mapping at U = −0.632 V, near the HOMO-derived peak. Whereas topography of the island shows similar height for all fullerene molecules (Fig. 3b), the dI/dU map reveals strong inhomogeneity with considerable variation of the brightness between different molecules (Fig. 3c). STS measurements at different molecules showed the variation of the HOMO peak from −0.45 to −0.61 eV as well as the variation of the transport gap from 0.95 to 1.18 V (Fig. 3a and Fig. S9†). We tentatively assign this variability to the different orientations of Tb2@C79N molecules in monolayers as well as different coordination geometry of the cage and metal substrate (the cells of the fullerene monolayer and metallic substrates are not commensurate). Similar variability of the MO peak caused by different molecular orientations was found in a C60 monolayer on Cu(100).80 Interestingly, the variation of the energies and the gap is more pronounced on Au(111) than on Cu(111), showing that Tb2@C79N molecules are more ordered on copper. This agrees with the results of XMCD studies discussed below, which show a considerably higher degree of ordering of Tb2 dimers in monolayers on Cu(111).
XPS and valence-band PES
DFT calculations discussed below showed that among the studied substrates, Cu(111) exhibits the strongest interactions with Tb2@C79N molecules. Thus, Tb2@C79N deposited on Cu(111) was studied by XPS using excitation at 800 eV. In addition to a submonolayer with a coverage of approximately 0.3 ML as estimated by STM, the measurements were also performed for a multilayer sample with a thickness of about 3 ML.The N 1s signal of Tb2@C79N is found at the binding energy of 401 eV. Neither the peak energy nor its shape changes with the level of coverage (Fig. 4a). This indicates that the nitrogen site of the azafullerene is not involved in the strong interaction with the copper substrate. Presumably, the molecules are landing on Cu(111) with the nitrogen oriented upside to avoid its contact with the metallic substrate (see results of DFT calculation below). The N 1s binding energy in Tb2@C79N is close to the N 1s binding energy in nitrogen-substituted C-sp2 compounds. For instance, pyridinic (6-membered ring) and pyrrolic (5-membered ring) nitrogen gives XPS signals at 398.3 ± 0.3 eV and 400.1 ± 0.3 eV,81 respectively, N-substituted graphene/graphite has a peak at 400–402 eV, whereas the N 1s binding energy in azafullerene C59N is 400.7 eV.81,82 For comparison, the N 1s binding energy of the endohedral nitride ion (N3−) in metallofullerenes of the M3N@C2n family is noticeably lower, 396–397 eV: 396.1 eV in Sc3N@C78,83 396.9 eV in Sc3N@C80,84 and 396.8 eV in TbSc2N@C80.85
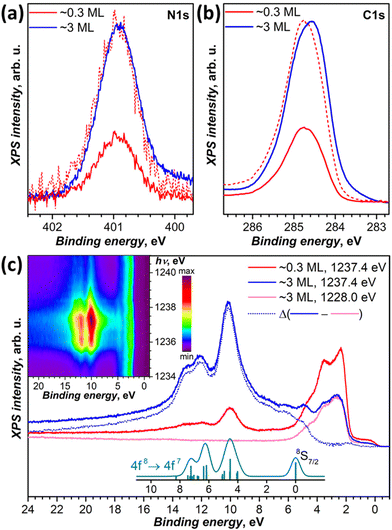 | ||
| Fig. 4 (a and b) XPS spectra of Tb2@C79N on Cu(111) in the N 1s (a) and C 1s (b) energy range, measurements are performed at 77 K with excitation at 800 eV for submonolayer (∼0.3 ML, red curves) and multilayer (∼3 ML, blue curves); dashed red curves are spectra of the submonolayer sample scaled to match intensity of the multilayer. (c) Valence band photoelectron spectra with excitation at 1228 eV (off-resonance, magenta) and at 1237.4 eV (in resonance with 3d → 4f excitation of Tb at the M5 edge) compared to theoretical intensity of 4f8 → 4f7 ionization transitions as calculated by Gerken91 (cyan, vertical bars are individual transition, and the curve is Gaussian broadening with the peak width of 0.6 eV). Blue dotted curve is the difference between in-resonance and off-resonance spectra. The inset shows variation of the PES intensity with the excitation photon energy between 1234 and 1241 eV measured with the step of 0.2 eV. | ||
The C 1s photoemission peak of Tb2@C79N multilayer has a maximum at 284.6 eV and full width at half-maximum of 1.1 eV. The peak energy is somewhat lower than in C60 (285.0–285.2 eV)86,87 or in metallofullerenes M3N@C80 with C80-Ih cage (285.2 eV for M = Sc,84 285.4 eV for M = Tm,88 285.9 eV for M = Dy89). The linewidth as well as the asymmetric shape of the peak is in line with those of EMFs with C80 fullerene cage.84,85,88,89 The C 1s peak of Tb2@C79N shows noticeable variation of the band shape and increase of the binding energy by ca. 0.2 eV when going from 3 ML to 0.3 ML coverage. Presumably, the fullerene–substrate interactions have a non-negligible influence on the C 1s core levels, unlike the N 1s level of the cage nitrogen. But the shift is not sufficiently strong to make a definitive conclusion on its nature. For comparison, in C60 adsorbed on Ag(110), a system with a strong fullerene–metal interactions and a sizeable charge transfer, the C 1s peak shifts to a lower binding energy by 0.7 eV on going from a monolayer to a multilayer coverage.90
We also studied valence-band photoelectron spectra (PES) using X-ray excitation with photon energy hνex varied in the 1228–1242 eV range. At hνex = 1228 eV, the PES spectrum is dominated by occupied states of Cu with strong peaks at the binding energies of 1.5–5.5 eV. Carbon and terbium have very small cross sections at this excitation energy. But when hνex is scanned through the Tb-M5 (3d → 4f) absorption edge, the resonantly enhanced Tb-4f photoemission appears at 5–15 eV below the Fermi level. The strongest Tb-4f emission is observed at hνex = 1237.4 eV (Fig. 4c). The Cu-based photoemission intensity remains virtually constant at these excitation energies. The spectra of 0.3 ML and 3 ML samples have the same resonant Tb-4f photoemission profile, which points to the absence of a strong interaction between Tb-4f electrons and the substrate. This is not surprising in the view of the localized nature of 4f electrons and shielding of endohedral Tb ions by the fullerene cage. The electron escape depth is short and most of the signal comes from the outermost layers. As a result, when the coverage of the substrate is increased from 0.3 to 3 ML, the resonant PES signal of Tb-4f increased considerably, whereas that of copper substrate decreased almost twice.
Off-resonance 4f8 → 4f7 photoemission intensity was computed by Gerken using the intermediate interaction model.91 According to his results, ionization of Tb3+ should give a stand-alone peak at the 4f7 ground state (8S7/2) and a complex multiplet at higher energies, between 4 and 8 eV above the 8S7/2-derived transition. The predicted multiplet structure corresponds well to a peak at 10.1 eV and a double peak at 12.1/12.9 eV below the Fermi level in the resonant PES spectrum of Tb2@C79N. At the same time, the 8S7/2 transition does not appear as sharp and well-resolved as predicted by theory. Instead, subtraction of the off-resonance spectrum leaves a broad band with multiple unresolved features at the binding energies of 5–7 eV. Presumably, the difference may be caused by the resonance nature of the spectra. Note that earlier the same theory gave very good agreement with X-ray valence band PES spectra of metallofullerenes Dy3N@C80,89 Tm3N@C80,92 and Tm@C8293 excited with Al Kα radiation (1486.6 eV). At that energy, the cross section of lanthanides is also very high, but there is no resonance with Dy-M5 or Tm-M5 absorption edges.
Computational modeling
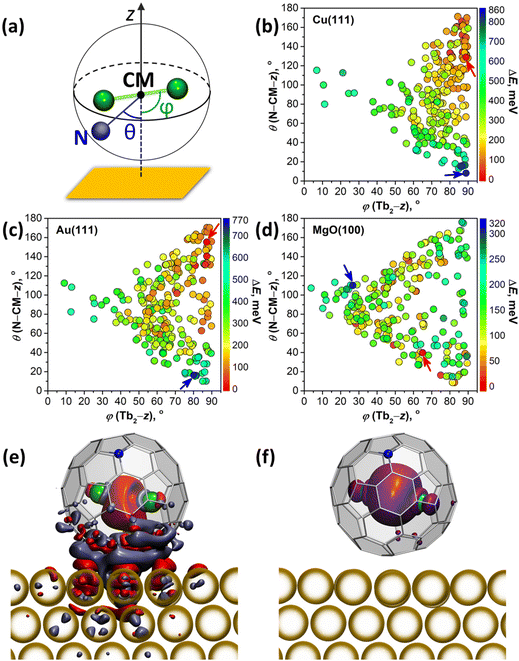
DFT calculations were performed to understand how interactions with metallic substrates can affect the molecular ordering and electronic structure of Tb2@C79N. In particular, we aimed to understand how the presence of the nitrogen atom in the fullerene cage affects the adsorption geometry of the molecule. Another question of interest was how Tb2 dimers are preferentially oriented inside the fullerene cage when it interacts with a substrate. Computations of an isolated Tb2@C79N molecule revealed that the nitrogen atom is located at the [5,6,6] position and that metal atoms tend to avoid close contact with nitrogen.14,30 The lowest energies were found then for the conformers, in which Tb2 atoms are located on the plane oriented perpendicular to the axis passing through the center of mass (CM) and the nitrogen atom. At the same time, rotation of the metal dimer in this plane leads to small energy variations, indicating that there is a certain flexibility for the dimer position. Our earlier theoretical studies of surface-supported Dy2ScN@C80 molecules showed that metallic substrates exhibit a significant orientational effect on the endohedral cluster.57 The latter tends to orient itself parallel to the surface to avoid interactions of endohedral metal atoms with a surface-contacted fragment of the fullerene cage. To summarize, these findings show that a reliable study of metallofullerene on the surface should consider various degrees of freedom of the whole molecule as well as its endohedral unit.For a comprehensive description of Tb2@C79N on Cu(111), Au(111), and MgO(100) substrates, we generated 240 starting configurations of an adsorbed Tb2@C79N molecule with different positions of the nitrogen and endohedral Tb2 dimer on each substrate94 and optimized them at the DFT level (see Methods for further details and ESI† for details of structure generation). Even with this large number of structures, complete sampling cannot be guaranteed because the parameter space is immense, but it is representative enough to find general trends in the preferable configurations. Two angles defined in Fig. 5a are used in the further discussion to parameterize the Tb2@C79N structure on the surface. The angle between the Tb2 bond and the normal to the substrate z is denoted as ϕ(Tb2–z); the values of ϕ close to 90° correspond to the parallel orientation of the Tb2 dimer versus the surface. The nitrogen position with respect to the substrate is described by the angle θ(N–CM–z) between the N–CM axis and the normal to the surface z; small values of θ correspond to the nitrogen atom facing the surface, whereas the values close to 180° correspond to the nitrogen facing upwards. Note that for the vast majority of optimized structures, the angle between the Tb2 bond and N–CM axis is within the 75°–90° range.
Fig. 5b–d and Fig. S12† plot distributions of ϕ(Tb2–z) and θ(N–CM–z) angles in optimized structures, whereas their relative energies are encoded in the color of the dots. The range of the relative energies obtained for optimized conformers depends considerably on the substrate. For an isolated Tb2@C79N molecule, the conformers span the energy range of 100 meV.30 For adsorbed molecules, the range of the energies increases to 860 meV (on Cu) and 770 meV (on Au). On the insulating MgO(100), the spread of values is reduced to 320 meV, which is still significantly higher than for the isolated molecule.
There is a clear tendency to avoid landing configurations, in which the nitrogen atom of the azafullerene cage is in close contact with the metal substrate. All structures with θ(N–CM–z) less than 20° are among the least stable configurations on Cu(111) and Au(111). On the other hand, for the most stable structures with ΔE < 100 meV, θ(N–CM–z) angles are higher than 96° on Cu(111) and 59° on Au(111). The avoidance of N-metal contacts is in line with N 1s XPS results for Tb2@C79N on Cu(111) discussed above. Note that there is no clear preference for the position of nitrogen for Tb2@C79N molecules on MgO.
Calculations also reveal the preference of the parallel orientation of Tb2 with respect to metallic substrates. For the most stable structures with ΔE < 100 meV, ϕ(Tb2–z) angles span the ranges of 73°–90° on Cu(111) and 50°–90° on Au(111). For the cut-off of 200 meV, the ranges increase to 54°–90° on Cu(111) and 39°–90° on Au(111). Thus, the effect is most pronounced for Cu(111), whereas on Au(111) the ordering effect of the substrate is weaker. For MgO, we do not find a preferential orientation of the Tb2 dimer. The lack of ordering effect on MgO can be explained by the weak electronic interactions between the fullerene π-system and the substrate. This is different on metal substrates, where hybridization of the fullerene π-system with the metal bands is much stronger.
The degree of charge transfer between the Tb2@C79N molecule and a substrate was determined by Bader analysis (Fig. S14†).95 Calculations show that Tb2@C79N molecules attain 0.4–0.6 electrons from Cu(111). On Au(111) the direction of the charge transfer is reversed, and fullerene molecules lose 0.05–0.2 electrons to the substrate. On MgO(100), Tb2@C79N molecules gain 0.10–0.15 electrons from the surface. Similar sign and magnitude of charging was found earlier for Dy2ScN@C80 on Au(111) and MgO(100) substrates.57 For Cu(111), the degree of the charge transfer appears to be overestimated by theory, as it leads to a considerable change of the electron density of states and appearance of the features near the Fermi level (Fig. S13†), which could not be observed in the STS measurements (Fig. 3a). Visualization of the difference electron density for Tb2@C79N on Au(111) in Fig. 5e (see Fig. S15† for Cu(111)) shows that the charge redistribution is mainly localized in the region between the fullerene and the substrate. Some excess of the electron density can be also seen in the area between Tb atoms, but the spin density distribution for this structure (Fig. 5f) proves that the single-electron nature of the Tb–Tb bond is preserved on Au(111).
X-ray absorption studies of Tb2@C79N films
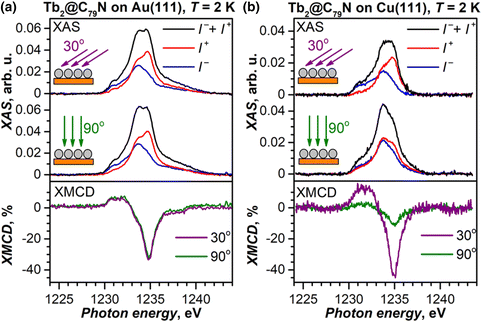
Submonolayers of Tb2@C79N on Cu(111) and Au(111) (∼0.2 ML, see Fig. S10 and S11† for STM topographies) were studied by X-ray absorption spectroscopy (XAS) at the Tb-M4,5 edge with circular-polarized X-rays. Both layers show XAS spectra typical for TbIII (see Fig. 6 for M5 edge and ESI† for full spectra) and develop X-ray magnetic circular dichroism (XMCD) in the presence of a magnetic field. The maximum of the XMCD signal at 1235 eV was then used to monitor the changes of the monolayer magnetization during magnetic field sweeps described below. As the X-ray beam and magnetic field were aligned parallel in the measurements, the XMCD intensity is proportional to the magnetization in the direction of the beam. Thus, the measurements at different incidences allow the determination of the preferential orientation of magnetic moments in the monolayer. For a Tb2@C79N monolayer on Au(111), polarized spectra and normalized XMCD intensity for the measurements in normal (90°) and grazing (30°) incidence are very similar (Fig. 6a). Thus, there is no discernable ordering of Tb2 dimers in Tb2@C79N adsorbed on gold. A completely different situation is found on Cu(111). Here, the XMCD signal at grazing incidence is 4 times stronger than at normal incidence. Since magnetic moments of Tb ions in Tb2@C79N are aligned along the Tb–Tb bond (Fig. 1), we conclude that Tb2 dimers in Tb2@C79N monolayer on Cu(111) are oriented parallel to the surface.Magnetic behavior of Tb2@C79N films on Au(111) and Cu(111)
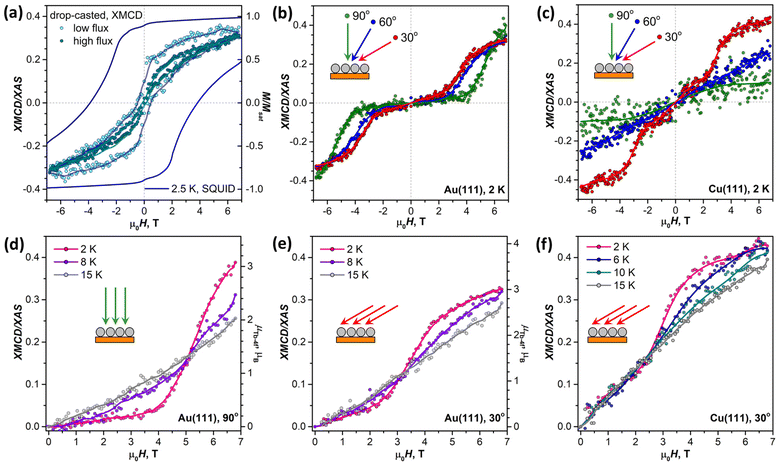
Before studying the magnetization dynamics in monolayer samples by XMCD, we made reference measurements of the magnetic hysteresis of the Tb2@C79N multilayer drop-casted onto a gold substrate. The studies of similarly prepared samples by SQUID magnetometry showed broad magnetic hysteresis at T = 2.5 K (Fig. 7a).30 The magnetic hysteresis recorded by XMCD technique is much narrower, despite the faster sweep rate. The further narrowing was observed when the X-ray flux was increased by a factor of 6 (see also Fig. S16 in ESI†). This proves that the X-ray irradiation considerably accelerates magnetic relaxation in Tb2@C79N. Such X-ray induced demagnetization was reported earlier in monolayers of metallofullerenes61,62,96 and TbPc2,46 but the effect in Tb2@C79N is more pronounced. Further measurements of (sub)monolayer films demonstrate that not only the demagnetization rate but also the population of valence orbitals may be affected by X-ray irradiation through secondary processes.In contrast to the multilayer sample, submonolayers of Tb2@C79N on Au(111) and Cu(111) did not show magnetic hysteresis. Instead, they revealed an unexpected shape of the magnetization curves characteristic for a ground state with a small magnetic moment. The effect is especially well seen for Au(111). Magnetization of the sample remains small up to the field of 2.5–4 T, and then increases fast above a certain threshold field. Such a behavior is expected for a system with a moderately-strong antiferromagnetic (afm) coupling of magnetic moments undergoing a metamagnetic transition in high field. While non-magnetized in small external fields, the system develops magnetization in high fields, when the ferromagnetically-coupled state (fm) becomes lower in energy due to the Zeeman effect. Interestingly, the threshold field changes from 2.5 T at the grazing incidence to 4 T at the normal incidence. Thus, there is some anisotropy of the Tb2 orientation in Tb2@C79N molecules adsorbed on Au(111), although much less pronounced than on Cu(111), and the parallel alignment is somewhat more preferable here as well. Hence a smaller magnetic field is required to switch between afm and fm states in grazing incidence. Sum rule analysis was performed to estimate the 4f-contribution to the magnetic moment of Tb ions in Tb2@C79N on Au(111). At 2 K and the field of 6.8 T, the Tb-4f moment (μTb-4f) is estimated as 3 ± 0.5μB. This value is considerably smaller than the 4.5μB expected for Tb3+ ions with easy-axis magnetic anisotropy in a disordered monolayer, which is not surprising given the fact that the magnetization is not saturated yet in this field (Fig. 7).
Similar switching between afm and fm states is found in submonolayer of Tb2@C79N on Cu(111). The switching field in grazing incidence is also close to 2.5 T as for Au(111). However, the transition between afm and fm states is not as pronounced as on Au(111). Besides, the sample on Cu(111) shows higher residual magnetization in smaller fields indicating that the molecules with afm and fm ground state can co-exist on Cu(111).
When temperature is increased from 2 K to 15 K (Fig. 7d–f), the transition between afm and fm states becomes less sharp. Presumably, the fm state becomes more thermally accessible at smaller fields, when it is still higher in energy than the afm state. At the same time, magnetization in higher fields, when the fm state is dominant, is smaller because the system requires a higher field to reach the saturation.
Tb2@C79N films on h-BN|Rh(111) and MgO|Ag(100)
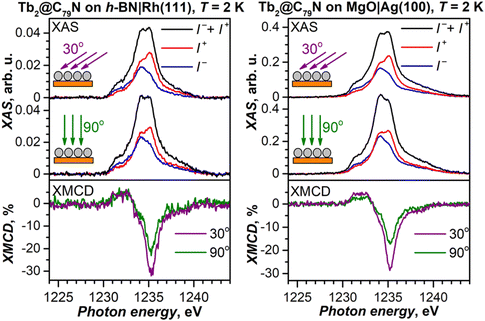
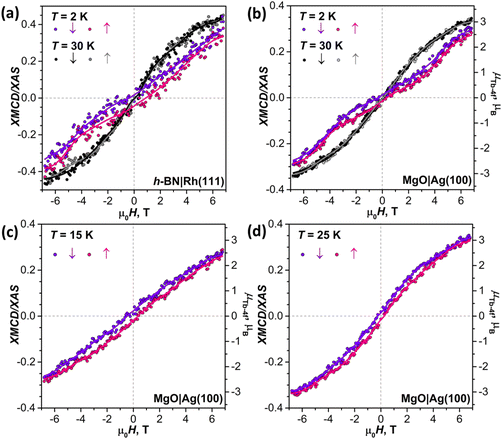
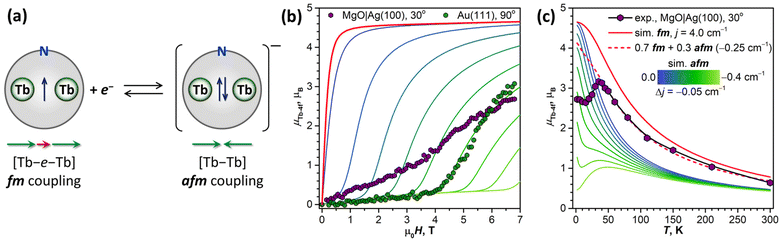
To decrease the electronic coupling of Tb2@C79N molecules with the substrate, we then used a thin layer of semiconductor (monolayer h-BN on Rh(111)) or insulator (5 ML of MgO on Ag(100)). Fullerene layers on these substrates were prepared by thermal evaporation. For MgO(5 ML)|Ag(100), the evaporation was carried out at a higher temperature and gave 1.5 ML coverage as determined by comparison of Tb-M4,5 XAS intensity to that of TbPc2 on MgO|Ag(100) from ref. 46 and 51. Tb-M5 XAS and XMCD spectra of Tb2@C79N on both substrates are shown in Fig. 8. The measurements in grazing incidence give a somewhat higher XMCD signal, indicating a slight preference of the parallel orientation of Tb2 dimer with respect to the surface, but the effect is less pronounced than on Cu(111) in Fig. 6b.In Fig. 9, magnetization curves measured at 2 K are compared to 30 K measurements. The concave shape of the low-temperature curves again points to the prevalence of the afm state in low fields, although it should co-exist with a fraction of molecules with large magnetic moment. Thus, the electronic decoupling of Tb2@C79N molecules from metals does not eliminate the afm ground state for some of them. At 30 K, magnetization curves show more typical outward curvature in the whole field range. Gradual transition from inward to outward curvature can be seen at intermediate temperatures (15 K and 25 K in Fig. 9c and d). Sum rule analysis for 30 K and 6.8 T gives the μTb-4f values of 3 ± 0.5μB, similar to the estimation on Au(111). It is clear from the shape of the magnetization curves that the magnetization is not saturated at this field. At lower temperatures, the μTb-4f values at 6.8 T are even smaller (Fig. 9 and 10).
At 2 K, Tb2@C79N on h-BN|Rh(111) and MgO|Ag(100) exhibits narrow magnetic hysteresis. Hysteresis on MgO|Ag(100) remains open up to 25 K (Fig. 9d). No hysteresis can be found at 30 K (Fig. 9a and b). The closing temperature of hysteresis in Tb2@C79N on MgO|Ag(100) agrees with bulk magnetic measurement of Tb2@C79N30 as well as bulk and monolayer measurements in monolayers of Tb2@C80(CH2Ph) derivatives on graphitic substrates.62
The origin of the antiferromagnetic state
The afm ground state of Tb2@C79N monolayers found in XMCD measurements was completely unexpected. Strong ferromagnetic coupling of Tb moments in Tb2@C79N is caused by the unpaired valence electron delocalized between two Tb ions (Fig. 1). The change of the magnetic ground state may indicate that the Tb–Tb bonding orbital changed its occupation by acquiring an additional electron (Fig. 10a). Earlier, we demonstrated that single-electron reduction of dimetallofullerenes M2@C80(CH2Ph) in solution leads to stable anions with two-fold occupied M–M bonding orbital and reduced magnetic anisotropy.16,23 In the absence of an unpaired valence electron, lanthanide–lanthanide interactions via two-electron M–M bond are presumably antiferromagnetic (Fig. 10a). Thus, unusual magnetic behavior is not caused by intact Tb2@C79N molecules, but results from the trapping of an extra electron.Reduction of adsorbed fullerenes could be caused by their strong hybridization with the metallic substrate and an electron transfer from the metal to the Tb–Tb bonding SOMO, as predicted by DFT for Tb2@C79N on Cu(111). In case of a fractional charge transfer between fullerene and metal, one may expect a non-zero DOS at the Fermi level, which however is not validated by the STM/STS results for Tb2@C79N on Cu(111) and Au(111), showing a considerable HOMO–LUMO gap (Fig. 3a). However, the metal–metal bonding MO hidden inside a fullerene cage may be not well accessible for STM, although we did observe the features of such orbitals in M2@C80(CH2Ph) molecules deposited on a graphene|Ir(111) substrate.97 Besides, when the charge transfer is integer, STS of the adsorbed anion may show a gapped pattern.
Deposition of Tb2@C79N on thin dielectric layers was aimed at the electronic decoupling of fullerenes from the underlying metals. The persistence of the afm state on h-BN|Rh(111) and MgO|Ag(100) could serve as an indication that the charge transfer from the substrate is not the reason for the unexpected magnetic behavior of Tb2@C79N. However, the charge transfer hypothesis still cannot be fully excluded by these data because there are examples of the electron transfer between Ag and adsorbate on MgO|Ag(100) substrates.98–104 For instance, pentacene molecules acquire one electron when deposited onto MgO(2 ML)|Ag(100).99 Variation of the MgO layer thickness and work-function resulted in the co-existence of neutral and charged pentacene molecules, and signatures of the charge transfer were observed up to the MgO thickness of 16 ML.100 Coexistence of Dy atoms and Dy+ ions with the ratio depending on the MgO thickness was recently demonstrated for Dy deposited on MgO|Ag(100).104 Such situations are less documented for adsorbates on h-BN|metal substrates,105 but not unimaginable either. For instance, C60 retains its charge state on h-BN|Ni(111) at low temperature, but the population of its LUMO is increased by 0.4 electrons at room temperature.106 Thus, there is no fundamental reason why an electron transfer cannot occur across the h-BN or MgO layers, and we cannot fully exclude such a possibility for Tb2@C79N on h-BN|Rh(111) and MgO|Ag(100). Importantly, a dielectric layer can stabilize the states of adsorbate molecules with an integer charge, whereas the direct contact with metal would usually give hybridized states with fractional charge transfer. Thus, in certain situations a thin dielectric layer may even stabilize the charged state of an adsorbate.
The electron transfer from the substrate is not the only plausible source of the surplus electron. The method employed to study magnetic properties of monolayers, XAS/XMCD, is by no means an innocent technique. The influence of the X-ray flux on the magnetization relaxation and the width of magnetic hysteresis was already discussed above (Fig. 5a). Absorption of an X-ray photon, 3d → 4f excitation, and subsequent decay of the core-hole results in the Auger process forming a cascade of secondary electrons, which are then collected as a drain current from the sample. But some can be trapped in the sample, especially an insulating one, leading to its charging and affecting the energies and intensities of measured signals.107–109 Although charging effects are not expected to play a strong role for molecular submonolayers on metals, the singly unoccupied Tb–Tb MO buried inside the fullerene cage and thus well-isolated from the substrate may be an efficient trap for such electrons. In this situation, irradiation with an X-rays might generate metastable Tb2@C79N− anions and change the magnetic properties of the sample. If our hypothesis on the secondary electron trapping is correct, then the afm state we observe is an artefact of the experimental technique (XMCD) and does not reflect the intrinsic magnetic behavior of the Tb2@C79N monolayer.
As an alternative to the intramolecular nature of the afm state, one might suggest that the non-magnetic ground state emerges as a result of the intermolecular antiferromagnetic coupling, whereas the charge state and intramolecular ferromagnetic coupling of Tb2@C79N molecules is preserved. Although we never observed measurable intermolecular magnetic coupling in bulk metallofullerene samples, the situation may be different in a monolayer on a metal, where such interactions may be mediated by conducting electrons of a metallic substrate in the spirit of the Ruderman–Kittel–Kasuya–Yosida mechanism.110–112 But this would require considerable electronic coupling of the fullerene with the underlying substrate and can be ruled out based on the experiments with h-BN and MgO, unlike the charge-transfer through these layer, which does not require hybridization. Thus, we consider the intramolecular origin of the afm state in Tb2@C79N monolayers as much more plausible.
Magnetic simulations
To get more insight into the magnetic properties of the Tb2@C79N monolayer, we simulated magnetization curves for Tb2@C79N in neutral and anionic states. Description of dimetallofullerenes with single-electron M–M bond used in ref. 19, 23, 24 and 30 is based on a three-center model, including two local Tb-4f moments with spin operators ĴTb and ligand-field (LF) Hamiltonians ĤLF, unpaired electron spin ŝ, and their exchange interactions, forming the following effective spin Hamiltonian: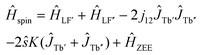 | (1) |
| Ĥspin = ĤLF′ + ĤLF′′ − 2j12ĴTb′ĴTb′′ + ĤZEE. | (2) |
In the first approximation, we assume that the ligand field terms for Tb ions in Tb2@C79N and Tb2@C79N− are similar, which allows the use results of ab initio calculations from ref. 30 in further modelling. Since XMCD at the Tb-M4,5 edge allows determination of Tb-4f moments only, we can use eqn (2) as an effective Hamiltonian for the neutral Tb2@C79N as well. The correct energy of the Tb2@C79N state with antiparallel alignment of Tb-4f moments is then obtained with the j12 constant of 4 cm−1. Following ab initio predictions, the quantization axes of the two Tb ions in Tb2@C79N are misaligned by 8°.
Fig. 10b shows simulated powder-averaged magnetization curves of Tb2@C79N− obtained with the Hamiltonian in eqn (2) and j12 values in the range of 0 to −0.4 cm−1 for T = 2 K. The shape of the curves with small magnetization at low field and fast increase above the threshold field corresponds well to the data measured for Tb2@C79N adsorbed on Au(111). The j12 value of −0.25 cm−1 gives the zero-field energy difference between afm and fm-coupled states of 36 cm−1 (4.5 meV) and the threshold field of 4.1 T. For other substrates, the Tb2@C79N− anion alone with afm ground state cannot reproduce magnetization data, which is probably caused by a co-existence of Tb2@C79N− anion and neutral Tb2@C79N molecules.
The coexistence of two types of species with different magnetic ground states can be further inferred from the temperature dependence of the Tb-4f magnetic moment, which was measured for Tb2@C79N on MgO|Ag(100) substrate in the field of 6.8 T. Between 2 K and 15 K, the μTb-4f value decreased slightly from 3.0 to 2.9μB, then increased to reach its maximum of 3.4μB at 35 K, and then showed gradual decrease at higher temperatures to the value of 0.7μB at 300 K (Fig. 10c). Note that the sum rule analysis gives the error up to 0.5μB due to uncertainty in integration limits and background, but the relative values of XMCD intensities are much more precise. We therefore determined the μTb-4f value from the sum rule analysis at 35 K and estimated other points from their relative XMCD intensities at the Tb-M5 edge.
The peak in the μTb-4f(T) dependence is only possible with the afm state (j12 < 0) contribution because the fm ground state (j12 > 0) is characterized by a gradual decay of μTb-4f in the whole temperature range. However, we cannot reproduce the shape of the μTb-4f(T) curve with Hamiltonian (2) and any single j12 value. The peak in simulated μTb-4f(T) curves develops only for j12 values more negative than −0.4 cm−1, but simulated μTb-4f values in the peak maximum are around 3 times smaller than experimental ones. At temperatures above 35 K, the experimental μTb-4f is considerably larger than calculated for any negative j12, but smaller than for j12 = 4 cm−1. In fact, the part of the curve above 35 K can be reproduced by a combination of two species, neutral Tb2@C79N with j12 of 4 cm−1 and Tb2@C79N− anion with j12 of −0.25 cm−1 in a 0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 ratio (Fig. 10c). This ratio is only qualitatively estimated because of uncertainties of sum rule analysis, but the prevalence of the neutral Tb2@C79N at higher temperatures is evident.
0.3 ratio (Fig. 10c). This ratio is only qualitatively estimated because of uncertainties of sum rule analysis, but the prevalence of the neutral Tb2@C79N at higher temperatures is evident.
Thus, the shape of the μTb-4f(T) curve with a peak at 35 K cannot be explained by any constant composition of the sample, and we suggest that the ratio between Tb2@C79N− and Tb2@C79N is changing with temperature. If the anionic state is metastable, as it would be if it were formed by the electron trapping, its lifetime should depend on the rate of the electron hopping between neighboring molecules. In molecular solids, the hopping is often an activated process with a certain energy barrier. Thus, when the hopping is activated, the Tb2@C79N− fraction in the sample may decrease considerably, which would lead to the increase of the average magnetic moment and appearance of the peak in the μTb-4f(T) curve.
Conclusions
In this work, we presented the first study of surface magnetism in lanthanide dimetallo-azafullerene monolayers on different substrates. In contrast to the single-molecule magnetism of the bulk Tb2@C79N with strongly ferromagnetic intramolecular coupling, its monolayers showed unexpected antiferromagnetic coupling between Tb magnetic moments. The coupling is moderately strong, and the ferromagnetically-coupled state becomes prevalent in higher magnetic fields. The origin of the antiferromagnetic ground state in a monolayer is presumably the formation of Tb2@C79N− anions with two-fold occupied Tb–Tb bonding orbital. The anions can be formed either by an electron transfer from the substrate or, more likely, by trapping secondary electrons formed in the course of X-ray absorption measurements. The coexistence of neutral and anionic species exhibiting different magnetic properties and the variation of their ratio with temperature and as a function of the substrate result in unconventional magnetization behavior of Tb2@C79N monolayers. On substrates with thin dielectric layers, h-BN|Rh(111) and MgO|Ag(100), we observed narrow magnetic hysteresis, presumably originating from the neutral Tb2@C79N molecules.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Computational resources were provided by ZIH/TU Dresden. The work was performed with financial support from Deutsche Forschungsgemeinschaft (grants PO 1602/7-1 and PO 1602/8-1 to A. A. P., LI 3055/3-1 to F. L., and AV 169/3-1 to S. M. A.), the Swedish Research Council (Grant No. 2015-00455), and Sklodowska Curie Actions cofounding project INCA 600398. We acknowledge the Paul Scherrer Institute for providing synchrotron beamtime at the X-treme and PEARL beamlines of the Swiss Light Source.References
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed.
- L. Spree and A. A. Popov, Dalton Trans., 2019, 48, 2861–2871 RSC.
- T. Wang and C. Wang, Small, 2019, 15, 1901522 CrossRef CAS PubMed.
- S. Yang, T. Wei and F. Jin, Chem. Soc. Rev., 2017, 46, 5005–5058 RSC.
- X. Lu, W. Shen and S. Hu, Chem. – Eur. J., 2020, 26, 5748–5757 CrossRef PubMed.
- A. A. Popov, Endohedral Fullerenes: Electron Transfer and Spin, Springer International Publishing, Cham, 2017 Search PubMed.
- W. Li, C.-R. Wang and T. Wang, Chem. Commun., 2021, 57, 10317–10326 RSC.
- R. T. Harding, S. Zhou, J. Zhou, T. Lindvall, W. K. Myers, A. Ardavan, G. A. D. Briggs, K. Porfyrakis and E. A. Laird, Phys. Rev. Lett., 2017, 119, 140801 CrossRef CAS PubMed.
- J. E. Grose, E. S. Tam, C. Timm, M. Scheloske, B. Ulgut, J. J. Parks, H. D. Abruña, W. Harneit and D. C. Ralph, Nat. Mater., 2008, 7, 884–889 CrossRef CAS PubMed.
- Endohedral Metallofullerenes: Basics and Applications, ed. X. Lu, L. Echegoyen, A. L. Balch, S. Nagase and T. AkasakaCRC Press, 2014 Search PubMed.
- U. Reuther and A. Hirsch, Carbon, 2000, 38, 1539–1549 CrossRef CAS.
- A. Hirsch and B. Nuber, Acc. Chem. Res., 1999, 32, 795–804 CrossRef CAS.
- J. C. Hummelen, B. Knight, J. Pavlovich, R. Gonzalez and F. Wudl, Science, 1995, 269, 1554–1556 CrossRef CAS PubMed.
- T. Zuo, L. Xu, C. M. Beavers, M. M. Olmstead, W. Fu, T. D. Crawford, A. L. Balch and H. C. Dorn, J. Am. Chem. Soc., 2008, 130, 12992–12997 CrossRef CAS PubMed.
- K. Nakao, N. Kurita and M. Fujita, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 11415–11420 CrossRef CAS PubMed.
- F. Liu, L. Spree, D. S. Krylov, G. Velkos, S. M. Avdoshenko and A. A. Popov, Acc. Chem. Res., 2019, 52, 2981–2993 CrossRef CAS PubMed.
- W. Fu, J. Zhang, T. Fuhrer, H. Champion, K. Furukawa, T. Kato, J. E. Mahaney, B. G. Burke, K. A. Williams, K. Walker, C. Dixon, J. Ge, C. Shu, K. Harich and H. C. Dorn, J. Am. Chem. Soc., 2011, 133, 9741–9750 CrossRef CAS PubMed.
- Z. Hu, B.-W. Dong, Z. Liu, J.-J. Liu, J. Su, C. Yu, J. Xiong, D.-E. Shi, Y. Wang, B.-W. Wang, A. Ardavan, Z. Shi, S.-D. Jiang and S. Gao, J. Am. Chem. Soc., 2018, 140, 1123–1130 CrossRef CAS PubMed.
- G. Velkos, D. S. Krylov, K. Kirkpatrick, X. Liu, L. Spree, A. U. B. Wolter, B. Buchner, H. C. Dorn and A. A. Popov, Chem. Commun., 2018, 54, 2902–2905 RSC.
- X. Wang, J. E. McKay, B. Lama, J. van Tol, T. Li, K. Kirkpatrick, Z. Gan, S. Hill, J. R. Long and H. C. Dorn, Chem. Commun., 2018, 54, 2425–2428 RSC.
- F. Cimpoesu, B. Frecus, C. I. Oprea, H. Ramanantoanina, W. Urland and C. Daul, Mol. Phys., 2015, 113, 1712–1727 CrossRef CAS.
- G. Rajaraman, M. K. Singh and N. Yadav, Chem. Commun., 2015, 51, 17732–17735 RSC.
- F. Liu, G. Velkos, D. S. Krylov, L. Spree, M. Zalibera, R. Ray, N. A. Samoylova, C.-H. Chen, M. Rosenkranz, S. Schiemenz, F. Ziegs, K. Nenkov, A. Kostanyan, T. Greber, A. U. B. Wolter, M. Richter, B. Büchner, S. M. Avdoshenko and A. A. Popov, Nat. Commun., 2019, 10, 571 CrossRef CAS PubMed.
- F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed.
- Y. Wang, J. Xiong, J. Su, Z.-Q. Hu, F. Ma, R. Sun, X.-Y. Tan, H.-L. Sun, B. Wang, Z. Shi and S. Gao, Nanoscale, 2020, 12, 11130–11135 RSC.
- C. Zhao, H. Meng, M. Nie, Q. Huang, P. Du, C. Wang and T. Wang, Chem. Commun., 2019, 55, 11511–11514 RSC.
- C. Zhao, H. Meng, M. Nie, L. Jiang, C. Wang and T. Wang, J. Phys. Chem. C, 2018, 122, 4635–4640 CrossRef CAS.
- Y. Feng, T. Wang, Y. Li, J. Li, J. Wu, B. Wu, L. Jiang and C. Wang, J. Am. Chem. Soc., 2015, 137, 15055–15060 CrossRef CAS PubMed.
- R. B. Zaripov, Y. E. Kandrashkin, K. M. Salikhov, B. Büchner, F. Liu, M. Rosenkranz, A. A. Popov and V. Kataev, Nanoscale, 2020, 12, 20513–20521 RSC.
- G. Velkos, D. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. Avdoshenko, V. Bezmelnitsyn, S. Davis, P. Faust, J. Duchamp, H. Dorn and A. A. Popov, Angew. Chem., Int. Ed., 2019, 58, 5891–5896 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503 RSC.
- C. Gould, K. R. McClain, J. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, J. Am. Chem. Soc., 2019, 141, 12967–12973 CrossRef CAS PubMed.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed.
- M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M. A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421 CrossRef CAS PubMed.
- L. Malavolti, V. Lanzilotto, S. Ninova, L. Poggini, I. Cimatti, B. Cortigiani, L. Margheriti, D. Chiappe, E. Otero, P. Sainctavit, F. Totti, A. Cornia, M. Mannini and R. Sessoli, Nano Lett., 2015, 15, 535–541 CrossRef CAS PubMed.
- J.-P. Kappler, E. Otero, W. Li, L. Joly, G. Schmerber, B. Muller, F. Scheurer, F. Leduc, B. Gobaut, L. Poggini, G. Serrano, F. Choueikani, E. Lhotel, A. Cornia, R. Sessoli, M. Mannini, M.-A. Arrio, P. Sainctavit and P. Ohresser, J. Synchrotron Radiat., 2018, 25, 1727–1735 CrossRef CAS PubMed.
- G. Serrano, L. Poggini, M. Briganti, A. L. Sorrentino, G. Cucinotta, L. Malavolti, B. Cortigiani, E. Otero, P. Sainctavit, S. Loth, F. Parenti, A.-L. Barra, A. Vindigni, A. Cornia, F. Totti, M. Mannini and R. Sessoli, Nat. Mater., 2020, 19, 546–551 CrossRef CAS PubMed.
- L. Margheriti, D. Chiappe, M. Mannini, P. E. Car, P. Sainctavit, M.-A. Arrio, F. B. de Mongeot, J. C. Cezar, F. M. Piras, A. Magnani, E. Otero, A. Caneschi and R. Sessoli, Adv. Mater., 2010, 22, 5488–5493 CrossRef CAS PubMed.
- M. Gonidec, R. Biagi, V. Corradini, F. Moro, V. De Renzi, U. del Pennino, D. Summa, L. Muccioli, C. Zannoni, D. B. Amabilino and J. Veciana, J. Am. Chem. Soc., 2011, 133, 6603–6612 CrossRef CAS PubMed.
- A. Lodi Rizzini, C. Krull, T. Balashov, A. Mugarza, C. Nistor, F. Yakhou, V. Sessi, S. Klyatskaya, M. Ruben, S. Stepanow and P. Gambardella, Nano Lett., 2012, 12, 5703–5707 CrossRef CAS PubMed.
- M. Mannini, F. Bertani, C. Tudisco, L. Malavolti, L. Poggini, K. Misztal, D. Menozzi, A. Motta, E. Otero, P. Ohresser, P. Sainctavit, G. G. Condorelli, E. Dalcanale and R. Sessoli, Nat. Commun., 2014, 5, 4582 CrossRef CAS PubMed.
- D. Klar, A. Candini, L. Joly, S. Klyatskaya, B. Krumme, P. Ohresser, J.-P. Kappler, M. Ruben and H. Wende, Dalton Trans., 2014, 43, 10686–10689 RSC.
- C. Nistor, C. Krull, A. Mugarza, S. Stepanow, C. Stamm, M. Soares, S. Klyatskaya, M. Ruben and P. Gambardella, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 184402 CrossRef.
- C. Wäckerlin, F. Donati, A. Singha, R. Baltic, S. Rusponi, K. Diller, F. Patthey, M. Pivetta, Y. Lan, S. Klyatskaya, M. Ruben, H. Brune and J. Dreiser, Adv. Mater., 2016, 28, 5195–5199 CrossRef PubMed.
- G. Cucinotta, L. Poggini, A. Pedrini, F. Bertani, N. Cristiani, M. Torelli, P. Graziosi, I. Cimatti, B. Cortigiani, E. Otero, P. Ohresser, P. Sainctavit, A. Dediu, E. Dalcanale, R. Sessoli and M. Mannini, Adv. Funct. Mater., 2017, 27, 1703600 CrossRef.
- A. Pedrini, L. Poggini, C. Tudisco, M. Torelli, A. E. Giuffrida, F. Bertani, I. Cimatti, E. Otero, P. Ohresser, P. Sainctavit, M. Suman, G. G. Condorelli, M. Mannini and E. Dalcanale, Small, 2018, 14, 1702572 CrossRef PubMed.
- G. Serrano, E. Velez-Fort, I. Cimatti, B. Cortigiani, L. Malavolti, D. Betto, A. Ouerghi, N. B. Brookes, M. Mannini and R. Sessoli, Nanoscale, 2018, 10, 2715–2720 RSC.
- K. Diller, A. Singha, M. Pivetta, C. Wäckerlin, R. Hellwig, A. Verdini, A. Cossaro, L. Floreano, E. Vélez-Fort, J. Dreiser, S. Rusponi and H. Brune, RSC Adv., 2019, 9, 34421–34429 RSC.
- M. Studniarek, C. Wäckerlin, A. Singha, R. Baltic, K. Diller, F. Donati, S. Rusponi, H. Brune, Y. Lan, S. Klyatskaya, M. Ruben, A. P. Seitsonen and J. Dreiser, Adv. Sci., 2019, 6, 1901736 CrossRef CAS PubMed.
- Y. Lan, S. Klyatskaya, M. Ruben, O. Fuhr, W. Wernsdorfer, A. Candini, V. Corradini, A. Lodi Rizzini, U. del Pennino, F. Troiani, L. Joly, D. Klar, H. Wende and M. Affronte, J. Mater. Chem. C, 2015, 3, 9794–9801 RSC.
- M. D. Korzyński, Z. J. Berkson, B. Le Guennic, O. Cador and C. Copéret, J. Am. Chem. Soc., 2021, 143, 5438–5444 CrossRef PubMed.
- A. Cornia, M. Mannini, R. Sessoli and D. Gatteschi, Eur. J. Inorg. Chem., 2019, 552–568 CrossRef CAS.
- L. Poggini, E. Tancini, C. Danieli, A. L. Sorrentino, G. Serrano, A. Lunghi, L. Malavolti, G. Cucinotta, A.-L. Barra, A. Juhin, M.-A. Arrio, W. Li, E. Otero, P. Ohresser, L. Joly, J. P. Kappler, F. Totti, P. Sainctavit, A. Caneschi, R. Sessoli, A. Cornia and M. Mannini, Adv. Mater. Interfaces, 2021, 8, 2101182 CrossRef CAS.
- C.-H. Chen, L. Spree, E. Koutsouflakis, D. S. Krylov, F. Liu, A. Brandenburg, G. Velkos, S. Schimmel, S. M. Avdoshenko, A. Fedorov, E. Weschke, F. Choueikani, P. Ohresser, J. Dreiser, B. Büchner and A. A. Popov, Adv. Sci., 2021, 8, 2000777 CrossRef CAS PubMed.
- D. S. Krylov, S. Schimmel, V. Dubrovin, F. Liu, T. T. N. Nguyen, L. Spree, C.-H. Chen, G. Velkos, C. Bulbucan, R. Westerström, M. Studniarek, J. Dreiser, C. Hess, B. Büchner, S. M. Avdoshenko and A. A. Popov, Angew. Chem., Int. Ed., 2020, 59, 5756–5764 CrossRef CAS PubMed.
- T. Greber, A. P. Seitsonen, A. Hemmi, J. Dreiser, R. Stania, F. Matsui, M. Muntwiler, A. A. Popov and R. Westerström, Phys. Rev. Mater., 2019, 3, 014409 CrossRef CAS.
- C. H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Westerström, C. Bulbucan, M. Studniarek, J. Dreiser, A. U. B. Wolter, B. Büchner and A. A. Popov, Nanoscale, 2018, 10, 11287–11292 RSC.
- R. Westerström, A.-C. Uldry, R. Stania, J. Dreiser, C. Piamonteze, M. Muntwiler, F. Matsui, S. Rusponi, H. Brune, S. Yang, A. Popov, B. Büchner, B. Delley and T. Greber, Phys. Rev. Lett., 2015, 114, 087201 CrossRef PubMed.
- F. Paschke, T. Birk, V. Enenkel, F. Liu, V. Romankov, J. Dreiser, A. A. Popov and M. Fonin, Adv. Mater., 2021, 33, 2102844 CrossRef CAS PubMed.
- L. Spree, F. Liu, V. Neu, M. Rosenkranz, G. Velkos, Y. Wang, S. Schiemenz, J. Dreiser, P. Gargiani, M. Valvidares, C.-H. Chen, B. Büchner, S. M. Avdoshenko and A. A. Popov, Adv. Funct. Mater., 2021, 31, 2105516 CrossRef CAS.
- A. Hemmi, C. Bernard, H. Cun, S. Roth, M. Klöckner, T. Kälin, M. Weinl, S. Gsell, M. Schreck, J. Osterwalder and T. Greber, Rev. Sci. Instrum., 2014, 85, 035101 CrossRef CAS PubMed.
- M. Corso, W. Auwärter, M. Muntwiler, A. Tamai, T. Greber and J. Osterwalder, Science, 2004, 303, 217–220 CrossRef CAS PubMed.
- M. Muntwiler, J. Zhang, R. Stania, F. Matsui, P. Oberta, U. Flechsig, L. Patthey, C. Quitmann, T. Glatzel, R. Widmer, E. Meyer, T. A. Jung, P. Aebi, R. Fasel and T. Greber, J. Synchrotron Radiat., 2017, 24, 354–366 CrossRef CAS PubMed.
- C. Piamonteze, U. Flechsig, S. Rusponi, J. Dreiser, J. Heidler, M. Schmidt, R. Wetter, M. Calvi, T. Schmidt, H. Pruchova, J. Krempasky, C. Quitmann, H. Brune and F. Nolting, J. Synchrotron Radiat., 2012, 19, 661–674 CrossRef CAS PubMed.
- J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- T. Sakurai, X. D. Wang, Q. K. Xue, Y. Hasegawa, T. Hashizume and H. Shinohara, Prog. Surf. Sci., 1996, 51, 263–408 CrossRef CAS.
- N. Neel, J. Kroger and R. Berndt, Appl. Phys. Lett., 2006, 88, 163101 CrossRef.
- M. Grobis, A. Wachowiak, R. Yamachika and M. F. Crommie, Appl. Phys. Lett., 2005, 86, 204102 CrossRef.
- I. Fernández Torrente, K. J. Franke and J. Ignacio Pascual, J. Phys.: Condens. Matter, 2008, 20, 184001 CrossRef.
- S. Vijayaraghavan, D. Écija, W. Auwärter, S. Joshi, K. Seufert, A. P. Seitsonen, K. Tashiro and J. V. Barth, Nano Lett., 2012, 12, 4077–4083 CrossRef CAS PubMed.
- M. Jung, D. Shin, S.-D. Sohn, S.-Y. Kwon, N. Park and H.-J. Shin, Nanoscale, 2014, 6, 11835–11840 RSC.
- D. R. Daughton and J. A. Gupta, Appl. Phys. Lett., 2011, 98, 133303 CrossRef.
- T. Susi, T. Pichler and P. Ayala, Beilstein J. Nanotechnol., 2015, 6, 177–192 CrossRef PubMed.
- K. Schulte, L. Wang, P. J. Moriarty, K. Prassides and N. Tagmatarchis, J. Chem. Phys., 2007, 126, 184707 CrossRef CAS PubMed.
- S. Hino, M. Zenki, T. Zaima, Y. Aoki, S. Okita, T. Ohta, H. Yagi, T. Miyazaki, R. Sumii, H. Okimoto, Y. Ito and H. Shinohara, J. Phys. Chem. C, 2012, 116, 165–170 CrossRef CAS.
- L. Alvarez, T. Pichler, P. Georgi, T. Schwieger, H. Peisert, L. Dunsch, Z. Hu, M. Knupfer, J. Fink, P. Bressler, M. Mast and M. S. Golden, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035107 CrossRef.
- R. Stania, A. P. Seitsonen, D. Kunhardt, B. Büchner, A. A. Popov, M. Muntwiler and T. Greber, J. Phys. Chem. Lett., 2018, 9, 3586–3590 CrossRef CAS PubMed.
- J. A. Leiro, M. H. Heinonen, T. Laiho and I. G. Batirev, J. Electron Spectrosc. Relat. Phenom., 2003, 128, 205–213 CrossRef CAS.
- A. Goldoni, C. Cepek, R. Larciprete, L. Sangaletti, S. Pagliara, G. Paolucci and M. Sancrotti, Phys. Rev. Lett., 2002, 88, 196102 CrossRef CAS PubMed.
- X. Liu, M. Krause, J. Wong, T. Pichler, L. Dunsch and M. Knupfer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085407 CrossRef.
- H. Shiozawa, H. Rauf, T. Pichler, D. Grimm, X. Liu, M. Knupfer, M. Kalbac, S. Yang, L. Dunsch, B. Buchner and D. Batchelor, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 195409 CrossRef.
- E. Magnano, S. Vandre, C. Cepek, A. Goldoni, A. D. Laine, G. M. Curro, A. Santaniello and M. Sancrotti, Surf. Sci., 1997, 377, 1066–1070 CrossRef.
- F. Gerken, J. Phys. F: Met. Phys., 1983, 13, 703–713 CrossRef CAS.
- M. Krause, X. J. Liu, J. Wong, T. Pichler, M. Knupfer and L. Dunsch, J. Phys. Chem. A, 2005, 109, 7088–7093 CrossRef CAS PubMed.
- T. Pichler, M. S. Golden, M. Knupfer, J. Fink, U. Kirbach, P. Kuran and L. Dunsch, Phys. Rev. Lett., 1997, 79, 3026–3029 CrossRef CAS.
- V. Dubrovin, L.-H. Gan, B. Büchner, A. A. Popov and S. M. Avdoshenko, Phys. Chem. Chem. Phys., 2019, 21, 8197–8200 RSC.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- J. Dreiser, R. Westerström, C. Piamonteze, F. Nolting, S. Rusponi, H. Brune, S. Yang, A. Popov, L. Dunsch and T. Greber, Appl. Phys. Lett., 2014, 105, 032411 CrossRef.
- F. Paschke, T. Birk, S. M. Avdoshenko, F. Liu, A. A. Popov and M. Fonin, Small, 2022, 18, 2105667 CrossRef CAS PubMed.
- G. Pacchioni and H. Freund, Chem. Rev., 2013, 113, 4035–4072 CrossRef CAS PubMed.
- M. Hollerer, D. Lüftner, P. Hurdax, T. Ules, S. Soubatch, F. S. Tautz, G. Koller, P. Puschnig, M. Sterrer and M. G. Ramsey, ACS Nano, 2017, 11, 6252–6260 CrossRef CAS PubMed.
- P. Hurdax, M. Hollerer, P. Puschnig, D. Lüftner, L. Egger, M. G. Ramsey and M. Sterrer, Adv. Mater. Interfaces, 2020, 7, 2000592 CrossRef CAS.
- L. Egger, M. Hollerer, C. S. Kern, H. Herrmann, P. Hurdax, A. Haags, X. Yang, A. Gottwald, M. Richter, S. Soubatch, F. S. Tautz, G. Koller, P. Puschnig, M. G. Ramsey and M. Sterrer, Angew. Chem., Int. Ed., 2021, 60, 5078–5082 CrossRef CAS PubMed.
- P. Hurdax, M. Hollerer, L. Egger, G. Koller, X. Yang, A. Haags, S. Soubatch, F. S. Tautz, M. Richter, A. Gottwald, P. Puschnig, M. Sterrer and M. G. Ramsey, Beilstein J. Nanotechnol., 2020, 11, 1492–1503 CrossRef CAS PubMed.
- A. Singha, D. Sostina, C. Wolf, S. L. Ahmed, D. Krylov, L. Colazzo, P. Gargiani, S. Agrestini, W.-S. Noh, J.-H. Park, M. Pivetta, S. Rusponi, H. Brune, A. J. Heinrich, A. Barla and F. Donati, ACS Nano, 2021, 15, 16162–16171 CrossRef CAS PubMed.
- F. Donati, M. Pivetta, C. Wolf, A. Singha, C. Wäckerlin, R. Baltic, E. Fernandes, J.-G. de Groot, S. L. Ahmed, L. Persichetti, C. Nistor, J. Dreiser, A. Barla, P. Gambardella, H. Brune and S. Rusponi, Nano Lett., 2021, 21, 8266–8273 CrossRef CAS PubMed.
- W. Auwärter, Surf. Sci. Rep., 2019, 74, 1–95 CrossRef.
- M. Muntwiler, W. Auwärter, A. P. Seitsonen, J. Osterwalder and T. Greber, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 121402 CrossRef.
- D. Vlachos, A. J. Craven and D. W. McComb, J. Synchrotron Radiat., 2005, 12, 224–233 CrossRef CAS PubMed.
- A. Cros, J. Electron Spectrosc. Relat. Phenom., 1992, 59, 1–14 CrossRef CAS.
- J. Cazaux, J. Electron Spectrosc. Relat. Phenom., 1999, 105, 155–185 CrossRef CAS.
- M. A. Ruderman and C. Kittel, Phys. Rev., 1954, 96, 99–102 CrossRef CAS.
- T. Kasuya, Prog. Theor. Phys., 1956, 16, 45–57 CrossRef.
- K. Yosida, Phys. Rev., 1957, 106, 893–898 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1nr08475e |
| ‡ Current address: Quantum Nanoscience, Peter Grünberg Institute, Jülich Research Centre, 52425 Jülich, Germany. |
| § Current address: Institute of Physics, Karlsruhe Institute of Technology (KIT), 76131 Karlsruhe, Germany. |
| ¶ Current address: Faculty of Mathematics and Natural Sciences-Physics Department, Bergische Universität Wuppertal, 42119 Wuppertal, Germany. |
| This journal is © The Royal Society of Chemistry 2022 |