Cubic versus hexagonal – phase, size and morphology effects on the photoluminescence quantum yield of NaGdF4:Er3+/Yb3+ upconverting nanoparticles†
Marta
Quintanilla
 *ab,
Eva
Hemmer
*ab,
Eva
Hemmer
 *ac,
Jose
Marques-Hueso
*ac,
Jose
Marques-Hueso
 d,
Shadi
Rohani
a,
Giacomo
Lucchini
d,
Shadi
Rohani
a,
Giacomo
Lucchini
 e,
Miao
Wang
a,
Reza R.
Zamani
e,
Miao
Wang
a,
Reza R.
Zamani
 f,
Vladimir
Roddatis
f,
Vladimir
Roddatis
 gh,
Adolfo
Speghini
gh,
Adolfo
Speghini
 e,
Bryce S.
Richards
e,
Bryce S.
Richards
 ij and
Fiorenzo
Vetrone
ij and
Fiorenzo
Vetrone
 *ak
*ak
aInstitut National de la Recherche Scientifique, Centre Énergie, Matériaux et Télécommunications (INRS - EMT), Université du Québec, 1650 Boul. Lionel-Boulet, Varennes, QC J3X 1P7, Canada. E-mail: fiorenzo.vetrone@inrs.ca
bUniversidad Autónoma de Madrid, Materials Physics Department, Avda. Francisco Tomás y Valiente 7, 28049 Madrid, Spain. E-mail: marta.quintanilla@uam.es
cUniversity of Ottawa, Department of Chemistry and Biomolecular Sciences, 10 Marie-Curie, Ottawa, ON K1N 6N5, Canada. E-mail: ehemmer@uottawa.ca
dHeriot-Watt University, Institute of Sensors, Signals and Systems, Edinburgh, EH14 4AS Scotland, UK
eNanomaterials Research Group, Department of Biotechnology, University of Verona and INSTM, RU of Verona, Strada Le Grazie 15, I-37134 Verona, Italy
fGeorg-August-Universität Göttingen, IV. Physikalisches Institut, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
gGeorg-August-Universität Göttingen, Institut für Materialphysik, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
hGFZ German Research Centre for Geosciences, Telegrafenberg, 14473 Potsdam, Germany
iKarlsruhe Institute of Technology (KIT), Institute of Microstructure Technology, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
jKarlsruhe Institute of Technology (KIT), Light Technology Institute, Engesserstrasse 13, 76131 Karlsruhe, Germany
kCentre Québécois sur les Matériaux Fonctionnels (CQMF)/Québec Centre for Advanced Materials (QCAM), INRS – EMT, Varennes, QC J3X 1P7, Canada
First published on 6th January 2022
Abstract
Upconverting nanoparticles (UCNPs) are well-known for their capacity to convert near-infrared light into UV/visible light, benefitting various applications where light triggering is required. At the nanoscale, loss of luminescence intensity is observed and thus, a decrease in photoluminescence quantum yield (PLQY), usually ascribed to surface quenching. We evaluate this by measuring the PLQY of NaGdF4:Er3+,Yb3+ UCNPs as a function of size (ca. 15 to 100 nm) and shape (spheres, cubes, hexagons). Our results show that the PLQY of α-phase NaGdF4 Er3+,Yb3+ surpasses that of β-NaGdF4 for sizes below 20 nm, an observation related to distortion of the crystal lattice when the UCNPs become smaller. The present study also underlines that particle shape must not be neglected as a relevant parameter for PLQY. In fact, based on a mathematical nucleus/hull volumetric model, shape was found to be particularly relevant in the 20 to 60 nm size range of the investigated UCNPs.
Introduction
Considerable effort is being paid to improve the performance of nanomaterials with the ability to emit light of wavelength shorter than that of the excitation light (i.e. with anti-Stokes properties) for a growing number of potential applications in fields as diverse as energy, optical sensing, environment, or health.1–5 At the forefront of these types of nanomaterials are trivalent lanthanide ion (Ln3+)-doped nanoparticles that follow an excitation scheme known as upconversion in which, through long-lived 4f energy states, multiple near-infrared (NIR) photons are converted into ultraviolet (UV) and/or visible photons.6,7 Despite promising results, better understanding of the relationship between the structural properties and luminescence intensity is required to gain the basic knowledge necessary to ultimately pave the way to more efficient upconverting nanoparticles (UCNPs).8–11 Photoluminescence quantum yield (PLQY) constitutes a direct measure of a material's efficiency in converting absorbed photons into emitted photons. Even if some efforts have been undertaken to facilitate the measurement of PLQY in upconverting materials,12 including for the first time sale of a commercial unit in 2019,13 its quantification is not trivial.14–18To date, most PLQY studies that consider UCNP size are based on a limited range of particle diameters, and thus, the establishment of trends and structure–property relationships remains a challenge. Moreover, nanoparticle size and morphology are closely related and linked to the particles’ crystal structure for some of the most common nanoparticle hosts for upconversion: NaLnF4 (Ln = Y, Gd) can crystallise in either α- (cubic, space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) or β- (hexagonal, space group P
m) or β- (hexagonal, space group P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) or P63/m) crystal phase. Smaller particles tend to present a spherical shape regardless of the crystal phase. However, when exceeding a critical size (typically 20 nm), they exhibit the shape of cubes or hexagons, as dictated by the crystal phase.19 With this in mind, we investigated the effect of size and shape on the PLQY of Er3+/Yb3+ co-doped α- and β-phase NaGdF4 nanoparticles. For this study, we took into account rarely considered structural changes at the lattice-level of the host material, demonstrating the relevance of the crystallographic parameters and strain of the host crystal lattice for upconversion PLQY.
or P63/m) crystal phase. Smaller particles tend to present a spherical shape regardless of the crystal phase. However, when exceeding a critical size (typically 20 nm), they exhibit the shape of cubes or hexagons, as dictated by the crystal phase.19 With this in mind, we investigated the effect of size and shape on the PLQY of Er3+/Yb3+ co-doped α- and β-phase NaGdF4 nanoparticles. For this study, we took into account rarely considered structural changes at the lattice-level of the host material, demonstrating the relevance of the crystallographic parameters and strain of the host crystal lattice for upconversion PLQY.
Previous theoretical and experimental studies on upconversion PLQY provide valuable knowledge required for the design of more efficient UCNPs.17,20–25 Yet, these studies focus on mainly three aspects; namely, (i) the environment of the UCNPs, including solvents and surfactants that can induce quenching through high-energy vibrations (phonons);25,26 (ii) the complicated relationship between excitation power and PLQY of the non-linear upconversion process;4,17,26–32 and (iii) dopant concentration dependency of PLQY,4,32–36 while one study addresses the relevance of scattering-related effects in larger particles.16 Still, some aspects remain the subject of discussion, including the role of the host material and why (also to what extent) some hosts perform better than others.36 The most commonly accepted reasons are based on the effect of a reduced multi-phonon relaxation probability when the cut-off phonon energy of the host material is small, or on the availability of multiple optical sites that lanthanide ions can occupy within the crystal lattice.37 Yet, further insight into the host material's properties is still chief for the design of more efficient UCNPs. Besides, effects of reducing the particle size below 100 nm are still under debate. In general, smaller UCNPs exhibit lower PLQY than larger ones.18,38 This fact is often attributed to environmental quenching,38–42 at least for sizes above 10 nm, in which the crystal host is thought to keep the properties of the bulk material (for smaller sizes there might be a phonon confinement effect).43–45 Luminescence quenching due to the local environment (e.g. solvent molecules) of the lanthanide ions affects smaller particles to a larger extent because a larger fraction of lanthanide ions are close to the particle surface. In addition, the particle surface is prone to have a high density of defects that can also influence emission probability. This structural issue even affects if core–shell interfaces are considered, instead of the external surface, as it has been demonstrated that the degree of intermixing at the interface also modifies the optical properties.46–48
This works revisits the commonly accepted theory of surface quenching as major origin for low PLQY in small UCNPs. PLQY was measured as a function of size, morphology, and crystal phase and correlated with structural data obtained by electron microscopy and X-ray diffraction analysis. For UCNPs smaller than 20 nm, distortion of the crystal lattice was found to have a significant impact on PLQY, in particular for α-NaGdF4 in which case the observed trends in PLQY could not be explained by surface quenching. Indeed, α-phase NaGdF4 were found to be more efficient upconverters than their β-phase counterparts in this size range. This is an important finding that limits the general agreement that UCNPs based on the β-phase of NaLnF4 (Ln = Gd, Y) are better emitters.19,49,50 Besides, a thorough analysis of PLQY in light of the development of the particle shape versus size was conducted with the help of a mathematical nucleus/hull volumetric model. For small UCNPs (sizes below 20 nm), the effect of the morphology was small compared to general surface quenching due to size reduction. However, the morphology should not be neglected for those of the UCNPs investigated the size of which falls within the 20 to 60 nm size range.
Results and discussion
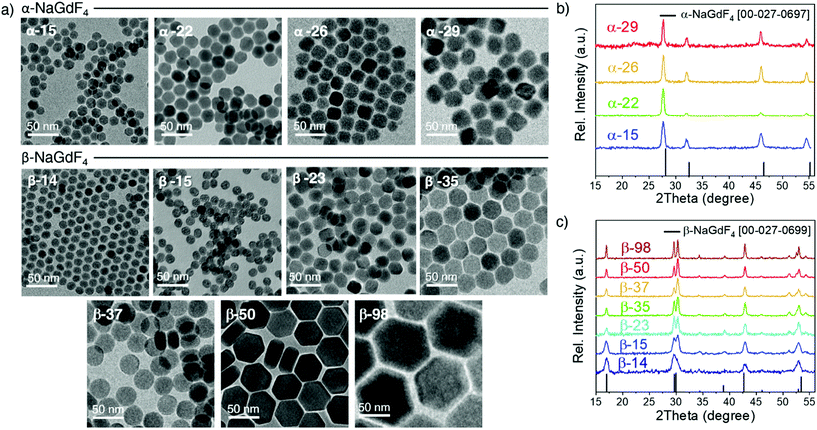
Oleate-capped Er3+/Yb3+ co-doped cubic (α)- and hexagonal (β)-NaGdF4 UCNPs of various sizes were prepared using the same reagents and synthetic route, which is based on a thermal decomposition strategy. The fact that all UCNPs were prepared following the same strategy allows for minimizing any effects that starting materials or synthetic routes may have on particle composition and structure and hence, PLQY, either due to a different level of impurities or to the presence of different surfactants. During the synthesis, metal trifluoroacetates, used as source of lanthanides, sodium and fluorine, were injected to a flask containing a hot mixture of 1-octadecene and oleic acid to trigger fast nucleation and growth (specific experimental details are provided in the ESI, section S1 and Table S1†). Size and phase control of the UCNPs was achieved by tuning the reaction parameters, i.e., reaction temperature (mainly affecting crystal phase) and precursor injection rate (mainly affecting particle size).Irrespective of their crystalline phase and size, all UCNPs were co-doped with 2 mol% Er3+ and 20 mol% Yb3+, an ion concentration that is most often used.51,52 The narrow size distribution (ESI, Fig. S1†) and crystal phase purity of the obtained UCNPs were confirmed by transmission electron microscopy (TEM) and powder X-ray diffraction (XRD) analysis (Fig. 1). Overall, this provided a set of α- and β-NaGdF4:Er3+/Yb3+ UCNPs (hereafter α- and β-NaGdF4) spanning the size range from 15 to almost 100 nm. As such, a comprehensive library of eleven UCNPs of different phases and sizes was available for PLQY assessment. It must be noted that the size range covered by the β-phase UCNPs is wider than that for the α-phase UCNPs. This is because of the thermodynamic stability of the respective crystal phase. For bulk NaGdF4, the temperature range in which the metastable α-phase can be observed is higher than room temperature, at which the thermodynamically stable β-phase is typically found. Indeed, in the bulk, the α-phase only exists at temperatures above 750 °C.53 However, for materials constituted by only a small number of unit cells – as in case of small nanoparticles – this restriction can be overcome, and it is possible to stabilize α-NaGdF4 UCNPs even at lower temperatures. Nonetheless, a size limitation for the α-phase remains and, if exceeded, inevitably triggers the α → β phase transformation.54 Elemental analysis (ICP-OES) experiments (ESI, Table S2†) were performed for all samples to confirm consistent sodium (Na+) to gadolinium (Gd3+) ratios and rule out the presence of any alternative non-stoichiometric composition. Further evidence for the high crystallinity of the UCNPs was obtained by high-resolution TEM (HRTEM) and selected area electron diffraction (SAED, representative morphologies are shown in Fig. 2; data for all other samples under investigation are shown in Fig. S2 of the ESI†), which demonstrated that the UCNPs were all single crystals. It is also clear from Fig. 1 and 2 that, even though the composition is the same for each sample, size and phase play an important role for the morphology of the UCNPs. Indeed, as shown in the top scheme of Fig. 2, for both crystal phases, the smaller UCNPs (∼15 nm diameter) had a spherical morphology, while larger UCNPs transformed into hexagonal plates or into cube-like structures in the case of hexagonal β-phase and cubic α-phase UCNPs, respectively. In the latter case, additional intermediate states in the form of truncated cubes appeared.54,55
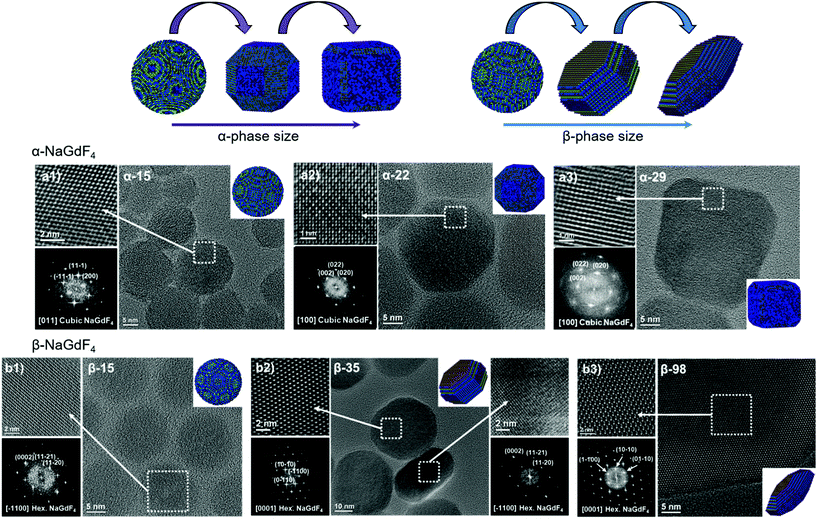 | ||
| Fig. 2 HRTEM images, SAED patterns and morphological models of selected (a) α- and (b) β-NaGdF4:Er3+/Yb3+ UCNPs (additional data available in Fig. S2†). | ||
As mentioned above, the main reason argued to explain the typically lower PLQY of smaller UCNPs is an increased probability of surface quenching. Underpinning this claim is the fact that the smaller the UCNPs are, the larger the percentage of ions near the surface is.28,56,57 Consequently, the observed variation in morphology gains relevance, as it determines the surface-to-volume ratio (S/V) of the UCNPs, which is the parameter typically used to quantify the fraction of material in close proximity to the surface. Therefore, careful analysis of the morphology of each batch of UCNPs was performed based on the HRTEM images given in Fig. 2 and S2.† The shape evolution is shown in the top scheme of Fig. 2.
Photoluminescence as a function of size and crystal phase
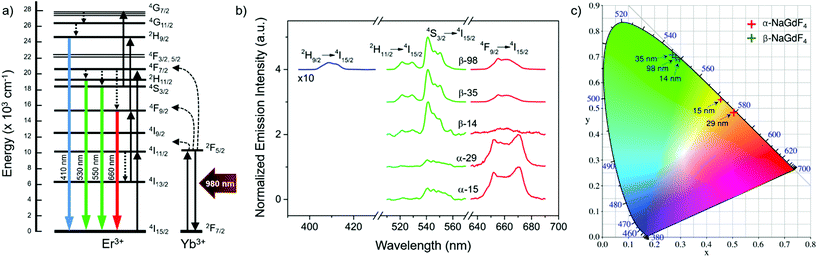
Er3+/Yb3+ co-doped materials present certain luminescent properties given by the distribution of their energy states, which is only weakly affected by the crystal host.58 Among these properties is the ability of Er3+ ions to generate visible emissions with blue, green and red wavelengths upon excitation with near-infrared light (around 980 nm), mainly absorbed by the Yb3+ ions (Fig. 3a).7 As an example, Fig. 3b shows the visible emission spectra obtained upon excitation at 980 nm, comparing the largest and smallest UCNPs of each crystal phase considered in this study. The complete upconversion mechanism that leads to these emissions has contributions of several simultaneous processes including energy transfer from Yb3+ to Er3+ and between Er3+ ions, as well as excited state absorption involving Er3+ ions. Among these processes, those accounting for higher probabilities are shown in the scheme of Fig. 3a, which includes the involved energy levels of Er3+ and Yb3+ ions, the main energy transfer steps between Yb3+ and Er3+ ions (curved dashed black arrows), excited state absorption and energy-transfer-triggered excitation (solid black arrows), radiative relaxations of Er3+ ions (coloured arrows), and non-radiative relaxation processes (straight dashed arrows).The resulting PLQY of the emission will be affected by all these simultaneous processes. Due to the multi-step and competitive character of upconversion, the relationship between PLQY and excitation intensity is not linear. Instead, it follows a power function that depends on the number of steps.59 Accordingly, there is a steep increase of PLQY with illumination intensity. Yet, it can be partially dampened as a result of the competition existing in each intermediate state between the probability of participating in excitation or in relaxation processes.17,26,27,30–32 This dampening, often called saturation, strengthens at higher illumination intensities and even dominates the trend above a certain excitation power density threshold. In this study, the laser excitation density was kept constant at 5.8 W cm−2, which is in the lower range of power densities applied in most of the related works and is below the saturation regime (see ESI, section S6†).17 Under these illumination conditions, emission spectra (Fig. 3b) were recorded on UCNP dispersions in hexane with a concentration of 75 mg mL−1. All spectra were normalised to their respective maximum emission.
Four emission bands were considered: one in the red wavelength region (Er3+ transition 4F9/2 → 4I15/2), two in the green region (Er3+ transitions 2H11/2 → 4I15/2 and 4S3/2 → 4I15/2), and a less intense one in the blue spectral region (Er3+ transition 2H9/2 → 4I15/2). The latter, though, was too weak to be measured for all samples. From the obtained spectra, it can be stated that the most intense emission band is the green one in the case of the hexagonal crystal phase (β-NaGdF4), while the red emission becomes more intense for UCNPs based on the cubic crystal phase (α-NaGdF4). Aiming to quantify to what extent these differences can be perceived, the CIE colour coordinates of the emissions given in Fig. 3b were plotted in a chromaticity diagram (CIE 1931, Fig. 3c). This analysis shows the relevance of the spectral difference between upconversion emissions originating from β- and α-phase UCNPs; the former mainly showed green emission, while the latter showed emission in the yellow-orange range. An effect of size was observed in both cases, though it seems larger in the case of the α-phase UCNPs despite the narrower size range considered. In terms of average human perception, small differences observed in the green range around 545 nm are less noticeable than in the yellow-orange range, around 570 nm.60 Accordingly, the colour differences observed for the α-phase are not only larger, but also lie in a range in which it is easier to be noticed by human eyes, thus size-control is in this case more important in applications in which a luminescent colour palette is an asset. On the other hand, the human eye presents a greater sensitivity to the green colour than to the yellow-orange one, which supports β-phase particles as optical labels.
In order to provide information about the emission intensity in absolute terms, the internal quantum yield needs to be considered, as given by:
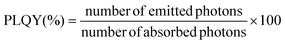 | (1) |
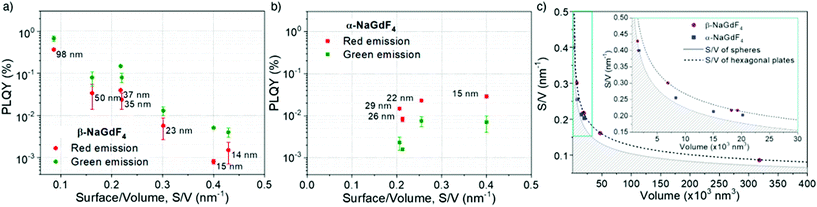
According to eqn (1), emission is normalised by absorption, which makes PLQY a purely intrinsic parameter. Absolute PLQY was measured using an integrating sphere with the same parameters used to record the emission spectra given in Fig. 3a (further experimental details are given in section S2 of the ESI†). The obtained values are plotted in Fig. 4a (hexagonal phase) and Fig. 4b (cubic phase) as a function of the surface-to-volume ratio, S/V (see Table S4 of the ESI† for details). In preparation of a meaningful comparison between UCNPs of various sizes and crystal phases, thermal effects due to laser heating that could affect any PLQY trends were ruled out (a more in-depth discussion is provided in the ESI, section S8†). Also, scattering effects can be considered negligible, given the small size of the UCNPs.16
The obtained PLQY values were below 1% for all samples, reaching values as low as 0.001% in some cases. Such low PLQY is expected for upconversion due to the non-linear nature of the process and the many alternative and competing relaxation routes. As values were small, experimental error might be large. To provide an uncertainty (error bars in Fig. 4a and b), each sample was measured at least twice and on different days, so they confirm the consistency of the obtained trends. Table 1 summarises the literature PLQY data for experimental conditions as close as possible to those applied in this study. Even though the comparison of PLQY values obtained under different experimental conditions (dopant concentration, particle size, excitation power, etc.) is difficult, Table 1 shows that our results are in the same range as those found by other authors. For the sake of comparison, the obtained results were also framed in the context of two additional popular upconversion host materials, LiYF4 and NaYF4, with equivalent S/V values. As this comparison is beyond the main subject of this work, these data can be found in the ESI, section S9.†
| Host | Concentration [Er3+], [Yb3+] (%) | Size (nm) | Excitation (W cm−2) | Solvent | Upconversion PLQY | Ref. |
|---|---|---|---|---|---|---|
| β-NaYF4 | 2, 20 | 30 | 150 | Hexane | 0.1% | 18 |
| β-NaYF4 | 5, 33 | 24 | 63 | Chloroform | 0.07% | 62 |
| β-NaYF4 | 2, 20 | 23 | 20 | Cyclohexane | 0.045% | 26 |
| β-NaYF4 | 3, 17 | 25 | ∼3 | Toluene | 0.01% | 17 |
| β-NaYF4 | 2, 15 | 28 | ∼10 | Toluene | ∼0.01% | 27 |
| β-NaGdF4 | 2, 20 | 4 | 420 | Cyclohexane | 4 × 10−5% | 11 |
| β-NaGdF4 | 2, 20 | 23 | 5.6 | Hexane | 0.018% | This work |
Effect of particle shape
For the sake of clarity, prior to a detailed discussion of the PLQY data, the choice of using S/V as a variable instead of particle diameter shall be rationalised. As mentioned above, only the smallest UCNPs are spheres and thus, have a well-defined diameter. Upon variation of the morphology from a spherical geometry, a more general parameter than diameter has to be introduced to allow for comparison. As PLQY is thought to be mainly affected by surface effects, a parameter considering the relevance of surface over volume seems practical and has to be accurately defined for each morphology. Since S/V has been used before, we followed this same approach.49 Aiming to evaluate S/V, a geometry-based formula has been defined for each shape found, i.e., spheres, cubes, truncated cubes and hexagonal plates, and has been applied to the corresponding UCNPs (detailed information in ESI, section S5†). Still, to provide an intuitive guide, data points in Fig. 4a and b, which are plotted versus S/V, are also labelled in the graph with the respective diameter (for spheres), diagonal length (for hexagons) or side length (for cubes and truncated cubes).A certain volume of material can be shaped in several different ways to produce a particle. If shape has an effect on PLQY, following a geometrical rationale, one would expect a better performance from spherical UCNPs as this shape minimises the surface area per unit of volume. Conversely, flat geometries, for instance hexagonal plates, will always have a larger surface per volume than a sphere of comparable volume. Fig. 4c visualises this general fact. The grey full line depicts the mathematical curve of S/V versus the volume of spherical nanoparticles. Given that the sphere mathematically minimises S/V, any value below this line does not exist (shaded area). The addition of the obtained experimental S/V data for β- and α-phase UCNPs to the plot shows that those UCNPs exhibiting cubic geometries (blue symbols) are closer to this optimal boundary than hexagonal plates (purple symbols). Experimental data points obtained for hexagonal UCNPs match well with the line that describes S/V versus volume calculated for a hexagonal geometry (black dashed line; see details on the calculation in the ESI, Fig. S3†). Note that for both crystal phases, a spherical geometry is only observed for the smallest UCNPs. Consequently, given the importance of S/V with respect to luminescence quenching effects, the morphology evolution towards cubes or hexagonal plates can be considered detrimental for PLQY. Both shapes induce a less than optimal S/V, whereas the hexagonal plate geometry is even more unfavourable than the cubic one. Nevertheless, one must keep in mind that larger UCNPs generally exhibit a higher PLQY as the volume gains relevance over the surface as the particles grow (see how the curves in Fig. 4c become less steep for larger particles). Consequently, these two trends – shape-induced S/V and size – compete against each other.
In light of these considerations, the PLQY evolution as a function of size and shape was analysed in more detail. The data obtained for β-NaGdF4 (Fig. 4a) and α-NaGdF4 (Fig. 4b) follow opposite trends. Interestingly, the PLQY of β-NaGdF4 was found to increase for larger UCNPs, while that of α-NaGdF4 decreased with size to such an extent that the PLQY of α-NaGdF4 surpasses that of β-NaGdF4 when the particle size becomes sufficiently small. This behaviour is noticeable since β-NaGdF4 is typically reported to be the most efficient host material for Er3+/Yb3+ upconversion when compared to α-NaGdF4.19,49,50 The switch of positions in this intensity ranking for small enough UCNPs has been previously suggested by few works comparing emission intensities or lifetimes, though none of these studies could systematically compare both phases.49,61 However, Fig. 4 corroborates their observations and provides further evidence that, indeed, there is a differentiating size-dependent behaviour. It is such that the PLQY of α-phase UCNPs surpasses the PLQY of β-phase UCNPs when a small-enough size regime is reached. This is, within our experimental conditions, below ∼20 nm.
Based on Fig. 4, β-NaGdF4 followed the expected trend that larger UCNPs emit more efficiently, which implies that the size change affects PLQY more strongly than shape change from spheres to hexagonal plates does.38,49 In the surface-quenching context, it is possible to understand an UCNP as a particle comprised of two different regions: (i) an emitting region in the particle core that remains mainly unaffected by the external environment, thus, behaving as close to bulk material as possible, and (ii) a surrounding external region that can be described as a hull and that is affected by quenching (see schemes given at Fig. 5, bottom).49,62 Hence, it is possible to establish a simplified volumetric model that allows visualizing the relevance of the particle's shape on the resulting PLQY, described by the following general expression:
| PLQY = ϕT(R) = (ϕSVS + ϕBVB)/VT | (2) |
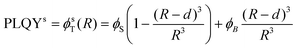 | (3a) |
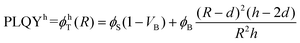 | (3b) |
It is worth discussing the meaning of d and ϕS and their influence on the total value of PLQY. Within this model, d, the hull thickness, should be understood as an effective depth reaching into the UCNP covering the area in which Ln3+ ions are strongly quenched. If we assume energy transfer from lanthanides to other molecules or defects as the main reason for quenching, d can be linked to the critical radius defined within the energy transfer theory. As a reference value, it has been experimentally demonstrated in analogous experiments that an inert shell (without any Ln3+ ion) of around 6 nm could avoid surface quenching.62 Our situation is different as there is no inert shell, but instead a strongly quenched area containing lanthanide ions. Accordingly, we are not only dealing with energy transfer to external molecules, as in the mentioned work, but also with migration processes that can transport energy from inner areas of the particle closer to the surface. Hence, we can expect our effective depth, d, to be longer than the previously reported value of 6 nm. For instance, a 10 nm surface region doped with Er3+ but largely non-emissive due to quenching has been defined for Ln2O3:Er3+ nanoparticles.63
Regarding ϕS, i.e., the PLQY contribution of the surface, its value would logically vary within the region defined by d. In particular, it should depend on the distance to the surface, r, since quenching is more likely the closer an emitting ion is to the outer environment (ϕS![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) ϕS(r)). Specifically, if we assume quenching effects led by dipole–dipole energy transfer, it should follow a function of 1/r6.
ϕS(r)). Specifically, if we assume quenching effects led by dipole–dipole energy transfer, it should follow a function of 1/r6.
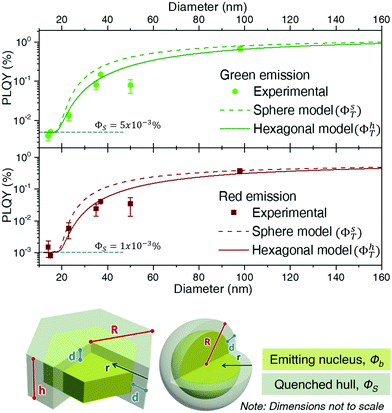
As ϕS is related to the hull only, it will govern the PLQY trend for particles with a radius, R, smaller or equal than d, as in this case there isn't a bulk region (in other words, the whole particle suffers quenching). The experimental values in this R ≤ d range can be used to set ϕS. Considering the discussion on d above, only two experimental data may fall within the size range in which we can a priori assume that the whole UCNP is strongly quenched, i.e., those obtained for UCNPs of sizes smaller than ∼15 nm in diameter. Thus, defining the dependence of ϕS on r, is not feasible. We can assume, instead, an effective constant for ϕS, which will be a fair approximation as long as R ≳ d. Within this approximation, a fit to the experimental data gives a ϕS of 0.001% for the red emission and 0.005% for the green upconversion emission. Such approximation makes the shape of the curve unrealistically flat for sizes below 20 nm (Fig. 5), but circumvents the need to increase the number of variables with parameters that we cannot reliably fit.
Having determined the surface contribution, ϕs, we can proceed to fit equations 3a and 3b to determine the bulk contribution, ϕb. By doing so, it becomes clear that given its small values, the surface contribution to the total PLQY is negligible for sizes slightly larger than ∼20 nm, since the bulk term dominates the trend. Indeed, most of the PLQY variation observed in Fig. 4c is due to the fact that when a quenching hull exists, not all of the material emits, while all of it absorbs.
As ϕb is the PLQY value of the material without surface quenching, i.e., that of larger crystals in which shape shouldn't play a role, both geometrical models (sphere and hexagonal) are fit with the same ϕb. From this fit we determined that the red emission was best modelled with ϕb equal to 0.7% and d equal to 8.9 nm, while the green emission requires a ϕb of 1.4% and a d of 8.4 nm. As predicted above, the fitted values of d are slightly larger than those reported in a previous study (d = 6 nm) which is consistent with the presence of energy migration.62 Besides, it is clear from Fig. 5 that the model based on a spherical geometry overestimates the PLQY of the UCNPs for particles smaller than ∼60 nm. It can be concluded that in a surface-quenching model, the shape of the UCNP plays a role that is connected to the different weight of the surface over the volume as a function of particle size (Fig. 4c).
Limitations of the surface-quenching model: the case of α-NaGdF4
It was not possible to fit this surface-quenching model to the PLQY values measured for α-NaGdF4 phase (Fig. 4b), as the observed trend was opposite to its predictions. Nonetheless, it is worth mentioning that such behaviour has been previously observed in experiments based on intensities or lifetimes, leading to the hypothesis that crystal defects and lattice distortion may play a key role in this case.19,49 This idea is consistent with the fact that the cubic phase of NaGdF4 is per se thermodynamically unstable at room temperature (as mentioned above) and can only be stabilised for small enough particle sizes, so certain lattice distortion as particles grow larger can be expected. Alternative hypotheses may include quenching through vibrational energy of surface ligands linked to uncontrolled concentrations of surfactants; or heterogeneous dopant ion distributions in the host lattice (inducing possible changes in the distance between Er3+ and Yb3+ ions). However, both aspects were ruled out as major reason for the observed PLQY trends (further optional reading is provided in the ESI, sections S10 and S11†). In light of this – and in the context of the observed size-dependent variation of PLQY – it seems reasonable to consider differences in the crystal lattice itself as a function of particle size, ultimately affecting its phase stability and PLQY.In order to gain deeper insight into the crystallographic characteristics of UCNPs, which may account for the PLQY variation, Rietveld refinement was applied to their XRD diffractograms (ESI, section S12†). Resulting lattice parameters of the cubic and hexagonal unit cells (a = b, c for the β-phase and a = b = c for the α-phase) for all samples under investigation are summarised in Table 2. The error represents the standard deviation of two fits for each sample, all of them with χ2 < 1.5. The volume of the unit cell was calculated from these lattice parameters (Fig. 6a and b), unveiling a contraction when particles become smaller, regardless the crystal phase. Comparison of the obtained data as a function of S/V showed that the contraction was stronger for the cubic phase (steeper slope, p, approximating the three values of lower S/V to a straight line: pβ ∼−0.06, pα ∼−3).
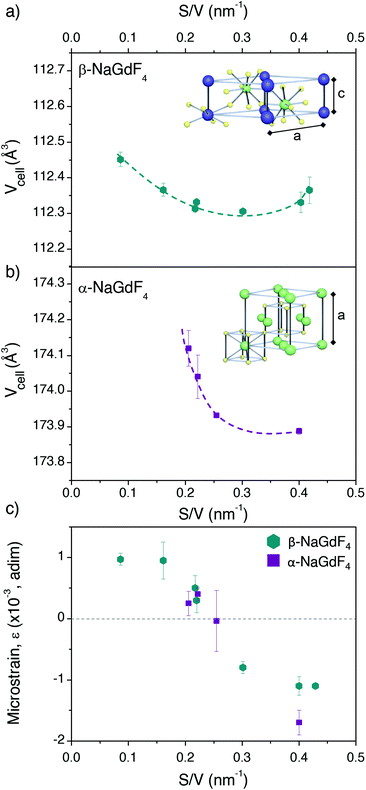 | ||
| Fig. 6 Unit cell volume calculated from the lattice parameters given in Table 2 and plotted versus the S/V ratio for (a) β- and (b) α-NaGdF4 UCNPs. Schemes depicting the ion positions within each unit cell are given as insets. (c) Microstrain parameters obtained for each sample as a function of S/V. | ||
| β-NaGdF4 | ||||
|---|---|---|---|---|
| S/V (nm−1) | a (Å) | c (Å) | Crystallite size (nm) | TEM size (nm) |
| 0.08(6) | 6.0317 ± 0.0004 | 3.5685 ± 0.0004 | 90 | 98 |
| 0.16(1) | 6.0285 ± 0.0003 | 3.5696 ± 0.0006 | 47 | 50 |
| 0.21(7) | 6.0276 ± 0.0002 | 3.5688 ± 0.0003 | 42 | 37 |
| 0.21(9) | 6.0275 ± 0.0002 | 3.5697 ± 0.0003 | 36 | 35 |
| 0.30(1) | 6.0272 ± 0.0002 | 3.5698 ± 0.0002 | 28 | 23 |
| 0.40(3) | 6.0279 ± 0.0003 | 3.571 ± 0.001 | 16 | 15 |
| 0.41(8) | 6.0270 ± 0.0009 | 3.5711 ± 0.0002 | 14 | 14 |
| α-NaGdF4 | ||||
|---|---|---|---|---|
| S/V (nm−1) | a (Å) | — | Crystallite size (nm) | TEM size (nm) |
| 0.20(6) | 5.5840 ± 0.0006 | 30 | 29 | |
| 0.22(2) | 5.5832 ± 0.0008 | 23 | 26 | |
| 0.25(5) | 5.58205 ± 0.00003 | 22 | 22 | |
| 0.40(0) | 5.5816 ± 0.0001 | 13 | 15 | |
In general, uniform lattice modifications, such as homogeneous doping, contribute to a shift of the XRD reflections and hence have an effect on lattice parameters and unit cell volumes when compared to an undoped material. Moreover, any deviation from perfect crystallinity, i.e., any distortion that is not uniform throughout the crystal, is also reflected in XRD patterns as it affects the width of the diffraction peaks. These deviations include the finite size of the crystal and microstrains related to surface tension, morphology or the presence of impurities. Such effects can thus be studied through the reflections’ half-width, βhkl. In particular, Williamson–Hall equation, which assumes that the different contributions to the width are additive, can be applied:64,65
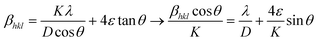 | (4) |
In this expression, the first addend is the contribution given by the crystallite size, i.e., the Scherrer formula, and the second addend is the contribution from microstrains. θ is the diffraction angle (in rad), ε is the strain parameter, λ the X-ray wavelength (1.5418 Å), D is the crystallite size and K is the Scherrer parameter. Typically, K takes values around 1, though it changes slightly depending on the crystallite geometry and the diffraction plane. Exact values for K are tabulated for a number of geometries, including all those considered here (ESI, section S13†).66,67
Given the different angle dependence of both addends, it is possible to rearrange the Williamson–Hall expression as in the right side of eqn (4). Such rearrangement allows to separately evaluate experimental data with respect to crystallite size and strain, which can be performed through a linear fit (Fig. S12†). The values of D obtained in this way are given in Table 2 together with the respective TEM sizes for comparison. The generally good agreement between both values indicates that the UCNPs are single crystallites, as it was already suggested by HRTEM. The strain parameter calculated for each sample is shown in Fig. 6c as a function of S/V, unveiling minimal strain in both phases. While strain appears to be size dependent, which is in agreement with Zhao et al., differences between crystal phases cannot be discerned.49
Summarizing the XRD results, strains might indeed play a role, as they change with size. Also, all UCNPs suffered a size-dependent cell contraction, which is more relevant for smaller sizes. Both, strain and lattice contraction, may contribute to variation in luminescence given that they influence the position of the lanthanide dopant ions within the lattice, which may affect the symmetry around the optical centres. In this context, it should be noted that electronic transitions in 4f lanthanide levels are parity forbidden by selection rules. However, asymmetric environments provoke mixing of opposite parity states, making f–f transitions partially allowed. From this perspective, highly asymmetric local environments of the lanthanide dopants account for a higher transition probability as well as higher relative intensities from electric dipole transitions. Accordingly, lattice distortion is an additional aspect influencing photoluminescence in UCNPs. A good example that supports this claim is the work of van Hest et al. showing, through a careful analysis of the emission of Eu3+ ions in nanocrystals, that surface defects play a role in lowering the symmetry of lanthanide optical centres, and constitute a major difference between nanocrystals and bulk samples.68
But why exactly would α and β phases be so different in that regard? Different effects can be expected for α-NaGdF4 and β-NaGdF4 UCNPs as both crystal phases can be differently affected by the observed changes. This is due to the differences between both phases regarding the symmetry of the sites occupied by the dopant ions. In the hexagonal phase lanthanides are mostly found in C1 symmetry sites, which is the lowest symmetry possible.69 Hence, even if defects may still involve a stronger deviation from the inversion symmetry, their effect will be weaker than in any other case, as has been demonstrated in Eu3+-doped nanoparticles.68 It should be noted that in the β-phase there is also a smaller fraction of lanthanides in more symmetric C3h sites (to be precise, there are twice as many ions in C1 than in C3h) that may benefit from the symmetry lowering induced by defects.69 In α-NaGdF4 UCNPs, instead, all lanthanides are in CS and C2 sites, which involve symmetry operations that can still be broken, and thus can be locally affected by defects.70–72 Consequently, we hypothesise that defects and lattice distortion can play a major role for UCNPs crystallised in the α-phase through symmetry relaxation, to the extent that it can compete with surface quenching. Ultimately, this gives rise to the dependence of PLQY with size (and shape) as seen in Fig. 4.
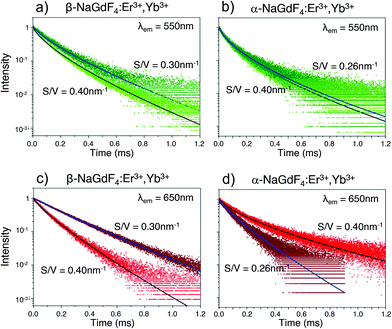
In addition, the multisite structure of β-NaGdF4 has been pointed out as a possible reason for its excellent performance as upconverting host material. This characteristic could be extended to the smaller α-NaGdF4 particles as defects would involve a larger number of differentiated optical sites.37,73 Such considerations are in line with previously published data and with our own results. However, confirming which one plays the major role would require additional experiments, likely with single-doped nanoparticles, that go beyond the scope of this current work. It is possible, though, to gain additional insight into the upconversion properties of α- and β-phase UCNPs by considering the emission decay behaviour of samples from both phases. The UC decay curves of the green (λem = 550 nm) and red (λem = 650 nm) emission of UCNPs dispersed in toluene are displayed in Fig. 7. As shown, each decay curve exhibits a remarkable deviation from single-exponential behaviour. This deviation is typical of structural situations in which lanthanide ions appear in a variety of local environments, resulting in multiple excited state lifetimes that all combined, create the observed non-exponential behaviour. In this case, a common approach to analyse the decay curves involves a fit using a multi-exponential function that reflects the multiple kinetic parameters.74,75 In the present case, following our PLQY volumetric nucleus/hull model, this approach would involve one lifetime linked to the inner region of the UCNPs where the local environment of the lanthanide ions is presumably homogeneous. In contrast, in the surrounding hull, as the luminescent ions approach the UCNP surface, the local site environment is expected to be more and more affected by strain, defects and surface quenching. Thus, lifetime variation is expected to be more pronounced than in the UCNP inner region. As the change from nucleus to hull is gradual, one or more exponential functions could be used to fit the contribution of the hull to the decay curves, resulting in an unnecessarily large number of parameters.76 Alternatively, the Kohlrausch function can be used, which offers a powerful tool to analyse non-exponential features of luminescence decays. This model has already been applied in disordered and ordered solid hosts, as well as in nanostructured materials,77,78 including lanthanide-doped nanomaterials.48,74 Following the Kohlrausch function, the emission intensity as a function of time I(t) is described as:
I(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(t/τ0)γ] exp[−(t/τ0)γ] | (5) |
The kinetic parameters obtained by fitting the emission decay curves (shown in Fig. 7) using eqn (5) are reported in Table 3. It can be noted that all fits generated γ values lower than 1, with generally smaller values for α-NaGdF4. This is indicative of less homogenous environments in case of α-NaGdF4 compared to β-NaGdF4. For the latter, both the time constants τ0 and γ decrease with decreasing particle size, either for the red or green emissions. However, a more pronounced decrease is observed for the red emission (see Table 3). This shortening of the lifetimes (τ0) can be reasonably explained by an increase of the distortion of the local environment when S/V increases (i.e., the UCNPs become smaller), which is consistent with an increase of the strain parameter, as shown in Fig. 6c. Similarly, for α-NaGdF4, the most significant effect is observed for the red emission, while neither τ0 nor γ vary much with particle size in the case of the green emission (see Table 3). Yet, noteworthy and in contrast to β-NaGdF4, the time constant τ0 of the red emission increases, suggesting a decrease of the distortion of the local environment around the lanthanide ions. Moreover, its γ value decreases most significantly with decreasing particle size, pointing to a larger heterogeneity in terms of luminescent centres. Importantly, these results agree with the trends observed for PLQY. In fact, both the PLQY and lifetimes of the β-NaGdF4 notably decreases as S/V increases (Fig. 4a). On the other hand, the PLQY of α-NaGdF4 smoothly increases with S/V, in particular for the red emission (Fig. 4b), again, as lifetime does.
| β-NaGdF4 | ||||
|---|---|---|---|---|
| S/V (nm−1) | λ em = 550 nm | λ em = 650 nm | ||
| τ 0 (ms) | γ | τ 0 (ms) | γ | |
| 0.30(1) | 0.114(1) | 0.75(1) | 0.208(1) | 0.92(1) |
| 0.40(3) | 0.081(1) | 0.71(1) | 0.096(1) | 0.82(1) |
| α-NaGdF4 | ||||
|---|---|---|---|---|
| S/V (nm−1) | λ em = 550 nm | λ em = 650 nm | ||
| τ 0 (ms) | γ | τ 0 (ms) | γ | |
| 0.26(1) | 0.057(1) | 0.61(1) | 0.090(1) | 0.82(1) |
| 0.40(0) | 0.054(1) | 0.62(1) | 0.121(1) | 0.65(1) |
Conclusions
Through detailed investigation of a set of NaGdF4:Er3+,Yb3+ UCNPs of different size, shape, and crystal phase, we have revisited the commonly applied surface quenching theory, used to explain why UCNPs typically account for lower PLQY values than the bulk material. Overall, the obtained results are consistent with the previously established theory; however, interestingly, some limitations were identified. In particular, it was confirmed that the behaviour of β-NaGdF4 PLQY can be largely explained based on the established theory, while this is not the case for α-NaGdF4. Indeed, in this case PLQY showed the opposite trend versus size than expected. To explain this, we propose that the increasing distortion of the cubic crystal lattice upon decrease of the particle size may be playing a particularly relevant role in this specific crystal phase, given its symmetry characteristics.Besides that, the results of this study show that an accurate model to describe how PLQY depends on UCNP size must also consider the shape of the particle as relevant parameter. This is particularly noteworthy for NaGdF4 UCNPs in the 20 to 60 nm size range, whereas quenching in smaller or larger UCNPs was found to no longer being affected by particle geometry (and its associated surface-to-volume ratio).
Author contributions
E.H., M.Q. and S.R. have worked on the synthesis of nanoparticles and their characterization; J.M-H measured PLQY; G.L and A.S. measured emission decay curves; and R.R.Z and V.R are responsible for HRTEM images. All authors have participated in conceptualization and discussion steps. M.Q. and E.H. wrote the manuscript, that was reviewed and edited by all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors appreciate the valuable comments of Dr Ian Howard and Dr Damien Hudry (both at KIT, Karlsruhe, Germany) during the final stages of the manuscript. Also, the authors thank Gwenaël Chamoulaud (UQAM, Montreal, Canada) for experimental support with the thermogravimetric measurements and gratefully acknowledge the use of equipment in the “Collaborative Laboratory and User Facility for Electron Microscopy” (CLUE, http://www.clue.physik.uni-goettingen.de). Prof. F. Vetrone is grateful for financial support from the Natural Sciences and Engineering Research Council (NSERC) of Canada and the Fonds de Recherche du Québec – Nature et Technologies (FRQNT) for supporting their research. E. Hemmer is thankful to the Alexander von Humboldt Foundation for financial support in the frame of the Feodor Lynen Research Fellowship. J. Marques-Hueso thanks the UK Engineering and Physical Sciences Research Council for support (EP/T013680/1). M. Quintanilla acknowledges the financial support of the Spanish Ministerio de Ciencia e Innovación through the project COLUMNAS (PID2019-110632RB-I00). B. S. Richards would like to acknowledge the financial support provided by the Helmholtz Association via (i) the Recruitment Initiative Funding; and (ii) the Research Field Energy – Program Materials and Technologies for the Energy Transition – Topic 1 Photovoltaics.References
- E. Z. Xu, C. Lee, S. D. Pritzl, A. S. Chen, T. Lohmueller, B. E. Cohen, E. M. Chan and P. J. Schuck, Opt. Mater.: X, 2021, 12, 100099 CAS.
- L. Y. Ang, M. E. Lim, L. C. Ong and Y. Zhang, J. Nanomed. Nanotechnol., 2011, 6, 1273–1288 Search PubMed.
- Y. Huang, A. Skripka, L. Labrador-Paez, F. Sanz-Rodriguez, P. Haro-Gonzalez, D. Jaque, F. Rosei and F. Vetrone, Nanoscale, 2018, 10, 791–799 RSC.
- S. K. W. MacDougall, A. Ivaturi, J. Marques-Hueso, K. W. Krämer and B. S. Richards, Sol. Energy Mater. Sol. Cells, 2014, 128, 18–26 CrossRef CAS.
- J. C. Goldschmidt and S. Fischer, Adv. Opt. Mater., 2015, 3, 510–535 CrossRef CAS.
- F. Auzel, C. R. Acad. Sci., 1966, 262, 1016–1019 Search PubMed.
- F. Auzel, in Spectroscopic Properties of Rare Earths in Optical Materials, ed. R. Hull, J. Parisi, R. M. Osgood Jr., H. Warlimont, G. Liu and B. Jacquier, Springer Berlin Heidelberg, 2005, ch. 5, pp. 266–319 Search PubMed.
- U. Resch-Genger and H. H. Gorris, Anal. Bioanal. Chem., 2017, 409, 5855–5874 CrossRef CAS PubMed.
- E. Hemmer, P. Acosta-Mora, J. Mendez-Ramos and S. Fischer, J. Mater. Chem. B, 2017, 5, 4365–4392 RSC.
- D. Hudry, I. A. Howard, R. Popescu, D. Gerthsen and B. S. Richards, Adv. Mater., 2019, 31, 1900623 CrossRef PubMed.
- C. Würth, S. Fischer, B. Grauel, A. P. Alivisatos and U. Resch-Genger, J. Am. Chem. Soc., 2018, 140, 4922–4928 CrossRef PubMed.
- P. S. May, A. Baride, M. Y. Hossan and M. Berry, Nanoscale, 2018, 10, 17212–17226 RSC.
- A. Skripka, A. Benayas, C. D. S. Brites, I. R. Martín, L. D. Carlos and F. Vetrone, Nano Lett., 2020, 20, 7648–7654 CrossRef CAS PubMed.
- C. Würth, M. Grabolle, J. Pauli, M. Spieles and U. Resch-Genger, Nat. Protoc., 2013, 8, 1535–11550 CrossRef PubMed.
- S. K. W. MacDougall, A. Ivaturi, J. Marques-Hueso and B. S. Richards, Rev. Sci. Instrum., 2014, 85, 063109 CrossRef PubMed.
- C. M. S. Jones, N. Panov, A. Skripka, J. Gibbons, F. Hesse, J.-W. G. Bos, X. Wang, F. Vetrone, G. Chen, E. Hemmer and J. Marques-Hueso, Opt. Express, 2020, 28, 22803–22818 CrossRef CAS PubMed.
- M. Kaiser, C. Würth, M. Kraft, I. Hyppanen, T. Soukka and U. Resch-Genger, Nanoscale, 2017, 9, 10051–10058 RSC.
- J.-C. Boyer and F. C. J. M. van Veggel, Nanoscale, 2010, 2, 1417–1419 RSC.
- F. Wang, Y. Han, C. S. Lim, Y. H. Lu, J. Wang, J. Xu, H. Y. Chen, C. Zhang, M. H. Hong and X. G. Liu, Nature, 2010, 463, 1061–1065 CrossRef CAS PubMed.
- A. Nadort, V. K. Sreenivasan, Z. Song, E. A. Grebenik, A. V. Nechaev, V. A. Semchishen, V. Y. Panchenko and A. V. Zvyagin, PLoS One, 2013, 8, e63292 CrossRef CAS PubMed.
- C. T. Xu, P. Svenmarker, H. Liu, X. Wu, M. E. Messing, L. R. Wallenberg and S. Andersson-Engels, ACS Nano, 2012, 6, 4788–4795 CrossRef CAS PubMed.
- S. Balabhadra, M. L. Debasu, C. D. S. Brites, R. A. S. Ferreira and L. D. Carlos, J. Lumin., 2017, 189, 64–70 CrossRef CAS.
- E. H. Eriksen, C. L. M. Hofmann, S. Fischer and J. C. Goldschmidt, Upconversion in a finite, one-dimensional photonic crystal: a simulation-based assessment of the potential for increasing the upconversion efficiency of β-NaYF4:Er3+, in Light, Energy and the Environment, Boulder, Colorado, 2017 Search PubMed.
- S. Fischer, D. Kumar, F. Hallermann, G. von Plessen and J. C. Goldschmidt, Opt. Express, 2016, 24, A460–A475 CrossRef CAS PubMed.
- M. Tan, M.-J. Monks, D. Huang, Y. Meng, X. Chen, Y. Zhou, S.-F. Lim, C. Würth, U. Resch-Genger and G. Chen, Nanoscale, 2020, 12, 10592–10599 RSC.
- C. Würth, M. Kaiser, S. Wilhelm, B. Grauel, T. Hirsch and U. Resch-Genger, Nanoscale, 2017, 9, 4283–4294 RSC.
- I. N. Stanton, J. A. Ayres, J. T. Stecher, M. C. Fischer, D. Scharpf, J. D. Scheuch and M. J. Therien, J. Phys. Chem. C, 2018, 122, 252–259 CrossRef CAS.
- H. Liu, C. T. Xu, D. Lindgren, H. Xie, D. Thomas, C. Gundlach and S. Andersson-Engels, Nanoscale, 2013, 5, 4770–4775 RSC.
- D. O. Faulkner, S. Petrov, D. D. Perovic, N. P. Kherani and G. A. Ozin, J. Mater. Chem., 2012, 22, 24330–24334 RSC.
- M. Pokhrel, G. A. Kumar and D. K. Sardar, J. Mater. Chem. A, 2013, 1, 11595–11606 RSC.
- M. Pokhrel, A. K. Gangadharan and D. K. Sardar, Mater. Lett., 2013, 99, 86–89 CrossRef CAS.
- S. Kuznetsov, Y. Ermakova, V. Voronov, P. Fedorov, D. Busko, I. A. Howard, B. S. Richards and A. Turshatov, J. Mater. Chem. C, 2018, 6, 598–604 RSC.
- A. Pilch, D. Wawrzynczyk, M. Kurnatowska, B. Czaban, M. Samoc, W. Strek and A. Bednarkiewicz, J. Lumin., 2017, 182, 114–122 CrossRef CAS.
- D. Yasyrkina, S. Kuznetsov, A. Ryabova, D. Pominova, V. Voronov, R. Ermakov and P. Fedorov, Nanosyst.: Phys., Chem., Math., 2013, 4, 648–656 CAS.
- S. Fischer, B. Fröhlich, K. W. Krämer and J. C. Goldschmidt, J. Phys. Chem. C, 2014, 118, 30106–30114 CrossRef CAS.
- S. Fischer, R. Martin-Rodriguez, B. Fröhlich, K. W. Krämer, A. Meijerink and J. C. Goldschmidt, J. Lumin., 2014, 153, 281–287 CrossRef.
- C. Renero-Lecuna, R. Martín-Rodríguez, R. Valiente, J. González, F. Rodríguez, K. W. Krämer and H. U. Güdel, Chem. Mater., 2011, 23, 3442–3448 CrossRef CAS.
- M. Kraft, C. Würth, V. Muhr, T. Hirsch and U. Resch-Genger, Nano Res., 2018, 11, 6360–6374 CrossRef CAS.
- H. Sun, L. Zhang, L. Wen, M. Liao, J. Zhang, L. Hu, S. Dai and Z. Jiang, Appl. Phys. B, 2005, 80, 881–888 CrossRef CAS.
- M. C. Tan, L. Al-Baroudi and R. E. Riman, ACS Appl. Mater. Interfaces, 2011, 3, 3910–3915 CrossRef CAS PubMed.
- F. C. J. M. van Veggel, C. Dong, N. J. J. Johnson and J. Pichaandi, Nanoscale, 2012, 4, 7309–7321 RSC.
- J. W. Stouwdam, G. A. Hebbink, J. Huskens and F. C. J. M. van Veggel, Chem. Mater., 2003, 15, 4604–4616 CrossRef CAS.
- J. J. H. A. van Hest, G. A. Blab, H. C. Gerritsen, C. de Mello Donega and A. Meijerink, J. Phys. Chem. C, 2018, 122, 3985–3993 CrossRef CAS PubMed.
- D. Li, Q. Shao, Y. Dong and J. Jiang, J. Phys. Chem. C, 2014, 118, 22807–22813 CrossRef CAS.
- Z. H. Li, D. Hudry, R. Heid, A. H. Said, M. D. Le, R. Popescu, D. Gerthsen, M. Merz, K. W. Krämer, D. Busko, I. A. Howard, B. S. Richards and F. Weber, Phys. Rev. B, 2020, 102, 165409 CrossRef CAS.
- D. Hudry, D. Busko, R. Popescu, D. Gerthsen, A. M. M. Abeykoon, C. Kübel, T. Bergfeldt and B. S. Richards, Chem. Mater., 2017, 29, 9238–9246 CrossRef CAS.
- D. Hudry, D. Busko, R. Popescu, D. Gerthsen, I. A. Howard and B. S. Richards, J. Mater. Chem. C, 2019, 7, 7371–7377 RSC.
- P. U. Bastian, S. Nacak, V. Roddatis and M. U. Kumke, J. Phys. Chem. C, 2020, 124, 11229–11238 CrossRef CAS.
- J. Zhao, Z. Lu, Y. Yin, C. McRae, J. A. Piper, J. M. Dawes, D. Jin and E. M. Goldys, Nanoscale, 2013, 5, 944–952 RSC.
- G. S. Yi and G. M. Chow, Adv. Funct. Mater., 2006, 16, 2324–2329 CrossRef CAS.
- F. Wang and X. G. Liu, J. Am. Chem. Soc., 2008, 130, 5642–5643 CrossRef CAS PubMed.
- S. Heer, K. Kömpe, H.-U. Güdel and M. Haase, Adv. Mater., 2004, 16, 2102–2105 CrossRef CAS.
- R. E. Thoma, H. Insley and G. M. Hebert, Inorg. Chem., 1966, 5, 1222–1229 CrossRef CAS.
- H.-X. Mai, Y.-W. Zhang, R. Si, Z.-G. Yan, L.-D. Sun, L.-P. You and C.-H. Yan, J. Am. Chem. Soc., 2006, 128, 6426–6436 CrossRef CAS PubMed.
- Z. L. Wang, J. Phys. Chem. B, 2000, 104, 1153–1175 CrossRef CAS.
- F. Wang, J. Wang and X. Liu, Angew. Chem., Int. Ed., 2010, 49, 7456–7460 CrossRef CAS PubMed.
- N. J. J. Johnson, S. He, S. Diao, E. M. Chan, H. Dai and A. Almutairi, J. Am. Chem. Soc., 2017, 139, 3275–3282 CrossRef CAS PubMed.
- B. Henderson and G. F. Imbusch, Optical spectroscpy of inorganic solids, Oxford University Press, Oxford, 1989 Search PubMed.
- M. Pollnau, D. R. Gamelin, S. R. Lüthi and H. U. Güdel, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3337–3346 CrossRef CAS.
- D. L. MacAdam, J. Opt. Soc. Am., 1942, 32, 247–274 CrossRef.
- H.-Q. Wang, R. D. Tilley and T. Nann, CrystEngComm, 2010, 12, 1993–1996 RSC.
- S. Fischer, N. D. Bronstein, J. K. Swabeck, E. M. Chan and A. P. Alivisatos, Nano Lett., 2016, 16, 7241–7247 CrossRef CAS PubMed.
- E. Hemmer, N. Venkatachalam, H. Hyodo, A. Hattori, Y. Ebina, H. Kishimoto and K. Soga, Nanoscale, 2013, 5, 11339–11361 RSC.
- A. Khorsand Zak, W. H. A. Majid, M. E. Abrishami and R. Yousefi, Solid State Sci., 2011, 13, 251–256 CrossRef CAS.
- E. Cantelar, J. A. Sanz-García, A. Sanz-Martín, J. E. Muñoz Santiuste and F. Cussó, J. Alloys Compd., 2020, 813, 152194 CrossRef CAS.
- J. I. Langford and A. J. C. Wilson, J. Appl. Crystallogr., 1978, 11, 102–113 CrossRef CAS.
- S. Lele and T. R. Anantharaman, Proc. Indian Acad. Sci. – Sect. A, 1966, 64, 261–271 CrossRef CAS.
- J. J. H. A. van Hest, G. A. Blab, H. C. Gerritsen, C. de Mello Donega and A. Meijerink, J. Phys. Chem. C, 2017, 121, 19373–19382 CrossRef CAS PubMed.
- A. Aebischer, M. Hostettler, J. Hauser, K. W. Krämer, T. Weber, H. U. Güdel and H.-B. Bürgi, Angew. Chem., Int. Ed., 2006, 45, 2802–2806 CrossRef CAS PubMed.
- D. Tu, Y. Liu, H. Zhu, R. Li, L. Liu and X. Chen, Angew. Chem., 2013, 125, 1166–1171 CrossRef.
- D. T. Tu, W. Zheng and X. Y. Chen, Angew. Chem., Int. Ed., 2015, 54, 1077–1078 CrossRef CAS PubMed.
- M. Karbowiak, J. Cichos and C. Rudowicz, Angew. Chem., Int. Ed., 2015, 54, 1074–1076 CrossRef CAS PubMed.
- P. Boutinaud, R. Mahiou, N. Martin and M. Malinowski, J. Lumin., 1997, 72–74, 809–811 CrossRef CAS.
- L. Sun, R. Gao, T. Pan, X.-C. Ai, L. Fu and J.-P. Zhang, Nanoscale, 2019, 11, 18150–18158 RSC.
- M. Wang, Y. Tian, F. Zhao, R. Li, W. You, Z. Fang, X. Chen, W. Huang and Q. Ju, J. Mater. Chem. C, 2017, 5, 1537–1543 RSC.
- J. W. Stouwdam and F. C. J. M. van Veggel, Langmuir, 2004, 20, 11763–11771 CrossRef CAS PubMed.
- M. N. Berberan-Santos, E. N. Bodunov and B. Valeur, Chem. Phys., 2005, 315, 171–182 CrossRef CAS.
- F. Priolo, G. Franzò, D. Pacifici, V. Vinciguerra, F. Iacona and A. Irrera, J. Appl. Phys., 2001, 89, 264–272 CrossRef CAS.
- S. Kim, B.-K. Yoo, Y. Choi, B.-S. Kim and O.-H. Kwon, Phys. Chem. Chem. Phys., 2018, 20, 11673–11681 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Including methods, further characterization details and more detailed discussions. See DOI: 10.1039/d1nr06319g |
| This journal is © The Royal Society of Chemistry 2022 |