Open Access Article
Open Access ArticleGraphical tools for the planning and interpretation of polyurethane foam based passive air sampling campaigns†
Yuening
Li
 ,
James M.
Armitage
and
Frank
Wania
,
James M.
Armitage
and
Frank
Wania
 *
*
Department of Physical and Environmental Sciences, University of Toronto Scarborough, 1265 Military Trail, Toronto, Ontario M1C 1A4, Canada. E-mail: frank.wania@utoronto.ca; Tel: +1-416-287-7225
First published on 15th February 2022
Abstract
Due to low cost and easy handling during sampling and extraction, passive air samplers (PASs) using polyurethane foam (PUF) as a sorbent have become the most commonly deployed PASs for semi-volatile organic compounds (SVOCs). However, depending on the scenario, PUF-PAS may not always be operating in the linear uptake phase, which implies the need to consider how temperature, wind speed, deployment length and chemical properties interact to determine the amount of a target chemical taken up and the fraction of a depuration compound (DC) being lost during deployment. Guidance is, therefore, necessary to quantitatively interpret curvi-linear uptake in the PUF-PAS and avoid selection of DCs unsuited to the deployment conditions. In this study, the PAS-SIM model is used to generate graphical tools that aid in addressing important questions frequently arising during the use of PUF-PASs. Specifically, we generated five charts that display (i) the inherent sampling rate as a function of wind speed and a chemical's molecular diffusivity, (ii) the length of the linear uptake period as a function of chemical properties, temperature and the acceptable deviation from linearity, (iii) the time to 95% equilibrium as influenced by chemical properties, temperature and wind speed, (iv) the dependence of the fractional loss of DCs on chemical properties, temperature, wind speed and deployment length, and (v) the influence of chemical properties, temperature and the total suspended particle concentration on the extent of sorption to atmospheric particles. The charts also facilitate the assessment of the influence of parameter uncertainty. It is hoped that these charts assist with planning and interpreting sampling campaigns based on a mechanistic and quantitative understanding of uptake in PUF-based PASs.
Environmental significanceEven though polyurethane foam based passive air samplers (PUF-PAS) are widely used for sampling semi-volatile organic chemicals, interpretation of the results is not always based on a comprehensive understanding of how these samplers work. While a number of numerical simulation models of the uptake in the PUF-PAS exist and could provide valuable guidance, they have not been widely adopted. In order to lower the thresholds for their adoption, this study makes simulation results of one such model accessible without the need to actually run it. This is accomplished through the construction of graphs, that allow variables such as the length of the linear uptake period, the time to equilibrium, and the fractional loss of depuration compounds to be obtained from the length, temperature, and wind speed of deployment and the chemical partitioning properties. |
1. Introduction
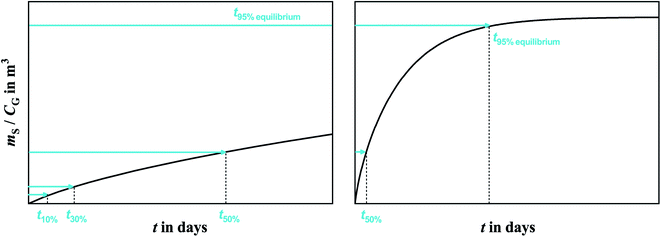
Polyurethane foam (PUF) is made by the reaction of di-isocyanates and polyols, and depending on the production method yields PUF-ether or PUF-ester. Due to the reasonably high and consistent sorptive capacity PUF-ether is a widely used sorbent in the sampling of semi-volatile organic compounds (SVOCs) from the atmosphere.1–6 Because of wide availability, easy handling and low cost of PUF compared to other sorbents, passive air samplers based on PUF (PUF-PASs) are commonly utilized for collecting SVOCs around the world.7–11The PUF-PAS was originally designed to be a linear uptake sampler, which implies that evaporation of target chemicals from the PUF is assumed to be negligible. If that assumption is valid, a volumetric air concentration averaged over the time of deployment in units of ng m−3 is obtained by simply dividing the amount of chemical sorbed to the PUF (mS in ng, possibly corrected for the amount in field blanks) by the product of the deployment period Δt in days and an inherent sampling rate SRinh in m3 day−1. This inherent sampling rate varies between chemicals, because their molecular diffusivity is somewhat dependent on molecular size. However, in many sampling scenarios, it is not valid to assume that the evaporation of chemical from the PUF is negligible. In that case, the sampler is said to leave the linear uptake period and enter the curvi-linear section of the generic uptake curve displayed in Fig. 1. When this transition occurs is chemical-specific, with more volatile chemicals having much shorter linear uptake periods than less volatile ones.
The real sampling rate of a chemical in the curvi-linear uptake period is lower than the inherent one. Because uptake curves in the curvi-linear uptake period can still appear to be linear (Fig. 1), these sampling rate are also referred to as “apparent” sampling rates SRapp. An alternative nomenclature refers to an effective sampling volume Veff, which is equivalent to the product of SRapp and deployment time. The volumetric air concentration during the deployment CG can then be calculated by the simple equation:
| CG = mS/(SRappΔt) = mS/Veff | (1) |
But not only is eqn (1) no longer valid if CG is variable during the sampling period,12 SRapp or Veff are also difficult to establish with high confidence. Li and Wania13 have shown that the uncertainty in the equilibrium partition ratio between PUF and the gas phase (KPUF/G) alone causes uncertainty in estimated Veff or SRapp of at least ∼50% and the uncertainty will be even higher when accounting for the influence of ambient conditions during the sampling, especially temperature and wind speed.14 While it is therefore often desirable to avoid sampling outside of the linear uptake range, use of the PUF-PAS in the curvi-linear regime is generally the rule rather than the exception. Sampling in the linear uptake range is more easily achieved by using a high uptake capacity sorbent such as styrene-divinylbenzene co-polymeric resin (commercial name XAD).
SRapp or Veff are functions of the sampled chemical, namely its molecular diffusivity and KPUF/G, the deployment conditions, most notably wind speed and temperature, and the deployment length. Theoretical methods for estimating SRapp or Veff have been presented.15 Alternatively, they can also be estimated from the measured fraction of a depuration compound (DC) lost from the PUF during the deployment of a PAS.16,17 Isotopically labelled SVOCs and chemicals that are not present in the sampled environment are often used as DCs to distinguish them from the SVOCs in the field. Importantly, using DCs does not prevent the uncertainty in KPUF/G from being carried forward to the uncertainty in SRapp or Veff, because KPUF/G of the DCs at the temperature of deployment need to be known.13
Alternatively, one could also envisage to use the PUF-PAS as an equilibrium sampler for volatile substances. If a chemical reaches equilibrium between PUF and atmospheric gas phase, the air concentration (in ng m−3) can be obtained by dividing the concentration of the chemical in the PUF (in ng m−3) by the KPUF/G (m3 air m−3 PUF) (Fig. 1).
When planning to use a PUF-PAS or after having used one, a number of questions often arise, such as:
• For how long can I deploy a PUF-PAS under specific meteorological conditions for my target compound(s) to remain in the linear uptake phase?
• Having deployed a sampler for a period of time under a set of conditions, can I use the SRinh for my target compound(s) or do I need to estimate an SRapp or Veff?
• How long would a deployment under a set of conditions need to be if I wanted my target compound(s) to reach equilibrium with the PUF?
• What deployment length can provide the best balance between the ability to detect a compound and being able to interpret the sequestered amount quantitatively?
• What DC(s) should I spike onto my PUF to make sure the fraction lost during a deployment of a particular length and under a set of conditions is suitable for deriving a SRapp reliably?
• Will the target chemical be sampled from the atmospheric gas phase or do I have to consider the possibility that some of it is being sampled with particles and therefore experiences different uptake kinetics?
As indicated above, several methods for estimating SRapp or Veff have been presented and could serve to answer such questions. Zhang and Wania18 developed a model to illustrate how the mass transfer processes in general and the sampling rate in particular is affected by various parameters, but it is not a model suitable for routine applications. Harner15 published a Microsoft Excel template to calculate the Veff based on the physicochemical parameters of target compounds, the deployment length and ambient conditions such as temperature and particle concentration. However, the template uses fixed constants, e.g., SRinh and particle concentration, and is only suitable for specific SVOCs. To solve this problem, Herkert et al.19 developed a MATLAB-based model to predict the Veff accounting for the influence of external wind speed and temperature. However, the user interface is not straightforward for new users. In addition, the model ignores any resistance to mass transfer within the PUF, the potential for degradation of chemicals sorbed to the sampler and the influence of aerosol.
The PAS-SIM model by Armitage et al.20 is a user-friendly Microsoft Excel-based model developed to quantitively simulate the transport of chemicals from the atmospheric gas phase to the sorbent of a PUF- or XAD-based PAS. PAS-SIM considers the potential existence of a sampler-side resistance to uptake and provides daily outputs for the amount sorbed to the PUF or XAD and the SRapp. In addition, the influence of different parameters is embedded in PAS-SIM, such as chemical properties, temperature, wind speed, deployment length, and atmospheric particle concentration. The performance of PAS-SIM model for XAD-PAS was evaluated using data for polychlorinated biphenyls, polycyclic aromatic hydrocarbons, and pesticides.20,21 Overall, these studies show that PAS-SIM model is capable of accounting for the influence of temperature and wind speed on passive sampling rates and modeled PAS uptake curves show a good agreement with the empirical data (generally within a factor of two).20,21
Even though these models have been developed, none of them are widely used. PUF-PAS derived data continue to be interpreted with generic sampling rates without consideration of the specific uptake conditions applicable to a particular set of compounds and deployments.22,23 Multiple DCs are often used without consideration of the specific deployment conditions, even though they are expensive and often do not yield the desired information.20 Possible reasons for this situation are a general reluctance to adopt numerical models and a lack of visualization of model outputs. The main objective of this study therefore is to use the PAS-SIM model, supplemented with theoretical calculations, to generate charts to provide graphical guidance on how to use PUF-PASs and to interpret data obtained from PUF-PASs. These charts allow anyone to benefit from the information provided by PAS-SIM without the need to actually run it. It is hoped that these charts facilitate the planning and interpretation of sampling campaigns based on a mechanistic and quantitative understanding of how the PUF-PAS functions.
2. Method
2.1 Characteristics of the PUF-based passive air sampler
In this study, the height (h), radius (r) and porosity (θ) of the PUF in the PUF-PAS are 0.0135 m, 0.07 m and 0.97, respectively. The total surface area of the PUF As of 0.037 m2 is calculated using:| As = 2 × π × r × (r + h) | (2) |
The total volume of the PUF Vs of 0.0002 m3 is obtained using:
| Vs = π × r2 × h | (3) |
In this study, the sampler is divided into 50 layers (n = 50) to calculate the mass transfer coefficient in the sampler.
2.2 Inherent sampling rate
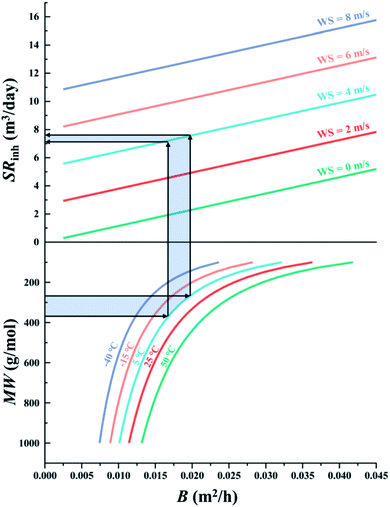
The first chart displays the inherent sampling rate for the PUF-PAS (SRinh in m3 day−1) as a function of a chemical's molecular diffusivity in the gas phase (B in m2 h−1) and external wind speed (WS in m s−1). Following the approach taken in PAS-SIM, SRinh was calculated using:| SRinh = kSAAS + 1.32 × WS | (4) |
According to two-film theory and assuming diffusion through the PUF material to make a negligible contribution to mass transfer,21kSA can be estimated as:
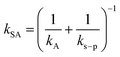 | (5) |
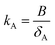 | (6) |
Here, δA under wind-still conditions is assumed to be 0.0075 m.21ks–pcan be obtained using:
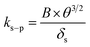 | (7) |
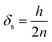 | (8) |
If the height of PUF is larger than the radius, PAS-SIM calculates the layer thickness as the ratio of radius and the number of layers. In this study, the height is less than the radius; thus, eqn (8) was used to calculate the diffusion path length on the sampler side.
B is a chemical-specific parameter that is influenced by ambient temperature. In PAS-SIM, B is estimated using the semi-empirical Fuller–Schettler–Giddings equation (eqn (9)):26
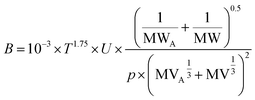 | (9) |
| U = 60 × 60/10000 | (10) |
When generating the data displayed in the chart, the molecular weight of SVOCs was set to range between 100 to 1000 g mol−1, and T from −40 to 50 °C. Atmospheric pressure was set to 1 atm.
2.3 Length of the linear uptake period
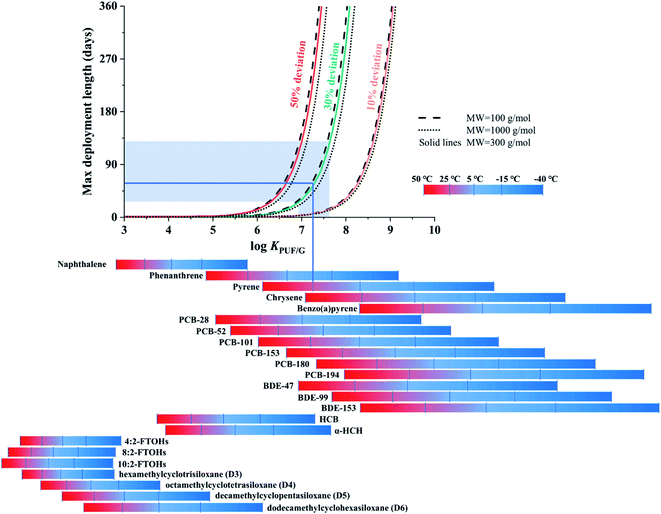
The second chart displays the length of the linear uptake period as a function of chemical properties, temperature, deployment length and the deviation from linearity a user is willing to accept. The data displayed in this chart were directly generated with PAS-SIM using molecular weights (MW) of 100, 300 or 1000 g mol−1 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (KPUF/G/m3 m−3) values ranging from 3 to 10. No aerosol is assumed to be present, wind speed is constant at 5 m s−1, and no degradation of target compound is assumed to occur during sampling.
(KPUF/G/m3 m−3) values ranging from 3 to 10. No aerosol is assumed to be present, wind speed is constant at 5 m s−1, and no degradation of target compound is assumed to occur during sampling.
Specifically, the percentage of the deviation from linearity was calculated using:
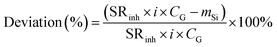 | (11) |
2.4 Time to equilibrium
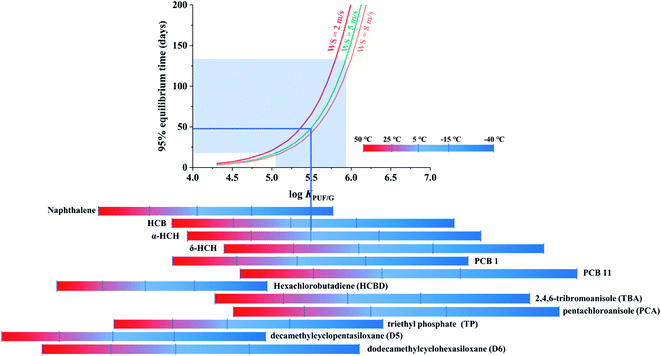
The third chart displaying the time to 95% equilibrium as influenced by chemical properties, temperature and wind speed was again based on data generated with PAS-SIM. A common molecular weight of 300 g mol−1, a range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G between 4 to 7 and three different wind speeds (2, 5 and 8 m s−1) were used. The time to 95% equilibrium is determined as the first day when mSi, as calculated by PAS-SIM for different log
KPUF/G between 4 to 7 and three different wind speeds (2, 5 and 8 m s−1) were used. The time to 95% equilibrium is determined as the first day when mSi, as calculated by PAS-SIM for different log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G, exceeds 0.95 times the mass at equilibrium.
KPUF/G, exceeds 0.95 times the mass at equilibrium.
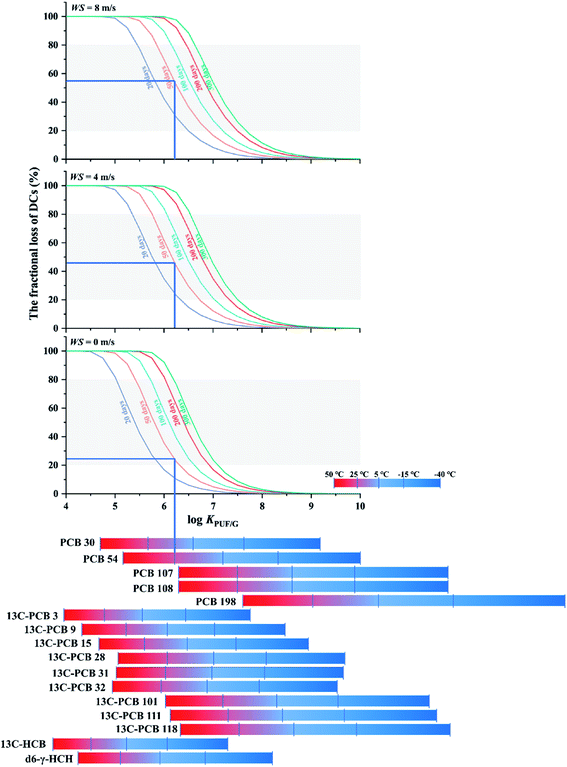
2.5 Fractional loss of depuration compounds
The fourth chart, displaying the fractional loss of a DC in its dependence on chemical properties, temperature, wind speed and deployment length, is based on data generated with a version of PAS-SIM (PUF-Depurator) specially developed for simulating the loss of DCs. A common molecular weight of 300 g mol−1, a range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G between 4 to 10, three different wind speeds (0, 4 and 8 m s−1) and deployment lengths between 20 and 300 days were used. The percent loss of a depuration compound (R) is estimated as:
KPUF/G between 4 to 10, three different wind speeds (0, 4 and 8 m s−1) and deployment lengths between 20 and 300 days were used. The percent loss of a depuration compound (R) is estimated as: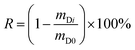 | (12) |
2.6 Particle sorption
The fifth chart displays the influence of the chemical's equilibrium partitioning ratio between particles and the gas phase (KQ/G) and the total suspended particle (TSP) concentration (CTSP in g particles m−3 air) on the extent of sorption of a compound to atmospheric particles, expressed as the percentage of a compound in the gas phase φG: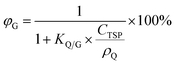 | (13) |
2.7 Estimating KPUF/G and KQ/G
In most of the charts in this study, a parameter is plotted against the logarithm of an equilibrium partitioning ratio (KPUF/G and KQ/G). To apply these charts to a specific chemical therefore requires knowledge of the partitioning ratio, either through measurement or by estimation. Because KPUF/G and KQ/G are functions of temperature, the partitioning ratio at the temperature of the sampler's deployment is required. To facilitate the placement of a number of commonly sampled SVOCs on the x-axes, we provide estimates of KPUF/G and KQ/G at different temperatures at the bottom of each of these plots. The KPUF/G was estimated using the following poly-parameter linear free energy relationship (ppLFER):6log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G15°C = 1.63S + 3.39A + 0.71L + 0.27V − 0.02 + log KPUF/G15°C = 1.63S + 3.39A + 0.71L + 0.27V − 0.02 + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρPUF ρPUF | (14) |
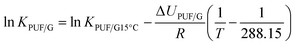 | (15) |
| ΔUPUF/G (J mol−1) = (−17.6S − 46.6A − 12.8V − 4.3L + 2.7) × 1000 + RT | (16) |
The KQ/G, required for the fifth charts, was similarly obtained with ppLFERs.28 Details are provided in the ESI.†
The solute descriptors for commonly targetted SVOCs and 16 commonly used DCs17,19,31–34 were taken from the UFZ LSER database,35 and are listed in Tables S1 and S2,† respectively. The calculation results and other data used in the making of the charts are compiled in Tables S3–S5.†
3. Results
Fig. 2 illustrates the inherent sampling rate's dependence on wind speed and a chemical's molecular diffusivity. The bottom panel in Fig. 2 shows the relationship between molecular weight MW and molecular diffusivity B. B is size-dependent, with small chemicals having a higher B compared to large chemicals. B is also a much stronger function of MW for smaller than for larger compounds, i.e. the rate at which B changes decreases as MW increases. The five lines in the bottom panel demonstrate that B increases with temperature, but this temperature dependence is not very dependent on MW as the five lines are generally equidistant. The top panel in Fig. 2 shows that SRinh increases linearly with both B and wind speed WS.We can use Fig. 2 to estimate the SRinh range we might expect for typical SVOCs under commonly encountered meteorological conditions (e.g., 5 °C and 4 m s−1). The light blue shaded area in Fig. 2 yields a SRinh around 7 and 7.8 m3 day−1 for commonly sampled SVOCs ranging in MW from 285 to 360 g mol−1 (e.g. HCB to PCB-153). We can expect this SRinh to vary only a little between chemicals and with temperature: the range of MW from 100 to 1000 g mol−1, which comprises all SVOCs conceivably being sampled with the PUF-PAS, translates into a change in SRinh of only ∼30% at −40 °C (e.g. from 6.1 to 8 m3 day−1 when WS is 4 m s−1) or ∼50% at 50 °C. Similarly, the temperature range of −40 to 50 °C, comprising all conceivable deployments, only results in a change in SRinh of 23% and 11% for chemicals with a MW of 100 and 1000 g mol−1, respectively. Clearly, wind speed is the dominant factor controlling SRinh.
Fig. 3 displays the length of the linear uptake period as a function of a chemical's KPUF/G. The relationship between this length and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G is not linear: as log
KPUF/G is not linear: as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G increases, the linear uptake period increases first very slowly, but eventually very rapidly. When this transition to a rapid increase occurs depends strongly on the acceptable deviation from linearity (comparing differently coloured lines in Fig. 3). For example, during a PUF-PAS deployment of one month, chemicals with a log
KPUF/G increases, the linear uptake period increases first very slowly, but eventually very rapidly. When this transition to a rapid increase occurs depends strongly on the acceptable deviation from linearity (comparing differently coloured lines in Fig. 3). For example, during a PUF-PAS deployment of one month, chemicals with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G above 6.5, 7.2 or 8.2 can be assumed to experience linear uptake, if deviations of 10, 30, or 50% are tolerated. During a seasonal deployment (90 days), these thresholds shift to slightly higher values above 6.8, 7.5 and 8.5. Because many of the SVOCs sampled with the PUF-PAS have a log
KPUF/G above 6.5, 7.2 or 8.2 can be assumed to experience linear uptake, if deviations of 10, 30, or 50% are tolerated. During a seasonal deployment (90 days), these thresholds shift to slightly higher values above 6.8, 7.5 and 8.5. Because many of the SVOCs sampled with the PUF-PAS have a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G in the range between 6.5 and 8.5 at temperatures typical of ambient deployment, the length of the linear uptake period is very strongly dependent on the applied linearity criterion. In fact, applying the strictest criterion (10%) very few SVOCs would remain in the linear uptake phase during typical deployment lengths. Different line styles in Fig. 3 indicate that the influence of the chemical's molecular weight on the length of the linear uptake period is minor.
KPUF/G in the range between 6.5 and 8.5 at temperatures typical of ambient deployment, the length of the linear uptake period is very strongly dependent on the applied linearity criterion. In fact, applying the strictest criterion (10%) very few SVOCs would remain in the linear uptake phase during typical deployment lengths. Different line styles in Fig. 3 indicate that the influence of the chemical's molecular weight on the length of the linear uptake period is minor.
The KPUF/G of selected chemicals is displayed in the bottom of Fig. 3–5 over the temperature range from −40 to 50 °C, with bars shaded in a color gradient from blue to red indicating different temperatures. The SVOCs cover a very wide range in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G over this very large, but environmentally relevant, temperature range (see also Table S3† in the ESI). The KPUF/G for the same chemical can vary over many orders of magnitude within this temperature range. Fig. 3 conveys that the PUF-PAS cannot be used as a linear uptake sampler for more volatile SVOCs with a log
KPUF/G over this very large, but environmentally relevant, temperature range (see also Table S3† in the ESI). The KPUF/G for the same chemical can vary over many orders of magnitude within this temperature range. Fig. 3 conveys that the PUF-PAS cannot be used as a linear uptake sampler for more volatile SVOCs with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G below ∼6, such as the fluorotelomer alcohols (FTOHs), the cyclic volatile methylsiloxanes (cVMS), or smaller polycyclic aromatic hydrocarbons (PAHs) such as naphthalene. Even with a high tolerance for non-linearity and at low temperatures, the linear uptake periods for such compounds are shorter than a few days. At warm temperatures, this is also the case for the less chlorinated PCBs and three-ring PAHs. On the other hand, the PUF-PAS can generally be assumed to function as a linear uptake sampler for compounds with a log
KPUF/G below ∼6, such as the fluorotelomer alcohols (FTOHs), the cyclic volatile methylsiloxanes (cVMS), or smaller polycyclic aromatic hydrocarbons (PAHs) such as naphthalene. Even with a high tolerance for non-linearity and at low temperatures, the linear uptake periods for such compounds are shorter than a few days. At warm temperatures, this is also the case for the less chlorinated PCBs and three-ring PAHs. On the other hand, the PUF-PAS can generally be assumed to function as a linear uptake sampler for compounds with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G above 8.5, as long as deployment periods do not exceed a few months. However, such SVOCs will often partition to atmospheric particles (see Fig. 6 below) and the sampling rate for particle-bound substances is uncertain and likely dependent on the size of the particles.
KPUF/G above 8.5, as long as deployment periods do not exceed a few months. However, such SVOCs will often partition to atmospheric particles (see Fig. 6 below) and the sampling rate for particle-bound substances is uncertain and likely dependent on the size of the particles.
The chart in Fig. 3 can be used to estimate the maximum deployment length of a PUF-PAS if the goal is to sample a specific chemical within the linear uptake phase under a specific set of deployment conditions. For example, if pyrene (MW is 202.25 g mol−1 (ref. 36)) is to be sampled in summer (25 °C) we can read from the respective bar below the diagram that its log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G is ∼7.25. Moving from this value on the x-axis up vertically until the line intersects with the 30% deviation curve, we can move left to obtain a maximum deployment length of ∼60 days on the y-axis. Much shorter and longer values would be obtained with a different tolerance for deviation from linearity. We can further explore graphically, how the uncertainty in KPUF/G propagates to the uncertainty in the length of linear uptake period. The uncertainty in log
KPUF/G is ∼7.25. Moving from this value on the x-axis up vertically until the line intersects with the 30% deviation curve, we can move left to obtain a maximum deployment length of ∼60 days on the y-axis. Much shorter and longer values would be obtained with a different tolerance for deviation from linearity. We can further explore graphically, how the uncertainty in KPUF/G propagates to the uncertainty in the length of linear uptake period. The uncertainty in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G of pyrene at 25 °C is approximately ±0.36,13 which is represented by the area shaded in light blue in Fig. 3. The maximum deployment lengths of 60 days thus has an uncertainty range from ∼30 to ∼130 days.
KPUF/G of pyrene at 25 °C is approximately ±0.36,13 which is represented by the area shaded in light blue in Fig. 3. The maximum deployment lengths of 60 days thus has an uncertainty range from ∼30 to ∼130 days.
Fig. 4 displays the time to 95% equilibrium as a function of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G, with three differently coloured lines indicating different wind speed conditions. Again the increase in t95%equilibrium is not linear with increasing log
KPUF/G, with three differently coloured lines indicating different wind speed conditions. Again the increase in t95%equilibrium is not linear with increasing log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G, but slow for more volatile SVOCs and faster for less volatile ones. While a higher WS shortens t95%equilibrium, the change in t95%equilibrium is not proportional to the change in WS, because the three curves are not equidistant. For example, as WS increases from 5 to 8 m s−1, t95%equilibrium increases less than if it increases from 2 to 5 m s−1.
KPUF/G, but slow for more volatile SVOCs and faster for less volatile ones. While a higher WS shortens t95%equilibrium, the change in t95%equilibrium is not proportional to the change in WS, because the three curves are not equidistant. For example, as WS increases from 5 to 8 m s−1, t95%equilibrium increases less than if it increases from 2 to 5 m s−1.
The transition from a t95%equilibrium of a few days to half a year occurs over a fairly small range in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G fom 4.5 to 6. The log
KPUF/G fom 4.5 to 6. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G of the most volatile SVOCs, such as 4:2-FTOHs or D3, are not included in Fig. 4, as they will reach 95% equilibrium very quickly within a few days, even at the coldest temperature (−40 °C). The plot does not displays the less volatile SVOCs either, such as chrysene, benzo(a)pyrene, and some highly halogenated PCBs and PBDEs, which have log
KPUF/G of the most volatile SVOCs, such as 4:2-FTOHs or D3, are not included in Fig. 4, as they will reach 95% equilibrium very quickly within a few days, even at the coldest temperature (−40 °C). The plot does not displays the less volatile SVOCs either, such as chrysene, benzo(a)pyrene, and some highly halogenated PCBs and PBDEs, which have log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G above 6.5, even at 50 °C, and thus always have t95%equilibrium in excess of 200 days. For the SVOCs that are displayed, it is readily apparent that the time to equilibrium is very strongly dependent on the deployment temperature. The chart suggests that the PUF-PAS could function as an equilibrium sampler for compounds such as naphthalene, hexachlorobutadiene (HCBD), triethyl phosphate (TP) and decamethylcyclopentasiloxane (D5), with t95%equilibrium in the range of typically used PUF-PAS deployment periods.
KPUF/G above 6.5, even at 50 °C, and thus always have t95%equilibrium in excess of 200 days. For the SVOCs that are displayed, it is readily apparent that the time to equilibrium is very strongly dependent on the deployment temperature. The chart suggests that the PUF-PAS could function as an equilibrium sampler for compounds such as naphthalene, hexachlorobutadiene (HCBD), triethyl phosphate (TP) and decamethylcyclopentasiloxane (D5), with t95%equilibrium in the range of typically used PUF-PAS deployment periods.
This chart can be used to estimate the time a specific chemical requires to approach equilibrium with the PUF of a PAS during a particular set of deployment conditions: find the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G value of the target substance at the temperature of the planned deployment on the x-axis, move up vertically to the intersection with the curve representing the WS of the planned deployment, and then read the t95%equilibrium from the y-axis. For instance, α-HCH sampled at 5 °C and an average WS of 5 m s−1 will reach 95% equilibrium within ∼50 days (blue lines in Fig. 4), whereas that time is only ∼10 days if the temperature is 25 °C. The uncertainty of KPUF/G of α-HCH at 5 °C is ±0.44,13 leading to a range in t95%equilibrium from ∼20 to ∼130 days (shaded area in Fig. 4).13
KPUF/G value of the target substance at the temperature of the planned deployment on the x-axis, move up vertically to the intersection with the curve representing the WS of the planned deployment, and then read the t95%equilibrium from the y-axis. For instance, α-HCH sampled at 5 °C and an average WS of 5 m s−1 will reach 95% equilibrium within ∼50 days (blue lines in Fig. 4), whereas that time is only ∼10 days if the temperature is 25 °C. The uncertainty of KPUF/G of α-HCH at 5 °C is ±0.44,13 leading to a range in t95%equilibrium from ∼20 to ∼130 days (shaded area in Fig. 4).13
More reliable SRapps can be obtained if the percentage loss of a DC is approximately between 20% and 80%.37 Because chemical properties, meterological conditions and deployment length jointly influence the extent of loss of DCs, choosing a DC that is lost to the appropriate extent is not trivial. Fig. 5 displays the dependence of the fractional loss of a DC on log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G, wind speed and deployment length. The three panels in the figure represent different assumed average wind speeds (0, 4, and 8 m s−1) and differently coloured lines in each panel are used to distinguish different deployment lengths. The grey shading represents loss between 20% to 80%. Bars at the bottom of the chart indicating the log
KPUF/G, wind speed and deployment length. The three panels in the figure represent different assumed average wind speeds (0, 4, and 8 m s−1) and differently coloured lines in each panel are used to distinguish different deployment lengths. The grey shading represents loss between 20% to 80%. Bars at the bottom of the chart indicating the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G at different temperatures of a number of SVOCs commonly used as DCs allow for the selection of the appropriate value along the x-axis.
KPUF/G at different temperatures of a number of SVOCs commonly used as DCs allow for the selection of the appropriate value along the x-axis.
The loss of a DC decreases with an increase in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G, the function resembling a sigmoidal curve, i.e. the loss is a particularly strong function of log
KPUF/G, the function resembling a sigmoidal curve, i.e. the loss is a particularly strong function of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G in a transitional log
KPUF/G in a transitional log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G range. Below that range, almost all of the DC is lost in a short period of time. Above that range, almost no loss occurs, even after longer deployments. Fig. 5 can aid in the identification of the DCs that have a log
KPUF/G range. Below that range, almost all of the DC is lost in a short period of time. Above that range, almost no loss occurs, even after longer deployments. Fig. 5 can aid in the identification of the DCs that have a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G in the desirable steep transition area under a given set of conditions. This is done as follows: estimate the wind speed during deployment (choose one of the three panels) and decide on a desired deployment length (choose one of the lines in that panel). This indicates the log
KPUF/G in the desirable steep transition area under a given set of conditions. This is done as follows: estimate the wind speed during deployment (choose one of the three panels) and decide on a desired deployment length (choose one of the lines in that panel). This indicates the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G range that will result in a loss between 20 and 80%. Finally choose a DC that has a log
KPUF/G range that will result in a loss between 20 and 80%. Finally choose a DC that has a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G in that range at the temperature of the planned deployment. The bottom part of Fig. 5 indicates that three groups of PCBs, namely congeners 101, 111 and 118, congeners 28, 31 and 32, and congeners 107 and 108 have very similar KPUF/G. It would not be necessary to pick more than one DC from each of these groups, as their fractional loss would be expected to be similar.
KPUF/G in that range at the temperature of the planned deployment. The bottom part of Fig. 5 indicates that three groups of PCBs, namely congeners 101, 111 and 118, congeners 28, 31 and 32, and congeners 107 and 108 have very similar KPUF/G. It would not be necessary to pick more than one DC from each of these groups, as their fractional loss would be expected to be similar.
Fig. 5 can also be used to estimate the expected fractional loss of a particular DC under a specific set of deployment conditions. For example, the blue lines indicate that half of the PCB-54 added to a PUF-PAS can be expected to be lost after a deployment of 50 days at 25 °C and a wind speed around 4 to 8 m s−1. Under windstill conditions, only about a quarter would be lost.
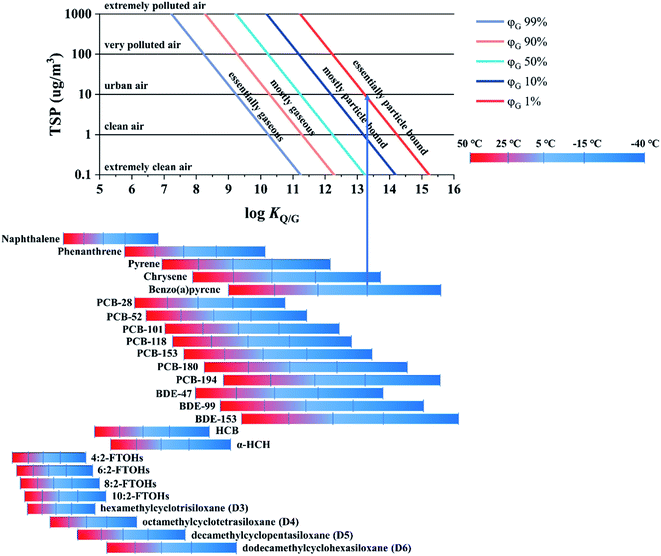
There is clear evidence that the PUF-PAS collects SVOCs in both the gas and particle phase.38–40 However, there is no consensus on whether the SR of particle-bound substances is similar to that of gaseous compounds. For example, Harner et al.39 reported that both gas- and particle-phase polycyclic aromatic hydrocarbons (PAHs) were sampled with a similar SR, whereas Klánová et al. found that the SR of particle-bound PAHs was 10 times lower than that of gaseous compounds.38 The inconsistency of the findings is likely because the uptake of particle-bound substances may be influenced by the atmospheric particles (concentration, composition, size distribution), the meteorological conditions (wind speed and its variability, angle of incidence), and the density of the PUF.25,40,41 Even though the chamber design was the same in these two studies38,39 the design of the PAS housing can also be a factor.42 The PAS-SIM model describes the uptake of gas phase compounds only and does not attempt to simulate the uptake of particle-bound substances. Modelling the particle uptake processes within the PUF-PAS would be extremely complex and require deployment-specific input information, such as data on the local wind conditions, the particles in the sampled atmosphere and the particle size distribution of the target compounds, that is typically not available.
The only purpose a model such as PAS-SIM can serve in this regard is therefore to estimate what fraction of the total atmospheric load of a target compound can be expected to be in the gas and particle phases under a specific set of deployment conditions. This information is provided in Fig. 6, which shows the extent of sorption to particles, expressed as the percentage of a compound in the gas phase, φG, as a function of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KQ/G and the total suspended particle (TSP) concentration. The charts in Fig. 2–5 can then be assumed to apply to the fraction in the gas phase. A user may also decide to refrain from a quantitative interpretation of data obtained for substances that are estimated to be mostly particle bound during a particular deployment.
KQ/G and the total suspended particle (TSP) concentration. The charts in Fig. 2–5 can then be assumed to apply to the fraction in the gas phase. A user may also decide to refrain from a quantitative interpretation of data obtained for substances that are estimated to be mostly particle bound during a particular deployment.
In the top panel of Fig. 6, five air pollution levels are defined based on the TSP concentration. Increasing either the TSP concentration or the KQ/G value will increase the extent of sorption to atmospheric particles. At the bottom of the plot, the KQ/G of a number of commonly sampled SVOCs is displayed, again within the temperature range −40 to 50 °C (numerical values of KQ/G and ΔUQ/G are reported in Table S5† in the ESI). One way to use this chart is as follows: find the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KQ/G value of the target compound at the temperature of the planned deployment. Move up vertically from there until you intersect with the TSP concentration prevailing in the sampled atmosphere, then read the extent of sorption to particles from the coloured line (e.g., benzo(a)pyrene is essentially particle bound, φG < 1%, in urban air in winter −15 °C).
KQ/G value of the target compound at the temperature of the planned deployment. Move up vertically from there until you intersect with the TSP concentration prevailing in the sampled atmosphere, then read the extent of sorption to particles from the coloured line (e.g., benzo(a)pyrene is essentially particle bound, φG < 1%, in urban air in winter −15 °C).
4. Discussion
For PUF-PAS users, there are two primary ways to use these charts to guide sampling and data interpretation:Chemical centred: if a user has target compounds or a group of target compounds and a region of potential deployment (i.e., a specific range of temperature and wind speed), these charts can help to establish how the PUF-PAS can be applied to measure these compounds: as a linear or an equilibrium sampler? For what lengths of deployment? Is the use of a DC necessary, e.g. because it is inevitable that sampling occurs in the curvi-linear region?
Deployment centred: if a user has deployed, or plans to deploy, samplers for a certain length of time under a particular set of meteorological condition, these charts help to establish what chemicals can be expected to be interpretable using linear uptake assumptions, equilibrium assumptions, or require the use of DCs within the curvi-linear range. If there are some unexpected data, these charts may help to explain whether these data are reasonable or not and what causes this situation.
In the chemical centred approach, the process of using the charts starts with the colored bars representing different chemicals at the bottom of Fig. 3–6 and proceeds to the corresponding upper panel. In the deployment centred approach, one starts with the upper panel and goes down to the bars.
In an application resembling a model sensitivity analysis, the charts may facilitate the identification of the parameters that will have the largest influence on the uptake of a particular set of target compounds during a particular set of deployment conditions. Attention can then be paid to the study design by assuring values for these parameters are appropriately chosen and well characterised.
Here we used KPUF/G values predicted for a selected group of SVOCs with ppLFERs to generate the bars at the bottom of Fig. 3–5. If a user is interested in other compounds not currently displayed, it is of course possible to predict KPUF/G at the desired temperature using eqn (14)–(16). Solute descriptors required for the ppLFER predictions of eqn (14) and (16) can be obtained for thousands of compounds from the UFZ-LSER database,35 or – if no such data are available – can be predicted from molecular structure using the quantitative structure property relationships implemented in the UFZ-LSER website.35 ppLFER estimates are uncertain and sometimes diverge from available experimental KPUF/G data.13 It is of course possible to use the charts with KPUF/G obtained by other means, e.g. experimentally determined values or values predicted with other techniques. Attention needs to be paid to using a KPUF/G in the appropriate units.
While we have tried to vary influential parameters within the entire plausible range and to depict the most commonly encountered scenarios when constructing the charts, they are inevitably based on only a limited set of data combinations. In particular, all of the charts assume invariant air concentrations, temperatures and wind speeds. Obviously, the PAS-SIM model itself is not constrained in the same way and is capable of simulating a much wider array of possible deployment scenarios, including those that allow for changes in many parameters over time. It is hoped that using the charts displayed here provides a gateway that helps PUF-PAS users to become familiar with the capabilities of the PAS-SIM models and to overcome the barriers to using the actual software.
Comparing Fig. 3 and 6 highlights that the range of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPUF/G in which the PUF-PAS can function as a true linear uptake sampler, where sorbed amounts can be interpreted with the help of inherent sampling rates, is very narrow and only includes a small number of commonly sampled SVOCs under a limited set of temperature conditions. In other words, when applied to a group of compounds or a range of temperature, the PUF-PAS is almost inevitably operating in the curvi-linear uptake regime, with all of the additional complexity and uncertainty this entails.13 The same applies to PASs using other sorbents with limited uptake capacity, such as polyethylene. High capacity sorbents such as XAD resin can widen the range of both SVOCs and temperatures for which true linear uptake can be achieved. This can reduce errors propagating from uncertain sorption coefficients and the need for, and the expense of, DCs.12
KPUF/G in which the PUF-PAS can function as a true linear uptake sampler, where sorbed amounts can be interpreted with the help of inherent sampling rates, is very narrow and only includes a small number of commonly sampled SVOCs under a limited set of temperature conditions. In other words, when applied to a group of compounds or a range of temperature, the PUF-PAS is almost inevitably operating in the curvi-linear uptake regime, with all of the additional complexity and uncertainty this entails.13 The same applies to PASs using other sorbents with limited uptake capacity, such as polyethylene. High capacity sorbents such as XAD resin can widen the range of both SVOCs and temperatures for which true linear uptake can be achieved. This can reduce errors propagating from uncertain sorption coefficients and the need for, and the expense of, DCs.12
The charts presented here provide only very limited guidance on the uptake of particle-bound substances in the PUF-PAS. This sampler takes up particle-bound SVOCs, because the housing design allows for wind to impinge on the sorbent (the foam), i.e., the double bowl design is a poor wind shelter. Large variations in the sampling rate for particle-bound SVOCs when using such a housing design are inevitable.42 These uncertainties are tolerated by PUF-PAS users, because this housing design allows for relatively high sampling rates and maybe also because they are interested in sampling particle-bound substances. Rather than interpreting data for compounds that are particle-bound during a PUF-PAS's deployment without consideration of the uncertainties this entails, we recommend refraining from such quantitative interpretation altogether. Alternatively, a user may consider relying on a sampler with a housing that acts as an effective wind shelter, i.e., largely prevents particle impaction on the sorbent. This facilitates quantitative interpretation and has the added benefit of a much weaker dependence of the sampling rate for gaseous compounds on wind speed.43 However, it comes at the cost of a lower sampling rate and the inability to record the presence of particle-bound substances.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from a Discovery Grant of the Natural Sciences and Engineering Research Council of Canada to FW and a Connaught Scholarship to YL is gratefully acknowledged.References
- T. F. Bidleman and C. E. Olney, Chlorinated Hydrocarbons in the Sargasso Sea Atmosphere and Surface Water, Science, 1974, 183(4124), 516–518 CrossRef CAS PubMed.
- T. F. Bidleman and C. E. Olney, High-Volume Collection of Atmospheric Polychlorinated Biphenyls, Bull. Environ. Contam. Toxicol., 1974, 11(5), 442–450 CrossRef CAS PubMed.
- T. F. Bidleman and L. Melymuk, Forty-Five Years of Foam: A Retrospective on Air Sampling with Polyurethane Foam, Bull. Environ. Contam. Toxicol., 2019, 102(4), 447–449 CrossRef CAS PubMed.
- D. Zhao, J. C. Little and S. S. Cox, Characterizing Polyurethane Foam as a Sink for or Source of Volatile Organic Compounds in Indoor Air, J. Environ. Eng., 2004, 130(9), 983–989 CrossRef CAS.
- T. Braun, J. D. Navratil and A. B. Farag, Polyurethane Foam Sorbents in Separation Science, CRC Press, Boca Raton, 1st edn, 1985 Search PubMed.
- I. Kamprad and K. U. Goss, Systematic Investigation of the Sorption Properties of Polyurethane Foams for Organic Vapors, Anal. Chem., 2007, 79(11), 4222–4227 CrossRef CAS PubMed.
- M. Mari, M. Schuhmacher, J. Feliubadaló and J. L. Domingo, Air Concentrations of PCDD/Fs, PCBs and PCNs Using Active and Passive Air Samplers, Chemosphere, 2008, 70(9), 1637–1643 CrossRef CAS PubMed.
- K. Pozo, T. Harner, S. C. Lee, R. K. Sinha, B. Sengupta, M. Loewen, V. Geethalakshmi, K. Kannan and V. Volpi, Assessing Seasonal and Spatial Trends of Persistent Organic Pollutants (POPs) in Indian Agricultural Regions Using PUF Disk Passive Air Samplers, Environ. Pollut., 2011, 159(2), 646–653 CrossRef CAS PubMed.
- Z. Zhang, L. Liu, Y.-F. Li, D. Wang, H. Jia, T. Harner, E. Sverko, X. Wan, D. Xu and N. Ren, Analysis of Polychlorinated Biphenyls in Concurrently Sampled Chinese Air and Surface Soil, Environ. Sci. Technol., 2008, 42(17), 6514–6518 CrossRef CAS PubMed.
- K. Pozo, T. Harner, F. Wania, D. C. G. Muir, K. C. Jones and L. A. Barrie, Toward a Global Network for Persistent Organic Pollutants in Air: Results from the GAPS Study, Environ. Sci. Technol., 2006, 40(16), 4867–4873 CrossRef CAS PubMed.
- K. Pozo, M. Palmeri, V. Palmeri, V. H. Estellano, M. D. Mulder, C. I. Efstathiou, G. L. Sará, T. Romeo, G. Lammel and S. Focardi, Assessing Persistent Organic Pollutants (POPs) in the Sicily Island Atmosphere, Mediterranean, Using PUF Disk Passive Air Samplers, Environ. Sci. Pollut. Res., 2016, 23(20), 20796–20804 CrossRef CAS PubMed.
- F. Wania and C. Shunthirasingham, Passive Air Sampling for Semi-Volatile Organic Chemicals, Environ. Sci.: Processes Impacts, 2020, 22(10), 1925–2002 RSC.
- Y. Li and F. Wania, Partitioning between Polyurethane Foam and the Gas Phase: Data Compilation, Uncertainty Estimation and Implications for Air Sampling, Environ. Sci.: Processes Impacts, 2021, 23(5), 723–734 RSC.
- S. Genualdi, S. C. Lee, M. Shoeib, A. Gawor, L. Ahrens and T. Harner, Global Pilot Study of Legacy and Emerging Persistent Organic Pollutants Using Sorbent-Impregnated Polyurethane Foam Disk Passive Air Samplers, Environ. Sci. Technol., 2010, 44(14), 5534–5539 CrossRef CAS PubMed.
- T. Harner, 2016_V1.3 Template for Calculating PUF and SIP Disk Sample Air Volumes, 2016 Search PubMed.
- C. Persoon and K. C. Hornbuckle, Calculation of Passive Sampling Rates from Both Native PCBs and Depuration Compounds in Indoor and Outdoor Environments, Chemosphere, 2009, 74(7), 917–923 CrossRef CAS PubMed.
- C. Moeckel, T. Harner, L. Nizzetto, B. Strandberg, A. Lindroth and K. C. Jones, Use of Depuration Compounds in Passive Air Samplers: Results from Active Sampling-Supported Field Deployment, Potential Uses, and Recommendations, Environ. Sci. Technol., 2009, 43(9), 3227–3232 CrossRef CAS PubMed.
- X. Zhang and F. Wania, Modeling the Uptake of Semivolatile Organic Compounds by Passive Air Samplers: Importance of Mass Transfer Processes within the Porous Sampling Media, Environ. Sci. Technol., 2012, 46, 9563–9570 CrossRef CAS PubMed.
- N. J. Herkert, S. N. Spak, A. Smith, J. K. Schuster, T. Harner, A. Martinez and K. C. Hornbuckle, Calibration and Evaluation of PUF-PAS Sampling Rates across the Global Atmospheric Passive Sampling (GAPS) Network, Environ. Sci.: Processes Impacts, 2018, 20(1), 210–219 RSC.
- J. M. Armitage, S. J. Hayward and F. Wania, Modeling the Uptake of Neutral Organic Chemicals on XAD Passive Air Samplers under Variable Temperatures, External Wind Speeds and Ambient Air Concentrations (PAS-SIM), Environ. Sci. Technol., 2013, 47(23), 13546–13554 CrossRef CAS PubMed.
- A. R. Restrepo, S. J. Hayward, J. M. Armitage and F. Wania, Evaluating the PAS-SIM Model Using a Passive Air Sampler Calibration Study for Pesticides, Environ. Sci.: Processes Impacts, 2015, 17(7), 1228–1237 RSC.
- L. Melymuk, P. Bohlin-Nizzetto, Š. Vojta, M. Krátká, P. Kukučka, O. Audy, P. Přibylová and J. Klánová, Distribution of Legacy and Emerging Semivolatile Organic Compounds in Five Indoor Matrices in a Residential Environment, Chemosphere, 2016, 153, 179–186 CrossRef CAS PubMed.
- W. Wang, Y. Wang, R. Zhang, S. Wang, C. Wei, C. Chaemfa, J. Li, G. Zhang and K. Yu, Seasonal Characteristics and Current Sources of OCPs and PCBs and Enantiomeric Signatures of Chiral OCPs in the Atmosphere of Vietnam, Sci. Total Environ., 2016, 542, 777–786 CrossRef CAS PubMed.
- J. Thomas, T. M. Holsen and S. Dhaniyala, Computational Fluid Dynamic Modeling of Two Passive Samplers, Environ. Pollut., 2006, 144(2), 384–392 CrossRef CAS PubMed.
- L. Tuduri, T. Harner and H. Hung, Polyurethane Foam (PUF) Disks Passive Air Samplers: Wind Effect on Sampling Rates, Environ. Pollut., 2006, 144(2), 377–383 CrossRef CAS PubMed.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental Organic Chemistry, John Wiley & Sons, Inc., Hoboken New Jersey, USA, 2nd edn, 2003 Search PubMed.
- F. Wania, Y. D. Lei, C. Wang, J. P. D. Abbatt and K. U. Goss, Novel Methods for Predicting Gas-Particle Partitioning during the Formation of Secondary Organic Aerosol, Atmos. Chem. Phys., 2014, 14(23), 13189–13204 CrossRef.
- H. P. H. Arp, R. P. Schwarzenbach and K. U. Goss, Ambient Gas/Particle Partitioning. 2: The Influence of Particle Source and Temperature on Sorption to Dry Terrestrial Aerosols, Environ. Sci. Technol., 2008, 42(16), 5951–5957 CrossRef CAS PubMed.
- D. Atkinson and G. Curthoys, The Determination of Heats of Adsorption by Gas-Solid Chromatography, J. Chem. Educ., 1978, 55(9), 564–566 CrossRef CAS.
- K. U. Goss, Adsorption of VOCs from the Gas Phase to Different Minerals and a Mineral Mixture, Environ. Sci. Technol., 1996, 30(7), 2135–2142 CrossRef CAS.
- C. Persoon and K. C. Hornbuckle, Calculation of Passive Sampling Rates from Both Native PCBs and Depuration Compounds in Indoor and Outdoor Environments, Chemosphere, 2009, 74(7), 917–923 CrossRef CAS PubMed.
- N. T. Petrich, S. N. Spak, G. R. Carmichael, D. Hu, A. Martinez and K. C. Hornbuckle, Simulating and Explaining Passive Air Sampling Rates for Semivolatile Compounds on Polyurethane Foam Passive Samplers, Environ. Sci. Technol., 2013, 47(15), 8591–8598 CAS.
- J. He and R. Balasubramanian, A Comparative Evaluation of Passive and Active Samplers for Measurements of Gaseous Semi-Volatile Organic Compounds in the Tropical Atmosphere, Atmos. Environ., 2010, 44(7), 884–891 CrossRef CAS.
- T. Harner, M. Shoeib, T. Gouin and P. Blanchard, Polychlorinated Naphthalenes in Great Lakes Air: Assessing Spatial Trends and Combustion Inputs Using PUF Disk Passive Air Samplers, Environ. Sci. Technol., 2006, 40(17), 5333–5339 CrossRef CAS PubMed.
- N. Ulrich, S. Endo, T. N. Brown, N. Watanabe, G. Bronner, M. H. Abraham and K.-U. Goss, UFZ-LSER database v 3.2.1 [Internet] http://www.ufz.de/lserd, accessed Nov 23, 2020.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen and B. Yu, et al., PubChem 2019 Update: Improved Access to Chemical Data, Nucleic Acids Res., 2019, 47(D1), D1102–D1109 CrossRef PubMed.
- H. S. Söderström and P.-A. Bergqvist, Passive Air Sampling Using Semipermeable Membrane Devices at Different Wind-Speeds in Situ Calibrated by Performance Reference Compounds, Environ. Sci. Technol., 2004, 38(18), 4828–4834 CrossRef PubMed.
- J. Klánová, P. Èupr, J. Kohoutek and T. Harner, Assessing the Influence of Meteorological Parameters on the Performance of Polyurethane Foam-Based Passive Air Samplers, Environ. Sci. Technol., 2008, 42(2), 550–555 CrossRef PubMed.
- T. Harner, K. Su, S. Genualdi, J. Karpowicz, L. Ahrens, C. Mihele, J. Schuster, J. P. Charland and J. Narayan, Calibration and Application of PUF Disk Passive Air Samplers for Tracking Polycyclic Aromatic Compounds (PACs), Atmos. Environ., 2013, 75, 123–128 CrossRef CAS.
- C. Chaemfa, E. Wild, B. Davison, J. L. Barber and K. C. Jones, A Study of Aerosol Entrapment and the Influence of Wind Speed, Chamber Design and Foam Density on Polyurethane Foam Passive Air Samplers Used for Persistent Organic Pollutants, J. Environ. Monit., 2009, 11(6), 1135–1139 RSC.
- A. A. May, P. Ashman, J. Huang, S. Dhaniyala and T. M. Holsen, Evaluation of the Polyurethane Foam (PUF) Disk Passive Air Sampler: Computational Modeling and Experimental Measurements, Atmos. Environ., 2011, 45(26), 4354–4359 CrossRef CAS.
- L. Melymuk, P. Bohlin, T. Harner, K. B. White, X. Wang, M. Yumiko, J. He, J. Li, J. Ma and W. Ma, Global Intercomparison of Polyurethane Foam Passive Air Samplers Evaluating Sources of Variability in SVOC Measurements, Environ. Sci. Policy, 2021, 125, 1–9 CrossRef CAS PubMed.
- X. Zhang, T. N. Brown, A. Ansari, B. Yeun, K. Kitaoka, A. Kondo, Y. D. Lei and F. Wania, Effect of Wind on the Chemical Uptake Kinetics of a Passive Air Sampler, Environ. Sci. Technol., 2013, 47, 7868–7875 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1em00559f |
| This journal is © The Royal Society of Chemistry 2022 |