Computational thermochemistry: extension of Benson group additivity approach to organoboron compounds and reliable predictions of their thermochemical properties

Abstract

High-level computational data for standard gas phase enthalpies of formation, entropies, and heat capacities are reported for 116 compounds of boron. A comparison of the results with extant experimental and computational benchmark values reveals important trends and clear outliers. Recommendations are made to revise some of the key quantities, such as the enthalpies of formation of orthoboric acid, trimethylthioborate, and triphenylborane, the last of which is found to be considerably in error. The uncertainties associated with the experimental values are found to exceed those of high-level calculations by a clear margin, prompting the redetermination of Benson group additivity contributions for boron-based groups on purely computational grounds. The applicability of the established group contribution values is demonstrated by estimating thermochemical data for large organoboron compounds that cannot be treated with high-level quantum chemical methods and comparing the results with existing experimental and computational values.

---

Introduction

The standard enthalpy (heat) of formation, Δ_fH, describes the change in enthalpy when one mole of a given compound forms from its constituent elements in their standard states.¹ Since enthalpy is a state function, the enthalpy change of any reaction, Δ_rH°, can be calculated by taking the difference of the sum of standard enthalpies of formation of the products (i) and that of the reactants (j), with each value multiplied by its stoichiometric coefficient ν_n: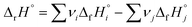 . While this approach works in principle for any reaction imaginable, it is in practise limited by the available experimental data. Specifically, the number of chemical compounds is currently counted in millions,² but the largest of thermochemical databases, such as the NIST Chemistry WebBook,³ contain only a few thousand entries. For this reason, chemistry software for hazard analysis, heat balance calculations, and process simulation, such as RMG-Py,⁴ CHETAH,⁵ and JTHERGAS,⁶ include modules that quickly estimate standard enthalpies of formation (and other thermochemical data) for molecules using their structures as the only input.

On-the-fly estimation of thermochemical properties of molecules typically employs group additivity methods that divide the species in question into well-defined and distinctive groups whose contributions to various physical properties are taken to be constant from one system to another.⁷ The properties of a compound of interest are then obtained by summing up the tabulated values of all groups present in the molecule. In some cases, the results can be further adjusted by considering higher order (nonlinear) interactions between primary groups or specific structural features such as the presence of rings or different isomers. Although the additivity of molecular properties is not strictly fulfilled beyond atomic and molecular masses, empirical group additivity methods are able to estimate the thermodynamic properties of a wide range of molecular species with excellent accuracy and are superior to quantum chemical calculations in terms of speed.

The accuracy of group additivity approaches depends on the reliability of the reference values that have been used to derive the individual contributions and this is one of the Achilles’ heels of the methodology. Even though standard enthalpies of formation of ‘classical’ organic species can often be estimated with high accuracy,^8,9 the same does not hold for more diverse chemical systems, like organo main group compounds, for which there are often not enough reliable thermochemical data.¹⁰ For example, difficulties encountered in analysing the combustion products of organoboron compounds made reliable calorimetric work problematic prior to the advent of fluorine-containing combustion promoters.^11,12 Lately, the accumulation of thermochemical data has slowed down considerably, largely owing to the retirement of the generation of researchers familiar with calorimetry along with lack of interest in the younger generation and insufficient funding for this type of work.¹³ This has spurred the development and use of high-accuracy quantum chemical methods, such as Feller-Peterson-Dixon (FPD),¹⁴ Weizmann-n (Wn),¹⁵ and HEAT protocols,¹⁶ whose accuracy is currently on-par with that of first-class calorimetric measurements and can be controlled by adjusting the underlying theoretical approximations.

The current contribution has two main goals:

First, high-level composite quantum chemical methods are used to calculate the standard enthalpies of formation for 116 boron compounds. The results are compared with experimental reference values and very high-level FPD data, where available. The W1X-1 ansatz¹⁷ used in the current work is a derivative of the Weizmann-1 protocol that can reach chemical accuracy, that is, mean absolute deviation (MAD) less than 4 kJ mol⁻¹, and is applicable to molecular systems with up to 20 non-hydrogen atoms when using server/workstation hardware. While high-level computational investigations of thermochemical properties of boron compounds have been performed before, our work is the first one using a large and diverse set of molecules with complex substituents. This allows, for example, an evaluation of the accuracy of literature data for large organoboron compounds, such as triphenylborane, for which several different experimental enthalpies of formation have been reported.

Second, boron-containing compounds have a plethora of applications in modern chemical industry. They are used as reagents in organic transformations,^18–21 components in materials for energy storage and conversion,^22–27 and as pharmaceuticals,^28–30 to name a few. Despite this, reliable data of their thermochemical properties are in many cases lacking and/or difficult to obtain by experimental means. At present, group additivity approaches offer no remedy to the problem as the only readily available compilation including boron is that of Benson and co-workers from 1969 and it is largely based on old calorimetric data using estimated quantities.³¹ In contrast, the consistency of computational data reported herein allows the derivation of significantly more accurate group contributions for 52 Benson groups and group pairs involving boron. These values enable a straightforward extension of group additivity methods to boron-based compounds.

Computational details

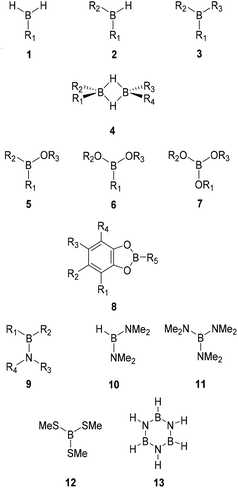
Following our previous work,^32,33 the W1X-1 composite method¹⁷ was employed to calculate the standard gas phase enthalpies of formation (Δ_fH°_298K, kJ mol⁻¹), entropies (S°_298K, J K⁻¹ mol⁻¹), and heat capacities (C_p, J K⁻¹ mol⁻¹) for 116 boron compounds including 40 monoboranes (1–3), 7 diboranes (4), 15 borinic acid derivatives (5), 23 boronic acid derivatives (6), 11 boric acid derivatives (7), 11 catecholboranes (8), 7 aminoboranes (9–11), one thioborate (12), and borazine (13) with alkyl (Me = methyl, Et = ethyl, Pr = propyl, ⁱPr = isopropyl, Bu = butyl, ^sBu = sec-butyl, ^tBu = tert-butyl), alkenyl (Vi = vinyl, All = allyl), aryl (Ph = phenyl, p-Tol = para-tolyl) and/or halogen substituents. The size of the examined systems was limited by the scaling of the W1X-1 method and the available hardware (computing nodes with 14 TB SSD disk, 36 CPU cores and 1 TB memory) that allowed the treatment of molecules with up to ca. 20 heavy atoms. Given the high computational cost of the W1X-1 method, results from the less demanding and thereby significantly faster CBS-QB3 composite method were used for comparison.³⁴ In both methods, the computational bottleneck is a conventional CCSD(T) calculation, but the biggest basis set used in W1X-1 is approximately twice the size of that in CBS-QB3. Consequently, the CBS-QB3 method is roughly two orders of magnitude faster than W1X-1. However, as described in detail in below, the largest differences between the two methods are observed for the biggest of systems, and it is generally not recommended to substitute W1X-1 data with CBS-QB3 values.

All structure optimizations were performed with the Gaussian 16 program package.³⁵ Extensive conformational scans were carried out at the B3LYP^36–39/cc-pV(T+d)Z^40,41 level of theory and only the lowest energy geometries were used as input for W1X-1 energy calculations. When applying the CBS-QB3 method, the geometries were reoptimized at the B3LYP/6-311G(2d,d,p)^42,43 level of theory, as required by the composite protocol. For very high-level work, an ensemble of conformers having statistically significant populations at 298 K should be used for the calculation of standard enthalpies of formation instead of a single low-energy conformer. However, Bolzmann averaging is significant only when the conformational space is large and it is computationally very expensive to include at the W1X-1 level of theory. Furthermore, it has been shown that the resulting correction is similar (to a few kJ mol⁻¹) in magnitude but opposite in sign to the correction for low-frequency internal rotations, and they effectively cancel out.⁴⁴ Thus, both corrections should either be included or omitted, and the latter avenue was followed in this work. It should also be noted that neither CBS-QB3 or W1X-1 uses a dispersion correction during geometry optimization, which could lead to inferior results for systems in which these effects are important.

The CBS-QB3 method was used as implemented in Gaussian 16.³⁵ Single point runs performed with the Molpro 2019.2 program system^45–47 were used to calculate the W1X-1 energies as a sum of four different terms, namely E_HF-CABS, E_ΔCCSD-F12b, E_Δ(T), and E_(C+R), following the protocol of Chan and Radom.¹⁷ The three non-relativistic components E_HF-CABS, E_ΔCCSD-F12b, and E_Δ(T) were extrapolated to the complete basis set (CBS) limit using cc-pVD/TZ-F12^48–51 (HF-CABS⁵² and CCSD-F12b^53,54) and aug′-cc-pV(D/T+d)Z^40,41 (CCSD(T))^55,56 basis sets and the extrapolation formula⁵⁷E_L = E_CBS + A_L^−α where L is the cardinal number of the basis sets (that is, 2 or 3) and α is a method-dependent exponent (5, 3.6725, and 2.0436 for HF-CABS, CCSD-F12b, and CCSD(T), respectively).¹⁷ The fourth energy component E_(C+R) is a combined core and scalar relativistic correlation term that was obtained as the difference of FC-MP2⁵⁸/cc-pCVTZ^59,60 and DKH-MP2^61,62/cc-pCVTZ^59,60 energies.

For the determination of standard enthalpies of formation, heat capacities, and entropies, the B3LYP level harmonic vibrational frequencies were scaled with 0.985 (W1X-1) or 0.990 (CBS-QB3). The calculation of entropies and heat capacities was carried out within the rigid rotor-harmonic oscillator approximation and treating rotation modes involving single bonds as hindered rotors using the procedure implemented in Gaussian 16.³⁵ A periodicity of 3 was used for all bonds to and within alkyl groups, whereas periodicity 2 was used for other single bonds. Symmetry numbers 3 and 2 were used for bonds with local C₃ and C₂ symmetries, respectively, while symmetry number 1 was used for all other bonds.

Standard gas phase enthalpies of formation were obtained using the atomization energy approach. The calculated atomic energies were corrected for spin–orbit (SO) coupling effects using the experimental values tabulated by Moore.⁶³ Reference values for the enthalpies of formation of gaseous atoms and thermal corrections for elements in their standard states were taken from NIST/JANAF Thermochemical Tables for elements H, C, N, O, F, and Cl.⁶⁴ For gaseous B, the uncertainty of the NIST/JANAF value, 560 ± 12 kJ mol⁻¹, is prohibitively large and there exits ample experimental^65,66 and computational^67–69 evidence that it should be revised upwards. To this end, we opted to use the value 570.3 ± 0.8 kJ mol⁻¹ recommended by Karton and Martin based on very high-level theoretical calculations and experimental data for BF₃.⁷⁰

The computed W1X-1 thermochemical parameters were used to derive Benson group contributions for 52 groups and group pairs containing boron. The contributions were determined by minimizing the squared differences between the computed thermochemical parameters and parameters calculated as sums of group contributions using a non-linear optimization algorithm COUENNE of the COIN-OR foundation⁷¹ as implemented in OpenSolver.^72,73 Literature values reported by Domalski and Hearing^74,75 were used for all carbon groups, while some of the groups were required to be fixed to avoid linear dependencies. Following Benson's example,³¹ the fixed group contributions are: E–(C)(H)₃≡C–(C)(H)₃ for any element E, B–(O)₃≡B–(S)₃≡B–(N)₃≡N–(C)₃, and B–(F)₂(C)≡B–(F)₂(C_D).

For the determination of enthalpy contributions, methyl repulsion correction terms of Domalski and Hearing were used for tertiary and quaternary carbon atoms, while ortho-corrections were employed in the case of adjacent fluorine atoms and hydroxyl groups in catecholboranes.^74,75 Steric crowding around boron atoms in diboranes was equated to what is known for substituted alkenes and a cis-correction term was used to describe repulsions between methyl groups.^74,75 Ring strain in the five-membered ring of catecholboranes was described with a single parameter that was optimized in the fitting procedure. Entropy contributions were corrected for optical isomerism (R ln n, where n is the total number of stereoisomers) and for internal (σ_int) and external (σ_ext) symmetries (–R ln σ_tot, where σ_tot = σ_extΠⁱ(σ_int)_i) (see ESI for details†).³¹

Results and discussion

Comparison of calculated gas phase standard enthalpies of formation of boron compounds with experimental and computational data

Before comparing the calculated W1X-1 and CBS-QB3 standard enthalpies of formation (Table 1) with experimental values and prior computational data (Table 2), an initial evaluation of the relative performance of the two methods is warranted. A detailed examination of the data in Table 1 shows that with only a few exceptions in boric acid derivatives and catecholboranes, the CBS-QB3 method predicts standard enthalpies of formation that are more endothermic than those obtained with the W1X-1 protocol. Even though the observed differences are well in line with the expected accuracy of the methods, gauged by the confidence intervals determined against large reference data sets (2σ values of ±14 and ±6 kJ mol⁻¹ for CBS-QB3⁷⁶ and W1X-1,¹⁷ respectively), the fact that the largest differences between the two methods are observed for the biggest of systems infers of systematic error. Previously,^32,33 we have ascribed this behaviour to inferior treatment of electron correlation effects in CBS-QB3 over W1X-1 that become more pronounced with increasing molecular size. However, since the W1X-1 method contains empirical parameters,¹⁷ the extrapolation exponents α fitted to data for small molecules, it is possible that also W1X-1 results have larger than anticipated error as the size of the system in question grows.

Table 1 Calculated gas phase standard enthalpies of formation (Δ_fH° 298K, kJ mol⁻¹), entropies (S° 298K, J K⁻¹ mol⁻¹), and heat capacities (C_p, J K⁻¹ mol⁻¹) of monoboranes 1–3, diboranes 4, borinic 5, boronic 6, and boric acid derivatives 7, catecholboranes 8, aminoboranes 9–11, thioborane 12, and borazine 13

Molecule	Chemical formula^a	ΔfH° 298K		S° 298K	C p 298K	C p 500K	C p 1000K
		W1X-1	CBS-QB3	W1X-1	W1X-1	W1X-1	W1X-1
a Used abbreviations: Me = methyl, Et = ethyl, Pr = propyl, ^iPr = isopropyl, Bu = butyl, ^sBu = sec-butyl, ^tBu = tert-butyl, Vi = vinyl, All = allyl, Ph = phenyl, p-Tol = para-tolyl.
1a	BH3	103.9	103.7	188.2	27.8	36.2	53.4
1b	BH2Me	32.2	36.7	250.0	46.8	67.5	102.7
1c	BH2Et	21.3	27.6	288.0	69.1	100.7	153.2
1d	BH2Vi	135.3	141.4	265.2	56.4	86.1	128.1
1e	BH2Pr	–0.7	7.6	322.1	91.4	135.4	204.6
1f	BH2^iPr	3.2	10.8	312.9	93.8	138.2	205.5
1g	BH2^sBu	–16.9	–7.8	345.9	115.0	174.2	259.2
1h	BH2^tBu	–22.6	–14.7	339.8	118.5	177.1	261.0
1i	BH2Ph	160.9	172.5	313.9	98.6	163.0	245.6
2a	BHMe2	–39.7	–31.1	291.0	68.0	99.8	152.1
2b	BHEtMe	–50.4	–40.2	332.4	89.8	132.1	202.2
2c	BHMeVi	64.0	74.0	315.6	79.7	120.6	180.6
2d	BHMePh	91.8	106.5	364.6	122.2	196.4	292.8
2e	BHEt2	–60.4	–48.7	354.9	113.2	166.6	253.4
2f	BHEtVi	53.7	65.2	345.0	100.1	151.5	227.4
2g	BHVi2	166.9	178.3	317.4	90.2	138.2	203.3
2h	BHPhVi	195.0	210.8	377.3	132.1	213.2	318.4
2i	BH^iPr2	–96.7	–83.5	417.0	161.5	238.6	356.7
2j	BHPh2	229.8	249.3	425.1	176.4	292.5	435.3
3a	BMe3	–109.6	–97.8	357.5	90.6	132.7	201.4
3b	BEtMe2	–121.3	–108.0	375.6	114.0	166.4	252.1
3c	BMe2Vi	–2.3	10.6	357.8	103.0	151.1	223.8
3d	BMe2Ph	26.1	43.3	404.4	146.4	228.6	340.6
3e	BEtMePh	16.1	34.5	459.1	164.2	258.5	389.9
3f	BMeVi2	105.4	119.5	378.6	114.4	167.5	245.0
3g	BMePhVi	133.7	151.9	426.2	159.0	246.2	362.3
3h	BMePh2	163.3	184.5	469.9	200.8	326.4	485.5
3i	BF2Me	–809.4	–806.1	296.3	56.6	79.9	111.8
3j	BEt3	–143.3	–127.5	423.4	161.7	235.6	354.2
3k	BEtVi2	96.3	112.1	392.7	138.1	204.7	300.9
3l	BEtF2	–819.0	–814.8	327.8	78.7	112.5	162.0
3m	BVi3	213.5	228.4	394.1	123.1	181.2	265.1
3n	BPhVi2	242.1	260.9	431.9	171.8	268.9	391.8
3o	BPh2Vi	268.4	289.9	480.5	213.6	346.3	512.9
3p	BF2Vi	–695.8	–691.9	306.7	71.5	101.3	137.1
3q	B^iPr3	–194.1	–177.9	503.5	235.0	349.2	515.4
3r	BBu3	–274.6	–248.7	632.4	292.6	436.8	659.3
3s	BPh3	293.3	317.3	517.2	256.4	422.9	630.5
3t	BF3	–1134.6	–1133.9	254.9	42.7	55.1	67.7
3u	BCl3	–404.3	–411.5	290.0	55.0	64.9	71.8
4a	B2H6	40.6	46.9	232.2	48.2	78.7	126.6
4b	B2H5Me	–16.8	–7.4	282.1	71.5	112.2	176.4
4c	1,1-B2H4Me2	–76.6	–64.5	314.3	95.5	145.9	226.1
4d	1,2-cis-B2H4Me2	–71.3	–59.0	314.2	94.0	144.7	225.8
4e	1,2-trans-B2H4Me2	–72.1	–59.9	314.1	95.5	145.7	226.1
4f	B2H3Me3	–129.2	–114.3	357.1	118.6	178.5	275.5
4g	B2H2Me4	–184.3	–166.8	381.9	141.3	211.1	324.9
5a	BH2OH	–274.0	–271.9	230.8	34.1	50.4	74.3
5b	BH2(OMe)	–245.8	–246.0	269.8	51.9	78.5	123.1
5c	BH2(OEt)	–280.2	–278.7	303.2	73.7	113.5	174.8
5d	BH2(OPh)	–121.3	–115.8	344.5	112.8	181.0	265.7
5e	BHMe(OH)	–347.3	–341.5	274.2	55.9	83.4	123.9
5f	BHEt(OH)	–358.0	–351.2	307.9	78.5	116.5	174.3
5g	BHPh(OH)	–210.6	–199.7	345.1	112.0	181.5	266.3
5h	BHMe(OMe)	–318.0	–314.7	312.7	74.3	111.3	172.6
5i	BHEt(OMe)	–329.0	–324.8	342.9	96.5	148.1	229.9
5j	BHPh(OMe)	–182.0	–173.7	384.0	133.3	213.0	318.9
5k	BMe2(OH)	–415.0	–406.3	317.8	77.4	116.1	173.7
5l	BMe2(OMe)	–381.7	–375.7	357.7	99.1	146.0	219.7
5m	BEtMe(OH)	–427.2	–417.1	348.7	99.0	148.8	223.6
5n	BMePh(OH)	–278.2	–264.8	387.0	136.0	214.6	314.0
5o	BMePh(OMe)	–244.6	–234.1	430.8	154.3	238.7	356.7
6a	BH(OH)2	–646.3	–642.5	256.7	48.1	70.5	97.1
6b	BH(OMe)2	–579.8	–581.9	338.8	84.0	126.3	190.2
6c	BH(^iPrO)2	–719.7	–716.7	462.1	179.9	268.3	394.7
6d	BMe(OH)2	–713.6	–707.3	304.8	70.2	103.6	146.4
6e	BMe(OH)(OMe)	–680.0	–676.9	342.3	88.5	131.9	192.7
6f	BMe(OMe)2	–646.1	–646.3	379.8	109.2	158.5	236.5
6g	BMe(OEt)(OMe)	–680.4	–679.2	411.7	130.5	195.2	290.6
6h	BMe(OEt)2	–713.8	–711.3	444.5	153.4	230.7	342.0
6i	BEt(OH)2	–724.8	–717.4	331.1	92.5	136.9	197.1
6j	BEt(OH)(OMe)	–690.9	–686.9	372.4	110.7	164.2	242.3
6k	BEt(OMe)2	–656.5	–656.2	412.5	130.9	191.3	286.9
6l	BVi(OH)2	–600.7	–593.7	316.5	86.8	124.4	166.5
6m	BVi(OH)(OMe)	–567.5	–563.6	362.5	100.4	148.7	214.0
6n	BVi(OMe)2	–531.7	–531.1	399.9	121.9	175.2	257.8
6o	B(All)(OH)2	–627.3	–618.2	349.5	106.2	154.9	219.4
6p	B(All)(OH)(OMe)	–594.2	–588.3	390.3	121.6	181.0	264.3
6q	B(All)(OMe)2	–552.7	–550.2	436.1	142.8	208.6	308.7
6r	BPh(OH)2	–572.6	–562.6	382.0	125.3	198.2	284.6
6s	BPh(OH)(OMe)	–539.8	–532.9	418.2	145.3	226.0	330.0
6t	BPh(OMe)2	–497.6	–494.1	448.1	169.3	256.2	378.5
6u	B(p-Tol)(OH)2	–605.8	–594.8	420.3	147.1	230.1	334.3
6v	B(p-Tol)(OH)(OMe)	–572.9	–565.1	457.9	166.8	257.4	379.5
6w	B(p-Tol)(OMe)2	–530.4	–526.0	487.4	187.4	286.4	426.7
7a	B(OH)3	–1002.1	–998.0	272.2	65.8	93.1	119.1
7b	B(OH)2(OMe)	–967.6	–966.8	323.5	83.4	119.4	164.5
7c	B(OH)2(OPh)	–842.9	–836.5	398.7	139.0	223.2	308.7
7d	B(OH)(OMe)2	–933.1	–935.8	365.1	101.3	145.6	209.5
7e	B(OH)(OMe)(OPh)	–809.2	–806.4	442.8	160.7	245.4	350.9
7f	B(OMe)3	–898.6	–905.4	396.4	119.1	173.0	255.9
7g	B(OEt)(OMe)2	–932.7	–937.7	437.6	141.1	208.8	309.3
7h	B(OMe)2(OPh)	–775.5	–776.5	484.2	179.0	272.2	396.2
7i	B(OEt)2(OMe)	–966.8	–970.4	469.8	162.9	244.8	362.8
7j	B(OMe)(OPh)2	–652.5	–648.5	559.8	243.0	376.5	539.9
7k	B(OEt)3	–1000.8	–1003.0	492.8	184.9	281.1	416.0
8a	C6H4O2BH	–409.1	–406.7	322.0	104.3	173.2	253.8
8b	C6H4O2BMe	–482.9	–478.8	371.8	127.8	206.2	303.2
8c	3-C6H3FO2BMe	–662.3	–662.6	390.4	140.1	217.2	310.5
8d	4-C6H3FO2BMe	–673.1	–672.9	389.5	140.4	217.8	310.8
8e	3,4-C6H2F2O2BMe	–834.8	–840.8	409.4	152.7	228.3	317.8
8f	3,5-C6H2F2O2BMe	–849.7	–853.8	408.8	152.8	228.7	318.0
8g	3,6-C6H2F2O2BMe	–836.9	–843.5	408.5	152.6	228.2	317.8
8h	4,5-C6H2F2O2BMe	–845.2	–850.7	407.6	153.0	228.8	318.1
8i	3,4,5-C6H2F2O2BMe	–1004.3	–1014.1	428.7	165.4	239.3	325.1
8j	3,4,6-C6H2F2O2BMe	–1006.8	–1016.9	427.6	165.2	239.2	325.1
8k	C6F4O2BMe	–1159.1	–1175.1	448.5	177.8	249.7	332.1
9a	BH2NH2	–81.9	–79.3	228.4	39.2	59.1	88.1
9b	BH2NHMe	–72.6	–70.2	270.7	58.1	88.4	137.5
9c	BH2NMe2	–70.0	–72.6	293.4	81.6	123.6	189.5
9d	BHMeNH2	–147.0	–140.5	275.8	62.2	92.5	137.8
9e	BMe2NH2	–211.0	–201.4	312.3	84.5	125.5	187.2
10	BH(NMe2)2	–160.2	–159.1	390.4	146.2	216.5	328.3
11	B(NMe2)3	–239.6	–241.5	461.0	215.3	315.6	469.4
12	B(SMe)3	–199.1	–199.7	435.1	152.8	203.2	270.1
13	B3N3H6	–495.7	–480.8	287.8	87.0	142.6	208.7

---

Table 2 Experimental (Exptl.) and calculated (FPD, W1X-1, and CBS-QB3) gas phase standard enthalpies of formation (Δ_fH° 298K, kJ mol⁻¹) of selected boron compounds

Molecule	Exptl.	FPD	W1X-1	CBS-QB3
BH3	106.7 ± 10.0^64	102.1^82	103.9	103.7
B2H6	41.0 ± 16.7^64	39.5^81	40.6	46.9
BF3	–1136.6 ± 0.8^82	−1135.5^82	–1134.6	–1133.9
BCl3	–403.0 ± 2.1^83	−404.6^82	–404.3	–411.5
BMe3	–125.0 ± 22.0^85	—	–109.6	–97.8
BEt3	–160.7 ± 15.0^85	—	–143.3	–127.5
B(OH)3	–992.3 ± 2.5^64	–1003.3^82	–1002.1	–998.0
B(SMe)3	–156.5 ± 2.5^90	—	–199.1	–199.7
B3N3H6	–510.0 ± 13.0^64	–497.1^92	–495.7	–480.8

---

As noted in the Introduction, experimentally determined thermochemical data for boron compounds are limited. Well-established standard enthalpies of formation exist only for nine species examined in the current work (Table 2) and many of these values are associated with large uncertainties (2σ confidence intervals). The scarcity of first-hand calorimetric data for boron compounds has led to the adoption of other means to arrive at the missing entities. For example, lacking direct measurements for many gaseous boron compounds, the vast compilation of Skinner⁷⁷ uses estimated quantities to calculate the standard enthalpy of formation for several systems, while other authors have taken advantage of the computer-analysed compilation of Pedley and Rylance from the 1970s to derive enthalpies of formation for boron compounds.⁷⁸ When compiling Table 2, we have carefully reviewed the existing literature and included experimental results that are backed up by ample amounts of data, are derived in the most straightforward manner, and/or do not rely on estimated ancillary data. Furthermore, most of the compounds in Table 2 are sufficiently small that there exist very high-level FPD benchmark values for comparison.

The NIST-JANAF standard enthalpies of formation of borane and diborane are 106.7 ± 10.0 and 41.0 ± 16.7 kJ mol⁻¹, respectively.⁶⁴ Of these, the value for borane is based on ion appearance potentials,⁷⁹ whereas the data for diborane is a weighted average of eight different experimental determinations. The compilation of Gurvich et al. quotes different numerical values for both borane and diborane, 88.0 ± 10.0 and 36.6 ± 2.0 kJ mol⁻¹,⁸⁰ respectively, that are, however, identical with NIST-JANAF values (within 2σ) and in good agreement with our calculated W1X-1 (103.9 and 40.6 kJ mol⁻¹) and CBS-QB3 (103.7 and 46.9 kJ mol⁻¹) results. The FPD enthalpies of formation have been reported for both borane and diborane.^81,82 The value for borane, 102.1 kJ mol⁻¹,⁸² is based on the Karton Martin enthalpy of formation of gaseous boron atom,⁷⁰ whereas the value for diborane, 41.6 kJ mol⁻¹,⁸¹ needs to be adjusted by −2.1 kJ mol⁻¹, giving 39.5 kJ mol⁻¹. Both FPD values are in good agreement with experimental data and results of our calculations.

Experimental standard enthalpies of formation of boron trifluoride and trichloride, −1136.6 ± 0.8⁸³ and −403.0 ± 2.1 kJ mol⁻¹,⁸⁴ respectively, have been determined using calorimetry. These values are statistically identical to those listed in the NIST-JANAF Thermochemical Tables⁶³ and in the compilation of Gurvich et al.⁸⁰ Our W1X-1 (−1134.6 and −404.3 kJ mol⁻¹) and CBS-QB3 (−1133.9 and −411.5 kJ mol⁻¹) results reproduce the experimental values for both boron trifluoride and trichloride, as is also the case for FPD data reported in the literature (−1135.5 and −404.6 kJ mol⁻¹).⁸² Consequently, it is without a doubt that the standard enthalpies of formation quoted for these molecules in thermochemical databases have been determined to the highest precision.

Table 2 includes experimental standard enthalpies of formation for two alkylboranes, −125.0 ± 22.0 and −160.7 ± 15.0 kJ mol⁻¹ for trimethyl- and triethylborane, respectively.⁸⁵ These values have been determined by combustion calorimetry. The associated uncertainties are very large in both cases, primarily because of the inability of the authors to accurately characterise the nature and thermodynamic states of combustion products. Unfortunately, there are no other experimental reports on the thermochemistry of these species and instead of very high-level FPD data, the published computational standard enthalpy of formation of trimethylborane, −107.9 kJ mol⁻¹, is based on isodesmic reactions modelled at the G3(MP2) level.⁸⁶ For this reason, the W1X-1 results for trimethyl- and triethylborane (−109.6 and −143.3 kJ mol⁻¹, respectively) set a new high-level computational benchmark for both compounds. Our values are identical (within 2σ) with the experimental data, supporting the validity of latter within the limits of the assigned uncertainties.

The NIST-JANAF standard enthalpy of formation of orthoboric acid,⁶⁴ −992.3 ± 2.5 kJ mol⁻¹, is based on calorimetric^12,87 and vapour pressure data.⁸⁸ Our W1X-1 and CBS-QB3 results (−1002.1 and −998.0 kJ mol⁻¹, respectively) are more exothermic than the literature value and the W1X-1 prediction is not identical with it within 2σ confidence intervals. This species has also been subjected to the FPD treatment, yielding −1003.3 kJ mol⁻¹ for its standard enthalpy of formation,⁸² in harmony with our W1X-1 value. This allows us to conclude that the established experimental standard enthalpy of formation of orthoboric acid is slightly too endothermic and should be adjusted accordingly.

The experimental standard enthalpy of formation of trimethylthioborate has been determined via enthalpy of hydrolysis.⁸⁹ The reported value, −156.5 ± 2.5 kJ mol⁻¹, is significantly more endothermic than our computational W1X-1 and CBS-QB3 results (−199.1 and −199.7 kJ mol⁻¹, respectively) even when considering 3σ confidence intervals. The authors of the original experimental work already noted that thermal effects from the evolution of gaseous methanethiol were neglected in the analysis, which could account for some of the difference between the numbers. Furthermore, boron–sulphur bond energy calculated from the data for trimethylthioborate was found to be approximately 20 kJ mol⁻¹ smaller than bond energies determined from experimental data for higher trialkylthioborates,⁸⁹ casting further doubt on the experimental enthalpy of formation of trimethylthioborate. Even though FPD benchmark result is not available for comparison, we are inclined to adjust the reference standard enthalpy of formation of trimethylthioborate to match the W1X-1 prediction.

The last experimental reference value to be considered is the standard enthalpy of formation of borazine, −510.0 ± 13.0 kJ mol⁻¹. This value is reported in the NIST-JANAF Thermochemical Tables⁶⁴ and is based on the original calorimetric determination of the enthalpy of combustion of borazine,⁹⁰ with minor adjustments to the ancillary values used in the derivation. For this molecule, our calculated W1X-1 and CBS-QB3 values (−495.7 and −480.8 kJ mol⁻¹, respectively) deviate from each other by as much as 15 kJ mol⁻¹, though the difference is still within the combined 2σ confidence interval of the two methods. However, only the W1X-1 value is identical (within 2σ) with the experimental value. Interestingly, the FPD value reported for this species is −483.3 kJ mol⁻¹,⁹¹ in seemingly better agreement with our CBS-QB3 result, but a later technical report by the same author quotes −497.1 kJ mol⁻¹ as the “recalculated heat of formation of borazine”,⁹² spot on with our W1X-1 prediction. Considering that the report adjusts all enthalpies given in the original publication by 4.6 kJ per mol per boron atom, a likely reason for the correction is the adoption of an updated standard enthalpy of formation for gaseous B from Karton and Martin.⁷⁰ The same reference value is also used by us and with this in mind we conclude that high-level computational predictions support the accuracy of the experimental standard enthalpy of formation of borazine within the reported confidence interval.

To summarize, the data in Table 2 shows that our W1X-1 results are in excellent agreement (within 1.5 kJ mol⁻¹) with FPD values, where available. Together with the extensive assessment of the performance of the W1X-1 method against G2 and G3/99 test sets by its developers, this result strongly supports the use of W1X-1 composite approach for the determination of standard enthalpies of formation of boron compounds, lending credence to the data in Table 1. Except for orthoboric acid and trimethylthioborate, high-level W1X-1 and FPD results uniformly imply that the experimental values given in Table 2 are accurate within the reported uncertainties. However, considering the consistency of the computational results and their much smaller error limits in comparison to experiments, we recommend that the calculated standard enthalpies of formation of borazine, borane, diborane, and trimethyl- and triethylborane are used in thermochemical work aiming to high-accuracy results. In the case of orthoboric acid, the literature value for its standard enthalpy of formation is slightly too endothermic and requires a minor revision. In contrast, the experimental standard enthalpy of formation of trimethylthioborate is considerably in error and the significantly more accurate W1X-1 prediction should be used in place of it.

Comparison of calculated gas phase standard enthalpies of formation of boron compounds with reference data used by Benson and co-workers

As noted above, many of the reference values reported by Skinner in his compilation⁷⁷ or in other works^93–97 take advantage of estimates to calculate the gas phase standard enthalpy of formation for several boron species. These data have also been used by Benson and co-workers to derive group contribution values for boron.³¹ Of the various boron compounds that Benson and co-workers have considered in their analysis, around half are among the systems calculated herein (Table 1). In the following, we compare our high-level W1X-1 predictions for these molecules to the data used by Benson (Table 3).

Table 3 Reference (Ref.) and calculated (W1X-1) gas phase standard enthalpies of formation (Δ_fH° 298K, kJ mol⁻¹) of selected boron compounds

Molecule	Ref.	W1X-1
BMe3	–122.4 ± 23.0^77	–109.6
BEt3	–152.8 ± 10.5^77	–143.3
BBu3	–283.3 ± 10.9^77	–274.6
BF2Me	–832.6 ± 12.6^77	–809.4
BF2Et	–875 ± 34^77	–819.0
BF2Vi	–715 ± 34^77	–695.8
BH(OMe)2	–582.4 ± 6.3^99	–579.8
BH(O^iPr)2	–729.7 ± 3.3^97	–719.7
B(OMe)3	–902.5 ± 4.1^93	–898.6
B(OEt)3	–1002.5 ± 5.0^96	–1000.8
B(NMe2)3	–275.7 ± 5.0^94	–239.6
BH2OH	–292.9 ± 4.2^100	−274.0
BH(OH)2	–643.5 ± 8.4^100	−646.3

---

The reference standard enthalpies of formation for trimetyl- and triethylborane used by Benson and co-workers, 122.4 ± 23.0 and −152.8 ± 10.5 kJ mol⁻¹,^31,77 respectively, have equally large uncertainties as the calorimetric data discussed in the previous section. Consequently, the two sets of values are statistically identical within the given uncertainties and thereby in good agreement with our calculated W1X-1 results (−109.6 and −143.3 kJ mol⁻¹, respectively). The reference value quoted for tributylborane,^31,77 −283.3 ± 10.9 kJ mol⁻¹, has been derived by Skinner and takes use of an estimated enthalpy of vaporization. Despite this, the value is in good agreement with our calculated W1X-1 enthalpy (−274.6 kJ mol⁻¹) and can be considered accurate within the limits of the given confidence intervals.

The compounds considered by Benson and co-workers include methyl, ethyl, and vinyl substituted difuoroboranes with reference values −826.6 ± 12.6, −875 ± 34, and −715 ± 34 kJ mol⁻¹, respectively.^31,77 These data have been derived from ion appearance potentials in electron impact measurements by Steele and co-workers.⁹⁸ Owing to the limitations of the method and the assumptions required to be made in the calculation of enthalpies of formation, some very large uncertainties have been assigned to the reported values. A comparison of the data with our W1X-1 enthalpies (−809.4, −819.0, and −695.8 kJ mol⁻¹, respectively) indicates that the authors have been wise in doing so as the reference values for methyl- and ethyldifluoroborane agree with computational predictions only within 3σ confidence intervals. This casts considerable doubt on the validity of these reference values.

The reference values for boronic acid esters dimethyl- and diisopropylboronate,³¹ −582.4 ± 6.3⁹⁹ and −729.7 ± 3.3 kJ mol⁻¹,⁹⁷ respectively, and boric acid esters trimethyl- and triethylborate,³¹ −902.5 ± 4.1⁹³ and −1002.5 ± 5.0 kJ mol⁻¹,⁹⁶ respectively, have been derived from hydrolysis enthalpies. All values are in good agreement with our W1X-1 calculations (−579.8, −719.7, −898.6, and −1000.8 kJ mol⁻¹, respectively), save for diisopropylboronate for which the difference between reference and computational values exceeds their combined 2σ confidence interval, albeit only slightly.

The reference value for tris(dimethylamino)borane given in Table 3, −275.7 ± 5.0 kJ mol⁻¹,^31,94 is based on its enthalpy of hydrolysis in an acidic solution. It differs significantly from the W1X-1 result (−239.6 kJ mol⁻¹) even when considering 3σ confidence intervals. In this case, the ancillary thermochemical data used in the derivation of the quantity appears just and the description of the original experimental work offers no immediate explanation to the discrepancy. Nevertheless, given the proven performance of W1X-1 in predicting the standard enthalpies of formation of boron compounds, we consider the calculated value to be the more accurate of the two.

Benson and co-workers have used the reference values −292.9 ± 4.2 and −643.5 ± 8.4 kJ mol⁻¹, for borinic and boronic acid, respectively.^31,100 These are from the work of Porter and Gupta and were determined by mass spectrometric kinetic analysis of the reaction of diborane with orthoboric acid. The reference value for boronic acid is an excellent match with our calculated W1X-1 result (−646.3 kJ mol⁻¹) but the value for borinic acid differs significantly from the W1X-1 prediction (−274.0 kJ mol⁻¹) even when considering 3σ confidence intervals. However, the ancillary data used to derive the experimental enthalpies are not entirely accurate (for example, 31.4 kJ mol⁻¹ was used for the gas phase enthalpy of formation of diborane) and the confidence intervals associated with them are, subsequently, too narrow.

Interestingly, the reference set of Benson and co-workers does not contain triphenylborane, a key species in boron chemistry. Its experimental standard enthalpy of formation, 130.1 ± 8.4 kJ mol⁻¹, is based on enthalpy of hydrolysis.¹⁰¹ A later investigation on the sublimation enthalpy of triphenylborane¹⁰² gave 155.4 ± 8.4 kJ mol⁻¹ for the enthalpy of formation using ancillary data from Pedley and Rylance.⁷⁸ These values are statistically different even within 3σ confidence intervals and also ca. 150 kJ mol⁻¹ less endothermic than our W1X-1 prediction in Table 1 (293.3 kJ mol⁻¹). Given the consistency of our computational results and the large number of ancillary data required to arrive at the experimental values, we strongly argue in favour of our computational prediction. It is plausible that the experimental data of triphenylborane was excluded by Benson and co-workers for its anomalously low value.

Considered as a whole, Table 3 demonstrates a problem common to all group contribution methods: the reliability of reference values used in the derivation of group contributions. Even though the majority of data are accurate within the given confidence intervals, large uncertainties are detrimental to the fitting process and lead to inaccurate group contributions and thereby to poor estimates of thermochemical properties. In some instances, such as with organosilicon compounds,³¹ inconsistencies in the reference data have completely prevented the determination of an internally consistent set of group contributions by experimental means. As shown by us^32,33 and by others,^103–107 a simple fix to the problem is offered by theoretical approaches and high-level composite methods in particular. In the following, we pursue this avenue and determine Benson group contributions for boron using the high-level W1X-1 data in Table 1.

Determination of Benson thermochemical group contributions for boron and their application in estimating the gas phase standard enthalpies of formation of boron compounds

Group contributions for 52 Benson groups and group pairs involving boron were derived from the W1X-1 thermochemical data by fitting and the results are presented in Tables 4 and 5 We have adopted the convention of Holmes and Aubry to round the values to the nearest integer to underline the fact that group contribution methods yield only reliable estimates of thermochemical parameters.^8,9 In the case of aryl substituted species, Benson groups such as C_B–(C_B)₂(B) always occur in pairs that prevents the easy assignment of unambiguous values for individual groups. Though some authors have chosen to assign arbitrary reference values to some key groups, we have opted to use group pair values. This is well-justified as the individual contributions have no physical meaning.

Table 4 Thermochemical Benson group contributions for standard enthalpies of formation (Δ_fH° 298K, kJ mol⁻¹), entropies (S° 298K, J K⁻¹ mol⁻¹), and heat capacities (C_p, J K⁻¹ mol⁻¹) derived from results of W1X-1 calculations

Group ^a	ΔfH° 298K	S° 298K	C p 298K	C p 500K	C p 1000K
a Values of groups B–(O)3≡B–(S)3≡B–(N)3 are set to match those of N–(C)3 by Domalski and Hearing.^74,75 b Values set to be identical to avoid linear dependencies. c HBR = bridging hydrogen.
B–(C)(H)2	74	134	21	28	41
B–(CD)(H)2	65	138	16	25	41
B–(H)2(N)	49	120	15	26	42
B–(H)2(O)	94	113	18	28	46
B–(C)2(H)	45	67	17	20	28
B–(CD)2(H)	26	69	9	16	29
B–(H)(N)2	77	38	13	21	34
B–(H)(O)2	102	27	15	25	35
B–(C)(CD)(H)	36	71	13	19	30
B–(C)(H)(N)	26	43	12	20	30
B–(C)(H)(O)	66	43	14	22	35
B–(C)3	16	–9	15	16	16
B–(C)2(CD)	12	–6	11	12	13
B–(C)2(N)	4	–32	9	14	18
B–(C)2(O)	42	–32	11	15	19
B–(C)(CD)2	8	–1	8	8	12
B–(C)(F)2^b	–766	180	31	40	50
B–(CD)(F)2^b	–766	180	31	40	50
B–(C)(O)2	73	–47	13	18	23
B–(CD)3	2	28	1	–2	3
B–(CD)(O)2	74	–36	11	15	19
C–(B)(C)(H)2	–11	28	22	33	50
C–(B)(CD)(H)2	–15	23	19	34	47
C–(B)(C)2(H)	19	–60	22	32	42
C–(B)(C)3	44	–140	21	31	35
CD–(B)(CD)(H)	44	12	19	30	40
N–(B)(H)2	–131	114	24	33	46
N–(B)(C)(H)	–79	32	18	23	33
N–(B)(C)2	–34	–57	15	19	24
O–(B)(H)	–373	116	16	23	30
O–(B)(C)	–296	34	10	11	15
S–(B)(C)	–63	52	20	21	19
B–(H)2(HBR)2 ^c	20	122	24	39	63
B–(C)(H)(HBR)2 ^c	6	42	22	34	51
B–(C)2(HBR)2 ^c	–11	–39	20	28	39
cis-Corr., B2H6	3	–1	–1	–1	0
Ring strain, BO2C2	–12	109	–19	–20	–6

---

Table 5 Thermochemical Benson group pair contributions for standard enthalpies of formation (Δ_fH° 298K, kJ mol⁻¹), entropies (S° 298K, J K⁻¹ mol⁻¹), and heat capacities (C_p, J K⁻¹ mol⁻¹) derived from results of W1X-1 calculations

Group pair	ΔfH° 298K	S° 298K	C p 298K	C p 500K	C p 1000K
B–(CB)(H)2 + CB–(CB)2(B)	92	84	31	49	70
B–(CB)2(H) + 2 × CB–(CB)2(B)	92	–41	40	64	83
B–(C)(CB)(H) + CB–(CB)2(B)	65	11	28	43	55
B–(CB)(CD)(H) + CB–(CB)2(B)	55	14	23	38	55
B–(CB)(H)(O) + CB–(CB)2(B)	90	–5	29	46	63
B–(C)2(CB) + CB–(CB)2(B)	42	–52	25	34	40
B–(C)(CB)2 + 2 × CB–(CB)2(B)	67	–120	39	59	72
B–(C)(CB)(CD) + CB–(CB)2(B)	36	–55	25	32	37
B–(C)(CB)(O) + CB–(CB)2(B)	68	–79	26	36	44
B–(CB)3 + 3 × CB–(CB)2(B)	86	–175	52	80	103
B–(CB)2(CD) + 2 × CB–(CB)2(B)	60	–118	37	57	74
B–(CB)(CD)2 + CB–(CB)2(B)	32	–58	23	33	41
B–(CB)(O)2 + CB–(CB)2(B)	106	–85	26	39	47
O–(B)(CB) + CB–(CB)2(O)	–279	43	11	11	13

---

Before discussing the application potential of the data in Tables 4 and 5 in more detail, we point out that the W1X-1 enthalpies given in Table 1 already illustrate that the underlying approximation of additivity of thermochemical properties holds well for organoboron compounds considered herein. For example, the calculated standard enthalpies of formation for the methylborane series BH₃, BH₂Me, BHMe₂, and BMe₃ (103.9, 32.3, −39.7, and −109.6 kJ mol⁻¹, respectively) show that each consecutive H-to-Me replacement on boron alters the standard enthalpy of formation by a constant factor of ca. −71 kJ mol⁻¹. The same is true for the corresponding ethyl series, in which case every H-to-Et replacement affects the enthalpy by ca. −82 kJ mol⁻¹. Similarly, a comparison between the methyl- and ethylborane series allows to determine the effect of Me-to-Et substitution on boron and this value turns out to be ca. −11 kJ mol⁻¹. The same correction applies equally well to any similar Me-to-Et replacement within compounds given in Table 1 as shown, for example, by the calculated standard enthalpies of formation for methyl- and ethyldifluoroborane (−809.4 and −819.0 kJ mol⁻¹, respectively) with a difference of ca. 10 kJ mol⁻¹. In contrast, if the Me-to-Et correction is calculated using Skinner's reference values,⁷⁷ two vastly different numbers are obtained: ca. −10 kJ mol⁻¹ from data for trimethyl- and triethylborane (−122.4 ± 23.0 and −152.8 ± 10.5 kJ mol⁻¹, respectively) or −48 kJ mol⁻¹ from methyl- and ethyldifluoroborane (−826.6 ± 12.6 and −875 ± 34 kJ mol⁻¹, respectively), which completely masks the validity of the additivity approximation.

Even though the individual Benson group contributions carry no physical meaning, it is instructive to compare the values in Table 4 to those originally reported by Benson and co-workers.³¹ The assessment of ten group contributions common to both studies shows that the agreement varies from excellent (C–(B)(C)(H)₂, difference of 2 kJ mol⁻¹) to very poor (O–(B)(H), difference of 110 kJ mol⁻¹). This is affected in part by minor variations in the reference values used in the two works (for example, B–(O)₃≡B–(S)₃≡B–(N)₃, 116.5^74,75vs. 102.1 kJ mol⁻¹)³¹ but even more so by the accuracy of the employed reference data as discussed above. In our case, the fitted group contributions fully reproduce the reference W1X-1 thermochemical data used to derive them in the case of enthalpies (MAD 1.6 kJ mol⁻¹, maximum deviation 11.0 kJ mol⁻¹) and heat capacities (MAD 0.8 J K⁻¹ mol⁻¹, maximum deviation 3.9 J K⁻¹ mol⁻¹), while a slightly poorer fit is found in the case of entropies (MAD 3.2 J K⁻¹ mol⁻¹, maximum deviation −19.1 J K⁻¹ mol⁻¹). Thus, the data in Tables 4 and 5 are fully self-consistent and allow for quick and reliable on-the-fly estimation of thermodynamic properties of a wide range of boron compounds within the limits of the employed parametrization.

To illustrate the usefulness of group contributions given in Tables 4 and 5, we used them to estimate the standard enthalpies of formation of 13 boron compounds for which experimental reference values have been reported by Skinner^77,93 and others (Table 6).⁸⁹ Even though the smallest of the systems in question could easily be subjected to W1X-1 treatment, molecules such as triheptyl- and trioctylborane have more than 20 non-hydrogen atoms, making high-level calculations prohibitively expensive in terms of both time and computational resources. In these cases, the use of group contribution method allows for a quick screening of the reference values for obvious outliers that could easily arise from the use of estimated thermochemical quantities.

Table 6 Reference (Ref.) and estimated (Benson) gas phase standard enthalpies of formation (Δ_fH° 298K, kJ mol⁻¹) of selected boron compounds

Molecule	Ref.	Benson
B^iBu3	–279.9 ± 5.4^77	–274
B^sBu3	–245.6 ± 25.1^77	–242
BHex3	–396.6 ± 10.9^77	–391
BHept3	–457.7 ± 8.4^77	−453
BOct3	–520.9 ± 8.4^77	–515
BF2^iPr	–887 ± 34^77	–832
BBu2(OH)	–546.4 ± 16.7^77	–520
B(OPr)3	–1091.6 ± 10.0^93	−1059
B(OBu)3	–1169.0 ± 10.5^93	−1121
B(SEt)3	–285.3 ± 2.9^89	–269
B(SPr)3	–334.7 ± 3.3^89	–331
B(SBu)3	–394.1 ± 4.2^89	–393
B(SPe)3	–463.2 ± 5.4^89	–454

---

As shown by the data in Table 6, standard enthalpies of formation calculated from Benson group contributions are in good agreement with the reference values in the majority of cases, thereby building confidence that the estimations made in deriving the reference values have been justified. The most obvious outlier is isopropyl difluoroborane, whose reference value, −887 ± 34 kJ mol⁻¹,⁷⁷ is associated with a very large uncertainty. Based on the earlier discussion pertaining to methyl- and ethyldifluoroborane, we conclude that the reference value for isopropyl difluoroborane continues the series and is most likely erroneous.

The estimated standard enthalpies of formation of heavier trialkylthioborates⁸⁹ are in good agreement with the reference values, excluding data for triethylthioborate. In the preceding analyses, we noted that the experimental value for trimethylthioborate,⁸⁹ though given with a narrow 2σ confidence interval, should be adjusted by ca. 40 kJ mol⁻¹ to −199.1 kJ mol⁻¹. We can now use the high-level W1X-1 computational data for it along with a correction term for Me-to-Et substitution on sulphur, −23 kJ mol⁻¹, calculated from experimental enthalpies of formation for dialkylsulfides,³ as another means to estimate the standard enthalpy of formation of triethylthioborate. Adding three correction terms to the W1X-1 enthalpy of trimethylthioborate gives −268 kJ mol⁻¹ as the standard enthalpy of formation of triethylthioborate, in excellent agreement with the estimate based on group contribution values alone. The data for tripropyl- and tributylborate in Table 6 can also be subjected to similar analysis, resulting in standard enthalpies of formation of −1063 and −1126 kJ mol⁻¹, respectively, based on the experimental values for triethylborate⁹⁶ and relevant dialkylethers.³ In further support of our enthalpy estimates in Table 6, we used the W1X-1 method to calculate the standard enthalpy of formation of triethylthioborate, the smallest of the three problematic systems discussed herein. The result, −270.0 kJ mol⁻¹, is another testament of the effectiveness of the group contribution method and the ability of the data in Tables 4 and 5 to yield reliable estimates of thermochemical properties.

As a final exercise demonstrating the usefulness of group contribution values in Tables 4 and 5, we used them to calculate the standard enthalpies of formation for a series of monosubstituted phenylboronic acids. These are an interesting class of compounds with diverse applications in synthesis and biological, medicinal, and materials chemistry.¹⁰⁸ Furthermore, substituted boronic acids are one of the few groups of organoboron compounds whose thermochemical properties have been investigated by computational means using Gaussian-n composite methods, the other being boroxines.^109–111 Specifically, Rao et al. have calculated the standard enthalpies of formation of selected monosubstituted phenylboronic acids and their different isomers at the G3 level of theory (Table 7).¹⁰⁹ As the parent compound is included amongst those in Table 1, we have now estimated the enthalpies of all systems investigated by Rao et al. with the help of group contributions derived herein. The expected uncertainties of the two different approaches are similar, making a comparison between them particularly illustrative.

Table 7 Comparison between calculated (G3) and estimated (Benson) standard gas phase enthalpies of formation (Δ_fH°, 298 K, kJ mol⁻¹) of monosubstituted phenylboronic acids

Molecule	Benson groups^a	G3^109	Benson	Diff.
a Literature values (kJ mol^−1) for Benson groups of carbon and oxygen taken from Domalski and Hearing:^74,75 CB–(CB)2(H) = 13.81, CB–(CB)2(C) = 23.64, C–(CB)(H)3 = –42.26, CB–(CB)2(N) = –1.30, N–(CB)(H)2 = 19.25, CB–(CB)2(O) = –4.75, O–(CB)(H) = –160.30, CB–(CB)2(F) = –181.26. b ortho-Corrections (kJ mol^−1): B(OH)2–CH3≡NO2–CH3 = 2.00, B(OH)2–NH2≡NO2−NH2 = –4.00, B(OH)2–OH≡COOH–OH = –20.00, B(OH)2–F≡CH3–F = –3.30.
C6H5B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 5 × CB–(CB)2(H)	−570.7	−571	0
p-C6H4(CH3)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(C), C–(CB)(H)3	−605.3	−603	2
m-C6H4(CH3)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(C), C–(CB)(H)3	−604.2	−603	1
o-C6H4(CH3)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(C), C–(CB)(H)3, o-corr.^b	−597.0	−601	−4
p-C6H4(NH2)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(N), N–(CB)(H)2	−570.9	−567	4
m-C6H4(NH2)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(N), N–(CB)(H)2	−565.1	−567	−2
o-C6H4(NH2)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(N), N–(CB)(H)2, o-corr.^b	−575.2	−571	4
p-C6H4(OH)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), O–(CB)(H), CB–(CB)2(O)	−751.5	−750	2
m-C6H4(OH)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), O–(CB)(H), CB–(CB)2(O)	−746.1	−750	−4
o-C6H4(OH)B(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), O–(CB)(H), CB–(CB)2(O), o-corr.^b	−765.8	−770	−4
p-C6H4FB(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(F)	−771.7	−766	6
m-C6H4FB(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(F)	−770.0	−766	4
o-C6H4FB(OH)2	CB–(CB)2(B) + B(CB)(O)2, 2 × O–(B)(H), 4 × CB–(CB)2(H), CB–(CB)2(F), o-corr.^b	−784.0	−769	15

---

The results in Table 7 are an excellent demonstration of the value of group contribution methods in thermochemical analyses. Standard enthalpies of formation calculated using Benson's method fully reproduce the G3 data (MAD of 3 kJ mol⁻¹) in all but a single case. This is because the ortho-isomer of fluorophenylboronic acid contains an intramolecular O−H⋯F hydrogen bond, whose enthalpic content has not been parametrized within the used group contributions. A value for it can, however, be obtained using an average of calculated data for related intramolecular hydrogen bonds,¹¹²ca. −10 kJ mol⁻¹, yielding −779 kJ mol⁻¹ for the estimated enthalpy, fully on par with the result from G3 level calculation (−784 kJ mol⁻¹). In contrast to the many hours of CPU time required to obtain the G3 data in Table 7, the estimates based on Benson group contributions were determined within a click of a single button. While this may seem like an insignificant saving of time and resources in the current case, it becomes less so when the number of thermochemical parameters to be estimated is counted in hundreds and/or if the size of the systems in question increases considerably.

Conclusions

It this contribution, we investigated 116 boron compounds with high-level composite quantum chemical methods to determine their thermochemical properties. The results were compared to FPD benchmark values as well as extant experimental data and reference values based on different estimations. The calculated thermochemical properties were used to derive Benson group contributions for standard gas phase enthalpy of formation, entropy, and heat capacity for 52 Benson groups and group pairs involving boron that can, in turn, be employed in estimating thermochemical propertied of compounds that have not been subjected to experimental studies and/or cannot be treated with high-level theoretical methods.

The most important results of this work can be summarized as follows:

High-level W1X-1 results are in excellent agreement with FPD benchmark values and indicate that the experimental gas phase standard enthalpies of formation of key boron compounds are, for the most part, accurate within the reported uncertainties. However, the 2σ confidence intervals of experimental values are often substantially larger than those of computational predictions, which can lead to considerable error, for example, if more than one of them are required to calculate an unknown quantity. In this respect, computational results suggest that the experimental standard enthalpy of formation of orthoboric acid, a key species to which many other reported enthalpies are related, is slightly too endothermic. High-level calculations also show that the standard enthalpies of formation reported for trimethylthioborate and triphenylborane are erroneous and should be replaced with the significantly more accurate W1X-1 predictions.

Many of the experimental thermochemical results reported for boron compounds are based on estimated or by other means approximated quantities. Computational analysis of a selected set of compounds from this category revealed that the very large uncertainties assigned to the reported values are well justified. In many cases, the given 2σ confidence intervals are still too conservative as significant differences are observed between reference values and high-level computational data. Nevertheless, the reported enthalpies are in many cases sufficiently accurate to be used as such in various applications. However, the combined use of these values, such as in a training set for the development of group additivity approaches, is beyond their applicability, and high-level computational data should be used instead to achieve sufficient accuracy.

Computationally derived Benson group contributions show that the approximation of additivity of thermochemical properties holds well also for boron compounds. This allows, for example, the accurate estimation of standard enthalpies of formation of many organoboron species irrespective of their size and complexity, provided that the necessary group contributions have been determined. Application of this approach to a diverse set of boron compounds demonstrated that the experimental reference values for several difluoroboranes, trialkylborates, and trialkylthioborates are noticeable outliers and, therefore, most likely in error. This conclusion was further supported by bond enthalpy considerations and accurate W1X-1 level results. In another example, the standard enthalpies of formation of monosubstituted phenylboronic acids were estimated with the group additivity method and the results fully reproduce the G3 level data with a fraction of the computational cost.

Even though group additivity methods might seem archaic in the era of high-performance computing, they offer a very powerful approach whenever thermochemical data are required for bigger molecular systems or for a large group of compounds. In these cases, high-level quantum chemical calculations become prohibitively expensive or even impossible. The results reported herein can be implemented in any thermochemical software utilizing Benson's approach, allowing their extension to boron compounds and, therefore, to new application areas. We note that even though machine learning models are becoming the state-of-the-art in numerous applications, the prediction of thermochemical properties making no exception, their adaptation beyond elements C, H, N, and O and wide-scale implementation will take time. In this respect, the high-level W1X-1 enthalpies reported herein can also be used to train the algorithms in machine learning models due to their significantly better accuracy over existing experimental data.

Author contributions

H. T. V.: conceptualization, investigation, formal analysis, writing – original draft preparation. J. M. R.: validation, supervision, writing – review & editing. E. T. K.: conceptualization, writing – original draft preparation. H. M. T.: resources, writing – review & editing, supervision, project administration, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Academy of Finland (grant number 324680) and the University of Jyväskylä are gratefully acknowledged for financial support.

References

1. D. Sherwood and P. Dalby, Modern Thermodynamics for Chemists and Biochemists, Oxford University Press, Oxford, 2018.  DOI:10.1093/oso/9780198782957.001.0001.
2. CAS REGISTRY®, https://www.cas.org/cas-data/cas-registry, (accessed August 2022).
3. NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, 20899, Maryland, USA.  DOI:10.18434/T4D303, (accessed August 2022).
4. M. Liu, A. G. Dana, M. S. Johnson, M. J. Goldman, A. Jocher, A. M. Payne, C. A. Grambow, K. Han, N. W. Yee, E. J. Mazeau, K. Blondal, R. H. West, C. F. Goldsmith and W. H. Green, J. Chem. Inf. Model., 2021, 61, 2686–2696,  DOI:10.1021/acs.jcim.0c01480.
5. B. K. Harrison, J. Test. Eval., 2016, 44, 1035–1049,  DOI:10.1520/JTE20160081.
6. E. S. Blurock, V. Warth, X. Grandmougin, R. Bounaceur, P.-A. Glaude and F. Battin-Leclerc, Energy, 2012, 43, 161–171,  DOI:10.1016/j.energy.2012.01.072.
7. Z. Kolská, M. Zábranský and A. Randova, in Thermodynamics – Fundamentals and Its Application in Science, ed. R. M. Morales-Rodriguez, IntechOpen, London, 2012, pp. 135–162.  DOI:10.5772/49998.
8. J. I. Holmes and C. Aubry, J. Phys. Chem. A, 2011, 115, 10576–10586,  DOI:10.1021/jp202721k.
9. J. I. Holmes and C. Aubry, J. Phys. Chem. A, 2012, 116, 7196–7209,  DOI:10.1021/jp303780m.
10. G. Pilcher, in Thermochemistry and Its Applications to Chemical and Biochemical Systems, ed. M. A. V. Ribeiro da Silva, D. Reidel Publishing Company, Dordrecht, 1984, pp. 353–366.
11. E. J. Prosen, W. H. Johnson and F. Y. Pergiel, J. Res. Natl. Bur. Stand., 1959, 62, 43–47,  DOI:10.6028/jres.062.008.
12. W. D. Good and M. Månsson, J. Phys. Chem., 1966, 70, 97–104,  DOI:10.1021/j100873a015.
13. R. Becerra, R. Walsh, in The Chemistry of Organic Silicon Compounds, ed. Z. Rappoport and Y. Apeloig, John Wiley & Sons, Ltd, Chichester, 1998, vol. 2, pp. 153–180.  DOI:10.1002/0470857250.
14. K. A. Peterson, D. Feller and D. A. Dixon, Theor. Chem. Acc., 2012, 131, 1079,  DOI:10.1007/s00214-011-1079-5.
15. A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108,  DOI:10.1063/1.2348881.
16. A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613,  DOI:10.1063/1.1811608.
17. B. Chan and L. Radom, J. Chem. Theory Comput., 2012, 8, 4259–4269,  DOI:10.1021/ct300632p.
18. N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483,  DOI:10.1021/cr00039a007.
19. D. V. Partyka, Chem. Rev., 2011, 111, 1529–1595,  DOI:10.1021/cr1002276.
20. T. S. De Vries, A. Prokofjevs and E. Vedejs, Chem. Rev., 2012, 112, 4246–4282,  DOI:10.1021/cr200133c.
21. Y. Li and X.-F. Wu, Angew. Chem., Int. Ed., 2020, 59, 1770–1774,  DOI:10.1002/anie.201914914.
22. G. R. Owen, Chem. Soc. Rev., 2012, 41, 3535–3546,  10.1039/c2cs15346g.
23. Z. Liu, J. Chai, G. Xu, Q. Wang and G. Cui, Coord. Chem. Rev., 2015, 292, 56–73,  DOI:10.1016/j.ccr.2015.02.011.
24. S. P. Fisher, A. W. Tomich, J. Guo and V. Lavallo, Chem. Commun., 2019, 55, 1684–1701,  10.1039/C8CC09663E.
25. Z. Huang, S. Wang, R. D. Dewhurst, N. V. Ignat'ev, M. Finze and H. Braunschweig, Angew. Chem., Int. Ed., 2020, 59, 8800–8816,  DOI:10.1002/anie.201911108.
26. X. Yang, G. Zhou and W.-Y. Wong, Chem. Soc. Rev., 2015, 44, 8484–8575,  10.1039/C5CS00424A.
27. X. Wang and S. Wang, Chem. Rec., 2019, 19, 1693–1709,  DOI:10.1002/tcr.201800165.
28. M. Scholz and E. Hey-Hawkins, Chem. Rev., 2011, 111, 7035–7062,  DOI:10.1021/cr200038x.
29. J. Magano and J. R. Dunetz, Chem. Rev., 2011, 111, 2177–2250,  DOI:10.1021/cr100346g.
30. K. Hu, Z. Yang, L. Zhang, L. Xie, L. Wang, H. Xu, L. Josephson, S. H. Liang and M.-R. Zhang, Coord. Chem. Rev., 2020, 405, 213139,  DOI:10.1016/j.ccr.2019.213139.
31. S. W. Benson, F. R. Cruickshank, D. M. Golden, G. R. Haugen, H. E. O'Neal, A. S. Rodgers, R. Shaw and R. Walsh, Chem. Rev., 1969, 69, 279–324,  DOI:10.1021/cr60259a002.
32. H. T. Vuori, J. M. Rautiainen, E. T. Kolehmainen and H. M. Tuononen, J. Comput. Chem., 2019, 40, 572–580,  DOI:10.1002/jcc.25740.
33. H. T. Vuori, J. M. Rautiainen, E. T. Kolehmainen and H. M. Tuononen, J. Phys. Chem. A, 2022, 126, 1729–1742,  DOI:10.1021/acs.jpca.1c09980.
34. J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542,  DOI:10.1063/1.481224.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford, Connecticut, USA, 2016. https://www.gaussian.com.
36. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211,  DOI:10.1139/p80-159.
37. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789,  DOI:10.1103/PhysRevB.37.785.
38. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652,  DOI:10.1063/1.464913.
39. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627,  DOI:10.1021/j100096a001.
40. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023,  DOI:10.1063/1.456153.
41. T. H. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253,  DOI:10.1063/1.1367373.
42. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648,  DOI:10.1063/1.438980.
43. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654,  DOI:10.1063/1.438955.
44. O. V. Dorofeeva and T. A. Suchkova, Chem. Phys. Lett., 2018, 698, 218–222,  DOI:10.1016/j.cplett.2018.03.029.
45. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. M. III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 2019.2, a package of ab initio programs, Stuttgart, Germany, 2019. https://www.molpro.net.
46. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253,  DOI:10.1002/wcms.82.
47. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107,  DOI:10.1063/5.0005081.
48. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102,  DOI:10.1063/1.2831537.
49. K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108,  DOI:10.1063/1.3009271.
50. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183,  DOI:10.1063/1.1445115.
51. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291,  10.1039/B204199P.
52. E. F. Valeev, Chem. Phys. Lett., 2004, 395, 190–195,  DOI:10.1016/j.cplett.2004.07.061.
53. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106,  DOI:10.1063/1.2817618.
54. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104,  DOI:10.1063/1.3054300.
55. G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918,  DOI:10.1063/1.443164.
56. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975,  DOI:10.1063/1.453520.
57. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252,  DOI:10.1016/S0009-2614(98)00111-0.
58. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622,  DOI:10.1103/PhysRev.46.618.
59. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585,  DOI:10.1063/1.470645.
60. K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560,  DOI:10.1063/1.1520138.
61. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155,  DOI:10.1016/0003-4916(74)90333-9.
62. B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748,  DOI:10.1103/PhysRevA.33.3742.
63. C. E. Moore, Atomic Energy Levels as Derived from the Analyses of Optical Spectra: Volume I, United States Department of Commerce – National Bureau of Standards, Washington D.C., 1971.
64. M. W. Chase Jr., NIST-JANAF Thermochemical Tables, American Institute of Physics, Woodbury, 4th edn, 1998.
65. E. Storms and B. Mueller, J. Phys. Chem., 1977, 81, 318–324,  DOI:10.1021/j100519a008.
66. B. Ruščić, C. A. Mayhew and J. Berkowitz, J. Chem. Phys., 1988, 88, 5580–5593,  DOI:10.1063/1.454569.
67. J. W. Ochterski, G. A. Petersson and K. B. Wiberg, J. Am. Chem. Soc., 1995, 117, 11299–11308,  DOI:10.1021/ja00150a030.
68. C. W. Bauschlicher, J. M. L. Martin and P. R. Taylor, J. Phys. Chem. A, 1999, 103, 7715–7718,  DOI:10.1021/jp991713a.
69. D. A. Dixon and M. Gutowski, J. Phys. Chem. A, 2005, 109, 5129–5135,  DOI:10.1021/jp0445627.
70. A. Karton and J. M. L. Martin, J. Phys. Chem. A, 2007, 111, 5936–5944,  DOI:10.1021/jp071690x.
71. P. Belotti, Couenne, version 0.5.6, Clemson, USA, 2015. https://www.coin-or.org/Couenne.
72. A. J. Mason, in Operations Research Proceedings 2011, ed. D. Klatte, H.-J. Lüthi and K. Schmedders, Springer, Berlin, Heidelberg, 2012, pp. 401–406.  DOI:10.1007/978-3-642-29210-1_64.
73. A. J. Mason, Opensolver, version 2.9.0, Auckland, New Zeeland, 2017. https://opensolver.org.
74. E. S. Domalski and E. D. Hearing, J. Phys. Chem. Ref. Data, 1993, 22, 805–1159,  DOI:10.1063/1.555927.
75. E. S. Domalski and E. D. Hearing, J. Phys. Chem. Ref. Data, 1988, 17, 1637–1678,  DOI:10.1063/1.555814.
76. J. M. Simmie and K. P. Somers, J. Phys. Chem. A, 2015, 119, 7235–7246,  DOI:10.1021/jp511403a.
77. H. A. Skinner, in Advances in Organometallic Chemistry, ed. F. G. A. Stone and R. West, Academic Press, New York, 1965, vol. 2, pp. 49–114.  DOI:10.1016/S0065-3055(08)60077-5.
78. J. B. Pedley and J. Rylance, in Sussex-N.P.L. computer analysed thermochemical data: organic and organometallic compounds, University of Sussex, Brighton, 1977.
79. T. P. Fehlner and W. S. Koski, J. Am. Chem. Soc., 1964, 86, 2733–2734,  DOI:10.1021/ja01067a052.
80. L. V. Gurvich, I. V. Veyts and C. B. Alcock, Thermodynamic properties of individual substances, Volume 3, Part 1, CRC Press, Boca Raton, 1991, pp. 1–112.
81. D. Feller, D. A. Dixon and K. A. Peterson, J. Phys. Chem. A, 1998, 102, 7053–7059,  DOI:10.1021/jp981734p.
82. D. J. Grant and D. A. Dixon, J. Phys. Chem. A, 2009, 113, 777–787,  DOI:10.1021/jp806627r.
83. G. K. Johnson, H. M. Feder and W. N. Hubbard, J. Phys. Chem., 1966, 70(1), 1–6,  DOI:10.1021/j100873a001.
84. W. H. Johnson, R. G. Miller and E. J. Prosen, J. Res. Natl. Bur. Stand., 1959, 62, 213–217,  DOI:10.6028/jres.062.037.
85. W. H. Johnson, M. V. K. Kilday and E. J. Prosen, J. Res. Natl. Bur. Stand., Sect. A, 1961, 65A, 215–219,  DOI:10.6028/jres.065A.025.
86. D. J. Grant, M. H. Matus, K. D. Anderson, D. M. Camaioni, S. R. Neufeldt, C. F. Lane and D. A. Dixon, J. Phys. Chem. A, 2009, 113, 6121–6132,  DOI:10.1021/jp902196d.
87. G. K. Johnson and W. N. Hubbard, J. Chem. Thermodyn., 1969, 1, 459–468,  DOI:10.1016/0021-9614(69)90004-4.
88. M. von Stackelberg, F. Quatram and J. Dressel, Z. Elektrochem., 1937, 43, 14–28,  DOI:10.1002/bbpc.19370430104.
89. A. Finch, P. J. Gardner and G. B. Watts, Trans. Faraday Soc., 1967, 63, 1603–1607,  10.1039/tf9676301603.
90. M. V. Kilday, W. H. Johnson and E. J. Prosen, J. Res. Natl. Bur. Stand., Sect. A, 1961, 65A, 101–104,  DOI:10.6028/jres.065A.012.
91. M. H. Matus, K. D. Anderson, D. M. Camaioni, T. Autrey and D. A. Dixon, J. Phys. Chem. A, 2007, 111, 4411–4421,  DOI:10.1021/jp070931y.
92. D. A. Dixon and A. J. Arduengo III, Main Group Element Chemistry in Service of Hydrogen Storage and Activation, The University of Alabama, Alabama, USA, 2010.  DOI:10.2172/989180.
93. T. Charnley, H. A. Skinner and N. B. Smith, J. Chem. Soc., 1952, 2288–2291,  10.1039/JR9520002288.
94. H. A. Skinner and N. B. Smith, J. Chem. Soc., 1953, 4025–4028,  10.1039/JR9530004025.
95. H. A. Skinner and N. B. Smith, J. Chem. Soc., 1954, 2324–2329,  10.1039/JR9540002324.
96. H. A. Skinner and N. B. Smith, J. Chem. Soc., 1954, 3930–3934,  10.1039/JR9540003930.
97. J. E. Bennett and H. A. Skinner, J. Chem. Soc., 1962, 2150–2153,  10.1039/JR9620002150.
98. W. C. Steele, L. D. Nichols and F. G. A. Stone, J. Am. Chem. Soc., 1962, 84, 1154–1158,  DOI:10.1021/ja00866a019.
99. W. J. Cooper and J. F. Masi, J. Phys. Chem., 1960, 64, 682–683,  DOI:10.1021/j100834a507.
100. R. F. Porter and S. K. Gupta, J. Phys. Chem., 1964, 68, 2732–2733,  DOI:10.1021/j100791a511.
101. A. Finch, P. J. Gardner, E. J. Pearn and G. B. Watts, Trans. Faraday Soc., 1967, 63, 1880–1888,  10.1039/TF9676301880.
102. W. Govorchin, A. S. Kana'an and J. M. Kanamueller, J. Chem. Thermodyn., 1984, 16, 703–709,  DOI:10.1016/0021-9614(84)90053-3.
103. S. Zu, Z. Xiong and C.-W. Zhou, Phys. Chem. Chem. Phys., 2022, 24, 18582–18599,  10.1039/D2CP01459A.
104. D. S. Farina Jr., S. K. Sirumalla, E. J. Mazeau and R. H. West, Ind. Eng. Chem. Res., 2021, 60, 15492–15501,  DOI:10.1021/acs.iecr.1c03076.
105. H. Janbazi, C. Schulz, I. Wlokas, H. Wang and S. Peukert, Int. J. Chem. Kinet., 2020, 52, 918–932,  DOI:10.1002/kin.21410.
106. R. J. Gills and W. H. Green, ChemSystemsChem, 2020, 2, e190005,  DOI:10.1002/syst.201900051.
107. A. Khalfa, M. Ferrari, R. Fournet, B. Sirjean, L. Verdier and P. A. Glaude, J. Phys. Chem. A, 2015, 119, 10527–10539,  DOI:10.1021/acs.jpca.5b07071.
108. Boronic Acids: Preparation and Applications in Organic Synthesis, Medicine and Materials, 1&2, ed. D. G. Hall, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2nd edn, 2011.
109. N. Z. Rao, J. D. Larkin and C. W. Bock, Struct. Chem., 2017, 28, 945–955,  DOI:10.1007/s11224-016-0897-4.
110. C. W. Bock and J. D. Larkin, Comput. Theor. Chem., 2012, 986, 35–42,  DOI:10.1016/j.comptc.2012.02.007.
111. K. L. Bhat, G. Markham, J. D. Larkin and C. W. Bock, J. Phys. Chem. A, 2011, 115, 7785–7793,  DOI:10.1021/jp202409m.
112. R. E. Rosenberg, J. Phys. Chem. A, 2018, 122, 4521–4529,  DOI:10.1021/acs.jpca.8b01148.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated total energies, energy corrections, and symmetry numbers for correction of optical isomerism and internal and external symmetries (PDF). Optimized molecular coordinates (XYZ). See DOI: https://doi.org/10.1039/d2dt02659g

---