Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Development of magnetocaloric coordination polymers for low temperature cooling
Mario
Falsaperna
and
Paul J.
Saines
 *
*
School of Physical Sciences, Ingram Building, University of Kent, Canterbury, CT2 7NH, UK. E-mail: P.Saines@kent.ac.uk
First published on 1st February 2022
Abstract
Caloric materials have attracted significant interest as replacements for conventional refrigeration, which is becoming increasingly important in our daily lives, yet poses issues for sustainability due to both energy consumption and loss of refrigerants into the atmosphere. Among caloric materials, which are key to solid state cooling technologies, those exhibiting the magnetocaloric effect (MCE), an entropy-driven phenomenon under cycled applied magnetic fields, are promising candidates for cryogenic cooling. These have potential to replace conventional cryogenics, particularly liquid He – an increasingly scarce and expensive resource. Amongst magnetocalorics, coordination polymers containing polyatomic ligands have been shown to be very promising materials due to their large entropy changes at low temperatures. One of the contributing factors to this peformance is their unique structural flexibility, as they can adopt a wide range of structures usually not accessible for conventional materials, such as close-packed metal oxides. The most researched materials for magnetocaloric applications are those containing Gd as their magnetic centre, as the combination of structure and the weakly interacting 4f orbitals of Gd3+ in these materials enables the fabrication of promising magnetocalorics that contain a high density of cations and thus exhibit a high entropy change as a function of their weight and volume at ultra-low cryogenic temperatures. Alongside this, there is a growing interest in magnetocaloric coordination polymers with their magnetocaloric effect optimised for lower applied fields that can be generated using permanent magnets through incorporating other magnetic cations, including lanthanides with greater magnetic anisotropy. When combined with tailored magnetic interactions this leads to promising entropy changes above 4 K, a typical base temperature for many cryogenic applications. This review discusses the most promising magnetocalorics among coordination polymers and MOFs, highlighting their structural characteristics, and concluding with a brief perspective on the future of this field.
1. Introduction
1.1 Conventional refrigeration and the alternative of solid-state caloric materials
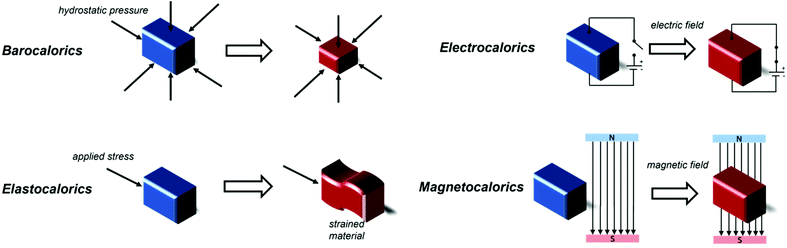
One of the major challenges of the past thirty years is combating climate change, which requires the reduction of energy consumption and of environmentally harmful greenhouse gas emissions. The International Institute of Refrigeration (IIR) estimates that, as of 2019, there are approximately 5 billion refrigeration, air conditioning and heat pump units worldwide that contribute to climate change, with 63% of this contribution being indirect due to the electricity consumption required for the functioning of the apparatuses and around 37% of it directly caused by leakage of refrigerant gases, e.g. fluorinated molecules.1 With refrigeration becoming increasingly important both in our daily lives as well as for more specific applications, such as in the food industry and food transportation,2 medicine and science,3,4 it is vital to find alternatives to traditional gas compression\expansion refrigeration technologies,5 for which, in general, energy efficiencies are typically limited to a maximum of 40–50% of Carnot efficiency;6 a theoretical thermodynamic cycle which provides insight into the upper limit a thermodynamic system achieves during conversion of heat into work. Limitations to their efficiency are often determined by technological limitations of the components of the refrigerating device, such as the compressor.6Solid-state caloric materials are an alternative for gas-based refrigeration, avoiding emissions of environmentally harmful or non-renewable gases. Furthermore, the predicted cooling efficiency for some of these materials is higher than that of traditional gas cooling, with above 60% of Carnot efficiency attained by some prototypes.7 It is possible to identify four main classes of materials for refrigeration depending on the external factors that drive their caloric effects, i.e. their heating and cooling process. These are namely barocalorics, elastocalorics, electrocalorics and, finally, magnetocalorics, on which this review focuses (see Fig. 1). In all cases, the cooling step typically occurs via an entropically driven process when the applied stimulus is removed. Electrocaloric materials are solids exhibiting the electrocaloric effect (ECE), where adiabatic depolarization upon the application of an external electric field results in a temperature change of the material.8 Polymeric materials such as the copolymer polyvinylidene fluoride-tetrafluoroethylene (PVDF-TFE) have shown to be promising candidates for electrocaloric applications,9 along with Rochelle salt (KNaC4H4O6·4H2O),10 KTaO3,11 BaTiO3 and SrTiO3,12,13 and NH4HSO4.14 It is also possible to achieve cooling with the application of mechanical stress or pressure when elastocaloric or barocaloric (BCE) materials are used. In materials exhibiting the elastocaloric effect (eCE), the change in temperature is caused by the uniaxial stress-induced Martensitic phase transformation process. Application of mechanical stress decreases the entropy of the material and releases latent heat, this is reversed when the mechanical stress is removed enabling the material to absorb heat from its surroundings.15 Elastocaloric materials focus on alloys, including Ni–Ti and Cu–Zn–Al,16 alongside Cu-, Fe- and Ni–Ti-based superelastic alloys.17 Barocalorics materials exhibit a thermal response due to isotropic compression from hydrostatic pressure, typically associated with a concurrent first-order phase transition.18 The BCE has been identified in many materials,19–21 including elastomeric polymers,22,23 including natural rubber,24,25 plastic crystals,26 magnetic memory shape alloys27 and coordination polymers, particularly inorganic–organic perovskites that have shown the so-called giant barocaloric effect, including [TPrA][Mn(dca)3],28,29 [(CH3CH2CH2)4N]Cd[N(CN)2]3([TPrA]Cd[dca]3)30 and [(CH3)4N]Mn[N3]3.31
The final group of caloric solids are magnetocalorics, which were first discovered by Weiss and Picard in 1917.32,33 The magnetocaloric effect (MCE) is driven by the application and removal of an external magnetic field. Many magnetocalorics show promising magnetocaloric effects, with some prototype devices existing for applications such as domestic refrigeration and air-conditioning,34 and as established candidates for subkelvin cooling with predicted energy efficiencies higher than 60% of the Carnot cycle.35,36 The so-called giant MCE (GMCE) is associated with first-order magneto-structural transitions that enable significantly higher magnetocaloric effects than known materials near ambient temperatures and modest applied magnetic fields, enabling their use in near ambient temperature applications. This term was first coined for Gd5Si2Ge2 at nearly 15 J kg−1 K−1 for a 2–0 T field change, double that of the best near ambient temperature magnetocalorics then known.37 Conversely magnetocalorics for low temperature cooling rely on gradual field induced magnetic ordering of paramagnetic spins.36,37
Amongst caloric materials magnetocalorics are particularly promising and thermodynamically efficient candidates for low temperature cooling. Cryogenic cooling has become increasingly relevant recently for technologies that are dependent on cooling to low and ultra-low temperatures such as hydrogen liquefaction,38 quantum computing,39 spintronics,40 medical imaging,3 and high-performance infrared sensing.41 Liquid cryogenics are conventionally used for this purpose, with liquid helium vital for reaching temperatures below the boiling point of liquid nitrogen (77 K), including the millikelvin regime. In particular, 4He can reach 2 K, while mixtures with 3He can be used in dilution refrigerators to reach temperatures below 0.1 K. With liquid helium becoming an increasingly scarce and expensive resource, it is essential to find alternatives suitable for low-temperature cryogenic cooling.42
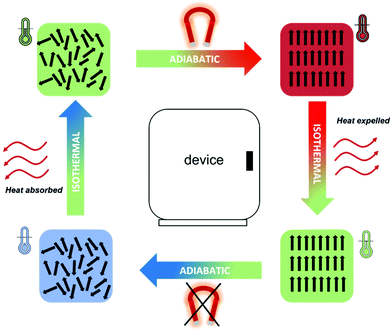
In magnetocalorics used at low temperatures, the application of an externally applied magnetic field induces a transition from a disordered paramagnetic state to an ordered magnetic state; the orientation of the magnetic moments along the direction of the field in magnetocaloric materials leads to a temperature change, ΔTad, in an adiabatic process. Heat can then be removed from the system whilst keeping the spins aligned with the magnetic field under isothermal conditions. In a subsequent step, removing the magnetic field under adiabatic conditions will result in the material cooling down due to the disordering of the spins. Due to this final temperature change, which results in the material having a lower temperature than its initial state, the material can then be used as a heat sink for cooling utilising the magnetic refrigeration process (see Fig. 2). The biggest accomplishment of magnetic refrigeration lies in the fact that the cooling process does not rely on the use of gases, therefore no refrigerant leakage or CO2 emission is possible, resulting in a much more environmentally friendly process.
1.2 Theory and measurements of the magnetocaloric effect
The MCE is an intrinsic property of all magnetic materials,43 but in order to classify them in terms of their magnetocaloric effect some parameters are necessary.44 The most commonly reported parameter in literature is the maximum magnetic entropy change, −ΔSmaxm (where the negative stems from the entropy conventionally decreasing when the field is applied) for a given applied magnetic field change, typically reported with respect to the mass in J kg−1 K−1. A second parameter, the volumetric entropy change, is easily obtained by considering the product between the former and the density of the material (−ΔSmaxm × ρ) and is reported as mJ cm−3 K−1. The magnetic entropy change can be determined by either direct or indirect measurements. In the former case, the total heat capacity CT of the material is measured, with this being the result of electronic Ce, lattice Cl and magnetic Cm contributions. Therefore, it is necessary to isolate the magnetic contribution, Cm, to determine the magnetic entropy change ΔSm, the relationship between the two given by ΔSm = ∫(Cm/T)dT. Indirect measurement of ΔSm requires determining the isothermal magnetisation of a material and applying the Maxwell relation, ΔSm(T,ΔH) = ∫[δM(T,H)/δT]HdH, therefore requiring measurements to be carried out as a function of temperature for a variety of magnetic fields. The indirect approach is the more commonly used approach in the initial characterisation of magnetocalorics. While the Clausius–Clapeyron method is an indirect method for calculating ΔSm for magnetocalorics that rely on first order transitions, as is the case for “giant” magnetocalorics such as Gd5Si2Ge2,45 this is largely not relevant for magnetocalorics for low temperature applications that rely on more gradual changes. A third parameter, the aforementioned adiabatic temperature change ΔTad, is a more direct measure of magnetocaloric effect. Nevertheless, this parameter is less well characterised for most new magnetocalorics as determining the adiabatic temperature, ΔTad, requires a detailed understanding of how its heat capacity changes as a function of temperature and applied field. This additional information often limits the availability of ΔTad for new materials, whose magnetocaloric effect parameters have been assessed by indirect measurements.Theoretically, the maximum entropy change −ΔSmaxm that can be extracted from a material corresponds to nRln(2J + 1), where R is the universal gas constant, n the number of unpaired spins and J the total angular momentum.46 Increasing the magnetic moment is then essential to increase the maximum realisable −ΔSmaxm, as well as minimising the diamagnetic components of the material, such as non-magnetic cations and coordination ligands, which negatively affects the entropy change with respect to its weight and volume. As a non-zero orbital angular momentum might result in zero-field splitting (ZFS) effects, which are responsible for splitting the ground spin state into a number of degenerate states and, as a consequence, lowering the magnetic entropy change, most magnetocalorics studied have negligible orbital momentum. Thus their maximum expected entropy corresponds to nRln(2S + 1), and it is therefore entirely dependent on the magnetic degrees of freedom, as expressed by the term (2S + 1), the spin multiplicity. Therefore, when choosing an appropriate metal for the fabrication of magnetocaloric materials, gadolinium is considered the best candidate, as the 4f orbitals of the Gd3+ cation are exactly half-filled, resulting in a total spin quantum number of S = 7/2, and due to it being strongly isotropic, i.e. it possesses zero orbital angular momentum and its magnetism is determined only by its spins, preventing any ZFS effects. As a result, considerable effort has been put into the design and characterization of gadolinium-based materials with oxides such as gadolinium gallium garnet Gd3Ga5O12 (GGG) and the iron-substituted derivatives Gd3(Ga1−xFex)5O12 (GGIG) well established as candidates for low-temperature cooling, superseding traditional metal salts due to the higher −ΔSmaxm, which stems from the higher density of magnetic cations in these oxides.47
More recently, molecule-based magnetic materials have been proposed for low- and ultra-low temperature applications.47 Molecule-based materials can adopt a wide variety of structures that are not easily obtained with traditional oxides due to the tendency of these to adopt close-packed structures. This, combined with their lack of significant intermolecular magnetic interactions, enables these molecule-based magnetocalorics to be used at lower temperatures. However, research on these materials has recently lost traction as their −ΔSmaxm with respect to their weight and, particularly, volume, is limited due to the use of large ligands for the fabrication of their structures.47,48
1.3 Beyond conventional materials: coordination polymers
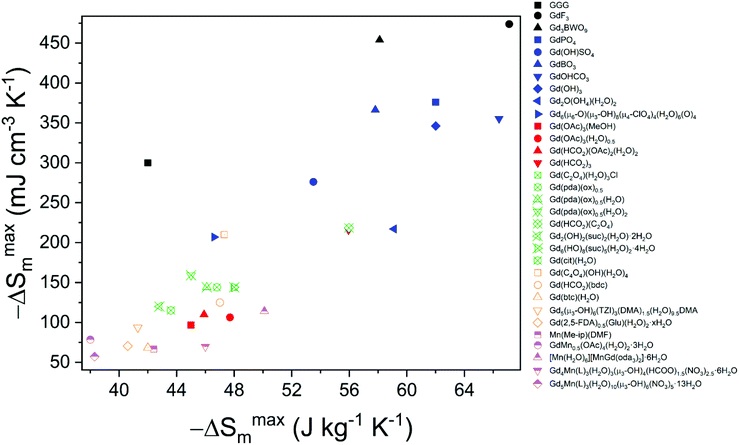
In contrast to discrete complexes and metal oxides, there has recently been significant interest in dense coordination polymers, including metal–organic frameworks (MOFs), as potential magnetocaloric materials.47,49–51 IUPAC provisionally defines coordination polymers as a coordination compound continuously extending in 1, 2 or 3 dimensions through coordination bonds.52 While according to IUPAC the definition of coordination bond is a covalent bond where two of the electrons forming the bond come from the same chemical entity, as the IUPAC definition itself acknowledges, the term “coordination” is also used with a wider connotation, generally to define the ligands surrounding a metal centre regardless of whether the character of the bond is covalent or ionic. With this in mind, and with the balance of covalent and ionic bonds being difficult to clearly discern for many materials, in this review we have used the term coordination polymers to describe any extended structures in which metals are linked by polyatomic ligands. The focus on polyatomic ligands is to avoid considering those more well-known compounds with monodentate ligands that would be generally considered salts e.g. oxides or halides. In doing so, we acknowledge this restriction is somewhat arbitrary and some of the materials reviewed here will likely possess predominantly ionic bonds and that some of the materials included may be considered by others to simply be salts. The varied structural topologies of coordination polymers offer more freedom in the tuning of their magnetic properties than is commonly found in oxides due to the structure directing effect of their polyatomic ligands leading to a variety of structures rather than the close packed arrays typically adopted by simple salts.53The variety of structures accessible with coordination polymers makes it possible to design three-dimensional structures containing low-dimensional motifs, such as one-dimensional magnetic chains or two-dimensional magnetic sheets, via the structure direct effect of the ligand.47,53 When these structural motifs are well isolated from one another, structures with a higher density of magnetic cations with long-range order occurring at very low temperatures can be realised due to the resulting weak interactions between these units. In addition to this, it is possible to design structures featuring competing magnetic interactions due to the arrangement of the cations in the crystal lattice, so-called geometric frustration,54 to further suppress the onset of long-range magnetic order to much lower temperatures and, therefore, allow for an even higher density of magnetic cations in the structure. Typically, this implies designing structures containing triangular motifs, responsible for the competition of antiferromagnetic interactions, such as the two-dimensional triangular or Kagome lattices,54,55 as well as pyrochlore structures,54 such as that of Gd2Ti2O7.56 While conventional materials can exhibit geometric frustration, GGG being a classic example,57 coordination polymers expand the scope for this through the plethora of topologies they can adopt. Coordination polymers featuring low dimensional units and/or magnetic frustration have been suggested to be excellent candidates for low-temperature cooling, highlighting that attention to the structural characteristics of materials plays a key role in the optimisation of their MCE. The combination of lower ordering temperatures in coordination polymers compared to metal oxides, which enables them to remain useful magnetocalorics at lower temperatures, and higher density of magnetic cations than is possible in molecular complexes, greatly enhances their −ΔSmaxm as a function of weight and volume, making them very promising candidates as magnetocalorics materials.47 Furthermore many coordination polymers have already been reported to have greater −ΔSmaxm than the benchmark oxides, such as GGG.
The coordination polymers and dense MOFs with the highest −ΔSmaxm, approximately 40 J kg−1 K−1 or higher for large field changes, tend to be found amongst materials with either purely inorganic (in which there are no C–H bonds) or carboxylate ligands. The majority of the magnetocaloric coordination polymers studied to date incorporate only lanthanides, primarily Gd3+, as their magnetic centres, although there has been recent interest in a handful of systems that feature both 3d and 4f metals as a future potential route to enhancing their magnetocaloric properties as seen previously in molecular magnetocalorics.47 In this review we will discuss the most promising magnetocalorics coordination polymers and dense MOFs known to date across these categories.
2. Coordination polymers containing inorganic ligands
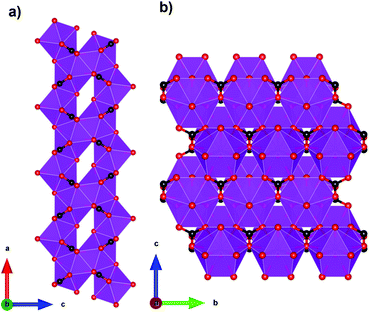
Coordination polymers with inorganic ligands are attractive as their smaller polyatomic anions typically allow denser packing of their magnetic cations than systems with larger organic ligands, increasing the magnetocaloric entropy change as a function of volume. Among inorganic coordination polymers, GdPO4 has attracted significant interest for having a higher −ΔSmaxm than GGG.58 At room temperature, this material adopts a monoclinic P21/n structure in which the nine-coordinate Gd3+ node is bound to four oxygens from the distorted tetrahedral phosphate groups (see Fig. 3), with an average Gd–O distance of 2.47 Å, and linked together in a chain-like fashion.59 The reported magnetic entropy change −ΔSmaxm for this material is 62.0 J kg−1 K−1 (376 mJ cm−3 K−1) at 2.1 K and an applied field change of 7 T, higher than that of the benchmark material, GGG, under the same conditions.47,58 The magnetic properties, including the MCE, of this material are largely attributed to the high density of Gd3+ cations in the structure, coupled with the presence of weak magnetic interactions and the low magnetocrystalline anisotropy, allowing for magnetic order only below 60 mK as a dipolar antiferromagnet.58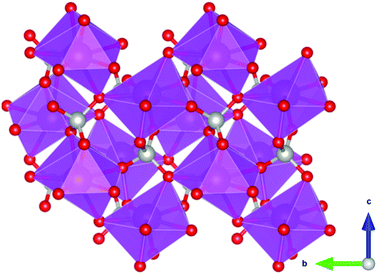 | ||
| Fig. 3 Crystal structure of GdPO4. The GdO9 polyhedra are bridged by the tetrahedral phosphate groups. Colour codes: Gd: purple, P: grey, O: red. | ||
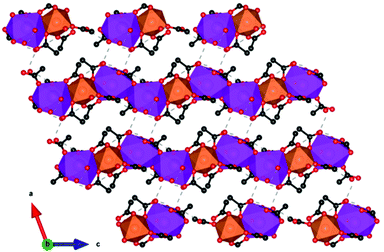
More recently, a Gd(OH)SO4 coordination polymer has been synthesised and it has been shown to exhibit a −ΔSmaxm comparable to that of GGG.60 This material crystallises in a monoclinic P21/n structure with the asymmetric unit consisting of one Gd3+ cation, one sulfate ion and a single hydroxy anion. The Gd cations are nine-coordinate and form a capped square antiprism coordination geometry, with six oxygens from the SO42− ligands, with two of the sulfate oxygens being μ2-bridging and three oxygens from the OH− anion, this being μ3-bridging.61 The Gd3+ cations are connected to form 1D-chains along the a-axis, and these further extend via hydroxy oxygens along the bc direction to form a three-dimensional framework (see Fig. 4).61 The magnetic coupling is negligible in this material with a Weiss constant, θW, of about −0.2 K. The magnetic entropy change −ΔSm of this material was extracted from magnetisation data using the Maxwell relation, with a −ΔSmaxm value of 53.5 J kg−1 K−1 (276 mJ cm−3 K−1) obtained at 2 K and for a 7 T field change, demonstrating a higher gravimetric −ΔSmaxm than GGG, but a comparable volumetric −ΔSmaxm to the benchmark material.47,62
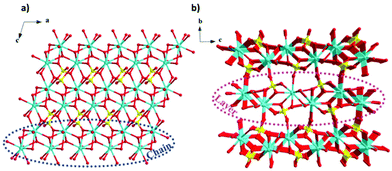 | ||
| Fig. 4 (a) Crystal structure of Gd(OH)SO4, with one-dimensional chains propagating along the a-axis and forming layers along the ac-plane, (b) with the latter stacking along the b-axis. Colour codes: Gd: cyan, O: red, S: yellow. The hydrogen atoms have been omitted for clarity. Reproduced from ref. 60 with permission from the Chinese Chemical Society (CCS), Institute of Chemistry of Chinese Academy of Sciences (IC), and the Royal Society of Chemistry. | ||
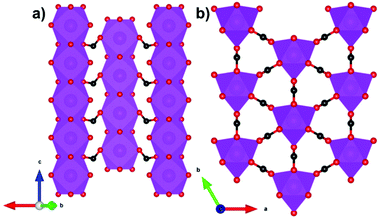
Another family of coordination polymers, the lanthanide orthoborates LnBO3, have proven to be viable magnetocalorics for liquid helium temperature regimes at both high and low applied magnetic fields.63 These materials adopt a monoclinic C2/c structure with triangular layers of Ln3+ cations separated by sheets of three-membered rings of corner sharing BO45− tetrahedra that form isolated B3O99− units.63 While the existence of antiferromagnetic interactions within triangular layers suggest the possibility of geometric frustration, the monoclinic symmetry results in the triangles being scalene and the difference in Ln–Ln distances among different triangles make this less likely than in higher symmetry systems.64,65 Consistent with this it was found that GdBO3 has a low frustration index, f, (θW, divided by Néel temperature) of f = 5.4/1.7 = 3.1, and although the Er and Dy analogues possess f > 10, consistent with highly frustrated systems it cannot be ruled out that this is partly due to crystal field effects on θW.63 In GdBO3, the average in-plane Gd–Gd distance is 3.84 Å, while the average interplane distance is 4.52 Å. The maximum magnetic entropy change −ΔSmaxm for this material is found to be 57.8 J kg−1 K−1 (366 mJ cm−3 K−1) for a field change of 9 T at 2 K.63 While this value is higher than the benchmark material, GGG, under the same conditions, the high magnetic field strength would limit its application to where superconducting magnets are employed. For a 2 T field change, −ΔSmaxm drops significantly, reaching values below 10 J kg−1 K−1 (about 60 mJ cm−3 K−1). Amongst other members of the LnBO3 series, it is worth noting that DyBO3 has been shown to outperform the Gd analogue at lower applied fields, with a −ΔSmaxm of 13.9 J kg−1 K−1 (92.5 mJ cm−3 K−1) for a field change of 2 T at 2 K.
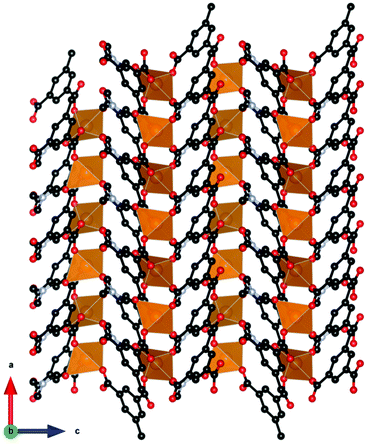
Among inorganic coordination polymers, the LnOHCO3 frameworks have the highest −ΔSmaxm as a function of weight. Work on these compounds started with GdOHCO3,66,67 which adopts an orthorhombic P212121 structure in which the Gd3+ cation is 10-coordinate, binding to five carbonate anions, three in a chelating fashion, and two hydroxide groups. These polyhedra connect in a face-sharing fashion to form zig-zag chains with short 3.82 Å Gd–Gd contacts (see Fig. 5). These chains are packed in a dense and distorted triangular lattice via edge-sharing connectivity. The MCE effect was determined via the Maxwell equation from the magnetisation data to give a −ΔSmaxm of 66.4 J kg−1 K−1 (355 mJ cm−3 K−1) at 1.8 K for a field change of 7 T, which is very similar to that determined from heat capacity measurements, 67.1 J kg−1 K−1 (359 mJ cm−3 K−1). An impressive ΔTad of 24 K was determined for a field change of 9 T from heat capacity measurements, which is the highest reported for a coordination polymer.
Interest in the magnetocaloric properties of GdOHCO3 led Dixey et al.68 to an investigation of other heavier lanthanides from Tb–Er, which were confirmed to adopt orthorhombic P212121 symmetry via neutron diffraction.68 Among these materials, TbOHCO3 and DyOHCO3 demonstrated promising magnetocaloric properties with higher entropy change than GdOHCO3 for field changes lower than 2 T, the maximum field strength achievable using a permanent magnet at temperatures above 4 K, where they could be potentially used to replace liquid He for a wider range of cryogenic cooling temperatures. Specifically, DyOHCO3 has a −ΔSmaxm of 33.3 J kg−1 K−1 (186 mJ cm−3 K−1) at 4 K and a field change of 2 T while TbOHCO3 has a −ΔSmaxm of 301.0 J kg−1 K−1 (169 mJ cm−3 K−1) compared to a value of 29.5 J kg−1 K−1 (158 mJ cm−3 K−1) for GdOHCO3 under the same conditions. The differences in −ΔSmaxm values between these compounds are even greater for a field change of 1 T (17.6 and 20.8 J kg−1 K−1, respectively for Dy and Tb; cf. 11.7 J kg−1 K−1 for Gd). These results are impressive when compared to the benchmark garnet oxides, with DyOHCO3 showing improved magnetocaloric properties than GGG's maximum for a 2 T field change up to 8 K. Unfortunately, attempts to optimise magnetocaloric entropy change further through synthesising solid solutions Gd1−xTbxOHCO3 and Gd1−xDyxOHCO3 were unsuccessful, with heterometallic compounds having lower entropy changes compared to the homometallic materials.
A further study by Dixey et al.69 indicated that the LnOHCO3 compounds with improved magnetocaloric properties above 4 K all exhibited significant magnetic diffuse scattering in their correlated paramagnetic phases. Reverse Monte Carlo (RMC) fits indicated this was a result of having non-collinear ferromagnetic coupled Ising-like spins within the zig-zag chains packed into a frustrated antiferromagnetic lattice. They suggested such arrangements allows the ferromagnetic Ising chains to be readily aligned with low applied magnetic fields once the antiferromagnetic interactions are supressed by it, therefore maximising the change in magnetisation under these conditions, resulting in a higher MCE, as expressed by the Maxwell relation. This is in contrast to GdOHCO3, which, as is typical in Gd coordination polymers, has predominantly antiferromagnetic coupling with a θW of about −1 K.55 Therefore, geometric frustration likely plays a key role in the optimisation of the MCE for this material, and indicates the important role structure plays in achieving such an optimisation, suggesting particular attention needs to focused on fabricating materials with similar structural motifs.
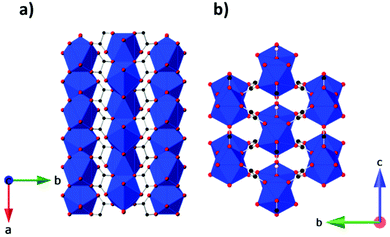
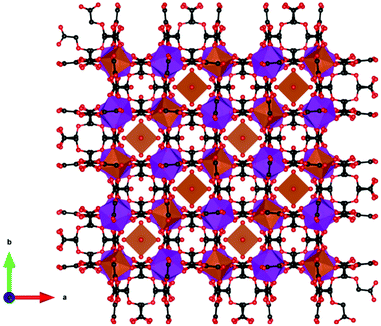
Other inorganic coordination polymers have also been reported to have high magnetic entropy changes. This includes weakly antiferromagnetically coupled Gd(OH)3 whose −ΔSmaxm is comparable to GdOHCO3 at 62.0 J kg−1 K−1 (346 mJ cm−3 K−1) at 2 K and 7 T, as determined from magnetisation data.70 This material adopts P63/m hexagonal symmetry with nine-coordinate Gd3+ connected via 9 different μ3-OH− groups into a 3D structure with 1D hexagonal channels (see Fig. 6). Gd2O(OH)4(H2O)2 is another promising material,70 with −ΔSmaxm values, determined from magnetisation data, of 59.1 J kg−1 K−1 at 2 K and 7 T, although its lower density leads to a significant decreased value as a function of volume of 217 mJ cm−3 K−1. This orthorhombic Cmcm structure features two distinct Gd3+ ions which are eight and nine coordinate. These are connected to form a 2D structure via connection of adjacent Gd2 ions through two OH− and one O2− bridges along the c-axis with adjacent Gd1 ion connected through two OH− bridges along the same direction; adjacent Gd1 and Gd2 ions are connected through three OH− bridges along the b-axis. These 2D structures are held together along the a-axis via hydrogen-bonding between the coordinated water molecules from adjacent 2D layers thus generating a 3D framework. A final inorganic polymer with −ΔSmaxm above 40 J kg−1 K−1 is [Gd6(μ6-O)(μ3-OH)8(μ4-ClO4)4(H2O)6](O)4,71 which crystallises in a monoclinic C2/c structure with relatively significant antiferromagnetic coupling (θW = −5.5 K) and has a −ΔSmaxm equal to 46.6 J kg−1 K−1 (207 mJ cm−3 K−1) at 2.5 K for a field change of 7 T, based on magnetisation data. This material has a complex structure comprised of hexanuclear octahedral clusters and four crystallographically distinct Gd cations. The [Gd6(μ6-O)(μ3-OH)8]8+ distorted octahedral clusters have six Gd3+ around one central μ6-oxo central atom and are connected by eight face-capping μ3-OH bridges. All Gd3+ cations are coordinated to nine oxygen atoms in a mono-capped square antiprism geometry. The octahedral clusters are connected to each other to form a 3D framework through ClO4− bridges, with every cluster bridged via twelve ClO4− ligands with every ligand linking three Gd6 clusters.
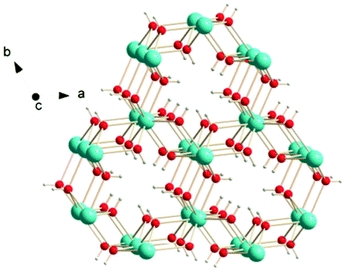 | ||
| Fig. 6 Crystal structure of Gd(OH)3. Colour codes: Gd: cyan, O: red, H: white. Reproduced from ref. 70 with permission from the Royal Society of Chemistry. | ||
3. Carboxylate-based coordination polymers
The other family of promising lanthanide coordination polymers that have shown significant promise as magnetocaloric materials are carboxylate-based frameworks. Amongst these materials those with extended 2D and 3D structures can generally be considered to be MOFs, albeit most of these are dense and, thus, lack significant porosity. Generally, these materials can be thought of as containing either small monocarboxylate ligands, slightly larger linear dicarboxylates or bulker aromatic carboxylates; where materials in this review contain more than one of these ligand types we have classified them according to the largest ligand type. The larger ligands involved in these materials, compared to purely inorganic coordination frameworks, leads to less densely packed structures, therefore, while their −ΔSmaxm as a function of weight are often similar, these coordination polymers typically have lower entropy changes as a function of volume.3.1 Monocarboxylate-based polymers
The denser monocarboxylate frameworks, which amongst the polymers containing organic ligands are generally reported to have the highest −ΔSmaxm, are either based on acetate or formate ligands. Acetate compounds commonly adopt 1D chain structures with coordination bonding only within these chains, with three such materials being reported to have high magnetocaloric entropy changes. Two examples of this are Gd(OAc)3(MeOH) and Gd(OAc)3(H2O)0.5, which adopt monoclinic P21/c and Cc symmetry, respectively (see Fig. 7).72 In Gd(OAc)3(MeOH), the Gd3+ are in a nine-coordinate capped square-antiprism geometry, while in Gd(OAc)3(H2O)0.5 there are two Gd in nine-coordinate, capped square-antiprismatic, and eight-coordinate, square antiprismatic, geometries. In both cases, the Gd within the chains are bridged by three acetate ligands, in a mixture of η2:η1 and syn–syn acetate geometries with Gd–Gd distances of 4.06 Å and 6.46 Å for Gd(OAc)3(MeOH) and Gd(OAc)3(H2O)0.5, respectively. In Gd(OAc)3(H2O)0.5 there are interchain hydrogen bond interactions between the water and acetate carboxylate groups while Gd(OAc)3(MeOH) only has weaker interchain interactions. Gd(OAc)3(MeOH) and Gd(OAc)3(H2O)0.5 have very weak ferromagnetic and antiferromagnetic coupling, respectively, with θW of −0.22 and 0.34 K. Magnetisation measurements indicate a −ΔSmaxm = 45.0 J kg−1 K−1 (96.8 mJ cm−3 K−1) and 47.7 J kg−1 K−1 (106 mJ cm−3 K−1) for a 7 T field change at 1.8 K for Gd(OAc)3(MeOH) and Gd(OAc)3(H2O)0.5, respectively.A third 1D acetate compound reported to have high magnetocaloric entropy change is weakly antiferromagnetically coupled Gd(HCO2)(OAc)2(H2O)2,73 which adopts monoclinic P21/m symmetry. Here it is the formate co-ligand which connects Gd within the chain, with Gd–Gd distances of 6.58 Å (see Fig. 8). Adjacent chains are rotated by 180° which allows for the formation of a dense network of hydrogen bonds in one direction perpendicular to the chain while chains in the third dimension are separated by methyl groups for the acetate ligand resulting in only weak intermolecular forces in this direction. The magnetocaloric properties of this compound were evaluated through both magnetisation and heat capacity data, both determining that −ΔSmaxm has a maximum of 45.9 J kg−1 K−1 (110 mJ cm−3 K−1) at 1.8 K for a field change of 7 T.
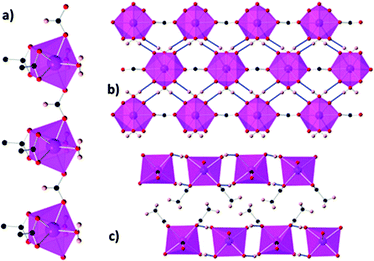 | ||
| Fig. 8 (a) Coordination chains of Gd(HCO2)(OAc)2(H2O)2 along the b-axis; (b) hydrogen-bonded chains forming sheets on the bc-plane; (c) packing of the sheets along the b-axis. Colour codes: Gd: purple, O: red, C: black, H: pink. Reproduced from ref. 73 with permission from the Royal Society of Chemistry. | ||
The other formate-containing compound in this grouping reported to have significant magnetocaloric properties is Gd(HCO2)3,74 which adopts an R3m rhombohedral structure featuring face-sharing chains with neighbouring chains connected through the formate ligand to yield a triangular lattice (see Fig. 9). The Gd cations are nine-coordinate in a tricapped trigonal prismatic geometry. The MCE of Gd(HCO2)3 is evaluated both indirectly from the magnetisation data and directly from heat capacity measurements. In the former case, the magnetic entropy changes for different applied field changes are obtained, which are similar to those from heat capacity data. At ∼1 K and for a field change of 7 T, the −ΔSmaxm is 55.9 J kg−1 K−1 or 216 mJ cm−3 K−1, with the large volumetric entropy change enabled by the dense structure. ΔTad was estimated to be approximately 22 K from heat capacity measurements. Direct measurements under quasi-adiabatic conditions suggest values of 2.47 and 0.51 K during magnetisation and demagnetisation for a 1–0 T field change, consistent with the values obtained from the indirect entropy-based measurements for such changes. The relative cooling power (RCP) of Gd(HCO2)3 was also estimated to be 522 mJ cm−3 K−1, which is higher than the 479 mJ cm−3 K−1 reported for Gd3Ga5O12.
The high entropy change of Gd(HCO2)3 has led to the investigation of analogues containing heavier lanthanides from Tb–Er.75 While the −ΔSmaxm of these compounds is lower at high fields than for Gd(HCO2)3, for field changes less than 2 T and for temperatures above 4 K Tb(HCO2)3 and, to a smaller extent, Ho(HCO2)3, have higher −ΔSm compared to the Gd analogue. Specifically, Tb(HCO2)3 outperforms Gd(HCO2)3 above 6 K for a 2–0 T field change and both Tb(HCO2)3 and Ho(HCO2)3 do so above 4 K for a 1–0 T field change, although the difference between Ho(HCO2)3 and Gd(HCO2)3 is very modest. Unlike the LnOHCO3 series the mixing of lanthanide cations is shown to be a promising route to optimising higher temperature and lower applied field MCE behaviour. In the series Gd1−xTbx(HCO2)3, for x = 0.2 and 0.4 and a field change of 1 T, there is improvement in the magnetic entropy change above 4 K compared to Gd(HCO2)3 with only a minimal loss in −ΔSmaxm at 2 K.
Strong diffuse magnetic scattering is observed from neutron diffraction of the paramagnetic phase of Tb(HCO2)3 with RMC fits indicating the presence of Ising-like spins parallel to the chain direction with strong ferromagnetic correlations within these units.75 There are also weaker frustrated antiferromagnetic interchain correlations within the triangular lattice. It has been suggested that the high entropy change of Tb(HCO2)3 under low applied fields is caused by ready alignment of the ferromagnetic Ising chains with the applied field once the interchain antiferromagnetic interactions are supressed. Further work has shown that this combination of interactions in Tb(HCO2)3 leads to a unique triangular Ising antiferromagnetic state below 1.6 K, which has long range 1D magnetic order with only short range antiferromagnetic correlations between these chains.76 Strong magnetic diffuse scattering has also been uncovered in Ho(HCO2)3 indicating the presence of similar magnetic interactions as in Tb(HCO2)3 while all other Ln(HCO2)3 lack such correlations, suggesting the ferromagnetic Ising chains in these systems is key to improving their −ΔSm at higher temperatures as opposed to the predominantly antiferromagnetic interactions in Gd(HCO2)3.77
3.2 Linear dicarboxylate-based polymers
Another extensively studied family of carboxylate magnetocalorics are those with linear dicarboxylate ligands, principally those containing the relatively small oxalate, succinate and citrate ligands. The oxalate ligand is the simplest of these, being comprised of two connected carboxylate groups. The first promising magnetocaloric to be reported using the oxalate ligand was very weakly antiferromagnetically coupled Gd(C2O4)(H2O)3Cl.78 This adopts a P21/n monoclinic structure with the Gd in a nine-coordinate capped squared antiprismatic geometry. Gd dimers, formed by edge-sharing polyhedra with an intradimer separation of 4.42 Å, are connected into 2D layers with shorter Gd–Gd distances of 5.84 Å along the a-axis, through μ4–η1:η2:η1:η2 bonded oxalates, and 6.31 Å along the c-axis, through μ–η2:η2 oxalates (see Fig. 10). The structure includes Owater–H⋯Ooxalate intralayer and Owater–H⋯Owater and Owater–H⋯Cl interlayer hydrogen bonds. Indirect methods indicate a −ΔSmaxm of 48.0 J K−1 kg−1 (144 mJ cm−3 K−1) at 2.2 K for a 7 T field change. Direct determination of the MCE effect via heat capacity measurements shows that the −ΔSmaxm values are consistent with those obtained from magnetisation data and that ΔTad is 16.9 K for the same magnetic field change.Another oxalate family shown to have good magnetocaloric properties are the Gd(pda)(ox)0.5(H2O)x (x = 0, 1, 2, pda = propionate) phases.79 All three compounds adopt P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) triclinic symmetry with nine coordinate Gd cations in the anhydrous form, which increase to 10 in the hydrated forms. The increase in the hydration state leads to a change from a 3D structure made of pillared layers in the anhydrous and monohydrate form to a 2D dihydrate structure with only weak C–H⋯O hydrogen bonding interactions between them. The layers in the 3D structure are connected by the carboxylate groups of the pda2− ligands with the oxalates pillaring the layers. In the dihydrate, the layers are comprised of cationic zig-zag Gd(pda) chains, which are connected to form 2D layers by the oxalate ligands. Despite the changes in dimensionality, all three materials retain similar weak ferromagnetic coupling, with θW between 0.3 and 0.7 K. Magnetisation measurements indicate −ΔSmaxm for these compounds are similar with regards to mass density at 46.8 J kg−1 K−1, 46.1 J kg−1 K−1 and 45.0 J kg−1 K−1 for the x = 0, 1 and 2 phases for a 7 T field change at 2 K, although the greater density of the hydrated phases increases their volumetric entropy change (cf. 128 mJ cm−3 K−1, 1512 mJ cm−3 K−1 and 159 mJ cm−3 K−1 for x = 0, 1 and 2, respectively).
triclinic symmetry with nine coordinate Gd cations in the anhydrous form, which increase to 10 in the hydrated forms. The increase in the hydration state leads to a change from a 3D structure made of pillared layers in the anhydrous and monohydrate form to a 2D dihydrate structure with only weak C–H⋯O hydrogen bonding interactions between them. The layers in the 3D structure are connected by the carboxylate groups of the pda2− ligands with the oxalates pillaring the layers. In the dihydrate, the layers are comprised of cationic zig-zag Gd(pda) chains, which are connected to form 2D layers by the oxalate ligands. Despite the changes in dimensionality, all three materials retain similar weak ferromagnetic coupling, with θW between 0.3 and 0.7 K. Magnetisation measurements indicate −ΔSmaxm for these compounds are similar with regards to mass density at 46.8 J kg−1 K−1, 46.1 J kg−1 K−1 and 45.0 J kg−1 K−1 for the x = 0, 1 and 2 phases for a 7 T field change at 2 K, although the greater density of the hydrated phases increases their volumetric entropy change (cf. 128 mJ cm−3 K−1, 1512 mJ cm−3 K−1 and 159 mJ cm−3 K−1 for x = 0, 1 and 2, respectively).
More recently, the magnetocaloric properties of the Ln(HCO2)(C2O4) phases have been assessed, specifically for the members where Ln = Gd3+, Tb3+, Dy3+ and Ho3+, and the oxalate ligand C2O42− is present. These coordination polymers adopt an orthorhombic Pnma structure, featuring face-sharing polyhedra forming zig-zag chains with adjacent chains connected by the formate and oxalate ligands forming a triangular lattice, hence exhibiting a similar topology to the Ln(HCO2)3 family of coordination polymers (see Fig. 11).80 The Ln3+ cations are nine-coordinate with a distorted monocapped square antiprism geometry, with three oxygen atoms from three formates and six from three oxalates, with these acting as a bichelating ligand utilizing both carboxylate groups. Among the members of this family, weakly antiferromagnetically coupled Gd(HCO2)(C2O4) has proven to be an interesting candidate for magnetic cooling with the magnetic entropy change determined via isothermal magnetisation measurements, indicating a −ΔSmaxm of 56.0 J kg−1 K−1 (218 mJ cm−3 K−1) for a 5 T field change at 2 K,81 with these values being the highest known for a dense MOF and higher than that of the closely related Gd(HCO2)3.74 The other members of this family have a lower −ΔSmaxm at high fields and, with the exception of Dy(HCO2)(C2O4) above 5 K for a 1–0 T field change and above 7 K for a 2–0 T field change, do not exceed Gd(HCO2)(C2O4) at lower applied fields.81 For the Tb and Ho phases, this is in direct contrast with the LnOHCO3 and Ln(HCO2)3 frameworks, which have similar face-sharing chains packed in distorted triangular lattices.68,75 Neutron diffraction experiments on Tb(HCO2)(C2O4) and Ho(HCO2)(C2O4) have shown these lack significant magnetic correlations above 1.5 K, this likely being the cause of a significantly poorer entropy change compared to their LnOHCO3 and Ln(HCO2)3 analogues; this highlights the importance of local magnetic interactions in determining the magnetocaloric properties at lower applied fields, and suggests small changes in structures influence these significantly.81
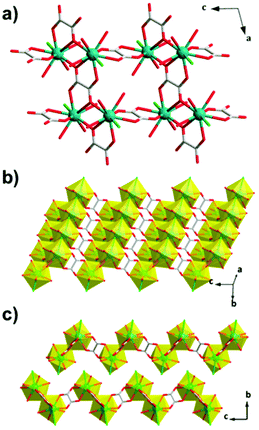
The succinate (suc) ligand is expanded from an oxalate by inclusion of two CH2 groups between its carboxylates. Two succinate frameworks have been reported to have promising magnetocaloric entropy changes, viz. Gd2(OH)2(suc)2(H2O)·2H2O and Gd6(OH)8(suc)5(H2O)2·4H2O, which adopt C2/c and P21/c symmetry, respectively.82 Gd2(OH)2(suc)2(H2O)·2H2O and Gd6(OH)8(suc)5(H2O)2·4H2O both adopt ladder-like structures with two and six distinct Gd cations, respectively, with one gadolinium in an eight coordinate environment in both structures and the remainder in nine coordinate environments (see Fig. 12). Gd2(OH)2(suc)2(H2O)·2H2O crystallises as a Gd–OH ladder that grows parallel to the b-axis and is comprised of two rows of Gd3+ ions with Gd–Gd distances ranging from 3.655 to 4.065 Å. These ladders are then connected along the a-axis and the c-axis via succinate ligands which serve as pillars to form the 3D network. Similarly, Gd6(OH)8(suc)5(H2O)2·4H2O adopts a three rail Gd–OH ladder where three rows of Gd3+ ions, connected by the succinate ligand, form the rungs of the ladder. The ladders extend along the b-axis and neighbouring Gd⋯Gd separations range from 3.656 and 4.049 Å. Magnetisation measurements of these weakly antiferromagnetically coupled phases indicate a −ΔSmaxm of 42.8 J kg−1 K−1 (120 mJ cm−3 K−1) and 48.0 J kg−1 K−1 (144 mJ cm−3 K−1) for a field change of 7 T at 2.6 K and 1.8 K, with ΔTad of 17 and 15 K, respectively.
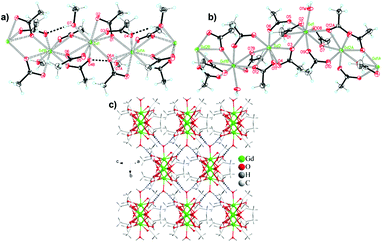
One citrate (cit) coordination polymer, which is related to the succinate ligand via replacement of a CH2 group with a C(OH)(CHCO2) group, has been reported to have potentially promising magnetocaloric entropy changes, namely Gd(cit)(H2O).83 This compound adopts monoclinic C2/c symmetry with GdO9 polyhedra connected by carboxylate O atoms in a μ2–η2 bridging mode to form a dimer (see Fig. 13). Neighbouring dimers are then bridged through carboxylate groups to form 1D ladder Gd3+ chains which are bridged by citrate ligands to from a 2D layer structure with weak ferromagnetic coupling indicated by a θW of 1.1 K. Magnetisation measurements indicate a −ΔSmaxm of 43.6 J kg−1 K−1 (115 mJ cm−3 K−1) for field change of 7 T at 2 K.
 | ||
| Fig. 13 Two-dimensional layer structure of Gd(cit)(H2O) showing two Gd ladder chains propagating along the b-axis. Colour codes: Gd: purple, C: black, O: red. Hydrogens are omitted for clarity. | ||
3.3 Cyclic carboxylate-based polymers
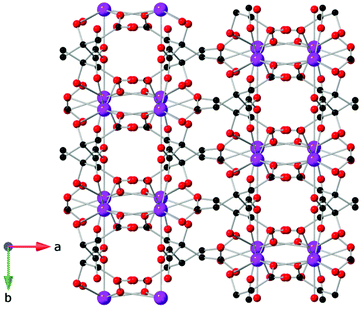
Compounds incorporating cyclic carboxylate ligands, which are amongst the most common ligands utilised in MOFs, have also been investigated as magnetocalorics. Amongst the first of these was Gd(C4O4)(OH)(H2O)4,84 which adopts a monoclinic P21/c structure with six coordinate Gd, which are bridged by the squarate ligand to form a 2D sheet in the bc-plane with an intralayer Gd–Gd separation of 6.48 Å (see Fig. 14). Interlayer coupling is via extensive hydrogen bonding between squarate oxygen atoms and water ligands. This phase has negligible magnetic interactions with indirect measurements of MCE properties indicating a −ΔSmaxm of 47.3 J kg−1 K−1 or 210 mJ cm−3 K−1 for a field change of 9 T at ∼3 K, with the volumetric density particularly high for a MOF containing a cyclic unit due to the dense structure enabled by the smaller squarate ligand. Another high performing magnetocaloric framework containing a cyclic carboxylate Gd(HCO2)(bdc),85 where bdc is the aromatic 1,4-benzenedicarboxylate ligand found in many MOFs structures. Here it leads to a monoclinic P21/c structure with edge-sharing dimeric GdO8 distorted trigonal dodecahedra, which are connected through the oxygen atoms of two formate ligands with intradimer Gd–Gd distances of 3.95 Å. These dimers are connected through the bdc carboxylate groups to generate layers that are pillared through the bdc linker. Gd(HCO2)(bdc) was found to be very weakly antiferromagnetically coupled. The −ΔSmaxm, calculated from magnetisation data, gives a value of 42.4 J kg−1 K−1 (113 mJ cm−3 K−1) for a 5 T field change at 2.25 K, with this increasing to 47.0 J kg−1 K−1 (125 mJ cm−3 K−1) for a field change of 9 T.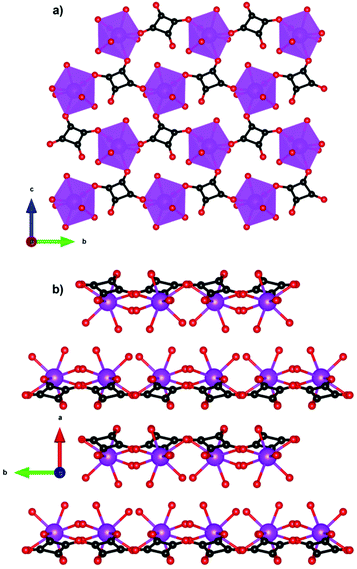 | ||
| Fig. 14 (a) Two-dimensional layers of Gd(C4O4)(OH)(H2O)4 on the bc-plane and (b) packing of the layers along the a-axis. Colour codes: Gd: purple, C: black, O: red. Hydrogens are omitted for clarity. | ||
More recently an evacuated porous benzenetricarboxylate (btc) framework, Gd(btc)(H2O),86 has been reported to have a surprisingly high θW of −6.2 K and good magnetocaloric entropy change at 1.8 K for a 5 T field change as a function of weight, 42 J kg−1 K−1. Its entropy change as a function of volume is, however, very modest at about 68 mJ cm−3 K−1, due to its low density structure. This structure, which adopts the chiral space groups of P4122 and P4322,87 features Gd cations connected via carboxylate groups of btc linkers to give 1D helical chains with Gd–Gd distances of 4.30 Å. These rods pack to give a 3D structure thanks to the connectivity of Gd3+ ions and btc3− ligands and features helical-shaped channels, with well-spaced Gd cations between chains with a minimum separation of 8 Å.
Two other frameworks with potential voids featuring cyclic carboxylates and with −ΔSmaxm above 40 J kg−1 K−1 have been reported, namely the weakly antiferromagnetically coupled Gd5(μ3-OH)6(TZI)3(DMA)1.5(H2O)9.5·DMA88 (where H3TZI is 5-(1H-tetrazol-5-yl)isophthalic acid and DMA is dimethylcetamide) and [Gd(2,5-FDA)0.5(Glu)(H2O)2]·xH2O89 (where FDA2− is furan-2,5-dicarboxylate and Glu2− is glutarate). Indirect measurements indicate a −ΔSmaxm of 41.3 J kg−1 K−1 and 40.6 J kg−1 K−1 at 2 K for a 7 T field change but, again, their porosity leads to a very modest volumetric −ΔSmaxm of 93.7 mJ cm−3 K−1 and 70.6 mJ cm−3 K−1 respectively. Gd5(μ3-OH)6(TZI)3(DMA)1.5(H2O)9.5·DMA forms a 3D framework in monoclinic C2/m symmetry. Its structure is based on the [Gd5(OH)6]9+ trigonal bipyramidal core built from eight and nine coordinate Gd linked together by six μ3-OH bridges and five syn–syn carboxylate bridges. These clusters are then connected by a μ2-H2O bridge to form 1D chains which are in turn connected by carboxylate groups of the TZI ligand to create the 3D framework. Gd(2,5-FDA)0.5(Glu)(H2O)2·xH2O adopts orthorhombic Pnma symmetry consisting of nine-coordinate Gd in monocapped square-antiprismatic polyhedra.89 These Gd are linked into Gd2O16 dimers by two bidentate chelating-bridged carboxylates. The dimers connected into 1D zig-zag chains via the 2,5-FDA ligand with neighbouring chains bridged together by two Glu ligands per dimer.
4. 4f–3d mixed-metal polymers
The other general group of magnetocaloric coordination polymers that should be considered are those containing transition metals, with the highest performing materials amongst these typically combining d5 Mn2+ with f7 Gd3+ to maximise their magnetic spin. Mn2+ is the transition metal of choice in 3d–4f systems due to it being readily available and having the most unpaired electrons possible in a transition metal. Indeed, despite their lower number of unpaired electrons (cf. to Gd3+), Mn2+ complexes can have high −ΔSmaxm, with respect to weight even in the absence of a lanthanide, as seen in Mn(Me-ip)(DMF) (where Me-ipH2 is 5-methylisophthalic acid).90 This material adopts a Pna21 orthorhombic structure which contains distorted octahedral Mn2+ in a coordination polymer comprised of chains of Mn cations connected by two carboxylate ligands with a Mn–Mn intrachain distance of 3.88 Å (see Fig. 15). Each chain is then connected to four adjacent ones via the Me-ip2− ligand with interchain Mn–Mn distance of 7.49 Å. The −ΔSmaxm for this system is calculated at 42.4 J kg−1 K−1 (66.7 mJ cm−3 K−1) for a field change of 8 T at 2 K. This is accompanied by weak antiferromagnetic coupling, with a θW of −0.59 K, indicating that despite the presence of only 3d cations the emergence of magnetic order should not prevent its use as a magnetocaloric until much lower temperatures.An interesting 3d–4f mixed coordination polymer is GdMn0.5(OAc)4(H2O)2·3H2O,91 which contains a low-dimensional motif, specifically the Gd3+–Mn2+ acetate chains with only very weak antiferromagnetic coupling within them. This compound has a −ΔSmaxm of 38.7 J kg−1 K−1 (78.7 mJ cm−3 K−1) for a field change of 7 T at 2.5 K It should be noted that this compound also shows an interesting −ΔSmaxm of 31.1 J kg−1 K−1 (63.2 mJ cm−3 K−1) for a field change of 3 T at ∼2 K, which is higher than that of the commercially available GGG under the same conditions. This compound crystallises in a triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) structure where each Gd ion is in a capped square-antiprism geometry and each Mn adopts an octahedral geometry. Two adjacent Gd3+ ions are bridged by two acetates while adjacent Gd3+ and Mn2+ ions are bridged by three acetates (see Fig. 16). This generates a 1D chain structure where pairs of Gd ions are separated by one Mn along the chain. Within the chains, the Gd–Gd distance is 4.277 Å whereas the Gd–Mn distance is 4.030 Å. Intrachain hydrogen bonds are present between one coordinated water molecule and two acetate ligands. Water tetramers, formed by two guest water molecules, support the main interactions between chains by enabling hydrogen bonding between coordinating carboxylate and water molecules.
structure where each Gd ion is in a capped square-antiprism geometry and each Mn adopts an octahedral geometry. Two adjacent Gd3+ ions are bridged by two acetates while adjacent Gd3+ and Mn2+ ions are bridged by three acetates (see Fig. 16). This generates a 1D chain structure where pairs of Gd ions are separated by one Mn along the chain. Within the chains, the Gd–Gd distance is 4.277 Å whereas the Gd–Mn distance is 4.030 Å. Intrachain hydrogen bonds are present between one coordinated water molecule and two acetate ligands. Water tetramers, formed by two guest water molecules, support the main interactions between chains by enabling hydrogen bonding between coordinating carboxylate and water molecules.
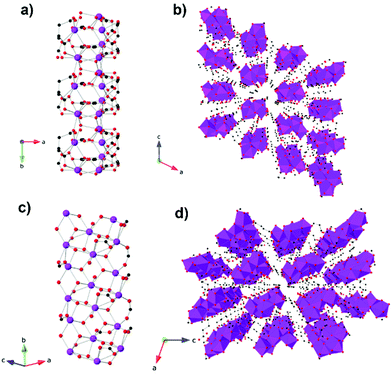
The remaining mixed 3d–4f coordination polymers with promising magnetocaloric properties are 3D frameworks with a net charge that is balanced by the presence of counterions in the pore space. These compounds all have respectable magnetocaloric entropy changes as a function of weight but, as for other porous magnetocalorics, they are much more modest as a function of volume. [Mn(H2O)6][MnGd(oda)3]2·6H2O (where oda2− is oxydiacetetate) is the only reported example of a promising magnetocaloric framework with an anionic charge.92,93 The framework is composed of nine coordinate Gd in a distorted tricapped trigonal prismatic geometry while Mn in an octahedral environment, with each 3d cation connected via carboxylate oxygen atoms to six 4f cations and vice versa (see Fig. 17). This leads to a cubic lattice with voids of alternatingly broad and narrow cavities that are occupied by [Mn(H2O)6]2+ units, which both balance the anionic charge of the framework and enhance the MCE of the material, and solvent water molecules, respectively. This weakly coupled ferromagnetic material (θW of 1.2) has been determined indirectly to exhibit −ΔSmaxm of 50.1 J kg−1 K−1 (114 mJ cm−3 K−1) at 1.8 K for field changes of up to 7 T. Heat capacity measurements under fields of up to 3 T were also performed giving properties that were consistent with those obtained from bulk magnetisation measurements with a ΔTad of 10.1 K for an applied field of 3 T.
Weakly antiferromagnetically coupled [Gd4Mn(L)3(H2O)3(μ3-OH)4(HCOO)1.5](NO3)2.5·6H2O (where H2L is 2,2′-dipyridine-4,4′-dicarboxylic acid) has the highest −ΔSmaxm amongst a series of cationic mixed 3d–4f frameworks, between which L is varied, with a value of 46.0 J kg−1 K−1 (70.0 mJ cm−3 K−1) for a field change of 7 T at 2 K.94 This compound adopts a cubic I213 symmetry with Gd3+ having two distinct coordination environments where Gd1 is eight coordinated with a dicapped trigonal prism geometry whereas Gd2 is six coordinated. These distinct cations are linked by OH− groups into a distorted cubane [Gd4O4] cluster six coordinate and three eight coordinate Gd with intracluster in which the Gd are arranged in a trigonal prism containing one Gd–Gd distances of 3.78 Å and 3.87 Å. The L2− ligands both link each [Gd4O4] cluster to three others but also to the octahedral Mn, which is coordinated only to nitrogen atoms from these ligands to six [Gd4O4] clusters, forming a 6,9-connected sqc topology. The clusters are bridged by formate ligands into a 3D framework with two unusual types of helical channels. The first of these is a larger L-helix with a pore diameter of 10.4 Å while the latter is an R-helix with the same helix pitch – that is the height of one complete helix turn of 20.7 Å, but a smaller pore diameter of 5.0 Å. Residual electron density has been used to suggest the pores of this compound are occupied by disordered H2O molecules and NO3− anions, the latter being required for charge balancing, but there is no direct confirmation of this through other techniques. Weakly antiferromagnetically coupled [Gd5Mn(L)3(H2O)10(μ3-OH)6](NO3)5·13H2O,94 (where H2L is 2,2′-dipyridine-4,4′-dicarboxylic acid) is another example of a 3D cationic framework with a high −ΔSmaxm of 38.3 J kg−1 K−1 (57.3 mJ cm−3 K−1) at 3 K for a field change of 7 T. This compound adopts hexagonal P3121 symmetry and contains [Gd5(COO)6(H2O)10(OH)6]3+ cluster nodes in which the five Gd cations are arranged in a distorted trigonal bipyramidal geometry, with the Gd cations bridged by six μ3-OH groups and encapsulated by the six carboxyl groups of three L2− ligands. Each cluster contains three crystallographically independent Gd3+ cation all of which are eight-coordinated with dicapped trigonal prismatic geometries in the apical positions and square antiprism geometries in the equatorial plane of the cluster. Every cluster connects to six adjacent ones through the L2− ligand which also connects the octahedral Mn to the Gd clusters, forming an overall 6,6-connected topology. The resulting channels in the structure contain free water molecules and NO3− counter anions.
5. Summary and perspective
This review has presented coordination polymers, based on polyatomic ligands, exhibiting MCE showing a high −ΔSmaxm, the most readily available measure of their potential magnetic cooling. These are dominated by materials in which Gd is the magnetic cation and have been grouped across four categories, based on the ligand type, i.e. inorganic, monocarboxylate, linear carboxylate and cyclic carboxylate (see Fig. 18). Among these, the best performing magnetocaloric materials are typically found to incorporate only inorganic-based ligands, such as phosphates, borates and carbonates to name a few, likely because these smaller ligands yield structures containing higher densities of Gd3+ cations. One of the best performing magnetocalorics in this category is GdPO4,58 which features a high density of Gd3+ in combination with weak magnetic interactions and low magnetocrystalline anisotropy, with a magnetocaloric entropy change of up to 62.0 J kg−1 K−1 (376 mJ cm−3 K−1) for a field change of 7 T, making this a very promising material for high field applications. Comparable materials are GdBO3,63 Gd(OH)3,70 and GdOHCO3,55 with the latter two having comparable and higher gravimetric magnetic entropy changes, respectively, but presenting a slightly lower volumetric entropy change.While there are a number of compounds associated with the other ligand groupings that exhibit −ΔSmaxm above 40 J kg−1 K−1, and thus comparable to the commonly used benchmark material GGG, they generally exhibit more modest entropy change values with respect to those incorporating only inorganic ligands. There are, however, some notable exceptions to this, specifically Gd(HCO2)3 and Gd(C2O4)(HCO2),74,81 that highlight that magnetocalorics with simple carboxylates can offer comparable entropy changes to purely inorganic frameworks. It can be seen that coordination frameworks with more complex ligands, particularly where these lead to more porous structures, generally have much lower MCE due to their relatively low density of magnetic cations. Such MOFs, however, retain scope for multifunctionality that could be either used to enhance their magnetocaloric properties, e.g. via inclusion of simple magnetic guests in their pores such as simple neutral lanthanide complexes analogous to [Mn(H2O)6][MnGd(oda)3]2·6H2O,92,93 or couple another function with good, if not excellent, magnetocaloric properties. In the pursuit of such multifunctionality, the use of simpler cyclic carboxylates, such as squarates,84 and relatively small pore sizes that provide space for the desired guest or functionality, but do not unnecessarily reduce overall density, appear a sensible route forward.
In contrast to the wide number of coordination polymers whose −ΔSm have been characterised further characterisation of the thermodynamic properties of even the most promising materials is very limited. It will be important to rectify this to enable the full potential of the most promising magnetocalorics to be determined. This can be emphasised by examination of Table 1, which compares the −ΔSmaxm and ΔTad of coordination polymers, for the limited number of materials where the later has been reported. This shows that some materials with high −ΔSmaxm have relatively more modest ΔTad, which is often considered a more direct measure of a magnetocalorics performance.
| Compound | ΔTad (K) | −ΔSmaxm (J kg−1 K−1) | T max (K) | ΔH (T) |
|---|---|---|---|---|
| GdPO4 | 24.6 | 62.0 | 2.1 | 7 |
| GdOHCO3 | 24 | 66.4 | 2 | 9 |
| Gd(HCO2)3 | 22 | 55.9 | ∼1 | 7 |
| Gd(C2O4)(H2O)3Cl | 16.9 | 48.0 | 2.2 | 7 |
| Gd2(OH)2(suc)2(H2O)·2H2O | ∼17 | 42.8 | 2.6 | 7 |
| Gd6(OH)8(suc)5(H2O)2·4H2O | 15 | 48 | 1.8 | 7 |
| Gd(btc)(H2O) | ∼14 | 42 | ∼20 | 5 |
| [Mn(H2O)6][MnGd(oda)3]2·6H2O | 10.1 | 42.6 | ∼2 | 3 |
Looking beyond Gd-based materials, it has been noted that, amongst the 4f coordination polymers, there are a handful of examples where metal cations with significant magnetocrystalline anisotropy feature improved entropy changes for lower field changes and higher temperatures compared to their Gd analogues. This renders these materials good candidates for a broader range of applications that require cooling above 4 K, as He is commonly used to do, rather than the <2 K temperatures at which Gd materials excel. This is particularly the case when lower applied fields are needed, which are more readily achieved and offer the potential of using a permanent magnet rather than a more energy demanding superconducting magnet.
Notably amongst these are DyOHCO3 and TbOHCO3,68 which have higher −ΔSm changes at and above 4 K than GdOHCO3 for field changes below 2 T, and Tb(HCO2)3 and Ho(HCO2)3,75 which offer similar improved magnetocaloric properties compared to Gd(HCO2)3. In contrast, in the Ln(HCO2)(C2O4) phases only the Dy analogue has a similar entropy change for low field applications compared to Gd(HCO2)(C2O4),81 with this enhancement found to be modest.81 The materials with improved −ΔSm for low applied fields also tend to exhibit strong diffuse magnetic scattering originating from a combination of low dimensional ferromagnetic coupling and geometrically frustrated magnetic interactions.77 This suggests such properties are dependent on a combination of the single ion anisotropy and tailored magnetic interactions and thus designing structures where local magnetic interactions are optimised might be key to improving the magnetocaloric properties for cooling using low applied fields. Examples thus far focus on cases where there are strong ferromagnetic interactions in chains but competing interactions between the chains due to geometric frustration. This enables the facile alignment of the moment on the chains along the direction of a modest external magnetic field while the frustration suppresses order to very low temperatures in the absence of an applied field. Similar behaviour might also be expected for well isolated chains in coordination polymers, such that the interchain interactions are weak enough that magnetic order does not occur until below the temperature at which these are useful magnetocalorics, although this would likely lead to lower −ΔSmaxm as a function of volume and, to a lesser extent, weight due to the dilution of the magnetic cations required by this additional spacing. It is also possible that other magnetic motifs may exhibit similar properties with anisotropic magnetic centres as indicated by the performance of DyBO3 compared to its Gd analogue.63 Thus investigation of the analogues of inorganic frameworks with anisotropic lanthanides offers a potential opportunity for improvement of magnetocaloric properties under lower fields with such materials, including Gd(OH)3, Gd(OH)SO4 and Gd2O(OH)4(H2O)2.
Finally, 3d–4f mixed-metal coordination polymers have been briefly reviewed, with Gd–Mn polymers showing −ΔSmaxm comparable to the other classes of materials discussed with respect to weight. Although the lower density of these mixed metal MOFs leads to their entropy change as a function of volume being quite modest, it should also be considered that the materials reported thus far commonly have cyclic dicarboxylates that, even in purely 4f materials, commonly lead to poorer MC properties. The greater availability and lower cost of transition metals, however, makes 3d–4f frameworks or, as seen in Mn(Me-ip)(DMF),90 even 3d frameworks attractive as a way of enabling the use of magnetocalorics with a reduced dependence on the use of lanthanides. Thus, the magnetocaloric properties of 3d–4f and 3d frameworks based on inorganic ligands or small carboxylates, e.g. formate and oxalate, are worth further exploration. While it is possible these will have stronger magnetic coupling than the 3d containing polymers explored in this review, this should not prove an impediment to their application as magnetocalorics, provided magnetic order is supressed to below the desired order temperature by e.g. geometric frustration. Additionally, through the promising −ΔSmaxm of GdMn0.5(OAc)4(H2O)2·3H2O for 3 T field changes,91 there is some indication of there being a potential route for maximising properties at lower applied magnetic fields.
In conclusion, a variety of coordination polymers featuring promising magnetocaloric properties have been reviewed, highlighting the influence of a material's structure, including incorporation of smaller polyatomic ligands and optimising magnetic interactions, through use of low dimensional motifs and magnetic frustration, as important factors to consider when designing materials for low-temperature magnetic cooling applications.
Author contributions
MF lead the investigation which PJS also contributed to, with both authors contributing to the writing of the manuscript. PJS conceptualised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank the Leverhulme Trust and Engineering and Physical Sciences Research Council for supporting this work through RPG-2018-268 and EP/T027886/1, respectively.References
- J.-L. DuPont, P. Domasnki, P. Lebrun and F. Ziegler, 38th Informatory Note on Refrigeration Technologies, 2019 Search PubMed.
- S. A. Tassou, J. S. Lewis, Y. T. Ge, A. Hadawey and I. Chaer, Appl. Therm. Eng., 2010, 30, 263–276 CrossRef.
- L. P. Ichkitidze, N. A. Bazaev, D. V. Telyshev, R. Y. Preobrazhensky and M. L. Gavrushina, Biomed. Eng., 2015, 48, 305–309 CrossRef.
- J. C. Doane and H. D. Stein, J. Int. Coll. Surg., 1951, 16, 346–349 CAS.
- A. H. Olafsdottir and H. U. Sverdrup, Biophys. Econ. Sustain., 2020, 5, 6 CrossRef.
- O. Sari and M. Balli, Int. J. Refrig., 2014, 37, 8–15 CrossRef.
- V. Franco, J. S. Blázquez, B. Ingale and A. Conde, Annu. Rev. Mater. Res., 2012, 42, 305–342 CrossRef CAS.
- J. F. Scott, Annu. Rev. Mater. Res., 2011, 41, 229–240 CrossRef CAS.
- P. F. Liu, J. L. Wang, X. J. Meng, J. Yang, B. Dkhil and J. H. Chu, New J. Phys., 2010, 12, 023035 CrossRef.
- G. G. Wiseman and J. K. Kuebler, Phys. Rev., 1963, 131, 2023 CrossRef CAS.
- W. N. Lawless, Phys. Rev. B: Solid State, 1977, 16, 433–439 CrossRef CAS.
- H.-X. Cao and Z.-Y. Li, J. Appl. Phys., 2009, 106, 094104 CrossRef.
- W. N. Lawless and A. J. Morrow, Ferroelectrics, 1977, 15, 159–165 CrossRef CAS.
- I. N. Flerov and E. A. Mikhaleva, Phys. Solid State, 2008, 50, 478–484 CrossRef CAS.
- S. Qian, Y. Geng, Y. Wang, J. Ling, Y. Hwang, R. Radermacher, I. Takeuchi and J. Cui, Int. J. Refrig., 2016, 64, 1–19 CrossRef CAS.
- J. Tušek, K. Engelbrecht, R. Millán-Solsona, L. Mañosa, E. Vives, L. P. Mikkelsen and N. Pryds, Adv. Energy Mater., 2015, 5, 1500361 CrossRef.
- K. Otsuka and C. M. Wayman, Shape memory materials, Cambridge university press, 1999 Search PubMed.
- C. M. Miliante, A. M. Christmann, E. O. Usuda, W. Imamura, L. S. Paixão, A. M. G. Carvalho and A. R. Muniz, Macromolecules, 2020, 53, 2606–2615 CrossRef CAS.
- S. Crossley, N. D. Mathur and X. Moya, AIP Adv., 2015, 5, 067153 CrossRef.
- L. Mañosa and A. Planes, Adv. Mater., 2017, 29, 1603607 CrossRef PubMed.
- C. Cazorla, Appl. Phys. Rev., 2019, 6, 041316 Search PubMed.
- W. Imamura, É. O. Usuda, L. S. Paixão, N. M. Bom, A. M. Gomes and A. M. G. Carvalho, Chin. J. Polym. Sci., 2020, 38, 999–1005 CrossRef CAS.
- A. M. G. Carvalho, W. Imamura, E. O. Usuda and N. M. Bom, Eur. Polym. J., 2018, 99, 212–221 CrossRef CAS.
- E. O. Usuda, N. M. Bom and A. M. G. Carvalho, Eur. Polym. J., 2017, 92, 287–293 CrossRef CAS.
- N. M. Bom, W. Imamura, E. O. Usuda, L. S. Paixão and A. M. G. Carvalho, ACS Macro Lett., 2017, 7, 31–36 CrossRef.
- B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S. Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510 CrossRef CAS PubMed.
- L. Mañosa, D. González-Alonso, A. Planes, E. Bonnot, M. Barrio, J.-L. Tamarit, S. Aksoy and M. Acet, Nat. Mater., 2010, 9, 478–481 CrossRef PubMed.
- J. M. Bermúdez-García, M. Sánchez-Andújar, S. Yáñez-Vilar, S. Castro-García, R. Artiaga, J. López-Beceiro, L. Botana, Á. Alegría and M. A. Señarís-Rodríguez, Inorg. Chem., 2015, 54, 11680–11687 CrossRef PubMed.
- J. M. Bermúdez-García, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga and M. A. Señarís-Rodríguez, Nat. Commun., 2017, 8, 15715 CrossRef PubMed.
- J. M. Bermúdez-García, S. Yáñez-Vilar, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga, M. Dilshad, X. Moya and M. A. Señarís-Rodríguez, J. Mater. Chem. C, 2018, 6, 9867–9874 RSC.
- J. Salgado-Beceiro, A. Nonato, R. X. Silva, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, E. Stern-Taulats, M. A. Señarís-Rodríguez, X. Moya and J. M. Bermúdez-García, Adv. Mater., 2020, 1, 3167–3170 RSC.
- E. Warburg, Ann. Phys., 1881, 249, 141–164 CrossRef.
- P. Weiss and A. Piccard, C. R. Acad. Sci., 1918, 166, 352–354 CAS.
- A. Waske, M. E. Gruner, T. Gottschall and O. Gutfleisch, MRS Bull., 2018, 43, 269–273 CrossRef CAS.
- C. Zimm, A. Jastrab, A. Sternberg, V. Pecharsky, K. Gschneidner, M. Osborne and I. Anderson, Advances in Cryogenic Engineering, Springer US, Boston, MA, 1998, pp. 1759–1766 Search PubMed.
- K. A. Gschneidner and V. K. Pecharsky, Int. J. Refrig., 2008, 31, 945–961 CrossRef.
- V. K. Pecharsky and K. A. Gschneidner, Phys. Rev. Lett., 1997, 78, 4494–4497 CrossRef CAS.
- U. Cardella, L. Decker and H. Klein, Int. J. Hydrogen Energy, 2017, 42, 13329–13338 CrossRef CAS.
- L. Gyongyosi and S. Imre, Comput. Sci. Rev., 2019, 31, 51–71 CrossRef.
- C. Mitra, Nat. Phys., 2015, 11, 212–213 Search PubMed.
- P. Martin, A. S. Royet, F. Guellec and G. Ghibaudo, Solid-State Electron., 2011, 62, 115–122 CrossRef CAS.
- A. Cho, Science, 2009, 326, 778–779 CrossRef CAS PubMed.
- V. K. Pecharsky and K. A. Gschneidner Jr., J. Magn. Magn. Mater., 1999, 200, 44–56 CrossRef CAS.
- I. Niknia, P. V. Trevizoli, T. V. Christiaanse, P. Govindappa, R. Teyber and A. Rowe, J. Appl. Phys., 2017, 121, 064902 CrossRef.
- A. Giguère, M. Foldeaki, B. Ravi Gopal, R. Chahine, T. K. Bose, A. Frydman and J. A. Barclay, Phys. Rev. Lett., 1999, 83, 2262–2265 CrossRef.
- A. M. Tishin, J. Alloys Compd., 1997, 250, 635–641 CrossRef CAS.
- Y. Z. Zheng, G. J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475 RSC.
- M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672–4676 RSC.
- N. R. Ram, M. Prakash, U. Naresh, N. S. Kumar, T. S. Sarmash, T. Subbarao, R. J. Kumar, G. R. Kumar and K. C. B. Naidu, J. Supercond. Novel Magn., 2018, 31, 1971–1979 CrossRef CAS.
- K. A. Gschneidner and V. K. Pecharsky, Annu. Rev. Mater. Sci., 2000, 30, 387–429 CrossRef CAS.
- Y. Mozharivskyj, Magnetocaloric Effect and Magnetocaloric Materials, Elsevier Inc., 2016 Search PubMed.
- S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O'Keeffe, M. P. Suh and J. Reedijk, CrystEngComm, 2012, 14, 3001 RSC.
- M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379 RSC.
- A. P. Ramirez, Annu. Rev. Mater. Sci., 1994, 24, 453–480 CrossRef CAS.
- M. Mekata, Phys. Today, 2003, 56, 12–13 CrossRef.
- S. S. Sosin, L. A. Prozorova, A. I. Smirnov, A. I. Golov, I. B. Berkutov, O. A. Petrenko, G. Balakrishnan and M. E. Zhitomirsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 094413 CrossRef.
- O. A. Petrenko, D. M. K. Paul, C. Ritter, T. Zeiske and M. Yethiraj, Physica B: Condens. Matter, 1999, 266, 41–48 CrossRef CAS.
- E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. de Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423 CrossRef.
- D. F. Mullica, D. A. Grossie and L. A. Boatner, Inorg. Chim. Acta, 1985, 109, 105–110 CrossRef CAS.
- Y. Han, S.-D. Han, J. Pan, Y.-J. Ma and G.-M. Wang, Mater. Chem. Front., 2018, 2, 2327–2332 RSC.
- R. A. Zehnder, C. S. Wilson, H. T. Christy, K. S. Harris, V. Chauhan, V. Schutz, M. Sullivan, M. Zeller, F. R. Fronczek, J. A. Myers, K. Dammann, J. Duck, P. M. Smith, A. Okuma, K. Johnson, R. Sovesky, C. Stroudt and R. A. Renn, Inorg. Chem., 2011, 50, 836–846 CrossRef CAS PubMed.
- B. Daudin, R. Lagnier and B. Salce, J. Magn. Magn. Mater., 1982, 27, 315–322 CrossRef CAS.
- P. Mukherjee, Y. Wu, G. I. Lampronti and S. E. Dutton, Mater. Res. Bull., 2018, 98, 173–179 CrossRef CAS.
- L. C. Chapon, P. Manuel, F. Damay, P. Toledano, V. Hardy and C. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 024409 CrossRef.
- A. I. Smirnov, L. E. Svistov, L. A. Prozorova, A. Zheludev, M. D. Lumsden, E. Ressouche, O. A. Petrenko, K. Nishikawa, S. Kimura, M. Hagiwara, K. Kindo, A. Y. Shapiro and L. N. Demianets, Phys. Rev. Lett., 2009, 102, 037202 CrossRef CAS PubMed.
- T. Tahara, I. Nakai, R. Miyawaki and S. Matsubara, Z. Krist., 2007, 222, 326–334 CrossRef CAS.
- Y.-C. Chen, L. Qin, Z.-S. Meng, D.-F. Yang, C. Wu, Z. Fu, Y.-Z. Zheng, J.-L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, J. Mater. Chem. A, 2014, 2, 9851–9858 RSC.
- R. J. C. Dixey and P. J. Saines, Inorg. Chem., 2018, 57, 12543–12551 CrossRef CAS PubMed.
- R. J. C. Dixey, G. B. G. Stenning, P. Manuel, F. Orlandi and P. J. Saines, J. Mater. Chem. C, 2019, 7, 13111–13119 RSC.
- Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long, L.-S. Zheng, Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long and L.-S. Zheng, Chem. Commun., 2015, 51, 7317–7320 RSC.
- Y.-L. Hou, G. Xiong, P.-F. Shi, R.-R. Cheng, J.-Z. Cui and B. Zhao, Chem. Commun., 2013, 49, 6066 RSC.
- F.-S. Guo, J.-D. Leng, J.-L. Liu, Z.-S. Meng and M.-L. Tong, Inorg. Chem., 2012, 51, 405–413 CrossRef CAS PubMed.
- G. Lorusso, M. A. Palacios, G. S. Nichol, E. K. Brechin, O. Roubeau and M. Evangelisti, Chem. Commun., 2012, 48, 7592–7594 RSC.
- G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656 CrossRef CAS PubMed.
- P. J. Saines, J. A. M. Paddison, P. M. M. Thygesen and M. G. Tucker, Mater. Horiz., 2015, 2, 528–535 RSC.
- D. R. Harcombe, P. G. Welch, P. Manuel, P. J. Saines and A. L. Goodwin, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 174429 CrossRef.
- R. J. C. Dixey, F. Orlandi, P. Manuel, P. Mukherjee, S. E. Dutton and P. J. Saines, Philos. Trans. R. Soc., A, 2019, 377, 20190007 CrossRef CAS PubMed.
- Y. Meng, Y.-C. Chen, Z.-M. Zhang, Z.-J. Lin and M.-L. Tong, Inorg. Chem., 2014, 53, 9052–9057 CrossRef CAS PubMed.
- S.-J. Liu, C. Cao, S.-L. Yao, T.-F. Zheng, Z.-X. Wang, C. Liu, J.-S. Liao, J.-L. Chen, Y.-W. Li and H.-R. Wen, Dalton Trans., 2017, 46, 64–70 RSC.
- S. Romero, A. Mosset and J. C. Trombe, J. Solid State Chem., 1996, 127, 256–266 CrossRef CAS.
- M. Falsaperna, G. B. G. Stenning, I. da Silva and P. J. Saines, J. Mater. Chem. C, 2021, 9, 13209–13217 RSC.
- Y.-C. Chen, F.-S. Guo, Y.-Z. Zheng, J.-L. Liu, J.-D. Leng, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, Chem. – Eur. J., 2013, 19, 13504–13510 CrossRef CAS PubMed.
- S.-J. Liu, C.-C. Xie, J.-M. Jia, J.-P. Zhao, S.-D. Han, Y. Cui, Y. Li and X.-H. Bu, Chem. – Asian J., 2014, 9, 1116–1122 CrossRef CAS PubMed.
- S. Biswas, A. Adhikary, S. Goswami and S. Konar, Dalton Trans., 2013, 42, 13331–13334 RSC.
- R. Sibille, T. Mazet, B. Malaman and M. François, Chem. – Eur. J., 2012, 18, 12970–12973 CrossRef CAS PubMed.
- V. Zeleňák, M. Almáši, A. Zeleňáková, P. Hrubovčák, R. Tarasenko, S. Bourelly and P. Llewellyn, Sci. Rep., 2019, 9, 15572–15580 CrossRef PubMed.
- L.-H. Xie, Y. Wang, X.-M. Liu, J.-B. Lin, J.-P. Zhang and X.-M. Chen, CrystEngComm, 2011, 13, 5849–5857 RSC.
- F. Liu, H. Huang, W. Gao, X.-M. Zhang and J.-P. Liu, CrystEngComm, 2017, 19, 3660–3665 RSC.
- M. Kumar, L.-H. Wu, M. Kariem, A. Franconetti, H. N. Sheikh, S.-J. Liu, S. C. Sahoo and A. Frontera, Inorg. Chem., 2019, 58, 7760–7774 CrossRef PubMed.
- C.-B. Tian, R.-P. Chen, C. He, W.-J. Li, Q. Wei, X.-D. Zhang and S.-W. Du, Chem. Commun., 2014, 50, 1915–1917 RSC.
- Y. Y. Pan, Y. Yang, L. S. Long, R. Bin Huang and L. S. Zheng, Inorg. Chem. Front., 2014, 1, 649–652 RSC.
- T. K. Prasad, M. V. Rajasekharan and J.-P. Costes, Angew. Chem., Int. Ed., 2007, 46, 2851–2854 CrossRef CAS PubMed.
- F. S. Guo, Y. C. Chen, J. L. Liu, J. D. Leng, Z. S. Meng, P. Vrábel, M. Orendác, M. L. Tong, M. Orendáč and M. L. Tong, Chem. Commun., 2012, 48, 12219–12221 RSC.
- P.-F. Shi, C.-S. Cao, C.-M. Wang and B. Zhao, Inorg. Chem., 2017, 56, 9169–9176 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |