Meta-stability through intermolecular interactions protecting the identity of atomic metal clusters: ab initio evidences in (Cu₅–Cu₅)_n (n < 3) cases

Abstract

Recent developments in new synthesis techniques have allowed the production of precise monodisperse metal clusters composed of a few atoms. These atomic metal clusters (AMCs) often feature a molecule-like electronic structure, which makes their physical and chemical properties particularly interesting in nanotechnology. Regarding potential applications, there is a major concern about the sintering of AMCs in nanoparticles due to the loss of their special properties. In this work, multireference ab initio theory is applied to demonstrate the formation of coupled AMC–AMC clusters in which the AMC partners maintain their ‘identity’ to a large extent in terms of their initial structures and atomic Mulliken charges, and their further oligomerization.

---

1 Introduction

Recent developments of highly selective experimental techniques enabling the synthesis of subnanometer metal clusters are pushing the understanding of these, more “molecular” than “metallic”, systems far beyond the present knowledge in materials science. In this way, when the atomic metal cluster (AMC) size is reduced to a small (less than 10) number of atoms, high stability and novel properties are achieved, that allow the AMC integration into materials. Additionally, interaction with the environment has the potential to boost the performance in applications particularly interesting in nanotechnology, including luminescence, sensing, bioimaging, theranostics, energy conversion, catalysis, and photocatalysis (see, e.g., ref. 1 and 2 for recent reviews). From a more fundamental point of view, it has also been shown how modification of popular materials such as TiO₂ with AMCs can convert them into “reporters” of fundamental surface polaron properties.^3–5 From the microscopic point of view, the above behaviour is explained in terms of the d-band of the metal splitting into a subnanometric network of discrete molecule-like d orbitals, with fluxional inter-connections having the length of a chemical bond (1–2 Å). The spatial structures of these molecular orbitals make all the metal atoms cooperatively active and accessible and confer molecular characteristics to the complexes, that are responsible of their stability and properties.

Among the different AMCs, copper clusters have attracted much attention as catalysts⁶ since they have shown important catalytic properties e.g. for the oxidation of CO,^7,8 the selective hydrogenation of olefin and carbonyl groups,^9,10 and in C–X (being X = C, N, S, P) bond forming reactions.¹¹ The oxidative dehydrogenation of cyclohexene on atomically precise subnanometer bimetallic Cu–Pd (tetramer) clusters is also worth mentioning.¹² Moreover, the work in ref. 13 showed an outstanding chemical and thermodynamical stability of atomic copper clusters in solution over the whole pH range. First-principles modelling, including methods beyond the state-of-the-art and an interplay with cutting-edge experiments, is helping to understand the special properties of AMCs at the most fundamental molecular level. Thus, the use of first-principles methods has disclosed the fundamental reasons why Cu₅ clusters experience a reversible oxidation,¹⁴ and are capable of increasing and extending into the visible region the solar absorption of TiO₂,¹⁵ also considering the decomposition and photo-activation of CO₂ as a prototypical (photo-)catalytic reaction.¹⁶

In spite of their potential applications, there is a major concern about the sintering of AMCs in metallic nanoparticles with the consequent loss of their special properties. In order to analyze the possible existence of metastable states in which Cu₅ preserves its identity, multireference Rayleigh Schrödinger (second-order) perturbation theory¹⁷ (RS2C) is applied here, allowing evidence of the formation and further oligomerization of coupled Cu₅–Cu₅ clusters at a high level of ab initio theory. It should be stressed that in our work preservation of identity at a molecular level encompasses a concept considerably broader than just aggregation by weak (dispersion-dominated) van der Waals (vdW) forces. It also includes the formation of covalent bonds between molecular sub-units, yet conserving their initial structures and, to a large extent, their atomic charge distributions.

2 Results and discussion

We optimized the Cu₅ cluster geometries in vacuum, their two main geometrical arrangements are shown in Fig. 1 (top panel): a planar trapezoidal two-dimensional (2D) structure with a spin quantum number equal to 1/2 and a trigonal bipyramidal tri-dimensional (3D) arrangement with spin equal to 3/2. In agreement with previous studies (see, e.g., ref. 11 and 18), the 2D structure is the most stable configuration by 0.6–0.7 eV (see Table 1). It can also be observed in Table 1 that the relative energies calculated at coupled-cluster and multireference perturbation levels of theory, using the largest active space, differ by less than 0.1 eV, thus indicating the accuracy of the latter.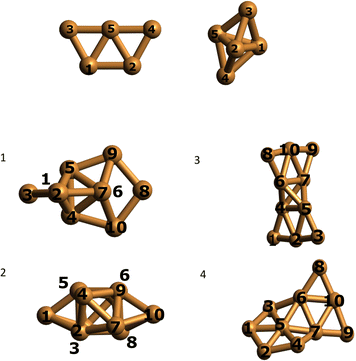

Fig. 1 Optimized structures of individual Cu₅ clusters (at the CCSD/Def2-TZVP level above) and coupled Cu₅–Cu₅ clusters (at the CAS(10,10)/cc-pVTZ-PP level below) in vacuum. Atom numbering included.

Table 1 Relative energies of Cu₅ clusters at coupled-cluster singles and doubles (CCSD/Def2-TZVP) and multireference Rayleigh Schrödinger (second-order) perturbation theory¹⁷ (RS2C/cc-pVTZ-PP) levels with respect to the lowest-energy structure (in eV). The spin multiplicity (2S + 1) is also indicated. The active space in the preceding multi-configurational calculations is specified as well (see Appendix). Within parentheses, we indicate the nature of the stationary point: Min denotes minimum and TS denotes a transition state

Cu5	2S + 1	CCSD	RS2C(5,5)	RS2C(7,7)
Planar (Min)	2	0	0	0
Planar (TS)	4	2.0	2.0	2.0
Bipyramidal (TS)	2	0.3	0.2	0.3
Bipyramidal (Min)	4	0.7	0.5	0.6

---

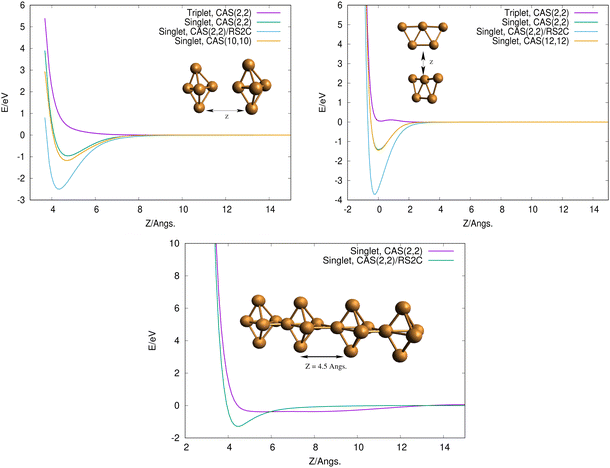
To get some insights on how 3D and 2D Cu₅ clusters interact as a function of their relative distances, we evaluated interaction energies keeping the intramolecular geometries fixed at the optimized values (see Fig. 2, top panels). Interestingly, for both structures, the interaction is repulsive in the triplet spin state but it becomes strongly attractive (by a few eV) in the singlet spin state. This outcome can be explained by considering that unpaired electrons occupying s-type orbitals on the two Cu₅ clusters feature repulsion/attraction to each other in parallel/anti-parallel spin configurations, producing repulsive/attractive inter-molecular interactions, as is the case for the interaction between two hydrogen atoms. It can also be observed that the attractive interaction is significantly enhanced when dynamical correlation is accounted for using the RS2C method (see the Appendix for the computational details). Interestingly, the interaction energies are hardly modified when the CASSCF space is enlarged from a minimal (2,2) space (2 electrons in 2 orbitals) to larger spaces (see Fig. 2, top panels).

Fig. 2 Top panels: scans of the interaction energy of two Cu₅ clusters as a function of the Z distance in vacuum. The geometries of the Cu₅ clusters have been kept fixed in the calculations. Top left panel: bypiramidal 3D structures. Top right panel: planar 2D structures. Bottom panel: interaction of two Cu₅–Cu₅ coupled clusters as a function of the Z distance, with the Cu₅–Cu₅ geometries fixed to those corresponding to the minimum in the top left panel. All calculations have been carried out with the cc-pVTZ-PP basis set.

Using the computational strategy described in the Appendix, the structures of coupled Cu₅–Cu₅ clusters shown in the middle and bottom panels of Fig. 1 have been obtained. The corresponding interaction energies are indicated in Table 2 at both multiconfigurational (referred to as DF-CASSCF) and multireference Rayleigh Schrödinger (second-order), internally contracted, perturbation levels of theory (denoted RS2C). With the exception of the structure labeled as ‘4’,¹⁹ note that the increase of the active space from that considering 10 electrons in 10 active orbitals [denoted as (10,10)] to that including 12 electrons in 12 active orbitals [referred to as (12,12)] modifies the energies up to 0.2 eV when dynamical correlation is not accounted for, while the consideration of the latter makes the interaction energies almost identical for both active spaces. It should be mentioned that the inclusion of the dynamical correlation with RS2C is crucial, accounting for ca. 70% of the attractive Cu₅–Cu₅ interaction in cluster 1 (−5.2 eV, see Table 2). This value agrees well with that obtained using the natural orbital coupled-cluster approach DLPNO-CCSD(T)²⁰ (−4.9 eV from ref. 21). The good agreement with the interaction energy and structure of the lowest-energy isomer obtained with the DFT-D4 ansatz (−5.4 eV from ref. 21) is also worth-mentioning. A similar coupled Cu₅–Cu₅ structure is also predicted to be more stable at the DFT-D4 level. Moreover (see Table S2 of the ESI†), the average values of the Cu–Cu bond lengths for the Cu₅ partners (2.5 Å) are in between those obtained through the DF-CASSCF and the RS2C optimizations (2.7 and 2.4 Å, respectively). It should also be considered that we are dealing with fluxional clusters bearing wide amplitude Cu–Cu motions (see below). For instance, an ab initio molecular dynamics simulation²¹ has shown that the values of Cu–Cu distances in circumpyrene-supported Cu₅–(O₂)₄ at 473 K experience large fluctuations (within 0.5 Å).

Table 2 Interaction energies (in eV) of coupled Cu₅–Cu₅ clusters at DF-CASSCF/cc-pVTZ-PP and RS2C/cc-pVTZ-PP energy levels (see Appendix for computational details). Within parentheses, we indicate the nature of the stationary point: Min denotes minimum and TS denoted a transition state

Cu5–Cu5	DF-CAS(10,10)/RS2C	DF-CAS(12,12)/RS2C
1 (Min)	−1.5/−5.2	−1.6/−5.2
2 (Min)	−1.5/−5.0	−1.7/−5.0
3 (Min)	−1.8/−2.3	−1.7/−2.3
4 (Min)	−1.4/−3.3	−2.3/−2.8
5 (TS)	−1.3/−4.7	−1.5/−4.7

---

In contrast to the case of isolated Cu₅ clusters, for which the 2D structures are energetically favored, it can be observed in Table 2 that the most stable (by ca. 2 eV) arrangements of coupled Cu₅–Cu₅ clusters correspond to coupled 3D structures. This structure (of D_2d symmetry) is similar to that reported in ref. 18 for Cu₁₀. The inclusion of dynamical correlation is clearly responsible for such behaviour. In fact, without considering it, the interaction energies are up to 0.7 eV more attractive upon the coupling of planar 2D structures than in the case of coupled 3D geometries.

We performed a Mulliken charge analysis of natural orbitals for both isolated Cu₅ and coupled Cu₅–Cu₅ clusters using the geometries optimized at the DF-CASSCF level (see Table 3). Note that Mulliken charges are larger in the 3D Cu₅ structure than in the 2D Cu₅ structure. As a result, the electrostatic contribution to the Cu₅–Cu₅ intermolecular interaction is favored when 3D Cu₅ clusters become coupled to each other. Most importantly, the values of Mulliken charges on all Cu atoms are (within numerical accuracy) the same for the two Cu₅ clusters within Cu₅–Cu₅ in clusters 1 and 3, leading to a symmetric structure of the complex with respect to the two Cu₅ units. It is remarkable that, in spite of being strongly bound (interaction Cu₅–Cu₅ energies of −5.2 eV using the RS2C method on geometries optimized at the DF-CASSCF level), the two Cu₅ clusters maintain their spatial arrangements in a symmetric way. Moreover, although the charge distributions in the coupled structures are not identical to those in isolated clusters, their modification is relatively modest on DF-CASSCF-based optimized structures. For the 3D structure of isolated Cu₅, atomic Mulliken charges vary in between −0.07 and 0.10 a.u., while in the lowest-energy Cu₅–Cu₅ structure found in this study, they range from −0.11 to 0.16 a.u. These modifications can be understood on the basis of polarization effects causing a higher electron localization on the peripheral, lower coordinated Cu atoms. The preservation of 3D and 2D Cu₅ structures in some of the coupled Cu₅–Cu₅ clusters is also clear in Fig. 1, being more evident in the case of the 2D geometries (see also Fig. S1 in the ESI†). Altogether, these outcomes indicate the protection of the identity of the Cu₅ partners, yet in a way differing significantly from that characterizing weakly bound van der Waals aggregates. Thus, recently, it has been shown that, upon heating, the Cu₅ sub-units of coupled Cu₅–Cu_5ne structures experience a decoupling through fluxional rotational motion but none spatial separation,²¹ in contrast to the case of vdW aggregates. Additionally, upon exposition to environmental O₂ molecules, a high oxygen gas pressure is necessary to achieve the individualization of Cu₅ sub-units.²¹

Table 3 Mulliken charges on the atoms of Cu₅ and coupled Cu₅–Cu₅ clusters for the most stable structures optimized at the DF-CASSCF/cc-pVTZ-PP level of theory. No symmetry has been imposed in the calculations. CCSD/Def2-TZVPP results are reported within parentheses for the sake of comparison

Individual Cu5 clusters
Label	2D (Min)	3D (Min)
1	–0.02	–0.07 (–0.06)
2	–0.03	–0.07 (–0.06)
3	0.01	0.10 (0.10)
4	0.01	0.10 (0.10)
5	0.03	–0.07 (–0.06)

---

Coupled Cu5–Cu5 clusters
Label	1 (Min)	2 (Min)	3 (Min)	4 (Min)
1	−0.11	−0.14	0.15	−0.04
2	−0.11	0.10	−0.21	−0.06
3	−0.10	0.04	0.15	−0.01
4	0.16	−0.28	−0.05	0.01
5	0.16	0.28	−0.04	0.09
6	0.16	−0.27	−0.04	0.02
7	0.16	0.03	−0.05	0.01
8	−0.10	0.09	0.15	0.02
9	−0.11	0.29	0.15	0.01
10	−0.11	−0.14	−0.21	−0.06

---

It is interesting to note that the energy difference between structures 1 and 2 in Fig. 1 is just 0.2 eV (see Table 2). Hence, the interconversion between them can be expected to be reversible. Although the potential energy landscape of Cu₅–Cu₅ clusters has been carefully explored (see Appendix), many local minima with similar energies could co-exist with those found in this work. The existence of many meta-stable states bearing very close energies is a typical feature characterizing atomic metal clusters due to their fluxional nature and associated wide amplitude inter-atomic motions. The concept of structural fluxionality has recently been advocated to explain the catalytic activity of AMCs (see, e.g., ref. 1, 16, 22 and 23). The occurrence of fluxional dynamics has also been suggested from recent spectroscopic observations.²⁴ Recent ab initio molecular dynamics simulations have also shown the fluxional rotational motion between the two Cu₅ units of the coupled Cu₅–Cu₅ clusters upon heating.²¹

Finally, to get some insight into the interaction between two coupled Cu₅–Cu₅ clusters, we evaluated the interaction energy as a function of their relative distance (see the bottom panel in Fig. 2). As expected from the closed-shell nature of the coupled clusters, the attractive interaction is extremely weak when the dynamical correlation is not accounted for. In contrast, the two coupled clusters become strongly bound (by ca. 2 eV) when the latter is included through the multireference RS2C perturbation method. Thus, the formation of covalent bonds between the clusters is clearly apparent in the minimum (see inset in the bottom panel of Fig. 2). The electrostatic contribution is expected to be responsible for the strong interaction between Cu₅ clusters, ultimately giving rise to their oligomerization. It can be expected that more stable structures might exist, even implying the sintering in a Cu₂₀ structure in which the Cu₅ clusters have lost their identity. However, it should be stressed that the existence of many metastable states of fluxional, but strongly bound, oligomers might quench such structural re-arrangements at experimentally relevant ranges of temperature. In this sense, it is worth pointing out that the individualization of Cu₅ clusters at certain conditions of oxygen pressure and temperature has been recently suggested, particularly in an O₂-rich environment.²¹

3 Conclusions

In the quest for a fundamental level understanding of the outstanding stability experimentally probed for AMCs such as Cu₅,¹³ we have explored the possibility that AMCs couple to each other in such a way that their initial structures are preserved and, although their initial charge distributions experience modifications due to polarization effects, initial charge patterns can yet be recognized in the combined clusters. This concept of ‘identity’ thus goes beyond the classical concept of preservation of identity through the formation of vdW aggregates. In this work, we have found clear ab initio evidences on the favored coupled cluster formation and oligomerization of Cu₅ clusters in such a way that the Cu₅ units to a large extent keep their identity in terms of their structures. This outcome is reflected in the geometrical arrangements and in the Mulliken charge analyses of the resulting electronic structures. Additionally, the existence of metastable states of coupled Cu₅ clusters bearing very close energies has been found and can be interpreted as a consequence of the cluster fluxional nature. Our results could be valuable in the interpretation of experimental spectroscopic measurements of the (photo-)catalytic activities of atomic metal clusters, calling for high-resolution scanning electron microscopic probes on the formation of coupled clusters and their further oligomerization. From a theoretical perspective, additional work is necessary to analyze the concept of oligomerization of AMCs, including, e.g., molecular dynamics simulations on surface-supported AMCs as a function of temperature and even stronger tests using different methods at high level ab initio theory, including some that allow an analysis of interaction energy contributions.

Author contributions

Both co-authors have contributed equally to the manuscript in all the required steps (investigation, writing and editing). All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Appendix

Computational methods and additional details

Density fitting single-state multi-configurational self-consistent-field (DF-CASSCF) calculations have been carried out, as implemented in the last version of the MOLPRO code.²⁵ We used the polarized correlation-consistent triple-ζ cc-pVTZ-PP basis set for copper atoms,²⁶ including a small (10-valence-electron) relativistic pseudopotential. The DF-CASSCF approach is employed to account for the most important non-dynamical correlation effects. Then, the internally contracted multireference Rayleigh Schrödinguer (second-order) perturbation theory RS2C method¹⁷ has been applied to cover dynamical correlation effects. The RS2C method is basically a modified version of CASPT2 (complete active space with second-order perturbation theory) developed by Celani and Werner,¹⁷ using CASSCF wave functions as a reference in the RS2C calculations. For complex 1 of the coupled Cu₅–Cu₅ clusters, the CASSCF wave functions comprise up to 226 512 configuration state functions (CFSs). The subsequent RS2C wave function consists of 700 × 10⁶ contracted CSFs. The RS2C method thus allows the use of reference wave functions with large active spaces and internally contracted configurations are used as a basis. For density fitting, the associated MP2FIT and JKFIT bases have been used in DF-CASSCF calculations. The diagonalization of the first-order reduced density matrix obtained from the wave function in DF-CASSCF calculations allowed us to obtain natural orbitals. An analysis of the Mulliken charges²⁷ was accomplished for both Cu₅ and Cu₅–Cu₅ clusters. Additionally, for the sake of comparison, Coupled Cluster Singles and Doubles (CCSD) calculations have been carried out as implemented in the GAUSSIAN 09 code.²⁸

Initial optimizations of the coupled Cu₅–Cu₅ cluster geometries were performed at PBE and B3LYP levels,^29,30 using D4 Grimme's parameterization³¹ to account for the dispersion correction. An excellent performance has been achieved with the predecessor PBE-D3(BJ) ansatz³² in describing both supported and unsupported subnanometer silver^3,33 and copper^16,34 clusters. We used the atom-centered Def2-SVP³⁵ basis set for copper atoms. All dispersion-corrected DFT-based calculations have been performed with the ORCA suite of programs (version 5.0.1).^36–38

We started our coupled Cu₅–Cu₅ cluster calculations with a bipyramidal arrangement for the Cu₅ sub-unit. In this way, we placed together two trigonal bypiramidal arrangements with the center of mass of one of them located in the origin of the coordinate system and the corresponding main symmetry axis along the Z axis. The position of the second Cu₅ molecule with respect to the first one was modified in a range of distances and orientations. For this, we varied the distance between the two centers of mass along each of the axes, making it equal to 4.0, 5.0 and 6.0 Å for X, 6.0 and 7.0 Å for Y, and 7.0 and 8.0 Å for displacements along the Z-axis. Regarding the angles we considered three rotations for each of the geometries, i.e. the first one around the X-axis and with values of 0, 60, and 90 degrees; the second one around the Z axis, taking angles of 0, 45, and 90 degrees; and the last one around the X axis and with values of 0, 60, 120, 180, 240, 300, 360 degrees. The resulting geometries were fully optimized at the dispersion-corrected DFT levels, and those corresponding to the lowest energies were selected for further optimizations through DF-CASSCF calculations. The active spaces in DF-CASSCF calculations [m electrons in m orbitals, referred as (m,m) active space] varied until convergence was achieved in the follow-up RS2C calculations of coupled Cu₅–Cu₅ cluster energies. In all cases we considered the singlet ground state of the clusters and no symmetry restrictions were imposed in the calculations. The results of the preliminary DFT calculations can be obtained from the authors upon request. Results on previous theoretical evaluations of copper cluster geometries are available in the literature, see for instance ref. 39 and 40, but as far as we are aware, the authors of these investigations applied DFT level and not multireference ab initio approaches, with the resulting geometries differing from those obtained in this work. All interaction energies (E_inter) were calculated as follows:

E_inter = {E_Cu5–Cu5}_Min − {E_Cu5–Cu5}_Asymp

where {E_Cu5–Cu5}_Min is the energy at the minimum and {E_Cu5–Cu5}_Asymp is that at the asymptotic limit, correlating with the corresponding two Cu₅ + Cu₅ fragments in their energetically most favored structures. For the sake of size consistency, both calculations were carried out using the same active space within the DF-CASSCF and RS2C methodologies.

Acknowledgements

We thank Lyudmila Moskaleva, Alexander O. Mitrushchenkov, and Alexander Zanchet for very useful discussions. This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) under Grant No. PID2020-117605GB-I00. This publication is also based upon work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). We are also greatly thankful for the support of the EU Doctoral Network PHYMOL 101073474 (project call reference HORIZON-MSCA-2021-DN-01. One of the authors (B. F.) acknowledges Xunta de Galicia (grant number ED431C 2021/40) for further financial support. The CESGA supercomputer center (Spain) is acknowledged for having provided the computational resources. We also acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).

Notes and references

1. M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759.
2. J. Juraj, A. Fortunelli and S. Vajda, Phys. Chem. Chem. Phys., 2022, 24, 12083–12115.
3. P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853.
4. P. López-Caballero, S. Miret-Artés, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Chem. Phys., 2020, 153, 164702.
5. M. P. de Lara-Castells and S. Miret-Artés, Europhys. News, 2022, 53, 7–9.
6. P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568.
7. A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901.
8. S. Hirabayashi and M. Ichihashi, Phys. Chem. Chem. Phys., 2014, 16, 26500–26505.
9. B. Yang, C. Liu, A. Halder, E. C. Tyo, A. B. F. Martinson, S. Seifert, P. Zapol, L. A. Curtiss and S. Vajda, J. Phys. Chem. C, 2017, 121, 10406–10412.
10. P. Maity, S. Yamazoe and T. Tsukuda, ACS Catal., 2013, 3, 182–185.
11. J. Oliver-Messeguer, L. Liu, S. García-García, C. Canós-Giménez, I. Domínguez, R. Gavara, A. Doménech-Carbó, P. Concepción, A. Leyva-Pérez and A. Corma, J. Am. Chem. Soc., 2015, 137, 3894–3900.
12. J. Jašik, S. Valtera, M. Vaidulych, M. Bunian, Y. Lei, A. Halder, H. Tarábková, M. Jindra, L. Kavan, O. Frank, S. Bartling and S. Vajda, Faraday Discuss., 2022 10.1039/D2FD00108J.
13. S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908.
14. D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. Lóopez-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. Calvino, M. Lopez-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv.13661081.v1.
15. M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500.
16. P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074.
17. P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557.
18. A. S. Chaves, G. G. Rondina, M. J. Piotrowski, P. Tereshchuk and J. L. F. Da Silva, J. Phys. Chem. A, 2014, 118, 10813–10821.
19. Dynamical correlation contributions associated to state ‘4’ are found to be rather dependent on the geometry. In this way, when the geometry optimized with the (12,12) space at DF-CASSCF level is used in the RS2C calculation with the (10,10) space, the resulting energy (−2.9 eV) differs by just 0.1 eV from that obtained considering the (12,12) space at RS2C level (−2.8 eV, see Table 2 of the main manuscript).
20. A. Kubas, D. Berger, H. Oberhofer, D. Maganas, K. Reuter and F. Neese, J. Phys. Chem. Lett., 2016, 7, 4207–4212.
21. J. Garrido-Aldea and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 24810–24822.
22. H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911.
23. Q.-Y. Fan, Y. Wang and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 3891–3897.
24. O. V. Lushchikova, H. Tahmasbi, S. Reijmer, R. Platte, J. Meyer and J. M. Bakker, J. Phys. Chem. A, 2021, 125, 2836–2848.
25. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
26. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244.
27. R. S. Mulliken, J. Chem. Phys., 1962, 36, 3428–3439.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.1, Gaussian Inc., Wallingford CT, 2009.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem. Lett., 1994, 98, 11623–11627.
31. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
32. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
33. M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119.
34. S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908.
35. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
36. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
37. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
38. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
39. U. J. Rangel-Peña, R. L. Camacho-Mendoza, S. González-Montiel, L. Feria and J. Cruz-Borbolla, J. Cluster Sci., 2021, 32, 1155–1173.
40. P. Jaque and A. Toro-Labbé, J. Chem. Phys., 2002, 117, 3208–3218.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of optimized structures appearing in Fig. 1, complex 1 structure and charges, Cu–Cu distance Table. See DOI: https://doi.org/10.1039/d2cp03537e

---