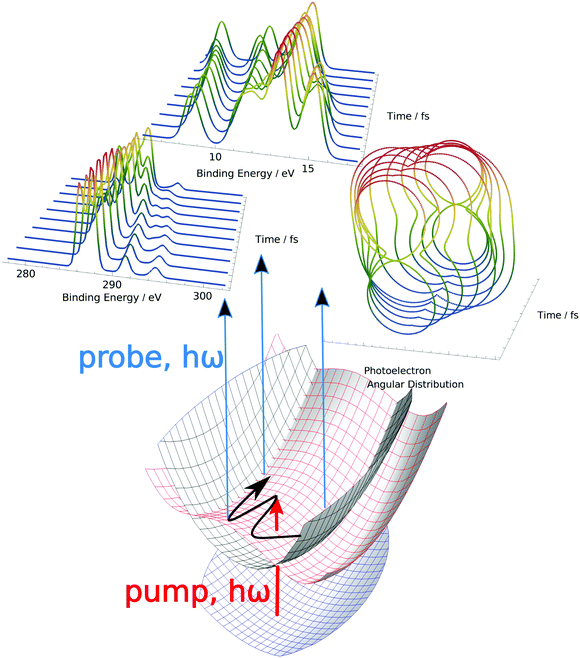
Time-resolved photoelectron spectroscopy: the continuing evolution of a mature technique

Abstract

Time-resolved photoelectron spectroscopy (TRPES) has become one of the most widespread techniques for probing nonadiabatic dynamics in the excited electronic states of molecules. Furthermore, the complementary development of ab initio approaches for the simulation of TRPES signals has enabled the interpretation of these transient spectra in terms of underlying coupled electronic–nuclear dynamics. In this perspective, we discuss the current state-of-the-art approaches, including efforts to push femtosecond pulses into vacuum ultraviolet and soft X-ray regimes as well as the utilization of novel polarizations to use time-resolved optical activity as a probe of nonadiabatic dynamics. We close this perspective with a forward-looking prospectus on the new areas of application for this technique.

---

1 Introduction

Imaging photo-initiated dynamics in molecules presents a number of challenges for both experiments and simulations. If the degrees of freedom of interest are primarily those directly related to the chemical bonds in a molecule, it is the time evolution of the valence electronic density and the coordinates of nuclei that are the primary quantities of import. These variables define both the relevant energy and time domains, with electronic and vibrational level spacings given by ≈4 eV and ≈0.1 eV, respectively. Thus, excitation by attosecond or femtosecond pulses will have sufficient bandwidth to prepare wave packets (coherent super-positions) of states with mixed electronic and nuclear characters.

It is this complex coupling of electronic and nuclear characters, and the corresponding time evolution of this admixture, that make the interpretation and assignment of a time-resolved observable quantity of these dynamics an ongoing theoretical and computational problem. Ideally, a well-chosen spectroscopic observable quantity would allow for a straight-forward disambiguation of these components so that the spectral features could be assigned using chemically intuitive concepts such as electronic states and vibrational modes. However, as with all observable quantities, changes in the measured signal arise not only just from the dynamics of the underlying wave packet, but also due to the time evolution of the spectroscopic quantity, which may itself exhibit a complex and non-intuitive mapping to the dynamics. For example, a significant change in the observed signal from a time-resolved experiment may arise from a change in the electronic character of the pump-prepared wave packet as a result of a non-adiabatic transition or, alternatively, may reflect the changes in the nuclear component of the wave packet via the coordinate dependence of the probe photon absorption cross-section.

In the face of these challenges and complexities, time-resolved photo-electron spectroscopy (TRPES) has emerged as a preeminent approach for probing ultrafast nonadiabatic dynamics in molecules.¹ This technique has a number advantages that arise from the choice of ionization as a universal probe process. First, ionization cross-sections will be sensitive to changes in both the electronic and nuclear components of a wave packet in a molecule. Vibrational motion on a potential energy surface will generally modulate the vertical ionization potential, which results in a shift of the kinetic energy of the outgoing election.² This observation has been particularly successful at identifying a large-amplitude motion in organic chromophores, such as torsion about carbon bonds in conjugated polyenes.³ Furthermore, simultaneous ionization to multiple cationic continua yields information on the electronic character of the wave packet. The different electronic components of the excited state wave packet will generally preferentially ionize to the different states of the cation, enabling their resolution via the time-dependence of the electron yield, corresponding to the different cationic continua.⁴ In addition, ionization is always an allowed process. While the ionization cross-section will display a coordinate and electronic state dependence, it will not be symmetry-forbidden; these symmetries will simply be reflected in the differential angular yields in an angle-resolved measurement of the photoelectron emission. Lastly, the measurement of time-evolving photoelectron angular distributions,^5–7 either completely or simply in the form of photoelectron anisotropy,⁸ can yield complementary insights into the electronic states and symmetries involved in the photoionization dynamics.

Importantly, this approach has proven amenable to simulations using ab initio computational techniques.^9–11 Numerous previous studies have shown that computationally tractable approximate ionization cross-sections are capable of yielding semi-quantitative agreement with energy-resolved experimental measurements.^12,13 In addition, significant progress has been made in the quantitative simulation of photoionization dynamics of polyatomic molecules,^14–18 including the first-principles simulation of energy- and angle-resolved measurements employing electronic wave functions with variational complexity sufficient to quantitatively describe molecular excited states.^19,20 When these computations are paired with trajectory or grid-based quantum dynamical approaches, purely ab initio TRPES may be determined. Accurate simulations of this type enable a degree of assignment of the spectral features that go far beyond the determination of empirical time constants. The underlying dynamics simulations will often allow for a mechanistic interpretation of the experimental and simulated TRPES in terms of time-evolving electronic states and nuclear configurations that define the wave packet.

In recent years, TRPES has continued to evolve with advances in source development and detection techniques. The tunable vacuum ultra-violet (VUV) or ultra-broad band (≈1 eV) light enables the preparation of wave packets with complex electronic characters, as well as the ability to probe the ensuing dynamics via the simultaneous projection onto numerous cationic continua. Following the development of photoelectron circular dichroism (PECD),²¹ the ability to generate pump pulses with complex polarizations, including the circularly polarized light, enables the measurement of circular dichroism in a time-resolved manner to image the chiral transient that arises in the excited state dynamics. Indeed, the ability to resolve not only the energy, but also the angular distributions of photoelectrons enables a far more detailed accounting of the ionization process, particularly if the molecular ensemble is aligned prior to photo-excitation. Advances in the development of velocity map imaging detectors greatly aids in the experimental determination of time-resolved photoelectron angular distributions in addition to the energy-resolved spectrum.

Lastly, the recent astonishing advances represented by X-ray free electron lasers (XFELs) enable truly novel investigations, in which the femtosecond timescale dynamics of photo-excited molecules may be performed in heretofore inaccessible energy regimes that enable atom-specific probes (via energy-resolved core–electron edges) of the electronic environment. In summary, an exhaustive account of the electronic and nuclear dynamics will not, in general, be possible in a single experiment and measuring a single observable quantity. Rather, a more complete picture of the photo-initiated dynamics in molecules is achieved via the combination of multiple time-resolved methodologies, many of which have only been developed and optimized in the last decade (Fig. 1 and 2).²²

Fig. 1 Time-resolved photoelectron spectroscopy as a probe of nonadiabatic dynamics in valence-excited electronic states. The pump pulse considered here will be assumed to be below the first ionization potential, while a variety of different probe pulses and detection schemes will be considered, especially the comparison between a valence photoionisation and a core–edge one.

Fig. 2 A Shadoks' view of time-resolved photoelectron spectroscopy for new users: a joint analysis of experimental and theoretical data leads to a quantitative interpretation of the photodynamics.

In the following, we will discuss a number of these advances, selected applications, and the implications of this recent work on the study of ultrafast nonadiabatic excited state molecular dynamics. We emphasize that this is not meant to be an exhaustive review. Rather, our purpose is to give a broad overview of the theoretical and experimental achievements made in TR-PES in the last approximately five years. It is our hope that this snapshot of the current “state of the art” approaches may be useful to both novice researchers in the field, as well as the external users of femtosecond TR-PES platforms, as they become familiar with this family of time-resolved spectroscopies. We close this work with what we believe are the most exciting applications for these techniques, which may be performed today or in the near future. We note that other recent reviews are complementary to this work and have influenced our thinking on a number of topics.^23,24

2 Complementarity of theory and experiment

The analysis of any time-resolved experiment will generally involve an attempt to quantify the evolution of the signal. For example, this may involve global or local “fits” of the signal to an analytic function, which itself is chosen from a chosen kinetic model. The underlying model may be constructed on the basis of chemical intuition or may be purely empirical. The result in either case is a set of time constants, which are determined so as to yield the best agreement between the model signal and the experimental result. If the model was chosen on the basis of chemical intuition, the empirical time constants may be mapped to changes in the electronic or nuclear structure of the wave packet (i.e. electronic state lifetimes and simple nuclear motion).

From the viewpoint of the simulation, ultrafast processes pose a particular challenge since they often defy description in terms of the statistical rate models that have proven successful for describing ground state chemical processes. For example, dynamics that proceed via passage through the regions of conical intersection will generally involve changes in the electronic character that is highly localized in time and coordinate space. The computational description of this type of dynamics requires the explicit consideration of the multi-dimensional potential energy surfaces and the coordinate dependence of the nonadiabatic coupling that facilitates transitions between electronic states. There exist numerous approaches for describing precisely these types of dynamics. Benchmark quantum dynamics are those that are preformed fully variationally, as exemplified by the multiconfigurational time-dependent Hartree (MCTDH) approach. This technique employs a grid-basis and a prescribed mathematical form of the potential energy surface(s). The earliest simulations of TRPES spectra were performed using numerical approaches and involved dynamics on both the neutral and cationic surfaces using model Hamiltonians.⁹

However, for dynamics that are more “chemical” in nature (i.e. large amplitude nuclear motion, bond breaking, and bond formation), the constraint that the potential energy surface be predetermined can be limiting. Indeed, it may not even be clear which degrees of freedom, and thus which regions of the potential energy surfaces, are most important for describing the coupled electronic–nuclear dynamics. This situation was greatly improved by the advent of trajectory-based quantum dynamics approaches, in which the potential energy surfaces are evaluated “on the fly” rather predetermined. In these approaches, the basis functions are localized in phase-space, and the equations of motion that determine their time evolution require only local information about the potential energy surfaces. Examples of these approaches include variational multiconfigurational Gaussians (v-MCG),²⁵ multi-configurational Ehrenfest (MCE),²⁶ and ab initio multiple spawning.²⁷ In addition, there are also semi-classical approaches, which are exemplified by the surface hopping family of methods, including surface hopping with arbitrary couplings (SHARC).²⁸ Here, the wave function (or the trajectory ensemble) is determined from a “swarm” of basis functions that evolve in the phase-space, each with an associated amplitude.

Indeed, recent efforts have shown^29–31 that a return to pre-determined surfaces of maximal flexibility is now possible thanks to advances in machine learning (ML) technologies. When performed employing the potential energy surfaces obtained from quantum chemistry computations, the computational cost of on-the-fly trajectory simulations is dominated by the evaluation of the electronic potential. When ML-derived surfaces are employed, this computational cost is shifted to the fitting of the surface; which may occur using classical trajectories to guide the fitting of the relevant regions of the coordinate space. Once this surface is determined, however, the evaluation of the potential and propagation of the trajectory basis is now highly computationally efficient. Even if the computational effort to determine a ML surface is comparable to an on-the-fly simulation, the advantage of the full-dimensional surface is that it enables a level of convergence and quantitative accuracy that is often inaccessible to ab initio on-the-fly approaches.

Once the dynamics have been simulated, it remains to couple them for the determination of the relevant ionization cross-sections. Importantly, all of these approaches are highly amenable to the approximate simulation of TRPES. Trajectory based methods inherently identify those regions of the coordinate space that are most important in describing the dynamics by providing discrete, enumerable number of phase space points at which the basis functions exist at any given time. What remains is to determine the ionization cross-section at these points. Again using quantum chemical methods, the electronic component of the ionization cross-section may be determined using a variety of approaches that differ in complexity and rigor.

One of the simplest approaches is to assume that the ionization cross-section to a specific cationic state may be approximated by the norm of the corresponding Dyson orbital: the one electron quantity that is determined by computing the overlap between the N-electron neutral and N − 1-electron cationic wave functions. While conceptually this can be thought of as a generalization of Koopmans' approximation, these quantities arise naturally in more detailed determinations of ionization cross-sections.^12,13 In a simple orbital picture, if the dominant neutral and cationic electronic configurations differ by a single electron, the overlap has the possibility of being large and the approximation predicts a correspondingly large one-photon ionization cross-section. Conversely, configurations that differ by more than a single orbital rotation will likely be small if orbital relaxation effects are not significant and thus the orbitals of the initial and final states remain roughly orthonormal.

However, the emergence of experiments that can capture the time-evolving angular momentum of the ionized electron clearly necessitates a description of the final state wave function that goes beyond just the cationic core. Numerous methods, including those based on Schwinger variational,¹⁴R-matrix theory,^32–34 or explicit time-dependent electronic structure computations,³⁵ can be coupled to direct dynamics simulations which can provide weighted time-evolving coordinate space representations of the wave packet as inputs to the computation. In summary, many advances have been made over the past decades that enable the accurate simulation of photo-ionization cross-sections employing complex molecular electronic wave functions.

Taken together, the result is that the purely ab initio simulations of TRPES are possible for both photo-physical and photo-chemical processes and provide semi-quantitative or better levels of agreement with experimental measurements. These developments have been key to enable interpretations of these experiments that go beyond empirical correlations and instead allow for the assignment of specific spectral features in terms of the transient electronic and nuclear characters derived from a wave packet simulation. This level of interplay between theory and experiment allows not only for the interpretation of a singular experiment, but also for understanding the spectroscopic response in terms of the underlying wave packet dynamics guides the proposal of new experiments and informs the design of measurements so that specific features of the wave packet more be explicitly imaged using particular observable quantities or energy ranges.

3 Current trends

3.1 Tunable vacuum ultraviolet time-resolved photoelectron spectroscopy

The ability to generate vacuum ultraviolet (VUV) fs-pulses on table-top set-ups enables the one-photon ionization of most organic chromophores in pump–probe time-resolved studies. But also, this ability enables a one-photon excitation just below the ionization threshold, with a subsequent transient population decay through an excited state manifold and down to the ground state(s), and even possibly the electronic states of reactive photoproducts. Indeed, in the case of gradient directed dynamics, the evolution of the nuclear wave packet “downhill” in low-lying excited states is often mirrored by an increasing binding energy of the outgoing electron. This increase in the effective ionization potential results from the conversion of the potential to the vibrational energy in the wave packet and concomitant shift of the dominant ionization channels to higher lying vibrational states of the cation. In practice, this can lead to “windowing” effects, where the decay of the ionization signal is due to a change in the photoionization dynamics, rather than the underlying excited state wave packet. In the absence of accurate simulations, disambiguating the wave packet and photoionization dynamics is difficult.

Therefore, in principle, the “ideal” ionizing probe pulse is one tuned to energies just below the ionization threshold. This energy precludes the possibility of the direct ionization of the ground electronic state (which may complicate the identification of the excited state signal) while enabling the ionization of the pump-initiated wave packet until electronic relaxation results in decay to the ground state. If this relaxation occurs on ultrafast time scales via a conical intersection, a sudden change in both the nuclear and electronic characters can then be potentially observed as a sudden change in the binding energy or ionization cross-section. A recent dramatic example of this was observed in the TR-PES of furan, where the time-dependent binding energy exhibits a distinct “kink” that the authors assign to return to the ground electronic state via a CI.³⁶

Alternatively, employing the VUV pulse as a pump pulse enables the preparation of complex electronic characters. As the excitation energy increases and approaches the ionization potential, the density of electronic states increases dramatically. The resulting wave packet will be an admixture of numerous electronic components. Furthermore, the ability to tune the excitation wavelength provides an additional means to control the character of the initially prepared wave packet. For example, tuning above or below predicted activation barriers on the excited state potential can give rise to a dramatically different temporal evolution, thereby confirming mechanistic predictions made by intuition or simulation. A recent study of the excited state dynamics of acetone utilized this ability to prepare wave packets at 159.4 and 154.2 nm and track the resulting electronic relaxation processes for both pump wavelengths via both TR-PES and quantum dynamics simulations.³⁷ In general, ensuring that the agreement between experiment and theory is maintained as the parameters that determine the composition of the excited state wave packet (e.g. pump wavelength) are varied and engender confidence in the underlying quantum dynamics simulations used to interpret the result.

In an “ideal” experiment, the pump pulse would prepare a well-characterized excited state wave packet, that is then probed on vibrational time-scales via one-photon ionization until the ground electronic state is re-populated. For organic photochemistry, this would involve pump and probe pulses both in the deep, vacuum, or extreme (DUV/VUV/EUV) ultraviolet range and a sub-30 fs cross-correlation. If the pulses become much shorter than this, the result will be an unavoidable loss in the discriminability in TR-PES: a 300 meV bandwidth corresponding to the convolution of two ∼10 fs pump and probe pulses are comparable to the typical energy splittings of excited valence cation states.

Few TR-PES experiments have utilized both DUV and EUV pulses.^37–39 Most of the published work in this area select one high order harmonic of the fundamental wavelength of the laser chain as a pump^40,41 or a probe.^42–44 In a number of cases, a significant effort has been expended to obtain a cross-correlation shorter than 32 fs.^40,45–47 An intense EUV source as a seeded FEL as FERMI has also been used as a probe pulse.^48,49 Even shorter time-resolution has been achieved in several of investigations on ultrafast charge-migration triggered by photoionization. But, in general, the sensitivity of such recent experiments lies exclusively in the transients of the mass spectrum.^50,51 Indeed, there are presently challenges to produce tunable ultrashort fs pulses, in the range of 6 to 10 eV, that will be stable enough for long acquisition times. In addition to the frequency mixing that delivers sub-10 fs-DUV pulse,^52–54 the optical soliton driven resonant dispersive wave (RDW) emission in gas-filled hollow fibers⁵⁵ becomes a promising source. It delivers ultrashort pulses up to a deep-UV (down to 113 nm) with a large tunability, stable over hours, in any polarisation state, at low cost and easy to implement. The first demonstration of these sources for TR-PES has recently been published and shows a high stability.⁵⁶ This RDW solution with its simplicity might soon prevails over the non-collinear non-resonant four wave mixing in a gas cell⁵⁷ or a selected high harmonic.

3.2 TR-photoelectron circular dichroism (PECD) and TR-photoexcitation-induced photoelectron circular dichroism (PXECD)

TR-PECD and TR-PXECD are two recent extensions of TR-PES that exhibit chiroptical sensitivity and take advantage of the full range of techniques amenable to photoelectron imaging. Information about the chiral potential is revealed in an asymmetry of the photoelectron angular momentum relative to the propagation axis of the light. By convention, this asymmetry is termed as “positive”, or forward, if the result is an excess of photoelectrons in the forward hemisphere for a left polarized ionization pulse. Conversely, it is termed as “negative” if this excess is in the backward hemisphere. It is then this photoelectron asymmetry that is the observable quantity of these chiroptical effects. In TR-PECD, the probe pulse is circularly polarized with a pump pulse linearly polarized, while, in TR-PXECD, this is reversed. Beyond this technical aspect, which is not so difficult to implement in any experimental set-up, why using circularly polarised light, in conjunction with a photoionisation probe, to interrogate light–matter interactions is useful? Briefly, it is because these techniques result in one of the largest circular dichroism effects ever measured: in the range of a few to several percent despite the random distribution of the molecules in the molecular jet and its low density.

In addition to the usual pump–probe delay, the basic building block of these CD spectroscopies is to record a differential signal between photoelectron images that have opposite helicities, but the same ellipticity. The result is a photoelectron asymmetry relative to the propagation axis of light pulses as shown in Fig. 3. This differential measurement needs to be normalized by the number of emitted photoelectrons to obtain a percentage of the asymmetry. Since PECD and PXECD, in contrast to circular dichroism observed in absorption processes, are both based only on a pure dipole interaction, these asymmetries are potentially quite large. One key difference between these two chiro-sensitive TR-PES is that TR-PECD is based on the transition dipole for ionization, while TR-PXECD depends on the phase relationship between the non-colinear dipoles of photoexcitation. Let's go in detail to differentiate the physics underlying TR-PECD and TR-PXECD.

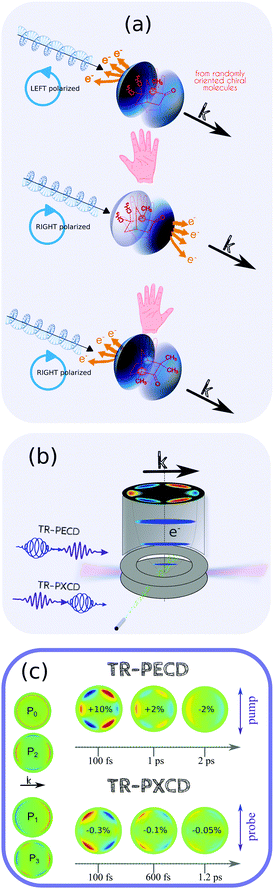Fig. 3 (a) TR-PECD and TR-PXECD appear both as an photoelectron asymmetry relative to the light propagation axis on the velocity map imaging spectrometer (VMIS) image. This asymmetry depends both on the handness of the molecule and the helicity of the light, as any other chiroptical effect. (b) This asymmetry is monitored with a velocity map imaging detector. In TR-PECD, the probe has to be circularly polarized, while, in TR-PXECD, it is the pump that is circularly polarized. (c) The asymmetry images can be fitted by a linear combination of the P_i=1,3 Legendre Polynomials (as shown in the column at left). The images of the photoelectron asymmetry recorded in TR-PECD and TR-PXECD for different pump–probe delays in the enantiopure 1R,4R-(+)-camphor are shown. Pump–probe ionization takes place at ∼9.3 eV with a pump excitation in the first Rydberg states of camphor. The colormap is the same for all the delays in each configuration. The indicated percentages correspond to the asymmetry of the forward hemisphere recorded with a left polarized probe (TR-PECD) or a pump (TR-PXECD). These data are published in ref. 58 and 59.

When chiral molecules are photoionized by a circularly polarized probe pulse, the forward/backward asymmetry of the emitted photoelectron, known as PECD, results from the spatial interference between the partial waves that define the continuum photoelectron. Their relative phases depend on both the initial bound-state wavefunction, the scattering of this electron in the chiral potential, and the partial waves that define the electron continuum. For chiral molecules, this phase information can survive even in an ensemble of randomly oriented nuclear structures due to the chirality inherent to the molecular electronic density. As with any other chiroptical phenomena, the sign of the asymmetry reverses with the handedness of the enantiomer or the helicity of the light. PECD is the ionization channel resolved as any other photoelectron spectroscopy and, for a same cation state, can become monotonically kinetic energy dependent. From a pragmatic point of view, the differential operation on the electron images generates positive and negative contributions that are straightforward to resolve, in contrast to TR-PES where the photoelectron bands generally span broad energy ranges. In PECD, these contributions are more readily resolved as the main information content is in the asymmetry of the angular distribution. The degree of asymmetry is quantified as a linear combination of the odd Legendre polynomial with the angle θ defined by the momentum of the electron relative to the propagation axis of the light. Following the first numerical calculation and first experimental verification of the PECD effect,^21,60 most of the published studies over the last two decades in this area have involved randomly oriented chiral molecules or clusters which are photoionized using tunable VUV light.⁶¹

Using synchrotron VUV light, and when only one photon is involved in the ionization process, the PECD simplifies to the amplitude of the Legendre P₁(cos θ) function. To date, only TR-PECD employing a one-photon probe has been reported, pushing the Legendre decomposition to a linear combination of P₁(cos θ) and P₃(cos θ) with this later contribution arising from the anisotropy of excitation created by the pump pulse.^58,62 This anisotropy is able to enhance or cancel the photoelectron asymmetry by selecting a molecular orientation, while the time-dependence appears as a decay of the P₃(cos θ) amplitude. More impressive is how a clear breakdown of the Franck–Condon approximation (BFCA) results in a dramatic flip of the sign of the asymmetry, thereby making PECD sensitive to vibrational effects.^63,64 As a result of this effect, which leads to geometry-induced phase shifts in the partial wave decomposition of the outgoing electron, vibrational wavepacket dynamics created by the pump in an electronic excited state can have a strong impact, as seen in Fenchone.⁵⁸ The BFCA can also be employed to explain why TR-PECD may depend on the pump polarisation.⁶² Indeed, employing a circularly polarised pump in the case of the BFCA, several molecular orientations will be selected each one with a slightly different vibrational wavepacket, resulting in interference detectable using TR-PECD.

In PXECD, when a circularly polarized pump in the (x,y) plane photoexcites a set of non-parallel moments of transition-different electronic states or vibrations with the BFCA, a 3D-electronic coherence is also created. This 3D-coherence is in fact a pseudo-vector whose amplitude depends on the coherence lifetime.⁶⁵ Due to the quantum beat, this pseudo-vector maps out a helix with its amplitude oscillating perpendicular to the common plane of all the moments for the corresponding transition, by defining the pump polarisation plane. This oscillation period along the z axis (along the propagation axis of the pump) is inversely proportional to the energy differences between the moments of transition, namely quantum beating energies. This induced dipole has an initial phase that depends mainly on the pump helicity. Its time evolution along the z axix switches the helix direction each half period of the quantum beating. In the peculiar case of a chiral molecular system, the molecular handedness enforces a preferential direction of the electronic helix.

To help visualize this 3D-coherence of the electron density created in the photoexcited neutral molecule, we consider the specific case in which photoionization occurs via a linearly polarised probe pulse. If the time-resolution is sufficiently short, the oscillations along the z axis appear to be asymmetrical on the photoelectron images, called photoexcitation-induced photoelectron circular dichroism (PXECD). Since the probe pulse is achiral, it is quite important to underscore that this TR-PXECD is not a result of the chirality of the Coulomb potential of the cation, like the PECD is. Instead, it is a result of the neutral wave packet dynamics via a possible vorticity and its initial phase along z fixed by the handedness of the molecule and the helicity of the pump. To observe these oscillations, sub-10 fs UV circularly polarized pulses are in general required. To date, these oscillations have not been observed; only the decay of the 3D coherence has been monitored with snapshots shown as example in Fig. 3(c).⁵⁹ Both techniques are used to investigate chiral molecular systems and, ideally in a near future, chiral transients associated with nuclear geometries in the vicinity of conical intersections from static achiral molecular systems. With the exception of the work performed by Ilchen et al. in the X-ray regime,⁶⁶ this chirosensitive TR-PES has only been applied to investigate the Rydberg bands of photoexcited chiral terpenes.⁵⁹ The next step is to photoexcite chemically more reactive valence states.

It has been shown that these appealing extensions of time-resolved electron imaging can be performed using kHz Ti:Sapphire laser systems and would be even easier to implement with the emerging multikHz Yb-doped fiber amplified laser. For the kHz repetition rate, artificial neural network analysis is an alternative solution to reduce the acquisition time by reliable handling of raw images made of sparse illuminated pixels as the ones encountered in TR-chiroptic PES.⁶⁷ As with any time-resolved technique, shorter the cross-correlation is, better is the sensitivity to the dynamics, as far as the VMI energy resolution is not drastically exceeded. From an experimental point of view, there is another important condition ideally to be fulfilled in TR-PECD: in general, lower is the kinetic energy of the outgoing electron, stronger is the asymmetry. Therefore, a tunable probe wavelength is of high benefit. This condition on the probe wavelength does not exist in TR-PXECD.

So far, these two spectroscopies have used the P-Basex fits of photoelectron images to disentangle through the decomposition of the Legendre polynomial and the molecular dynamics induced by the pump. While this is useful, it cannot be used to retrieve the real 3D angular distribution of the photoelectron asymmetry. Indeed, the pump through its electronic excitation breaks the cylindrical symmetry required to extract the 3D distribution of the photoelectron from the P-Basex fit. One way to settle this issue is to implement a tomographic approach in these TR-PECD and TR-PXECD. This is unfortunately highly time consuming at kHz but manageable at hundreds of kHz.

The reliable quantitative prediction of TR-PECD and TR-PXECD effects relies on the accuracy of the underlying quantum chemistry calculations of the transition dipole moments involving both bound and continuum states. This is a highly demanding task since photoelectron dichroisms are inherently differential phenomena which require an accurate description of both the amplitude and the phase of the transition dipoles. Moreover, an average over all the molecular orientations is required to obtain the appropriate angular dependencies. Chiral molecules are generally “large” so that coupling nuclear dynamics simulations using accurate quantum chemical methods to ab initio descriptions of the photoionization process are not practical. Therefore, the theoretical simulation of electronic transitions usually relies on fixed-nuclei mean field approaches which have been found accurate enough in many static cases.^{62,64,68–70} Coupling the electronic and nuclear degrees of freedom to describe TR dichroisms remains a great challenge for large chiral molecules, and remains an outstanding problem due to difficulties analogous to those described in Section 2. An unambiguous evaluation of the phases is critical and depends on the electronic basis used to characterize the states populated by the pump pulse, as well as the partial wave description of the continuum. This will be particularly challenging if the vibronic wave packet is spatially extended. Last but not least, the PECD effect is stronger at the lowest kinetic energies of the photoelectrons, exacerbating the sensitivity to the molecular potential and thus the quality of its description with precise minute structural detail. Similarly, the relaxation of the ionic core due to nuclear motion or induced by the Coulomb interaction with the outgoing photoelectron, as well as the electron spin have not been considered so far.

4 Future directions

4.1 TR-XPS

If the nonadiabatic dynamics of interest involve the time evolution of the valence electronic density and nuclear configurations, i.e. chemical processes, probing the valence electrons directly via ionization with UV-VUV light would seem to be the most appropriate strategy as discussed already above. In the case of wave packet dynamics, this electronic density may be the result of a complex super-position of different electronic characters. The canonical conception of TR-PES would state that via the projection of the wave packet onto multiple cationic continua, the differing ionization cross-sections for each of electronic components would enable the identification of each of the electronic characters. This is the basis for Koopmans' correlation picture in which,^4,71 in ideal or well-chosen cases, the different electronic states that comprise an excited state wave packet will have very different ionization cross-sections to the cationic states accessible by the probe pulse.

While true in principle, in many cases where the neutral electronic states are highly coupled (as is generally the case in ultrafast nonadiabatic processes) and the ionization process only accesses the lowest few cationic states, ionization cross-sections for each component electronic state in the wave packet will be of similar magnitude, regardless of the cationic state accessed. When coupled with large amplitude nuclear motion, which will also broaden the photoelectron band due vibronic coupling and FC overlap considerations, in practice, the observed signal may be significantly broadened in energy with a poorly contrasted time delay-variations, thereby precluding assignment of the various electronic state components.

Another strategy is to push the energy of the probe photon into the X-ray regime. Then, the nature of the probe process is changed qualitatively. In this case, the core-ionized manifold of states is used to spatially image the evolution of the valence electronic density. This has a number of advantages. First, X-ray pulses are extremely high above threshold, enabling access to many core-ionized states near a specific edge feature. However, second and more importantly, the core–hole created by this probe is highly localized in the coordinate space. Thus, even though the initial valence electronic states that comprise the neutral wave packet are delocalized over the nuclear framework, ideally each atomic core in the molecule will provide its own view of this evolving charge density via the ionization process. The ability to generate element specific probes of electron density will be especially useful if the electronic character evolves around the transient charge formation at localized sites on the molecular framework. In addition, the associated transient chemical shifts would be potentially observable via TR-XPS.

Early work using this approach focused precisely on this: transient charge formation and migration. Early synchrotron^72,73 and subsequent XFEL studies^74,75 interrogated charge carrier recombination at semiconductor interfaces. Modern XFEL facilities can now deliver a near vibrational time-scale resolution in the soft X-ray regime, allowing for the direct probing of the 1s electrons of elements relevant for organic photo-chemistry.⁷⁶ In summary, these studies can be considered direct analogs to the valence spectroscopies discussed previously. The widespread application of this approach to femtosecond time-scale dynamics has been limited mainly by the (now historical) sub-1KHz repetition rate of the XFEL sources. The corresponding acquisition time to achieve the reasonable signal:noise ratio in a typical femtosecond resolution (i.e. vibrational time-scales) has made such studies traditionally very challenging.

An initial application of this technique to the excited state dynamics in the gas phase involved the dissociation dynamics of methyl iodide following excitation at 272 nm.⁷⁷ The soft x-ray probe was sufficient to ionize the 4d electrons from the iodine atom, and the time-resolved shift in the observed binding energy was assigned to the prompt dissociation of the molecule to CH₃ and the I atom. Studies are now underway that apply these techniques to non-adiabatic dynamics in the excited states of polyatomic molecules.

The brightness of these new light sources also enable alternative experiments in which an X-ray pulse serves as both the pump and the probe. In such experiments, the primary question is the preparation and subsequent imaging of core–hole dynamics in molecules.⁷⁸ While these experiments provide an exciting demonstration of the power of these light-sources, we will refrain from further discussion of them as our focus here is on the interrogation of chemical processes.

Despite the current scarcity of circularly polarized light at X-FELs, combined with their limited accessibility, there is an obvious interest to investigate the chirality of molecular potential by probing in the X-ray range. Indeed, as being element specific, the outgoing electron is potentially emitted from a localised orbital with an initial wavefunction that is achiral since spherically symmetric. For instance, PECD larger than 10% has been observed from C 1s,⁷⁹ thereby motivating investigations in the time domain. The first studies have been recently published with the K-edge of fluorine used to probe the dissociation of trifluoromethyloxirane dication resulting from the Auger decay and charge migration dynamics.⁶⁶ This pioneering experiment is an important stimulus for forthcoming investigations.

In the context of TR-PXECD, it would be of great interest to combine an ultrashort UV-circularly polarized light (CPL) pump pulse and a X-ray linearly polarized probe. Indeed, while the oscillating 3D-coherence of PXECD is highly delocalised, we could scrutinize thanks to the inner-shell probe and its spatial extension through this elemental localised ideal probe. Then, comparing the TR-PXECD probed in the valence range and in the X-ray range would provide a better glance if the electron density is a key participant for chirally driven electronic relaxation especially around conical intersections.

4.2 Probing electronic coherences

Much of the previously discussed work has focused on using time-resolved photoelectron spectroscopy to discern the flow of electronic state populations and thereby determine the instantaneous electronic character of a prepared wave packet. However, there has been a recent surge of interest in not only experimentally probing the electronic populations, but also the electronic coherences between states that facilitate the flow of the wave packet amplitude from one state to another. Various time-resolved techniques have been proposed for this endeavor, including linear and non-linear spectroscopies involving ultashort atto- and femto-second pulses, including those in the X-ray energy regime.⁷⁶ Here, we will highlight a couple of these approaches, and how TRPES may be employed to image this aspect of wave packet dynamics.

Theoretical studies and first-principles simulation^80–83 have demonstrated that the magnitude of the photo-ionization signal in a time-dependent study will be modulated not only by the state populations that define an excited state wave packet, but also by the coherences that arise from the coupling between the electronic states. Theoretical models predict that in the case of the conical intersection mediated dynamics, passage through the seam region will give rise to transient coherences in the vicinity of the degeneracy associated with the population transfer. If such signals were to be observed, they would represent one of the most direct observations of conical intersection dynamics, as these coherences are themselves a direct consequence of the degeneracy between the electronic states (in contrast to rapid changes in the population which only infer the role of a CI region). The observation of these signals would be challenging, and theoreticians have proposed the use of, for example, atto-second pulse trains to resolve the modulations in the photo-ionization signal.⁸³

A completely different proposal for observing electronic coherences in molecules employs TRPES to probe rotational wave packets.⁷ In most cases, the ultrafast dynamics in the excited electronic states of molecules are conceived of and simulated in the molecular frame, even though experiments are carried out in the laboratory frame (LF). Most ultrafast studies are primarily concerned with the internal degrees of freedom, in which the coupled electronic–nuclear wave packet evolves on atto- and femtosecond time scales. The rotational degree of freedom evolves on time-scale orders of magnitude larger than this and is often ignored. However, neglecting the coupling to the rotational degree of freedom is an approximation that can have significant consequences on the subsequent simulation of an experimental observable. The nonadiabatic dynamics that follow from electronic excitation will depend on the lab frame orientation of the molecule, as will the measurement (necessarily in the lab frame), which records the response of the ensemble of all orientations. However, in some cases, this can also be leveraged as an advantage, as all the relevant density matrix elements that define these dynamics may be extracted from the response of initially un-oriented molecules.

A rotational wave packet in ammonia, prepared with a femtosecond pump pulse, was employed in this manner. Time-resolved photoelectron angular distributions were employed to determine the so-called electronic angular distribution moments (EADMs) and thereby completely separate the electronic population dynamics from electronic coherences.⁷ This study employed VUV-TR-PES, but any ultrafast angle-resolved scattering observable could yield analogous information. In this work, by measuring the lab-frame angular distribution, the authors could experimentally measure the corresponding LF anisotropies, β_LM(t,ε), analyze the time evolution of these quantities, and compare to wave packet simulations. It was observed that while the time evolution of the β₀₀ moment related to the total ionization cross-section was sensitive to the population dynamics, the β₄₀ moment evinced the time-evolving coherences that characterized the the vibronic wave packet. This important result for TR-PES was in compelling agreement with theory. A key advantage of these experiments is that they can be performed using existing techniques and yet still be used to extract a wealth of information on the wave packet dynamics.

4.3 Coincidence measurements

We have already discussed the recent developments that enable probe photon energies in the 7–12 eV range to follow the complete evolution of the electron binding energies of an excited state wave packet. But inevitably, as soon as the total pump–probe energy exceeds excitation energies to the higher excited states of the cation, the branching ratio to dissociative photoionisation increases dramatically such that the assignment of TR-PES becomes even more challenging. One way to tackle this issue is to implement the coincident detection of photoelectrons as a function of emitted ions that stem from the very same ionization event. This spectroscopy, termed time-resolved photoelectron-photoion-coincidence spectroscopy (TR-PEPICO), was first reported more than two decades ago, but, to date, only a few such studies have been performed.^84–87 The necessity to maintain a low coincidence/ionization rate is challenging at laser source repetition rates near 1 kHz, resulting in time-consuming measurements. Such experiments are generally incompatible with the standard stability of most of the Ti:Sa laser sources, despite the clever statistical approaches developed to reduce the acquisition time in such experiments.^88,89

A revolution is underway with DUV-EUV sources developed from the Ytterbium high average power driving laser beam at repetition rates higher than 100 kHz and that display a wonderful stability over days. For instance, a VUV-DUV source with MHz repetition rates (based on highly cascaded harmonic generation (HHG) in rare gas-filled hollow-core negative-curvature fiber) has been developed to produce VUV photon fluxes as high as 10¹⁰–10¹⁴ photons s⁻¹ in the 7–11 eV range before monochromatisation.⁹⁰ An alternative is to produce HHG from an UV driving field. For example, at 166 kHz, the stability of high-power third-order harmonic at 85.7 nm (14.5 eV) of a 257 nm driving field, selected by a single SiO₂ plate under 30° grazing incidence, combined with 150 nm thick indium foil, has been tested for several hours with a flux of 4 × 10¹¹ photons s⁻¹ on molecular targets.⁹¹ Obviously, other VUV wavelengths can be produced based on high harmonic generation with lower cascaded harmonics of the 1 μm driving field or its second harmonic.⁹² The main challenge is however to handle appropriately the drifting pointing of the EUV beam resulting from thermal effects in the monochromatisation stage. These thermal effects are induced by the high average power level of the driving fundamental field. This can be largely overcome by using an annular driving field for HHG and then a simple pinhole to filter out the intense driving beam. This old concept of HHG has been tested with such high repetition rate sources, showing an absorption-limited HHG regime with only a (27 ± 13)% lower conversion efficiency with an annular driving field compared to the Gaussian beam.⁹³ This kind of set-up will ease the recombination of the pump and probe beams. There is no doubt that such high average power sources are of high practical importance for the future of TR-PEPICO investigations.

For instance, pump–probe experiments with ultra broadband pulses, in which charge migrations are investigated, have mainly relied on the transients of fragment yields induced by dissociative ionisation paths.^94,95 A TR-PEPICO spectroscopy would result in enhanced sensitivity by filtering the photoelectrons produced in coincidence with the fragmented ion signal that shows the highest pump–probe contrast. This would ease a direct mapping of the electronic redistribution and the assignment of new photoreaction pathways that are correlation-driven by the electronic coherence.⁹⁶

4.4 Fourier transform approaches

Such high power (>100 W) Ytterbium femtosecond laser sources can be also combined with the fast acquisition of VMIS images with no deadtime in order to implement Fourier transform analysis. Here, as with all Fourier-based approaches, the modulation of any parameter at a known frequency can be transcribed onto the measured signal and used to extract “background-free” photoelectron images on the pixel-by-pixel basis. For example, recent results were obtained by modulating the S₃ Stokes parameter of the pump pulse.⁹⁷ By varying the proportion of photons that are circularly polarized at regular intervals, it was possible to modulate the electronic content of the Rydberg wavepacket created by two-photon transitions, which then display different non-adiabatic dynamics.⁹⁷

The high repetition rate of such cutting-edge femtosecond sources allows for the implementation of more sophisticated Fourier analysis in photoelectron spectroscopy. Coherent multidimensional spectroscopy (CMS) with a sequence of four ultrashort optical pulses using with a locked-phase relationship and modulation, is used as a pump pulse to induce a nonlinear response in the sample. This latter one is then probed by photoionisation induced by a fifth pulse. The oscillating signal with the two variable delays is then Fourier transformed to yield multidimensional frequency correlation maps on the photoelectron spectrum. This multidimensional photoelectron spectroscopy based on a magnetic bottle spectrometer has been achieved showing an increasing sensitivity.⁹⁸ Indeed, the optical phase modulation allows an efficient single-counting detection once combined with the multichannel software-based lock-in amplification.⁹⁹ The next challenging step is to implement this CMS with an imaging photoelectron spectrometer to obtain access not only to the kinetic energy but also to the modulation in angular distributions.

4.5 Into highly diluted samples and complex systems

These amplified Ytterbium laser sources with a typical flux of several 10^16–18 photons s⁻¹ allow investigations of highly diluted samples using TR-PES. A recent example was an investigation into the photoreactivity on the surface of aerosolized functionalized nanoparticles.^100,101 In such set-ups, which are germane to photocatalysis, photochemical energy conversion or even electrochemistry, the charge transfer between surface terminating ligands and nanodots could be investigated by TR-PES to directly interrogate the electronic structures involved in these dynamics. Similar processes may also be investigated in thermo-labile bio-relevant charged molecules using electrosprayed sources combined with ion traps.^102,103 Here again, the low duty cycle of the ion traps could be compensated by using this high repetition rate-intense laser source on the few tenth of ms burst of charged molecules released.

There have been several TR-PES investigations performed on chromophores dissolved in liquid jets with a total pump–probe energy below the potential of ionisation^104–106 and above with as main issue the pump–probe contrast.^107–109 It has been shown that the effective attenuation length of the emitted electron from a water jet is quite constant for the kinetic energy in the range of 5 to 40 eV, indicating that a similar depth of the liquid jet around 2 nm is then probed.¹¹⁰ All the technical aspects of TR-PES on the liquid jet with a table-top laser source have been recently addressed by T. Suzuki.¹¹¹ The merging of the liquid jet and TR-PES allows the impact of the surrounding solvent environment to be investigated using a systematic approach that compares dynamics in different derivatives. Sensitivity to the charge-transfer-to-solvent process as well as the resulting relaxation “cooling” of the solvent shell are then possible.

5 Conclusions

The ability to observe and interpret the complex, coupled electronic–nuclear wave packet dynamics in the excited electronic states of polyatomic molecules has been significantly advanced by the co-development of time-resolved photoelectron spectroscopy and first-principles simulation techniques that are based on nonadiabatic dynamics computations. The former is a widely applicable and highly sensitive probe of the evolution of both the nuclear and electronic characters of the vibronic wave packet, while the latter enables the interpretation of the time-evolving signal in terms of time-evolution of nuclear structures and electronic state populations. New developments in high repetition-rate photon sources suitable for time-resolved studies enable femtosecond-duration pulses in new energy regimes.

Furthermore, these technological developments are likewise motivating advances in the theoretical and computational sides so that simulation can be employed to aid in the interpretation of these new spectroscopies. As this family of time-resolved techniques matures and continues to evolve, we look forward to experiments and simulations that go beyond the empirical measurement of wave packet dynamics and rationalization of the results and toward the preparation of the specific excited state dynamics to achieve particular reactive outcomes guided by truly predictive computations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

B. Pons, Y. Mairesse, B. Fabre, and A. Stolow are gratefully acknowledged for many valuable discussions. I. Seidu is thanked for assistance in the preparation of the figures.

References

1. A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758.
2. R. Spesyvtsev, T. Horio, Y.-I. Suzuki and T. Suzuki, J. Chem. Phys., 2015, 142, 074308.
3. A. E. Boguslavskiy, O. Schalk, N. Gador, W. J. Glover, T. Mori, T. Schultz, M. S. Schuurman, T. J. Martínez and A. Stolow, J. Chem. Phys., 2018, 148, 164302.
4. V. Blanchet, M. Z. Zgierski and A. Stolow, J. Chem. Phys., 2001, 114, 1194–1205.
5. J. G. Underwood and K. L. Reid, J. Chem. Phys., 2000, 113, 1067–1074.
6. C. Z. Bisgaard, O. J. Clarkin, G. Wu, A. M. D. Lee, O. Geßner, C. C. Hayden and A. Stolow, Science, 2009, 323, 1464–1468.
7. V. Makhija, K. Veyrinas, A. E. Boguslavskiy, R. Forbes, I. Wilkinson, R. Lausten, S. P. Neville, S. T. Pratt, M. S. Schuurman and A. Stolow, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 114001.
8. O. Schalk and A. E. Boguslavskiy, J. Phys. Chem. A, 2017, 121, 9612–9618.
9. M. Seel and W. Domcke, J. Chem. Phys., 1991, 95, 7806–7822.
10. Y. Arasaki, K. Takatsuka, K. Wang and V. McKoy, Chem. Phys. Lett., 1999, 302, 363–374.
11. H. R. Hudock, B. G. Levine, A. L. Thompson, H. Satzger, D. Townsend, N. Gador, S. Ullrich, A. Stolow and T. J. Martínez, J. Phys. Chem. A, 2007, 111, 8500–8508.
12. M. Spanner, S. Patchkovskii, C. Zhou, S. Matsika, M. Kotur and T. C. Weinacht, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 053406.
13. S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540.
14. R. R. Lucchese, K. Takatsuka and V. McKoy, Phys. Rep., 1986, 131, 147–221.
15. T. N. Rescigno, B. H. Lengsfield and A. E. Orel, J. Chem. Phys., 1993, 99, 5097–5103.
16. C. M. Oana and A. I. Krylov, J. Chem. Phys., 2009, 131, 124114.
17. D. Khuseynov, C. C. Blackstone, L. M. Culberson and A. Sanov, J. Chem. Phys., 2014, 141, 124312.
18. J. B. Williams, C. S. Trevisan, M. S. Schöffler, T. Jahnke, I. Bocharova, H. Kim, B. Ulrich, R. Wallauer, F. Sturm, T. N. Rescigno, A. Belkacem, R. Dörner, T. Weber, C. W. McCurdy and A. L. Landers, Phys. Rev. Lett., 2012, 108, 233002.
19. Y. Arasaki, K. Takatsuka, K. Wang and V. McKoy, J. Chem. Phys., 2010, 132, 124307.
20. K. Wang, V. McKoy, P. Hockett and M. S. Schuurman, Phys. Rev. Lett., 2014, 112, 113007.
21. I. Powis, J. Chem. Phys., 2000, 112, 301–310.
22. T. Suzuki, Faraday Discuss., 2021, 228, 11–38.
23. H. Zettergren, A. Domaracka, T. Schlathölter, P. Bolognesi, S. Díaz-Tendero, M. Łabuda, S. Tosic, S. Maclot, P. Johnsson, A. Steber, D. Tikhonov, M. C. Castrovilli, L. Avaldi, S. Bari, A. R. Milosavljević, A. Palacios, S. Faraji, D. G. Piekarski, P. Rousseau, D. Ascenzi, C. Romanzin, E. Erdmann, M. Alcamí, J. Kopyra, P. Limão-Vieira, J. Kočišek, J. Fedor, S. Albertini, M. Gatchell, H. Cederquist, H. T. Schmidt, E. Gruber, L. H. Andersen, O. Heber, Y. Toker, K. Hansen, J. A. Noble, C. Jouvet, C. Kjær, S. B. Nielsen, E. Carrascosa, J. Bull, A. Candian and A. Petrignani, Eur. Phys. J. D, 2021, 75, 152.
24. N. Kotsina and D. Townsend, Phys. Chem. Chem. Phys., 2021, 23, 10736–10755.
25. G. Richings, I. Polyak, K. Spinlove, G. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308.
26. D. V. Shalashilin, J. Chem. Phys., 2009, 130, 244101.
27. M. Ben-Nun, J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175.
28. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
29. Y. Guan, D. H. Zhang, H. Guo and D. R. Yarkony, Phys. Chem. Chem. Phys., 2019, 21, 14205–14213.
30. B. Jiang, J. Li and H. Guo, J. Phys. Chem. Lett., 2020, 11, 5120–5131.
31. J. Westermayr and P. Marquetand, Mach. Learn.: Sci. Technol., 2020, 1, 043001.
32. P. G. Burke and K. T. Taylor, J. Phys. B: At., Mol. Opt. Phys., 1975, 8, 2620–2639.
33. M. Tashiro, K. Morokuma and J. Tennyson, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 022706.
34. M. Tashiro, J. Chem. Phys., 2010, 132, 134306.
35. X. Li, N. Govind, C. Isborn, A. E. DePrince and K. Lopata, Chem. Rev., 2020, 120, 9951–9993.
36. S. Adachi, T. Schatteburg, A. Humeniuk, R. Mitrić and T. Suzuki, Phys. Chem. Chem. Phys., 2019, 21, 13902–13905.
37. R. Forbes, S. P. Neville, M. A. B. Larsen, A. Röder, A. E. Boguslavskiy, R. Lausten, M. S. Schuurman and A. Stolow, J. Phys. Chem. Lett., 2021, 12, 8541–8547.
38. M. Williams, R. Forbes, H. Weir, K. Veyrinas, R. J. MacDonell, A. E. Boguslavskiy, M. S. Schuurman, A. Stolow and T. J. Martinez, J. Phys. Chem. Lett., 2021, 12, 6363–6369.
39. Y. Liu, P. Chakraborty, S. Matsika and T. Weinacht, J. Chem. Phys., 2020, 153, 074301.
40. E. G. Champenois, L. Greenman, N. Shivaram, J. P. Cryan, K. A. Larsen, T. N. Rescigno, C. W. McCurdy, A. Belkacem and D. S. Slaughter, J. Chem. Phys., 2019, 150, 114301.
41. V. Svoboda, C. Wang, M. D. J. Waters and H. J. Wörner, J. Chem. Phys., 2019, 151, 104306.
42. A. Ciavardini, M. Coreno, C. Callegari, C. Spezzani, G. De Ninno, B. Ressel, C. Grazioli, M. de Simone, A. Kivimäki, P. Miotti, F. Frassetto, L. Poletto, C. Puglia, S. Fornarini, M. Pezzella, E. Bodo and S. Piccirillo, J. Phys. Chem. A, 2019, 123, 1295–1302.
43. Y. Nitta, O. Schalk, H. Igarashi, S. Wada, T. Tsutsumi, K. Saita, T. Taketsugu and T. Sekikawa, J. Phys. Chem. Lett., 2021, 12, 674–679.
44. T. J. A. Wolf, R. M. Parrish, R. H. Myhre, T. J. Martínez, H. Koch and M. Gühr, J. Phys. Chem. A, 2019, 6897–6903.
45. T. Latka, V. Shirvanyan, M. Ossiander, O. Razskazovskaya, A. Guggenmos, M. Jobst, M. Fieß, S. Holzner, A. Sommer, M. Schultze, C. Jakubeit, J. Riemensberger, B. Bernhardt, W. Helml, F. Gatti, B. Lasorne, D. Lauvergnat, P. Decleva, G. Halász, A. Vibók and R. Kienberger, Phys. Rev. A, 2019, 99, 063405.
46. T. Horio, Y.-i. Suzuki and T. Suzuki, J. Chem. Phys., 2016, 145, 044307.
47. S. Karashima, A. Humeniuk, R. Uenishi, T. Horio, M. Kanno, T. Ohta, J. Nishitani, R. Mitrić and T. Suzuki, J. Am. Chem. Soc., 2021, 143, 8034–8045.
48. R. J. Squibb, M. Sapunar, A. Ponzi, R. Richter, A. Kivimäki, O. Plekan, P. Finetti, N. Sisourat, V. Zhaunerchyk, T. Marchenko, L. Journel, R. Guillemin, R. Cucini, M. Coreno, C. Grazioli, M. Di Fraia, C. Callegari, K. C. Prince, P. Decleva, M. Simon, J. H. D. Eland, N. Došli, R. Feifel and M. N. Piancastelli, Nat. Commun., 2018, 9, 63.
49. S. Pathak, L. M. Ibele, R. Boll, C. Callegari, A. Demidovich, B. Erk, R. Feifel, R. Forbes, M. Di Fraia, L. Giannessi, C. S. Hansen, D. M. P. Holland, R. A. Ingle, R. Mason, O. Plekan, K. C. Prince, A. Rouzée, R. J. Squibb, J. Tross, M. N. R. Ashfold, B. F. E. Curchod and D. Rolles, Nat. Chem., 2020, 12, 795–800.
50. E. P. MÅnsson, S. Latini, F. Covito, V. Wanie, M. Galli, E. Perfetto, G. Stefanucci, H. Hübener, U. De Giovannini, M. C. Castrovilli, A. Trabattoni, F. Frassetto, L. Poletto, J. B. Greenwood, F. Légaré, M. Nisoli, A. Rubio and F. Calegari, Commun. Chem., 2021, 4, 73.
51. M. Hervé, V. Despré, P. Castellanos Nash, V. Loriot, A. Boyer, A. Scognamiglio, G. Karras, R. Brédy, E. Constant, A. G. G. M. Tielens, A. I. Kuleff and F. Lépine, Nat. Phys., 2021, 17, 327–331.
52. Y. Kida and T. Kobayashi, J. Opt. Soc. Am. B, 2011, 28, 139–148.
53. M. Galli, V. Wanie, D. P. Lopes, E. P. MÅnsson, A. Trabattoni, L. Colaizzi, K. Saraswathula, A. Cartella, F. Frassetto, L. Poletto, F. Légaré, S. Stagira, M. Nisoli, R. Martínez Vázquez, R. Osellame and F. Calegari, Opt. Lett., 2019, 44, 1308.
54. L. Bruder, L. Wittenbecher, P. V. Kolesnichenko and D. Zigmantas, Opt. Express, 2021, 29, 25593.
55. A. Lekosiotis, C. Brahms, F. Belli, T. F. Grigorova and J. C. Travers, Opt. Lett., 2021, 46, 4057.
56. N. Kotsina, F. Belli, S.-F. Gao, Y.-Y. Wang, P. Wang, J. C. Travers and D. Townsend, J. Phys. Chem. Lett., 2019, 10, 715–720.
57. M. Ghotbi, P. Trabs, M. Beutler and F. Noack, Opt. Lett., 2013, 38, 486.
58. A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Légaré, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, J. Phys. Chem. Lett., 2016, 7, 4514–4519.
59. S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Mašín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484–489.
60. N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190.
61. L. Nahon, G. A. Garcia and I. Powis, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 322–334.
62. V. Blanchet, D. Descamps, S. Petit, Y. Mairesse, B. Pons and B. Fabre, Phys. Chem. Chem. Phys., 2021, 23, 25612–25628.
63. G. A. Garcia, H. Dossman, L. Nahon, S. Daly and I. Powis, ChemPhysChem, 2017, 18, 500.
64. H. Ganjitabar, G. A. Garcia, L. Nahon and I. Powis, J. Chem. Phys., 2020, 153, 034302.
65. A. G. Harvey, Z. Mašín and O. Smirnova, J. Chem. Phys., 2018, 149, 064104.
66. M. Ilchen, P. Schmidt, N. M. Novikovskiy, G. Hartmann, P. Rupprecht, R. N. Coffee, A. Ehresmann, A. Galler, N. Hartmann, W. Helml, Z. Huang, L. Inhester, A. A. Lutman, J. P. MacArthur, T. Maxwell, M. Meyer, V. Music, H.-D. Nuhn, T. Osipov, D. Ray, T. J. A. Wolf, S. Bari, P. Walter, Z. Li, S. Moeller, A. Knie and P. V. Demekhin, Commun. Chem., 2021, 4, 119.
67. C. Sparling, A. Ruget, N. Kotsina, J. Leach and D. Townsend, ChemPhysChem, 2021, 22, 76–82.
68. B. Darquié, N. Saleh, S. K. Tokunaga, M. Srebro-Hooper, A. Ponzi, J. Autschbach, P. Decleva, G. A. Garcia, J. Crassous and L. Nahon, Phys. Chem. Chem. Phys., 2021, 23, 24140–24153.
69. A. D. Müller, E. Kutscher, A. N. Artemyev and P. V. Demekhin, J. Chem. Phys., 2020, 152, 044302.
70. R. E. Goetz, C. P. Koch and L. Greenman, J. Chem. Phys., 2019, 151, 074106.
71. M. Schmitt, S. Lochbrunner, J. P. Shaffer, J. J. Larsen, M. Z. Zgierski and A. Stolow, J. Chem. Phys., 2001, 114, 1206–1213.
72. J. P. Long, B. S. Itchkawitz and M. N. Kabler, J. Opt. Soc. Am. B, 1996, 13, 201–208.
73. A. Baraldi, M. Barnaba, B. Brena, D. Cocco, G. Comelli, S. Lizzit, G. Paolucci and R. Rosei, J. Electron Spectrosc. Relat. Phenom., 1995, 76, 145–149.
74. S. Neppl, A. Shavorskiy, I. Zegkinoglou, M. Fraund, D. S. Slaughter, T. Troy, M. P. Ziemkiewicz, M. Ahmed, S. Gul, B. Rude, J. Z. Zhang, A. S. Tremsin, P.-A. Glans, Y.-S. Liu, C. H. Wu, J. Guo, M. Salmeron, H. Bluhm and O. Gessner, Faraday Discuss., 2014, 171, 219–241.
75. S. Neppl and O. Gessner, J. Electron Spectrosc. Relat. Phenom., 2015, 200, 64–77.
76. L. Young, K. Ueda, M. Gühr, P. H. Bucksbaum, M. Simon, S. Mukamel, N. Rohringer, K. C. Prince, C. Masciovecchio, M. Meyer, A. Rudenko, D. Rolles, C. Bostedt, M. Fuchs, D. A. Reis, R. Santra, H. Kapteyn, M. Murnane, H. Ibrahim, F. Légaré, M. Vrakking, M. Isinger, D. Kroon, M. Gisselbrecht, A. LHuillier, H. J. Wörner and S. R. Leone, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 032003.
77. F. Brauße, G. Goldsztejn, K. Amini, R. Boll, S. Bari, C. Bomme, M. Brouard, M. Burt, B. C. de Miranda, S. Düsterer, B. Erk, M. Géléoc, R. Geneaux, A. S. Gentleman, R. Guillemin, I. Ismail, P. Johnsson, L. Journel, T. Kierspel, H. Köckert, J. Küpper, P. Lablanquie, J. Lahl, J. W. L. Lee, S. R. Mackenzie, S. Maclot, B. Manschwetus, A. S. Mereshchenko, T. Mullins, P. K. Olshin, J. Palaudoux, S. Patchkovskii, F. Penent, M. N. Piancastelli, D. Rompotis, T. Ruchon, A. Rudenko, E. Savelyev, N. Schirmel, S. Techert, O. Travnikova, S. Trippel, J. G. Underwood, C. Vallance, J. Wiese, M. Simon, D. M. P. Holland, T. Marchenko, A. Rouzée and D. Rolles, Phys. Rev. A, 2018, 97, 043429.
78. N. Berrah, L. Fang, B. Murphy, T. Osipov, K. Ueda, E. Kukk, R. Feifel, P. van der Meulen, P. Salen, H. T. Schmidt, R. D. Thomas, M. Larsson, R. Richter, K. C. Prince, J. D. Bozek, C. Bostedt, S.-I. Wada, M. N. Piancastelli, M. Tashiro and M. Ehara, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16912–16915.
79. V. Ulrich, S. Barth, S. Joshi, U. Hergenhahn, E. Mikajlo, C. J. Harding and I. Powis, J. Phys. Chem. A, 2008, 112, 3544–3549.
80. K. Bennett, M. Kowalewski and S. Mukamel, Faraday Discuss., 2015, 177, 405–428.
81. K. Bennett, M. Kowalewski and S. Mukamel, J. Chem. Theor. Comput., 2016, 12, 740–752.
82. S. Jiang and K. Dorfman, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9776–9781.
83. D. Jadoun and M. Kowalewski, J. Phys. Chem. Lett., 2021, 12, 8103–8108.
84. J. Davies, J. LeClaire, R. Continetti and C. Hayden, J. Chem. Phys., 1999, 111, 1–4.
85. V. Stert, W. Radloff, C. Schulz and I. Hertel, Eur. Phys. J. D, 1999, 5, 97–106.
86. P. Hockett, C. Z. Bisgaard, O. J. Clarkin and A. Stolow, Nat. Phys., 2011, 7, 612–615.
87. W. K. Peters, D. E. Couch, B. Mignolet, X. Shi, Q. L. Nguyen, R. C. Fortenberry, H. B. Schlegel, F. Remacle, H. C. Kapteyn, M. M. Murnane and W. Li, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E11072–E11081.
88. J. Mikosch and S. Patchkovskii, J. Mod. Opt., 2013, 60, 1439–1451.
89. M. Rumetshofer, P. Heim, B. Thaler, W. E. Ernst, M. Koch and W. von der Linden, Phys. Rev. A, 2018, 97, 062503.
90. D. E. Couch, D. D. Hickstein, D. G. Winters, S. J. Backus, M. S. Kirchner, S. R. Domingue, J. J. Ramirez, C. G. Durfee, M. M. Murnane and H. C. Kapteyn, Optica, 2020, 7, 832.
91. J. Bourgalais, N. Carrasco, L. Vettier, A. Comby, D. Descamps, S. Petit, V. Blanchet, J. Gaudin, Y. Mairesse and B. Marty, J. Phys. Chem. A, 2021, 125, 3159–3168.
92. A. Comby, E. Bloch, S. Beauvarlet, D. Rajak, S. Beaulieu, D. Descamps, A. Gonzalez, F. Guichard, S. Petit, Y. Zaouter, V. Blanchet and Y. Mairesse, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 234003.
93. R. Klas, A. Kirsche, M. Tschernajew, J. Rothhardt and J. Limpert, Opt. Express, 2018, 26, 19318.
94. E. Perfetto, A. Trabattoni, F. Calegari, M. Nisoli, A. Marini and G. Stefanucci, J. Phys. Chem. Lett., 2020, 11, 891–899.
95. A. Trabattoni, M. Galli, M. Lara-Astiaso, A. Palacios, J. Greenwood, I. Tavernelli, P. Decleva, M. Nisoli, F. Martín and F. Calegari, Philos. Trans. R. Soc., A, 2019, 377, 20170472.
96. J. Delgado, M. Lara-Astiaso, J. González-Vázquez, P. Decleva, A. Palacios and F. Martín, Faraday Discuss., 2021, 228, 349–377.
97. S. Beauvarlet, E. Block, D. Rajak, D. Descamps, B. Fabre, S. Petit, B. Pons, Y. Mairesse and V. Blanchet, Phys. Chem. Chem. Phys., 2021 10.1039/D1CP05618B.
98. D. Uhl, U. Bangert, L. Bruder and F. Stienkemeier, Optica, 2021, 8, 1316.
99. D. Uhl, L. Bruder and F. Stienkemeier, Rev. Sci. Instrum., 2021, 92, 083101.
100. P. Rupp, C. Burger, N. G. Kling, M. Kübel, S. Mitra, P. Rosenberger, T. Weatherby, N. Saito, J. Itatani, A. S. Alnaser, M. B. Raschke, E. Rühl, A. Schlander, M. Gallei, L. Seiffert, T. Fennel, B. Bergues and M. F. Kling, Nat. Commun., 2019, 10, 4655.
101. P. Rosenberger, P. Rupp, R. Ali, M. S. Alghabra, S. Sun, S. Mitra, S. A. Khan, R. Dagar, V. Kim, M. Iqbal, J. Schötz, Q. Liu, S. K. Sundaram, J. Kredel, M. Gallei, C. Costa-Vera, B. Bergues, A. S. Alnaser and M. F. Kling, ACS Photonics, 2020, 7, 1885–1892.
102. J. N. Bull, C. S. Anstöter and J. R. R. Verlet, Nat. Commun., 2019, 10, 5820.
103. A. P. Veenstra, L. Monzel, A. Baksi, J. Czekner, S. Lebedkin, E. K. Schneider, T. Pradeep, A.-N. Unterreiner and M. M. Kappes, J. Phys. Chem. Lett., 2020, 7, 2675–2681.
104. F. Buchner, A. Lübcke, N. Heine and T. Schultz, Rev. Sci. Instrum., 2010, 81, 113107.
105. F. Buchner, B. Heggen, H.-H. Ritze, W. Thiel and A. Lübcke, Phys. Chem. Chem. Phys., 2015, 17, 31978–31987.
106. B. A. Erickson, Z. N. Heim, E. Pieri, E. Liu, T. J. Martinez and D. M. Neumark, J. Phys. Chem. A, 2019, 123, 10676–10684.
107. N. Engel, S. I. Bokarev, A. Moguilevski, A. A. Raheem, R. Al-Obaidi, T. Möhle, G. Grell, K. R. Siefermann, B. Abel, S. G. Aziz, O. Kühn, M. Borgwardt, I. Y. Kiyan and E. F. Aziz, Phys. Chem. Chem. Phys., 2017, 19, 14248–14255.
108. R. Al-Obaidi, M. Wilke, M. Borgwardt, J. Metje, A. Moguilevski, N. Engel, D. Tolksdorf, A. Raheem, T. Kampen, S. Mähl, I. Y. Kiyan and E. F. Aziz, New J. Phys., 2015, 17, 093016.
109. L. Longetti, T. R. Barillot, M. Puppin, J. Ojeda, L. Poletto, F. van Mourik, C. A. Arrell and M. Chergui, Phys. Chem. Chem. Phys., 2021, 23, 25308–25316.
110. Y.-I. Suzuki, K. Nishizawa, N. Kurahashi and T. Suzuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 010302.
111. T. Suzuki, J. Chem. Phys., 2019, 151, 090901.

---