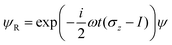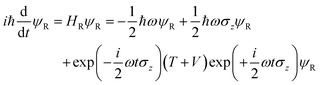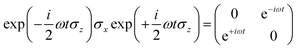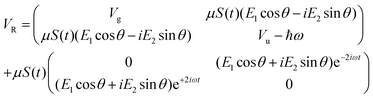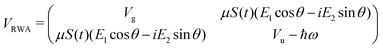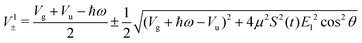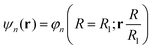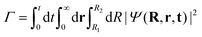Circularly polarized light-induced potentials and the demise of excited states
Sebastián
Carrasco
 a,
José
Rogan
bc,
Juan Alejandro
Valdivia
a,
José
Rogan
bc,
Juan Alejandro
Valdivia
 bc,
Bo Y.
Chang
bc,
Bo Y.
Chang
 d,
Vladimir S.
Malinovsky
d,
Vladimir S.
Malinovsky
 a and
Ignacio R.
Sola
a and
Ignacio R.
Sola
 *e
*e
aU.S. Army Research Laboratory, Adelphi, Maryland 20783, USA
bDepartamento de Física, Facultad de Ciencias, Universidad de Chile, Casilla 653, Santiago 7800024, Chile
cCentro Para la Nanociencia y la Nanotecnolgía, CEDENNA, Chile
dSchool of Chemistry(RIBS), Seoul National University, Seoul 08826, Republic of Korea
eDepartamento de Química Física, Universidad Complutense, 28040 Madrid, Spain. E-mail: isola@quim.ucm.es
First published on 29th December 2021
Abstract
In the presence of strong electric fields, the excited states of single-electron molecules and molecules with large transient dipoles become unstable because of anti-alignment, the rotation of the molecular axis perpendicular to the field vector, where bond hardening is not possible. We show how to overcome this problem by using circularly polarized electromagnetic fields. Using a full quantum description of the electronic, vibrational, and rotational degrees of freedom, we characterize the excited electronic state dressed by the field and analyze its dependence on the bond length and angle and the stability of its vibro-rotational eigenstates. Although the dynamics is metastable, most of the population remains trapped in this excited state for hundreds of femtoseconds, allowing quantum control. Contrary to what happens with linearly polarized fields, the photodissociation occurs along the initial molecular axis, not perpendicular to it.
1 Introduction
The quantum treatment of the dynamics of a molecule in all its degrees of freedom is an imposing computational challenge. Owing to the hierarchy of masses and the consequent different scales of motion, for coupled degrees of freedom one often describes each slower motion based on the average potential created by the faster motion, reducing the dimensions of the problem.1–5 In addition, it is customary to treat the nuclear (slower) motions using a classical or semiclassical approach. Such approximations do not allow one to describe the back-action of the slower motion on to the faster one, inducing decoherence, although the former effect can be approximately described by averaging over trajectories. In addition, when the time-scale of the motions is not very different, as at nuclear configurations where the electronic states are nearly degenerate (e.g. at conical intersections) and particularly with lighter atoms, the approximations are deemed to fail and a full quantum treatment is necessary. This is particularly the case for the hydrogen molecular cation and its isotopes. We have recently developed a model and computational scheme to integrate the time-dependent Schrödinger equation (TDSE) for one-electron molecules in 3-electronic plus 2-nuclear degrees of freedom (internuclear distance and angle of the molecular axis with respect to a fixed axis) in the presence of electromagnetic fields.6The first excited state of H2+ or any other one-electron molecule is dissociative, corresponding to the anti-bonding character of its molecular orbital. However, under an electric field, the ground and first excited electronic states become mixed so that their corresponding dressed potentials feature bond softening7–10 and bond hardening.11–14 With field intensities of the order of or larger than TW/cm2, bond hardening in the excited dressed potential is enough to support several bound vibrational states. Many quantum control schemes rely on bond hardening to control the bond length of molecules15–19 to generate huge dipole moments,20–22 or to control the photofragment velocity and angular distribution23–26 requiring the previous alignment of the molecules with the external field.27,28 Diatomic molecules can be aligned by means of different techniques, more so if the molecules have a permanent dipole, and a single strong non-resonant field (perhaps the same used for bond-hardening) can be used for this purpose. It is customary to assume that the molecules may remain aligned at least during the short period of time during which one acts on or control their dynamics with ultrafast laser pulses. While this is true in the ground state of the molecule, we recently found that the converse is the norm in the excited state,29 even when the molecule had a permanent dipole moment and is subject to a constant electric field, as in HD+.6 Then, anti-alignment, that is, the alignment of the molecular axis perpendicular to the polarization of the field, moves the molecule out of the influence of the field in as short a time as a molecular vibration, leading to fast photodissociation.
Anti-alignment was first predicted using a semiclassical model, where the nuclear motion was treated classically, allowing for bond-hardening in those molecules initially aligned with the field.29 Therefore, one could anticipate a control mechanism relying on laser alignment in the ground state before sending the population to the excited potential dressed by a field or, alternatively, a control process that would filter those molecules initially aligned with the field, the only ones to survive after the excitation. But using a full quantum description, we observed that the angular width of the initial wave function is always enough to induce total dissociation.6 In fact, aided by dephasing, a very narrow angular wave packet anti-aligns more rapidly than a wider distribution. The survival time in the excited state only depends on the average angle and not on the angular dispersion. In addition, the anti-alignment process was strong enough to beat the dipole-induced alignment when the molecule had an initial dipole moment, as in the HD+ isotope. The question then is are all strong field control scenarios based upon bond hardening in the excited states doomed to fail?
When working with electromagnetic fields, rather than static or ac electric fields, we expect some differences to occur. The field frequency selects the geometry of the excited potential that is resonant with the ground potential, forcing a stronger reshaping of the light-induced potentials30–35 (LIPs) and trapping population at selected internuclear distances in the excited state. This is not the case, however, when the molecular axis is perpendicular to the polarization and θ = π/2. Then the coupling is zero and the molecule dissociates, while some population may be transferred to the ground potential by non-adiabatic processes in the vicinity of θ = π/2. In the representation of the LIPs, this process can be seen as fast internal conversion through a light-induced conical intersection35–41 or LICI, using the language of Photochemistry, and it is possible even in diatomic molecules, including the rotational degree of freedom. There have been a plethora of studies concerning how to probe the LICIs and how to use them as a resource to control photochemical or photophysical processes, but if anything, one expects that the presence of LICIs will make it harder to stabilize the excited states of single electron molecules.
But the frequency is not the only control knob that electromagnetic fields provide: one can use the vectorial properties of the field to control the dynamics via the polarization of light. The selection rules of different spectroscopic techniques crucially depend on whether one uses linearly or circularly polarized fields.42,43 It is also well known that the polarization of the field directly affects the electronic motion, as observed for instance in the yields of ionization and high harmonic generation.44 Although circularly polarized fields are often used as enantio-sensitive signals that probe the chirality of the media (e.g. in measurements of circular dichroism or in photo-electron currents upon ionization45–48) they have also been proposed to control the dynamics.49,50 As an example, two pulses of circularly polarized light with different wavelengths could orient molecules,51,52 although simpler schemes were suggested.27,28 This is a field under development, as the technology of pulse shaping including the full vectorial properties of light is now available53 and a further step is being taken for creating synthetic chiral light.54
In this work we show the effects and dynamics of antialignment with electromagnetic fields, rather than electric pulses, and study the role of polarization. Both by using a theoretical model and by solving the TDSE for the electronic, vibrational and rotational degrees of freedom, we find that bond hardening in the excited state of H2+ is stable (actually meta-stable) using circularly polarized fields. Hence, the molecule survives in the excited state for the duration of short pulses. In contrast, there is antialignment that leads to fast photodissociation when using linearly polarized fields, while the effect of elliptically polarized fields stands in between both extremes. In Section 2, we outline the theoretical model. In Section 3, we introduce the numerical method used to solve the TDSE. Section 4 discusses the dynamics and dissociation in the excited state under different initial conditions and fields, and finally, conclusions are provided in Section 5.
2 Theory: excited state stability under linear and circularly polarized fields
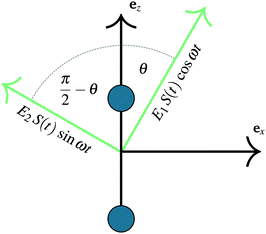
As previously outlined, a strong field can induce bond hardening in the first excited dressed state of H2+, enough to support several bound vibrational states, but the orientation of the molecular axis with the electric field makes such bond-hardening to be dependent on the nature of the polarization properties of light. To understand the origin of the stability or instability of the excited electronic state conditional to the polarization properties of the dressing field, we present here a model which allows one to predict the average properties of the light-induced potentials under certain approximations. This will be confronted with the numerical results in Section 4 which avoid the approximations.Consider two isolated electronic states of a diatomic molecule (e.g. the ground Vg(R) and the first excited state Ve(R)) that lies in the plane perpendicular to the axis of propagation of the field ey. In the length gauge and dipole approximation, the coupling with the external, linearly polarized field E1(t) (see Fig. 1) adds the term
E(t)·r = E1(t)S(t)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ez + sin ez + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ex)·(zez + xex) ex)·(zez + xex) | (1) |
=E1S(t)z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (2) |
E(t)·r = zE1S(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) + zE2S(t) cos(ωt) + zE2S(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) sin(ωt) | (3) |
The potential energy matrix can be written as
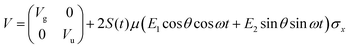 | (4) |
the TDSE becomes
where we have used the 2 × 2 Pauli matrices σx and σz, and the unit matrix I, for notational convenience. Since we are interested in the potential energy dressed by the field, we will omit the kinetic energy operator T from our consideration. In principle, a time-dependent transformation adds non-adiabatic terms to the kinetic energy, which are often neglected under the adiabatic approximation. Because of
we obtain
Following the rotating wave approximation (RWA), after neglecting non-resonant high frequency terms, we obtain the matrix
with eigenvalues or LIPs,
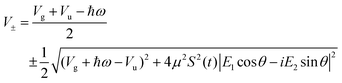 | (5) |
In this case, these dressed potentials show bond-hardening in the excited state and bond-softening in the ground state except in the surroundings of θ = ±π/2, where there is a LICI. The molecule dissociates through the LICI if the molecular axis rotates perpendicular to the field. The dependence of Vl± on θ explains that any wave packet will be subject to a torque. The direction of the torque toward the LICI or anti-alignment effect is due to the polarization in the excited state, and it was numerically predicted even when the molecule has a permanent dipole (as in HD+).6 The consequence is that any vibrational wave function created in Vl+ will dissociate in the time-scale of a molecular rotation: the potential does not bare any bound state.
In similar lines, setting E1 = E2 in eqn (5), we obtain the dressed potentials for an anti-clockwise polarized field
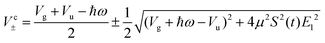 | (6) |
3 Numerics: quantum model of the hydrogen molecular cation under time-dependent fields
To model the dynamics of a hydrogen molecular ion under a time-dependent field, we will include electronic, vibrational and rotational degrees of freedom treated in a fully quantum way, to account for the correlation of the different degrees of freedom and the effect of decoherence that one motion can induce in the others. On the other hand, to reduce the dimensionality of the system, we study the dynamics of the molecules that lie in the plane perpendicular to the axis of propagation of the field.Following the procedure shown in ref. 6, we solve numerically the TDSE in the position representation (discretized in a grid), given by
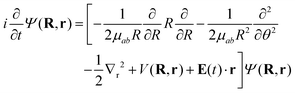 | (7) |
Considering this, eqn (7) becomes
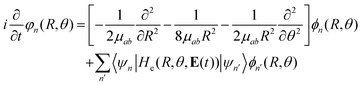 | (8) |
| He(R, θ, 0)φn(R = R0; r) = He,nφn(R = R1; r) |
In this way, we can calculate the matrix elements 〈ψn|He(R, θ, E(t))|ψn′〉 as a function of R, θ, and E(t). To calculate the eigenfunctions for R1 = 2a0, we use the well-established prolate spheroidal treatment for an electron in a two-center molecule.55–57
Finally, we solve eqn (8) by propagating all nuclear wave functions ϕn′(R, θ) over a grid of 128 points between R = 0.1a0 and R = 10a0, and 32 points between θ = −π and θ = π, using a Strang method with a three operator-splitting scheme.58,59
4 Results
4.1 The ground state of circularly polarized light-induced potentials
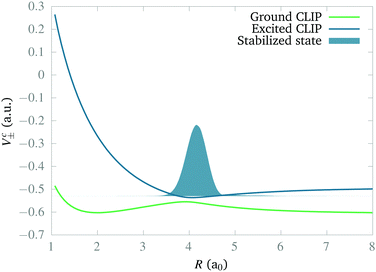
In this section we study the nature of the light-induced potential created by a strong field of circular polarization, which we call a CLIP. We will do so by characterizing its fundamental vibro-rotational state and other states near its equilibrium geometry. First, we calculate the CLIPs. For that, we employ eqn (6). For the examples in this work, we choose E1 = E2 = 0.02 a.u. and ω = 0.1 a.u. The field amplitude controls the strength of the bond hardening, and the frequency, the position of the minimum. These parameters are within the range of values where one can typically observe bond hardening in light-induced potentials, avoiding substantial ionization. To have enough intensity, in practice, most experiments are performed with 800 nm lasers and the dressing is achieved by the action of one and three photons. In this work we avoid these complications by choosing a larger frequency. The CLIPs are shown in Fig. 2, As observed, the ground CLIP Vc− exhibits bond softening, while the excited CLIP Vc+ exhibits bond hardening, with a minimum at R0 ≈ 4.1a0 that in principle supports several bound states. Both curves are separated by an avoided crossing near the minima with an energy gap of ∼0.19 a.u.Then, we need to isolate the ground vibrational state of the excited CLIP. To do so, we will use a dynamic approach, by propagating an initial Gaussian wave packet in a linear combination of the ground and excited electronic states centered at R0, under a circularly polarized field, adding an artificial imaginary potential at small and large internuclear distances, namely,
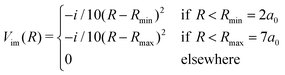 | (9) |
Naturally, the question is why the dynamics works to find the ground vibrational state of the excited CLIP. The answer is that our simulations show that this state is not stable (as expected from the model in Section 2) but metastable. Indeed, a wave packet can remain in the excited CLIP for an appreciable time (e.g. during several vibrational periods) while dissociating slowly. But as the wave packet sits or moves around the avoided crossing, there is a non-negligible probability of crossing to the lowest CLIP by non-adiabatic coupling, induced by the kinetic term, which we did not include in the model. Henceforth, the ground vibrational state is the one that remains after a relatively long dynamics. To test this, in Fig. 3, we create the system in different initial states and calculate the remaining population as a function of time. As we can observe, the population in all cases of study decays exponentially, as one can expect from a metastable state. In particular, the wave packets that are initially Gaussian in the radial coordinate, resembling the expected vibrational ground state, are the most slowly decaying, independent of the angular distribution. In contrast, a Gaussian displaced to larger bond distances or a function created as a Gaussian times a linear-term, resembling the first excited vibrational state, decays faster. Finally, we must remark that the initial state, created as a superposition of the ground and excited electronic states by hand, initially decays faster due to transient effects (the electronic components of the wave function are not similar to those of the true electronic eigenfunction of the dressed Hamiltonian) that are filtered during the first stage of the dynamics, before reaching the slow exponential-decay regime. Only after reaching this steady regime we consider that the wave functions obtained are the vibrational and electronic eigenstates (or electronic eigenstates times a nuclear wave packet) that we show in the paper.
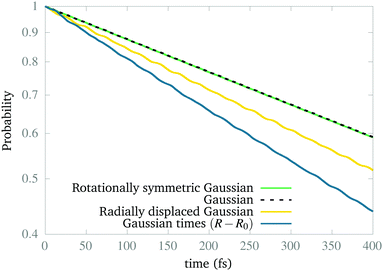 | ||
| Fig. 3 Population decay in the presence of a circularly polarized field for a set of different initial wave packets initially created in Vc+, measured as the norm of the wave function in the grid. | ||
4.2 Dynamics and metastability
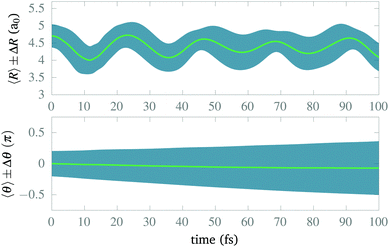
After isolating the vibrational ground state, we now proceed to study its stability and the stability of the CLIP in the proximity of the equilibrium geometry. From now on, we remove the imaginary potential for low internuclear distances, allowing the system to be in the ground electronic state. In Fig. 4, we show the average and standard deviation in R and θ under a circularly polarized field for a nuclear wave packet that is the ground state displaced by 0.5a0 (∼ 1.5σR, where σR is the standard deviation of the initial state in the radial direction). Likewise, we choose a Gaussian wave packet in the angle, centered at θ = 0 with width σθ = 0.2π. As expected, we observe vibrations in the LIP with a 23 fs period during the 100 fs of simulation with a fairly constant standard deviation (although slightly increasing because of dephasing and dissociating fragments), indicating a high degree of stability. In the angle, the average remains the same as there is no torque, but the packet naturally spreads as the potential is flat on θ (it does not depend on the angle). The spreading in the angle is slower than in R as the rotational quantum is smaller than the vibrational one.In Fig. 5, we present some snapshots from the first period of oscillation of the wave packet dynamics considered in Fig. 4. The dynamics shows the typical vibration of the packet, where it spreads mostly at the classical turning points, and squeezes in the initial position, characteristic of harmonic motion. However, we also observe the gradual emergence of a second maximum due to the anharmonic nature of the CLIP. At certain times, the spreading enlarges due to the dissociation of small components of the packet (for instance, at t = 11.25 fs, around θ = 0, R = 6a0). The slow decay of population to Vc− leads to photodissociation in the excited electronic state, V2, as both curves correlate at large R (see Fig. 2). The electronic population dynamics is subtle. The CLIP is created by the periodic electron dynamics induced by the circularly polarized field, but the dynamics is no longer periodic when the nuclei move. Consequently, the electron loses its synchronization with the field and the wave function is no longer in the exact mix of the ground and first excited electronic states that creates the CLIP. Indeed, the circularly polarized field period is of the order of 1 fs, which is not that far from the timescale of the nuclear dynamics, so the electron cannot instantly adapt to the movement.
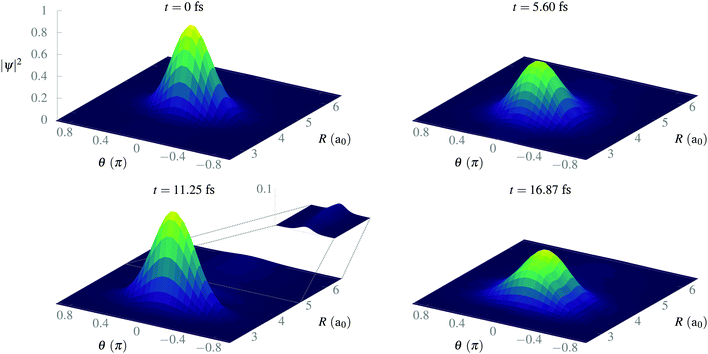 | ||
| Fig. 5 Snapshots of the time evolution of a Gaussian wave packet initially displaced 0.5a0 from R0, with σR = 0.34a0 and σθ = 0.2π in the presence of a circularly polarized field. | ||
4.3 Analysis of photofragments
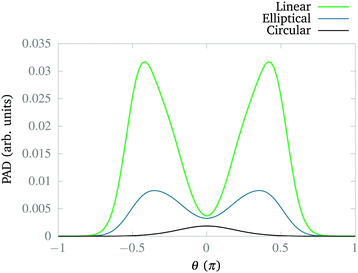
So far, we have explored the nature of the CLIPs and concluded that they sustain a metastable state that slowly dissociates. One question that remains is what happens with the dissociating fragments of the wave packet. Can the amplitudes of the linearly polarized fields that create the circular polarization be modified to observe the fingerprints of other effects, such as the anti-alignment with the field in the excited electronic state? To explore this, we created a wave packet with a Gaussian distribution in R and θ, centered approximately at R0 and θ = 0. Then, we solved the TDSE with circularly, elliptically, and linearly polarized fields. Finally, we compared the final angular distribution of the dissociating fragments. We calculate the photo-angular distribution (PAD) in the following way:where R1 is set to 6a0 in order to ignore the stabilized part of the wavepacket and R2 is set to 10a0, the boundary of the simulation. In practice, we observed that the shape of the PADs does not strongly depend on time after the first ∼10 fs so that there is no need to integrate over time except to obtain the exact yields, which can be easily inferred from the norm of the wave function.
In Fig. 6, we present the distribution for the three cases. First, we can observe that the linear polarization dissociates more strongly than the other two cases, followed by the elliptical case. Second, the elliptical and linear cases show maxima around θ ± π/2 indicating anti-alignment, as we expected from the corresponding CLIPs. Note that the maxima are displaced because a fragment has to travel from θ = 0, the position of the wave packet. Finally, for the circular polarization, the fragments just travel radially, as observed in Fig. 5. Typically, the anti-alignment and subsequent photodissociation with linearly or elliptically polarized fields is faster than the dissociation through non-adiabatic couplings that induce the metastability of the wave packets in the CLIP.
5 Conclusions
Excited states of single-electron molecules are unstable under strong linearly polarized laser pulses. In spite of bond-hardening, due to the polarizability of the molecule (the effect of a charge transfer that creates a transient dipole that increases linearly with the internuclear distance), the same polarizability is responsible for anti-alignment, leading to fragmentation at perpendicular orientations of the polarization vector in the excited state.Under the effect of circularly polarized fields, we have shown that the light-induced potential does not show any light-induced conical intersection. Bond hardening allows the wave packet to sustain vibrational motion in the LIP. The LIP is independent of the angle, so an initial rotational wave packet slowly disperses in the flat potential at a rate inversely proportional to the moment of inertia. Due to non-adiabatic couplings, the vibrational motion leads to a slow decay in the continuum, so that all eigenstates of the CLIP are meta-stable. However, the states survive for a few hundreds of femtoseconds, enough to allow for many different quantum control actions.
In this work we have shown the results for constant one-color fields, but the emerging picture clearly indicates what will be the main results when using ultrashort femtosecond pulses. Initially, we expect some steeper decay in the population as the pulse amplitude increases and before the electronic populations adjust to the LIP. If the pulse is slow, then the wave packet will adiabatically change adapting to the LIP. Then, depending on the polarizability of the field, either the molecule will anti-align and dissociate or the molecular axis will remain at its initial state, where the molecule slowly dissociates. We have identified the simplest experimental observable to distinguish both situations, namely the photofragment angular distributions. We believe that previous experiments may show indications of anti-alignment.60 A more thorough study of these dynamical effects will be explored in future studies and we hope to motivate further experiments using both linearly and circularly polarized pulses to control the photodissociation of simple molecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Army Research Laboratory under Cooperative Agreement Numbers W911NF-21-2-0037 (S. C.), National Agency for Research and Development (ANID) under Fondecyt Award No. 1190703 (J. A. V.), Fondecyt Award No. 1190662 (J. R.), and CEDENNA through “Financiamiento Basal para Centros Científicos y Tecnológicos de Excelencia” under Award No. AFB180001 (J. R. and J. A. V.), the Quantum Computing Technology Development Program (NRF-2020M3E4A1079793) (B. Y. C.) and MINECO CTQ2015-65033-P (I. R. S.).Notes and references
- S. A. Rice and M. Zhao, Optical Control of Molecular Dynamics, Wiley, 2000 Search PubMed.
- M. Shapiro and P. Brumer, Principles of the Quantum Control of Molecular Processes, Wiley & Sons, Hoboken, 2003 Search PubMed.
- C. Brif, R. Chakrabarti and H. Rabitz, in Control of quantum phenomena, ed. S. A. Rice and A. R. Dinner, Wiley-Blackwell, 2012, vol. 148, pp. 1–76 Search PubMed.
- G. A. Worth and G. W. Richings, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2013, 109, 113–139 RSC.
- I. R. Sola, B. Y. Chang, S. A. Malinovskaya and V. S. Malinovsky, in Chapter Three - Quantum Control in Multilevel Systems, ed. E. Arimondo, L. F. DiMauro and S. F. Yelin, Academic Press, 2018, vol. 67 of Advances In Atomic, Molecular, and Optical Physics, pp. 151–256 Search PubMed.
- S. Carrasco, J. Rogan, J. A. Valdivia and I. R. Sola, Phys. Chem. Chem. Phys., 2021, 23, 1936–1942 RSC.
- P. H. Bucksbaum, A. Zavriyev, H. G. Muller and D. W. Schumacher, Phys. Rev. Lett., 1990, 64, 1883–1886 CrossRef CAS PubMed.
- A. Zavriyev, P. H. Bucksbaum, H. G. Muller and D. W. Schumacher, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 5500–5513 CrossRef CAS PubMed.
- B. Yang, M. Saeed, L. F. DiMauro, A. Zavriyev and P. H. Bucksbaum, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, R1458–R1461 CrossRef CAS PubMed.
- S. W. Allendorf and A. Szöke, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 518–534 CrossRef CAS PubMed.
- A. Giusti-Suzor and F. H. Mies, Phys. Rev. Lett., 1992, 68, 3869–3872 CrossRef CAS PubMed.
- G. Yao and S.-I. Chu, Chem. Phys. Lett., 1992, 197, 413–418 CrossRef CAS.
- A. Zavriyev, P. H. Bucksbaum, J. Squier and F. Saline, Phys. Rev. Lett., 1993, 70, 1077–1080 CrossRef CAS PubMed.
- E. E. Aubanel, J.-M. Gauthier and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, 2145–2152 CrossRef CAS PubMed.
- B. Y. Chang, H. Rabitz and I. R. Sola, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 68, 031402 CrossRef.
- B. Y. Chang, S. Lee and I. R. Sola, J. Chem. Phys., 2004, 121, 11118–11128 CrossRef CAS PubMed.
- I. R. Sola, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 033401 CrossRef.
- B. Y. Chang, S. Shin and I. R. Sola, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 063414 CrossRef.
- B. Y. Chang, S. Shin, A. Palacios, F. Martn and I. R. Sola, ChemPhysChem, 2013, 14, 1405–1412 CrossRef CAS PubMed.
- G. G. Balint-Kurti, S. Zou and A. Brown, in Optimal Control Theory for Manipulating Molecular Processes, ed. S. A. Rice and A. R. Dinner, John Wiley & Sons, Inc., 2008, vol. 138, pp. 43–94 Search PubMed.
- B. Y. Chang, S. Shin, A. Palacios, F. Martn and I. R. Sola, J. Chem. Phys., 2013, 139, 084306 CrossRef PubMed.
- B. Y. Chang, S. Shin, A. Palacios, F. Martn and I. R. Sola, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 043001 CrossRef CAS.
- B. Y. Chang, S. Shin, J. Santamaria and I. R. Sola, J. Chem. Phys., 2009, 130, 124320 CrossRef PubMed.
- B. Y. Chang, S. Shin and I. R. Sola, J. Chem. Phys., 2009, 131, 204314 CrossRef PubMed.
- M. E. Corrales, J. Gonzalez-Vazquez, G. Balerdi, I. R. Sola, R. de Nalda and L. Bañares, Nat. Chem., 2014, 6, 785 CrossRef CAS PubMed.
- M. E. Corrales, R. de Nalda and L. Bañares, Nat. Commun., 2017, 8, 1345 CrossRef PubMed.
- H. Stapelfeldt and T. Seideman, Rev. Mod. Phys., 2003, 75, 543–557 CrossRef CAS.
- T. Seideman and E. Hamilton, Adv. At., Mol., Opt. Phys., 2005, 52, 289–329 CAS.
- B. Y. Chang, S. Shin, J. González-Vázquez, F. Martn, V. S. Malinovsky and I. R. Sola, Phys. Chem. Chem. Phys., 2019, 21, 23620–23625 RSC.
- J. Yuan and T. F. George, J. Chem. Phys., 1978, 68, 3040–3052 CrossRef CAS.
- A. D. Bandrauk and M. L. Sink, J. Chem. Phys., 1981, 74, 1110–1117 CrossRef CAS.
- B. M. Garraway and K. A. Suominen, Phys. Rev. Lett., 1998, 80, 932–935 CrossRef CAS.
- I. R. Sola, B. Y. Chang, J. Santamaria, V. S. Malinovsky and J. L. Krause, Phys. Rev. Lett., 2000, 85, 4241–4244 CrossRef CAS PubMed.
- P. Emil, B. Joachim and G. Stefanie, New J. Phys., 2009, 11, 105035 CrossRef.
- B. Y. Chang, I. R. Sola and S. Shin, Int. J. Quantum Chem., 2016, 116, 608–621 CrossRef CAS.
- N. Moiseyev, M. Šindelka and L. S. Cederbaum, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 221001 CrossRef.
- G. J. Halász, M. Šindelka, N. Moiseyev, L. S. Cederbaum and Á. Vibók, J. Phys. Chem. A, 2012, 116, 2636–2643 CrossRef PubMed.
- P. V. Demekhin and L. S. Cederbaum, J. Chem. Phys., 2013, 139, 154314 CrossRef PubMed.
- G. J. Halász, Á. Vibók and L. S. Cederbaum, J. Phys. Chem. Lett., 2015, 6, 348–354 CrossRef PubMed.
- A. Csehi, G. J. Halász, L. S. Cederbaum and A. Vibók, J. Phys. Chem. Lett., 2017, 8, 1624–1630 CrossRef CAS PubMed.
- C. Fábri, B. Lasorne, G. J. Halász, L. S. Cederbaum and Á. Vibók, J. Phys. Chem. Lett., 2020, 11, 5324–5329 CrossRef PubMed.
- M. Auzinsh, D. Budker and S. Rochester, Optically polarized atoms: understanding light-atom interactions, Oxford University Press, 2010 Search PubMed.
- Z. B. Rudzikas, A. A. Hikitin and A. F. Kholtygin, Leningrad Izdatel Leningradskogo Universiteta, 1990 Search PubMed.
- M. Ivanov, P. Corkum, T. Zuo and A. Bandrauk, Phys. Rev. Lett., 1995, 74, 2933 CrossRef CAS PubMed.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187 CrossRef PubMed.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, Phys. Rev. Lett., 2019, 122, 013204 CrossRef CAS PubMed.
- Y. Fujimura, L. González, K. Hoki, J. Manz and Y. Ohtsuki, Chem. Phys. Lett., 1999, 306, 1–8 CrossRef CAS.
- M. Shapiro, E. Frishman and P. Brumer, Phys. Rev. Lett., 2000, 84, 1669 CrossRef CAS PubMed.
- D. V. Zhdanov and V. N. Zadkov, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 011401 CrossRef.
- C. Chen, J. Wu and H. Zeng, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 033409 CrossRef.
- T. Brixner, G. Krampert, T. Pfeifer, R. Selle, G. Gerber, M. Wollenhaupt, O. Graefe, C. Horn, D. Liese and T. Baumert, Phys. Rev. Lett., 2004, 92, 208301 CrossRef CAS PubMed.
- D. Ayuso, O. Neufeld, A. F. Ordonez, P. Decleva, G. Lerner, O. Cohen, M. Ivanov and O. Smirnova, Nat. Photonics, 2019, 13, 866–871 CrossRef CAS.
- M.-G. Baik, M. Pont and R. Shakeshaft, Phys. Rev. A: At., Mol., Opt. Phys., 1996, 54, 1570 CrossRef CAS PubMed.
- G. L. Kamta and A. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 011404 CrossRef.
- G. L. Kamta and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 053407 CrossRef.
- T. Sørevik, T. Birkeland and G. Okša, J. Comput. Appl. Math., 2009, 225, 56–67 CrossRef.
- R. I. McLachlan and G. R. W. Quispel, J. Phys. A: Math. Gen., 2006, 39, 5251 CrossRef.
- M. Kübel, M. Spanner, Z. Dube, A. Y. Naumov, S. Chelkowski, A. D. Bandrauk, M. J. Vrakking, P. B. Corkum, D. Villeneuve and A. Staudte, Nat. Commun., 2020, 11, 1–8 Search PubMed.
| This journal is © the Owner Societies 2022 |