Excited state absorption of DNA bases in the gas phase and in chloroform solution: a comparative quantum mechanical study

Abstract

We study the excited state absorption (ESA) properties of the four DNA bases (thymine, cytosine, adenine, and guanine) by different single reference quantum mechanical methods, namely, equation of motion coupled cluster singles and doubles (EOM-CCSD), singles, doubles and perturbative triples (EOM-CC3), and time-dependent density functional theory (TD-DFT), with the long-range corrected CAM-B3LYP functional. Preliminary results at the Tamm–Dancoff (TDA) CAM-B3LYP level using the maximum overlap method (MOM) are reported for thymine. In the gas phase, the three methods predict similar One Photon Absorption (OPA) spectra, which are consistent with the experimental results and with the most accurate computational studies available in the literature. The ESA spectra are then computed for the ππ* states (one for pyrimidine, two for purines) associated with the lowest-energy absorption band, and for the close-lying nπ* state. The EOM-CC3, EOM-CCSD and CAM-B3LYP methods provide similar ESA spectral patterns, which are also in qualitative agreement with literature RASPT2 results. Once validated in the gas phase, TD-CAM-B3LYP has been used to compute the ESA in chloroform, including solvent effects by the polarizable continuum model (PCM). The predicted OPA and ESA spectra in chloroform are very similar to those in the gas phase, most of the bands shifting by less than 0.1 eV, with a small increase of the intensities and a moderate destabilization of the nπ* state. Finally, ESA spectra have been computed from the minima of the lowest energy ππ* state, and found in line with the available experimental transient absorption spectra of the nucleosides in solution, providing further validation of our computational approach.

---

1 Introduction

Pump–probe spectroscopy is the key tool to investigate fast photoinduced dynamics.^1–3 In transient absorption experiments, the excited state prepared by the pump pulse can further absorb the probe pulse, a process known as excited state absorption (ESA), which, together with the ground state bleaching and the stimulated emission, determines the observed signal.^1,2 Each excited electronic state has its characteristic ESA spectrum, making the correct interpretation of this phenomenon fundamental to disentangle the photoactivated dynamics.^1,2 This is a quite challenging task due to the large congestion of the excited electronic states in the high energy region and, at the same time, to the ‘interference’ of emission and ground state absorption processes, making the contribution of quantum mechanical calculations crucial.^4–14 In this respect, in a very recent study¹⁵ we considered the two lowest-energy excited states of uracil and benchmarked the ESA spectra computed by TD-DFT and the widely used CAM-B3LYP functional,¹⁶ with those provided by some accurate wavefunction-based methods, namely equation of motion coupled cluster singles and doubles (EOM-CCSD),¹⁷ singles, doubles and perturbative triples (EOM-CC3)¹⁸ and three methods of the Algebraic Diagrammatic Construction family, namely ADC(2), ADC(2)-x and ADC(3).¹⁹ Our investigation was presented shortly after a comprehensive study of the ESA from ππ* of DNA bases at the RASPT2 level by Jaiswal et al.¹³

In this study, we take further steps towards a full assessment of the performance of different single reference electronic structure methods in calculations of the ESA spectra. In particular, we extend our comparative analysis to all DNA bases: thymine, cytosine, adenine, and guanine (see Fig. 1). For these species, we compute one-photon absorption (OPA) and ESA spectra at the Franck–Condon (FC) point, for the first (or two first) lowest-energy ππ* states plus the lowest-energy nπ* state, in gas phase. In this first task, we compare the predictions of TD-DFT/CAM-B3LYP, EOM-CCSD, and EOM-CC3. At least for the lowest-energy ππ* states, the results of the recent RASPT2 study mentioned above¹³ provide an additional useful check, especially for what concerns the possible effect of double excitations. Using thymine as test case, we also carry out exploratory ESA calculations using the MOM-TDA approach. The ESA spectra are in this case obtained by computing, at CAM-B3LYP TDA level, the OPA of non-aufbau solutions of the Kohn–Sham equations corresponding to the dominant Molecular Orbital (MO) excitation in the excited states of interest. These higher energy KS solutions can be interpreted as single-determinant approximations to the excited states of the system and are optimized using the MOM approach.²⁰ MOM-TDDFT (and even MOM-CCSD) is often used to obtain X-ray absorption spectra of valence excited states, i.e. to simulate valence pump-core probe spectra,^21–24 but hardly explored for ESA in the UV-vis region.

Fig. 1 The molecules considered in the study: (a) thymine; (b) cytosine; (c) adenine; (d) guanine.

Having assessed the accuracy of CAM-B3LYP, in a second step of our analysis we use this method to compute the ESA for all the bases in chloroform solution, simulated by means of the polarizable continuum model (PCM).²⁵ Finally, we compute the ESA in chloroform from the minima of the lowest-energy bright states, in order to allow a more direct comparison between our predictions and the available experimental spectra.

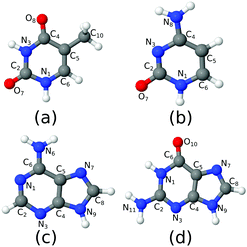
We selected the DNA bases for two different reasons. On one side, they are fairly complex heterocyclic molecules, pyrimidines (thymine and cytosine) and purines (adenine and guanine) with exocyclic substituents (carbonyl and amino groups) strongly coupled with the π ring. As a consequence, several excited states with different character (ππ*, nπ*, πσ*, and Rydberg states) lay close in energy in the FC region.²⁶ They constitute therefore challenging, and, at the same time, probative test cases. On the other side, the photoactivated dynamics of nucleobases is of great biological relevance, since absorption of UV light by DNA can trigger many potentially dangerous oxidative processes.^27–29 For this reason, many time-resolved experiments and computational studies are available for nucleobases, providing extremely useful data for any comparative analysis.^26,30–35

2 Computational details

C _s-Symmetry structures of all molecules were optimised at the CAM-B3LYP/6-311+G(d,p) level of theory (Fig. 1), to allow for perfect separation of the ππ* and nπ* systems. We checked that this approximation has a negligible effect on the computed spectra. In the following they will be referred to as the FC point. TD-DFT calculations using the CAM-B3LYP functional were carried out with Dalton.³⁶ The EOM-CCSD and EOM-CC3 calculations in gas phase were performed using e^T.³⁷ The aug-cc-pVDZ basis set was used in all cases. Test calculations were performed at the CAM-B3LYP level, computing the spectra also with the minimal 6-31G(d) basis set. The results are shown in the ESI.† The spectra in chloroform solution were obtained applying PCM²⁵ in chloroform, without any further geometry optimization. In fact, as we show for the OPA spectra in Fig. S10 (ESI†), the additional effect due to re-optimization in PCM is only marginal. The absolute minima of the lowest-energy bright excited state for each base were optimized at the PCM/CAM-B3LYP/6-311+G(d,p) level. C_s-Symmetry minima of the same state have also been located, under the constraint of planarity, at the CAM-B3LYP/6-311+G(d,p) level. TD-DFT calculations in the Tamm–Dancoff approximation (TDA) were run with Turbomole³⁸ and Q-Chem.³⁹ The MOM-TDA ESA calculations on thymine were also performed with Q-Chem.³⁹ The latter results are reported in the Fig. S22 (ESI†) and briefly discussed in the following section. Unless otherwise specified, in the main text we report and discuss the full TD-DFT results (i.e. considering the off-diagonal coupling term between ‘excitations’ and ‘de-excitations’). Tables collecting the TD-DFT, EOM-CCSD and EOM-CC3 OPA and ESA (energies and oscillator strengths) for each electronic transition are given in the ESI.†

Here and in the ESI,† smooth lines for electronic OPA and ESA spectra are simply obtained by applying a phenomenological Lorentzian broadening with half width at half maximum (HWHM) equal to 0.0045563 hartree (1000 cm⁻¹) to the stick transitions. Therefore, we do not explicitly account for vibronic effects since this would require a considerable additional effort. It is worth noticing that, using vibronic approaches, Avila Ferrer et al.⁴⁰ have shown that quadratic couplings, and in particular those arising from the changes of the normal mode frequencies between the initial and final state, are expected to introduce a ∼0.1 eV red shift of the center of gravity of the spectrum with respect to the vertical transition. Using the classical nuclear ensemble approach and analysing a data set of 28 organic molecules Bai et al.⁴¹ obtained the estimate of (0.1 ± 0.08) eV for the red shift between the maximum of the spectrum and the vertical excitation. Moreover, in a recent contribution⁴² we have shown that even neglecting quadratic couplings, but including inter-state nonadiabatic couplings, vibronic effects cause a ∼0.1–0.2 eV red-shift of the OPA maxima of nucleobases in gas phase.⁴² In Section S1.3 (ESI†), we plot together computed and available experimental OPA spectra. However, for the reasons discussed above and taking into account under which experimental conditions the spectra were measured (in some cases at very high temperature, in some cases involving more than one tautomer, while we only consider one), we here keep the discussion on the accuracy of the computed vertical transitions on a qualitative base.

The first ionization energy (IE) of the ground state was obtained at the EOM-CCSD and EOM-CC3 level as excitation into a bath orbital.^43–45 For CAM-B3LYP, we computed the IE as difference between the total energy of the cation and the total energy of the neutral at the FC geometry (ΔSCF). Estimates of the first ionization energy of the excited states were calculated as difference between the first IE of the ground state and the excitation energy of the valence excited state of interest, according to the vertical approximation. A summary of IEs for all systems is presented in ESI† in Table S1. For a characterization of the relevant excited states in terms of natural transition orbitals (NTO), see Fig. S1 (ESI†).

To facilitate the discussion, we report in Fig. S2–S5 in ESI† a comparison of our OPA and ESA spectra with those constructed from the RASPT2/ANO-L energies and oscillator strengths of ref. 13.

As detailed in Table S2 (ESI†), for thymine and cytosine at least 40 excited states have been included in the ESA calculations for all the methods considered. This enabled us to obtain spectra up to 4 eV. For adenine and guanine, at the EOM-CC3 and EOM-CCSD level it was only possible to include a smaller number of states. As a consequence, the computed spectra cover a smaller energy region, i.e. up to 1–1.8 eV for EOM-CC3, up to 2–2.8 eV for EOM-CCSD, and up to ∼3 eV for CAM-B3LYP.

3 Results

The results presented in Sections 3.1–3.4 all refer to OPA and ESA spectra computed at the ground state equilibrium geometry. For each nucleobase, we first analyse the OPA spectra in the gas phase, making a quick comparison with literature data (experiments and calculations). A comparison between TD-CAM-B3LYP and PCM/TD-CAM-B3LYP spectra then provides insights on the solvent effect. Analogously, we first discuss, for each excited state, the ESA in the gas phase computed by the different methods here examined and, finally, we check for the effect of the solvent on the computed ESA. Finally, in Section 3.5 we discuss ESA spectra computed at the minima of the lowest-energy excited bright states.

3.1 Thymine

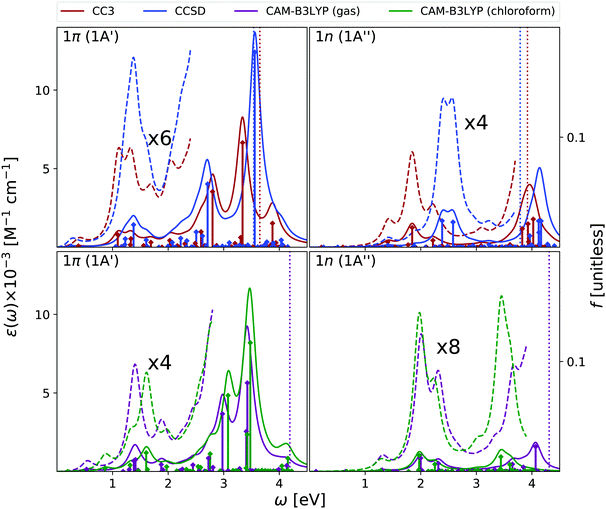
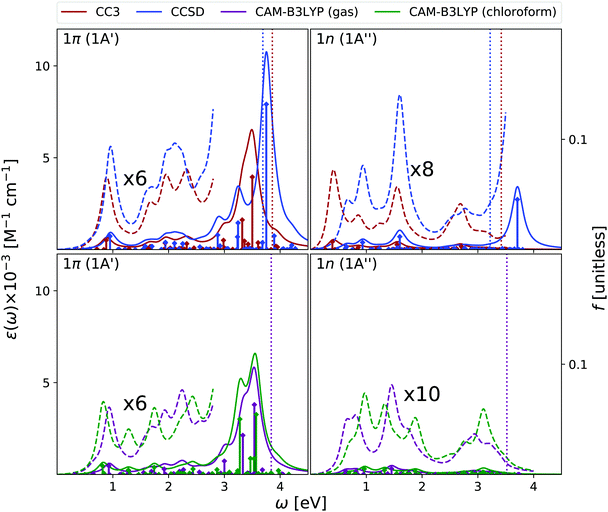
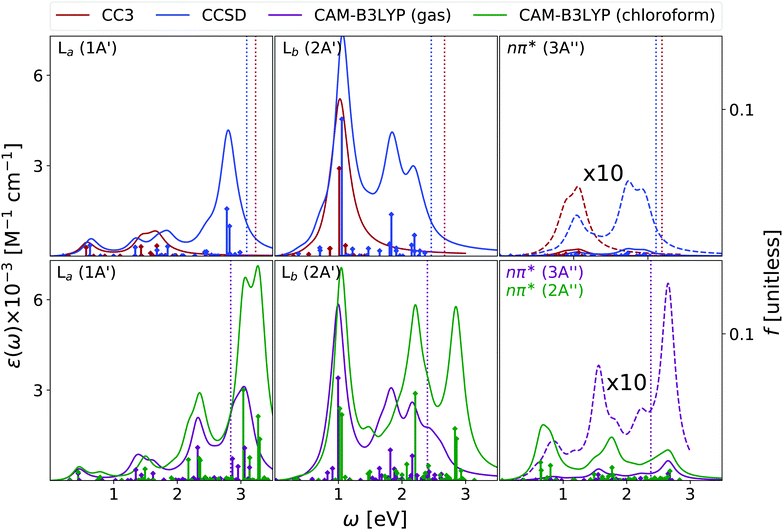
Fig. 2 shows that the OPA spectra computed in the gas phase by CAM-B3LYP and EOM-CC3 are fairly similar. They exhibit two bands slightly above 5 eV and at ∼6.5 eV, with similar intensity, followed by a more intense one at ∼7.8 eV. The EOM-CCSD spectrum has a similar shape, with a uniform blue-shift of ∼0.2 eV. The RASPT2 spectrum is also similar to the CAM-B3LYP one, but for a small uniform red-shift.^9,13 As it is shown in the Fig. S6 (ESI†), all the spectra are consistent with the available experimental ones (see ref. 42 and 13 for a discussion). The EOM-CC3 peaks are blue shifted by ∼0.4 eV with respect to the experiments,⁴⁶ a value which is expected to be partially due to the absence of vibronic effects in the present calculation (additional discussion in the ESI†).^40,42 The lowest energy band is associated to a ππ* state, with HOMO → LUMO character, though in the gas phase the lowest energy excited state is a nπ* state. This picture is very similar to the one we analyzed in detail in our previous study on uracil.¹⁵

Fig. 2 Thymine. Upper panel: OPA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels of theory in gas phase. Bottom panel: OPA at CAM-B3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (ΔSCF at DFT level). HWHM = 0.0045563 hartree.

Inclusion of solvent effects has a very modest influence on the OPA spectrum, apart from a general increase of the intensities, likely due to the linear response implementation of PCM in TD-DFT.^47,48 The most significant consequence is the destabilization (by ∼0.23 eV) of the nπ* state, confirming a trend already evidenced in the literature.^26,49 As a consequence, the nπ* state is S₁ in the gas phase and S₂ in chloroform.

As shown in Fig. 3, EOM-CC3 and CAM-B3LYP predict similar gas phase ESA spectra for the lowest-energy bright state, the former being, on the average, slightly red-shifted. We observe a broad absorption band in the 1–2.5 eV range, due to several, closely lying, weak transitions with a prominent peak at ∼1.5 eV and another, smaller, at ∼2 eV. Then, two very large peaks are predicted at ∼3 and ∼3.5 eV. On balance, the EOM-CCSD spectrum is also similar to the EOM-CC3 one, though with more intense peaks.

Fig. 3 Thymine. Upper panels: ESA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels of theory in gas phase. Bottom panels: ESA at CAM-B3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. The spectra in dashed line are enhanced by the factor given in the figures. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (see Section 2 for details). HWHM = 0.0045563 hartree.

Overall, these spectra are consistent with the predictions of RASPT2,^9,13 taking into account that, due to the selection of the active space and the basis set employed there, the number of excited states in RASPT2 is smaller and only ππ* transitions are considered.^9,13 Indeed, according to RASPT2, the ESA spectrum is made up of two peaks at 1.2 and 1.5 eV, a smaller one at ∼2 eV, and two more intense ESA transition at ∼3 and ∼3.5 eV,¹³ see also Fig. S2 (ESI†).

The gas phase ESA spectrum computed for the lowest energy nπ* state in the gas phase (see Fig. 3) is rather similar to the one predicted for uracil,¹⁵ with two weak bands peaking at ∼2 eV and ∼4 eV. Also in this case, EOM-CC3 and CAM-B3LYP spectra are very similar, while according to EOM-CCSD the lowest energy band is blue shifted by ∼0.5 eV.

Like for OPA, inclusion of solvent effect has limited effect on the computed ESA, which is dominated by transitions between states with the same symmetry. As a consequence, the ESA spectra computed in chloroform are very similar to those obtained in the gas phase, yet some differences appear. For example, the lowest energy ESA band exhibits a small, but well visible, red-shift in chloroform. This is due to the small separation induced by the solvent between the 2A′ and 3A′ transitions, which are instead almost iso-energetic in the gas phase. A more important effect is observed for the second ESA band of the nπ* state, which is red-shifted by ∼0.6 eV in chloroform.

To conclude this section, we briefly comment on TDA versus TD-DFT for the OPA spectrum, as well as on MOM-TDA versus regular TDA quadratic response for ESA. With reference to Fig. S22 (ESI†), TDA and TD-DFT yield similar spectral shape for the OPA and ESA spectra, the main difference is a small blue shift in energy, and a more peaked shape of the intense band at around 8 eV. The TDA ESA spectra obtained from the MOM-optimized 1n and 1π states differ more noticeably from those yielded by TDA quadratic response, as even more blue-shifted compared to TD-DFT. Even though the intensities are of comparable size, noticeable intensity redistribution is moreover observed between the peaks. Given these results, and keeping in mind that the final excited states obtained from MOM-TDA are significantly spin-contaminated, it is unclear whether MOM-TDA linear response is a valuable alternative to quadratic response TDA/TD-DFT to obtain ESA spectra. Further studies are clearly needed.

3.2 Cytosine

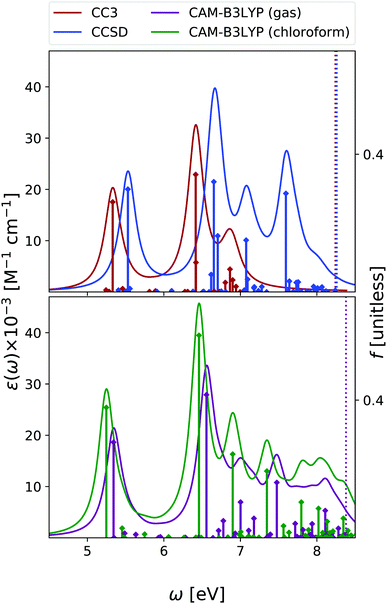
In the case of cytosine, we focused our analysis on the keto-amino tautomer, which is the most stable in condensed phase¹¹ and the one present within DNA. Note, however, that other tautomers are more stable in gas phase,^50,51 and they have to be included when comparing the experimental and the computed OPA spectra. A complete analysis at non-adiabatic vibronic level was provided by some of us in ref. 51. Moreover, in ref. 42 we also showed that, alike the case of the other nucleobases, even for cytosine vibronic effects are expected to red-shift the predicted OPA maximum.

In Fig. 4 we report the OPA spectra computed with EOM-CC3 and EOM-CCSD in the gas phase, and at the TD-CAM-B3LYP level both in the gas phase and in chloroform. EOM-CC3 predicts four prominent peaks below 7 eV, and, after a broad and rather structureless absorption band, another peak just above 8 eV. EOM-CCSD and TD-CAM-B3LYP provide very similar spectral patterns, for what concerns the relative energy and intensity of the main peaks, but the spectra are almost uniformly shifted by 0.2–0.3 eV. A detailed description of the lowest energy excited states of cytosine can be found in ref. 42 and 52. The S₁ state is a ππ* transition, with predominant HOMO → LUMO character, while the S₂ nπ* state involves the excitation from the lone pair of the nitrogen in position 3 towards the LUMO. The three methods applied in this study provide OPA spectral shapes very similar to those obtained by RASPT2/ANO-L,^9,13 which are in almost quantitative agreement with EOM-CC3, apart from a more intense central peak and a slight shift of the band at 8 eV, see Fig. S3 (ESI†). We refer to Fig. S7 (ESI†) for a comparison with existing experimental data.

Fig. 4 Cytosine. Upper panel: OPA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels in gas phase. Bottom panel: OPA at CAM-B3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (ΔSCF at DFT level). HWHM = 0.0045563 hartree.

Inclusion of solvent effects has the same, small, impact on the OPA spectrum, as we have already discussed for Thy – that is, a general increase of the intensities and a destabilization (by ∼0.3 eV) of the nπ* states.

In Fig. 5 we report the ESA computed at the same level of theory as the OPA. In the gas phase, the three methods predict quite similar ESA spectra for the lowest energy ππ* state. We observe a first peak just below 1 eV and another broad band centered at ∼2 eV. However, the presence of many very weak transitions, associated to Rydberg states, makes the entire spectrum below 3 eV very congested and not well resolved. After a peak at ∼3 eV, at ∼3.5 eV we then find two intense transitions, which give rise to a very strong band. The main quantitative difference between the three spectra is a blue-shift of the most intense peak predicted by EOM-CCSD. These spectra are consistent with those computed at the RASPT2/ANO-L level (see Fig. S3, ESI†), especially when considering that in this latter study only ππ* transitions are included.^9,13 At this latter level of theory, after two weak transitions at ∼0.9 eV and ∼2.2 eV, a strong peak at 3.35 eV is found.

Fig. 5 Cytosine. Upper panels: ESA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels of theory in gas phase. Bottom panels: ESA at TD-CAM-B3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. The spectra in dashed line have been enhanced by the factor indicated. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (ΔSCF at DFT level). HWHM = 0.0045563 hartree.

The gas phase ESA spectrum of the lowest energy nπ* state is generally weaker than the one of the ππ* state, but in the low-energy region where it is more intense. Therefore, it is possible that, if it is sufficiently populated, nπ* can actually contribute to the spectral signal at low energies.

As for thymine, inclusion of solvent effect has very little impact on the computed ESA. The most significant difference between the spectra computed in chloroform and in the gas phase is the small red-shift of the lowest energy peak, due to the slight destabilization of the lowest energy ππ* state in chloroform. Moreover, in solution the most prominent peak, at ∼3.5 eV, is better resolved.

3.3 Adenine

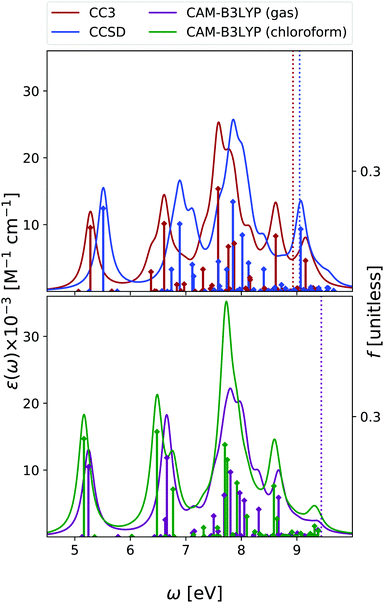
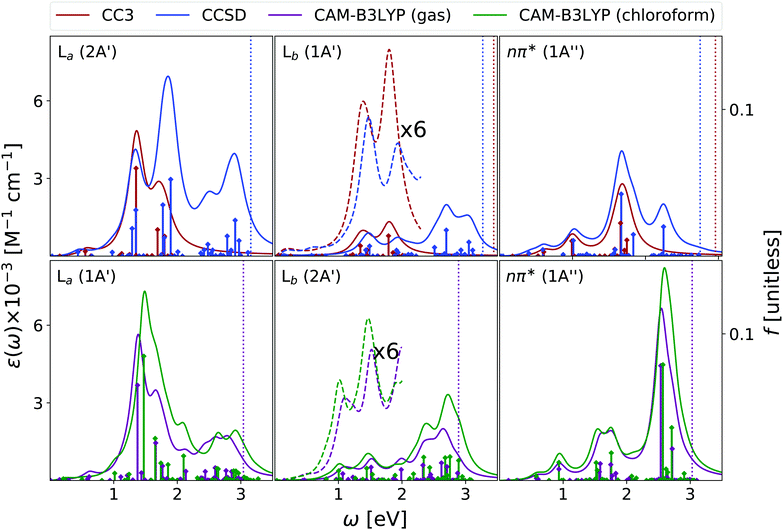
We have analysed the 9-H tautomer of adenine, since it is the most stable even in gas-phase,⁴² and is the species present in DNA.

In the OPA spectrum (see Fig. 6), EOM-CC3, EOM-CCSD and TD-CAM-B3LYP predict one intense peak falling at ∼5.3 eV, a more intense one at ∼6.5 eV, and a very broad absorption in the 7–8 eV region. These predictions appear in good agreement with the available experimental results, (see the spectra collected in ref. 13, as well as Fig. S8 in the ESI†) but for an uniform blue-shift of ∼0.35 eV, which is partially due to the lack of vibronic effects in our calculations. The lowest energy band is due to two ππ* transitions usually labelled as L_a and L_b, according to the Platt nomenclature. The former, more intense, has a predominant HOMO → LUMO character, the latter, rather weak, a more significant HOMO → LUMO+1 contribution.²⁶ Additionally, there is a close lying nπ* state, which corresponds to a transition from the N1 and N3 lone pairs to the LUMO π* orbital.²⁶ Confirming previous studies,^26,53,54 at the TD-CAM-B3LYP level, L_a is more stable than L_b, whereas EOM-CCSD and EOM-CC3 provide the opposite trend. However, assessing the exact energy ordering between L_a and L_b, which are strongly vibronically coupled,⁴² is not relevant for the present study, as we shall compute the ESA of both states.

Fig. 6 Adenine. Upper panel: OPA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels in gas phase. Bottom panel: OPA at CAM-B3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (ΔSCF at DFT level). Note that for CAM-B3LYP in gas phase the first intense peak is L_a, with nπ* almost overlapping with it. Then L_b follows. In solution, the first intense peak is L_a, followed by L_b and then by nπ*. HWHM = 0.0045563 hartree.

Also for adenine, inclusion of solvent effects by PCM has a modest effect on the computed OPA. We observe a small red-shift of the lowest energy bands and the ‘usual’ increase in the intensity. The nπ* state is confirmed to be destabilized in chloroform, by ∼0.25 eV.

We start our analysis of the ESA (see Fig. 7) for the L_b state, the lowest energy one at the EOM-CCSD/CC3 level. Due to the large computational cost, the EOM-CC3 spectrum is limited to the 20 lowest energy states. As a consequence, we limit our discussion to the 0–2 eV energy window. Here, EOM-CC3 and CAM-B3LYP spectra are similar, with a first band peaking just above 1 eV, followed by a peak, slightly more intense, at 1.5 eV. The EOM-CCSD spectrum is also similar, but for a blue-shift of the two peaks and for the inversion of their relative intensity. At higher energy, both EOM-CCSD and TD-CAM-B3LYP provide a broad absorption band between 2 and 3 eV, with two main peaks at ∼2.3 and ∼2.7 eV. In the investigated energy range, these spectra are in line with those obtained at the RASPT2 level,^13,55 see Fig. S4 (ESI†).

Fig. 7 Adenine. Upper panels: ESA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels in gas phase. Bottom panels: ESA at CAMB3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. The spectra in dashed line were enhanced by the factors indicated in the figures. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (DSCF at DFT level). It was assumed that EOM-CC3 provides the same order of states as EOM-CCSD. HWHM = 0.0045563 hartree.

Concerning the absorption from L_a, EOM-CC3 and TD-CAM-B3LYP predict extremely close spectra, but for a small blue-shift of the latter. An intense band appears between 1 and 2 eV, peaking at ∼1.4 eV, with a shoulder at 1.7 eV and a very long tail in the red. Then, shallow absorption in the 2–3 eV energy range is predicted by TD-CAM-B3LYP. The EOM-CCSD spectrum is quite similar, but the relative intensity of the lowest energy main peaks is reverted with respect to the predictions of EOM-CC3 and CAM-B3LYP. Significant absorption is then predicted between 2 and 3 eV, with a prominent peak around 2.5 eV, not obtained by TD-CAM-B3LYP.

The spectra in Fig. 7 are in good agreement with the ESA computed in this energy window at the RASPT2 level, which for L_a predicts a strong peak just above 1 eV, and for L_b three bands of increasing intensity at ∼1, 2, and 2.5 eV.¹³

EOM-CC3, EOM-CCSD and TD-CAM-B3LYP agree in yielding a rather substantial ESA also for the nπ* state. All the computed spectra show a first band peaking at ∼1 eV, with a long red-wing, and then several peaks between 1.5 and 2 eV, giving rise to a band, broader according to CAM-B3LYP, peaking at ∼1.8 eV. Then, CAM-B3LYP yields a very intense peak a 2.5 eV, which is, at least partially, also present at the EOM-CCSD level.

The spectra reported in Fig. 7 show that inclusion of solvent effect has a very limited impact on the computed ESA. Besides the small increase of the intensity, we observe a slight blue-shift of the most intense band of L_a, with the peaks present in the gas phase almost coalescing in a single one.

3.4 Guanine

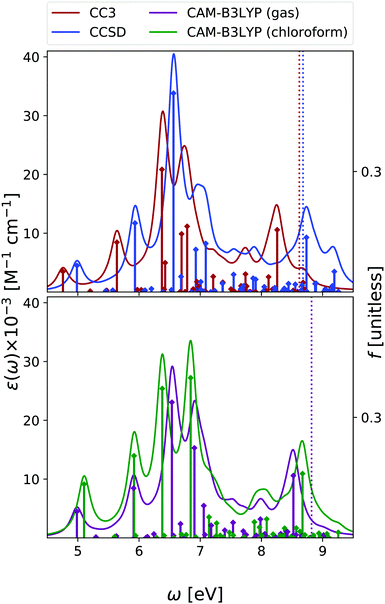
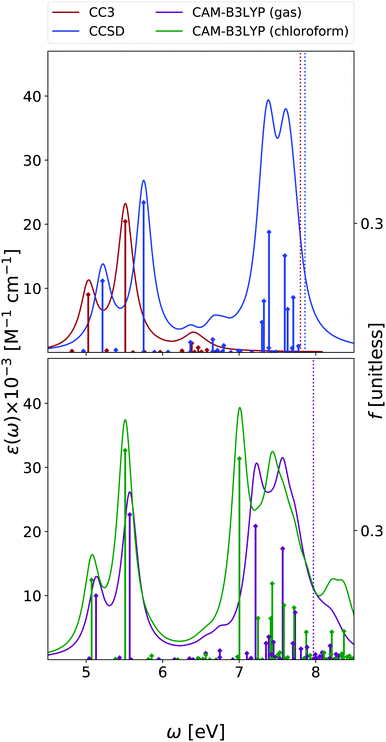
We focus our analysis on the 9-H tautomer, which is the one present in the DNA. On the other hand, as discussed in a recent study,⁴² in the comparison with experimental spectra obtained in the gas phase, the contribution of the 7-H tautomer should be considered.⁴² Due to the size and the large number of excited states of guanine, our EOM-CC3 and EOM-CCSD analysis for OPA is limited to the lowest energy 6.7 eV and 7.8 eV, respectively. The ESA spectra cover only up to 2.5 eV range at most at CCSD level, and 1.6 eV for CC3.

As shown in Fig. 8, in agreement with previous studies,²⁶ including the RASPT2 one,^13,56 for the 9-H tautomer, TD-CAM-B3LYP and EOM-CC3 predict a strong OPA above 5 eV, with two peaks at 5.0–5.1 eV and at 5.5 eV, the most intense one. The EOM-CCSD spectrum is more intense and slightly blue-shifted with respect to the EOM-CC3/TD-CAM-B3LYP ones. Then another intense multi-peaked band is found above 7 eV, according to both TD-CAM-B3LYP and EOM-CCSD. Also for guanine one should recall that inclusion of vibronic effects is expected to introduce a red-shift of the spectra by 0.1–0.2 eV.⁴²

Fig. 8 Guanine. Upper panel: OPA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels in gas phase. Bottom panel: OPA at CAM-B3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (ΔSCF at DFT level). HWHM = 0.0045563 hartree.

The lowest energy band is due to two bright ππ* transitions, which, as for adenine, are usually labelled as L_a and L_b. For guanine, however, L_b is twice as intense as L_a. As already discussed,^42,57 the lowest energy dark excited state is a mixed πσ*/Rydberg transition, which corresponds to S₁ in the gas phase and to S₂ in chloroform. For consistency with the other bases, we instead focus on the lowest energy nπ* state, which involves an excitation from the oxygen lone pair to the π* LUMO and it is almost isoenergetic with L_b in the gas phase.

According to EOM-CC3, EOM-CCSD, and TD-CAM-B3LYP the first peak in the gas phase ESA spectrum of L_a (see Fig. 9) falls at ∼0.5 eV and corresponds to the L_a → L_b transition. The three methods also agree in predicting two additional fairly intense transitions, of similar intensity, in the 1–2 eV spectral range. At 2.4–2.5 eV both EOM-CCSD and TD-CAM-B3LYP provide an intense band, followed, according to CAM-B3LYP of an even stronger band above 3 eV. These spectra are similar to those predicted by RASPT2,¹³ but for small energy shifts and changes in the relative intensity of the transitions in the range 1.5–2.5 eV.

Fig. 9 Guanine. Upper panel: ESA at EOM-CCSD/aug-cc-pVDZ and EOM-CC3/aug-cc-pVDZ levels in gas phase. Bottom panel: ESA at CAMB3LYP/aug-cc-pVDZ level of theory in gas phase and in chloroform solution. The spectra in dashed line are enhanced by the factor indicated in the figures. Geometry optimized in the gas phase enforcing C_s symmetry. The vertical lines indicate the first ionisation energy in the gas phase (ΔSCF at DFT level). HWHM = 0.0045563 hartree.

The most intense L_b ESA peak below 3 eV falls instead at ∼1 eV, according to EOM-CC3, EOM-CCSD and TD-CAM-B3LYP. The latter method then predicts two other intense peaks just below and above 2 eV. RASPT2 also predicts a strong band centered around 1 eV, but no strong peak is then found until 3 eV (i.e. the rather strong transitions around 2 eV are missing),¹³ see Fig. S5 (ESI†).

Finally, the ESA spectrum of the lowest energy nπ* state exhibits many transitions, but rather weak (see Fig. 9), with EOM-CC3, EOM-CCSD and TD-CAM-B3LYP methods providing fairly similar spectral patterns in the low-energy region. A first band is predicted just below 1 eV and a second one, more intense, at ∼1.5 eV (according to CAM-B3LYP) and ∼1.8 eV (according to EOM-CCSD). In the high energy part of the spectrum, the TD-CAM-B3LYP method predicts a band at ∼2.7 eV.

The qualitative trends associated to the inclusion of solvent effects are the same discussed until now: a general increase in the intensity, and ∼0.25 eV blue-shift of the lowest-energy nπ* state. Interestingly, the ESA spectrum computed in solution for this latter state is significantly more intense than in the gas phase. For guanine some additional transitions also appear in the blue-wing. However, this is likely due to the stabilization of some excited states associated to fairly intense transitions that ‘enter’ among the excited states considered when computing the spectrum.

3.5 ESA of ππ* at ππ*-minima

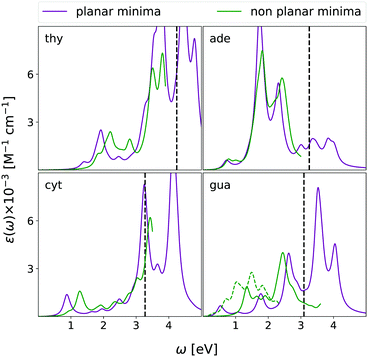
As discussed in the introduction, the reliable computation of ESA is an important step towards the interpretation of Transient Absorption experiments (TAS). Unfortunately, a direct comparison with experiments is not easy. First, the experimental spectra are affected by additional processes, such as ground state bleaching and stimulated emission, that are not considered in our calculations, and could mask the ESA in the high energy region, i.e., in our case, at λ < 350 nm. Moreover, TAS^58,59 also monitors ultrafast dynamical processes, involving several excited states, where the role of vibronic effects and even that of the characteristics of the laser fields (time duration, central frequency, shape) are very important. These effects are expected to be particularly influential for nucleobases, whose bright excited-state lifetime in chloroform is ultrashort (≤1 ps),^58–60 since the path from the FC point to the lowest energy Conical Intersection (CoI) with the ground state S₀ is characterized by a very small, or vanishing energy barrier.²⁶ In this scenario, only the direct simulation of the TAS spectra or, at least, a complete characterization of the ESA along the decay path from the FC point to the CoI, both well beyond the scope of this study, could provide the basis of a fully reliable assignment of the experimental results.

On the other hand, though for nucleobases ESA in the FC region could affect the experimental TAS, ESA from the minima of the bright states is expected to play an important role in determining the spectral signal, and, therefore, TAS experiments can provide a meaningful test of the accuracy of our predictions. As final step of our analysis, we have therefore computed the ESA from the minima of the lowest-energy ππ* bright states for all the nucleobases, where the ring exhibits significant deviations from planarity. For adenine and guanine, we focused on the L_a minimum, which, independently of the predictions concerning the relative stability with respect to L_b in the FC region, is associated to the lowest energy minimum, according to the vast majority of electronic structure methods.²⁶

For all nucleobases, in addition to the absolute minimum, we also computed the ESA from the planar pseudo-minimum of the lowest-energy bright state, optimized in C_s symmetry. In fact, due to the absence of a large energy barrier, the photo-excited wave-packet is expected to rapidly pass through the non planar region of the potential energy surface (PES). If we further consider that non-planar structures should be characterized by lower oscillator strengths, it is possible that also ESA from the planar minima could provide a significant contribution to the TAS, especially in the ultrafast time-regime, where the system approximately preserves a planar configuration. Moreover, for these structures, the signals from ππ* and nπ* states are separated, and this allows a more in-depth analysis. As final caveat before comparing our predictions with experimental TAS, please keep in mind that the experiments were carried out on bulky nucleoside derivatives,^58,59 whereas we here study the bare nucleobase.

As reported in Fig. 10, the spectra computed at the planar pseudo-minimum and at the absolute one are quite similar. The latter spectra are, on the average, slightly blue-shifted, confirming the trend highlighted for uracil.¹⁵

Fig. 10 CAMB3LYP/aug-cc-pVDZ ESA in chloroform solution (equilibrium PCM) from the ππ* state at the ‘planar’ ππ* constrained minimum (purple curves) and the absolute ππ*-minimum (green curves) of all four nucleobases. The dashed green curve reports the spectrum of a strongly distorted minimum found for Gua (see text for details). A vertical dashed line indicates the estimated value of the first ionization energy in the excited state obtained as IE of the ground state minus the energy of ππ* computed for planar structure. HWHM = 0.0045563 hartree.

Thymine. The computed spectrum of thymine shows a first small peak at ∼1.2 eV (∼1000 nm), followed by a band, covering the range 1.5–2.5 eV (800–500 nm) and peaking at ∼2 eV (∼650 nm). We then find a peak at ∼3 eV (∼400 nm) (a shoulder for the planar minimum), preceding a very intense ESA band at higher energy. The computed spectrum is consistent with the experimental ones, measured for a substituted thymidine in the 350–720 nm range at different times in ref. 59 and reproduced for the reader's convenience in Fig. S11 of the ESI.† Especially in the fs- and ps-timescale, they exhibit a band at ∼400 nm preceding a broad band, rising at ∼500 nm and peaking at ∼700 nm, very close, however, to the limit of the observation window.

Cytosine. For cytosine, our calculations predict a rather weak and broad absorption between 1 eV and 2.5 eV, with a first band peaking 1.2 eV (at 0.9 eV for the ‘planar’ structure), followed by a band starting above 2 eV (∼620 nm) and peaking at ∼2.5 eV (500 nm). Then, two strong bands are obtained at 3.2 eV (400 nm) and 4.5 eV (275 nm) in the planar minimum. Our predictions seem to agree with the available experimental data, which cover the range between 350 and 700 nm, considering that cytosine emits at 350 nm, and therefore a comparison with our ESA is difficult in that region. In the 2-dimensional experimental spectrum of a substituted cytidine, reported in the ESI of ref. 58 and reproduced in Fig. S12 of the ESI,† a weak and broad band, with shallow maxima at ∼500 and ∼600 nm is indeed present, more visible in the sub-ps timescale.

Adenine. The most prominent peak in the spectrum computed for adenine falls at ∼1.8 eV (690 nm) and is followed by another peak at ∼2.2 eV (560 nm). At higher energies, a broad band peaking above 3.0 eV (∼410 nm) is found. Also in this case, the computed spectrum is consistent with the available transient absorption spectra reported for a substituted adenine in the 350–720 nm range at different times in ref. 59, and reproduced for the reader' convenience in Fig. S13 of the ESI.† In fact, especially in the fs- and ps-timescale, it features a peak at ∼400 nm and a broad band growing from λ > 500 nm up to the limit of the observation range, at ∼720 nm. Interestingly, we correctly predict the higher ESA intensity of adenine with respect to thymine. On the other hand, the intensity of the 400 nm feature is underestimated by our calculations.

Guanine. Geometry optimization of the L_a state first leads to a low-energy gradient (∼0.001 a.u.) region where the distortion of the planarity is rather small. The spectra computed at a representative structure of this region is reported by the bold green curve of the fourth panel in Fig. 10. For this ‘planar’ minimum of guanine we then predict, below 3 eV, three bands of increasing intensity, peaking at ∼0.5 eV, ∼1.8 eV and ∼2.6 eV (480 nm). They are followed by an intense peak at 3.5 eV (350 nm). The ESA spectrum computed in the non-planar minimum exhibits a first peak at 1.2 eV, followed by two peaks at ∼1.8 eV (∼690 nm). An intense transition at ∼2.5 eV (490 nm) is then found. In the experimental spectrum of a substituted guanosine, reported as a 2-dimensional plot in ref. 58 and reproduced in Fig. S12 of the ESI,† we indeed find a broad band in the 400–620 nm region, with a maximum at ∼480 nm. Moreover, there is a very strong ESA band at ∼350 nm, which also agrees with our prediction. We should again recall that in principle, in this region, transient absorption spectra are also affected by the stimulated emission (SE) signal. The good agreement with ESA computations thus suggests that SE is rather weak. At the adopted level of theory, a strongly distorted minimum is also found, where the energy gap with S₀ (2.4 eV) and the oscillator strength (0.06) are small. It is not possible to assess whether this minimum provides any contribution to the experimental TAS. It could be considered representative of the contribution from the part of the path close to the crossing region with S₀, where there is a strong mixing between nπ* and ππ* transitions. The ESA computed in this structure (see Fig. 10 dashed green line), indeed shows a very broad, multi-peaked band with a maximum around 1.5 eV.

Finally, we note that the computed spectra exhibit an extremely small dependence on the solvation regime (equilibrium vs. non-equilibrium)^25,48,61 used in the PCM/TD-CAM-B3LYP calculations (see Fig. S23, ESI†).

4 Concluding remarks

We have carried out a thorough exploration of the absorption spectra of the four DNA bases, in the gas phase and in the low-polarity solvent chloroform, resorting to three single reference quantum mechanical methods: EOM-CC3, EOM-CCSD and TD-CAM-B3LYP. Our main focus was the calculation of the ESA spectra, which is fundamental for the assignment and the interpretation of the pump and probe spectra.

The three investigated methods provide similar shapes for the OPA spectra, which are also in good agreement with those obtained with other multi-reference QM methods.^13,26 As a rule of thumb, EOM-CCSD spectra are, more or less uniformly, blue-shifted by 0.2–0.3 eV with respect to the EOM-CC3 ones, which are very close to the CAM-B3LYP ones. The largest quantitative discrepancy between EOM-CC3 and CAM-B3LYP OPA spectra is found for cytosine and it is smaller than 0.25 eV. The spectra are consistent with the available experiments, apart from a moderate shift in the position, generally smaller for EOM-CC3. However, it should be remarked that a direct comparison is not trivial (see Section S1.3, ESI,† for a more detailed discussion).

The ESA spectra computed in the gas phase by EOM-CC3, EOM-CCSD, and TD-CAM-B3LYP are also in nice agreement, for both ππ* and nπ* states. In particular, EOM-CC3 and TD-CAM-B3LYP are, in general, quite close, most of the predicted peaks being within 0.1 eV. The predicted spectral shapes are also compliant with the RASPT2 results, which are available for ππ* states only.¹³ This result, together with the similarity between EOM-CC3 and EOM-CCSD results, indicates that the role of double excited states is rather limited, at least in the investigated energy window (0–3.5 eV). The ESA spectra of the considered nπ* states, are, in general, less intense than those of the ππ* states, but, interestingly, their contribution cannot be safely neglected. Moreover, it should be highlighted that while the ππ* and nπ* are decoupled by symmetry in C_s, they can mix at non-planar geometries like those visited in the path toward the CoI with the ground electronic state. Whereas we computed the ESA at the non-planar lowest-energy state minima, full characterization of the ESA along the entire path would be more computationally demanding.

In this respect, it is comforting that the present data provide an important validation of the less computationally-demanding TD-CAM-B3LYP approach, which yields spectra very close to those of EOM-CC3 and in good agreement with the RASPT2 ones. This outcome can pave the way to the study of larger oligonucleotides, which, at the moment, can only be tackled at the TD-DFT level. Already for a dinucleotide, the number of excited states to be considered, even in a small energy window, strongly increases, making brute force approaches unfeasible for wavefunction-based QM methods. On the other hand, as discussed above, the use of purposely tailored procedures (e.g., a ‘wise’ selection of the active space) is more difficult for non ‘symmetric structures’ and could it make difficult to obtain a well-balanced description in all the regions of the PES. Yet, very encouraging results on the treatment of larger systems, including solvated systems, with CC accuracy come from the latest advances in multilevel coupled cluster theory.^62–65

Another interesting feature of TD-CAM-B3LYP is the relatively small dependence of the computed spectra on the size of the basis set. As shown in the ESI,† the spectra obtained at the TD-CAM-B3LYP/6-31G(d) level are fairly similar to the ones reported here, but for a moderate, almost uniform, blue-shift. It is, however, clear that a small basis set would make it impossible to study Rydberg transitions and, in general, additional tests may be needed to definitively assess the reliability of TD-CAM-B3LYP. Once validated the accuracy of TD-CAM-B3LYP/aug-cc-pvdz calculations in the gas phase, we have exploited this method in the subsequent part of our study, focused on chloroform solution. Based on our experience,⁶¹ a continuum model as PCM should be sufficient to reproduce solvent effect in such non hydrogen-bonding solvent. Inclusion of solvent effect has a rather small, though visible, effect on the spectra. The spectral shapes are similar to those computed in the gas phase and the peaks are only slightly shifted (usually ≤0.1 eV). On the other hand, the lowest energy nπ* states are relatively destabilized in chloroform by 0.2–0.3 eV with respect the bright ππ* states. As a consequence, solvent could have an important ‘indirect’ impact on the computed TAS, by simply modifying the population transfer between the bright and dark excited states.

In the last part of our analysis, we have computed, for all the four DNA bases, the ESA from the minima of the lowest energy ππ* states in order to compare our predictions with the available TAS spectra in chloroform. Always keeping in mind all the caveats discussed in the preceding subsection, our computed spectra are fully consistent with the experimental ones, for what concerns the position and the relative intensity of the large majority of the peaks. Taken together, the data reported here provide very encouraging indications on the possibility of computing and assigning the ESA spectra of medium size molecules, not only in the gas phase but also in solution. It is clear that many challenges are still ahead (inclusion of vibronic effects, of explicit solute–solvent interactions, direct simulation of TAS spectra, just to name a few). Moreover, additional benchmark tests would be desirable, for what concerns especially the high energy region, where it could not be possible to discard the role of double excited states. However, it seems that, at least in the visible, the computation of the ESA of oligonucleotides in solution is now at hand.

Finally, we presented a preliminary test on thymine of the applicability of a MOM-TDA based approach to the computation of ESA. The results (reported in ESI†) were noticeably different from those obtained from quadratic-response TD-DFT, which definitely calls for a future, more in-depth, analysis.

Author contributions

R. I., F. S., and S. C. conceptualized and supervised the project. D. A. F. carried out the TDA and TDDFT calculations and prepared all graphical material. S. C. performed the MOM-TDA calculations. A. C. P. and H. K. performed the EOM-CCSD and EOM-CC3 calculations. R. I., F. S., and S. C. prepared the first draft of the manuscript. All authors discussed the science and revised the article to its final form.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Vishal Kumar Jaiswal, Dr Ivan Rivalta and Dr Marco Garavelli (University of Bologna) for providing the full set of RASPT2 ESA data from ref. 13, and Dr Martha Yaghoubi Jouybari (ICCOM-CNR) for preliminary TD-DFT calculations. S. C. thanks Dr Andrew Gilbert (Q-Chem) for discussion. This work has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Skodowska-Curie European Training Network [grant agreement no. 765739 (COSINE-COmputational Spectroscopy In Natural sciences and Engineering, D. A. F., A. C. P., H. K., and S. C.) and no. 765266 (LightDyNAmics, R. I. and F. S.). S. C. acknowledges financial support from the Independent Research Fund Denmark-DFF-FNU RP2 (grant no. 7014-00258B). A. C. P., S. C., and H. K. acknowledge the Research Council of Norway through FRINATEK projects 263110 and 275506.

Notes and references

1. M. Maiuri, M. Garavelli and G. Cerullo, J. Am. Chem. Soc., 2020, 142, 3–15.
2. T. A. A. Oliver, R. Soc. Open Sci., 2018, 5, 171425.
3. S. S. K. Raavi and C. Biswas, Femtosecond pump–probe spectroscopy for organic photovoltaic devices, Digital Encyclopedia of Applied Physics, John Wiley & Sons, Ltd, 2019, pp. 1–49.
4. C. Ruckebusch, M. Sliwa, P. Pernot, A. de Juan and R. Tauler, J. Photochem. Photobiol., C, 2012, 13, 1–27.
5. P. Cronstrand, O. Christiansen, P. Norman and H. Ågren, Phys. Chem. Chem. Phys., 2000, 2, 5357–5363.
6. S. Ling, S. Schumacher, I. Galbraith and M. Paterson, J. Phys. Chem. C, 2013, 117, 6889–6895.
7. J.-C. Denis, A. Ruseckas, G. J. Hedley, A. B. Matheson, M. J. Paterson, G. A. Turnbull, I. D. W. Samuel and I. Galbraith, Phys. Chem. Chem. Phys., 2016, 18, 21937–21948.
8. D. N. Bowman, J. C. Asher, S. A. Fischer, C. J. Cramer and N. Govind, Phys. Chem. Chem. Phys., 2017, 19, 27452–27462.
9. A. Giussani, J. Segarra-Martí, A. Nenov, I. Rivalta, A. Tolomelli, S. Mukamel and M. Garavelli, Theor. Chem. Acc., 2016, 135, 121.
10. A. J. Pepino, J. Segarra-Martí, A. Nenov, R. Improta and M. Garavelli, J. Phys. Chem. Lett., 2017, 8, 1777–1783.
11. L. Martínez-Fernández, A. J. Pepino, J. Segarra-Martí, J. Jovaiš, I. Vaya, A. Nenov, D. Markovitsi, T. Gustavsson, A. Banyasz, M. Garavelli and R. Improta, J. Am. Chem. Soc., 2017, 139, 7780–7791.
12. M. Schmid, L. Martinez-Fernandez, D. Markovitsi, F. Santoro, F. Hache, R. Improta and P. Changenet, J. Phys. Chem. Lett., 2019, 10, 4089–4094.
13. V. K. Jaiswal, J. Segarra-Martí, M. Marazzi, E. Zvereva, X. Assfeld, A. Monari, M. Garavelli and I. Rivalta, Phys. Chem. Chem. Phys., 2020, 22, 15496–15508.
14. L. González, D. Escudero and L. Serrano-Andrés, Chem. Phys. Chem., 2012, 13, 28–51.
15. D. A. Fedotov, A. C. Paul, P. Posocco, F. Santoro, M. Garavelli, H. Koch, S. Coriani and R. Improta, J. Chem. Theory Comput., 2021, 17, 1638–1652.
16. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118.
17. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
18. A. C. Paul, R. H. Myhre and H. Koch, J. Chem. Theory Comput., 2021, 0, 0.
19. A. Dreuw and M. Wormit, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82–95.
20. A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171.
21. A. Bhattacherjee, C. D. Pemmaraju, K. Schnorr, A. R. Attar and S. R. Leone, J. Am. Chem. Soc., 2017, 139, 16576–16583.
22. T. Northey, J. Norell, A. E. A. Fouda, N. A. Besley, M. Odelius and T. J. Penfold, Phys. Chem. Chem. Phys., 2020, 22, 2667–2676.
23. S. Tsuru, M. L. Vidal, M. Pápai, A. I. Krylov, K. B. Møller and S. Coriani, Struct. Dyn., 2021, 8, 024101.
24. V. Scutelnic, S. Tsuru, M. Pápai, Z. Yang, M. Epshtein, T. Xue, E. Haugen, Y. Kobayashi, A. I. Krylov, K. B. Møller, S. Coriani and S. R. Leone, Nat. Commun., 2021, 12, 5003.
25. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
26. R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593.
27. J. S. Taylor, Acc. Chem. Res., 1994, 27, 76–82.
28. J. Cadet, T. Douki and J.-L. Ravanat, Photochem. Photobiol., 2015, 91, 140–155.
29. T. Douki, Photochem. Photobiol. Sci., 2013, 12, 1286–1302.
30. C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019.
31. K. Kleinermanns, D. Nachtigallová and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342.
32. C. T. Middleton, K. de La Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernández and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239.
33. M. Barbatti, A. C. Borin and S. Ullrich, Top. Curr. Chem., 2015, 355, 1–32.
34. S. Mai, M. Richter, P. Marquetand and L. González, Top. Curr. Chem, 2015, 355, 99–154.
35. W. J. Schreier, P. Gilch and W. Zinth, Annu. Rev. Phys. Chem., 2015, 66, 497–519.
36. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansik, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Salek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269.
37. S. D. Folkestad, E. F. Kjønstad, R. H. Myhre, J. H. Andersen, A. Balbi, S. Coriani, T. Giovannini, L. Goletto, T. S. Haugland, A. Hutcheson, I.-M. Høyvik, T. Moitra, A. C. Paul, M. Scavino, A. S. Skeidsvoll, Å. H. Tveten and H. Koch, J. Chem. Phys., 2020, 152, 184103.
38. S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107.
39. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavoevi, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801.
40. F. J. Avila Ferrer, J. Cerezo, E. Stendardo, R. Improta and F. Santoro, J. Chem. Theory Comput., 2013, 9, 2072–2082.
41. S. Bai, R. Mansour, L. Stojanović, J. Toldo and M. Barbatti, J. Mol. Model., 2020, 26, 107.
42. J. A. Green, M. Yaghoubi Jouybari, D. Aranda, R. Improta and F. Santoro, Molecules, 2021, 26, 1–23.
43. J. F. Stanton and J. Gauss, J. Chem. Phys., 1999, 111, 8785–8788.
44. S. Coriani and H. Koch, J. Chem. Phys., 2015, 143, 181103.
45. S. Coriani and H. Koch, J. Chem. Phys., 2016, 145, 149901.
46. L. B. Clark, G. G. Peschel and I. Tinoco, J. Phys. Chem., 1965, 69, 3615–3618.
47. R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103.
48. M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708.
49. R. Improta and V. Barone, Top. Curr. Chem., 2015, 355, 329–358.
50. G. Bazsó, G. Tarczay, G. Fogarasi and P. G. Szalay, Phys. Chem. Chem. Phys., 2011, 13, 6799–6807.
51. Y. Liu, L. Martínez Fernández, J. Cerezo, G. Prampolini, R. Improta and F. Santoro, Chem. Phys., 2018, 515, 452–463.
52. M. Yaghoubi Jouybari, Y. Liu, R. Improta and F. Santoro, J. Chem. Theory Comput., 2020, 16, 5792–5808.
53. F. Santoro, R. Improta, T. Fahleson, J. Kauczor, P. Norman and S. Coriani, J. Phys. Chem. Lett., 2014, 5, 1806–1811.
54. S. K. Khani, R. Faber, F. Santoro, C. Hättig and S. Coriani, J. Chem. Theory Comput., 2019, 15, 1242–1254.
55. A. Nenov, A. Giussani, J. Segarra-Mart, V. K. Jaiswal, I. Rivalta, G. Cerullo, S. Mukamel and M. Garavelli, J. Chem. Phys., 2015, 142, 212443.
56. J. Segarra-Mart, A. J. Pepino, A. Nenov, S. Mukamel, M. Garavelli and I. Rivalta, Theor. Chem. Acc., 2018, 137, 47.
57. V. Karunakaran, K. Kleinermanns, R. Improta and S. A. Kovalenko, J. Am. Chem. Soc., 2009, 131, 5839–5850.
58. K. Röttger, H. J. B. Marroux, M. P. Grubb, P. M. Coulter, H. Böhnke, A. S. Henderson, M. C. Galan, F. Temps, A. J. Orr-Ewing and G. M. Roberts, Angew. Chem., Int. Ed., 2015, 54, 14719–14722.
59. K. Röttger, H. J. B. Marroux, A. F. M. Chemin, E. Elsdon, T. A. A. Oliver, S. T. G. Street, A. S. Henderson, M. C. Galan, A. J. Orr-Ewing and G. M. Roberts, J. Phys. Chem. B, 2017, 121, 4448–4455.
60. K. Röttger, H. J. B. Marroux, H. Böhnke, D. T. J. Morris, A. T. Voice, F. Temps, G. M. Roberts and A. J. Orr-Ewing, Faraday Discuss., 2016, 194, 683–708.
61. R. Improta, UV-Visible Absorption and Emission Energies in Condensed Phase by PCM/TD-DFT Methods, in Computational Strategies for Spectroscopy, ed. V. Barone, John Wiley & Sons, 2012, ch. 1, pp. 37–75.
62. R. H. Myhre, A. M. J. Sánchez de Merás and H. Koch, J. Chem. Phys., 2014, 141, 224105.
63. S. D. Folkestad, E. F. Kjønstad, L. Goletto and H. Koch, J. Chem. Theory Comput., 2021, 17, 714–726.
64. L. Goletto, T. Giovannini, S. D. Folkestad and H. Koch, Phys. Chem. Chem. Phys., 2021, 23, 4413–4425.
65. S. D. Folkestad and H. Koch, J. Chem. Theory Comput., 2020, 16, 6869–6879.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04340d

---