 Open Access Article
Open Access ArticleTerahertz pump–probe of liquid water at 12.3 THz
Fabio
Novelli
 *a,
Claudius
Hoberg
*a,
Claudius
Hoberg
 a,
Ellen M.
Adams
a,
J. Michael
Klopf
a,
Ellen M.
Adams
a,
J. Michael
Klopf
 b and
Martina
Havenith
b and
Martina
Havenith
 *a
*a
aDepartment of Physical Chemistry II, Ruhr University Bochum, 44780 Bochum, Germany. E-mail: fabio.novelli@rub.de; martina.havenith@rub.de
bInstitute of Radiation Physics, Helmholtz-Zentrum Dresden-Rossendorf, Dresden, Germany
First published on 17th September 2021
Abstract
The dynamical complexity of the hydrogen-bonded water network can be investigated with intense Terahertz (THz) spectroscopy, which can drive the liquid into the nonlinear response regime and probe anharmonicity effects. Here we report single-color and polarization-dependent pump–probe experiments at 12.3 THz on liquid water, exciting the librational mode. By comparing results obtained on a static sample and a free-flowing water jet, we are able to disentangle the distinct contributions by thermal, acoustic, and nonlinear optical effects. We show that the transient transmission by the static water layer on a time scale of hundreds of microseconds can be described by thermal (slow) and acoustic (temperature-dependent) effects. In addition, during pump probe overlap we observe an anisotropic nonlinear optical response. This nonlinear signal is more prominent in the liquid jet than in the static cell, where temperature and density perturbations are more pronounced. Our measurements confirm that the THz excitation resonates with the rotationally-damped motion of water molecules, resulting in enhanced transient anisotropy. This model can be used to explain the non-linear response of water in the frequency range between about 1 and 20 THz.
Introduction
Water is one of the most studied and least understood liquids.1 While several anomalies in the thermodynamic, macroscopic properties of liquid water are well documented,2–4 on the microscopic scale water is characterized by a dynamical, tetrahedral network of hydrogen bonded (HB) molecules rearranging on the picosecond timescale.5–9 Terahertz (THz) spectroscopy represents a possible experimental approach to study the water network dynamics. THz radiation is strongly absorbed10–15 by the HB network modes5–8 and provides a sensitive tool to study solute–solvent interactions.16–24Intense THz can be used to perform nonlinear experiments and unveil the transient couplings of the different HB modes.25–34 The first results detailing the nonlinear response of water in the THz frequency range are recent,27,28,32,33,35 and the molecular interpretation is still a matter of ongoing discussion. Tcypkin et al.32,33 performed a series of z-scan measurements at ∼1 THz on liquid water and associated the third-order nonlinear signal to cascaded second-order anharmonicity of the intramolecular O–H stretching modes. Based on their model, only small variations of the nonlinear signal as a function of frequency are predicted from 0.3 to 3.5 THz (see Fig. S7 in ref. 32). Also Ghalgaoui et al.35 recently measured the nonlinear response of liquid water at ∼1 THz, but proposed a different explanation. They suggested that, while a water molecule experiences fluctuating electric fields of about 100 MV cm−1 in the bulk liquid at equilibrium, the superposition of ≥0.25 MV cm−1 single-cycle external fields at ∼1 THz should separate and then accelerate an electron from the parent ion, leading to the ionization of water.35
In our previous study,27 we focused our investigation on the frequency range of the librational mode. Experimentally, we observed a large transient anisotropy of liquid water upon librational excitation using single-color pump–probe experiments at 12.3 THz. The third order response exclusively associated to the transient birefringence, χε3, was found to exceed previously reported values in the optical range36–53 by several orders of magnitude.27 Accompanying simulations could rationalize these experimental results, i.e., we derived an approximation of the experimental response by a simpler time evolving variable that can be calculated using molecular dynamics (MD) simulations.27 In the classical limit, the frequency-dependent nonlinear response function of a sample, S(ν), can be written as 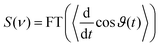 , where ϑ(t) is the time-dependent angle between the direction of the applied electric field and the molecular dipole, and
, where ϑ(t) is the time-dependent angle between the direction of the applied electric field and the molecular dipole, and 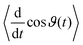 indicates the average derivative of ϑ(t) in the unit volume. In other words, the response of a sample depends crucially on the orientation changes of each water dipole with respect to the external field. These changes are facilitated upon excitation of the librational mode, which mainly involves a rotation of the water molecule in the surrounding hydration cage. The linear response function of liquid water was computed without external fields using MD simulations of the AMOEBA14 water model,27 resulting in a broad spectrum extending from about 0 to 35 THz and peaking at ∼17 THz (see Fig. 4 and Fig. S6 in ref. 27). We simulated the nonlinear response of water by applying an additional electric field. In this case, we found that the nonlinear signal yields a large response at the pump frequency of 12.3 THz, while the nonlinear response at 1 THz pumping is about 10x smaller. Thus, we proposed that the pump excitation at 12.3 THz is in resonance with the reorientation time scale of water dipoles in their hydration cages, and that applying an external field at this frequency might induce a large transient anisotropy in a homogeneous liquid phase.27
indicates the average derivative of ϑ(t) in the unit volume. In other words, the response of a sample depends crucially on the orientation changes of each water dipole with respect to the external field. These changes are facilitated upon excitation of the librational mode, which mainly involves a rotation of the water molecule in the surrounding hydration cage. The linear response function of liquid water was computed without external fields using MD simulations of the AMOEBA14 water model,27 resulting in a broad spectrum extending from about 0 to 35 THz and peaking at ∼17 THz (see Fig. 4 and Fig. S6 in ref. 27). We simulated the nonlinear response of water by applying an additional electric field. In this case, we found that the nonlinear signal yields a large response at the pump frequency of 12.3 THz, while the nonlinear response at 1 THz pumping is about 10x smaller. Thus, we proposed that the pump excitation at 12.3 THz is in resonance with the reorientation time scale of water dipoles in their hydration cages, and that applying an external field at this frequency might induce a large transient anisotropy in a homogeneous liquid phase.27
In our previous publication,27 owing to a large dichroic background, we were not able to dissect the different contributions and quantify the total nonlinear response of liquid water. Therefore, in the current paper we report new measurements at 12.3 THz with long and tunable macropulses. Furthermore, we compare the results obtained in a static cell with THz-pump THz-probe measurements in a free-flowing jet. This allows us to separate thermal, acoustic, and nonlinear responses. The deduced total effective third-order response is χeff3 ≈ 7.2 × 10−13 cm2 V−2, which to the best of our knowledge is the largest reported to date for liquid water in the THz range.28,32,33,35
Experimental
We performed pump–probe transmission experiments at 12.3 THz in pure water. We measured both a ∼15 μm thick water layer in a static cell with ∼0.5 mm thick diamond windows (Diamond Materials), as well as a water jet, free-flowing from a nozzle, with a ∼23 μm thickness estimated from the known absorption coefficient of liquid water10–15 at 12.3 THz, the intensity transmitted by the sample at equilibrium, and the Beer–Lambert law. The static diamond cell is magnetically attached to a copper plate that is stabilized to 20 ± 0.05°C with a chiller. The water jet uses a recirculating liquid with a total volume of about 0.5 L at room temperature (21 ± 0.1 °C) for the duration of the experiment.The FELBE free electron laser (FEL) was operated in continuous (CW) mode at 12.3 THz, emitting a total power of approximately 10 W on the user table. The micropulses are about 3 ps long (full width at half maximum, FWHM) and the repetition rate is 13 MHz, i.e., there is a ∼77 ns delay between two consecutive micropulses. We used two synchronized choppers to obtain the pump and probe macropulses. The probe is chopped at 53 Hz with a duty cycle of 50%. The probe macropulses (grey in Fig. 1b) are ∼9.4 ms long (“probe ON time”) and separated by ∼9.4 ms (“probe OFF time”). The single micropulse probe fluence is ϕpr ∼ 1 μJ cm−2. We chop the pump synchronously at 53 Hz with a duty cycle of 3%. The pump macropulses (green in Fig. 1b) are 283 μs long (“pump ON time”) and separated by ∼18.6 ms (“pump OFF time”). With the adjustable phase delay of the chopper, we set the “pump ON time” in the middle of the “probe ON time”. The pump micropulse fluence is set to ϕPU ∼ 300 μJ cm−2, with a corresponding intensity of IPU ∼ ϕPU/(3 ps) ∼ 100 MW cm−2 and peak field amplitude of54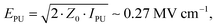 with Z0 ∼ 376.7 Ω vacuum impedance.
with Z0 ∼ 376.7 Ω vacuum impedance.
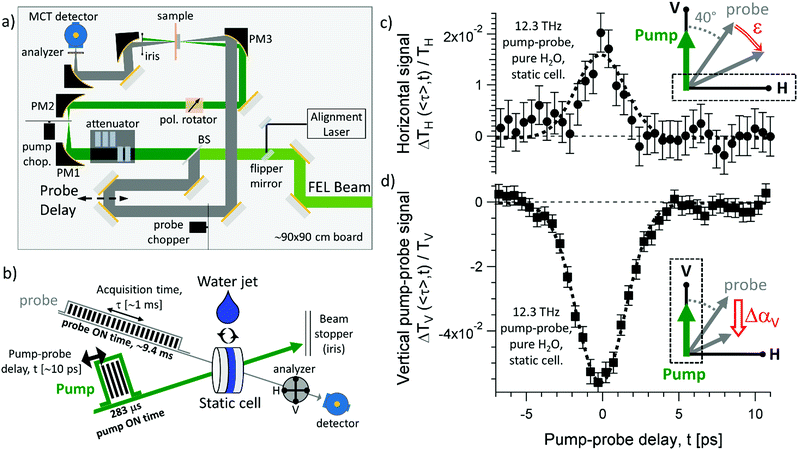 | ||
| Fig. 1 Experimental setup and benchmark measurements. (a) Complete schematic diagram of the experimental setup. The FEL beam is split into the pump and probe beams and routed to the sample with a 75 mm focal parabolic mirror (PM3). The intensity and polarization of the pump beam are adjusted as needed, and a pair of parabolic mirrors with focal lengths of 75 mm (PM1) and 50 mm (PM2) reduces its size. In this way, the pump spot is safely larger than the probe spot at the sample position. The probe is delayed with a mechanical stage, and two synchronized choppers are used to control the duration of the pump and probe macropulses. (b) Zoomed in cartoon at the sample position. The pump (green) and probe (grey) macropulses are obtained with synchronized choppers. The acquisition time of the probe, τ, is about 1 ms long with 1 μs steps. The pump–probe delay, t, spans few picoseconds and refers to the pump–probe micropulse delay. We measured either water in a static cell or in a free-flowing jet, and collect the vertical (V) or horizontal (H) components of the probe radiation. (c) The horizontal pump–probe trace measured from the static cell at 12.3 THz, averaged over the pump macropulse length. It displays a positive bump at pulse overlap that is dominated by the birefringent term (ε), as established previously.27 (d) The vertical pump–probe trace from a static water layer, averaged over the pump macropulse. The negative signal at t ∼ 0 is mostly affected by dichroism27 (Δα). Please note that, for display purposes, we subtracted from the two traces in panels (c) and (d) the same, time-independent offset of −6.8%, which is due to the average heating of the liquid in the static cell. This effect was observed before, as detailed in the ESI of ref. 27. | ||
The “ON times” of the pump (283 μs) and probe (9.4 ms) macropulses are short enough to safely avoid water boiling during a macropulse. Trivially, if boiling occurs we observe a large increase of the transmission saturating the detector, because liquid water, but not vapor, absorbs strongly at10–15 12.3 THz. The “OFF times” of the pump (18.6 ms) and probe (9.4 ms) macropulses are sufficiently long to ensure that the sample is equilibrated between subsequent macropulses. In fact, the thermalization time of a l ∼ 6 μm thick water cylinder (which is about one penetration depth10–15 at 12.3 THz) can be estimated as55–58τth ∼ l2/D ∼ 300 μs, with D thermal diffusivity. Additional information about thermal effects is given in the Discussion section.
A 90-degree off-axis parabolic mirror (PM) with 2′′ diameter and 75 mm effective focal length focuses both pump and probe beams into the sample. We set the linear polarization of the probe beam to an angle θ = 40° with respect to the linear polarization of the pump beam. The pump is aligned on the vertical direction (V). The spot sizes of probe (∼400 μm, 1/e2 diameter) and pump (∼700 μm) beams were measured with a camera (Ophir Pyrocam IV). We used two additional PMs to collimate and focus the THz radiation into the detector (Judson J15D26-M204-S01M-60) and beam blockers to filter out the pump scattering. We put an analyzer–polarizer (Infraspecs P01, with polarization contrast better than 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in front of the detector to select either the vertical (V) or horizontal (H) components of the THz probe intensity transmitted by the sample. In this way, we can measure the “vertical” (ΔTV/TV) or “horizontal” pump–probe trace (ΔTH/TH). With an acquisition card (National Instruments PCIe-5764), we detect the probe transmitted by the sample for 1 ms (probe acquisition time, τ, in Fig. 1b) with a resolution of 1 μs, and performed these measurements over a range of about 15 ps of pump–probe delay around the micropulse overlap time, t ∼ 0 ps, at 0.5 ps intervals of pump–probe delay. The noise level of the transient transmission is estimated from repeated measurements to ca. ±0.5% (see, e.g., Fig. 1c and d).
1) in front of the detector to select either the vertical (V) or horizontal (H) components of the THz probe intensity transmitted by the sample. In this way, we can measure the “vertical” (ΔTV/TV) or “horizontal” pump–probe trace (ΔTH/TH). With an acquisition card (National Instruments PCIe-5764), we detect the probe transmitted by the sample for 1 ms (probe acquisition time, τ, in Fig. 1b) with a resolution of 1 μs, and performed these measurements over a range of about 15 ps of pump–probe delay around the micropulse overlap time, t ∼ 0 ps, at 0.5 ps intervals of pump–probe delay. The noise level of the transient transmission is estimated from repeated measurements to ca. ±0.5% (see, e.g., Fig. 1c and d).
About 1% pump scattering still reaches the detector, see Fig. 2a and 3a. The scattering is a factor of five smaller than the pump–probe signals as seen in Fig. 1–3. The pump scattering was measured separately with the probe blocked, and removed as an offset from the corresponding pump–probe trace. The rise and decay times of the pump scatter, i.e., the approximate time it takes for the pump macropulse to reach a plateau in the acquisition time, amounts to few microseconds.
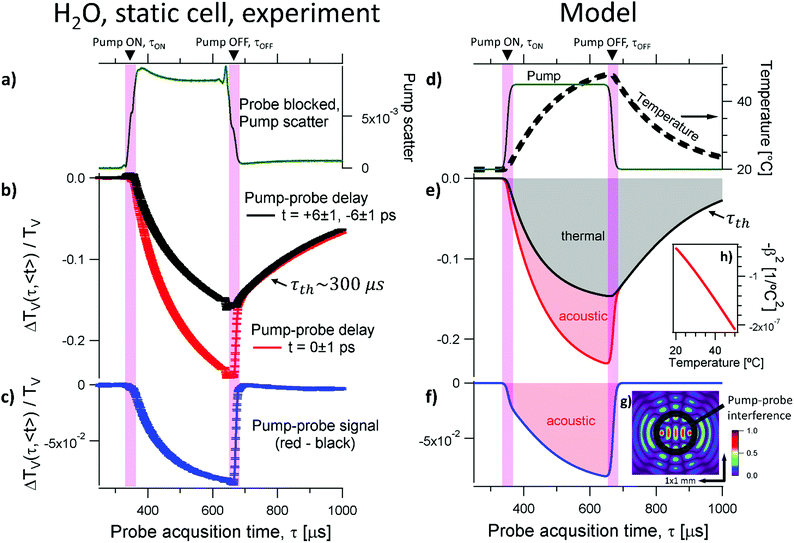 | ||
| Fig. 2 Pump–probe results at 12.3 THz for water in a static cell. (a) The pump scatter shows the approximate times at which the pump is turned on (τON) and off (τOFF). (b) Pump–probe signal as a function of the acquisition time, τ, at few significant pump–probe micropulse delays. The black line is obtained by averaging the pump–probe signal away from pulse overlap, i.e., between t = +5 ps and t = +7 ps or, equivalently, t = −5 ps and t = −7 ps. The response is dominated by thermal effects with a time constant τth ∼ 300 μs. The signal at pump–probe overlap, red curve, is averaged between t = −1 ps and t = +1 ps. (c) The different response at pulse overlap is estimated by the difference between the red and black curves in panel b. (d) The temperature change of the water layer in the static cell induced by the pump pulses, as estimated from eqn (1) and (2), is shown with the thick dashed black line. The simulation uses a simple pump envelope (green). (e) The simulated variation of the transmission of the water sample induced solely by a temperature change (black curve), and including also an acoustic component (red). (f) Simulated pump–probe signal (blue), estimated as the difference of the red and black curves in panel e. (g) Color map of the calculated acoustic grating obtained at the spatial and temporal overlap of pump and probe pulses, together with surface acoustic waves propagating outwards. (h) The thermal expansivity of liquid water, β(°T), depends strongly on temperature. | ||
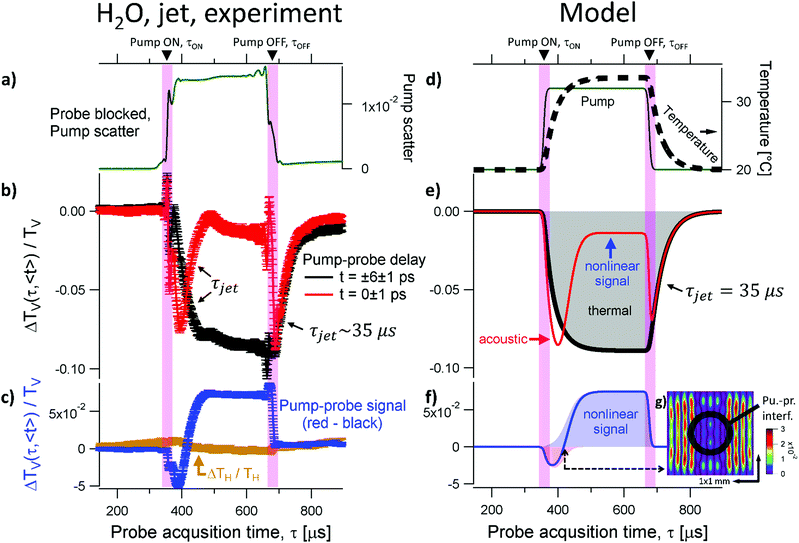 | ||
| Fig. 3 Pump–probe results at 12.3 THz for water in a free-flowing jet. (a) The pump is measured by blocking the probe pulse entirely. (b) Pump–probe signal as a function of the acquisition time, τ, at few significant pump–probe micropulse delays. The black line is obtained by averaging the pump–probe signal away from pulse overlap, i.e., between t = +5 ps and t = +7 ps or, equivalently, t = −5 ps and t = −7 ps. The response is dominated by the time it takes for the water to flow away, τjet ∼ 35 μs. The signal at pump–probe overlap, red curve, is averaged between t = −1 ps and t = +1 ps. (c) The different response at pulse overlap is estimated to the difference between the red and black curves in panel b. The orange curve is the tiny signal detected by rotating the analyzer–polarizer to transmit the horizontal component of the probe radiation. (d) The temperature change of the water layer in the jet induced by the pump pulses, and estimated from eqn (3) and (4), is shown with the thick dashed black line. The simulation uses a simple pump envelope (green). (e) The simulated variation of the transmission of the water sample induced solely by a temperature change that is determined by the jet speed (black curve), and including also acoustic (red curve, red arrow) and nonlinear optical (red curve, blue arrow) components. (f) Simulated pump–probe signal (blue), estimated as the difference of the red and black curves in panel e. (g) Estimated residue of the acoustic grating obtained by adding up patterns like the ones shown in Fig. 2g, but displaced in the vertical direction by the liquid flow, see the main text for details. | ||
Based on our previous results,27 any pump frequency resonant with the relaxation time scale of the reorientation of a water molecule in its hydration cage should trigger an enhanced anisotropy in the liquid. However, there are several technical limitations. Firstly, we avoided frequency ranges with high water vapor absorption. Secondly, we selected the central output frequency of the FEL to optimize the magnitude of the signal at the detector. Thirdly, all the optical elements used must work properly at the chosen frequency. Taking all three restrictions into consideration, we selected a single-color pump–probe frequency of 12.3 THz.
Results
In Fig. 1c and d we show the relative change of the transmitted probe intensity (ΔT/T) averaged over the pump macropulse time (〈τ〉) and as a function of the pump–probe delay (t). As shown in Fig. 1c and d), we detect a positive (negative) pump–probe signal at pulse overlap (t ∼ 0) when the analyzer is set to pass the horizontal (vertical) component of the probe light, ΔTH(〈τ〉, t ∼ 0)/TH > 0 (ΔTV(〈τ〉, t ∼ 0)/TV < 0). The signals are about half the magnitude of the ones we reported before, see Fig. 2 in ref. 27. We note that a quantitative comparison between the experiments reported here, performed in Dresden, with the previous ones from Nijmegen is difficult because of the different electron accelerators used. The micropulse fluence was 3.1 mJ cm−2 in ref. 27 and 300 μJ cm−2 here, while the pump macropulse duration was 8 μs in ref. 27 and 283 μs here.In ref. 27 we observed an anisotropic signal resulting from dichroism and birefringence. In short, dichroism describes how the transient absorption coefficient (Δα) varies with the polarization direction of the radiation, and the birefringence (ε) accounts for the change in polarization orientation induced by the anisotropic index of refraction. If the pump is vertically (V) polarized, the birefringent term depends on the angle (θ) between the linear polarizations of the pump and probe beams, while the dichroic term along V is unaffected. We found27 that the magnitude of the horizontal pump–probe signal is mostly related to the birefringent term (see the inset in Fig. 1c here, or Fig. 3c in ref. 27), while the dichroism dominates the vertical pump–probe trace (see the inset in Fig. 1d here or Fig. 2a in ref. 27, which shows that ΔTV/TV is weakly dependent on the probe polarization angle). In order to address the origin of both the transient dichroism as well as the increase of the signal during the macropulse, we performed additional vertical pump–probe measurements (ΔTV/TV) in a static cell (Fig. 2) and in a water jet (Fig. 3). The key advantage with respect to previous experiments27 is that the probe macropulse is longer than the pump, allowing investigation of extended dynamics.
The left column of Fig. 2 shows the results obtained from water in a static cell. Fig. 2a displays the intensity of the pump scatter (green) obtained by blocking the probe beam as a function of the acquisition time (τ). As marked by the purple bands and the black arrows, the pump macropulse is switched on approximately at τON ∼ 370 μs, and off at τOFF ∼ 650 μs. The black curve in Fig. 2b displays the relative change of the probe transmission beyond pump–probe overlap. This is identical at positive or negative delays (see Fig. 1d at t = −6 ps and t = +6 ps). The black curve represents the responses both before (t = −6 ± 1 ps) and after (t = +6 ± 1 ps) the pump–probe overlap, averaged within ±1 ps, which are indistinguishable within the measurement error. The black curve in Fig. 2b decreases slowly after the pump is turned on (τ > τON) and reaches a value of about ΔTV/TV ∼ −15% when the pump macropulse is turned off (τ ∼ τOFF). After the pump is off (τ > τOFF), the signal slowly recovers with an exponential process with a time constant τth ∼ 300 μs.
The red curve in Fig. 2b displays the transient signal at pump–probe overlap, t = 0 ± 1 ps. This curve decreases quickly after the pump is turned on, and reaches a value of about ΔTV/TV ∼ −23% just before the pump macropulse is turned off (τ ≲ τOFF). When the pump is off (τ ∼ τOFF) the signal changes abruptly, rising up to ca. ΔTV/TV ∼ −15% within few microseconds. After the pump has been turned off (τ > τOFF), the signal slowly recovers with an exponential process with a time constant τth ∼ 300 μs, i.e., with the same time constant as before. The pump–probe signal can be estimated as the difference of the transient responses (red minus black trace, Fig. 2b), and is shown with the blue curve in Fig. 2c. This curve displays a slowly increasing and negative transient signal during the pump macropulse (τON < τ < τOFF), which keeps decreasing during the pump macropulse, in agreement with previous observations.27
Since in a static cell the laser spot can induce a thermal gradient in the liquid, we wanted to compare these results to the ones obtained in a free flowing liquid jet. The left column of Fig. 3 shows the experimental results obtained from a free-flowing water jet. The pump–probe signal away from pulse overlap (black in Fig. 3b) quickly drops when the pump is turned on (τ ∼ τON) and, after a characteristic exponential decay with a time constant τjet ∼ 35 μs, will equilibrate at a negative value of ΔTV/TV = −8 ± 1% (τON < τ < τOFF). A weak, linear decrease of the transient transmission between about τ ∼ 450 μs and τ ∼ 650 μs might indicate an underlying, additional slow process. After the pump is off (τ ∼ τOFF) the signal recovers, rising almost all the way up to ΔTV/TV ∼ 0, with a similarly fast rise time with a τjet ∼ 35 μs constant.
The red curve in Fig. 3b displays the transient signal at pump–probe overlap, t = 0 ± 1 ps, for the water jet. This curve decreases quickly after the pump is turned on (τ > τON), reaching a value of about ΔTV/TV ∼ −7.5% after approximately 35 μs from the onset of the pump macropulse (τ ∼ τON + 35 μs ∼ 400 μs). The signal then reverses sign, increasing with a rise time of τjet ∼ 35 μs and reaching a plateau of ΔTV/TV = −1.1 ± 0.5% at τ ∼ τON + 100 μs ∼ 470 μs. When the pump is turned off (τ ∼ τOFF) the signal at pulse overlap (red in Fig. 3b) changes abruptly, dropping down to ΔTV/TV = −8 ± 1% within few microseconds. After the pump is off (τ > τOFF), the signal quickly recovers and approaches ΔTV/TV ∼ 0, again with a characteristic time of ca. τjet ∼ 35 μs.
The difference between the red and the black curve (see Fig. 3b) is displayed with the blue curve in Fig. 3c. This shows a fast changing and complex transient during the pump macropulse (τON < τ < τOFF), and a fast drop down to approximately zero, within few microseconds, when the pump is off (τ ∼ τOFF). Initially, the pump–probe signal shown in blue in Fig. 3c is negative and decreasing (τON < τ < τON + 35 μs) up to a minimum turning point of ΔTV/TV ∼ −5% at τ ∼ 400 μs. After this, the signal increases and reaches a positive plateau of ΔTV/TV ∼ +7% (τON + 100 μs ∼ 470 μs < τ < τOFF). When the pump is turned off (τ ∼ τOFF), the signal abruptly drops to zero for τ > τOFF.
For comparison, the orange curve in Fig. 3c displays the horizontal pump–probe signal (ΔTH/TH) obtained by rotating the analyzer to transmit only the horizontal component of the probe light, while leaving all the other experimental conditions unaltered. Thus, we clearly observe an anisotropy in the polarization of the signal also in the water jet, i.e., the orange and blue curves in Fig. 3c are obviously different.
Finally, we would like to point out two important details. First, the recovery times (τjet for the jet in Fig. 3, and τth for the static cell in Fig. 2) are independent on the pump–probe delay. We selected ±6 ps for display purposes only, because the pump–probe signal is centered around pulse overlap and extends only for few picoseconds around it (see Fig. 1c and d). Second, the time it takes for the signal to disappear when the pump is turned off depends also on how “sharp” the pump macropulses are in time. Given the fact that the pump macropulses are obtained with a mechanical chopper (Fig. 1a and b), the rise and decay times of the pump macropulses amount to few microseconds. See, for example, the purple bands at τ = τOFF in Fig. 2a and 3a.
Discussion
Often, pump–probe experiments are performed with tabletop laser setups running at a repetition rate of few kilohertz. In these conditions, both thermal55–58 (τth ∼ 300 μs) as well as acoustic59,60 (τac ∼ 0.3 μs as detailed in a paragraph below) effects can typically be disregarded, because they are slower than the optical nonlinear dynamics (∼10 fs to ∼10 ps), and faster than the delay between subsequent pulses (see, e.g., the Table 4.1.1. in ref. 61). In contrast, FELs are bright but they typically operate at a repetition rate of tens of MHz, emitting macropulses lasting several microseconds. In these experimental conditions, thermal and acoustic effects can also be present,62 together with nonlinear optical responses.61In spectroscopy, thermal effects originate from the fact that the optical properties of a material can be temperature dependent.10–12 The timescale of a thermal response is restricted by the thermal diffusivity (D = D(°T), which is temperature dependent) and the sample geometry. For a thin cylinder of thickness l the fastest thermalization time constant is approximately equal to55–58τth ∼ l2/D. If we take a water cylinder with thickness given by the inverse of the absorption coefficient (αwat) at 12.3 THz at the temperature °T = 20 °C, we have 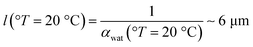 , and the thermalization time is τth(°T = 20 °C) ∼ l2(°T = 20 °C)/D(°T = 20 °C) ∼ 300 μs. This timescale agrees very well with both the rise and decay times of the transient transmission of the static cell, away from pulse overlap (black curve in Fig. 2b). Thus, we suggest that these processes are indicative of the macroscopic thermal response.
, and the thermalization time is τth(°T = 20 °C) ∼ l2(°T = 20 °C)/D(°T = 20 °C) ∼ 300 μs. This timescale agrees very well with both the rise and decay times of the transient transmission of the static cell, away from pulse overlap (black curve in Fig. 2b). Thus, we suggest that these processes are indicative of the macroscopic thermal response.
In the following we provide semi-quantitative models in order to reproduce the magnitude and the time scales of the transient signals. The steady-state temperature increase,63–67 Δ°Ti, induced by the single i-th pump micropulse in a water layer with thickness l depends on the micropulse fluence (ϕPU,i), possible interface effects limiting the amount of absorbed radiation67 (percentage of energy dissipated by contact with a surface, q, and/or radiation lost at interfaces due to indexes mismatch, f(n(°T))), and the temperature-dependent specific heat of water (CP(°T)):
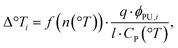 | (1) |
 are the Fresnel coefficients68 describing the intensity transmitted at the air-diamond and diamond-water interfaces. ndia = 2.37 is the index of refraction of diamond, nair = 1, and nwat (°T) is the temperature-dependent index of refraction of liquid water.10–12 We perform a simple numerical simulation in steps of 1/13 MHz ∼ 77 ns, and assume that the energy of each single pump micropulse is instantaneously converted into a temperature increase of water viaeqn (1). As we are not in steady state, this temperature gradient decays exponentially as a function of time with the thermalization constant55–58τth = l2/D(°T), with
are the Fresnel coefficients68 describing the intensity transmitted at the air-diamond and diamond-water interfaces. ndia = 2.37 is the index of refraction of diamond, nair = 1, and nwat (°T) is the temperature-dependent index of refraction of liquid water.10–12 We perform a simple numerical simulation in steps of 1/13 MHz ∼ 77 ns, and assume that the energy of each single pump micropulse is instantaneously converted into a temperature increase of water viaeqn (1). As we are not in steady state, this temperature gradient decays exponentially as a function of time with the thermalization constant55–58τth = l2/D(°T), with 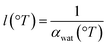 and αwat(°T) temperature-dependent absorption coefficient.10–12 The black dashed curve in Fig. 2d shows the transient temperature of the water layer during the pump macropulse, estimated from eqn (2):
and αwat(°T) temperature-dependent absorption coefficient.10–12 The black dashed curve in Fig. 2d shows the transient temperature of the water layer during the pump macropulse, estimated from eqn (2):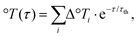 | (2) |
Optoacoustic effects originate from the fact that the optical properties of a medium can change as a result of density variations,62 which can trigger the generation of acoustic waves.70–76 When radiation is strongly absorbed, as in the case of Terahertz spectroscopy on liquid water,59,60 thermoacoustic effects dominate. In first approximation, the absorption triggers thermal expansion that, in turn, can induce a pressure wave with associated mass displacement and density perturbations.59,60,63–67,71,76–83 The timescale of an acoustic phenomenon is determined by the speed of sound84 (v ∼ 1500 m s−1 for liquid water at 20 °C) and the sample geometry. The time it takes for a surface acoustic wave (moving on the surface of the liquid water sample, perpendicular to the optical table) to travel through the probe spot size (∼400 μm) is 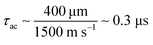 . The amplitude of a propagating acoustic wave is proportional to the coefficient of thermal expansion,67β = β(°T), which is strongly dependent on temperature in liquid water (Fig. 2h). Thus, the increase of the signal at pump–probe overlap during the pump macropulse, and the abrupt drop when the pump is turned off, are both consistent with an acoustic phenomenon (see the red curve in Fig. 2b, and the blue curve in Fig. 2c, between τON and τOFF).
. The amplitude of a propagating acoustic wave is proportional to the coefficient of thermal expansion,67β = β(°T), which is strongly dependent on temperature in liquid water (Fig. 2h). Thus, the increase of the signal at pump–probe overlap during the pump macropulse, and the abrupt drop when the pump is turned off, are both consistent with an acoustic phenomenon (see the red curve in Fig. 2b, and the blue curve in Fig. 2c, between τON and τOFF).
When the pump and probe beams overlap in space and time, their interference can induce a grating.85 This could account for the experimental fact that the pump–probe signal is present only at pulse overlap (t ∼ 0 in Fig. 1–3). The spatial period (Λ) of the interference pattern depends on the laser wavelength (λ), and the angle between the propagation directions of the pump and probe beams (ψ), 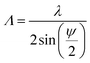 (see, e.g., paragraph 2.2.1 in ref. 85). In our case, considering the experimental parameters, the period of the interference pattern at pump probe pulse overlap is Λ ∼ 180 μm, which can be compared with the probe spot size of ∼400 μm. The intensity modulation of the interference pattern, which is the relative variation between maxima and minima, can be estimated by the ratio between the electric field amplitudes85 of probe and pump as
(see, e.g., paragraph 2.2.1 in ref. 85). In our case, considering the experimental parameters, the period of the interference pattern at pump probe pulse overlap is Λ ∼ 180 μm, which can be compared with the probe spot size of ∼400 μm. The intensity modulation of the interference pattern, which is the relative variation between maxima and minima, can be estimated by the ratio between the electric field amplitudes85 of probe and pump as 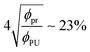 . The transient gratings have different relaxation timescales.78,79,85–88 An acoustic grating67,78–82 is strongly dependent on temperature (Fig. 2h), and decays quickly, on a timescale of τac ∼ 0.3 μs. A thermal grating decays on a much longer timescale,78,79 determined by τth ∼ 300 μs. Considering the short laser pulses used here (FWHM ∼ 3 ps) and the ∼77 ns delay between subsequent micropulses, the contribution by the acoustic grating should be much larger than that of a thermal grating.62 A simplistic cartoon of the acoustic grating generated at the water surface is given in Fig. 2g, which is obtained by taking two separate point sources of spherical waves68 within the laser spot. This qualitative model includes both the interference region at the spatial and temporal overlap of pump and probe (indicated by the black circle, “Pump–probe interference”), as well as the propagation of acoustic waves on the surface, away from the interference region.78
. The transient gratings have different relaxation timescales.78,79,85–88 An acoustic grating67,78–82 is strongly dependent on temperature (Fig. 2h), and decays quickly, on a timescale of τac ∼ 0.3 μs. A thermal grating decays on a much longer timescale,78,79 determined by τth ∼ 300 μs. Considering the short laser pulses used here (FWHM ∼ 3 ps) and the ∼77 ns delay between subsequent micropulses, the contribution by the acoustic grating should be much larger than that of a thermal grating.62 A simplistic cartoon of the acoustic grating generated at the water surface is given in Fig. 2g, which is obtained by taking two separate point sources of spherical waves68 within the laser spot. This qualitative model includes both the interference region at the spatial and temporal overlap of pump and probe (indicated by the black circle, “Pump–probe interference”), as well as the propagation of acoustic waves on the surface, away from the interference region.78
In our previous study we found27 that all the pump–probe signals from liquid water at 12.3 THz are proportional to the pump intensity and are independent from the probe. This is consistent with any process that requires two pump photons and one probe photon, which includes the diffraction of a pump photon from a transient grating. The pump photon diffracted in the probe direction can either enhance or suppress the transmitted intensity, depending on the sign of the coupling term (see, e.g., paragraph 7.4 and eqn (7.4.15) in ref. 61). The amount of scattered light depends on the diffraction efficiency (η), which is proportional to the square of the modulation of the index of refraction (η ∝ Δn2) induced in the sample by the intensity pattern.78 In turn, the change in the index of refraction is proportional to the density variation (Δn ∝ Δρ),59,78 and the acoustic density perturbation scales linearly with the thermal expansion coefficient (Δρ ∝ β(°T)).67,78–82 Thus, the contribution from an acoustic grating to the detected pump–probe signal from liquid water should be proportional to67,78β2(°T). In order to obtain the red curve in Fig. 2e, we take the change in temperature as given by the black curve in Fig. 2e, and add a term bβ2(°T), where b is a fitting parameter. By fixing b = −1.5 × 104, it is possible to qualitatively reproduce the experimentally observed trend and the size of the pump–probe signal from liquid water in the static cell at pump–probe overlap (t ∼ 0). Compare the red curves in Fig. 2b and e, and the blue curves in Fig. 2c and f.
We expect a different result in case of a free-flowing water jet. In this case, the thermalization is restricted by the speed of the jet, rather than by thermal diffusion. When the water has travelled by about one full laser spot size, the temperature within the probed volume is equilibrated at an average temperature, which remains constant as long as the laser pump macropulse is on. The water flow of the jet amounts to ca. 2.9 × 103 mm3 s−1. The syringe tip used as nozzle has an initial radius of 0.4 mm. The tip is squeezed with pliers to the shape of a few micrometre thin slit, and was optimized with a trial-and-error approach to obtain a flat profile. Here, we give a rough over-estimate of the jet speed by assuming a perfectly round nozzle. With this approximation, the time (τjet) it takes for the jet to move one full probe spot size away (400 μm) is smaller than 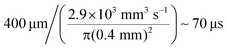 . Thus, we find good agreement of the decay constant of the signal observed at τ > τOFF (see the black curve in Fig. 3b) with the travel time of the jet, τjet ∼ 35 μs. We stress that the same time constant is observed when the pump macropulse is off for both the black and the red curves in Fig. 3b, and at τ ∼ 400 μs at pump–probe overlap (red curve in Fig. 3b). We note that changing the flow rate is expected to change τjet. However, we found that changing the speed strongly affects the shape, dimensions, and the fluctuations of the jet. As the jet is only stable enough at a flow speed close to 2.9 × 103 mm3 s−1, in the current experiments we could not reliably measure how τjet depends on the jet velocity.
. Thus, we find good agreement of the decay constant of the signal observed at τ > τOFF (see the black curve in Fig. 3b) with the travel time of the jet, τjet ∼ 35 μs. We stress that the same time constant is observed when the pump macropulse is off for both the black and the red curves in Fig. 3b, and at τ ∼ 400 μs at pump–probe overlap (red curve in Fig. 3b). We note that changing the flow rate is expected to change τjet. However, we found that changing the speed strongly affects the shape, dimensions, and the fluctuations of the jet. As the jet is only stable enough at a flow speed close to 2.9 × 103 mm3 s−1, in the current experiments we could not reliably measure how τjet depends on the jet velocity.
We can now extend the thermal model developed above (eqn (1) and (2)). The temperature increase triggered by a single pump micropulse in the water jet is
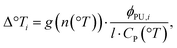 | (3) |
 because there is only an air–water interface. Please note that there is no energy dissipated by contact to a temperature-stabilized diamond surface, so the parameter q is absent in eqn (3). The temperature profile expected for the jet is akin to eqn (2),
because there is only an air–water interface. Please note that there is no energy dissipated by contact to a temperature-stabilized diamond surface, so the parameter q is absent in eqn (3). The temperature profile expected for the jet is akin to eqn (2),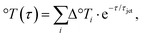 | (4) |
We expect different acoustic effects in a free-flowing jet with respect to water in a static cell. The interference of a pair of pump and probe micropulses interacting with the liquid at spatial and temporal overlap would result in patterned surface acoustic waves as shown in the color map in Fig. 2g. However, the following pulses will “write” a spatially shifted pattern, since water has travelled a distance 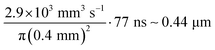 between two subsequent pairs of pump and probe micropulses. When the liquid has moved by one spot size (400 μm, which approximately takes a time τjet), we expect the acoustic grating to be averaged or washed out. This is highlighted by the estimated residue in Fig. 3g, where we summed up
between two subsequent pairs of pump and probe micropulses. When the liquid has moved by one spot size (400 μm, which approximately takes a time τjet), we expect the acoustic grating to be averaged or washed out. This is highlighted by the estimated residue in Fig. 3g, where we summed up 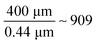 patterns like the single one shown in Fig. 2g, each shifted by the spatial offset of 0.44 μm. The resulting interference fringes at spatial and temporal overlap are shown in Fig. 3g. Please note that the amplitude of the pattern in Fig. 3g amounts to only 3% of the one shown in Fig. 2g. Thus, we expect that the signal from an acoustic grating at pump–probe overlap should only be present at the beginning of the pump macropulse, at τ ∼ τON, when measuring the free-flowing jet. After the water has travelled one spot size, the remaining pump–probe signal cannot be attributed anymore to a diffraction grating, but rather to a nonlinear optical signal as indicated in Fig. 3f.
patterns like the single one shown in Fig. 2g, each shifted by the spatial offset of 0.44 μm. The resulting interference fringes at spatial and temporal overlap are shown in Fig. 3g. Please note that the amplitude of the pattern in Fig. 3g amounts to only 3% of the one shown in Fig. 2g. Thus, we expect that the signal from an acoustic grating at pump–probe overlap should only be present at the beginning of the pump macropulse, at τ ∼ τON, when measuring the free-flowing jet. After the water has travelled one spot size, the remaining pump–probe signal cannot be attributed anymore to a diffraction grating, but rather to a nonlinear optical signal as indicated in Fig. 3f.
By taking into account a combination of acoustic and nonlinear effects, it is possible to account for the trend and the magnitude of the detected signal at pump–probe overlap in the water jet, see Fig. 3. The model, red curve in Fig. 3e, includes the same thermal component calculated previously without fitting parameters (the black curve in Fig. 3e) and includes an acoustic term bβ2(°T)(1 − s(τ)), where b = −1.5 × 104 has the same value used for the water in the static cell (Fig. 2). We introduce the sigmoid function s(τ) to qualitatively account for the fact that the acoustic effects are present only close to τ ∼ τON and absent after the acoustic grating is washed out (Fig. 3g). The sigmoid function is 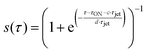 , with c being a fitting parameter describing the middle point of the sigmoid (time at which the value of s(τ) is half of the maximum value), and d fitting parameter for the exponential slope, describing how steep s(τ) switches from maximum (1) to minimum (0). The results of the simulation obtained from the fitting parameters c = 2 and d = 0.5 are shown by the red curve in Fig. 3e and by the blue curve in Fig. 3f. After the acoustic grating vanishes at τ ∼ 400 μs, the pump–probe signal from the water jet becomes positive. We propose that this is the nonlinear optical signal, as shown in Fig. 3e and f. In our model, this signal is described by a transmission change defined by a quantity a·s(τ), where s(τ) is the function described above and a = ΔTV/TV = +7% is the magnitude of the nonlinear optical signal measured experimentally between about τON + 100 μs ∼ 470 μs and τOFF, see Fig. 3c. Overall, we find that a combination of acoustic and nonlinear optical signals is sufficient to account for the magnitude and the temporal evolution of the measured response by the liquid water jet, as can be seen by comparing the red curves in Fig. 3b and e, and the blue curves in Fig. 3c and f.
, with c being a fitting parameter describing the middle point of the sigmoid (time at which the value of s(τ) is half of the maximum value), and d fitting parameter for the exponential slope, describing how steep s(τ) switches from maximum (1) to minimum (0). The results of the simulation obtained from the fitting parameters c = 2 and d = 0.5 are shown by the red curve in Fig. 3e and by the blue curve in Fig. 3f. After the acoustic grating vanishes at τ ∼ 400 μs, the pump–probe signal from the water jet becomes positive. We propose that this is the nonlinear optical signal, as shown in Fig. 3e and f. In our model, this signal is described by a transmission change defined by a quantity a·s(τ), where s(τ) is the function described above and a = ΔTV/TV = +7% is the magnitude of the nonlinear optical signal measured experimentally between about τON + 100 μs ∼ 470 μs and τOFF, see Fig. 3c. Overall, we find that a combination of acoustic and nonlinear optical signals is sufficient to account for the magnitude and the temporal evolution of the measured response by the liquid water jet, as can be seen by comparing the red curves in Fig. 3b and e, and the blue curves in Fig. 3c and f.
MD simulations suggest that optical phonon-like modes at THz frequencies can couple water89 to proteins in solution.23,90,91 Elton and Fernández-Serra89 indicated that optical modes in the librational band of pure bulk water can propagate up to a distance of 2 nm. Conti-Nibali et al.23,90 suggested that optical THz modes of a solvated protein spread to the hydration water, indicating an efficient solute–solvent coupling at these THz frequencies. The coupled protein–water acoustic modes were also investigated in more detail by Heyden et al.91 These modes reveal correlated protein–water vibrations that extend up to 1 nm from the protein surface, which also depend on the specific chemistry of the protein surface. We note that the acoustic mode that has been emphasized in this work, and that is only relevant when the static cell is used, is not in the THz range but at the much lower frequency of 8.3 MHz. In fact, the frequency of the acoustic mode associated to the grating can be estimated by the speed of sound divided by the period of the interference pattern, i.e., 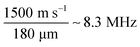 .
.
Previously,27 we performed a full set of polarization-dependent experiments, and we estimated a lower limit for the third-order birefringence of bulk water, χε3 ∼ 1.3 × 10−15 cm2 V−2, which is at least three orders of magnitude larger than the refractive response at VIS and NIR frequencies, see the first two rows of Table 1. This birefringent signal was estimated from27 a transmission change of 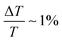 (compare, e.g., the dark and light blue curves in Fig. 2b of ref. 27) for IPu = 900 MW cm−2. Please note that the single pump micropulse intensity used in ref. 27 is 9× times larger than the one used here. Given the fact that the nonlinear signals are proportional to the pump intensity,27 we expect a birefringent signal of ca. 1%/9–0.11% for the experiments reported in the present study, which is below the noise level of ±0.5%. Thus, here we are unable to detect the birefringent component of the nonlinear signal. However, even given the lower pump intensity, the water jet reveals a large nonlinear signal,
(compare, e.g., the dark and light blue curves in Fig. 2b of ref. 27) for IPu = 900 MW cm−2. Please note that the single pump micropulse intensity used in ref. 27 is 9× times larger than the one used here. Given the fact that the nonlinear signals are proportional to the pump intensity,27 we expect a birefringent signal of ca. 1%/9–0.11% for the experiments reported in the present study, which is below the noise level of ±0.5%. Thus, here we are unable to detect the birefringent component of the nonlinear signal. However, even given the lower pump intensity, the water jet reveals a large nonlinear signal, 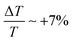 (Fig. 3c).
(Fig. 3c).
| Frequency | Technique | χ 3 [cm2 V−2] | Ref. |
|---|---|---|---|
| Transient refraction along one axis, χn3 | |||
| VIS, NIR | SPM, z-scan, SF, Kerr, THG | χ n 3 ≈ 2.6 × 10−18 | 36–53 |
| Transient birefringence, χε3 | |||
| 12.3 THz | pol-Pp, static | χ ε 3 ≈ 1.3 × 10−15 | 27 |
| Effective total third-order response, χeff3 | |||
| 12.3 THz | pol-Pp, jet | χ eff 3 ≈ 7.2 × 10−13 | This work |
| 1 THz | z-Scan, jet | χ eff 3 ≈ 4.5 × 10−13 | 32 and 33 |
| 1 THz | z-Scan, static | χ eff 3 ≈ 4.4 × 10−13 | 28 |
| 1 THz | Pp, jet | χ eff 3 ≈ 2.3 × 10−13 | 35 |
Different experimental techniques are sensitive to different contributions to the total third-order response of a material. For example, some works36–53 report the third-order response that depends only on the refraction change along one direction (χn3), others the difference between the transient refraction along two perpendicular directions,27 or birefringence, χε3. In general, the third-order nonlinear THz signal of bulk water stems from the transient changes of both refraction as well as absorption.28 In our case, the nonlinear signal is given by the difference between the red and black curves in Fig. 3b, as shown in blue in Fig. 3c. In order to compare it with previous results obtained with different experimental techniques, we introduce an effective total third-order coefficient, χeff3. A pump–probe signal originates from two pump photons with the same wavevector creating a population state.61,92,93 The probe interacts with this population state and a nonlinear signal is generated in the probe direction. When a power detector is used, the probe heterodynes the nonlinear signal, and the intensity-dependent nonlinear transmission is 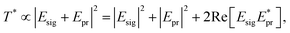 where Epr and Esig are the electric fields of probe and nonlinear signal, respectively. Recalling that the signal is obtained by third-order mixing61,92,93 (
where Epr and Esig are the electric fields of probe and nonlinear signal, respectively. Recalling that the signal is obtained by third-order mixing61,92,93 (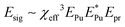 with EPu pump field), that the probe intensity transmitted by the sample at equilibrium is T ∝ |Epr|2, and assuming Esig ≪ Epr, the relative variation of the transmission in a pump–probe experiment is
with EPu pump field), that the probe intensity transmitted by the sample at equilibrium is T ∝ |Epr|2, and assuming Esig ≪ Epr, the relative variation of the transmission in a pump–probe experiment is 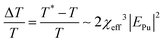 . To the first approximation, if we use the relation between field amplitude and intensity of a monochromatic wave,
. To the first approximation, if we use the relation between field amplitude and intensity of a monochromatic wave, 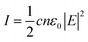 with c speed of light, n index of refraction, and ε0 vacuum permittivity, we obtain
with c speed of light, n index of refraction, and ε0 vacuum permittivity, we obtain
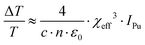 | (5) |
For the water jet we measured 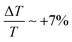 (Fig. 3c), and by using eqn (5) with IPu = 100 MW cm−2 and10n = nwat = 1.55, we estimate χeff3 ∼ 7.2 × 10−13 cm2 V−2 at 12.3 THz. This value is the largest reported to date for liquid water in the THz range and, as outlined in Table 1, is roughly twice as large as the ones reported by Tcypkin et al.32,33 and Ghalgaoui et al.35 at ∼1 THz.
(Fig. 3c), and by using eqn (5) with IPu = 100 MW cm−2 and10n = nwat = 1.55, we estimate χeff3 ∼ 7.2 × 10−13 cm2 V−2 at 12.3 THz. This value is the largest reported to date for liquid water in the THz range and, as outlined in Table 1, is roughly twice as large as the ones reported by Tcypkin et al.32,33 and Ghalgaoui et al.35 at ∼1 THz.
The cascaded intramolecular anharmonicity model proposed by Tcypkin et al.32,33 neglected the librational contribution and displays a weak frequency dependence (see, e.g., Fig. S7 in ref. 3). Thus, this model seems unable to explain the larger third-order response we found in liquid water at 12.3 THz. Let us now consider the field-ionization scenario proposed by Ghalgaoui et al.35 Since the ponderomotive energy is inversely proportional to the frequency of the pump field,35 the effect should be much smaller at 10 THz than at 1 THz. In fact, the ponderomotive energy of an electron driven by an external field with a field amplitude of 0.27 MV cm−1 at 12.3 THz should be more than 1000x smaller than in ref. 35, i.e., we can exclude field-induced water ionization here. Conversely, the transient anisotropy model as introduced previously by us27 predicts a smaller nonlinear response at 1 THz w.r.t. 12.3 THz and is, thus, qualitatively in agreement with all of the experimental observations reported to date.27,28,32,33,35 The transient anisotropy should be larger at 12.3 THz, which is closer to the time scale of the reorientation relaxation as observed experimentally.
Conclusions
Previously, we reported27 a giant transient birefringence in liquid water at 12.3 THz in a liquid cell. Here we report a comparison between the result in a cell and a liquid jet using longer macropulses, which allowed us to measure over longer time scales. While we were able to reproduce our previous observations (Fig. 1), we also investigated the different contributions to the transient change in the THz pump–probe response. Upon comparison of the results obtained on a static water cell (Fig. 2) with a free-flowing jet (Fig. 3) we suggest that the increase of the signal during the macropulse could originate from an acoustic phonon at 8.3 MHz. The anisotropic nonlinear signal observed here in the water jet at 12.3 THz confirms that driving the reorientation of hydrogen-bonded molecules induces a giant response, and it could help rationalize all the available nonlinear experiments performed on water at THz frequencies.27,28,32,33,35 As the rotationally damped motion of HB molecules in the librational band is resonantly driven at 12.3 THz, our results might open the door to the manipulation of solvation dynamics via strong fields, possibly also at interfaces. Considering that the technique outlined here is sensitive to ion hydration,27 we suggest that it might also help to elucidate the dynamical properties of the hydration water of different anions and cations in future investigations.94Author contributions
Conceptualization: F. N., M. H. Data curation: F. N., C. H., J. M. K. Formal analysis: F. N., C. H., J. M. K. Funding acquisition: M. H. Investigation: F. N., C. H., E. A., J. M. K. Methodology: F. N. Project administration: F. N. Resources: M. H., J. M. K. Software: F. N., C. H. Supervision: F. N., M. H. Validation: F. N., C. H., E. A. Visualization: F. N. Writing – original draft: F. N. Writing – review & editing: all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge D. Welzel for experimental support. M. H. acknowledges funding by the ERC Advanced Grant 695437 “THz calorimetry”. This work is part of the Cluster RESOLV funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy–EXC 2033–390677874–RESOLV.Notes and references
- P. Ball, Water—an enduring mystery, Nature, 2008, 452, 291–292 CrossRef CAS PubMed.
- P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. M. Pettersson, Water: A Tale of Two Liquids, Chem. Rev., 2016, 116, 7463–7500 CrossRef CAS PubMed.
- A. Nilsson and L. G. M. Pettersson, The structural origin of anomalous properties of liquid water, Nat. Commun., 2015, 6, 8998 CrossRef CAS PubMed.
- C. A. Angell, Insights into Phases of Liquid Water from Study of Its Unusual Glass-Forming Properties, Science, 2008, 319, 582–587 CrossRef CAS PubMed.
- M. Cho, G. R. Fleming, S. Saito, I. Ohmine and R. M. Stratt, Instantaneous normal mode analysis of liquid water, J. Chem. Phys., 1994, 100, 6672–6683 CrossRef CAS.
- M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Dissecting the THz spectrum of liquid water from first principles via correlations in time and space, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12068–12073 CrossRef CAS PubMed.
- F. Novelli, B. Guchhait and M. Havenith, Towards Intense THz Spectroscopy on Water: Characterization of Optical Rectification by GaP, OH1, and DSTMS at OPA Wavelengths, Materials, 2020, 13, 1311 CrossRef CAS.
- D. J. Cook, J. X. Chen, E. A. Morlino and R. M. Hochstrasser, Terahertz-field-induced second-harmonic generation measurements of liquid dynamics, Chem. Phys. Lett., 1999, 309, 221–228 CrossRef CAS.
- H. Elgabarty and T. D. Kühne, Tumbling with a limp: local asymmetry in water's hydrogen bond network and its consequences, Phys. Chem. Chem. Phys., 2020, 22, 10397–10411 RSC.
- H. R. Zelsmann, Temperature dependence of the optical constants for liquid H2O and D2O in the far IR region, J. Mol. Struct., 1995, 350, 95–114 CrossRef CAS.
- W. J. Ellison, Permittivity of Pure Water, at Standard Atmospheric Pressure, over the Frequency Range 0–25THz and the Temperature Range 0–100 °C, J. Phys. Chem. Ref. Data, 2007, 36, 1–18 CrossRef CAS.
- I. Bergonzi, L. Mercury, J.-B. Brubach and P. Roy, Gibbs free energy of liquid water derived from infrared measurements, Phys. Chem. Chem. Phys., 2014, 16, 24830–24840 RSC.
- J. E. Bertie and Z. Lan, Infrared Intensities of Liquids XX: The Intensity of the OH Stretching Band of Liquid Water Revisited, and the Best Current Values of the Optical Constants of H2O(l) at 25 °C between 15
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 1 cm−1, Appl. Spectrosc., 1996, 50, 1047–1057 CrossRef CAS.
000 and 1 cm−1, Appl. Spectrosc., 1996, 50, 1047–1057 CrossRef CAS. - J.-J. Max and C. Chapados, Isotope effects in liquid water by infrared spectroscopy. III. H2O and D2O spectra from 6000 to 0 cm−1, J. Chem. Phys., 2009, 131, 184505 CrossRef PubMed.
- P. Lunkenheimer, S. Emmert, R. Gulich, M. Köhler, M. Wolf, M. Schwab and A. Loidl, Electromagnetic-radiation absorption by water, Phys. Rev. E, 2017, 96, 062607 CrossRef CAS PubMed.
- D. R. Martin and D. V. Matyushov, Terahertz absorption of lysozyme in solution, J. Chem. Phys., 2017, 147, 084502 CrossRef PubMed.
- S. Ebbinghaus, S. J. Kim, M. Heyden, X. Yu, U. Heugen, M. Gruebele, D. M. Leitner and M. Havenith, An extended dynamical hydration shell around proteins, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20749–20752 CrossRef CAS.
- Y. He, P. I. Ku, J. R. Knab, J. Y. Chen and A. G. Markelz, Protein dynamical transition does not require protein structure, Phys. Rev. Lett., 2008, 101, 2–5 Search PubMed.
- G. Acbas, K. A. Niessen, E. H. Snell and A. G. Markelz, Optical measurements of long-range protein vibrations, Nat. Commun., 2014, 5, 3076 CrossRef PubMed.
- K. A. Niessen, M. Xu, D. K. George, M. C. Chen, A. R. Ferré-D’Amaré, E. H. Snell, V. Cody, J. Pace, M. Schmidt and A. G. Markelz, Protein and RNA dynamical fingerprinting, Nat. Commun., 2019, 10, 1–10 CrossRef CAS.
- J. W. Bye, S. Meliga, D. Ferachou, G. Cinque, J. A. Zeitler and R. J. Falconer, Analysis of the Hydration Water around Bovine Serum Albumin Using Terahertz Coherent Synchrotron Radiation, J. Phys. Chem. A, 2014, 118, 83–88 CrossRef CAS.
- J. Monroe, M. Barry, A. DeStefano, P. A. Gokturk, S. Jiao, D. Robinson-Brown, T. Webber, E. J. Crumlin, S. Han, M. S. Shell, P. Aydogan Gokturk, S. Jiao, D. Robinson-Brown, T. Webber, E. J. Crumlin, S. Han and M. S. Shell, Water Structure and Properties at Hydrophilic and Hydrophobic Surfaces, Annu. Rev. Chem. Biomol. Eng., 2020, 11, 1–35 CrossRef.
- V. Conti Nibali and M. Havenith, New Insights into the Role of Water in Biological Function: Studying Solvated Biomolecules Using Terahertz Absorption Spectroscopy in Conjunction with Molecular Dynamics Simulations, J. Am. Chem. Soc., 2014, 136, 12800–12807 CrossRef CAS PubMed.
- K. J. Tielrooij, N. Garcia-Araez, M. Bonn and H. J. Bakker, Cooperativity in Ion Hydration, Science, 2010, 328, 1006–1009 CrossRef CAS PubMed.
- P. Zalden, L. Song, X. Wu, H. Huang, F. Ahr, O. D. Mücke, J. Reichert, M. Thorwart, P. K. Mishra, R. Welsch, R. Santra, F. X. Kärtner and C. Bressler, Molecular polarizability anisotropy of liquid water revealed by terahertz-induced transient orientation, Nat. Commun., 2018, 9, 2142 CrossRef PubMed.
- H. Elgabarty, T. Kampfrath, D. J. Bonthuis, V. Balos, N. K. Kaliannan, P. Loche, R. R. Netz, M. Wolf, T. D. Kühne and M. Sajadi, Energy transfer within the hydrogen bonding network of water following resonant terahertz excitation, Sci. Adv., 2020, 6, eaay7074 CrossRef CAS PubMed.
- F. Novelli, L. Ruiz Pestana, K. C. Bennett, F. Sebastiani, E. M. Adams, N. Stavrias, T. Ockelmann, A. Colchero, C. Hoberg, G. Schwaab, T. Head-Gordon and M. Havenith, Strong Anisotropy in Liquid Water upon Librational Excitation Using Terahertz Laser Fields, J. Phys. Chem. B, 2020, 124, 4989–5001 CrossRef CAS.
- F. Novelli, C. Y. Ma, N. Adhlakha, E. M. Adams, T. Ockelmann, D. Das Mahanta, P. Di Pietro, A. Perucchi and M. Havenith, Nonlinear terahertz transmission by liquid water at 1 THz, Appl. Sci., 2020, 10, 20–23 Search PubMed.
- H. Zhao, Y. Tan, R. Zhang, Y. Zhao, C. Zhang and L. Zhang, Anion–water hydrogen bond vibration revealed by the terahertz Kerr effect, Opt. Lett., 2021, 46, 230 CrossRef PubMed.
- H. Zhao, Y. Tan, L. Zhang, R. Zhang, M. Shalaby, C. Zhang, Y. Zhao and X.-C. Zhang, Ultrafast hydrogen bond dynamics of liquid water revealed by terahertz-induced transient birefringence, Light: Sci. Appl., 2020, 9, 136 CrossRef CAS.
- M. Zhukova, M. Melnik, I. Vorontsova, A. Tcypkin and S. Kozlov, Estimations of low-inertia cubic nonlinearity featured by electro-optical crystals in the thz range, Photonics, 2020, 7, 1–7 CrossRef.
- A. Tcypkin, M. Zhukova, M. Melnik, I. Vorontsova, M. Kulya, S. Putilin, S. Kozlov, S. Choudhary and R. W. Boyd, Giant Third-Order Nonlinear Response of Liquids at Terahertz Frequencies, Phys. Rev. Appl., 2021, 15, 054009 CrossRef CAS.
- A. N. Tcypkin, M. V. Melnik, M. O. Zhukova, I. O. Vorontsova, S. E. Putilin, S. A. Kozlov and X.-C. Zhang, High Kerr nonlinearity of water in THz spectral range, Opt. Express, 2019, 27, 10419 CrossRef CAS PubMed.
- S. Ashihara, N. Huse, A. Espagne, E. T. J. J. Nibbering and T. Elsaesser, Ultrafast Structural Dynamics of Water Induced by Dissipation of Vibrational Energy, J. Phys. Chem. A, 2007, 111, 743–746 CrossRef CAS PubMed.
- A. Ghalgaoui, L.-M. Koll, B. Schütte, B. P. Fingerhut, K. Reimann, M. Woerner and T. Elsaesser, Field-Induced Tunneling Ionization and Terahertz-Driven Electron Dynamics in Liquid Water, J. Phys. Chem. Lett., 2020, 11, 7717–7722 CrossRef CAS PubMed.
- Z. W. Wilkes, S. Varma, Y. H. Chen, H. M. Milchberg, T. G. Jones and A. Ting, Direct measurements of the nonlinear index of refraction of water at 815 and 407 nm using single-shot supercontinuum spectral interferometry, Appl. Phys. Lett., 2009, 94, 1–4 CrossRef.
- B. A. Rockwell, W. P. Roach, M. E. Rogers and M. W. Mayo, C. a Toth, C. P. Cain and G. D. Noojin, Nonlinear refraction in vitreous humor, Opt. Lett., 1993, 18, 1792–1794 CrossRef CAS PubMed.
- N. J. Harrison and B. R. Jennings, Laser-induced birefringence measurement for pure liquids, Meas. Sci. Technol., 1992, 3, 120–125 CrossRef CAS.
- P. P. Ho and R. R. Alfano, Optical Kerr effect in liquids, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 2170–2187 CrossRef CAS.
- F. Kajzar and J. Messier, Third-harmonic generation in liquids, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 2352–2363 CrossRef CAS.
- D. Débarre and E. Beaurepaire, Quantitative characterization of biological liquids for third-harmonic generation microscopy, Biophys. J., 2007, 92, 603–612 CrossRef PubMed.
- V. Shcheslavskiy, G. Petrov and V. V. Yakovlev, Nonlinear optical susceptibility measurements of solutions using third-harmonic generation on the interface, Appl. Phys. Lett., 2003, 82, 3982–3984 CrossRef CAS.
- R. Barille, L. Canioni, L. Sarger and G. Rivoire, Nonlinearity measurements of thin films by third-harmonic-generation microscopy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 067602 CrossRef CAS.
- B. M. Novac, F. A. Banakhr, I. R. Smith, L. Pécastaing, R. Ruscassié, A. S. De Ferron and P. Pignolet, Determination of the Kerr Constant of Water at 658 nm for Pulsed Intense Electric Fields, IEEE Trans. Plasma Sci., 2012, 40, 2480–2490 CAS.
- R. K. Khanna, E. Dempsey and G. Parry, Jones, Kerr constant of water from 280 to 350 K at 632.8 nm, Chem. Phys. Lett., 1978, 53, 542–544 CrossRef CAS.
- W. L. Smith, P. Liu and N. Bloembergen, Superbroadening in H2O and D2O by self focused picosecond pulses from a YAIG: ND laser, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 15, 2396–2403 CrossRef CAS.
- Z. Blaszczak and P. Gauden, Method for the determination of the value of the optical Kerr constant in weakly anisotropic liquids, Rev. Sci. Instrum., 1987, 58, 1949–1951 CrossRef CAS.
- N. J. Harrison and B. R. Jennings, Laser-Induced Kerr Constants for Pure Liquids, J. Phys. Chem. Ref. Data, 1992, 21, 157–163 CrossRef CAS.
- T. Y. F. Tsang, Optical third-harmonic generation at interfaces, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 4116–4125 CrossRef CAS PubMed.
- O. Clay, C. B. Schaffer, J. A. Squier and D. Kleinfeld, in SPIE Commercial and Biomedical Applications of Ultrafast Lasers VI, ed. J. Neev, S. Nolte, A. Heisterkamp and C. B. Schaffer, 2006, vol. 6008, p. 610809 Search PubMed.
- A. Brodeur and S. L. Chin, Band-Gap Dependence of the Ultrafast White-Light Continuum, Phys. Rev. Lett., 1998, 80, 4406–4409 CrossRef CAS.
- E. T. J. Nibbering, M. A. Franco, B. S. Prade, G. Grillon, C. Le Blanc and A. Mysyrowicz, Measurement of the nonlinear refractive index of transparent materials by spectral analysis after nonlinear propagation, Opt. Commun., 1995, 119, 479–484 CrossRef CAS.
- W. Liu, O. Kosareva, I. S. Golubtsov, A. Iwasaki, A. Becker, V. P. Kandidov and S. L. Chin, Femtosecond laser pulse filamentation versus optical breakdown in H2O, Appl. Phys. B: Lasers Opt., 2003, 76, 215–229 CrossRef CAS.
- B. Liu, H. Bromberger, A. Cartella, T. Gebert, M. Först and A. Cavalleri, Generation of narrowband, high-intensity, carrier-envelope phase-stable pulses tunable between 4 and 18 THz, Opt. Lett., 2017, 42, 129 CrossRef CAS PubMed.
- P. Keblinski, D. G. Cahill, A. Bodapati, C. R. Sullivan and T. A. Taton, Limits of localized heating by electromagnetically excited nanoparticles, J. Appl. Phys., 2006, 100, 1–6 CrossRef.
- H. H. Richardson, M. T. Carlson, P. J. Tandler, P. Hernandez and A. O. Govorov, Experimental and theoretical studies of light-to-heat conversion and collective heating effects in metal nanoparticle solutions, Nano Lett., 2009, 9, 1139–1146 CrossRef CAS PubMed.
- Z. Qin and J. C. Bischof, Thermophysical and biological responses of gold nanoparticle laser heating, Chem. Soc. Rev., 2012, 41, 1191–1217 RSC.
- T. Q. Luong, Y. Xu, E. Bründermann, D. M. Leitner and M. Havenith, Hydrophobic collapse induces changes in the collective protein and hydration low frequency modes, Chem. Phys. Lett., 2016, 651, 1–7 CrossRef CAS.
- M. Tsubouchi, H. Hoshina, M. Nagai and G. Isoyama, Plane photoacoustic wave generation in liquid water using irradiation of terahertz pulses, Sci. Rep., 2020, 10, 18537 CrossRef CAS PubMed.
- S. Yamazaki, M. Harata, Y. Ueno, M. Tsubouchi, K. Konagaya, Y. Ogawa, G. Isoyama, C. Otani and H. Hoshina, Propagation of THz irradiation energy through aqueous layers: Demolition of actin filaments in living cells, Sci. Rep., 2020, 10, 9008 CrossRef CAS PubMed.
- R. W. Boyd, Nonlinear Optics, Academic Press, 3rd edn, 2007 Search PubMed.
- D. I. Kovsh, D. J. Hagan and E. W. Van, Stryland, Numerical modeling of thermal refraction in liquids in the transient regime, Opt. Express, 1999, 4, 315 CrossRef CAS.
- A. Vogel and V. Venugopalan, Mechanisms of pulsed laser ablation of biological tissues, Chem. Rev., 2003, 103, 577–644 CrossRef CAS PubMed.
- C. Tian, Z. Xie, M. L. Fabiilli, S. Liu, C. Wang, Q. Cheng and X. Wang, Dual-pulse nonlinear photoacoustic technique: a practical investigation, Biomed. Opt. Express, 2015, 6, 2923 CrossRef PubMed.
- A. D. Kraus and A. Bejan, Heat Transfer Handbook, John Wiley & Sons, Inc., Hoboken, New Jersey, 2003 Search PubMed.
- G. Paltauf and H. Schmidt-Kloiber, Microcavity dynamics during laser-induced spallation of liquids and gels, Appl. Phys. A: Mater. Sci. Process., 1996, 62, 303–311 CrossRef.
- R. J. D. Miller, R. Casalegno, K. A. Nelson and M. D. Fayer, Laser-induced ultrasonics: A dynamic holographic approach to the measurement of weak absorptions, optoelastic constants and acoustic attenuation, Chem. Phys., 1982, 72, 371–379 CrossRef CAS.
- E. Hecht, Optics, Pearson, 5th edn, 2017 Search PubMed.
- Appendix B Thermophysical Properties of Water, in Drying Phenomena, John Wiley & Sons, Ltd, 2015, pp. 457–459 DOI:10.1002/9781118534892.app2.
- F. Sedlmeier, S. Shadkhoo, R. Bruinsma and R. R. Netz, Charge/mass dynamic structure factors of water and applications to dielectric friction and electroacoustic conversion, J. Chem. Phys., 2014, 140, 054512 CrossRef PubMed.
- V. E. Gusev and A. A. Karabutov, Laser Optoacoustics, American Institute of Physics, New York, 1991 Search PubMed.
- S. Å. Ellingsen and I. Brevik, Electrostrictive fluid pressure from a laser beam, Phys. Fluids, 2011, 23, 096101 CrossRef.
- I. Brevik, Experiments in phenomenological electrodynamics and the electromagnetic energy-momentum tensor, Phys. Rep., 1979, 52, 133–201 CrossRef.
- I. Brevik, Radiation forces and the Abraham-Minkowski problem, Mod. Phys. Lett. A, 2018, 33, 1–15 CrossRef.
- A. B. Gojani, R. Bejtullahu and S. Obayashi, On two optomechanical effects of laser-induced electrostriction in dielectric liquids, Jpn. J. Appl. Phys., 2014, 53, 092703 CrossRef.
- J. Prakash, M. M. Seyedebrahimi, A. Ghazaryan, J. Malekzadeh-Najafabadi, V. Gujrati and V. Ntziachristos, Short-wavelength optoacoustic spectroscopy based on water muting, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 4007–4014 CrossRef CAS PubMed.
- A. Vogel, N. Linz, S. Freidank and G. Paltauf, Femtosecond-laser-induced nanocavitation in water: Implications for optical breakdown threshold and cell surgery, Phys. Rev. Lett., 2008, 100, 1–4 Search PubMed.
- H. Eichler and H. Stahl, Time and frequency behavior of sound waves thermally induced by modulated laser pulses, J. Appl. Phys., 1973, 44, 3429–3435 CrossRef.
- K. A. Nelson, R. J. D. D. Miller, D. R. Lutz and M. D. Fayer, Optical generation of tunable ultrasonic waves, J. Appl. Phys., 1982, 53, 1144–1149 CrossRef CAS.
- Q. Shen, A. Harata and T. Sawada, Theory of Transient Reflecting Grating in Fluid/Metallic Thin Film/Substrate Systems for Thin Film Characterization and Electrochemical Investigation, Jpn. J. Appl. Phys., 1996, 35, 2339–2349 CrossRef CAS.
- K. A. Nelson and M. D. Fayer, Laser induced phonons: A probe of intermolecular interactions in molecular solids, J. Chem. Phys., 1980, 72, 5202–5218 CrossRef CAS.
- K. A. Nelson, R. Casalegno, R. J. D. Miller and M. D. Fayer, Laser-induced excited state and ultrasonic wave gratings: Amplitude and phase grating contributions to diffraction, J. Chem. Phys., 1982, 77, 1144–1152 CrossRef CAS.
- D. Kim, M. Ye and C. P. Grigoropoulos, Pulsed laser-induced ablation of absorbing liquids and acoustic-transient generation, Appl. Phys. A: Mater. Sci. Process., 1998, 67, 169–181 CrossRef CAS.
- S. C. Santucci, D. Fioretto, L. Comez, A. Gessini and C. Masciovecchio, Is there any fast sound in water?, Phys. Rev. Lett., 2006, 97, 1–4 CrossRef PubMed.
- H. J. Eichler, P. Günter and D. W. Pohl, Laser-Induced Dynamic Gratings, Springer-Verlag, Berlin Heidelberg GmbH, 1986 Search PubMed.
- N. Gedik, J. Orenstein, R. Liang, D. A. Bonn and W. N. Hardy, Diffusion of Nonequilibrium Quasi-Particles in a Cuprate Superconductor, Science, 2003, 300, 1410–1412 CrossRef CAS PubMed.
- N. Gedik, J. Orenstein, R. Liang, D. A. Bonn and W. N. Hardy, Transient Gratings Formed by Nonequilibrium Quasiparticles in YBa2Cu3O6.5, J. Supercond., 2004, 17, 117–120 CrossRef CAS.
- C. A. Dennett and M. P. Short, Thermal diffusivity determination using heterodyne phase insensitive transient grating spectroscopy, J. Appl. Phys., 2018, 123, 215109 CrossRef.
- D. C. Elton and M. Fernández-Serra, The hydrogen-bond network of water supports propagating optical phonon-like modes, Nat. Commun., 2016, 7, 10193 CrossRef CAS PubMed.
- V. Conti Nibali, G. D’Angelo, A. Paciaroni, D. J. Tobias and M. Tarek, On the Coupling between the Collective Dynamics of Proteins and Their Hydration Water, J. Phys. Chem. Lett., 2014, 5, 1181–1186 CrossRef CAS PubMed.
- M. Heyden and D. J. Tobias, Spatial Dependence of Protein-Water Collective Hydrogen-Bond Dynamics, Phys. Rev. Lett., 2013, 111, 218101 CrossRef PubMed.
- P. Hamm, Principles of Nonlinear Optical Spectroscopy: A Practical Approach or: Mukamel for Dummies, 2005.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, New York, 1995 Search PubMed.
- G. Schwaab, F. Sebastiani, M. Havenith, M. Havenith-Newen, G. Schwaab and F. Sebastiani, Ion Hydration and Ion Pairing as Probed by THz Spectroscopy, Angew. Chem., Int. Ed., 2019, 58, 3000–3013 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |
