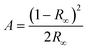Open Access Article
Open Access ArticleExploring the influence of polymorphism and chromophore co-ligands on linkage isomer photoswitching in [Pd(bpy4dca)(NO2)2]†‡
Ben A.
Coulson
and
Lauren E.
Hatcher
 *
*
School of Chemistry, Cardiff University, Main Building, Park Pl, Cardiff CF10 3AT, UK. E-mail: HatcherL1@cardiff.ac.uk
First published on 19th April 2022
Abstract
The polymorphic Pd(II)–nitrite complex [Pd(bpy4dca)(NO2)2] (1) (bpy4dca = 2,2′-bipyridine-4,4′-dicarboxylic acid methyl ester) is shown to undergo photoinduced nitro → nitrito linkage isomer switching in two crystal forms, to varying excited state population levels. Detailed photocrystallographic kinetic studies, structural analyses of the ground and photoexcited states and density functional theory calculations all combine to explain the unusually high maximum excited state population of 80% in 1, where other linkage isomer complexes containing strong chromophore co-ligands have traditionally been challenging to excite. Comparison of the photo-response in crystals for forms I and II reveals that, while the local crystal packing environment has a role in controlling the maximum photostationary population that can be achieved, the rate of isomerisation is comparable across different nitrite ligand environments. Our results reinforce the hypothesis that a complex combination of steric, electronic and kinetic factors govern the progress of linkage isomer switching in the solid-state and highlight the need for better understanding of the structural dynamics involved in isomer switching at the molecular level.
Introduction
Photoswitches are materials containing some fragment that can undergo a structural change in response to light irradiation. Typically, they can exist in one of two (meta)stable, structurally-distinct states, A and B, that are in equilibrium such that, while A → B switching occurs photochemically, B → A back-conversion is thermally-activated. A wide variety of organic,1–3 inorganic,4–6 and organometallic7–10 photoswitchable molecules are known and are well-studied for applications including optoelectronics, photocatalysis, data storage and solar energy.11–16For many real-world applications, it is convenient to have materials that can switch in the solid state. To fully-analyse structure changes in solid media, it is also desirable to study them by in situ single-crystal X-ray diffraction (SCXRD) as this provides highly-accurate, 3D structure information at stages of the photoreaction. For these “photocrystallography” studies, we additionally require that switching occurs in a single-crystal-to-single-crystal manner. This can be challenging, particularly where switching requires a large structural rearrangement. Steric hinderance due to the close packing of molecules in the crystalline state often results in incomplete photoactivation and may even preclude switching altogether, resulting in a complete loss of functionality. Where molecules cannot be switched in the “neat” single-crystal, approaches to dilute the photoactive species in a solid matrix have been explored, e.g. incorporation into porous solids such as silica-based materials,17 metal organic frameworks,18–20 or other supramolecular solids.21–24 While many such approaches are successful in providing the necessary space for solid state switching to proceed, the introduction of a complex framework structure can make analysis challenging. This is particularly true for photocrystallographic studies, as framework materials often produce only weakly diffracting crystals. The low resolution diffraction data make it difficult to obtain atomic-scale 3D structure solutions, which are critical to understand the target molecular switching process in detail.
An alternative approach is to rationally design molecular photoswitches whose crystal structure can accommodate the required rearrangements. This route is based on the “reaction cavity” concept, originally proposed by Cohen25 and later championed by Ohashi et al.26,27 Here, we define a reaction cavity as the region surrounding the photoactive part of the system, such that all necessary atomic rearrangements will occur within the cavity volume. It is then possible to design the surrounding crystalline environment in a way that maximises the reaction cavity space, for example by choosing ancillary fragments with high steric demands (e.g. bulky counterions, co-ligands or co-formers). These bulky, photoinert fragments can then dominate the crystal packing and will remain unchanged on illumination, allowing photoswitching to proceed to high completeness within the reaction cavity volume.
A group of photoswitches that are well-studied in reference to these design principles are solid-state linkage isomers. These switchable organometallics contain ambidentate ligands whose coordination geometry can be switched by exposing the crystal to external stimuli such as light or heat.28 Photoinduced linkage isomers exist as long-lived metastable states in the crystal, with excited state (ES) lifetimes that are temperature dependent.29 A variety of linkage isomers have been studied, including nitrosyl, sulfur dioxide, dinitrogen and nitrite complexes.30–36 While the structure changes involved in photoswitching are relatively modest, involving movement of only a few atoms, early studies were nevertheless hampered by relatively low ES populations in the single-crystal. This changed following a seminal study by Raithby, Warren et al. in 2009, in which complete, 100% photoswitching was achieved in single-crystals of the nickel–nitrite complex [Ni(dppe)(NO2)Cl] (dppe = 1,2-bis(diphenylphosphino)ethane).35 This study led to a dedicated approach by us,37–39 and others,40,41 in designing linkage isomer crystals by considering the steric demands of ancillary groups. This has been particularly successful for group 10 metal-nitrite systems, with 6 materials reported to achieve 100%, reversible nitro → nitrito photoswitching in the single-crystal.35,37–39,42
It is notable that all of the nitrite complexes that undergo high ES photoconversion contain ancillary fragments and/or co-ligands that are not, in themselves, strong chromophores. In particular, the most successful complexes contain co-ligands that have aliphatic backbones, e.g. 1,2-bis(phosphino)ethane or ethylenediamine derivatives. Anecdotal evidence from our research over the last 10 years indicates that compounds having co-ligands with extended pi-systems (bipyridine, biquinoline, phenanthroline etc.) led to crystals with lower,43 or even no photoswitching capability under the typical conditions used by us to study linkage isomers of this type (e.g. T = 100–150 K, λ = 390–450 nm). This is unfortunate, given the wide range of molecular design space that is excluded by this limitation.
Despite the obvious influence of steric factors on solid state photoswitching, the above observations reinforce the fact that the electronic structure of the molecular photoswitch must also impact the achievable ES population level in the crystal.44 Prior work has shown it can be difficult to deconvolute the impact of steric and electronic effects on the solid state photoreaction; ideally to study these influences separately we require crystal systems that contain identical photoswitchable molecules in differing crystal environments. This has been achieved in a handful of molecular crystal systems where Z′ > 1, which have more than one crystallographically independent photoswitch in the asymmetric unit.45,46 However, in these crystals it is difficult to be certain that photoswitching in one molecule does not adversely influence the environment at the second, i.e. via the creation of additional steric strain on molecule #2 as a result of switching in molecule #1. Another option would be to study photoswitching in two different polymorphs of the same complex. Theoretically, as both crystals contain chemically identical species, the effect of the different crystal packing environments on switching can be more systematically studied. However, the availability of suitable polymorphic systems for systematic study is, unsurprisingly, low.
Thus, to better understand all of the above factors, we initiated a systematic investigation of linkage isomer systems containing planar aromatic co-ligands, paying particular attention for the propensity for polymorphism. As part of this programme, we here-in report the design, synthesis and photocrystallographic study of two different polymorphs of the simple aromatic linkage isomer complex 1: [Pd(bpy4dca)(NO2)2] (bpy4dca = 2,2′-bipyridine-4,4′-dicarboxylic acid methyl ester), and attempt to rationalise its photoswitching behaviour in terms of steric, electronic and kinetic control factors.
Experimental
Synthetic procedures
All manipulations were carried out in air. Palladium(II) acetate, bpy4dca were purchased from Merck Life Science. Potassium nitrite was purchased from Acros Organics. All reagents were used as received without the need for further purification.Potassium tetranitropalladate was prepared by the reaction of palladium(II) acetate and potassium nitrite, as previously described.38 bpy4dca was prepared by Fischer esterification following a literature procedure.47 The crystal structure of bpy4dca is not previously reported in the CSD, and was obtained from a single-crystal grown by slow evaporation of the powder product from chloroform (see ESI‡ §1 for further information).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of acetonitrile to deionised water (15 mL). After 3 h the resulting yellow solution was allowed to very slowly cool to room temperature. As the product complex is only sparingly soluble, thin, needle-like crystals of 1 formed as the reaction mixture cooled. Needle crystals for SCXRD study were collected after the mixture was allowed to stand at room temperature overnight.
1 mixture of acetonitrile to deionised water (15 mL). After 3 h the resulting yellow solution was allowed to very slowly cool to room temperature. As the product complex is only sparingly soluble, thin, needle-like crystals of 1 formed as the reaction mixture cooled. Needle crystals for SCXRD study were collected after the mixture was allowed to stand at room temperature overnight.
NMR (1H, ppm). 8.83 (2H, d, 1.1 Hz), 8.50 (2H, dd, 0.7 Hz, 5.8 Hz), 8.10 (2H, dd, 1.8 Hz, 5.8 Hz), 4.00 (6H, s).
FT-IR (ATR, cm−1). 3061 (w), 2960 (w), 1716 (s), 1616 (w), 1560 (w), 1402 (s), 1348 (s), 1319 (br), 1257 (vs), 1066 (br), 1028 (w), 980 (w), 815 (w), 762 (s), 710 (s).
Powder X-ray diffraction
Variable temperature powder X-ray diffraction (PXRD) data were collected on a Rigaku Gemini A Ultra diffractometer using an Atlas CCD detector and an Enhance Ultra CuKα X-ray source (λ = 1.54056 Å). The temperature was controlled with an Oxford Cryosystems Cryojet XL liquid nitrogen flow device. A lightly ground powder sample was loaded onto a Mitegen microloop and data were collected via the Powder Pattern tool in CrysAlisPRO.48 2D diffraction data were recorded between 2θ = 7° and 50°, with fast rotation of the sample around the φ-axis and the Atlas detector in 1 × 1 binning mode.Single-crystal X-ray crystallography
Standard single-crystal X-ray diffraction (SCXRD) experiments were performed on the same dual-source Rigaku Gemini A Ultra system described above, now using MoKα radiation (λ = 0.71073 Å). Data collection, indexing and integration procedures were performed with CrysAlisPRO.48 Structures were solved by dual-space methods using SHELXT,49 and refined by full-matrix least squares on F2 using SHELXL.50Photocrystallography
In situ irradiation of the crystal was achieved using modified version of a bespoke LED array,51 placing 4 LEDs (Kingbright L-7113QBC-D blue LEDs, dominant λ = 465 nm, 16° viewing angle) at a distance of c.a. 1 cm away from the crystal in a uniform arc. The design of the LED set-up allows for in situ illumination of the crystal without impeding the SCXRD data collection. The LED array was controlled remotely using a Raspberry Pi Zero W computer. An electrical circuit diagram and photograph of the illumination set-up is provided in the ESI,‡ §2. SCXRD data collection and processing were completed as described above. To identify any ES isomer, the photoexcited X-ray data were first refined against the ground state (GS) atomic coordinates by full-matrix least squares on F2 with SHELXL using a LIST 3 instruction. A Fourier electron density difference map (often called a “photodifference map”) was then produced and used to identify new residual features corresponding to the ES isomer. Any significant difference peaks around NO2 were then used as the basis for a standard disorder refinement in SHELXL using PART instructions, allowing the GS-to-ES isomer ratio to be refined freely from the ES diffraction data in the final model.Diffuse reflectance measurements
Solid-state diffuse reflectance spectra were collected using an OceanOptics Flame miniature spectrometer and a DH-mini UV-vis-NIR light source. Spectra were collected on evenly-ground powders prepared from pure single-crystals, using the Ocean View control software (version 1.6.5) and data were post-processed using the adjacent-average smoothing method (5 pts). Experimental diffuse reflectance data were converted to absorption profiles using the Kubelka–Munk function:where A = calculated absorbance and R = diffuse reflectance.52
Density functional theory (DFT) calculations
All DFT calculations were performed with the B3LYP53,54 hybrid density functional using Gaussian09 (Revision C.01).55 In the gas phase, geometry optimisations were performed using the quasi-relativistic pseudopotential and associated basis set (SDD) for palladium and a 6-311+G(d) basis set for all other atoms. Frequency calculations to confirm the nature of the stationary points, molecular orbitals, electronic transitions (TD-DFT) and single point energies (“tight” convergence criteria) were all calculated at the optimised geometries using the same basis set combination. Molecular orbitals were visualised using the program Avogadro,56 while simulated UV/vis spectra were plotted following a standard procedure.57Results and discussion
Crystallisation of 1 and polymorphic transitions
Complex 1 initially crystallises as long, thin yellow needles when the reaction mixture is cooled and then left to stand at ambient temperature overnight. These needle-like crystals were initially used to confirm the structure of 1 by SCXRD at 150 K. Although weakly-diffracting and inherently twinned, the needles were sufficient to confirm the expected atomic connectivity of 1.Upon ageing in their supernatant acetonitrile/water mixture at ambient temperature, the needle crystals were observed to undergo a transformation. After 2–3 days, the needles break down into a microcrystalline powder and, on ageing in solution for a further 2–4 weeks, large block-like yellow crystals had formed (Fig. S5, ESI‡). Structure determination of this block morphology by SCXRD confirmed that the chemical structure of 1 remains unchanged, but the crystal structure has transformed to a second polymorphic form.
Aging a dry sample of the needle crystals for the same time period showed no change in the crystal habit, indicating that 1 undergoes a solvent-mediated polymorphic transformation. Attempts to reproduce this solvent-mediated phase transition through repeat crystallisation experiments gave mixed results. While all batches initially formed the expected long needles, herein assigned as metastable polymorph I, which break down into the microcrystalline powder over a few days in solution, growth of the large, block-like crystals of polymorph II was not consistent. In some vials, thicker needle crystals were observed instead of blocks, which were also confirmed as polymorph II by SCXRD. These observations indicate that the formation and crystal growth of polymorph II is very sensitive to the crystallisation conditions, with the observed variation in crystal size and habit possibly attributable to subtle changes in the concentration of 1 in each crystallisation batch.
PXRD experiments were run to further investigate the phase transition series. A dry sample of 1, isolated immediately after crystallisation, was analysed at 150 K. Comparison of the experimental PXRD pattern to simulated patterns for forms I and II (Fig. S6, ESI‡) indicates that the precipitated sample contains a mixture of form I and II crystals, even when isolated at this early stage. This shows that there is already some form II present at, or soon after, precipitation of 1 from the reaction mixture, which can then template the complete form I → form II transformation in solution over time. Finally, PXRD of the microcrystalline powders obtained on needle breakdown after 2–3 days in solution confirmed these samples to contain polymorph II only (Fig. S7, ESI‡). This confirms that the I → II phase transition occurs at this stage, regardless of whether larger form II blocks are later obtained.
Ground-state (GS) crystal structures
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , with two molecules of 1 in the asymmetric unit (Z′ = 2). In both molecules the Pd(II) centre adopts a strained square planar geometry, due to the bite angle of the chelating bpy4dca ligand (molecule a, angle N(3)–Pd(1)–N(4) = 79.8(6)° and RMS deviation of 0.0477 from the plane for Pd(1), N(1), N(2), N(3) and N(4); molecule b, angle N(7)–Pd(2)–N(8) = 79.5(6)° and RMS deviation of 0.0502 from the plane for Pd(2), N(5), N(6), N(7) and N(8)). In both molecules, the nitrite ligands adopts solely nitro-(η1-NO2) coordination geometry in this ground state (GS) structure. The diffraction data quality for form I is not that high, reflecting the fact that form I crystallises as thin needles that produce only limited diffraction intensity and are inherently twinned. However, the data are sufficient to confirm the atomic connectivity and the standard uncertainties on the bond distances and angles are reasonable enough to allow fair comparison between datasets.
, with two molecules of 1 in the asymmetric unit (Z′ = 2). In both molecules the Pd(II) centre adopts a strained square planar geometry, due to the bite angle of the chelating bpy4dca ligand (molecule a, angle N(3)–Pd(1)–N(4) = 79.8(6)° and RMS deviation of 0.0477 from the plane for Pd(1), N(1), N(2), N(3) and N(4); molecule b, angle N(7)–Pd(2)–N(8) = 79.5(6)° and RMS deviation of 0.0502 from the plane for Pd(2), N(5), N(6), N(7) and N(8)). In both molecules, the nitrite ligands adopts solely nitro-(η1-NO2) coordination geometry in this ground state (GS) structure. The diffraction data quality for form I is not that high, reflecting the fact that form I crystallises as thin needles that produce only limited diffraction intensity and are inherently twinned. However, the data are sufficient to confirm the atomic connectivity and the standard uncertainties on the bond distances and angles are reasonable enough to allow fair comparison between datasets.
| Poly I (GS) | Poly I (ES) | Poly II (GS) | Poly II (GS) | |
|---|---|---|---|---|
| Irradiation time (λ = 465 nm)/min | 0 | 480 | 0 | 240 |
| X-ray radiation wavelength/Å | 0.71073 | 0.71073 | 0.71073 | 0.71073 |
| Empirical formula | C14H12N4O8Pd1 | C14H12N4O8Pd1 | C14H12N4O8Pd1 | C14H12N4O8Pd1 |
| Formula weight | 470.68 | 470.68 | 470.68 | 470.68 |
| Temperature/K | 150 | 150 | 150 | 150 |
| Crystal system | Triclinic | Triclinic | Monoclinic | Monoclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/n | P21/n |
| a/Å | 8.4976(9) | 8.4570(17) | 8.4629(3) | 8.5145(3) |
| b/Å | 13.812(2) | 13.863(2) | 7.7277(3) | 7.8127(3) |
| c/Å | 15.5449(19) | 15.648(4) | 24.8938(7) | 24.8999(6) |
| α/° | 63.761(14) | 63.84(2) | 90 | 90 |
| β/° | 82.994(9) | 83.505(18) | 95.196(3) | 93.874(3) |
| γ/° | 78.512(11) | 79.366(16) | 90 | 90 |
| Volume/Å3 | 1602.5(4) | 1617.4(6) | 1621.33(10) | 1652.59(10) |
| Z | 4 | 4 | 4 | 4 |
| ρ calc/g cm−3 | 1.951 | 1.933 | 1.928 | 1.892 |
| μ/mm−1 | 1.215 | 1.204 | 1.201 | 1.178 |
| F(000) | 936 | 936 | 936 | 936 |
| Crystal size/mm | 0.25 × 0.05 × 0.02 | 0.25 × 0.05 × 0.02 | 0.3 × 0.2 × 0.1 | 0.3 × 0.2 × 0.1 |
| Reflections (independent) | 6168 (3599) | 6230 (2439) | 6851 (3315) | 6854 (3383) |
| Goodness of fit on F2 | 0.956 | 0.920 | 1.019 | 1.024 |
| R int | 0.0978 | 0.1327 | 0.0425 | 0.0372 |
| R 1 [I ≧ 2σ(I)] | 0.0764 | 0.1072 | 0.0393 | 0.0435 |
| wR2 [all data] | 0.2454 | 0.3464 | 0.0780 | 0.0917 |
| Largest difference peak and hole/e Å−3 | 1.80 and −1.15 | 1.82 and −1.31 | 0.77 and −0.61 | 0.99 and −0.99 |
Crystal Explorer fingerprint plots can be used to give a visual representation of the differences in the intermolecular interactions, and so crystal packing environments, between the polymorphs.58,59 A full set of fingerprint plots for each of the 3 crystallographically independent molecules are given in the ESI‡ (Table S2), and highlight the key interactions in each polymorph. The fingerprint plots are similar in shape for all molecules and intermolecular contacts in both polymorphs. The key difference between the molecules appears to involve the C⋯H contacts, with form I molecule a involved in considerably shorter and stronger C⋯H contacts compared to molecule b and polymorph II. This results from a short contact between the H(14B) on a methyl group and C(2) in pyridine in a neighbouring a molecule.
Overlays of the independent molecules of 1 in polymorph I (a and b) with that of polymorph II using the CCDC software Mercury60 also give an indication of the differences in the molecular geometry between the different crystal forms (Table S3‡). Comparison of polymorph I molecule a with form II shows the geometry is largely similar, with a RMSD of 0.1712 across the whole molecule. The most significant deviations involve the methyl groups of the ester, with a maximum displacement of 0.38 Å. Comparing form I, molecule b with form II, the RMSD is slightly larger at 0.3006, with more significant deviations in the NO2 ligands, as well as the methyl ester groups.
Choice of excitation wavelength
As our prior experience indicated that linkage isomer complexes containing strong chromophores often display little or no photoswitching, care was taken when designing photocrystallography experiments with 1, particularly in selecting the excitation source wavelength. It is also known that where the ES absorbs at the chosen excitation wavelength it is possible to both populate and depopulate the ES on irradiation, creating a photostationary equilibrium that limits the maximum ES population that can be achieved.44,61 Thus, the choice of excitation wavelength is key. To help guide wavelength choice, the diffuse reflectance spectrum was collected on a lightly ground powder sample of as-synthesised 1, confirmed by PXRD to contain a mixture of forms I and II (Fig. S6‡). The absorption profile, obtained using the Kubelka–Munk transform (Fig. 3), was used to select suitable excitation wavelengths. The high absorption recorded between 250 and 425 nm indicates that excitation wavelengths in this region will be strongly absorbed by the complex, while wavelengths outside the absorption band (>500 nm) are not expected to promote linkage isomerism. Prior research has indicated that selecting a wavelength in the tail of the absorption band helps to maximise the penetration of the excitation light through the single crystal, thereby maximising the measured level of photoactivation.62,63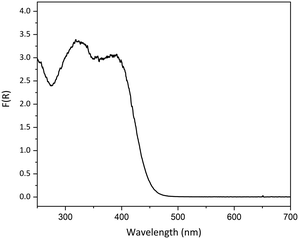 | ||
| Fig. 3 Solid-state absorption profile for a powdered sample of as-synthesised crystals of 1, converted from the experimental diffuse reflectance spectrum using the Kubelka–Munk transformation. | ||
To test this hypothesis for 1, and to ensure a suitable range of excitation conditions were trialled, a series of preliminary experiments were first run with a well-diffracting crystal of polymorph II. A crystal was irradiated for 1 h at 150 K, using 4 different LED wavelengths across the absorption profile: 390 nm, 405 nm, 465 nm and 500 nm, after which time a steady-state photocrystallography dataset was collected. The results of these preliminary studies are summarised in Table S4.‡
For near-UV wavelengths (390 nm, 405 nm) no change in the coordination of the nitro-(η1-NO2) ligands could be discerned from the photodifference map, however the crystal quality and diffraction intensity was observed to decrease with exposure to both wavelengths and particularly at λ = 390 nm. Irradiation at λ = 500 nm similarly showed no excitation in either nitrite ligand, but at this wavelength the crystal quality remained high following irradiation. Finally, irradiation at λ = 465 nm produced a significant change in the photodifference map, with both nitrite ligands found to photoswitch from GS nitro-(η1-NO2) to above 50% of the ES endo-nitrito-(η1-ONO) isomer. These results agree with prior research62,63 and a possible explanation is that wavelengths near the maxima of the absorption peak (λ = 390 nm and 405 nm) are too strongly absorbed in the outer layers of the crystal, limiting the transmission of excitation light through the sample and causing the observed crystal damage. Conversely, choosing a wavelength in the tail of the absorption band can help minimise crystal damage, while simultaneously promoting photoisomerisation to a high conversion percentage due to the improved penetration depth of the excitation light through the crystal bulk. Finally, the observation that a wavelength entirely outside the absorption maximum (500 nm) induced no change in the nitrite ligand geometry or the crystal quality is unsurprising and indicates that light of too low energy cannot produce any significant photo-response.
Steady-state photocrystallography at λ = 465 nm
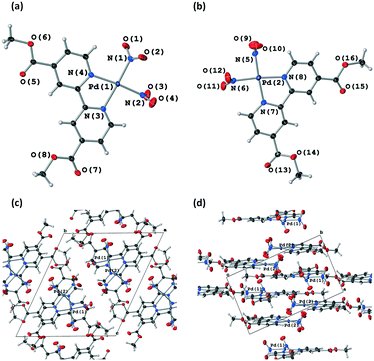
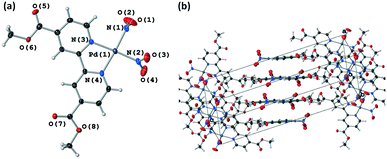
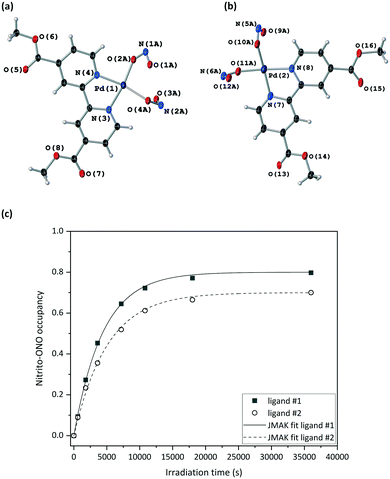
Fig. 4(a) and S8‡ show that the crystal structure remains largely unchanged on photoactivation, excepting the change in nitrite binding mode. An increase in the unit cell volume of 1.93% was found on excitation, which is a fairly large change compared with other photoactive linkage isomers.36,38,43,45
The excitation profiles for both ligands in Fig. 4(b) are sigmoidal, as seen for similar linkage isomer crystals.38,45,64 To extract kinetic information on the population dynamics of the GS → ES reaction, the excitation profiles can be fitted to the Johnson–Mehl–Avrami–Kolmogorov (JMAK) kinetic model:65–67
| a(t) = a∞ + (a0 − a∞)exp[−ktn] |
Variable temperature parametric studies were next run to determine the point at which the ES is no longer metastable. The photoinduced nitrito-(η1-ONO) isomer occupancy remains stable up to 210 K, at which temperature the ES begins to decay thermally back to the GS arrangement for both nitrite ligands #1 and #2 (Table S5‡).
A crystal was mounted at 200 K and a GS structure was first obtained in the dark at this temperature (Table 2). The GS structure is similar to that obtained at 150 K, with the exception that nitro-(η1-NO2) ligand #2 displays some disorder that was modelled in all datasets collected at this higher temperature (Fig. S9‡). The same crystal was then irradiated in situ on the diffractometer, with the irradiation paused and SCXRD datasets collected at regular intervals to obtain the photoexcitation profile for the crystal at 200 K. In line with other studies,37 the nitrito-(η1-ONO) isomer population level increased at higher temperature, with maximum ES occupancy levels of 80% for nitrite ligand #1 and 70% for nitrite ligand #2 in the 200 K photostationary state.
| Poly II (GS) | Poly II (ES) | |
|---|---|---|
| Irradiation time (λ = 465 nm)/min | 0 | 600 |
| X-ray radiation wavelength/Å | 0.71073 | 0.71073 |
| Empirical formula | C14H12N4O8Pd1 | C14H12N4O8Pd1 |
| Formula weight | 470.68 | 470.68 |
| Temperature/K | 200 | 200 |
| Crystal system | Monoclinic | Monoclinic |
| Space group | P21/n | P21/n |
| a/Å | 8.5278(3) | 8.5715(4) |
| b/Å | 7.7446(3) | 7.8480(4) |
| c/Å | 24.9228(8) | 24.9357(13) |
| α/° | 90 | 90 |
| β/° | 95.023(3) | 93.900(5) |
| γ/° | 90 | 90 |
| Volume/Å3 | 1639.69(10) | 1673.52(15) |
| Z | 4 | 4 |
| ρ calc/g cm−3 | 1.907 | 1.868 |
| μ/mm−1 | 1.187 | 1.163 |
| F(000) | 936 | 936 |
| Crystal size/mm | 0.3 × 0.2 × 0.1 | 0.3 × 0.2 × 0.1 |
| Reflections (independent) | 7216 (3345) | 7306 (3414) |
| Goodness of fit on F2 | 1.033 | 1.014 |
| R int | 0.0399 | 0.0487 |
| R 1 [I ≧ 2σ(I)] | 0.0382 | 0.0482 |
| wR2 [all data] | 0.0804 | 0.0956 |
| Largest difference peak and hole/e Å−3 | 0.65/−0.57 | 0.89/−0.96 |
As for the 150 K experiments, the excitation profile at 200 K was fitted to the JMAK model, allowing the extraction of kinetic information. The difference between the values of k at the two different nitrite positions is just statistically significant. However, if errors on the experimental values – for example the error on the temperature measurement from the cryostream – are also taken into account, then the difference between these k values is small enough that they can still be considered to be similar. However, data fitting showed that the photoreaction proceeds more slowly at higher temperature, with smaller rate constants k of (0.227 ± 0.004) × 10−3 s−1 (ligand #1) and (0.198 ± 0.006) × 10−3 s−1 (ligand #2) at 200 K, compared to (0.392 ± 0.017) × 10−3 s−1 (ligand #1) and (0.392 ± 0.016) × 10−3 s−1 (ligand #2) 150 K. It also took a much longer time (10 h) to reach the photostationary state at 200 K than it did at 150 K. This result is to be expected, as it is known that the nitro and nitrito isomers are subject to a thermodynamic equilibrium.29 At any temperature, the forwards nitro → nitrito photoreaction is in competition with the thermally-activated nitrito → nitro back-reaction. Thus, the reverse nitrito → nitro process is more favoured and so occurs at a faster rate at 200 K than at 150 K, causing the rate of the forwards nitro → nitrito photoreaction to be slower at the higher temperature.
Variable temperature parametric studies conducted for the photoexcited state obtained at 200 K showed similar results to the 150 K photocrystallography study, with decay of the ES measurable by 210 K.
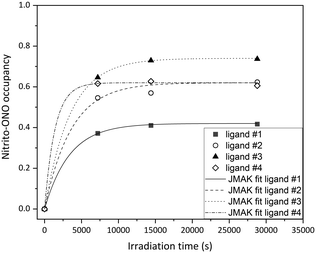
All four crystallographically independent nitrite ligands in form I are found to undergo nitro → nitrito photoisomerisation, with a photostationary state achieved after 8 h irradiation. The final excitation levels at each nitrite position are more varied in form I, with maximum ES occupancies of 42% for ligand #1, 62% for ligand #2, 74% for ligand #3 and 62% for ligand #4.
As for polymorph II, the crystal structure of form I remains largely unchanged on photoactivation, excepting the change in the nitrite ligand coordination. A moderate increase of 0.93% in the unit cell volume between the GS and photostationary ES was observed, which is considerably smaller than that seen for form II and is more in-line with other nitrite linkage isomers that display incomplete photoswitching in the single-crystal.43,45
The excitation profiles for all four nitrite ligands were fitted to the JMAK model, providing kinetic information (Fig. 6). The values of k refined from the data indicate that the reaction rates are similar for ligands #1, #2 and #3 when statistical errors are taken into account. Conversely, the analysis for ligand #4 indicates that the photoreaction here proceeds more quickly, with a value of k > 2× larger than at the other sites. However, it should be noted that the error on this value is very high and it is therefore unreliable. More data points between 0 h and 2 h irradiation would be necessary to confirm whether nitro → nitrito switching proceeds more quickly in ligand #4 compared with ligands #1–#3.
Finally, variable temperature parametric studies following the decay of the ES in form I were not possible as the diffraction intensity from the needle crystals was too weak at elevated temperatures.
Rationalising the photoresponse of 1
An attempt to rationalise the photoexcitation behaviour of 1 can be made by considering the photoreaction kinetics, the steric influences on the nitrite ligands from the surrounding crystal environment, and the electronic structure and resulting photophysical properties. Comparison can be made both between the individual nitrite ligand sites and also between the different polymorphic forms.C–H⋯O bond analysis does help to rationalise the increase in photoactivity in form II on warming, however (Table S8‡). All intermolecular C–H⋯O contacts are found to lengthen significantly at 200 K, while the D–H⋯A bond angle typically remains similar or becomes more acute. This is consistent with a weakening of the hydrogen bonding interactions, which can serve to facilitate the higher levels of photoactivation observed in form II crystals at higher temperature and is consistent with behaviour reported for other, related crystal systems.37
After photoswitching, the ES nitrito ligands will (re)form new close-contacts and it is feasible that the ES geometry adopted may be driven, in part, by the formation of stabilising interactions to nitrito-(η1-ONO). Fig. S13 and Table S9‡ summarise the key interactions involving the photoexcited ligands in I and II. As for the GS, no obvious trends in the C–H⋯O interactions arise that can account for the observed ES population levels at each nitrite site.
A final way to rationalise the photoresponse at each ligand site, in terms of structure, is to consider topochemical factors. It has long been understood that solid-state reactions should be topotactic, i.e. they will proceed in a way that minimises the amount of atomic or molecular movement in the structure.69,70 The application of these ideas to 1 dictates that the nitrite ligand most likely to achieve the highest level of photoswitching in the single crystal is the one that requires the smallest change in its surrounding crystalline environment. A common way to assess the impact of the local crystalline environment on nitro → nitrito switching is to utilise the “reaction cavity” concept.25,26 A comparison of the available reaction cavity volume, Vc, at each nitrite site provides an assessment of the space available for the required atomic rearrangements. It would be expected that, for a topotactic transformation, a large Vc will correlate with a high photoconversion to the nitrito-(η1-ONO) isomer. An estimation of Vc for each of the individual nitrite groups in the GS structures of forms I and II was made using the void space calculation tool in Mercury (further details of this procedure are included in the ESI‡).60 The results of the reaction cavity analyses for individual nitrite sites are given in Table 3. There is a trend between the GS Vc and the nitrito-(η1-ONO) population achieved, in that the nitrite site with the lowest ES population (form I ligand #1, 45%) has the smallest Vc at 24.34 Å3, while all other sites achieving higher ES population levels (60–80%) have much larger Vc. However, there is poor correlation among the ligand sites in the higher ES population bracket (Fig. S14‡).
| Polymorph | Nitrite ligand # | Nitrito-ONO occupancy | V c per unit cell (Å3) | V c per moleculea (Å3) |
|---|---|---|---|---|
| a V c per molecule was obtained by dividing the value obtained per unit cell by Z for each structure, allowing direct comparison of reaction cavities for forms I and II. | ||||
| I | #1 | 0.42 | 48.86 | 24.43 |
| I | #2 | 0.62 | 75.30 | 37.65 |
| I | #3 | 0.74 | 67.78 | 33.89 |
| I | #4 | 0.62 | 80.48 | 40.24 |
| II | #1 | 0.71 | 148.31 | 37.08 |
| II | #2 | 0.68 | 141.44 | 35.36 |
Comparing the reaction cavities for form II at 150 and 200 K (Table S10‡) shows no significant trend between Vc and the ES population level, indicating that the reaction cavity concept does not explain the increase in photoactivity on warming.
All of the above observations highlight the limitations of rationalising ES population levels with respect to steric factors alone, particularly for crystals containing multiple isomerising ligands. In both forms I and II it is likely that ES conversion at one site will influence switching at other sites in that crystal (either via induced steric strain or due to the rearrangement of influential intermolecular interactions). Thus, it is impossible to deconvolute the effects of excitation at multiple sites when analysis is limited to static, photostationary X-ray structures.
On assessing the effect of the differing crystal packing environments in I and II, it is interesting to first compare the ES structures adopted in each form. Inspection of Fig. 4(a) and 5(a) and Table S11‡ shows that a different ES molecule is accessed in each polymorph. In form II, the two nitrito-(η1-ONO) ligands coordinated to Pd(1) point in the same direction (i.e. both “up” in relation to the Pd(1), N(1), N(2), N(3), N(4) square plane). By contrast, the form I ES molecule contains two nitrito-(η1-ONO) ligands oriented in opposing directions (i.e. one “up”, one “down” in relation to the square plane). Reaction cavity analysis (Table 3) makes no clear distinction in the volumes occupied by “up” or “down” ligands; thus, it is unlikely that the geometry preference is governed by steric crowding in the crystal lattice. Assessment of C–H⋯O interactions also provides no real insight into the geometry preference: for all ligands it is possible to identify alternative C–H donors had the nitrito ligand oriented itself in the opposing direction. It is likely instead that the combined sum of all weak intermolecular interactions make one ES geometry more favourable than the other in each case.
Finally, it can be said that the photoreaction in form II is more efficient than in form I: not only does it proceed more quickly, but a higher over ES population level is achieved when averaging across all nitrite sites. Reaction cavity analyses for assessing the crystal structures as a whole, rather than taking isolated cavities for individual ligands, provide a better rationale for these observations: for polymorph I, a total Vc of 282.48 Å3 is calculated for the unit cell, whereas form II displays a larger overall Vc of 287.45 Å3 indicating that, where crystals contain multiple isomerisable groups, it is more accurate to consider the reactions cavities as a whole across the full crystal structure.
Density functional theory (DFT)
Finally, gas-phase DFT calculations were used to further explore the molecular and electronic structures of 1 in each polymorph.The geometries of form I molecules a and b and the lone molecule of 1 in form II were first optimised [DFT(B3LYP)/6-311+G(d) for light atoms, DFT(B3LYP)/SDD for Pd], starting from the GS SCXRD structures. Interestingly, form I molecules a and b both optimise to the same geometry, with identical single point energies (Fig. S15‡). Comparing the optimised geometry of 1 in forms I and II, subtle differences were still observed, with a RMSD of 0.3996 between molecules but only a small single point energy difference of 1 kJ mol−1. Both optimised geometries are confirmed to be minima by frequency calculations and the key difference is in the orientation of the nitro-(η1-NO2) ligands. The ES structures were also optimised from SCXRD structures. Again, form I molecules a and b optimise to the same geometry and retain the up/down orientation of nitrito-(η1-ONO) ligands observed experimentally. The optimised ES structure of form II retains the up/up arrangement seen by photocrystallography and calculations indicate that this geometry is only slightly less stable than the up/down arrangement, by 4 kJ mol−1. These calculations reinforce the conclusions of the steric analyses, indicating that solid state interactions in the surrounding crystal structure must influence the geometry preference in each case.
Calculated absorption spectra were also obtained for I and II using TDDFT (Fig. 7). Relative changes in the optical spectra can rationalise the switching behaviour seen experimentally. Fig. 7 shows that there are only subtle differences in the calculated GS absorption profiles between forms I and II, both displaying λmax(GS) = 270 nm, with absorption tailing off by ∼500 nm. Despite being calculated in the gas phase, the spectra compare well to the experimental diffuse reflectance spectrum (Fig. 3 and S16‡) and the similarity between forms I and II indicate that subtle differences in molecular geometry have little influence on the absorption properties. The calculated ES spectra for each polymorph differ more significantly than those of the GS, which may be expected given the larger difference in the ES geometries adopted. However, the key difference is the presence of an additional, higher-energy band overlapping with the main absorbance (ca. 250 nm), with the spectra again comparing well in the experimental photoexcitation region of 390–500 nm. The key comparison is between the GS and ES spectra, with the ES spectra displaying a significant red-shift in the main absorption maxima (Δλ = 30 nm, λmax(ES) = 300 nm) in addition to the formation of a new peak centred at 380 nm. This shows that the 465 nm excitation light is absorbed more strongly by the nitrito-(η1-ONO) ES than it is by the GS, which has implications for ES population levels. If the ES absorbs the excitation light more strongly, then as the outer layers of the crystal are excited these will act as a barrier to photoswitching, preventing the excitation light from penetrating well through the crystal bulk and ultimately limiting the ES population level that can be achieved. This is one possible explanation for the incomplete ES photoconversion seen for both polymorphs of 1. A second possible explanation is that, as the ES isomer absorbs the 465 nm excitation light, there is also potential for it to also depopulate the ES to some extent, setting up a photostationary equilibrium.44,61 This would also account for the incomplete photoconversion seen.
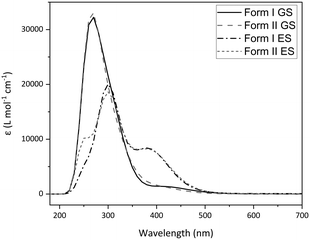 | ||
| Fig. 7 Calculated absorption spectra for 1 obtained by gas-phase TDDFT, comparing polymorphs I and II in their optimised GS and ES geometries. | ||
Molecular orbitals (MOs) and orbital energies were also calculated for GS molecules and used to assess the electronic transitions required to break the Pd–NO2 bond and facilitate switching. Initial results showed that forms I and II produce very similar outputs (Fig. S17 and S18‡) and as such the remainder of this analysis uses solely form II. Inspection of the frontier MOs for 1 (Fig. 8) shows the HOMO has a significant contribution from Pd and NO2 moieties (56% LCAO-MO contribution) and the localisation of electron density across Pd1, N1 and N2 indicates that this is a bonding MO. Conversely, the LUMO is primarily composed of bpy4dca (93%) and has little contribution from either Pd or NO2. In fact, a significant contribution from Pd and NO2 is not seen until LUMO+3 (29%) and the localisation of density indicates this is an antibonding-type orbital, with clear nodes between Pd and both NO2 ligands. The analysis of frontier MOs suggests that the HOMO → LUMO+3 transition will break the Pd–NO2 bonds and facilitate linkage isomer switching. TDDFT shows that the HOMO → LUMO+3 transition contributes to ESs in the region of 411–431 nm, with strongest contribution to ES #6 (411.39 nm, f = 0.0225, 44% contribution). These outputs (calculated in the gas phase) are slightly blue-shifted compared to the wavelengths used for solid state switching.
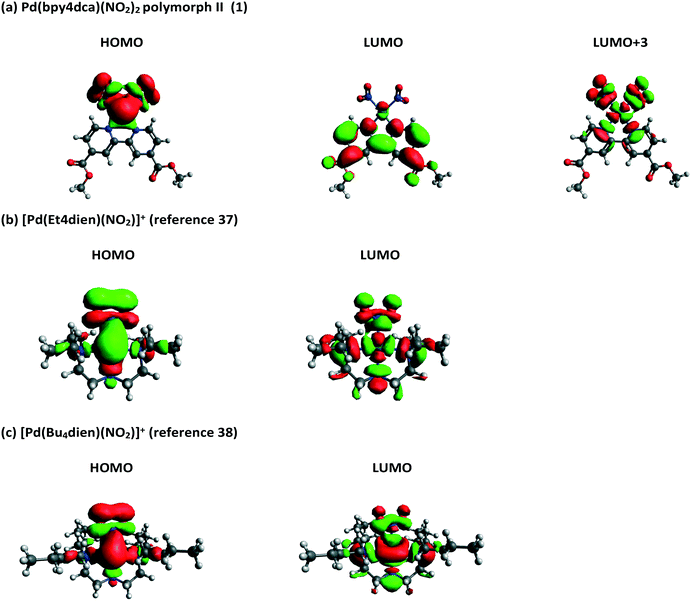 | ||
| Fig. 8 Calculated frontier molecular orbitals for (a) 1 (polymorph II) and two other Pd(II)–nitrite molecules reported in the literature, capable of 100% conversion to a nitrito-(η1-ONO) excited state: (b) [Pd(Et4dien)(NO2)]+,37 and (c) [Pd(Bu4dien)(NO2)]+.38 | ||
These MO calculations are most interesting when compared to other Pd(II)–nitrite linkage isomer complexes published in the literature. The frontier MOs for two compounds capable of 100% nitro → nitrito switching, [Pd(Bu4dien)(NO2)]+,38 and [Pd(Et4dien)(NO2)]+,37 are shown in Fig. 8, while three further complexes capable of lower ES photoconversion are included in the ESI‡ (Fig. S19–S23).71 For all other Pd(II)–nitrite systems reported, MO contributions and localisation of electron density indicates that the main HOMO → LUMO transition is most likely to cause Pd–NO2 bond-breaking, in contrast to 1. The presence of the strong chromophore bpy4dca in 1 clearly inserts other, accessible LUMOs between the desired MOs for Pd–NO2 bond-breaking, making it difficult to access the transition required for linkage isomerism in these systems. This rationale may explain why it was previously challenging to design effective linkage isomer switches that contain strong chromophores as co-ligands.
Conclusions
This study has confirmed by photocrystallography that complex 1, [Pd(bpy4dca)(NO2)2] shows the highest level of nitro → nitrito photoconversion recorded to-date for a nitrite linkage isomer complex containing a co-ligand that is, in itself, a strong chromophore. Informed selection of the appropriate excitation conditions leads to a maximum of 80% ES population in form I. DFT studies provide some rationale the observed photophysical properties of 1 and most interestingly confirm that the presence of the aromatic bpy4dca ligand causes a re-ordering of frontier MOs compared to other Pd(II) linkage isomer materials that do not contain co-ligands with extended pi-systems. This explains why it can be harder to access the transition required for linkage isomer switching in the presence of aromatics, insight that can be applied in future to design a wider variety of linkage isomer switches for new and varied applications.Single-crystal and PXRD studies also confirm that 1 exists in two different polymorphic forms, I and II, and that irreversible conversion of I into II occurs when form I needles are aged in their supernatant solution for a few days. Both polymorphs are confirmed to undergo photoinduced linkage isomer switching, with photocrystallographic kinetic studies showing that the overall photoreaction is more efficient in form II than form I.
As seen previously by us,45 and others,72 the independent nitrite ligand sites in both forms achieve different maximum photostationary ES populations, a factor that must be affected, at least in part, by the crystal packing environment at each site. Despite this, weak C–H⋯O hydrogen bond analysis is insufficient to explain the trends in photoactivity between sites, either in terms of preferred ES geometry or maximum ES population. Hydrogen bond analysis does help to rationalise the observed increase in functionality at higher experiment temperatures, however, in agreement with previous observations.37
The reaction cavity concept goes some way to explaining the trends in ES population level, particularly when cavity volumes are considered across the structure as a whole. However, analysis of the reaction cavities for individual nitrite sites did not show convincing trends, likely reflecting the fact that, for structures containing multiple photoactive ligands, the switching process is not independent at each site. This point is reinforced by the results of photocrystallographic kinetic analysis, which show that the independent nitrite ligand sites in the same crystal structure isomerise at very similar rates.
In summary, the results of this study reinforce our belief that the nitro → nitrito isomerism process is governed by a complex balance of steric, electronic and kinetic factors and that it is difficult to deconvolute each of these influences. Our ability to uncover convincing trends between structural parameters and the ES populations at each nitrite site is also limited by the fact that steady-state photocrystallographic analysis can only provide static crystal structures of the GS and photostationary ES states and gives no insight into the dynamic structure changes that occur in real time, as individual isomerisation events take place. Time-resolved diffraction studies with materials like 1 would provide vital information and are the subject of future investigation.
Author contributions
L. E. H. was responsible for the conceptualization, funding acquisition and administration of the research programme that produced this work, for the synthesis and photocrystallographic study of 1 and for the formal analysis of all XRD and DFT data. B. A. C. was responsible for collection, data curation and formal analysis of all other analytical data. All authors were involved in writing, reviewing and editing the draft and final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. E. H. and B. A. C. are grateful for to the Royal Society for support (URF\R1\191104). In performing DFT calculations we acknowledge the support of the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via Welsh Government. We also thank Dr Timothy Easun at Cardiff University for the use of the OceanOptics Flame miniature spectrometer to collect diffuse reflectance spectra.Notes and references
- R. Klajn, Chem. Soc. Rev., 2014, 43, 148–184 RSC.
- S. Crespi, N. A. Simeth and B. König, Nat. Rev. Chem., 2019, 3, 133–146 CrossRef CAS.
- S. L. Gilat, S. H. Kawai and J.-M. Lehn, Chem. – Eur. J., 1995, 1, 275–284 CrossRef CAS.
- P. Zeng, Z. Liu, Z. Hu, J. Zhai and L. Jiang, RSC Adv., 2013, 3, 22853–22856 RSC.
- S. D. Stranks and H. J. Snaith, Nat. Nanotechnol., 2015, 10, 391–402 CrossRef CAS PubMed.
- X. Wu, et al. , Sci. Adv., 2017, 3, e1602388 CrossRef PubMed.
- L. E. Hatcher, J. M. Skelton, M. R. Warren and P. R. Raithby, Acc. Chem. Res., 2019, 52, 1079–1088 CrossRef CAS PubMed.
- J.-F. Letard, J. Mater. Chem., 2006, 16, 2550–2559 RSC.
- I. I. Vorontsov, T. Graber, A. Y. Kovalevsky, I. V. Novozhilova, M. Gembicky, Y.-S. Chen and P. Coppens, J. Am. Chem. Soc., 2009, 131, 6566–6573 CrossRef CAS PubMed.
- K. Kalyanasundaram, Coord. Chem. Rev., 1982, 46, 159–244 CrossRef CAS.
- J. M. Cole, K. Y. M. Yeung, G. Pace, S. O. Sylvester, D. Mersch and R. H. Friend, CrystEngComm, 2015, 17, 5026–5031 RSC.
- H. Tsai, R. Asadpour, J.-C. Blancon, C. C. Stoumpos, O. Durand, J. W. Strzalka, B. Chen, R. Verduzco, P. M. Ajayan, S. Tretiak, J. Even, M. A. Alam, M. G. Kanatzidis, W. Nie and A. D. Mohite, Science, 2018, 360, 67 CrossRef CAS PubMed.
- M. Goulkov, D. Schaniel and T. Woike, J. Opt. Soc. Am. B, 2010, 27, 927–932 CrossRef CAS.
- L. Zeng, X. Guo, C. He and C. Duan, ACS Catal., 2016, 6, 7935–7947 CrossRef CAS.
- S.-P. Luo, E. Mejia, A. Friedrich, A. Pazidis, H. Junge, A.-E. Surkus, R. Jackstell, S. Denurra, S. Gladiali, S. Lochbrunner and M. Beller, Angew. Chem., Int. Ed., 2013, 52, 419–423 CrossRef CAS PubMed.
- A. Maldotti, Photochemistry, 2011, 39, 88–111 CAS.
- N. Alarcos, B. Cohen, M. Ziółek and A. Douhal, Chem. Rev., 2017, 117, 13639–13720 CrossRef CAS PubMed.
- T. L. Easun, J. Jia, J. A. Calladine, D. L. Blackmore, C. S. Stapleton, K. Q. Vuong, N. R. Champness and M. W. George, Inorg. Chem., 2014, 53, 2606–2612 CrossRef CAS PubMed.
- D. Hermann, H. Emerich, R. Lepski, D. Schaniel and U. Ruschewitz, Inorg. Chem., 2013, 52, 2744–2749 CrossRef CAS PubMed.
- J. W. Brown, B. L. Henderson, M. D. Kiesz, A. C. Whalley, W. Morris, S. Grunder, H. Deng, H. Furukawa, J. I. Zink, J. F. Stoddart and O. M. Yaghi, Chem. Sci., 2013, 4, 2858–2864 RSC.
- S. L. Zheng, M. Messerschmidt and P. Coppens, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 644–649 CrossRef CAS PubMed.
- S. L. Zheng, M. Gembicky, M. Messerschmidt, P. M. Dominiak and P. Coppens, Inorg. Chem., 2006, 45, 9281–9289 CrossRef CAS PubMed.
- D. Samanta, J. Gemen, Z. Chu, Y. Diskin-Posner, L. J. W. Shimon and R. Klajn, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9379–9384 CrossRef CAS PubMed.
- A. B. Grommet, L. M. Lee and R. Klajn, Acc. Chem. Res., 2020, 53, 2600–2610 CrossRef CAS PubMed.
- M. D. Cohen, Angew. Chem., Int. Ed. Engl., 1975, 14, 386–393 CrossRef.
- Y. Ohashi, Crystallogr. Rev., 2013, 19, 2–146 CrossRef CAS.
- Y. Ohashi, Acc. Chem. Res., 1988, 21, 268–274 CrossRef CAS.
- L. E. Hatcher and P. R. Raithby, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2013, 69, 1448–1456 CrossRef CAS PubMed.
- L. E. Hatcher, J. M. Skelton, M. R. Warren, C. Stubbs, E. L. da Silva and P. R. Raithby, Phys. Chem. Chem. Phys., 2018, 20, 5874–5886 RSC.
- P. Coppens, I. Novozhilova and A. Kovalevsky, Chem. Rev., 2002, 102, 861–884 CrossRef CAS PubMed.
- M. D. Carducci, M. R. Pressprich and P. Coppens, J. Am. Chem. Soc., 1997, 119, 2669–2678 CrossRef CAS.
- A. Y. Kovalevsky, K. A. Bagley and P. Coppens, J. Am. Chem. Soc., 2002, 124, 9241–9248 CrossRef CAS PubMed.
- K. F. Bowes, J. M. Cole, S. L. G. Husheer, P. R. Raithby, T. L. Savarese, H. A. Sparkes, S. J. Teat and J. E. Warren, Chem. Commun., 2006, 2448–2450 RSC.
- D. V. Fomitchev, K. A. Bagley and P. Coppens, J. Am. Chem. Soc., 2000, 122, 532–533 CrossRef CAS.
- M. Warren, S. Brayshaw, A. Johnson, S. Schiffers, P. Raithby, T. Easun, M. George, J. Warren and S. Teat, Angew. Chem., 2009, 121, 5821–5824 CrossRef.
- L. E. Hatcher, M. R. Warren, D. R. Allan, S. K. Brayshaw, A. L. Johnson, S. Fuertes, S. Schiffers, A. J. Stevenson, S. J. Teat, C. H. Woodall and P. R. Raithby, Angew. Chem., Int. Ed., 2011, 50, 8371–8374 CrossRef CAS PubMed.
- L. E. Hatcher and P. R. Raithby, CrystEngComm, 2017, 19, 6297–6304 RSC.
- L. E. Hatcher, CrystEngComm, 2016, 18, 4180–4187 RSC.
- L. E. Hatcher, J. Christensen, M. L. Hamilton, J. Trincao, D. R. Allan, M. R. Warren, I. P. Clarke, M. Towrie, D. S. Fuertes, C. C. Wilson, C. H. Woodall and P. R. Raithby, Chem. – Eur. J., 2014, 20, 3128–3134 CrossRef CAS PubMed.
- A. E. Phillips, J. M. Cole, T. d'Almeida and K. S. Low, Phys. Rev. B, 2010, 82, 155118 CrossRef.
- B. Cormary, S. Ladeira, K. Jacob, P. G. Lacroix, T. Woike, D. Schaniel and I. Malfant, Inorg. Chem., 2012, 51, 7492–7501 CrossRef CAS PubMed.
- M. R. Warren, T. L. Easun, S. K. Brayshaw, R. J. Deeth, M. W. George, A. L. Johnson, S. Schiffers, S. J. Teat, A. J. Warren, J. E. Warren, C. C. Wilson, C. H. Woodall and P. R. Raithby, Chem. – Eur. J., 2014, 20, 5468–5477 CrossRef CAS PubMed.
- L. E. Hatcher, CrystEngComm, 2018, 20, 5990–5997 RSC.
- D. Schaniel and T. Woike, Phys. Chem. Chem. Phys., 2009, 11, 4391–4395 RSC.
- L. E. Hatcher, E. J. Bigos, M. J. Bryant, E. M. MacCready, T. P. Robinson, L. K. Saunders, L. H. Thomas, C. M. Beavers, S. J. Teat, J. Christensen and P. R. Raithby, CrystEngComm, 2014, 16, 8263–8271 RSC.
- A. Makal, J. Benedict, E. Trzop, J. Sokolow, B. Fournier, Y. Chen, J. A. Kalinowski, T. Graber, R. Henning and P. Coppens, J. Phys. Chem. A, 2012, 116, 3359–3365 CrossRef CAS PubMed.
- S. A. Labb, C. J. Masteran, S. G. Albright, B. Ali, H. A. Chapman, Y. Cheng, R. M. Cusic, N. B. Hartlove, A. N. Marr, M. Timmons and S. J. Friese, Synlett, 2020, 31, 1384–1388 CrossRef CAS.
- CrysAlisPro data collection and data reduction GUI, Rigaku, version 171.40.67a ( 2021).
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- S. K. Brayshaw, J. W. Knight, P. R. Raithby, T. L. Savarese, S. Schiffers, S. J. Teat, J. E. Warren and M. R. Warren, J. Appl. Crystallogr., 2010, 43, 337–340 CrossRef CAS.
- M. P. Fuller and P. R. Griffiths, Anal. Chem., 1978, 50, 1906–1910 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.1), Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- Creating UV/Visible Plots from the Results of Excited States Calculations, Gaussian Inc., viewed 27 September 2021, <https://gaussian.com/uvvisplot/>.
- J. J. McKinnon, F. P. A. Fabbiani and M. A. Spackman, Cryst. Growth Des., 2007, 7, 755–769 CrossRef CAS.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- A. A. Mikhailov, V. Y. Komarov, A. S. Sukhikh, D. P. Pishchur, D. Schaniel and G. A. Kostin, New J. Chem., 2020, 44, 18014–18024 RSC.
- I. Abdelmoty, V. Buchholz, L. Di, C. Guo, K. Kowitz, V. Enkelmann, G. Wegner and B. M. Foxman, Cryst. Growth Des., 2005, 5, 2210–2217 CrossRef CAS.
- V. Enkelmann, G. Wegner, K. Novak and K. B. Wagener, J. Am. Chem. Soc., 1993, 115, 10390–10391 CrossRef CAS.
- S. E. Bajwa, T. E. Storr, L. E. Hatcher, T. J. Williams, C. G. Baumann, A. C. Whitwood, D. R. Allan, S. J. Teat, P. R. Raithby and I. J. S. Fairlamb, Chem. Sci., 2012, 3, 1656–1661 RSC.
- M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1940, 8, 212–224 CrossRef CAS.
- M. Avrami, J. Chem. Phys., 1941, 9, 177–184 CrossRef CAS.
- G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, 1997 Search PubMed.
- M. D. Cohen and G. M. J. Schmidt, J. Chem. Soc., 1964, 1996–2000 RSC.
- M. D. Cohen, G. M. J. Schmidt and F. I. Sonntag, J. Chem. Soc., 1964, 2000–2013 RSC.
- M. R. Warren, S. K. Brayshaw, L. E. Hatcher, A. L. Johnson, S. Schiffers, A. J. Warren, S. J. Teat, J. E. Warren, C. H. Woodall and P. R. Raithby, Dalton Trans., 2012, 41, 13173–13179 RSC.
- P. Coppens, J. Sokolow, E. Trzop, A. Makal and Y. Chen, J. Phys. Chem. Lett., 2013, 579–582, DOI:10.1021/jz400013b.
Footnotes |
| † Dedicated to Paul R. Raithby, celebrating a career in inorganic and organometallic chemistry, on the occasion of his 70th birthday. |
| ‡ Electronic supplementary information (ESI) available. CCDC 2151937 (bpy4dca), 2151942–2151945 (polymorph I) and 2151954–2151981 (polymorph II) contain the crystallographic data for this paper. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00213b |
| This journal is © The Royal Society of Chemistry 2022 |