Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intermolecular interactions in the solid-state structures of isoflavones: the relationship between supramolecular structure, torsion angle, and macroscopic properties†
Eric
Sperlich
 *,
Alexandra
Kelling
,
George
Kwesiga
*,
Alexandra
Kelling
,
George
Kwesiga
 and
Bernd
Schmidt
and
Bernd
Schmidt

Institut fuer Chemie, Universitaet Potsdam, Karl-Liebknecht-Straße 24-25, D-14476 Potsdam-Golm, Germany. E-mail: eric.sperlich@uni-potsdam.de
First published on 13th June 2022
Abstract
The molecular structures of three closely related isoflavones have been determined by single crystal X-ray diffraction and have been analysed by geometry matching with the CSD, Hirshfeld surface analysis and analysis of stacking interactions with the Aromatic Analyser program (CSD). The formation of the supramolecular structure by non-covalent interactions was studied and substantial differences in the macroscopic properties e.g., the solubility, were correlated with hydrogen bonding and π-stacking interactions. Moreover, a correlation between the supramolecular structure, the torsion angle (between benzopyran group and aryl group), and macroscopic properties was determined in the three compounds.
Introduction
Isoflavones are secondary plant metabolites with a 3-aryl benzopyran skeleton.1 Numerous bioactivities have been reported for these natural products,2 but their ability to bind to the human estrogen receptor (hERα) and their occurrence in plants relevant for human nutrition, e.g. soybeans, has probably attracted most of the attention in this regard.2,3Our interest in isoflavones stems from phytochemical investigations into the genus Erythrina. Many of the plants belonging to this genus are used in ethnopharmacology for the treatment of inflammation and infectious diseases,4e.g. malaria.5 One example is Erythrina sacleuxii, a tree indigenous in Kenya and Tanzania.6,7 An isoflavone that has so far only been isolated from this source by Yenesew and co-workers is 5-deoxy-3′-prenylbiochanin A (4).6 This natural product shows promising antiplasmodial activity against both chloroquine sensitive and resistant strains of Plasmodium falciparum, with IC50 values in the micromolar range.6 With the aim to expand the investigation into the anti-infective activities of secondary plant metabolites from E. sacleuxii to bacterial pathogens we have recently developed a synthesis of 5-deoxy-3′-prenylbiochanin A (4) in order to obtain sufficient amounts of material for antibacterial testing.8 Our synthesis started from a conveniently accessible MOM-protected flavanone 1, which underwent an oxidative rearrangement9 mediated by the hypervalent iodine reagent PIFA to the isoflavone 2. Deprotection of 2 furnished isoflavone 3, which was finally reacted with 2-methyl-2-butene in a cross metathesis reaction to give 5-deoxy-3′-prenylbiochanin A (4) (Scheme 1).
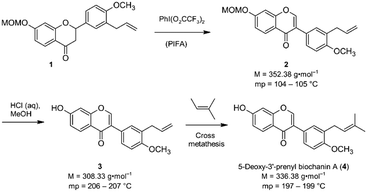 | ||
| Scheme 1 Key steps of our synthesis of 5-deoxy-3′-prenylbiochanin A (4).8 | ||
In the course of this investigation, we noted that the target molecule 5-deoxy-3′-prenylbiochanin A (4) and its two precursors 2 and 3 have remarkably different macroscopic properties. Compound 2 has a melting point which is ca. 100 K lower than the melting points measured for 3 and 4. Compound 3 has a melting point which is 10 K higher than the melting point of the structurally closely related natural product 4. There are also very large differences in the solubility behaviour of the three compounds, despite the structural similarities. Thus, 2 has good solubility in polar and nonpolar organic solvents, 4 dissolves only in polar organic solvents including ethanol and 3 is soluble only in DMSO. The solubility behaviour is one of the important properties of pharmaceutical compounds, as it directly affects the dissolution rate and therefore the bioavailability of the drug. Particularly important is the solubility in water and ethanol, as they are the usual media for drug delivery. Improving drug solubility has been a significant area of the pharmaceutical research for many years. Thus, especially the synthesis of more soluble polymorphs10 and co-crystals11 has been intensively studied.
Current investigations are concerned with the prediction of macroscopic properties of pharmaceutical compounds12 and the relationship between the supramolecular structure of a drug and some of its physiochemical properties, e.g. solubility and melting point.13 The melting point and the solubility behaviour of crystalline compounds depend directly on the lattice energy, which in the case of molecular compounds mainly results from the type and count of intermolecular interactions.14 By analysing the supramolecular structure of a compound, its macroscopic properties can be understood, explained, and predicted for similar compounds.15
Within this work, the solid-state structures of the structurally very similar compounds 2, 3, and 4 are investigated and the relationship between the supramolecular structure, the conformation (in particular the torsion angles) and the different melting points and the solubilities is discussed. For this purpose, the short non-covalent intermolecular interactions are determined, compared, and discussed.
Results and discussion
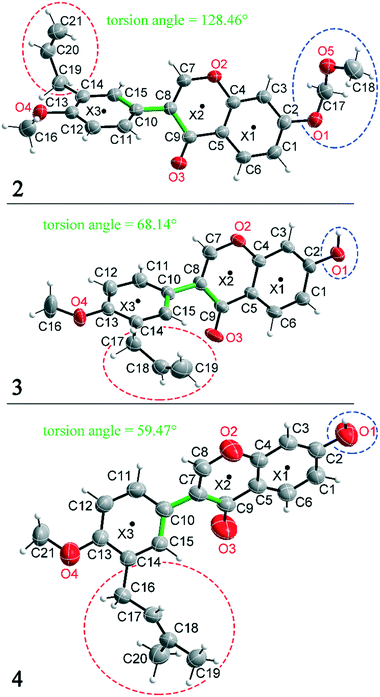
Compounds 2, 3 and 4 are 3-aryl benzopyran derivatives, that differ only with respect to the substituent on the C2 and C14 atoms. The molecular structures of the three compounds are shown in Fig. 1 with atomic numbering. Compound 2 is substituted at C2 by a methoxymethoxy group, while compounds 3 and 4 have a hydroxyl group at this position (Fig. 1 – blue dashed circles). The C14 atom in compound 2 and 3 is functionalized by an allyl group, in compound 4 a prenyl group is present (Fig. 1 – red dashed circles). Despite the major similarities of the molecular structures of 2–4, there are large differences in the crystal structure due to the different arrangement of the molecules in the solid-state. Thus, the three compounds even crystallize in different crystal systems. The crystal structure of compound 4 has already been published,8 but for better comparability of the structures the crystallographic data and the refinement data of all three compounds are listed in Table 1. Compound 2 crystallizes in the orthorhombic space group Pna21 with Z = 4, compound 3 in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z = 2, and compound 4 in the monoclinic space group P21/n with Z = 4. It is remarkable that compounds 3 and 4 crystallize in various orientations despite their molecular similarity.
with Z = 2, and compound 4 in the monoclinic space group P21/n with Z = 4. It is remarkable that compounds 3 and 4 crystallize in various orientations despite their molecular similarity.
| Compound | 2 | 3 | 4 (ref. 8) |
|---|---|---|---|
| Formula | C21H20O5 | C19H16O4 | C21H20O4 |
| M [g mol−1] | 352.37 | 308.32 | 336.37 |
| T [K] | 210 | 210 | 288 |
| Crystal system | Orthorhombic | Triclinic | Monoclinic |
| Space group | Pna21 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P21/n |
| a [Å] | 17.9139(2) | 8.0184(16) | 14.8274(4) |
| b [Å] | 14.6001(4) | 8.4831(17) | 8.16970(10) |
| c [Å] | 6.6911(7) | 11.867(2) | 15.5656(4) |
| α [°] | 90 | 104.02(3) | 90 |
| β [°] | 90 | 94.03(3) | 114.139(2) |
| γ [°] | 90 | 101.24(3) | 90 |
| V [Å3] | 1750.02(19) | 762.2(3) | 1720.67(7) |
| Z | 4 | 2 | 4 |
| ρ calc [g cm−3] | 1.337 | 1.343 | 1.298 |
| μ [mm−1] | 0.095 | 0.094 | 0.089 |
| F(000) | 744 | 324 | 712 |
| Refl. collected | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225 225 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 354 354 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 586 586 |
| Indep. reflection | 6617 | 4636 | 3955 |
| R int | 0.0504 | 0.0336 | 0.028 |
| Refl. I > 2σ(I) | 5353 | 3467 | 3600 |
| Parameter | 237 | 212 | 307 |
| R 1/wR2 [I > 2σ(I)] | 0.0427/0.1062 | 0.0465/0.1318 | 0.040/0.112 |
| R 1/wR2 [all data] | 0.0584/0.1137 | 0.0638/0.1419 | 0.043/0.117 |
| Min./max. Δρ[10−6 e pm−3] | −0.141/0.334 | −0.245/0.344 | −0.17/0.20 |
| GooF | 1.039 | 1.079 | 1.040 |
| CCDC | 2121813 | 2121812 | 2013149 |
Due to the different arrangement of the molecules in the solid-state, the lattice energies, melting points and solubilities of the compounds also show significant differences (see Table 2). Compound 2, for example, has the lowest lattice energy with −175.70 kJ mol−1, a melting point at 104 °C and is soluble in almost all solvents listed in Table 2. Compound 3 has the highest lattice energy with −201.75 kJ mol−1, melts at 207 °C and is the least soluble in the solvents shown. The compound 4 has a lattice energy of −194.00 kJ mol−1, a melting point at 198 °C and has a solubility behaviour that lies between that of compounds 2 and 3. To determine the influence of the different solid-state structures on the macroscopic properties, the geometric conformation parameters and the intermolecular non-covalent interactions in compounds 2–4 were investigated.
All three compounds were checked for geometry using the Program Mogul (CSD-Core) and compared with structurally related compounds from the crystal structure database (CSD). This shows that in compound 3 an unusual torsion angle occurs between the benzopyran group with X1 and X2 and the aryl group with X3 (illustrated with green bonds in Fig. 1). Fig. 2 shows the diagram of the Mogul search in which the torsion angles of the three title compounds were compared with in total 640 chemically similar structures deposited in the CSD. The largest number of compounds has a torsion angle of 45° (resp. 135°). Overall, only three compounds have a similarly small torsion angle as compound 3, and two of the compounds (CSD code POFDIA and UWIJIU) are also 3-aryl benzopyran derivatives with the same positioning of the hydroxy group on the benzopyran ring. For this reason, we suspect that the strongly deviating torsion angles are directly related to the 3-aryl benzopyran skeleton, and that this is due to intermolecular interactions.
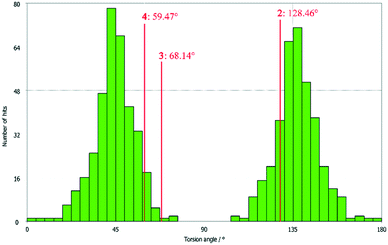 | ||
| Fig. 2 Diagram of the torsion angles of the three title compounds compared with 640 chemically similar structures deposited in the CSD (Mogul search). | ||
Deviations from the ideal 45° angle are expected to occur when both aromatics (i.e., the aryl group and the benzopyran group) are independently influenced by intermolecular interactions. Moreover, a particularly large deviation from the ideal torsion angle should only be possible through the formation of strong intermolecular interactions at both aromatics. Accordingly, it can be assumed that the deviation of the torsion angle in the compounds is an indication of the strength of the intermolecular interactions that occur. Looking at the three title compounds, the deviation from the ideal torsion angle actually correlates with the calculated lattice energy in the compounds. Compound 2 has the lowest lattice energy and the torsion angle deviates by only 6.54° from the ideal 135° angle, compound 4 has a higher lattice energy and the torsion angle deviates by 14.47° from the ideal 45° angle, and compound 3 with the highest lattice energy shows a deviation of 23.14°. To verify this hypothesis and to analyse the reason for the different conformations and deviating torsion angles, Hirshfeld surface analysis was performed on the molecular structures of all three compounds, from which information on the short intermolecular contacts in the solid-state structure was obtained. The Hirshfeld surface analysis can be used to determine the contribution of various intermolecular contacts to the total surface area of a molecule (Fig. 3). Thus, for the molecules of the compounds 2–4, particularly short contacts of the form H⋯H, C⋯H/H⋯C, O⋯H/H⋯O, C⋯O/O⋯C, C⋯C and O⋯O are found with decreasing frequency.
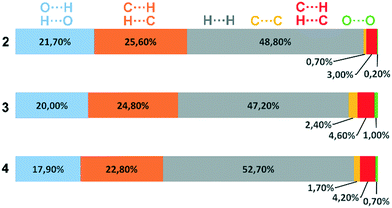 | ||
| Fig. 3 Representation of the composition of the Hirshfeld surface from different intermolecular contacts. | ||
To discuss the conformation, lattice energy and thus the melting points and solubilities of the three compounds, the contacts that lead to an attractive interaction between the molecules are most relevant. The dominant structure directing features are the hydrogen bonds with O acceptors, i.e., O⋯H/H⋯O contacts, and the stacking interactions with the C⋯C (offset-face-to-face) and C⋯H/H⋯C contacts (edge-to-face).
Before discussing these dominant interactions, we will briefly discuss the other contacts (H⋯H, C⋯O/O⋯C, and O⋯O) and their influence on the conformation of the molecules. The images of the 2D fingerprint plots of the H⋯H, C⋯O/O⋯C, and O⋯O contacts are listed in the ESI.† The shortest H⋯H contacts in all three title compounds are located at a distance of about 2.4 Å, which corresponds to the van der Waals distance between the two atoms and thus has a destabilizing effect on the crystal packing.16 The largest number of H⋯H contacts are located at a distance of 2.9 Å to 3.3 Å in the region that is most stabilizing for the intermolecular potential. Overall, it can be said that the few short destabilizing H⋯H contacts are compensated by many longer stabilizing contacts and that the H⋯H contacts overall lead to a stabilization of the molecular crystals. However, despite the high percentage of H⋯H contacts, these interactions have rather a small influence on the orientation of the molecules in the solid-state (and thus on the torsion angles) since there are many contacts acting on the molecules from all sides in a similarly populated way. Short C⋯O/O⋯C contacts could indicate the formation of strong dipole interactions, or tetrel bridges. The shortest C⋯O/O⋯C distances are located in all three compounds at about 3.2 Å (van der Waals radius of C and O = 3.22 Å (ref. 17)), which is slightly longer than typical distance for tetrel bonding interactions with σ-holes on C atoms,18 but no orientation of the atoms with respect to each other is obtained that is typical for this type of interaction. In fact, these shortest C⋯O/O⋯C contacts in the three compounds do not result from the formation of strong C⋯O/O⋯C interactions, but from the orientation of the molecules with the formation of H-bridges and stacking interactions. Therefore, the C⋯O/O⋯C contacts also do not possess much influence on the supramolecular arrangement of the molecules. Short O⋯O contacts could indicate the formation of weak chalcogen bridges between the molecules. In compound 2, the shortest contacts are at 3.6 Å and thus in the stabilizing potential region; in compounds 3 and 4, the shortest contacts are at 3.2 Å and result from the formation of the O–H⋯O hydrogen bonds. Since the percentage of O⋯O contacts in the three compounds is very low and the shortest contacts in 2 and 3 are formed due to hydrogen bonds, the O⋯O contacts are also not considered to have a significant effect on the arrangement of the molecules in the solid-state. For this reason, the supramolecular structure and conformation of the three title compounds are discussed as follows, taking into account hydrogen bonding and stacking interactions.
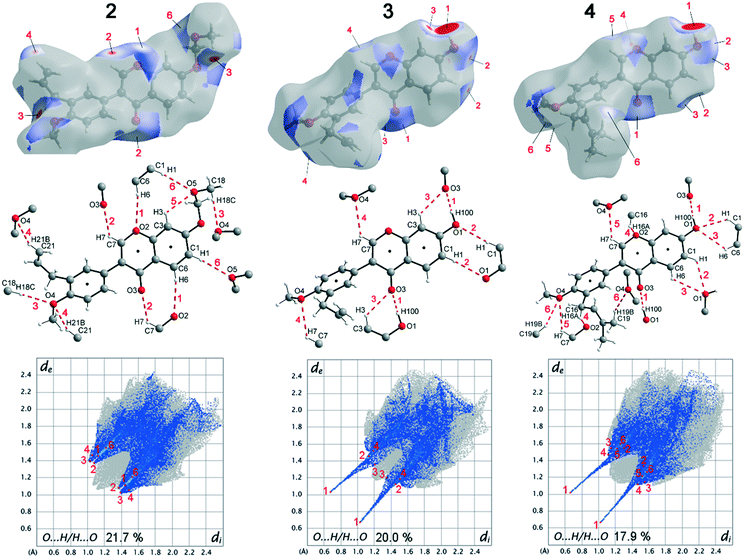
When comparing the percentage of O⋯H/H⋯O surface contacts in the three compounds, these occur most frequently in 2 with 21.7%, followed by 3 with 20.0% and the smallest percentage with 17.9% is found in 4. In contrast to other investigations,19 there does not seem to be any direct dependence of the melting point on the percentage of O⋯H/H⋯O surface contacts. One reason for the large number of O⋯H/H⋯O contacts in 2 is the fact that there are five oxygen atoms in the molecule, whereas in 3 and 4 there are only four O atoms. In addition, the percentage says something about the amount of surface contacts and not directly about the contact distance and thus about the bond strength. To analyse the strength of the O⋯H/H⋯O contacts, the strongest hydrogen bonds with O-acceptor for the three compounds are shown in Fig. 4.
The Hirshfeld surface of the O⋯H/H⋯O contacts (top), the molecular view with atom labels (center) and the 2D fingerprint plot of the O⋯H/H⋯O contacts (bottom) are shown. In compound 2, 11 hydrogen bonds with O-acceptor result for each molecule, and these are 6 symmetry-independent hydrogen bonds. For each molecule, the hydrogen bonds 1, 2, 3, 4 and 6 are present twice, since the molecule acts once as a proton donor and the second time as a proton acceptor. Only the intramolecular hydrogen bond 5 is single. When looking at the 2D plot of the O⋯H/H⋯O contacts of compound 2 (Fig. 4, bottom left), it can be seen that the contacts of hydrogen bonds 1, 2, 3, and 4 are in the same region and thus the hydrogen bonds have similar bond strengths. The hydrogen bond 6 has a slightly larger proton-acceptor distance. The fact that the molecule acts as donor and acceptor for the hydrogen bonds 1, 2, 3, 4 and 6 respectively, results in two points on the 2D plot for each of these hydrogen bonds. Since the hydrogen bond 5 is not formed between different molecules but intramolecularly, it cannot be mapped on the Hirshfeld surface and is consequently missing on the 2D plot.
In compound 3, each molecule forms a total of 8 hydrogen bonds, four symmetry-independent bonds 1, 2, 3 and 4, in which each molecule is involved both as a proton donor and as a proton acceptor. When looking at the Hirshfeld surface of compound 3 in Fig. 4 (top, center), it is evident that hydrogen bond 1 has a particularly large red area on the surface. In contrast to the other hydrogen bonds, this is an O–H⋯O hydrogen bond with a particularly high bond strength. It is formed between the hydroxyl group with O1 and the O3 of the keto group. This can also be seen on the 2D plot of the O⋯H/H⋯O contacts of compound 3. Here, there are two sharp spikes, at very small di and de values, which illustrate the particularly short contact of the atoms involved and thus the very large strength of the hydrogen bond. All other contacts shown in Fig. 4 (top, center) are C–H⋯O hydrogen bonds. The proton acceptor atom O3 forms a bifurcated hydrogen bond, in which bond 3 is formed as well as bond 1. A ring-shaped dimeric hydrogen bond 2 is formed between the atoms C1–H1⋯O1, which is strengthened by π-bond cooperativity.20 In addition, the somewhat weaker bond 4 is formed. Also in compound 4, very strong O–H⋯O hydrogen bonds 1 and a total of five other symmetry-independent C–H⋯O hydrogen bonds 2, 3, 4, 5, and 6 are present, resulting in a total of 12 O-acceptor hydrogen bonds for each molecule. The 2D fingerprint plot is similar to that of compound 3, also resulting in two sharp spikes for the O–H⋯O hydrogen bond 1 and the C–H⋯O hydrogen bonds 2, 3, 4, 5, and 6 are much weaker.
The bond distances and angles of all hydrogen bonds with O-acceptor of the three compounds 2–4 are shown in Table 4. Since the positions of the hydrogen atoms in 4 were freely refined, a column with the sum of D–H and H⋯A is also given in Table 4, which simplifies the comparison of the hydrogen bond strengths of compounds 2–4.
As can be seen from Fig. 2, compound 2 has the largest number of O⋯H/H⋯O contacts, but since these are relatively weak C–H⋯O hydrogen bonds, this results in the lowest lattice energy and the best solubility of all three compounds. In compounds 3 and 4, two very strong O–H⋯O hydrogen bonds 1 are present in each case, which are the reason for the significantly higher lattice energy of these two compounds. The fact that compound 3 has a higher lattice energy than compound 4 cannot be concluded from Table 4. This is because the O–H⋯O hydrogen bonds 1, seem to be somewhat stronger for compound 4. In compound 3, slightly stronger C–H⋯O hydrogen bonds are present, but compound 4 forms significantly more of these short C–H⋯O hydrogen bonds. The reason for the deviating torsion angles between the aryl groups and the benzopyran groups also cannot be explained on the basis of the hydrogen bonds alone. However, it can be concluded that the orientation of the benzopyran group in 3 and 4 is stabilized by the strong one-dimensional linked O–H⋯O hydrogen bonds 1. Looking at the aryl group in 3 and 4, it can be seen that no very strong hydrogen bond is formed here, except for hydrogen bond 6 in compound 4, the D–H⋯A angles are about 130°.
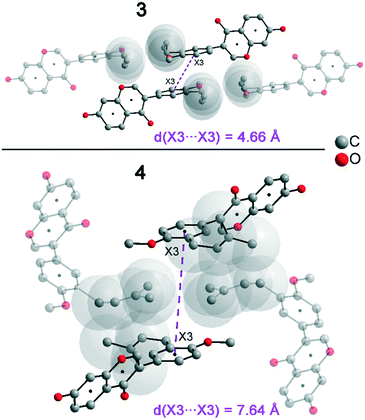
In addition to hydrogen bonds, the formation of attractive interactions between the aromatic rings of the molecules occurs in compounds 2–4. These offset-face-to-face and edge-to-face stacking interactions can be analysed using the program Aromatic Analyser (CSD-Materials). This program uses a neural network model to analyse the distances and orientations of aromatic rings to each other. Each stacking interaction is scored from 0 to 10, with high scores indicating strong interactions and low scores indicating weak interactions. Table 3 shows all stacking interactions in compounds 2–4 with a score above 6, Fig. 5 shows these stacking interactions in molecular environment. The stacking interactions can also be analysed by imaging the C⋯C contacts on the Hirshfeld surface. Fig. S3 in the ESI† shows these Hirshfeld surfaces (top), below is the representation of the molecular structure, and at the bottom is the 2D plot for the C⋯C contacts. Each molecule in compound 2 forms strong stacking interactions with a total of four neighbour molecules (see Fig. 5, left). In each case, two symmetry-equivalent interactions occur between the aryl groups 1 and the benzopyran groups 2. The interacting aromatics arrange at an angle of 62.62° (1) and 22.07° (2). Unlike in compounds 3 and 4, parallel-displaced stacking interactions do not form in 2. The reason is probably repulsion between the bulky methoxymethoxy and allyl groups of neighbouring molecules. Within the solid-state, the stacking results in intermolecular chains that expand along the crystallographic c-axis (see packing picture in the ESI†). The fact that there are no directional interactions, such as strong hydrogen bonds or parallel-displaced or T-shaped stacking interactions, acting on the molecules in 2, means that the deviation of the torsion angle is low, at 128.46°, compared to the ideal 135° angle. In compound 3, each molecule also forms four stacking interactions (see Fig. 5, center), resulting in a particularly strong parallel-displaced stacking interaction 1 between the benzopyran groups of neighbouring molecules with an aromatic–aromatic distance of 3.7 Å. In addition, there is the formation of two symmetry-equivalent stacking interactions 2 between the benzopyran groups and the aryl groups with a relative orientation of 68.37°. Since the orientation of the benzopyran groups in 3 are already fixed by the formation of the strong O–H⋯O hydrogen bonds 1 and the stacking interaction 1, the aromatic–aromatic distance of stacking interaction 2 is also fixed; only the orientation of the aryl ring with respect to the benzopyran ring is variable. The aryl ring rotates such that in addition to 2 a parallel-displaced stacking interaction 3 is formed between neighbouring aryl groups. The arrangement of the molecules in 4 is similar to the arrangement in 3. A parallel-displaced stacking interaction 1 between neighbouring benzopyran rings and two symmetry-equivalent stacking interactions 2 between the benzopyran and aryl rings with a relative orientation of 58.46° are also formed. However, unlike 3, the stacking interaction between the aryl rings is absent (interaction 3 in compound 3). Due to the absence of this interaction, the orientation of the aryl ring depends mainly on stacking interaction 2, since the benzopyran ring is fixed by the O–H⋯O hydrogen bonds 1 and the stacking interaction 1, as in 3. For this reason, a more energetically favourable interaction 2 is formed in compound 4 compared to compound 3. This is also evident from the score of the interactions in Table 3. This score is slightly higher at 7.5 for interaction 2 in compound 4 than in compound 3 (score = 7.4), since in 3 the orientation of the aryl ring is also influenced by stacking interaction 3. The question is why no stacking interaction is formed between the aryl rings of neighbouring molecules in compound 4. Fig. 6 shows the arrangement of neighbouring aryl groups in compounds 3 and 4. It can be seen that the reason for the missing strong stacking interaction in 4 is the location of the bulky prenyl substituents. These arrange themselves exactly between the aryl rings, resulting in a centroid-centroid distance of 7.64 Å. The smaller allyl substituents in 3 intercalate into the interstitial space in such a way that the strong parallel-displaced stacking interaction 3 is possible. This observation is also consistent with the higher C⋯C contact percentage (Fig. 3) in compound 3 (2.4%) compared to 4 (1.7%). Interestingly, the relative orientation of interaction 2 in compound 3 and 4 corresponds geometrically exactly to the torsion angle between the benzopyran and aryl rings in the respective compound. This means that the different torsion angles of compound 3 (68.37°) and 4 (58.46°) can be clearly justified by the absence of stacking interaction 3 and the strengthening of stacking interaction 2 in compound 4. Also, the higher lattice energy, higher melting point and lower solubility behaviour of compound 3 compared to 4 can be explained by the additional stacking interaction 3.
| Compound 2 | d(X⋯X) [Å] | Rel. orientation [°] | Score |
|---|---|---|---|
| 1 (X3⋯X3) (two times) | 5.22 | 62.62 | 7.8 |
| 2 (X1⋯X1) (two times) | 5.20 | 22.07 | 6.7 |
| Compound 3 | d(X⋯X) [Å] | Rel. orientation [°] | |
| 1 (X1⋯X1) | 3.70 | 0 | 8.4 |
| 2 (X1⋯X3) (two times) | 5.32 | 68.37 | 7.4 |
| 3 (X3⋯X3) | 4.66 | 0 | 7.4 |
| Compound 4 | d(X⋯X) [Å] | Rel. orientation [°] | |
| 1 (X1⋯X1) | 4.00 | 0 | 8.9 |
| 2 (X1⋯X3) (two times) | 5.26 | 58.46 | 7.5 |
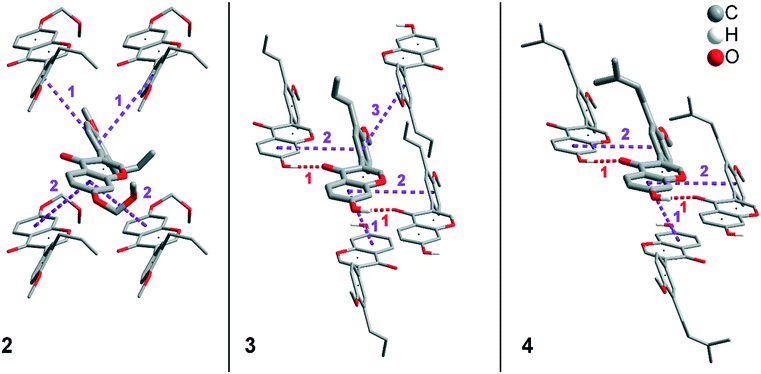 | ||
| Fig. 5 Strong stacking interactions and hydrogen bonds in compounds 2 (left), 3 (middle), and 4 (right). Non-acidic H atoms have been omitted. | ||
| Compound 2 | D–H [Å] | H⋯A [Å] | D⋯A [Å] | ∑ (D–H + H⋯A) [Å] | D–H⋯A [°] |
|---|---|---|---|---|---|
| 1 (C6–H6⋯O2) | 0.94 | 2.72 | 3.59 | 3.66 | 154.2 |
| 2 (C7–H7⋯O3) | 0.94 | 2.56 | 3.25 | 3.50 | 130.6 |
| 3 (C18–H18C⋯O4) | 0.97 | 2.54 | 3.50 | 3.51 | 174.6 |
| 4 (C21–H21B⋯O4) | 0.94 | 2.67 | 3.51 | 3.61 | 148.7 |
| 5 (C3–H3⋯O5) | 0.94 | 2.46 | 3.00 | 3.40 | 116.8 |
| 6 (C1–H1⋯O5) | 0.94 | 2.75 | 3.67 | 3.69 | 167.1 |
| Compound 3 | D–H [Å] | H⋯A [Å] | D⋯A [Å] | ∑ (D–H + H⋯A) [Å] | D–H⋯A [°] |
|---|---|---|---|---|---|
| 1 (O1–H100⋯O3) | 0.94 | 1.74 | 2.67 | 2.68 | 174.5 |
| 2 (C1–H1⋯O1) | 0.94 | 2.66 | 3.55 | 3.60 | 157.9 |
| 3 (C3–H3⋯O3) | 0.94 | 2.57 | 3.23 | 3.51 | 128.2 |
| 4 (C7–H7⋯O4) | 0.94 | 2.77 | 3.40 | 3.71 | 125.4 |
| Compound 4 | D–H [Å] | H⋯A [Å] | D⋯A [Å] | ∑ (D–H + H⋯A) [Å] | D–H⋯A [°] |
|---|---|---|---|---|---|
| 1 (O1–H100⋯O3) | 0.89 | 1.77 | 2.66 | 2.66 | 170.5 |
| 2 (C1–H1⋯O1) | 1.01 | 2.75 | 3.41 | 3.76 | 123.1 |
| 3 (C6–H6⋯O1) | 0.96 | 2.88 | 3.48 | 3.84 | 121.7 |
| 4 (C16–16A⋯O2) | 0.99 | 2.63 | 3.37 | 3.62 | 132.0 |
| 5 (C7–H7⋯O4) | 0.97 | 2.73 | 3.39 | 3.70 | 125.8 |
| 6 (C19–H19⋯O4) | 1.00 | 2.78 | 3.69 | 3.78 | 150.6 |
Conclusions
In the present work, the conformation, and intermolecular interactions of the 3-aryl-benzopyran derivates 2–4 have been investigated by single crystal X-ray analysis, mogul geometry search (CSD-Core), Hirshfeld surface analysis and the program Aromatic Analyser (CSD-Materials) with the aim to comprehend the different physicochemical properties. Despite the very similar molecular structure there are very large differences between the three compounds in terms of lattice energy, melting point and solubility behaviour. The low lattice energy and melting point of 2 (104 °C) can be clearly attributed to the absence of strong intermolecular O–H⋯O hydrogen bonds. Moreover, the repulsion between the bulky methoxymethoxy group on the benzopyran ring and the allyl substituents on the aryl ring prevents the formation of strong parallel-displaced stacking interactions. The absence of strong intermolecular interactions and the substitution of more nonpolar groups compared to compounds 3 and 4 also explains the good solubility in organic solvents.The significantly higher melting points of 3 (207 °C) and 4 (198 °C) and the lower solubility, especially in organic nonpolar solvents can be clearly attributed to the OH group at C2 and the formation of strong one-dimensional O–H⋯O hydrogen bonds. The fact that compound 3 has a higher lattice energy, a higher melting point and a lower solubility behaviour than 4 cannot be explained on the basis of the hydrogen bonds, because these are similarly numerous and similarly strong in both compounds. Looking at the stacking interactions formed by the rings, it can be seen that both compounds form strong parallel-displaced stacking interactions between the benzopyran rings and two stacking interactions between benzopyran and aryl rings. These interactions are even somewhat stronger in compound 4. In addition, however, another strong parallel-displaced stacking interaction is formed between the aryl rings of neighbouring molecules in compound 3, which does not occur in 4. This interaction is the reason for the divergent macroscopic properties in the two compounds. The reason for the absence of this stacking interaction in 4 can be clearly explained by the intercalation of the bulky prenyl substituents between the molecules, which prevent a spatially close arrangement of the aromatics in the solid-state. The different solubility behaviour of 3 and 4 can be attributed to the stacking interaction, since the lattice energy in 3 is slightly higher than in 4 due to the additional interaction. Therefore, compound 4 is soluble in ethanol, for example, and 3 is not. All in all, it can be said that the good solubility and low melting point of 2 is mainly explained by the absence of strong hydrogen bonds and the repulsion between the bulky methoxymethoxy and allyl groups of neighbouring molecules, but the difference between 3 and 4 results from the different number and thus strength of stacking interactions. In addition, a correlation between the conformation of the three title compounds, the supramolecular structure and the lattice energy was observed. According to a geometry analysis in the CSD, the ideal torsion angle between the benzopyran ring and the aryl ring is 45° and 135°, respectively. In compound 2 in which only weak hydrogen bonds and four non-parallel displaced stacking interactions are formed, the two rings are not affected by strong directing interactions. This results in a torsion angle of 128.46°, with a relatively small deviation of 6.54° from the ideal angle. In both compound 3 and compound 4, the benzopyran ring is fixed by strong O–H⋯O hydrogen bonds and parallel-displaced stacking interactions. Therefore, the torsion angle formed in the two compounds depends only on the interactions on the aryl ring. In compound 4, only one strong stacking interaction acts on the aryl ring, and this leads to a deviation of 14.47° from the ideal torsion angle between the aromatics. In compound 3, in addition to the stacking interaction, which is also present in 4, another strong stacking interaction acts on the aryl ring. To allow the parallel-displaced arrangement of this stacking interaction, the aryl ring must rotate even further, which is why there is a deviation of 23.14° from the ideal 45° torsion angle in compound 3. This means in the three title compounds, a greater deviation from the ideal torsion angle occurs with the increase in the number and strength of intermolecular interactions. Since the lattice energy and melting point also increase and the solubility decreases, the trend of these macroscopic properties can be recognised here indirectly from the deviation of the torsion angle from the ideal 45° or 135° angle.
Experimental
Materials, synthesis and measurements
The experimental procedures for the synthesis of compounds 2, 3 and 4 (ref. 8 and 21) and their 1H NMR, 13C{1H} NMR, IR and HRMS spectral data have been reported previously by us.8 All the compounds were recrystallized from methanol. Melting points were measured using a SMP-10 instrument from Bibby Scientific (Stuart) and are uncorrected.X-ray crystal structure analysis
The crystal structures of the compounds 2, 3 and 4 were determined by single crystal structure analysis. Suitable single crystals were selected using an optical microscope and were separated with oil. Fig. 7 shows the analysed crystal of the compound 3. X-ray crystal structure analysis was performed on a Stadivari diffractometer (Stoe) with Mo-Kα radiation (λ = 0.71073 Å). The data were corrected using the program X-Area22 and the structure was solved by direct methods and refined against F2 on all data by full-matrix least-squares using the SHELX suite of programs.23 The crystal structure was visualized with Diamond.24 The data (2: CCCD 2121813; 3: CCDC 2121812; 4: CCDC 2013149) can be obtained free of charge from The Cambridge Crystallographic Data Centre.Lattice energy calculation
The lattice energies of the three compounds were calculated using the program CrystalExplorer 21.5,25 with the CIF of the compounds used as the input file. For the calculation of the lattice energy, one molecule of the compound was marked and a cluster of neighbouring molecules at least 20 Å distance was created and all incomplete molecules were completed. All molecules within this cluster interacting with the central molecule were considered and the default benchmarked B3LYP/6-31G(d,p) energy model was used for the calculation. The individual amounts and compositions of the calculated lattice energy are shown in the ESI.†Mogul CSD search
The configuration (bond lengths, bond angles and torsion angles) of all three title compounds was analysed using the program Mogul (CSD-Core) and compared with 640 structurally similar compounds from the CSD. Organometallic compounds and powder structures were excluded from the search. Only compounds from CSD version 5.43 were used for the analysis. All results of the Mogul Geometry Check can be found in the ESI.†Hirshfeld surface analysis
The molecular Hirshfeld surfaces (HS) and the 2D fingerprint plot were obtained using the CIF of 2, 3 and 4 as input file in the program Crystal Explorer 17.25 The HS was calculated using a high surface resolution, with the dnorm surfaces mapped over the colour scale range of −0.1 (red) to 1.4 Å (blue). The red spots on the Hirshfeld surface indicate the closest interactions between the atoms of neighbouring molecules. The 2D fingerprint plot was displayed with the di and de distances on the axes in the range of 0.4–2.6 Å. The di is the distance from the HS to the nearest atom internal to the surface, and de is the distance from the Hirshfeld surface to the nearest external atom.26Aromatic Analyser
The program Aromatic Analyser (CSD-Materials) was used to determine the stacking interactions. All results of the Aromatic Analyser search (score > 0) can be found in the ESI.†Funding
This work was supported by the German Academic Exchange Service (DAAD) with a PhD scholarship (grant number: 57381412) for George Kwesiga. Open access fees were covered by the Potsdam Graduate School (PoGS).Conflicts of interest
There are no conflicts to declare.Acknowledgements
Synthetic assistance by Mr. Andreas Foß is gratefully acknowledged.Notes and references
- M. S. Abdelfattah, M. K. Kharel, J. A. Hitron, I. Baig and J. Rohr, J. Nat. Prod., 2008, 71, 1569–1573 CrossRef CAS PubMed.
- V. R. Preedy, Isoflavones, Chemistry, analysis, function and effects, RSC Publishing, Cambridge, 2013, vol. 5 Search PubMed.
- R. Simons, H. Gruppen, T. F. H. Bovee, M. A. Verbruggen and J.-P. Vincken, Food Funct., 2012, 3, 810–827 RSC.
- L. A. Mitscher, S. Drake, S. R. Gollapudi and S. K. Okwute, J. Nat. Prod., 1987, 50, 1025–1040 CrossRef CAS PubMed.
- K. Kaur, M. Jain, T. Kaur and R. Jain, Bioorg. Med. Chem., 2009, 17, 3229–3256 CrossRef CAS PubMed.
- A. W. Andayi, A. Yenesew, S. Derese, J. O. Midiwo, P. M. Gitu, O. J. Jondiko, H. Akala, P. Liyala, J. Wangui, N. C. Waters, M. Heydenreich and M. G. Peter, Planta Med., 2006, 72, 187–189 CrossRef CAS PubMed.
- M. C. Gessler, M. H. H. Nkunya, L. B. Mwasumbi, M. Heinrich and M. Tanner, Acta Trop., 1994, 56, 65–77 CrossRef CAS PubMed.
- G. Kwesiga, A. Kelling, S. Kersting, E. Sperlich, M. von Nickisch-Rosenegk and B. Schmidt, J. Nat. Prod., 2020, 83, 3445–3453 CrossRef CAS PubMed.
- (a) F. Singh and T. Wirth, Synthesis, 2013, 45, 2499–2511 CrossRef CAS; (b) B. Zhang, X. Li, B. Guo and Y. Du, Chem. Commun., 2020, 56, 14119–14136 RSC.
- (a) M. Pudipeddi and A. T. M. Serajuddin, J. Pharm. Sci., 2005, 94, 929–939 CrossRef CAS PubMed; (b) R. Censi and P. Di Martino, Molecules, 2015, 20, 18759–18776 CrossRef CAS PubMed.
- (a) D. Douroumis, S. A. Ross and A. Nokhodchi, Adv. Drug Delivery Rev., 2017, 117, 178–195 CrossRef CAS PubMed; (b) M. Karimi-Jafari, L. Padrela, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18, 6370–6387 CrossRef CAS.
- A. Jouyban, J. Pharm. Pharm. Sci., 2019, 22, 466–485 CAS.
- M. J. Webber and R. Langer, Chem. Soc. Rev., 2017, 46, 6600–6620 RSC.
- A. J. Edwards, C. F. Mackenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, Faraday Discuss., 2017, 203, 93–112 RSC.
- F. Musil, S. De, J. Yang, J. E. Campbell, G. M. Day and M. Ceriotti, Chem. Sci., 2018, 9, 1289–1300 RSC.
- I. Dance, New J. Chem., 2003, 27, 22–27 RSC.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Rec., 2016, 16, 473–487 CrossRef PubMed.
- S. Grabowsky, P. M. Dean, B. W. Skelton, A. N. Sobolev, M. A. Spackman and A. H. White, CrystEngComm, 2011, 14, 1083–1093 RSC.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- G. Kwesiga, E. Sperlich and B. Schmidt, J. Org. Chem., 2021, 86, 10699–10712 CrossRef CAS PubMed.
- STOE & Cie GmbH, X-Area, software package for collecting single-crystal data on STOE area-detector diffractometers, for image processing, for the correction and scaling of reflection intensities and for outlier rejection, STOE & Cie GmbH, Darmstadt, 2018 Search PubMed.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed; (b) G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- K. Brandenburg and H. Putz, Crystal Impact Diamond, Diamond - Crystal and Molecular Structure Visualization, Bonn, Germany, 2020 Search PubMed.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The crystallographic data (2: CCCD 2121813; 3: CCDC 2121812; 4: CCDC 2013149). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2ce00169a |
| This journal is © The Royal Society of Chemistry 2022 |