Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A neutral, acyclic, borataalkene-like ligand for group 11 metals: L- and Z-type ligands side by side†‡
Felix
Krämer
a,
Michael
Radius
a,
Helga
Berberich
a,
Israel
Fernández
 *b and
Frank
Breher
*b and
Frank
Breher
 *a
*a
aInstitute of Inorganic Chemistry, Karlsruhe Institute of Technology (KIT), Engesserstr. 15, Karlsruhe 76131, Germany. E-mail: breher@kit.edu
bDepartamento de Química Orgánica I, Facultad de Ciencias Químicas and Centro de Innovación en Química Avanzada (ORFEO-CINQA), Universidad Complutense de Madrid, Madrid 28040, Spain. E-mail: israel@quim.ucm.es
First published on 21st February 2022
Abstract
The overall neutral α-borylated phosphorus ylide Ph3PC(Me)BEt2 behaves like a polar borataalkene and can act as acyclic, ambiphilic π-type ligand with L- and Z-type functionalities side by side. In the complexes [MX{η2-Ph3PC(Me)BEt2}] (M = Cu, (Ag), Au; X = Cl, NTf2), the bonding is dominated by the highly nucleophilic ylidic carbon atom (L-type ligand). The Lewis acidic boron atom furnishes nonetheless a small but significant bonding contribution (Z-type ligand).
Boron-based ligands for transition metal complexes have received considerable attention for many years.1 Among others, one focus of interest refers to ambiphilic chelate ligands featuring an L-type donor entity and a Z-type acceptor unit suitable to stabilize metal→boron interactions.2 Boron-based π-ligands have also been studied, most often cyclic structures.3 Acyclic boron-based π-ligands,4 however, are relatively scarce and only a few transition metal complexes have been described.5 Interests in these types of ligands are rooted in their isoelectronic relationship to olefin ligands (Scheme 1),6 which have been studied in great detail during the past decades and are important intermediates in catalytic processes or serve as leaving groups in starting materials and as steering ligands in homogeneous catalysis, for instance.7 An inherent feature of anionic borataalkenes8 is their flexibility to potentially act as a “classical” π-ligand according to the well-known Dewar–Chatt–Duncanson (DCD) model6,7 or as ambiphilic L-/Z-type ligand (Scheme 1).9
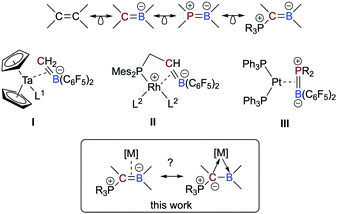 | ||
| Scheme 1 Isolectronic relationship between olefins and heteroalkenes and selected complexes consisting of anionic and neutral, acyclic boron-based π-ligands from the literature. Scope of this work. | ||
Piers and co-workers presented in 1999 the first example of an electron-poor, “early” Ta(0) complex featuring an anionic, C6F5-substituted borataalkene ligand (I in Scheme 1), which was synthesized by converting a Ta-bound alkylidene into the η2-coordinated [H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B(C6F5)2]− ligand.10 Quantum chemical calculations predicted that the latter species readily converts to boryl-substituted methyl ligand, most likely due to steric congestion. In 2020, Erker succeeded in isolating complexes of “late”, i.e. electron-rich metals bearing an anionic P/C
B(C6F5)2]− ligand.10 Quantum chemical calculations predicted that the latter species readily converts to boryl-substituted methyl ligand, most likely due to steric congestion. In 2020, Erker succeeded in isolating complexes of “late”, i.e. electron-rich metals bearing an anionic P/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B chelate ligand (II).11 Neutral heteroelement analogs of η2-bound olefins are, however, very rare. To the best of our knowledge, only one example has been described in the literature. Amgoune and Bourissou described the synthesis and full characterization of the platinum complexes [(Ph3P)2Pt(η2-{R2P
B chelate ligand (II).11 Neutral heteroelement analogs of η2-bound olefins are, however, very rare. To the best of our knowledge, only one example has been described in the literature. Amgoune and Bourissou described the synthesis and full characterization of the platinum complexes [(Ph3P)2Pt(η2-{R2P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B(C6F5)2})] (III; R = tBu, Cy) and performed an in-depth quantum-chemical analysis.12 Although the BP-based π-ligand is bound symmetrically, the polar electronic profile of the ligand is also reflected in its partially asymmetric bonding mode featuring characteristics of both a DCD-type π-ligand and an ambiphilic L-/Z-type ligand.
B(C6F5)2})] (III; R = tBu, Cy) and performed an in-depth quantum-chemical analysis.12 Although the BP-based π-ligand is bound symmetrically, the polar electronic profile of the ligand is also reflected in its partially asymmetric bonding mode featuring characteristics of both a DCD-type π-ligand and an ambiphilic L-/Z-type ligand.
In this context, we recently reported on a highly polarized π-bond13 consisting of a ylide carbon atom and a boron atom within the α-borylated phosphorus ylide Ph3PC(Me)BEt2 (L1, Scheme 2).14 As exemplified in small molecules activation, the competition for the lone-pair of electrons between the boryl (BR2) and phosphonyl (PR3) substituents results in electronic frustration within this overall neutral, highly polarized borataalkene-like molecule. We now hypothesized that species L1 would be a promising candidate to act as an acyclic, ambiphilic π-type ligand with L- and Z-type functionalities side by side.15 Note that a cyclic analog possessing the 9-borataphenanthrene anion has been recently published by Martin and co-workers.16 Reported herein is the successful realization of our hypothesis by the synthesis and (full) characterization of electron-rich, “late” transition metal complexes of L1 and a detailed analysis of their bonding situation.
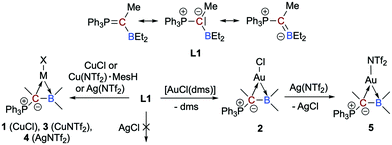
We were able to synthesize the anticipated group 11 complexes [MCl{η2-Ph3PC(Me)BEt2}] (M = Cu: 1; M = Au: 2) either by reacting CuCl with L1 in CH2Cl2 (74% isolated yield) or via the substitution of the CO in [AuCl(CO)] with L1, but only in poor yields (no reaction with [Ph3PAuCl]). To our delight, when the gold(I) complex [AuCl(dms)] (dms = dimethyl sulfide) is used as a precursor, however, an isolated yield of 91% for 2 could be achieved (Scheme 2). The mixture of L1 with AgCl in 1,2-Cl2C2H4 at 60 °C showed no reaction due to insolubility of AgCl.
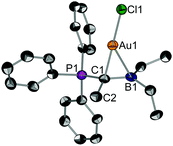
Suitable single crystals of 2 for X-ray diffraction were obtained by slow solvent evaporation of a saturated CH2Cl2 solution. The title compound crystallizes in the space group P21/c (Fig. 1). Most notably, the P1–C1 (178.2 pm) and the C1–B1 bond (155.2 pm) in 2 are considerably elongated as compared to the free pro-ligand L1 (171.7 pm and 149.2 pm, respectively). This clearly shows that the electron density from the ylidic carbon atom is involved in the C1–Au bond and, thus, is no longer available for both π-interactions with σ*(PC) or p(B) orbitals. The gold atom is coordinated in a linear fashion by the ylidic carbon atom and the chloride ligands (∠C1–Au1–Cl1 = 178.2°). The C1–Au1–Cl1 axis is slightly tilted towards the boron atom (∠B1–C1–Au1 = 80.0°) indicating bonding interaction between the boron center and the gold atom. The short B–Au distance of 239.4 pm found in the solid-state is a strong indication for a Au→B interaction. The distance is in the same region found for gold complexes of polydentate B/P ligands.17
The 1H NMR spectra of 1 and 2 in d8-toluene display line broadening at room temperature due to dynamic processes, in particular for the ethyl groups bound to boron. Variable temperature NMR investigations revealed energy barriers of ∼16 (for 1) and ∼15 (for 2) kcal mol−1 (for further details, see section S5, ESI‡). We assumed that this dynamic process is associated with the rotation around the Cylide–B bond. Indeed, density functional theory (DFT) calculations at the dispersion-corrected BP86-D3/def2-TZVPP level (ESI‡) indicate that the activation barrier associated with the Cylide–B rotation in 1 and 2 is 17.5 and 17.8 kcal mol−1, respectively. Both values agree reasonably well with the experimental ones (Fig. S1, ESI‡). Interestingly, the rotation along the Cylide–B bond has a dramatic impact on the bonding situation in the corresponding transition state TS. As depicted in Fig. S1 (ESI‡), the relatively short B–Au distance of 241.4 pm in 2 is significantly longer in TS (314.3 pm), thus indicating that the Au⋯B interaction in the latter saddle-point can be considered as negligible.
Furthermore, the 11B NMR signal of 2 at a chemical shift of δ(11B) = 53.6 ppm shifted upfield compared to the free pro-ligand L1 (cf. δ(11B) = 56.5 ppm).18 This is reminiscent of the 11B highfield shift of the boron–gold complexes featuring Au→B interactions (Chart S1, ESI‡).17
To check the accessibility of other group 11 complexes, we also prepared the whole series of {M(NTf2)} complexes 3–5 (3: Cu, 4: Ag, 5: Au; Scheme 2). It turned out, however, that only highly sensitive, oily products are formed. Due to this, a full characterisation was not possible. We have nevertheless performed comprehensive NMR studies and the results are convincing (e.g.11B NMR chemical shifts of δ(11B) = 53.3 ppm for 3, 58.5 ppm for 4, 53.8 ppm for 5, respectively, and δ(31P) = 31.3 ppm (d, 2JAgP = 27,8 Hz) for 4 in d8-toluene).
Again, line broadening at room temperature was observed for all complexes due to the dynamic process associated with the rotation around the Cylide–B bond. Variable temperature NMR investigations on 3–5 revealed slightly lower energy barriers of ∼15 (for 3 and 4) and ∼14 (for 5) kcal mol−1.
To further investigate the bonding situation in the newly prepared complexes, we first explored the electronic structure of the pro-ligand L1 with the help of DFT calculations. From the computational studies it becomes clear that pro-ligand L1 is best described by the zwitterionic resonance structure (Fig. S2, ESI†) with a negative charge on the carbon atom (i.e. ylide) and only to a lesser extent by the borataalkene structure. This is confirmed by comparing the charges and Wiberg Bond Indices of related species (see Table S1, ESI‡). Indeed, the computed HOMO can be viewed as a lone-pair at the carbon atom, which is slightly delocalized into the adjacent vacant pz atomic orbital of boron (see below). The latter finding is reflected in the computed C–B Wiberg bond Index of 1.24, which suggests a partial, highly polarized C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) B bond.
B bond.
More quantitative insight into the bonding situation of the {MCl} complexes (M = Cu, Ag, Au) can be gained by means of the energy decomposition analysis (EDA) method computed at the relativistic ZORA-BP86-D3/TZ2P//BP86-D3/def2-TZVPP level. From the data in Table 1, columns 2–4, it becomes evident that the main contribution to the bonding between L1 and {MCl} comes from the electrostatic interactions (measured by the ΔVelstat term), which contribute ca. 65% to the total interaction (ΔEint). This is consistent with the zwitterionic nature of pro-ligand L1 commented above. Despite that, the orbital interactions (ΔEorb) are also significant, albeit to a lesser extent (ca. 30%). In contrast, interactions coming from dispersion forces (ΔEdisp) are much less important in the L1···{MCl} interaction (ca. 5%).
| [MCl{η2-Ph3PC(Me)BEt2}] | [(MNTf2){η2-Ph3PC(Me)BEt2}] | [AuCl{η2-Ph3PC(Me)BR2}] | ||||||
|---|---|---|---|---|---|---|---|---|
| M = Cu | M = Ag | M = Au | M = Cu | M = Ag | M = Au | R = CF3 | R = OMe | |
| ΔEint | −72.6 | −57.2 | −79.4 | −91.4 | −74.4 | −101.8 | −73.5 | −80.6 |
| ΔEPauli | 124.1 | 120.6 | 182.0 | 130.0 | 131.5 | 204.0 | 192.8 | 175.4 |
| ΔVelstat | −127.6 | −120.5 | −173.8 | −134.0 | −129.2 | −194.0 | −170.7 | −171.7 |
| ΔEorb | −56.0 | −46.5 | −75.0 | −62.6 | −54.4 | −88.4 | −83.0 | −71.4 |
| ΔEorb(ρ1) | −24.6 | −22.4 | −40.0 | −27.6 | −25.6 | −47.6 | −37.7 | −41.4 |
| ΔEorb(ρ2) | −13.6 | −8.4 | −14.9 | −12.3 | −8.7 | −14.5 | −25.3 | −9.9 |
| ΔEorb(rest) | −17.8 | −15.7 | −20.1 | −22.7 | −20.1 | −26.3 | −20.0 | −20.1 |
| ΔEdisp | −13.1 | −10.8 | −12.5 | −24.9 | −22.3 | −23.4 | −12.5 | −12.8 |
| r(M–C)/Å | 1.979 | 2.178 | 2.132 | 1.971 | 2.175 | 2.100 | 2.144 | 2.126 |
| r(M–B)/Å | 2.318 | 2.556 | 2.414 | 2.322 | 2.501 | 2.447 | 2.258 | 2.589 |
The natural orbital for chemical valence (NOCV) extension of the EDA method was applied next to further partitioning the orbital term into its main pair-wise interactions. According to the EDA-NOCV, two main orbital interactions dominate the total ΔEorb term, namely the donation from the lone-pair at the carbon atom to the σ*(M–Cl) and the π-backdonation from a doubly-occupied d atomic orbital at the transition metal to the vacant pz atomic orbital of the boron atom, denoted as ρ1 and ρ2, respectively (see Fig. 2). The σ-donation LP(C)→σ*(M–Cl) (ρ1) is significantly stronger than the π-backdonation (ρ2). When inspecting the influence of the coordinated group 11 metal, it becomes clear that M = Au leads to stronger interactions in all contributions and that the (hypothetical) silver complexes exhibit the lowest values when compared to Au or Cu complexes. This, however, is consistent with recent computations of Bayat et al.19a on phosphorus ylide complexes of group 11 metals and recent bonding analyses of related Au(I) complexes.19b This also correlates with the highest promotion energy for Ag(I) in the series Cu(I) (8.25 eV) < Ag(I) (9.94 eV) > Au(I) (7.83 eV) and the lowest electron affinity in the series Cu(I) (7.72 eV) > Ag(I) (7.59 eV) < Au(I) (9.22 eV). Moreover, the Au→pz(B) backdonation is comparable to that found in those complexes having a single anchor boron ligand (Chart S1, ESI‡), which were confirmed to exhibit a significant Au→B interaction.20 This backdonation is also validated by the NBO method, which provides a noticeable Au→B WBI of 0.25 and locates a significant stabilizing delocalization from the doubly-occupied d-atomic orbital of gold to the pz-atomic orbital of boron (associated ΔE(2) = −14.2 kcal mol−1). Therefore, our EDA-NOCV analysis indicates that the orbital interactions in 2 can be described as two donor–acceptor interactions involving the highly nucleophilic ylidic carbon atom as the dominant ligating atom (L-type ligand) and the Lewis acidic boron atom, which furnishes a weaker yet noticeable bonding contribution as a Z-type ligand. Results above suggest that the Au→pz(B) backdonation can be efficiently modulated by modifying either the geometry or the Lewis acidity of the BR2 moiety. For instance, in the rotated TS (Fig. S1, ESI‡), the Au–B bond distance is significantly longer than in that in 2 as a consequence of the position of the pz atomic orbital of boron, which is much less available to accept electron density from the gold atom. As a result, this saddle-point becomes destabilized with respect to 2 and exhibits an almost negligible Au→pz(B) π-backdonation (ΔEorb(ρ2) < −1 kcal mol−1).
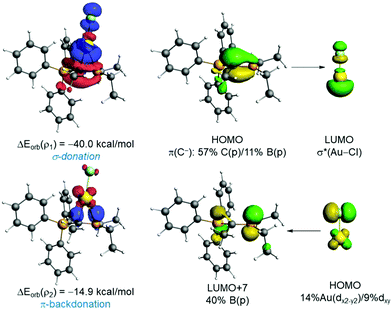 | ||
| Fig. 2 Deformation densities and associated molecular orbitals of the most important orbital interactions of 2 using the fragments AuCl and L1 (Table 1) together with the corresponding stabilizing energies ΔEorb(ρ1) and ΔEorb(ρ2). The colour code used to represent the flow of charge is red→blue. | ||
To check the influence of the Lewis acidity of the BR2 fragment, we attached both a strong electron-withdrawing (CF3) and electron-donor (OMe) groups directly to the boron atom. From the data in Table 1, columns 7 and 8, the replacement of the ethyl groups by CF3 significantly enhances the Au→pz(B) π-backdonation, which becomes almost twice as strong as that in the parent 2 (ΔEorb(ρ2) = −25.3 kcal mol−1). This is reflected in a markedly shorter Au–B bond (225.8 pm). At variance, the presence of the donor methoxy groups provokes the opposite effect and the Au→pz(B) π-backdonation becomes weaker (ΔEorb(ρ2) = −9.9 kcal mol−1) whereas the corresponding Au–B is much longer (258.9 ppm). We also studied the effect of the M-bound anion and compared {MCl} with {M(NTf2)} (cf.Table 1, columns 5–7). When changing X− = Cl− to (NTf2)−, the interaction between the {MX} and the ligand L1 becomes clearly stronger. This is mainly due to a significant increase in the orbital interactions (the electrostatic term also increases albeit to a lesser extent). In particular, the LP(C)→σ*(M–X) (ρ1) interaction becomes stronger because the M(NTf2) fragment is a much better acceptor as compared to {MCl}.20 For this same reason, the Au→pz(B) π-backdonation is slightly weaker.
In summary, this case study clearly depicts that the polar π-bond of the α-borylated phosphorous ylide differs significantly from a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π-bond and is even more polar than the phosphinoborane published by Amgoune and Bourissou.12 In the {MCl} complexes 1 and 2, the highly nucleophilic ylidic carbon atom is the dominant ligating atom (L-type ligand). The Lewis acidic boron atom furnishes a small but significant bonding contribution as a Z-type ligand. Thus, the bonding is asymmetric from both the geometric and the electronic perspectives. The overall neutral, acyclic pro-ligand L1 indeed behaves like a polar borataalkene ligand, which is induced by the competition for the lone-pair of electrons. Quantum chemical calculations predict that the strength of the Au→B interaction can be increased by introducing electron-withdrawing groups and decreased by π-donating substituents on boron. We also provided experimental and computational evidence that the L-type ligand contribution can be increased upon moving from X− = Cl− to (NTf2)−. Thus, it appears that the whole continuum between ambiphilic L-/Z-type coordination and DCD-type π-coordination can be covered by fully exploring the coordination chemistry of variously substituted α-borylated phosphorous ylides. Investigations in this direction are currently performed in our laboratories.
C π-bond and is even more polar than the phosphinoborane published by Amgoune and Bourissou.12 In the {MCl} complexes 1 and 2, the highly nucleophilic ylidic carbon atom is the dominant ligating atom (L-type ligand). The Lewis acidic boron atom furnishes a small but significant bonding contribution as a Z-type ligand. Thus, the bonding is asymmetric from both the geometric and the electronic perspectives. The overall neutral, acyclic pro-ligand L1 indeed behaves like a polar borataalkene ligand, which is induced by the competition for the lone-pair of electrons. Quantum chemical calculations predict that the strength of the Au→B interaction can be increased by introducing electron-withdrawing groups and decreased by π-donating substituents on boron. We also provided experimental and computational evidence that the L-type ligand contribution can be increased upon moving from X− = Cl− to (NTf2)−. Thus, it appears that the whole continuum between ambiphilic L-/Z-type coordination and DCD-type π-coordination can be covered by fully exploring the coordination chemistry of variously substituted α-borylated phosphorous ylides. Investigations in this direction are currently performed in our laboratories.
This work was supported by the Karlsruhe Institute of Technology (KIT) and the Spanish MCIN/AEI/10.13039/501100011033 (Grants PID2019-106184GB-I00 and RED2018-102387-T to I. F.)
Conflicts of interest
There are no conflicts to declare.Notes and references
- Selected reviews: (a) J. T. Goettel and H. Braunschweig, Coord. Chem. Rev., 2019, 380, 184 CrossRef CAS; (b) H. Braunschweig, R. D. Dewhurst and A. Schneider, Chem. Rev., 2010, 110, 3924 CrossRef CAS PubMed; (c) J. Takaja, Chem. Sci., 2021, 12, 1964 RSC.
- Selected reviews: (a) G. Bouhadir and D. Bourissou, Chem. Soc. Rev., 2015, 45, 1065 RSC; (b) A. Amgoune and D. Bourissou, Chem. Commun., 2011, 47, 859 RSC; (c) I. Kuzu, I. Krummenacher, J. Meyer, F. Armbruster and F. Breher, Dalton Trans., 2008, 5836 RSC; (d) F. G. Fontaine, J. Boudreau and M. H. Thibault, Eur. J. Inorg. Chem., 2008, 5439 CrossRef CAS; (e) H. Kameo and H. Nakazawa, Chem. – Asian J., 2013, 8, 1720 CrossRef CAS PubMed.
- (a) W. Siebert, Adv. Organomet. Chem., 1980, 18, 301 CrossRef CAS; (b) R. N. Grimes, in Boron-containing Rings Ligated to Metals in Comprehensive Organometallic Chemistry III, ed. R. H. Crabtree, D. M. P. Mingos and C. E. Housecroft, Elsevier Ltd, Oxford, 2007 Search PubMed.
- D. J. H. Emslie, B. E. Cowie and K. B. Kolpin, Dalton Trans., 2012, 41, 1101 RSC.
- Early work on π-complexes of amino-9-fluorenylideneborane: (a) S. Helm and H. Nöth, Angew. Chem., Int. Ed. Engl., 1988, 27, 1331 CrossRef; (b) S. Channareddy, G. Linti and H. Nöth, Angew. Chem., Int. Ed. Engl., 1990, 29, 199 CrossRef; (c) S. W. Helm, G. Linti, H. Nöth, S. Channareddy and P. Hofmann, Chem. Ber., 1992, 125, 73 CrossRef CAS.
- R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, Wiley, Hoboken, NJ, 7th edn, 2019, ch. 5 Search PubMed.
- C. Defieber, H. Grützmacher and E. M. Carreira, Angew. Chem., Int. Ed., 2008, 47, 4482 CrossRef CAS PubMed.
- R. J. Maza, J. J. Carbó and E. Fernández, Adv. Synth. Catal., 2021, 363, 2274 CrossRef CAS.
- (a) M. L. H. Green, J. Organomet. Chem., 1995, 500, 127 CrossRef CAS; (b) M. L. H. Green and G. Parkin, J. Chem. Educ., 2014, 91, 807 CrossRef CAS.
- (a) K. S. Cook, W. E. Piers and S. J. Rettig, Organometallics, 1999, 18, 1575 CrossRef CAS; (b) K. S. Cook, W. E. Piers, T. K. Woo and R. McDonald, Organometallics, 2001, 20, 3927 CrossRef CAS; (c) K. S. Cook, W. E. Piers and R. McDonald, J. Am. Chem. Soc., 2002, 124, 5411 CrossRef CAS PubMed.
- K. Watanabe, A. Ueno, X. Tao, K. Škoch, X. Jie, S. Vagin, B. Rieger, C. G. Daniliuc, M. C. Letzel, G. Kehr and G. Erker, Chem. Sci., 2020, 11, 7349 RSC.
- A. Amgoune, S. Ladeira, K. Miqueu and D. Bourissou, J. Am. Chem. Soc., 2012, 134, 6560 CrossRef CAS PubMed.
- D. Munz and K. Meyer, Nat. Rev. Chem., 2021, 5, 422 CrossRef CAS.
- (a) M. Radius and F. Breher, Chem. – Eur. J., 2018, 24, 15744 CrossRef CAS PubMed; (b) M. Radius, E. Sattler, H. Berberich and F. Breher, Chem. – Eur. J., 2019, 25, 12206 CrossRef CAS PubMed.
- To a degree, the boron containing allyl type ligands can be seen as neighboring L- and Z-type ligands: (a) M. W. Drover and J. C. Peters, Dalton Trans., 2018, 47, 3733 RSC; (b) F. Jiang, P. J. Shapiro, F. Fahs and B. Twamley, Angew. Chem., Int. Ed., 2003, 42, 2651 CrossRef CAS PubMed; (c) K. B. Kolpin and D. J. H. Emslie, Angew. Chem., Int. Ed., 2010, 49, 2716 CrossRef CAS PubMed.
- T. A. Bartholome, A. Kaur, D. J. D. Wilson, J. L. Dutton and C. D. Martin, Angew. Chem., Int. Ed., 2020, 59, 11470 CrossRef CAS PubMed.
- Selected examples: (a) M. Sircoglou, S. Bontemps, M. Mercy, N. Saffon, M. Takahashi, G. Bouhadir, L. Maron and D. Bourissou, Angew. Chem., Int. Ed., 2007, 46, 8583 CrossRef CAS PubMed; (b) M. Sircoglou, S. Bontemps, G. Bouhadir, N. Saffon, K. Miqueu, W. Gu, M. Mercy, C.-H. Chen, B. M. Foxman, L. Maron, O. V. Ozerov and D. Bourissou, J. Am. Chem. Soc., 2008, 130, 16729 CrossRef CAS PubMed; (c) A. Ueno, K. Watanabe, C. G. Daniliuc, G. Kehr and G. Erker, Chem. Commun., 2019, 55, 4367 RSC.
- This should not be the case, because upon coordination, the ylidic carbon atom possesses less electron density and the signal should be shifted downfield: (a) H. Nöth and B. Wrackmeyer, Chem. Ber., 1981, 114, 1150 CrossRef; (b) B. Wrackmeyer, Z. Naturforsch., B: J. Chem. Sci., 2015, 70, 421 CrossRef CAS.
- (a) M. Bayat, A. Sedghi, L. Ebrahimkhani and S. Sabounchei, Dalton Trans., 2017, 46, 207 RSC; (b) M. Navarro, J. Miranda-Pizarro, J. J. Moreno, C. Navarro-Gilabert, I. Fernández and J. Campos, Chem. Commun., 2021, 57, 9280 RSC.
- J. J. Cabrera-Trujillo and I. Fernández, Dalton Trans., 2020, 49, 3129 RSC.
Footnotes |
| † Dedicated to Prof. Cameron Jones on the occasion of his 60th birthday. |
| ‡ Electronic supplementary information (ESI) available. CCDC 2131093. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d2cc00199c |
| This journal is © The Royal Society of Chemistry 2022 |