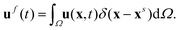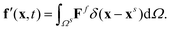DOI:
10.1039/D0SM01662D
(Paper)
Soft Matter, 2021,
17, 3560-3568
Magttice: a lattice model for hard-magnetic soft materials†
Received
15th September 2020
, Accepted 29th November 2020
First published on 7th December 2020
Abstract
Magnetic actuation has emerged as a powerful and versatile mechanism for diverse applications, ranging from soft robotics, biomedical devices to functional metamaterials. This highly interdisciplinary research calls for an easy to use and efficient modeling/simulation platform that can be leveraged by researchers with different backgrounds. Here we present a lattice model for hard-magnetic soft materials by partitioning the elastic deformation energy into lattice stretching and volumetric change, so-called ‘magttice’. Magnetic actuation is realized through prescribed nodal forces in magttice. We further implement the model into the framework of a large-scale atomic/molecular massively parallel simulator (LAMMPS) for highly efficient parallel simulations. The magttice is first validated by examining the deformation of ferromagnetic beam structures, and then applied to various smart structures, such as origami plates and magnetic robots. After investigating the static deformation and dynamic motion of a soft robot, the swimming of the magnetic robot in water, like jellyfish's locomotion, is further studied by coupling the magttice and lattice Boltzmann method (LBM). These examples indicate that the proposed magttice model can enable more efficient mechanical modeling and simulation for the rational design of magnetically driven smart structures.
1 Introduction
Hard-magnetic soft materials, usually made by embedding hard magnetic neodymium-iron-boron (NdFeB) microparticles into soft matrix-like silicone elastomers, have attracted great attention due to their various remarkable features such as the response to remote external stimuli, fast actuation, excellent flexibility, and stretchability.1–7 Promising applications include soft robotics,8–14 machines and actuators,15–20 microfluidics,21–25 biomedical devices10,13,14,26–30 (e.g., endovascular neurosurgery10 and smart catheters29), and multifunctional architected materials and meta-structures,8,25,31–37 just to name a few. The rapid developments of the field also call for efficient and accurate modeling and simulation platforms to rationalize the design, because these smart structures usually undergo very large and nonlinear deformation in complicated working environments, e.g., confined, enclosed spaces, combined liquid and solid terrain and brain's narrow and winding vasculature.9,14,20,38 For example, Hu et al.9 made untethered small-scale robots that can perform various complicated forms of locomotion, such as walking, jumping, rolling, and swimming by designing a harmonic magnetization profile in a magneto-elastic, rectangular sheet. These locomotion modes require a sophisticated control scheme to maneuver the robot as highly nonlinear deformation and multiphysics couplings are inevitable. An efficient and accurate modeling platform can provide a solid foundation for identifying the optimum control scheme and reduce the experimental trial-and-error.
Among various numerical techniques,32–39 finite element methods (FEMs) are widely used to simulate the nonlinear and active deformation of ferromagnetic materials.32,39 For example, Zhao et al.32 derived a finite element simulation scheme for the hard-magnetic soft materials and implemented it into the FEM software ABAQUS through a user-defined element (UEL). This robust and powerful platform has greatly promoted the computational contributions to the design of magnetic smart structures. However, it is still difficult to include the multiphysics interactions into the framework of UEL in ABAQUS, such as fluid–structure interactions. Besides, the commercial software's parallel simulation capabilities are also constrained by the setup of the computational environments and the availability of the research licenses. Lattice models are another kind of numerical techniques for simulating elastic solids that are efficient and easy to integrate with other methods for multiphysics problems.40–48 For example, lattice spring gel models have been applied to study the fluid-driven motion of microcapsules on compliant surfaces.44,49 Recently, the authors derived irregular lattice models directly from the FEM framework,46 and further coupled the lattice model with the lattice Boltzmann method (LBM) for complicated fluid–structure interactions (e.g., the platform of OpenFSI50). Although the simplicity and powerfulness of the lattice model make it very promising, there is still a lack of a rigorous derivation to include the magnetic forces.
In this work, we present a modeling and simulation platform of hard-magnetic soft materials that combines the advantages of the recently developed FEM schemes and lattice models, named ‘magttice’. We show that the magnetic actuation can be incorporated into the existing lattice model as nodal forces, which can be pre-computed if the external magnetic field is uniform. We implement the magttice model into the open-source molecular dynamics package, LAMMPS, and leverage its highly parallelized simulation capability and the versatile simulation techniques for multiphysics problems, such as fluid–structure interactions, by coupling the magttice model with the LBM. We then apply the magttice model to investigate the folded deformation of an origami plate, nonlinear deformation, and swimming of small-scale robots made by using a magnetic strip. These examples indicate that the proposed magttice model can enable more efficient mechanical modeling and simulation for the rational design of magnetically driven smart structures.
2 Computational model and benchmark
For hard-magnetic soft materials under moderate deformation (i.e., strain less than 30%), Zhao et al.32 have shown that the strain energy density (U) can be expressed as the summation of elastic energy (i.e., the neo-Hookean model) and magnetic energy| | 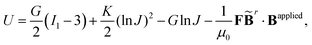 | (1) |
where G is the shear modulus, K is the bulk modulus, I1 = λ12 + λ22 + λ32 for plane strain deformation is the first invariant of the right Cauchy–Green deformation tensor, λi, i = 1, 2, 3 is the principal stretches and J is the determinant of the deformation gradient tensor F, μ0 is the vacuum permeability, ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) r and Bapplied denote the residual and applied magnetic flux densities, respectively. Note that
r and Bapplied denote the residual and applied magnetic flux densities, respectively. Note that ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) r is defined in the reference configuration. The strain energy density in eqn (1) is derived for ideal hard-magnetic soft materials,32 whose magnetic flux density is linearly related to the applied magnetic field. For more general cases, higher-order terms of the magnetic flux density should be included in the strain energy density function.39,51,52 For large deformation, the soft matrix will exhibit strain hardening (i.e., 30% for PDMS53) and thus requires modifying the elastic strain energy density in eqn (1). Since many applications utilize large geometry nonlinear deformation with small stretching or compression, we focus on the neo-Hookean model. It should also be noted that viscoelasticity is not included in the current model and has been shown to play an important role in the deformation of magnetic soft materials.54,55 All these nonlinearities in mechanical deformation and magnetic interactions are important and interesting research topics, which will be studied in our future work.
r is defined in the reference configuration. The strain energy density in eqn (1) is derived for ideal hard-magnetic soft materials,32 whose magnetic flux density is linearly related to the applied magnetic field. For more general cases, higher-order terms of the magnetic flux density should be included in the strain energy density function.39,51,52 For large deformation, the soft matrix will exhibit strain hardening (i.e., 30% for PDMS53) and thus requires modifying the elastic strain energy density in eqn (1). Since many applications utilize large geometry nonlinear deformation with small stretching or compression, we focus on the neo-Hookean model. It should also be noted that viscoelasticity is not included in the current model and has been shown to play an important role in the deformation of magnetic soft materials.54,55 All these nonlinearities in mechanical deformation and magnetic interactions are important and interesting research topics, which will be studied in our future work.
The lattice model is derived based on energy equivalence through comparing with the finite element model. In the framework of the FEM, the deformation gradient tensor F in an irregular element can be calculated as:56
| | 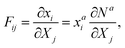 | (2) |
where
Na(
X1,
X2,
X3) is the shape function for a hexahedron element,
a = 1, 2,…,8, and
i,
j,
k = 1, 2, 3. The energy associated with
I1 can be written as:
| | 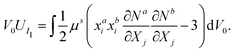 | (3) |
By rearranging the summations in eqn (3), the energy can be obtained in the lattice model (28 lattice springs in a general case Fig. 1(a)) with the form46
| | 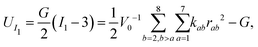 | (4) |
where
rab =
xa −
xb. Comparing above two energy expressions, we can easily calculate
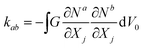
,
j = 1, 2, 3,
a = 1, 2,…,7,
b = 2, 3,…,8. The volumetric energy is calculated with an averaged volumetric strain (
Fig. 1),
| | 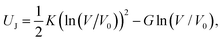 | (5) |
where
V and
V0 represent the lattice's volumes at the deformed and undeformed (reference) configurations, respectively. The spring constants
kab can be computed following the same procedure of calculating thestiffness matrix in the FEM. In short, the lattice model leverages FEM techniques to rewrite the strain energy inside a hexahedron element as a summation of energies associated with lattice stretching and volumetric changes. Note that the bulk modulus
K is usually not directly reported in the literature, and here we just set as
K = 20
G to mimic the nearly incompressible condition of polymers and soft materials.
57,58
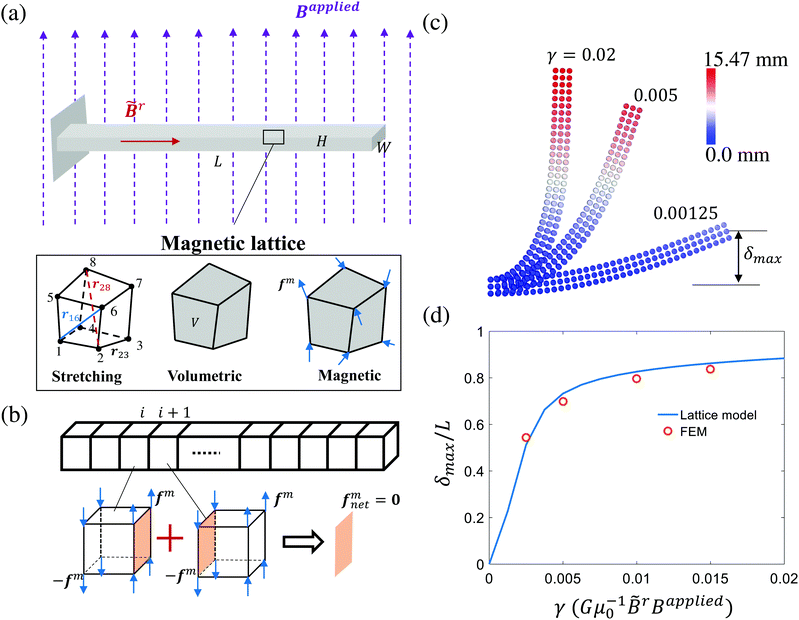 |
| | Fig. 1 Computational model and benchmark of the proposed magttice model. (a) Illustration of the proposed magttice model for ferromagnetic materials. (b) Diminished magnetic forces for the interior part of a beam with uniformly residual and external magnetic fields. (c) Deformed configurations of a representative beam (length L = 17.5 mm, width W = 5 mm, and height H = 1 mm) at different external magnetic fields. The dimensionless variable 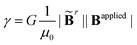 characterize the effective strength of magnetic forces, in comparison to the elasticity. (d) The normalized maximum displacement as a function of γ. The finite element solution is taken from previous work done by Zhao et al.32 characterize the effective strength of magnetic forces, in comparison to the elasticity. (d) The normalized maximum displacement as a function of γ. The finite element solution is taken from previous work done by Zhao et al.32 | |
For the magnetic energy density, it can also be pre-computed as
| | | Umagnetic = V0−1(−fm)aixai, | (6) |
where
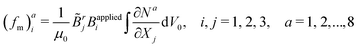
can be considered as general nodal forces associated with the magnetic actuation (
Fig. 1(a)). It is noted that
eqn (6) is valid only for spatially uniform external magnetic field because additional forces should be considered due to the gradient of the field.
59 For a given external magnetic field that is characterized by the applied magnetic flux density
Bapplied, it is interesting to note that
fm is a dead force under large deformation whose direction does not change along with the deformation. Therefore, the magnetic forces can be easily incorporated into the same framework through added nodal forces in the job script of LAMMPS simulations. This enables us to directly simulate active deformations due to magnetic forces in OpenFSI,
50 which is based on LAMMPS and already has lattice models for pure mechanics structures. For temporally changing and spatially uniform external magnetic field, we will show in the following sections (Section 3) that the updates of the magnetic forces can be directly done within the LAMMPS script without re-running the integration in
eqn (6). This will significantly simplify the simulations of the dynamic motions of magnetic robots, such as swimming in water.
Viewing the magnetic actuation as forces can also help simplify the modeling systems. Taking a ferromagnetic beam structure as an example with ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) r = [1, 0, 0]T and Bapplied = [0, 0, 1]T (Fig. 1(a) and (b)), the magnetic forces applied to the interior nodes will be cancelled out by summing the forces of the adjacent elements. This will lead to zero internal forces and non-zero nodal forces at the two ends, which is consistent with the recent observations in the modeling of the magnetic actuation of ferromagnetic beams with the elastic model.60 We further simulate the deformed configurations of the representative ferromagnetic beam (length L = 17.5 mm, width W = 5 mm, and height H = 1 mm) using the proposed magttice model (Fig. 1(c)), where we have G = 330 kPa, K = 20 G and
r = [1, 0, 0]T and Bapplied = [0, 0, 1]T (Fig. 1(a) and (b)), the magnetic forces applied to the interior nodes will be cancelled out by summing the forces of the adjacent elements. This will lead to zero internal forces and non-zero nodal forces at the two ends, which is consistent with the recent observations in the modeling of the magnetic actuation of ferromagnetic beams with the elastic model.60 We further simulate the deformed configurations of the representative ferromagnetic beam (length L = 17.5 mm, width W = 5 mm, and height H = 1 mm) using the proposed magttice model (Fig. 1(c)), where we have G = 330 kPa, K = 20 G and 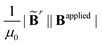 as a tunable parameter. As shown in Fig. 1(d), our simulation results are in excellent agreement with FEM results reported by Zhao et al.32
as a tunable parameter. As shown in Fig. 1(d), our simulation results are in excellent agreement with FEM results reported by Zhao et al.32
3 Applications to smart structures
Since the magttice model has been validated through a benchmark of beam bending simulation, we further demonstrate its capability of handling nonlinear and coupling deformation of smart structures with inhomogeneous residual magnetic fields. These examples include origami plates and magnetic robots, which represent structures with discretely and continuously nonuniform residual magnetic flux density, respectively.
3.1 Origami plate
Miura-ori folds have been created by encoding alternating oblique patterns of ferromagnetic domains in a simple rectangular structure (Fig. 2(a)). This is a representative example of non-uniform spatial residual magnetic flux density. We adopt the same geometries (Fig. 2(a)) and material properties in a previous work,32 where we have 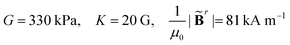 and |Bapplied| = 200 mT. After discretizing the origami plate into a 3D lattice, we compute the magnetic forces at each node. We then let the structure deform under magnetic forces and relax to its final equilibrium configuration by adding damping in the simulation. As depicted in Fig. 2(b), the magttice model can successfully capture the Miura-ori folds. It is interesting to note that forces concentrate on the domain boundaries with zero values in the interior of the domains (Fig. 2(c)). This can provide guidance for developing more efficient reduced-order models, such as plates and shells with active components, to understand the ferromagnetic origami plates’ mechanical behaviors with a much larger number of unit cells.
and |Bapplied| = 200 mT. After discretizing the origami plate into a 3D lattice, we compute the magnetic forces at each node. We then let the structure deform under magnetic forces and relax to its final equilibrium configuration by adding damping in the simulation. As depicted in Fig. 2(b), the magttice model can successfully capture the Miura-ori folds. It is interesting to note that forces concentrate on the domain boundaries with zero values in the interior of the domains (Fig. 2(c)). This can provide guidance for developing more efficient reduced-order models, such as plates and shells with active components, to understand the ferromagnetic origami plates’ mechanical behaviors with a much larger number of unit cells.
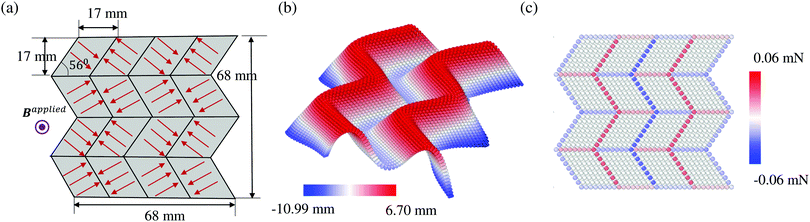 |
| | Fig. 2 Origami plate for Miura-ori folds. (a) The initial planar structure with an alternating ferromagnetic domain. The thickness of the plate is taken as 1 mm. (b) The deformed Miura-ori folds. (c) The distribution of the magnetic forces. | |
3.2 Statically deformed configuration of the magnetic strip
We next apply the magttice model to small-scale soft-bodied robots made by using magnetic strips with continuous and nonuniform residual magnetic flux density. We take the magneto-elastic, rectangular sheet in the work of Hu et al.9 as a representative structure and first focus on the statically deformed configurations. As shown in Fig. 3 (the central schematic), a flat sheet is placed on a solid platform and has a harmonic magnetization profile with βR = 45°. We model the same robot used in their work, with length L = 3.7 mm, width w = 1.5 mm, and thickness h = 185 μm. The material properties are also obtained from the same work, such as G = 33 kPa, K = 20 G, density ρ = 1.86 g cm−3 and 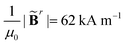 . In the following discussions, we keep all the geometrical and material properties the same, unless otherwise noted. To search for the static configuration after applying the external magnetic field, we gradually increase |Bapplied| in the simulations. After having |Bapplied| = 20 mT, the structure will be further relaxed for a sufficiently long time through a damped dynamic simulation until the changes of displacements become negligible. A pure repulsive interaction is assigned between the sheet and platform to describe the non-penetration conditions of the real platform. Gravity is also included in the simulation, whose important role will be discussed in detail in Section 3.3.
. In the following discussions, we keep all the geometrical and material properties the same, unless otherwise noted. To search for the static configuration after applying the external magnetic field, we gradually increase |Bapplied| in the simulations. After having |Bapplied| = 20 mT, the structure will be further relaxed for a sufficiently long time through a damped dynamic simulation until the changes of displacements become negligible. A pure repulsive interaction is assigned between the sheet and platform to describe the non-penetration conditions of the real platform. Gravity is also included in the simulation, whose important role will be discussed in detail in Section 3.3.
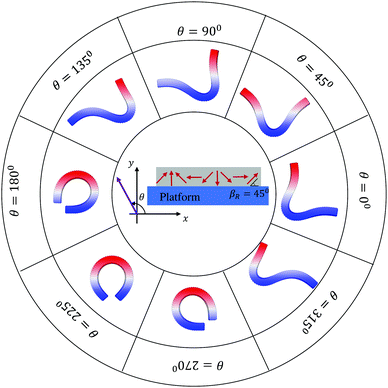 |
| | Fig. 3 Static configurations of the magnetic robot at different external magnetic fields. | |
Hu et al.9 already showed that the robot's final configurations depended on the direction of the external magnetic field and had “C” and “V” stable configurations. To demonstrate these aspects, we run eight simulations by varying the direction θ from 0° to 315°. As shown in Fig. 3, a “V” shape is observed when θ is closer to 45° and a “C” shape can be obtained when θ is closer to 215°. Furthermore, rigid body rotation can be noticed for θ = 90°, 180°, 270°, and 315°. These findings are all in excellent agreement with the analytical solutions and experiments in the previous study.9 However, the configurations for θ = 135° and θ = 315° are more complicated, which is neither a “V” nor a “C” shape. In addition, there is no rigid body rotation and two contact points between the robot and the platform.
3.3 Rigid body motion of the magnetic strip
The case with θ = 135° or θ = 315° seems an outlier in terms of the rigid body rotation and the deformation mode. It motivates us to further examine the effects of magnetic and gravity forces applied on the robot. We notice that there is a competition between the magnetic force and gravity. Focusing on the moment at point A, the magnetic force tends to generate rigid rotation to push the strip away from the ground, while the gravity creates moments to pull the strip down to the ground. Since the rigid body rotation is also coupled with the large nonlinear elastic deformation (Fig. 4(a)), we do not pursue the analytical formula of the moment applied to point A (center of the edge (x = 0, y = 0)) at a given deformed configuration. Instead, we quantify the competition between magnetic and gravitational forces (along the negative y direction) by gradually tuning the value of density and the magnitude of the applied magnetic flux density |Bapplied|. When the rigid body rotation happens, only one contact point exists between the magnetic strip and platform, the tangential line of the valley of the “V” shape can be used as an indicator of the extent of the rigid body rotation. For the normal value of gravity on earth, no rigid body rotation is observed, even for a large magnetic magnitude as 20 mT (Fig. 4(b) and (c)). When reducing the gravity by a factor of 2, rigid body rotation begins when the magnetic magnitude is larger than 6.25 mT. And the strip reaches a plateau (∼60°) of the rotation angle (Fig. 4(b) and (c)). In our simulations, we can set the gravity equal to 0 (e.g., the microgravity environment) and observe almost immediate rigid body rotation (Fig. 4(b)). The theoretical rotation limit (90°) is reached for magnetic magnitude as small as 5 mT (Fig. 4(c)). These examples clearly show that gravity plays an important role in determining the magnetic stripe's deformation modes, which can alter the performance of the magnetic robotic jumping, turning, and swimming. Furthermore, this also calls for more systematic simulations of the nonlinear deformation of ferromagnetic structures to design more efficient magnetic robots under different working conditions, to which the newly proposed magttice model can play an important role.
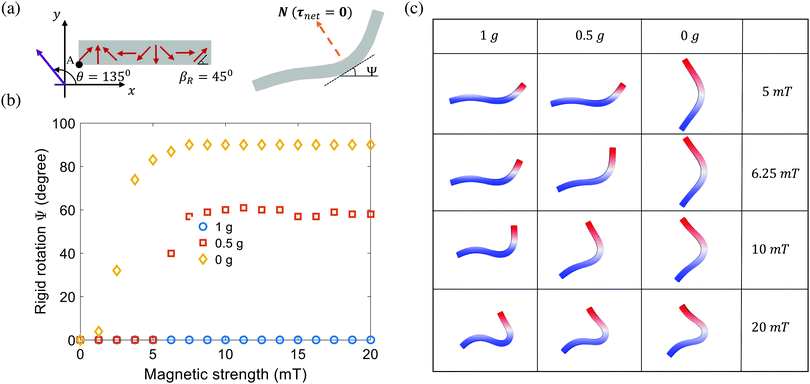 |
| | Fig. 4 Competing effect of magnetic forces and the gravity on the rigid body motion. (a) Schematics of the rigid body rotation. (b) Rigid rotation as a function of magnetic strength and gravity. (c) Representative deformed configurations of the robot under different magnetic and gravitational forces. | |
3.4 Turning of the magnetic robot
Uniform external magnetic fields with a changing direction are usually necessary to maneuver robots for various forms of locomotion, such as rolling, jumping, and swimming. To model the homogeneous external magnetic field with a changing direction, we can link the new (B′applied) and original (Bapplied) applied magnetic flux densities through a rigid body rotation matrix| | 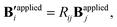 | (7) |
where Rij is the component of the matrix R for a given rotational angle Δθ (Δθ > 0 for counter-clockwise rotation), such that| | 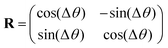 | (8) |
Substituting eqn (7) and (8) into the magnetic force defined by eqn (8), the new forces associated with the rotating external magnetic field can be expressed as| | | (fm′)ia = Rij(fm)ia, i, j = 1, 2, 3, a = 1,2,…,8. | (9) |
We only need to compute the magnetic forces at each node once for a given θ and directly compute the new magnetic forces after rotating the external magnetic field to θ + Δθ based on eqn (9). It enables us to simulate the external magnetic field's rotation by just modifying the variables in the input script of LAMMPS.
We demonstrate this function by using the robot turning-deformation as an example. The robot is first deformed into a “C” shape by setting θ = 225° and |Bapplied| = 16.9 mT. Then we perform three sequential rotations along the clockwise direction with Δθ = −45°. The robot is rotating with the external magnetic field and maintains the “C” shape (Fig. 5) (see Movie 1 of ESI†). Following this deformation sequence, it is very interesting to note that a “C” shape can be achieved for θ = 90°. This is different from the “C” shape starting from the fixed direction of the external magnetic field (Fig. 3), indicating that the structure is bi-stable.
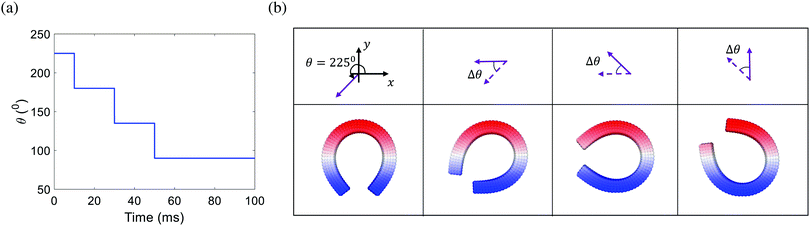 |
| | Fig. 5 (a) Time variation of the direction of the external magnetic field. (b) Structures with spatially varied residual magnetic flux for robotic-turn. Here we set Δθ = −45°. | |
3.5 Swimming of magnetic robots
To demonstrate this magttice platform's capability to model the multiphysics problem, fluid–structure interactions, we investigate the swimming of the magnetic robot and compare it with the experimental study in terms of the swimming gaits of the soft robot. As shown in the experiments by Hu et al.9 and our simulations, the soft magnetic robot's asymmetric shape can alternate between the “C”- and “V”-shapes under periodic B with time-varying magnitude along the principal axis. When the soft magnetic robot is immersed in water, this shape-changing mechanism can push it to swim upwards and overcome gravity, which manifests a gait similar to jellyfish swimming.15,61,62 In the simulation, we model the same robot used in the experimental study, with length L = 3.7 mm (x-direction), width w = 1.5 mm (y-direction), and thickness h = 185 μm (z-direction). It is placed in a fluid domain with size Lx = 16 mm, Ly = 8 mm and Lz = 16 mm with center initially at (Lx/2, Ly/2, Lz/4). To model the swimming motion of the robot in water, a fluid–structure interaction framework is introduced. Here, we briefly review the computational method used in this framework, which is detailed in our recent work.50 The fluid is governed by the Navier–Stokes equation (NSE)| | 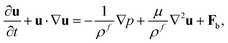 | (10) |
where ρf, u, and p are the fluid density, velocity, and pressure, respectively. μ is the dynamic viscosity of the fluid, and Fb is the body force. Instead of solving the NSE directly, we use the LBM to solve the discrete Boltzmann equation that can recover incompressible NSE through Chapman–Enskog analysis,63 due to its high efficiency and accuracy. In our simulation scheme, the D3Q19 model is used64 (Fig. 6(a)), where the fluid particles have possible discrete velocities in 19 directions. The explicit parameter underpinning the LBM is density distribution function fi(x,t), which is associated with the macroscopic properties of fluid as| | 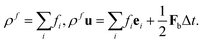 | (12) |
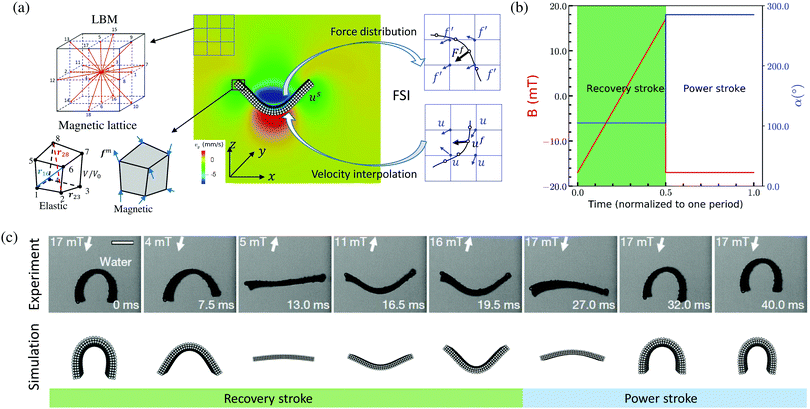 |
| | Fig. 6 Swimming of the magnetic robot. (a) Fluid–structure interaction scheme for the swimming of the magnetic robot. (b) Sequence of the applied magnetic field Bapplied, α is equal to 360°–θ. (c) Comparison of the gaits of the magnetic robot in one period: from recovery stroke to power stroke. The experimental results are adapted from Hu et al.9 | |
The magnetic robot is represented by a flat sheet and accounted for by the magttice model introduced in Section 2. The mechanical properties of the magnetic robot are the same as those in the experimental study (G = 33 kPa, K = 20 G, density ρ = 1.86 g cm−3 and 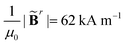 ). The coupling between the magnetic robot and fluid is fulfilled by the immersed boundary method (IBM), which has been extensively used to study the fluid–structure interaction problems.48,50,65,66,67 In IBM, the FSI force Ff is calculated as
). The coupling between the magnetic robot and fluid is fulfilled by the immersed boundary method (IBM), which has been extensively used to study the fluid–structure interaction problems.48,50,65,66,67 In IBM, the FSI force Ff is calculated as
| | | Ff = β(uf(t) − us(t)), | (13) |
where
β is the force coefficient,
us(
t) is the velocity of the structure, and
uf(
t) is the fluid velocity at the position where the structure locates.
uf(
t) is interpolated from its surrounding fluid velocity as
| | 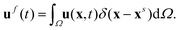 | (14) |
where
δ is a smoothed approximation of the Dirac delta interpolation function. To reflect the existence of the structure in the fluid, the FSI force will be spread into the surrounding fluid mesh as
| | 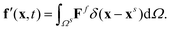 | (15) |
The sequence of Bapplied is given in Fig. 6(b), where the maximum Bapplied, Bappliedmax = 17 mT and frequency f = 25 Hz. Accordingly, the robot can perform locomotion when B is oscillating along the direction α = 105° and α = 285°. In one period, the prescribed Bapplied sequence can make the robot demonstrate a slow recovery stroke, in which the robot changes from the “C”-shape to “V”-shape (0–19.5 ms as shown in Fig. 6(c)). Following is a fast power stroke (19.5–32 ms as shown in Fig. 6(c)), which takes the robot back to the “C”-shape. From the comparison of the configuration evolution of the magnetic robot between experiment and simulation results (cf.Fig. 6(c)), we can see that the current fluid–structure interaction platform can capture the whole swimming gaits of the robot underwater. Furthermore, the asymmetry of the “C”-shape and “V”-shape makes the robot experiences more propulsion in power stroke than the reduction in recovery stroke. This net propulsion will propel the robot to move upwards along the z-direction. It resembles that of an actual jellyfish swimming,61 and it is also observed in our simulation (see Movie 2 of ESI†).
4 Conclusion
We derived a lattice model for hard-magnetic soft materials, so-called magttice. In the magttice model, the elastic energies are described by lattice stretching and volumetric changes, and the magnetic energy is modeled as potential energy associated with given nodal forces. Within this magttice model, the magnetic actuation can be incorporated into the existing lattice model in the OpenFSI package (https://github.com/huilinye/OpenFSI) directly through variables in the job script of LAMMPS simulations. Tuning the magnitude and direction of the applied magnetic flux density can also be realized in the script, without modifying any source code, if the external magnetic field is spatially uniform. The proposed magttice model is powerful and easy to use, as demonstrated by the examples in this study, including the origami plate and magnetic robots. Besides excellent agreements with the previous FEM simulations and experiments, our numerical analysis also revealed that magnetic forces would only exist at the domain boundaries under a uniform external magnetic field if the residual magnetic flux density is uniform within the domain. This finding will help develop a more efficient reduced-order model for structures with many domain structures, such as origami plates. Besides, we found that gravity plays an important role in the soft magnetic robots’ rigid body rotation. This may provide theoretical guidance for designing soft magnetic robots working in environments with different gravities, such as microgravity in outer space. Lastly, the magnetic robot swimming modeling confirms the capability of handling nonlinear and multiphysics coupled deformations, with which another path to design soft robots for biomedical applications, such as medical micro/nanorobots, is explored.14
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
H. Y. and Y. L. would like to acknowledge the support by the National Science Foundation under grant no. OAC-1755779. T. Z. acknowledges the support of the National Science Foundation under grant no. CMMI-1847149. H. Y. and Y. L. are grateful for the support from the Department of Mechanical Engineering at the University of Connecticut. Y. L. is partially supported by ASME Robert M. and Mary Haythornthwaite Research Initiation Award. T. Z. acknowledges the support from the Department of Mechanical and Aerospace Engineering at Syracuse University. H. Y. was partially supported by a fellowship grant from GE's Industrial Solutions Business Unit under a GE–UConn partnership agreement. The views and conclusions contained in this document are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of Industrial Solutions or UConn. This research also benefited in part from the computational resources and staff contributions provided by the Booth Engineering Center for Advanced Technology (BECAT) at the University of Connecticut. The authors also acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin (Frontera project and the National Science Foundation award 1818253) and Comet cluster at San Diego Supercomputer Center (National Science Foundation award 1341698) (SDSC) for providing HPC resources that have contributed to the research results reported within this paper.
Notes and references
- J. Ginder, S. Clark, W. Schlotter and M. Nichols, Int. J. Mod. Phys. B, 2002, 16, 2412–2418 CrossRef CAS.
- Y. Li, J. Li, W. Li and H. Du, Smart Mater. Struct., 2014, 23, 123001 CrossRef.
-
W. Li, K. Kostidis, X. Zhang and Y. Zhou, IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2009, pp. 233–238.
- H. Böse, R. Rabindranath and J. Ehrlich, J. Intell. Mater. Syst. Struct., 2012, 23, 989–994 CrossRef.
- S. Hong, Y. Jung, R. Yen, H. F. Chan, K. W. Leong, G. A. Truskey and X. Zhao, Lab. Chip, 2014, 14, 514–521 RSC.
- S. Kashima, F. Miyasaka and K. Hirata, IEEE Trans. Magn., 2012, 48, 1649–1652 Search PubMed.
- S. Opie and W. Yim, J. Intell. Mater. Syst. Struct., 2011, 22, 113–125 CrossRef.
- S. Wu, Q. Ze, R. Zhang, N. Hu, Y. Cheng, F. Yang and R. Zhao, ACS Appl. Mater. Interfaces, 2019, 11, 41649–41658 CrossRef CAS PubMed.
- W. Hu, G. Z. Lum, M. Mastrangeli and M. Sitti, Nature, 2018, 554, 81–85 CrossRef CAS PubMed.
- Y. Kim, G. A. Parada, S. Liu and X. Zhao, Sci. Robot, 2019, 4, 7329 CrossRef PubMed.
- T. Xu, J. Zhang, M. Salehizadeh, O. Onaizah and E. Diller, Sci. Robot., 2019, 4, 4494 CrossRef PubMed.
- S. Wu, C. M. Hamel, Q. Ze, F. Yang, H. J. Qi and R. Zhao, Adv. Intell. Syst., 2020, 2000060 CrossRef.
- K. E. Peyer, L. Zhang and B. J. Nelson, Nanoscale, 2013, 5, 1259–1272 RSC.
- Z. Wu, Y. Chen, D. Mukasa, O. S. Pak and W. Gao, Chem. Soc. Rev., 2020, 49, 8088–8112 RSC.
-
Z. Ren, T. Wang, W. Hu and M. Sitti, Robotics: Science and Systems, 2019.
- G. Mao, M. Drack, M. Karami-Mosammam, D. Wirthl, T. Stockinger, R. Schwödiauer and M. Kaltenbrunner, Sci. Adv., 2020, 6, eabc0251 CrossRef CAS PubMed.
- H.-W. Huang, M. S. Sakar, A. J. Petruska, S. Pané and B. J. Nelson, Nat. Commun., 2016, 7, 1–10 Search PubMed.
- H. Song, H. Lee, J. Lee, J. K. Choe, S. Lee, J. Y. Yi, S. Park, J.-W. Yoo, M. S. Kwon and J. Kim, Nano Lett., 2020, 20(7), 5185–5192 CrossRef CAS PubMed.
- J. Cui, T.-Y. Huang, Z. Luo, P. Testa, H. Gu, X.-Z. Chen, B. J. Nelson and L. J. Heyderman, Nature, 2019, 575, 164–168 CrossRef CAS PubMed.
- Y. Kim, H. Yuk, R. Zhao, S. A. Chester and X. Zhao, Nature, 2018, 558, 274–279 CrossRef CAS PubMed.
- F. Fahrni, M. W. Prins and L. J. van IJzendoorn, Lab Chip, 2009, 9, 3413–3421 RSC.
- S. Zhang, Z. Cui, Y. Wang and J. den Toonder, Lab Chip, 2020, 20, 3569–3581 RSC.
- S. Khaderi, C. Craus, J. Hussong, N. Schorr, J. Belardi, J. Westerweel, O. Prucker, J. Rühe, J. D. Toonder and P. Onck, Lab Chip, 2011, 11, 2002–2010 RSC.
- J. Belardi, N. Schorr, O. Prucker and J. Rühe, Adv. Funct. Mater., 2011, 21, 3314–3320 CrossRef CAS.
- H. Gu, Q. Boehler, H. Cui, E. Secchi, G. Savorana, C. De Marco, S. Gervasoni, Q. Peyron, T.-Y. Huang and S. Pane,
et al.
, Nat. Commun., 2020, 11, 1–10 Search PubMed.
- X. Zhao, J. Kim, C. A. Cezar, N. Huebsch, K. Lee, K. Bouhadir and D. J. Mooney, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 67–72 CrossRef CAS PubMed.
-
H. K. Yap, J. H. Lim, F. Nasrallah, F.-Z. Low, J. C. Goh and R. C. Yeow, IEEE International Conference on Rehabilitation Robotics (ICORR), 2015, pp. 735–740.
- P. R. Buckley, G. H. McKinley, T. S. Wilson, W. Small, W. J. Benett, J. P. Bearinger, M. W. McElfresh and D. J. Maitland, IEEE Trans. Biomed. Eng., 2006, 53, 2075–2083 Search PubMed.
- H. Gu, S. W. Lee, J. Carnicelli, T. Zhang and D. Ren, Nat. Commun., 2020, 11, 1–11 Search PubMed.
- S. Zhang, P. Zuo, Y. Wang, P. R. Onck and J. M. den Toonder, ACS Appl. Mater. Interfaces, 2020, 12(24), 27726–27736 CrossRef CAS PubMed.
- K. Yu, N. X. Fang, G. Huang and Q. Wang, Adv. Mater., 2018, 30, 1706348 CrossRef PubMed.
- R. Zhao, Y. Kim, S. A. Chester, P. Sharma and X. Zhao, J. Mech. Phys. Solids, 2019, 124, 244–263 CrossRef CAS.
- G. Z. Lum, Z. Ye, X. Dong, H. Marvi, O. Erin, W. Hu and M. Sitti, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E6007–E6015 CrossRef CAS PubMed.
- J. Li, T. D. Pallicity, V. Slesarenko, A. Goshkoderia and S. Rudykh, Adv. Mater., 2019, 31, 1807309 CrossRef PubMed.
- A. Goshkoderia, V. Chen, J. Li, A. Juhl, P. Buskohl and S. Rudykh, Phys. Rev. Lett., 2020, 124, 158002 CrossRef CAS.
-
S. M. Montgomery, S. Wu, X. Kuang, C. D. Armstrong, C. Zemelka, Q. Ze, R. Zhang, R. Zhao and H. J. Qi, 2020, arXiv preprint arXiv:2006.12721.
- K. H. Lee, K. Yu, H. Al Ba’ba’a, A. Xin, Z. Feng and Q. Wang, Research, 2020, 2020, 4825185 CrossRef PubMed.
- W. Gao, D. Kagan, O. S. Pak, C. Clawson, S. Campuzano, E. Chuluun-Erdene, E. Shipton, E. E. Fullerton, L. Zhang and E. Lauga,
et al.
, Small, 2012, 8, 460–467 CrossRef CAS PubMed.
- K. Danas, S. Kankanala and N. Triantafyllidis, J. Mech.
Phys. Solids, 2012, 60, 120–138 CrossRef CAS.
- M. Ostoja-Starzewski, Appl. Mech. Rev., 2002, 55, 35–60 CrossRef.
- X. He, M. Aizenberg, O. Kuksenok, L. D. Zarzar, A. Shastri, A. C. Balazs and J. Aizenberg, Nature, 2012, 487, 214–218 CrossRef CAS PubMed.
- O. Kuksenok and A. C. Balazs, Sci. Rep., 2015, 5, 1–7 Search PubMed.
- O. Kuksenok and A. C. Balazs, Mater. Horiz., 2016, 3, 53–62 RSC.
- A. Alexeev, R. Verberg and A. C. Balazs, Macromolecules, 2005, 38, 10244–10260 CrossRef CAS.
- V. V. Yashin and A. C. Balazs, J. Chem. Phys., 2007, 126, 124707 CrossRef PubMed.
- T. Zhang, Extreme Mech. Lett., 2019, 26, 40–45 CrossRef.
- P. Dayal, O. Kuksenok and A. C. Balazs, Langmuir, 2009, 25, 4298–4301 CrossRef CAS PubMed.
- H. Ye, Z. Shen and Y. Li, Comput. Mech., 2018, 62, 457–476 CrossRef.
- G. A. Buxton, R. Verberg, D. Jasnow and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 056707 CrossRef PubMed.
- H. Ye, Z. Shen, W. Xian, T. Zhang, S. Tang and Y. Li, Comput. Phys. Commun., 2020, 256, 107463 CrossRef CAS.
- A. Dorfmann and R. Ogden, Eur. J. Mech. A Solids, 2003, 22, 497–507 CrossRef.
- S. Kankanala and N. Triantafyllidis, J. Mech. Phys. Solids, 2004, 52, 2869–2908 CrossRef CAS.
- T. K. Kim, J. K. Kim and O. C. Jeong, Microelectron. Eng., 2011, 88, 1982–1985 CrossRef CAS.
- P. Saxena, M. Hossain and P. Steinmann, Int. J. Solids Struct., 2013, 50, 3886–3897 CrossRef.
- D. Garcia-Gonzalez, Smart Mater. Struct., 2019, 28, 085020 CrossRef CAS.
-
T. Belytschko, W. K. Liu, B. Moran and K. Elkhodary, Nonlinear finite elements for continua and structures, John wiley & sons, 2013 Search PubMed.
- S. Tang, Y. Li, Y. Yang and Z. Guo, Soft Matter, 2015, 11, 7911–7919 RSC.
- Z. Zhou, Y. Li, W. Wong, T. Guo, S. Tang and J. Luo, Soft Matter, 2017, 13, 6011–6020 RSC.
-
L. Dorfmann and R. W. Ogden, Nonlinear theory of electroelastic and magnetoelastic interactions, Springer, 2014, vol. 1 Search PubMed.
- L. Wang, Y. Kim, C. F. Guo and X. Zhao, J. Mech. Phys. Solids, 2020, 104045 CrossRef.
- B. J. Gemmell, J. H. Costello, S. P. Colin, C. J. Stewart, J. O. Dabiri, D. Tafti and S. Priya, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17904–17909 CrossRef CAS PubMed.
- Z. Ren, W. Hu, X. Dong and M. Sitti, Nat. Commun., 2019, 10, 1–12 CrossRef CAS PubMed.
-
S. Succi, The lattice Boltzmann equation: for fluid dynamics and beyond, Oxford University Press, 2001 Search PubMed.
- F. Mackay, S. T. Ollila and C. Denniston, Comput. Phys. Commun., 2013, 184, 2021–2031 CrossRef CAS.
- C. S. Peskin, Acta Numer., 2002, 11, 479–517 CrossRef.
- F.-B. Tian, H. Luo, L. Zhu, J. C. Liao and X.-Y. Lu, J. Comput. Phys., 2011, 230, 7266–7283 CrossRef CAS.
- H. Ye, H. Wei, H. Huang and X.-Y. Lu, Phys. Fluids, 2017, 29, 021902 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Simulation movies for turning and swimming of the magnetic robot. See DOI: 10.1039/d0sm01662d |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Ying
Li
a,
Ying
Li
 ab and
Teng
Zhang
ab and
Teng
Zhang
 *cd
*cd
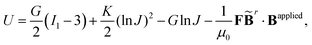
![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) r and Bapplied denote the residual and applied magnetic flux densities, respectively. Note that
r and Bapplied denote the residual and applied magnetic flux densities, respectively. Note that ![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) r is defined in the reference configuration. The strain energy density in eqn (1) is derived for ideal hard-magnetic soft materials,32 whose magnetic flux density is linearly related to the applied magnetic field. For more general cases, higher-order terms of the magnetic flux density should be included in the strain energy density function.39,51,52 For large deformation, the soft matrix will exhibit strain hardening (i.e., 30% for PDMS53) and thus requires modifying the elastic strain energy density in eqn (1). Since many applications utilize large geometry nonlinear deformation with small stretching or compression, we focus on the neo-Hookean model. It should also be noted that viscoelasticity is not included in the current model and has been shown to play an important role in the deformation of magnetic soft materials.54,55 All these nonlinearities in mechanical deformation and magnetic interactions are important and interesting research topics, which will be studied in our future work.
r is defined in the reference configuration. The strain energy density in eqn (1) is derived for ideal hard-magnetic soft materials,32 whose magnetic flux density is linearly related to the applied magnetic field. For more general cases, higher-order terms of the magnetic flux density should be included in the strain energy density function.39,51,52 For large deformation, the soft matrix will exhibit strain hardening (i.e., 30% for PDMS53) and thus requires modifying the elastic strain energy density in eqn (1). Since many applications utilize large geometry nonlinear deformation with small stretching or compression, we focus on the neo-Hookean model. It should also be noted that viscoelasticity is not included in the current model and has been shown to play an important role in the deformation of magnetic soft materials.54,55 All these nonlinearities in mechanical deformation and magnetic interactions are important and interesting research topics, which will be studied in our future work.
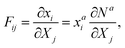
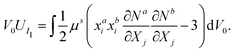
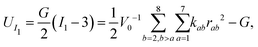
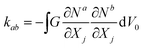 , j = 1, 2, 3, a = 1, 2,…,7, b = 2, 3,…,8. The volumetric energy is calculated with an averaged volumetric strain (Fig. 1),
, j = 1, 2, 3, a = 1, 2,…,7, b = 2, 3,…,8. The volumetric energy is calculated with an averaged volumetric strain (Fig. 1),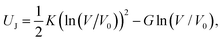

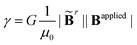 characterize the effective strength of magnetic forces, in comparison to the elasticity. (d) The normalized maximum displacement as a function of γ. The finite element solution is taken from previous work done by Zhao et al.32
characterize the effective strength of magnetic forces, in comparison to the elasticity. (d) The normalized maximum displacement as a function of γ. The finite element solution is taken from previous work done by Zhao et al.32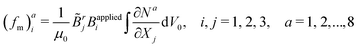 can be considered as general nodal forces associated with the magnetic actuation (Fig. 1(a)). It is noted that eqn (6) is valid only for spatially uniform external magnetic field because additional forces should be considered due to the gradient of the field.59 For a given external magnetic field that is characterized by the applied magnetic flux density Bapplied, it is interesting to note that fm is a dead force under large deformation whose direction does not change along with the deformation. Therefore, the magnetic forces can be easily incorporated into the same framework through added nodal forces in the job script of LAMMPS simulations. This enables us to directly simulate active deformations due to magnetic forces in OpenFSI,50 which is based on LAMMPS and already has lattice models for pure mechanics structures. For temporally changing and spatially uniform external magnetic field, we will show in the following sections (Section 3) that the updates of the magnetic forces can be directly done within the LAMMPS script without re-running the integration in eqn (6). This will significantly simplify the simulations of the dynamic motions of magnetic robots, such as swimming in water.
can be considered as general nodal forces associated with the magnetic actuation (Fig. 1(a)). It is noted that eqn (6) is valid only for spatially uniform external magnetic field because additional forces should be considered due to the gradient of the field.59 For a given external magnetic field that is characterized by the applied magnetic flux density Bapplied, it is interesting to note that fm is a dead force under large deformation whose direction does not change along with the deformation. Therefore, the magnetic forces can be easily incorporated into the same framework through added nodal forces in the job script of LAMMPS simulations. This enables us to directly simulate active deformations due to magnetic forces in OpenFSI,50 which is based on LAMMPS and already has lattice models for pure mechanics structures. For temporally changing and spatially uniform external magnetic field, we will show in the following sections (Section 3) that the updates of the magnetic forces can be directly done within the LAMMPS script without re-running the integration in eqn (6). This will significantly simplify the simulations of the dynamic motions of magnetic robots, such as swimming in water.
![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) r = [1, 0, 0]T and Bapplied = [0, 0, 1]T (Fig. 1(a) and (b)), the magnetic forces applied to the interior nodes will be cancelled out by summing the forces of the adjacent elements. This will lead to zero internal forces and non-zero nodal forces at the two ends, which is consistent with the recent observations in the modeling of the magnetic actuation of ferromagnetic beams with the elastic model.60 We further simulate the deformed configurations of the representative ferromagnetic beam (length L = 17.5 mm, width W = 5 mm, and height H = 1 mm) using the proposed magttice model (Fig. 1(c)), where we have G = 330 kPa, K = 20 G and
r = [1, 0, 0]T and Bapplied = [0, 0, 1]T (Fig. 1(a) and (b)), the magnetic forces applied to the interior nodes will be cancelled out by summing the forces of the adjacent elements. This will lead to zero internal forces and non-zero nodal forces at the two ends, which is consistent with the recent observations in the modeling of the magnetic actuation of ferromagnetic beams with the elastic model.60 We further simulate the deformed configurations of the representative ferromagnetic beam (length L = 17.5 mm, width W = 5 mm, and height H = 1 mm) using the proposed magttice model (Fig. 1(c)), where we have G = 330 kPa, K = 20 G and 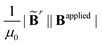 as a tunable parameter. As shown in Fig. 1(d), our simulation results are in excellent agreement with FEM results reported by Zhao et al.32
as a tunable parameter. As shown in Fig. 1(d), our simulation results are in excellent agreement with FEM results reported by Zhao et al.32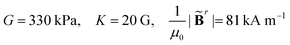 and |Bapplied| = 200 mT. After discretizing the origami plate into a 3D lattice, we compute the magnetic forces at each node. We then let the structure deform under magnetic forces and relax to its final equilibrium configuration by adding damping in the simulation. As depicted in Fig. 2(b), the magttice model can successfully capture the Miura-ori folds. It is interesting to note that forces concentrate on the domain boundaries with zero values in the interior of the domains (Fig. 2(c)). This can provide guidance for developing more efficient reduced-order models, such as plates and shells with active components, to understand the ferromagnetic origami plates’ mechanical behaviors with a much larger number of unit cells.
and |Bapplied| = 200 mT. After discretizing the origami plate into a 3D lattice, we compute the magnetic forces at each node. We then let the structure deform under magnetic forces and relax to its final equilibrium configuration by adding damping in the simulation. As depicted in Fig. 2(b), the magttice model can successfully capture the Miura-ori folds. It is interesting to note that forces concentrate on the domain boundaries with zero values in the interior of the domains (Fig. 2(c)). This can provide guidance for developing more efficient reduced-order models, such as plates and shells with active components, to understand the ferromagnetic origami plates’ mechanical behaviors with a much larger number of unit cells.
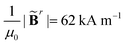 . In the following discussions, we keep all the geometrical and material properties the same, unless otherwise noted. To search for the static configuration after applying the external magnetic field, we gradually increase |Bapplied| in the simulations. After having |Bapplied| = 20 mT, the structure will be further relaxed for a sufficiently long time through a damped dynamic simulation until the changes of displacements become negligible. A pure repulsive interaction is assigned between the sheet and platform to describe the non-penetration conditions of the real platform. Gravity is also included in the simulation, whose important role will be discussed in detail in Section 3.3.
. In the following discussions, we keep all the geometrical and material properties the same, unless otherwise noted. To search for the static configuration after applying the external magnetic field, we gradually increase |Bapplied| in the simulations. After having |Bapplied| = 20 mT, the structure will be further relaxed for a sufficiently long time through a damped dynamic simulation until the changes of displacements become negligible. A pure repulsive interaction is assigned between the sheet and platform to describe the non-penetration conditions of the real platform. Gravity is also included in the simulation, whose important role will be discussed in detail in Section 3.3.
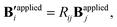
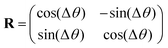

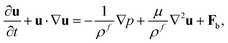
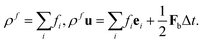

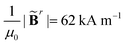 ). The coupling between the magnetic robot and fluid is fulfilled by the immersed boundary method (IBM), which has been extensively used to study the fluid–structure interaction problems.48,50,65,66,67 In IBM, the FSI force Ff is calculated as
). The coupling between the magnetic robot and fluid is fulfilled by the immersed boundary method (IBM), which has been extensively used to study the fluid–structure interaction problems.48,50,65,66,67 In IBM, the FSI force Ff is calculated as