Open Access Article
Open Access ArticlePair distribution function and 71Ga NMR study of aqueous Ga3+ complexes†
Ida Gjerlevsen
Nielsen
 a,
Sanna
Sommer
a,
Sanna
Sommer
 a,
Ann-Christin
Dippel
a,
Ann-Christin
Dippel
 b,
Jørgen
Skibsted
b,
Jørgen
Skibsted
 c and
Bo Brummerstedt
Iversen
c and
Bo Brummerstedt
Iversen
 *a
*a
aCenter for Materials Crystallography, Department of Chemistry, Interdisciplinary Nanoscience Center (iNANO), Aarhus University, 8000 Aarhus C, Denmark. E-mail: bo@chem.au.dk
bDeutsches Elektronen-Synchrotron DESY, D-22607 Hamburg, Germany
cDepartment of Chemistry, iNANO, Aarhus University, 8000 Aarhus C, Denmark
First published on 14th October 2021
Abstract
The atomic structures, and thereby the coordination chemistry, of metal ions in aqueous solution represent a cornerstone of chemistry, since they provide first steps in rationalizing generally observed chemical information. However, accurate structural information about metal ion solution species is often surprisingly scarce. Here, the atomic structures of Ga3+ ion complexes were determined directly in aqueous solutions across a wide range of pH, counter anions and concentrations by X-ray pair distribution function analysis and 71Ga NMR. At low pH (<2) octahedrally coordinated gallium dominates as either monomers with a high degree of solvent ordering or as Ga-dimers. At slightly higher pH (pH ≈ 2–3) a polyoxogallate structure is identified as either Ga30 or Ga32 in contradiction with the previously proposed Ga13 Keggin structures. At neutral and slightly higher pH nanosized GaOOH particles form, whereas for pH > 12 tetrahedrally coordinated gallium ions surrounded by ordered solvent are observed. The effects of varying either the concentration or counter anion were minimal. The present study provides the first comprehensive structural exploration of the aqueous chemistry of Ga3+ ions with atomic resolution, which is relevant for both semiconductor fabrication and medical applications.
Introduction
The atomic structures of ions and clusters in aqueous solution are of essential importance across chemical disciplines.1–3 Undergraduate chemistry text books inevitably devote considerable attention to describing the atomic structures of complex ions providing this fundamental information as a basis for all chemists. However, the structures of ion complexes are difficult to determine in their solvated form, and direct information is often lacking. Most structural tools, such as EXAFS or NMR, are challenged as information on atomic positions beyond the first coordination sphere is fuzzy, while information from IR and Raman spectroscopies is indirect and limited to bond identification and symmetry information.3,4 Therefore “solvated structures” for decades have mostly been probed indirectly using, for example, single-crystal X-ray or neutron diffraction, and it remains an open question whether the observed solid-state structures are representative of the solvated regime. As an example, several gallium structures of varying sizes and coordination have been determined using single-crystal X-ray diffraction.5–13 While solid state structures presumably have given insight into unknown solvated structures, many structures remain impossible to crystallize and fundamental uncertainty remains due to the structural perturbations caused by the solvent and the highly dynamic character of a solution. Recent developments of the total scattering (TS) and pair distribution function (PDF) techniques are changing the scientific landscape, as the accessibility and quality of data and modelling possibilities have increased enormously. Building on pioneering early PDF analysis,14–16 in recent years a range of solution structures have been refined with atomic resolution using these techniques.4,17,18 These advances inspired us to revisit central, and previously characterised solution systems, to provide updated structural information. Here we re-examine the aqueous Ga3+ system using X-ray TS to unravel its complex solution chemistry.The aqueous Ga3+ system is of significant technological interest since Ga2O3 is a promising semiconductor material for applications, e.g., in gas sensors and solar cells.19 Fabrication of both nanostructures and thin films has been reported from Ga3+ salts in aqueous solution.20–23 Due to the high sensitivity to disorder in semiconductors, an atomistic understanding of the nucleation and growth mechanism of solids from solution is important for tailoring suitable materials. Such understanding rests on the structure of the ions in solution, sometimes coined the precursor structure (PS), since that is the origin point of the formation reaction.17,24 Aqueous Ga3+ chemistry is also interesting for medical applications as both radioactive and stable gallium nitrates are used for diagnostic and therapeutic purposes in cancer and bone diseases, while other gallium compounds have anti-inflammatory and anti-microbial effects.25,26 Hence, the aqueous chemistry of Ga3+ must be understood on a structural level including the effects of concentration, pH and counter ions.
Experimentally, there is consensus in the literature that Ga3+ in water coordinates octahedrally to oxygen at low pH and tetrahedrally at high pH. In general chemistry textbooks, this is often written as [Ga(H2O)6]3+ at low pH and [Ga(OH)4]− at high pH. In the intermediate range there are reports on both amorphous Ga(OH)3, solid GaOOH and the Keggin structure ([GaO4Ga12(OH)24(H2O)12]7+).26–29 Different theoretical approaches have also been applied to the hydrated salts, supporting pH regions with either octahedral, Keggin or tetrahedral motifs.30–32 Several new gallium clusters have been discovered by single-crystal X-ray diffraction in the pursuit to confirm the presence of the Keggin structure, but structural information of the actual Ga Keggin ion remains elusive.8–13 In general, characterisation of aqueous gallium chemistry is less extensive than for the well-studied aluminium system, and group trends in the periodic table between the two systems have guided the analysis of various data on gallium systems and suggested similar structures.27–29
Here we use X-ray TS and subsequent PDF analysis in combination with 71Ga NMR to investigate the atomic structures of aqueous Ga3+ complexes across the entire pH range, for three different counter ions (nitrate, chloride, sulfate) and Ga3+ concentrations in the 0.5–2 M range. Through this comprehensive parameter study we provide an understanding of the complex interplay between the Ga3+ species and its chemical environment, and our study reiterates the often neglected complexity of solvent chemistry.
Experimental
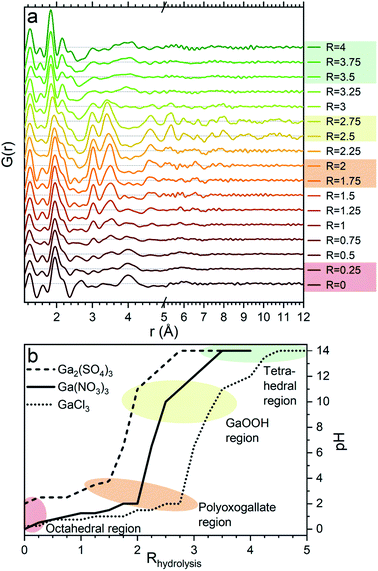
Aqueous solutions of Ga(NO3)3·xH2O (99.9%, Alfa Aesar), Ga2(SO4)3·xH2O (≥99.99%, Sigma-Aldrich) and GaCl3 (anhydrous, 99.99+%, Acros Organics) with a concentration of 1 M were made by adding demineralized water to the salts. For each salt, a pH series was made by adding varying volumes of 4 M NaOH solution to the 1 M Ga3+ solution to obtain hydrolysis ratios, R, ranging from 0 to 4 for Ga(NO3)3 and Ga2(SO4)3 and from 0 to 5 for GaCl3, each with steps of 0.25. The hydrolysis ratio is given by R = [OH−]/[Ga3+]. [OH−] and [Ga3+] denote the concentrations in the final solution of NaOH and gallium ions, respectively, which are calculated based on the used volumes and concentrations (1 and 4 M) of the stock solutions. As an unknown amount of crystal water is present in the precursor powders, the three different gallium stock solutions will have slightly different Ga3+ concentrations. This results in a small shift between the calculated and actual hydrolysis ratios. Consequently, the pH is not the same for the same hydrolysis ratio R in the three series, see Fig. 1b. The calculated hydrolysis ratio, R, will remain the denominator for different samples throughout, as the actual hydrolysis ratio remains unknown and the pH of the samples are not unique. Regarding the pH, it is worth noticing that the slightly elevated pH for the gallium sulfate solutions at low R can be explained by the weakly basic nature of the sulfate ion.An additional series was made for Ga2(SO4)3 with R = 1–1.6 and steps of 0.1. Furthermore, 0.5 and 2 M Ga3+ solutions were made from all the three salts to investigate concentration effects at R = 0. Addition of NaOH was also done to achieve solutions of R = 2 at the different concentrations.
TS data were collected for all solutions in 1.45 mm Kapton tubes at beamline P21.1, PETRA, Hamburg, Germany. Measurements were conducted with a wavelength of λ = 0.1204 Å and an instrumental Qmax of 28.8 Å−1. Data of diluted NaOH solutions with concentrations corresponding to the gallium solution data were used as backgrounds. Integration and calibration were done using Dioptas.33 The program xPDFsuite34 was used for the subtraction and transformation of the data to PDFs using Qmin = 1.12–1.25 and Qmax = 22.0–28.8 Å−1 (maximizing Qmax and minimising noise and termination ripples).
Modelling of the structures was performed using the DiffPy-CMI software.35 For the small structural motifs a cluster approach was employed including anion contributions and box restraints to the atomic positions. A crystalline approach was used for GaOOH.
Single-pulse 71Ga NMR spectra were obtained either at 14.09 T (νL(71Ga) = 182.8 MHz) on a solid-state Varian-Direct Drive spectrometer using a 4 mm CP/MAS probe, or at 9.39 T (νL(71Ga) = 121.9 MHz) on a liquid-state Bruker Avance III HD spectrometer equipped with a standard 5 mm liquid-state NMR probe. Solutions were prepared with Ga(NO3)3·xH2O and D2O (99.90% D, Euriso-top) as described above for the ratios R = 1.0, 1.5, 1.6, 1.7, 1.8, 1.9, 1.95, 2.0 and 2.1 and analysed at 14.09 T. In addition, a series was made for R = 0 with concentrations of 0.01, 0.05, 0.1, 0.5, 1 and 2 M, which were studied at 9.39 T. The spectra were acquired for samples of the clear supernatant of the solutions, as obtained after 5 min of centrifugation at 5000 rpm.
Results and discussion
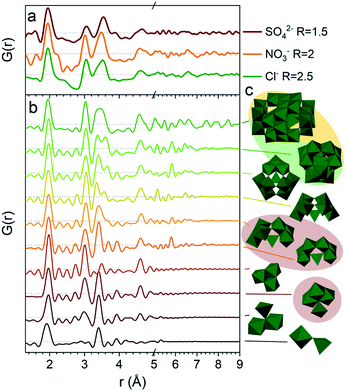
The PDFs of the pH series of the gallium nitrate solutions are presented in Fig. 1a, while the similar series for gallium sulfate and chloride are shown in Fig. S1.† When the signals from the anions are accounted for, the remaining signal is assumed to arise from the gallium structures in the solution. Modelling of the anion signals is discussed further in the ESI.† Four distinct structural regions appear across the full pH range for all three anions, Fig. 1b (see also Fig. S1†). The four identified structural regions are: (1) the octahedral region for pH < 2, (2) the polyoxogallate region for pH ≈ 2–3, (3) the GaOOH region for 4 < pH < 12 and (4) the tetrahedral region for pH > 12. The different regions will be discussed separately below. The hydrolysis ratio R, given as the concentration of OH− from NaOH divided by the concentration of Ga3+ from the gallium salts (R = [OH−]/[Ga3+]), will denominate the samples through the study as the pH value is not unique for all samples.Octahedral region
The 1 M Ga3+ solution without added NaOH (R = 0) shows structural correlations at 1.95, 2.73 and 4 Å, Fig. 1a. The correlation at 1.95 Å corresponds to the gallium–oxygen distance for an octahedrally coordinated Ga3+ ion, whereas the distance for tetrahedrally coordinated oxygen is 1.85 Å in various gallium oxide crystal structures, Fig. 2. The oxygen–oxygen distance in the octahedron gives rise to the signal at 2.73 Å.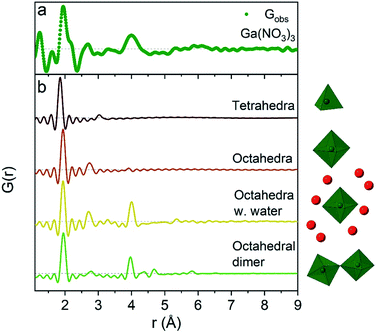 | ||
| Fig. 2 Comparison of (a) the R = 0 Ga(NO3)3 PDF data with (b) calculated PDFs for four small gallium–oxygen structures. From the top the first structure is from the β-Ga2O3 crystal structure,36 the second and third are from Ga(NO3)3·9H2O37 and the fourth from the study by Sommer et al.17 | ||
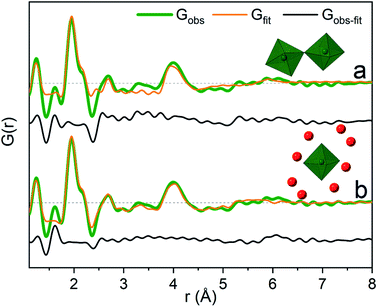
The significant peak at 4 Å is not explained by the simple octahedral coordination around Ga3+ (Fig. 2) and as the peak is quite wide it requires careful consideration during modelling. An octahedral dimer model has previously been suggested for this feature, which describes both the distances and the intensity ratio of the 1.95 and 4 Å peaks when refined (Fig. 3a).17 We have reanalysed the dimer model, and significantly better fits of the 4 Å peak can be obtained if the atoms of the dimer are allowed to relax where Rw changes from 0.499 for the model published by Sommer et al.17 to 0.412 for a relaxed model (see ESI Fig. S3 and S4†). However, the improved dimer model comes at the expense of increasing the number of refined parameters. We show below that the 4 Å feature alternatively can be modelled with an octahedral monomer surrounded by ordered solvent molecules (Fig. 3b). The monomer model with solvent molecules provides a much better fit (Rw decreases to 0.284), but again at the expense of more parameters. It is therefore important to scrutinize the different models.
To exemplify the different structural features in the monomer and dimer models we have calculated partial PDFs as seen in Fig. 4. The partial PDFs clearly show that Ga–O is the 2 Å peak, while Ga–O and Ga–Ga describe the 4 Å peak. The O–O only makes a small contribution to the PDF and describes the 2.8 Å peak for both models. The N–O distance in nitrate accounts for the shoulder at 2.2 Å (see also the ESI† for anion features).
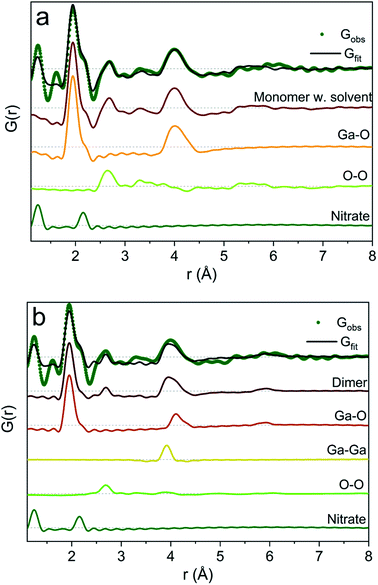 | ||
| Fig. 4 Model calculation of partial PDF contribution to (a) the monomer with the solvent and (b) the dimer model. | ||
It is difficult to determine the exact number of solvent molecules in the monomer model as additional fitting parameters naturally will improve the agreement with the data. In Fig. 5 we show fits using different numbers of water molecules (oxygen atoms) surrounding the central monomer unit. In Fig. 5a the oxygen positions are fixed at the values from the crystal structure,37 while in Fig. 5b the oxygen positions are refined with a box restraint of ±0.2 Å. As seen in Fig. 5a the shape of the 4 Å peak is too sharp in the crystalline model, but when the oxygen positions are refined a broadening can be achieved which better describes the peak shape in the PDF, Fig. 5b. Use of four or six oxygen atoms is not sufficient to fully describe the 4 Å peak, whereas eight oxygen atoms give a satisfactory description. Further increasing the number of oxygen results in slight improvement in the fits, but with a substantial increase in the fitting parameters. 16 oxygens give slightly too large intensity in the 4 Å peak. It appears that on balance the best model has eight oxygen atoms, but since the system is highly dynamic it is reasonable to expect a significant range of solvent molecules. The dimer as reported by Sommer et al.17 gives a narrow signal for the 4 Å peak, which is similar to the crystal model for the monomer (Fig. S4b†). For a better description refinement of atomic positions was done with altering box restraints (Fig. S4c and Table S1†) resulting in the model presented in Fig. 3 and 4 with a box restraint of ±0.9 Å. The dimer model and the solvated monomer model both produce satisfactory and quite similar fits of the PDF and it is not possible to firmly differentiate between the two based on the present data.
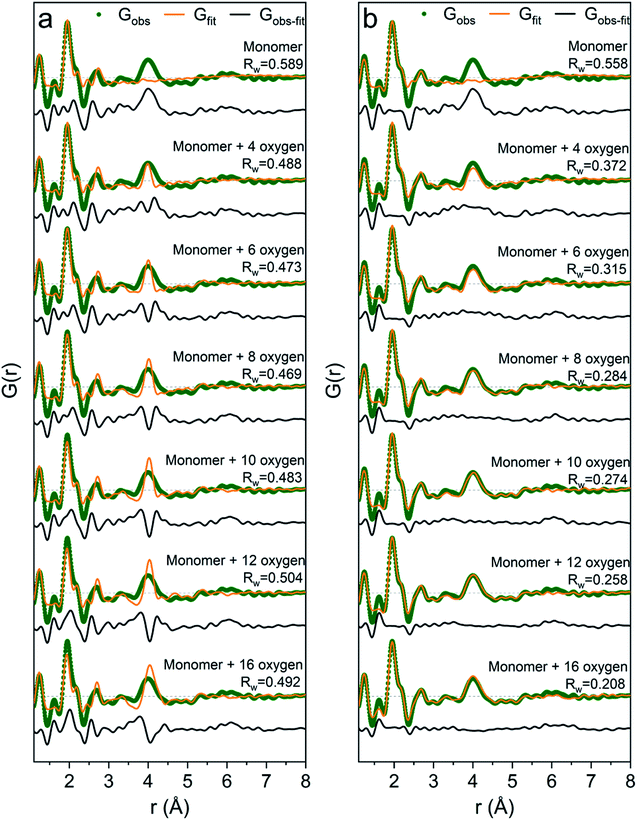 | ||
| Fig. 5 PDFs of Ga(NO3)3R = 0 fitted with: (a) the monomer model with different number of solvent oxygen atoms with positions fixed at values in a crystal structure37 and (b) the same models with refined oxygen positions and a box restraint of ±0.2 Å. | ||
In the solvated monomer model, the oxygen–oxygen distances between the first and second hydration shell refine to 2.59–3.27 Å. These values are within the normal range of oxygen–oxygen distances in water,1,38 confirming that the refined structure is physically sensible. Hydration shells beyond the first are often observed as broad signals;24,39–41 in contrast to this, in this respect, a quite narrow peak at 4 Å was observed. This indicates a specific ordering dictated by hydrogen bonds in the solvent model. For the dimer model, on the other hand, the peak at 4 Å appears quite wide for a specific rigid Ga–Ga distance, but this can be explained by dynamically varying Ga–O–Ga angles. In the dimer model the effect of an ordered solvation shell must be limited as it would lead to an over-description of the 4 Å peak.
Previously reported EXAFS data are also equally well described by the two different structural models (Table S3 and Fig. S5–S9†). Theoretical studies have not included a dimer model, and therefore its relative stability with respect to the solvated monomer model is unknown. It should be noted that the two models and their refinements are not considered to be uniquely correct and mutually exclusive models for the structures in the solution, but rather as examples of possible structures. Indeed most likely many slightly different structures are present in a dynamic solution, where the two presented models capture the structural characteristics of the actual structures. A mixture is possible – the present PDF data cannot differentiate between the two models.
The above observations are in general agreement with the literature, which describes the structure as an octahedrally coordinated Ga3+ ion at R = 0 based on EXAFS, NMR, Raman spectroscopy and theoretical calculations.27–32,42 Only a few of these studies treat the structure beyond the first coordination shell of six water molecules, and the structure is often simply written as [Ga(H2O)6]3+.30,31 The present modelling clearly shows that a higher degree of structural complexity (and order) is present in the aqueous solution.
While the X-ray scattering signal from hydrogen atoms is low and difficult to describe in the PDF models, it is still possible to consider the ligated species from a chemical perspective. As the pH is measured to be approximately 0 for the R = 0 solutions (except for the Ga2(SO4)3 solution due to the basic properties of the anion) hydrolysis must occur as [Ga(H2O)6]3+ → [Ga(OH)x(H2O)6−x](3−x)+ + xH+ with x ≈ 1 to give the correct pH. This makes [Ga(OH)(H2O)5]2+ a more chemically correct description of the gallium species at pH ≈ 0 rather than the commonly used [Ga(H2O)6]3+. If we include this chemical consideration then the modelled dimeric species can be written as [Ga2O(H2O)10]4+, while it is [Ga(OH)(H2O)5(H2O)8]2+ for the solvated monomer model.
When NaOH is added to the solutions (increasing R) the signal at 4 Å gradually disappears, while the remaining signal is left unchanged, Fig. 1a. The 4 Å distance corresponds to either the Ga–Ga distance in the dimer or the solvent coordination. The disappearance of a peak at 4 Å suggests that either the dimer breaks down or the solvent coordination becomes less significant. This might be caused by a deprotonation of [Ga(OH)(H2O)5]2+ which in turn would reduce the electrostatic ordering of the second water coordination. Addition of counter ions might also be a part of the explanation for lower ordering of the solvent or breaking of the dimer in the octahedral region. Additional ions are known to affect the bulk water structure,2,43 and they would likely result in a less ordered structure around Ga3+.
Polyoxogallate region
A larger structure gradually forms with increasing R. New peaks appear first at 3.1 and 3.5 Å and their heights become similar to the Ga–O peak at 1.95 Å which is observed for R = 2 (Fig. 1a). With correlations extending to at least 8 Å, the structure must be a polyoxogallate cluster.Several different polyoxogallates have been reported with the first being the Ga13 Keggin ion with the nominal stoichiometry [GaO4Ga12(OH)24(H2O)12]7+.28 This structure was suggested based on potentiometric measurements and 71Ga NMR (observing both tetrahedral and octahedral coordination), and combined with gallium's similarity to aluminium where the Al13 Keggin ion is well established.28 Several studies have sought to crystallise the Ga13 Keggin structure, but these resulted in different polyoxogallate clusters of varying sizes: Ga8, Ga9, Ga12, planar Ga13, Ga30 and Ga32 (full nominal composition in Table S4†).8–13 Importantly, no study specifically has observed the atomic positions in the suggested Ga13 Keggin structure.
For the present data the β-, γ- and δ-Ga13 Keggin isomers derived from aluminium crystal structures along with the Ga30 and Ga32 structures give the best descriptions of the PDF (Rw = 0.45, 0.37, 0.40, 0.36, 0.38, respectively, Fig. 6a and Table S5†). The remaining gallium structures and other common polyoxometalate clusters fail to describe the data (Table S5 and Fig. S10†). It has not been possible using only the PDF data to firmly determine which of the structures are present. Further information on the modelling can be found in the ESI.†
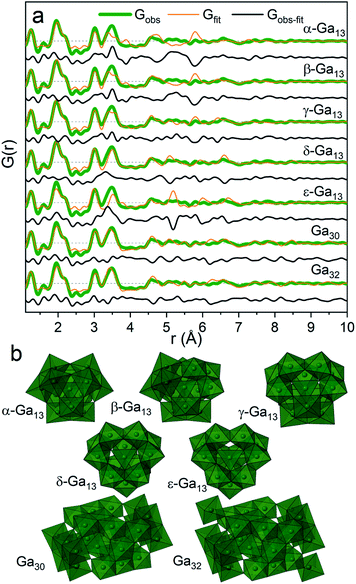 | ||
| Fig. 6 (a) PDF refinements of the five Keggin isomers as well as Ga30 and Ga32 for the Ga(NO3)3 solution with R = 2. (b) The different polyoxogallate structures. | ||
The different polyoxogallate structures are shown in Fig. 6b. The Keggin structures consist of four trimers of edge-sharing Ga–O octahedra surrounding a tetrahedrally coordinated Ga atom. For the α-Ga13 isomer, the trimers are connected by corner-sharing between neighbouring trimer units. Isomerization occurs by rotation of a trimer with 60° around its center. In this way, the bonding between the trimers shifts to being edge-sharing for the ε-isomer. A previous theoretical study reported the γ-Ga13 Keggin isomer as the most stable structure at the pH interval above the octahedral regime,32 while a combined NMR and EXAFS study suggests the ε-Ga13 isomer. For comparison, the Al13 Keggin ion has been observed as γ-, δ- and ε-iosomers.44
The Ga30 and Ga32 structures both have similar structural motifs to the Keggin ions with four tetrahedrally coordinated Ga atoms in the center surrounded by planes of edge-sharing Ga–O octahedra. The Ga32 structure is indistinguishable from the Ga30 structure except for the addition of two octahedra in opposite corners of the structure.
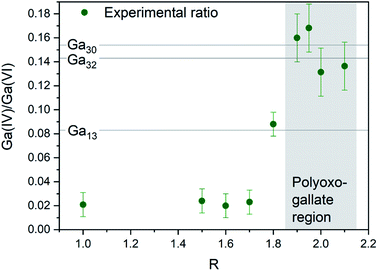
The Ga13, Ga30 and Ga32 structures have different ratios of tetrahedrally to octahedrally coordinated Ga3+ (Fig. 7, lines). The experimental ratios of Ga(IV)/Ga(VI) were determined by spectral integration over the characteristic ranges for Ga(IV) at ≈ 180 ppm and Ga(VI) at ≈ 0 ppm, giving values of 0.13–0.17(2) for samples with R ≈ 2 and pH matching the polyoxogallate region (Fig. 7 and S11, S12†). As the structures in the neighbouring pH regions solely consist of octahedrally coordinated Ga3+, it is assumed that no free tetrahedrally coordinated Ga3+ is present in the solutions. In that case the measured NMR ratios clearly suggest that Ga30 and/or Ga32 structures dominate the solutions with R ≈ 2, where the PDF signal of the polyoxogallate is strongest.
At R = 1.8, a lower Ga(IV)/Ga(VI) ratio is observed, and this may have two explanations: (1) the combination of an octahedrally coordinated Ga3+ and a Ga30/Ga32 structure, or (2) a Ga13 Keggin structure, which transitions to the Ga30/Ga32 structure upon further OH− addition. The first explanation is the simplest with only one stable polyoxogallate structure. This matches previous reports, where there is no evidence of more than one structure in the interval between the octahedral structure at the lowest pH and the GaOOH structure at intermediate pH. Thus, the present data suggest that the Ga13 Keggin structure does not exist for Ga3+ in aqueous solution, and in reality the polyoxogallate is a Ga30/Ga32 structure. The misinterpretation presumably is due to weak experimental evidence in combination with a tendency to correlate Ga data with the well-known Al13 Keggin structure. It should be noted that the Ga30 and Ga32 moieties have been observed in crystal structures,11,13 whereas the Ga13 structure has never been firmly demonstrated.
The formation of large polyoxogallates must originate from one of the octahedral [Ga(OH)(H2O)5]2+ structures. With the addition of OH− the reaction for the Ga30 could be:
| 30[Ga(OH)(H2O)5]2+ + 48OH− → [Ga30O16(OH)46(H2O)16]12+ + 150H2O | (1) |
GaOOH region
At elevated pH (10–12) the solutions show PDF correlations up to 20 Å, and the peak positions match those of crystalline GaOOH.45 The GaOOH structure consists of octahedrally coordinated Ga with both edge- and corner-sharing motifs. Below 5 Å the correlations are very similar to those observed for the polyoxogallate structure (Fig. 1a). This is explained by the very similar local coordination of Ga in GaOOH and the polyoxogallate structure, where edge-sharing octahedra dominate. Above 5 Å the correlations are stronger for the GaOOH region data and at 5.3 Å a new and distinct peak appears, which clearly distinguishes the newly formed structure from the polyoxogallate regime. The peak corresponds to the Ga–Ga distance in GaOOH, which is not present in the polyoxogallate structures. The transition from the polyoxogallate cluster to GaOOH occurs with addition of only a small amount of NaOH. Assuming the polyoxogallate structure to be Ga30 the reaction could be:| [Ga30O16(OH)46(H2O)16]12+ + 12OH− → 30GaOOH + 30H2O | (2) |
Both these reactions, as well as the reactions from Ga13 and Ga32 to GaOOH require only a small amount of OH− (see the ESI†), and this agrees with the observed abrupt transition.
The strongest signal from GaOOH is for the R = 2.5 solution (Fig. 1a). Modelling of the PDF was attempted with several different models (ESI Tables S7, S8 and Fig. S13†). A two-phase GaOOH model is necessary to describe the relative peak intensities, and both atomic positions, particle size and unit cell parameters were refined individually for each phase (Fig. 8 and Table S9†). The model suggests that distorted GaOOH structures are present with bimodal size distribution or anisotropic size. The refined particle sizes are approximately 25 Å and 10 Å for the two phases, respectively.
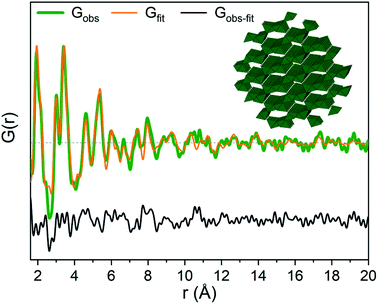 | ||
| Fig. 8 GaOOH modelled using two GaOOH phases at R = 2.5 for Ga(NO3)3 solution. The refined structure of the large GaOOH phase is shown as the inset. | ||
Tetrahedral region
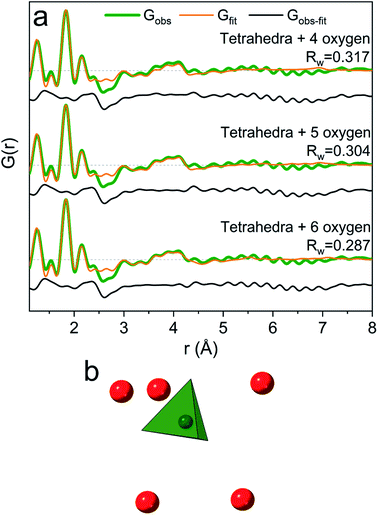
When the pH is raised above 12 the long-range order of the GaOOH nanoparticles disappears. The only remaining sharp peak (besides the anion signals) is the Ga–O peak, which shifts from 1.95 Å to 1.85 Å revealing a transformation from octahedral to tetrahedral Ga. The transition may be described as GaOOH + OH− + H2O → [Ga(OH)4]−. Modelling using a Ga–O tetrahedron and anion contributions describes the PDF data below 3 Å very well, but as for the octahedral region (R = 0) a peak at 4 Å is not accounted for in a simple monomer model (Fig. 2). The peak is broader and weaker than for the R = 0 data, and a structure of tetrahedral dimers is therefore unlikely. This leaves solvent ordering as an obvious possibility. No crystal structure exists for a tetrahedral coordinated Ga3+ with surrounding oxygen, thus the solvent oxygen was placed manually and their positions refined. The number of surrounding oxygens was varied. For four oxygens the signal at 4 Å is not fully described, while the PDF data can be very well described by including five to six oxygen atoms from ordered water molecules (Fig. 9a). As for the octahedral model, the model with the lowest amount of oxygen, i.e., five, could be the best for the description of the system, while it is reasonable to expect a range of solvent molecules. The structure is illustrated in Fig. 9b.The inclusion of five solvent molecules in the model results in a structure which can be written as [Ga(OH)4(H2O)5]−. The nearest neighbour O–O distances between the first and second hydration shells are 3.15–3.60 Å, which is mostly within the normal O–O distance in water.1,38 Further details on the modelled cluster are given in Tables S10 and S11.† As for the octahedral models it should be noted that this is not a unique model, but rather a representation of possible similar structures.
Assuming the monomer models to be correct then it is interesting to observe that the solvent molecules behave differently around octahedrally (R = 0) and tetrahedrally (R = 4) coordinated Ga3+ ions. More water molecules are ordered in the second coordination shell around the octahedral Ga3+ than around the tetrahedral Ga3+ (eight versus five oxygens, respectively). This can only partly be explained by geometrical considerations due to the size difference of the first coordination shell (six versus four water molecules). The O–O distances between the coordination shells are generally shorter in the octahedral model (2.59–3.27 Å for Ga(NO3)3) than in the tetrahedral model (3.15–3.60 Å for Ga(NO3)3). For octahedral Ga3+ (low pH) stronger attraction to the inner complex [Ga(OH)(H2O)5]2+ is expected, while the tetrahedral complex at high pH is [Ga(OH)4]−. Despite the large size of the first shell of the octahedral complex, the charge density is larger than that for the tetrahedral complex. This makes stronger hydrogen bonds possible and therefore relatively less solvent ordering is observed for the tetrahedral complex.2 However, one should remember that the ion concentration increases with increasing R-values. As ions are known to affect the bulk water structure2,43 this may affect the solvent ordering around the Ga3+ ions, and thereby partly explain the observed differences between aqueous octahedral and tetrahedral Ga3+ species.
Effect of counter anions
So far we have only discussed the PDFs for the Ga(NO3)3 solutions, and we now turn to the Ga2(SO4)3 and GaCl3 solutions. For the octahedral (pH < 2), tetrahedral (pH > 12) and GaOOH (9 < pH < 12) regions, the PDFs are very similar across the three salts, and this directly demonstrates that the counter anions in the solution have a limited effect on the aqueous gallium structure. As shown in the ESI,† the models used for the Ga(NO3)3 solutions can also be used to obtain satisfactory fits to the PDFs from the Ga2(SO4)3 and GaCl3 solutions (Fig. S3, S4, S14, S15 and Tables S1, S2, S19, S11†). For the GaOOH region a small difference is observed. Here, the refined sizes for the two GaOOH phases are approximately 25 and 10 Å for the Ga(NO3)3 and Ga2(SO4)3 solutions, while they are 15 and 8 Å for the GaCl3 solution. This indicates that the chloride ions might impede the growth of GaOOH crystals.More pronounced differences are observed for the polyoxogallate region. As seen in Fig. 10a the PDFs of the Ga(NO3)3 and GaCl3 solutions have very similar peaks and relative intensities, when the anion contribution is accounted for, and the GaCl3 solution therefore contains the same polyoxogallate structure as the Ga(NO3)3 solution (the Ga30/Ga32 moiety). For the Ga2(SO4)3 series with R = 1.5 the PDF peaks above 5 Å are weak and the ratio of the peaks at 3.1 and 3.5 Å is different from the other two solutions. Since derivatives of Keggin ions are known with octahedra or full trimers removed,46 different alterations of the Ga13 and Ga30 structures were used to fit the Ga2(SO4)3 data (Fig. S16†). Removal of more than half of the edge-sharing octahedra gives satisfactory fits (red shaded structures in Fig. 10b and c). These structural motifs include one or two trimers of octahedra connected to a central tetrahedron by corner-sharing.
The structural motifs describing the Ga2(SO4)3 data are part of the Ga30, Ga32 and Ga13 Keggin structures, and it is possible that they are intermediates in the formation of these larger polyoxogallate structures at a different R-value. However, PDFs of samples with R between 1 and 1.6 contradict this possibility, since similar PDFs are obtained across the entire polyoxogallate region for the Ga2(SO4)3 solutions (Fig. S17†). Since the anions represent the primary difference between the different salts, the sulfate must be the origin of the different behaviour, and it may coordinate with the clusters and stabilize smaller structures.
The transitions between the octahedral region and the polyoxogallate region are different for the three counter ions (Fig. S1†). For the Ga2(SO4)3 series the peak at 3.5 Å is somewhat more pronounced than the one at 3.1 Å already at low R, whereas for Ga(NO3)3 these two peaks have similar intensity throughout the series. GaCl3 seems to follow the same trend as Ga(NO3)3 even though it is harder to distinguish, as the broad signal from Cl–O bonding at 3.2 Å is present in the same area. The similar intensity ratio of these peaks is seen for the full Ga30, Ga32 and Ga13 Keggin structures previously identified for Ga(NO3)3R = 2 (Fig. 10b and c structures marked with yellow/green). This indicates that the full Ga30/Ga32/Ga13 structure could form directly without intermediates, while not all possible intermediates can be excluded.
Based on EXAFS and NMR data on a similar pH series for Ga(NO3)3 and GaCl3, Michot et al. suggested the presence of distinct trimers/tetramers before the signals from the Keggin ion arise.29 Such isolated trimers do not give rise to a significant peak at 3.5 Å (Fig. 10), and thus clearly the models proposed by Michot et al. cannot describe the present PDF data.
Effect of precursor concentration
The salt concentration has been reported to influence the structures in aqueous solution based on calculated Gibbs energies from a group additivity method.32 Here we have investigated concentrations of 0.5, 1 and 2 M for all three salts at R = 0 and R = 2 (Fig. 11), and the PDFs are virtually identical across this concentration interval. The most noticeable difference is that the noise level is higher at low concentrations due to the lower scattering signal relative to the background. The present PDF data do not support appreciable effects of concentration on the solution structures of Ga3+.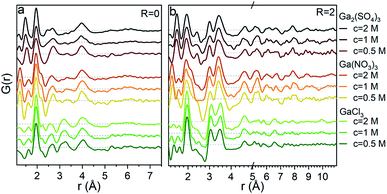 | ||
| Fig. 11 PDF data for aqueous solutions of Ga(NO3)3, GaCl3, and Ga2(SO4)3 with concentrations of 0.5, 1 and 2 M. (a) R = 0 and (b) R = 2. The variations between the salts is due to differences in pH as outlined in Fig. 1b and Table S12.† | ||
We also investigated a concentration series from 0.05 to 2 M for Ga(NO3)3 at R = 0 by 71Ga NMR. A significant increase of the linewidth was observed at lower concentrations (Fig. S18, S19 and Table S13†), indicating a more rigid environment around Ga3+ or increased dynamics at low concentration. However, the linewidth of the 71Ga NMR signal is nearly the same for the 0.5–2 M solutions, supporting the PDF observations. Further dilution leads to an increase in pH up to 2. Michot et al. observed linewidth broadening with addition of NaOH to Ga3+ solutions in their NMR data.29 Thus, the line broadening might be caused by a change in pH and compared to small increases in R-values.
Concluding remarks
Aqueous structures of metal ions represent one of the most basic pieces of information in chemistry, and every general chemistry text book will touch on this issue. Even so the experimental data used to deduce solution structures of metal ions are often weak and indirect, and conclusions are often quite speculative. The most concrete structural information comes from local structural probes such as NMR and EXAFS, but these techniques are challenged when looking beyond the first coordination sphere. Here we have introduced X-ray total scattering and PDF analysis to probe the aqueous structures of Ga3+ ions across pH and using three different counter ions (sulfate, chloride and nitrate). Since the PDF implicitly probes both short range and long range order, very detailed structural models can be obtained, and the present study exposes a huge complexity in solution phase structures including the ordering of adjacent solvent molecules to both first and second coordination spheres.For aqueous Ga3+ four structural motifs are identified with variation in pH. At low pH (<2), Ga3+ is octahedrally coordinated, and the PDFs can be modelled either with a corner-sharing dimer or with a monomer further surrounded by eight ordered water molecules. Both models are significantly more complex than previously established models in the literature. Above a pH of 12, a tetrahedrally coordinated Ga3+ ion is present, and also here it is essential to include ordered solvent molecules in the model to properly describe the PDFs. Usually the structures in these two pH ranges are described as free Ga3+ ions, [Ga(H2O)6]3+ and [Ga(OH)4]−, respectively. The present PDF data show that such simplistic structures are incorrect, and even the simplest aqueous metal ion systems contain complex structures that must influence their chemical behaviour.
At pH ≈ 2–3, polyoxogallate structures are observed. The PDFs can be described by both the β-, γ- and δ-Ga13 Keggin isomers and the previously reported Ga30 and Ga32 structures. However, 71Ga NMR spectroscopy strongly indicates that Ga30/Ga32 species must be present at pH ≈ 2–3. Our data therefore question the actual existence of the Ga13 Keggin ion. The three structures Ga13/Ga30/Ga32 share many structural similarities, which may explain why the Ga13 Keggin ion has been the prevalent structural suggestion in this pH interval.
At neutral and slightly elevated pH, nanosized GaOOH particles form, with a slightly distorted atomic structure. The particles are observed to have a bimodal size distribution, but overall the sizes range between 8 and 25 Å.
The nature of the counter anion (sulfate, chloride, nitrate) has little effect on the solution structures of Ga3+. Only in the polyoxogallate region of the sulfate solutions there is a difference, and the large Ga13/Ga30/Ga32 structures observed for chloride and nitrate are absent. Instead, the sulfate ion stabilizes smaller structures containing trimer(s) of octahedra, which are corner-sharing with a tetrahedron. These smaller structures are also part of the Ga13/Ga30/Ga32 structures, but it does not appear to be an intermediate in the formation of the larger structures since it is not observed for the other counter ions when the pH is altered.
Change in metal ion concentration from 0.5 M to 2 M has no effect on the solution structures observed by PDF in contradiction with previous reports. We observe an effect on the 71Ga NMR linewidths when the concentration change is very large, but since the metal ion concentration correlates strongly with the pH, a pure concentration effect is not documented.
The study highlights similarities between the aqueous gallium system and the more extensively studied aluminium system, but it also showcases the importance of not just relying on expected chemical similarities as seen, e.g. with the difference of polyoxometallate structures. The similarities and differences observed for the solvated gallium ions can in turn form the basis for further understanding of the behaviour of gallium ions in different applications such as during hydrothermal formation of gallium oxides.
The present work has unravelled a fascinating, but hitherto unappreciated, structural complexity even for simple metal ions in solution. The data presented here touch on the most basic chemical information available, and such information is widely used, e.g. for rationalising electrochemical data in Pourbaix diagrams. It appears that the structures of metal ions in solution should systematically be revisited using the powerful analytical probe of X-ray total scattering, which is now becoming more widely available due to advances in synchrotron radiation technology. Such work could provide more complex and precise information about solvated species and form a better basis for rationalising the solution chemistry of metal ions.
Author contributions
IGN measured data, carried out data analysis, wrote the initial manuscript, and contributed to discussion and editing. SS carried out data analysis. ACP measured data and edited the manuscript. JS measured data, carried out data analysis and edited the manuscript. BBI designed the project, conducted supervision, discussion, resource acquisition, validation, review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the beamtime at PETRA III, Deutsches Elektronen-Synchrotron, DESY, a member of the Helmholtz Association (HGF). We thank the P21.1 beamline staff for beamline support. This work was supported by DanScatt and the Villum Foundation. Affiliation with the Aarhus University Center for Integrated Materials Research is gratefully acknowledged (iMAT). We are grateful for the assistance during beamtime provided by Martin Roelsgaard, Nils Lau Nyborg Broge, Frederik Søndergaard-Pedersen, Magnus Kløve Kjær and Rasmus S. Christensen.References
- Y. Marcus, Effect of Ions on the Structure of Water: Structure Making and Breaking, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS PubMed.
- B. Hribar, N. T. Southall, V. Vlachy and K. A. Dill, How Ions Affect the Structure of Water, J. Am. Chem. Soc., 2002, 124, 12302–12311 CrossRef CAS PubMed.
- H. Ohtaki and T. Radnai, Structure and dynamics of hydrated ions, Chem. Rev., 1993, 93, 1157–1204 CrossRef CAS.
- E. D. Bøjesen and B. B. Iversen, The chemistry of nucleation, CrystEngComm, 2016, 18, 8332–8353 RSC.
- J. Storre, C. Schnitter, H. W. Roesky, H.-G. Schmidt, M. Noltemeyer, R. Fleischer and D. Stalke, A Novel Approach for the Stabilization and Structural Characterization of Group 13 Organometallic Hydroxides:The Way to Well Defined Crystalline Methylalumoxanes, J. Am. Chem. Soc., 1997, 119, 7505–7513 CrossRef CAS.
- J. Storre, T. Belgardt, D. Stalke and H. W. Roesky, Synthesis and Structure of the First Organometallic Galloxane Hydroxide Mes6Ga6O4(OH)4, Angew. Chem., Int. Ed., 1994, 33, 1244–1246 CrossRef.
- J. Storre, A. Klemp, H. W. Roesky, H.-G. Schmidt, M. Noltemeyer, R. Fleischer and D. Stalke, Hydrolysis of Trimesitylgallium and Trimesitylaluminum:Structures Along a Reaction Pathway, J. Am. Chem. Soc., 1996, 118, 1380–1386 CrossRef CAS.
- J. C. Goodwin, S. J. Teat and S. L. Heath, How Do Clusters Grow? The Synthesis and Structure of Polynuclear Hydroxide Gallium(III) Clusters, Angew. Chem., Int. Ed., 2004, 43, 4037–4041 CrossRef CAS PubMed.
- J. Storre, A. Klemp, H. W. Roesky, R. Fleischer and D. Stalke, Synthesis and Characterization of (MesGaO)9 (Mes = Me3C6H2) and Crystal Structure of the First Galloxane Comparable to Catalytically Active Aluminum Compounds, Organometallics, 1997, 16, 3074–3076 CrossRef CAS.
- C. C. Landry, C. J. Harlan, S. G. Bott and A. R. Barron, Galloxane and Alumoxane Hydroxides: [Ga12tBu12(μ3-O)8(μ-O)2(μ-OH)4] and [Al6tBu6(μ3-O)4(μ-OH)4], Angew. Chem., Int. Ed., 1995, 34, 1201–1202 CrossRef CAS.
- O. A. Gerasko, E. A. Mainicheva, D. Yu. Naumov, N. V. Kuratieva, M. N. Sokolov and V. P. Fedin, Synthesis and Crystal Structure of Unprecedented Oxo/Hydroxo-Bridged Polynuclear Gallium(III) Aqua Complexes, Inorg. Chem., 2005, 44, 4133–4135 CrossRef CAS PubMed.
- E. Rather, J. T. Gatlin, P. G. Nixon, T. Tsukamoto, V. Kravtsov and D. W. Johnson, A simple organic reaction mediates the crystallization of the inorganic nanocluster [Ga13(μ3-OH)6(μ2-OH)18(H2O)24](NO3)15, J. Am. Chem. Soc., 2005, 127, 3242–3243 CrossRef CAS PubMed.
- W. H. Casey, M. M. Olmstead, C. R. Hazlett, C. Lamar and T. Z. Forbes, A New Nanometer-Sized Ga(III)-Oxyhydroxide Cation, Inorganics, 2015, 3, 21–26 CrossRef CAS.
- H. A. Levy, P. A. Agron and M. D. Danford, Structure of Silico-Tungstic Acid in Aqueous Solution, J. Chem. Phys., 1959, 30, 1486–1488 CrossRef CAS.
- M. Sandström, I. Persson and S. Ahrland, On the Coordination around Mercury(II), Cadmium(II) and Zinc(II) in Dimethyl Sulfoxide and Aqueous Solutions. An X-ray Diffraction, Raman and Infrared Investigation, Acta Chem. Scand., Ser. A, 1978, 32, 607–625 CrossRef.
- A. H. Narten and H. A. Levy, Liquid Water: Molecular Correlation Functions from X-Ray Diffraction, J. Chem. Phys., 1971, 55, 2263–2269 CrossRef CAS.
- S. Sommer, I. G. Nielsen and B. B. Iversen, Group 13 Precursor Structures and Their Effect on Oxide Nanocrystal Formation, Chem.–Eur. J., 2020, 26, 1022–1026 CrossRef CAS PubMed.
- M. Juelsholt, T. L. Christiansen and K. M. Ø. Jensen, Mechanisms for Tungsten Oxide Nanoparticle Formation in Solvothermal Synthesis: From Polyoxometalates to Crystalline Materials, J. Phys. Chem. C, 2019, 123, 5110–5119 CrossRef CAS.
- S. J. Pearton, J. Yang, P. H. Cary, F. Ren, J. Kim, M. J. Tadjer and M. A. Mastro, A review of Ga2O3 materials, processing, and devices, Appl. Phys. Rev., 2018, 5, 011301 Search PubMed.
- L. S. Reddy, Y. H. Ko and J. S. Yu, Hydrothermal Synthesis and Photocatalytic Property of β-Ga2O3 Nanorods, Nanoscale Res. Lett., 2015, 10, 364 CrossRef PubMed.
- E. A. Cochran, K. N. Woods, D. W. Johnson, C. J. Page and S. W. Boettcher, Unique chemistries of metal-nitrate precursors to form metal-oxide thin films from solution: materials for electronic and energy applications, J. Mater. Chem. A, 2019, 7, 24124–24149 RSC.
- D. Chen, Y. Xu, Z. An, Z. Li and C. Zhang, Thin-film transistors based on wide bandgap Ga2O3 films grown by aqueous-solution spin-coating method, Micro Nano Lett., 2019, 14, 1052–1055 CrossRef CAS.
- H. Y. Playford, A. C. Hannon, E. R. Barney and R. I. Walton, Structures of Uncharacterised Polymorphs of Gallium Oxide from Total Neutron Diffraction, Chem.–Eur. J., 2013, 19, 2803–2813 CrossRef CAS PubMed.
- S. Sommer, E. D. Bøjesen, H. Reardon and B. B. Iversen, Atomic Scale Design of Spinel ZnAl2O4 Nanocrystal Synthesis, Cryst. Growth Des., 2020, 20, 1789–1799 CrossRef CAS.
- C. R. Chitambar, Medical Applications and Toxicities of Gallium Compounds, Int. J. Environ. Res. Public Health, 2010, 7, 2337–2361 CrossRef CAS PubMed.
- L. R. Bernstein, Mechanisms of Therapeutic Activity for Gallium, Pharmacol. Rev., 1998, 50, 665–682 CAS.
- S. M. Bradley, R. A. Kydd and R. Yamdagni, Comparison of the Hydrolyses of Gallium(III) and Aluminium(III) Solutions by Nuclear Magnetic Resonance Spectroscopy, J. Chem. Soc., Dalton Trans., 1990, 2653–2656 RSC.
- S. M. Bradley, R. A. Kydd and R. Yamdagni, Detection of a new polymeric species formed through the hydrolysis of gallium(III) salt solutions, J. Chem. Soc., Dalton Trans., 1990, 413–417 RSC.
- L. J. Michot, E. Montargès-Pelletier, B. S. Lartiges, J.-B. d'Espinose de la Caillerie and V. Briois, Formation Mechanism of the Ga13 Keggin Ion:A Combined EXAFS and NMR Study, J. Am. Chem. Soc., 2000, 122, 6048–6056 CrossRef.
- W. W. Rudolph, C. C. Pye and G. Irmer, Study of gallium(III) nitrate hydrate and aqueous solutions: Raman spectroscopy and ab initio molecular orbital calculations of gallium(III) water clusters, J. Raman Spectrosc., 2002, 33, 177–190 CrossRef CAS.
- W. W. Rudolph and C. C. Pye, Gallium(III) hydration in aqueous solution of perchlorate, nitrate and sulfate. Raman and 71-Ga NMR spectroscopic studies and ab initio molecular orbital calculations of gallium(III) water clusters, Phys. Chem. Chem. Phys., 2002, 4, 4319–4327 RSC.
- L. A. Wills, X. Qu, I.-Y. Chang, T. J. L. Mustard, D. A. Keszler, K. A. Persson and P. H.-Y. Cheong, Group additivity-Pourbaix diagrams advocate thermodynamically stable nanoscale clusters in aqueous environments, Nat. Commun., 2017, 8, 15852 CrossRef CAS PubMed.
- C. Prescher and V. B. Prakapenka, DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration, High Pressure Res., 2015, 35, 223–230 CrossRef CAS.
- X. Yang, P. Juhas, C. L. Farrow and S. J. L. Billinge, xPDFsuite: an end-to-end software solution for high throughput pair distribution function transformation, visualization and analysis, 2014, arXiv:1402.3163.
- P. Juhas, C. L. Farrow, X. Yang, K. R. Knox and S. J. L. Billinge, Complex modeling: a strategy and software program for combining multiple information sources to solve ill posed structure and nanostructure inverse problems, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 562–568 CrossRef PubMed.
- J. Åhman, G. Svensson and J. Albertsson, A Reinvestigation of β-Gallium Oxide, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 1336–1338 CrossRef.
- A. D. Hendsbee, C. C. Pye and J. D. Masuda, Hexaaquagallium(III) trinitrate trihydrate, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, i65 CrossRef CAS PubMed.
- U. Bergmann, A. Di Cicco, P. Wernet, E. Principi, P. Glatzel and A. Nilsson, Nearest-neighbor oxygen distances in liquid water and ice observed by x-ray Raman based extended x-ray absorption fine structure, J. Chem. Phys., 2007, 127, 174504 CrossRef PubMed.
- M. Zobel, R. B. Neder and S. A. J. Kimber, Universal solvent restructuring induced by colloidal nanoparticles, Science, 2015, 347, 292–294 CrossRef CAS PubMed.
- S. L. J. Thomä, S. W. Krauss, M. Eckardt, P. Chater and M. Zobel, Atomic insight into hydration shells around facetted nanoparticles, Nat. Commun., 2019, 10, 995 CrossRef PubMed.
- M. W. Terban, D. Banerjee, S. Ghose, B. Medasani, A. Shukla, B. A. Legg, Y. Zhou, Z. Zhu, M. L. Sushko, J. J. D. Yoreo, J. Liu, P. K. Thallapally and S. J. L. Billinge, Early stage structural development of prototypical zeolitic imidazolate framework (ZIF) in solution, Nanoscale, 2018, 10, 4291–4300 RSC.
- P. Lindqvist-Reis, A. Muñoz-Páez, S. Díaz-Moreno, S. Pattanaik, I. Persson and M. Sandström, The Structure of the Hydrated Gallium(III), Indium(III), and Chromium(III) Ions in Aqueous Solution. A Large Angle X-ray Scattering and EXAFS Study, Inorg. Chem., 1998, 37, 6675–6683 CrossRef CAS PubMed.
- M. Śmiechowski and I. Persson, Hydration of Oxometallate Ions in Aqueous Solution, Inorg. Chem., 2020, 59, 8231–8239 CrossRef PubMed.
- S. E. Smart, J. Vaughn, I. Pappas and L. Pan, Controlled step-wise isomerization of the Keggin-type Al13 and determination of the γ-Al13 structure, Chem. Commun., 2013, 49, 11352–11354 RSC.
- S.-J. Li, C. Zheng and K. C. Lobringn, Refinement of the crystal structure of gallium oxide hydroxide, GaO(OH), Z. Kristallogr. - Cryst. Mater., 2003, 218, 11–12 CAS.
- A. Müller, F. Peters, M. T. Pope and D. Gatteschi, Polyoxometalates:VeryLarge Clusters -NanoscaleMagnets, Chem. Rev., 1998, 98, 239–271 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc05190c |
| This journal is © The Royal Society of Chemistry 2021 |