Open Access Article
Open Access ArticleHow natural materials remove heavy metals from water: mechanistic insights from molecular dynamics simulations†
Fabio
Pietrucci
 a,
Mauro
Boero
a,
Mauro
Boero
 b and
Wanda
Andreoni
b and
Wanda
Andreoni
 cd
cd
aSorbonne Université, Muséum National d'Histoire Naturelle, CNRS, UMR 7590, Institut de Minéralogie, de Physique des Matériaux et de Cosmochimie (IMPMC), 4 Pl Jussieu, F-75005 Paris, France. E-mail: fabio.pietrucci@sorbonne-universite.fr
bUniversité de Strasbourg, Institut de Physique et Chimie des Matériaux de Strasbourg (IPCMS), CNRS, UMR 7504, 23 rue du Loess, F-67034 Strasbourg, France. E-mail: mauro.boero@ipmc.unistra.fr
cEcole Polytechnique Fédérale de Lausanne (EPFL), Institut de Physique, CH-1015 Lausanne, Switzerland. E-mail: wanda.andreoni@epfl.ch
dIstituto Italiano di Tecnologia (IIT), Via Morego 30, I-16163 Genova, Italy
First published on 11th January 2021
Abstract
Water pollution by heavy metals is of increasing concern due to its devastating effects on the environment and on human health. For the removal of heavy metals from water sources, natural materials, such as spent-coffee-grains or orange/banana/chestnut peels, appear to offer a potential cheap alternative to more sophisticated and costly technologies currently in use. However, in order to employ them effectively, it is necessary to gain a deeper understanding – at the molecular level – of the heavy metals-bioorganic-water system and exploit the power of computer simulations. As a step in this direction, we investigate via atomistic simulations the capture of lead ions from water by hemicellulose – the latter being representative of the polysaccharides that are common components of vegetables and fruit peels − as well as the reverse process. A series of independent molecular dynamics simulations, both classical and ab initio, reveals a coherent scenario which is consistent with what one would expect of an efficient capture, i.e. that it be fast and irreversible: (i) binding of the metal ions via adsorption is found to happen spontaneously on both carboxylate and hydroxide functional groups; (ii) in contrast, metal ion desorption, leading to solvation in water, involves sizable free-energy barriers.
1 Introduction
Lead, cadmium, mercury and arsenic are common pollutants of fresh and waste waters and constitute a threat to human and animal health as well as to agriculture.1–3 Concern has increased dramatically over the years and led to several different strategies to reduce water contamination by heavy metals, including adsorption onto active carbon, membrane filtration and chemical precipitation.4 An especially interesting strategy is based on inexpensive and natural materials obtained from waste produced in industrial or agricultural processes, e.g., coffee residues such as spent-coffee-grains (SCG), dried tea leaves, chestnut shells, orange or lemon peels [see e.g., ref. 5–22].Despite obvious economic and environmental advantages, this technology has not yet been exploited on a large scale.
A vast quantity of reports on the “performance” of natural materials is scattered in the scientific literature, from which it appears, however, that understanding of the chemistry involved in the metal capture has rarely been the research focus. Attempts to identify specific responsible components have mainly relied on FTIR or XPS, namely on the comparison of the spectra of the dried material before and after immersion in polluted water [see, e.g., ref. 6, 11, 17, 23 and 24]. The interpretation, however, is not easy. Even in cases when one can distinguish the response of different functional groups, one cannot ignore the fact that the same group is present in many different constituents. On the other hand, the complexity of the systems to be investigated explains the lack of simulations at the molecular level which could provide useful insights into the relevant mechanisms.
The scope of the present paper is to explore the potential of state-of-the-art computer experiments for research in this field and to start by studying, via atomistic models and molecular dynamics (MD) simulations, the interaction of polysaccharides – common components of vegetables and fruit peels – with heavy metals immersed in water.
More precisely, our investigation aims at clarifying how adsorption/desorption processes take place, namely at characterizing the driving mechanisms, the nature of the ion adsorption sites and the energetics. As a prototype of highly toxic metals we have chosen lead, which is mainly detected as Pb2+ in aqueous environments. As reference polysaccharide(s) we have selected hemicellulose(s) because of its (their) special structural characteristics: amorphous, partially or fully soluble in water and heterogeneous, namely consisting of chains of diverse monosaccharides. Moreover, hemicellulose was found amongst the dominant components of SCG and coffee silverskin.15,19,24
2 Methods
Here we give a brief account of the models and methodologies used in our simulations, both classical and ab initio MD. A detailed description is given in the ESI.†2.1 Classical MD
Among the major groups of hemicellulose constituents, mannans are detected in larger percentage in SCG.15,24 They consist15 of β (1-4) linked D-mannose substituted every about 100 residues, at O6, with a single D-galactose (Gal). On this basis, we construct an oligomer model with the sequence (Man20GlcA10Man20)Gal(Man20GlcA10Man20)Gal(Man20GlcA10Man20)Gal(Man20GlcA10Man20) where Man = D-mannose, Gal = D-galactose, GlcA = D-glucuronic acid (see Fig. S1†). This is the system simulated using classical molecular dynamics, solvated in explicit water (31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782 molecules) and with 20 Pb2+ ions that neutralize the negative charges associated with 40 carboxylate anions (COO–). Other functional groups are present in the organic that contain oxygen and can thus also act as adsorption centers for the lead ions, namely 570 hydroxy (C–OH) and 406 ether (–COC–) groups. As force-fields we use GLYCAM_06 (ref. 25) for the organic subsystem, TIP3P26 for water and a standard Coulomb plus Lennard-Jones potential for the lead ions.27
782 molecules) and with 20 Pb2+ ions that neutralize the negative charges associated with 40 carboxylate anions (COO–). Other functional groups are present in the organic that contain oxygen and can thus also act as adsorption centers for the lead ions, namely 570 hydroxy (C–OH) and 406 ether (–COC–) groups. As force-fields we use GLYCAM_06 (ref. 25) for the organic subsystem, TIP3P26 for water and a standard Coulomb plus Lennard-Jones potential for the lead ions.27
2.2 Ab initio MD
The atomistic model simulated with ab initio MD corresponds to a cut from the one considered above. It consists of 4 organic chains, namely Man3, Man3, Man4, Man1GlcA8 (saturated with H at the ends) (842 atoms) containing 8 carboxylates (COO), 53 hydroxy (C–OH) and 34 (–COC–) ether groups, 4 Pb atoms and 149 water molecules. The system is neutral and – as verified – after equilibration the Pb atoms were ionized, with Bader charges in the range 1.5–1.7. By ab initio MD we denote Car–Parrinello MD that is based on density-functional-theory (DFT), and, in particular, with gradient-corrected exchange-correlation functionals28 and semi-empirical corrections for van-der-Waals interactions.292.3 Metadynamics
Calculation of activated events implies the use of acceleration procedures to empower MD. We have chosen metadynamics30,31 (MTD) as enhanced configurational sampling method in both classical and ab initio approaches. The path collective variables (CV)32 (S, Z) introduced in ref. 33 are adopted since they are uniquely suited for the study of reactions in complex systems such as aqueous solutions because all atoms in the system (metal ions, organic and solvent) can in principle be allowed to participate in the reaction under study. In this case, in addition to the Pbs, oxygens of the organic are included as well as those of all water molecules. All mathematical expressions as well as all details of the simulation protocol we have followed are reported in the ESI.† Here we recall that path collective variables S and Z are defined relative to an initial (guessed) reference path between two states (e.g., from an ion-organic bound state to a dissociated state). S monitors the progression along the reference path whereas Z measures the distance from it. The effectiveness of the path CVs relies on the metric chosen to define the distance between actual and reference configurations. The distance metric introduced in ref. 33 is based on the coordination pattern of all the atoms participating in the process.To inspect the results of MTD simulations, we plot the free-energy surface (FES) in the CV space reconstructed from the bias potential.34 We further analyze it in terms of the Pb–O coordination number (see the ESI†) relative to the first shell, with a cutoff of 3.3 Å.
We remark that the values estimated for the free-energy barriers (FEBs) are affected by a statistical error of at least 5 kcal mol−1, with a tendency to overestimation because the FES is estimated from the bias potential accumulated until the “forward” (or the “backward”) transition occurs, without attaining the regime of multiple forward and backward transitions.
3. Results and discussion
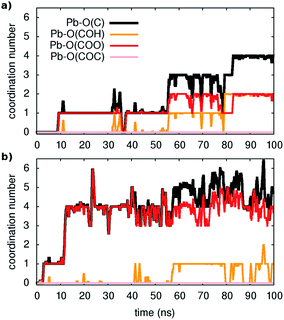
The key questions we tackle are: How easy is the metal capture? Do all types of oxygen-containing groups in the model act as adsorption sites and if yes to what extent? How easy is the metal ion detachment from the organic? How do water molecules participate in these reactions?First, three distinct unbiased MD simulations were run at room temperature, starting from configurations with all metal ions fully solvated and far away from the organic. As shown in Fig. 1 (and Fig. S2 and S3†), adsorption occurs spontaneously within tens of nanoseconds. Moreover, as illustrated in the examples of Fig. 1, four-five oxygen atoms succeed in binding to a given Pb ion within 100 ns and all three types of functional groups containing oxygen contribute to the metal capture to some extent although, as expected from their larger partial negative charge, carboxylates are the principal chelating agents.
As a second step, the desorption process was investigated via four independent MD-MTD simulations – also at room temperature – starting with Pb2+ located in different environments. We employ the S path coordinate as the main indicator of the “degree of adsorption”: the region with S < 1.2 includes configurations with Pb2+ tightly bound to the organic (Fig. 2A), while the region with S > 1.6 includes configurations with Pb2+ dissociated from the organic and fully solvated by water molecules (Fig. 2D). The region 1.2 < S < 1.6 (see Fig. 2B and C) includes transition pathways between A and D. Fig. 3 shows the FES reconstructed from two (a and b) out of four (a–d; see Fig. S4†) simulations. As expected, the bound state corresponds to a deep free-energy minimum, while the transition region towards the dissociated state features an almost monotonic growth of the free energy. The relative stability of the dissociated state cannot be quantified from MTD simulations due to the absence of reverse (association) transitions. However, as we have reported above, unbiased MD clearly indicates that at room temperature the barriers for association are of the order of kT (∼1 kcal mol−1). On the contrary, all four MTD simulations reveal that desorption involves sizable barriers: the estimated values from the bias accumulated until full dissociation are 32 (a), 45 (b), 56 (c) and 32 kcal mol−1 (d).
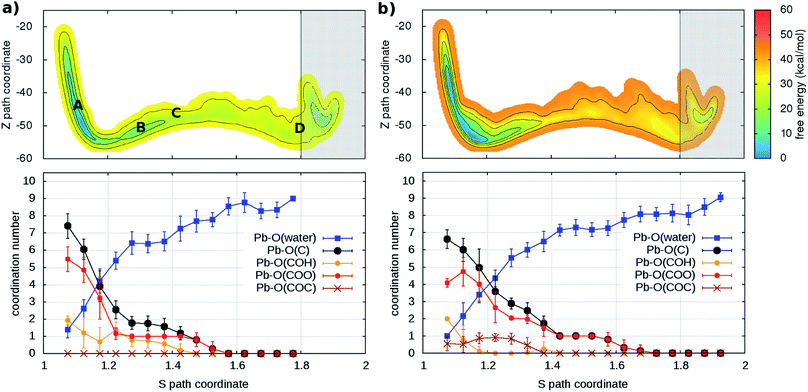 | ||
| Fig. 3 (Upper panels) Free energy surface for the unbinding of Pb reconstructed from two ((a) and (b)) out of four (see Fig. S4†) independent classical metadynamics simulations in different environments. The shaded area (S > 1.8) represents the region where the bias profile is not representative of the free energy, due to lack of reverse transition (binding). Note in (a) the location of the configurations of Fig. 2. (Lower panels) Evolution of coordination number of Pb and O atoms of water molecules and different groups in the organic (see legend) as a function of the S path coordinate. Vertical bars represent standard deviations. | ||
In order to understand the link between the free-energy profile and the structural evolution of the system, we exploit the correlation between the path coordinate S and the Pb2+–O coordination pattern. The latter can be further dissected into the coordination numbers of Pb2+ with oxygen atoms belonging to its different potential adsorption species: water or the organic via carboxylate- (–COO−), hydroxy- (C–OH) and ether groups (–COC–) (Fig. 3 and S4†). In the bound state (S < 1.2), carboxylate groups are the main chelating agents (coordination between 4 and 6) in agreement with the results of the simulations of the capture process. Hydroxy groups also make an important contribution (coordination between 1 and 4) while ether groups are seldom in contact. Moreover, water molecules (up to 4) coordinate the cation, indicating that the binding pocket is not dry. The loss of contacts with organic groups during the unbinding is systematically compensated by that of water molecules, until full solvation. To a good approximation, Pb2+ is constantly coordinated to 7–9 oxygen atoms, in agreement with the coordination number computed from the pair distribution function of the solvated ion (Fig. S5†).
Analysis of the MD trajectories of solvated Pb2+ indicates an average lifetime of 189 ± 27 ps for water molecules in the first shell (with standard deviation 186 ps, i.e. close to the average as expected for Poisson statistics of rare water unbinding events). For comparison with pure water, the lifetime of a tagged molecule in the first shell is 8.3 ± 1.6 ps (with standard deviation 7.5 ps). We remark that such a long lifetime for the first solvation shell hampers the brute-force sampling of the dynamics of Pb2+- in water and justifies our MTD protocol based on CVs that include the solvent.
Turning on to discuss the results of ab initio MD, some more clarifications of our model and protocol are necessary. DFT calculations are expected to provide a better description of the relevant intermolecular interactions (Pb–water; Pb–organic, water–organic, water–water etc.). Still, when comparison is made with classical MD, one should care about the effects of the unavoidable limitations in the model size and in the length of the MD trajectories (20–40 times shorter than in classical MD). First, we notice that, although offering several possibilities for Pb adsorption, the size limitations do not allow more than one hydration shell to complete after detachment from the organic. However, we can characterize in detail the early steps of the desorption and of the reverse reaction. MTD was applied, at room temperature, to two out of four Pb ions having different local environments. The FEBs for desorption (Fig. 4 and S6†) estimated from the bias accumulated until the most dissociated state are 103 and 59 kcal mol−1. On the other hand, the estimated FEBs relative to the removal of the metal ions from solvated configurations – end points of the unbinding simulations – and re-capture by the organic are 30 and 10 kcal mol−1 (Fig. 5 and S7†). Inspection of the atomic trajectories suggests that these barriers correspond to the displacement of water molecules from the path of approach of the metal ion to the organic.
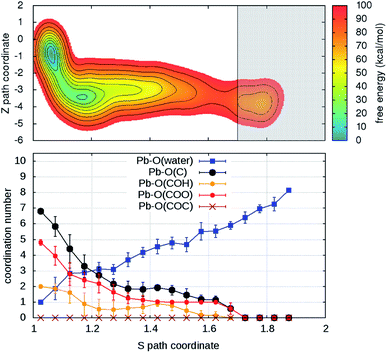 | ||
| Fig. 4 (Upper panel) Free energy surface for the unbinding of Pb reconstructed from one out of two (Fig. S6†) independent ab initio metadynamics simulations in different environments. The shaded area (S > 1.7) represents the region where the bias profile is not representative of the free energy, due to lack of reverse transition (binding). (Lower panel) Evolution of the coordination numbers of Pb and O belonging to water and to different organic functional groups, as a function of the S path coordinate. The vertical bars represent standard deviations of coordination numbers. | ||
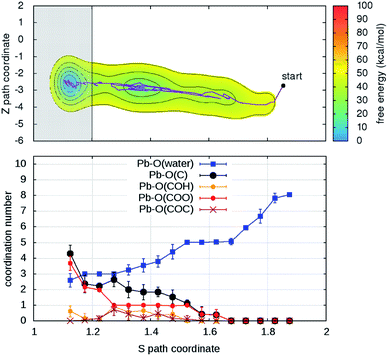 | ||
| Fig. 5 (Upper panel) Free energy surface for the binding of Pb reconstructed from one out of two ab initio metadynamics simulations (see Fig. S7† for both) started from the end (unbound state, S > 1.8) of the simulation in Fig. 4. In the shaded area – S < 1.2 – the bias is not representative of the free-energy. (Lower panel) Evolution of the coordination of Pb with oxygen atoms belonging to water and to different organic functional groups as function of the S path coordinate. | ||
The slow relaxation of the solvent is expected to cause a more severe overestimation of the FEBs relative to classical MD. In order to quantify this statement, we have repeated the four classical MD simulations in Fig. 3 with the MTD setup adjusted to that of ab initio simulations (see ESI†). The values thus estimated from the bias potentials (Fig. S8†) are indeed higher by a factor of at least 1.6. Once applied to our estimates from DFT-MD, this result explains at large the seeming quantitative discrepancy with classical MD.
Before passing on to further discussion of our results, we should recall that the experimental information on the binding of heavy metals at the molecular level is very limited and comes from FTIR and XPS spectra. In both cases, measurements refer to dry samples of bio-organic materials (e.g., chestnut shells,11 blend coffee,6 marine algae,35 SCG36) and are taken both before and after having been immersed into aqueous solutions containing heavy metal ions. Any change induced by immersion in polluted water onto the spectral features attributed to a given atom (C or O for XPS) or a functional group (for FTIR) has been interpreted as caused by its binding with the metal ions. From both XPS and FTIR investigations, it has thus been shown that Pb2+ affects the response of multiple oxygen-based functional groups, namely carboxyl, hydroxy, ether and alcoholic groups.11,35 These variations are generally minor, and especially so for C1s/O1s or IR peak positions. For example, the shift of IR peak positions it at most ∼10 cm−1. Only recent XPS data on SCGs18 were interpreted as demonstrating an exclusive binding of Pb to carboxylates. This argument was further emphasized as support for the application of the Langmuir model in its simplest form (single-site adsorption), assuming that all adsorbents are identical. However, the spectra resolution does not seem to be adequate to support these conclusions.37 We remark that the characterization provided by either XPS or FTIR is insufficient to either identify the components of the material that contribute to this response or exclude some.
We have used the ab initio MD trajectories to try and identify possible clear variations induced by Pb in the vibrational spectra calculated before and after injection of the metal ions. The major changes are blue-shifts (∼20 cm−1) of the stretching modes of carbon-oxygen bonds in carboxylates (Fig. S9†).
From comparison of the results of all our simulations, a coherent picture emerges of the equilibrium configurations as well as of binding and unbinding processes.
(i) The tendency of the Pb ion to bind to diverse oxygen-based functional groups – that we observed in the extensive classical MD simulations (Fig. 2 and 3) – is also seen in the ab initio simulations in Fig. 4. These observations are consistent with the experimental data mentioned above.
(ii) The adsorption locations are never dry, namely water molecules participate in the Pb–organic bound states. This is reminiscent of other biological environments, such as active sites in protein–ligand complexes or at protein–protein interfaces.38–40
(iii) The gradual replacement of the organic residues with water molecules in the first coordination shell accompanies the ion removal from the organic and vice versa in the adsorption process, with the bound state corresponding to a coordination of 8–9 in classical MD (Fig. 3 and S4†) and 8 or 6 in ab initio MD (Fig. 4 and S6†). The reduced availability of binding sites in the latter case explains the difference.
(iv) The ion uptake from water by the organic is easy, fast and irreversible, as can be expected for an efficient capture.
4. Conclusions
Several bioorganic materials such as SCG are known to be efficient agents for the capture of toxic metals from water but knowledge of their functioning at the molecular level is missing. Motivated by the importance of the related issues we have used modeling and advanced molecular dynamics protocols to gain new insights into the dynamics of the uptake of lead ions from aqueous solutions by hemicellulose – a most relevant component of SCG – as well as their release back to water.In summary, our simulations were able to predict – from scratch – that the polymer can indeed act as a very efficient capture agent for lead ions, namely in a fast and irreversible manner: by offering multiple and effective adsorption sites (oxygen-based functional groups), components like hemicellulose – as our simulations show – can easily capture the metal ions at room temperature whereas overcoming a range of sizable barriers is required for their desorption under the same conditions. Moreover, the twofold role of water emerges, namely not only as a competitor of the polymer for the uptake of the metal ions, but also as its “partner” in the bound metal–polymer states, thus satisfying the eagerness of lead for high coordination with oxygen atoms.
Experimental investigation of biosorption of heavy metals in polluted water, also using standard spectroscopies such as XPS or FTIR, is made on samples of real and thus highly complex systems. This makes it difficult – if not impossible – to identify amongst the numerous components of the real system (various polysaccharides, lipids, phenols, proteins…) those that are mainly responsible for the capture of the metal ions via adsorption and to locate their binding sites. However, this knowledge is crucial in the search of alternative bio-inspired adsorbents. Therefore, the information one obtains from molecular simulations of single components can be exploited in an optimum way within a systematic combined strategy where also specific experiments are planned for single components in polluted water.
From a methodological viewpoint: the need of a metadynamics protocol like ours, namely including all solvent molecules as potential participants in the events, is proven. It becomes also clear that improving on quantitative assessments will have to mainly rely on methodological advances in alleviating the time-scale problem,31,41 given the slow reorganization of the hydrogen-bond network to accommodate changes in coordination with the metal ion.
In conclusion, although our study has characterized model systems, the knowledge we have gained about the mechanism of ion adsorption can be extended to more realistic complex scenarios. We believe that the deepening of our understanding of the physics and chemistry underlying water pollution by heavy metals or organic waste is essential for progress on the utilization of available materials as effective removal agents and also for the design of bio-inspired (supra)molecular systems and nanostructures. In this challenging task, application of state-of-the-art simulation methods on simplified but still realistic models could play a central role, as is currently the case for protein science42,43 and drug discovery.44,45
Author contributions
The authors contributed equally to this work.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The research presented here was made possible thanks to the support from PRACE (WASHME; PRA12-3086) at CINECA. Other computer grants are also acknowledged: from Grand Equipement National de Calcul Intensif (GENCI) (under allocation DARI-A0060906092; A008090609; A0050910143; A0070811069) and ISCRA at CINECA. We wish to thank Roberto Cingolani, Athanassia Athanassiou and Despina Fragouli for stimulating discussions and Massimiliano Guarrasi and Piero Lanucara for technical help at CINECA.References
- L. Järup, Br. Med. Bull., 2003, 68, 167–182 CrossRef.
- S. Chowdhury, M. A. J. Mazumder, O. Al-Attas and T. Husain, Sci. Total Environ., 2016, 569–570, 476–488 CrossRef CAS.
- C. F. Carolina, P. S. Kumara, A. Saravanana, G. J. Joshibaa and Mu. Naushad, J. Environ. Chem. Eng., 2017, 5, 2782–2799 CrossRef.
- Heavy Metals in Water: Presence, Removal and Safety, ed. S. Sharma, The Royal Society of Chemistry, London, 2015 Search PubMed.
- K. S. Low, C. K. Lee and S. C. Liew, Process Biochem., 2000, 36, 59–64 CrossRef CAS.
- M. Minamisawa, H. Minamisawa, S. Yoshida and N. Takai, J. Agric. Food Chem., 2004, 52, 5606–5611 CrossRef CAS.
- Z. Xuan, Y. Tang, X. Li, Y. Liu and F. Luo, Biochem. Eng. J., 2006, 31, 160–164 CrossRef CAS.
- X. Li, Y. Tang, Z. Xuan, Y. Liu and F. Luo, Sep. Purif. Technol., 2007, 55, 69–75 CrossRef CAS.
- A. Demirbas, J. Hazard. Mater., 2008, 157, 220–229 CrossRef CAS.
- D. Sud, G. Mahajan and M. P. Kaur, Bioresour. Technol., 2008, 99, 6017–6027 CrossRef CAS.
- G. Vazquez, M. Calvo, M. S. Freire, J. Gonzalez-Alvarez and G. Antorrena, J. Hazard. Mater., 2009, 172, 1402–1414 CrossRef CAS.
- R. S. D. Castro, L. Caetano, G. Ferreira, P. M. Padilha, M. J. Saeki, L. F. Zara, M. A. U. Martines and G. R. Castro, Ind. Eng. Chem. Res., 2011, 50, 3446–3451 CrossRef CAS.
- L. Agwaramgbo, N. Lathan, S. Edwards and S. Nunez, J. Environ. Prot., 2013, 4, 741–745 CrossRef CAS.
- F. J. Cerino-Córdova, P. E. Díaz-Flores, R. B. García-Reyes, E. Soto-Regalado, R. Gómez-González, M. T. Garza-González and E. Bustamante-Alcántara, Int. J. Environ. Sci. Technol., 2013, 10, 611–622 CrossRef.
- R. Campos-Vega, G. Loarca-Pina, H. Vergara-Castaneda and B. D. Oomah, Trends Food Sci. Technol., 2015, 45, 24–36 CrossRef CAS.
- J. Fang, B. Gao, Y. Sun, M. Zhang and S. K. Sharma, in ref. 4, Ch. 14, pp. 281–295.
- R. Lavecchia, F. Medici, M. S. Patterer and A. Zuorro, Chem. Eng. Trans., 2016, 47, 295–300 Search PubMed.
- A. A. Chavan, J. Pinto, I. Liakos, I. S. Bayer, S. Lauciello, A. Athanassiou and D. Fragouli, ACS Sustainable Chem. Eng., 2016, 4, 5495–5502 CrossRef CAS.
- I. Anastopoulos, M. Karamesouti, A. C. Mitropoulos and G. Z. Kyzas, J. Mol. Liq., 2017, 229, 555–565 CrossRef CAS.
- A. N. Babu, D. S. Reddy, G. S. Kumar, K. Ravindhranath and G. V. K. Mohan, J. Environ. Manage., 2018, 218, 602–612 CrossRef.
- J. McNutt and Q. He, J. Ind. Eng. Chem., 2019, 71, 78–88 CrossRef CAS.
- L. Joseph, B.-M. Jun, J. R. V. Flora, C. M. Park and Y. Yoon, Chemosphere, 2019, 229, 142–159 CrossRef CAS.
- D. Pujol, C. Liu, J. Gominho, M. À. Olivella, N. Fiol, I. Villaescusa and H. Pereira, Ind. Crops Prod., 2013, 50, 423–429 CrossRef CAS.
- L. F. Ballesteros, J. A. Teixeira and S. I. Mussatto, Food Bioprocess Technol., 2014, 7, 3493–3503 CrossRef CAS.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2008, 29, 622–655 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- A. S. de Araujo, M. T. Sonoda, O. E. Piro and E. E. Castellano, J. Phys. Chem. B, 2007, 111, 2219–2224 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891–894 CrossRef.
- S. J. Grimme, Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U.S.A., 2002, 99, 12562–12566 CrossRef CAS.
- G. Bussi, A. Laio and P. Tiwari, in Handbook of Materials Modeling – Methods: Theory and Modeling, ed. W. Andreoni, and S. Yip, Springer Nature Switzerland AG 2020, Ch. 27 Search PubMed.
- D. Branduardi, F. L. Gervasio and M. Parrinello, J. Chem. Phys., 2007, 126, 054103–054112 CrossRef.
- F. Pietrucci and A. M. Saitta, Proc. Natl. Acad. Sci. U.S.A., 2015, 112, 15030–15035 CrossRef CAS.
- F. Pietrucci, Reviews in Physics, 2017, 2, 32–45 CrossRef.
- P. X. Sheng, Y.-P. Ting, J. P. Chen and L. Hong, J. Colloid Interface Sci., 2004, 275, 131–141 CrossRef CAS.
- C. M. Futalan, J. Kim and J.-J. Yee, Water Sci. Technol., 2019, 79, 1029–1041 CrossRef CAS.
- O 1s spectra are deconvoluted into two (instead of typical three) components and ascribed to oxygen atoms involved in either single (C–O) or double (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) bonds. Only the peak position of the latter appears to be sensitive to the interaction with the metal ions, whereas the height and surface areas of both contributions are affected. The broad spectral feature ascribed to C
O) bonds. Only the peak position of the latter appears to be sensitive to the interaction with the metal ions, whereas the height and surface areas of both contributions are affected. The broad spectral feature ascribed to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds has a half-height width of about 2 eV. Note that the core binding energies of the oxygen atoms in C
O bonds has a half-height width of about 2 eV. Note that the core binding energies of the oxygen atoms in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds and in C–OH groups differ by less than 1 eV: see e.g., G. P. Lopez, D. G. Castner and B. D. Ratner, XPS O1s Binding Energies for Polymers Containing Hydroxyl, Ether, Ketone and Ester Groups, Surf. Interface Anal., 1991, 17, 267–272 CrossRef CAS.
O bonds and in C–OH groups differ by less than 1 eV: see e.g., G. P. Lopez, D. G. Castner and B. D. Ratner, XPS O1s Binding Energies for Polymers Containing Hydroxyl, Ether, Ketone and Ester Groups, Surf. Interface Anal., 1991, 17, 267–272 CrossRef CAS. - F. Spyrakis, M. H. Ahmed, A. S. Bayden, P. Cozzini, A. Mozzarelli and G. E. Kellogg, J. Med. Chem., 2017, 60, 6781–6827 CrossRef CAS.
- J. Schiebel, R. Gaspari and T. Wulsdorf, et al. , Nat. Commun., 2018, 9, 3559 CrossRef.
- M. Maurer and C. Oostenbrink, J. Mol. Recognit., 2019, 32, e2810–e2828 CrossRef CAS.
- B. P. Uberuaga and D. W. Perez, in Handbook of Materials Modeling – Methods: Theory and Modeling, ed. W. Andreoni and S. Yip, Springer Nature Switzerland AG, 2020, Ch. 32 Search PubMed.
- M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652 CrossRef CAS.
- M. Karplus, Angew. Chem., 2014, 53, 9992–10005 CrossRef CAS.
- M. De Vivo, M. Masetti, G. Bottegoni and A. Cavalli, J. Med. Chem., 2016, 59, 4035–4061 CrossRef CAS.
- L. Riccardi, V. Genna and M. De Vivo, Nat. Rev. Chem., 2018, 2, 100–112 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information on structural models and computational methods, details of the metadynamics protocols, additional illustrations of the simulation results (Fig. S2–S9) discussed in the main text. See DOI: 10.1039/d0sc06204a |
| This journal is © The Royal Society of Chemistry 2021 |