Open Access Article
Open Access ArticleTautomers of N-acetyl-D-allosamine: an NMR and computational chemistry study
Wojciech
Plazinski
 a,
Mattias U.
Roslund
a,
Mattias U.
Roslund
 b,
Elin
Säwén
b,
Olof
Engström
b,
Petri
Tähtinen
b,
Elin
Säwén
b,
Olof
Engström
b,
Petri
Tähtinen
 c and
Göran
Widmalm
c and
Göran
Widmalm
 *b
*b
aJerzy Haber Institute of Catalysis and Surface Chemistry, Polish Academy of Sciences, 30-239 Krakow, Poland
bDepartment of Organic Chemistry, Arrhenius Laboratory, Stockholm University, S-106 91 Stockholm, Sweden. E-mail: goran.widmalm@su.se
cDepartment of Chemistry, University of Turku, 20014 Turku, Finland
First published on 4th August 2021
Abstract
D-Allosamine is a rare sugar in Nature but its pyranoid form has been found α-linked in the core region of the lipopolysaccharide from the Gram-negative bacterium Porphyromonas gingivalis and in the chitanase inhibitor allosamidin, then β-linked and N-acetylated. In water solution the monosaccharide N-acetyl-D-allosamine (D-AllNAc) shows a significant presence of four tautomers arising from pyranoid and furanoid ring forms and anomeric configurations. The furanoid ring forms both showed 3JH1,H2 ≈ 4.85 Hz and to differentiate the anomeric configurations a series of chemical shift anisotropy/dipole–dipole cross-correlated relaxation NMR experiments was performed in which the α-anomeric form showed notable different relaxation rates for its components of the H1 doublet, thereby making it possible to elucidate the anomeric configuration of each of the furanoses. The conformational preferences of the different forms of D-AllNAc were investigated by 3JHH, 2JCH and 3JCH coupling constants from NMR experiments, molecular dynamics simulations and density functional theory calculations. The pyranose form resides in the 4C1 conformation and the furanose ring form has the majority of its conformers located on the South–East region of the pseudorotation wheel, with a small population in the Northern hemisphere. The tautomeric equilibrium was quite sensitive to changes in temperature, where the β-anomer of the pyranoid ring form decreased upon a temperature increase while the other forms increased.
Introduction
Carbohydrates are an integral part of biological systems including plants, invertebrates and mammals. The glycan structures may be highly complex1,2 and interactions with glycans3 or proteins4,5 are essential in many biochemical processes. In humans only ten monosaccharides are used to build glycoconjugates whereas in bacteria the number of different monosaccharides utilized in structure formation is one to two orders of magnitude higher, although some monosaccharides are significantly more prevalent.6 The rare sugar D-allosamine (C3-epimer of D-glucosamine) (Scheme 1) is a constituent of allosamidin,7 a chitanase inhibitor.8,9,10–14 Its structure consists of two N-acetylated D-allosamine residues and an aglycon part being an aminocyclitol derivative termed allosamizoline. The residues in the pseudotrisaccharide, β-D-AllpNAc-(1→4)-β-D-AllpNAc-(1→4)-allosamizoline, all originate from D-glucosamine and the latter residue is a fused bicyclic ring system containing a highly oxygenated cyclopentanoid structure and a dimethylaminooxazoline ring.15,16 Interestingly, also α-linked D-allosamine has been found as a structural component in Nature, then in the core region of the lipopolysaccharide from Porphyromonas gingivalis W50.17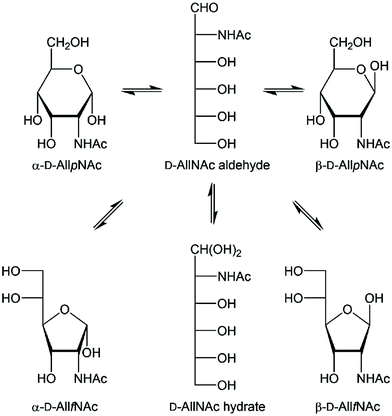 | ||
| Scheme 1 Schematic of the equilibria of tautomeric acyclic and ring forms of N-acetyl-D-allosamine in water solution. The four different ring forms are readily observable by 1H NMR spectroscopy. | ||
In structural characterization of carbohydrates, the use of gas or liquid chromatography is often the choice when standards are available and routine analyses are to be carried out. However, when novel sugar residues or substituent modifications are present one often relies on information from NMR spectroscopy experiments for a de novo structural analysis.18 A reducing monosaccharide can be present in several forms, illustrated for N-acetyl-D-allosamine in Scheme 1 showing the pyranoid and furanoid ring forms in which the α- or β-anomeric forms are possible, the aldehyde form and the hydrate form, resulting in six different structures in equilibrium in water solution for this hexose sugar. The relative populations of aldohexoses in general can be assessed via13C NMR spectroscopy, using in particular D-[1-13C]aldoses, which was done for the eight different D-aldohexoses.19 The hydrate and aldehyde forms were all present to <1% whereas the extent of furanoid ring forms varied depending on the stereoisomer. For example, in D-glucose the pyranoid ring form make up >99% while in D-galactose both the α-D-galactofuranose and β-D-galactofuranose are present to 2% and 4%, respectively. NMR spin–spin coupling constants of anomeric atoms are often used to address the anomeric configuration of a sugar residue. For pyranoses one can rely on the 1JC1,H1 coupling constant, which differs by ∼10 Hz between the two anomeric forms,20 but not for furanoses where the value usually is 175–180 Hz, in practice independent of the anomeric configuration. In some cases the anomeric configuration of furanosides can determined based on the 3JH1,H2 coupling constant such as for β-D-Galf where it is small, ∼1–2 Hz, while for α-D-Galf it is large, ∼5 Hz.21–23
The continued development of the computerized approach CASPER for structural investigation of carbohydrates based on NMR chemical shift predictions24,25 would benefit from assignment of both 1H and 13C NMR chemical shift data for the monosaccharide N-acetyl-D-allosamine. Whereas the NMR resonance assignments to the pertinent α- and β-anomeric pyranose ring forms were straightforward (vide infra) the assignment to the minor furanose ring forms were not, since both the α-D-AllfNAc and β-D-AllfNAc showed 3JH1,H2 ≈ 4.85 Hz, in stark contrast to e.g. the galactofuranose case described above, indicating that different conformational averaging takes place in the allo-configured furanoses. This prompted us to investigate methods for determination of the anomeric configuration in the D-AllfNAc residues and equilibria between different tautomeric forms of the monosaccharide. To this end we have, in particular, applied chemical shift anisotropy/dipole–dipole cross-correlated relaxation (CSA/DD CCR) NMR experiments, molecular dynamics (MD) simulations and density functional theory (DFT) calculations, which we hereby report on.
Materials and methods
NMR spectroscopy
NMR experiments were carried out on 700 MHz Bruker Avance III and 500 MHz Bruker Avance spectrometers equipped with 5 mm CryoProbes. For the NMR chemical shift assignments of N-acetyl-D-allosamine the experiments were performed at 25 °C (1H and 13C) and at 65 °C (13C) in D2O (unless otherwise stated) at a concentration of 90 mM using standard 1D and 2D NMR techniques, viz., 1H,13C-HSQC, 1H,1H-TOCSY (τmix = 10, 30, 60, 90 and 110 ms) and 1H,13C-H2BC experiments. The 1H NMR chemical shifts and coupling constants were refined iteratively with the integral transform fitting mode and the total line-shape mode of the PERCH NMR iterator PERCHit;26,27 starting values were extracted from 1D 1H,1H-TOCSY experiments. 1H NMR chemical shifts were referenced to external sodium 3-trimethylsilyl-(2,2,3,3-2H4)-propanoate (TSP) in D2O (δH 0.00) and 13C NMR chemical shifts were referenced to external dioxane in D2O (δC 67.40). Measurements of the temperature dependence on the ratio of the integrals of the anomeric protons were performed by 1D 1H NMR experiments at six different temperatures in the range 20–65 °C; sufficiently long relaxation delays (>5 × T1) were used to ensure accurate integration.The 1H T1 inversion recovery NMR experiments were carried out at a spectrometer frequency of 700 MHz and a temperature of 25 °C. The detection pulse angle was set to 15° in order to retain the potential asymmetry of the longitudinal relaxation rates of the doublet component of the anomeric proton of each tautomer.28 Seven mixing times ranging from 10 ms to 15 s were used and sufficiently long relaxation delays (>5 × T1) were used to ensure full recovery of the signal between the scans.
Measurements of the heteronuclear carbon–proton coupling constants at 25 °C and 70 °C were performed with the 1H,13C-J-HMBC experiment.29 To scale the splitting of the doublet components in the indirect dimension the experiments used a scaling factor κ of 17.3 and 20.6 at the lower temperature, and 20.6 and 25.8 at the higher temperature, calculated from κ = Δ/tmax1 where Δ was set to be at least 0.6/JminCH. A spectral width of 5 ppm and a carrier position at 4 ppm was used for 1H whereas 13C used a spectral width of 90 ppm and a carrier position at 60 ppm. The experiments were performed with 512 × 2048 points in F1 and F2, respectively, and 32 scans per t1 increment with the echo/antiecho method. Forward linear prediction to 1024 points in F1, subsequent zero-filling to 2048 × 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 points and a 90° shifted squared sine-bell function was applied prior to Fourier transformation. The J-HMBC spectrum was processed in magnitude mode. Coupling constants were extracted from 1D-projections of the resonances of interest through rescaling of peak separation by κ−1. The reported values at each temperature are the average from the two measurements with different scaling factors.
384 points and a 90° shifted squared sine-bell function was applied prior to Fourier transformation. The J-HMBC spectrum was processed in magnitude mode. Coupling constants were extracted from 1D-projections of the resonances of interest through rescaling of peak separation by κ−1. The reported values at each temperature are the average from the two measurements with different scaling factors.
Computer simulations
The saccharides under consideration were the four tautomers of AllNAc: α-AllfNAc, β-AllfNAc, α-AllpNAc and β-AllpNAc. The computations involved MD simulations performed with classical force fields to sample conformational space and ab initio calculations to obtain J coupling constants.The MD simulations were carried out within the GROMACS 2016.4 package.30 To describe the interactions within the system either the GROMOS (α-AllfNAc and β-AllfNAc)31,32 or the CHARMM33 (α-AllpNAc and β-AllpNAc) force field was applied. The GROMOS parameters were based on the furanose-dedicated extension of the 56A6CARBO set32 whereas the N-acetyl (NAc) group was described by non-bonded parameters taken from the 53a6 set34 and bonded parameters generated by the Automated Topology Builder server.35 The torsional parameters describing the interactions at the NAc/ring interface were unchanged with respect to the furanose-dedicated set,32 in which the role of one of the hydroxyl oxygen atoms is played by the topologically analogous nitrogen atom.
The considered MD systems consisted of one saccharide molecule solvated by water molecules within a cubic computational box simulated under periodic boundary conditions. The box edges (of initial dimensions corresponding to 3.1 × 3.1 × 3.1 nm3) were preoptimized by a 1 ns constant-pressure MD equilibration at 1 bar and 298 K, ensuring an effective solvent density appropriate for the conditions in the subsequent production simulations. After equilibration, all simulations were carried out for 100 ns. The data, saved every 1 ps, consisted of torsion angle values describing the conformation of exocyclic groups as well as the parameters describing the ring geometry. In the case of pyranose forms of AllNAc, the simulations were initiated from the 4C1 chair conformation, which was identified as the favorable one in the independent metadynamics simulations (vide infra).
The temperature was maintained close to its reference value (298 K) by applying the V-rescale thermostat,36 whereas for the constant pressure (1 bar, isotropic coordinate scaling) the Parrinello–Rahman barostat37 was used with a relaxation time of 0.4 ps. The equations of motion were integrated with a time step of 2 fs using the leap-frog scheme.38 The translational center-of-mass motion was removed every timestep separately for the solute and the solvent. The full rigidity of the water molecules was enforced by application of the SETTLE procedure.39 Some details regarding the simulation set-up varied, depending on the used force field. In the case of CHARMM, the TIP3P model of water40 was applied. The hydrogen-containing solute bond lengths were constrained by application of the LINCS procedure with a relative geometric tolerance of 10−4.41,42 The electrostatic interactions were modeled by using the particle-mesh Ewald method43 with the cut-off set to 1.2 nm, while van der Waals interactions (Lennard-Jones potentials) were switched off between 1.0 and 1.2 nm. In the case of GROMOS, the SPC model of water44 was applied. The solute bond lengths were constrained by application of the LINCS procedure with a relative geometric tolerance of 10−4.41,42 The non-bonded interactions were calculated using a single cut-off distance set to 1.4 nm and a Verlet list scheme. The reaction-field correction was applied to account for the mean effect of the electrostatic interactions beyond the long-range cut-off distance, using a relative dielectric permittivity of 61 as appropriate for the SPC water model.45
The analysis of the unbiased MD simulations included: (i) the occurrence of hydrogen bonding; (ii) the population of the hydroxymethyl group rotamers of the pyranose forms of AllNAc; (iii) the conformation of the ring of the furanose forms of AllNAc; (iv) the population of the individual conformers, distinguished on the basis of the rotation of the exocyclic groups. In step (i), the default, GROMACS-inherent geometrical criteria were applied. During step (ii), the conformation of the O5–C5–C6–O6 torsion angle (ω) was assigned to one of the three possible staggered conformers, based on its value, i.e., gt (staggered conformation at 60°), gg (−60°), and tg (180°). In step (iii), the Altona–Sundaralingam46 coordinates expressing the pseudorotation phase (P) and amplitude (ϕm) were used according to the mathematical definition by Huang et al.47 The corresponding P vs. ϕm free energy maps were constructed by using the Boltzmann inversion method. The purpose of step (iv) was to optimize the J coupling constant calculations. Each saccharide structure present in the MD trajectory was analyzed with respect to the conformation of the exocyclic, rotatable bonds. The conformation of all such bonds in the monosaccharide molecule was assigned to be one of the three possible staggered conformers, based on the smallest deviation from the optimal value. The results of such assignment were sorted and the 200 most frequently occurring combinations were subjected to the subsequent calculations of the J coupling constants.
The enhanced-sampling free energy calculations were restricted to the case of α-AllpNAc and β-AllpNAc and were focused on the free energy changes associated with the pyranose ring distortion. The metadynamics simulations along the Cremer–Pople θ parameter48 were performed by using PLUMED 2.2 software.49 The well–tempered metadynamics50 relied on Gaussian local functions of widths 2.86°, an initial deposition rate of 0.01 kJ mol−1 ps−1 and a temperature parameter ΔT (see eqn (2) in the study by Barducci et al.50) of 1788 K. The duration of metadynamics simulations was 100 ns and the convergence was checked by calculating ring-inversion free energy values as a function of time. The remaining details of the simulation set-up were identical to those described earlier for the case of unbiased MD simulations.
The values of the nJCH and nJHH coupling constants were calculated according to the multi-step protocol proposed by Gaweda and Plazinski.51 In the first step the unbiased, explicit solvent molecular dynamics simulations within the classical force field were carried out for each of the considered tautomers (according to the protocol described above). The aim of this step was to provide the information about the possible conformers of the saccharide molecule and the corresponding populations. In the next step, the most populated conformers were extracted from the MD trajectory and subjected to ab initio-based geometry optimization in the presence of implicit solvent. For each of the fully optimized structures the nJCH and nJHH coupling constants were calculated. The final values of either nJCH or nJHH assigned to the given pair of atoms were calculated according to the following equation:
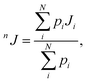 | (1) |
The ab initio calculations were performed in Gaussian09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 at the DFT/B3LYP/6-311+G(d,p) level of theory53,54 and in the presence of implicit, aqueous solvent (COSMO model).55 The geometry optimization was performed by using the default criteria, except for the use of the tight keyword, tightening the cut-offs on forces and step size. Subsequently, J coupling constants, which in effect respond immediately as electronic structure instantaneously adjusts to any comparatively slow change in nuclear position (Born–Oppenheimer approximation),56 were calculated for the fully optimized structures using the GIAO (gauge-independent atomic orbital) approach57 at the same level of theory. The mixed keyword was invoked to request a two-step spin–spin coupling calculation.58
52 at the DFT/B3LYP/6-311+G(d,p) level of theory53,54 and in the presence of implicit, aqueous solvent (COSMO model).55 The geometry optimization was performed by using the default criteria, except for the use of the tight keyword, tightening the cut-offs on forces and step size. Subsequently, J coupling constants, which in effect respond immediately as electronic structure instantaneously adjusts to any comparatively slow change in nuclear position (Born–Oppenheimer approximation),56 were calculated for the fully optimized structures using the GIAO (gauge-independent atomic orbital) approach57 at the same level of theory. The mixed keyword was invoked to request a two-step spin–spin coupling calculation.58
The relative populations of particular tautomers of AllNAc were calculated from known average DFT energies of each of the considered individual species (i.e. α-AllfNAc, β-AllfNAc, α-AllpNAc and β-AllpNAc) and the Boltzmann ratio. The average energies were calculated according to the following equation:
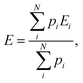 | (2) |
Results and discussion
NMR chemical shift and spin–spin coupling constants
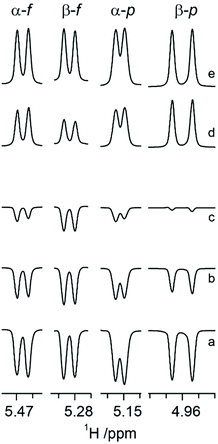
The one-dimensional 1H and 13C NMR spectra of N-acetyl-D-allosamine in D2O revealed that four tautomeric forms were present to a significant extent. One- and two-dimensional NMR experiments suitable for resonance assignments of carbohydrates59 were employed to assign resonances from each tautomer, followed by NMR spin-simulation27 to refine 1H NMR chemical shifts and nJHH coupling constants, i.e., a seven-proton spin system for each of the tautomeric forms. From the 3JH1,H2 and 1JC1,H1 coupling constants together with the chemical shifts of the anomeric carbons as well as the low chemical shifts of ∼67 ppm for their C4 resonances (Table 1) it was evident that the spin systems having the anomeric proton at δH 5.153 and 3JH1,H2 3.8 Hz originated from α-D-AllpNAc and that at δH 4.960 and 3JH1,H2 8.7 Hz originated from β-D-AllpNAc being present to ∼22% and 66%, respectively, at 25 °C, since the pyranose rings reside in the 4C1 conformation for which 3JH4,H5 ≈ 10 Hz for both anomeric forms. The spin systems having anomeric protons at δH 5.466 and δH 5.284 had 3JH1,H2 ≈ 4.85 Hz as well as 1JC1,H1 ≈ 179 Hz, with relative populations of ∼7% and ∼4%, respectively; the high chemical shifts of ∼85 ppm for their C4 resonances (Table 1) supported the fact that these tautomers originate from the furanoid ring form. In addition, 13C NMR chemical shift data in D2O are reported at an elevated temperature commonly used in the NMR chemical shift prediction program CASPER60,61 as well as nitrogen-15 and proton chemical shifts of the amide groups in water solution (Table 1). Although a comparison to published 13C NMR chemical shifts for the anomeric carbons of D-allose, which differ by ∼5 ppm between the α- and β-anomeric forms,19 suggests that the lower 13C NMR chemical shift of 96.06 ppm and the higher 1H chemical shift of 5.466 ppm originate from α-D-AllfNAc whereas the higher 13C NMR chemical shift of 100.58 ppm and the lower 1H chemical shift of 5.284 ppm originate from β-D-AllfNAc, a general approach to the determination the anomeric configuration of sugars should be applied to prove the stereochemistry at the anomeric center.| Monosaccharide | 1 | 2 | 3 | 4 | 5 | 6d | Me | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
NHe | % | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 J H1,H2 | 3 J H2,H3 | 3 J H3,H4 | 3 J H4,H5 | 3 J H5,H6pro-R/H6pro-S | 2 J H6pro-R,H6pro-S | ||||||
a ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1JC1,H1 coupling constants from a coupled HSQC experiment at 11.7 T.
b 1JC1,H1 coupling constants from a coupled HSQC experiment at 11.7 T.
b ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13C NMR chemical shifts of D-AllNAc in D2O at 65 °C.
c 13C NMR chemical shifts of D-AllNAc in D2O at 65 °C.
c ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4JH1,H3.
d The resonance assignments to H6pro-R and H6pro-S are tentative.
e 4JH1,H3.
d The resonance assignments to H6pro-R and H6pro-S are tentative.
e ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15N NMR chemical shifts in 95% H2O and 5% D2O at 5 °C. 15N NMR chemical shifts in 95% H2O and 5% D2O at 5 °C.
|
|||||||||||
| α-D-AllfNAc | 1H | 5.466 | 4.211 | 4.332 | 4.159 | 3.790 | 3.623, 3.738 | 2.099 | 7.80 | 7.4 | |
| J HH | 4.84 | 6.69 | 2.41 | 5.03 | 6.88, 4.00 | −11.72 | |||||
| 13C/15N | 96.06 [178.7]a | 54.95 | 69.47 | 86.21 | 72.30 | 63.11 | 22.57 | 175.15 | 115.7 | ||
| 13Cb | 96.17 | 54.90 | 69.71 | 86.21 | 72.36 | 63.27 | 22.65 | 175.06 | |||
| β-D-AllfNAc | 1H | 5.284 | 4.172 | 4.465 | 3.911 | 3.800 | 3.640, 3.773 | 2.076 | 8.39 | 4.3 | |
| J HH | 4.86 | 5.72 | 3.40 | 6.60 | 6.79, 2.36 | −11.45 | |||||
| 13C/15N | 100.33 [179.2]a | 58.71 | 70.85 | 84.50 | 72.84 | 63.19 | 22.62 | 175.49 | 116.8 | ||
| 13Cb | 100.58 | 58.79 | 70.80 | 84.72 | 72.88 | 63.33 | 22.70 | 175.39 | |||
| α-D-AllpNAc | 1H | 5.153 | 4.000 | 4.106 | 3.704 | 4.034 | 3.813, 3.887 | 2.080 | 8.17 | 22.3 | |
| J HH | 3.84, −1.01c | 3.06 | 3.09 | 10.32 | 5.19, 2.27 | −12.32 | |||||
| 13C/15N | 91.91 [174.9]a | 50.64 | 70.58 | 66.84 | 67.72 | 61.56 | 22.64 | 174.75 | 122.1 | ||
| 13Cb | 92.00 | 50.71 | 70.67 | 67.04 | 67.91 | 61.81 | 22.74 | 174.66 | |||
| β-D-AllpNAc | 1H | 4.960 | 3.779 | 4.097 | 3.686 | 3.818 | 3.725, 3.892 | 2.057 | 8.41 | 66.0 | |
| J HH | 8.69 | 2.82 | 3.07 | 10.20 | 5.94, 2.26 | −12.31 | |||||
| 13C/15N | 93.18 [166.3]a | 55.08 | 70.54 | 67.32 | 74.62 | 62.01 | 22.72 | 174.86 | 122.4 | ||
| 13Cb | 93.33 | 55.09 | 70.64 | 67.53 | 74.67 | 62.21 | 22.82 | 174.82 | |||
Since long-range heteronuclear 2JCH and 3JCH coupling constants depend on conformation and stereochemical arrangements62 we also measured some of these by the J-HMBC experiment29 in the same way as previously reported for a milk oligosaccharide63 and the data are reported in Table 2. It is evident that some coupling constants differ between the four tautomeric forms, such as 3JH1,C3, 3JH1,C4, and 2JH2,C1 in the furanoses and 3JH1,C3 and 3JH1,C5 in the pyranoses, the magnitudes of which can be useful for structural and conformational analysis of AllNAc-containing compounds. In the 4C1 conformation of the pyranoses (vide supra) the torsion angles H1–C1–C2–C3 and H1–C1–O5–C5 will for the α-anomeric form be in an antiperiplanar arrangement resulting in a large coupling constant whereas for the β-anomeric form these torsion angles will be in a synclinal arrangement and as a result thereof the coupling constants will be smaller. Both pyranose ring forms have in common a large value of the 3JH3,C1 coupling constant (antiperiplanar arrangement for the torsion angle H3–C3–C2–C1) characteristic for the allo-configuration. In contrast to both anomeric forms of D-Glcp, for which |2JH4,C3| ≈ 5 Hz,62 the corresponding coupling constants in D-AllpNAc are smaller in magnitude with |2JH4,C3| < 2 Hz (Table 2), where the main difference between the compounds is the stereochemistry at C3, with an equatorial hydroxyl group in the former and an axial one in the latter compound.
| Atom pair | α-D-AllfNAc | β-D-AllfNAc | α-D-AllpNAc | β-D-AllpNAc | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 °C | 70 °C | MD/DFT | 25 °C | 70 °C | MD/DFT | 25 °C | 70 °C | MD/DFT | 25 °C | 70 °C | MD/DFT | ||
| H1 | C2 | 2.03 | 2.04 | 3.15 | 1.24 | 1.47 | 2.42 | ||||||
| C3 | 4.54 | 4.05 | 4.14 | 1.46 | 1.53 | 1.31 | 4.60 | 4.77 | 4.78 | 1.15 | 1.42 | 0.98 | |
| C4 | 6.13 | 6.35 | 7.17 | 2.90 | 2.77 | 4.30 | |||||||
| C5 | 5.84 | 5.86 | 6.42 | 1.20 | 1.43 | 1.38 | |||||||
| H2 | C1 | 1.50 | 1.52 | 1.39 | 5.25 | 4.75 | 4.30 | 3.02 | 2.87 | 2.18 | 7.78 | 7.69 | 6.52 |
| CO | 2.86 | 2.71 | 3.21 | 3.12 | 3.09 | 3.04 | 3.14 | ||||||
| H3 | C1 | 5.42 | 5.36 | 4.97 | 4.13 | 3.96 | 4.26 | 5.60 | 5.42 | 6.18 | 6.14 | 5.87 | |
| C2 | 3.73 | 2.65 | 3.93 | 3.95 | 2.86 | ||||||||
| C4 | 1.68 | 1.62 | 3.33 | 4.26 | 4.10 | 3.02 | |||||||
| C5 | 2.91 | 2.71 | 3.05 | 2.86 | 2.46 | 2.75 | 4.97 | 4.73 | 4.78 | ||||
| H4 | C1 | 2.59 | 4.09 | ||||||||||
| C2 | 1.50 | 1.02 | |||||||||||
| C3 | 4.43 | 4.47 | 3.65 | 4.63 | 3.79 | 1.88 | 1.76 | 3.49 | 1.90 | 1.64 | 3.05 | ||
| C5 | 2.97 | 2.78 | 3.03 | ||||||||||
| C6 | 2.10 | 1.89 | 3.23 | 3.84 | 3.40 | 3.78 | 3.82 | ||||||
| H5 | C1 | 1.68 | 1.75 | 2.85 | |||||||||
| C3 | 4.19 | 3.83 | 4.40 | 2.03 | 2.20 | 1.82 | 1.89 | ||||||
| C4 | 4.21 | 2.89 | 1.93 | 2.21 | |||||||||
| C6 | 3.25 | 2.97 | 3.32 | 2.93 | 3.13 | ||||||||
| H6pro-R | C4 | 2.10 | 3.10 | 2.27 | 1.93 | 2.75 | 1.42 | 1.61 | |||||
| C5 | 3.08 | 4.20 | 2.31 | 4.01 | 3.16 | 3.26 | 2.97 | ||||||
| H6pro-S | C4 | 2.26 | 2.44 | 4.34 | 2.45 | 2.28 | 2.36 | ||||||
| C5 | 1.27 | 2.50 | |||||||||||
Chemical shift anisotropy/dipole–dipole cross-correlated relaxation NMR experiments
It has been reported that CSA/DD CCR is an important relaxation mechanism that is manifested by multiplet asymmetries in NMR inversion-recovery experiments where the monitoring pulse angle is small.28 The anomeric configuration of ribonucleosides64 as well as that of hexopyranoses65 have been determined by the application of CSA/DD CCR NMR experiments, since in the compounds investigated the CSA/DD CCR rates differed for the doublet components of the anomeric proton due to cross-correlation between CSA and DD interactions,66–68 thereby facilitating the structural differentiation between the α- and β-anomeric configurations in sugar residues. This prompted us to explore the approach based on CSA/DD CCR to the different tautomers of N-acetyl-D-allosamine.For N-acetyl-D-allosamine the peak-asymmetry of the anomeric doublet in each tautomer is due to the interference between the H1 CSA and the H1–H2 DD interactions. The spectral region of anomeric resonances reveals from the inversion-recovery experiments (Fig. 1) that the doublet components of the anomeric proton at 5.153 ppm relax with different rates, fully consistent with the α-anomeric configuration of this pyranose form of AllNAc. Inspection of the resonances from the anomeric protons of the tautomers having the furanose ring form reveals that it is the doublet at 5.466 ppm that shows notable different relaxation rates for its components thereby assigning this tautomer to α-D-AllfNAc and the one having its anomeric 1H NMR chemical shift at 5.284 ppm to β-D-AllfNAc.
Computational investigation of conformational preferences
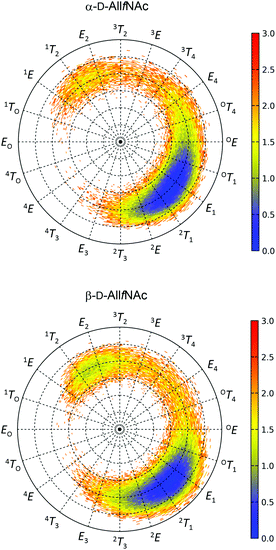
The free energy maps illustrating the conformational preferences of five-membered rings of α-AllfNAc and β-AllfNAc are shown in Fig. 2. The preferences displayed by α-AllfNAc agree with the expectations based on the stereoelectronic endo-anomeric effect;69 the ‘ideal’ pseudo-axial arrangement of the anomeric hydroxyl group corresponds to the OT1 ring geometry. For α-AllfNAc, the most frequently appearing shapes include: OT1, E1, 2T1 and 2E, i.e., canonical conformers located on the Southern hemisphere of the pseudorotation wheel. However, due to a high flexibility of the ring, a much broader region of the conformational phase space is accessible and the disallowed region on the pseudorotation wheel includes relatively narrow set of shapes between 1TO and 4T3. This region corresponds to a very short distance between the NH and HO3 groups and the enhancement of the corresponding, unfavorable interactions. Overall, the conformation of the α-AllfNAc ring is nearly identical to that calculated for unfunctionalized α-D-allofuranose.32Interestingly, the conformational properties exhibited by the ring of β-AllfNAc are very similar to those of α-AllfNAc, including both the conformationally-restricted and the favorable regions that differ only by a larger population of conformers located on the Northern hemisphere of the pseudorotation wheel for β-AllfNAc, in the vicinity of 1T2 and E2. Such an alteration is expected due to the inverted configuration at the anomeric center and the anomeric effect-related tendencies to shift the conformational equilibrium towards the 1TO geometry. However, the magnitude of such shift is significantly lower in comparison to those predicted for either unfunctionalized D-allofuranose or D-ribofuranose,32i.e., compounds of analogous topological orientation of ring substituents.70,71 This finding may be explained by the combined influence of the conformationally-restricted rotation of the N-acetyl group around the C–N bond and its interactions with the ring substituents. The preferred orientation of the NH group with respect to the aliphatic hydrogen atom at C2 is antiperiplanar; thus, interactions of the NH hydrogen atom with the pseudo-axially arranged aliphatic H4 hydrogen atom are unavoidable if the ring is in a conformation close to E2. As a consequence, the population of the Northern conformers is reduced in comparison to the expectations based on the behavior of unfunctionalized compounds. The HO2 hydroxyl hydrogen atoms (structurally-analogous to HN) in either D-ribofuranose or unfunctionalized D-allofuranose are allowed to rotate freely and can avoid the unfavorable interactions with pseudo-axially oriented aliphatic hydrogens at C1 and C4. Thus, a more balanced equilibrium between both North and South conformers is observed for β-anomers of compounds lacking the N-acetyl group at C2.
In addition to the analysis based on the values of the pseudorotation phase, it is worth noting the similarities between the variabilities of the ring puckering amplitudes calculated for both α-AllfNAc and β-AllfNAc. In both cases the pseudorotation phase varies from ∼20° to ∼40° with an average equal to 30° (α-AllfNAc) or 32° (β-AllfNAc), which agrees with results from a report on aldohexofuranoses and methyl glycosides thereof.32
One-dimensional free energy profiles illustrating the conformational preferences of six-membered rings of α-AllpNAc and β-AllpNAc are shown in Fig. 3. Independently of the considered anomer, the conformer type that strongly dominates over the remaining ones is always the 4C1 chair. The population of a second conformation, which in both cases is the inverted 1C4 chair, is smaller than 0.1%, i.e., can be considered negligible. Thus, a more detailed analysis focused on the boat and skew ring shapes was not performed. Regarding the most favorable 4C1 geometries, both the deviation from the ‘ideal’ 4C1 conformation (where θ = 0) and the magnitude of the puckering amplitude (also expressed by the Cremer–Pople definition) are in accordance with the values typical for regular hexopyranoses.72
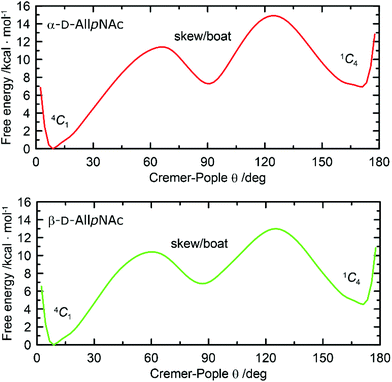 | ||
| Fig. 3 Free energy as a function of the Cremer–Pople parameter θ for (top) α-D-AllpNAc and (bottom) β-D-AllpNAc. | ||
A comparison to the ring-inversion free energies calculated for allopyranose within the same force field73 reveals that introducing the N-acetyl group results in a shift of the conformational equilibrium. More precisely, the ring-inversion free energies are notably enhanced in comparison to the unfunctionalized compounds, by ∼6 kcal mol−1 for the α-anomer and by 2.2 kcal mol−1 for β-anomer. This can be explained by the energetically unfavorable axial orientation of the N-acetyl group and its interactions with the 1,3-syn-axially oriented hydroxyl group at C4 occurring when the pyranose ring is found in the 1C4 conformation.
Calculation of NMR spin–spin coupling constants
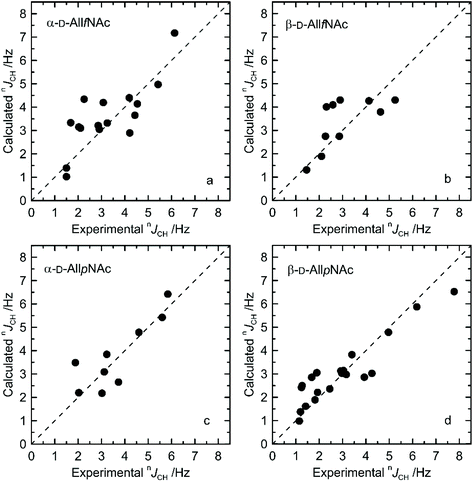
The agreement between measured and theoretically-predicted J coupling constants are shown graphically in Fig. 4 and 5. The average magnitude of deviation from the experiment is lower in the case of pyranoses (0.5–0.6 Hz) in comparison to furanoses (0.7–1 Hz). All deviations have a non-systematic character.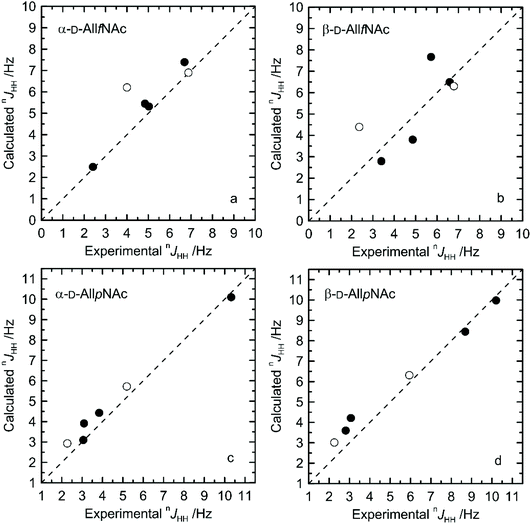 | ||
| Fig. 4 Calculated vs. experimental nJHH presented as absolute values for (a) α-D-AllfNAc, (b) β-D-AllfNAc, (c) α-D-AllpNAc and (d) β-D-AllpNAc; 3JH5,H6 are shown by empty circles. | ||
 | ||
| Fig. 5 Calculated vs. experimental nJCH presented as absolute values for (a) α-D-AllfNAc, (b) β-D-AllfNAc, (c) α-D-AllpNAc and (d) β-D-AllpNAc. | ||
Deviations of larger magnitude for J values are observed in the case of furanose forms of AllNAc. Besides the factors related to the inaccuracies of the theoretical models and calculation methodology, the additional reason for this may be a larger flexibility of the furanoses in comparison to pyranoses. A relatively flat potential energy surface characteristic of furanoses makes them more prone to conformational rearrangements at the stage of geometry optimization, preceding the final J coupling constant calculations. This effect can influence the final nJCH and nJHH values due to two opposite tendencies. Firstly, it can reduce the inaccuracies inherent in the classical force field and optimize the corresponding J coupling constant values. Secondly, the geometry optimization-induced structural rearrangements can be much larger in comparison to pyranoses, which leads to underestimation of the off-equilibrium structures. Assuming the same level of accuracy of both applied force fields and the obtained magnitudes of deviation from the experiment for both furanoses and pyranoses, it can be speculated that that the latter effect is more pronounced in the case of the considered systems.
Furthermore, from the perspective of the ring conformational equilibrium, one may note that the structures belonging to both hemispheres of the pseudorotation wheel contributed to the final nJCH and nJHH values calculated for furanose forms of AllNAc. The corresponding North vs. South ratio is equal to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 1
5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for α-AllfNAc and β-AllfNAc, respectively. The deviation of these numbers from the predictions of the free energy maps presented in Fig. 2 originates from the fact that the MD-extracted structures were preoptimized at the DFT level of theory, prior to calculation of J coupling constants. This element of the computational protocol may perturb the ring geometry in the case of the furanose forms. In the case of the pyranose forms, α-AllpNAc and β-AllpNAc, the structures subjected to the J coupling constant calculations always displayed the 4C1 geometry, i.e., consistent with that identified in the metadynamics simulations.
2 for α-AllfNAc and β-AllfNAc, respectively. The deviation of these numbers from the predictions of the free energy maps presented in Fig. 2 originates from the fact that the MD-extracted structures were preoptimized at the DFT level of theory, prior to calculation of J coupling constants. This element of the computational protocol may perturb the ring geometry in the case of the furanose forms. In the case of the pyranose forms, α-AllpNAc and β-AllpNAc, the structures subjected to the J coupling constant calculations always displayed the 4C1 geometry, i.e., consistent with that identified in the metadynamics simulations.
Rotamer populations of hydroxymethyl groups
The theoretically-predicted populations of the hydroxymethyl group rotamers of both pyranose tautomers using the Karplus-type relationships and limiting 3JHH coupling constant values developed by Stenutz et al.74 are in an excellent agreement with the experimental data (Table 3). The maximal deviation does not exceed 4% of relative population of the given conformer. Both α- and β-anomeric forms display a highly similar trend in the corresponding population orders, i.e., gt ≈ gg > tg. This trend is consistent with the reports for other monosaccharides exhibiting analogous orientations of both the hydroxymethyl group and the vicinal hydroxyl group at C4, i.e., for glucopyranose and mannopyranose (cf. the compilation of the experimental data in Table 8 in the work by Hansen and Hünenberger31).| Monosaccharide | gt | gg | tg | |||
|---|---|---|---|---|---|---|
| NMR | MD | NMR | MD | NMR | MD | |
| α-D-AllpNAc | 45 | 48 | 46 | 46 | 9 | 6 |
| β-D-AllpNAc | 53 | 54 | 38 | 41 | 9 | 5 |
Tautomeric equilibrium as a function of temperature
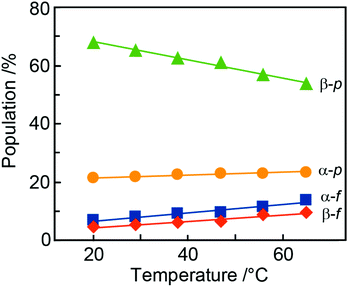
During the NMR-based analysis of AllNAc it was observed that the tautomeric equilibrium was quite affected by changes in temperature. The relative amount of the different tautomers in D2O75 varied in a linear way as a function of temperature (Fig. 6 and Table 4), where the β-anomer of the pyranoid form decreased upon a temperature increase, whereas the other forms increased. This behavior is reminiscent of the temperature dependence of D-fructose for which the β-anomeric form decreases, roughly by the same amount as for β-D-AllpNAc, while the other forms increase as temperature increases.76 The same temperature dependence does also occur for D-glucose, albeit to a negligible extent.77 The tautomeric equilibrium of D-glucose consists of the α-anomeric form ∼38% and the β-anomeric form ∼62%, with only trace amounts <0.3% of any of the other four forms whereas D-allose has the pyranoid α-anomeric form to ∼15% and the β-anomeric form to ∼77%, with small portions of the furanoid forms, viz., the α-anomeric form is present to ∼3% and the β-anomeric form to ∼5%; the hydrate and aldehyde forms are negligible, <0.01%.19 Notably, already in 1947 Hassel and Ottar78 proposed that the β-anomeric form of D-allopyranose should be favored over its α-anomeric form as a result of energetically unfavorable hydroxyl group interactions on the same side of the pyranose ring, i.e., axially oriented OH groups at both C1 and C3. Thus, the single difference in stereochemistry at C3 between glucose and allose leads to large changes in the relative populations of the tautomers.| Temp | α-D-AllfNAc | β-D-AllfNAc | α-D-AllpNAc | β-D-AllpNAc |
|---|---|---|---|---|
| NMR experiment | ||||
| 20 | 6.7 | 4.4 | 21.2 | 67.7 |
| 29 | 7.8 | 5.3 | 21.6 | 65.3 |
| 38 | 9.0 | 6.1 | 22.5 | 62.4 |
| 47 | 9.6 | 6.4 | 22.9 | 61.1 |
| 56 | 11.6 | 8.7 | 23.0 | 56.7 |
| 65 | 13.6 | 9.4 | 23.3 | 53.7 |
| MD/DFT calculations | ||||
| 25 | 1.1 | 0.4 | 16.9 | 81.5 |
The β-anomeric form is predominant over the α-anomeric form for AllpNAc in the temperature range 20–65 °C. This may in part be due to a disfavorable 1,3-syndiaxial interaction (Hassel–Ottar effect)78,79 between the hydroxyl groups at C1 and C3 of the α-anomeric form of AllpNAc. D-Xylose in water solution shows an α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β ratio of 1
β ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for its pyranoid ring form and MD simulations of the anomeric forms of D-xylopyranose80,81 in the 4C1 chair conformation concluded that the β-anomeric form is favored as a result of increased accessible surface area of the anomeric hydroxyl group thereby facilitating a greater hydrogen bonding ability.
2 for its pyranoid ring form and MD simulations of the anomeric forms of D-xylopyranose80,81 in the 4C1 chair conformation concluded that the β-anomeric form is favored as a result of increased accessible surface area of the anomeric hydroxyl group thereby facilitating a greater hydrogen bonding ability.
The populations calculated on the basis of the DFT energies agree qualitatively with the experimental data, indicating: (i) larger populations of pyranoses in comparison to furanoses; (ii) a larger population of the α-anomeric form of the furanose whereas for the pyranose ring form the β-anomer predominates. Considering the relatively low magnitude of deviations from the experimental values (4–16%, cf.Table 1vs.Table 4) and the approximate character of the calculations (data relying only on the DFT energies with neglected entropic contributions) the agreement with the measured populations is quite satisfactory.
To investigate hydrogen bonding occurrences in general and more specifically whether the favored β-anomeric configuration of AllpNAc in water solution also can be rationalized by increased hydrogen bonding to solvent as compared to its α-anomeric counterpart, the MD simulations were analyzed to this end (Table 5).
| Hydrogen bonding type | α-D-AllfNAc | β-D-AllfNAc | α-D-AllpNAc | β-D-AllpNAc |
|---|---|---|---|---|
| Intra-solute | 0.18 | 0.05 | 0.75 | 0.01 |
| Solute-solvent | 9.94 | 10.54 | 8.90 | 10.53 |
| Intra-solute involving OH(anomeric) | 0.17 | 0.03 | 0.74 | 0.00 |
| OH(anomeric)-solvent | 1.72 | 2.16 | 1.06 | 2.06 |
The intra-solute (i.e. taking place within monosaccharide molecule) hydrogen bonds are relatively rare and occur, on average, <1 per timeframe. The major contribution to this value comes from hydrogen bonds involving the anomeric hydroxyl group. In contrast, hydrogen bonds of the solute-solvent type are very frequent occurring ∼10 per timeframe and are clear indicators of the intensive interactions between monosaccharide and water. In agreement with the expectations expressed in previous paragraph, the β-anomeric configuration of AllpNAc favors the formation of solute-solvent hydrogen bonding compared to the α-configured monosaccharide. This is demonstrated by the total number of solute-solvent hydrogen bonds observed for those two anomeric forms (8.9 vs. 10.5 for α-AllpNAc and β-AllpNAc, respectively), but also by the particular contributions to this value, from hydrogen bonds emanating the anomeric hydroxyl moiety (∼1 vs. ∼2 for α-AllpNAc and β-AllpNAc, respectively). The above differences can be explained on stereochemical grounds, referring to the orientation of the anomeric hydroxyl group which can be either axial (α-AllpNAc) or equatorial (β-AllpNAc). The latter configuration essentially prevents the formation of hydrogen bond with the rest of the monosaccharide molecule as the potential donors and acceptors are too distant. Instead, the interactions with solvent are preferred. On the other hand, in the case of α-AllpNAc two syn-axially oriented hydroxyl groups exist, capable of creating some hydrogen bonding. The trends characteristic for pyranoid forms of AllNAc are not as pronounced in the case of the two furanoses (Table 5), which in part may be due to the much higher flexibility of the ring in both of the anomeric forms of AllfNAc. A representative set of highly populated structures is given in Fig. 7 in which the arrangement H2–C2–N–HN has an antiperiplanar orientation and the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–N–HN has a trans conformation, similar to those observed for methyl 3-acetamido-3,6-dideoxy-α-D-galactopyranoside.82
C–N–HN has a trans conformation, similar to those observed for methyl 3-acetamido-3,6-dideoxy-α-D-galactopyranoside.82
 | ||
| Fig. 7 Representative structures for highly populated conformations of (a) α-D-AllfNAc, (b) β-D-AllfNAc, (c) α-D-AllpNAc and (d) β-D-AllpNAc. | ||
Conclusions
The tautomers of N-acetyl-D-allosamine in water solution arising from pyranoid and furanoid ring forms and the different anomeric configurations have been characterized by 1H and 13C NMR chemical shift data as well as nJHH and nJCH coupling constants, some of which are characteristic for the stereochemical arrangements within the monosaccharide. As the 1H NMR chemical shifts of H1 of the furanoses were similar and the 3JH1,H2 essentially indistinguishable we relied on a series of CSA/DD CCR NMR experiments to differentiate between the α- and β-anomeric configurations. The rotamer distribution of the hydroxymethyl group of the pyranose tautomers was determined using 3JH5,H6 coupling constant values and was found similar to those of hexopyranoses with the manno- or gluco-configuration. The MD simulations reproduced the relative populations of the ω torsion angle very well for both of the anomeric forms of D-AllpNAc, the rings of which reside in the 4C1 conformation. The furanose ring form display a preferred South–East region of the pseudorotation wheel, but is still very flexible with populations on the Northern hemisphere. A procedure based on sampling of the conformational space by MD simulations, selecting the representative set of conformers, geometry preoptimization at the DFT/B3LYP/6-311+G(d,p) level of theory, followed by calculation of J coupling constants, showed an overall good agreement of computed coupling constants to those determined from NMR experiments. The computational approach relying on the DFT energies was also able to reproduce relative populations of the tautomeric equilibrium for AllNAc in qualitative agreement with NMR data. The combined use of NMR spectroscopy and computational chemistry has facilitated a detailed investigation of structure, conformation and dynamics of N-acetyl-D-allosamine, underscoring the successful methodological approach as well as obtaining valuable information on the monosaccharide for future studies of either synthesized compounds83 or those isolated from Nature and containing D-AllNAc.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by grants from the Swedish Research Council and The Knut and Alice Wallenberg Foundation (GW), Magnus Ehrnrooths Stiftelse (MUR) and Polish National Science Centre (contract financed in 2016–2020 under Project No. 2015/18/E/ST4/00234 SONATA BIS) (WP). CSC – IT Center for Science, Finland, is acknowledged for computational resources. We thank Dr Clas Landersjö for his contribution to the project at the initial part of the study.References
- J. F. G. Vliegenthart, Proc. Jpn. Acad., 2017, B93, 64–86 CrossRef PubMed.
- Y. Watanabe, Z. T. Berndsen, J. Raghwani, G. E. Seabright, J. D. Allen, O. G. Pybus, J. S. McLellan, I. A. Wilson, T. A. Bowden, A. B. Ward and M. Crispin, Nat. Commun., 2020, 11, 2688 CrossRef CAS PubMed.
- C. J. Day, E. N. Tran, E. A. Semchenko, G. Tram, L. E. Hartley-Tassell, P. S. K. Ng, R. M. King, R. Ulanovsky, S. McAtamney, M. A. Apicella, J. Tiralongo, R. Morona, V. Korolik and M. P. Jennings, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E7266–E7275 CrossRef CAS PubMed.
- J. Poole, C. J. Day, M. Von Itzstein, J. C. Paton and M. P. Jennings, Nat. Rev. Microbiol., 2018, 16, 440–452 CrossRef CAS PubMed.
- B. Wiseman, R. G. Nitharwal, G. Widmalm and M. Högbom, Nat. Commun., 2021, 12, 369 CrossRef CAS PubMed.
- A. Adibekian, P. Stallforth, M.-L. Hecht, D. B. Werz, P. Gagneux and P. H. Seeberger, Chem. Sci., 2011, 2, 337–344 RSC.
- S. Sakuda, A. Oisgai, S. Matsumoto, A. Suzuki and K. Koseki, Tetrahedron Lett., 1986, 27, 2475–2478 CrossRef CAS.
- S. Sakuda, A. Isogai, S. Matsumoto and A. Suzuki, J. Antibiot., 1987, 40, 296–300 CrossRef CAS PubMed.
- A. Germer, M. G. Peter and E. Kleinpeter, J. Org. Chem., 2002, 67, 6328–6338 CrossRef CAS PubMed.
- A. Germer, S. Klod, M. G. Peter and E. Kleinpeter, J. Mol. Model., 2002, 8, 231–236 CrossRef CAS PubMed.
- F. V. Rao, D. R. Houston, R. G. Boot, J. M. F. G. Aerts, S. Sakuda and D. M. F. van Aalten, J. Biol. Chem., 2003, 278, 20110–20116 CrossRef CAS PubMed.
- F. H. Cederkvist, S. F. Saua, V. Karlsen, S. Sakuda, V. G. H. Eijsink and M. Sørlie, Biochemistry, 2007, 46, 12347–12354 CrossRef CAS PubMed.
- J. Baban, S. Fjeld, S. Sakuda, V. G. H. Eijsink and M. Sorlie, J. Phys. Chem. B, 2010, 114, 6144–6149 CrossRef CAS PubMed.
- G. Huang, D. Peng, X. Mei, X. Chen, F. Xiao and Q. Tang, J. Enzyme Inhib. Med. Chem., 2015, 30, 863–866 CrossRef CAS PubMed.
- Z. Zhou, S. Sakuda and Y. Yamada, J. Chem. Soc., Perkin Trans. 1, 1992, 1649–1652 RSC.
- S. Sakuda, Y. Sugiyama, Z. Y. Zhou, H. Takao, H. Ikeda, K. Kakinuma, Y. Yamada and H. Nagasawa, J. Org. Chem., 2001, 66, 3356–3361 CrossRef CAS PubMed.
- N. A. Paramonov, J. Aduse-Opoku, A. Hashim, M. Rangarajan and M. A. Curtis, J. Bacteriol., 2009, 191, 5272–5282 CrossRef CAS PubMed.
- G. Widmalm, Carbohydr. Res., 2013, 378, 123–132 CrossRef CAS PubMed.
- Y. Zhu, J. Zajicek and A. S. Serianni, J. Org. Chem., 2001, 66, 6244–6251 CrossRef CAS PubMed.
- D. R. Bundle and R. U. Lemieux, Methods Carbohydr. Chem., 1976, 7, 79–86 CAS.
- M. V. Svensson, X. Zhang, E. Huttunen and G. Widmalm, Biomacromolecules, 2011, 12, 2496–2501 CrossRef CAS PubMed.
- M. Linnerborg, R. Wollin and G. Widmalm, Eur. J. Biochem., 1997, 246, 565–573 CrossRef CAS PubMed.
- M. R. Richards, Y. Bai and T. L. Lowary, Carbohydr. Res., 2013, 374, 103–114 CrossRef CAS PubMed.
- M. Lundborg and G. Widmalm, Anal. Chem., 2011, 83, 1514–1517 CrossRef CAS PubMed.
- M. Lundborg, C. Fontana and G. Widmalm, Biomacromolecules, 2011, 12, 3851–3855 CrossRef CAS PubMed.
- R. Laatikainen, M. Niemitz, W. J. Malaisse, M. Biesemans and R. Willem, Magn. Reson. Med., 1996, 36, 359–365 CrossRef CAS PubMed.
- G. F. Pauli, S.-N. Chen, D. C. Lankin, J. Bisson, R. J. Case, L. R. Chadwick, T. Gödecke, T. Inui, A. Krunic, B. U. Jaki, J. B. McAlpine, S. Mo, J. G. Napolitano, J. Orjala, J. Lehtivarjo, S.-P. Korhonen and M. Niemitz, J. Nat. Prod., 2014, 77, 1473–1487 CrossRef CAS PubMed.
- C. Dalvit and G. Bodenhausen, Chem. Phys. Lett., 1989, 161, 554–560 CrossRef CAS.
- A. Meissner and O. W. Sørensen, Magn. Reson. Chem., 2001, 39, 49–52 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- H. S. Hansen and P. H. Hünenberger, J. Comput. Chem., 2011, 32, 998–1032 CrossRef CAS PubMed.
- K. Nester, K. Gaweda and W. Plazinski, J. Chem. Theory Comput., 2019, 15, 1168–1186 CrossRef PubMed.
- O. Guvench, S. N. Greene, G. Kamath, J. W. Brady, R. M. Venable, R. W. Pastor and A. D. Mackerell Jr., J. Comput. Chem., 2008, 29, 2543–2564 CrossRef CAS PubMed.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- K. B. Koziara, M. Stroet, A. K. Malde and A. E. Mark, J. Comput.-Aided Mol. Des., 2014, 28, 221–233 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- R. W. Hockney, Methods Comput. Phys., 1970, 9, 135–211 Search PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Intermolecular Forces, Springer, Dordrecht, 1981, vol. 14, pp. 331–342 Search PubMed.
- T. N. Heinz, W. F. van Gunsteren and P. H. Hünenberger, J. Chem. Phys., 2001, 115, 1125 CrossRef CAS.
- C. Altona and M. Sundaralingam, J. Am. Chem. Soc., 1972, 94, 8205–8212 CrossRef CAS PubMed.
- M. Huang, T. J. Giese, T. S. Lee and D. M. York, J. Chem. Theory Comput., 2014, 10, 1538–1545 CrossRef CAS PubMed.
- D. Cremer and J. A. Pople, J. Am. Chem. Soc., 1975, 97, 1354–1358 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- K. Gaweda and W. Plazinski, Phys. Chem. Chem. Phys., 2017, 19, 20760–20772 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- W. J. Hehre, L. Radom, P. V. R. Schleyer and J. Pople, AB INITIO Molecular Orbital Theory, John Wiley, New York, 1986 Search PubMed.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- C. Lorenz and N. L. Doltsinis, in Handbook of Computational Chemistry, ed. J. Leszczynski, Springer Science+Business Media B.V., 2012, pp. 195–238 Search PubMed.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- W. Deng, J. R. Cheeseman and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 1028–1037 CrossRef CAS PubMed.
- G. Widmalm, in Comprehensive Glycoscience, ed. J. Barchi Jr., Elsevier Inc., 2nd edn, 2021, pp. 340–373 Search PubMed.
- P.-E. Jansson, L. Kenne and G. Widmalm, J. Chem. Inf. Model., 1991, 31, 508–516 CrossRef CAS PubMed.
- J. Ståhle and G. Widmalm, in New Developments in NMR, ed. K. Kato and T. Peters, The Royal Society of Chemistry, 2017, pp. 335–352 Search PubMed.
- M. Oikawa, S. Adachi and S. Kusumoto, Org. Lett., 2005, 7, 661–664 CrossRef CAS PubMed.
- E. Säwén, F. Hinterholzinger, C. Landersjö and G. Widmalm, Org. Biomol. Chem., 2012, 10, 4577–4585 RSC.
- K. Pichumani, T. Chandra, X. Zou and K. L. Brown, J. Phys. Chem. B, 2006, 110, 5–8 CrossRef CAS PubMed.
- K. Pichumani, X. Zou, T. Chandra and K. L. Brown, Magn. Reson. Chem., 2007, 45, 734–738 CrossRef CAS PubMed.
- L. Di Bari, J. Kowalewski and G. Bodenhausen, J. Chem. Phys., 1990, 93, 7698–7705 CrossRef CAS.
- L. Mäler, F. A. A. Mulder and J. Kowalewski, J. Magn. Reson., Ser. A, 1995, 117, 220–227 CrossRef.
- D. Canet, in New Developments in NMR, ed. D. Canet, Royal Society of Chemistry, 2018, pp. 1–60 Search PubMed.
- D. Horton, Encycl. Biophys., 2013, pp. 93–94 Search PubMed.
- E. Hatcher, O. Guvench and A. D. MacKerell, J. Phys. Chem. B, 2009, 113, 12466–12476 CrossRef CAS PubMed.
- X. Wang and R. J. Woods, J. Biomol. NMR, 2016, 64, 291–305 CrossRef CAS PubMed.
- W. Plazinski, A. Lonardi and P. H. Hünenberger, J. Comput. Chem., 2016, 37, 354–365 CrossRef CAS PubMed.
- W. Plazinski and A. Plazinska, Pure Appl. Chem., 2017, 89, 1283–1294 CAS.
- R. Stenutz, I. Carmichael, G. Widmalm and A. S. Serianni, J. Org. Chem., 2002, 67, 949–958 CrossRef CAS PubMed.
- H. Okumura, I. Azuma, M. Kiso and A. Hasegawa, Carbohydr. Res., 1983, 117, 298–303 CrossRef CAS.
- T. Barclay, M. Ginic-Markovic, M. R. Johnston, P. Cooper and N. Petrovsky, Carbohydr. Res., 2012, 347, 136–141 CrossRef CAS PubMed.
- S. R. Maple and A. Allerhand, J. Am. Chem. Soc., 1987, 109, 3168–3169 CrossRef CAS.
- O. Hassel and B. Ottar, Acta Chem. Scand., 1947, 1, 929–943 CrossRef CAS.
- G. A. Jeffrey, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 89–103 CrossRef PubMed.
- R. K. Schmidt, M. Karplus and J. W. Brady, J. Am. Chem. Soc., 1996, 118, 541–546 CrossRef CAS.
- C. Höög and G. Widmalm, J. Phys. Chem. B, 2001, 105, 6375–6379 CrossRef.
- O. Engström, H. Mobarak, J. Ståhle and G. Widmalm, J. Phys. Chem. B, 2017, 121, 9487–9497 CrossRef PubMed.
- J. Zhang, N. N. H. M. Eisink, M. D. Witte and A. J. Minnaard, J. Org. Chem., 2019, 84, 516–525 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |