Unraveling high-pressure gas storage mechanisms in shale nanopores through SANS†
Received
6th May 2021
, Accepted 3rd August 2021
First published on 4th August 2021
Abstract
As storage rocks rather than source rocks, shale reservoirs can potentially serve as energy storehouses for energy security and sequester CO2 in the long term to mitigate climate change. Despite extensive studies investigating the geochemical and geophysical properties of shale and gas adsorption and transport in the shale matrix, limited studies have been devoted to characterizing nanoscale gas storage mechanisms in shale at elevated high pressure. In this study, contrast-matching small-angle neutron scattering (SANS) has been conducted to quantify the gas storage mechanisms and capacity in three shale samples up to elevated high pressure using deuterated methane. The three-phase Porod invariant method is uniquely used to estimate the average scattering length density (SLD) in open pores over the measured pore range, in which open pores, closed pores, and rock matrix are the three phases. The estimated average SLD in open pores is smaller than the SLD of the bulk phase at the pressure between 10 MPa and the contrast-matched point (∼60–70 MPa, which is sample-dependent), while it is higher than that of the bulk at the pressure below 10 MPa and above the contrast-matched pressure, indicating a variation of average adsorbed phase density over the measured pressure range for the measured shale samples. The average adsorbed phase volume could first increase and then decrease with increasing pressure until the high-pressure region. Three essential factors, including the final injection pressure, total organic carbon (TOC), and accessible porosity, could be used to screen a potential targeted shale reservoir and maximize methane storage and long-term CO2 sequestration.
Environmental significance
Although intensive studies have been reported to characterize gas adsorption and storage in natural and synthesized nanoporous materials over decades, the long-standing question of how gas is stored in nanopores at high pressure is not well understood. In this study, we have used contrast-matching small-angle neutron scattering (SANS) to characterize nanoscale gas storage behaviors in shale nanopores at high pressure. The essential findings are that (1) adsorbed phase density could be lower than bulk phase density at the pressure above 10 MPa and below the contrast-matched point (∼60–70 MPa, which is sample-dependent) while it could be higher than bulk phase density at the pressure below 10 MPa and above the contrast-matched pressure; (2) three essential factors, including the final injection pressure, total organic carbon (TOC), and the accessible porosity, will serve as the criteria for screening a potential targeted shale reservoir and maximizing gas storage and CO2 sequestration. This study will have an implication on CO2-enhanced gas recovery and CO2 sequestration in unconventional gas reservoirs, which is beneficial to climate change mitigation.
|
1. Introduction
Among the energy sources, natural gas is considered an abundant, reliable, and clean energy source.1 Due to the technical maturity of horizontal well drilling and hydraulic fracturing,2 natural gas exploitation and development in the United States have been heavily focused on shale reservoirs in recent decades.3 Although the commercial development of shale gas reservoirs has been conducted in the past decades, fluid transport dynamics in shale remain poorly understood, with many specificities left unexplained.4 One of the critical challenges for long-term shale gas production optimization is the lack of a reliable multi-scale and multi-mechanics gas transport model.4 Meanwhile, the increasing trend of anthropogenic greenhouse gas emissions, e.g., methane and CO2, is alarming for global warming and its associated climate change.5 One reason for the increase in atmospheric CO2 concentration is power generation by burning fossil fuels, which has adverse effects on the earth's ecological environment due to the rise of the global average temperature.5 The net emission of CO2 must approach zero to meet the Paris Agreement's criterion of limiting the increase of global temperature within 2 °C or 1.5 °C above pre-industrial levels.6 According to the research agenda for CO2 removal and reliable sequestration,6 several feasible negative-emission technologies and research and development plans have been identified, including (1) biological CO2 sequestration in soils, forests, and wetlands; (2) synchronized bioenergy production and CO2 capture; (3) coupling direct-air-capture and geological sequestration; and (4) enhancing geologic carbon mineralization or “weathering”. CO2-enhanced shale gas recovery and CO2 sequestration in depleted shale gas reservoirs could be a cost-effective strategy to permanently store densified CO2 in subsurface shale formations. With various mineral and organic matter, shale rock has hierarchical pore structures, including micro-fractures and macro-/meso-/micropores.7–11 Methane or CO2 is primarily stored as a free phase through gas compression in fracture voids and macropores and as both bulk and adsorbed phases in meso-/micropores in shales.12,13 In general, the gas sorption capacity in shale is low due to the low total organic carbon (TOC) content,12–15 and the adsorbed phase density is usually obtained either by using an empirical value13,16 or curve fitting16,17 or by analytical/molecular simulation methods,18,19 which could cause inaccuracy, to determine the actual sorption capacity given in situ pressure and temperature conditions. The total gas storage capacity in shale is the sum of the bulk phase and adsorbed phase gases. Therefore, understanding the gas storage behaviors in shale nanopores has practical applications in gas transport modeling and estimating methane or carbon storage potential in shale reservoirs.20 The understanding could determine the injection rate and the potential of CO2 sequestration in shale reservoirs to meet the challenge of climate change mitigation.21
Numerous techniques can be successfully used to characterize pore structure in shale,22,23 including invasive and noninvasive methods. However, only a few studies have been devoted to characterizing gas storage and condensation behaviors in shale nanopores under in situ pressure and temperature conditions. Fortunately, small-angle neutron scattering (SANS) can be used to noninvasively quantify the structures of total nanopores in shale.24–27 Combining SANS with the contrast-matching method, or so-called contrast-matching SANS, pore accessibility10,28–30 and gas behaviors in pores31,32 can be invasively quantified. Therefore, contrast-matching SANS is an excellent choice to determine gas storage behaviors in shale confined nanopores under in situ gas injection.33 This study focuses on the characterization of the nanopore structures of three shale samples and gas storage behaviors in accessible nanopores through in situ contrast-matching SANS measurements. Deuterated methane (CD4) injection was used in this study because high-pressure CD4 can have a relatively high scattering length density (SLD) than CO2, which can reach or approach the contrast-matched condition of the shale samples with relatively high SLDs. We found that the Illinois shale sample with the highest TOC has the lowest pore accessibility. With the increase of injection gas pressure, the adsorbed methane density in shale nanopores could be higher than the bulk phase density at relatively low pressure, lower than the bulk phase density at relatively high pressure, and again higher than the bulk phase density at even higher pressure beyond the contrast-matched point. TOC could be the determining factor of gas storage in micropores because of the high affinity of gas, leading to high adsorption. For free compression gas storage, accessible porosity of macro-/mesopores could be the controlling factor of total gas storage capacity. Apparently, the total gas storage will depend on the final equilibrium pressure in shale reservoirs. We believe the current research will improve the fundamental understanding of methane storage and long-term CO2 sequestration in shale reservoirs.
2. Materials and methods
2.1 Sample preparation and characterization
Three shale powder samples, pulverized to 60–80 mesh sizes (0.177–0.25 mm) using a mortar, were prepared from fresh block samples collected from different shale formations, including Marcellus Formation in Pennsylvania, USA, Illinois Basin in Indiana, USA, and Longmaxi Formation in Sichuan, China. Marcellus Formation describes the upper Eifelian and lower Givetian stage mudrock-dominated strata lying in the Middle Devonian timescale.34 The shale outcrop fresh blocks were obtained in Frankstown, Pennsylvania. The collected shale in Illinois Basin is a roof shale above the Coal V (Springfield Coal Member, Petersburg Formation, Pennsylvania System) or so-called Springfield coal and below the Alum Cave Limestone Member, Dugger Formation.35,36 Roof shale is a black fissile marine shale.35,36 Roof shale fresh blocks were obtained from Bear Run Surface Mine in Carlisle, Indiana. Longmaxi Formation located in the Yangtze area is in the Lower Silurian timescale.37 Shale outcrop fresh blocks were obtained in Yibin, Sichuan, China.
The pulverized samples were oven-dried for 24 hours at 80 °C, and all the dried samples were sealed in airtight Ziploc bags before the contrast-matching SANS and the sorption/diffusion measurements. X-ray diffraction (XRD) and carbon/sulfur determination using a LECO CS230 analyzer were conducted to obtain the mineralogical information and the TOC of the samples, respectively, as shown in Table S1 in the ESI.† We can find that the Marcellus shale is quartz-rich, containing more than 70% quartz. The Longmaxi shale also has a relatively high amount of quartz at nearly 50%, with an addition of 20% calcite. The chemical compositions were used to estimate the effective scattering length density (SLD) of each shale sample. We can see that the sample with a relatively high TOC content has a relatively low estimated effective SLD. The estimated SLDs were used for SANS data analysis to characterize the information of nanopore structures quantitatively.
2.2 Contrast-matching SANS measurement
The contrast-matching SANS measurements were conducted using the vSANS instrument at the NIST Center for Neutron Research (NCNR). Each dried powder sample was filled into an aluminum capsule, and then the aluminum capsule was placed into a high-pressure cell, as shown in Fig. S1.† The thickness is about 1 mm, and the illuminated area or beam size through the sample is about half an inch in diameter. The neutron wavelength λ was set at 6 Å. A small λ helps to minimize the multiple scattering effect. The neutron wavelength spread Δλ/λ was 0.12. Two configurations were used for the measurements. The first configuration, named NG7, uses the sample-to-detector distances of 1.93 m for the four front detectors and of 9.13 m for the four middle detectors to cover a scattering vector Q range between ∼4.8 × 10−3 and ∼0.34 Å−1, corresponding to a length scale d, or pore diameter, range between ∼1.3 × 103 and ∼18.6 Å, where the relationship d = 2π/Q was used. The second configuration, named NG2, uses the sample-to-detector distances of 4.13 m for the four front detectors and of 19.13 m for the four middle detectors to cover a Q range between ∼2.5 × 10−3 and ∼0.16 Å−1, corresponding to a d range between ∼2.5 × 103 and ∼38.6 Å. Both the NG7 and NG2 configurations were used to measure the Marcellus shale and Longmaxi shale samples. Only the NG7 configuration was used to measure the Illinois shale sample due to limited beam time.
All three shale samples were dosed with deuterated methane (CD4) using incremental gas pressure for the contrast-matching SANS measurements. The maximum conducting pressure was 70 MPa for the Marcellus shale and the Longmaxi shale samples and 60 MPa for the Illinois shale sample. Scattering counts were measured under vacuum condition first and then under each incremental pressure with 10 MPa as the pressure interval till the maximum conducting pressure for each sample. The time between pressure steps is about 20 min. Scattering counts were measured under vacuum condition again after the methane injection for all the samples. After the data acquisition, the obtained 2D scattering profiles were radially averaged to 1D scattering profiles for each configuration using the Igor macros vSANS procedures.38 1D scattering profiles at two sample-to-detector distances were merged for each configuration. For the Marcellus shale and Longmaxi shale samples using two configurations during the measurements, 1D scattering profiles of the two configurations were further merged.
3. Results and discussion
This section first provides the interpretation of SANS data analyses and pore structure information of the measured shale samples as baseline information. Then, we estimate the average SLDs in the accessible pores, giving gas condensation information under confinement and gas storage mechanisms. Finally, we provide the implication of gas storage in underground shale reservoirs.
3.1 SANS data analyses and pore structures of the measured shales
The background-subtracted scattering intensities as a function of Q and methane pressure for the Marcellus shale are shown in Fig. 1 and for the Longmaxi shale and Illinois shale samples in Fig. S2 and S4 in the ESI.† The flat scattering background was estimated by fitting the scattering intensity in the Q range from 0.3 Å−1 to the highest Q value for the scattering profile either under vacuum or under CD4 saturation for each shale. We can see that the scattering intensity decreases with increasing pressure at the middle and low Q regions. However, the scattering intensities do not have a noticeable change and have higher uncertainties at the high Q region. By choosing specific Q values at the middle, low, and high Q regions, the scattering intensity at each Q value as a function of pressure can be demonstrated in detail, and the data can be compared (Fig. 2, S3, and S5†). The scattering intensity at the representative middle or low Q value rapidly decreases as gas pressure increases and gradually decreases with further increasing pressure for all the samples (Fig. 2a and b, S3a and b, and S5a and b†). This is because the increase in SLD of CD4 as a function of gas pressure is known to be nonlinear, as shown in Table S2 and Fig. S6 in the ESI.† The SLD of CD4 rapidly increases with increasing pressure before 30 MPa, followed by a gentle and gradual increase of the SLD after 30 MPa. However, there is no clear trend between scattering intensity and gas pressure at the representative high Q value for each sample (Fig. 2c, S3c, and S5c†), indicating that either CD4 is already highly densified at small nanopores before 10 MPa or limited fine pores are accessible to the guest gas or incoherent background has already surpassed the elastic intensity of fine pores which was subtracted initially.39 Condensation effects prevent an accurate determination of the accessible porosity for fine pores in shale.28 We can tell that the Marcellus shale sample has reached the contrast-matched condition at ∼60 MPa at low Q and at ∼40 MPa at middle Q (Fig. 2a and b). However, the Longmaxi shale and Illinois shale samples did not reach the contrast-matched point experimentally but were approaching it (Fig. S3a and b and S5a and b†). Reaching the contrast-matched point at a smaller pressure at the middle Q region than the low Q region indicates a smaller SLD of the solid matrix surrounding middle-sized pores than large-sized pores for the Marcellus shale sample. Since most mineral matter have a higher SLD than organic carbon, organic matter in Marcellus shale could contain smaller pores than mineral matter.9,40 Another possible reason could be a higher degree of gas densification in smaller pores.32,39 We have shown the intensities before and after CD4 injection (Fig. S7†), and the intensity has a negligible change before and after CD4 saturation with multiple pressure steps for each shale sample. This indicates no permanent pore damage in the measured shale samples after high-pressure gas injection.
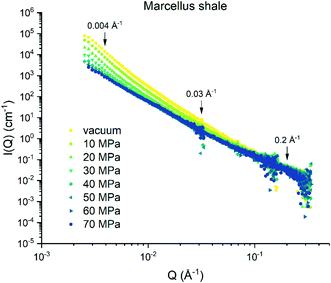 |
| | Fig. 1 Scattering intensity as a function of methane pressure for the Marcellus shale sample. | |
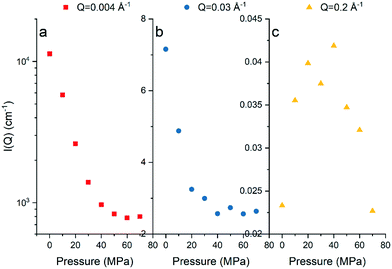 |
| | Fig. 2 Scattering intensity as a function of methane pressure at (a) Q of 0.004 Å−1, (b) Q of 0.03 Å−1, and (c) Q of 0.2 Å−1 for the Marcellus shale sample. | |
The pore accessibilities of the three shale samples were estimated by a previously determined method using the scattering intensities under vacuum and contrast-matched conditions:41,42
| | 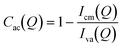 | (1) |
where
Iva(
Q) and
Icm(
Q) are the background-subtracted scattering intensities under vacuum and contrast-matched conditions, respectively. Since we used powder samples, the estimated pore accessibility should be the volumetric and statistical average pore accessibility of each shale sample,
40 where the results are shown in
Fig. 3a. We can find that the pore accessibilities of the three shale samples decrease with increasing
Q in general, which provides direct evidence that the smaller pore is less accessible. The pore accessibilities of the Marcellus shale and Longmaxi shale samples are higher than that of Illinois shale, which could be because of lower amounts of organic matter in the Marcellus shale and Longmaxi shale samples in comparison with the Illinois shale. The Longmaxi shale has the smallest TOC and has the highest pore accessibility among the measured samples. We can also see that pore accessibility at the high
Q region has relatively high error bars. This is because the scattering intensities under vacuum and contrast-matched conditions are very close at high
Q.
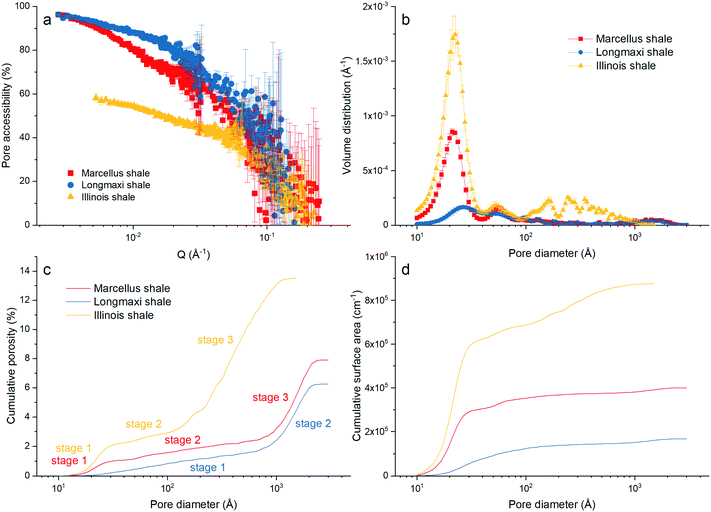 |
| | Fig. 3 (a) Pore accessibility, (b) pore volume distribution, and cumulative (c) porosity and (d) surface area of the three shale samples. | |
Furthermore, the pore volume distributions of the shale samples were estimated by the model fitting method.39,40,43 The background-subtracted 1D scattering profiles under vacuum condition were used to fit using the maximum entropy (MaxEnt) method in the Igor macros Irena package.44 Without using a statistical function of pore size distribution, the MaxEnt method can provide a more accurate result in multimodal pore volume distribution for a given two-phase porous material. The background-subtracted scattering intensity can be expressed as45
| | 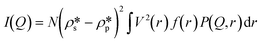 | (2) |
where
N is the pore number density;
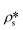
and
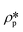
are the SLDs of the solid matrix and the pores;
r is the spherical radius;
V(
r) is the spherical volume;
f(
r) is the pore size distribution; and
P(
Q,
r) is the spherical form factor. The SLD of the pores
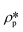
, should be zero under vacuum condition. The estimated effective SLD of each shale sample shown in Table S2
† was used for the solid matrix SLD. The upper and lower limits of the pore diameter were set as 3000 Å and 10 Å for the model fitting of the Marcellus shale and Longmaxi shale samples. However, for the Illinois shale sample, a smaller upper limit of the pore diameter (1500 Å) was used because only the NG7 configuration was used for the measurement due to the limited beam time. Thus, the probed pore diameter range is 1–300 nm for the Marcellus and Longmaxi shale samples and 1–150 nm for the Illinois shale. The results of pore volume distributions with uncertainties are shown in
Fig. 3b. The unit of volume distribution is cm
3 (cm
3 Å)
–1,
i.e., d
V/(
V·d
D). We can find that the pore volume distributions of all the shale samples are multimodal. The main peak at the pore diameter of ∼20 Å and a small peak at the pore diameter of ∼55 Å are shown in the volume distributions of the Marcellus shale and Illinois shale samples. However, a relatively lower and broader hump at the pore range around 20–300 Å is shown in the volume distribution of the Longmaxi shale sample. We can see multiple peaks at larger pores ranging between 100 Å and 1000 Å for the Illinois shale sample, in which the volume distribution is higher than those of the other two shale samples due to the relatively higher pore population in larger sized pores. The Marcellus and Longmaxi shale samples have very similar pore volume distributions at pore diameters greater than ∼100 Å, and both have a small hump at pores around 1500 Å.
In addition, the cumulative porosities and surface areas of the three samples were estimated based on the estimated pore volume distributions. The cumulative porosity and surface area can be estimated as43,44
where
A(
r) is the spherical surface area. The results of cumulative porosities and surface areas are shown in
Fig. 3c and d. A three-stage porosity increases with increasing pore size for the Marcellus shale and Illinois shale samples and a two-stage increase of porosity for the Longmaxi shale sample, as shown in
Fig. 3c. A rapid increase at the pore diameter around 30 Å for the Marcellus shale and Illinois shale samples is because of the major peak of volume distribution (
Fig. 3b). Then, porosity gradually increases till ∼150 Å for the Illinois shale sample and till ∼1000 Å for the Marcellus shale sample. After that, porosity rapidly increases till the upper pore limit, which the SANS instrument can measure, for these two samples. In contrast, the Longmaxi shale sample has a moderate porosity increase before 1000 Å and a rapid increase of porosity after 1000 Å. Overall, the Illinois shale sample has a much higher total porosity than the other two shale samples at the pore size of 1500 Å, which is the maximum measured pore size of the Illinois shale sample. The surface area rapidly increases at pore size around 250 Å and gradually increases further for the Illinois shale sample. The surface area of the Marcellus shale sample also rapidly increases at the pore with a size of ∼250 Å but barely increases afterward. The Longmaxi shale sample seems to have a gradual increase of surface area over the entire pore range.
To characterize the nanopore structure evolution under different pressure conditions for the shale samples, we have applied a global scattering function integrated Guinier approximation and power-law scattering, a unified scattering model, for data fitting, in which the unified scattering model is superior to differentiate multiple structures in multiscale in a hierarchical porous medium. The method has been successfully used in shale in previous studies.25,46 The unified scattering equation to describe multiple interrelated structural levels over a broad range of Q without considering background can be expressed as47
| | 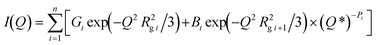 | (5) |
| | 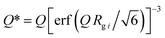 | (6) |
where the first term in
eqn (5) is Guinier's exponential form, and the second term is the structurally limited power-law form.
Q* is the modified scattering vector
Q containing a three-dimensional Gaussian probability function, which accounts for the finite structural effect in the power-law region.
G is the classic Guinier prefactor;
Rg is the radius of gyration describing the domain size;
B is the power-law prefactor;
P is the power-law exponent; and
i is the structural level, in which
i = 1 refers to the largest-size structural level. The fitting of each scattering profile was conducted using SasView.
48 The representative model fitting profiles can be found in Fig. S8,
† and the fitting parameters can be found in Fig. S9 and S10 and Tables S3–S5.
† A detailed discussion can be found in the ESI.
†
3.2 The average SLD in open pores
We have used the bulk phase SLD of the injected gases to estimate pore volume and surface area changes with increased gas pressure in our previous studies.39,43 The method ignores the contribution of the SLD of adsorbed phase density in pores. To characterize the average SLD or average density fluctuation in pores under elevated pressure conditions for the shale samples, the structure-free Porod invariant method considering three-phase approximation (i.e., solid matrix, open pores, and closed pores, as shown in Fig. 4) can be used. The three-phase Porod invariant equation may be expressed as49| | 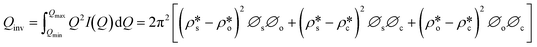 | (7) |
where Qmax and Qmin are the maximum and minimum Q, which can be measured by the configuration of SANS experiments; 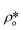 and
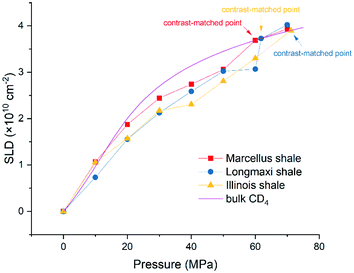
and 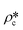 are the SLDs of the open and closed pores, respectively; and ∅s, ∅o, and ∅c are the volume fractions of the solid matrix, open pores, and closed pores, respectively. Qinv can be estimated using the experimentally obtained scattering intensity under different pressure conditions, which is shown in Fig. 5. Note that the Q range to estimate the Porod invariant was set as 2.8 × 10−3–0.25 Å−1, 2.5 × 10−3–0.21 Å−1, and 5.3 × 10−3–0.25 Å−1 for the Marcellus shale, Longmaxi shale, and Illinois shale samples, respectively. Then the results can be more precisely compared among different pressure conditions for each sample, although some portion of high Q was ignored. The Marcellus shale sample may already reach the contrast-matched point at the pressure around 60 MPa on average over the estimated pore range (Fig. 5). The SLD of CD4 at 60 MPa at room temperature is about 3.7 × 1010 cm−2, which is slightly smaller than the estimated effective SLD (∼3.9 × 1010 cm−2) from the chemical compositions of the Marcellus shale. It suggests that slightly more open nanopores accessible to CD4 are in the matrix with a smaller SLD, which could be organic matter. In contrast, the Longmaxi shale sample may approach the contrast-matched point at the pressure around 70 MPa, and the Illinois shale sample may not reach the contrast-matched point over the pressure range measured (Fig. 5). It is unexpected for the two samples because the estimated effective SLD of the Longmaxi shale sample (∼4.4 × 1010 cm−2) is higher than the SLD of CD4 at the highest pressure (70 MPa), which is ∼3.9 × 1010 cm−2, and the estimated effective SLD of the Illinois shale sample (∼3.4 × 1010 cm−2) is less than the SLD of CD4 at the pressure of 60 MPa (∼3.7 × 1010 cm−2). The results suggest that more open nanopores accessible to CD4 are in the Longmaxi shale sample matrix with a lower SLD, which could be organic matter, while in the matrix of the Illinois shale sample with a higher SLD, which could be clay minerals such as glauconite.
are the SLDs of the open and closed pores, respectively; and ∅s, ∅o, and ∅c are the volume fractions of the solid matrix, open pores, and closed pores, respectively. Qinv can be estimated using the experimentally obtained scattering intensity under different pressure conditions, which is shown in Fig. 5. Note that the Q range to estimate the Porod invariant was set as 2.8 × 10−3–0.25 Å−1, 2.5 × 10−3–0.21 Å−1, and 5.3 × 10−3–0.25 Å−1 for the Marcellus shale, Longmaxi shale, and Illinois shale samples, respectively. Then the results can be more precisely compared among different pressure conditions for each sample, although some portion of high Q was ignored. The Marcellus shale sample may already reach the contrast-matched point at the pressure around 60 MPa on average over the estimated pore range (Fig. 5). The SLD of CD4 at 60 MPa at room temperature is about 3.7 × 1010 cm−2, which is slightly smaller than the estimated effective SLD (∼3.9 × 1010 cm−2) from the chemical compositions of the Marcellus shale. It suggests that slightly more open nanopores accessible to CD4 are in the matrix with a smaller SLD, which could be organic matter. In contrast, the Longmaxi shale sample may approach the contrast-matched point at the pressure around 70 MPa, and the Illinois shale sample may not reach the contrast-matched point over the pressure range measured (Fig. 5). It is unexpected for the two samples because the estimated effective SLD of the Longmaxi shale sample (∼4.4 × 1010 cm−2) is higher than the SLD of CD4 at the highest pressure (70 MPa), which is ∼3.9 × 1010 cm−2, and the estimated effective SLD of the Illinois shale sample (∼3.4 × 1010 cm−2) is less than the SLD of CD4 at the pressure of 60 MPa (∼3.7 × 1010 cm−2). The results suggest that more open nanopores accessible to CD4 are in the Longmaxi shale sample matrix with a lower SLD, which could be organic matter, while in the matrix of the Illinois shale sample with a higher SLD, which could be clay minerals such as glauconite.
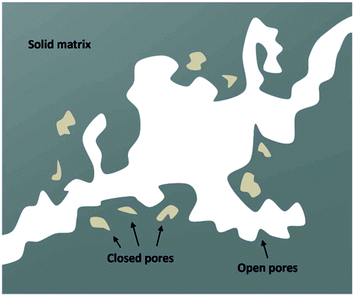 |
| | Fig. 4 A schematic of the three-phase system in shale matrix. | |
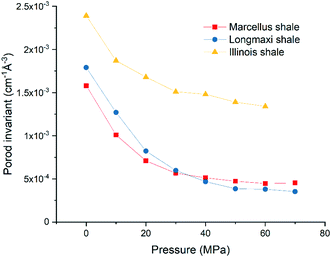 |
| | Fig. 5 Porod invariant as a function of pressure for the three shale samples. | |
In order to estimate the average SLD in open pores, 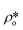 , using eqn (7), the volume fractions of the solid matrix, open pores, and closed pores, ∅s, ∅o, and ∅c, need to be quantified. The average SLD in closed pores,
, using eqn (7), the volume fractions of the solid matrix, open pores, and closed pores, ∅s, ∅o, and ∅c, need to be quantified. The average SLD in closed pores, 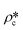 is equal to zero since the guest fluid does not have access to closed pores, and there may be no residual fluid inside closed pores.
is equal to zero since the guest fluid does not have access to closed pores, and there may be no residual fluid inside closed pores. 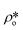 is equal to zero under vacuum condition because of empty open pores and equal to
is equal to zero under vacuum condition because of empty open pores and equal to 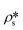 under contrast-matched condition. Thus, in both conditions, the three-phase Porod invariant equation reduces to the two-phase one:
under contrast-matched condition. Thus, in both conditions, the three-phase Porod invariant equation reduces to the two-phase one:
| | 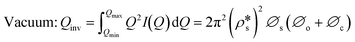 | (9) |
| | 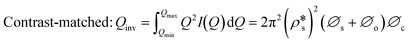 | (10) |
where the volume fraction of total pores equals
∅o +
∅c. Since ∼60 MPa could be the contrast-matched pressure of the Marcellus shale sample, the SLD of CD
4 at 60 MPa (3.7 × 10
10 cm
−2) was used as the SLD of the sample along with the
Qinv at that pressure to quantify volume fractions of total and closed pores and the average SLD in open pores in the Marcellus shale sample. However, parabolic curve-fitting using the last five data points may give the smallest
Qinv and the contrast-matched pressure for the Longmaxi shale and Illinois shale samples. The estimated
Qinv and pressure at the contrast-matched point could be 3.40 × 10
−4 cm
−1 Å
−3 and 61.8 MPa for the Longmaxi shale sample and 1.33 × 10
−3 cm
−1 Å
−3 and 71.1 MPa for the Illinois shale sample. The approximate contrast-matched SLD can be obtained, which is 3.73 × 10
10 cm
−2 for the Longmaxi shale sample and 3.90 × 10
10 cm
−2 for the Illinois shale sample. The estimated contrast-matched SLDs were used to estimate the volume fractions of total and closed pores and the average SLD in open pores. Table S6
† shows the estimated volume fractions of open and closed pores and the corresponding average pore accessibility. We can find that the Longmaxi shale sample has the highest volume fraction of open pores. However, the Illinois shale sample has the highest volume fraction of closed pores, as expected, because of the highest amount of organic matter among the three shale samples. Accordingly, the Illinois shale sample has the smallest pore accessibility on average, consistent with the size-dependent result shown in
Fig. 3a. In addition, Pearson correlation analysis was conducted using the variables TOC, maturity, contrast-matched SLD, the volume fraction of total pores, and pore accessibility. The correlation coefficients are shown in Table S7.
† We can find that TOC and total pores are positively correlated. A highly negative correlation is shown between TOC and pore accessibility. However, since we have only measured three shale samples, those correlations may be different using more samples with diverse mineral and organic components, and thus further study will be needed.
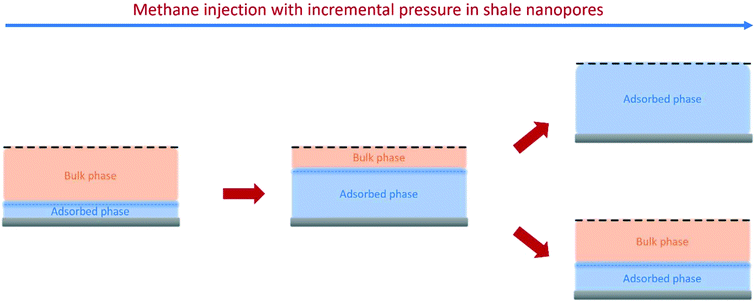
Using the estimated volume fractions of open and closed pores and the contrast-matched SLDs, the average SLD in open pores over the specified pore range as a function of pressure for each sample can be quantified, as shown in Fig. 6. The assumption is that the volume fractions of open and closed pores do not change under pressurized conditions, which may hold for shale rocks. The SLD of bulk CD4 as a function of pressure is also shown in the figure for comparison. Note that the Q range for estimation of the average SLD in pores was set as 2.8 × 10−3–0.25 Å−1, 2.5 × 10−3–0.21 Å−1, and 5.3 × 10−3–0.25 Å−1 for the Marcellus shale, Longmaxi shale, and Illinois shale samples, respectively. By using the relationship d = 2π/Q, the pore diameter range is 2.3 × 103–25 Å, 2.5 × 103–30 Å, and 1.2 × 103–25 Å for the Marcellus shale, Longmaxi shale, and Illinois shale samples, respectively. We can find that the average SLDs of the three samples over the quantified pore range are smaller than that of bulk CD4 when the pressure is lower than the contrast-matched pressure of each sample except for the SLDs at the pressure of 10 MPa for the Marcellus shale and Illinois shale samples (Fig. 6). When the pressure is higher than the contrast-matched pressure, the average SLD in pores becomes greater than the SLD of the bulk phase for the Marcellus shale and Longmaxi shale samples. It is well known that the stored gas in shale nanopores could include both bulk gas and adsorbed gas. The average SLD in open pores may be expressed as
| | 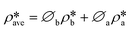 | (11) |
where
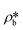
and
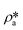
are the SLDs of the bulk phase and adsorbed phase, respectively; and
∅b and
∅a are the volume fractions of the bulk phase and adsorbed phase, respectively, in which the sum of
∅b and
∅a is equal to one. A higher
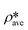
than
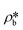
suggests a higher
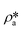
than
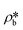
on average in the integrated pore range and
vice versa. The measured samples' results hypothetically indicate that the adsorbed phase density,
ρa, in shale macro-/mesopores on average could be higher than the bulk phase density,
ρb, at the low-pressure region (<∼10 MPa) because of surface adsorption (
Fig. 7). However, the average
ρa could become smaller than the
ρb at a higher pressure because of the increase of adsorbed phase volume,
Va, in which surface adsorption could convert to partial pore-filling adsorption (
Fig. 7). When the gas pressure is even higher, there could be two situations: (1) the completion of pore-filling adsorption occurs, in which
Va increased to be the pore volume and (2) the decrease of
Va occurs (
Fig. 7). The second situation may be more likely in shale macro-/mesopores because these nanopores may not have enough overlapped energy from the pore surface to provide a possible complete pore-filling adsorption. From a laboratory perspective, the excess or Gibbs adsorption capacity can be directly estimated either by gravimetric or by volumetric methods.
50 In contrast, the absolute adsorption capacity, representing the actual adsorption capability, can only be estimated by correcting the excess adsorption capacity through assumptions. The usual assumption of constant adsorbed phase density
13,16 could have less error in relatively low pressure than higher pressure regions. The assumption of monolayer sorption volume or pore volume as constant adsorbed phase volume
51,52 could have higher errors for sorption capacity estimation. However, since we only measured three shale samples and do not have data points at relatively low-pressure (<10 MPa) and significantly high-pressure regions (>70 MPa) because of limited beam time, further research, either experimental or computational approaches, needs to be conducted to prove the hypothetical mechanisms.
 |
| | Fig. 6 Average SLD in open pores as a function of pressure for the three shale samples. | |
 |
| | Fig. 7 Schematic of the hypothetical mechanisms of methane sorption and compression at elevating pressure in idealized shale nanopores (the black dashed line is the centerline in pores; the gray area is the shale matrix). | |
From a previous study, SLD evidently varies with scattering vector Q or pore size in shales.28 For a system with 100% accessible pores with a certain total scattering intensity, a higher SLD of the matrix will have a higher SLD in open pores. For a system with less than 100% accessible pores with a certain total scattering intensity, the effect will be less evident because a higher SLD of the matrix will have a higher scattering intensity of closed pores, and the scattering intensity of open pores reduces. The result will also depend on size-dependent pore accessibility. Another case for a system with less than 100% accessible pores is with certain both total scattering intensity and scattering intensity at contrast-matched conditions. This situation indicates a certain scattering intensity for accessible pores, similar to the first case. Because of the existence of Q-dependent SLD in shale,28 we have used three separate Q ranges for the Marcellus and Longmaxi shale samples and two separate Q ranges for the Illinois shale sample to estimate Porod invariants as a function of pressure using eqn (7), as shown in Fig. S11,† and further estimate the average SLDs in open pores, as shown in Fig. S12.† The approximate segmentation is based on the definition of meso-/macropores. The determined contrast-matched pressures and corresponding SLDs are shown in Table S8.† We can see that mesopores have a lower average SLD than macropores for all the samples when pressure is higher than 10 MPa, indicating a smaller average adsorbed phase density in mesopores. A possible reason could be that occupation of gas molecules or adsorbed phase volume at low pressure (<10 MPa) in mesopores is relatively higher than that in macropores. When pressure continuously increases, lesser gas molecules could be adsorbed in mesopores, in which the average adsorbed phase density will be smaller in mesopores.
3.3 The implication on methane storage and CO2 sequestration in shale reservoirs
For carbon storage or sequestration in subsurface formations, all the potential phases, including bulk phase, chemically reacted phase(s), physically adsorbed phase, and even dissolved phase(s), will contribute to the total gas storage or sequestration in shale reservoirs. In this study, since we used a single-phase dry gas, the stored phases could only be the bulk and adsorbed gas phases. From the previous section, the average SLDs in nanopores under different pressure conditions were quantified. The gas density and SLD of CD4 have an approximately linear correlation, shown in Table S2.† The total gas storage in shale nanopores may be estimated by| | | m = ρaveVo/ms = ρave[(Vo/Vt)/(Vs/Vt)]/(ms/Vs) ≅ ρave(∅o/∅s)/ρhe | (12) |
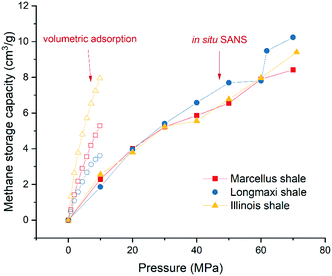
where ρave is the average gas density in pores; Vo, Vs, and Vt are the volumes of open pores, solid matrix, and total matrix, respectively; ms is the mass of the solid matrix; ρhe is the helium density; and m is the total gas storage capacity per unit mass. The helium densities of 2.55 g cm−3, 2.72 g cm−3, and 2.07 g cm−3 were used for the Marcellus shale, Longmaxi shale, and Illinois shale samples, respectively. The estimated methane storage capacities as a function of pressure for the three measured shale samples are shown in Fig. 8. The excess adsorption capacities of the shale samples are also shown for comparison, although they were measured in the low-pressure region. Detailed information on the experimental operation and adsorption capacity estimation can be found in our previous study,15 and a schematic of the experimental system is shown in Fig. S13.† All the volumetric adsorption capacities are higher than the methane storage capacities obtained by in situ SANS at the low-pressure region for the samples (Fig. 8). One possible reason could be that pores with overall sizes contribute to the volumetric adsorption, while only a limited pore range was used to estimate methane storage capacity from in situ SANS data. As mentioned in the previous section, the pore diameter range for the estimation is 2.3 × 103–25 Å for the Marcellus shale sample, 2.5 × 103–30 Å for the Longmaxi shale sample, and 1.2 × 103–25 Å for the Illinois shale sample. We can see that the micropore region was excluded entirely in the estimation because the measured high Q limit of the SANS profiles is not high enough to reach the length scale of micropores. Even though the high Q limit is high enough to access the length scale of micropores, the scattering background could be higher than the scattering of micropores, restricting the micropore information to be quantified. If we assume that most of the volumetric adsorption capacity is the gas storage in micropores because of high specific surface area,11 we can see that the micropore gas storage at the pressure of ∼10 MPa is as high as the total gas storage in macro-/mesopores at the pressure of ∼60 MPa for the Illinois shale (yellow curves in Fig. 8). The sample is highly organic-rich with a TOC of ∼30%. The storage capacity in adsorption in micropores is approximately four times higher than the storage capacity of both bulk and adsorbed gas in macro-/mesopores at the pressure of ∼10 MPa. We may conclude that adsorption could dominate total gas storage in nanopores at relatively low pressure in a highly organic-rich shale sample. For the relatively less organic-rich shale samples, i.e., Marcellus shale and Longmaxi shale samples, the gas adsorption in micropores is less dominant than the total gas storage in the low-pressure region (red and blue curves in Fig. 8). At the pressure of 20 MPa, the total gas capacity is slightly higher than the adsorption one for the Longmaxi shale sample. The total gas capacity is very similar to the adsorption one at the pressure of 30 MPa for the Marcellus shale sample. It is interesting to find that the adsorption capacity has a positive correlation with TOC, and the total gas storage capacity at the pressure of 10 MPa also has a positive correlation with TOC, although only three shale samples were measured here. The total gas storage capacities at the pressures of 20 MPa and 30 MPa are similar among these samples. When the pressure is beyond 30 MPa, Longmaxi shale with the highest number of open pores has the highest total gas storage capacity. The results suggest that a target shale reservoir with a high gas storage capacity either for methane storage or CO2 sequestration could depend on three essential factors: the final equilibrium pressure, TOC, and accessible porosity. TOC seems to only affect the gas storage capacity at relatively low pressure. However, other factors such as geological fault, reservoir depth, and cap rock quality will be considered for gas storage security in the long term. Indeed, the gas injection rate will depend on the intrinsic permeability and diffusion in fractures and pores in complex shale.
 |
| | Fig. 8 Methane storage capacity in open pores as a function of pressure for the three shale samples. | |
4. Conclusions
This study provides an investigation of high-pressure gas storage mechanisms of three shale samples using in situ SANS measurements with the contrast-matching method using deuterated methane. From basic characterization, the Marcellus shale and Longmaxi shale samples are quartz-rich, and the Illinois shale sample has the highest TOC. The Marcellus shale and Longmaxi shale samples have higher pore accessibility than the Illinois shale sample. However, the Illinois shale has the highest cumulative porosity and surface area among the measured samples.
Based on the three-phase Porod invariant method, the average SLD in open pores over the measured pore range of the measured shale samples can be obtained. The estimated average SLD in open pores is smaller than the SLD of the bulk phase at the pressure between 10 MPa and the contrast-matched point (∼60–70 MPa, which is sample-dependent). The results could indicate a lower average adsorbed phase density in open pores than bulk phase density in this pressure range. In contrast, the estimated average SLD in open pores is higher than the SLD of the bulk phase at the pressure below 10 MPa and above the contrast-matched pressure. At these pressure conditions, the average adsorbed phase density could be higher than the bulk phase density. Hypothetically, the average adsorbed phase volume could first increase and then decrease with increasing pressure until the very high-pressure region. However, further study needs to be conducted at low-pressure and very high-pressure regions to confirm the results and mechanisms, and more samples also need to be considered.
In addition, the gas storage capacities of the shales were estimated. The results are compared with the previously measured gas adsorption capacities of the same shale samples. TOC has a positive correlation with both the gas adsorption capacity and storage capacity at low pressure. Longmaxi shale, with the highest pore accessibility and open porosity, has the highest gas storage capacity at high pressure. Therefore, three essential factors, including the final injection pressure, TOC, and accessible porosity, could be used to search and maximize methane storage and long-term CO2 sequestration in depleted shale reservoirs.
Author contributions
SL and RZ designed the research; RZ and SL performed the research; RZ, LF, TPB, and GS conducted the measurements; RZ analyzed and interpreted the data; RZ drafted the manuscript; all authors gave feedback and contributed to the writing of the manuscript.
Conflicts of interest
The authors declare no competing financial interests.
Acknowledgements
The authors would like to thank Nichole Wonderling for providing the measurement and data analysis of X-ray diffraction at the Penn State Materials Characterization Lab. The authors want to thank Yun Liu for the help with vSANS measurement and data reduction at the NIST Center for Neutron Research (NCNR). Access to CHRNS vSANS was provided by the Center for High Resolution Neutron Scattering, a partnership between the National Institute of Standards and Technology and the National Science Foundation under Agreement No. DMR-2010792. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement No 654000.
References
-
EIA, Annual Energy Outlook 2020: With Projections to 2050, Government Printing Office, 2020.
- R. W. Howarth, A. Ingraffea and T. Engelder, Natural gas: Should fracking stop?, Nature, 2011, 477, 271–275 CrossRef CAS PubMed.
- R. A. Kerr, Natural Gas From Shale Bursts Onto the Scene, Science, 2010, 328, 1624–1626 CrossRef CAS PubMed.
- L. Cueto-Felgueroso and R. Juanes, Forecasting long-term gas production from shale, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19660–19661 CrossRef CAS PubMed.
-
V. Masson-Delmotte, P. Zhai, H.-O. Pörtner, D. Roberts, J. Skea, P. R. Shukla, A. Pirani, W. Moufouma-Okia, C. Péan and R. Pidcock, Global warming of 1.5 C, An IPCC Special Report on the impacts of global warming of, 2018, vol. 1.
-
E. National Academies of Sciences and Medicine, Negative emissions technologies and reliable sequestration: a research agenda, National Academies Press, 2019 Search PubMed.
- C. Bousige, C. M. Ghimbeu, C. Vix-Guterl, A. E. Pomerantz, A. Suleimenova, G. Vaughan, G. Garbarino, M. Feygenson, C. Wildgruber, F. J. Ulm, R. J. M. Pellenq and B. Coasne, Realistic molecular model of kerogen's nanostructure, Nat. Mater., 2016, 15, 576–582 CrossRef CAS PubMed.
- G. R. Chalmers, R. M. Bustin and I. M. Power, Characterization of gas shale pore systems by porosimetry, pycnometry, surface area, and field emission scanning electron microscopy/transmission electron microscopy image analyses: Examples from the Barnett, Woodford, Haynesville, Marcellus, and Doig units, AAPG Bull., 2012, 96, 1099–1119 CrossRef CAS.
- X. Gu, D. R. Cole, G. Rother, D. F. R. Mildner and S. L. Brantley, Pores in Marcellus Shale: A Neutron Scattering and FIB-SEM Study, Energy Fuels, 2015, 29, 1295–1308 CrossRef CAS.
- C. R. Clarkson, N. Solano, R. M. Bustin, A. M. M. Bustin, G. R. L. Chalmers, L. He, Y. B. Melnichenko, A. P. Radlinski and T. P. Blach, Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion, Fuel, 2013, 103, 606–616 CrossRef CAS.
- Y. Wang, Y. Zhu, S. Liu and R. Zhang, Pore characterization and its impact on methane adsorption capacity for organic-rich marine shales, Fuel, 2016, 181, 227–237 CrossRef CAS.
- T. F. Rexer, E. J. Mathia, A. C. Aplin and K. M. Thomas, High-Pressure Methane Adsorption and Characterization of Pores in Posidonia Shales and Isolated Kerogens, Energy Fuels, 2014, 28, 2886–2901 CrossRef CAS.
- Y. Wang, Y. M. Zhu, S. M. Liu and R. Zhang, Methane adsorption measurements and modeling for organic-rich marine shale samples, Fuel, 2016, 172, 301–309 CrossRef CAS.
- R. Heller and M. Zoback, Adsorption of methane and carbon dioxide on gas shale and pure mineral samples, J. Unconv. Oil Gas Resour., 2014, 8, 14–24 CrossRef.
- L. Fan and S. Liu, A novel experimental system for accurate gas sorption and its application to various shale rocks, Chem. Eng. Res. Des., 2021, 165, 180–191 CrossRef CAS.
- M. Gasparik, A. Ghanizadeh, P. Bertier, Y. Gensterblum, S. Bouw and B. M. Krooss, High-Pressure Methane Sorption Isotherms of Black Shales from The Netherlands, Energy Fuels, 2012, 26, 4995–5004 CrossRef CAS.
- H. Tian, T. F. Li, T. W. Zhang and X. M. Xiao, Characterization of methane adsorption on overmature Lower Silurian-Upper Ordovician shales in Sichuan Basin, southwest China: Experimental results and geological implications, Int. J. Coal Geol., 2016, 156, 36–49 CrossRef CAS.
- Y. X. Ma and A. Jamili, Modeling the density profiles and adsorption of pure and mixture hydrocarbons in shales, J. Unconv. Oil Gas Resour., 2016, 14, 128–138 CrossRef.
- K. Mosher, J. He, Y. Liu, E. Rupp and J. Wilcox, Molecular simulation of methane adsorption in micro- and mesoporous carbons with applications to coal and gas shale systems, Int. J. Coal Geol., 2013, 109, 36–44 CrossRef.
- J. Berthonneau, A. Obliger, P. L. Valdenaire, O. Grauby, D. Ferry, D. Chaudanson, P. Levitz, J. J. Kim, F. J. Ulm and R. J. M. Pellenq, Mesoscale structure, mechanics, and transport properties of source rocks' organic pore networks, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 12365–12370 CrossRef CAS PubMed.
- S. Fuss, J. G. Canadell, G. P. Peters, M. Tavoni, R. M. Andrew, P. Ciais, R. B. Jackson, C. D. Jones, F. Kraxner, N. Nakicenovic, C. Le Quéré, M. R. Raupach, A. Sharifi, P. Smith and Y. Yamagata, Betting on negative emissions, Nat. Clim. Change, 2014, 4, 850–853 CrossRef CAS.
-
L. M. Anovitz and D. R. Cole, in Pore-Scale Geochemical Processes, ed. C. I. Steefel, S. Emmanuel and L. M. Anovitz, 2015, vol. 80, pp. 61–164 Search PubMed.
-
L. M. Anovitz and D. R. Cole, Analysis of the Pore Structures of Shale Using Neutron and X-Ray Small Angle Scattering, Geological Carbon Storage, 2019, pp. 71–118 Search PubMed.
- J. Bahadur, Y. B. Melnichenko, M. Mastalerz, A. Furmann and C. R. Clarkson, Hierarchical Pore Morphology of Cretaceous Shale: A Small-Angle Neutron Scattering and Ultrasmall-Angle Neutron Scattering Study, Energy Fuels, 2014, 28, 6336–6344 CrossRef CAS.
- S. Lee, T. B. Fischer, M. R. Stokes, R. J. Klingler, J. Ilavsky, D. K. McCarty, M. O. Wigand, A. Derkowski and R. E. Winans, Dehydration effect on the pore size, porosity, and fractal parameters of shale rocks: Ultrasmall-angle X-ray scattering study, Energy Fuels, 2014, 28, 6772–6779 CrossRef CAS.
- M. D. Sun, B. S. Yu, Q. H. Hu, Y. F. Zhang, B. Li, R. Yang, Y. B. Melnichenko and G. Cheng, Pore characteristics of Longmaxi shale gas reservoir in the Northwest of Guizhou, China: Investigations using small-angle neutron scattering (SANS), helium pycnometry, and gas sorption isotherm, Int. J. Coal Geol., 2017, 171, 61–68 CrossRef CAS.
- H. E. King, A. P. R. Eberle, C. C. Walters, C. E. Kliewer, D. Ertas and C. Huynh, Pore Architecture and Connectivity in Gas Shale, Energy Fuels, 2015, 29, 1375–1390 CrossRef CAS.
- L. F. Ruppert, R. Sakurovs, T. P. Blach, L. He, Y. B. Melnichenko, D. F. R. Mildner and L. Alcantar-Lopez, A USANS/SANS study of the accessibility of pores in the Barnett shale to methane and water, Energy Fuels, 2013, 27, 772–779 CrossRef CAS.
- X. Gu, D. F. R. Mildner, D. R. Cole, G. Rother, R. Slingerland and S. L. Brantley, Quantification of Organic Porosity and Water Accessibility in Marcellus Shale Using Neutron Scattering, Energy Fuels, 2016, 30, 4438–4449 CrossRef CAS.
- J. Bahadur, L. F. Ruppert, V. Pipich, R. Sakurovs and Y. B. Melnichenko, Porosity of the Marcellus Shale: A contrast matching small-angle neutron scattering study, Int. J. Coal Geol., 2018, 188, 156–164 CrossRef CAS.
- K. L. Stefanopoulos, T. G. A. Youngs, R. Sakurovs, L. F. Ruppert, J. Bahadur and Y. B. Melnichenko, Neutron Scattering Measurements of Carbon Dioxide Adsorption in Pores within the Marcellus Shale: Implications for Sequestration, Environ. Sci. Technol., 2017, 51, 6515–6521 CrossRef CAS PubMed.
- A. P. R. Eberle, H. E. King, P. I. Ravikovitch, C. C. Walters, G. Rother and D. J. Wesolowski, Direct Measure of the Dense Methane Phase in Gas Shale Organic Porosity by Neutron Scattering, Energy Fuels, 2016, 30, 9022–9027 CrossRef CAS.
-
Y. B. Melnichenko, Small-Angle Scattering from
Confined and Interfacial Fluids: Applications to Energy Storage and Environmental Science, Springer International Publishing, 2015 Search PubMed.
- D. Kohl, R. Slingerland, M. Arthur, R. Bracht and T. Engelder, Sequence stratigraphy and depositional environments of the Shamokin (Union Springs) Member, Marcellus Formation, and associated strata in the middle Appalachian Basin, AAPG Bull., 2014, 98, 483–513 CrossRef.
-
R. H. Shaver, Compendium of Paleozoic rock-unit stratigraphy in Indiana: A revision, Department of Natural Resources, 1986 Search PubMed.
-
C. E. Wier, Geology and mineral deposits of the Jasonville Quadrangle, Indiana Geological Survey, Indiana, 1952.
- C. Zou, D. Dong, S. Wang, J. Li, X. Li, Y. Wang, D. Li and K. Cheng, Geological characteristics and resource potential of shale gas in China, Pet. Explor. Dev., 2010, 37, 641–653 CrossRef CAS.
- S. Kline, Reduction and analysis of SANS and USANS data using IGOR Pro, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- S. M. Liu, R. Zhang, Z. Karpyn, H. Yoon and T. Dewers, Investigation of accessible pore structure evolution under pressurization and adsorption for coal and shale using small-angle neutron scattering, Energy Fuels, 2019, 33, 837–847 CrossRef CAS.
- R. Zhang, S. Liu, L. He, T. P. Blach and Y. Wang, Characterizing anisotropic pore structure and its impact on gas storage and transport in coalbed methane and shale gas reservoirs, Energy Fuels, 2020, 34, 3161–3172 CrossRef CAS.
- Y. B. Melnichenko, L. He, R. Sakurovs, A. L. Kholodenko, T. Blach, M. Mastalerz, A. P. Radlinski, G. Cheng and D. F. R. Mildner, Accessibility of pores in coal to methane and carbon dioxide, Fuel, 2012, 91, 200–208 CrossRef CAS.
- R. Zhang, S. Liu, J. Bahadur, D. Elsworth, Y. Melnichenko, L. He and Y. Wang, Estimation and modeling of coal pore accessibility using small angle neutron scattering, Fuel, 2015, 161, 323–332 CrossRef CAS.
- S. Liu and R. Zhang, Anisotropic pore structure of shale and gas injection-induced nanopore alteration: A small-angle neutron scattering study, Int. J. Coal Geol., 2020, 103384, DOI:10.1016/j.coal.2020.103384.
- J. Ilavsky and P. R. Jemian, Irena: tool suite for modeling and analysis of small-angle scattering, J. Appl. Crystallogr., 2009, 42, 347–353 CrossRef CAS.
-
O. Glatter and O. Kratky, Small angle X-ray scattering, Academic Press, 1982 Search PubMed.
- Y. Wang, Y. Qin, R. Zhang, L. He, L. M. Anovitz, M. Bleuel, D. F. R. Mildner, S. Liu and Y. Zhu, Evaluation of Nanoscale Accessible Pore Structures for Improved Prediction of Gas Production Potential in Chinese Marine Shales, Energy Fuels, 2018, 32, 12447–12461 CrossRef CAS.
- G. Beaucage, Approximations leading to a unified exponential power-law approach to small-angle scattering, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS.
-
http://www.sasview.org/
.
- W. Wu, Small-angle X-ray study of particulate reinforced composites, Polymer, 1982, 23, 1907–1912 CrossRef CAS.
- Y. Belmabkhout, M. Frère and G. D. Weireld, High-pressure adsorption measurements. A comparative study of the volumetric and gravimetric methods, Meas. Sci. Technol., 2004, 15, 848–858 CrossRef CAS.
- K. Murata, M. El-Merraoui and K. Kaneko, A new determination method of absolute adsorption isotherm of supercritical gases under high pressure with a special relevance to density-functional theory study, J. Chem. Phys., 2001, 114, 4196–4205 CrossRef CAS.
- R. Pini, Interpretation of net and excess adsorption isotherms in microporous adsorbents, Microporous Mesoporous Mater., 2014, 187, 40–52 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1en00419k |
| ‡ Present address: Chemical Sciences Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA. |
| § Present address: Department of Civil and Environmental Engineering, University of Strathclyde, Glasgow G1 1XQ, UK. |
|
| This journal is © The Royal Society of Chemistry 2021 |
 a,
Shimin
Liu
a,
Shimin
Liu
 *a,
Long
Fan
a,
Tomasz P.
Blach
b and
Guijie
Sang§
a
*a,
Long
Fan
a,
Tomasz P.
Blach
b and
Guijie
Sang§
a

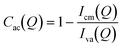

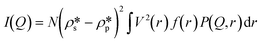
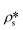 and
and 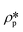 are the SLDs of the solid matrix and the pores; r is the spherical radius; V(r) is the spherical volume; f(r) is the pore size distribution; and P(Q, r) is the spherical form factor. The SLD of the pores
are the SLDs of the solid matrix and the pores; r is the spherical radius; V(r) is the spherical volume; f(r) is the pore size distribution; and P(Q, r) is the spherical form factor. The SLD of the pores 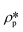 , should be zero under vacuum condition. The estimated effective SLD of each shale sample shown in Table S2† was used for the solid matrix SLD. The upper and lower limits of the pore diameter were set as 3000 Å and 10 Å for the model fitting of the Marcellus shale and Longmaxi shale samples. However, for the Illinois shale sample, a smaller upper limit of the pore diameter (1500 Å) was used because only the NG7 configuration was used for the measurement due to the limited beam time. Thus, the probed pore diameter range is 1–300 nm for the Marcellus and Longmaxi shale samples and 1–150 nm for the Illinois shale. The results of pore volume distributions with uncertainties are shown in Fig. 3b. The unit of volume distribution is cm3 (cm3 Å)–1, i.e., dV/(V·dD). We can find that the pore volume distributions of all the shale samples are multimodal. The main peak at the pore diameter of ∼20 Å and a small peak at the pore diameter of ∼55 Å are shown in the volume distributions of the Marcellus shale and Illinois shale samples. However, a relatively lower and broader hump at the pore range around 20–300 Å is shown in the volume distribution of the Longmaxi shale sample. We can see multiple peaks at larger pores ranging between 100 Å and 1000 Å for the Illinois shale sample, in which the volume distribution is higher than those of the other two shale samples due to the relatively higher pore population in larger sized pores. The Marcellus and Longmaxi shale samples have very similar pore volume distributions at pore diameters greater than ∼100 Å, and both have a small hump at pores around 1500 Å.
, should be zero under vacuum condition. The estimated effective SLD of each shale sample shown in Table S2† was used for the solid matrix SLD. The upper and lower limits of the pore diameter were set as 3000 Å and 10 Å for the model fitting of the Marcellus shale and Longmaxi shale samples. However, for the Illinois shale sample, a smaller upper limit of the pore diameter (1500 Å) was used because only the NG7 configuration was used for the measurement due to the limited beam time. Thus, the probed pore diameter range is 1–300 nm for the Marcellus and Longmaxi shale samples and 1–150 nm for the Illinois shale. The results of pore volume distributions with uncertainties are shown in Fig. 3b. The unit of volume distribution is cm3 (cm3 Å)–1, i.e., dV/(V·dD). We can find that the pore volume distributions of all the shale samples are multimodal. The main peak at the pore diameter of ∼20 Å and a small peak at the pore diameter of ∼55 Å are shown in the volume distributions of the Marcellus shale and Illinois shale samples. However, a relatively lower and broader hump at the pore range around 20–300 Å is shown in the volume distribution of the Longmaxi shale sample. We can see multiple peaks at larger pores ranging between 100 Å and 1000 Å for the Illinois shale sample, in which the volume distribution is higher than those of the other two shale samples due to the relatively higher pore population in larger sized pores. The Marcellus and Longmaxi shale samples have very similar pore volume distributions at pore diameters greater than ∼100 Å, and both have a small hump at pores around 1500 Å.
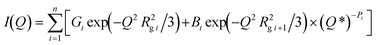
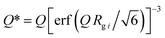
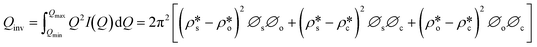
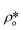 and
and 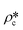 are the SLDs of the open and closed pores, respectively; and ∅s, ∅o, and ∅c are the volume fractions of the solid matrix, open pores, and closed pores, respectively. Qinv can be estimated using the experimentally obtained scattering intensity under different pressure conditions, which is shown in Fig. 5. Note that the Q range to estimate the Porod invariant was set as 2.8 × 10−3–0.25 Å−1, 2.5 × 10−3–0.21 Å−1, and 5.3 × 10−3–0.25 Å−1 for the Marcellus shale, Longmaxi shale, and Illinois shale samples, respectively. Then the results can be more precisely compared among different pressure conditions for each sample, although some portion of high Q was ignored. The Marcellus shale sample may already reach the contrast-matched point at the pressure around 60 MPa on average over the estimated pore range (Fig. 5). The SLD of CD4 at 60 MPa at room temperature is about 3.7 × 1010 cm−2, which is slightly smaller than the estimated effective SLD (∼3.9 × 1010 cm−2) from the chemical compositions of the Marcellus shale. It suggests that slightly more open nanopores accessible to CD4 are in the matrix with a smaller SLD, which could be organic matter. In contrast, the Longmaxi shale sample may approach the contrast-matched point at the pressure around 70 MPa, and the Illinois shale sample may not reach the contrast-matched point over the pressure range measured (Fig. 5). It is unexpected for the two samples because the estimated effective SLD of the Longmaxi shale sample (∼4.4 × 1010 cm−2) is higher than the SLD of CD4 at the highest pressure (70 MPa), which is ∼3.9 × 1010 cm−2, and the estimated effective SLD of the Illinois shale sample (∼3.4 × 1010 cm−2) is less than the SLD of CD4 at the pressure of 60 MPa (∼3.7 × 1010 cm−2). The results suggest that more open nanopores accessible to CD4 are in the Longmaxi shale sample matrix with a lower SLD, which could be organic matter, while in the matrix of the Illinois shale sample with a higher SLD, which could be clay minerals such as glauconite.
are the SLDs of the open and closed pores, respectively; and ∅s, ∅o, and ∅c are the volume fractions of the solid matrix, open pores, and closed pores, respectively. Qinv can be estimated using the experimentally obtained scattering intensity under different pressure conditions, which is shown in Fig. 5. Note that the Q range to estimate the Porod invariant was set as 2.8 × 10−3–0.25 Å−1, 2.5 × 10−3–0.21 Å−1, and 5.3 × 10−3–0.25 Å−1 for the Marcellus shale, Longmaxi shale, and Illinois shale samples, respectively. Then the results can be more precisely compared among different pressure conditions for each sample, although some portion of high Q was ignored. The Marcellus shale sample may already reach the contrast-matched point at the pressure around 60 MPa on average over the estimated pore range (Fig. 5). The SLD of CD4 at 60 MPa at room temperature is about 3.7 × 1010 cm−2, which is slightly smaller than the estimated effective SLD (∼3.9 × 1010 cm−2) from the chemical compositions of the Marcellus shale. It suggests that slightly more open nanopores accessible to CD4 are in the matrix with a smaller SLD, which could be organic matter. In contrast, the Longmaxi shale sample may approach the contrast-matched point at the pressure around 70 MPa, and the Illinois shale sample may not reach the contrast-matched point over the pressure range measured (Fig. 5). It is unexpected for the two samples because the estimated effective SLD of the Longmaxi shale sample (∼4.4 × 1010 cm−2) is higher than the SLD of CD4 at the highest pressure (70 MPa), which is ∼3.9 × 1010 cm−2, and the estimated effective SLD of the Illinois shale sample (∼3.4 × 1010 cm−2) is less than the SLD of CD4 at the pressure of 60 MPa (∼3.7 × 1010 cm−2). The results suggest that more open nanopores accessible to CD4 are in the Longmaxi shale sample matrix with a lower SLD, which could be organic matter, while in the matrix of the Illinois shale sample with a higher SLD, which could be clay minerals such as glauconite.
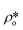 , using eqn (7), the volume fractions of the solid matrix, open pores, and closed pores, ∅s, ∅o, and ∅c, need to be quantified. The average SLD in closed pores,
, using eqn (7), the volume fractions of the solid matrix, open pores, and closed pores, ∅s, ∅o, and ∅c, need to be quantified. The average SLD in closed pores, 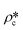 is equal to zero since the guest fluid does not have access to closed pores, and there may be no residual fluid inside closed pores.
is equal to zero since the guest fluid does not have access to closed pores, and there may be no residual fluid inside closed pores. 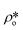 is equal to zero under vacuum condition because of empty open pores and equal to
is equal to zero under vacuum condition because of empty open pores and equal to 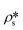 under contrast-matched condition. Thus, in both conditions, the three-phase Porod invariant equation reduces to the two-phase one:
under contrast-matched condition. Thus, in both conditions, the three-phase Porod invariant equation reduces to the two-phase one: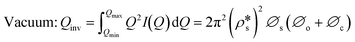
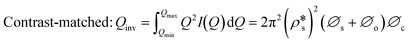
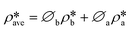
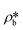 and
and 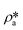 are the SLDs of the bulk phase and adsorbed phase, respectively; and ∅b and ∅a are the volume fractions of the bulk phase and adsorbed phase, respectively, in which the sum of ∅b and ∅a is equal to one. A higher
are the SLDs of the bulk phase and adsorbed phase, respectively; and ∅b and ∅a are the volume fractions of the bulk phase and adsorbed phase, respectively, in which the sum of ∅b and ∅a is equal to one. A higher 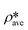 than
than 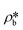 suggests a higher
suggests a higher 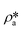 than
than 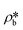 on average in the integrated pore range and vice versa. The measured samples' results hypothetically indicate that the adsorbed phase density, ρa, in shale macro-/mesopores on average could be higher than the bulk phase density, ρb, at the low-pressure region (<∼10 MPa) because of surface adsorption (Fig. 7). However, the average ρa could become smaller than the ρb at a higher pressure because of the increase of adsorbed phase volume, Va, in which surface adsorption could convert to partial pore-filling adsorption (Fig. 7). When the gas pressure is even higher, there could be two situations: (1) the completion of pore-filling adsorption occurs, in which Va increased to be the pore volume and (2) the decrease of Va occurs (Fig. 7). The second situation may be more likely in shale macro-/mesopores because these nanopores may not have enough overlapped energy from the pore surface to provide a possible complete pore-filling adsorption. From a laboratory perspective, the excess or Gibbs adsorption capacity can be directly estimated either by gravimetric or by volumetric methods.50 In contrast, the absolute adsorption capacity, representing the actual adsorption capability, can only be estimated by correcting the excess adsorption capacity through assumptions. The usual assumption of constant adsorbed phase density13,16 could have less error in relatively low pressure than higher pressure regions. The assumption of monolayer sorption volume or pore volume as constant adsorbed phase volume51,52 could have higher errors for sorption capacity estimation. However, since we only measured three shale samples and do not have data points at relatively low-pressure (<10 MPa) and significantly high-pressure regions (>70 MPa) because of limited beam time, further research, either experimental or computational approaches, needs to be conducted to prove the hypothetical mechanisms.
on average in the integrated pore range and vice versa. The measured samples' results hypothetically indicate that the adsorbed phase density, ρa, in shale macro-/mesopores on average could be higher than the bulk phase density, ρb, at the low-pressure region (<∼10 MPa) because of surface adsorption (Fig. 7). However, the average ρa could become smaller than the ρb at a higher pressure because of the increase of adsorbed phase volume, Va, in which surface adsorption could convert to partial pore-filling adsorption (Fig. 7). When the gas pressure is even higher, there could be two situations: (1) the completion of pore-filling adsorption occurs, in which Va increased to be the pore volume and (2) the decrease of Va occurs (Fig. 7). The second situation may be more likely in shale macro-/mesopores because these nanopores may not have enough overlapped energy from the pore surface to provide a possible complete pore-filling adsorption. From a laboratory perspective, the excess or Gibbs adsorption capacity can be directly estimated either by gravimetric or by volumetric methods.50 In contrast, the absolute adsorption capacity, representing the actual adsorption capability, can only be estimated by correcting the excess adsorption capacity through assumptions. The usual assumption of constant adsorbed phase density13,16 could have less error in relatively low pressure than higher pressure regions. The assumption of monolayer sorption volume or pore volume as constant adsorbed phase volume51,52 could have higher errors for sorption capacity estimation. However, since we only measured three shale samples and do not have data points at relatively low-pressure (<10 MPa) and significantly high-pressure regions (>70 MPa) because of limited beam time, further research, either experimental or computational approaches, needs to be conducted to prove the hypothetical mechanisms.






