Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of substituent position on aminobenzoate relaxation pathways in solution†
Natércia d. N.
Rodrigues
 *ab,
Jack M.
Woolley
*ab,
Jack M.
Woolley
 a,
Konstantina M.
Krokidi
a,
Maria A.
Tesa-Serrate
c,
Matthew A. P.
Turner
ad,
Nicholas D. M.
Hine
a,
Konstantina M.
Krokidi
a,
Maria A.
Tesa-Serrate
c,
Matthew A. P.
Turner
ad,
Nicholas D. M.
Hine
 d and
Vasilios G.
Stavros
d and
Vasilios G.
Stavros
 *a
*a
aUniversity of Warwick, Department of Chemistry, Coventry, CV4 7AL, UK. E-mail: natercia.rodrigueslopes@lubrizol.com; v.stavros@warwick.ac.uk
bLipotec SAU, Calle Isaac Peral, 17 Pol. Ind. Camí Ral, 08850 Barcelona, Spain
cEdinburgh Instruments, 2 Bain Square, Kirkton Campus, Livingston, EH54 7DQ, UK
dUniversity of Warwick, Department of Physics, Coventry, CV4 7AL, UK
First published on 6th October 2021
Abstract
The negative effects of ultraviolet radiation (UVR) on human skin have led to the widespread use of sunscreens, i.e. skincare products containing UV filters to absorb, reflect or otherwise block UVR. The mechanisms by which UV filters dissipate energy following photoexcitation, i.e. their photodynamics, can crucially determine a molecule's performance as a sunscreen UV filter. In this work, we evaluate the effects of substituent position on the in-solution relaxation pathways of two derivates of methyl anthranilate (an ortho compound that is a precursor to the UV filter meradimate), meta- and para-methyl anthranilate, m-MA and p-MA, respectively. The photodynamics of m-MA were found to be sensitive to solvent polarity: its emission spectra show larger Stokes shifts with increasing polarity, and both the fluorescence quantum yield and lifetimes for m-MA increase in polar solvents. While the Stokes shifts for p-MA are much milder and more independent of solvent environment than those of m-MA, we find its fluorescence quantum yields to be sensitive not only to solvent polarity but to the hydrogen bonding character of the solvent. In both cases (m- and p-MA) we have found common computational methods to be insufficient to appropriately model the observed spectroscopic data, likely due to an inability to account for explicit solvent interactions, a known challenge in computational chemistry. Therefore, apart from providing insight into the photodynamics of anthranilate derivatives, the work presented here also provides a case study that may be of use to theoretical chemists looking to improve and develop explicit solvent computational methods.
Introduction
The ultraviolet (UV) radiation that reaches the Earth's surface, mostly UVB (280–315 nm) and UVA (315–400 nm),1 plays an important role in life sustaining processes such as photosynthesis in plants2 or the production of vitamin D in human skin.2,3 Nevertheless, UV radiation may also have destructive effects on living organisms. UVB radiation, being more energetic, can cause more direct damage by being absorbed directly by DNA and thus causing mutagenic photolesions which may lead to skin cancer.4,5 UVA is commonly associated with skin pigmentation and skin aging, but it is also the source of oxidative stress, which may equally cause DNA mutations and lead to skin cancer.6,7 Moreover, the higher abundance of UVA radiation at the Earth's surface, in addition to its ability to penetrate deeper into the skin, constitute further risks which justify the need for photoprotection against UVA as well as UVB.6While human skin is naturally equipped with its own forms of photoprotection, in the form of melanin, a pigment which absorbs harmful radiation before it reaches vulnerable skin cells, this protection is a delayed response that is often insufficient against overexposure to solar radiation.8,9 In order to complement the skin's natural forms of photoprotection, the use of sunscreens – commercial formulations containing chemical UV filters, physical UV blockers or, often, both – is now common practice. The chemical UV filters contained in commercial sunscreen formulations are required to be non-toxic to humans and the environment while allowing for the production of a pleasant formulation. In addition, an ideal UV filter should dissipate excess energy efficiently, without undergoing or inducing any potentially harmful photochemistry. From a photophysical perspective, this translates to short-lived excited states, with excited state population returning to the electronic ground state (S0) within a picosecond (10−12 second) lifetime or less, typically via internal conversion (IC).10–12 Fast excited state relaxation ensures not only that the UV filter is less vulnerable to harmful photochemistry but also that it is quickly ‘recycled’ and thus able to re-absorb UV radiation. In turn, this ‘recycling’ of the UV filter ensures the commercial sunscreen formulation maintains its photoprotective performance for longer periods of time.
The anthranilates constitute one of the families of chemical UV filters currently employed in commercial sunscreen formulations.13 Anthranilates are molecules for which the ortho positioning of an amine and an ester functional group facilitates an intramolecular hydrogen bond between them. Menthyl anthranilate, or meradimate, a UV filter currently approved by the Food and Drug Administration of the United States of America for use in commercial sunscreen formulations,13 has previously been studied in order to establish its photophysics and hence the mechanisms by which it dissipates excess energy. In one such study, which combined experimental and computational insight, it has been found that absorption of UVA/UVB radiation leads both meradimate and its precursor methyl anthranilate (an ortho compound, o-MA) to undergo an incomplete excited state intramolecular proton transfer, for which the hydrogen atom is dislocated along the N–H–O hydrogen bond,14 being unable to then access any nearby conical intersections (CIs) that would allow IC to take place. As a result, the excited state population is trapped in the S1 state and relaxation happens mostly via radiative pathways, i.e. fluorescence and phosphorescence.14 This scenario is non-ideal for a sunscreen molecule, not only due to the formation of often undesirable triplet states but also because excess energy persists for longer periods of time, making the molecules more vulnerable to reactive relaxation pathways.10–12
In previous work carried out in the gas-phase, it has been shown that changing the substituent position (and thus disturbing the intramolecular hydrogen bond) of the anthranilates has a significant impact on both the resulting absorption spectra and the observed photodynamics.15 Specifically, it has been suggested that, in the gas-phase, the relaxation pathway of methyl-3-aminobenzoate, (m-MA, see Fig. 1 for molecular structure) may involve prefulvenic CIs, that is, ring distortions which push one of the carbon atoms in the six membered ring away from the ring plane.15 On the other hand, the long gas-phase lifetime (>1.2 ns) of the excited state of methyl-4-aminobenzoate (p-MA, see Fig. 1) was suggested to be due to the stability afforded by the charge transfer characteristic of this state.15 Moreover, it was established that while both m-MA and p-MA fluoresce in solution, luminescence is non-unity (<100%) and hence alternative, non-radiative pathways must be involved in the photodynamics of these molecules.15
In the present work, we investigate the effects of substituent position on the ultrafast photodynamics of these aminobenzoates, m-MA and p-MA, in solution, having pursued both experimental work and computational modelling. We evaluate also the effects of environment polarity and protic characteristics on the photodynamics of these molecules. In a sunscreen context, the ultrafast photodynamics of solvated p-MA are particularly interesting, since p-MA is the ester derivative of para-aminobenzoic acid (PABA), a once widely used UV filter that lost its place in commercial sunscreen formulations due to photosensitivity and photoallergy concerns.16,17
Experimental methods
i. Steady-state spectroscopy
The UV/Vis absorption spectra of m-MA (methyl-3-aminobenzoate, Alfa Aesar, ≥98%) and p-MA (methyl-4-aminobenzoate, Aldrich, 98%) were obtained using an Agilent Cary 60 UV/Vis spectrophotometer for separate solutions of each molecule dissolved in cyclohexane (CHX, Merck, ≥99.7%), acetonitrile (ACN, Fisher Scientific, ≥99.8%), and ethanol (EtOH, VWR, absolute) to a concentration of approximately 10−6 M. Temperature-dependent UV/Vis absorption spectra were also obtained for equivalent solutions using an Agilent Cary 60 UV/Vis spectrophotometer equipped with a temperature control unit (TC 1 Temperature Controller, Quantum NorthWest); these spectra can be found in the ESI,† Section 1 (S1).The emission spectra for both m-MA and p-MA were obtained for each solution with a Horiba Scientific Fluorolog®-3. The same instrument was used to determine fluorescence quantum yields for these solutions, as presented in the ESI,† in Section 2 (S2). Fluorescence lifetimes were also determined, albeit employing different equipment: for m-MA, the fluorescence lifetimes were obtained with the Horiba Scientific Fluorolog®-3, while for p-MA these were measured using a Time-Correlated Single Photon Counting (TCSPC) technique. Further details on the procedures followed for these measurements are given in Section 3 of the ESI† (S3).
ii. Transient electronic absorption spectroscopy (TEAS)
The transient electronic absorption spectroscopy (TEAS) set-up used in the present experiments has been described previously in greater detail18–20 and it will therefore be only briefly summarised here, with specific details pertaining to the present work being provided. TEAS measurements were obtained for separate solutions of m-MA and p-MA dissolved in CHX, ACN and EtOH to a concentration of 10−3 M. To ensure that fresh sample is interrogated with each laser pulse, the sample solutions were recirculated through a flow cell (Harrick Scientific), consisting of two CaF2 windows separated by 100 μm thick PTFE spacers (500 μm for m-MA, for improved signal), using a SIMDOS 02 diaphragm pump (KNF Neuberger UK Ltd).The fundamental 800 nm output (12 W, 1 kHz) of a commercial femtosecond (fs) Ti:Sapphire regenerative amplified laser system (Spectra-Physics, Dual Ascend Pumped Spitfire Ace) seeded by a Mai Tai (Spectra-Physics), was split into four fractions of approximately equal power (3.5 W), each one having a separate recompression grating. A 2.5 W fraction of one of these beams was seeded into an optical parametric amplifier (Topas-Prime with UV extension, Light Conversion) to generate the pump pulses used in the reported TEAS experiments. The pump wavelength (λpu) was centred at the absorption maxima (λmax) for each solution. Moreover, the power of the pump pulse was set to 0.4–0.6 mW, and power dependence studies were carried out in order to ensure single-photon dynamics at these powers; see Section 4 of the ESI† for more details (S4). The probe pulses (λpr), on the other hand, were generated by focusing 5% of the remaining 1 W of the 800 nm fundamental beam into a CaF2 window (2 mm thick, vertically translated to avoid damage), thus creating the broadband white light continuum (320–720 nm); the 800 nm beam was further attenuated with a variable neutral density filter as required to produce stable white light. The relative polarisation between the pump and probe beams was held at magic angle (54.7°) by means of a λ/2 waveplate in order to negate any rotational dynamics.
At the sample-laser interaction point, λpu photoexcites the species of interest and λpr probes the resulting excited state at predetermined pump–probe time interval delays (Δt), thus allowing for excited state dynamics to be monitored. Pump–probe delays ranging from −1 ps to 3 ns (where Δt = 0 corresponds to the pump and probe pulses arriving at the sample at the same time) are achieved by translating a hollow gold retroreflector on a motorized optical delay line (Newport M-IMS500CCHA) in the λpr beam path. Between −1 and 1 ps, the Δt step size is fixed, and after that it is increased as described by Megerle et al.;21 this is to ensure an optimum balance between detailed mapping of the dynamics and reasonable acquisition times. The portion of the probe beam transmitted through the sample was collected using a fibre-coupled spectrometer (Avantes, AvaSpec-ULS1650F). Changes in optical density (ΔOD) were calculated from the measured probe intensities transmitted through the sequentially excited and non-excited sample as prepared by employing a mechanical chopper in the pump beam path.
The transient absorption spectra (TAS) collected as just described are chirped, i.e. Δt = 0 is different for each λpr, due to group velocity dispersion (GVD) artefacts;22 this chirp was corrected in the data herein presented using the KOALA package.23 When extracting quantitative dynamical information from the TAS with a global fitting procedure within the Glotaran software package,24 a third order polynomial is included in the algorithm to account for this chirp effect. The algorithm within Glotaran also convolves the Gaussian instrument response function (IRF) with exponential functions following a sequential kinetic model (i.e. assuming 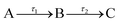 ) to extract time constants (τn) and their associated evolution associated difference spectra (EADS) for each data set collected, as further detailed in S5 of the ESI.† The setup used in these experiments provides an IRF with a full width at half maximum of ∼70–140 fs (depending on solvent, λpu and λpr, see S6 of the ESI†). The quality of the fits was evaluated upon inspection of the resulting residuals and fit lineouts, also shown in the ESI,† in S7.
) to extract time constants (τn) and their associated evolution associated difference spectra (EADS) for each data set collected, as further detailed in S5 of the ESI.† The setup used in these experiments provides an IRF with a full width at half maximum of ∼70–140 fs (depending on solvent, λpu and λpr, see S6 of the ESI†). The quality of the fits was evaluated upon inspection of the resulting residuals and fit lineouts, also shown in the ESI,† in S7.
Finally, ‘long-time’ transient absorption spectra (Δt = 0–100 ns, LT-TAS) were also obtained for p-MA. For these LT-TAS measurements, solutions of p-MA were prepared in CHX, ACN, and EtOH, adjusting the concentration to an optical density between 0.3 and 0.5 OD at 266 nm. The solutions were placed in quartz cuvettes and studied without further preparation. LT-TAS measurements were then performed for these solutions in an LP980-KS spectrometer (Edinburgh Instruments Ltd) configured with a visible PMT detector for kinetic data and an ICCD detector for spectral data acquisition. These detectors were mounted on different ports of the LP980 spectrograph, allowing rapid switching between spectral and kinetic detection. Pump pulses at 266 nm were produced by a Litron Nano S 130-10 laser (Litron Lasers Ltd). The pump pulse width was ∼5 ns and its energy was ∼8 mJ pulse−1. The white light probe beam was generated by the Xe lamp in the LP980 spectrograph, operating in pulsed mode and producing pulses with a duration of 6 ms. Pump-only and probe-only backgrounds were subtracted automatically by the L900 software when necessary. Spectral and kinetic ΔOD curves were calculated automatically by L900.
Computational methods
All calculations were conducted using the NWCHEM software package.25 Initially, the geometries of m-MA and p-MA were optimised at the PBE0/cc-pVTZ level of theory.26m-MA can relax into two possible forms, one with the methyl group pointing towards the amine group and one with it pointing away. Both m-MA structures were investigated but gave very similar results; as such, hereafter we restrict discussion to the structure with the methyl group pointing away from the amine group, as this structure had a slightly lower ground state energy. Following geometry optimisation, both m-MA and p-MA were reoptimized using an implicit solvent model27,28 for each of the three solvents, CHX, ACN, and EtOH, using default parameters from the Minnesota Solvent Descriptor Database.29 Vertical excitation calculations were then conducted for each of these structures with each choice of implicit solvent, using the same level of theory as before, in both the singlet and triplet manifold.Reaction coordinates were probed in implicit-solvent ethanol along the static rotation coordinate of both the amino and ester groups of m-MA and p-MA (see Fig. 6 and ESI†) through equidistant steps along the coordinate. Vertical excitations were calculated at each step, again using the PBE0/cc-pVTZ level of theory. This process was repeated for rotations of the amino and ester groups of both m-MA and p-MA, as well as the rotation of the N(CH3)2 group of the methylated version of p-MA (see discussion below and Section 8 of the ESI,† S8).
Results and discussion
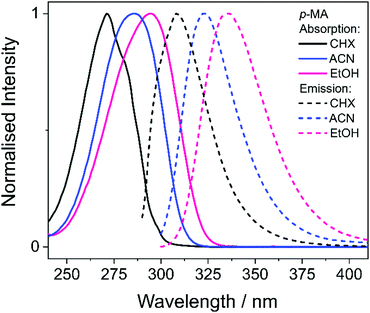
i. Photodynamics of m-MA
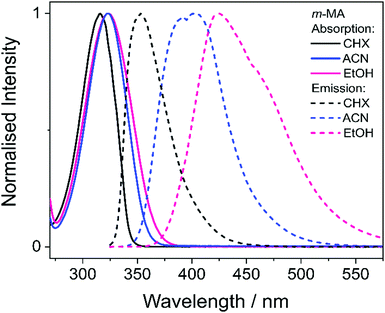
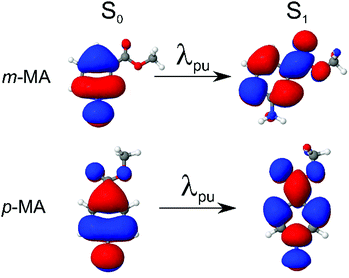
We first present and discuss the steady-state spectroscopy measurements obtained for m-MA, namely the absorption and emission spectra shown in Fig. 2. While the absorption bands of m-MA seem to be relatively unaltered regardless of solvent environment, its emission bands reveal a considerable solvatochromic effect, with both the Stokes shifts and the spectral features of the emission being heavily dependent on solvent polarity. In particular, the observed Stokes shifts, i.e. the energy difference between peak absorption and peak emission, increase significantly with increasing solvent polarity, taking values of 37 nm (3317 cm−1) in CHX, 77 nm (5960 cm−1) in ACN and 102 nm (7431 cm−1) in EtOH (see Fig. 2). This behaviour is characteristic of π-conjugated intramolecular donor–acceptor systems, in which excited states with charge-transfer (CT) character are particularly sensitive to the solvent environment.30–33 In fact, the electron density calculated for the transition between the ground state (S0) and the first excited singlet state (S1) of m-MA, shown in Fig. 3, reveal some migration of electron density from the amino group to the ester group upon photoexcitation, suggesting that the S1 state of m-MA does carry some CT character.Photoinduced CT processes are often accompanied by a significant geometry change as excited state population relaxes from the Franck–Condon (vertical excitation) region towards the energy minimum of the CT state. It might be expected that it would be possible to find computational evidence for this CT energy minimum, despite the difficulties associated with calculating states with CT character in TDDFT. However, in scans either along a particular reaction coordinate or along a linear interpolation of internal coordinates, we were unable to locate this energy minimum in our studies; none of the potential energy cuts (PECs) produced for m-MA reveal a landscape that would justify a significant drive towards an energy minimum (see ESI†), and the relaxed geometry of m-MA remains similar to its Franck–Condon geometry. A full investigation of the energy surface of the S1 state of m-MA may well require an explicit representation of the solvent, but the computational effort required to locate this minimum is beyond the scope of this study.
We offer two further possible explanations for the lack of computational evidence for a CT energy minimum, the existence of which is strongly suggested by our experimental observations (see Fig. 2). First of all, it is possible that there is a small barrier on the pathway from the Franck–Condon region towards the CT energy minimum. Geometry optimisation calculations would stop upon encountering this barrier, thus identifying a local minimum in the vicinity of the Franck–Condon region but not the global minimum that would explain the experimental data in Fig. 2. This would imply that this barrier is sufficiently small so that the light sources employed in our experiments – both steady-state and ultrafast – provide sufficient energy to the system to overcome said barrier. We have previously reported on calculated large energy barriers along the rotation of both the amino and the ester group of m-MA, as well as a large barrier along a linear interpolation of internal coordinates.15 However, these previously reported barriers were calculated in the gas-phase, and it is likely that these results are not comparable to the present observations in solution, particularly given the observed sensitivity of m-MA to solvent environment, as discussed above. In addition, it is a common observation that polar solvents stabilize CT states, and therefore it is entirely plausible that these barriers would be lower in a solvent environment (and in particular in polar solvents).34
The inability of our computational methods to locate a CT energy minimum could also be due to difficulties with appropriately accounting for explicit solvent effects. While we have used an implicit ethanol model to generate PECs for m-MA in solution (see ESI†), this would only account for electrostatic solvent effects, for which interactions can mostly be understood as interactions between dipole moments. However, it is likely that the interactions between m-MA and any solvent also include specific, more complex, solvent interactions such as hydrogen bonding, which can only be properly accounted for with explicit solvent models. These calculations are computationally demanding, as computational cost scales unfavourably with system size. The amount of statistically varied snapshots it would require to accurately calculate excited state energies for these systems is large,35 and these calculations would need to be run individually for each and every step along the molecular coordinate. Therefore, the current computational tools and resources at our disposal may be insufficient to accurately model systems such as solvated m-MA.
Finally, we note here that states with nπ* character, for example, could also be particularly sensitive to solvent environment.36 However, as the computational results presented in Table 1 suggest, the S1 state of m-MA does not have nπ* character. While we have also found that the S2 state of m-MA is indeed an nπ* state, the large S1–S2 vertical energy difference for m-MA in all solvents (7582 cm−1 in CHX, 8630 cm−1 in ACN and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 082 cm−1 in EtOH) makes it highly unlikely for an S2 → S1 transition to take place in the vicinity of the Franck–Condon region. As such, we proceed with this discussion under the assumption that photoexcitation to the S1 state of m-MA results in population of an excited state with at least some CT character, making it sensitive to solvent environment.
082 cm−1 in EtOH) makes it highly unlikely for an S2 → S1 transition to take place in the vicinity of the Franck–Condon region. As such, we proceed with this discussion under the assumption that photoexcitation to the S1 state of m-MA results in population of an excited state with at least some CT character, making it sensitive to solvent environment.
| State | CHX | ACN | EtOH | ||||||
|---|---|---|---|---|---|---|---|---|---|
| eV | Character | Oscillator strength | eV | Character | Oscillator strength | eV | Character | Oscillator strength | |
| m-MA | |||||||||
| S2 | 4.97 | nπ* | 0.0002 | 5.01 | nπ* | 0.0002 | 5.12 | nπ* | 0.0003 |
| S1 | 4.03 | ππ* | 0.0532 | 3.94 | ππ* | 0.0529 | 3.87 | ππ* | 0.0524 |
| T2 | 3.50 | ππ* | — | 3.49 | ππ* | — | 3.48 | ππ* | — |
| T1 | 3.06 | ππ* | — | 3.00 | ππ* | — | 2.94 | ππ* | — |
| p-MA | |||||||||
| S2 | 4.78 | ππ* | 0.3345 | 4.71 | ππ* | 0.0283 | 4.71 | ππ* | 0.0180 |
| S1 | 4.77 | ππ* | 0.1489 | 4.66 | ππ* | 0.4830 | 4.60 | ππ* | 0.5048 |
| T2 | 4.01 | ππ* | — | 3.92 | ππ* | — | 3.94 | ππ* | — |
| T1 | 3.20 | ππ* | — | 3.14 | ππ* | — | 3.10 | ππ* | — |
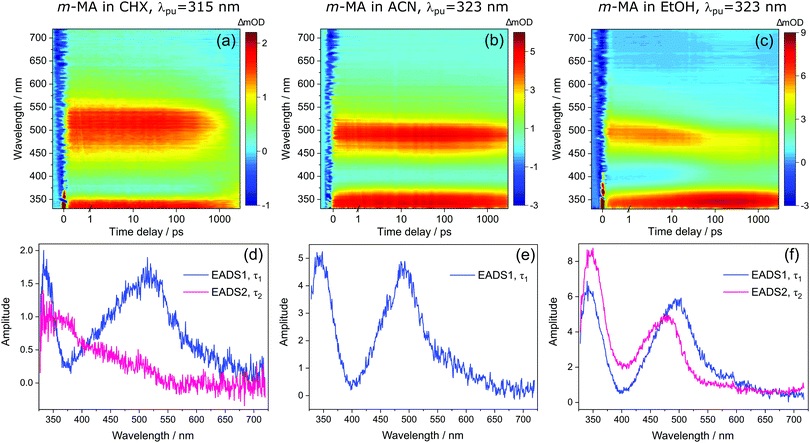
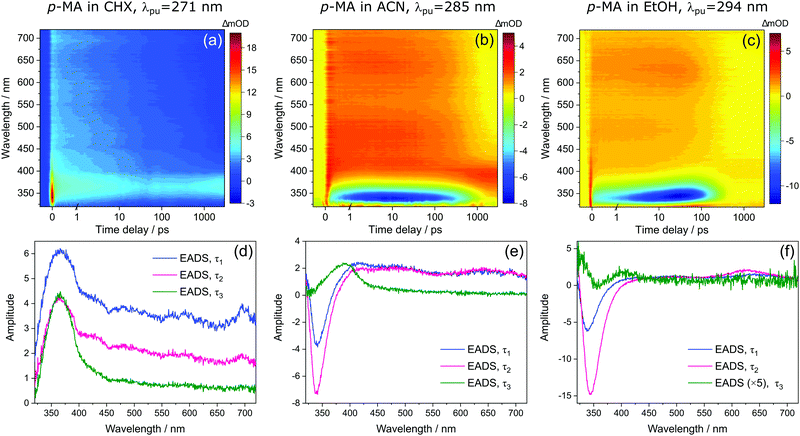
Despite the significant differences in the emission spectra, the transient absorption spectra (TAS) obtained for m-MA are similar across the solvents studied, as can be seen in Fig. 4. In all solvents, the TAS seem to be predominantly described by two excited state absorption features which are present immediately after photoexcitation at the λmax for each solution. However, given that photoexcitation of m-MA is likely to result in exclusive population of the S1 state (see Table 1 and discussion above), the appearance of the TAS in Fig. 4 is best explained by a strong, broad excited state absorption feature which is overlapped by a negative stimulated emission feature. The stimulated emission feature would correspond to the dip in signal observed at approximately 350–400 nm (depending on solvent), which also broadly matches the m-MA emission in each solvent, as presented Fig. 2.
The hypothesis of a single excited state absorption feature overlapped by a stimulated emission feature appropriately accounts for the evolution of EADS1 into EADS2 for m-MA in CHX (see Fig. 4(d)). Within τ1 = 1690 ± 160 ps, the dip at ∼360 nm disappears, leaving behind a single, broad excited state absorption feature which remains for τ2 > 3 ns. Assuming the dip at ∼360 nm does indeed correspond to a stimulated emission feature, this would imply that τ1 in this case corresponds to the fluorescence lifetime. In fact, the value of τ1 extracted from these experiments is in remarkable agreement with the previously reported fluorescence lifetime of m-MA in CHX of τFl ∼ 1.7 ns,15 which supports our assignment of τ1 to the fluorescence lifetime of m-MA in CHX.
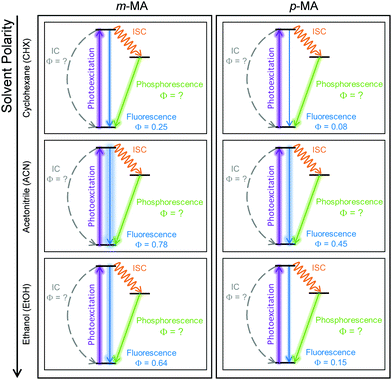
The relatively fast fluorescence observed for m-MA in CHX, along with the small Stokes shift observed in this case (37 nm, Fig. 2), suggests that emission takes place from the close vicinity of the Franck–Condon region. However, as evidenced by the TAS in Fig. 4, some of the excited state population remains in the S1 state of m-MA beyond the temporal window of the present experiments (Δt = 3 ns), suggesting the existence of a nearby energy minimum where excited state population can be trapped. The non-unity quantum yield of fluorescence previously reported for m-MA in CHX (ΦFl = 0.25),15 implies that alternative relaxation pathways play a significant role in excited state relaxation in this case, which could also be acting as efficient sinks for excited state population and thus contributing to the observed fast fluorescence lifetimes. These alternative pathways could include intersystem crossing (ISC) onto the triplet manifold and subsequent phosphorescence, or internal conversion (IC) onto the ground state, even though we have no direct evidence of either relaxation pathway. While we have been unable to computationally identify a conical intersection (CI) between the S1 and S0 states of m-MA in implicit solvent, we have previously reported on several prefulvenic (ring distortion) CIs that may be accessible to MA, thus facilitating IC.15
The photodynamics of m-MA were also studied in two polar solvents, a polar aprotic solvent, ACN, and a polar protic solvent, EtOH, in order to evaluate any potential effects of the hydrogen bonding. In both ACN and EtOH, the TAS of m-MA are slightly different to that observed in CHX. Taking forward the assumption that the dip in signal, which in ACN is centred at ∼400 nm (see Fig. 4(e)), corresponds to a stimulated emission feature overlapping a broader excited state absorption feature, we can conclude that photoexcitation of the S1 state of m-MA in ACN results in trapped excited state population: both the excited state absorption and the stimulated emission feature are immediately present in the TAS and remain for τ1 > 3 ns. This is consistent with the fluorescence lifetime measured for m-MA in ACN, τFl = 10.24 ± 0.02 ns (see ESI†), corroborating the long-lived S1 state and respective fluorescence observed in the TAS. The trapping of excited state population in S1, as evidenced by both the TAS and the fluorescence lifetime measurements of m-MA in ACN, is also consistent with the existence of a relatively deep energy minimum along the S1 state which, as discussed above, we could not locate with computational methods. In contrast to what was observed for m-MA in CHX, fluorescence is the dominant relaxation pathway of m-MA in ACN, taking place with a quantum yield of ΦFl = 0.78 ± 0.02 (see Table 2 and ESI†). The remaining excited state population may once again relax to the ground state via either intersystem crossing (ISC) and subsequent phosphorescence, or via a minor IC coordinate; we do not, however, have direct evidence of either. The previously mentioned prefulvenic CIs15 may still be accessible for m-MA in ACN, but given the significantly increased quantum yield of fluorescence, these CIs are likely not energetically favourable for m-MA in ACN (cf. CHX).
| Solvent | m-MA | ||||
|---|---|---|---|---|---|
| τ 1/ps | τ 2/ns | τ Fl /ns | Φ Fl | Stokes shift (nm/cm−1) | |
| a The values of τFl for m-MA were determined using the Horiba Scientific Fluorolog®-3, while those of p-MA were determined by TCSPC (see ESI for further details). Superscript numbers denote the reference from which the value was taken. | |||||
| CHX | 1690 ± 160 | >3 | 1.715 | 0.2515 | 37/3317 |
| ACN | >3000 | — | 10.24 ± 0.02 | 0.78 ± 0.02 | 77/5960 |
| EtOH | 22.4 ± 0.9 | >3 | 14.00 ± 0.03 | 0.64 ± 0.02 | 102/7431 |
| Solvent | p-MA | |||||
|---|---|---|---|---|---|---|
| τ 1/ps | τ 2/ps | τ 3/ps | τ Fl /ns | Φ Fl | Stokes shift (nm cm−1) | |
| CHX | 3.84 ± 0.05 | 460 ± 10 | >3 | 1.949 ± 0.003 | 0.0815 | 37/4433 |
| ACN | 1.35 ± 0.02 | 526 ± 6 | >3 | 1.029 ± 0.002 | 0.45 ± 0.001 | 37/4005 |
| EtOH | 12.8 ± 0.1 | 135 ± 1 | >3 | 0.390 ± 0.001 | 0.15 ± 0.07 | 41/4162 |
In the case of m-MA in EtOH, two time constants are extracted from the TAS shown in Fig. 4 (see Table 2). The first, τ1 = 22.4 ± 0.9 ps, is associated with a decrease in signal of both the excited state absorption and the stimulated emission features as EADS1 evolves into EADS2, as shown in Fig. 4(f); there also seems to be some spectral shifts taking place alongside this signal decay but the overlapping of the excited state absorption and stimulated emission features may artificially create these apparent blue/red shifts, and as such we will not be drawing any conclusions from them. Nevertheless, this initial step is likely associated with vibrational cooling on the S1 state, whereby significant geometry and solvent rearrangements take place.37 The fact that this initial vibrational cooling is visible in EtOH and not in ACN, along with the relatively long time constant associated with it in EtOH (τ1 = 22.4 ± 0.9 ps), suggests that the S1 energy minimum is further away from the Franck–Condon region in EtOH than ACN, therefore requiring a more significant geometry rearrangement. This hypothesis is also confirmed by the emission spectra in Fig. 2, where it is clear that the Stokes shift for m-MA is largest in EtOH (when compared to CHX and ACN).
Finally, after the vibrational cooling taking place within τ1, the overlapped excited state absorption and stimulated emission features present in the TAS of m-MA in EtOH persist for τ2 > 3 ns, as was observed in ACN. This is once again taken as an indication of a long-lived S1 state from which relaxation takes place predominantly via fluorescence, which is confirmed by the long fluorescence lifetime, τFl = 14.00 ± 0.03 ns, and high fluorescence quantum yield, ΦF = 0.64 ± 0.02, which we measured for m-MA in EtOH (see Table 2 and ESI†). While the quantum yield of fluorescence of m-MA is markedly higher in polar solvents (ACN and EtOH c.f. CHX), it is unexpectedly lower in EtOH when compared with ACN, which could be indicative of the effect of hydrogen bonding overcoming polarity effects. The lower fluorescence quantum yield of m-MA in EtOH may also be due to the S1 energy minima in this solvent being better coupled with the triplet manifold, facilitating ISC at the expense of fluorescence. However, while computationally we have determined the existence of energetically accessible triplet states (see Table 1), our experiments do not provide direct evidence of their population. Moreover, as previously discussed for CHX and ACN, it is also not possible to discard a minor contribution from IC to the excited state relaxation of m-MA in EtOH.
In summary, we hypothesise that the ultrafast photodynamics of m-MA in solution are determined by the solvent-dependent energy and landscape of its S1 state, which we suggest has significant CT character. We further hypothesise that the energy minimum of this S1 CT state is located further from the Franck–Condon region with increasing solvent polarity, resulting in increased geometry rearrangement and thus leading to the significant Stokes shifts observed (see Fig. 2). This S1 CT energy minimum is likely to be stabilized by polar solvents, leading to an increasingly deeper energy minima where excited state population can get trapped, which would also account for the experimentally observed longer fluorescence lifetimes and larger quantum yields in polar solvents (ACN and EtOH vs CHX). The non-unity quantum yields of fluorescence for m-MA in solution, particularly in CHX, imply that either ISC and subsequent phosphorescence and/or IC must contribute to the relaxation of m-MA to some extent, even though we have gathered no direct evidence of either. Nevertheless, we conclude that polar solvents enhance the trapping of excited state population in the long-lived S1 state, therefore negatively affecting the suitability of m-MA for use in sunscreens.
ii. Photodynamics of p-MA
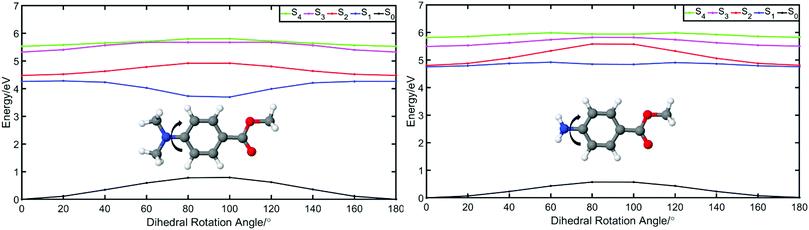
We start this discussion by first analysing the steady-state measurements obtained for p-MA, a close analogue of other aminobenzoates which are known to undergo twisted intramolecular charge transfer (TICT) upon photoexcitation.38 Dual fluorescence is characteristic of the donor–acceptor TICT systems whose excited states have a double energy well, with minima corresponding to the vertical excitation and the twisted molecular configurations. The double fluorescence observed for TICT systems, in particular the intensity ratio between the two emission peaks, has been shown to be both temperature and solvent polarity dependent.38,39 However, as shown in Fig. 5, the emission spectra of p-MA (at room temperature) are single peaked regardless of solvent polarity, in contrast with what is observed when the NH2 group is replaced by a N(CH3)2 group, as reported and reviewed by Lippert et al.38 While the lack of double fluorescence in p-MA had already been reported by Aleksiejew et al.,40 the reasoning for this marked difference remained elusive.In order to elucidate the reasons for a lack of double fluorescence in p-MA when compared to its methylated amine form, we have produced PECs along the rotation of both the NH2 and the N(CH3)2 groups with respect to the benzene ring, as shown in Fig. 6. This rotational motion would correspond to the ‘twist’ undergone by TICT systems. It is clear that the S1 state of the methylated p-MA has a marked energy minimum at the point in N(CH3)2 rotation where the methyl units are positioned on the plane perpendicular to that of the ring (90° dihedral angle). On the S2 state, on the other hand, there is a barrier along the TICT coordinate which traps excited state population in the locally excited minimum, from which fluorescence can also take place.38 The relative positions of the S1 and S2 states and barriers is affected by solvent polarity and ultimately defines the observed fluorescence spectra, including the double fluorescence observed by Lippert et al.38
When the equivalent rotation is evaluated for the NH2 group in p-MA, no TICT energy minimum is evident: the S1 excited state is virtually isoenergetic across the rotation coordinate (from 0° to 180°) and hence there is no driving force for a ‘twist’ to take place as it would for a TICT system. The lack of pronounced Stokes shifts in p-MA, regardless of solvent polarity as shown in Fig. 5, is also indicative of no large geometry changes taking place in the excited state. Given the small Stokes shifts observed for p-MA in any of the three solvents studied (see Table 2 for Stokes shift values), it is plausible to assume that the implicit ethanol PECs in Fig. 6 would be unaffected by solvent. Finally, it is worth noting that the lack of double fluorescence observed for p-MA is also consistent with the behaviour of its acid form, para-aminobenzoic acid (PABA), which was one of the earliest patented sunscreens and was very commonly used prior to its prohibition in cosmetic use in the European Union.41,42 Similar to what we report here for p-MA, PABA was also found to have single peak fluorescence, revealing a lack of photoexcited TICT.41
Bearing in mind the above observations, we now move to present and discuss the TAS obtained for p-MA in the different solvents studied, shown in Fig. 7. We consider first the excited states accessed upon photoexcitation of p-MA at its absorption maxima in each solvent. The first and second excited electronic states of p-MA (S1 and S2, respectively) are nearly isoenergetic in CHX, with an energy difference between them of just 80 cm−1, as revealed by our vertical excitation energy calculations (Table 1). The close energies of these S1 and S2 states are also evidenced by the absorption spectrum of p-MA in CHX (shown in Fig. 5), which shows a main peak centred at 271 nm (S2), with a discernible shoulder at 281 nm (S1). These observations are in line with those reported by Aleksiejew et al.40 Despite the larger energy differences between the S1 and S2 states of p-MA in ACN and EtOH (404 cm−1 and 888 cm−1, respectively), the bandwidth of ∼500 cm−1 of the laser pulses used in the present TEAS experiments is likely to result in simultaneous photoexcitation of both the S1 and S2 states in p-MA, albeit to a lesser extent in EtOH. In addition, in CHX the oscillator strength of the S2 state of p-MA has been calculated to be larger than that of the S1, as shown in Table 1. In ACN and EtOH, the calculated oscillator strength of the S2 state is significantly smaller than that of the respective S1 states (see Table 1). Neverthless, given the small S1–S2 energy gaps determined by our calculations for p-MA, the discussion hereon assumes that both the S1 and S2 states of p-MA can be populated, to some extent, upon photoexcitation at λpu = 271 nm, 285 nm and 294 nm in CHX, ACN, and EtOH, respectively.
Despite significant differences in the time constants obtained from the TAS for p-MA shown (see Table 2), the observed spectral features can be explained by the same combination of photophysical processes in all three solvents. When photoexciting p-MA in either EtOH or ACN at their respective absorption maxima (λpu = 294 nm and 285 nm, respectively), a strong stimulated emission feature is observed at approximately 340 nm. This stimulated emission feature sensibly matches with the fluorescence of p-MA reported in Fig. 5; its absence in the TAS for CHX is likely due to the emission wavelength (∼310 nm according to the spectra in Fig. 5) being outside of our TEAS probe window (320–720 nm) in this case. However, given the proximity of the S1 and S2 states of p-MA in all three solvents, as just discussed, we cannot discard the possibility that this stimulated emission feature originates from the S2 state, rather than the S1, which could be possible despite Kasha's rule and despite the low oscillator strength of the S2 → S0 transition (see Table 1) due to the fact that stimulated emission is a phenomenon facilitated by laser conditions. Furthermore, in both ACN and CHX, a broad excited state absorption feature spanning 400–700 nm is also present, while in EtOH this feature is much less obvious (albeit still present). Given that, in EtOH, photoexcitation of p-MA is likely to populate mainly the S1 state (see above), we suggest that the broad feature covering the red-edge of the probe window corresponds to excited state absorption from the S2 state of p-MA (most obvious in CHX and ACN, where population of the S2 state is more likely).
In all solvents, the evolution of EADS1 into EADS2 consists mainly of changes in signal intensity, with no large spectral shifts. This behaviour is indicative of mild geometry relaxation, likely taking place alongside solvent rearrangement. In particular, the stimulated emission features in the polar solvents become more intense within τ1, indicating excited state population migration towards an energy minimum from which fluorescence is more efficient. There is no evidence of IC between two states, nor of any drastic geometry change during τ1 (on either the S1 or S2 states); in EtOH, the evolution from EADS1 to EADS2 does evidence a slight red shift of the stimulated emission feature (see Fig. 4(f)), but this is likely associated with a geometry relaxation that leads to more significant vibrational cooling within τ1 in this case. This combination of processes, i.e. vibrational cooling via mild geometry relaxation and solvent rearrangement, is therefore suggested to take place within τ1 = 3.84 ± 0.05 ps in CHX, τ1 = 1.35 ± 0.02 ps in ACN, and τ1 = 12.8 ± 0.1 ps in EtOH.
It is worth noting here the significant differences in τ1 across solvents, which do not follow the polarity trend. It is plausible that the different contributions from the S2 state to this initial vibrational cooling step (which is minimal in EtOH) may introduce these differences and thus contribute to the lack of a trend along increasing solvent polarity. Nevertheless, and in particular for the case of p-MA in EtOH, for which τ1 is significantly longer, the variations in the time over which vibrational cooling takes place are likely explained by different levels of solvent interactions. The temperature-dependent UV/Vis spectra of p-MA presented in the ESI† (see S1) reveal a blue shift in absorption with increasing temperature which is more pronounced in the polar solvents. This effect has been previously reported to be related to hydrogen bonding:43 while polar solvents stabilize the excited state, the increasing temperature disturbs hydrogen bonds and the solvent stabilizing effect is increasingly lost. As a result, the energy of the excited state increases with increasing temperature and a blue shift is observed in UV/Vis absorption, as we have observed for p-MA (see ESI†). The different strengths of hydrogen bonding between p-MA and each solvent may therefore afford varying flexibility to the solvent cage encompassing each p-MA molecule, thus justifying different timescales of vibrational cooling. Specifically, we suggest that a stronger solvent interaction between p-MA and EtOH would impede the geometry relaxation and solvent rearrangement motions, leading to the longer τ1 observed (see Table 2).
We then assign τ2 in all solvents to migration of excited state population from S2 to S1, but this conclusion follows a different rationale in different solvents. In the case of p-MA in CHX, as EADS2 evolves into EADS3 (see Fig. 7(d)), the broad S2 excited state absorption (400–700 nm) decays significantly, while the S1 excited state absorption (∼390 nm), remains almost unchanged beyond the temporal window of these experiments, Δt = 3 ns. As such, it is plausible to suggest that a S2 → S1 transition takes place within τ2 = 460 ± 10 ps; we take confidence in discarding the possibility that τ2 would correspond to S1 decay due to our TCSPC experiments, which have revealed a fluorescence lifetime of τFl = 1.949 ± 0.003 ns (for photoexcitation at 279 nm and monitoring the emission at 340 nm, see ESI†). A time constant corresponding to this fluorescence lifetime is likely not captured in the TAS for p-MA in CHX because the stimulated emission feature would be outside of the probe window of the TEAS experiments. Finally, the third time constant extracted for these TAS, τ3 > 3 ns, reveals that some excited state population remains trapped beyond the temporal window of the presented TEAS experiments (Δt = 3 ns), mostly on the S1 state.
With respect to the red edge of the probe window of these experiments, the observation in polar solvents is similar to that just described for CHX. The broad excited state absorption between 400–700 nm decays significantly as EADS2 evolves into EADS3, particularly for p-MA in ACN (see Fig. 7(e)). In addition, the stimulated emission feature seen in the data for both ACN and EtOH (not present in CHX), also disappears within τ2. We hypothesize that the stimulated emission feature present in the TAS for p-MA in ACN and EtOH originates from the S2 state and that its decay, along with the decay of the broad 400–700 nm ESA, both correspond to an S2 → S1 transition (as was the case in CHX), taking place within τ2 = 526 ± 6 ps in ACN and within τ2 = 135 ± 1 ps in EtOH (see Table 2). The significantly shorter τ2 extracted for p-MA in EtOH, when compared to ACN and CHX, suggests a faster S2 → S1 transition in this case. The S2/S1 internal conversion may be faster in EtOH due to the larger energy difference between the two states: this energy gap may result not only in less population of the S2 state but could also lead to a more energetically favourable S2/S1 CI which enhances the driving force for motion from the S2 state towards the S2/S1 CI. As was discussed for CHX, we take confidence in assuming τ2 does not correspond to S1 decay because our TCSPC experiments have revealed fluorescence lifetimes (for photoexcitation at 279 nm and monitoring the emission at 340 nm, see ESI†) of τFl = 1.029 ± 0.002 ns in ACN and τFl = 390 ± 1 ps in EtOH, which do not match the respective τ2 values extracted from the TAS.
Finally, EADS3 for p-MA in both ACN and EtOH consist of a final excited state absorption feature which we assign to excited state population trapped in the S1 state, which persists for τ3 > 3 ns in both solvents. The double-peaked appearance of this excited state absorption in EtOH suggests it may still be overlapped with some residual stimulated emission intensity, as previously discussed for m-MA. Apart from fluorescence taking place within the aforementioned lifetimes, the excited state population that remains trapped in the S1 state beyond the temporal window of these TEAS experiments (Δt = 3 ns) would necessarily decay via alternative relaxation pathways.
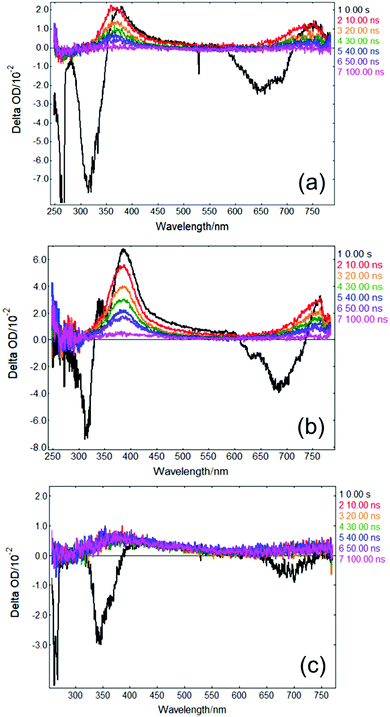
In order to gather further insight into the fate of excited state population of photoexcited solvated p-MA beyond 3 ns, we obtained ‘long-time’ transient absorption spectra (LT-TAS), with a temporal window of 0–100 ns, which can be seen in Fig. 8. The LT-TAS obtained for p-MA in all solvents reveal an excited state absorption feature centred at approximately 400 nm, and another expanding between ∼650–750 nm. While the excited state absorption feature at 400 nm in the LT-TAS is fortuitously close to the one assigned to the S1 state in the ultrafast TAS (see Fig. 7), we argue here that these are not the same feature, i.e. what is observed in the LT-TAS at 400 nm does not originate from the S1 state as previously assigned in the ultrafast TAS, but instead corresponds to an excited state absorption from a triplet state. Despite their similarities, close inspection of the LT-TAS (see Fig. 8) reveals that the spectral shape of the 400 nm excited state absorption feature is not the same as the one at the same wavelength in the TAS, since the LT-TAS feature has a broader wing extending into the red edge of the probe window. In addition, both excited state absorption features in the LT-TAS (at 400 nm and between ∼650–750 nm) seem to decay concurrently, which is at odds with a scenario where excited state population from an S1 state migrates onto a triplet state; in this case, one could expect one of the features decaying as the other grows, or each feature decaying at different rates. Since neither scenario matches the experimental observation, we suggest that within the time window between 3–10 ns, to which the present experiments are blind, ISC takes place, populating at least two different triplet states: one which is nearly isoenergetic with the S1 state of p-MA and happens to have a similar excited state absorption cross-section, and a second one which shows in the LT-TAS at ∼650–750 nm. Each of these triplet states can result from either direct population from the singlet manifold or, alternatively, they can be the result of IC within the triplet manifold also taking place within the 3–10 ns time window which cannot be monitored with the present experiments.
As a caveat, we note here that it is also possible that τ2 in all solvents could entail ISC directly from S2 and S1 onto nearby triplet states, with the feature visible in EADS3 at ∼390 nm corresponding already to a triplet state which then persists into the timescales of the LT-TAS; the second triplet excited state absorption feature between ∼650–750 nm would then result from IC within the triplet manifold. However, this hypothesis is relatively less likely given that such an efficient rate of ISC would be at odds with the fluorescence lifetimes we measured for p-MA in all three solvents studied (see earlier discussion and ESI†), all of which are significantly longer than τ2.
The combination of all spectroscopic data collected for p-MA reveals an excited state behaviour for which the longest fluorescence lifetime is observed in a different solvent to the highest fluorescence quantum yield (CHX vs ACN, respectively). While the fluorescence lifetime of p-MA in different solvents follows a polarity trend (it increases with decreasing polarity, following the order EtOH < ACN < CHX) the same cannot be said for the fluorescence quantum yield, which increases in the order CHX < EtOH < ACN. Moreover, if we assume the strength of the LT-TAS features to be correlated to the extent of triplet state population (rather than to a weak probe transition), it can also be said that the efficiency of ISC is different in the different solvents, being notably less efficient in EtOH (see Fig. 8). This behaviour points to a complex combination of relaxation pathways in p-MA which are affected in different ways by the solvent environment; particularly, it points to a scenario where alternative relaxation pathways compete with fluorescence, acting as efficient sinks for excited state population, but of which we have only indirect evidence. In summary, we find that excited state relaxation of p-MA in either CHX, ACN or EtOH proceeds via radiative pathways, with the relative contributions of each photophysical process being significantly affected by solvent polarity. We further suggest that the hydrogen bonding character of the solvent environment plays a particularly important role in the photodynamics of p-MA, potentially determining the activation/deactivation of its non-radiative decay pathways.
It is interesting to note that solvent environment has a critical effect on the photodynamics observed for both m-MA and p-MA, as summarized in Fig. 9. This is in stark contrast with o-MA, for which the photodynamics in both the gas-phase and in either polar or non-polar solvent were previously found to be virtually unaltered,14 most likely due to the stabilizing effect of the intramolecular hydrogen bond. The difference in the extent of solvent effects on the photodynamics of these systems is particularly interesting given that the S1 states of both o-MA and m-MA have some CT character (see ref. 14 and discussion above), but only the S1 CT state of m-MA seems to be affected by solvent environment. In addition, while a CT character state was also previously suggested to account for the photodynamics of p-MA in the gas-phase,15 in this work we find no compelling evidence for the existence of such a state in solution. Substituent position is therefore found to significantly alter the photodynamics of these anthranilate derivatives, and also to impact their sensitivity to solvent environment.
In a sunscreen context, the work presented here reveals that photoexcitation of both m-MA and p-MA populates long-lived excited states upon photoexcitation, similar to what was observed in o-MA,14 and as such these are not ideal sunscreen candidates. However, while it can be said that radiative decay pathways play a significant role in the photodynamics of o-MA, m-MA, and p-MA, they each show a balance between radiative and non-radiative relaxation pathways upon which solvent environment has distinct effects. As such, a finer understanding of the photodynamics of m- and p-MA in solution is crucial not only for the understanding of their intramolecular dynamics, but importantly for a more detailed understanding of solute–solvent interactions more generally. Unfortunately, we find that gathering such detailed mechanistical insight for these systems is hindered by their complexity, which has revealed a challenge for the computational methods at our disposal. The work presented here may therefore serve as a case study of two molecules for which specific solvent interactions critically alter their photodynamics, supporting the case for the development of improved explicit solvent computational methods.
Conclusions
The present work explores the photodynamics of two aminobenzoate derivatives, m- and p-MA, in order to evaluate the effects of substituent position and solvent environment on their photodynamic behaviour. We find that m-MA behaves similarly to the previously studied methyl anthranilate, presenting evidence of excited state relaxation via radiative decay pathways. We find experimental evidence to suggest the S1 state of m-MA has charge-transfer character that is sensitive to solvent environment, presumably leading to a deep S1 energy minimum where excited state population can become trapped. The photodynamics of p-MA were found to be complex and also sensitive to solvent environment, in particular to the extent of hydrogen bonding, with fluorescence being significantly quenched in EtOH. We find, therefore, that despite the loss of the intramolecular hydrogen bond present in o-MA,14 the photodynamics of both m- and p-MA remain long-lived, and their excited state relaxations retain significant contributions from radiative decay pathways, a non-ideal behaviour for sunscreen UV filters.Finally, we note that the computational methods at our disposal for this study have revealed insufficient to appropriately model the experimental observations here reported for both m- and p-MA. The experimental data here reported may serve as a benchmark in future development of explicit solvent computational models.
Author contributions
N. d. N. R. was responsible for conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, validation, visualization, and writing (both original draft and review & editing). J. M. W. was responsible for formal analysis, investigation, validation and writing (review & editing). K. M. K. was responsible for formal analysis, investigation and writing (review & editing). M. A. T.-S. was responsible for formal analysis and investigation. M. A. P. T. was responsible for conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, and writing (review & editing). N. D. M. H. was responsible for funding acquisition, resources, software, supervision and writing (review & editing). V. G. S. was responsible for funding acquisition, project administration, resources, supervision and writing (review & editing).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Michael Staniforth and Dr Neil Cole-Filipiak for fruitful discussion throughout the preparation of this manuscript. The authors would also like to thank the Warwick Centre for Ultrafast Spectroscopy (WCUS; http://go.warwick.ac.uk/wcus) for use of the Cary 60 UV/Vis spectrophotometer and Horiba Scientific Fluorolog®-3, and Prof. Sebastien Perrier for use of the temperature-controlled Agilent Cary 60 UV/Vis spectrophotometer. N. d. N. R. thanks the University of Warwick's Institute of Advanced Study and Institute for Advanced Teaching and Learning for a joint Early Career Fellowship, and the support and funding received from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 844177 – SUNNRL. J. M. W. thanks the FETOpen grant BoostCrop (Grant agreement 828753) for postdoctoral funding. K. M. K. thanks the Engineering and Physical Sciences Research Council (EPSRC) for doctoral funding. M. A. P. T. thanks the Engineering and Physical Sciences Research Council (EPSRC) for a PhD studentship through the EPSRC Centre for Doctoral Training in Molecular Analytical Science, grant number EP/L015307/1. Computing facilities were provided by the Scientific Computing Research Technology Platform of the University of Warwick. We acknowledge the use of Athena at HPC Midlands+, which was funded by the EPSRC by Grant EP/P020232/1, in this research, as part of the HPC Midlands+ consortium. V. G. S. thanks the EPSRC for equipment grants (EP/J007153 and EP/N010825) and the Royal Society and Leverhulme Trust for a Royal Society Leverhulme Trust Senior Research Fellowship.References
- ISO 21348, 2007, 20.
- B. L. Diffey, Solar ultraviolet radiation effects on biological systems, Phys. Med. Biol., 1991, 36, 299–328 CrossRef PubMed
.
- M. F. Holick, Sunlight, UV-radiation, vitamin D and skin cancer: How much sunlight do we need?, Adv. Exp. Med. Biol., 2008, 624, 1–15 CrossRef PubMed
.
- J. A. Lo and D. E. Fisher, The melanoma revolution: From UV carcinogenesis to a new era in therapeutics, Science, 2014, 346, 945–949 CrossRef PubMed
.
- R. P. Sinha and D.-P. Häder, UV-induced DNA damage and repair: a review, Photochem. Photobiol. Sci., 2002, 1, 225–236 CrossRef PubMed
.
- F. R. de Gruijl, Methods Enzymol., 2000, 359–366 Search PubMed
.
- C. Battie, S. Jitsukawa, F. Bernerd, S. Del Bino, C. Marionnet and M. Verschoore, New insights in photoaging, UVA induced damage and skin types, Exp. Dermatol., 2014, 23, 7–12 CrossRef PubMed
.
- M. Brenner and V. J. Hearing, The Protective Role of Melanin Against UV Damage in Human Skin, Photochem. Photobiol., 2008, 84, 539–549 CrossRef PubMed
.
- B. A. Gilchrest and M. S. Eller, DNA Photodamage Stimulates Melanogenesis and Other Photoprotective Responses, J. Investig. Dermatology Symp. Proc., 1999, 4, 35–40 CrossRef PubMed
.
- N. D. N. Rodrigues, M. Staniforth and V. G. Stavros, Photophysics of sunscreen molecules in the gas phase: a stepwise approach towards understanding and developing next-generation sunscreens, Proc. R. Soc. A, 2016, 472, 20160677 CrossRef PubMed
.
- N. d. N. Rodrigues and V. G. Stavros, From Fundamental Science to Product: A Bottom-up Approach to Sunscreen Development, Sci. Prog., 2018, 101, 8–31 CrossRef CAS PubMed
.
- L. A. Baker and V. G. Stavros, Observing and Understanding the Ultrafast Photochemistry in Small Molecules: Applications to Sunscreens, Sci. Prog., 2016, 99, 282–311 CrossRef CAS PubMed
.
- D. R. Sambandan and D. Ratner, Sunscreens: An overview and update, J. Am. Acad. Dermatol., 2011, 64, 748–758 CrossRef CAS PubMed
.
- N. D. N. Rodrigues, N. C. Cole-Filipiak, M. D. Horbury, M. Staniforth, T. N. V. Karsili, Y. Peperstraete and V. G. Stavros, Photophysics of the sunscreen ingredient menthyl anthranilate and its precursor methyl anthranilate: A bottom-up approach to photoprotection, J. Photochem. Photobiol., A, 2018, 353, 376–384 CrossRef CAS
.
- N. d. N. Rodrigues, N. C. Cole-Filipiak, M. A. P. Turner, K. Krokidi, G. L. Thornton, G. W. Richings, N. D. M. Hine and V. G. Stavros, Substituent position effects on sunscreen photodynamics: A closer look at methyl anthranilate, Chem. Phys., 2018, 515, 596–602 CrossRef
.
- P. J. Osgood, S. H. Moss and D. G. Davies, The Sensitization of Near-Ultraviolet Radiation Killing of Mammalian Cells by the Sunscreen Agent Para-aminobenzoic Acid, J. Invest. Dermatol., 1982, 79, 354–357 CrossRef PubMed
.
- T. Wong and D. Orton, Sunscreen allergy and its investigation, Clin. Dermatol., 2011, 29, 306–310 CrossRef PubMed
.
- S. E. Greenough, M. D. Horbury, J. O. F. Thompson, G. M. Roberts, T. N. V. Karsili, B. Marchetti, D. Townsend and V. G. Stavros, Solvent induced conformer specific photochemistry of guaiacol, Phys. Chem. Chem. Phys., 2014, 16, 16187 RSC
.
- S. E. Greenough, G. M. Roberts, N. A. Smith, M. D. Horbury, R. G. McKinlay, J. M. Żurek, M. J. Paterson, P. J. Sadler and V. G. Stavros, Ultrafast photo-induced ligand solvolysis of cis-[Ru(bipyridine) 2 (nicotinamide)2]2+: experimental and theoretical insight into its photoactivation mechanism, Phys. Chem. Chem. Phys., 2014, 16, 19141–19155 RSC
.
- J. M. Woolley, M. Staniforth, M. D. Horbury, G. W. Richings, M. Wills and V. G. Stavros, Unravelling the Photoprotection Properties of Mycosporine Amino Acid Motifs, J. Phys. Chem. Lett., 2018, 9, 3043–3048 CrossRef PubMed
.
- U. Megerle, I. Pugliesi, C. Schriever, C. F. Sailer and E. Riedle, Sub-50 fs broadband absorption spectroscopy with tunable excitation: putting the analysis of ultrafast molecular dynamics on solid ground, Appl. Phys. B: Lasers Opt., 2009, 96, 215–231 CrossRef
.
- I. Walmsley, L. Waxer and C. Dorrer, The role of dispersion in ultrafast optics, Rev. Sci. Instrum., 2001, 72, 1–29 CrossRef
.
- M. P. Grubb, A. J. Orr-Ewing and M. N. R. Ashfold, KOALA: A program for the processing and decomposition of transient spectra, Rev. Sci. Instrum., 2014, 85, 064104 CrossRef PubMed
.
- J. J. Snellenburg, S. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkum, Glotaran: A Java -Based Graphical User Interface for the R Package TIMP, J. Stat. Softw., 2012, 49(3), 1–22 Search PubMed
.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef
.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef
.
- D. M. York and M. Karplus, A Smooth Solvation Potential Based on the Conductor-Like Screening Model, J. Phys. Chem. A, 1999, 103, 11060–11079 CrossRef
.
- A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC
.
- P. Winget, D. M. Dolney, D. J. Giesen, C. J. Cramer and D. G. Truhlar, Minnesota solvent descriptor database for DFT calculation, Minnesota Solvent Descriptor Database, 1999, Retrieved from http://amsol.chem.umn.edu/solvation/mnsddb.pdf, https://comp.chem.umn.edu/solvation/mnsddb.pdf Search PubMed.
-
N. J. Turro, Molecular Photochemistry, University Science Press, Menlo Park, CA, 1991 Search PubMed
.
-
J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer US, Boston, MA, 2nd edn, 1999 Search PubMed
.
- G. Ramakrishna and T. Goodson, Excited-State Deactivation of Branched Two-Photon Absorbing Chromophores: A Femtosecond Transient Absorption Investigation, J. Phys. Chem. A, 2007, 111, 993–1000 CrossRef PubMed
.
- H. Song, K. Wang, Z. Kuang, Y. S. Zhao, Q. Guo and A. Xia, Solvent modulated excited state processes of push–pull molecule with hybridized local excitation and intramolecular charge transfer character, Phys. Chem. Chem. Phys., 2019, 21, 3894–3902 RSC
.
-
J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer US, Boston, MA, 2006, pp. 205–235 Search PubMed
.
- N. D. M. Hine, P. D. Haynes, A. A. Mostofi, C.-K. Skylaris and M. C. Payne, Linear-scaling density-functional theory with tens of thousands of atoms: Expanding the scope and scale of calculations with ONETEP, Comput. Phys. Commun., 2009, 180, 1041–1053 CrossRef CAS
.
- S. Yabumoto, S. Shigeto, Y.-P. Lee and H. Hamaguchi, Ordering, Interaction, and Reactivity of the Low-Lying nπ* and ππ* Excited Triplet States of Acetophenone Derivatives, Angew. Chem., Int. Ed., 2010, 49, 9201–9205 CrossRef CAS PubMed
.
- E. T. J. Nibbering, H. Fidder and E. Pines, ULTRAFAST CHEMISTRY: Using Time-Resolved Vibrational Spectroscopy for Interrogation of Structural Dynamics, Annu. Rev. Phys. Chem., 2005, 56, 337–367 CrossRef CAS PubMed
.
-
E. Lippert, W. Rettig, V. Bonačić-Koutecký, F. Heisel and J. A. Miehé, in Advances in Chemical Physics, ed. I. P. S. A. Rice, John Wiley & Sons, Inc, 1987, pp. 1–174 Search PubMed
.
- J. Catalán, On the dual emission of p-dimethylaminobenzonitrile and its photophysical implications, Phys. Chem. Chem. Phys., 2013, 15, 8811 RSC
.
- M. Aleksiejew and J. R. Heldt, Experimental and theoretical studies of electronic
energy states of methyl benzoate derivatives, J. Lumin., 2007, 126, 665–676 CrossRef CAS
.
- C. T.-L. Chan, C. Ma, R. C.-T. Chan, H.-M. Ou, H.-X. Xie, A. K.-W. Wong, M.-L. Wang and W.-M. Kwok, A long lasting sunscreen controversy of 4-aminobenzoic acid and 4-dimethylaminobenzaldehyde derivatives resolved by ultrafast spectroscopy combined with density functional theoretical study, Phys. Chem. Chem. Phys., 2020, 22, 8006–8020 RSC
.
- ECHA: European Chemicals Agency, Cosmetic Products Regulation, Annex II – Prohibited Substances, https://echa.europa.eu/cosmetics-prohibited-substances, (accessed 6 July 2021).
- M. Ito, The effect of temperature on ultraviolet absorption spectra and its relation to hydrogen bonding, J. Mol. Spectrosc., 1960, 4, 106–124 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03759e |
| This journal is © the Owner Societies 2021 |