Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Caveat when using ADC(2) for studying the photochemistry of carbonyl-containing molecules†
Emanuele
Marsili
 ,
Antonio
Prlj
,
Antonio
Prlj
 * and
Basile F. E.
Curchod
* and
Basile F. E.
Curchod
 *
*
Department of Chemistry, Durham University, Durham DH1 3LE, UK. E-mail: antonio.prlj@durham.ac.uk; basile.f.curchod@durham.ac.uk
First published on 4th June 2021
Abstract
Several electronic-structure methods are available to study the photochemistry and photophysics of organic molecules. Among them, ADC(2) stands as a sweet spot between computational efficiency and accuracy. As a result, ADC(2) has recently seen its number of applications booming, in particular to unravel the deactivation pathways and photodynamics of organic molecules. Despite this growing success, we demonstrate here that care has to be taken when studying the nonradiative pathways of carbonyl-containing molecules, as ADC(2) appears to suffer from a systematic flaw.
The theoretical description of photophysics and photochemistry of molecules and materials has matured enough that nowadays most experimental observations can be successfully interpreted and sometimes predicted fully in silico. Ab initio calculations have contributed substantially to understanding the molecular mechanisms behind the human and animal vision,1 optimizing solar cells2 and light-emitting devices,3 designing molecular motors and rotors,4 dyes5 or photochemical switches,6 understanding complex photobiological,7 atmospheric8 or interstellar9 phenomena, etc. The processes underlying all these applications involve the interplay and interconversion between ground and excited electronic states.
Molecular electronic states are rigorously obtained as the solutions of the time-independent electronic Schrödinger equation. While an exact solution of this Schrödinger equation is an unattainable goal for nearly all molecular systems, a number of approximate electronic-structure methods has been developed and used to study realistic molecular systems. The ground state of a standard closed-shell organic molecule is typically well described by a single closed shell electronic configuration, using popular electronic-structure methods like Kohn-Sham density-functional theory (DFT) or Møller-Plesset perturbation theory up to second-order (MP2). In more challenging situations, one needs to resort to so-called multireference approaches, where the ground-state wavefunction is described by a linear combination of multiple electronic configurations with sizable weights. Along with the ground state, excited states can also be obtained with methods like extended multi-state complete active space second-order perturbation theory (XMS-CASPT2) and multi-reference configuration interaction singles and doubles (MR-CISD).10,11 Such multireference methods often require the careful selection of key orbitals forming an active space, and are truly applicable only to relatively small molecular systems due to their computational burden. However, they allow for an accurate description of conical intersections (CIs) and their branching space–key ingredients for the understanding of nonradiative processes.
Substantially cheaper than multireference methods, strategies based on a single reference or on DFT have gained a large popularity in the computations of excited states. Linear-response time-dependent density-functional theory (TDDFT), an extension of DFT to excited states, is perhaps the most popular method for excited states nowadays. TDDFT (and its Tamm-Dancoff approximation, TDA) has become a convenient tool to support, predict, or interpret the experimental data in molecular spectroscopy,12 and can be combined with excited-state molecular dynamics simulations.13 Over the years, different failures of standard TDDFT (and underlying DFT) approximations have been documented for certain types of excited states (e.g. charge-transfer states, doubly-excited states), meaning that the use of TDDFT requires careful benchmarks with respect to higher levels of theory.14 Importantly, gaining knowledge in the failures of TDDFT approximations has also contributed to a better and safe use of this efficient electronic-structure method.
A commonly employed single-reference method is the algebraic diagrammatic construction of second order, ADC(2), an extension of MP2 to excited states.15 ADC(2) is not as computationally affordable as TDDFT, but also not as computationally cumbersome as multireference approaches. It shares the black-box nature of TDDFT, which makes it an appealing approach for wide applications in spectroscopy and molecular dynamics. Just like in TDDFT, the accuracy of ADC(2) critically depends on the quality of the ground-state reference–situations where MP2 fails to describe the ground electronic state are detrimental for the description of the excited states. Nevertheless, ADC(2) appears to be a more reliable method than TDDFT, granting a balanced description of excited-state energies for standard organic molecules, with a relatively low mean error around 0.2 eV.15 While the development of ADC(2) method dates back to 1982,16 its wide applications to photochemistry and photophysics are not older than a decade. Among relevant studies, Tuna et al.17 showed that ADC(2) does not properly describe the topology of conical intersections between the ground (S0) and the first excited (S1) singlet state (while multireference methods do), yet it can still predict reasonable crossing energies and geometries. Plasser et al.18 investigated the application of different single-reference methods in excited-state molecular dynamics of adenine, placing ADC(2) as a serious competitor to the commonly-accepted TDDFT for nonadiabatic dynamics. Following these reports, an explosion of studies employing ADC(2) in excited-state dynamics appeared in the literature,19–33 also mapping the reaction paths between the Franck-Condon (FC) geometry and the electronic states crossings,28–45 and calculating absorption properties of functional molecules.46,47 The community has gained a large confidence with ADC(2), to the point where many studies employing it do not contain systematic comparisons with high-level multireference methods.19,24,26–29,38–42 This is understandable though considering that the latter studies involve middle-sized or bigger molecular systems. For these systems ADC(2) is an ace in the hole, appearing as an ideal compromise between accuracy and computational efficiency.
In this communication, we highlight what appears to be a systematic issue of ADC(2) in describing some electronic states of molecule bearing a carbonyl group, which concerns a large class of molecules like chromophores, nucleobases, or atmospheric volatile organic compounds. Such systems possess characteristic low-lying singlet excited state of n(O)π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) character (shortened by nπ* in the following), where n(O) is the lone pair orbital associated to the oxygen of the carbonyl group and π*(C
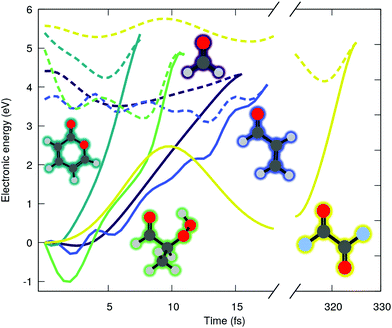
O) character (shortened by nπ* in the following), where n(O) is the lone pair orbital associated to the oxygen of the carbonyl group and π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) refers here to an unoccupied π-type orbital localized either fully on the carbonyl functional group or partially when delocalization is possible. We start our investigation by examining the ADC(2) excited-state dynamics of small molecules bearing carbonyl moiety. Fig. 1 shows the time evolution of the ground (solid lines) and excited (dashed lines) state electronic energies following the molecular dynamics initiated by a nπ* photoexcitation. The electronic states were computed with the spin-component-scaled (SCS) variant of MP2/ADC(2), which was recently shown to improve the potential energy surfaces,48 combined with a def2-SVP basis set (abbreviated SVP in the following, see ESI† for the full computational details and a comparison between SCS-ADC(2) and ADC(2)–in the following we will note SCS-MP2/ADC(2) to denote the combination of SCS-MP2 for S0 and SCS-ADC(2) for the excited states). Inspecting the time trace of the electronic energies for five different carbonyl-bearing molecules, namely formaldehyde, (anti-)acrolein, pyrone, 2-hydroperoxy-propanal (2-HPP), and oxalyl fluoride, reveals a common feature: all the systems appear to possess an easily accessible nonradiative decay channel via a S1/S0 crossing, achieved by an ultrafast elongation of the C
O) refers here to an unoccupied π-type orbital localized either fully on the carbonyl functional group or partially when delocalization is possible. We start our investigation by examining the ADC(2) excited-state dynamics of small molecules bearing carbonyl moiety. Fig. 1 shows the time evolution of the ground (solid lines) and excited (dashed lines) state electronic energies following the molecular dynamics initiated by a nπ* photoexcitation. The electronic states were computed with the spin-component-scaled (SCS) variant of MP2/ADC(2), which was recently shown to improve the potential energy surfaces,48 combined with a def2-SVP basis set (abbreviated SVP in the following, see ESI† for the full computational details and a comparison between SCS-ADC(2) and ADC(2)–in the following we will note SCS-MP2/ADC(2) to denote the combination of SCS-MP2 for S0 and SCS-ADC(2) for the excited states). Inspecting the time trace of the electronic energies for five different carbonyl-bearing molecules, namely formaldehyde, (anti-)acrolein, pyrone, 2-hydroperoxy-propanal (2-HPP), and oxalyl fluoride, reveals a common feature: all the systems appear to possess an easily accessible nonradiative decay channel via a S1/S0 crossing, achieved by an ultrafast elongation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Interestingly, a similar nonradiative pathway showed up in the excited-state dynamics of the nucleobase thymine, accounting for 61% of radiationless decay in gas phase,49 and 54% in water.26 The decay channel associated with C
O bond. Interestingly, a similar nonradiative pathway showed up in the excited-state dynamics of the nucleobase thymine, accounting for 61% of radiationless decay in gas phase,49 and 54% in water.26 The decay channel associated with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O elongation was also identified in a guanine derivative,32 though it was argued that other deactivation mechanisms would prevail. Interestingly, all these studies employed ADC(2) method. As such, a nonradiative decay channel mediated by the C
O elongation was also identified in a guanine derivative,32 though it was argued that other deactivation mechanisms would prevail. Interestingly, all these studies employed ADC(2) method. As such, a nonradiative decay channel mediated by the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O elongation appears to be a general and well-established feature in excited-state dynamics of carbonyl-containing molecules. Can it really be the case? In fact, more systematic studies of cytosine33,50 and guanine31 derivatives photophysics cast some shadow of doubt on these observations. In these studies, ADC(2) predictions were compared to the results from a high-level multireference method, finding some conspicuous discrepancies. What does that mean for the molecules shown in Fig. 1? We will show in the following that such an easily-accessible deactivation pathway is an artefact of the MP2/ADC(2) method that end users should be aware of.
O elongation appears to be a general and well-established feature in excited-state dynamics of carbonyl-containing molecules. Can it really be the case? In fact, more systematic studies of cytosine33,50 and guanine31 derivatives photophysics cast some shadow of doubt on these observations. In these studies, ADC(2) predictions were compared to the results from a high-level multireference method, finding some conspicuous discrepancies. What does that mean for the molecules shown in Fig. 1? We will show in the following that such an easily-accessible deactivation pathway is an artefact of the MP2/ADC(2) method that end users should be aware of.
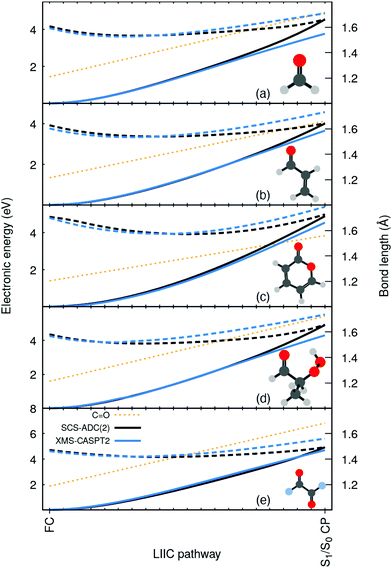
To highlight the artificial nature of these nonradiative pathways, we optimized the S0 minimum geometry–the Franck-Condon (FC) point–with SCS-MP2/SVP and the S1/S0 crossing point (S1/S0 CP) with SCS-MP2/ADC(2)/SVP. We then interpolated geometries in internal coordinates between these two critical points and computed electronic energies both with SCS-MP2/ADC(2) and XMS-CASPT2/SVP (see ESI† for additional details on these calculations, active space, SCS-ADC(2) vs. ADC(2), and influence of the basis set). Surprisingly, XMS-CASPT2 shows an entirely different behavior when the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is extended beyond 1.4 Å. The intersection observed between S0 and S1 (nπ*) at the SCS-MP2/ADC(2) level is not present at the XMS-CASPT2 for all molecules. Any attempt to locate the crossing at XMS-CASPT2 level did not lead to a structure resembling the S1/S0 CP of SCS-MP2/ADC(2). In other words, SCS-MP2/ADC(2) suggests the presence of an easily accessible S1/S0 CP, while XMS-CASPT2 strongly indicates that the crossing is not easily accessible–whether it is much higher in energy or does not exist at all. Importantly, such a discrepancy between the two methods is systematic for all five molecules. We also note that ADC(2) shows the same artificial crossings (see ESI†).
O bond is extended beyond 1.4 Å. The intersection observed between S0 and S1 (nπ*) at the SCS-MP2/ADC(2) level is not present at the XMS-CASPT2 for all molecules. Any attempt to locate the crossing at XMS-CASPT2 level did not lead to a structure resembling the S1/S0 CP of SCS-MP2/ADC(2). In other words, SCS-MP2/ADC(2) suggests the presence of an easily accessible S1/S0 CP, while XMS-CASPT2 strongly indicates that the crossing is not easily accessible–whether it is much higher in energy or does not exist at all. Importantly, such a discrepancy between the two methods is systematic for all five molecules. We also note that ADC(2) shows the same artificial crossings (see ESI†).
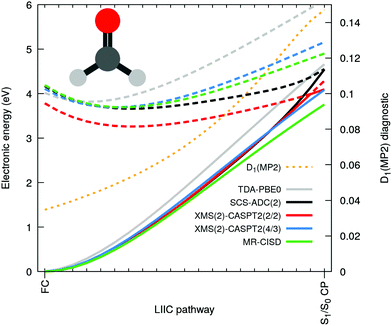
Let us now focus on the case of formaldehyde to gain deeper insights in this issue. Fig. 3 shows the same electronic-energy profiles as in Fig. 2 but now for five different methods: TDA-PBE0/SVP (grey), SCS-ADC(2)/SVP (black), XMS(2)-CASPT2(2/2)/SVP (red), XMS(2)-CASPT2(4/3)/SVP (blue) and MR-CISD(4/3)/SVP (green). For details about these methods see ESI.† The high-level methods XMS(2)-CASPT2(4/3) and MR-CISD both agree on the absence of an intersection at the SCS-MP2/ADC(2) S1/S0 CP geometry. The D1 diagnostic (dashed orange) measures the degree of multiconfigurational character for the MP2 ground state. The quick D1 surge beyond the recommended limit value of 0.0451 (and even the less conservative value of 0.1 proposed by others52) indicates that the S0 state acquires a multiconfigurational character along the pathway. In other words, the single-reference wavefunction that serves as reference for perturbation theory is no more adequate for large D1 values. Interestingly, the PBE0 ground state appears to have an incorrect shape in comparison to high-level methods, but as the S1 electronic energy is also raising steeply along the profile, the S1/S0 CP is (fortuitously) avoided. The artificial S1/S0 CP of SCS-MP2/ADC(2) can be explained by the combination of two recurring factors for all molecules bearing a carbonyl group: (i) the MP2 ground state is not adequate and overestimates the S0 energy when stretching the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and (ii) the curvature of the nπ* state along the CO stretching coordinate is too small. The poor description of S1 can be correlated with an increasing contribution of doubly-excited configurations along the interpolation pathway (see Fig. S2 in the ESI†). Such contributions cannot be optimally described by ADC(2) since the treatment of double excitations in ADC(2) is very limited.15 Finally, the point (ii) resonates with earlier findings that ADC(2) was inaccurate in describing the nπ* state of cytosine,48 (even if SCS-ADC(2) was shown to perform better), while it has been pointed out that ADC(2) performs less accurately when describing nπ* transition, yielding too low frequencies associated with the carbonyl stretching.53 Another study also showed that ADC(2) already overestimates the C
O bond and (ii) the curvature of the nπ* state along the CO stretching coordinate is too small. The poor description of S1 can be correlated with an increasing contribution of doubly-excited configurations along the interpolation pathway (see Fig. S2 in the ESI†). Such contributions cannot be optimally described by ADC(2) since the treatment of double excitations in ADC(2) is very limited.15 Finally, the point (ii) resonates with earlier findings that ADC(2) was inaccurate in describing the nπ* state of cytosine,48 (even if SCS-ADC(2) was shown to perform better), while it has been pointed out that ADC(2) performs less accurately when describing nπ* transition, yielding too low frequencies associated with the carbonyl stretching.53 Another study also showed that ADC(2) already overestimates the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond length of formaldehyde at its S1 minimum.54
O bond length of formaldehyde at its S1 minimum.54
Based on the considerations above, we could reproduce the S1/S0 CP using XMS-CASPT2 by employing a minimal active space constituted only by two electrons in n(O) and the π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (XMS(2)-CASPT2(2/2) in Fig. 3). Such a small active space does not include the π orbital, which is a key contributor to the multiconfigurational character of the S0 along the pathway, when the closed-shell configuration starts to strongly mix with a ππ* contribution (see Fig. S2 in the ESI†). As a result, XMS(2)-CASPT2(2/2) leads, as for MP2, to a poor description of the ground-state reference wavefunction on which perturbation theory is applied, ultimately leading to a failure of the method when reaching the S1/S0 CP region (in stark contrast with XMS(2)-CASPT2(4/3) and MR-CISD, both including the π orbital). Therefore, the failure of XMS-CASPT2 caused by the small active space appears to mimic that of SCS-ADC(2). The very same trends are systematically reproduced for the other four compounds, as depicted in Fig. S6 in the ESI.† Hence, our observations point towards (i) a too shallow S1(nπ*) along the elongation of the CO bond combined with (ii) a bad reference for MP2 destabilizing too rapidly the ground state to explain the fast and artificial decay observed in the excited-state dynamics. We note that the point (ii) resonates with earlier findings that ADC(2) tends to have energy gaps between S1 and S0 closing too rapidly even still far from the crossing region (e.g. ref. 55 and 56).
O) (XMS(2)-CASPT2(2/2) in Fig. 3). Such a small active space does not include the π orbital, which is a key contributor to the multiconfigurational character of the S0 along the pathway, when the closed-shell configuration starts to strongly mix with a ππ* contribution (see Fig. S2 in the ESI†). As a result, XMS(2)-CASPT2(2/2) leads, as for MP2, to a poor description of the ground-state reference wavefunction on which perturbation theory is applied, ultimately leading to a failure of the method when reaching the S1/S0 CP region (in stark contrast with XMS(2)-CASPT2(4/3) and MR-CISD, both including the π orbital). Therefore, the failure of XMS-CASPT2 caused by the small active space appears to mimic that of SCS-ADC(2). The very same trends are systematically reproduced for the other four compounds, as depicted in Fig. S6 in the ESI.† Hence, our observations point towards (i) a too shallow S1(nπ*) along the elongation of the CO bond combined with (ii) a bad reference for MP2 destabilizing too rapidly the ground state to explain the fast and artificial decay observed in the excited-state dynamics. We note that the point (ii) resonates with earlier findings that ADC(2) tends to have energy gaps between S1 and S0 closing too rapidly even still far from the crossing region (e.g. ref. 55 and 56).
We note that we also investigated the case of the aforementioned thymine nucleobase. Our rational explanation for the failure of both ADC(2) and XMS(2)-CASPT2(2/2) is clearly confirmed for this additional molecule: both ADC(2) and XMS(2)-CASPT2(2/2) predict an artificial S1/S0 crossing, which is verily avoided when using a suitably high level of theory (Fig. S7, ESI†).
In summary, the electronic-structure method ADC(2) is a rising star to study the photochemistry and photophysics of organic molecules, but its pitfalls still need to be fully uncovered. The unexpected failures of ADC(2) for carbonyl-containing compounds were discussed in several case studies but the systematic nature of these errors in the context of S1/S0 crossing points has not been widely recognized. The recurrence of artificial S1/S0 crossings upon C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O elongation closely resembles the predictions from multireference methods with an inadequate active space, which prevents the proper description of both ground and excited state, and leads to the unphysical nonradiative decay channels in molecular dynamics. Similar issues are expected for molecules bearing a C
O elongation closely resembles the predictions from multireference methods with an inadequate active space, which prevents the proper description of both ground and excited state, and leads to the unphysical nonradiative decay channels in molecular dynamics. Similar issues are expected for molecules bearing a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S group, based on the results presented in ref. 57. Considering the omnipresence of C
S group, based on the results presented in ref. 57. Considering the omnipresence of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functional group and the increasing interest in using ADC(2) to study photochemical deactivation pathways, our current findings should serve as a warning bell for future research in the field.
O functional group and the increasing interest in using ADC(2) to study photochemical deactivation pathways, our current findings should serve as a warning bell for future research in the field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant agreement No. 803718, project SINDAM). This article is based upon work from COST Action CA18212–Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology), and made use of the facilities of the Hamilton HPC Service of Durham University.Notes and references
- S. Gozem, H. L. Luk, I. Schapiro and M. Olivucci, Chem. Rev., 2017, 117, 13502–13565 CrossRef CAS PubMed.
- T. Le Bahers, T. Pauporté, P. P. Lainé, F. Labat, C. Adamo and I. Ciofini, J. Phys. Chem. Lett., 2013, 4, 1044–1050 CrossRef CAS PubMed.
- R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, et al. , Nat. Mater., 2016, 15, 1120–1127 CrossRef PubMed.
- J. Michl and E. C. H. Sykes, ACS Nano, 2009, 3, 1042–1048 CrossRef CAS PubMed.
- A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356 RSC.
- A. Fihey, A. Perrier, W. R. Browne and D. Jacquemin, Chem. Soc. Rev., 2015, 44, 3719–3759 RSC.
- M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458 CrossRef CAS PubMed.
- J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical kinetics and dynamics, Prentice Hall, Upper Saddle River, NJ, 1999 Search PubMed.
- R. C. Fortenberry and T. D. Crawford, Annual Reports in Computational Chemistry, Elsevier, 2011, vol. 7, pp. 195–214 Search PubMed.
- J. W. Park, R. Al-Saadon, M. K. MacLeod, T. Shiozaki and B. Vlaisavljevich, Chem. Rev., 2020, 120, 5878–5909 CrossRef CAS PubMed.
- H. Lischka, D. Nachtigallova, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361 CrossRef CAS PubMed.
- C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- B. F. E. Curchod, U. Rothlisberger and I. Tavernelli, ChemPhysChem, 2013, 14, 1314–1340 CrossRef CAS PubMed.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS.
- A. Dreuw and M. Wormit, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82–95 CAS.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395 CrossRef CAS.
- D. Tuna, D. Lefrancois, Ł. Wolański, S. Gozem, I. Schapiro, T. Andruniów, A. Dreuw and M. Olivucci, J. Chem. Theory Comput., 2015, 11, 5758–5781 CrossRef CAS PubMed.
- F. Plasser, R. Crespo-Otero, M. Pederzoli, J. Pittner, H. Lischka and M. Barbatti, J. Chem. Theory Comput., 2014, 10, 1395–1405 CrossRef CAS PubMed.
- M. A. Kochman, A. Tajti, C. A. Morrison and R. J. D. Miller, J. Chem. Theory Comput., 2015, 11, 1118–1128 CrossRef CAS PubMed.
- M. A. Kochman and B. Durbeej, J. Phys. Chem. A, 2019, 123, 6660–6673 CrossRef CAS PubMed.
- M. Sapunar, A. Ponzi, S. Chaiwongwattana, M. Mališ, A. Prlj, P. Decleva and N. Došlić, Phys. Chem. Chem. Phys., 2015, 17, 19012–19020 RSC.
- A. Prlj, B. F. E. Curchod and C. Corminboeuf, Phys. Chem. Chem. Phys., 2015, 17, 14719–14730 RSC.
- M. A. Kochman and B. Durbeej, J. Phys. Chem. A, 2020, 124, 2193–2206 CrossRef CAS PubMed.
- F. Siddique, M. Barbatti, Z. Cui, H. Lischka and A. J. A. Aquino, J. Phys. Chem. A, 2020, 124, 3347–3357 CrossRef CAS PubMed.
- M. Barbatti, J. Am. Chem. Soc., 2014, 136, 10246–10249 CrossRef CAS PubMed.
- H. Lischka, M. Barbatti, F. Siddique, A. Das and A. J. A. Aquino, Chem. Phys., 2018, 515, 472–479 CrossRef CAS.
- B. Milovanović, J. Novak, M. Etinski, W. Domcke and N. Došlić, Phys. Chem. Chem. Phys., 2021, 23, 2594–2604 RSC.
- A. Prlj, A. Fabrizio and C. Corminboeuf, Phys. Chem. Chem. Phys., 2016, 18, 32668–32672 RSC.
- J. Novak, A. Prlj, N. Basarić, C. Corminboeuf and N. Došlić, Chem. – Eur. J., 2017, 23, 8244–8251 CrossRef CAS PubMed.
- M. Dommett and R. Crespo-Otero, Phys. Chem. Chem. Phys., 2017, 19, 2409–2416 RSC.
- G. Gate, R. Szabla, M. R. Haggmark, J. Šponer, A. L. Sobolewski and M. S. de Vries, Phys. Chem. Chem. Phys., 2019, 21, 13474–13485 RSC.
- M. A. Kochman, M. Pola and R. J. D. Miller, J. Phys. Chem. A, 2016, 120, 6200–6215 CrossRef CAS PubMed.
- R. Szabla, R. W. Góra and J. Šponer, Phys. Chem. Chem. Phys., 2016, 18, 20208–20218 RSC.
- M. Rivera, L. Stojanović and R. Crespo-Otero, J. Phys. Chem. A, 2021, 125, 1012–1024 CrossRef CAS PubMed.
- X. Liu, T. N. V. Karsili, A. L. Sobolewski and W. Domcke, J. Phys. Chem. B, 2015, 119, 10664–10672 CrossRef CAS PubMed.
- M. De Vetta, L. González and I. Corral, ChemPhotoChem, 2019, 3, 727–738 CrossRef CAS.
- D. Tuna and W. Domcke, Phys. Chem. Chem. Phys., 2016, 18, 947–955 RSC.
- M. Barbatti and H. Lischka, Phys. Chem. Chem. Phys., 2015, 17, 15452–15459 RSC.
- R. Szabla, H. Kruse, P. Stadlbauer, J. Šponer and A. L. Sobolewski, Chem. Sci., 2018, 9, 3131–3140 RSC.
- A. Prlj, L. Vannay and C. Corminboeuf, Helv. Chim. Acta, 2017, 100, e1700093 CrossRef.
- M. Mališ, J. Novak, G. Zgrablić, F. Parmigiani and N. Došlić, Phys. Chem. Chem. Phys., 2017, 19, 25970–25978 RSC.
- D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 122–127 CrossRef CAS PubMed.
- M. J. Janicki, S. J. Roberts, J. Šponer, M. W. Powner, R. W. Góra and R. Szabla, Chem. Commun., 2018, 54, 13407–13410 RSC.
- K. E. Szkaradek, P. Stadlbauer, J. Šponer, R. W. Góra and R. Szabla, Chem. Commun., 2020, 56, 201–204 RSC.
- A. Prlj, L. M. Ibele, E. Marsili and B. F. E. Curchod, J. Phys. Chem. Lett., 2020, 11, 5418–5425 CrossRef CAS PubMed.
- D. Leifert, D. G. Artiukhin, J. Neugebauer, A. Galstyan, C. A. Strassert and A. Studer, Chem. Commun., 2016, 52, 5997–6000 RSC.
- J.-H. Li, G. Gryn*ova, A. Prlj and C. Corminboeuf, Chem. Commun., 2017, 53, 2423–2426 RSC.
- A. Tajti, L. Tulipán and P. G. Szalay, J. Chem. Theory Comput., 2020, 16, 468–474 CrossRef PubMed.
- L. Stojanović, S. Bai, J. Nagesh, A. F. Izmaylov, R. Crespo-Otero, H. Lischka and M. Barbatti, Molecules, 2016, 21, 1603 CrossRef PubMed.
- D. Hu, Y. F. Liu, A. L. Sobolewski and Z. Lan, Phys. Chem. Chem. Phys., 2017, 19, 19168–19177 RSC.
- C. L. Janssen and I. M. B. Nielsen, Chem. Phys. Lett., 1998, 290, 423–430 CrossRef CAS.
- A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036 CrossRef.
- C. Hättig, Adv. Quantum Chem., 2005, 50, 37–60 CrossRef.
- Š. Budzák, G. Scalmani and D. Jacquemin, J. Chem. Theory Comput., 2017, 13, 6237–6252 CrossRef PubMed.
- D. Jacquemin, I. Duchemin and X. Blase, J. Chem. Theory Comput., 2015, 11, 5340–5359 CrossRef CAS PubMed.
- Ł. Kielesiński, O. W. Morawski, C. A. Barboza and D. T. Gryko, J. Org. Chem., 2021, 86, 6148–6159 CrossRef PubMed.
- S. Mai, A. J. Atkins, F. Plasser and L. González, J. Chem. Theory Comput., 2019, 15, 3470–3480 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, supporting calculations, xyz files for all LIICs presented. See DOI: 10.1039/d1cp02185k |
| This journal is © the Owner Societies 2021 |