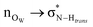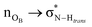On the role of water in the hydrogen bond network in DESs: an ab initio molecular dynamics and quantum mechanical study on the urea–betaine system†
Renato
Contreras
a,
Lucas
Lodeiro
 *a,
Nicolás
Rozas-Castro
a and
Rodrigo
Ormazábal-Toledo
*a,
Nicolás
Rozas-Castro
a and
Rodrigo
Ormazábal-Toledo
 *ab
*ab
aDepartamento de Química, Facultad de Ciencias, Universidad de Chile, Las Palmeras 3425, Casilla 653, Santiago, Chile. E-mail: lucas.lodeiro@ug.uchile.cl
bCentro Integrativo de Biología y Química Aplicada (CIBQA), Universidad Bernardo OHiggins, Santiago 8370854, Chile. E-mail: rodrigo.ormazabal@ubo.cl
First published on 23rd December 2020
Abstract
We herein report an ab initio molecular dynamics study on a natural DES composed of urea and betaine in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, as a test case for evaluating the water effect. The article deals with a theoretical study using both ab initio molecular dynamics and quantum chemistry computations in order to unravel the role of water in the nanostructure of a urea–betaine mixture. Preliminary molecular dynamics outcomes (both radial and spatial distribution functions) suggest that water promotes the association between urea and betaine by increasing the hydrogen bond network and precluding the aggregation of urea molecules. In other words, the presence of water allows a less restrictive hydrogen bond network, presenting a regimen where the strong hydrogen bond interactions are replaced by a wide variety of weaker hydrogen bond interactions. On the other hand, in a water free DES there is a regimen where strong urea–betaine interactions are dominant. It is shown that second order perturbation theory energy analysis provides cogent insights into charge spreading and hydrogen bond patterns. A vibrational analysis (both IR and power spectrum) over the ab initio molecular dynamics trajectories in the water free DES as well as in the urea–betaine–water systems reveals that our results are consistent with the second order perturbation theory analysis and with the hydrogen bond network pattern.
2 ratio, as a test case for evaluating the water effect. The article deals with a theoretical study using both ab initio molecular dynamics and quantum chemistry computations in order to unravel the role of water in the nanostructure of a urea–betaine mixture. Preliminary molecular dynamics outcomes (both radial and spatial distribution functions) suggest that water promotes the association between urea and betaine by increasing the hydrogen bond network and precluding the aggregation of urea molecules. In other words, the presence of water allows a less restrictive hydrogen bond network, presenting a regimen where the strong hydrogen bond interactions are replaced by a wide variety of weaker hydrogen bond interactions. On the other hand, in a water free DES there is a regimen where strong urea–betaine interactions are dominant. It is shown that second order perturbation theory energy analysis provides cogent insights into charge spreading and hydrogen bond patterns. A vibrational analysis (both IR and power spectrum) over the ab initio molecular dynamics trajectories in the water free DES as well as in the urea–betaine–water systems reveals that our results are consistent with the second order perturbation theory analysis and with the hydrogen bond network pattern.
1 Introduction
Deep eutectic solvents (DESs) are commonly recognized as a “new class” of ionic liquids (ILs). This relationship is based upon the similar physicochemical properties of both solvents, namely, density, viscosity, vapor pressure, polarity, chemical stability, etc.1,2 Despite this similarity, ILs and DESs are fundamentally different classes of solvents, mostly due to the presence of neutral species in the latter.3 However, DESs are generally regarded as a cheaper and eco-friendly alternatives to ILs for many applications.4Typically, DESs are binary mixtures of a quaternary ammonium or phosphonium salt and an organic species capable of forming Hydrogen Bonds (HBs) with itself, the anion and/or the cation of the quaternary salt. The main characteristic of these systems is their large Melting Point Depression (MPD) with respect to the ideal mixture behavior. During the last few years, related mixtures presenting large MPD have been reported.1,5,6
Abbot et al. reported systems composed of quaternary ammonium salts and amide derivatives, formed by heating the components up to 80 °C and stirring until a homogeneous liquid was formed. These mixtures were called Deep eutectic solvents, to emphasize their large MPD. The most extensively studied DES is the mixture formed by choline chloride (ChCl) and urea in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio (commonly known as reline).7,8 Based on NMR and FAB-MS spectra, Abbot and coworkers suggested that charge transfer from the anion (Cl−) to urea may be the main factor responsible for the electrostatic interaction depletion, thereby promoting the observed MPD.9 Besides that, the results obtained from gas phase ab initio computations for a set of pairs (i.e., urea–urea, urea–Cl−, Ch–Cl−, etc.) allowed us to understand MPD by means of entropy increase, induced by the existence of a large number of different possible hydrogen bonded moieties.
2 ratio (commonly known as reline).7,8 Based on NMR and FAB-MS spectra, Abbot and coworkers suggested that charge transfer from the anion (Cl−) to urea may be the main factor responsible for the electrostatic interaction depletion, thereby promoting the observed MPD.9 Besides that, the results obtained from gas phase ab initio computations for a set of pairs (i.e., urea–urea, urea–Cl−, Ch–Cl−, etc.) allowed us to understand MPD by means of entropy increase, induced by the existence of a large number of different possible hydrogen bonded moieties.
In this line, Welton and Hunt proposed that reline may be considered as an “alphabet soup” of HBs.10 However, the structure of DESs has proven to be complex in the sense that it can be variable from one system to another depending on the molecules chosen to form the DES. For instance, charge spreading was investigated, using ab initio molecular dynamics (AIMD) simulations, in reline and other related DESs, by including ethyleneglycol and oxalic acid as Hydrogen Bond Donors (HBDs). Interestingly, the results obtained showed that the charge transfer from the chloride anion to the neutral organic HBD is not dominant, compared to charge transfer towards choline cations.11,12 Similarly to ionic liquids, DESs display low vapor pressure (i.e. almost null volatile residues13), a wide liquid range, and chemical, thermal and electrochemical stability.1,3,14 However, several advantages over ILs have been proposed for DESs, namely, the starting materials are cheaper and they require less synthetic steps than ILs. Moreover, generally, DESs are composed of biodegradable and non-toxic components.15
One of the first applications of DESs was for electrochemical finishing of metals, for instance, Au and Pt nanocrystal electrodeposition controlled by water content in ChCl-based DESs,16,17 and also the electropolishing of Ni-based super alloy turbine blades.18 Similarly to ILs, DESs can be used for gas capture of CO219,20 and SO2.21–23 Moreover, DESs have been used in biocatalysis due to the possibility of dissolving enzymes without losing their activity.24 Moreover, recently DESs were used for biomass processing, especially by their capability to dissolve lignin fractions.25 Other related works concern the extraction processes of bioactive compounds, such as phenolic compounds,26 flavonoids,27 polysaccharides28 and proteins.29,30
Because of its great ability to form HBs, water is expected to interact with DESs. Indeed, DESs of type II composed of hydrated metal salts and quaternary ammonium salts (for instance CrCl3·6H2O with ChCl)31 exhibit improved transport properties over anhydrous metal salt systems, thereby demonstrating the huge effect of water content on the properties of DESs. In the same line, in hydrated reline, the use of neutron total scattering and empirical potential structure refinement reveals that its nanostructure retains up to 42 wt% of water.32 This response may be related to solvophobic sequestration of water into nanostructured domains around cholinium cations. However above 51 wt% of water, the DES structure is disrupted, thereby suggesting that the DES–water mixture is best described as an aqueous solution of DES components.32
The effect of water was studied theoretically by means of classical molecular dynamics simulations, and may be classified into three zones depending on the molar fraction of water. At low water fractions (<5 wt%), urea–urea and urea–cation moieties establish a HB network revealing a non-monotonic behavior.33 At intermediate water fractions (5–25 wt%), the components of reline are mainly hydrated with water, with the Cl− anion being mostly solvated (over urea and choline). At higher molar fractions of water (>25 wt%) both urea and anions show changes of the transport properties such as viscosity and conductivity.33
In other ChCl-based DESs, with glycerol or ethyleneglycol as an organic HBD, water also affects the structure and transport properties.34 For instance, pulsed field gradient NMR was used to probe self-diffusion of molecular and ionic species, revealing that stronger hydrophilic interactions appear while water is added to the system.34 However, these studies concern only a few types of DESs, and to date the role of water in the formation of the eutectic mixture is not clear. Moreover, the chemical origin of MPD brought about by water in DESs still remains elusive. In this sense, the “alphabet soup” of HBs in DES–water mixtures are fascinating systems that should give deeper insights into nanostructured domains and intermolecular interactions in DESs. For this reason, in this paper, we seek for insights into the water effect on a model natural DES (NADES), composed of urea and trimethylglycine (betaine) in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio. In this sense, the article deals with a theoretical study using both classical and ab initio molecular dynamics in order to unravel the role of water in the MPD of a model NADES. The article is organized as follows: firstly we analyze the structural influence of water by studying various types of radial distribution functions; later we analyze the influence of water on the electronic properties (charge and electronic structure); and finally, we compare the role of water in the vibrational spectrum of the NADES.
2 ratio. In this sense, the article deals with a theoretical study using both classical and ab initio molecular dynamics in order to unravel the role of water in the MPD of a model NADES. The article is organized as follows: firstly we analyze the structural influence of water by studying various types of radial distribution functions; later we analyze the influence of water on the electronic properties (charge and electronic structure); and finally, we compare the role of water in the vibrational spectrum of the NADES.
2 Systems under study
The systems under study are urea–betaine mixtures in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
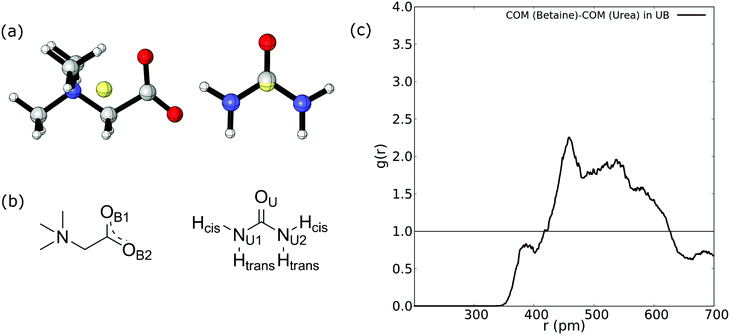
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molecular ratio, as described elsewhere.35–38 We prepared two systems based upon this ratio: a water free urea–betaine mixture (named UB) and a urea–betaine–water system (named UBW) with 2.1 wt% of water (0.091 molar fraction). The UB system consists of 18 urea and 12 betaine molecules, while the UBW system consists of 18 urea, 12 betaine and 3 water molecules. A snapshot of both mixtures is presented in Fig. 1.
2 molecular ratio, as described elsewhere.35–38 We prepared two systems based upon this ratio: a water free urea–betaine mixture (named UB) and a urea–betaine–water system (named UBW) with 2.1 wt% of water (0.091 molar fraction). The UB system consists of 18 urea and 12 betaine molecules, while the UBW system consists of 18 urea, 12 betaine and 3 water molecules. A snapshot of both mixtures is presented in Fig. 1.
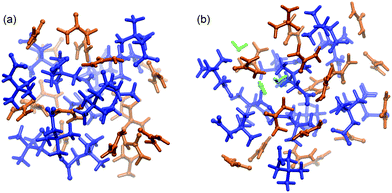 | ||
| Fig. 1 Simulation boxes (ball and stick model) of (a) UB and (b) UBW systems. The color code is as follows: blue (betaine), orange (urea), and green (water). | ||
3 Computational details
3.1 Classical molecular dynamics
Classical molecular dynamics simulations were performed with Gromacs version 5.1.439 with OPLS-AA force field40,41 (urea and betaine) and TIP5P42 (water). The atomic charges for urea and betaine molecules were obtained within the CHelp-G scheme as implemented in Gaussian-09, at the MP2/cc-pVTZ level of theory for isolated molecules, as previously suggested.43 The initial simulation cubic cell was generated with Packmol version 16.261,44 and was minimized with the steepest descent algorithm as the first step. After that, a 1 ns simulation in the NVT ensemble, with a time step of 1 fs, was carried out to thermalize. The production run was carried out in the isothermal–isobaric ensemble (NPT) for 70 ns. The first 10 ns were used as equilibrium, and the last 60 ns were used to obtain statistical information (average volume). During the production run, the temperature was kept constant at 298.15 K using a Nosé–Hoover chain thermostat with a coupling time constant of 100 fs in NVT and NPT. The pressure was controlled at 1 bar through a Parrinello–Rahman barostat45,46 with a coupling time constant of 2.0 ps. All calculations were done with a 0.7 nm cutoff radius.3.2 Ab initio molecular dynamics
After classical molecular dynamics, we performed an ab initio molecular dynamics (AIMD) simulation based on the Born–Oppenheimer approach, using the canonical ensemble (NVT) and periodic boundary conditions with CP2K 5.1,47,48 starting from the last snapshot of the classical molecular dynamics.The wavefunctions and the electronic density were represented and extrapolated by the hybrid Gaussian and Augmented Plane Wave (GAPW) method within the QuickStep module.49 Force evaluations were performed using the BLYP50,51 functional with the Grimme correction scheme (DFT-D3) to account for vdW interactions.52 The valence electron (Kohn–Sham) wavefunctions of all elements were expanded using the DZVP-MOLOPT-SR Gaussian basis set,53 with the corresponding GTH pseudopotential.54 Explicit valence shells included are H(1s), C(2s2p), N(2s2p), and O(2s2p). The density was represented with a plane wave energy cutoff of 280 Ry and a four level multigrid with a relative cutoff of 40 Ry. Along the simulation, the temperature was kept constant by using the Nosé–Hoover chain thermostat55–57 at 298.15 K with a coupling time constant of 50 fs. A convergence criterion of 10−5, for SCF cycles, was used. The simulation was carried out for 15 ps for equilibrium and thermalization using a 0.5 fs time step to integrate the dynamic equations. Afterwards, the trajectory productions were extended up to 70 ps to obtain the physical properties as a statistical average over all configurations. The cubic simulation cell volume (3.019 nm3 and 3.145 nm3 for UB and UBW systems, respectively) and the initial atomic configuration were set equal to the average volume and the last frame of classical molecular production dynamics simulations, respectively.
3.3 Data analysis
The TRAVIS program package58 was used for post-processing data and analyze the results obtained from AIMD. Static functions such as radial distribution function (RDF), spatial distribution function (SDF), and spectroscopic/vibrational data (namely, power spectrum,59 vibrational modes60 and IR spectrum61 using fluctuating Hirshfeld-I atomic partial charges) were computed using a well-known procedure.62 Atomic partial charges were obtained by the improved partitioning scheme of the electron density based on the model by Hirshfeld.63,64 Hirshfeld-I partial atomic charges were obtained along the AIMD trajectory, using multiple Gaussians to expand the atomic density. Finally, a set of clusters were generated from the AIMD trajectory using TRAVIS. A set of 30 different clusters were obtained along the trajectory of the UBW systems. Roughly, the clusters were obtained by putting a molecule of betaine or urea in the middle of a box and using a cutoff radius of 500 pm to find the neighborhood molecules (betaine, urea and/or water). Commonly, the clusters had between 60 and 150 atoms. A natural population analysis was carried out for these clusters to obtain information regarding the interaction between urea, betaine, and water. Natural Bond Orbital (NBO) analysis was performed at the BLYP/cc-pVTZ level of theory using Gaussian 09.654 Results and discussion
4.1 Influence of water on the structure of the urea–betaine mixture
Firstly, we compute the center-of-mass/center-of-mass radial distribution function (COM–COM RDF) of the betaine–urea pair in the UB mixture. In the case of betaine, COM is located near the α carbon atom, and in urea it is very close to the carbon atom. For reference, Fig. 2(a) shows the COM of betaine and urea. Considering the position of COM, the RDF in Fig. 2(a) is difficult to analyze since it does not include explicit information about hydrogen atoms promoting a HB network in urea (see Fig. 2(b)).Moreover, it has been demonstrated that both hydrogen atoms in urea nitrogen atoms display different behavior depending on their chemical environment66–68 (see Fig. 2(b)); hereby we have labeled them as cis and trans hydrogen. In this sense, the COM–COM RDF in Fig. 2(c) shows that zones near α carbon in betaine and Cα in urea are correlated showing a low-intensity peak near 390 pm, followed by a higher peak at 459 pm and a diffuse zone above 500 pm. However, short range interactions, such as HBs, may not be properly displayed. For this reason we followed the analysis by considering different atoms in the RDF of betaine and urea as displayed in Fig. 3.
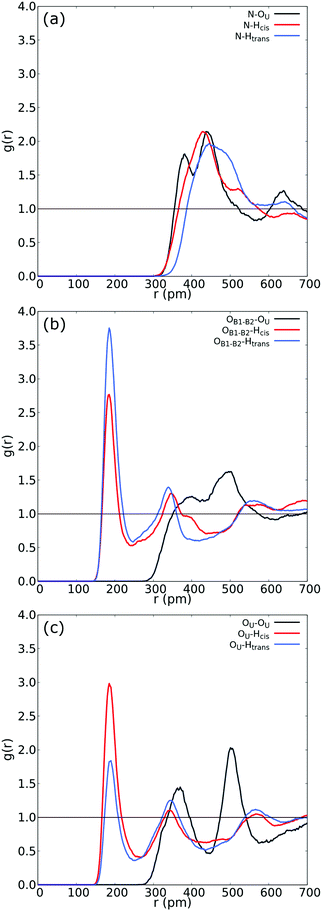 | ||
| Fig. 3 (a) RDF between N in betaine and both Htrans (blue), both Hcis (red) and OU (black) in urea. (b) RDF between OB1 and OB2 in betaine and both Htrans (blue), both Hcis (red) and OU (black) in urea in the UB mixture. (c) Intermolecular RDF between OU in urea and both Htrans (blue), both Hcis (red) and OU (black) in urea in the UB mixture. For atom labelling, please refer to Fig. 2(b). | ||
Fig. 3 reveals an interesting feature in the UB mixture: the interaction between betaine and urea is mainly by means of oxygens in betaine and hydrogens in urea. Moreover, the shape, size, and distance of RDF of the nitrogen atom in betaine and different atoms in urea are quite similar to those observed in the COM–COM RDF in Fig. 2(a). This result is natural since COM in betaine is centered close to Cα (and near the nitrogen atom). However, in Fig. 3(b) hydrogen atoms reveal a different response, mainly related to the HB network in the UB mixture. For instance, the RDF considering oxygen atoms in betaine and Htrans atoms in urea presents a higher peak (g(r) = 3.75) with respect to Hcis (g(r) = 2.77). This difference may be traced to a different interaction towards oxygen atoms in both betaine and urea: Htrans atoms prefer the interaction towards betaine, while Hcis atoms are mainly associated with oxygen in the remaining ureas through intermolecular interactions. To test this prognosis, in Fig. 3(c) the RDF between OU in urea and both Htrans and Hcis in urea is displayed. Notably, peak intensities associated with both sets of atoms are inverted with respect to those obtained in Fig. 3(b), displaying values of g(r) = 1.84 and g(r) = 2.98 for Htrans and Hcis, respectively. On the other hand, the interaction between oxygen atoms in different urea molecules appears as a pair of peaks at larger distances (r = 365 pm and r = 501 pm), probably due to long-range interactions, promoted by the HB network, more than an interaction between oxygen atoms themselves.
The next task is to analyze the effect of water molecules in the UBW mixture. At this point, a reviewer prompted us to consider that there exists a significant movement of the molecules within the system. We obtained diffusion coefficients by computing the mean-square displacement. The values obtained were De = 5.49 × 10−11 m2 s−1 and De = 7.50 × 10−11 m2 s−1 for UB and UBW, respectively. Even though these values are quite small, they may be considered in the range of highly viscous liquids as suggested elsewhere.69–71 On the other hand, it is well-known that the GGA functionals suffer from a self-interaction error.72 This error entails to an overestimation of the strength of hydrogen bonding, underestimating the diffusion coefficient.73 In other words, by using GGA functionals, the system evolves to an overstructured liquid. However, as suggested by Galli,74 the GGA functionals (such as BLYP) give reasonably good liquid structures and description of vibrational properties of liquids. In order to start this analysis, we obtained the COM–COM RDF of betaine and urea for comparing the responses due to the presence of water molecules (see Fig. 4). Together with the COM–COM RDF of betaine and urea in the UBW system, Fig. 4(a) shows the results presented in Fig. 3(a) for a better comparison. Even though both COM–COM RDFs display a similar broad shaped response, several differences may be related to the presence of 2% of water. Firstly, the peak at r = 388 pm in the UB mixture appears as a shoulder at a similar distance suggesting that water precludes short-range interactions between oxygen atoms in betaine and urea. However, the broad band at 450–550 pm presents a higher intensity compared to the UB mixture, suggesting that other interactions may dominate due to the presence of water in the UBW mixture.
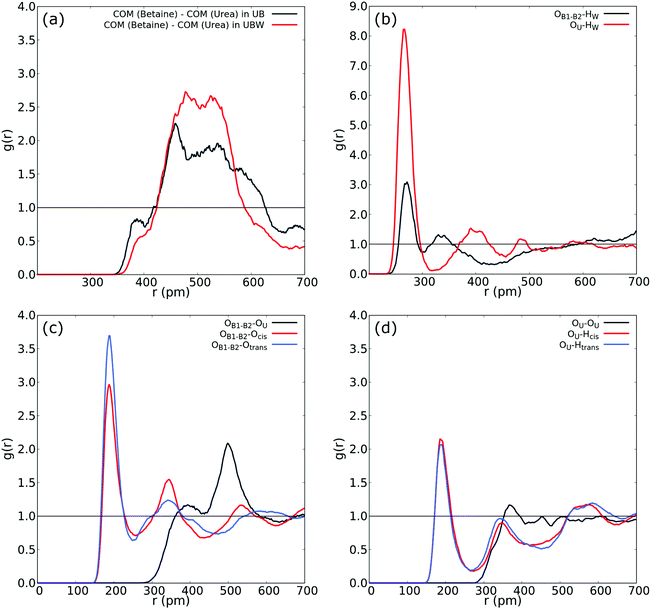 | ||
| Fig. 4 (a) COM–COM RDF of the urea and betaine pair in the UBW mixture. (b) RDF between oxygen in water and oxygen in urea (red), and OB1 and OB2 in betaine. (c) RDF between OB1 and OB2 in betaine and both Htrans (blue), both Hcis (red) and OU (black) in urea in the UBW mixture. (d) Intermolecular RDF in urea between OU and both Htrans (blue), both Hcis (red) and OU (black) in the UBW mixture. For atom labelling, please refer to Fig. 2(b). | ||
Fig. 4(b) shows atom-to-atom RDF relating water and oxygens in urea (red line) and betaine (black line). This comparison reveals that urea presents a higher peak at r = 266 pm with an intensity of g(r) = 8.22; in contrast betaine presents a low intensity peak with g(r) = 3.09 at a similar distance (r = 270 pm). In this sense, Fig. 4(b) suggests that there exists a tendency of water to form a HB network with oxygen in urea. Moreover, this interaction might be related to the presence of a different HB network that promotes a new nanostructure. Fig. 4(c) shows that the atom-to-atom RDF between oxygen atoms in betaine and Htrans in urea is similar to that observed in Fig. 3(b); however, the peak intensity in the correlation with Hcis is g(r) = 2.76 and g(r) = 2.96 in the UB and UBW mixtures, respectively. This result suggests that water promotes the association between urea and betaine by increasing the HB network and, consequently, the entropy of the system as proposed previously by Welton.10 Another interesting feature observed in the UBW mixture is revealed in RDF presented in Fig. 4(d). Note that the correlation between different urea molecules is diminished due to the presence of water molecules. In this sense, the RDF intensity in the intermolecular correlation between OU and Hcis in urea passes from g(r) = 2.82 in UB to g(r) = 2.15 in UBW. This result is relevant because it suggests, as discussed above, that water promotes the association between urea and betaine, thereby precluding the self-association of urea.
The SDF plots shown in Fig. 5 give us valuable information regarding the position that some important atoms take along the dynamics. For instance we can observe that the Hcis atoms (red) in the UBW system are spread over a larger, although discontinuous, volume around betaine in Fig. 5(c), compared with UB in Fig. 5(a). Similarly, in Fig. 5(b) and (d) we can observe an increase in the volume region covered by Hcis (red) and Htrans (blue) when passing from UB to UBW. Also, in Fig. 5(b) and (d) some evidence for urea–urea network disruption can be assessed. In other words, if we look at the OU (green) portion in Fig. 5(b), it reminds us of the solid structure of urea, with quite localized interactions (i.e. smaller covered regions). On the other hand, the OU (green) regions in Fig. 5(d) show a much more delocalized cloud, and practically the loss of Htrans–OU interaction. So, as already said, the presence of water promotes a change in the way urea interacts with urea in UBW systems, compared with the UB system. Similarly, in Fig. 5(b) and (d), the volume observed between urea and other urea molecules suggests that HB formation is similarly distributed but with important differences in the shape. For instance, note that the interaction between Htrans and OU looks more delocalized in Fig. 5(d); a similar result was obtained for the Hcis and OU atoms. Even though the interaction observed in Fig. 5(d) in blue color was computed as the Htrans and Htrans self-interaction, we think that the observed volume is a response of the rotation of the Htrans atom assisted by the OU interaction. The delocalization of the interaction may be related to the proposal by Hunt and Welton: water enhances the entropy of the system by spreading the components making a flexible structure. In other words, the presence of water allows a less restrictive HB network, increasing Ssystem and, consequently, depleting the molecular cohesion of the components.
4.2 Charge spread brought about by water
According to Kirchner and coworkers, the presence of chloride in different DESs based on choline chloride promotes the charge spreading of negative charge in the mixture.11,12 Considering these findings, we calculated partial charges using an improved partitioning scheme of the electron density based on the Hirshfeld-I model.63,64 The results obtained are presented in Table 1 for selected atoms in urea and betaine in both mixtures, namely UB and UBW, as well as in the gas phase.| Atom | q (UB) | q (UBW) | q (gas phase) |
|---|---|---|---|
| OU | −0.40 | −0.40 | −0.46 |
| Hcis | +0.24 | +0.25 | +0.31 |
| Htrans | +0.24 | +0.25 | +0.29 |
| OB1 | −0.37 | −0.37 | −0.45 |
| OB2 | −0.37 | −0.37 | −0.45 |
| NB | +0.21 | +0.21 | +0.19 |
| OW | — | −0.54 | −0.64 |
| HW | — | +0.26 | +0.32 |
Notably, the variations observed in UB and UBW mixtures are marginal and may be related to the presence of a neutral molecule such as water. Previously, Kirchner and coworkers reported variations of almost 0.5e brought about by the addition of chloride in the DES compared to the gas phase computation.11 The presence of a negative ion in the mixture must promote a more efficient charge spreading than the presence of a neutral (and, in this case, polar) molecule. In this sense, our results point out to a negligible charge spreading brought about by water since all species in the mixture are neutral (urea) or zwitterionic (betaine), revealing that water contributes in a more efficient way to the formation of an extensive HB network.
An important feature observed in Table 1 reveals that there exists a difference in partial charges observed in the gas phase with respect to the solvated phase, in either the UB or UBW mixture. Even though our charge spread is small compared to that previously obtained,11,12 it is in the same line as the proposal made by other authors: ab initio molecular dynamics simulations might be used to obtain partial charges that should be used as an ansatz for a systematic calculation of the non-polarizable force field of DESs. However, charge spreading brought about by adding water is marginal revealing that the water effect may be related to the probability of HB appearance, rather than a change of the electronic distribution of betaine or urea.
4.3 Electronic structure of the UBW mixture
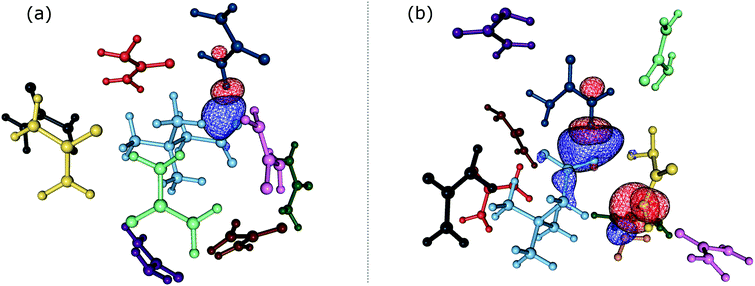
In order to gain insights into the electronic structure of the UBW system, we performed a NBO analysis. The shape and orientation of natural orbitals show overlap between lone pair orbitals in oxygen and σ anti-bonding orbitals in the O–H bond, as shown in Fig. 6. This overlap is an indicator of the HB strength, which is expected to be observed in DES systems. Also, the nature of the orbitals implicated in HB formation processes is an expected one. Note that, there is no evidence for other kinds of interactions in the NBO analysis. As shown in Fig. 6, this procedure allows us to consider not only the interacting pair, but a more complete interaction with neighborhood molecules, resembling the solvent bulk. Even though the bulk of the solvent cannot be completely described using a portion of the simulation box (clusters), it is a better approach than considering only a couple of molecules.In Table S1 of the ESI† we present the complete set of values obtained from our electronic analysis, summarized in Table 2. The second column in Table 2 shows the mean second-order perturbation energies, E(2), which are associated with the HB strength. Also, Table 2 emphasizes that the stronger interactions occur between oxygen in urea or betaine and hydrogen atoms in water. The next columns in Table 2 display the most probable second order perturbation theory energies, the standard deviation obtained from the statistical distribution of the energies and the total number of interactions considered in the distribution. For this distribution only the interactions presenting E(2) ≥ 2.0 kcal mol−1 were considered. Note that there are values of E(2) and 〈E〉 that are quite similar to each other. On the other hand there are two interactions shown in Table 2 that differ considerably from this trend (≥4.0 kcal mol−1). These interactions are OB → HW and OU → HW. This difference may be related, in the first case, to a poor sampling, which means that this interaction even though is one of the greatest occurs rarely. On the other hand, in the case of OU → HW the sampling obtained reveals a wide range of interactions (up to 36.5 kcal mol−1) introducing artifacts in the statistic. In both cases this response may be related to the higher standard deviation shown in Table 2.
| Donor → acceptora | 〈E(2)〉b | E (2)MP | σ | N |
|---|---|---|---|---|
| a Donor → Acceptor contributions are in all cases n → σ* HB interactions. b Mean second order perturbation theory energies (in kcal mol−1 units) computed with interactions over 2.0 kcal mol−1. c Most probable second order perturbation theory energies on histogram distribution with a 0.5 kcal mol−1 window, interactions over 2.0 kcal mol−1. d Standard deviation of interactions over 2.0 kcal mol−1. e Total number of interactions considered over 2.0 kcal mol−1. | ||||
| OB → Hcis | 4.7 | 6.3 | 5.5 | 34 |
| OB → Htrans | 5.7 | 5.3 | 6.0 | 45 |
| OB → HW | 15.4 | 9.8 | 7.7 | 9 |
| OU → Hcis | 5.4 | 4.3 | 5.8 | 41 |
| OU → Htrans | 3.9 | 3.8 | 6.4 | 25 |
| OU → HW | 11.3 | 7.3 | 7.9 | 35 |
| OW → Hcis | 4.2 | 4.3 | 5.8 | 16 |
| OW → Htrans | 3.9 | 2.3 | 4.8 | 16 |
Comparing the information given in Table 2 with Fig. 3(b), we can see that the peak intensity may be related to the N value for the corresponding interactions. For instance, the number of interactions obtained for OB → HW is N = 9 and for OU → HW is N = 35. Moreover, in Table 2 we can see that the strength of the former HB is greater, which could be related to the electron rich nature of the carbonyl group.
Considering the values of 〈E〉 and N, it is possible to note that the stronger interactions are not the most likely observed in the dynamics, which seems contradictory. This fact may be explained in terms of intrinsic entropy increase, due to the existence of two different regimes driven by the water presence. A water free DES is the most ordered nanostructure, suggesting stronger interactions; meanwhile in the UBW system there are plenty weaker interactions and a loss of the ordered nanostructure, suggesting a melting point depletion. This may be related with the following: (i) the strong interaction regimen in the water free DES retains a non-malleable nanostructure allowing the access to just a few microstates, and (ii) the weak interaction regimen in the UBW system disorders the nanostructure allowing the access to a great number of microstates. In other words, our results suggest that water in the UBW system promotes an increase of the entropy. This proposal is not new, and was previously discussed by Hunt and Welton, elsewhere.10 In our case, for instance, this response was obtained for the limit case of OB → HW and OB → Htrans. Note that for the former there exist only N = 9 interactions, but all of them present E(2) ≥ 6.8 kcal mol−1. However, for OB → Htrans, there are an important number of interactions (N = 45), but they exhibit a wide range of values.
Also, the OU → HW interaction shows major angular dispersion compared to OB → HW, as shown in Fig. S2 of the ESI.† There is a dependence of the HB strength on the angle comprised by X–H⋯Y, with X the atom covalently attached to the hydrogen and Y atoms of the HB donor atom. Because of the greater angular dispersion observed for the OU → HW HB, the E(2) values are spread over a wider range. Despite the fact that both OU → HW and OB → HW interactions are HB interactions, here we can appreciate how different are these two kinds of HB interactions. The relationship between distance and angle with HB strength is not a fully understood matter, and the values of angles and distances associated with the HB observed in the UBW system are listed in Tables S2–S5 of the ESI.†
Interestingly, the HB interaction energies reported by Hunt and Welton10 are systematically higher compared with those reported by us. This situation is mainly due to the fact that the reported computations were obtained from gas phase stationary dimers, trimers, and tetramers, while in our case, we used bigger clusters with 6 to 10 molecules, obtained from computations considering the thermal effect.
4.4 Vibrational analysis
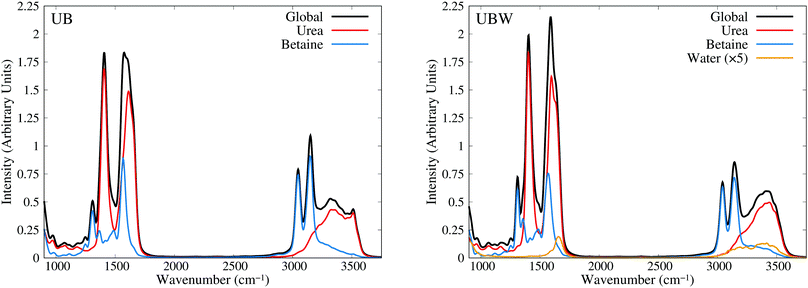
Until now, all analyses were carried out using geometrical and energetic functions, which provide information from different conformations along the AIMD trajectories, but not from their temporal correlations. For this purpose, we compute the power spectrum (vibrational density of states) along the AIMD production trajectories, for UB and UBW systems. Since this property is calculated by means of atomic velocity autocorrelation functions, the power spectrum can be easily decomposed into molecular contributions,59 as shown in Fig. 7 from 900 to 3750 cm−1 (full power spectra in Fig. S3 of the ESI†). We selected this spectral range, since the vibrational modes of the characteristic functional groups of urea, betaine and water exist in this range. It is worth mentioning that the intensity of the power spectrum is proportional to the number of vibrational modes and their broadening. In order to assign different peaks and vibrational modes, we computed them using single reference molecules for each constituent, which enables us to project molecular vibrational modes from the AIMD trajectories.60 Also, a signal deconvolution were performed using Lorentzian functions, in peak overlapping cases to check the positions of vibrational modes (see Fig. S4 and S5 in ESI†). Fig. 7 shows well resolved groups of vibrational modes: X–H (X = C and N) stretching vibrational modes over 3000 cm−1 and functional group and angular vibrational modes below 1700 cm−1.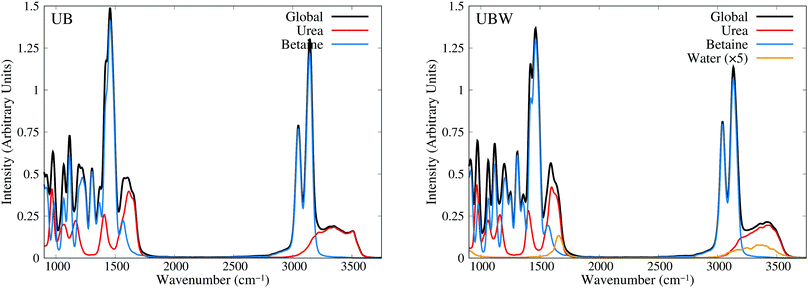 | ||
| Fig. 7 Power spectra obtained from AIMD for UB and UBW mixtures, showing the global and molecule decomposed spectrum. The water plot in UBW was enhanced by a factor of 5, for better visualization. | ||
For the UB mixture, the N–H stretching of the urea molecule (symmetrical and asymmetrical) is in a widespread range, from 3000 to 3600, with the maximum at 3350 cm−1. These broad signals are expected for HB active hydrogens. On the other hand, the C–H stretching of the betaine molecule is well localized into two peaks: one peak (composed of four symmetrical modes) at 3047 and the other peak (composed of seven asymmetrical modes) at 3143 cm−1 (see the deconvolution in Fig. S4 of the ESI†). These well localized signals are expected for HB inactive hydrogen atoms.
In the other group (signals below 1700 cm−1), urea presents seven vibrational modes, as reported elsewhere,75–77 with three of them being overlapped in the range of 1500 to 1700 cm−1 (see the deconvolution in Fig. S5 of the ESI†). The assignment is as follows: 965 cm−1 (symmetrical C–N stretching), 1065 cm−1 and 1166 cm−1 (asymmetrical and symmetrical NH2 rocking), 1407 cm−1 (asymmetrical C–N stretching), 1571 cm−1 (C–O carbonyl stretching), and 1613 cm−1 and 1655 cm−1 (asymmetrical and symmetrical NH2 bending).
In the case of betaine, there are several peaks in this range, with two of them being of interest:78–80 1567 cm−1 (asymmetrical C–O carboxyl stretching) and 1304 cm−1 (symmetrical C–O carboxyl stretching). The higher peak computed is mainly due to the presence of CH2 bending, and rocking vibrations (below 1300 cm−1), but they are not relevant for the purpose of our discussion, since they are HB inactive.
In the UBW mixture the vibrational mode assignment is highly similar. Just the water vibrational modes were added. Symmetrical and asymmetrical O–H stretching are present in the same widespread range as N–H ones. At 1567 cm−1 the well known H2O angular vibrational mode is located. Notwithstanding the contributions of water vibrational modes to power spectra are negligible due to the low amount of water in the mixture. However the simple fact of incorporating water in the mixture modifies the position and shape of some vibrational modes of urea and betaine.
As a last check, in the assignment of vibrational modes, we computed the IR spectra for both mixtures, using fluctuating Hirshfeld-I atomic partial charges. Since this property is calculated by means of molecular dipole autocorrelation functions, the IR spectrum can be easily decomposed into molecular contributions,61 as seen in Fig. 8 from 900 to 3750 cm−1 (full IR spectra in Fig. S6, ESI†). In the IR spectra we expected intense signals mainly at the positions of heteronuclear stretching vibrational modes, that is, the C–O carboxyl (symmetric and asymmetric), C–O carbonyl, C–N asymmetric, and X–H stretching, as well as the low signal intensity of bending and rocking C–H vibrational modes. As Fig. 8 shows, the urea signals are dominant over the other signals in the spectra. The differences in shape and position between UB and UBW IR spectra are the same as in the power spectra.
In order to gain more insights into the effect of water on the urea–betaine mixture, we compared the power spectra of UB and UBW. The main discussion was based on the shape and position of main vibrational modes. Variations less than ±5 cm−1 in position will not be commented. In the group of X–H vibrational modes, an evident change in the shape and position of maximum of N–H stretching vibrational modes is observed. The range between 3000 cm−1 and 3600 cm−1 is maintained, but the distribution and shape change, moving to higher wavenumbers. The maximum in the UBW mixture is located at 3450 cm−1 (+100 cm−1 with respect to the UB mixture). In the case of C–H stretching vibrational modes, a slight decrease in the height of the asymmetric vibrational mode peak is observed. Deconvolution in Fig. S4 of the ESI† shows that the broadening of these signals is enhanced by the presence of water in the mixture, and this explains the decrease of the height by means of peak thickening. Finally, for the C–O stretching modes, there are three main changes, i.e. their position shifts to higher values. The changes were +6 cm−1, +7 cm−1, and +12 cm−1 for asymmetric carboxyl, symmetric carboxyl, and carbonyl C–O stretching modes, respectively.
The shifts of C–O and N–H stretching vibrational modes to higher wavenumbers suggest that the inclusion of water in the mixture promotes the strengthening of these bonds. Since all of them are HB active, the discussion presented above about the delocalization of the HB interaction is consistent with our vibrational analysis results: going from a regimen where strong interactions are dominant to a regimen where these strong HB interactions are replaced by a wide variety of weaker HB interactions. These results are in the same line with NBO results.
The wavenumber values for C–O stretching modes are lower than computed or experimental ones in gas phase for each molecule. Moreover, C–O carbonyl stretching is close to the value for crystalline urea.76,77 Crystalline urea has a structured HB network, where Hcis and Htrans are clearly differentiated. In our case, it is observed that in the UB mixture there exists a pseudo structured HB network between urea molecules, as shown in Fig. 3(c). The differentiation of hydrogen atoms is present, and the OU⋯OU shows well defined and separated peaks, which resembles an organized neighborhood of urea fragments around the urea molecule. These differences disappear in the UBW mixture as clearly shown in the RDF (Fig. 4). In this case, Hcis and Htrans have highly similar RDF, and the OU⋯OU no longer has peaks, and the RDF is approximately flat over 400 pm. These findings imply that at room temperature the UB mixture still maintains some structured solid state like HB network among urea molecules, and the inclusion of a small amount of water disrupts it. It is worth mentioning that the shift of the C–O carbonyl stretching vibrational mode to a higher wavenumber, in UBW with respect to the UB mixture, is practically the same as observed between crystalline urea and urea in solution.75
5 Conclusions
A complete ab initio molecular dynamics + quantum mechanical approach has been presented in order to microscopically characterize the water effect on a natural DES composed of urea and betaine in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio. Both ab initio molecular dynamics and quantum chemistry calculations have been performed in order to unravel the role of water in the nanostructure of a urea–betaine mixture. Preliminary molecular dynamics outcomes suggest that water promotes the association between urea and betaine by increasing the HB network and precluding the aggregation of urea molecules, consequently, increasing the entropy of the system, in agreement with previous proposals. In other words, the presence of water allows a less restrictive HB network, thereby increasing the entropy of the system and consequently, depleting the molecular cohesion of the components. Quantum chemical population analysis shows that charge spreading brought about by adding water is marginal, thereby revealing that the water effect may be related to the probability of HB appearance, rather than a change of the electronic distribution of betaine or urea. It is shown that second order perturbation energy analysis provides a cogent methodology that nicely complements charge spreading and HB patterns. Finally, vibrational analysis over the ab initio molecular dynamics trajectories in the water free DES as well as in the urea–betaine–water systems reveals that the simple fact of incorporating water in the mixture modifies the position (to higher wavenumbers) and shape of HB active hydrogen stretching modes in urea, and C–O carbonyl and carboxyl stretching modes of urea and betaine, respectively, in a way which is consistent with the second order perturbation energy analysis and with the HB network pattern predicted for the model system. We expect the present results to be useful for the design of new task specific NADESs for different applications in chemistry and related fields.
2 ratio. Both ab initio molecular dynamics and quantum chemistry calculations have been performed in order to unravel the role of water in the nanostructure of a urea–betaine mixture. Preliminary molecular dynamics outcomes suggest that water promotes the association between urea and betaine by increasing the HB network and precluding the aggregation of urea molecules, consequently, increasing the entropy of the system, in agreement with previous proposals. In other words, the presence of water allows a less restrictive HB network, thereby increasing the entropy of the system and consequently, depleting the molecular cohesion of the components. Quantum chemical population analysis shows that charge spreading brought about by adding water is marginal, thereby revealing that the water effect may be related to the probability of HB appearance, rather than a change of the electronic distribution of betaine or urea. It is shown that second order perturbation energy analysis provides a cogent methodology that nicely complements charge spreading and HB patterns. Finally, vibrational analysis over the ab initio molecular dynamics trajectories in the water free DES as well as in the urea–betaine–water systems reveals that the simple fact of incorporating water in the mixture modifies the position (to higher wavenumbers) and shape of HB active hydrogen stretching modes in urea, and C–O carbonyl and carboxyl stretching modes of urea and betaine, respectively, in a way which is consistent with the second order perturbation energy analysis and with the HB network pattern predicted for the model system. We expect the present results to be useful for the design of new task specific NADESs for different applications in chemistry and related fields.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).Notes and references
- Q. Zhang, K. De Oliveira Vigier, S. Royer and F. Jérôme, Chem. Soc. Rev., 2012, 41, 7108–7146 RSC.
- D. Carriazo, M. C. Serrano, M. C. Gutiérrez, M. L. Ferrer and F. del Monte, Chem. Soc. Rev., 2012, 41, 4996–5014 RSC.
- M. Francisco, A. van den Bruinhorst and M. C. Kroon, Angew. Chem., Int. Ed., 2013, 52, 3074–3085 CrossRef CAS.
- C. Ruß and B. König, Green Chem., 2012, 14, 2969–2982 RSC.
- L. I. Tomé, V. B. Ao, W. da Silva and C. M. Brett, Appl. Mater. Today, 2018, 10, 30–50 CrossRef.
- A. Paiva, R. Craveiro, I. Aroso, M. Martins, R. L. Reis and A. R. C. Duarte, ACS Sustainable Chem. Eng., 2014, 2, 1063–1071 CrossRef CAS.
- S. Zahn, Phys. Chem. Chem. Phys., 2017, 19, 4041–4047 RSC.
- C. F. Araujo, J. A. P. Coutinho, M. M. Nolasco, S. F. Parker, P. J. A. Ribeiro-Claro, S. Rudić, B. I. G. Soares and P. D. Vaz, Phys. Chem. Chem. Phys., 2017, 19, 17998–18009 RSC.
- A. P. Abbott, G. Capper, D. L. Davies, R. K. Rasheed and V. Tambyrajah, Chem. Commun., 2003, 70–71 RSC.
- C. R. Ashworth, R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2016, 18, 18145–18160 RSC.
- S. Zahn, B. Kirchner and D. Mollenhauer, ChemPhysChem, 2016, 17, 3354–3358 CrossRef CAS.
- V. Alizadeh, F. Malberg, A. A. H. Pádua and B. Kirchner, J. Phys. Chem. B, 2020, 124, 7433–7443 CrossRef CAS.
- M. J. Earle, J. M. S. S. Esperança, M. A. Gilea, J. N. Canongia Lopes, L. P. N. Rebelo, J. W. Magee, K. R. Seddon and J. A. Widegren, Nature, 2006, 439, 831–834 CrossRef CAS.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082 CrossRef CAS.
- H. Vanda, R. Verpoorte, P. G. L. Klinkhamer and Y. H. Choi, Natural Deep Eutectic Solvents: From Their Discovery to Their Applications, John Wiley & Sons, Ltd, 2019, ch. 4, pp. 61–81 Search PubMed.
- A. Li, Y. Chen, K. Zhuo, C. Wang, C. Wang and J. Wang, RSC Adv., 2016, 6, 8786–8790 RSC.
- L. Wei, Y.-J. Fan, N. Tian, Z.-Y. Zhou, X.-Q. Zhao, B.-W. Mao and S.-G. Sun, J. Phys. Chem. C, 2012, 116, 2040–2044 CrossRef CAS.
- N. Dsouza, M. Appleton, A. Ballantyne, A. Cook, R. Harris and K. S. Ryder, MATEC Web Conf., 2014, 14, 13007 CrossRef.
- I. Adeyemi, M. R. Abu-Zahra and I. Alnashef, Energy Procedia, 2017, 105, 1394–1400 CrossRef CAS.
- X. Li, M. Hou, B. Han, X. Wang and L. Zou, J. Chem. Eng. Data, 2008, 53, 548–550 CrossRef CAS.
- D. Yang, M. Hou, H. Ning, J. Zhang, J. Ma, G. Yang and B. Han, Green Chem., 2013, 15, 2261–2265 RSC.
- B. Liu, F. Wei, J. Zhao and Y. Wang, RSC Adv., 2013, 3, 2470–2476 RSC.
- S. Sun, Y. Niu, Q. Xu, Z. Sun and X. Wei, Ind. Eng. Chem. Res., 2015, 54, 8019–8024 CrossRef CAS.
- P. Domínguez de María, N. Guajardo and S. Kara, Enzyme Catalysis: In DES, with DES, and in the Presence of DES, John Wiley & Sons, Ltd, 2019, ch. 13, pp. 257–271 Search PubMed.
- M. Zuo, X. Zeng, Y. Sun, X. Tang and L. Lin, Processing of Biomass in Deep Eutectic Solvents, John Wiley & Sons, Ltd, 2019, ch. 12, pp. 235–255 Search PubMed.
- K. M. Jeong, Y. Jin, D. E. Yoo, S. Y. Han, E. M. Kim and J. Lee, Food Chem., 2018, 251, 69–76 CrossRef CAS.
- Y. Dai, G.-J. Witkamp, R. Verpoorte and Y. H. Choi, Anal. Chem., 2013, 85, 6272–6278 CrossRef CAS.
- M. Sharma, J. Prakash Chaudhary, D. Mondal, R. Meena and K. Prasad, Green Chem., 2015, 17, 2867–2873 RSC.
- K. Xu, Y. Wang, Y. Huang, N. Li and Q. Wen, Anal. Chim. Acta, 2015, 864, 9–20 CrossRef CAS.
- Q. Zeng, Y. Wang, Y. Huang, X. Ding, J. Chen and K. Xu, Analyst, 2014, 139, 2565–2573 RSC.
- A. P. Abbott, G. Capper, D. L. Davies and R. K. Rasheed, Chem. – Eur. J., 2004, 10, 3769–3774 CrossRef CAS.
- O. S. Hammond, D. T. Bowron and K. J. Edler, Angew. Chem., Int. Ed., 2017, 56, 9782–9785 CrossRef CAS.
- D. Shah and F. S. Mjalli, Phys. Chem. Chem. Phys., 2014, 16, 23900–23907 RSC.
- C. DAgostino, L. F. Gladden, M. D. Mantle, A. P. Abbott, E. I. Ahmed, A. Y. M. Al-Murshedi and R. C. Harris, Phys. Chem. Chem. Phys., 2015, 17, 15297–15304 RSC.
- C.-X. Zeng, S.-J. Qi, R.-P. Xin, B. Yang and Y.-H. Wang, J. Mol. Liq., 2016, 219, 74–78 CrossRef CAS.
- N. Li, Y. Wang, K. Xu, Y. Huang, Q. Wen and X. Ding, Talanta, 2016, 152, 23–32 CrossRef CAS.
- N. Kumar and N. Kishore, J. Chem. Phys., 2013, 139, 115104 CrossRef.
- N. Kumar and N. Kishore, Chem. Phys., 2014, 443, 133–141 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922 CrossRef CAS.
- L. Lodeiro, R. Contreras and R. Ormazábal-Toledo, J. Phys. Chem. B, 2018, 122, 7907–7914 CrossRef CAS.
- L. Martínez, R. Andrade, E. Birgin and J. Martínez, J. Comput. Chem., 2009, 30, 13 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- The CP2K developers group, 2018, CP2K is freely available from https://www.cp2k.org.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS.
- K. Wendler, M. Brehm, F. Malberg, B. Kirchner and L. Delle, Site, J. Chem. Theory Comput., 2012, 8, 1570–1579 CrossRef CAS.
- M. Thomas, M. Brehm, O. Hollóczki, Z. Kelemen, L. Nyulászi, T. Pasinszki and B. Kirchner, J. Chem. Phys., 2014, 141, 024510 CrossRef.
- M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622 RSC.
- M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- H. Tanaka, H. Touhara, K. Nakanishi and N. Watanabe, J. Chem. Phys., 1984, 80, 5170–5186 CrossRef CAS.
- H. Tanaka, K. Nakanishi and H. Touhara, J. Chem. Phys., 1985, 82, 5184–5191 CrossRef CAS.
- E. S. Boek and W. J. Briels, J. Chem. Phys., 1993, 98, 1422–1427 CrossRef CAS.
- C. A. Nkuku and R. J. LeSuer, J. Phys. Chem. B, 2007, 111, 13271–13277 CrossRef CAS.
- A. M. Sakita, R. Della Noce, C. S. Fugivara and A. V. Benedetti, Phys. Chem. Chem. Phys., 2016, 18, 25048–25057 RSC.
- M. Kowsari, S. Alavi, M. Ashrafizaadeh and B. Najafi, J. Chem. Phys., 2008, 129, 224508 CrossRef CAS.
- A. P. Gaiduk, F. Gygi and G. Galli, J. Phys. Chem. Lett., 2015, 6, 2902–2908 CrossRef CAS.
- T. Todorova, A. P. Seitsonen, J. Hutter, I.-F. W. Kuo and C. J. Mundy, J. Phys. Chem. B, 2006, 110, 3685–3691 CrossRef CAS.
- C. Zhang, D. Donadio, F. Gygi and G. Galli, J. Chem. Theory Comput., 2011, 7, 1443–1449 CrossRef CAS.
- D. Hadži, J. Kidrič, Ž. V. Kneževic and B. Barlič, Spectrochim. Acta, Part A, 1976, 32, 693–704 CrossRef.
- B. Rousseau, C. Van Alsenoy, R. Keuleers and H. O. Desseyn, J. Phys. Chem. A, 1998, 102, 6540–6548 CrossRef CAS.
- R. Keuleers, H. O. Desseyn, B. Rousseau and C. Van Alsenoy, J. Phys. Chem. A, 1999, 103, 4621–4630 CrossRef CAS.
- Z. Dega-Szafran, K. Roszak, F. Safari, A. Komasa, A. Katrusiak and M. Szafran, J. Mol. Struct., 2020, 1206, 127695 CrossRef.
- J. Baran, A. Barnes, B. Engelen, M. Panthöfer, A. Pietraszko, H. Ratajczak and M. Sledz, J. Mol. Struct., 2000, 550–551, 21–41 CrossRef CAS.
- J.-J. Max and C. Chapados, J. Phys. Chem. A, 2004, 108, 3324–3337 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06078j |
| This journal is © the Owner Societies 2021 |