Rapid relaxation NMR measurements to predict rate coefficients in ionic liquid mixtures. An examination of reaction outcome changes in a homologous series of ionic liquids†
Daniel C.
Morris
 ab,
Stuart W.
Prescott
ab,
Stuart W.
Prescott
 *a and
Jason B.
Harper
*a and
Jason B.
Harper
 *b
*b
aSchool of Chemical Engineering, University of New South Wales, Sydney, NSW 2052, Australia. E-mail: s.prescott@unsw.edu.au; Fax: +61 2 9385 6141; Tel: +61 2 9385 4692
bSchool of Chemistry, University of New South Wales, Sydney, NSW 2052, Australia. E-mail: j.harper@unsw.edu.au
First published on 6th April 2021
Abstract
A series of ionic liquids based on the 1-alkyl-3-methylimidazolium cations were examined as components of the solvent mixture for a bimolecular substitution process. The effects on both the rate coefficient of the process and the NMR spin–spin relaxation of the solvent components of changing either the alkyl chain length or the amount of ionic liquid in the reaction mixture were determined. At a constant mole fraction, a shorter alkyl chain length resulted in a greater rate coefficient enhancement and a longer relaxation time, with the opposite effects for a longer alkyl chain length. For a given ionic liquid, increasing the proportion of salt in the reaction mixture resulted in a greater rate coefficient and a shorter relaxation time. The microscopic origins of the rate coefficient enhancement were determined and a step change found in the activation parameters on increasing the alkyl chain length from hexyl to octyl, suggesting notable structuring in solution. Across a range of ionic liquids and solvent compositions, the relaxation time from NMR measurements was shown to relate to the reaction rate coefficient. The approach of using fast and simple NMR relaxation measurements to predict reaction outcomes was exemplified using a morpholinium-based ionic liquid.
Introduction
Choosing the right solvent for a given application allows control over reaction outcomes, such as rate coefficients and selectivities; solvent effects of molecular solvents are well-described.1 Given the potential drawbacks of molecular solvents (such as volatility2), current research has been increasingly focussed on alternatives such as ionic liquids,3–5 which are arbitrarily defined as salts with a melting point below 100 °C.6 They have properties consistent with their ionic nature, such as negligible volatility7 and low flammability,8 which make them desirable over molecular solvents. Problems arise however when trying to predict the effect an ionic liquid will have on a given reaction outcome, as the solvent effects of such systems generally are not well understood (for a key early example see Earle et al.9), not least due to the vast range of different cation–anion combinations10 that can be used to tailor the physicochemical properties of the final salt.11In recent years, much work has gone into developing an understanding of ionic liquid solvent effects through the investigation of well-known organic processes, with work from groups including those of D’Anna,12–16 Pavez,17–20 and Welton,21–29 along with the Harper group (for a review see Hawker et al.30), contributing significantly. The Menschutkin reaction of benzyl bromide 1 with pyridine 2 (Scheme 1), a bimolecular nucleophilic substitution (SN2) process, has been the subject of numerous studies in reaction mixtures containing ionic liquids.31–42 Such studies have investigated the microscopic origins of the enhancement of the bimolecular rate coefficient (k2) in ionic liquid, with molecular dynamics and deconvolution studies33,34 indicating the origin of this effect lies in an interaction between the lone pair of electrons on the pyridine 2 and the cationic charged centre of the ionic liquid, with a large dependence on the accessibility of such charge. This interaction results in stabilisation of, and ordering of the ionic liquid about, the starting materials and manifests in the activation parameters for the process. On moving to a reaction mixture containing an ionic liquid, increases are seen in both the entropy of activation (ΔS‡, which decreases the activation energy) and the enthalpy of activation (ΔH‡, which increases the activation energy). The former effect is larger, resulting in an overall lowering of the activation energy and an entropy-driven rate coefficient enhancement. Importantly, the key interactions differ from those of other related bimolecular processes, such as those reported by Welton on SN2 processes with charged nucleophiles,22–26 so direct comparison to previous cases of ionic liquid solvent effects on this reaction is key.
 | ||
| Scheme 1 The Menschutkin reaction of benzyl bromide 1 with pyridine 2 to form benzylpyridinium bromide 3, studied in reaction mixtures consisting of varying proportions of ionic liquid and acetonitrile.31–42 | ||
Current understanding of ionic liquid solvent effects on this particular reaction allows the prediction of the general effects a given liquid will have on the rate coefficient by considering factors such as the cation structure and the proportion of ionic liquid in reaction mixture (for examples, see ref. 38). Although significant progress has been made in building this predictive framework and understanding the specific interactions that drive reaction outcomes, prediction of rate coefficient data is still typically qualitative; quantitative analysis requires extensive kinetic studies. It would hence be desirable to find alternative methods to predict quantitative rate coefficient data, such as using physical measurement techniques.
Solvent relaxation NMR (observed as either spin–lattice, T1, or spin–spin, T2, relaxation times) is a different technique to typical NMR spectroscopy and focuses on the time taken for the magnetic spin states of nuclei to return to equilibrium populations.43,44 Unlike spectroscopic NMR in which the NMR signal is Fourier transformed to provide chemical shifts and coupling constants, which may be used for the identification of unknown compounds, relaxation NMR is a time domain measurement probing the local physical and chemical environment around the NMR-active nucleus.45 While for spectroscopic NMR experiments, perdeuterated solvents are typically used so as to minimise the signal from the (uninteresting) solvent and permit the spectra of the desired molecules to be collected, solvent relaxation NMR rarely uses deuterated solvents as it is actually the 1H nuclei within the solvent that are measured. Since Fourier transforms to produce narrow-line spectra are not needed for relaxation NMR studies, and multipulse sequences can mitigate the effects of diffusion within the sample, there is no need for the extremely homogeneous magnetic field provided by the expensive superconducting magnet of spectroscopic systems; solvent relaxation NMR measurements are routinely performed in electromagnet, permanent magnet, and earth's magnetic field instruments, and linewidths upwards of 100 ppm are common.46 Since 1H is present in the solvent system in comparatively large quantities compared to a typical spectroscopic NMR experiment, the hardware requirements for the receiver chain of the instrument are modest, and the low-power amplifiers of bench-top instruments are sufficient.46,47
Solvent relaxation measurements are sensitive to the characteristic time for molecular reorientation (the correlation time, τc), and it is here that we must allow that there are two separate relaxation rates within the cylindrical coordinate system in the NMR, with a longitudinal relaxation time, T1, and a transverse relaxation time, T2, emerging from the Bloch equations as time constants for the first-order relaxations to equilibrium. Standard relationships between T1, T2 and τc are arrived at after considerable mathematics and, as this ground has been covered by many authors in the past, the interested reader is directed towards the work of seminal texts such as those by Carrington and McLachlan,48 and Farrar and Becker,45 or more recent work by Kowalewski and Mäler.49 In considering the links between τc, T1, and T2, Cooper et al.44 note that the sensitivity of the experiment to molecular motion can be enhanced by moving to low-field instruments; with the expense and complexity of a high-field superconducting spectroscopic NMR being unnecessary, the low-field bench-top instrument with its low purchase price and low running costs is a compelling hardware alternative.
In the context of ionic liquids, there is considerable literature covering the dynamics of ionic liquids, ion identity, and self-assembled nanostructures within the ionic liquid determined by X-ray and neutron scattering techniques.50–55 By indirectly probing τc, relaxation measurements are sensitive to molecular motion and solvent structuring, providing information about solvent–solvent,50–52,54 solvent–solute,56 and solvent–surface interactions.44,57,58 Applying this technique to ionic liquid mixtures may be able to provide useful information about the system dynamics and, in particular, T2 tends to be significantly influenced by entropic differences such as extent of molecular structuring in solution.59 As noted above, reaction kinetics in ionic liquid mixtures are sensitive to the entropy of the solvent, solvent structuring and solvent dynamics; the symmetry with the factors affecting T2 is pleasing and forms the basis for the work described here. Since both reaction and relaxation rate coefficients are influenced by solution structuring and solution entropy, it may be possible to correlate T2 of different ionic liquid mixtures with the corresponding k2 enhancement behaviours observed for the SN2 reaction outlined in Scheme 1. Importantly, low field T2 measurements are fast, taking less than one minute, permitting significant data to be obtained rapidly; T2 measurements can also be performed on inexpensive benchtop instruments.
Relaxation NMR measurements are not the only time-domain NMR measurements available for study of the dynamics of solvent molecules such as ionic liquids, with pulsed-field gradient NMR diffusion measurements yielding considerable information on solvent dynamics and the interactions between solvent and solute. Diffusion measurements are highly sensitive to relevant features, such as the formation of molecular clusters within the solvent and ion pairing, and have been applied to ionic liquids.50,60 Particularly, work on diffusion in mixtures of ionic liquids has shown the importance of the solvent composition (which affects boundary conditions), the presence of “cage” and “jump” events and the potential of this method to evaluate interactions between solute and solvent.61 While some low-field benchtop instrumentation is available to perform diffusometry, the throughput of the measurement is much less than the relaxometry measurements, precluding its use in exploratory or screening studies.
The ionic liquids literature has established the importance of solvent structuring on the chemical kinetics of reactions performed in ionic liquids and their mixtures with other solvents,30 with the initial solvent structure significantly influencing the solvent reorganisation that is needed to take the reactants to their transition state and thus the entropic contribution to the activation energy. As noted above, NMR relaxation measurements are also sensitive to solvent structures and it is for this reason that the relationships between relaxation rates and reaction rate coefficients were explored in this work. From the NMR perspective, both T1 and T2 are sensitive to solvent reorganisation dynamics and the Bloembergen–Purcell–Pound formulation43 indicates that T1 and T2 would both be sensitive for the systems of interest here; however, from a purely practical point of view, the two-component fitting that is described in detail here is more robust with more points in the time domain measurement, and thus T2 measurements (with thousands of points acquired in seconds from a traditional CPMG sequence) are preferred over T1 measurements (relatively few points over a longer period of time from a traditional inversion recovery pulse sequence).
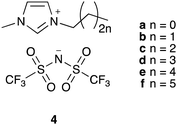
To explore the potential to correlate physical measurements of ionic liquid mixtures with kinetic outcomes in those mixtures, we investigated the effects of a homologous series of ionic liquid – the 1-alkyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imides ([C2n+2C1im][N(SO2CF3)2], 4a–f; Fig. 1) – on the rate coefficient of the reaction shown in Scheme 1. This series was selected because altering the steric nature of the cation is known to affect the value of k2 (for example, see ref. 34) and such changes are also expected to influence T2 for each system, indicating these data might be correlated. Hence, the work described in this manuscript details the relaxation behaviour of components of mixtures containing a range of proportions of the [C2n+2C1im][N(SO2CF3)2] 4 series of ionic liquids, as well as their effect on reaction kinetics, and any links between these results.
Experimental
The ionic liquids 4a–f were synthesised according to literature methods, through alkylation of particularly N-methylimidazole with the appropriate n-alkyl bromide, both freshly distilled immediately before use, followed by anion metathesis; full experimental details are given in the ESI.†Benzyl bromide 1 was distilled and stored over molecular sieves at 6 °C away from light until use, pyridine 2 was distilled and stored over molecular sieves and sodium hydroxide pellets at −20 °C until use, acetonitrile was distilled from phosphorous pentoxide and stored in an inert nitrogen atmosphere until use.62 Each of the ionic liquids 4a–f and 5 was dried in vacuo for at least 5 hours to result in a water concentration of less than 100 ppm as measured by Karl–Fischer titration.
Kinetic analyses investigating the effect of varying proportions of ionic liquid were carried out under pseudo-first order conditions (ca. 0.5 ml of reaction mixture, minimum 10-fold excess of pyridine 2 – ca. 0.5 mol L−1, ca. 3 mg benzyl bromide 1) and followed using 1H NMR spectroscopy at 295.35 K on either a Bruker Avance III 400 (400 MHz, 1H), Bruker Avance III 500 (500 MHz, 1H) or Bruker Avance III 600 (600 MHz, 1H), using a TBI, BBO or BBFO probe. Results were shown to be consistent between spectrometers and probes. The temperature of the spectrometer was set and measured using an external thermocouple prior to each experiment. Details of all solvent compositions are given in Tables S1–S5 (ESI†).
Reactions were monitored until at least 95% of the starting material 1 was consumed. Spectra were processed using MestReNova software to measure depletion of the integral at δ ca. 4.6 ppm representing the benzylic protons on the starting material 1. Fitting of the resultant data allowed calculation of the pseudo-first order rate coefficient (kobs), which was subsequently divided by the initial concentration of the nucleophile, 2, to determine the second order rate coefficient for each reaction (k2). All rate coefficient data is provided in Table S6 (ESI†). Activation parameters for each temperature dependence study were obtained by fitting the data to the bimolecular form of the Eyring equation;31,63 the corresponding Eyring plots are presented in the ESI† as Fig. S2.
Relaxation measurements were taken using a Mageleka MagnoMeter XRS bench-top NMR spectrometer (13.5 MHz, 1H, 295.35 ± 1 K) using 5 mm NMR tubes containing the same samples used for kinetic analyses of each system, except for systems containing salt 4b. For that case, where kinetics data were already available, stock solutions were made mirroring the compositions used in previous studies.37 The T2 relaxation time was measured using the CPMG pulse sequence64,65 with a 90° pulse length of ca. 4.7 μs and a pulse spacing between the 180° pulses of 1.0 ms. Echoes were collected out to at least five times the apparent T2 of the sample to ensure that the entire relaxation profile was observed, meaning that between 200 and 9000 echo cycles were collected depending on the sample, with most samples being around 2000 echo cycles. A recycle delay of at least five times the measured T1 for each system was allowed. T1 relaxation times for each system were acquired through application of the inversion recovery method on the same instrument. The manufacturer-recommended CPMG protocol for the instrument was used, which records a single scan without phase cycling; the ratio of the signal to the rms noise in the CPMG trace was greater than 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
Results and discussion
Kinetic analyses
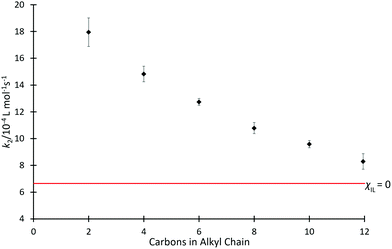
Kinetics studies were initially completed for mixtures containing each of the ionic liquids [C2n+2C1im][N(SO2CF3)2] 4 in acetonitrile, at the same, high mole fraction (χILca. 0.8) (Fig. 2); high proportions of salt in the reaction mixture have been shown previously to have the greatest effects on reaction outcome for this particular reaction (for example, see ref. 37 and 38). For those reaction mixtures that contain each of the six ionic liquids 4a–f (χILca. 0.8), the rate coefficients are all measurably faster than in neat acetonitrile; this is consistent with previous reports (see, most recently, ref. 42). A clear trend is seen with an increase in the length of alkyl chain, which results in a decrease in the rate coefficient.Since alkyl chains have similar electronic properties irrespective of their length, the cations of these ionic liquids would be expected to have similar electronic character; any small change would not be expected to result in the large change in the key interactions identified above that would be needed to explain the observed changes in rate coefficient. Notably, however, the steric features of the cation become more significant across the series as chain length increases. The observed trend is consistent with greater steric hindrance from the larger alkyl chains reducing the cation–nucleophile interaction, which is known to cause the rate coefficient enhancement and thus the decreasing rate coefficient with increasing chain length.33 The trend appears to approach an asymptotic value of k2 (near that observed in acetonitrile) as chain length increases, however, investigating this further is impractical due to solubility limitations of higher homologues of [C2n+2C1im][N(SO2CF3)2] in acetonitrile.66 The origins of this trend will be revisited below.
The above data demonstrate the effects of each of the ionic liquids 4 on the rate coefficient of the reaction shown in Scheme 1. However, ionic liquids are frequently used in mixtures with molecular solvents and the proportion of salt in the mixture can have a significant effect,30 so it is of interest to consider the solvent effects of mixtures containing the ionic liquids 4. Previous studies have investigated the dependence of k2 for the reaction of species 1 and 2 on the proportion of [C4C1im][N(SO2CF3)2] 4b in the reaction mixture (see, for example, ref. 37 and 38), with an initially rapid increase in rate coefficient seen at low values of χIL, followed by a slower, but steady increase at higher mole fractions. To determine whether this behaviour is affected by the length of the alkyl chain, rate coefficient data was determined in mixtures containing [C2n+2C1im][N(SO2CF3)2] 4a, c, d, f at different proportions in acetonitrile (Fig. 3). The equivalent data for ionic liquid 4b has been reported,37 whilst the small change in rate coefficient enhancement for the higher homologues suggested that determining the data for all salts 4d–f was likely redundant and, as such, ionic liquid 4e was left out of the series.
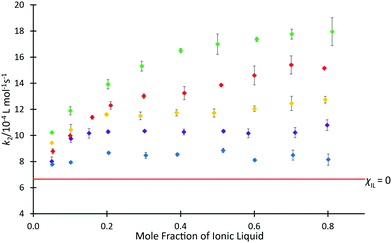 | ||
Fig. 3 The bimolecular rate coefficient (k2) for the reaction of benzyl bromide 1 and pyridine 2 at 22.2 °C in mixtures containing different proportions of either [C2C1im][N(SO2CF3)2] 4a ( ), [C4C1im][N(SO2CF3)2] 4b ( ), [C4C1im][N(SO2CF3)2] 4b ( ),37 [C6C1im][N(SO2CF3)2] 4c ( ),37 [C6C1im][N(SO2CF3)2] 4c ( ), [C8C1im][N(SO2CF3)2] 4d( ), [C8C1im][N(SO2CF3)2] 4d( ), or [C12C1im][N(SO2CF3)2] 4f ( ), or [C12C1im][N(SO2CF3)2] 4f ( ) in acetonitrile, and in acetonitrile ( ) in acetonitrile, and in acetonitrile ( ). Uncertainties are reported as the standard deviation of at least triplicate results. Some uncertainties fall within the size of the markers used. ). Uncertainties are reported as the standard deviation of at least triplicate results. Some uncertainties fall within the size of the markers used. | ||
The mole fraction dependence of the rate coefficients in mixtures containing one of the homologous series 4 in acetonitrile clearly varies with the length of the alkyl chain. For the ionic liquid with longest chain considered, [C12C1im][N(SO2CF3)2] 4f, an increase in the value of k2 compared to acetonitrile was observed up to χILca. 0.05, followed by only minor variations in the rate coefficient. That is, the plot is flatter than seen previously for mixtures containing [C4C1im][N(SO2CF3)2] 4b.37 Similar plateau-like behaviour was also seen in the [C8C1im][N(SO2CF3)2] 4d system, though the magnitude of rate coefficient was consistently higher than the twelve-carbon system 4f at equivalent mole fractions.
In contrast, the shorter-chain systems investigated, ([C2C1im][N(SO2CF3)2] 4a and [C6C1im][N(SO2CF3)2] 4c) both exhibit similar behaviour to [C4C1im][N(SO2CF3)2] 4b, with increases in k2 occurring across the entire range of solvent compositions. At each mole fraction, the ionic liquid with the shorter alkyl substituent 4a consistently resulted in the largest enhancement of rate coefficient for the ionic liquids considered. The magnitude of the rate coefficient enhancement in mixtures containing [C6C1im][N(SO2CF3)2] 4c was not as large as for the two-carbon system 4a, consistent with the previously observed trend of increasing length of alkyl chain causing a decrease in k2 (see for example, ref. 38). Despite this, there is still an additional benefit to the reaction rate seen for each increasing proportion of ionic liquid. Observing the trends present in these data, particularly the tendency of the larger homologues to cause a plateau in k2 values at higher mole fractions, it was suggested that steric hindrance may not be the only influence on rate coefficient.
In order to further understand the microscopic origins of the rate coefficient enhancements seen and to compare them to those reported previously, temperature dependent studies were carried out. These experiments were carried out at the same, high proportion of ionic liquid (χILca. 0.8); this proportion has been considered previously (see, for example, ref. 38) and might be considered most similar to ‘in an ionic liquid only’ (mole fractions higher than this are impractical due to dilution by the reagent in excess, pyridine 2, under pseudo-first order conditions). The activation parameters obtained are presented in Table 1.
| Solvent | χ IL | ΔH‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/kJ mol−1 a/kJ mol−1 |
ΔS‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/J K−1 mol−1 a/J K−1 mol−1 |
|---|---|---|---|
| a Uncertainties quoted are derived from the fit of the linear regression. b Data reproduced from Hawker et al.36 c Data reproduced from Yau et al.31 | |||
| Acetonitrileb | 0 | 44.7 ± 0.8 | −220 ± 3 |
| 4a | 0.81 | 50.2 ± 0.8 | −192 ± 3 |
| 4b | 0.86 | 49.9 ± 0.8 | −195 ± 3 |
| 4c | 0.79 | 49.5 ± 0.5 | −198 ± 2 |
| 4d | 0.79 | 53.8 ± 0.7 | −185 ± 2 |
| 4f | 0.80 | 54.1 ± 1.0 | −186 ± 3 |
In all cases, on moving from acetonitrile to mixtures containing each of the ionic liquids 4a–d, f, there is an increase in both the entropy of activation and the enthalpy of activation. (Note that the magnitude of the activation entropy decreases, but the value increases; that is, it becomes more positive.) These changes are consistent with what has been seen previously for other ionic liquids (for example, see ref. 38) and suggests that the microscopic origin of the rate coefficient increase seen is both the same in each case here and consistent with that seen previously. Increases in both the activation enthalpy and entropy are the result of increased organisation of the solvent around the starting material(s); the increase in the entropy of activation dominates, resulting in the rate coefficient increase.
Of note here, however, is that the magnitude of the changes in activation parameters are different across the systems 4a–d, f considered. That is, the change in each of the enthalpy and entropy of activation on moving from acetonitrile to an ionic liquid is not the same for each of the cases containing the salts 4a–d, f. For the mixtures containing the salts with imidazolium cations with the shorter alkyl chains (4a–c), the enthalpy and entropy of the reaction have the same value (ca. 50 kJ mol−1 and ca. −195 J K−1 mol−1, respectively), values that are consistent with those previously reported for the reaction in mixtures containing a range of mono-cationic ionic liquids (for example, see ref. 24 and 38); the change in the activation entropies for the cases involving salts 4a and 4c are beyond the uncertainty limits, however, this difference is very small compared to the other differences considered here and previously. Hence, any changes in microscopic interactions that determine rate coefficients are sufficiently small as not to be measurable. These similarities are consistent with previous evaluation of activation parameters, where the effects of different ionic liquids in terms of microscopic interactions is effectively indistinguishable.38 While the activation parameter data are indistinguishable for the reaction in either ionic liquids 4a–c or 4d, e, the rate coefficient data differ (Table 1). This result is due to uncertainties in the activation parameter data which, whilst reasonable, are large relative to the differences between the rate coefficients measured.
For the mixtures containing salts based on imidazolium cations with the longer alkyl chains (4d, f), the values of the activation parameters differ from both cases involving the shorter alkyl chain systems (4a–c) as well as other previously reported mono-cationic systems (for example, see ref. 24 and 38). Significant increases in both ΔH‡ and ΔS‡ are seen for the mixtures containing each of the salts 4d and 4f relative to the cases involving the salts 4a-c, though no distinction can be made between the 4d and 4f cases.
These different activation parameters suggest changes in the interactions involving the ionic liquids 4d, f that would result either from a different or (more likely) an additional interaction than is observed for the salts 4a–c. To our knowledge, the only example in which such a change has been seen previously involved ionic liquids containing cations made up of two imidazolium centres linked by an alkyl chain; the dependence of the effect on the length of the alkyl chain implied that this is the result of a bidentate interaction.40 Such interactions are not the cause here, rather structuring in solution is postulated to be the underlying origin.
The change in activation parameters for this reaction in mixtures containing the homologous series 4 occurs as the chain length increases from six to eight carbons. The change occurring at this point suggests that it might be related to a greater degree of organisation in the solvent mixture that has to be overcome on reaction occurring and one potential origin is the formation of aggregates. This argument is similar to that around the change in structuring seen at charged interfaces between heptyl and decyl substituents.67 Note that the changes in the activation parameters observed take into account both changes to the organisation of the solvent and changes to the key interaction between the cation of the ionic liquid and the nucleophile 2; deconvoluting these effects simply with these data is not possible though computational studies in the gas phase suggest that there is a decrease in the key interaction on increasing chain length on the cation.41
Relaxation time analyses
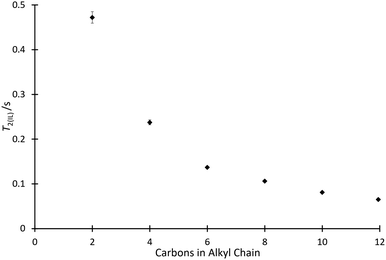
With the effect of the homologous series of salts 4 on k2 determined, it was of interest to consider how other physical measurements vary with the solvent composition. As such, 1H solvent relaxation NMR was used to determine the spin–spin relaxation times of mixtures containing the ionic liquids 4.The T2 data for the systems of interest exhibited behaviour which deviated from a single exponential, and hence two exponential components were resolved from the data using a non-linear least squares regression (using SciPy68) to give T2(IL) (referring to the relaxation time of the ionic liquid component of the solution) and T2(non-IL) (referring to the relaxation time of the non-ionic liquid component of the solution) for each solvent mixture considered. (The procedure for two-component fitting is included in the ESI,† along with specific parameters used for each individual mixture.) Initially considered were mixtures containing the ionic liquids 4a–f at χILca. 0.8 (Fig. 4). This proportion matches the proportion considered in the kinetic analyses above, allowing comparison.
The relaxation data show that as the length of the alkyl chain increases for the [C2n+2C1im][N(SO2CF3)2] 4 series, there is a decrease in the spin–spin relaxation time component due to the ionic liquid.‡ The trend shown in Fig. 4 is similar to that shown in Fig. 2 and this will be commented on further below. Compounds with larger molecular weights tend to exhibit shorter relaxation times and this has been shown for, particularly, simple hydrocarbons.69,70 Of interest, when considering a power law for the relationship of the chain length with relaxation time, as has been done previously for alkanes,69 a linear relationship was found with the length of the alkyl chain, not with the increase in overall molecular weight (for example, see Fig. S10 and S11, ESI†). Importantly, this suggests that other features changing in the solvent, particularly increased structuring in the bulk solution, are important.
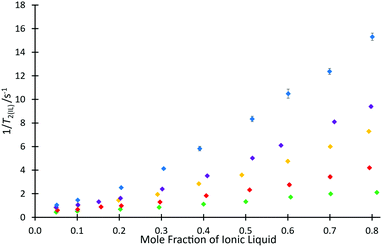
To investigate the ability for fast and simple relaxation time measurements to predict the reaction behaviour with different cations of this homologous series, the same measurements of T2(IL) were performed for each ionic liquid mixture that was studied in the kinetic analyses across different proportions of ionic liquid and molecular solvent in the reaction mixture (hence, salt 4e was excluded). These data are plotted as 1/T2(IL) against mole fraction of ionic liquid (Fig. 5), to more clearly depict the differences in relaxation behaviours; as is standard practice, the relaxation rate, 1/T2(IL), is used here as it is indicative of the number and strength of intermolecular interactions through their input on the molecular correlation time.43,44
For every system, there is a clear trend of increasing relaxation rate as the mole fraction of ionic liquid increases.‡ At a macroscopic length scale, this result clearly follows well known correlations between solution viscosity and relaxation rates; however, given that solvent structuring is understood to control the rate coefficient for this reaction (see, for example, ref. 31), it is possible to go beyond a mere correlation with viscosity and look for molecular level explanations of both the NMR and reaction rate data presented here. Further, it is noted that viscosity alone does not explain the observed reaction rate coefficient data (Fig. 3), with higher viscosity solutions exhibiting higher rate coefficients for each individual ionic liquid, but lower rate coefficients on moving to longer alkyl chain lengths. It is seen that the relaxation rates are consistent with the changing composition of solution affecting the microscopic structure that determines relaxation. Also notable is that at any mole fraction, the values of 1/T2(IL) are all consistently higher in ionic liquid systems containing longer alkyl chains; this trend is indicative of changing solution dynamics owing to changing solvent structures and demonstrates that changing the alkyl chain length has a consistent and measurable impact on the solvent structure and therefore reactions undertaken in them.
This difference can be rationalised not only by noting that including a longer alkyl chain results in an increase to the molecular mass of the cation and consequently an expected reduction in the relaxation time, but this trend also reflects a higher degree of structuring in the longer chained systems. Analysis of the ratio of relaxation times for any two ionic liquids across the solvent compositions considered is also useful; it might be expected that if structuring were the same in all cases then this value would remain constant. This is not the case (see Fig. S12, ESI†), showing that there is increased structuring with increased proportion of ionic liquid in the reaction mixture. Further, the change is greater the longer the alkyl chain, with a notable difference between the hexyl 4c and octyl 4d cases.
Another consideration worth noting is a change in the solvent that contributes the greater number of spins; this occurs at χILca. 0.2 (depending on the salt) and relates to a transition seen previously where the solvent contributing the greatest volume fraction changes.53 One may see this point as the one in which the solvent changes from “ionic liquid dissolved in acetonitrile” to “acetonitrile dissolved in ionic liquid”, noting that with longer alkyl chains on the salt, smaller mole fractions of ionic liquid will be required to reach this point (though the changes are not large given the relative size of acetonitrile and the ionic liquids 4; see ESI†). Such a change in solvent composition is expected to result in a change in solvent structure and it is conceivable that the change in solvent manifests as the change in slope seen in Fig. 5, noting that the process is gradual and is more pronounced the longer the alkyl chain on the cation (see Fig. S13–S17, ESI†).
Correlating relaxation behaviour with rate coefficients and its potential application
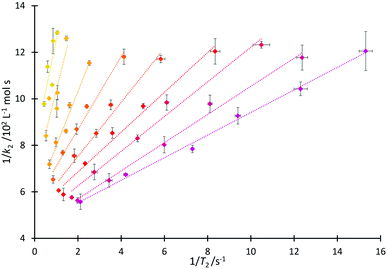
That both T2 and k2 are sensitive to structure and dynamics within the solvent invites further investigation of these data. In the case of the homologous series 4, increased structuring in solution associated with longer alkyl sidechains would be expected to cause a faster T2 relaxation time, consistent with the trend observed in Fig. 4 and matching the discussion above. Including longer alkyl side chains would also be expected to cause steric hindrance (and organisation in solution) which would vary the extent of interaction of the cation of the salt with pyridine 2 and thus affect the value of k2, again as has been argued above. As such, it is proposed that it may be possible to draw correlations linking T2 and k2.A linear relationship was observed for 1/k2 with 1/T2(IL), producing the correlation depicted in Fig. 6 (see Fig. S18 and S19, ESI,† for other relationships that were considered but found to be inadequate). From this figure, it can be seen that at a high mole fraction of ionic liquid in the reaction mixture, the correlation of 1/k2 and 1/T2(IL) is excellent. The fits remain extremely good for all of the proportions of salt in the reaction mixture considered, down to low mole fractions (χIL < 0.2) where the smaller dynamic ranges likely affect the correlation. (There are similar correlations between the rate and the spin–spin relaxation time measured for the non-ionic liquid component of the reaction mixture; this will become significant in subsequent correlations (vide infra).) These linear relationships shown in Fig. 6 are important as they allow the calculation of the rate coefficient of the reaction in mixtures containing any member of this series 4. Importantly, this could be extended to other members of the homologous series (the differences between different series are highlighted below); that is, taking data from one system as the basis for predicting an outcome in another.
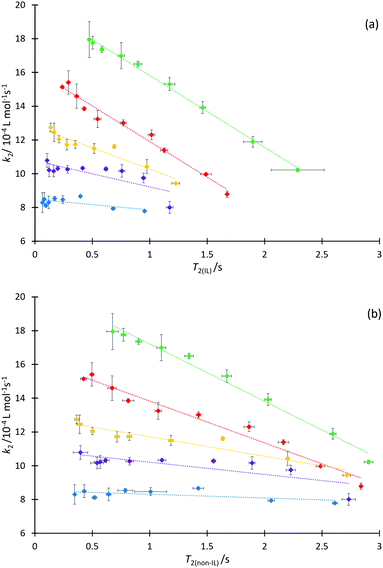
We next consider each of the ionic liquids 4a–f as the solvent composition was varied. Solvent structuring and the associated interactions with the starting material 2 would also be expected to vary across the proportion of ionic liquid in the mixture, with this variation differing according to the identity of the ionic liquid and the structuring it imparts onto the solvent mixture. The behaviour of each individual ionic liquid at varied proportions in the reaction mixture is more complex than at a single mole fraction (the cases represented in Fig. 6 above), however excellent correlations were observed on plotting k2 and T2(IL) directly (Fig. 7a), contrasting the inverse relationship seen across the homologous series as was seen for individual mole fractions shown in Fig. 6 (other correlations of 1/T2(IL) against either k2 or 1/k2 did not give as good a fit and were considered inappropriate, see Fig. S20 and S21, ESI†). It is particularly worth noting here that the contribution to T2 from the remainder of the solution, T2(non-IL), also has an excellent correlation with the rate coefficient (Fig. 7b).
Immediately obvious from these plots is that the fits are best for systems with the shorter alkyl chains. Likely contributing to this effect is that the range of the kinetic data decreases significantly with increasing alkyl chain length. Bearing in mind the previously presented argument (that the change in activation parameter data was a function of the onset of organisation in solution), the deviations seen here indicate that perhaps structuring alone cannot influence T2 significantly enough to accurately mirror the trend in the mole fraction dependent behaviour of k2 in systems which exhibit such significant ordering, though it is important to understand why this is the case.
It is known that the rate coefficient enhancement of this reaction in ionic liquids is entropically driven and that it is increased structuring/reduced solvent dynamics within the solvent system that principally leads to this change in entropy (see, for example, ref. 38); as described above, that same reduction in solvent dynamics leads to a decrease in T2.49 Decreases observed in T2 are a direct result of increased order and structuring in solution (such as due to longer alkyl chains), however as the proportion of ionic liquid is varied, other factors also contribute to T2 values. At a constant mole fraction however, there is no significant variation in the molar ratio of cations affecting relaxation of the observed proton signals; the mixtures are as similar as possible such that the only significant contribution to variation in T2(IL) should be any dynamical differences due to changing the alkyl chain length.
The data shown in Fig. 5–7 indicate that a small number of kinetics measurements can be used alongside more extensive relaxation NMR measurements to predict reaction rate coefficients. Whilst rate coefficient prediction directly, without any kinetics measurements, is not possible we demonstrate the power of this approach using solvent mixtures containing the ionic liquid 4-butyl-4-methylmorpholinium bis(trifluoromethanesulfonyl)imide ([C4C1mo][N(SO2CF3)2], 5; Fig. 8) and previously published rate coefficient data.38 NMR relaxation times for this system were measured as a function of the proportion of salt 5 in the reaction mixture, showing similar behaviour (see Fig. S22, ESI†) to ionic liquids 4a–d, f (Fig. 5). While the salts 4 and 5 are different, and organisation in solution would be expected to also differ, it is possible to use an empirical relationship between the rate coefficients and the relaxation time to predict the reaction rate coefficient for a given mixture. This relationship requires two additional rate coefficient measurements, that then allow us to interpolate further k2 values from:
| k2(predicted) = 3.40 × 10−3 − 8.51 × 10−4 × T2(non-IL) | (1) |
 | ||
| Fig. 8 The morpholinium-based ionic liquid 5 that was considered to demonstrate the ability to predict reaction outcome. | ||
In Fig. 9, we use rate coefficient data at χIL = 0.0 and 0.7 for salt 5 to determine the two unknown coefficients for the correlation, thereby determining k2 as a function of χIL for salt 5 (see ESI,† Table S19, for further details). This figure also shows previously reported mole fraction dependent kinetic data for the ionic liquid 5, demonstrating that the relaxation NMR-based prediction and the experimentally determined reaction rate coefficients are consistent, along with the potential utility of this method. The ability to determine the equivalent data along a homologous series is anticipated, though no such data currently exists in literature for the morpholinium salts to allow comparison.
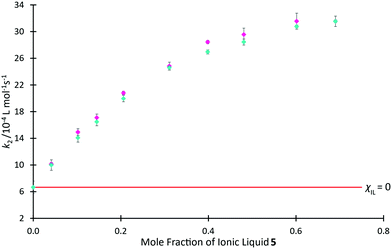 | ||
Fig. 9 The experimentally measured value of k2 ( ) associated with the reaction of benzyl bromide 1 and pyridine 2 when performed in mixtures containing varying proportions of [C4C1mo][N(SO2CF3)2] 5 in acetonitrile, reproduced from Hawker et al.,38 compared to the predicted value of k2 ( ) associated with the reaction of benzyl bromide 1 and pyridine 2 when performed in mixtures containing varying proportions of [C4C1mo][N(SO2CF3)2] 5 in acetonitrile, reproduced from Hawker et al.,38 compared to the predicted value of k2 ( ) calculated using T2(non-IL) for mixtures with the same compositions. Uncertainties are reported as either the standard deviation of replicate results (experimental k2) or the propagation of uncertainties associated with each of the two points used to form the prediction equation as well as the individual T2(non-IL) value used in calculation of each point (predicted k2).§ ) calculated using T2(non-IL) for mixtures with the same compositions. Uncertainties are reported as either the standard deviation of replicate results (experimental k2) or the propagation of uncertainties associated with each of the two points used to form the prediction equation as well as the individual T2(non-IL) value used in calculation of each point (predicted k2).§ | ||
It is important to reiterate that these predicted data are based on linear approximations involving other kinetic data; they are not based on relaxation NMR measurements only. With this in mind, the relaxation NMR measurements reported here utilise inexpensive bench-top NMR hardware with each measurement taking ca. 30 s to complete. With just two kinetic NMR experiments, the relaxation measurements were used to generate robust mathematical models to predict the reaction rate coefficient as a function of mole fraction across the entire mole fraction series, saving many hours of (expensive) high-field NMR time.
It is appropriate to reflect on the predictions described in this section and the implications for future research on such solvent mixtures. It is anticipated that future spectrally resolved NMR relaxation, NMR diffusion, small-angle X-ray scattering and inelastic neutron scattering experiments will further elucidate the structure–function relationships that are being probed by the NMR relaxometry measurements described here.
Conclusions
Ionic liquids in the [C2n+2C1im][N(SO2CF3)2] 4 homologous series all affected the bimolecular rate coefficient for the reaction of benzyl bromide 1 and pyridine 2, with increases seen across different proportions of salt in the reaction mixture as seen previously. The longer the alkyl chain, the smaller the rate coefficient enhancement, noting that temperature dependent studies have shown that upon increasing alkyl chain length from six to eight carbons, there is a step-change in each of the activation enthalpy and activation entropy associated with the strength of the specific microscopic interactions responsible for the rate constant enhancement. This latter result is significant as it is the first time a simple, mono-cationic system has displayed measurably different activation parameters for the Menschutkin reaction, compared to other ionic liquid mixtures.Changes similar to those seen in the rate coefficient data were observed in the spin–spin relaxation time of these mixtures. Each ionic liquid in the homologous series exhibited a different dependence of relaxation rate on mole fraction due to dynamical differences caused by changing alkyl chain length. Comparison of these NMR relaxation data with kinetic data allowed correlation of relaxation time with rate coefficient such that accurate, quantitative determination of k2 across the homologous series at the same mole fraction is possible using NMR relaxometry. This outcome is particularly important because it is the first example demonstrating a relationship between rate coefficient data in ionic liquids and a separate, simple, rapid physical measurement that could be used to obtain a rate coefficient, overcoming the need for extensive kinetic analysis.
In a single ionic liquid, closer correlation across mole fraction seems to be favoured by systems which exhibit less structuring. Hence, T2 measurements might be used as a tool to obtain quantitative values of k2 at any mole fraction, with more accurate data available in systems with larger dynamic ranges of k2. Significantly, this was demonstrated for an example salt outside the initial homologous series considered. Here, we also demonstrate a strong nexus between NMR relaxation times, reaction kinetics and solvent structures that is both informative in explaining the causal links and transformative in providing additional predictive power.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
DCM and JBH acknowledge financial support from the Australian Research Council Discovery Project Funding Scheme (Project DP180103682). We would like to thank Prof. Mark Rutland (KTH, Stockholm) for useful discussions on organisation in solution, Dr Ron Haines (UNSW Sydney) for regular meetings and advice on sensible data presentation, and Dr Alyssa Gilbert for synthesis of additional ionic liquid to analyse. The authors also acknowledge the NMR facility in the Mark Wainwright Analytical Centre at the University of New South Wales for high-field NMR support and Mageleka for provision of the MagnoMeter XRS low field NMR spectrometer. DCM would like to thank his brother, Adrian Morris, for countless coding interventions to allow more efficient data processing.Notes and references
- M. B. Smith and J. March, March's advanced organic chemistry: reactions, mechanisms, and structure, Wiley-Interscience, New York, 2007 Search PubMed.
- G. S. Gardner and J. E. Brewer, Ind. Eng. Chem., 1937, 29, 179–181 CrossRef CAS.
- T. Welton, Chem. Rev., 1999, 99, 2071–2083 CrossRef CAS PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- T. Welton, Biophys. Rev., 2018, 10, 691–706 CrossRef CAS PubMed.
- J. S. Wilkes, J. Mol. Catal. A: Chem., 2004, 214, 11–17 CrossRef CAS.
- F. Heym, B. J. M. Etzold, C. Kern and A. Jess, Green Chem., 2011, 13, 1453–1466 RSC.
- S. Zhang, N. Sun, X. He, X. Lu and X. Zhang, J. Phys. Chem. Ref. Data, 2006, 35, 1475–1517 CrossRef CAS.
- M. J. Earle, S. P. Katdare and K. R. Seddon, Org. Lett., 2004, 6, 707–710 CrossRef CAS PubMed.
- J. D. Holbrey and K. R. Seddon, Clean Prod. Processes, 1999, 1, 223–226 Search PubMed.
- C. Dai, J. Zhang, C. Huang and Z. Lei, Chem. Rev., 2017, 117, 6929–6983 CrossRef CAS PubMed.
- F. D’Anna, V. Frenna, R. Noto, V. Pace and D. C. Spinelli, J. Org. Chem., 2006, 71, 5144–5150 CrossRef PubMed.
- F. D’Anna, V. Frenna, S. La Marca, R. Noto, V. Pace and D. C. Spinelli, Tetrahedron, 2008, 64, 672–680 CrossRef.
- F. D’Anna, S. La Marca and R. Noto, J. Org. Chem., 2008, 73, 3397–3403 CrossRef PubMed.
- F. D’Anna, S. La Marca, P. Lo Meo and R. Noto, Chem. – Eur. J., 2009, 15, 7896–7902 CrossRef PubMed.
- F. D’Anna, D. Millan and R. Noto, Tetrahedron, 2015, 71, 7361–7366 CrossRef.
- D. Millán, M. Rojas, P. Pavez, M. Isaacs, C. Diazb and J. G. Santosa, New J. Chem., 2013, 37, 3281–3288 RSC.
- P. Pavez, D. Millan, J. I. Morales, E. A. Castro, A. C. Lopez and J. G. Santos, J. Org. Chem., 2013, 78, 9670–9676 CrossRef CAS PubMed.
- P. Pavez, D. Millán, C. Cocq, J. G. Santos and F. Nome, New J. Chem., 2015, 39, 1953–1959 RSC.
- P. Pavez, D. Millan, J. I. Morales, M. Rojas, D. Cespedes and J. G. Santos, Org. Biomol. Chem., 2016, 14, 1421–1427 RSC.
- T. Fischer, A. Sethi, T. Welton and J. Woolf, Tetrahedron Lett., 1999, 40, 793–796 CrossRef CAS.
- N. L. Lancaster, T. Welton and G. B. Young, J. Chem. Soc., Perkin Trans. 2, 2001, 2267–2270 RSC.
- A. Aggarwal, N. L. Lancaster, A. R. Sethi and T. Welton, Green Chem., 2002, 4, 517–520 RSC.
- N. L. Lancaster, P. A. Salter, T. Welton and G. B. Young, J. Org. Chem., 2002, 67, 8855–8861 CrossRef CAS PubMed.
- L. Crowhurst, N. L. Lancaster, J. M. P. Arlandis and T. Welton, J. Am. Chem. Soc., 2004, 126, 11549–11555 CrossRef CAS PubMed.
- N. L. Lancaster and T. Welton, J. Org. Chem., 2004, 69, 5986–5992 CrossRef CAS PubMed.
- L. Crowhurst, R. Falcone, N. L. Lancaster, V. Llopis-Mestre and T. Welton, J. Org. Chem., 2006, 71, 8847–8853 CrossRef CAS PubMed.
- I. Newington, J. M. Perez-Arlandis and T. Welton, Org. Lett., 2007, 9, 5247–5250 CrossRef CAS PubMed.
- J. P. Hallett, C. L. Liotta, G. Ranieri and T. Welton, J. Org. Chem., 2009, 74, 1864–1868 CrossRef CAS PubMed.
- R. R. Hawker and J. B. Harper, Adv. Phys. Org. Chem., 2018, 52, 49–85 CrossRef CAS.
- H. M. Yau, A. G. Howe, J. M. Hook, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2009, 7, 3572–3575 RSC.
- H. M. Yau, S. J. Chan, S. R. D. George, J. M. Hook, A. K. Croft and J. B. Harper, Molecules, 2009, 14, 2521–2534 CrossRef CAS PubMed.
- H. M. Yau, A. K. Croft and J. B. Harper, Faraday Discuss., 2012, 154, 365–371 RSC.
- E. E. L. Tanner, H. M. Yau, R. R. Hawker, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 6170–6175 RSC.
- S. T. Keaveney, D. V. Francis, W. Cao, R. S. Haines and J. B. Harper, Aust. J. Chem., 2015, 68, 31–35 CrossRef CAS.
- R. R. Hawker, J. Panchompoo, L. Aldous and J. B. Harper, ChemPlusChem, 2016, 81, 574–583 CrossRef CAS PubMed.
- K. S. Schaffarczyk McHale, R. R. Hawker and J. B. Harper, New J. Chem., 2016, 40, 7437–7444 RSC.
- R. R. Hawker, R. S. Haines and J. B. Harper, Chem. Commun., 2018, 54, 2296–2299 RSC.
- K. S. Schaffarczyk McHale, M. J. Wong, A. K. Evans, A. Gilbert, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2019, 17, 9243–9250 RSC.
- K. T.-C. Liu, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2020, 18, 7388–7395 RSC.
- A. Schindl, R. R. Hawker, K. S. Schaffarczyk McHale, K. T.-C. Liu, D. C. Morris, A. Y. Hsieh, A. Gilbert, S. W. Prescott, R. S. Haines, A. K. Croft, J. B. Harper and C. M. Jäger, Phys. Chem. Chem. Phys., 2020, 22, 23009–23018 RSC.
- T. L. Greaves, K. S. Schaffarczyk McHale, R. F. Burkart-Radke, J. B. Harper and T. C. Le, Phys. Chem. Chem. Phys., 2021, 23, 2742–2752 RSC.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- C. L. Cooper, T. Cosgrove, J. S. van Duijneveldt, M. Murray and S. W. Prescott, Soft Matter, 2013, 9, 7211–7228 RSC.
- T. C. Farrar and E. D. Becker, Pulse and Fourier Transform NMR: Introduction to Theory and Methods, Academic Press, 1971 Search PubMed.
- C. A. Michal, J. Magn. Reson., 2020, 319, 106800 CrossRef CAS PubMed.
- D. Fairhurst and S. W. Prescott, Spectrosc. Eur., 2011, 23, 13–16 CAS.
- A. D. Carrington and A. M. McLachlan, Introduction to Magnetic Resonance, Harper & Row, New York, 1969 Search PubMed.
- J. Kowalewski and L. Maler, Nuclear Spin Relaxation in Liquids. Theory, Experiments, and Applications, CRC Press, New York, 2nd edn, 2019 Search PubMed.
- S. S. Bystrov, V. V. Matveev, Y. S. Chernyshev, V. Balevičius and V. I. Chizhik, J. Phys. Chem. B, 2019, 123, 2362–2372 CrossRef CAS PubMed.
- R. Nanda and K. Damodaran, Magn. Reson. Chem., 2018, 56, 67–72 CrossRef PubMed.
- S. K. Panja and S. Saha, Magn. Reson. Chem., 2018, 56, 95–102 CrossRef CAS PubMed.
- S. T. Keaveney, T. L. Greaves, D. F. Kennedy and J. B. Harper, J. Phys. Chem. B, 2016, 120, 12687–12699 CrossRef CAS PubMed.
- M. Kunze, S. Jeong, E. Paillard, M. Schönhoff, M. Winter and S. Passerini, Adv. Energy Mater., 2011, 1, 274–281 CrossRef CAS.
- L. Aguilera, J. Völkner, A. Labrador and A. Matic, Phys. Chem. Chem. Phys., 2015, 17, 27082–27087 RSC.
- A. O. Seyedlar, J. P. d. A. Martins, P. J. Sebastião, M. J. J. Beira, S. Stapf, F. V. Chávez and C. Mattea, Magn. Reson. Chem., 2018, 56, 108–112 CrossRef PubMed.
- D. Fairhurst, T. Cosgrove and S. W. Prescott, Magn. Reson. Chem., 2015, 54, 521–526 CrossRef PubMed.
- D. Fairhurst, R. Sharma, T. Cosgrove and S. W. Prescott, Powder Technol., 2021, 377, 545–552 CrossRef CAS.
- G. L. Burrell, I. M. Burgar, Q. Gong, N. F. Dunlop and F. Separovic, J. Phys. Chem. B, 2010, 114, 111436 CrossRef PubMed.
- S. S. Bystrov, V. V. Matveev, A. V. Egorov, Y. S. Chernyshev, V. A. Konovalov, V. Balevičius and V. I. Chizhik, J. Phys. Chem. B, 2019, 123, 9187–9197 CrossRef CAS PubMed.
- S. T. Keaveney, K. S. Schaffarczyk McHale, J. W. Stranger, B. Ganbold, W. S. Price and J. B. Harper, ChemPhysChem, 2016, 17, 3853–3862 CrossRef CAS PubMed.
- W. L. F. Armarego and C. L. L. Chai, Purification of Laboratory Chemicals, Butterworth-Heinemann, Oxford, 2013 Search PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- H. Y. Carr and E. M. Purcell, Phys. Rev., 1954, 94, 630 CrossRef CAS.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- S. Watanabe, G. A. Pilkington, A. Oleshkevych, P. Pedraz, M. Radiom, R. Welbourn, S. Glavatskih and M. W. Rutland, Phys. Chem. Chem. Phys., 2020, 22, 8450–8460 RSC.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. P. Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G.-L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko, Y. Vázquez-Baeza and SciPy Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- D. E. Freed, J. Chem. Phys., 2007, 126, 174502 CrossRef PubMed.
- P. M. Singer, D. Ashthagiri, W. G. Chapman and G. J. Hirasaki, J. Magn. Reson., 2017, 277, 15–24 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: General experimental; details of the syntheses of the ionic liquids 4a–f and 5; exact composition details of mixtures used in kinetic analyses; rate coefficient data for each of the ionic liquids 4a, c–f; exact compositions and rate coefficient data for temperature dependence analyses at χILca. 0.8; eyring plots used to determine activation parameters; procedure for multi-component exponential fitting of relaxation data; exact compositions and associated fitting parameters for mixtures of salts 4 used in relaxation analyses; mole fraction dependent relaxation data for salts 4; plots of single and two component exponential fits obtained in relaxation analyses of mixtures including ionic liquids 4a–d, f; initially considered correlations of k2 and T2; exact compositions and associated fitting parameters for mixtures of salt 5 used in relaxation analyses; mole fraction dependent relaxation data for salt 5; methodology and results for predicting k2 in mixtures containing salt 5. See DOI: 10.1039/d0cp06066f |
| ‡ There is also a similar trend present in the second exponential component representing the rest of the solution. These data are included in the ESI.† |
| § Due to the limited solubility of salt 5, the maximum proportion of ionic liquid used in the kinetic studies of the reaction shown in Scheme 1 was χILca. 0.7.38 |
| This journal is © the Owner Societies 2021 |