Magnetic and vibrational properties of small chromium clusters on the Cu(111) surface

Abstract

The structure and magnetic properties of small Cr clusters, Cr₃ and Cr₄, adsorbed on the Cu(111) surface have been investigated using density functional theory (DFT) calculations and their vibrational properties have been studied within calculations based on tight-binding second moment approximation interatomic interaction potentials (TBSMA). It has been shown that the magnetic ordering in the Cr clusters significantly affects their crystal structure and symmetry, which influences the vibrational modes of the clusters and nearest neighbor copper atoms. In turn, these modes select potentially possible structures of Cr₃ and Cr₄, prohibiting the lowest total energy cluster structure as dynamically unstable.

---

1 Introduction

The unique chemical, physical and magnetic properties of transition metals play an important role in determining the observed phenomena in such systems of reduced symmetry as atomic clusters,¹ surfaces,² thin films,^3,4 and complex multilayer structures.⁵ The existence of surface and interface states, a reduced coordination number, and atomic symmetry in the surface layer lead to new properties that differ from the properties of bulk systems.⁶ Magnetic clusters have drawn significant attention due to both fundamental understanding of low dimensional magnetism and some remarkable technological applications including high-density recording and data storage.^7,8 They also have attractive properties which could be seen as having promising potential use in catalysis including nanomaterial-based catalysts,⁹ biomedicine and tissue specific targeting,¹⁰ magnetically tunable colloidal photonic crystals,¹¹ microfluidics,¹² and magnetic resonance imaging.¹³ Among magnetic clusters chromium ones are most intriguing, particularly in the respect of their magnetic properties showing a unique size dependence.¹⁴ The structure, and electronic and magnetic properties of small free and supported Cr and other transition metal magnetic clusters have been extensively investigated experimentally^15–19 and theoretically.^20–25 There has been found a strong interplay between the atomic structure and magnetic order in the clusters. Thus, for Cu(111) surface supported small clusters of Fe, Mn, and Cr it has been revealed that the Fe clusters show ferromagnetic order regardless of the cluster geometry. In contrast, for the Mn and Cr clusters, the antiferromagnetic exchange interaction between nearest neighbors was found to cause collinear antiferromagnetic ordering when the geometry allows it.²² Despite the important role that vibrations play in understanding low-dimensional structure phenomena, much less attention had been paid to investigation of vibrational properties and these studies were restricted to the study of free magnetic clusters.^16,19,24

The interplay of the spin and vibrational degrees of freedom is central to many interesting phenomena, ranging from magnetoelectric effects to superconductivity. For example, in magnetic perovskite oxides it has a strong influence on the structural transformations accompanied by the magnetic transitions.^26,27 A high degree of interrelation between the magnetic structure, lattice vibrations and electronic conductivity was also revealed in NaOsO₃ and h-FeS, demonstrating a metal–insulator transition.^28,29 Strong spin–phonon coupling and its implications for superconductivity in iron pnictides were discussed³⁰ and anisotropy of the phonon modes depending on the spin order was revealed.³¹ Apart from 3D materials, the coupling between the spin and vibrational degrees of freedom is also important in recently discovered 2D ferromagnetic Fe₃GeTe₂, where it results in anomalous softening of phonons below T_C and gives rise to significantly enhanced Raman scattering susceptibility, activating new Raman modes at low temperatures.³² At the same time the study of the influence of the magnetic configuration on the vibrational properties (and vice versa) of small adsorbed magnetic clusters has not been reported to date.

In the present work we scrutinize the correlation between the atomic structure, and magnetic and vibrational properties of Cu(111) supported small Cr clusters. The structural and magnetic properties of trimer and tetramer clusters on Cu(111) are studied within non-collinear density functional theory (DFT). The vibrational properties of the Cr clusters on the Cu(111) surface are explored using tight-binding second moment approximation (TBSMA) interatomic interaction potentials, which were used earlier for calculation of various properties of the transition metal cluster/substrate adsorption system.^33,34 We discuss the dependence of the vibrational spectra on the cluster atomic structure, which strongly depends on their magnetic configuration and the role of these vibrations in controlling the cluster structure.

2 Calculation methods

To study the magnetic characteristics of the Cr trimers and tetramers on the Cu(111) surface we use the slab supercell approach, where the slab consists of seven Cu layers and the vacuum spacing amounts to 10 Å. To exclude direct cluster–cluster interactions we use a 4 × 4 supercell with the cluster atoms arranged in fcc hollow sites on both surfaces of the slab. Fig. 1 shows the initial geometry of the Cu(111) surface with the Cr clusters and the corresponding unit cells for the trimer (Fig. 1a) and tetramer (Fig. 1b). Total energy calculations were performed with the Vienna Ab initio Simulation Package (VASP)^35,36 and within the projected augmented wave (PAW) method to describe the valence and core electrons.^37,38 The exchange–correlation effects were described in the generalized gradient approximation with the Perdew–Burke–Ernzerhof functional.³⁹ To determine the equilibrium geometry the two upper layers of the slab have been relaxed and the other layers are fixed. To study the non-collinear magnetic structures of Cr clusters the fully unconstrained method developed by Hobbs et al.,⁴⁰ which allows both the atomic and magnetic structures to relax simultaneously and self-consistently, was implemented. The local spin moments on atoms were determined inside the Wigner–Seitz spheres.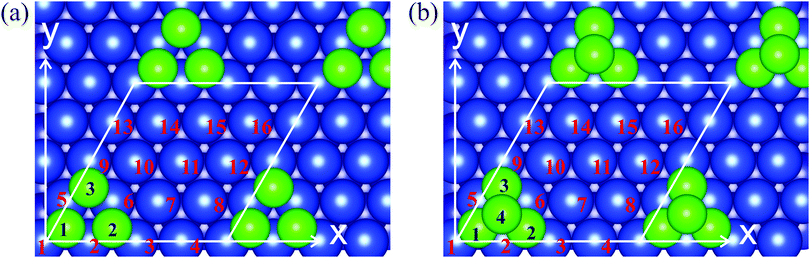

Fig. 1 The atomic structure of (a) Cr₃/Cu(111) and (b) Cr₄/Cu(111). The green circles with numerals represent Cr atoms and blue circles with numerals indicate the Cu surface atoms in the unit cell.

It was shown earlier²⁴ that the vibrational frequencies of the free chromium dimer and trimer calculated using DFT with different exchange–correlation functionals are generally too soft as compared to the experiment. In the present study the vibrational properties of small chromium clusters on the Cu(111) surface have been calculated using tight-binding second moment approximation interatomic interaction potentials fitted to the bulk lattice properties of Cr and Cu⁴¹ and for Cr–Cu interactions a half-sum of the potentials was used. Despite the fact that the TB potentials are constructed for the bulk, they display good transferability to surface and cluster environments. In the previous studies of vibrations of free clusters^42,43 and cluster/substrate systems^34,44,45 using the tight-binding approach very good agreement with available experimental results was demonstrated.

To simulate the substrate surface a thin-film model of a two-dimensional periodic slab consisting of 31 atomic layers of Cu(111) was used. The Cr clusters were placed on both surfaces of the film. This thickness is sufficient to avoid interactions between two opposite surfaces of the slab.^46–49 Relaxations of the cluster atoms and two Cu(111) surface atomic layers were extracted from ab initio calculations. The calculations of vibrational spectra were carried out by the dynamical matrix method. Diagonalizing the matrix gives the eigenfrequencies and polarization vectors of vibrations. The local vibrational densities were obtained by projecting eigenmodes onto atoms of interest in a given X, Y or Z direction.

3 Results and discussion

3.1 Magnetic properties and atomic structure of adsorbed chromium clusters

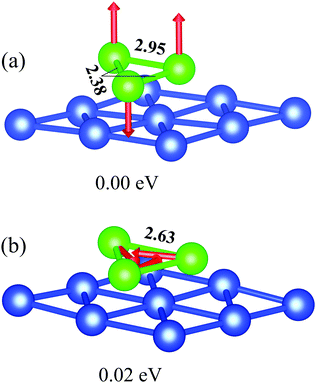
As shown in ref. 50 and 51, the most stable structure of the free-standing Cr₃ cluster is almost a right angled scalene triangle with bond lengths of 1.61, 2.52, and 3.09 Å, which is formed by a dimer with a short bond length and antiparallel but not equal magnetic moments on the dimer atoms and a distant third atom with more than twice the magnetic moment value. Whereas, in ref. 52 it was demonstrated that the ground state atomic structure for the trimers on the (111) surface of noble metals is an equilateral triangle with a noncollinear arrangement of the in-plane oriented magnetic moments on cluster atoms having an angle of 120° to each other. Examples are Cr and Mn trimers on Cu(111)^22,53 and Cr clusters on Au(111).²¹ However, for Cr₃ on Cu(111) our calculations give a non-equilateral triangle as the lowest energy structure with a ferrimagnetic configuration (Fig. 2a) where two parallel magnetic moments of 3.78 μ_B are aligned perpendicular to the surface layer and a magnetic moment of 3.48 μ_B on the third atom of the trimer is oriented in the opposite direction. This configuration is of 20 meV more favorable as compared with the “120°” noncollinear configuration (Fig. 2b) for the Cr₃ cluster on Cu(111). The magnetic moments on each atom for the latter configuration are equal to 3.84 μ_B. This value is larger than the calculated magnetic moments found for Cr₃ on Au(111), 3.16 μ_B.²¹ The ferromagnetic configurations of the Cr trimer, irrespective of the magnetic moments being aligned parallel or perpendicular to the surface plane, characterized by atomic magnetic moments of 4.1 μ_B, are energetically much less favorable compared with the ground state. For all considered configurations the magnetic cluster induces a small, about 0.02–0.04 μ_B, magnetic moment on the nearest substrate atoms.

Fig. 2 Atomic and magnetic structures of the adsorbed ferrimagnetic and noncollinear antiferromagnetic Cr trimers on Cu(111). The red arrows show the atomic magnetic moments; bond lengths are given in Angstroms.

The relaxation of Cr₃/Cu(111) leads to alteration of the bond lengths in the trimer depending on the magnetic configuration and to rippling of the upper Cu layer. The calculated equilibrium bond length in the equilateral noncollinear Cr₃ cluster is 2.63 Å (Fig. 2b). Note that in free-standing Cr₃ the equilateral structure with a bond length of 2.51 Å and a noncollinear arrangement of atomic magnetic moments was found at 0.64 eV higher in energy as compared with the ground state structure.⁵⁰ The Δz distance between the Cr₃ cluster atoms and copper layer is 2.10 Å for atoms (1,3,9) and it is 2.08 Å for atoms (2,5,6), see Fig. 1a. Adsorption of the “120°” noncollinear Cr₃ cluster also leads to rippling of the surface layer by 0.13 Å in the vicinity of the cluster and to a small (∼0.03 Å) in-plain shift of the nearest Cu atoms (1,3,9) and (2,5,6) by 0.04 Å and 0.03 Å, respectively, away from the cluster center. The resulting relative contractions of the first interlayer distance in the vicinity of the cluster are Δ₁₂ = −1.9% for the nearest Cu atoms (1,3,9), and Δ₁₂ = −0.7% for Cu atoms (2,5,6).

In the lowest energy magnetic configuration (Fig. 2a) the bond length between atoms with parallel magnetic moments equals 2.95 Å, while it is shorter (like in the free trimer^50,51), 2.38 Å, between atoms with antiparallel magnetic moment alignment. At that, the former atoms lie higher by 0.06 Å compared to those with antiparallel magnetic moments, which results in much larger rippling of the surface layer of Cu(111), 0.18 Å, and consequently in more complicated relaxation Δ₁₂ of the nearest Cu atoms, which varies from −2.8% to +2.8%.

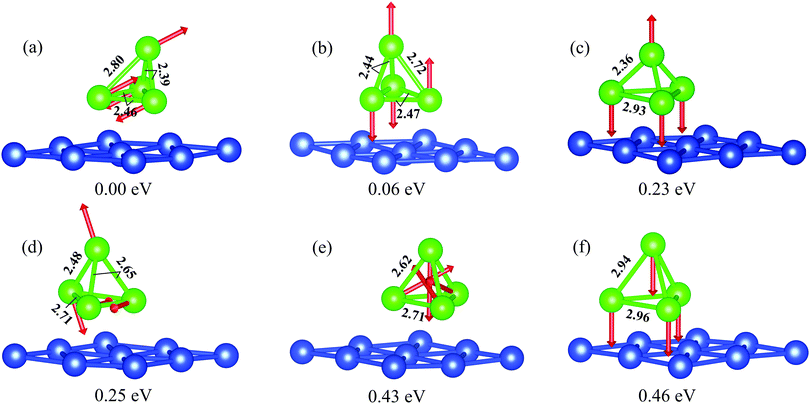
The most stable geometry of free-standing Cr₄ is a twisted two-dimer structure^50,51 in which the antiferromagnetic Cr dimers with relatively short bond length (1.63 Å) are separated by a relatively large distance (2.73 Å). The atomic magnetic moments in the ground-state structure are equal to 2 μ_B. Among the considered isomers of free-standing Cr₄, a distorted tetrahedron with antiferromagnetically arranged magnetic moments (3.71 μ_B) has an energy of 0.42 eV higher compared to the ground state.⁵⁰ On the other hand, it was shown earlier that for Cr₄ on Cu(111), as well as for adsorbed Fe₄ and Mn₄ clusters, the distorted tetrahedron is a ground state structure.²² According to ref. 22, the Cr₄ cluster on the Cu(111) surface exhibits collinear antiferromagnetic ordering. The reduced neighbor coordination for the top Cr atom affects its magnetic moment, which is 4.2 μ_B in contrast to 3.6 μ_B for the base tetrahedron atoms, and so the full magnetic moment of the cluster is nonzero.

We have considered Cr₄ on Cu(111) with a regular tetrahedron geometry and different collinear and noncollinear, ferromagnetic, antiferromagnetic and ferrimagnetic magnetic configurations as a starting point. Several resulting configurations obtained by simultaneous relaxation of the atomic and magnetic structures are shown in Fig. 3. The collinear antiferromagnetic structure found in ref. 22 as the ground state for Cr₄/Cu(111) (Fig. 3b) in our calculations shows magnetic moments of 3.57 and 3.81 μ_B for the base and top cluster atoms, respectively. However, this magnetic structure has an energy of 60 meV higher compared with the structure where all magnetic moments are tilted by 63.6° to the surface normal (Fig. 3a). The atomic magnetic moment on the base tetrahedron atoms in this case amounts to 3.53 μ_B, while the top atom carries a magnetic moment of 3.70 μ_B. Among the resulting structures, the tetramers with ferromagnetic ordering are most unfavorable, irrespective of the fact that the atomic magnetic moments are aligned parallel or perpendicular to the surface (Fig. 3f). The noncollinear magnetic structure (Fig. 3e), similar to that found for Mn₄/Cu(111)²² as the stable one, has an energy close to the ferromagnetic configuration. The collinear ferrimagnetic structure (Fig. 3c) and the structure where the atomic magnetic moments are pairwise antiparallel (Fig. 3d) are more than 200 meV less favorable with respect to the most stable magnetic structure.

Fig. 3 Atomic and magnetic structures of the adsorbed Cr tetramers on Cu(111). The red arrows show atomic magnetic moments; bond lengths are given in Angstroms; and the values below each panel are the relative total energies of different magnetic configurations (b–f) with respect to the ground state shown in panel (a).

The magnetic configuration strongly affects the atomic structure of the adsorbed Cr₄ cluster. Triangular pyramid clusters characterized by C_3v point group symmetry are obtained for the ferromagnetic, ferrimagnetic and noncollinear magnetic configurations, whereas for the other considered magnetic configurations the symmetry of the cluster is lowered to C_1v. Among the C_3v symmetry clusters the largest bond lengths between base atoms and between top and base atoms were found for the ferromagnetic configuration (Fig. 3f) (2.96 and 2.94 Å, respectively) and the smallest Cr–Cr interatomic distances were found for the noncollinear configuration (Fig. 3e) (2.71 and 2.62 Å, respectively). Comparing the structure of the latter with the trimer with a noncollinear magnetic configuration, one can see that the bond lengths between base atoms in Cr₄ with a C_3v structure are by 3% larger than those in the C_3v trimer.

For the ground-state cluster with tilted magnetic moments and the cluster with a non-tilted collinear antiferromagnetic configuration, the base atoms no longer form an equilateral triangle (see Fig. 3a and b, respectively). The bond length between the base atoms with antiparallel magnetic moment orientation in the tilted (non-tilted) structure is 2.46 (2.47) Å, whereas it is 2.85 (2.77) Å between atoms with the same direction of the magnetic moments. The bond length between the top and base atoms carrying parallel magnetic moments is 2.80 (2.72) Å and that between the top atom and base atoms with antiparallel magnetic moments amounts to 2.39 (2.45) Å, which are different too. In both cases the distances between atoms with antiparallel magnetic moments are shorter, like in the stable free tetramer.

The structure of the cluster also affects the relaxation of the surrounding substrate atoms. For Cr₄ clusters with C_3v symmetry the relaxation of the substrate is similar to that in Cr₃/Cu(111) with the “120°” noncollinear configuration. For instance, for the noncollinear magnetic configuration (Fig. 3e) the distance Δz between the Cr₄ base atoms and the copper surface layer is 2.13 Å for Cu atoms (1,3,9) and it is 2.11 Å for atoms (2,5,6), see Fig. 1b. The relative contractions of the first interlayer distances in the vicinity of the cluster are a bit smaller with respect to the case of Cr₃ adsorption.

For clusters with C_1v symmetry, besides the base atoms of the tetramer forming an isosceles triangle, their heights depend on the magnetic moment direction. In the ground state magnetic structure, the atoms with parallel magnetic moments lie by 0.08 Å higher than the atoms with opposite magnetic moments, whereas for the magnetic configuration with non-tilted magnetic moments this difference in the positions of the base atoms is even larger, 0.18 Å. It results in different interactions of the cluster atoms with neighboring atoms of the substrate and consequently in much larger rippling of the surface copper layer. For instance, for the ground state cluster it amounts to 0.18 Å. Whereas for the cluster with C_3v symmetry the relaxation of the neighboring atoms can be described for two groups of atoms, (1,3,9) and (2,5,6), for the C_1v clusters it is even more complicated. For the lowest energy magnetic configuration the relaxation of the neighboring atoms is more complicated: Δ₁₂ varies from +2.2% for the Cu atom lying at the edge of the triangle formed by Cr atoms with parallel magnetic moments to −2.8% at the corner formed by the Cr atoms with antiparallel magnetic moments. The variation in relaxation of neighboring Cu atoms for the non-tilted collinear antiferromagnetic configuration of the tertramer is noticeably smaller and also is sign alternating, from +0.5% to −1.7%, respectively.

3.2 Vibrational characteristics of adsorbed chromium clusters

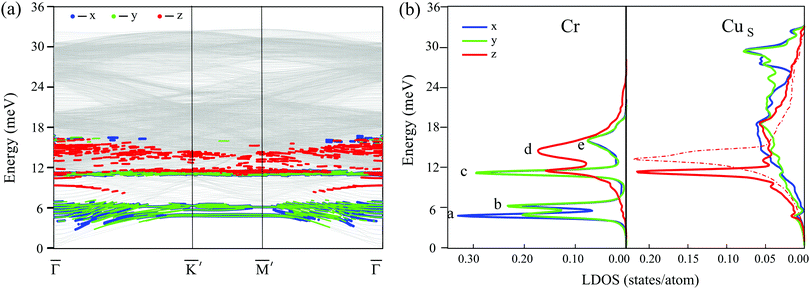
The lowest energy ferrimagnetic configuration of the adsorbed Cr₃ cluster demonstrates imaginary vibrational frequencies in the spectrum, which indicates dynamical instability of this configuration. In contrast, the trimers with “120°” noncollinear and ferromagnetic configurations have all frequencies real. Fig. 4a shows the calculated phonon dispersion curves for Cr₃/Cu(111) with the “120°” noncollinear antiferromagnetic configuration of the Cr atomic magnetic moments. As can be seen, the in-plane (XY) polarized vibrations of the cluster arise mostly at ∼6 meV in the spectrum. At the Brillouin zone (BZ) center they appear as resonance states mixed with vibrations of the substrate and become localized at the BZ boundary. At higher energy, 10–17 meV, the Cr Z-polarized vibrations dominate with the exception of a well localized in-plane mode at ∼11 meV. The character of the cluster vibrations can be better identified from the local density of states (LDOS) projected onto Cartesian directions and analysis of the atomic displacements. Fig. 4b shows the local density of states of the Cr₃ cluster atoms (left side) and Cu surface atoms (right side). In the low-frequency region one can see two localized peaks corresponding to the in-plane vibrations of the cluster. The lowest energy peak at 4.8 meV (a) corresponds to a frustrated translation (FT) mode determined by the XY displacements of the entire cluster. The second peak at 6.3 meV (b) is a frustrated rotation (FR) mode arising from rotational displacements of the cluster relative to its center of mass. The low-frequency FT and FR vibrations of Cr₃ are weakly coupled to low-frequency vibrations of the nearest Cu atoms. The strongly localized third peak (c) at 11.2 meV is produced by degenerate deformation and antisymmetric XY polarized vibrational modes of the cluster. Such degeneracy of the deformation and antisymmetric vibrational modes is inherited from the free clusters with C_3v symmetry and is typical for non-magnetic trimers on the (111) surface.⁴⁴ Both these vibrations, being modified by vertical displacements of Cr atoms, are strongly hybridized with the Rayleigh wave (RW) of the substrate, which shifts down by 1.9 meV compared to the RW mode of the clean Cu(111) surface (Fig. 4b, right side, dashed-dot curve). The broad peak (d) at 14.5 meV originates from the shear-vertical vibration of cluster atoms coupled with vibrations of the nearest copper atoms. The highest energy peak (e) at 16.1 meV is produced by an optical-like in-plane vibration of the trimer, weakly coupled to the vertical displacements of the nearest Cu atoms.

Fig. 4 (a) Calculated phonon dispersion curves for Cr₃/Cu(111) with the “120°” noncollinear antiferromagnetic configuration of the Cr atomic magnetic moments. Blue, green, and red dots denote respectively X, Y, and Z-polarized vibrational modes of the cluster. (b) Local density of states projected onto the Cr atoms (left) and surface layer atoms of the copper substrate (right). The dashed-dot red line shows the LDOS for Z-polarized vibrations (Rayleigh wave) of clean Cu(111).

Despite the fact that the cluster with a ferromagnetic configuration possesses the same C_3v symmetry as the cluster with a “120°” noncollinear alignment of the Cr atomic magnetic moments, its phonon spectrum is markedly different. Though the Z polarized peaks in the LDOS remain almost at the same energies, the in-plane vibrational modes are changed substantially, experiencing softening. At that, the FR mode becomes mixed with optical-like vibrations and gives rise to a peak at 4.6 meV, while degenerate deformation and antisymmetric XY polarized vibrational modes appears below, at 4.0 meV.

Turning to tetramers, we consider first the cluster possessing the same C_3v symmetry as that of the stable configuration of the Cr trimer. Among the cluster geometries with C_3v symmetry, the clusters with ferrimagnetic and ferromagnetic configurations show imaginary eigenvalues in the spectra, which indicates dynamical instability of the system, and only the Cr₄ cluster with noncollinear antiferromagnetic atomic magnetic moment alignment (Fig. 3e) has no imaginary frequencies. The local density of vibrational states of this cluster is demonstrated in Fig. 5a. Like in the Cr₃ case, the lowest energy peaks in the LDOS, (a) at 3.8 meV and (b) at 6.3 meV, are determined by the FT and RT vibrations of the cluster, respectively. The (c) and (d) peaks originate from XY deformation vibrations of the cluster and peak (c) at 7.4 meV is contributed to a greater extent by the displacements of the top atom of the tetramer, whereas peak (d) at 10 meV is predominantly contributed by vibrations of the base atoms of the cluster. This mode is strongly coupled with Z polarized vibrations of the substrate atoms and hence it also has a significant Z component. At that, the energy of the main RW peak in the Cu_S LDOS is almost the same (11.5 meV) as in the case of the trimer with a non-collinear magnetic configuration. At higher energies a broad Cr LDOS peak with two maxima, (e) (16.5 meV) and (f) (17.2 meV), is produced by a mixture of deformation and antisymmetric (e) modes as well as symmetric (f), predominantly Z polarized vibrations of the cluster, accompanied by complex vibrations of the neighbouring substrate atoms.

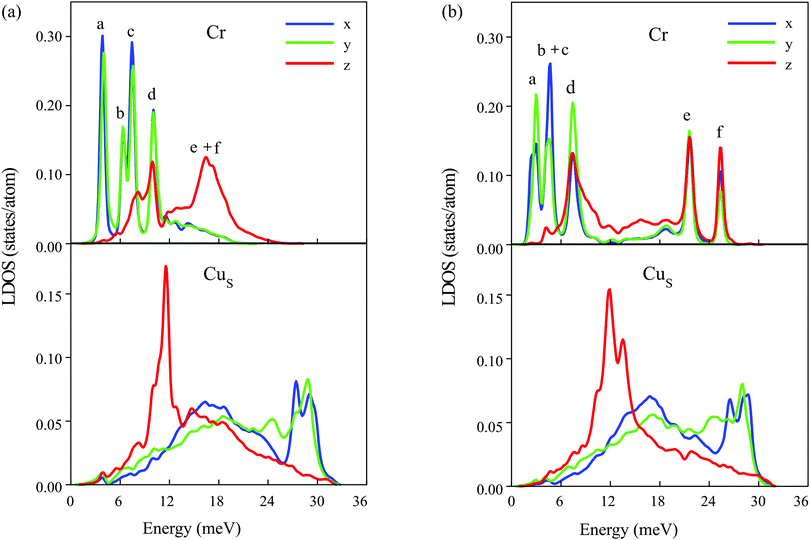Fig. 5 Local density of states projected onto the Cr atoms (top) and surface layer atoms of the copper substrate (bottom) for (a) the Cr₄ cluster with a noncollinear magnetic configuration possessing C_3v symmetry (Fig. 3e) and (b) for the Cr tetramer with a collinear antiferromagnetic configuration having C_1v symmetry (Fig. 3b).

Now let's turn to the magnetic configurations of the Cr tetramer characterized by the lowered C_1v symmetry and more complex relaxation of the neighboring substrate atoms. The lowest energy magnetic configuration with antiferromagnetically aligned atomic magnetic moments tilted to the surface normal (Fig. 3a) demonstrates imaginary vibrational frequencies and thus it is dynamically unstable. The next favorable magnetic configuration of the Cr₄ cluster, with non-tilted magnetic moments (Fig. 3b), also possessing C_1v symmetry, was found to be a stable one. The LDOSs for this cluster and for the surface layer atoms of the Cu(111) substrate are shown in Fig. 5b. As can be seen from comparison of panels (a) and (b), the lowering of the cluster symmetry leads to significant changes in the vibrational spectrum. First, the frequency of the FT mode goes down to 3 meV. Two different modes, RT and deformation vibrations of the cluster caused by displacements of the top atom of the tetramer, now appear as a single peak (b + c) at 4.7 meV. The (d) peak, preliminary contributed by complex deformation vibrations of the base atoms of the cluster, also appears at a significantly lower frequency (7.5 meV) compared to the cluster with C_3v symmetry. In addition, this mode is significantly less hybridized with Z polarized vibrations of the substrate atoms. At the same time, due to the much larger rippling of the copper surface layer and complex relaxation in the vicinity of the Cr₄ cluster, in this case the peak in the Cu_S LDOS related to the RW mode of the Cu(111) surface becomes much broader and splits into two peaks despite the fact that in this energy region vibrational states of the cluster are almost absent. The lowering symmetry of the Cr₄ cluster also significantly modifies its high-frequency modes. First of all, these modes become of much higher frequency, and, instead of predominantly Z character in the C_3v cluster, peaks (e) and (f) in the LDOS acquire mixed polarization. At that, the mixed deformation and antisymmetric vibrations of the cluster contribute to the lower peak (f) at 21.6 meV, whereas the symmetric (optical-like) vibrations give rise to peak (e) at 25.3 meV. However, it should be emphasized again that these vibrations are more complex compared to those in the C_3v symmetry cluster due to the more complex crystal structure of the Cr₄ cluster with a collinear antiferromagnetic configuration.

4 Conclusion

In summary, we have presented the results of the study of the magnetic, structural and vibrational properties of the chromium trimer and tetramer adsorbed on the Cu(111) surface. We have considered a series of magnetic configurations for the clusters and found that for both the trimer and tetramer the clusters with the lowest energy magnetic configuration are dynamically unstable. For the trimer the dynamically stable configuration is a “120°” noncollinear magnetic configuration which has the structure of an equilateral triangle characterized by C_3v point group symmetry. The phonon spectrum of this structure demonstrates modification of the proper modes of the trimer due to their mixing with vibrations of neighboring copper atoms like in the case of non-magnetic atom trimers on Cu(111). The dynamically stable structure for the Cr₄ cluster is a collinear antiferromagnetic configuration with magnetic moments aligned along the surface normal. In this structure the cluster is characterized by C_1v symmetry. Comparing it with the Cr tetramer with C_3v symmetry as realized for example in the case of noncollinear antiferromagnetic alignment of the Cr magnetic moments, we found that lowering the cluster symmetry to C_1v leads to substantial modification of the vibrational spectrum. It is expressed in considerable softening of the low-frequency frustrated translation and frustrated rotation modes as well as the modes determined by the deformation vibrations of the cluster, and, on the other hand, in large hardening of the high-frequency modes along with modification of their polarization. Thus, our results disclose a complex interplay between the magnetic ordering in small adsorbed chromium clusters, their atomic structure and the vibrational properties of the clusters, which should affect their electronic characteristics and chemical properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Government Research assignment for ISPMS SB RAS, Project No. III.23.2.9. E. V. C. acknowledges partial support from Saint Petersburg State University (Grant No. ID 51126254).

References

1. M. Martins and W. Wurth, J. Phys.: Condens. Matter, 2016, 28, 503002.
2. M. Donath, Surf. Sci. Rep., 1994, 20, 251–316.
3. A. B. Schmidt, M. Pickel, M. Donath, P. Buczek, A. Ernst, V. P. Zhukov, P. M. Echenique, L. M. Sandratskii, E. V. Chulkov and M. Weinelt, Phys. Rev. Lett., 2010, 105, 197401.
4. P. Poulopoulos and K. Baberschke, J. Phys.: Condens. Matter, 1999, 11, 9495–9515.
5. T. Hirahara, S. V. Eremeev, T. Shirasawa, Y. Okuyama, T. Kubo, R. Nakanishi, R. Akiyama, A. Takayama, T. Hajiri, S.-I. Ideta, M. Matsunami, K. Sumida, K. Miyamoto, Y. Takagi, K. Tanaka, T. Okuda, T. Yokoyama, S.-I. Kimura, S. Hasegawa and E. V. Chulkov, Nano Lett., 2017, 17, 3493–3500.
6. F. J. Himpsel, J. E. Ortega, G. J. Mankey and R. F. Willis, Adv. Phys., 1998, 47, 511–597.
7. J. Bansmann, S. Baker, C. Binns, J. Blackman, J.-P. Bucher, J. Dorantes-Dávila, V. Dupuis, L. Favre, D. Kechrakos, A. Kleibert, K.-H. Meiwes-Broer, G. Pastor, A. Perez, O. Toulemonde, K. Trohidou, J. Tuaillon and Y. Xie, Surf. Sci. Rep., 2005, 56, 189–275.
8. C. F. Hirjibehedin, C. P. Lutz and A. J. Heinrich, Science, 2006, 312, 1021–1024.
9. N. Sharma, H. Ojha, A. Bharadwaj, D. P. Pathak and R. K. Sharma, RSC Adv., 2015, 5, 53381–53403.
10. R. Sensenig, Y. Sapir, C. MacDonald, S. Cohen and B. Polyak, Nanomedicine, 2012, 7, 1425–1442.
11. H. Hu, C. Chen and Q. Chen, J. Mater. Chem. C, 2013, 1, 6013–6030.
12. S. Yaman, M. Anil-Inevi, E. Ozcivici and H. C. Tekin, Front. Bioeng. Biotechnol., 2018, 6, 192.
13. Z. R. Stephen, F. M. Kievit and M. Zhang, Mater. Today, 2011, 14, 330–338.
14. F. W. Payne, W. Jiang and L. A. Bloomfield, Phys. Rev. Lett., 2006, 97, 193401.
15. V. Bondybey and J. English, Chem. Phys. Lett., 1983, 94, 443–447.
16. D. P. DiLella, W. Limm, R. H. Lipson, M. Moskovits and K. V. Taylor, J. Chem. Phys., 1982, 77, 5263–5266.
17. W. L. Brien, B. P. Tonner, G. R. Harp and S. S. P. Parkin, J. Appl. Phys., 1994, 76, 6462–6464.
18. J. Lawler, R. Van der Kraan, H. Van Kempen and A. Quinn, J. Magn. Magn. Mater., 1997, 165, 195–198.
19. L. Fang, B. Davis, H. Lu and J. R. Lombardi, J. Phys. Chem. A, 2001, 105, 9375–9378.
20. A. N. Andriotis and M. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 10069–10081.
21. H. J. Gotsis, N. Kioussis and D. A. Papaconstantopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 014436.
22. A. Bergman, L. Nordström, A. Burlamaqui Klautau, S. Frota-Pessôa and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 224425.
23. F. Ruipérez, M. Piris, J. M. Ugalde and J. M. Matxain, Phys. Chem. Chem. Phys., 2013, 15, 2055–2062.
24. R. Würdemann, H. H. Kristoffersen, M. Moseler and M. Walter, J. Chem. Phys., 2015, 142, 124316.
25. O. López-Estrada, S. López-Olay, A. Aburto and E. Orgaz, J. Phys. Chem. C, 2016, 120, 23892–23897.
26. C. Cazorla, O. Diéguez and J. Íñiguez, Sci. Adv., 2017, 3, e1700288.
27. S. Nikolaev, V. Mazurenko and A. Rudenko, Solid State Commun., 2013, 164, 16–21.
28. S. Calder, J. H. Lee, M. B. Stone, M. D. Lumsden, J. C. Lang, M. Feygenson, Z. Zhao, J.-Q. Yan, Y. G. Shi, Y. S. Sun, Y. Tsujimoto, K. Yamaura and A. D. Christianson, Nat. Commun., 2015, 6, 8916.
29. D. Bansal, J. L. Niedziela, S. Calder, T. Lanigan-Atkins, R. Rawl, A. H. Said, D. L. Abernathy, A. I. Kolesnikov, H. Zhou and O. Delaire, Nat. Phys., 2020, 16, 669–675.
30. T. Egami, B. V. Fine, D. Parshall, A. Subedi and D. J. Singh, Adv. Condens. Matter Phys., 2010, 164916.
31. G. Q. Huang, Z. W. Xing and D. Y. Xing, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014511.
32. L. Du, J. Tang, Y. Zhao, X. Li, R. Yang, X. Hu, X. Bai, X. Wang, K. Watanabe, T. Taniguchi, D. Shi, G. Yu, X. Bai, T. Hasan, G. Zhang and Z. Sun, Adv. Funct. Mater., 2019, 29, 1904734.
33. F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33.
34. S. D. Borisova, S. V. Eremeev, G. G. Rusina and E. V. Chulkov, Phys. Status Solidi C, 2010, 7, 2596–2599.
35. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
36. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
38. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. D. Hobbs, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 11556–11570.
41. M. A. Karolewski, Radiat. Eff. Defects Solids, 2001, 153, 239–255.
42. A. N. Andriotis and M. Menon, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 10069–10081.
43. S. D. Borisova, G. G. Rusina and E. V. Chulkov, Phys. Solid State, 2010, 52, 838–843.
44. S. D. Borisova, S. V. Eremeev, G. G. Rusina, V. S. Stepanyuk, P. Bruno and E. V. Chulkov, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075428.
45. L. Vitali, S. D. Borisova, G. G. Rusina, E. V. Chulkov and K. Kern, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 153409.
46. G. G. Rusina, S. V. Eremeev, P. M. Echenique, G. Benedek, S. D. Borisova and E. V. Chulkov, J. Phys.: Condens. Matter, 2008, 20, 224007.
47. K. Volgmann, H. Gawronski, C. Zaum, G. G. Rusina, S. D. Borisova, E. V. Chulkov and K. Morgenstern, Nat. Commun., 2014, 5, 5089.
48. S. D. Borisova, G. G. Rusina, S. V. Eremeev and E. V. Chulkov, J. Phys.: Condens. Matter, 2019, 31, 125001.
49. G. G. Rusina, S. D. Borisova, S. V. Eremeev, I. Y. Sklyadneva, E. V. Chulkov, G. Benedek and J. P. Toennies, J. Phys. Chem. C, 2016, 120, 22304–22317.
50. P. Ruiz-Díaz, J. L. Ricardo-Chávez, J. Dorantes-Dávila and G. M. Pastor, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 224431.
51. R. Mecheref, S. Bouarab, M. Zemirli and A. Vega, Eur. Phys. J. D, 2017, 71, 90.
52. G. M. Stocks, M. Eisenbach, B. Újfalussy, B. Lazarovits, L. Szunyogh and P. Weinberger, Prog. Mater. Sci., 2007, 52, 371–387.
53. A. Bergman, L. Nordström, A. Burlamaqui Klautau, S. Frota-Pessôa and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 174434.

---