Nucleation behaviour of racemic and enantiopure histidine

Abstract

Nucleation of DL- and L-histidine is examined using induction time measurements and their nucleation rates have been deduced. Results indicate a much slower nucleation for the racemic form compared to the pure enantiomer form. The effect of temperature and supersaturation on the nucleation rate is also described. Classical nucleation theory (CNT) is used to determine the interfacial energy, the nucleation energy barrier, and the nucleus size for both compounds. The large difference between the nucleation rates for the pure enantiomer and the racemic compound have so far not led to satisfactory preferential crystallization; however second harmonic generation analysis demonstrates the presence of non-centrosymmetric domains embedded within the racemic crystals implying that improving control over the nucleation conditions may lead to more efficient preferential crystallisation and symmetry breaking.

---

Introduction

Crystallization is an important industrial process; it is commonly used in several important industries including pharmaceuticals,¹ chemicals,² food,³ pigments,⁴ and microelectronics,⁵ in which crystallization is often used as a final separation and purification step to control the crystal size, shape, composition, and structure.⁶ Crystallization is used to manipulate the end-product's physical and chemical properties (polymorph, solubility, morphology, density, size, size distribution, etc.)⁷ especially in the pharmaceutical industry, because many pharmaceutical ingredients are manufactured in a solid, crystalline form. Ultimate control over the crystallization process requires a control of the most crucial step: ‘nucleation’.

Nucleation can happen through different mechanisms that can be divided into two categories:^6–8 primary nucleation and secondary nucleation. The critical nucleus may emerge either homogeneously or heterogeneously on a foreign surface such as dust particles or the wall of the container.^9,10 Heterogeneous nucleation is often faster and more common than homogeneous nucleation because a surface is always present in the reaction environment.¹¹ However, nucleation is difficult to control because several factors (e.g. nucleation rate, the number of molecules needed to form a nucleus of a critical size, the energy barrier, etc.)⁶ can play a major role in the nucleation onset.

In this study, racemic and enantiopure histidine (Scheme 1) have been selected as model compounds, as control over nucleation is one of the pathways to accomplish chiral resolution through crystallisation. We aim to compare the nucleation behaviour of the racemic and enantiopure materials. To the best of our knowledge, this kind of studies are rare.¹²

Scheme 1 Chemical structure of D-histidine. The chiral centre is denoted with an asterisk.

We will apply a previously developed method based on induction time measurements^13,14 to determine the nucleation kinetics of the model compounds. The experimental data will be analysed against classical nucleation theory^15,16 based on Arrhenius rate laws. In addition, the effect of temperature and supersaturation is studied.

Materials and methods

Materials

Racemic (DL) and enantiopure (L)-histidine (purity ≥ 99.0%) were purchased from Merck and used as received. Water used in this work is demineralized water.

Solubility measurements. The solubilities (s) of the model compounds in water were determined for several temperatures using the Crystal16® multiple-reactor system (Technobis, The Netherlands)¹⁷ in a volume of 1 mL. A suspension of DL-histidine and L-histidine with known concentration was prepared in 1 mL of water in the standard HPLC glass vials equipped with a magnetic stirrer and stirred at 700 rpm. The heating and cooling rate were set to 0.2 °C min⁻¹. The saturation temperature is taken when the transmissivity of light through the sample reaches 100% (clear point). The saturation temperature was measured 4 times per sample and the average value is taken as the solubility.

Induction time measurements. The induction time (t_i), representing the time required to detect crystals in a solution once reaching constant supersaturation, was determined using the Crystal16 under different conditions (4 different concentrations and 4 different saturation temperatures). A calculated amount of DL-histidine and L-histidine was dissolved in a suitable amount of water by heating above the saturation temperature to make sure that all crystals were dissolved. The clear solution was then cooled down in the Crystal16 to the target temperature, 25, 20, 15, or 10 °C for L-histidine and 15, 10, 7, or 5 °C for DL-histidine with a cooling rate of 5 °C min⁻¹. The moment at which the set temperature was reached is taken as time zero (t₀) after which a constant temperature was maintained. Once a spontaneous crystallization happens, the light transmission decreases. The difference between the moment when the transmissivity started to decrease and t₀ was taken as t_i.¹⁸ Heat-cool cycles were repeated many times for each vial to ensure a statistically relevant number of datapoints.

X-ray Diffractometry (PXRD). Powder X-ray diffraction (PXRD) analyses were performed at room temperature using a D8 Discover diffractometer (Bruker analytic X-ray Systems, Germany) with Bragg–Brentano geometry. The instrument is equipped with a copper anticathode (40 kV, 40 mA, Kα radiation (λ = 1.5418 Å)), and a Lynx Eye linear detector. The diffraction patterns were recorded with a scan rate of 0.04° (2θ) in the angular range of 3–30° 2θ, with a counting time of 4 s per step.

SHG microscopy. Insight X3 single laser with automated dispersion compensation (Spectra-Physics, Santa Clara, USA) and a TCS SP8 MP confocal microscope (Leica Microsystems, Wetzlar, Germany) performed confocal microscopy as well as two-photon microscopy and fluorescence lifetime imaging of the samples. The laser cavity had over 2.44 W of average power at 900 nm and was tunable from 680 nm to 1300 nm. The repetition rate was 80 MHz and the temporal width at the output of the cavity was around 120 fs (<100 fs between 850 nm and 1050 nm). The laser was controlled with the LASX Leica software. Two Leica hybrid descanned detectors (HyD) were used to record images. For two-photon imaging experiments, fluorescence was collected after the microscope objective via a dichroic beam splitter, transparent to wavelengths greater than 815 nm. Microscope objectives were long working distance dry Leica objectives (HC PL Fluotar 5× NA 0.15, HC PL Fluotar 10× NA 0.3 or HC PL APO 20× NA 0.4 CS2) or oil-immersion Leica objective (HC PL APO 40× NA 1.30 CS2). An electro-optical modulator adjusted the laser power at the entrance of the confocal system.

To check if the sample produce fluorescence, an emission spectral scan is performed. Typically, the sample is excited at a given wavelength (e.g., 1200 nm or 900 nm) while scanned through the emission wavelength (e.g., in the 385–780 nm range). The SHG and THG should appear at the half and at the third of the excitation wavelength, respectively. The spectral acquisition was performed using an internal hybrid detector. Collected photons were dispersed by a prism and a specific motorized split mirror selected the spectral detected band before the hybrid detector. Acquisitions were performed between 385 nm and 780 nm every 3 nm and a spectral bandwidth of 5 nm.

The samples are prepared by deposition of few mg on a microscope slide.

Kurtz & Perry test. Fig. S1† shows the experimental setup used for the SHG measurements. A Nd:YAG Q-switched laser (Quantel) operating at 1.06 μm was used to deliver up to 360 mJ pulses of 5 ns duration with a repetition rate of 10 Hz. An energy adjustment device made up of two polarizers (P) and a half-wave plate (λ/2) allowed the incident energy to vary from 0 to ca. 200 mJ per pulse. A RG1000 filter was used after the energy adjustment device to remove light from laser flash lamps. The samples (few mg of powder) were placed in a vial and were irradiated with a beam (4 mm in diameter).

The signal generated by the sample (diffused light) was collected into an optical fiber (500 μm of core diameter) and directed onto the entrance slit of a spectrometer (Ocean Optics). A boxcar integrator allowed an average spectrum (spectral range 490–590 nm) with a resolution of 0.1 nm to be recorded over 3 s (30 pulses).

According to Kurtz and Perry SHG powder method,¹⁹ SHG signal intensities were compared to the signal of a reference compound (α-quartz powder – 45 μm average size).

Theory

Classical nucleation theory. As nucleation is regarded as a random process, the nucleation rate can be obtained with a cumulative probability distribution of the induction time (t_i) as reported elsewhere.¹⁴ The cumulative probability P(t) to detect crystals at a time t is given by:

P(t) = 1 − C exp(−JV(t_i − t_g)) (1)

where J is the nucleation rate (m⁻³ s⁻¹), V is volume in m³, t_i is the experimentally determined induction time in seconds (s) and t_g (growth time) is the time needed for the formed nuclei to grow to a detectable size. An additional parameter is introduced to this equation, C, which is used to compensate for the finite cooling rate of the equipment at high supersaturations. C is a correction factor representing all samples having crystallized before reaching the target temperature.

Experimentally, the cumulative probability function, P(t), is defined as follows:

P(t) = M⁺(t)/M (2)

In which M represents the total number of experiments and M⁺(t) is the number of experiments in which crystals are detected at time t. Plotting the data obtained through eqn (2), the nucleation rate J can be determined by fitting the plot with eqn (1).

According to the classical nucleation theory (CNT), the nucleation rate for a given supersaturation, β, is defined as:^20,21

J = Aβ exp(−B/ln² β) (3)

A (m⁻³ s⁻¹) is a kinetic parameter proportional to the number of nucleation-active centres in the system and B is a dimensionless thermodynamic parameter proportional to the thermodynamic barrier (ΔG*) specified by:

B = (16πv₀²γ³)/(3k³T³) (4)

γ is the interfacial energy of the surface of the nucleus given in J m². k is the Boltzmann constant (1.380649 × 10⁻²³ J K⁻¹), T is the temperature in kelvin (K) and υ₀ is the molecular volume calculated to be 180 × 10⁻³⁰ m³ for histidine, the same value was obtained elsewhere.¹⁴

The critical Gibbs free energy (ΔG*) representing the energy barrier that the system must overcome to form a critical nucleus (kJ mol⁻¹), and the critical number of molecules in the nucleus n* (molecules) can be calculated using these equations:^7,22

ΔG* = (16πv₀³γ³)/3k²T² ln² β = BkT/ln² β (5)

n* = (32πv₀²γ³)/3k³T³ ln³ β (6)

Prediction of nucleation kinetics. According to CNT for homogeneous nucleation, the kinetic parameter A for interface-transfer control is given by:²¹

A_l,hom = (4π/3v₀)^1/3(γ/kT)^1/2Ds (7)

s, the solubility, is represented in mol m⁻³ in eqn (7). D (m² s⁻¹) is the diffusion coefficient^23–25 (see ESI†). The kinetic parameter for volume-diffusion can be found in the ESI.†

The interfacial energy γ can be predicted with the aid of the Stefan–Skapski–Turnbull formula²¹ connecting γ to ln(1/s):

γ_predicted = 0.514kT/v₀^2/3 ln(1/N_Av₀s) (8)

As proposed by Nielsen and Söhnel, the interfacial energy is represented with a corrected shape factor equal to 0.514 for spherical clusters.²⁰

Using the previous equations, J for interface-transfer control can be presented as:

J = a_IT/η(ln(ρ_c/Ms))^0.5sβ exp(−b_I((ln²(ρ_c/Ms))/(ln² β)) (9)

J for volume-diffusion control, a_I, and b_I can be found in ESI.†

Results and discussion

Solubility and induction time measurements

The solubility (s) curves of the two crystal forms (pure enantiomer L and racemic DL) of histidine in demineralized water are shown in Fig. 1. As seen in this figure, the solubility of L-histidine in water is higher than that of DL-histidine. Each point is the average of 4 data points. The solid lines are a fit to the experimental data, and they have been used to determine the supersaturation ratio β = C₀/s, where C₀ is the initial concentration of the solution at the targeted nucleation temperatures.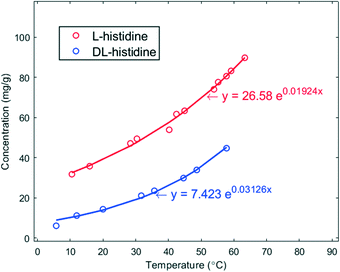

Fig. 1 Solubility curves in mg g⁻¹ of L- (red) and DL-histidine (blue) in water as a function of temperature in °C. The solid lines are fits of the data.

The nucleation kinetics of these compounds was determined using the induction time method, as reported elsewhere.^13,14 Experiments were performed with various initial concentrations at four nucleation temperatures (25, 20, 15, and 10 °C for L-histidine and 15, 10, 7, and 5 °C for DL-histidine). Each experimental run was carried out several times leading to a total number of at least 112 induction time data points per supersaturation ratio. The variation in the measured induction times at one supersaturation reflects the stochastic character of nucleation.

Using eqn (1), the nucleation rates for the different supersaturation ratios have been calculated. Its dependence on the supersaturation and on the temperature has been determined. Experimental conditions and results are shown in Table 1 and Fig. S2† for both enantiomer and racemic crystals. The high supersaturation used in the case of DL-histidine is related to the very slow nucleation rate seen in this system at low β. For instance, a sample at 15 °C with a β = 2.2 needs an average of 24 h to crystallize. Such high β could not be used in the case of L-histidine since the nucleation is too rapid. As expected, the nucleation rate J increases with increasing supersaturation and for the same supersaturation level the nucleation rate J decreases with decreasing temperature.

Table 1 Measured nucleation rate J (m⁻³ s⁻¹) for L-histidine and DL-histidine as a function of temperature and supersaturation

Compound	T (°C)	C 0 (mg g^−1)	β	J (m^−3 s^−1)
L-Histidine	25	67.7	1.6	516.9
		74.4	1.7	2392.0
		77.9	1.8	2773.3
		83.4	1.9	5914.2
	20	67.7	1.7	1185.3
		74.4	1.9	3506.3
		77.9	2.0	3658.1
		83.4	2.1	7112.6
	15	67.7	1.9	2239.9
		74.4	2.1	4939.7
		77.9	2.2	5206.7
		83.4	2.4	10 401.0
	10	67.7	2.2	5063.0
		74.4	2.3	6232.8
		77.9	2.4	7062.0
		83.4	2.6	15 070.0
DL-Histidine	15	33.0	2.7	252.7
		34.5	2.8	270.2
		36.0	2.9	863.9
		38.0	3.1	1168.3
	10	33.0	3.6	501.0
		34.5	3.7	620.8
		36.0	3.9	1473.1
		38.0	4.1	2244.9
	7	33.0	4.5	668.3
		34.5	4.7	1201.6
		36.0	4.9	1543.5
		38.0	5.2	2384.0
	5	33.0	5.7	848.1
		34.5	5.9	1227.2
		36.0	6.2	2230.3
		38.0	6.5	2572.7

---

The experimental cumulative probability distributions P(t) as a function of the measured induction times t_i in seconds are given in Fig. S3 and S4 in the ESI.†

Nucleation kinetic parameters

The temperature dependence of the nucleation rate can be modelled with an Arrhenius-type equation. The natural logarithm of J/β is a linear function of ln⁻² β as shown in eqn (3); the data have been accordingly plotted in Fig. 2. The resulting slopes and intercepts are used to determine the experimental thermodynamic parameter B_exp and kinetic parameter A_exp respectively. The considered model does not afford an understanding of the origins of the experimentally observed not perfect linear plots and variations for L-histidine at different temperature as seen in Fig. 2. Polymorphism of L-histidine (LHISTD01, LHISTD10) might be a reason for the relatively scattered data, however, XRD measurements of the final powders did not provide any proof that a second polymorph was present.²⁶

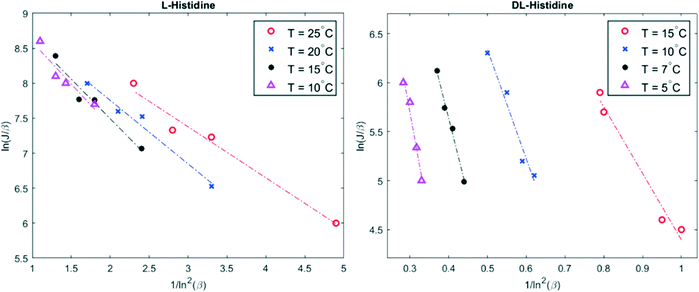Fig. 2 Plot of ln(J/β) versus 1/ln² β for four different temperatures. The experimental data are given by colored marker shapes and the dotted lines are the best fit to the experimental points.

The values of the parameters a_I, b_I, a_D and b_D are obtained from eqn (S5)–(S7)† and are reported in the ESI,† Table S1. These values are used to calculate the corresponding theoretical values of the kinetic A_I(predicted) and thermodynamic B_I(predicted) parameters using eqn (9).

The prediction of the kinetic parameter for homogeneous interface-transfer control A_{I,hom(predicted)} is obtained from eqn (7). The thermodynamic parameter B_{hom(predicted)} is obtained theoretically by substituting γ_predicted in eqn (4). The results are very similar to the one obtained by substituting a_I and b_I in eqn (9).

Experimental values of the interfacial energy (γ_exp) have been obtained from the B_exp values using eqn (4). The theoretical values of the interfacial energies (γ_predicted) have been calculated using eqn (8).

All results for L and DL-histidine are presented and compared in Table 2.

Table 2 Comparison between the parameters obtained from the experimental data and from theory

Compound	T (°C)	B exp	A exp (m^−3 s^−1)	γ exp (mJ m^−2)	B I(predicted)	B hom(predicted)	A I(predicted) (m^−3 s^−1)	A I,hom(predicted) (m^−3 s^−1)	γ (predicted) (mJ m^−2)
These parameters were calculated using. a Eqn (3). b Eqn (4). c Eqn (9) and (3). d Eqn (8) and (4). e Eqn (7). f Eqn (8).
L-Histidine	25	0.73	1.4 × 10^4	4.5	92	98	7.7 × 10^35	7.8 × 10^35	23.2
	20	0.91	1.5 × 10^4	4.7	99	106	6.2 × 10^35	6.3 × 10^35	23.5
	15	1.13	1.7 × 10^4	5.0	108	115	4.9 × 10^35	5.0 × 10^35	23.7
	10	1.2	1.8 × 10^4	5.0	117	124	3.9 × 10^35	3.9 × 10^35	23.9
DL-Histidine	15	6.8	7.1 × 10^4	9.1	230	240	1.9 × 10^35	1.9 × 10^35	30.4
	10	11.1	14.8 × 10^4	10.5	270	270	1.3 × 10^35	1.3 × 10^35	31.7
	7	15.7	15.1 × 10^4	11.7	310	330	9.4 × 10^34	9.5 × 10^34	32.9
	5	21.8	20.6 × 10^4	12.9	350	380	7.2 × 10^34	7.2 × 10^34	34.1

---

Only the results for interface-transfer control are shown here, those for volume-diffusion control obtained by linearizing the equation of J for volume-diffusion control (eqn (S4)†) by plotting ln (J/β ln β) in terms of ln⁻² β can be found in the ESI† (Fig. S5 and Table S2).

As represented in Table 2, with increasing the value of the temperature, the kinetic factor A and the thermodynamic factor B decrease in both systems. Considering that with increasing the value of A (higher concentration of nucleation sites and/or higher attachment frequency) and with decreasing the value of B (low energy barrier), it is easier for the solute molecules to aggregate together and to cross the free energy barrier. Thus, in this case increasing the nucleation temperature favours the nucleation process mainly in kinetic aspect.

The experimental values of A are 30–31 orders of magnitude lower than the predicted values for homogeneous nucleation A_I,hom, which can be viewed as a strong indication that the primary nucleation of histidine (L and DL) crystals is actually heterogeneous. This finding does not come as a surprise as previous papers have found a similar disagreement between experimental and theoretical values and ascribed this to heterogeneous nucleation.^14,25,27 It may be related to the low concentration of nucleation sites in the solution or to the low attachment frequency of molecules to the nucleus.¹³ However, these explanations could not be further explored with the current experimental setup.

As is shown in Table 2, the values of the kinetic parameter, A, the thermodynamic parameters, B and the interfacial energies γ for DL-histidine are larger than those obtained for L-histidine. Although the experimental values for both compounds are lower than the predicted ones, it is in fact close to those calculated from nucleation data for other organic compounds.^25,28,29

According to eqn (5) and (6), low interfacial energy is related to smaller critical nucleus size (proportional to γ). In the next part, the nucleation behaviour of the current systems will be discussed with respect to CNT in relation to the effect of γ on the critical nucleus size.

Energy barrier and cluster size

Within the CNT framework, by using B_exp values inferred from nucleation data, the thermodynamic activation barrier ΔG* and the number of molecules per nucleus n* at different temperatures have been determined in the supersaturation range of 1.7–2.4 for L-histidine and 2.6–3.6 for DL-histidine respectively (see ESI†).

It is clear from the results that as supersaturation or temperature increases, ΔG* and n* values become smaller. The nucleation barrier of DL-histidine is found to be higher than the one for L-histidine also explaining the slower nucleation of the racemic form vs. the pure enantiomer form.

Such a behaviour is of interest for the chiral resolution process; however, the observed, much faster nucleation of enantiopure crystals has not yet led to the crystallization of the conglomerate. In fact, the solubility of the stable racemic form is extremely low in comparison to the conglomerate. Given the solubility curves in Fig. 1, at 20 °C, the solubility of the racemic compound is 13.9 mg g⁻¹, whereas that of the conglomerate is two times that of the pure enantiomer 78.1 mg g⁻¹. This difference is extreme.³⁰ Thus, to reach at 20 °C a supersaturation of β > 1 with respect to the metastable conglomerate, where nucleation can be expected, the supersaturation with respect to the racemic form will be β ≥ 5.6. This obviously is a large impediment to nucleate the conglomerate as the high supersaturation counteracts the fast nucleation.

Microscopic behaviour observed by SHG

The Kurtz and Perry test has been performed on two racemic samples: the racemic compound as received from the manufacturer and the recrystallized solid at high supersaturation (up to β ≈ 15) under quiescent conditions. Although small, both clearly show a SHG effect (Fig. S8 and S9†).

SHG microscopy on these samples (laser excitation of 900 nm) confirms the presence of domains which are non-centrosymmetric embedded in the crystals (Fig. 3 and S10†). These domains can be differentiated from the very weak SHG surface effect and must therefore be non-centrosymmetric crystallites. This is inconsistent with the centrosymmetric crystal space group P2₁/c of the racemic crystals. On the other hand, the PXRD patterns of the samples match the calculated one, based on P2₁/c. Hence, above the detection threshold for PXRD, no other polymorphic form (which could have been non-centrosymmetric) has been observed. It appears therefore likely that some deviations in the 50–50 composition is tolerated by the ‘racemic’ crystal lattice. Considering the foregoing nucleation analysis, it is possible that in the highly supersaturated racemic system, initial nucleation of enantiomerically enriched crystals occurs. However, subsequently, crystal growth is taken over by the more stable and less soluble racemic crystal. These observations are consistent with a report on limited preferential enrichment observed for histidine³¹ and would explain the weak SHG effect in line with symmetry breaking through crystallisation.^32,33 It also explains, in the case of the racemic compound, why CNT may not work as the nucleation is clearly not a simply homogeneous process.

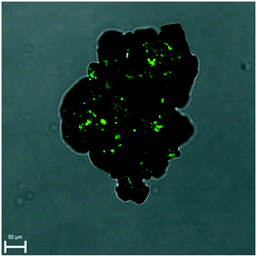Fig. 3 Overlay of SHG and microscope image demonstrating small non-centrosymmetric domains in the racemic crystal.

Conclusions

Nucleation induction time in water has been determined for two systems: racemic histidine and pure enantiomer of histidine. The effect of the temperature and the supersaturation ratio on the nucleation rate is presented. Classic nucleation theory does not describe the data correctly and this is likely due to heterogeneous instead of homogeneous nucleation as concluded before.³⁴ It is observed experimentally that the nucleation of DL-histidine is much slower than that of L-histidine for the same level of supersaturation and at the same temperature. This has not led to preferential crystallisation of the conglomerate due to the large differences in solubility between the conglomerate and the stable racemic compound. For the racemic compound, although the crystal structure is globally compatible with the P2₁/c space group, non-centrosymmetric domains are observed by SHG microscopy. As a partial reason, why CNT does not apply, the SHG signal implies that nucleation processes can in certain cases be highly complex phenomena in which the initially nucleating form loses out to the faster growing form that appears through secondary nucleation and growth, which possibly occurs on the nuclei of the initially nucleating form. Harnessing such phenomena may lead to better optimization of preferential crystallisation and separation of enantiomers by preferential enrichment.

List of symbols and abbreviations

N A	Avogadro's constant
k	Boltzmann constant
D	Diffusion coefficient
ΔG*	Gibbs free energy
t g	Growth time
t i	Induction time
C 0	Initial concentration
γ	Interfacial energy
A	Kinetic parameter
ν 0	Molecular volume
J	Nucleation rate
n*	Number of molecules in the nucleus
P(t)	Probability distribution
L	Pure enantiomer
DL	Racemic compound
SHG	Second harmonic generation
s	Solubility ratio
V	Solution volume
β	Supersaturation
B	Thermodynamic parameter
THG	Third harmonic generation
PXRD Powder	X-ray diffraction

Author contributions

All authors contributed equally.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research received funding as part of the NACRE Project by the European Regional Development Fund (FEDER) and the Normandy region. The authors thank Jules Kachaner for help with the experimental work during his internship at the SMS laboratory.

References

1. J. Chen, B. Sarma, J. M. B. Evans and A. S. Myerson, Cryst. Growth Des., 2011, 11, 887–895.
2. P. A. Larsen, D. B. Patience and J. B. Rawlings, IEEE Control Syst., 2006, 26, 70–80.
3. A. B. N. Brito and M. Giulietti, Cryst. Res. Technol., 2007, 42, 583–588.
4. S. Suzuki and J. Mizuguchi, Dyes Pigm., 2004, 61, 69–77.
5. P. Muhammed Shafi and A. Chandra Bose, AIP Adv., 2015, 5, 057137.
6. H.-H. Tung, E. L. Paul, M. Midler and J. A. McCauley, Crystallization of Organic Compounds: An Industrial Perspective, John Wileys & Sons, 2009.
7. P. G. Vekilov, Cryst. Growth Des., 2010, 10, 5007–5019.
8. P. G. Vekilov, Nat. Mater., 2012, 11, 838–840.
9. R. P. Sear, J. Phys. Chem. B, 2006, 110, 4985–4989.
10. X. Y. Liu, J. Chem. Phys., 2000, 112, 9949–9955.
11. A. Myerson, Handbook of Industrial Crystallization, Butterworth-Heinemann, USA, 2002.
12. A. Robin, P. Iavicoli, K. Wurst, M. S. Dyer, S. Haq, D. B. Amabilino and R. Raval, Cryst. Growth Des., 2010, 10, 4516–4525.
13. S. A. Kulkarni, S. S. Kadam, H. Meekes, A. I. Stankiewicz and J. H. Ter Horst, Cryst. Growth Des., 2013, 13, 2435–2440.
14. S. Jiang and J. H. Ter Horst, Cryst. Growth Des., 2011, 11, 256–261.
15. M. Vollmer, Kinetik der Phasenbildung, Verlag Theodor Steinkopff, Dresden, 1939.
16. A. E. Nielsen, Kinetics of Precepitation, Pergamon Press, Oxford, 1964.
17. C. Brandel and J. H. ter Horst, Faraday Discuss., 2015, 179, 199–214.
18. J. W. Mullin, Crystallization, Butterworth, London, 4th edn, 2001.
19. S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813.
20. D. Kashchiev and G. M. van Rosmalen, Cryst. Res. Technol., 2003, 38, 555–574.
21. D. Kashchiev, Nucleation: Basic Theory With Applications, Butterworth-Heinemann, Oxford, first, 2000.
22. M. P. Anisimov, Usp. Khim., 2003, 72, 664–706.
23. J. T. Edward, J. Chem. Educ., 1970, 47, 261–270.
24. M. Laliberte, J. Chem. Eng. Data, 2007, 52, 1507–1508.
25. C. Lindenberg and M. Mazzotti, J. Cryst. Growth, 2009, 311, 1178–1184.
26. M. Kitamura, J. Chem. Eng. Jpn., 1993, 26, 303–307.
27. R. J. Davey, S. L. M. Schroeder and J. H. Ter Horst, Angew. Chem., Int. Ed., 2013, 52, 2166–2179.
28. L. T. Padro and A. Nenes, Atmos. Chem. Phys. Discuss., 2007, 7, 2325–2355.
29. L. D. Shiau and H. P. Wang, J. Cryst. Growth, 2016, 442, 47–51.
30. G. Coquerel, J. Pharm. Pharmacol., 2015, 67, 869–878.
31. S. Iwama, PhD thesis, University of Tokyo, March 2012, (thesis in Japanese).
32. H. Takahashi, Y. Numao, J. Motokawa, S. Clevers, G. Coquerel, H. Tsue and R. Tamura, Chem. - Eur. J., 2019, 25, 16405–16413.
33. G. Coquerel and M. Hoquante, Symmetry, 2020, 12, 1796.
34. D. Gebauer, P. Raiteri, J. D. Gale and H. Cölfen, Am. J. Sci., 2018, 318, 969–988.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ce01199e

---