On the lipid flip-flop and phase transition coupling†
Lionel
Porcar
a and
Yuri
Gerelli
 *b
*b
aInstitut Laue-Langevin, avenue des Martyrs, 38000 Grenoble, France
bDepartment of Life and Environmental Sciences, Università Politecnica delle Marche, Via Brecce Bianche, 60131 Ancona, Italy. E-mail: y.gerelli@univpm.it
First published on 8th August 2020
Abstract
We measured the passive lipid flip-flop of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) in solid supported lipid bilayers across their main gel to fluid (Lβ → Lα) phase transition. By performing time and temperature resolved neutron reflectometry experiments, we demonstrated that asymmetric systems prepared in the gel phase are stable for at least 24 hours. Lipid flip-flop was found to be intrinsically linked to the amount of lipid molecules in the fluid phase. Moreover, the increase of this amount during the broad phase transition was found to be the main key factor for the timing of the flip-flop process. By measuring different temperature scan rate, we could demonstrate that, in the case of supported bilayers and for the temperature investigated, the lipid flip flop is characterised by an activation energy of 50 kJ mol−1 and a timescale on the order of few hours. Our results demonstrate the origin on the discrepancies between passive flip-flop in bulk systems and at interfaces.
1 Introduction
Biological membranes have a complex composition and consist of a continuous double layer (bilayer) of lipid molecules in which membrane proteins and sugar (forming glycolipids and glycoproteins) are embedded.1 Such a bilayer is formed, in turns, by two individual and opposite amphiphilic monolayers, also called leaflets. The distribution of molecular components in membranes can be both laterally heterogeneous and transversely asymmetric. This heterogeneity makes them sites of vital biochemical activities.2 For example, in most of the eukaryotic cells, compositional asymmetry is the result of a complex regulation process in which lipids are synthesised in the endoplasmic reticulum and then actively or passively transported from the site of synthesis to the Golgi apparatus first, and next to the cell membrane.3 Once these components reach the cell membrane, they can self-organise, for example, into the so-called lipid rafts4–6 giving rise to lateral heterogeneity, but also be distributed in a different ratio between inner and outer leaflets, giving rise to structural asymmetry.7 Indeed, structural asymmetry in cell membranes is of fundamental importance to ensure the correct functioning of living cells.8 Among other processes, loss of asymmetry in eukaryotic membranes is known to lead to cell apoptosis and therefore the understanding of dynamical processes promoting and loosening structural asymmetry plays an essential role in engineering safer drug treatments.9,10 More specifically, in the case of phospholipids, several physiological processes, such as blood coagulation and elimination of aged cells, are linked to transversal phospholipid motion.11–13 This motion is generally called translocation or lipid flip-flop (LFF), a process that in vivo is regulated and controlled by membrane proteins. In the present work, we refer to lipid flip-flop as to the spontaneous and passive, thermally activated inside-outside (and vice-versa) diffusion of lipid molecules in bilayers.14 Despite its fundamental role in cell regulation and potential impact on drugs development, features and energetic of LFF are still largely debated not only for in vivo systems but also for model systems.15,16 LFF in model systems has been studied since the ‘70s.The early results from Kornberg and McConnell indicated the timescale of flip-flop, for spin-labelled egg phosphatidylcholine, to be on the order of several hours in physiological conditions.14 Later, Bretscher17 postulated that specific enzymes, called flippase, were responsible for LFF but this idea was at first neglected, as the predominant belief was that formation of transient non-bilayer structures facilitated LFF. It is nowadays accepted that, in living cells, mono- and bi-directional active lipid transporters are mediating LFF, thus regulating the asymmetric distribution of lipid components in membranes. In the last decade, experiments have been mostly focusing on the passive LFF (i.e., non-mediated by flippase) because the investigation of the fundamental mechanism is easier in simplified model systems. Recently, the role of non-specific peptides on the passive LFF were investigated by preincorporating antimicrobial peptides in large unilamellar vesicles.18 These experiments indicated that without any specific activity, the presence of peptides within the lipid matrix was sufficient to accelerate the LFF rate with respect to the one observed for peptide-free vesicles. One of the future steps will be the investigation of LFF in more complex multi-component membranes systems, including proteins and in particular flippases. All the experiments referenced and carried out in this work relate to passive LFF monitored either through molecular exchange or spontaneous loss of asymmetry in isotopically asymmetric lipid systems.
Experimental methods, allowing to track the diffusion of given molecules within a chemically identical environment are few. Until the early 2000s, the majority of experiments were based on the use of fluorescent- or spin-labeled lipids, while it is now accepted that these probes do not accurately convey the dynamics and thermodynamics of native lipid motion.19 On the other hand, the use of isotopic labeling (as 1H–2H replacement) is expected to perturb less these native lipid motions since the change in shape and conformation of the molecule is very limited. However, 1H–2H replacement might have a non negligible impact on molecular interactions where hydrogen bonding is a significant factor. This method has been largely used in combination with small angle neutron scattering19,20 (SANS), neutron reflectometry21,22 (NR), nuclear magnetic resonance23 (NMR) and sum frequency generation vibrational spectroscopy24–26 (SFGVS). Some of these techniques were used to probe the features of LFF in solution (SANS and NMR) while NR and SFGVS were used for experiments at surfaces. A class of techniques not requiring any labeling strategy at all is that of computer simulations which have been used to track the LFF at different time- and length scales.2,16,27,28
So far, experimental investigations are providing contradictory results, indicating LFF timescales that differ of orders of magnitude: for example, reported LFF half times for phospholipid in fluid phase range from seconds (or subseconds) to hours to days or weeks.23 The correct determination of LFF rates and energetic remains nowadays a challenge, but in the last five years a coherent picture describing the lipid flip-flop is a slow motion started to emerge.19,20,23,29 In the recent work of Marquardt and co-workers,23 the authors addressed many aspects of these discrepancies between studies in solution and at interfaces, pointing out the role of defects as main passive force in timing the LFF process. Through Monte Carlo simulations they demonstrated that the presence of 1% defects (in terms of surface coverage) was enough to speed up the LFF process. In particular, they indicated that defects can facilitate LFF not only for bilayers in fluid phase, but also for bilayers in gel phase, corroborating the experimental observations of Liu and Conboy.24 Because of the acceleration promoted by defects, LFF in fluid phase was expected to be too fast to be experimentally measured. This point is of crucial interested for surface sensitive techniques, since the presence of such a small fraction of defects is almost unavoidable considering the sample preparation approaches available at the moment. Indeed, the presence of topological defects was pointed out by the authors as the origin of the discrepancies between LFF rates measured in bulk (in vesicles) and at interfaces (in solid-supported lipid bilayers).
Another result presented in the work of Marquardt23 was the influence of the phase change on the LFF rate in asymmetric large unilamellar vesicles composed by hydrogenous and partially deuterated DPPC molecules. Interestingly, they reported an increase of LFF rate if measurements were carried out at the main phase transition. In this case, the LFF rate was a factor of 2 greater than the measured one in the fully melted fluid phase and a factor of 5 greater than the expected rate as extrapolated from the fluid phase measurements.23 This accelerated LFF was attributed to enhanced volume fluctuations that might increase the probability of a translocation event. The same effect was already reported for DPPC small unilamellar vesicles labelled with fluorescent phospholipids.30
In this manuscript, we present a new investigation of the LFF in isotopically asymmetric solid-supported lipid bilayers by means of neutron reflectometry. In particular, we have investigated the interplay between phase change and LFF rate across the gel-to-fluid phase transition. Our results indicated that the growth of fluid domains during the phase transition, hypothesized in,31,32 can accelerate the LFF rate. However, they also demonstrated that isotopic asymmetry in SLBs was unaltered if the system was kept in the gel-phase despite the presence of a limited number of topological defects.
2 Experimental
2.1 Sample preparation
DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) and d75DPPC (1,2-dipalmitoyl-d62-sn-glycero-3-phosphocholine-1,1,2,2-d4-N,N,N-trimethyl-d9) were purchased from Avanti Polar Lipids (Alabaster, USA). Lipids were dissolved in chloroform (purchased from Merck Millipore) at 1 mg ml−1 concentration and stored at −20 °C until their use. Ultra-pure water and D2O were supplied by the Institut Laue Langevin (ILL, Grenoble). All water solution were degassed prior to their use. This step was essential for high-temperature experiments because it allowed to avoid formation of air bubbles inside the sample cell. Isotopically asymmetric solid supported lipid bilayers (SLBs) were deposited on the top of the polished surface of silicon single crystals (cut along the 111 plane, polished with 3 Å RMS roughness) by Langmuir Blodgett (LB) and Langmuir Schaefer (LS) deposition techniques.33 The properties of the silicon substrates and the deposition procedure are the same as those reported in an earlier work of our group.32 The only difference for the preparation of the samples described in this manuscript is in the type of lipid molecules used; for all the samples described in the manuscript, the first monolayer, deposited by LB, was always composed by deuterated d75DPPC molecules, while the second one, deposited by LS, was always composed by hydrogenous DPPC lipids. Both monolayers were deposited from a Langmuir film prepared at a surface pressure of 50 mN m−1 (Lβ, gel phase).Once deposited, samples were sealed within solid–liquid flow cells for neutron reflectometry experiments directly under water. Samples were kept prior to the measurements at 20 °C, a temperature lower than the melting temperature of DPPC SLBs.32 Solid–liquid cells were provided by the ILL and were equipped by a water reservoir made of PEEK in contact with the surface of the substrate, and by two metallic plates allowing for a precise temperature regulation. The water reservoir was connected to inlet and outlet valves allowing the exchange of the water subphase.
2.2 Neutron reflectometry
Neutron reflectometry (NR) measurements were performed on the neutron reflectometer D1734 (ILL, Grenoble, France) operated in time-of-flight mode. The instrument was configured as described in.32 Samples, deposited at the solid–liquid interface, were measured in the initial asymmetric and in the final mixed states exploiting the contrast variation method,35i.e., using D2O, H2O, a 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 (V/V) D2O
34 (V/V) D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixture (named 4MW), and a 38
H2O mixture (named 4MW), and a 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 (V/V) D2O
62 (V/V) D2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixture named silicon-matched water (SiMW). Each set of four reflectivity curves measured in these water solutions, was co-refined to obtain the structural description of initial and final states of the SLBs. The result of the modeling of such NR data is a scattering length density (SLD or ρ) profile along the vertical direction (z) with respect to the plane of the supporting interface.36 An SLD profile reflects the distribution of nuclei within the sample and therefore it gives information about the structure and location of different molecular species within the SLB.37 An important feature of the SLD is its variation upon isotopic substitution.35,38 Because of this, the value of an SLD can differ for two chemically identical molecular species differing only by their isotopic composition. SLD profiles are generated from the structural parameters obtained via the modeling of the reflectivity curves through a slab model. Each slab is characterised by a thickness, a total SLD value and by an interfacial roughness modeled by an error function. Details about the full modeling approach for an SLB can be found elsewhere.39
H2O mixture named silicon-matched water (SiMW). Each set of four reflectivity curves measured in these water solutions, was co-refined to obtain the structural description of initial and final states of the SLBs. The result of the modeling of such NR data is a scattering length density (SLD or ρ) profile along the vertical direction (z) with respect to the plane of the supporting interface.36 An SLD profile reflects the distribution of nuclei within the sample and therefore it gives information about the structure and location of different molecular species within the SLB.37 An important feature of the SLD is its variation upon isotopic substitution.35,38 Because of this, the value of an SLD can differ for two chemically identical molecular species differing only by their isotopic composition. SLD profiles are generated from the structural parameters obtained via the modeling of the reflectivity curves through a slab model. Each slab is characterised by a thickness, a total SLD value and by an interfacial roughness modeled by an error function. Details about the full modeling approach for an SLB can be found elsewhere.39
Kinetics measurements were performed in a single contrast not to affect the system during its evolution exploiting a novel operation mode available at the D17 instrument,40 using the time- and temperature-resolved (TTR-NR) approach recently used by our group to study the phase transition in SLBs composed by DPPC.32 The core of the TTR-NR kinetics measurements is the use of a time-resolved temperature profile. The evolution of the samples reported in this work was monitored using two different temperature ramps; in one case the temperature was changed step-wise, with 5 °C steps every 22 minutes from 30 °C to 40 °C and with 1 °C steps every 15 minutes from 40 °C to 60 °C. Thermal equilibrium (within ±0.1 °C) was reached in less than 1 minute for every step and reflectivity data corresponding to non-equilibrated states were not included in the analysis. Alternatively, the temperature was changed continuously, i.e., without any intermediate constant temperature steps, from 32 °C to 60 °C with a rate of 1.74 °C min−1. This implies that during fast scans, the temperature of a single acquisition has a ±0.87 °C uncertainty. For both ramps, reflectivity curves were acquired in the range 0.019 Å−1 < Q < 0.16 Å−1 every 30 seconds. If no changes were visible between two consecutive acquisitions, during data reduction measurements were binned to a 1 minute interval to increases data statistics. Details about the instrumental configuration used are given in.32
As described in recent works,31,32,41 the phase transition of a DPPC SLB is broad and starts at approximately 40 °C and it is characterized by the coexistence of fluid and gel phase lipids. We accounted for this fact in the analysis allowing only the fraction of fluid molecules undergo LFF events. The phase behaviour of each leaflet of the SLB was modeled as reported in ref. 32. In particular, the amount of lipids in the fluid phase, as a function of temperature, was empirically described by a Φ parameter for each leaflet, as
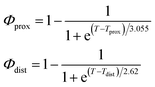 | (1) |
In eqn (1), Tprox = 47.8 °C and Tdist = 44.09 °C were determined empirically from the analysis of the Φ parameters for DPPC and d75DPPC.32 These data are reproduced in the ESI.† The two temperatures indicate the mid-point of the broad phase transition for proximal and distal leaflets and they were not assumed to change significantly upon lipid deuteration. The Φprox and Φdist parameters were used to account for the changes induced by the phase transition on the SLD, thickness and hydration levels as32
| Xj = (1 − Φ)Xgj + ΦXfj, | (2) |
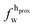 ,
, 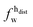 ) and tails (
) and tails (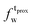 ,
, 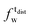 ). g and f refers to the value of the parameters in the gel and fluid phase. Eqn (2) was also used to determine to the head-groups (ρDPPCh,
). g and f refers to the value of the parameters in the gel and fluid phase. Eqn (2) was also used to determine to the head-groups (ρDPPCh, 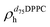 ) and tails (ρDPPCt,
) and tails (ρDPPCt, 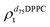 ) SLD values for the individual hydrogenated and deuterated lipid molecules. Being the phase transition acting differently on the two leaflets, all the above quantities were calculated twice, for the proximal and distal leaflets respectively.
) SLD values for the individual hydrogenated and deuterated lipid molecules. Being the phase transition acting differently on the two leaflets, all the above quantities were calculated twice, for the proximal and distal leaflets respectively.
For the LFF analysis, the amount of deuterated lipids in each leaflet was determined from the individual SLD values (during the data modeling) as
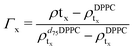 | (3) |
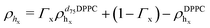 | (4) |
| Δρtprox(t,T) = e−2kf(T)[t−t0(T)] | (5) |
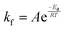 | (6) |
In eqn (6), A is a pre-exponential factor and R the universal gas constant. For a given temperature, the LFF half-time can be evaluated as
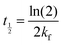 | (7) |
3 Results and discussion
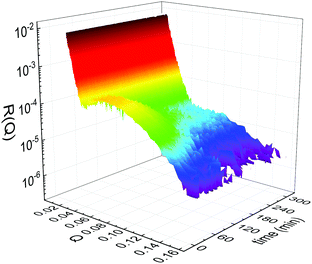
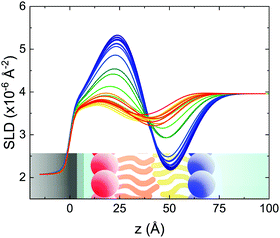
Static NR measurements performed at 25 °C, i.e., well below the phase transition temperature of each leaflet of the bilayer, indicated that the initial structure of the SLBs was indeed asymmetric in terms of isotopic composition (SLD profiles and reflectivity curves reported in the ESI†). However, an initial degree of mixing (ranging from 3%, Γ0 = 0.03, to 10%, Γ0 = 0.10) induced during the sample depositions was observed. It is worth mentioning that for other samples, excluded from the analysis, the initial degree of mixing reached even the 30% because of mishandling of the sample during its preparation. Sample preparation is therefore a crucial step for the success of the experiment. Despite the intrinsic difference in terms of SLD values, the structural parameters characterising the all asymmetric SLBs described in this work were in full agreement with those reported for pure d75DPPC and DPPC bilayers.32 Once the SLB evolution stopped, i.e., at high temperature, corresponding to the end of the LFF kinetics, contrast variation measurements were performed, without lowering the temperature, to characterize the sample structure in its fully mixed state (SLD profiles and reflectivity curves reported in the ESI†). Again, the parameters obtained resulted in agreement with those reported for a fluid DPPC bilayer32 and were used as a reference for the evolution of the sample during the analysis of reflectivity curves measured according to temperature scans.As described in the experimental section, a key assumption of the model requires lipid molecules to be in the fluid phase to be able to undergo LFF events. Since the phase transition to the fluid phase in SLBs has been shown to take place in a large temperature range,31,32,42 it was expected to observe a similar temperature dependence for the LFF process. For this reason, the evolution of the mixing kinetics was studied with two different temperature ramps, one including steps at constant temperature and a continuous one. Starting and ending temperatures were the same, but the overall temperature-time rates were different, being 0.063 °C min−1 the one for the constant-temperature steps profile and 1.74 °C min−1 that of the continuous temperature profile. These two scans are named slow and fast in the following. In Fig. 1 the reflectivity curves measured during the slow scan are shown. Changes in the shape and intensity of the curves are clearly visible and are indicative of a structural modification of the SLB. All the corresponding SLD profiles obtained according to the modeling of TTR-NR data are reported in the ESI.† The SLD profiles obtained for the sample measured with the fast scan are reported in Fig. 2.
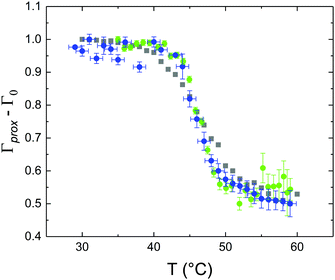
These profiles were calculated assuming only two free parameters, namely ρtprox and ρtdist, i.e., the SLD values of the tail region for proximal and distal leaflet respectively. They can be therefore used to better evaluate temperature and time dependence of the LFF process. The values of these parameters, obtained from the modeling of the TTR-NR data (fast scan), are reported in Fig. 3. The temperature evolution of the two parameters was not biased by any link between them and the symmetric trend confirmed that the changes reported for the SLD profiles were actually originated by the progression of the LFF process. Because of this symmetric behaviour (confirmed for all samples) all the further analysis are reported for the ρtprox parameter only. As already mentioned, the initial isotopic composition of the samples was not fully asymmetric because of a pre-mixing taking place during sample preparation. This explain why the low-temperature ρt values did not correspond to those of pure DPPC or d75DPPC tail regions. The variation in SLD indicated that the original asymmetry was kept when both leaflets are in the gel phase while LFF starts above 40 °C, in combination with the appearance of the SLB phase transition.32 The mixing was completed when the temperature reached approximately 55 °C. The same temperature dependence was found for the ρt parameters obtained from the analysis of the TTR-NR data measured according to the slow temperature ramp. As mentioned already, because of the arbitrary degree of initial mixing Γ0 between the samples, the ρt do not overlap exactly between different samples. For this reason, the mixing data compared in terms of Γprox(T) − Γ0, i.e., in terms of the amount of deuterated molecules in the proximal leaflet (eqn (3)), in Fig. 4. The original ρtprox data are reported in the ESI† material. The temperature evolution of Γprox was, for both scans, the same within the experimental accuracy. It is worth noting that the measurements were performed independently and on two different samples, confirming thus the high confidence in the results obtained. For comparison purposes, Γprox(t,T), was obtained also from a Monte Carlo simulation in which, an originally asymmetric system was able to mix following the assumption made for our experimental model. In brief, the system was populated initially by molecules in the gel phase; if a molecule was in the gel phase it was not allowed to move to the opposite layer. As temperature increased, the number of molecules in the fluid phase increased as described from eqn (1). In this case the molecules were allowed to undergo random flip-flop events. To reproduce the experimental conditions, for each temperature step the evolution of the system was observed for different times. Only in case of very short observation times, the system did not evolve into a fully mixed state. The time-averaged Γprox obtained from the MC simulation is overlapping with the experimental data. Minor differences are present at low temperature, where flip-flop events were observed in the simulation but not in the data. This might be related to the appropriateness of eqn (1) in describing the real system at the boundaries of its evolution. The surprising result is that, independent of the scan rate, the time-average evolution of the LFF is the same. This might indicate that temperature changes play a more important role than time in determining the LFF kinetics. In particular, it is worth recalling that between approx. 42 °C and 55 °C, DPPC SLBs are characterised by a gel–fluid phase coexistence. It was already pointed out23,30 that in presence of phase coexistence, enhanced structural fluctuations might accelerate the LFF not only in bi-dimensional bilayers but also in vesicles. Here we report a consistent result for which, the increasing amount of lipid molecules in fluid phase accelerate instantaneously the LFF. As reported for symmetric bilayers phase transition might occur through the appearance and growth of fluid-in-gel domains.31,42 The growth of fluid domains was reported to be extremely fast so that, for a given temperature, their size, once increased, stays constant with time32 as indicated by the thermotropic nature of the main phase transition. In the case of the asymmetric bilayers investigated in this work, the variation in Γprox induced by thermal effects is predominant. However, once temperature is equilibrated, the LFF is clearly visible through slower changes in the Γprox(t,T = const.) (or ρtprox(t,T = const.)) parameter. To investigate the possible interplay between time and temperature the LFF progression was monitored according to the slow temperature scan. All the ρtprox values obtained according to the slow scan are shown, as a function of time, in Fig. 5, and colors indicate the different temperatures.
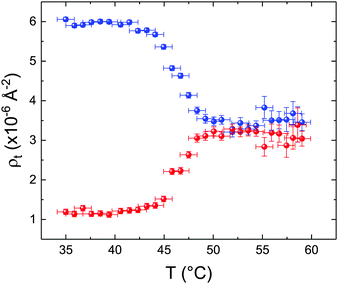 | ||
| Fig. 3 Temperature dependence for ρtprox (proximal leaflet, blue symbols) and ρtdist (distal leaflet, red symbols) obtained from the analysis of the fast TTR-NR measurements. | ||
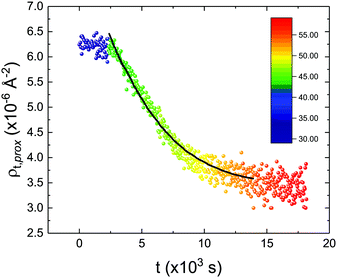 | ||
| Fig. 5 Time evolution of the ρtprox parameter obtained from the analysis of the TTR-NR data measured according to the constant temperature steps profile. Values obtained at different temperatures are labelled with different colors in the graph. The model of the time-dependent kinetic evolution (eqn (5)) is plotted as full line for the temperature range analysed. | ||
The time dependence of the ρtprox is clearly visible that above a certain temperature, the LFF process, if observed on a timescale slow enough, appears as a continuous process. However, since temperature changes, the kinetic of the system can not be described by a single exponential process. In fact, by assuming an Arrhenius-like behaviour (assumption based on the results present in literature19,20,23,24), the rate constant of the LFF has to change as temperature changes. The data shown in Fig. 5 were therefore analysed by using eqn (5) and (6) in which this temperature dependence was directly accounted for. The model could be applied only to a restricted temperature range, i.e., from approx. 42 °C up to ∼54 °C. The low temperature could not be analysed since the system did not show any kinetics, while for the high-temperature regime, data resulted to be too scattered. The model shows a good agreement with the experimental data. The global activation energy resulted Ea = 50 ± 5 kJ mol−1 corresponding to a half-time ranging from t1/2 ∼ 60 min in the low temperature regime (green part of the curve) up to t1/2 ∼ 30 min for the high temperature regime (orange region). Some deviations are however present at short time and a model with a double activation energy could describe the data with better accuracy. However, on the basis of our experimental data, we could not justify the presence of two different activation energies. The corresponding values for the temperature-dependent rate constant are reported in Fig. 6, together with the values for the same constant obtained by Liu24 (SLBs) and by Marquardt23 (vesicles).
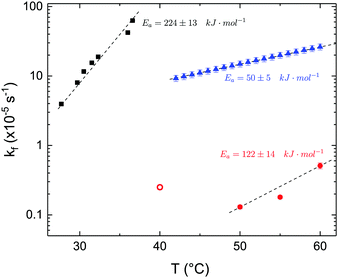 | ||
| Fig. 6 LFF rate constants kf obtained in the present work (asymmetric DPPC SLB, blue triangles), from Liu and Conboy24 (asymmetric DPPC SLB, black squares) and from Marquardt and coworkers23 (asymmetric DPPC vesicles in fluid phase, red solid circles, and in gel–fluid coexistence, red open circle). Values of activation energy reported for the three samples are also indicated. Dashed lines are guides for the eye. | ||
By comparing the present results to those reported in literature, it is possible to state that for the SLBs we investigated, LFF was not observed if samples were kept in the gel phase. This statement is surely valid for a timescale reaching 24 hours. Because of the limited amount of time available for neutron scattering experiments, a longer timescale could not be investigated. The initial level of mixing observed remained constant during these 24 h, allowing us to conclude that it was induced during the sample preparation and not by real LFF events as already reported for other asymmetric systems for which flip-flop was strongly hindered.43 In our opinion, this observation rules out a major role of defects (always present to a certain extent in LB-LS samples) in rendering the flip-flop in the gel phase as fast as detected in SFGVS experiments.24,26 On the other hand, defects might have an impact on the flip-flop rate during the phase transition. In fact, the values for activation energy found in the present work and, more importantly, the values of the rate constant kf, suggested that LFF in SLBs is faster than in vesicles. One justification might be the unavoidable presence of defects and the second one the presence of a broader temperature interval characterised by phase coexistence. Faster flip-flop was also reported in defect-free bilayers coating silica nanoparticles44 and this was explained in terms of increased disorder in the bilayer structure as induced by the presence of the supporting silica surface. However, the measure of this enhanced disorder was indeed a broader phase transition profile (compared to the one of free standing vesicles). A broad phase transition was also reported in the case of asymmetric vesicles,23 and it was related to the coexistence of fluid and gel phase lipids. In this last case, the activation energy was on the order of 120 kJ mol−1, i.e., greater by a factor of 2.4 with respect to the one we found for SLBs. The values of kf differed by almost two orders of magnitude (Fig. 6). Because of these differences also the half time for the LFF in SLBs resulted much shorter than those reported for vesicles at similar temperatures. It is therefore clear that, because of the behaviour of the phase transition of SLBs,32 there is a strong role of temperature changes that can accelerate, or better tune, the LFF progression. In fact, while the time-dependence of the LFF is slow, changes in temperature and therefore changes in the number of lipids in the fluid phase produce larger changes on the mixing. Enhanced fluctuations at the phase transition might be the mechanism at the origin of this effect, and it could explain the large discrepancies observed so far in studies performed at interfaces and in solution.15,44
4 Conclusions
Time and temperature resolved neutron reflectometry allowed us to investigate the lipid flip-flop mechanism in solid supported lipid bilayers. An intrinsic interplay between the phase transition profile and the progression of the LFF has been described. In particular, temperature effects were found to be the main driving force for the definition of the LFF time-scale. Measurements performed during the phase transition from the gel to the fluid phase, but a constant temperature, allowed us to determine that the LFF is indeed a relatively slow process also in SLBs, in partial agreement with several results obtained from bilayers in solution and already published.19,20,23,44 However, because of the intrinsic coupling between phase transition and LFF timescale present for solid-supported bilayers, we demonstrated that the same system, at a solid interface or in bulk did not behave in the exactly same way. In fact, the time scale of LFF in solution resulted to be much longer than the one observed for SLBs. However, the difference in the observed flip-flop rates might be also a result of the presence of a small and limited amount of defects, almost unavoidable in SLBs. As demonstrated by Marquardt and co-workers,23 a small amount of defects might have large consequences on the LFF process. Even if our data indicate that this effect is indeed smaller than the one the authors reported, we cannot exclude that the measured timescale might be affected, to some extents, by a limited number of defects present in the SLBs studied in the present work. A conclusive answer to this point might require an extensive investigation of LFF in SLBs with a controlled number of defects. On the other hand, we demonstrated that it is indeed possible to measure the lipid flip-flop in SLBs above their melting temperature and that asymmetric samples could be prepared and kept unaltered in the gel phase. Our results provided a clarification of the discrepancies reported in literature between the lipid flip-flop features determined in solution and at interfaces, suggesting that planar systems are intrinsically different for those obtained with the same molecules in solution.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Institut Laue – Langevin for the awarded beamtime (DOIs: 10.5291/ILL-DATA.9-13-852 and 10.5291/ILL-DATA.TEST-2786) on the neutron reflectometer D17 and the Partnership for Soft Condensed Matter for the financial support provided as well for the access to sample preparation and complementary characterisation facilities. The authors gratefully thank Bill Hamilton for discussion and proof reading assistance during the preparation of the manuscript. YG thanks Felix Roosen-Runge for the fruitful discussions about the LFF kinetics.References
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Science, New York, 4th edn, 2002 Search PubMed.
- G. Parisio, A. Ferrarini and M. M. Sperotto, Int. J. Adv. Eng. Sci. Appl. Math., 2016, 8, 134–146 CrossRef.
- V. W. Hsu, S. Y. Lee and J. S. Yang, The evolving understanding of COPI vesicle formation, 2009.
- K. Simons and E. Ikonen, Nature, 1997, 387, 569–572 CrossRef CAS PubMed.
- K. Simons and W. L. Vaz, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 269–295 CrossRef CAS PubMed.
- K. Simons and M. J. Gerl, Nat. Rev. Mol. Cell Biol., 2010, 11, 688–699 CrossRef CAS PubMed.
- J. D. Nickels, S. Chatterjee, C. B. Stanley, S. Qian, X. Cheng, D. A. A. Myles, R. F. Standaert, J. G. Elkins and J. Katsaras, PLoS Biol., 2017, 15, e2002214 CrossRef PubMed.
- H. Lodish, A. Berk, C. A. Kaiser, M. Krieger, M. P. Scott, A. Bretscher, H. Ploegh and P. Matsudaira, et al., Molecular cell biology, Macmillan, 2008 Search PubMed.
- S. W. Fesik, Nat. Rev. Cancer, 2005, 5, 876–885 CrossRef CAS PubMed.
- A. P. Demchenko, Exp. Oncol., 2012, 34, 263–268 CAS.
- J. F. Tait and D. Gibson, J. Lab. Clin. Med., 1994, 123, 741–748 CAS.
- E. M. Bevers, T. Wiedmer, P. Comfurius, S. J. Shattil, H. J. Weiss, R. F. Zwaal and P. J. Sims, Blood, 1992, 79, 380–388 CrossRef CAS.
- Transmembrane Dynamics of Lipids, ed. P. F. Devaux and A. Herrmann, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2011 Search PubMed.
- R. D. Kornberg and H. M. McConnell, Biochemistry, 1971, 10, 1111–1120 CrossRef CAS PubMed.
- J. S. Allhusen and J. C. Conboy, Acc. Chem. Res., 2017, 50, 58–65 CrossRef CAS PubMed.
- A. A. Gurtovenko and I. Vattulainen, J. Phys. Chem. B, 2007, 111, 13554–13559 CrossRef CAS PubMed.
- M. S. Bretscher, Nat. New Biol., 1972, 236, 11 CrossRef CAS PubMed.
- M. H. L. Nguyen, M. DiPasquale, B. W. Rickeard, M. Doktorova, F. A. Heberle, H. L. Scott, F. N. Barrera, G. Taylor, C. P. Collier, C. B. Stanley, J. Katsaras and D. Marquardt, Langmuir, 2019, 35, 11735–11744 CrossRef CAS PubMed.
- S. Garg, L. Porcar, A. C. Woodka, P. D. Butler and U. Perez-Salas, Biophys. J., 2011, 101, 370–377 CrossRef CAS PubMed.
- M. Nakano, M. Fukuda, T. Kudo, H. Endo and T. Handa, Phys. Rev. Lett., 2007, 98, 238101 CrossRef PubMed.
- Y. Gerelli, L. Porcar and G. Fragneto, Langmuir, 2012, 28, 15922–15928 CrossRef CAS PubMed.
- Y. Gerelli, L. Porcar, L. Lombardi and G. Fragneto, Langmuir, 2013, 29, 12762–12769 CrossRef CAS PubMed.
- D. Marquardt, F. A. Heberle, T. Miti, B. Eicher, E. London, J. Katsaras and G. Pabst, Langmuir, 2017, 33, 3731–3741 CrossRef CAS PubMed.
- J. Liu and J. C. Conboy, Biophys. J., 2005, 89, 2522–2532 CrossRef CAS PubMed.
- T. C. Anglin and J. C. Conboy, Biophys. J., 2008, 95, 186–193 CrossRef CAS PubMed.
- T. C. Anglin, M. P. Cooper, H. Li, K. Chandler and J. C. Conboy, J. Phys. Chem. B, 2010, 114, 1903–1914 CrossRef CAS PubMed.
- M. M. Sperotto and A. Ferrarini, The Biophysics of Cell Membranes, Springer, Singapore, 2017, pp. 29–60 Search PubMed.
- R.-X. Gu, S. Baoukina and D. P. Tieleman, J. Chem. Theory Comput., 2019, 15, 2064–2070 CrossRef CAS PubMed.
- M. Markones, C. Drechsler, M. Kaiser, L. Kalie, H. Heerklotz and S. Fiedler, Langmuir, 2018, 34, 1999–2005 CrossRef CAS PubMed.
- K. John, S. Schreiber, J. Kubelt, A. Herrmann and P. Müller, Biophys. J., 2002, 83, 3315–3323 CrossRef CAS PubMed.
- H.-L. Wu, Y. Tong, Q. Peng, N. Li and S. Ye, Phys. Chem. Chem. Phys., 2016, 18, 1411–1421 RSC.
- Y. Gerelli, Phys. Rev. Lett., 2019, 122, 248101 CrossRef CAS PubMed.
- M. C. Petty and W. A. Barlow, in Langmuir-Blodgett Films, ed. G. Roberts, Springer, US, Boston, MA, 1990, pp. 93–132 Search PubMed.
- T. Saerbeck, R. Cubitt, A. Wildes, G. Manzin, K. H. Andersen and P. Gutfreund, J. Appl. Crystallogr., 2018, 51, 249–256 CrossRef CAS.
- T. L. Crowley, E. M. Lee, E. A. Simister and R. K. Thomas, Phys. B, 1991, 173, 143–156 CrossRef.
- J. Fitter, T. Gutberlet and J. Katsaras, Neutron Scattering in Biology: Techniques and Applications, Springer, 2006, vol. 1st, p. 736 Search PubMed.
- Y. Gerelli, EPJ Web Conf., 2020, 236, 04002 CrossRef.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- Y. Gerelli, J. Appl. Crystallogr., 2016, 49, 330–339 CrossRef CAS.
- R. Cubitt, T. Saerbeck, R. A. Campbell, R. Barker and P. Gutfreund, J. Appl. Crystallogr., 2015, 48, 2006–2011 CrossRef CAS.
- D. Keller, N. B. Larsen, I. M. Møller and O. G. Mouritsen, Phys. Rev. Lett., 2005, 94, 025701 CrossRef PubMed.
- A. F. Xie, R. Yamada, A. A. Gewirth and S. Granick, Phys. Rev. Lett., 2002, 89, 246103 CrossRef PubMed.
- L. A. Clifton, M. W. A. Skoda, E. L. Daulton, A. V. Hughes, A. P. Le Brun, J. H. Lakey and S. A. Holt, J. R. Soc., Interface, 2013, 10, 20130810 CrossRef PubMed.
- B. Wah, J. M. Breidigan, J. Adams, P. Horbal, S. Garg, L. Porcar and U. Perez-Salas, Langmuir, 2017, 33, 3384–3394 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Characterisation of static NR datasets, additional SLD profiles for the slow sample, temperature dependence of the Φ parameters, details about Monte Carlo simulation and comparison between ρtprox data obtained at different temperatures. See DOI: 10.1039/d0sm01161d |
| This journal is © The Royal Society of Chemistry 2020 |