Open Access Article
Open Access ArticleDriving high quantum yield NIR emission through proquinoidal linkage motifs in conjugated supermolecular arrays†
Erin J. Peterson ,
Wei Qi,
Ian N. Stanton,
Peng Zhang
,
Wei Qi,
Ian N. Stanton,
Peng Zhang and
Michael J. Therien
and
Michael J. Therien *
*
Department of Chemistry, French Family Science Center, Duke University, 124 Science Drive, Durham, North Carolina 27708-0346, USA. E-mail: michael.therien@duke.edu
First published on 5th August 2020
Abstract
High quantum yield NIR fluorophores are rare. Factors that drive low emission quantum yields at long wavelength include the facts that radiative rate constants increase proportional to the cube of the emission energy, while nonradiative rate constants increase in an approximately exponentially with decreasing S0–S1 energy gaps (in accordance with the energy gap law). This work demonstrates how the proquinoidal BTD building blocks can be utilized to minimize the extent of excited-state structural relaxation relative to the ground-state conformation in highly conjugated porphyrin oligomers, and shows that 4-ethynylbenzo[c][1,2,5]thiadiazole (E-BTD) units that terminate meso-to-meso ethyne-bridged (porphinato)zinc (PZnn) arrays, and 4,7-diethynylbenzo[c][1,2,5]thiadiazole (E-BTD-E) spacers that are integrated into the backbone of these compositions, elucidate new classes of impressive NIR fluorophores. We report the syntheses, electronic structural properties, and emissive characteristics of neoteric PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD fluorophores. Absolute fluorescence quantum yield (ϕf) measurements, acquired using a calibrated integrating-sphere-based measurement system, demonstrate that these supermolecules display extraordinary ϕf values that range from 10–25% in THF solvent, and between 28–36% in toluene solvent over the 700–900 nm window of the NIR. These studies underscore how the regulation of proquinoidal conjugation motifs can be exploited to drive excited-state dynamical properties important for high quantum yield long-wavelength fluorescence emission.
Introduction
Low band gap π-conjugated molecules and oligomers are central to function in electro-optic applications that span excitonic solar cells,1–7 field-effect transistors,8,9 optical power limiting (OPL),10 dye-sensitized solar cells (DSSCs),11,12 photon-upconversion (UC) technologies,13–17 long-wavelength light-emitting diodes,18–20 nonlinear optics (NLO),21–24 and biological imaging.25–27 Desirable low band gap materials for these applications typically feature singlet manifold transitions (S0 → S1, S0 → Sn, and S1 → Sn) that possess large absorptive oscillator strengths covering broad spectral domains that include the near-infrared (NIR).Driving high fluorescence quantum yields is perhaps the most demanding design challenge for low band gap chromophores. Engineering augmented S0 → S1 transition oscillator strength is not sufficient to realize correspondingly high S1 → S0 fluorescence quantum yields (ϕf values), particularly as the optical band gap is diminished: while it is often the case that a large S0 → S1 absorptive extinction coefficient is correlated with a correspondingly large S1 → S0 radiative rate constant congruent with the Strickler–Berg relationship,28 most strongly absorbing NIR chromophores are not impressive emitters, due to the substantial S1 state non-radiative rate constants (knr values) that ensue from the energy gap law.29
With respect to high oscillator strength NIR absorbers, meso-to-meso ethyne-bridged (porphinato)zinc (PZnn) arrays (Chart 1A)17,30–46 constitute a notable exception to these generalizations. These supermolecules – conjugated structures realized from strong coupling of simple chromophoric building blocks – manifest such strong electronic and excitonic interactions between the constituent (porphinato)zinc oscillators that entirely unique photophysical entities are defined. PZnn structures, for example, possess fluorescence quantum yields comparable to the most impressive NIR laser dyes in the 750–900 nm regime,41 and rival the highest reported for organic dyes in this spectral window;47–49 importantly, PZnn emitters do not suffer from the commonly cited drawbacks of tricarbocyanine dyes that include poor photostability and fluorescence quantum yields that drop precipitously with decreasing solvent polarity.25,50,51PZnn chromophores feature low energy Q-state derived π–π* excited-states that are polarized exclusively along the long molecular axis, and lowest energy transitions that gain in intensity and progressively red-shift with increasing numbers of PZn units. Extended conjugation in these highly polarizable chromophores drives red-shifting of PZnn fluorescence spectra. Because triplet excitons are more spatially confined than singlet excitons in these systems,31,34,35,39,52,53 an unusual dependence of ϕf magnitude upon increasing emission wavelength [λmax(S1 → S0)] is manifest that confounds that anticipated simply from the energy gap law.41 Because of this disparity in lowest energy singlet (S1) and triplet (T1) state delocalization, diminished S1–T1 intersystem crossing rate constants (kisc values) track with increasing conjugation in PZnn chromophores, and serve to partly counter-balance the impact of augmented Franck–Condon mediated internal conversion rate constants (kic values) that typically accompany diminished S0–S1 energy gaps in the NIR. These impressive PZnn photophysical properties have been exploited in a wide range of fluorescence imaging applications.54–61
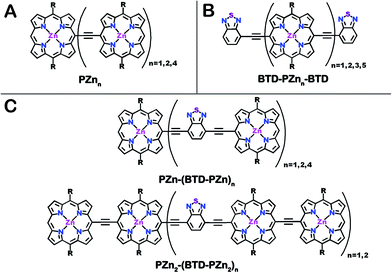 | ||
| Chart 1 Chemical structures for (A) benchmark PZnn, (B) BTD-PZnn-BTD and (C) PZn2-(BTD-PZn2)n and PZn-(BTD-PZn)n fluorophores. R = [2,6-bis(3,3-dimethyl-1-butyloxy)phenyl]. | ||
The photophysical properties of PZnn chromophores may be extensively modulated via incorporation of proquinoidal units into these emblematic conjugated arrays. For example, proquinoidal spacer (Sp) moieties such as 4,7-diethynylbenzo[c][1,2,5]thiadiazole (E-BTD-E), 6,13-diethynylpentacene (E-PC-E), 4,9-diethynyl-6,7-dimethyl[1,2,5]thiadiazolo[3,4-g]quinoxaline (E-TDQ-E), and 4,8-diethynylbenzo[1,2-c:4,5-c′]bis([1,2,5]thiadiazole) (E-BBTD-E) that link bis[(porphinato)zinc] units can be utilized to modulate the relative degrees of quinoidal character that characterize the ground and electronically excited singlet states in these highly conjugated supermolecules.62 Recent work highlights how electronic modulation of proquinoidal conjugation motifs can also be exploited as a powerful means to modulate independently the dynamics of excited-state relaxation pathways in these systems, enabling, for example, exceptional NIR absorbers that possess long-lived electronically excited triplet states (τT1 > μs) that are generated at unit quantum yield.63 In this contribution, we (i) show how proquinoidal BTD building blocks can be utilized to minimize the extent of excited-state structural relaxation relative to the ground-state conformation in highly conjugated porphyrin oligomers, and (ii) demonstrate that 4-ethynylbenzo[c][1,2,5]thiadiazole (E-BTD) units that terminate PZnn chromophores (Chart 1B), and E-BTD-E spacers that are integrated into the backbone of these compositions (Chart 1C), enable elucidation of new classes of impressive NIR fluorophores.
Results and discussion
Synthesis
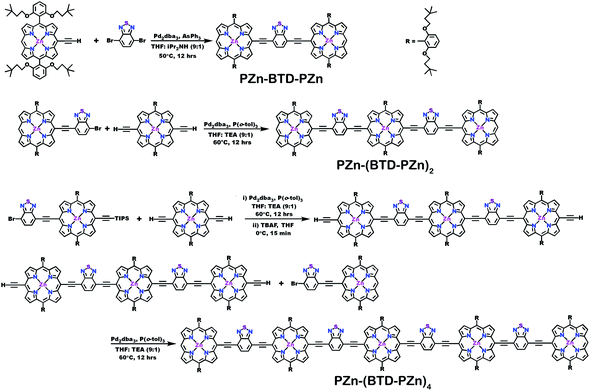
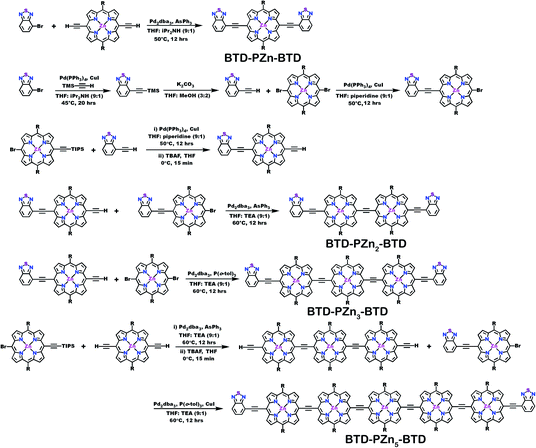
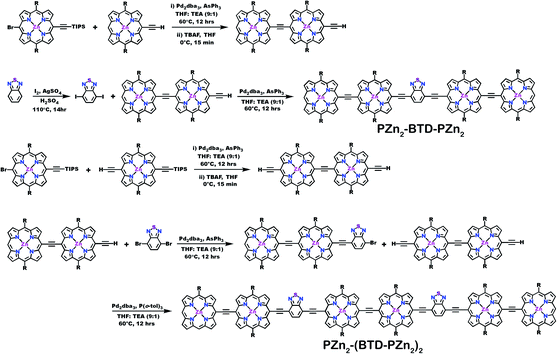
Schemes 1–3 outline the synthetic strategies for the fabrication of BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n chromophores. These structures were synthesized by palladium (Pd)-mediated cross-coupling reactions involving appropriately substituted (porphinato)zinc(II) (PZn) compounds, BTD spacers, and terminal BTD units. These structures exploit [2,6-bis(3,3-dimethyl-1-butyloxy)phenyl] groups as 10- and 20-meso-porphyrin substituents, which facilitate solubility and straightforward assignment of 1H-NMR spectra.37,64 The nature of the functionalized PZn, PZnn, and BTD moieties used in the syntheses of these BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n arrays varied with the degree of conjugation in the precursor molecules. Synthetic details may be found in the ESI.†Steady-state absorption and emission spectroscopy of BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n chromophores
Steady-state electronic absorption and fluorescence spectra recorded for reference PZnn chromophores (PZn2, PZn3, and PZn5; Fig. 1A),17,30–46,54–56,58,59,61,63,65 as well as PZn-(BTD-PZn)n [PZn-BTD-PZn,62PZn-(BTD-PZn)2, and PZn-(BTD-PZn)4; Fig. 1B], PZn2-(BTD-PZn2)n [PZn2-BTD-PZn2 and PZn2-(BTD-PZn2)2; Fig. 1C], and BTD-PZnn-BTD [BTD-PZn-BTD,66BTD-PZn2-BTD, BTD-PZn3-BTD, and BTD-PZn5-BTD; Fig. 1D] arrays, are shown in Fig. 1. The overall characteristics of the electronic absorption spectra for these PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD chromophores resemble those described previously for dimeric and multimeric PZn compounds that feature a meso-to-meso ethyne-linkage topology (PZnn arrays); these spectra exhibit two distinct intense absorption manifolds that are derived from the porphyrin B- (Soret, S0 → S2) and Q-band (S0 → S1) transitions.30,32–34,37,38,40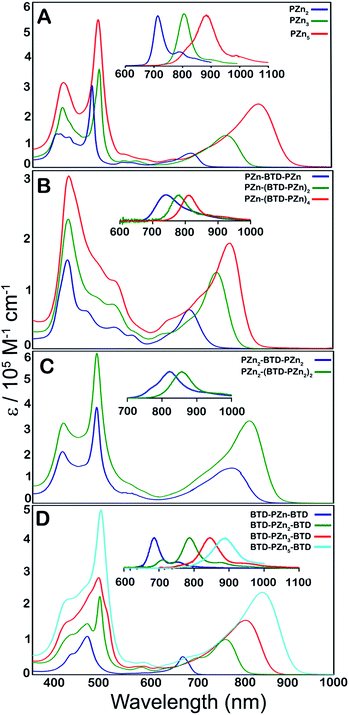 | ||
| Fig. 1 Electronic absorption and emission spectra (figure panel insets) recorded for: (A) benchmark PZnn chromophores (see ref. 30 and 41), and (B) PZn-(BTD-PZn)n, (C) PZn2-(BTD-PZn2)n, and (D) BTD-PZnn-BTD compositions. Experimental conditions: T = 298 K, THF solvent. | ||
The observed perturbations from these benchmark PZnn spectra trace their origin to the proquinoidal BTD units that are connected to the porphyrin macrocycle meso carbons via ethynyl moieties. Previous investigations demonstrate that the nature of proquinoidal unit conjugation to the PZn macrocycle exerts a pronounced impact on the magnitude of B- and Q-state mixing;62,63,66 for example, for PZn–(proquinoidal Sp)–PZn chromophores, the long axis-polarized Q state (Qx) absorption maxima can be modulated from 689 to 1006 nm, depending upon the extent of the quinoidal resonance contribution to the electronically excited singlet state.62 A combination of semi-empirical electronic structure calculations and electrochemical data underscore the cardinal role that PZn and proquinoidal fragment orbital energy differences play in fixing the radical cation and anion state energy levels in these structures.62,63
The principles that informed design of these PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD chromophores stem from prior work that examined the photophysics of (porphinato)metal–(proquinoidal Sp)–(porphinato)metal super-molecules.63 This work highlighted the central importance of the magnitude of the energy separation between the (porphinato)metal and proquinoidal Sp fragment frontier orbitals in determining whether radiative, internal conversion, or intersystem crossing decay channels dominated the relaxation dynamics of the initially prepared electronically excited states of these complexes. When the (porphinato)metal and proquinoidal Sp fragment LUMO levels featured energy separations on the order of a few tenths of an eV, as they are for the 5-ethynyl-PZn, 4-ethynyl-BTD, and 4,7-diethynyl-BTD fragments of these PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD structures, chromophores having multiconfigurational S1 states characterized by a modest degree of charge transfer (CT) character are anticipated; such supermolecules were shown to display large S1 → S0 radiative rate constants and substantial fluorescence quantum yields. Other factors that informed the blueprint of the Fig. 1B–D supermolecules included insights derived from monomeric PZn complexes in which ethynyl-BTD units were used to expand conjugation at the macrocycle meso-carbon position;66 these designs led to PZn chromophores characterized by enhanced transfer of B-to-x-polarized Q-state oscillator strength, intensified Qx absorption bands, chromophore structural rigidification, spectrally narrow fluorescence emission bands, small magnitude Stokes shifts, and enhanced radiative rate constant magnitudes relative to simple benchmark PZn complexes.
Fluorescence emission metrics of BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n chromophores
Long wavelength absorption maxima (λmax, S0 → S1), corresponding extinction coefficient measurements, fluorescence (S1 → S0) emission maxima, full-width at fluorescence half-maximum (FWHM), Stokes shifts, fluorescence lifetimes (τF), radiative rate constant (kr), non-radiative rate constant (knr), and fluorescence quantum yield (ϕf) data, are tabulated in Table 1 for the PZnn, PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD supermolecules.| λ max (S0 → S1)a [nm] | ε g@λmax (S0 → S1) [M−1 cm −1] | λ max (S1 → S0) [nm] | FWHM (S1 → S0) [cm−1] | Stokes shiftb (cm−1) | ϕ f , | τ F [ns] | k r [×108 s−1] | k nr [×108 s−1] | |
|---|---|---|---|---|---|---|---|---|---|
| a Numbers in parentheses are spectral breadths (full-widths at half-maximum, FWHM) of the respective transitions in units of cm−1. b Stokes shifts values correspond to the difference in energy between the low energy (Qx) absorption (S0 → S1) and fluorescence (S1 → S0) band maxima. c Fluorescence quantum yields (ϕf values) were determined using an integrating sphere-based absolute emission quantum yield measurement system (see ESI). d Values in parentheses represent those determined in toluene solvent. e These values were determined using S0 → S2 excitation (483 nm). Fluorescence lifetimes were measured via time-correlated single-photon-counting using a picosecond fluorescence lifetime measurement system. f Excited-state relaxation constants were calculated based on the following equations: τS1 = 1/(kr + knr), ϕf = kr × τS1. | |||||||||
| PZn-BTD-PZn | 689 (1194) | 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
741 | 1605 | 1018 | 0.25 (0.31) | 1.6 | 1.6 | 4.7 |
| PZn-(BTD-PZn)2 | 745 (1178) | 132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
784 | 977 | 543 | 0.22 (0.36) | 1.1 | 2.0 | 7.1 |
| PZn-(BTD-PZn)4 | 777 (1558) | 184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
811 | 846 | 490 | 0.16 (0.29) | 0.8 | 2.0 | 11 |
| BTD-PZn-BTD | 674 (672) | 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
687 | 727 | 281 | 0.13 (0.13) | 1.3 | 1.0 | 6.7 |
| BTD-PZn2-BTD | 765 (1243) | 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
787 | 802 | 365 | 0.23 (0.30) | 1.4 | 1.6 | 5.5 |
| BTD-PZn3-BTD | 809 (1663) | 157![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
846 | 872 | 510 | 0.16 (0.29) | 0.8 | 2.0 | 11 |
| BTD-PZn5-BTD | 847 (1675) | 238![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
888 | 1008 | 587 | 0.10 (0.28) | 0.6 | 1.7 | 15 |
| PZn2-BTD-PZn2 | 780 (1822) | 145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
822 | 926 | 688 | 0.14 (0.34) | 0.6 | 2.3 | 14 |
| PZn2-(BTD-PZn2)2 | 816 (1582) | 340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
857 | 1154 | 586 | 0.12 (0.36) | 0.5 | 2.4 | 18 |
| PZn2 | 695 (1082) | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
711 | 810 | 324 | 0.14 (0.16) | 1.09 | 1.3 | 7.9 |
| PZn3 | 770 (1386) | 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
806 | 875 | 580 | 0.19 (0.27) | 1.13 | 1.7 | 7.1 |
| PZn5 | 842 (1562) | 230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
883 | 955 | 551 | 0.09 (0.11) | 0.45 | 2.0 | 20 |
These fluorescence quantum yield data correspond to absolute measurements, acquired using a calibrated integrating-sphere-based measurement system, which collects photons emitted from the sample following excitation through NIR wavelengths that range up to 1100 nm (see ESI† for a complete system description). Note in this regard that minor differences between the Table 1ϕf data acquired for PZnn chromophores and those reported originally41 stem from the fact that these earlier ϕf values were determined via the reference method. Table 2 displays comparative integrated oscillator strengths of the B- and Q-band spectral regions of BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n chromophores relative to corresponding PZnn benchmarks.
| Oscillator strength B-band regionb | Oscillator strength Q-band regionc | Total oscillator strength | |
|---|---|---|---|
a Integrated oscillator strengths (f) were calculated based on the following expression: 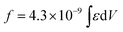 , where ε is the experimental extinction coefficient, and ν is the energy (in wave numbers) of the absorption. Values noted derive from electronic absorption spectra recorded in THF solvent. b Oscillator strengths calculated over the following wavelength domains: PZn-BTD-PZn (∼360 to 600 nm); PZn-(BTD-PZn)2 (∼360 to 600 nm); PZn-(BTD-PZn)4 (∼360 to 605 nm); BTD-PZn-BTD (∼360 to 560 nm); BTD-PZn2-BTD (∼360 to 560 nm); BTD-PZn3-BTD (∼360 to 560 nm); BTD-PZn5-BTD (∼360 to 560 nm); PZn2-BTD-PZn2 (∼360 to 610 nm); PZn2-(BTD-PZn2)2 (∼360 to 610 nm). c Oscillator strengths calculated over the following wavelength domains: PZn-BTD-PZn (∼600 to 760 nm); PZn-(BTD-PZn)2 (∼600 to 820 nm); PZn-(BTD-PZn)4 (∼600 to 900 nm); BTD-PZn-BTD (∼560 to 720 nm); BTD-PZn2-BTD (∼560 to 850 nm); BTD-PZn3-BTD (∼560 to 910 nm); BTD-PZn5-BTD (∼560 to 1050 nm); PZn2-BTD-PZn2 (∼610 to 860 nm); PZn2-(BTD-PZn2)2 (∼610 to 920 nm). d Ref. 41. , where ε is the experimental extinction coefficient, and ν is the energy (in wave numbers) of the absorption. Values noted derive from electronic absorption spectra recorded in THF solvent. b Oscillator strengths calculated over the following wavelength domains: PZn-BTD-PZn (∼360 to 600 nm); PZn-(BTD-PZn)2 (∼360 to 600 nm); PZn-(BTD-PZn)4 (∼360 to 605 nm); BTD-PZn-BTD (∼360 to 560 nm); BTD-PZn2-BTD (∼360 to 560 nm); BTD-PZn3-BTD (∼360 to 560 nm); BTD-PZn5-BTD (∼360 to 560 nm); PZn2-BTD-PZn2 (∼360 to 610 nm); PZn2-(BTD-PZn2)2 (∼360 to 610 nm). c Oscillator strengths calculated over the following wavelength domains: PZn-BTD-PZn (∼600 to 760 nm); PZn-(BTD-PZn)2 (∼600 to 820 nm); PZn-(BTD-PZn)4 (∼600 to 900 nm); BTD-PZn-BTD (∼560 to 720 nm); BTD-PZn2-BTD (∼560 to 850 nm); BTD-PZn3-BTD (∼560 to 910 nm); BTD-PZn5-BTD (∼560 to 1050 nm); PZn2-BTD-PZn2 (∼610 to 860 nm); PZn2-(BTD-PZn2)2 (∼610 to 920 nm). d Ref. 41. |
|||
| PZn-BTD-PZn | 2.11 | 0.72 | 3.52 |
| PZn-(BTD-PZn)2 | 4.65 | 1.03 | 5.67 |
| PZn-(BTD-PZn)4 | 5.98 | 1.58 | 7.57 |
| BTD-PZn-BTD | 2.24 | 0.37 | 2.63 |
| BTD-PZn2-BTD | 3.54 | 0.89 | 4.42 |
| BTD-PZn3-BTD | 5.23 | 1.53 | 6.76 |
| BTD-PZn5-BTD | 7.64 | 2.10 | 9.74 |
| PZn2-BTD-PZn2 | 6.04 | 1.30 | 7.35 |
| PZn2-(BTD-PZn2)2 | 10.49 | 2.84 | 13.32 |
| PZn2 | 2.134 | 0.303 | 2.438 |
| PZn3 | 3.240 | 0.716 | 3.956 |
| PZn5 | 5.986 | 1.622 | 7.608 |
Table 1 highlights that E-BTD units that terminate PZnn chromophores (Fig. 1A) give rise to BTD-PZnn-BTD supermolecules (Fig. 1D) in which λmax(S1 → S0) for BTD-PZn2-BTD, BTD-PZn3-BTD, and BTD-PZn5-BTD redshift by 1358, 587, and 64 cm−1, respectively, relative to their PZn2, PZn3, and PZn5 benchmarks. Note that as a function of the number of PZn units in these arrays, BTD-PZnn-BTD and PZnn supermolecules display similarly narrow fluorescence FWHM values as well as modest Stokes shifts; these energy differences between the low energy (Qx) absorption (S0 → S1) and fluorescence (S1 → S0) band maxima of these chromophores range from 325–585 cm−1. A key spectroscopic ramification of terminal ethynyl-BTD conjugation to these PZnn frameworks is highlighted in the data chronicled in Table 2, which contrasts the integrated oscillator strengths of the B- and Q-band regions of the electronic absorption spectra of these chromophores. Note that the integrated Q-state oscillator strengths of these BTD-PZnn-BTD chromophores are augmented by more than 50% relative their corresponding PZnn benchmark. These factors, coupled with a diminished nonradiative rate constant, play important roles in driving the substantial, long-wavelength emission quantum yield manifest by BTD-PZn5-BTD (ϕf = 0.28) relative to that for the parent PZn5 chromophore (ϕf = 0.11) in low dielectric toluene solvent (Table 1).
PZn-(BTD-PZn)n chromophores (Fig. 1B) contrast the electronic spectral properties of BTD-PZnn-BTD supermolecules; PZn-BTD-PZn, PZn-(BTD-PZn)2, and PZn-(BTD-PZn)4 display Qx state absorption maxima that are blue-shifted 126, 436, and 994 cm−1 with respect to the λmax(S0 → S1) transitions of their respective PZn2, PZn3, and PZn5 benchmarks (Table 1, Fig. 1); this effect derives from the fact that 4,7-diethynylbenzo[c][1,2,5]thiadiazole provides diminished PZn–PZn electronic coupling relative to the ethynyl linker. While PZn-BTD-PZn displays an augmented Stokes shift (1018 cm−1) relative to PZn2 (324 cm−1) due to the greater cumulenic character in its relaxed electronically excited S1 state,62 the Stokes shifts manifest for PZn-(BTD-PZn)2, PZn-(BTD-PZn)4, PZn3, and PZn5 are similar in magnitude (∼560 cm−1), congruent with more modest structural differences between the relaxed S0 and S1 states for these supermolecules (vide infra).
PZn-BTD-PZn, PZn-(BTD-PZn)2, and PZn-(BTD-PZn)4 display fluorescence emission maxima centered at 741, 784, and 811 nm, respectively, and substantial fluorescence quantum yields in THF solvent [ϕf(PZn-BTD-PZn) = 0.25; ϕf(PZn-(BTD-PZn)2) = 0.22; ϕf(PZn-(BTD-PZn)4) = 0.16]. Similar to that observed for BTD-PZnn-BTD chromophores, fluorescence quantum yields are significantly enhanced in nonpolar solvent; note in this regard that ϕf(PZn-(BTD-PZn)4) is amplified to 29% in toluene (Table 1).
Fig. 1C highlights the absorptive and emissive spectral properties that ensue when PZn2 chromophores are linked by 4,7-diethynylbenzo[c][1,2,5]thiadiazole units. These PZn2-(BTD-PZn2)n chromophores display dramatic Qx absorption band intensification with increasing conjugation (Tables 1 and 2); note in this regard that PZn2-(BTD-PZn2)n is an exceptional long-wavelength absorber (ε(816 nm) = 340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1; Table 1). PZn2-BTD-PZn2 and PZn2-(BTD-PZn2)2 emit respectively at 822 and 857 nm in THF solvent, with corresponding quantum yields of 14 and 12%. As demonstrated for both PZn-(BTD-PZn)n and BTD-PZnn-BTD chromophores, these fluorescence quantum yields are dramatically enhanced in toluene solvent [ϕf(PZn2-BTD-PZn2) = 0.34; ϕf(PZn2-(BTD-PZn2)2) = 0.36]. These data acquired for PZn2-(BTD-PZn2)n designs suggest additional approaches to realize related frameworks that make possible high quantum yield NIR emission that include electronic modulation of the proquinoidal units that both terminate supermolecules that utilize PZnn building blocks, as well as those that are integrated into the conjugated backbones of these compositions.
000 M−1 cm−1; Table 1). PZn2-BTD-PZn2 and PZn2-(BTD-PZn2)2 emit respectively at 822 and 857 nm in THF solvent, with corresponding quantum yields of 14 and 12%. As demonstrated for both PZn-(BTD-PZn)n and BTD-PZnn-BTD chromophores, these fluorescence quantum yields are dramatically enhanced in toluene solvent [ϕf(PZn2-BTD-PZn2) = 0.34; ϕf(PZn2-(BTD-PZn2)2) = 0.36]. These data acquired for PZn2-(BTD-PZn2)n designs suggest additional approaches to realize related frameworks that make possible high quantum yield NIR emission that include electronic modulation of the proquinoidal units that both terminate supermolecules that utilize PZnn building blocks, as well as those that are integrated into the conjugated backbones of these compositions.
Computed electronic structures of BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n chromophores
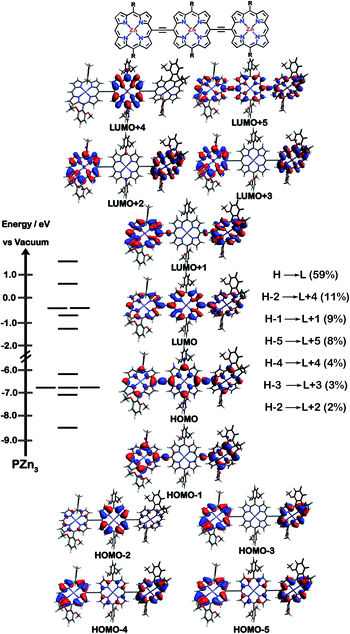
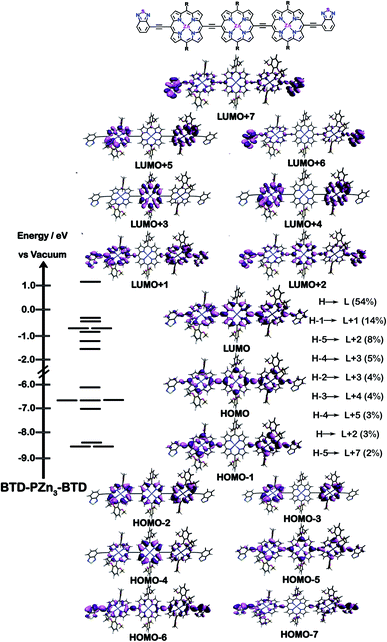
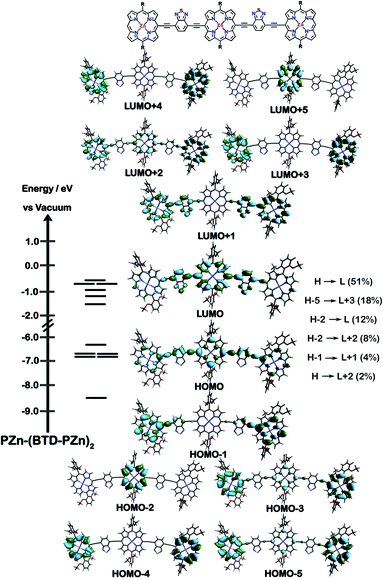
The natures of the low energy S1 states of BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n chromophores were probed through frontier orbital (FO) population and transition matrix eigenvector analyses derived using TD-DFT methods. Fig. 2–4 show FO diagrams for BTD-PZn3-BTDand PZn-(BTD-PZn)2, along with those for the PZn3 benchmark, and highlight the prominent one-electron configurations that contribute to their respective lowest energy Qx transitions; related data for the PZn2-(BTD-PZn2)2 chromophore is presented in the ESI.†The natures and energy separations between the PZn3, BTD-PZn3-BTD, and PZn-(BTD-PZn)2 FOs underscore the x-polarized nature of the lowest energy excited state for these supermolecules, and the globally delocalized character of their respective S1 excited states. The low-lying excited states of these supermolecules are described by extensive configuration interaction (CI). The S0 → S1 transitions of PZn3, BTD-PZn3-BTD, and PZn-(BTD-PZn)2 have large contributions (∼55%) from the one electron HOMO → LUMO (H → L) configuration, and highlight the importance of quinoidal resonance contributions to this low-lying excited state; this resonance contribution plays a key role in the solvent-dielectric dependent fluorescence quantum yields evidenced in THF and toluene solvent.
For PZn3 (Fig. 2), seven single excitation configurations describe the transition matrix eigenvector; in contrast, nine and six single excitation configurations describe respectively the transition matrix eigenvectors for BTD-PZn3-BTD and PZn-(BTD-PZn)2. For PZn3, the transition eigenvector is dominated by configurations (representing an ∼82% weighting in the CI expansion) that do not redistribute to a significant degree electron density. For BTD-PZn3-BTD and PZn-(BTD-PZn)2, the relative importance of such single excitation configurations that do not redistribute significantly electron density drops respectively to 74 and 22%, highlighting the increased importance of single-excitation configurations that redistribute electron density in the CI expansions that describe the S0 → S1 transition eigenvectors for these supermolecules. While the bandgap represented by ΔEHOMO–LUMO varies to a minor degree and spans ∼4.5 to 4.8 eV, note that the FO bandwidth in these Fig. 2–4 fluorophores varies significantly: ΔH−5–L+5 for PZn3 is 9.77 eV but only 7.76 eV for PZn-(BTD-PZn)2, a decrease of 2.01 eV.
Note that as supermolecular conjugation evolves from PZn3 to BTD-PZn3-BTD and PZn-(BTD-PZn)2, an increased degeneracy of energy eigenvalues is manifest in the Fig. 2–4 FOs. This increased density of states (DOS) evident in BTD-PZn3-BTD and PZn-(BTD-PZn)2 derives from the mixing of BTD and PZn frontier orbitals. Congruent with Fermi's Golden Rule, transition probability correlates with increased DOS. This larger DOS near the HOMO and LUMO levels serve to increase the multi-reference nature of the S1 state wave function; S1 configurations that involve these delocalized and mixed frontier orbitals will thus exhibit enhanced S1 state wave function spatial delocalization. This computational trend is in line with the experimentally determined transition moments, wherein Qx-transition oscillator strengths for BTD-PZn3-BTD and PZn-(BTD-PZn)2 exceed that of PZn3. Note also that this dispersion of FO energies, which decreases progressively from PZn3 to BTD-PZn3-BTD to PZn-(BTD-PZn)2 (Fig. 2–4), is correlated with increased π conjugation which is reflected in the computed electronic delocalization range function for these fluorophores (ESI†); due to the nature of these orbitals and their diminished energy gaps within the filled and empty regimes of the FO manifold, a greater weighted fraction of single excitation configurations having charge resonance character is manifest, congruent with the augmented Qx absorption oscillator strengths observed for BTD-PZnn-BTD and PZn-(BTD-PZn)n relative to PZnn (Fig. 1, Tables 1 and 2).
Conclusions
We describe a design strategy for (porphinato)zinc-based supermolecules that possess large NIR fluorescence quantum yields. These PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD fluorophores feature either 4-ethynylbenzo[c][1,2,5]thiadiazole (E-BTD) units that terminate meso-to-meso ethyne-bridged (porphinato)zinc (PZnn) arrays, or 4,7-diethynylbenzo[c][1,2,5]thiadiazole (E-BTD-E) spacers that are integrated into the backbone of these compositions. PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD chromophores are characterized by enhanced transfer of B-to-x-polarized Q-state oscillator strength relative to their corresponding PZnn benchmarks, intensified Qx absorption bands, supermolecule structural rigidification, spectrally narrow fluorescence emission bands, small magnitude Stokes shifts, and large radiative rate constant magnitudes. TD-DFT calculations point to the importance of a greater weighted fraction of single excitation configurations having charge resonance character that describe the S0 → S1 transition matrix eigenvector in PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD emitters relative to PZnn oscillators in driving these spectroscopic and dynamical properties. Collectively, these systems define an unusual family of intensely absorbing vis-NIR absorbers that display strikingly high fluorescence quantum yields (ϕf values) over the 700–900 nm regime of the NIR. These THF ϕf values for PZn-(BTD-PZn)n, PZn2-(BTD-PZn2)n, and BTD-PZnn-BTD supermolecules, perhaps without peer in a solvent of this dielectric strength over this spectral window, range from 10–25%; notably these ϕf values are dramatically amplified in hydrophobic media and thus contrast the behavior of classic tricarbocyanine NIR dyes, displaying fluorescence quantum yields ranging from 28–36% in toluene solvent. Because these BTD-PZnn-BTD, PZn-(BTD-PZn)n, and PZn2-(BTD-PZn2)n supermolecules display extraordinarily large NIR fluorescence quantum yields in hydrophobic solvent, these designs underscore new opportunities to evolve NIR-emissive nano- and mesoscale vesicles for fluorescence imaging applications in which the emissive irradiance exceeds the impressive metrics already established for such structures that membrane-disperse PZnn fluorophores.54–61,65Experimental section
Synthesis and characterization
The synthetic procedures and corresponding characterization data of all new compounds, complete with the reaction schemes, are given in the ESI.†Instrumentation
Electronic absorption spectra were recorded on a Shimadzu UV-1700 spectrophotometer. Steady-state emission spectra were recorded on a FLS920 spectrometer that utilized a xenon lamp (Xe900) as the excitation light source and an extended red sensitive PMT (Hamamatsu R2658P side window photomultiplier, spectral range: 200–1010 nm) for detection. Emission spectra were corrected using a calibration curve supplied with the instrument.Fluorescence lifetime measurements
Time-resolved emission spectra were recorded using a Hamamatsu C4780 picosecond fluorescence lifetime measurement system. This system employs a Hamamatsu Streakscope C4334 as its photon-counting detector; a Hamamatsu C4792-01 synchronous delay generator electronically generated all time delays. The excitation light source chosen was a Hamamatsu 405 nm diode laser. Fluorescence lifetimes were acquired in single-photon-counting mode using Hamamatsu HPD-TA software and analyzed using the Hamamatsu fitting module.Quantum yield measurements
A Hamamatsu C9920-03 Absolute Quantum Yield Measurement System was employed to make the quantum yield measurements. Excitation initiates from a Xe-lamp, where the wavelength is selected by a monochromator, and passed through a 1 mm optical excitation fiber. The inside of the sphere is coated with Spectralon (Labsphere, Inc.) that has at least 99% reflectance over the 350–1650 nm spectral window. Added detail regarding these measurements is provided in the ESI.†Time-dependent density functional theory calculations
All electronic structure calculations were performed upon model compounds in which aliphatic chains were truncated to methyl groups (ESI†). Structure optimization and linear response calculations were performed with density functional theory (DFT) using Gaussian 16, revision C.01.67 The M11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68 functional was employed for all calculations. Optimizations were performed with minimal symmetry constraints using tight optimization criteria with the 6-311g(d) basis set implemented. Selected frontier orbital wave functions were plotted as isosurfaces (iso = 0.02) using Avogadro.69 TD-DFT result files were post-processed using the GaussSum package;70 this software partitions the wave function amplitudes onto atomic components using Mulliken population analysis,71 and parses the electronic configurations contributing to each excitation.
68 functional was employed for all calculations. Optimizations were performed with minimal symmetry constraints using tight optimization criteria with the 6-311g(d) basis set implemented. Selected frontier orbital wave functions were plotted as isosurfaces (iso = 0.02) using Avogadro.69 TD-DFT result files were post-processed using the GaussSum package;70 this software partitions the wave function amplitudes onto atomic components using Mulliken population analysis,71 and parses the electronic configurations contributing to each excitation.
Conflicts of interest
No competing financial interests have been declared.Acknowledgements
This work was funded by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, of the U.S. Department of Energy through Grant DE-SC0001517. The authors are grateful for support made available through the Extreme Science and Engineering Discovery Environment (XSEDE) Comet at the San Diego Supercomputer Center through allocation CHE190106, which is supported by the National Science Foundation through Grant ACI-1548562. E. J. P. acknowledges the National Science Foundation for a Graduate Research Fellowship.References
- A. Ajayaghosh, Chem. Soc. Rev., 2003, 32, 181–191 RSC.
- L.-Y. Lin, Y.-H. Chen, Z.-Y. Huang, H.-W. Lin, S.-H. Chou, F. Lin, C.-W. Chen, Y.-H. Liu and K.-T. Wong, J. Am. Chem. Soc., 2011, 133, 15822–15825 CrossRef CAS PubMed.
- Z. Li, T.-H. Park, J. Rawson, M. J. Therien and E. Borguet, Nano Lett., 2012, 12, 2722–2727 CrossRef CAS PubMed.
- G. Li, R. Zhu and Y. Yang, Nat. Photonics, 2012, 6, 153–161 CrossRef CAS.
- Y. F. Deng, J. Liu, J. T. Wang, L. H. Liu, W. L. Li, H. K. Tian, X. J. Zhang, Z. Y. Xie, Y. H. Geng and F. S. Wang, Adv. Mater., 2014, 26, 471–476 CrossRef CAS PubMed.
- C. Liu, K. Wang, X. Gong and A. J. Heeger, Chem. Soc. Rev., 2016, 45, 4825–4846 RSC.
- G. Li, W.-H. Chang and Y. Yang, Nat. Rev. Mater., 2017, 2, 17043 CrossRef CAS.
- Y.-J. Cheng, S.-H. Yang and C.-S. Hsu, Chem. Rev., 2009, 109, 5868–5923 CrossRef CAS PubMed.
- Y. Zhao, Y. Guo and Y. Liu, Adv. Mater., 2013, 25, 5372–5391 CrossRef CAS PubMed.
- C. W. Spangler, J. Mater. Chem., 1999, 9, 2013–2020 RSC.
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef.
- A. Hagfeldt, G. Boschloo, L. C. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS.
- T. N. Singh-Rachford, A. Nayak, M. L. Muro-Small, S. Goeb, M. J. Therien and F. N. Castellano, J. Am. Chem. Soc., 2010, 132, 14203–14211 CrossRef CAS PubMed.
- J. Z. Zhao, S. M. Ji and H. M. Guo, RSC Adv., 2011, 1, 937–950 RSC.
- J. Z. Zhao, W. H. Wu, J. F. Sun and S. Guo, Chem. Soc. Rev., 2013, 42, 5323–5351 RSC.
- J.-H. Olivier, Y. Bai, H. Uh, H. Yoo, M. J. Therien and F. N. Castellano, J. Phys. Chem. A, 2015, 119, 5642–5649 CrossRef CAS PubMed.
- J. C. Ostrowski, K. Susumu, M. R. Robinson, M. J. Therien and G. C. Bazan, Adv. Mater., 2003, 15, 1296–1300 CrossRef CAS.
- A. C. Grimsdale, K. L. Chan, R. E. Martin, P. G. Jokisz and A. B. Holmes, Chem. Rev., 2009, 109, 897–1091 CrossRef CAS PubMed.
- L. Dou, Y. Liu, Z. Hong, G. Li and Y. Yang, Chem. Rev., 2015, 115, 12633–12665 CrossRef CAS PubMed.
- D. N. Beratan, J. N. Onuchic and J. W. Perry, J. Phys. Chem., 1987, 91, 2696–2698 CrossRef CAS.
- D. N. Beratan, J. Phys. Chem. Lett., 1989, 93, 3915–3920 CrossRef CAS.
- T. V. Duncan, K. Song, S.-T. Hung, I. Miloradovic, A. Nayak, A. Persoons, T. Verbiest, M. J. Therien and K. Clays, Angew. Chem., Int. Ed., 2008, 47, 2978–2981 CrossRef CAS PubMed.
- G. Heimel, ACS Cent. Sci., 2016, 2, 309–315 CrossRef CAS PubMed.
- J. V. Frangioni, Curr. Opin. Chem. Biol., 2003, 7, 626–634 CrossRef CAS PubMed.
- M. Y. Berezin and S. Achilefu, Chem. Rev., 2010, 110, 2641–2684 CrossRef CAS PubMed.
- L. Yuan, W. Lin, K. Zheng, L. He and W. Huang, Chem. Soc. Rev., 2013, 42, 622–661 RSC.
- S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- V. S.-Y. Lin, S. G. DiMagno and M. J. Therien, Science, 1994, 264, 1105–1111 CrossRef CAS PubMed.
- P. J. Angiolillo, V. S.-Y. Lin, J. M. Vanderkooi and M. J. Therien, J. Am. Chem. Soc., 1995, 117, 12514–12527 CrossRef CAS.
- V. S.-Y. Lin and M. J. Therien, Chem.–Eur. J., 1995, 1, 645–651 CrossRef CAS.
- R. Kumble, S. Palese, V. S.-Y. Lin, M. J. Therien and R. M. Hochstrasser, J. Am. Chem. Soc., 1998, 120, 11489–11498 CrossRef CAS.
- R. Shediac, M. H. B. Gray, H. T. Uyeda, R. C. Johnson, J. T. Hupp, P. J. Angiolillo and M. J. Therien, J. Am. Chem. Soc., 2000, 122, 7017–7033 CrossRef CAS.
- P. J. Angiolillo, K. Susumu, H. T. Uyeda, V. S.-Y. Lin, R. Shediac and M. J. Therien, Synth. Met., 2001, 116, 247–253 CrossRef CAS.
- J. T. Fletcher and M. J. Therien, Inorg. Chem., 2002, 41, 331–341 CrossRef CAS PubMed.
- K. Susumu and M. J. Therien, J. Am. Chem. Soc., 2002, 124, 8550–8552 CrossRef CAS PubMed.
- I. V. Rubtsov, K. Susumu, G. I. Rubtsov and M. J. Therien, J. Am. Chem. Soc., 2003, 125, 2687–2696 CrossRef CAS PubMed.
- P. J. Angiolillo, H. T. Uyeda, T. V. Duncan and M. J. Therien, J. Phys. Chem. B, 2004, 108, 11893–11903 CrossRef CAS.
- K. Susumu, P. R. Frail, P. J. Angiolillo and M. J. Therien, J. Am. Chem. Soc., 2006, 128, 8380–8381 CrossRef CAS PubMed.
- T. V. Duncan, K. Susumu, L. E. Sinks and M. J. Therien, J. Am. Chem. Soc., 2006, 128, 9000–9001 CrossRef CAS PubMed.
- P. R. Frail, K. Susumu, M. Huynh, J. Fong, J. M. Kikkawa and M. J. Therien, Chem. Mater., 2007, 19, 6062–6064 CrossRef CAS.
- T. V. Duncan, T. Ishizuka and M. J. Therien, J. Am. Chem. Soc., 2007, 129, 9691–9703 CrossRef CAS PubMed.
- T. V. Duncan, P. R. Frail, I. R. Miloradovic and M. J. Therien, J. Phys. Chem. B, 2010, 114, 14696–14702 CrossRef CAS PubMed.
- J. Rawson, P. J. Angiolillo and M. J. Therien, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13779–13783 CrossRef CAS PubMed.
- Y. Bai, J.-H. Olivier, H. Yoo, N. F. Polizzi, J. Park, J. Rawson and M. J. Therien, J. Am. Chem. Soc., 2017, 139, 16946–16958 CrossRef CAS PubMed.
- R. R. Birge and F. J. Duarte, Kodak Optical Products, Kodak Publication, Rochester, New York, 1990, Publication JJ-169B Search PubMed.
- J. Gayton, S. A. Autry, W. Meador, S. R. Parkin, G. A. Hill Jr, N. I. Hammer and J. H. Delcamp, J. Org. Chem., 2019, 84, 687–697 CrossRef CAS PubMed.
- W. E. Meador, S. A. Autry, R. N. Bessetti, J. N. Gayton, A. S. Flynt, N. I. Hammer and J. H. Delcamp, J. Org. Chem., 2020, 85, 4089–4095 CrossRef CAS PubMed.
- S. Reindl, A. Penzkofer, S.-H. Gong, M. Landthaler, R. M. Szeimies, C. Abels and W. Bäumler, J. Photochem. Photobiol., A, 1997, 105, 65–68 CrossRef CAS.
- Y. Lin, R. Weissleder and C.-H. Tung, Bioconjugate Chem., 2002, 13, 605–610 CrossRef CAS PubMed.
- P. J. Angiolillo, J. Rawson, P. R. Frail and M. J. Therien, Chem. Commun., 2013, 49, 9722–9724 RSC.
- S. Richert, G. Bullard, J. Rawson, P. J. Angiolillo, M. J. Therien and C. R. Timmel, J. Am. Chem. Soc., 2017, 139, 5301–5304 CrossRef CAS PubMed.
- P. P. Ghoroghchian, P. R. Frail, K. Susumu, D. Blessington, A. K. Brannan, F. S. Bates, B. Chance, D. A. Hammer and M. J. Therien, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2922–2927 CrossRef CAS PubMed.
- P. P. Ghoroghchian, P. R. Frail, K. Susumu, T.-H. Park, S. P. Wu, H. T. Uyeda, D. A. Hammer and M. J. Therien, J. Am. Chem. Soc., 2005, 127, 15388–15390 CrossRef CAS PubMed.
- N. A. Christian, M. C. Milone, S. S. Ranka, G. Li, P. R. Frail, K. P. Davis, F. S. Bates, M. J. Therien, P. P. Ghoroghchian, C. H. June and D. A. Hammer, Bioconjugate Chem., 2007, 18, 31–40 CrossRef CAS PubMed.
- P. P. Ghoroghchian, P. R. Frail, G. Li, J. A. Zupancich, F. S. Bates, D. A. Hammer and M. J. Therien, Chem. Mater., 2007, 19, 1309–1318 CrossRef CAS PubMed.
- N. A. Christian, F. Benencia, M. C. Milone, G. Li, P. R. Frail, M. J. Therien, G. Coukos and D. A. Hammer, Mol. Imaging Biol., 2009, 11, 167–177 CrossRef PubMed.
- G. P. Robbins, R. L. Saunders, J. B. Haun, J. Rawson, M. J. Therien and D. A. Hammer, Langmuir, 2010, 26, 14089–14096 CrossRef CAS PubMed.
- N. P. Kamat, Z. Liao, L. E. Moses, J. Rawson, M. J. Therien, I. J. Dmochowski and D. A. Hammer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13984–13989 CrossRef CAS PubMed.
- C. L. Hofmann, M. C. O'Sullivan, A. Detappe, Y. Yu, X. Yang, W. Qi, C. D. Landon, M. J. Therien, M. W. Dewhirst, P. P. Ghoroghchian and G. M. Palmer, Nanoscale, 2017, 9, 13465–13476 RSC.
- K. Susumu, T. V. Duncan and M. J. Therien, J. Am. Chem. Soc., 2005, 127, 5186–5195 CrossRef CAS PubMed.
- Y. Bai, J. Rawson, S. A. Roget, J.-H. Olivier, J. Lin, P. Zhang, D. N. Beratan and M. J. Therien, Chem. Sci., 2017, 8, 5889–5901 RSC.
- H. T. Uyeda, Y. Zhao, K. Wostyn, I. Asselberghs, K. Clays, A. Persoons and M. J. Therien, J. Am. Chem. Soc., 2002, 124, 13806–13813 CrossRef CAS PubMed.
- T. V. Duncan, P. P. Ghoroghchian, I. V. Rubtsov, D. A. Hammer and M. J. Therien, J. Am. Chem. Soc., 2008, 130, 9773–9784 CrossRef CAS PubMed.
- K. Susumu and M. J. Therien, J. Porphyrins Phthalocyanines, 2015, 19, 205–218 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016 Search PubMed.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic details, characterization data, additional spectroscopic and computational data. See DOI: 10.1039/d0sc03446k |
| This journal is © The Royal Society of Chemistry 2020 |