Open Access Article
Open Access ArticleThermal effects – an alternative mechanism for plasmon-assisted photocatalysis†
Yonatan
Dubi
 ad,
Ieng Wai
Un
bc and
Yonatan
Sivan
ad,
Ieng Wai
Un
bc and
Yonatan
Sivan
 *bd
*bd
aDepartment of Chemistry, Ben-Gurion University, Israel
bSchool of Electrical and Computer Engineering, Ben-Gurion University of the Negev, Israel
cJoan and Irwin Jacobs TIX Institute, National Tsing Hua University, Taiwan
dIlse Katz Center for Nanoscale Science and Technology, Ben-Gurion University, Israel. E-mail: jdubi@bgu.ac.il
First published on 21st April 2020
Abstract
Recent experiments claimed that the catalysis of reaction rates in numerous bond-dissociation reactions occurs via the decrease of activation barriers driven by non-equilibrium (“hot”) electrons in illuminated plasmonic metal nanoparticles. Thus, these experiments identify plasmon-assisted photocatalysis as a promising path for enhancing the efficiency of various chemical reactions. Here, we argue that what appears to be photocatalysis is much more likely thermo-catalysis, driven by the well-known plasmon-enhanced ability of illuminated metallic nanoparticles to serve as heat sources. Specifically, we point to some of the most important papers in the field, and show that a simple theory of illumination-induced heating can explain the extracted experimental data to remarkable agreement, with minimal to no fit parameters. We further show that any small temperature difference between the photocatalysis experiment and a control experiment performed under external heating is effectively amplified by the exponential sensitivity of the reaction, and is very likely to be interpreted incorrectly as “hot” electron effects.
I. Introduction
Many chemical reactions are catalyzed in the presence of metallic nanoparticles (NPs). The catalysis ensues via low activation energy pathways which become accessible only in the presence of the NPs.1,2 Typically, high-temperatures are used to further catalyze these reactions. However, besides being highly energy-consuming, and beside the associated shortened catalyst lifetimes,3 thermal activation is non-selective, leading to accompanying undesired reactions to take place and to loss of yield and efficiency, see ref. 4 and references therein.In recent decades, it was suggested to further catalyze chemical reactions of reactants chemically bonded (adsorbed) to the metal catalyst surface via photo-excitation of the electrons in the metal; this typically happens with “standard” metal catalysts such as Pd, Pt, Ru, Rh etc. The excited electrons can almost immediately (“directly”) cross the metal-catalyst interface,5,6 occupy the high-energy orbitals of the adsorbed molecular species and lead to faster chemistry;6–9 this mechanism is sometimes also referred to as “chemical interface damping”.10–13
Another suggested mechanism (dubbed the “hot carrier mechanism” or “indirect” plasmon-assisted photocatalysis), involves excitation of electrons inside (bulk) plasmonic metal NPs, exploiting the ability of inert metal NPs to focus the electromagnetic fields around themselves. This so-called “plasmon” excitation is unique to noble metals, is strongly sensitive to particle size and shape, and is well-known for leading, e.g., to improved sensing capabilities, surface-enhanced Raman spectroscopy signals etc. As the plasmons decay, a non-equilibrium (aka “hot”) carrier distribution is generated such that electrons in the high-energy tail of this distribution can tunnel out of the metal into high-energy orbitals of the surrounding molecules, and then catalyse the chemical reaction.
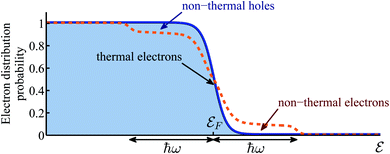
However, not only it may be difficult to distinguish between the above two mechanisms5,6,14,15, one must account for the build up of temperature that follows the decay (thermalization) of the “hot” electrons.16 In that sense, the relative importance of thermal and non-thermal effects in illuminated plasmonic NPs remained an issue under debate.5,17–20 Specifically, the main question that arises in this context is how does the photon energy absorbed in the plasmonic NPs split between the generation of high energy non-thermal (“hot”) electrons (i.e., those having energies far above the Fermi energy, and do not belong to the Fermi–Dirac distribution), and the regular (even if transient) heating of the NPs, which involves electrons close to the Fermi energy which do obey Fermi–Dirac statistics, see Fig. 1. The majority of previous (experimental as well as theoretical) studies concluded that the thermal effects are negligible compared to non-thermal electron action. This conclusion led to a rapid growth of interest in plasmon-assisted photocatalysis, mostly as a viable pathway towards cheap and efficient way to produce “green” fuels7,9,21–26 that supposedly circumvents the known limitations of thermo-catalysis which were discussed above.
In this article, we provide evidence that shows that, in contrast to the paradigm described above, the reported faster reaction rates are in many cases much more likely due to mere heating of the NPs, such that non-thermal effects play a negligible role in plasmon-assisted photocatalysis. This pure thermal interpretation is based (see Section II) on our first-principles theory in which the electron distribution and temperatures were computed self-consistently for the first time, see ref. 27. This theory showed that the power going to generation of “hot” electrons is a very small fraction of the total absorbed energy, which thus goes in its entirety to heating. Then, we propose a purely thermal theory based on the Fermi golden rule28 and the Arrhenius law which provides an alternative interpretation of the experimental data.
In Section III, we focus on a few of the seminal papers on plasmonic photocatalysis, which have claimed to isolate the “hot”-electron contribution in specific bond-dissociation reactions. These papers also provided (nearly) complete records of their experimental approach and data. First, we identify experimental errors that led to an underestimate of the temperature rise, hence, the role of thermal effects. Second, we provide support to our claim by showing that the alternative theory described in Section II, which only takes into account heating effects, can not only explain experimental results in a simple and physically transparent way, but can also provide remarkable fits to all the published results of these papers, with the minimum number of fit parameters. When possible, the values of these fit parameters are corroborated with a detailed calculation of the thermal response of the metal NP configurations used in the experiments, see ESI Section I.† It is crucial to emphasize that our analysis of previous work in Section III relies exclusively on the data reported in the papers themselves, i.e., it has no element of speculation whatsoever.
Finally, Section IV is devoted to a discussion of our results, of the limitations of the external heating control experiments employed so far, of different charge-based mechanisms potentially associated with other types of chemical reactions (e.g., oxidation–reduction reactions) and of possible future steps.
II. Heating vs. non-thermal effects: general argument
Before demonstrating our claim against the “hot electrons”-based explanations, it is useful to understand its theoretical basis. In a recent paper,27 we developed a formalism to calculate the electron distribution in an illuminated metal NP, where the only physical assumption is that due to electron–electron interactions, the electron distribution relaxes towards a Fermi-distribution, a physically-intuitive assumption that underlies almost all previous theoretical studies of this problem. The main difference with respect to previous theoretical studies of this problem is that we accounted for the heat transfer from the phonons to the environment and its dependence on the NP size and shape and on the environment's thermal properties. This approach allowed us to provide a qualitative prediction of the steady-state electron distribution, and to define and calculate electron and phonon temperatures unambiguously.The main results of ref. 27 were – (i) the electron and phonon temperatures are nearly equal; accordingly, they are denoted below by T. T depends only on the illumination intensity, NP size and shape and the thermal conductivity of the host. (ii) The efficiency of non-thermal (“hot”)-electron generation is ∼10−10 to 10−7 (for the low intensities typically used in photocatalysis experiments), i.e., only about one billionth of the energy provided by the illumination goes to creating non-thermal (“hot”) electrons, while the rest goes to heating. The latter result can be simply understood by noting that the electron relaxation time, which leads to thermalization, is about 106 times faster than the relaxation time in standard gain materials (e.g., semiconductors or laser dye).28,29 Accordingly, a ∼106 stronger illumination intensity is required to balance it and to establish a substantial level of deviation from thermal equilibrium; these illumination levels are far above the damage threshold for metals, and the resulting temperatures are well above the melting temperatures. These claims are in agreement with the findings of ref. 6, which showed experimentally that the number of high energy electrons that tunnel out from the metal to the surface is negligible in comparison to the number of high energy electrons directly generated in the dielectric (TiO2) surface. They are also in accord with the findings in ref. 30, which use careful-than-before temperature measurements to show the absence of non-thermal effects.
The conventional way in which the temperature affects the rate of chemical reactions can be seen via the Arrhenius law of chemical reactions. This law, derived empirically in 1889, shows that the reaction rate R is given by
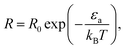 | (1) |
In ref. 28, we employed a Fermi golden rule type argument to show that under optical illumination, the reaction rate enhancement would be proportional to the number of “hot” electrons at the relevant energy, R0 ∼ Ne, which is in turn proportional to the illumination intensity, Iinc, thus yielding R0 ∼ Iinc. This turns out to be a rather general result, even when more elaborate tunneling process are accounted for.27 We emphasize that this simple theory is at odds with the claims on the dependence of the activation energy on the reaction rate, the same claims that underlie the growing interest in plasmon-assisted photocatalysis.
This simple theory already shows that the faster reactions reported experimentally are very unlikely to originate from the presence of high energy non-thermal electrons. Indeed, although the absolute number of these “hot” electrons was calculated to be very small even under illumination,27 the increase in their number from dark to illumination is dramatic, up to 10–12 orders of magnitude (depending on the activation energy). This implies that the reaction rate should be faster by 10–12 orders of magnitude under illumination; clearly, this is much larger than the experimentally observed photocatalysis.
An implied conclusion is that the photo-catalytic rate enhancement is not due to high energy non-thermal (“hot”) electrons, but comes only from heating. Such a dependence arises from the dependence of the actual reactor temperature T on the illumination intensity, which for sufficiently low intensity, can be written as
| T(Iinc) = Tdark + aIinc, | (2) |
Eqn (1) and (2) imply that the dependence of the reaction rate R on temperature is a temperature-shifted Arrhenius law, i.e., a simple Arrhenius form, with a temperature that depends on the incident illumination intensity Iinc. In this context, it should be emphasized that although theoretical arguments were laid out in Papers I–IV, they were not used to fit the data, and cannot be used for other, similar systems. Thus, eqn (1) and (2) constitute the first ever attempt to quantitatively match experimental data of plasmon-assisted photocatalysis experiment to any sort of theory.
III. Experimental data explained by heating
To corroborate our claim regarding the dominance of thermal effects over non-thermal effects, we go back to some of the seminal papers in the field45–48 (denoted as Papers I–IV hereafter) and extract the experimentally measured data.49 Below, we point to the central shortcoming of each experiment, which led to a significant over-estimate of the non-thermal electron contribution to photocatalysis, and show how the data of these papers can be fully understood and very well-fitted with the simple theory presented in Section II. For doing that, we had to distinguish between T(Iinc) (the actual temperature of the reactor), Tdark (the temperature of the reactor in the dark) and TM, which is the experimentally measured temperature. Eqn (2) can be then rewritten as| T(Iinc) = Tdark + aIinc = TM + ãIinc. | (3) |
As we describe below, in Papers I–IV, TM is different from T(Iinc), an observation which explains their difficulties to distinguish correctly between thermal and non-thermal effects. When possible (see ESI Section II†), we compute the photothermal conversion coefficient a by solving the heat equation for the relevant catalyst pellet geometries under a set of reasonable assumptions. It should be noted, however, that in Papers I–IV, some of the heat generated by the absorption of light in the metal NPs is removed by convection. Since a detailed calculation of the underlying equations for the relevant macroscopic structures is beyond the capabilities of standard computational approaches, we have estimated the convection to show that it would have only a small effect on the overall temperature profile, see ESI Section V†).
A. Analysis of papers I and II
In ref. 45 [Paper I], Mukherjee et al. demonstrated enhanced H2 dissociation in the presence of illuminated Au NPs in a thick TiO2 layer.50 The central results in I are shown in their Fig. 2(e), where the reaction rate under illumination (in which case the measured temperature climbs to 30 °C) is compared to the reaction rate in the dark, with the system being heated up externally to the same temperature. The observed ∼5.2-fold increase in reaction rate under illumination was attributed to “hot”-electron-induced catalysis due to an opening of a “hot”-electron-initiated channel in the reaction energy surface, reducing the reaction energy barrier from ∼4.5 eV to ∼1.7 eV. The latter value was a result of a DFT calculation rather than of an actual measurement.The entire analysis in paper I is based on controlling the reactor temperature. However, as demonstrated in ref. 30, 51 and 52 (and later motivated Paper IV), the temperatures can vary substantially inside the chemical reactor and they decay rapidly away from it; specifically, the temperature of the reactor can be very different (by 100 s of degrees K) from the temperature measured by a thermocouple placed a few mm away (see ref. 13 and 53). As shown in great detail in ref. 54, the temperature measurements in I and II underestimated the reactor temperature, thus preventing a correct interpretation of the experimental results.
As an alternative explanation, we now show that the experimental data of Paper I can be explained using a pure thermal effect, namely, eqn (1) and (2). To start, from the reaction rate as a function of temperature in the dark (black circles in Fig. 4(c) of Paper I, inset of Fig. 2(A)) we extract the reaction activation energy by performing an Arrhenius fit. Although an energy scale of εa ∼ 1.7 eV is claimed, the simple fit to the experimentally measured data yields a value of εa ∼ 0.23 eV. This is a surprisingly low value, which is not discussed in I. A possible explanation for such a low barrier is that the reaction is catalyzed by the oxide supporting the NPs via a heterolytic fragmentation path. Indeed, heterolytic cleavage reactions have been observed to have very low activation barriers.55,56 Either way, this already shows that the reaction pathway computed in Paper I does not manifest itself in the reported experimental data.
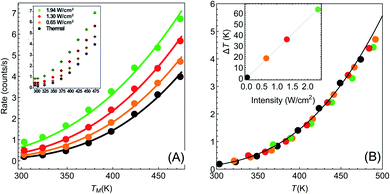 | ||
| Fig. 2 Temperature dependence of reaction rates (data from Paper I). (A) Reaction rate as a function of (measured) temperature for different illumination intensities Iinc = 0, 0.65, 1.3, 1.94 W cm−2 (black, orange, red and green points, respectively). Solid circles are data extracted from I (which is shown in its original form in the inset). Solid lines are fits to eqn (1)–(3), with no fitting parameters, showing remarkable agreement between experiment and theory. (B) Same data as in (A), with the temperatures for each intensity shifted by the temperature rise given in eqn (3). With this shift, all data points fall on a single exponential curve (R2 = 0.9956). Inset: temperature shifts as a function of intensity. | ||
Armed with this value for εa and the understanding that the real temperature of the catalytic surface is larger than the measured temperature under illumination, we ask: what temperature will give a rate which is 5.2 times larger than the reaction rate measured in the dark? This is simple to answer, since all is needed is to compare reaction rates given by eqn (1). The resulting temperature is T ≈ 362 K, an increase of 65 K compared to the ambient temperature Tdark = 297 K, rather than just 6 K as deduced originally in I. From this, together with the known incident laser intensity Iinc = 2.4 W cm−2, we extract the photothermal conversion coefficient (eqn (3)), ã = 27.2 K cm2 W−1.57
It is now a simple matter to understand the dependence of the reaction rates under illumination as a function of temperature. In Fig. 2(A) we plot the data from Paper I; reaction rate as a function of temperature for different illumination intensities. The solid lines are the lines according to eqn (1)–(3), with no fitting parameters (since all the information is already known). The temperature shifts as a function of intensities are plotted in the inset of Fig. 2(B), and the solid line is eqn (3) with ã = 27.2 K cm2 W−1. In Fig. 2(B) we plot the same data (rate as a function of temperature for different intensities), with the temperatures for each intensity shifted according to eqn (3). The resulting data falls onto a single exponential curve (eqn (1)). Thus, overall, the data from Paper I shows excellent fit to a shifted Arrhenius law with essentially no fitting parameters.
In ref. 46 [Paper II], a similar experiment (H2 dissociation with Au NPs) is reported, the only essential difference from Paper I is that the host is replaced, from TiO2 (in I) to SiO2. This results in a ∼150-fold enhancement of the reaction rate under illumination compared with the reaction rate in the dark; since a ∼5-fold enhancement was reported in Paper I under the same conditions, the exchange of the substrates (TiO2 to SiO2) amounts roughly to a 30-fold improvement.
This result has a very simple, purely thermal explanation. The thermal conductivity of SiO2 is about ∼5–10 times smaller than that of TiO2 so that the temperature rise in the Au NPs on SiO2 upon illumination is ∼5–10 larger33,34 as confirmed in the calculations described in ESI Section II.† Accordingly, the reaction rate (which depends exponentially on the inverse temperature, eqn (1)) becomes even more strongly enhanced, in fact, by a 25–100-fold increase, as observed experimentally. Further corroboration for this analysis comes from the data of Paper II itself, which can be fitted (again with remarkable accuracy) to an Arrhenius curve, albeit with a photothermal conversion coefficient which is ∼12 times larger than that found in Paper I, in line with the reduced thermal conductivity of SiO2 (see ESI Section I†).
B. Analysis of Paper III
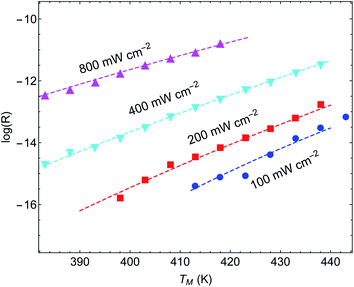
Another important example is the work of Christopher et al. [ref. 47, Paper III], where O2 dissociation in ethylene epoxidation is studied. In this work, 75 nm side-long Ag nano-cubes were placed on α-Al2O3 particles inside the reactor, and it is demonstrated that the reaction rate exhibits super-linear dependence on illumination intensity (Fig. 2(a) in III). Further, they demonstrated that upon illumination the reaction rate increases as a function of the external heating, manifested by an intensity-dependent reaction activation energy (Fig. 2(c) in III). Both these effects were attributed to plasmon-induced photocatalysis, and the former was specifically regarded as a unique characteristic of “hot” electron action, which cannot be observed by simply heating up the sample. Paper III then introduces an elaborate qualitative theory to explain these findings. They, however, dismissed the possibility of a thermal effect, based on a calculation they made in an earlier paper,58 which we show below to be erroneous.59 Nevertheless, once the reactor temperature is calculated correctly, the purely thermal model reproduces quantitatively the data of III with great accuracy.To show this, in Fig. 3 we plot the reaction rate as a function of illumination intensity for different (externally-measured) temperatures. From the measured data, one can extract the activation energy εa = 1.17 eV and the photo-thermal conversion coefficient ã = 40 K cm2 W−1. It is important to note that εa and ã can be determined by any two data sets (say blue circles and red squares) and the other curves are then reproduced essentially without any additional parameters (except the pre-exponential coefficient R0). Remarkably, the main acclaimed novelty in Paper III which was associated strictly with non-thermal electrons, namely, the super-linear dependence of the reaction rate on illumination intensity, is nicely reproduced by the (purely-thermal) temperature-shifted Arrhenius law, eqn (1) and (2).
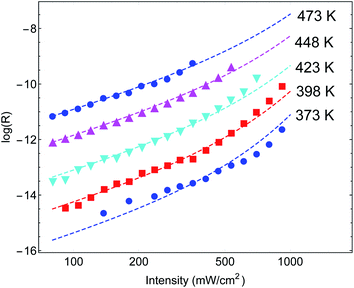 | ||
| Fig. 3 Reaction rates at different (measured) temperatures as a function of incident intensity. The symbols are data from Paper III, whereas the dashed lines are theoretical curves based on eqn (1)–(3). | ||
The fitted value of the photo-thermal conversion coefficient, ã = 40 K cm2 W−1, can be also obtained by an independent calculation under some reasonable assumptions based on a single particle temperature calculation,33 the procedure described in ref. 36 for calculating the temperature rise due to the collective contributions of multiple NPs, and the sample description provided in the original manuscript III itself. The details of this calculation are given in ESI Section II.† Notably, the value we obtained is much higher than in an earlier publication58 on which Paper III relies. However, the value obtained in ref. 58 (namely, a ∼ 1.7 × 10−5 K cm2 W−1) was calculated for a single NP, and did not take into account inter-NP heating (see ESI Section II,† as well as the discussion in ref. 60), therefore underestimating the total heating by ∼4 orders of magnitude.
Further support for the thermal interpretation of III is provided in Fig. 4, where we show the reaction rate as a function of (externally-measured) temperatures for different illumination intensities. Using the same activation energy from the previous fit, only one data set is required to determine the photothermal conversion coefficient a, which is found to be ã ∼ 160 K cm2 W−1; again, very good agreement is observed between the experimental data and the pure thermal explanation. This value is different from the value required for fitting the data of Fig. 3, which may be due to the fact that different samples were used (this information is not available in Paper III). We note that a similar fit can be obtained also to the data of ref. 58 (specifically, Fig. 1(b) and 3(b)), which was claimed by the same authors to be incompatible with a heating model (see ESI Section III†).
 | ||
| Fig. 4 Reaction rates under different illumination intensity as a function of measured temperature. The symbols are data from Paper III, whereas the dashed lines are theoretical curves based on eqn (1)–(3). Here, temperatures were varied externally using a heater. | ||
Finally, we point out that the thermal theory presented here can reproduce also the Kinetic Isotope Effect (KIE) reported in III (see ESI Section IV†) if one allows the photothermal conversion coefficient a to differ by ∼5% between the two isotopes. In that sense, essentially all the effects which were attributed to “hot” electrons in III can be fully reproduced with a thermal model that uses the actual reactor temperature.
C. Analysis of Paper IV
In a more recent paper [ref. 48, Paper IV], experiments are performed which are similar to those presented in Papers I and II, with several changes.61 First, the reaction considered is different (ammonia decomposition), meaning that the reaction activation energy would be different. More importantly, the temperature of the reactor was evaluated by correlating the readings of a thermocouple (again placed several mm away from the pellet) and a thermal imaging camera. This is a crucial change, since by this one can extract an (averaged) temperature value of the actual reaction that the enables the approximate isolation of the photo-thermal effects (page 12 in the ESI† to Paper IV). The reaction rate is then measured as a function of temperature for different illumination intensities (Fig. 5(A)) and subtract the photothermal contribution. An Arrhenius fit to these data yields an intensity-dependent activation energy, which is the central result of Paper IV. However, as explained briefly in a recent Technical Comment62 and in much greater detail in ref. 54 (written in response to the series of incorrect claims in ref. 53), the temperature measurements in Paper IV suffer from a series of systematic experimental errors that invalidate its conclusions; in particular, the temperatures reported in Paper IV are roughly 2-fold lower than what we deduce below from their own data.62 Instead, we offer here again a pure thermal explanation based on eqn (1)–(3) which remarkably reproduces the experimental data of IV.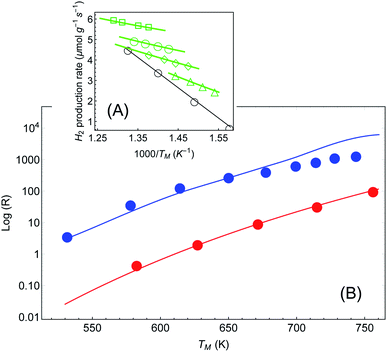 | ||
| Fig. 5 Reaction rates under different illumination intensity as a function of inverse (average measured) temperature (data from Paper IV). (A) Points correspond to the experimental data of ref. 48 for the reaction rate for 〈Iinc〉 = 0, 1.6, 2.4, 3.2 and 4 W cm−2 (empty circles, triangles, diamonds, disks and squares, respectively). The solid lines are a fit to eqn (1)–(3). The parameters (activation energy εa and photothermal conversion factor ã) are extracted from the open circles (in the dark) and the solid squares (〈Iinc〉 = 4 W cm−2) only. The curves for the rest of the data sets are obtained without additional fit parameters. Image borrowed from ref. 62. (B) Reaction rate as a function of (measured) temperature, in the dark (red) and under illumination (3.2, 4, 4.8, …, 9.6 W cm−2) with no external heating (blue). Points are data from ref. 48, solid red line is an Arrhenius fit, and solid blue line is a shifted Arrhenius fit (eqn (1) and (2)) with no additional parameters (except prefactor, see text). | ||
For the sake of clarity, we follow the procedure we used to apply the Arrhenius law to the experimental data (as described also above and briefly in ref. 62). In Fig. 5(A) we plot the reaction rate as a function of the measured inverse temperature for different illumination intensities, taken from the data of Paper IV. We fit a shifted Arrhenius law to the data for the reaction rate in the dark, and under laser illumination of (average) intensity 3.2 W cm−2 and wavelength 550 nm. These two data sets (empty circles and filled squares in Fig. 5(A), respectively) yield εa ∼ 1.3 eV and ã = 180 K cm2 W−1; unlike the case of Paper I, the value of activation energy obtained from our fit is similar to that found in Paper IV. With these parameters we can fit the rest of the data, with no additional fit parameters. A remarkable agreement between the theory and the data is evident. Furthermore, this value confirms our estimate of a 2-fold underestimate of the temperature in Paper IV; indeed, for Iinc = 3.2 W cm−2, we get T = TM + ãIinc ∼ 530 + 180 × 3.2 ∼ 1110.
In similarity to the calculation performed for Paper III (ESI Section II†), the fitted value of the photo-thermal conversion coefficient of Paper IV can also be obtained by an independent calculation based on the sample description provided in the original manuscript IV itself as well as the procedure described in ref. 36. However, since the source used in Paper IV is pulsed, the expression for the temperature rise due to a single illuminated particle has to be based on the time-dependent solution, as described e.g., in ref. 35. Again, the procedure, described in ESI Section II,† yields a value which is close to the one obtained from the fit.
Further support for the thermal interpretation of Paper IV is provided in Fig. 5(B) where the reaction rate is plotted as a function of measured temperature. The data points, taken from Paper IV, represent the following experimental procedure. The red points are the reaction rate in the dark (the temperature of the reactor is set by an external heater). The blue points, on the other hand, were obtained by illuminating the reactor with various intensities, measuring the resulting temperatures TM(Iinc) (without any external heating), and plotting the reaction rate as a function of this temperature. The data shows an apparent increase of ∼2 orders of magnitude in the reaction rate, one of the central results of IV.
To generate the shifted Arrhenius plot, we first fit the data in the dark to an Arrhenius curve (eqn (1), εa = 1.28 eV), and then invert TM(Iinc) to obtain the intensities Iinc(TM). The reaction rate, eqn (1), i.e., 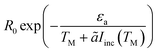 , is then plotted as a function of TM, with ã = 180 K cm2 W−1 and εa obtained from the previous fit, leaving only the prefactor R0 as a fit parameter. The good fit to the experimental data demonstrates the consistency of our theory and confirms that the faster reaction under illumination is related to the fact that T is much higher than TM; we expect the fit to improve once the thermo-optic (nonlinear) response discussed above (ref. 38 and 39) shall be included.
, is then plotted as a function of TM, with ã = 180 K cm2 W−1 and εa obtained from the previous fit, leaving only the prefactor R0 as a fit parameter. The good fit to the experimental data demonstrates the consistency of our theory and confirms that the faster reaction under illumination is related to the fact that T is much higher than TM; we expect the fit to improve once the thermo-optic (nonlinear) response discussed above (ref. 38 and 39) shall be included.
Notably, the temperatures our fit predicts are sufficiently high such that NP melting might be expected (see, e.g., claim in ref. 53). The nonlinear fit to the data of Fig. 5(B) described above shows that the reaction temperatures were in practice much lower than the linear prediction. Even then, the possibility of NP melting is shown in ESI Section VI† and in [ref. 44, pp. 271–272] to have, at most, a mild effect on the reaction rate.
Finally, we can follow the procedure used in Fig. 5(A) for the data presented in IV regarding the dependence of the reaction rate on the laser wavelength. All we need to assume is that a = a(λ) now depends on the wavelength, and hence ΔT = ΔT(λ). In Fig. 6 we plot the reaction rate as a function of the measured inverse temperature for different illumination wavelengths. The points are data from IV and the solid lines are fits to a shifted Arrhenius law, eqn (1) and (2). Again, we find excellent fit between our theory and the experimental data. The inset shows the resulting temperature rise ΔT = ãIinc (corresponding, roughly, to the maximal value reached in Fig. 2(a) of Paper IV) as a function of wavelength, where the colored points correspond to the different curves in the main figure. The solid line is a fit to a Lorentzian, with a maximum corresponding to the plasmon resonance (at 540 nm).
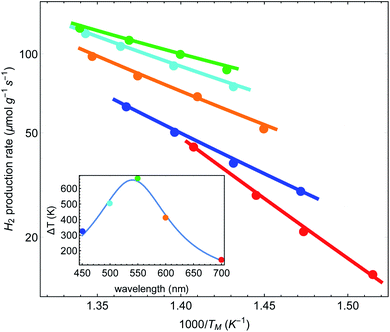 | ||
| Fig. 6 Reaction rates as a function of inverse (average measured) temperature, for different illumination wavelengths (data from Paper IV). Points correspond to original data of ref. 48, and lines are fits to a shifted Arrhenius (eqn (1)–(3)). Inset: the fitted (effective) temperatures as a function of wavelength, showing maximal heating close to the plasmon resonance. | ||
As an independent test, we computed the absorption cross-section of the Cu–Ru NPs using permittivity data from ref. 63; the resulting cross-section was essentially identical to those shown in the ESI of IV (Fig. S12A†). It is then a simple matter to fit the absorption cross-section to the data points. Notably, while the long wavelength side of the fit is satisfactory, the short wavelength side of the fitted curve exceeds the two extracted data points (data not shown); a similar discrepancy is seen in the deduced activation energy in IV (see their Fig. 2(c)). This discrepancy in the short wavelength might originate from the fact that in this spectral regime some of the absorption causes interband transitions (at ∼2.1 eV for Cu) rather than intraband transitions, as in the longer wavelength side of the spectrum. In interband transitions, potentially not all the absorbed photon energy is converted to heat because some of the energy is required to transfer the valence band electron across the bandgap to the conduction band, and change the relative populations of the d and s–p bands. Thus, the heating is lower compared to what one could have expected based on just the absorption cross-section. This possibility was also raised in Paper IV.
IV. Discussion
The evidence we provided above suggests that in the specific papers discussed, there was nothing special in using plasmonic NPs for photocatalysis; it proved to be yet another application for the use of plasmonic NPs as efficient heat sources.31,33,34,64–69 Unlike the common perception (as e.g., reflected in papers I–III), we show that the presence of a large number of particles in the samples leads to a collective macroscopic (rather than localized) heating effect which is orders of magnitude greater than the small amount of heating provided by a single NP. Specifically, our results demonstrate that the data of Papers I–IV can essentially be explained with a simple Arrhenius theory, the only requirement is that the temperature of the reactor is evaluated accurately. In Papers I–III, the origin of the discrepancy between the measured temperature and the actual reactor temperature is simple to understand; its origin is in the fact that a thermometer was placed away from the reactor pellet (or at least from the illuminated surface of the pellet), thus discarding any temperature gradients which appear in the reactor and beyond it (as was recently discussed in ref. 30, 51, 52, 54 and 60).In Paper IV, a substantial effort is made to overcome this, by using a thermal camera. However, even with this improvement, there may be several sources for temperature ambiguity. For instance, the use of a thermal camera for materials of low emissivity would result in a systematic temperature under-estimation.54,62 Furthermore, the authors of Paper IV seem to use the thermal camera's default settings, where the emissivity is set to be 0.95, although the aluminum oxide emissivity is evaluated in the camera's manual to be ∼0.16–0.46, and only comprises about 20% of the sample. For a thorough discussion of all the technical and conceptual errors in ref. 48 and 53, see ref. 54.
Another source of error are temperature gradients within the sample due to the non-uniform illumination (specifically, due to the finite penetration depth of light), or even temperature transients which are impossible to reproduce in a control experiment based on external heating. In fact, in ref. 30 it was shown that temperature gradients should be expected even in the dark control experiments, either due to the gas flow or due to non-uniform external heating. Thus, any attempt to subtract the thermocatalysis control results necessarily leads to an incorrect interpretation of the difference between the thermal contributions in the dark control and the photocatalysis experiments as “hot” electron action. Similar difficulties will arise if one attempts to compute the temperature of the reaction – any small error will be incorrectly interpreted as “hot” electron action.
Since the temperature recorded by the camera is an average over space (and time), while the reaction rate is exponentially sensitive to temperature changes, this methodology effectively overlooks the fact that the reaction occurs preferably in the higher temperature regions (and/or times in which the temperature peaks), thus, necessarily underestimating the thermal contribution. This is nothing but the well known mathematical statement that 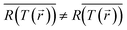 (especially for exponential functions). The associated errors (due to inhomogeneities, transients, calculation-based averaging etc.) can in fact be huge. For example, for the conditions of Paper IV, where the temperature drops to less than 50% along the axis of the sample (see Fig. S6(b)†), there is an orders of magnitude difference between the reaction rates on the top and bottom of the pellet. This suggests that the inhomogeneities must be minimized in order to allow the distinction between thermal and non-thermal effects. This can be achieved by using thinner pellets,70 very dilute NP suspensions, or ultimately, by studying a single particle.71–75 Even then, it would be critical to employ advanced thermometry techniques to image the temperature distribution in the samples, see e.g., ref. 20 and 75–80. The bottom line of the above discussion is that a thermocatalysis control experiment (i.e., using external heating to achieve uniform and steady-state heating of the pellet) can only identify “hot” electron contributions which are far larger compared to the errors associated with the temperature non-uniformities, transients and measurement inaccuracies.
(especially for exponential functions). The associated errors (due to inhomogeneities, transients, calculation-based averaging etc.) can in fact be huge. For example, for the conditions of Paper IV, where the temperature drops to less than 50% along the axis of the sample (see Fig. S6(b)†), there is an orders of magnitude difference between the reaction rates on the top and bottom of the pellet. This suggests that the inhomogeneities must be minimized in order to allow the distinction between thermal and non-thermal effects. This can be achieved by using thinner pellets,70 very dilute NP suspensions, or ultimately, by studying a single particle.71–75 Even then, it would be critical to employ advanced thermometry techniques to image the temperature distribution in the samples, see e.g., ref. 20 and 75–80. The bottom line of the above discussion is that a thermocatalysis control experiment (i.e., using external heating to achieve uniform and steady-state heating of the pellet) can only identify “hot” electron contributions which are far larger compared to the errors associated with the temperature non-uniformities, transients and measurement inaccuracies.
An orthogonal approach for separating thermal from non-thermal effects is to perform the same measurements with illumination at gradually longer wavelengths (so-called action-spectrum measurements, e.g.ref. 81). “Hot” electrons created under such low-energy illumination will not have enough energy to contribute to the reaction. Therefore, if the reaction is indeed based on a “hot” electron mechanism, a significant drop in the reaction rate will occur for sufficiently long wavelength. This is, in fact, the principle underlying the use of “hot” electrons for photo-detection – a photon is detected only if it has sufficient energy to cross the Schottky barrier and travel to the detector on the semiconductor side; otherwise, the contact is considered to be Ohmic, see e.g., ref. 25 and 82–86. A similar mechanism ensures “hot” electron action in upconversion experiments.87,88 In contrast, the thermal mechanism we propose predicts that under these conditions there will be no drop in the photo-catalytic enhancement, since the system will heat up even under low-energy illumination. Notably, wavelength dependence of the reaction rate is frequently recorded in plasmon-assisted photocatalysis studies. We are not aware of any report of a sharp decrease of reaction rate for long wavelengths; this further supports our purely thermal interpretation of the experimental data. Yet, the failure to observe such a sharp drop might be caused by the use of white light sources rather than monochromatic sources. Thus, more careful wavelength dependence studies might be worthwhile performing.
Having said all the above, it is important to mention that we have focused on a specific set of (photo)catalytic reactions, namely, bond-dissociation reactions in pellet geometries and solid–gas reactions, but plasmonic enhancement of other reactions has been reported, e.g., in oxidation–reduction reactions, where charge transfer is an integral part of the reaction.81,89–95 In other studies, the control experiments were performed carefully (see e.g., ref. 19 and 96 as a few select examples out of many), and some previous papers reported selective photocatalytic action that seemingly cannot be explained just using our simplistic thermal model.91,92,96–99 A possible explanation for the non-negligible role of non-thermal effects in those studies is the longer lifetime of tunnelled carriers achieved e.g., by the use of hole scavengers;91,92,100 this approach makes the photocatalysis problem more similar to photodetection experiments (e.g., ref. 25, 82–85, 101 and 102), which without doubt rely on high energy non-thermal electrons. Another potential way to distinguish between thermal and thermal effects is to study reactions in which the contributions these effects is opposite (see e.g., ref. 98 and 99). The theoretical approach of ref. 27, together with the detailed thermal calculations of ref. 33, 35 and 36 (as demonstrated in the current manuscript), existing theory of electron tunnelling (see e.g., ref. 27 and 103) and the vast knowledge accumulated on heterogeneous catalysis on the various chemical parameters that affect the reaction rate can now provide the necessary framework to perform a case by case analysis of the relative efficiency of non-thermal and thermal effects, the relative importance of the optical and chemical aspects in these previously published papers, as well as in future papers on the topic.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Dr A. Milo, Dr J. Baraban and Prof. M. Bar Sadan for valuable discussions and critical reading of the manuscript. YS and IWU were partially supported by Israel Science Foundation (ISF) grant no. 899/16.References
- L. Liu and A. Corma, Metal catalysts for heterogeneous catalysis: from single atoms to nanoclusters and nanoparticles, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- K. Watanabe, D. Menzel, N. Nilius and H.-J. Freund, Photochemistry on metal nanoparticles, Chem. Rev., 2006, 106, 4301–4320 CrossRef CAS PubMed.
- C. T. Campbell, S. C. Parker and D. E. Starr, The effect of size-dependent nanoparticle energetics on catalyst sintering, Science, 2002, 298, 811814 CrossRef PubMed.
- A. Naldoni, et al., Solar-powered plasmon-enhanced heterogeneous catalysis, Nanophotonics, 2016, 5, 112–133 CAS.
- M. Bonn, et al., Phonon- versus electron-mediated desorption and oxidation of CO on Ru(0001), Science, 1999, 285, 1042 CrossRef CAS PubMed.
- S. Tan, et al., Plasmonic coupling at a metal/semiconductor interface, Nat. Photonics, 2017, 11, 806812 CrossRef.
- W. Hou and S. B. Cronin, A review of surface plasmon resonance-enhanced photocatalysis, Adv. Funct. Mater., 2013, 23, 1612–1619 CrossRef CAS.
- C. Boerigter, U. Aslam and S. Linic, Mechanism of charge transfer from plasmonic nanostructures to chemically attached materials, ACS Nano, 2016, 10, 6108–6115 CrossRef CAS PubMed.
- J. L. Brooks, C. L. Warkentin, D. Saha, E. L. Keller and R. R. Frontiera, Toward a mechanistic understanding of plasmon-mediated photocatalysis, Nanophotonics, 2018, 7, 1697–1724 CAS.
- H. Hövel, S. Fritz, A. Hilger, U. Kreibig and M. Vollmer, Width of cluster plasmon resonances: bulk dielectric functions and chemical interface damping, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 18178 CrossRef PubMed.
- J. Olson, et al., Optical characterization of single plasmonic nanoparticles, Chem. Soc. Rev., 2015, 44, 40–57 RSC.
- B. Foerster, et al., Chemical interface damping depends on electrons reaching the surface, ACS Nano, 2017, 11, 2886–2893 CrossRef CAS PubMed.
- B. Seemala, et al., Plasmon-mediated catalytic O2 dissociation on ag nanostructures: hot electrons or near fields?, ACS Energy Lett., 2019, 4, 1803–1809 CrossRef CAS.
- C. Chen and R. Osgood, Direct observation of the local-field-enhanced surface photochemical reactions, Phys. Rev. Lett., 1983, 50, 1705 CrossRef CAS.
- R. T. Kidd, D. Lennon and S. R. Meech, Surface plasmon enhanced substrate mediated photochemistry on roughened silver, J. Chem. Phys., 2000, 113, 8276–8282 CrossRef CAS.
- M. Bauer, A. Marienfeld and M. Aeschlimann, Hot electron lifetimes in metals probed by time-resolved two-photon photoemission, Prog. Surf. Sci., 2015, 90, 319376 CrossRef.
- J. Culver, M. Li, Z.-J. Sun, R. Hochstrasser and A. Yodh, Temperature-dependent coupling of low frequency adsorbate vibrations to metal substrate electrons, Chem. Phys., 1996, 205, 159–166 CrossRef CAS.
- A. J. Leenheer, P. Narang, N. S. Lewis and H. A. Atwater, Solar energy conversion via hot electron internal photoemission in metallic nanostructures: efficiency estimates, J. Appl. Phys., 2014, 115, 134301 CrossRef.
- R. Kamarudheen, G. W. Castellanos, L. P. J. Kamp, H. J. H. Clercx and A. Baldi, Quantifying photothermal and hot charge carrier effects in plasmon-driven nanoparticle syntheses, ACS Nano, 2018, 12, 8447–8455 CrossRef CAS PubMed.
- R. M. Sarhan, et al., The importance of plasmonic heating for the plasmon-driven photodimerization of 4-nitrothiophenol, Sci. Rep., 2019, 9, 3060 CrossRef PubMed.
- T. Hirakawa and P. V. Kamat, Photoinduced electron storage and surface plasmon modulation in Ag@ TiO2 clusters, Langmuir, 2004, 20, 5645–5647 CrossRef CAS PubMed.
- G. Baffou and R. Quidant, Nanoplasmonics for chemistry, Chem. Soc. Rev., 2014, 43, 3898 RSC.
- C. Clavero, Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices, Nat. Photonics, 2014, 8, 95–103 CrossRef CAS.
- M. Moskovits, The case for plasmon-derived hot carrier devices, Nat. Nanotechnol., 2015, 10, 6 CrossRef CAS PubMed.
- W. Li and J. Valentine, Harvesting the loss: surface plasmon-based hot electron photodetection, Nanophotonics, 2016, 6, 177–191 Search PubMed.
- X. Wu, E. Jaatinen, S. Sarina and H. Y. Zhu, Direct photocatalysis of supported metal nanostructures for organic synthesis, J. Phys. D: Appl. Phys., 2017, 50, 283001 CrossRef.
- Y. Dubi and Y. Sivan, “hot electrons” in metallic nanostructures - non-thermal carriers or heating?, Light: Sci. Appl., 2019, 8, 89 CrossRef PubMed.
- Y. Sivan, I. W. Un and Y. Dubi, Assistance of plasmonic nanostructures to photocatalysis – just a regular heat source, Faraday Discuss., 2019, 214, 215–233 RSC.
- Y. Sivan, S. Xiao, U. K. Chettiar, A. V. Kildishev and V. M. Shalaev, Frequency-domain simulations of a negative-index material with embedded gain, Opt. Express, 2009, 17, 24060 CrossRef CAS PubMed.
- X. Li, X. Zhang, H. O. Everitt and J. Liu, Light-induced thermal gradients in ruthenium catalysts significantly enhance ammonia production, Nano Lett., 2019, 19, 1706–1711 CrossRef CAS PubMed.
- A. O. Govorov and H. H. Richardson, Generating heat with metal nanoparticles, Nano Today, 2007, 2, 30–38 CrossRef.
- H. H. Richardson, et al., Experimental and theoretical studies of light-to-heat conversion and collective heating effects in metal nanoparticle solutions, Nano Lett., 2009, 9, 1139–1146 CrossRef CAS PubMed.
- G. Baffou, R. Quidant and F. J. G. de Abajo, Nanoscale control of optical heating in complex plasmonic systems, ACS Nano, 2010, 4, 709–716 CrossRef CAS PubMed.
- G. Baffou and R. Quidant, Thermo-plasmonics: using metallic nanostructures as nano-sources of heat, Laser Photonics Rev., 2013, 7, 171–187 CrossRef CAS.
- G. Baffou and H. Rigneault, Femtosecond-pulsed optical heating of gold nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035415 CrossRef.
- G. Baffou, et al., Photoinduced heating of nanoparticle arrays, ACS Nano, 2013, 7, 6478–6488 CrossRef CAS PubMed.
- H.-Y. Wu, et al., Ultrasmall all-optical plasmonic switch and its application to superresolution imaging, Sci. Rep., 2016, 6, 24293 CrossRef CAS PubMed.
- Y. Sivan and S.-W. Chu, Nonlinear plasmonics at high temperatures, Nanophotonics, 2017, 6, 317–328 CAS.
- I. Gurwich and Y. Sivan, A metal nanosphere under intense continuous wave illumination - a unique case of non-perturbative nonlinear nanophotonics, Phys. Rev. E, 2017, 96, 012212 CrossRef CAS PubMed.
- D. T. Owens, C. Fuentes-Hernandez, J. M. Hales, J. W. Perry and B. Kippelen, A comprehensive analysis of the contributions to the nonlinear optical properties of thin Ag films, J. Appl. Phys., 2010, 107, 123114 CrossRef.
- H. Reddy, et al., Temperature-dependent optical properties of single crystalline and polycrystalline silver thin films, ACS Photonics, 2017, 4, 1083–1091 CrossRef CAS.
- H. Reddy, U. Guler, A. V. Kildishev, A. Boltasseva and V. M. Shalaev, Temperature-dependent optical properties of gold thin films, Opt. Mater. Express, 2016, 6, 2776–2802 CrossRef CAS.
- P.-T. Shen, et al., Temperature- and -roughness dependent permittivity of annealed/unannealed gold films, Opt. Express, 2016, 24, 19254 CrossRef CAS PubMed.
- J. Aizpurua, et al., Theory of hot electrons: general discussion, Faraday Discuss., 2019, 214, 245–281 RSC.
- S. Mukherjee, et al., Hot electrons do the impossible: plasmon-induced dissociation of H2 on Au, Nano Lett., 2013, 13, 240–247 CrossRef CAS PubMed.
- S. Mukherjee, et al., Hot-electron-induced dissociation of H2 on gold nanoparticles supported on SiO2, J. Am. Chem. Soc., 2014, 136, 64–67 CrossRef CAS PubMed.
- P. Christopher, H. Xin, A. Marimuthu and S. Linic, Singular characteristics and unique chemical bond activation mechanisms of photocatalytic reactions on plasmonic nanostructures, Nat. Mater., 2012, 11, 1044–1050 CrossRef CAS PubMed.
- L. Zhou, et al., Quantifying hot carrier and thermal contributions in plasmonic photocatalysis, Science, 2018, 362, 69 CrossRef CAS PubMed.
- This was done by digitizing the images, so some numerical errors ∼1% might arise, but they do not affect our claims.
- Note that the illustration in Paper I shows that the Au NPs are dispersed just on the surface of the TiO2 layer. However, judging from the reported mass concentrations etc., one has to conclude that the Au NPs are dispersed in the whole oxide thickness.
- H. Li, M. Rivallan, F. Thibault-Starzyk, A. Traverta and F. C. Meunier, Effective bulk and surface temperatures of the catalyst bed of FT-IR cells used for in situ and operando studies, Phys. Chem. Chem. Phys., 2013, 15, 7321 RSC.
- X. Zhang, et al., Plasmon-enhanced catalysis: distinguishing thermal and nonthermal effects, Nano Lett., 2018, 18, 1714–1723 CrossRef CAS PubMed.
- L. Zhou, et al., Response to Comment on “quantifying hot carrier and thermal contributions in plasmonic photocatalysis”, Science, 2019, 364, aaw9545 CrossRef PubMed.
- Y. Sivan, J. Baraban and Y. Dubi, Experimental practices required to isolate thermal effects in plasmonic photo-catalysis - lessons from recent experiments, OSA Continuum, 2020, 3, 483–497 CrossRef.
- Z. Song, et al., Heterolytic dissociative adsorption state of dihydrogen favored by interfacial defects, Appl. Surf. Sci., 2018, 433, 862–868 CrossRef CAS.
- J. Joubert, et al., Heterolytic splitting of H2 and CH4 on γ-alumina as a structural probe for defect sites, J. Phys. Chem. B, 2006, 110, 23944–23950 CrossRef CAS PubMed.
- In contrast to Papers III and IV described below, there was no sufficient information in I and II to enable a reliable calculation of the photothermal conversion coefficient ã.
- P. Christopher, H. Xin and S. Linic, Visible-light-enhanced catalytic oxidation reactions on plasmonic silver nanostructures, Nat. Chem., 2011, 3, 467 CrossRef CAS PubMed.
- We should note, however, that some thermal measurements were described in private correspondence with the authors of Paper III. These are expected to be published in the future and will clarify further the reasoning that led the authors to claim that a pure thermal effect cannot explain the experimental findings.
- G. Baffou, I. Bordacchini, A. Baldi and R. Quidant, Simple experimental procedures to discern photothermal processes in plasmon-driven chemistry, 2020, arxiv:2001.08402.
- Similarly to I, the illustration in Paper IV is limited to the immediate vicinity of the metal NP; this gives the impression that the Cu–Ru NPs are sparsely spaced on a solid oxide substrate. However, judging from the reported mass concentrations etc., one has to conclude that the metal NPs are dispersed in the whole oxide thickness, and that the oxide is highly porous (fill factor of 90% air).
- Y. Sivan, J. Baraban, I. W. Un and Y. Dubi, Comment on “Quantifying hot carrier and thermal contributions in plasmonic photocatalysis”, Science, 2019, 364, eaaw9367 CrossRef CAS PubMed.
- P. B. Johnson and R. W. Christy, Optical constants of noble metals, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- D. Boyer, P. Tamarat, A. Maali, B. Lounis and M. Orrit, Photothermal imaging of nanometer-sized metal particles among scatterers, Science, 2002, 297, 1160–1163 CrossRef CAS PubMed.
- L. R. Hirsch, et al., Nanoshell-mediated near-infrared thermal therapy of tumors under magnetic resonance guidance, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13549–13554 CrossRef CAS PubMed.
- K. Sokolov, Nanotechnology: Tiny thermometers used in living cells, Nature, 2013, 150, 36 CrossRef PubMed.
- U. Guler, A. Boltasseva and V. M. Shalaev, Refractory plasmonics, Science, 2014, 334, 263 CrossRef PubMed.
- O. Neumann, et al., Solar vapor generation enabled by nanoparticles, ACS Nano, 2013, 7, 42–49 CrossRef CAS PubMed.
- D. F. Swearer, et al., Plasmonic photocatalysis of nitrous oxide into N2 and O2 using Aluminum-Iridium antenna-reactor nanoparticles, ACS Nano, 2019, 13(7), 8076–8086 CrossRef CAS PubMed.
- Note that transverse gradients are very hard to avoid, see ESI Section II.†.
- E. Cortés, et al., Plasmonic hot electron transport drives nano-localized chemistry, Nat. Commun., 2017, 8, 14880 CrossRef PubMed.
- C.-Y. Wu, et al., High-spatial-resolution mapping of catalytic reactions on single particles, Nature, 2017, 541, 511–515 CrossRef CAS PubMed.
- F. Sterl, et al., Nanoscale hydrogenography on single magnesium nanoparticles, Nano Lett., 2018, 18, 4293–4302 CrossRef CAS PubMed.
- M. Vadai, D. Angell, F. Hayee, K. Sywtu and J. Dionne, In-situ observation of plasmon-controlled photocatalytic dehydrogenation of individual palladium nanoparticles, Nat. Commun., 2018, 9, 4658 CrossRef PubMed.
- E. Pensa, et al., Spectral screening of the energy of hot holes over a particle plasmon resonance, Nano Lett., 2019, 19, 1867–1874 CrossRef CAS PubMed.
- M. Honda, Y. Saito, N. I. Smith, K. Fujita and S. Kawata, Nanoscale heating of laser irradiated single gold nanoparticles in liquid, Opt. Express, 2011, 19, 12375–12383 CrossRef CAS PubMed.
- M. Mecklenburg, et al., Nanoscale temperature mapping in operating microelectronic devices, Science, 2015, 347, 629 CrossRef CAS PubMed.
- J. T. Hugall and J. J. Baumberg, Demonstrating photoluminescence from Au is electronic inelastic light scattering of a plasmonic metal: the origin of SERS backgrounds, Nano Lett., 2015, 15, 2600–2604 CrossRef CAS PubMed.
- X. Xie and D. G. Cahill, Thermometry of plasmonic nanostructures by anti-stokes electronic raman scattering, Appl. Phys. Lett., 2016, 109, 183104 CrossRef.
- A. Carattino, M. Caldarola and M. Orrit, Gold nanoparticles as absolute nano-thermometers, Nano Lett., 2017, 18, 874–880 CrossRef PubMed.
- S. Sarina, et al., Photon energy threshold in direct photocatalysis with metal nanoparticles: key evidence from the action spectrum of the reaction, J. Phys. Chem. Lett., 2017, 8, 2526–2534 CrossRef CAS PubMed.
- I. Goykhman, B. Desiatov, J. Khurgin, J. Shappir and U. Levy, Locally oxidized silicon surface-plasmon Schottky detector for telecom regime, Nano Lett., 2011, 11, 2219–2224 CrossRef CAS PubMed.
- I. Goykhman, B. Desiatov, J. Khurgin, J. Shappir and U. Levy, Waveguide based compact silicon Schottky photodetector with enhanced responsivity in the telecom spectral band, Opt. Express, 2012, 20, 28594 CrossRef PubMed.
- S. Mubeen, et al., An autonomous photosynthetic device in which all charge carriers derive from surface plasmons, Nat. Nanotechnol., 2013, 8, 247–251 CrossRef CAS PubMed.
- A. Giugni, et al., Hot-electron nanoscopy using adiabatic compression of surface plasmons, Nat. Nanotechnol., 2013, 8, 845852 CrossRef PubMed.
- S. Ishii, et al., Hot electron excitation from titanium nitride using visible light, ACS Photonics, 2016, 3, 1552–1557 CrossRef CAS.
- G. V. Naik and J. A. Dionne, Photon upconversion with hot carriers in plasmonic systems, Appl. Phys. Lett., 2015, 107, 133902 CrossRef.
- G. V. Naik, A. J. Welch, J. A. Briggs, M. L. Solomon and J. A. Dionne, Hot-carrier-mediated photon upconversion in metal-decorated quantum wells, Nano Lett., 2017, 17, 4583–4587 CrossRef CAS PubMed.
- P. Xu, et al., Mechanistic understanding of surface plasmon assisted catalysis on a single particle: cyclic redox of 4-aminothiophenol, Sci. Rep., 2013, 3, 1–6 Search PubMed.
- E. Peiris, et al., Plasmonic switching of the reaction pathway: visible-light irradiation varies the reactant concentration at the solid-solution interface of a gold-cobalt catalyst, Angew. Chem., Int. Ed., 2019, 58, 1–6 CrossRef PubMed.
- S. Yu, A. J. Wilson, J. Heo and P. K. Jain, Plasmonic control of multi-electron transfer and C–C coupling in visible-light-driven CO2 reduction on Au nanoparticles, Nano Lett., 2018, 18, 2189–2194 CrossRef CAS PubMed.
- S. Yu and P. K. Jain, Plasmonic photosynthesis of C1–C3 hydrocarbons from carbon dioxide assisted by an ionic liquid, Nat. Commun., 2019, 10, 2022 CrossRef PubMed.
- Y. Tian and T. Tatsuma, Plasmon-induced photoelectrochemistry at metal nanoparticles supported on nanoporous TiO2, Chem. Commun., 2004, 1810–1811 RSC.
- Z. Gong, J. Ji and J. Wang, Photocatalytic reversible reactions driven by localized surface plasmon resonance, Catalysts, 2019, 9, 193 CrossRef.
- J. Huang, et al., Plasmon-induced optical control over dithionite-mediated chemical redox reactions, Faraday Discuss., 2019, 214, 455–463 RSC.
- X. Li, H. O. Everitt and J. Liu, Confirming nonthermal plasmonic effects enhance CO2 methanation on Rh/TiO2 catalysts, Nano Res., 2019, 19, 1706–1711 CAS.
- X. Zhang, et al., Product selectivity in plasmonic photocatalysis for carbon dioxide hydrogenation, Nat. Commun., 2017, 8, 14542 CrossRef CAS PubMed.
- X. Dai, Q. Wei, T. Duong and Y. Sun, Selective transfer coupling of nitrobenzene to azoxybenzene on rh nanoparticle catalyst promoted by photoexcited hot electrons, Chem. Nanostruct. Mater., 2019, 5, 10001007 Search PubMed.
- H. Huang, et al., Unraveling surface plasmon decay in coreshell nanostructures toward broadband light-driven catalytic organic synthesis, J. Am. Chem. Soc., 2016, 138, 6822–6828 CrossRef CAS PubMed.
- Y. Dong, P. Jiang and W. Xie, Harvesting hot electrons on Au nanoparticle monolayer by efficient compensation of holes, Applied Materials Today, 2019, 14, 201–206 CrossRef.
- M. W. Knight, et al., Embedding plasmonic nanostructure diodes enhances hot electron emission, Nano Lett., 2013, 13, 1687–1692 CrossRef CAS PubMed.
- S. Mubeen, G. Hernandez-Sosa, D. Moses, J. Lee and M. Moskovits, Plasmonic photosensitization of a wide band gap semiconductor: converting plasmons to charge carriers, Nano Lett., 2011, 11, 5548–5552 CrossRef CAS PubMed.
- M. Grajower, J. Khurgin and U. Levy, The role of surface roughness in plasmonic-assisted internal photoemission schottky photodetectors, ACS Photonics, 2018, 5, 4030–4036 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc06480j |
| This journal is © The Royal Society of Chemistry 2020 |