Unveiling the optical parameters of vanadium dioxide in the phase transition region: a hybrid modeling approach

Abstract

The phase change behavior of vanadium dioxide (VO₂) has been widely explored in a variety of optical and photonic applications. Commonly, its optical parameters have been studied in two extreme regimes: hot (metallic) and cold (insulating) states. However, in the transition temperatures, VO₂ acts like an inherent metamaterial with mixed metallic-insulating character. In this range, the portions of metallic and insulating inclusions are tuned by temperature, and therefore a gradual change of optical parameters can be achieved. In this paper, a universal hybrid modeling approach is developed to model VO₂ in the intermediate region. For this aim, the measured reflectivity data, is analyzed and matched through the transfer matrix method (TMM) simulations where an effective medium theory (EMT) is employed. Based on the findings of this approach, not only the relative portions of inclusions are tailored but also their grain shapes are significantly altered in the transition range. Finally, the modeling approach is testified by experimental findings through dynamic device applications operating at short and mid infrared wavelengths. In addition, the hysteretic behaviors on electrical, optical, and structural parameters of the VO₂ film along the heating and cooling cycles are demonstrated by the experiments and scrutinized by the simulations.

---

Introduction

Vanadium dioxide (VO₂) is an exotic material in which its phase changes from an insulator to a metal after a conveniently accessible transition temperature (∼68 °C).¹ This phase transition is reversible, that is, when it reduces from higher temperatures to lower temperatures, the phase transition from metal to insulator occurs. For this reason, it has been the most attractive material among the phase change materials since its discovery in 1959.² The material, having the insulating phase at room temperature and metallic phase at high temperature, would be in an intermediate phase when approaching the transition point either from higher or lower temperatures. In other words, VO₂ is an inherent metamaterial in atomic scales. The phase transition of the VO₂ can be triggered thermally,^3–6 electrically,^7–9 optically,¹⁰ and mechanically.¹¹ The electrical and optical properties of the VO₂ before, during, and after the phase transition differ considerably in the spectra of interest. Many applications have been developed from radio frequency (RF) to optical spectrum, employing this phase transition character. Some of these applications are infrared (IR) camouflage,^12–14 smart thermochromic coatings,^15,16 IR sensors,^17,18 optical diode-like structures,^19,20 optical metasurfaces,^21,22 switching,^23,24 and terahertz devices.^25,26 The electrical and spectral optical properties of the VO₂ depend on the quality of the VO₂ film, i.e. the type of growth, growth conditions, substrate type, etc.^27,28 Thin VO₂ films can be grown on different substrates by various techniques. The main growth techniques are sol–gel deposition,^15,29–31 sputtering,^32–35 pulsed laser deposition (PLD),^36–39 chemical vapor deposition (CVD),^40–44 and reactive evaporation.⁴⁵ Some widespread substrates employed for VO₂ growth are sapphire (Al₂O₃),⁴⁶ titanium dioxide,⁴⁷ silicon,⁴⁸ germanium,⁴⁹ and gallium nitride.⁵⁰ In addition, VO₂ thin film growth on graphene⁵¹ and hexagonal boron nitride (hBN),⁵² which are transferable to flexible substrates, were reported. The diversity of VO₂ growth and applications calls for a detailed knowledge on the optical parameters of VO₂ at relevant operating temperatures and the wavelengths. Although many reports^3–6,19,51 have extracted the refractive index of VO₂ in hot or metal (m-VO₂) and cold or insulator (i-VO₂) states, its optical behavior in the transition region has not been scrutinized. This is the regime in which material itself operates as a metamaterial. To our knowledge, there has not been much comprehensive study on the spectral optical parameter extraction of VO₂ depending on the temperature and specific to VO₂ growth conditions, except for one recent study.⁵³

This paper shows a comprehensive study of extracting optical parameters in all phase transition regimes of VO₂ starting from a bare film and eventually to a device application in the short-wavelength infrared (SWIR) and mid-wavelength infrared (MWIR) spectra. The spectral optical parameters of the VO₂ at each temperature during the heating and cooling cycles are modeled utilizing an effective medium theory (EMT) approach in the electromagnetic simulations. Thanks to fine adjustments of parameters in the EMT modeling, spectral measurements and simulations are matched at every specific temperature. In this way, the size and shape changes in the metallization regions inside an ultrathin (∼90 nm thick) grown VO₂ film, which take place on an atomic scale during phase transition, are discovered by extensive experiments and simulations, based on the applied temperature intensity and direction. Our method concludes that the volume of metalized VO₂ regions is directly proportional to the applied temperature as expected. However, the most notable observation of this modeling approach is its prediction on optical behavior of VO₂ film in the phase transition regime. For the first time, our study reveals that the shape of metallic inclusions in the VO₂ layer differs only in the transition region compared to other regimes. In addition, the hysteretic behaviors, occurring in various parameters during the heating and cooling processes, are explored by the experiments and simulations. Finally, as a proof-of concept study, we design a tunable device, using the extracted optical parameters, and we theoretically and experimentally demonstrate its operation in the SWIR and MWIR wavelengths. Moreover, we make additional numerical simulations of the final device to enlighten the physics behind the operating mechanism, and its angular and the polarization dependency. While most of the previously reported studies concentrated on the optical character of VO₂ in only hot and cold states, accurate modeling of the material behavior in the intermediate transition region can be used to design multi-functional linearly tunable optical systems.

Materials and methods

Growth of VO₂ thin films

RF magnetron sputtering technique was used to deposit VO₂ thin film on double side polished c-plane sapphire substrate. A vanadium oxide target was used as the source material. Deposition pressure was 2.4 × 10⁻³ mbar and argon (Ar) flow was 7 sccm. Deposition rate was ∼0.4 Å s⁻¹. The thickness of deposited VO₂ film was 90 nm. Post annealing was done at 400 °C for 1 hour in atmospheric tube furnace under Ar flow of 4 cm³ min⁻¹. The sapphire substrate was selected for its superior transmittance up to 6 μm mid infrared wavelengths.

Fabrication of the samples

Following the growth and annealing of VO₂ on the sapphire substrate, three 5 × 5 mm samples were diced for the fabrication of samples A, B, and C. The bare film referred as “sample A” was used for temperature dependent electrical and FTIR reflectivity measurements of the grown VO₂. “Sample B” was prepared depositing 100 nm of gold (Au) on one of diced VO₂ samples by electron-beam evaporation system. The chamber pressure was 1 × 10⁻⁵ mbar while the deposition rate was 2 Å s⁻¹. For the fabrication of “sample C”, firstly 520 nm of SiO₂ was deposited on the VO₂ by plasma-enhanced chemical vapor deposition (PECVD). The PECVD temperature was 250 °C and the process pressure was 80 Pa with 300 sccm N₂O flow rate while the RF power was 50 W. After the SiO₂ deposition, 100 nm Au was deposited by electron-beam evaporation with the same process parameters described for “sample B”.

Electrical measurements

4-Probe sheet resistance technique utilizing Agilent B1500A Semiconductor Parameter Analyzer was performed to measure the dc electrical sheet resistance of “sample A” while changing the temperature from 25 °C to 90 °C and back down. During these temperature cycles, we chose a relatively fine resolution of 2 °C in the expected material phase transition region, and a resolution of 5 °C elsewhere. A thermoelectric cooling (TEC) chuck was used as the heating stage. A 10 A/12 V TEC controller (Arroyo Instruments 5310) was operated to control the temperature. At each temperature measurement, we waited at least 60 seconds for the temperature to settle.

Optical measurements

The infrared spectral reflectivity measurements of the samples were carried out using an IR microscope (Bruker Hyperion 2000) and the Fourier transform infrared (FTIR) spectrometer (Bruker Vertex 70v) with a liquid nitrogen cooled mercury cadmium telluride detector and mid-IR source. Reflected light was collected with a 15× magnification reflective objective (numerical aperture 0.4). To calibrate, a thick gold layer coated on sapphire substrate was used as the background in the reflection measurement. In order to change the temperature from the room temperature (T = 25 °C) to the high temperature (T = 90 °C) during the heating and from T = 90 °C to T = 25 °C during the cooling, the samples were placed on a heating stage that is mounted on the IR microscope, with a temperature controller (Arrayo TEC). After adjusting the controller of the heating stage, we waited at least 60 seconds to let the sample arrive to the desired temperature.

Simulations

In the Transfer Matrix Method (TMM), the field within each layer could be treated as superposition of forward-traveling (transmitted) and backward-traveling (reflected) wave with a wave number k and a transfer matrix could represent the propagation through interface or within medium. By cascading the transfer matrix for each layer, the entire system transfer matrix can be obtained, deriving the spectral transmittance (T) and spectral reflectivity (R) of the structure.⁵⁴ The mathematical details of these derivations and the incidence angle and the polarization modeling using TMM were given by Kocer et al.⁵⁵ The absorbed power and electric field intensity distributions along “sample C” were computed via finite-difference time-domain (FDTD) simulations with a commercial software from Lumerical Solutions.⁵⁶ While a TM polarized plane wave of 4 μm was sent at normal incidence in the FDTD simulations, periodic boundary conditions were applied along transverse axes perpendicular to the light propagation axis, and PML (perfectly matched layers) boundary conditions were selected along the propagation axis. Then, the electric field and absorbed power distributions were determined within the frequency profile and power monitors.

Results and discussion

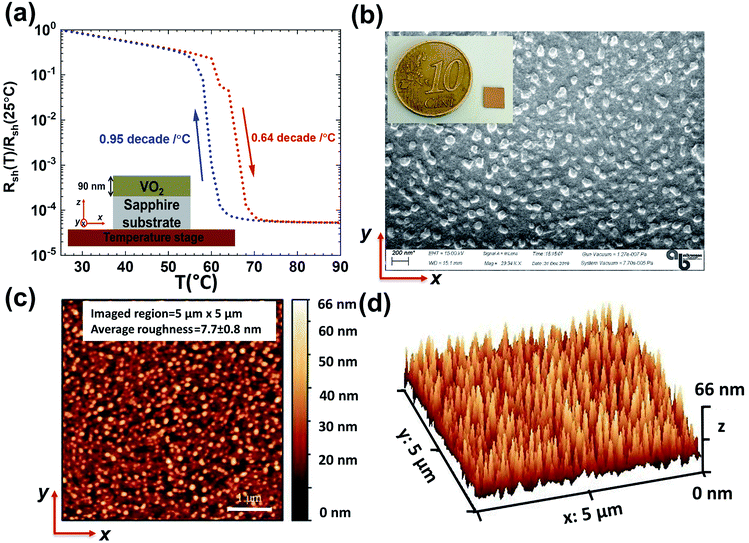
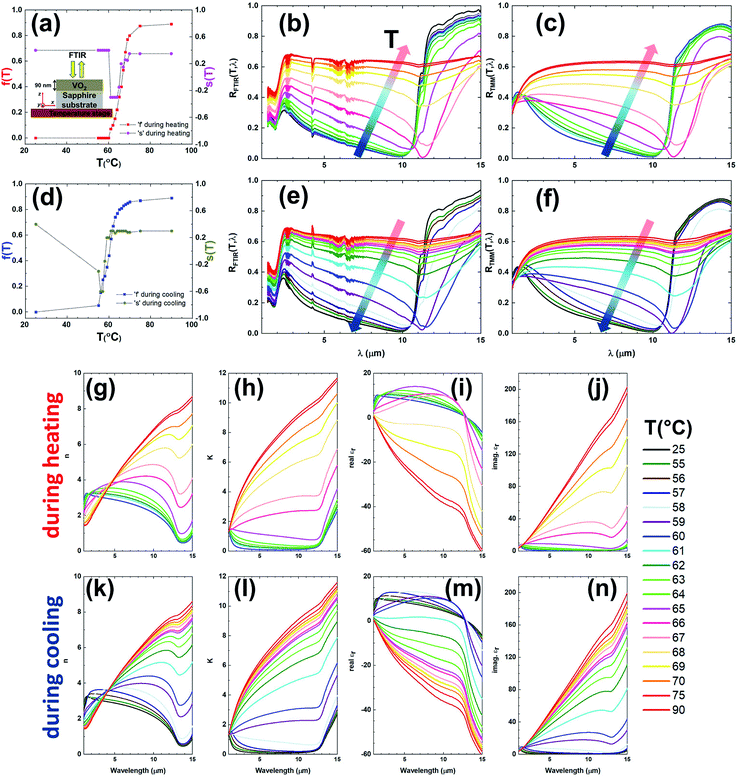
The fabrication of the bare film (referred as “sample A”) involves growing of a 90 nm VO₂ layer on the c-plane sapphire by RF magnetron sputtering. Then, we place it in a temperature controlled stage to make electrical resistance measurements as shown in the inset of Fig. 1a. Utilizing the 4-probe sheet resistance technique, we measure the dc electrical sheet resistance of the “sample A” while changing the temperature from 25 °C to 90 °C and back down (during heating step size of 2 °C in the range of 60–80 °C and 5 °C outside of this range, and during the cooling step size of 2 °C in the range of 50–80 °C and 5 °C outside of this range). In each temperature measurement during the heating and cooling cycles, we wait at least 60 s to allow the temperature to settle. Fig. 1a exhibits the mentioned measurement results as the normalized dc sheet resistance R_sh(T)/R_sh(25 °C). It shows more than four orders of magnitude change between cold (T = 25 °C) and hot (T = 90 °C) states. In addition, when we compare the blue (during cooling) and red (during heating) curves in the Fig. 1a, it is seen that the normalized dc sheet resistance shows a hysteretic behavior, which is elucidated later. It is also evident that the transition of the resistance in our sample across the phase transition region is steeper (during cooling: 0.95 decade per °C and during heating: 0.64 decade per °C) when we compare it with a similar structure⁵⁷ in the literature. Overall, the electrical measurements prove that our growth method achieves an appropriate VO₂ material that can change its phase in a reversible manner, by switching from the insulating state to the conductive state with a rather steep slope according to the temperature shift. In order to visualize the structural morphology and uniformity of the VO₂ film, the scanning electron microscope (SEM) image of the top surface of the “sample A” is obtained in Fig. 1b. The inset is the optical image of the top of the real sample next to a coin as well. The SEM image reveals that the surface morphology of the VO₂ film seems to be continuous with multi domains due to the magnetron sputtering. To assess the surface roughness of the VO₂ film, we use atomic force microscopy (AFM) measurement on the top surface of the “sample A”. The resulting 2D and 3D AFM images are seen in Fig. 1c and d, respectively. According to AFM imaging, the average surface roughness (R_a) is found to be 7.7 ± 0.8 nm. This value of R_a is much smaller than the wavelengths (λ ≥ 1 μm) in our study. Therefore, in the simulations at these wavelengths, we can treat the top of the VO₂ film as if it was smooth.

Fig. 1 (a) Electrical characterization of VO₂ ultrathin film (“sample A”) as a function of temperature during heating (red colored) and cooling (blue colored). The inset depicts the x–z side view of the “sample A” on a temperature stage. (b) Scanning electron microscope image of the “sample A”. Inset: Optical image of the “sample A” and size comparison with a coin of 10 eurocents. (c) 2D and (d) 3D atomic force microscopy images of the “sample A”.

After the electrical and surface characterizations of “sample A”, we start IR spectral reflectivity measurements using an IR microscope (Bruker Hyperion 2000) that is coupled to the Fourier transform infrared (FTIR) spectrometer (Bruker Vertex 70v). As seen in the inset of Fig. 2a, “sample A” is placed on a temperature controlled stage that is mounted inside the IR microscope/FTIR. The sample is exposed to near normal incidence of the IR light at wavelengths of 1 to 15 μm. In the heating step, the temperature increases from 25 °C to 90 °C and vice versa in the cooling process. As can be seen in the temperature values shown in the lower right side of Fig. 2, which we use in the heating and cooling phases, the reflectivity measurements R_FTIR(T,λ) are made between 55 °C and 70 °C in one degree steps. Since VO₂ material phase transition is between 55 °C and 70 °C, the reflectivity measurements in this range are done in fine steps compared to the other ranges. An optically thick gold mirror is used for the normalization in the reflectivity measurements. In addition, we perform the FTIR measurements during the cooling and the heating after staying at least 60 s at each temperature to sense the set temperature correctly. As a result, the spectral plots for the R_FTIR(T,λ) are given in Fig. 2b (during heating) and Fig. 2e (during cooling). The small resonating features at 4.2 μm are due to absorption of the atmospheric CO₂ molecules, which exist in the measurement environment. Considering the R_FTIR(T,λ) spectra during the heating (the cooling), we observe that these reflectivities do not switch monotonously from low (high) to high (low) temperatures. These characteristics stem from the complicated interaction between the effective medium formed when VO₂ is in an intermediate material state during these temperature transitions and the underlying sapphire substrate. In both of the spectra in the heating (Fig. 2b) and the cooling (Fig. 2e) periods, this situation can be especially viewed at 11.3 μm wavelength. Namely, when the material state of the VO₂ is an insulator at the room temperature (T = 25 °C) and a metal at the elevated temperature (T = 90 °C), the reflectivity values, which are quite high, are approaching zero suddenly at the intermediate temperatures. Furthermore, the sapphire substrate is not transmitting at this wavelength, but highly reflective. Therefore, the sudden drop of the reflectance at this particular wavelength at a certain temperature can be attributed to the absorption inside the VO₂ layer, which turns to the intermediate material state or inherent metamaterial. In addition, the reflectivity spectrum at 11.3 μm wavelength has a hysteresis, which is discussed later in the text. Since the VO₂ exhibits such a complex optical behavior related to the temperature changes, it is important to reveal the spectral optical parameters of the VO₂ depending on the temperature values in the case of temperature rise or decrease.

Fig. 2 During heating: (a) Looyenga effective-medium theory parameters of f(T) and s(T), (b) measured spectral reflectivity of R_FTIR(T,λ) and (c) simulated spectral reflectivity of R_TMM(T,λ). Inset (a) is x–z side view of the “sample A” on a temperature stage. During cooling: (d) Looyenga effective-medium theory parameters of f(T) and s(T), (e) measured spectral reflectivity of R_FTIR(T,λ) and (f) simulated spectral reflectivity of R_TMM(T,λ). Extracted infrared spectral optical parameters of VO₂ in “sample A” during heating: (g) real and (h) imaginary parts of the refractive indices, and (i) real and (j) imaginary parts of relative dielectric permittivities. Extracted infrared spectral optical parameters of VO₂ in “sample A” during cooling: (k) real and (l) imaginary parts of the refractive indices, and (m) real and (n) imaginary parts of relative dielectric permittivities. The colored horizontal lines on the right refer to the temperatures applied during heating and cooling.

VO₂ at and near the phase transition behaves like a natural metamaterial that contains metallic and insulating inclusions that are much smaller than the wavelength of the incident light. In addition, the sizes of the metallic and insulating domains vary depending on the temperature. As the temperature increases, the volume occupied by the metallic domains increases, while the one for the insulating domains decreases, and the opposite occurs when the temperature decreases. Therefore, the spectral optical parameters of VO₂ at different temperatures can be better assessed by an appropriate EMT. In our study, we implement a method utilizing an EMT. This method is based on the theoretical convergence to the reflectivity values obtained experimentally by performing the electromagnetic simulations of the “sample A” with Transfer Matrix Method (TMM)^54,55 as follows.

R_TMM(T,λ,ε_eff(T,λ)) ≈ R_FTIR(T,λ) (1)

The key parameter in eqn (1) is the ε_eff(T,λ) that represents the effective complex relative dielectric permittivity of the VO₂ layer in the “sample A”. Although there are many EMT models developed in the past to deal with the intermediate states of VO₂, we use EMT based on the Looyenga mixing rule,^53,58 as it has the more versatile modeling capabilities described below.

ε^s(T)_eff(T,λ) = (1 − f(T))ε^s(T)_ins(λ) + f(T)ε^s(T)_met(λ) (2)

Here, f(T) is the temperature dependent volume fraction of the metal-phase VO₂ domains, and it changes as 0 ≤ f(T) ≤ 1. s(T) is the temperature dependent shape of the metallic inclusions in the VO₂ layer, and it changes as −1 ≤ s(T) ≤ 1. The complex relative permittivities of the full insulator VO₂, ε_ins(λ), and full metal VO₂, ε_met(λ), are taken from an earlier experimental study⁵³ where they were found through the spectroscopic ellipsometry. Note that ε_ins(λ) corresponds to the complex relative permittivity of the VO₂ for f(T) = 0 and ε_met(λ) is for f(T) = 1. In the TMM simulations of “sample A”, the complex refractive index of the sapphire substrate is taken as Al₂O₃ in the Palik database.⁵⁹ The temperature dependent complex refractive index of the VO₂, N(T,λ), in the “sample A” is easily obtained by N(T,λ) = (ε_eff(T,λ))^0.5 = n(T,λ) + jK(T,λ). In order to fulfill the convergence in eqn (1) as much as possible in the temperature values during the heating and cooling cycles at the wavelengths of 1–15 μm, we tune the parameters of f(T) and s(T) through the TMM simulations as seen in Fig. 2a and d. The resulting values of R_TMM(T,λ) are indicated in Fig. 2c and f. Once the required parameters f(T) and s(T) are correctly determined, it can be seen that the simulation results in Fig. 2c and f closely converge with the corresponding measurement results in Fig. 2b and e. This convergence can be seen more thoroughly by looking at 2D maps of R_FTIR(T,λ) and R_TMM(T,λ), which are depicted in the ESI (Fig. S1†) as well. Moreover, we can easily observe the behavior of the f(T) and s(T) parameters that we found with the cooperative study of the measurements and simulations in Fig. 2a and d. In the temperature regime in which the material phase of VO₂ changes, f(T) alters in direct proportion with the temperature, while s(T), which is positive in other regions, becomes negative by forming a valley in this region. This behavior of f(T), which is also compatible with the literature,⁵³ means that the volume of the metalized VO₂ expands as the temperature increases, as expected. On the other hand, such behavior in the s(T) parameter is revealed by our study for the first time to our knowledge. With this finding, we can deduce that the shape of the metallic inclusions in the VO₂ layer is very different in the material transition region compared to the other regions (i-VO₂ and m-VO₂), while in the other regions it is approximately the same. The physics of our findings on s(T) can be elucidated as follows. By heating the material in the insulating phase, metallic inclusions which are initially two-dimensional circular (three-dimensional spherical) symmetry emerge on a sub wavelength scale as illustrated in the graphic of table of contents entry. When the material enters the transition zone, as a result of the metal inclusions merging with each other, the mentioned symmetry in their patterns is disrupted. As the heating continues, the material leaves the transition zone and initial symmetry reappears in dimensionally growing metallic inclusions. When the material is cooled from the high temperatures in the metal phase, the above-mentioned physical changes in metallic inclusions occur reversibly with a certain hysteresis. That is, at high temperatures, the large symmetrical situation deteriorates in the intermediate region, and it is reproduced in small size after crossing the intermediate region. Furthermore, both f(T) and s(T) have hysteresis, which we will touch upon later, depending on the increase or decrease of the applied temperature.

Following the agreement between FTIR and TMM spectral reflection through f(T) and s(T) adjustments, we can extract the temperature dependent spectral optical parameters of the VO₂ presented in Fig. 2g–n. For this purpose, we apply a systematic approach. At first, we calculate the temperature dependent real and imaginary components of the spectral optical parameters of the VO₂ in the heating phase by placing the parameters we identified in Fig. 2a in eqn (2). In this manner, the real part of the refractive index, n(T,λ), the imaginary part of the refractive index, K(T,λ), the real part of the relative dielectric permittivity, real ε_eff(T,λ), and the imaginary part of the relative dielectric permittivity, imag. ε_eff(T,λ), are given in Fig. 2g, h, i, and j, respectively. Next, when we insert the data from Fig. 2d in eqn (2), the mentioned optical parameters in the heating phase are now calculated for the cooling phase, and the results are presented in Fig. 2k–n, respectively. The aforementioned parameters are illustrated as 2D maps during heating and cooling in the ESI (Fig. S2 and S3†). Here, the important contour lines such as n(T,λ) = 1 (close to air) and real ε_eff(T,λ) = 0 (epsilon near-zero, ENZ) are shown separately for the heating and cooling conditions, and their behaviors are explained comparatively.

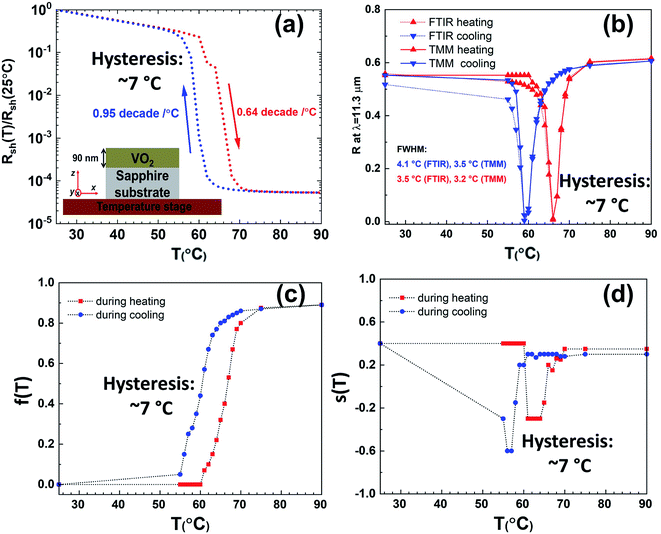
For the “sample A” in the inset of Fig. 3a, the hysteretic behaviors we encounter during the electrical/optical measurements and the optical simulations are exhibited collectively in Fig. 3. For all of the figure of merits whose hystereses are plotted here, the red colored data reflects the heating and the blue colored ones reflect the cooling state. Fig. 3a implies that the normalized dc sheet resistance has a hysteresis width of about 7 °C between the linearly sloping curves of 0.95 decade per °C and 0.64 decade per °C. This hysteresis width is close to the findings of an experimental study⁵⁷ similar to our growth conditions except the VO₂ thickness was two times of the ours. Fig. 3b shows another hysteresis we experienced. During the cooling and heating, the difference between the reflectivity drops occurring at the wavelength of 11.3 μm is found as ∼7 °C by means of compatible FTIR measurements and TMM simulations. In addition, when full width at half maximum (FWHM) values are quantitatively compared with the experiments and the simulations in the cooling and the heating phases, it is seen that they are not very different from each other as given inside the Fig. 3b. The last hysteretic behaviors are indicated in the EMT parameters of f(T) and s(T) in Fig. 3c and d, respectively. Comparing the red and the blue colored data in terms of the hysteresis, we observe that maximum width across the linear region in f(T) and the difference between the dips of the valleys in s(T) are ∼7 °C. Furthermore, the additional hystereses of the optical parameters at some selected wavelengths are also illustrated in the ESI (Fig. S4†). After all, the common feature of the four different hystereses in the main text and four in the ESI† is that they are all of the same value (i.e. ∼7 °C). Although the hysteretic behaviors with the same value are rarely seen in one or two parameters of VO₂ in the literature,⁵⁷ the hysteretic behaviors with the same value in more than two different parameters are disclosed for the first time in this study.

Fig. 3 Hysteretic behaviors observed in (a) normalized electrical resistance, (b) experimental (FTIR) and simulated (TMM) reflectivity (R) from the “sample A” at λ = 11.3 μm, effective-medium theory parameters of (c) f(T) and (d) s(T) as the applied temperature increases and decreases. Inset (a) is x–z side view of “sample A” on a temperature stage.

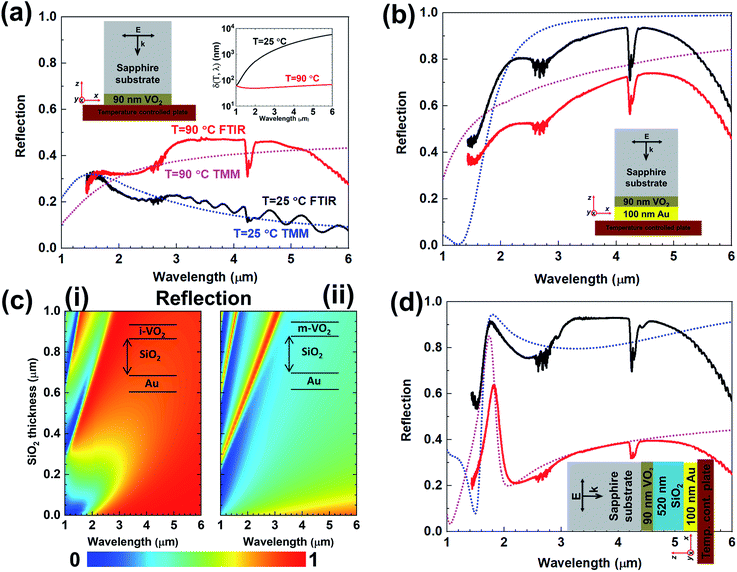
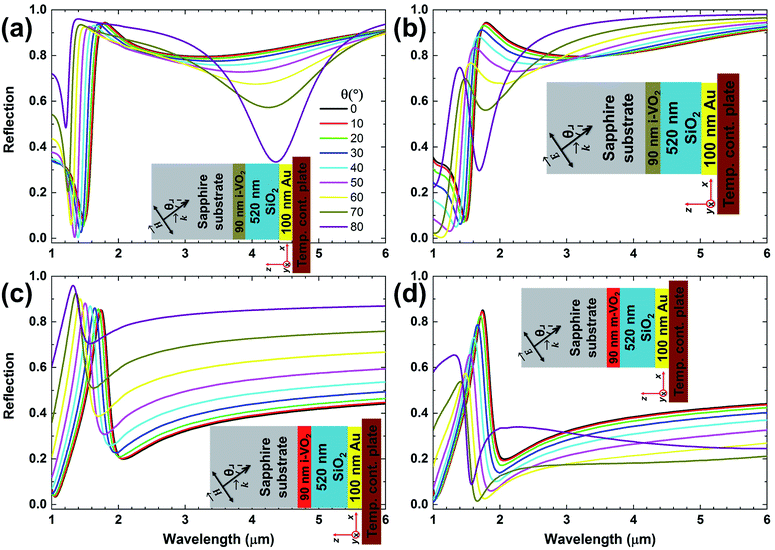
After implementing the proposed optical parameter extraction, a proof-of-concept study is carried out to demonstrate a device application using the optical parameters of the VO₂ film, which we have revealed as a result of the experimental and the theoretical studies of the material and optical properties described above in detail. Our goal is to design and experimentally show a tunable device⁶⁰ at SWIR and MWIR wavelengths using “sample A” and its optical parameters. We also employ a planar and lithography-free device architecture to benefit the ease of the fabrication.⁶¹ We will follow a three-step theoretical and experimental process toward the specified goal. Firstly, shown in Fig. 4a (left inset), we illuminate “sample A” from the sapphire side at the normal incidence in SWIR and MWIR wavelengths and perform the FTIR measurements and the TMM simulations under the conditions of T = 25 °C and T = 90 °C. Since the sapphire is highly transmissive and lossless in our wavelength range (1 μm ≤ λ ≤ 6 μm), we set its refractive index as 1.70 in the simulations.^3,4 Utilizing the spectral optical data of the VO₂ that we have already extracted in the Fig. 2, we pick the optical parameters at T = 25 °C where the VO₂ is an insulator (i-VO₂) and T = 90 °C where the VO₂ is a metal (m-VO₂). When we compare the measured and simulated spectral reflections in Fig. 4a, it is seen that the experiments and simulations are compatible and there is a certain contrast between the reflection spectra in two different temperature conditions. This contrast can be easily explained with the field intensity in the VO₂, I(T,λ,z). It decays as I(T,λ,z) ∼ exp{−z/δ(T,λ)}. δ(T,λ) is the skin depth and expressed as δ(T,λ) = λ/4πK(T,λ), which is dependent on the wavelength and the imaginary part of the refractive index of the VO₂. Taking the K(T,λ) from Fig. 2 at T = 25 °C and T = 90 °C, we calculate the spectral skin depth at these temperatures in the right inset of the Fig. 4a. Since the δ(T = 25 °C,λ) is much higher than the thickness of the VO₂, the incoming IR light can pass through the i-VO₂ layer with higher transmission, lower reflection, and negligible absorption, whereas the opposite situation occurs at T = 90 °C. Namely, the transmission decreases and the absorption and reflection increase due to the δ(T = 90 °C,λ), which is smaller than the VO₂ thickness. According to the well-known conservation of the power, the sum of reflection (R), transmission (T), and absorption (A) ratios is fixed as R + T + A = 1. If we block the transmission completely, it is reduced to A + R = 1. The second step of our study is now targeted toward this purpose such that we coat an optically thick gold (Au) layer (∼100 nm) on the VO₂ side displayed in the inset of the Fig. 4b as “sample B”. In this case, the transmission will no longer occur. Here and the later simulations, we select “Au (gold)-CRC” as the Au's spectral refractive index from the material library of Lumerical, a commercially available finite-difference time-domain (FDTD) simulation software package.⁵⁶ As seen in Fig. 4b, the simulated and measured reflectivity contrast reverses compared to “sample A”. At T = 25 °C, the IR illumination at λ > 2 μm can pass through the i-VO₂ without much loss, hitting the thick Au layer and almost the majority is reflected back. At T = 90 °C, the same illumination is absorbed more in the transitions from the lossy m-VO₂, so the reflection is relatively reduced compared to the previous situation. Although we have a fairly good agreement between the simulations and the measurements to estimate the reflection contrast, it is necessary to explain the deviation observed between them. This might primarily have been originated from the fact that the refractive index of the experimental 90 nm thick Au structure might be somewhat different than the bulk index of the “Au (gold)-CRC”. Secondly, the experimental sapphire index may exhibit slightly dispersive and lossy characteristics instead of the constant one, which was not considered in our simulations. In order to further rise this reflection contrast, we incorporate a SiO₂ spacer layer between VO₂ and Au as the last step. We investigate the effect of the thickness of this spacer layer via numerical simulations in Fig. 4c at T = 25 °C and T = 90 °C separately. To accurately simulate the device response, we measure the spectral refractive index of the SiO₂ film using variable angle spectroscopic ellipsometer in the ESI (Fig. S5†). Then, we fabricate the structure (“sample C”) with the 520 nm thick SiO₂ layer as seen in the inset of Fig. 4d. In Fig. 4d, we finally achieve broadband and tunable reflection at SWIR and MWIR wavelengths through the experiments and simulations that give quite close results. Some minor discrepancies that do not affect our main purpose are caused by the aforementioned reasons, and unavoidable imperfections during the fabrication and measurements. Moreover, we enlighten the physics behind this exclusive operating mechanism by the additional electromagnetic simulations given in the ESI (Fig. S6–S8†). To assess the angular and the polarization dependency of the proposed device, TMM simulations are carried out for four different illumination and temperature conditions, which are depicted as insets in Fig. 5. In “TE” or “s” polarization, the electric field is normal to the incidence (x–z) plane, whereas it is inside the incidence plane in “TM” or “p” polarization. The angle of incidence varies in all cases from 0° to 80° in 10° steps. In Fig. 5, the sub-items in each row show the effect of polarization at a constant temperature, while those in each column are the effect of the material state at constant polarization. We can elucidate the comments about these findings as follows. First, the desired device performance can be achieved in TM polarization (Fig. 5b and d) up to higher incidence angles compared to TE polarization (Fig. 5a and c). Secondly, it is also possible to say that the device performance up to 50° of incidence is almost maintained for both polarization conditions. Therefore, it would not be wrong to claim that our design is considerably independent in terms of the polarization and the angle of incidence.

Fig. 4 (a) Simulated (TMM) and measured (FTIR) power reflection spectra of the structure shown in left inset (“sample A”) at T = 25 °C and T = 90 °C. Right inset: the spectral skin depth of VO₂ at T = 25 °C and T = 90 °C, (b) TMM and FTIR reflection spectra of the structure shown in inset (“sample B”) at T = 25 °C and T = 90 °C, (c) reflection map with respect to the thickness of SiO₂ layer (which is added between VO₂ and Au layers of “sample B”) (i) at T = 25 °C and (ii) at T = 90 °C. The bottom color bar applies both. (d) TMM and FTIR reflection spectra of the structure shown in inset (“sample C”) at T = 25 °C and T = 90 °C. Solid red (T = 90 °C) and black (T = 25 °C) curves represent FTIR power reflections, whereas dotted pink (T = 90 °C) and blue (T = 25 °C) curves represent TMM power reflections in (a), (b) and (d).

Fig. 5 The angular dependence of infrared reflection when VO₂ is insulator under (a) TE and (b) TM polarized illuminations and when VO₂ is metallic under (c) TE and (d) TM polarized illuminations. The x–z side views of the simulated geometries and illumination conditions are pictured in the insets. The horizontal colored lines in inset (a) stand for incidence angles and apply to all.

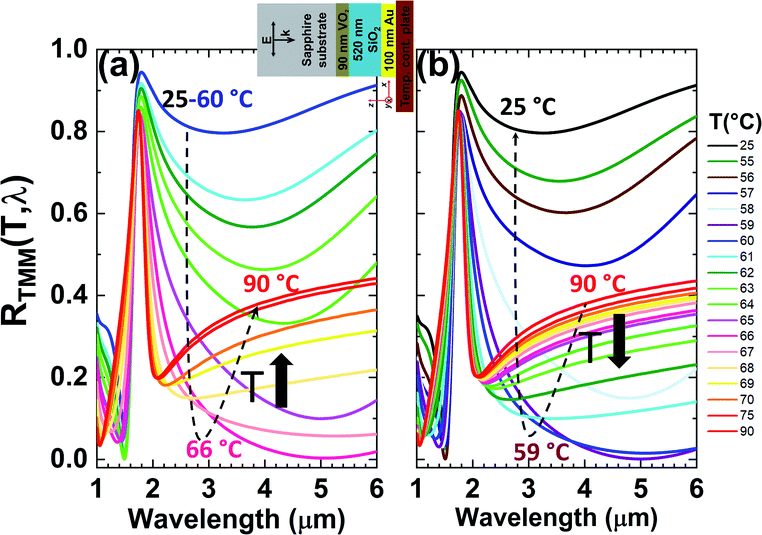
Finally, utilizing the temperature dependent optical parameters of VO₂ extracted in Fig. 2, we made additional TMM simulations of the “sample C” as seen in Fig. 6 in order to understand the effect of the intermediate states of the VO₂. The simulated geometry and the simulation conditions are shown in the inset of Fig. 6a. The resulting spectral reflectivities, R_TMM(T,λ), during heating and cooling cycles are given in Fig. 6a and b, respectively. It is possible to interpret the results here comparatively with the help of temperature trajectories drawn by black dashed lines in the figures. During the heating (Fig. 6a): the reflectivities between T = 25 °C and T = 60 °C are high and of the same value. From T = 60 °C to T = 66 °C, R_TMM(T,λ) is inversely proportional to the temperature. From T = 66 °C to T = 90 °C, R_TMM(T,λ) rises in direct proportion to the temperature. During the cooling (Fig. 6b): from T = 90 °C to T = 59 °C, the reflectivity decreases directly with the temperature. From T = 59 °C to T = 25 °C, its behavior turns to opposite by rising as the temperature drops. Although the spectral reflectivities at extreme temperatures (T = 90 °C to T = 90 °C) are the same in both heating and cooling conditions, the hystericity in VO₂ shows its effect on the intermediate regime and causes the R_TMM(T,λ) to differ in the intermediate regions.

Fig. 6 Simulated spectral reflectivity of R_TMM(T,λ) of the “sample C” during (a) heating and (b) cooling cycles. Inset (a) is x–z side view of the simulated “sample C” on the temperature stage and illumination conditions. The dashed black curved lines drawn to guide the eye represent the trajectories of the temperatures during heating and cooling. The colored horizontal lines on the right refer to the temperatures applied during heating and cooling.

Conclusions

In conclusion, we conducted an experimental study that included all of the stages, starting from an ultra-thin VO₂ film growth, examining the electrical and the optical parameters, extracting the temperature-dependent IR optical parameters, and eventually utilizing these parameters for the demonstration of a dynamic device operating at SWIR and MWIR wavelengths. By analyzing and matching the measured FTIR reflection data with TMM simulations where an EMT is incorporated, we found the spectral optical parameters of the VO₂ at the desired temperatures and wavelengths during the heating and cooling stages. Our method explained that not only the volume of metalized VO₂ inclusions is directly proportional to the applied temperature, but also for the first time it is unveiled that the shape of metallic inclusions in the VO₂ layer differs only in the transition region. Moreover, it was found that all of the hystereses in many different parameters mentioned interestingly have the same value (i.e. ∼7 °C). Finally, we realized the design of a device capable of broadband and tunable reflection that operates at SWIR and MWIR wavelengths by showing all of its stages with experiments and simulations. Additional numerical simulations were carried out to understand the physics behind the operating mechanism, and the angular and the polarization dependency. Our work, which sheds light on all of the stages from material parameters to device application, theoretically and experimentally, contributes to the still vivid field of VO₂, which has a lot of optical and photonic applications.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

E. Ozbay and H. Kurt acknowledge partial support from the Turkish Academy of Sciences (TUBA). This paper includes parts from M. Cihan Cakir's studies that will be presented as his PhD Thesis “Temperature Tunable Nanophotonic Structures”. All of the authors express their gratitude to M. C. Soydan (NANOTAM, Bilkent Unv.) for the ellipsometry measurements of SiO₂.

References

1. A. Cavalleri, T. Dekorsy, H. H. W. Chong, J. C. Kieffer and R. W. Schoenlein, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 161102.
2. F. J. Morin, Phys. Rev. Lett., 1959, 3, 34.
3. H. Kocer, S. Butun, E. Palacios, Z. Liu, S. Tongay, D. Fu, K. Wang, J. Wu and K. Aydin, Sci. Rep., 2015, 5, 13384.
4. H. Kocer, S. Butun, B. Banar, K. Wang, S. Tongay, J. Wu and K. Aydin, Appl. Phys. Lett., 2015, 106, 161104.
5. H. Kocer, A. Ozer, S. Butun, K. Wang, J. Wu, H. Kurt and K. Aydin, IEEE J. Sel. Top. Quantum Electron., 2019, 25, 1–7.
6. M. J. Dicken, K. Aydin, I. M. Pryce, L. A. Sweatlock, E. M. Boyd, S. Walavalkar, J. Ma and H. A. Atwater, Opt. Express, 2009, 17, 18330–18339.
7. M. R. M. Hashemi, S. H. Yang, T. Wang, N. Sepulveda and M. Jarrahi, Sci. Rep., 2016, 6, 35439.
8. G. Stefanovich, A. Pergament and D. Stefanovich, J. Phys.: Condens. Matter, 2000, 12, 8837–8845.
9. Y. Kim, P. C. Wu, R. Sokhoyan, K. Mauser, R. Glaudell, G. K. Shirmanesh and H. A. Atwater, Nano Lett., 2019, 19, 3961–3968.
10. A. Cavalleri, C. Toth, C. W. Siders, J. A. Squier, F. Raksi, P. Forget and J. C. A. Kieffer, Phys. Rev. Lett., 2001, 87, 237401.
11. N. B. Aetukuri, A. X. Gray, M. Drouard, M. Cossale, L. Gao, A. H. Reid, R. Kukreja, H. Ohldag, C. A. Jenkins, E. Arenholz, K. P. Roche, H. A. Dürr, M. G. Samant and S. S. P. Parkin, Nat. Phys., 2013, 9, 661–666.
12. S. Chandra, D. Franklin, J. Cozart, A. Safaei and D. Chanda, ACS Photonics, 2018, 5, 4513–4519.
13. L. Xiao, J. Liu, W. Zhao, Y. Jia, Q. Zhao, K. Liu, Y. Wu, Y. Wei, S. Fan and K. Jiang, Nano Lett., 2015, 15, 8365–8370.
14. M. A. Kats, R. Blanchard, S. Zhang, P. Genevet, C. Ko, S. Ramanathan and F. Capasso, Phys. Rev. X, 2013, 3, 041004.
15. Y. Gao, H. Luo, Z. Zhang, L. Kang, Z. Chen, J. Du, M. Kanehira and C. Cao, Nano Energy, 2012, 1, 221–246.
16. T. C. Chang, S. H. Bao, S. D. Ji, H. J. Luo and P. Jin, Adv. Manuf., 2018, 6, 1–19.
17. M. Gurvitch, S. Luryi, A. Polyakov and A. Shabalov, J. Appl. Phys., 2009, 106, 104504.
18. H. Ma, X. Zhang, Z. Zhang, Y. Wang, G. Wang, F. Liu, R. Cui, C. Huang, M. Wang, Y. Wei, K. Jiang, L. Pan and K. Liu, J. Mater. Chem. C, 2019, 7, 12095–12103.
19. C. Wan, E. H. Horak, J. King, J. Salman, Z. Zhang, Y. Zhou, P. Roney, B. Gundlach, S. Ramanathan, R. H. Goldsmith and M. A. Kats, ACS Photonics, 2018, 5, 2688–2692.
20. A. Ozer, H. Kocer and H. Kurt, J. Nanophotonics, 2018, 12, 046022.
21. J. Rensberg, S. Zhang, Y. Zhou, A. S. McLeod, C. Schwarz, M. Goldflam, M. Liu, J. Kerbusch, R. Nawrodt, S. Ramanathan, D. N. Basov, C. Capasso, C. Ronning and M. A. Kats, Nano Lett., 2016, 16, 1050–1055.
22. F. Ligmajer, L. Kejík, U. Tiwari, M. Qiu, J. Nag, M. Konečný, T. Šikola, W. Jin, R. F. F. Haglund, A. Kannatassen and D. Y. Lei, ACS Photonics, 2018, 5, 2561–2567.
23. M. Soltani, M. Chaker, E. Haddad, R. V. Kruzelecky and D. Nikanpour, J. Vac. Sci. Technol., A, 2004, 859–864.
24. S. Kumar, F. Maury and N. Bahlawane, Sci. Rep., 2016, 6, 37699.
25. F. Ding, S. Zhong and S. I. Bozhevolnyi, Adv. Opt. Mater., 2018, 6, 1701204.
26. Z. Song, A. Chen and J. Zhang, Opt. Express, 2020, 28, 2037–2044.
27. R. E. Marvel, R. R. Harl, V. Craciun, B. R. Rogers and R. F. Haglund, Acta Mater., 2015, 91, 217–226.
28. K. Liu, S. Lee, S. Yang, O. Delaire and J. Wu, Mater. Today, 2018, 21, 875–896.
29. D. P. Partlow, S. R. Gurkovich, K. C. Radford and L. J. Denes, J. Appl. Phys., 1991, 70, 443.
30. S. Lu, L. Hou and F. Gan, Adv. Mater., 1997, 9, 244246.
31. B. G. Chae, H. T. Kim, S. J. Yun, B. J. Kim, Y. W. Lee, D. H. Youn and K. Y. Kang, Electrochem. Solid-State Lett., 2005, 9, C12.
32. C. H. Griffiths and H. K. Eastwood, J. Appl. Phys., 1974, 45, 2201–2206.
33. C. C. Y. Kwan, C. H. Griffiths and H. K. Eastwood, Appl. Phys. Lett., 1972, 20, 93–95.
34. F. Beteille, L. Mazerolles and L. Livage, Mater. Res. Bull., 1999, 34, 2177–2184.
35. D. Brassard, S. Fourmaux, M. Jean-Jacques, J. C. Kieffer and M. A. Khakani, Appl. Phys. Lett., 2005, 87, 051910.
36. D. Fu, K. Liu, T. Tao, K. Lo, C. Cheng, B. Liu, R. Zang, H. A. Bechtel and J. Wu, J. Appl. Phys., 2013, 113, 043707.
37. D. H. Kim and H. S. Kwok, Appl. Phys. Lett., 1994, 65, 3188–3190.
38. Y. X. Guo, Y. F. Liu, C. W. Zou, Z. M. Qi, Y. Y. Wang, Y. Q. Xu, X. L. Wang, F. Zhang and R. Zhou, Appl. Phys. A, 2014, 115, 1245–1250.
39. R. McGee, A. Goswami, B. Khorshidie, K. McGuire, K. Schofield and T. Thundant, Acta Mater., 2017, 137, 12–21.
40. R. L. Remke, R. M. Walser and R. W. Bene, Thin Solid Films, 1979, 61, 73–82.
41. C. B. Greenberg, Thin Solid Films, 1983, 110, 73–82.
42. Y. Takahashi, M. Kanamori, H. Hashimoto and Y. Moritani, J. Mater. Sci., 1989, 24, 192–198.
43. T. Maruyama and Y. Ikuta, J. Mater. Sci., 1993, 28, 5073–5078.
44. T. D. Manning, I. P. Parkin, M. E. Pemble, D. Shell and D. Vernardou, Chem. Mater., 2004, 16, 744–749.
45. J. Nag and R. F. Haglund, J. Phys.: Condens. Matter, 2008, 20, 264016.
46. D. H. Kim and H. S. Kwok, Appl. Phys. Lett., 1994, 65, 3188–3190.
47. Y. Muraoka and Z. Hiroi, Appl. Phys. Lett., 2002, 80, 583–585.
48. K. Okimura and N. Kubo, Jpn. J. Appl. Phys., 2005, 44, 1150–1153.
49. Z. Yang, C. Ko and S. Ramanathan, J. Appl. Phys., 2010, 108, 073708.
50. Y. Zhou and S. Ramanathan, J. Appl. Phys., 2012, 112, 074114.
51. H. Kim, Y. Kim, K. S. Kim, H. Y. Jeong, A.-R. Jang, S. H. Han, D. H. Yoon, K. S. Sulh, H. S. Shin, T. Y. Kim and W. S. Yang, ACS Nano, 2013, 7, 5769–5776.
52. S. Genchi, M. Yamamoto, K. Shigematsu, S. Aritomi, R. Nouchi, T. Kanki, K. Watanabe, T. Tabiguchi, Y. Murakami and H. Tanaka, Sci. Rep., 2019, 9, 2857.
53. C. Wan, Z. Zhang, D. Woolf, C. M. Hessel, J. Rensberg, J. M. Hensley, Y. Xiao, A. Shahsafi, J. Salman, S. Richter, Y. Sun, M. M. Qazilbash, R. Schmidt-Grund, C. Ronning, S. Ramanathan and M. A. Kats, Ann. Phys., 2019, 531, 1900188.
54. P. Yeh, Optical Waves in Layered Media, Wiley, 2005.
55. H. Kocer, S. Butun, Z. Li and K. Aydin, Sci. Rep., 2015, 5, 8157.
56. Lumerical page, https://www.lumerical.com/products/fdtd/.
57. M. A. Kats, D. Sharma, J. Lin, P. Genevet, R. Blanchard, Z. Yang, M. M. Qazilbash, D. N. Basov, S. Ramanathan and F. Capasso, Appl. Phys. Lett., 2012, 101, 221101.
58. H. Looyenga, Dielectric constants of mixtures, Physica, 1965, 31, 401–406.
59. E. D. Palik, Handbook of Optical Constants of Solids, Elsevier, 1998.
60. H. Hajian, A. Ghobadi, B. Butun and E. Ozbay, J. Opt. Soc. Am. B, 2019, 36, F131–F143.
61. A. Ghobadi, H. Hajian, B. Butun and E. Ozbay, ACS Photonics, 2018, 5, 4203–4221.

---

Footnote

† Electronic supplementary information (ESI) available: The measured and simulated spectral reflectivity maps of “sample A” during heating and cooling, maps of extracted infrared spectral optical parameters of VO₂ in “sample A” during heating and cooling, additional hysteretic behaviors, ellipsometer spectral data for SiO₂, numerical simulations to enlighten the physics behind the operating mechanism of the tunable device (SuppInfo1). Moving one and two-dimensional spatial representation of electric fields at T = 25 °C and T = 90 °C calculated for “sample C” at a wavelength of 4 μm (SuppInfo2). See DOI: 10.1039/d0ra05890d

---