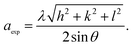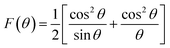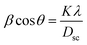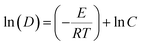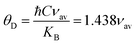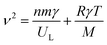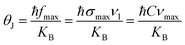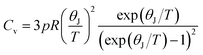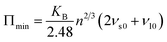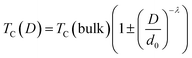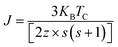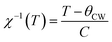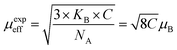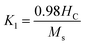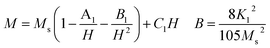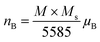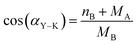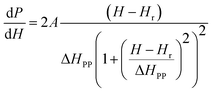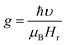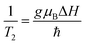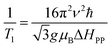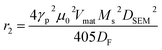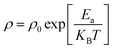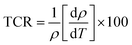Magnetic and spectroscopic properties of Ni–Zn–Al ferrite spinel: from the nanoscale to microscale

Abstract

This article presents the annealing effect on the structural, elastic, thermodynamic, optical, magnetic, and electric properties of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ (NZFAO) nanoparticles (NPs). The samples were successfully synthesized by the sol–gel method followed by annealing of the as-synthesized at 600, 800, 900, 1050, and 1200 °C. This approach yielded the formation of a highly crystalline structure with crystallite size ranging from 17 nm to 40 nm. X-ray diffraction (XRD), scanning electron microscopy (SEM) techniques, as well as energy disperse spectroscopy (EDS), Fourier transform infrared (FTIR) and Raman spectroscopy, were used in order to determine the structural and morphological properties of the prepared samples. Rietveld XRD refinement reveals that Ni–Zn–Al ferrite nanoparticles crystallize in inverse cubic (Fd3̄m) spinel structure. Using FTIR spectra, the elastic and thermodynamic properties were estimated. It was observed that the particle size had a pronounced effect on elastic and thermodynamic properties. Magnetic measurements were performed up to 700 K. The prepared ferrite samples present the highest Curie temperature, which decreases with increasing particle size and which is consistent with finite-size scaling. The thickness of the surface shell of about 1 nm was estimated from size-dependent magnetization measurements using the core–shell model. Besides, spin resonance, magnetostriction, temperature coefficient of resistance (TCR), and electrical resistivity properties have been scientifically studied and appear to be different according to their size. The optical properties of synthesized NZFAO nanoparticles were investigated, and the differences caused by the particle sizes are discussed on the basis of the phonon confinement effect. This effect was also inspected by the Raman analysis. Tuning of the physical properties suggests that the Ni–Zn–Al ferrite samples may be promising for multifunctional diverse applications.

---

Introduction

Over the past several years, ferrites spinels AFe₂O₄, where A is a divalent transition metal (Ni, Zn, Fe, Cr, Mn, Co, …) have attracted great interest due to their good biocompatibility, low toxicity and their magnetism.^1,2 These materials are currently considered among the most successful magnetic nanoparticles (MNPs) for technological and medical applications e.g., magnetocaloric refrigerators, magnetic memory, solar water oxidation, electrochemical supercapacitor applications, biological applications, lithium-ion batteries, contrast enhancement in magnetic resonance imaging (MRI) and magnetic fluid hyperthermia.^3–10 Therefore, an understanding of the structural and magnetic properties of spinels is of great importance from both a fundamental and an applied point of view. These properties can be controlled by synthesis methods, annealing temperature and/or by doping suitable elements into the A-site or B-site to change the structural parameters and/or the distribution cation.

The ferrite spinel has a face-centered cubic (fcc) structure, which consists of a cubic close-packed oxygen lattice. The unit cell of a spinel ferrite consists of 16 trivalent iron ions, 8 divalent metal ions (M) and 32 oxygen ones. The spinel structure contains two interstitial sites, occupied by metal cations with octahedral (B) and tetrahedral (A) oxygen coordination. In general, the cationic distribution between the two sites is quantified by the inversion degree (γ), which is defined as the fraction of divalent ions in the octahedral sites. In the normal spinel configuration, the Fe³⁺ ions occupy the octahedral sites, while the tetrahedral sites contain the M²⁺, giving the empirical formula (M²⁺)^A[Fe³⁺]^BO₄. On the other hand, in inverse spinels, half of the Fe³⁺ occupy the tetrahedral sites, while the octahedral sites contain the M²⁺ and the other half of Fe³⁺ ions, yielding the empirical formula (Fe³⁺)^A[M²⁺Fe³⁺]^BO₄. The structure can also be mixed spinels. However, superexchange interactions between magnetic atoms located in the same kind of interstitial sites (J_A–A and J_B–B) lead to two ferromagnetically ordered sub-lattices. On the other hand, the dominant antiferromagnetic interactions between magnetic ions in the A and B sites (J_A–B) induce a non-compensated antiferromagnetic order between the two sub-lattices inducing (ferrimagnetism). In the case of nanoparticles, the larger surface area creates surface relaxation, surface bond bending, surface effect and consequently spins canting which modifies the contribution of each interaction. The relation between structures and physical properties for nano ferrites requires a careful consideration. Therefore, various methods, including, forced hydrolysis in polyol, ball milling, coprecipitation, sol–gel auto-combustion and hydrothermal/solvothermal method etc.,^3,11–14 have extensively been developed to synthesize nano-spinel ferrite with different sizes and shapes. Ball milling method is favorable to produce a highly crystalline nanostructure, but always leads to agglomeration in high reaction temperature and long time. By contrast, sol–gel method is preferred due to the better control over the shape and size for particle synthesis in low temperature and low time of process with remarkable purity and high amount. Also, this method offers an advantage due to its high quality production, its low cost.¹⁵

Ni–Zn ferrite is a member of the class of the spinel ferrites which is widely touted for its applications in magnetic, magnetooptical and magnetodielectric devices. Under normal conditions, spinel Ni–Zn ferrites is a typical ferrimagnetic material possessing mixed spinel structure (Fe_i³⁺M_1−i²⁺)[M_i²⁺Fe_2−i³⁺]O₄,^16,17 where i is the inversion degree, () and [] represent tetrahedral and octahedral positions respectively, which belongs to Fd3̄m space group. The cation arrangement can vary between two extreme cases. One of them is the normal spinel (i = 0), where all the divalent elements occupy tetrahedral A sites and all the trivalent elements occupy octahedral B sites. The other one is the inverse spinel (i = 1), where all the divalent elements occupy octahedral B sites and all trivalent elements are equally distributed between tetrahedral A sites and octahedral B sites. Spinels with the cation distribution intermediate between normal and inverse (i.e., partially inverse spinels; 0 < i < 1) are also very frequent.¹⁸

Furthermore, Ni–Zn ferrites are characterized by high surface area, chemical stability, high saturation magnetization, high Curie temperature, low coercivity (soft magnetic), high permeability, high dielectric constant, low losses, semiconductor dielectric transition and they can find wide application in the high frequency region of electronics devices.¹⁹ On substitution of Zn²⁺ in Ni ferrite the Fe³⁺ ions migrate from (A) to [B] site and consequently the Fe_A–O–Fe_B interaction becomes feeble. Several studies have reported the dependence of magnetic properties of Ni–Zn ferrites on their microstructure, sintering temperature and preparation method, these properties can be changed and tuned by aluminum doping.^20,21 The introduction of Al³⁺ ions leads to significant variations of cation distribution over the A and B sites depending on the method of synthesis and Al concentration, additional non-magnetic ions Al³⁺ on octahedral B site reduces saturation magnetization by increasing the resistivity.²¹

The electrical properties displayed macroscopically by the ferrite are a direct consequence of their cationic arrangement since both nickel and iron possess different electronic characters depending on the interstice they occupy inside the lattice. For nanometric Ni–Zn ferrites, it is possible to obtain good electric properties and high performance at relatively low sintering temperature. Recently, Li et al.²² examined the dielectric properties and direct-current resistivity of Al-substituted Ni–Zn–Co ferrite nanoparticles. Also, the magnetic properties of Ni–Zn ferrite nanocrystals depend on different sizes, shapes, and synthesis methods. Beji et al.¹¹ prepared a series of polyol-made Ni–Zn ferrite nanoparticles with varying annealing temperatures to optimize the structural and magnetic properties and found that heating at different temperatures ranged from 400 to 800 °C provides changes of the magnetic properties of these particles. In our earlier work,²³ we investigated the dielectric properties of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ annealed at 600, 900, and 1200 °C. It was found that the dielectric properties of the system improved on increasing the temperature. Moreover, K. Praveena et al.²⁴ discussed the effect of annealing temperature in dynamic magnetic properties of Ni_0.4Zn_0.2Mn_0.4Fe₂O₄ nanoparticles. However, their discussion was limited to the resonance field and g-value which are major imprints of the material characteristics, but other key spin resonance parameters that can provide an even more detailed understanding of the properties of materials required to enhance the performance of the device must be reported. To the best of our knowledge, there is no report performed to understand the effect of particle size on the relaxation mechanism, transverse relaxivity, magnetostrictive, thermodynamic, and elastic properties of Ni–Zn–Al ferrite in detail. A better understanding of these physical properties of Ni–Zn–Al ferrite is, therefore, highly beneficial to tune the properties for diverse technological applications.

Herein, the main aim of this framework is to synthesize and study nanoscale and bulk materials based on nickel–zinc ferrites. We are interested in determining the effects of particle size changes in the nano to micro-regime by annealing temperature at 600, 800, 900, 1050, and 1200 °C and characterized with different aspects such as structural, morphological, magnetic, elastic, thermodynamic, magnetostriction, optical and electric properties. A detailed investigation of the dynamic magnetic properties was carried out by an electron spin resonance (ESR) study and the spin resonance parameters were also estimated. Interestingly, the synthesized nanoparticles at low temperature possess excellent transverse relaxivity r₂ and can be used as T₂ contrast efficacy in imaging application. Hence, these synthesized materials will not only seem to be an ideal material for examining the size effect on the physical properties of nanomaterial but also have broad applications in the future.

Experimental section

Synthesis

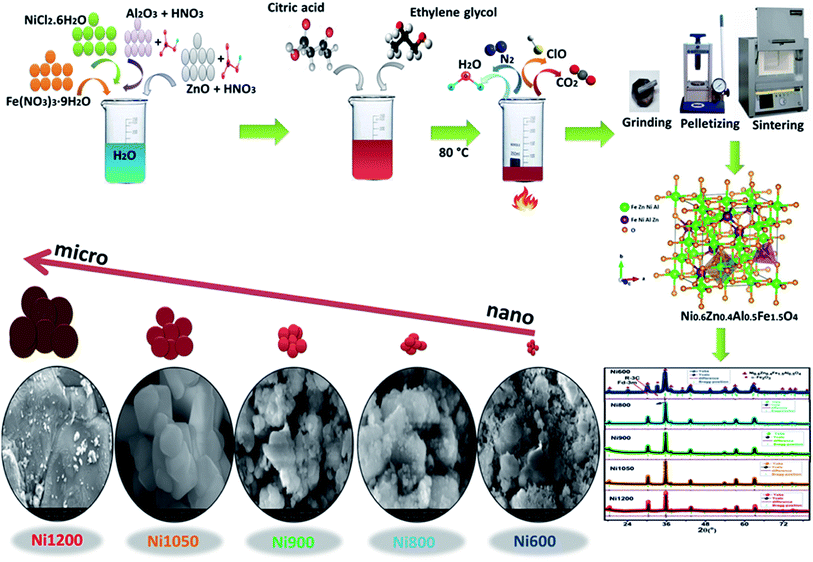
All the chemical reactants in this work were purchased from Sigma-Aldrich and used without further purification. Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ nanoparticles were successfully prepared through the sol–gel method. The process was described in detail elsewhere.²³ In a typical preparation, analytical purity grade Fe(NO₃)₃·9H₂O and NiCl₂·6H₂O were dissolved in distilled water. The oxides powders ZnO and Al₂O₃ of purity (99.99%) were dissolved in nitric acid. The obtained solution was added to the previous one. We mixed this solution with citric acid (C₆H₈O₇) with molar ratio 1 : 1.5 of metal cation (Ni + Fe + Zn + Al) to citric acid flowed by the addition of ethylene glycol (C₂H₆O₂). The resulting solutions were heated to 80 °C with magnetic stirring to remove the excess water and to form a gel. To decompose the organic matter, the as prepared powder was annealed at 500 °C for 6 hours in an electrical muffle furnace and cooled slowly to room temperature. Finally, the obtained powder was then separated into five sets (Ni600), (Ni800), (Ni900), (Ni1050) and (Ni1200) were pelletized and annealed at 600, 800, 900, 1050 °C for 6 h and 1200 °C for 24 h, respectively. Chemical reaction of the prepared sample is shown in Fig. 1.

Fig. 1 Chemical reaction of Ni_0.6Zn_0.4Al_0.5Fe_1.5O₄ synthesized by sol–gel method.

Characterizations and measurements

The structural characterization was carried out by X-ray diffraction at room temperature. The ferrite nanoparticles were characterized using a powder X-ray diffraction (XRD) with a Bruker D8 diffractometer with Cu Kα radiation (λ = 1.5406 Å) and a step size of 0.015° width from 15° to 80°. Morphological characterization was carried out using Merlin scanning electron microscopy (SEM) equipped with an energy-dispersive X-ray spectrometer (EDXS). The particle size was estimated by image processing of SEM's pictures using ImageJ software. Thermogravimetric analysis (TGA) and the differential thermal analysis (DTA) were carried out using the Setaram Instrument. The sample was heated up to 1000 °C with a heating rate 10 °C min⁻¹ in argon atmosphere with nitrogen flow of 40 ml min⁻¹. The Raman spectra were recorded using a SENTERRA spectrometer from Bruker Company with laser excitation of 532 nm at room temperature. Room temperature Fourier transform infrared (FTIR) spectra were obtained using Thermo Scientific Nicolet 6700 FTIR Spectrometer in the region 400–4000 cm⁻¹ with diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) technique. Absorption spectra were registered on a UV-3600 Spectrophotometer (SHIMADZU, Japan) for the UV/visible/IR range. The magnetostriction measurements were made on the NZFAO pellets using the small angle rotation magnetization method. The magnetic isotherms M(H) were recorded at room temperature under a magnetic field up to 4 T using a SQUID magnetometer. Measurements of the intrinsic magnetic temperature (T_C) were carried out using differential sample magnetometer MANICS in a field up to 1 kOe. Additionally, the electron spin resonance (ESR) measurements were carried out on a Bruker ESP-300E spectrometer operating in the X band 9.3 GHz and with a field modulation of 2 GHz. A thin silver film is deposited through a circular mask of 8 mm of diameter on both sides of the pellet by thermal evaporation. A plane capacitor configuration is obtained and permits the investigation of electrical properties of the synthesized material. Measurements are conducted with an Agilent 4294A analyzer under vacuum with signal amplitude of 20 mV.

Result and discussion

Thermal analysis

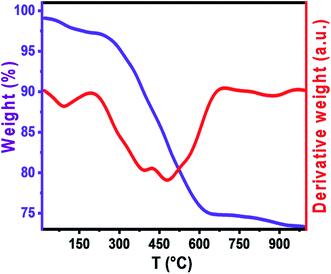
Thermal analysis is performed to understand the decomposition behavior of the Ni–Zn ferrite precursors and the formation of metal oxides, Fig. 2 shows the TGA and DTA curves of the as prepared sample which were performed up to temperature of 1000 °C at the heating rate 10 °C min⁻¹ in argon gas to observe different changes in the form of endothermic and exothermic peaks which show the phase transition during the heat treatment. Moreover total weight loss is 24% which is the sum of two parts. The first broad weight loss of ∼2% in the temperature range below 200 °C is assigned to the dehydration of residual water. The second weight loss of ∼22%, between 200 °C and 630 °C on TGA curve, which may be due to the autocatalytic oxidation–reduction reaction between the nitrate and citrate acid. For temperature higher than 630 °C, the sample attains the stability in terms of weight and the weight loss at about this temperature possibly corresponds to the formation of metal oxide phase of ferrite Ni_0.6Zn_0.4Al_0.5Fe_1.5O₄. We can conclude from TGA and DTA that the organic compounds were eliminated above 630 °C. Thus, the sample was further annealed at temperature from 600 °C.

Fig. 2 TGA and DTA curves corresponding to solid sample obtained from NZAFO gel.

Structural analysis

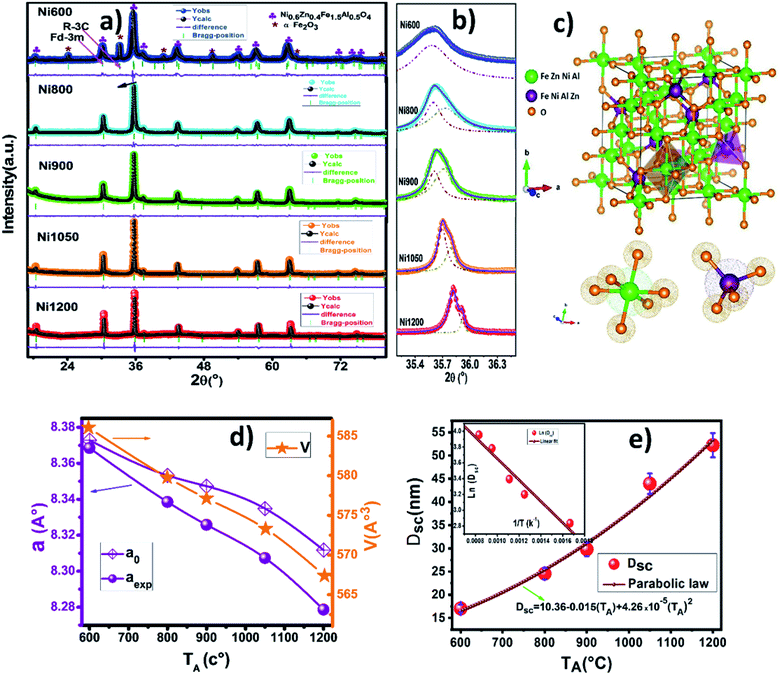
Fig. 3a depicts the Rietveld refined X-ray powder diffraction (XRD) patterns for Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ samples annealed at 600, 800, 900, 1050 and 1200 °C using the FULLPROF program.²⁵ The reflections from the atomic planes (111), (220), (311), (400), (422), (511), (440), (620), (533) and (622) are identified and confirm the formation of single phase cubic spinel structure with Fd3̄m space group. For the sample annealed at 600 °C (Ni600), we notice the appearance of some peaks due to rhombohedral symmetry R3̄c as a second phase (Fe₂O₃) designated by (*) which disappeared at higher annealing temperature. The hematite phase has been observed by several authors, up to the calcination temperature of 900 °C.²⁶ No diffraction peaks of other structures were detected in the other samples, which indicated that high purity crystalline. The Rietveld refinement parameters are listed in Table S1 (ESI).† We have observed a low value of goodness of fit (χ²) which suggests that the refining of the samples is effective and that the obtained samples are of good quality. From Fig. 3b, it is observed that the width at half maximum of (311) peak decreases with increase in annealing temperature. Diffraction peaks become narrower and sharper with increasing temperature, thus demonstrating that the average size of the crystallites increases accordingly. The crystal structure of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ along with the different Wyckoff sites occupied by the Ni, Zn, Al, Fe and O atoms are shown in Fig. 3c.

Fig. 3 (a) Rietveld refined X-ray diffraction patterns of Ni_0.6Zn_0.4Al_0.5Fe_1.5O₄ annealed at 600, 800, 900, 1050 and 1200 °C. (b) Zoomed views in the 2θ interval of 35.1–36.3 (°). (c) Unit cell of the sample showing the tetrahedral (A) and octahedral [B] sites. (d) Lattice parameters and volume of the ferrites compounds against annealing temperature. (e) D_sc versus the annealing temperature T_A, where the solid line shows the fit to the parabolic law and the fitted values are shown.

The lattice constant (a_exp) of Ni–Zn nanoparticles was determined from X-ray data analysis using the relation:¹²

where λ is X-ray wavelength, θ is the diffraction angle and h, k, and l are Muller indices.

The volume of the unit cell for a cubic system has been calculated from the following equation: V = a_exp³. All the obtained lattice parameters and volume of the ferrite's compounds are plotted against annealing temperature in Fig. 3d. A decrease in the lattice parameter with increasing annealing temperature could be attributed to a decrease in particle surface stress and the higher crystal structure of larger particles. In addition, many metal oxides exhibit lattice parameter with a reduction in particle size which may be due to cation/anion vacancies, finite size effect, lattice stress etc. A similar variation of lattice parameter has been reported previously for Ni–Zn ferrite nanoparticles.^11,21 The true values of the lattice parameter “a₀” also are determined using the extrapolation function F(θ) by plotting the calculated “a_exp” values of each diffraction peak versus the Nelson–Riley (N–R) function for each reflection of the studied Ni–Zn–Al ferrites:¹²

The values of the lattice constant “a_exp” are depicted in the Fig. S1 (ESI)† as a function of F(θ) for all samples. As seen from the Fig. 3d, the true values of the lattice parameter are observed to be slightly higher than the experimental values. It is also evident that both “a₀” and “a_exp” and volume decreased as the size of particles increased. Lattice parameters (a₀, a_exp and a_R measured from Rietveld refinement), density, porosity, crystallite size and surface area of all annealed samples are given in Table S1.† Density plays an important role in controlling the properties of polycrystalline ferrites. The X-ray density deduced from XRD data (ρ_X-ray) increases when increases annealing temperature rises, from 5.04 g cm⁻³ for Ni600 to 5.15 g cm⁻³ for Ni1200. Therefore, it has been noticed that the annealing temperature influences the densification process. In other words, during the sintering process, a force that is generated by the thermal energy drives the grains to grow over pores and as a result reduces the pores volume and their grain boundaries. The values of bulk density (ρ_th) also increase whereas the porosity (P) decreases with increasing the particles size, revealing that annealing temperature enhances the disorder of spinel ferrite system. The sol–gel process is known for synthesizing materials with high surface area (S). As it can be seen from Table S1,† the specific surface area varied in the range 69.8–22.2 (m² g⁻¹). Therefore, a high surface area of ferrite is needed for sensing and supercapacitor application.¹²

The crystallite size was calculated from the line broadening of the most intense (311) peak using the classical Scherer formula:^12,21

where D_sc is crystalline size, K is shape factor (0.9), λ is wavelength of Cu Kα radiation (1.5406 Å), θ the diffraction Bragg angle of the most intense peak (311) and β is half width of (311) peak in radian. It is clear that from Fig. 3e that, the crystallite size increases as the annealing temperature increases from 600 °C to 1200 °C. Particularly, the crystallite size increases significantly when the sample is annealed above 900 °C. The growth of the crystallites can be attributed to coalescence by solid-state diffusion and it is in agreement with the increase in density. The corresponding crystallite size D_sc versus the annealing temperatures is fitted in Fig. 3f. The estimated values of D_sc versus the annealing temperature T_A are plotted, revealing an increase with the increase in the particle size. The red solid curve indicates the fit of the experimental data by a theoretical curve using parabolic law. The obtained fit parameters are listed in the inset of Fig. 2f. According to Coble's theory,²⁷ the logarithm variation of crystallite size for NZAFO NPs with annealing temperature is shown in the inset of Fig. 3f. The activation energy of grain growth can also be calculated by the modified Arrhenius equation:
where E is the activation energy, C is the specific reaction rate constant, T is the absolute temperature and R is the ideal gas constant. The crystallite growth activation energy of nickel ferrite synthesized by high-energy ball milling with Fe₂O₃ and NiO was found to be 64.4 kJ mol⁻¹ as reported by Hajalilou et al.²⁸ By comparison, this value is higher than the present value of 11.3 kJ mol⁻¹. This means that the growth of Ni–Zn–Al ferrite crystallite prepared by the sol–gel method required less energy to overcome the kinetic barrier. Thus, it is one of the reasons for obtaining phase Ni–Zn–Al spinel ferrite at lower temperature.

The lattice strain (ε) was calculated from the Williamson–Hall method (figure not shown here). It is evident from Table S1† that strain is constantly decreasing with the increase in the crystallite size. This is evident because of the ratio of the number of atoms at the surface to the one of atoms inside the volume decreases when the crystallite size increases, reducing the number of broken bonds for surface atoms, hence reducing the strain.

The physical properties of ferrites are sensitive to the cation's nature, the valance state and their distribution on tetrahedral A and octahedral B sites of the spinel structure. Thus, understanding of the cation distribution is essential in understanding the intricate structural and physical property relationship. The distribution of cations in the various spinel ferrite systems has been estimated from Mossbauer, XPS, X-ray diffraction, and Raman measurements.^29–31 Bestha et al.³² reported that the intensities of (220), (422), and (400) planes are sensitive to cations on tetrahedral (A-) and octahedral (B-) site. In our studies, the distribution of cations was estimated from XRD data by using the Bertaut method.^32,33 From the best-matched intensity ratio, the cation distribution was estimated and the values are presented in Table S1.†

On the basis of estimated cation distribution, the value of ionic radius per molecule at the tetrahedral (r_A) and octahedral (r_B), theoretical lattice constant (a_th), oxygen positional parameter (u), tetrahedral bond lengths (d_AL), octahedral bond lengths (d_BL), tetrahedral edge length (d_AE), shared (d_BE), unshared octahedral edge lengths (d_BEU), jump length of the tetrahedral (L_A) and octahedral (L_B) for various samples has been determined using the relation (S5–S13) (ESI).† The values of all estimated structural parameters are shown in Table S1.† As shown in Table S1,† the variations of experimental (a_exp) and theoretical lattice parameter (a_th) with increasing annealing temperature are the same. Moreover, the theoretical lattice constant values are in close agreement with the experimentally derived values from XRD data. This result validates the estimated cation distribution from the XRD data. The oxygen positional parameter (u) is slightly greater than ideal value of 0.375. This has been attributed to the adjustment of the structure to accommodate differences in the relative effective radii of cations in the spinel structure.

L_A and L_B were observed to show a decreasing trend with an increase in the size of crystallites. The decreased behavior so observed can be correlated to the decrease in lattice parameter and to the decrease in distance between magnetic ions. It is also observed that L_A > L_B which indicates that the electron hopping between ions at A and B sites is less probable than that between B and B sites.

The strength of magnetic exchange interaction has direct dependence on bond angles and inverse dependence on interionic distances.³⁴ Fig. S3 (ESI)† shows the interionic distances and bond angles between ions of spinel ferrites. The bond lengths and bond angles between the cations are calculated by the relations (S14–S27) (ESI) and are listed in Table S2.†

Morphological analysis

To obtain an accurate estimation of the microstructure and morphology of the nano-crystals, scanning electron microscopy has been performed. The SEM images of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ nanoparticles are shown in Fig. 4a–j, which demonstrates that the samples (Ni600, Ni800 and Ni900) are in nanoregime. At higher annealing temperature (>900 °C), a broad size of particle is observed for Ni1050 and Ni1200 samples. All samples showed a tendency towards agglomeration can be due to electrostatic effects as well as an artifact of the drying of aqueous suspensions and to magnetic interaction arising among of nanoparticles, revealing the formation of spherical and uniformly distributed nanoparticles. A similar behavior of nanoparticle agglomeration has been reported of Co₃O₄ nanoparticles.³⁵ The observed asymmetric distribution can be described using a Lorentz distribution function as shown in Fig. 4k–o. Based on SEM images, the average grain size was found to be around 13, 20, 30, and 180 nm for Ni600, Ni800, Ni900 and Ni1050 samples respectively, and around 4 μm of the bulk sample (Ni1200). In fact, the annealing temperature increases the size of the grains. This increase is due to the coalescence of crystallites at increasing temperature. As shown, a clear difference between Ni600, Ni1050 and the bulk sample. The micrographs manifest grain boundaries and clear grains with non-uniform grain size distribution of Ni1200. The grains are almost homogeneously distributed throughout the sample surface. This observation is consistent with the results observed by XRD analysis, discussed earlier. Comparing the grain size obtained by SEM with crystallite size obtained from XRD analysis, it can be concluded that each grain of sample annealed at 600, 800 and 900 °C almost of single crystallite nature while the grains of sample annealed at 1050 and 1200 °C consist of agglomeration of many crystallites. The elemental analysis of the Fe600, Fe900 and Fe1200 samples, measured using EDX at room temperature, are shown in Fig. S3 (ESI).† The spectrum confirms the presence of all chemical elements Fe, Al, Zn, Ni and O in the synthesized Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ samples, which confirms that there was no loss of any integrated elements and no contamination during the process of annealing. The result of EDX predicted the required proportion of the constituents as well as the chemical purity of the samples, denoting a homogeneous chemical composition.

Fig. 4 SEM images of Ni_0.6Zn_0.4Al_0.5Fe_1.5O₄ ferrite samples; (a and f) Ni600, (b and g) Ni800, (c and h) Ni900, (d and i) Ni1050, (e and j) Ni1200. The representative histograms of size distribution for of Ni_0.6Zn_0.4Al_0.5Fe_1.5O₄ and their respective average size calculation by Lorentz fitting of size histograms, (k) Ni600, size is about 13.6 nm, (l) Ni800, size is about 22.2 nm, (m) Ni900, size is about 37.6 nm, (n) Ni1050, size is about 180 nm, (o) Ni1200, size is about 4 μm.

Raman analysis

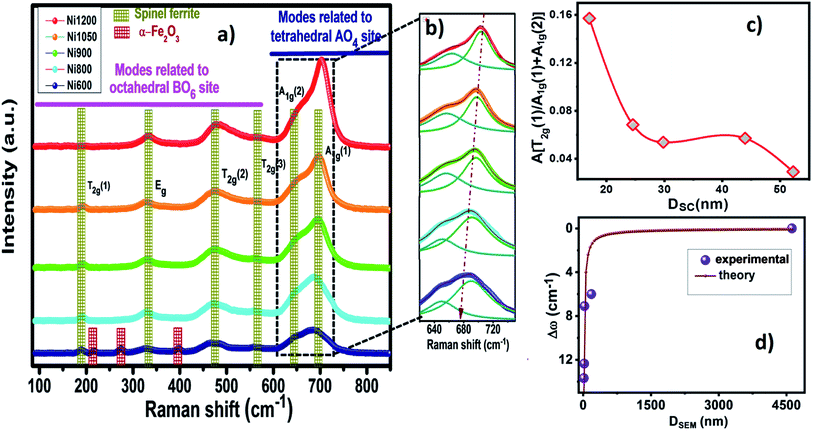
Further structural and complementary details can be obtained by the analysis of the Raman spectra. Confocal Raman spectroscopy has been widely used as an effective tool to investigate the cation disorder, the lattice dynamics and structure transition in ferrites due of their sensitivity and their high spatial resolution to explore atomic vibrations. In order to verify the chemical impurity and to confirm the formation of our simples, Raman spectra at room temperature in the region of 120 cm⁻¹ to 850 cm⁻¹ by using 540 nm laser excitation of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ nanoparticles and bulk synthesized by annealing at 600, 800, 900, 1050 and 1200 °C are presented in Fig. 5a. The factor group analysis predicts the following modes in spinel:³⁶

ζ = A_1g(R) + E_g(R) + T_1g + 3T_2g + 2A_2u + 2E_u + 4T_1u(IR) + 2T_2u

where, (IR) and (R) indicate infrared active vibrational and Raman modes, respectively. For spinel ferrite, it is well known that the group theory predicts that five Raman active modes (A_1g + E_g + 3T_2g) are observed at ambient conditions and they are associated to the motion of O ions and both the A-site and B-site ions and four infrared active modes (4T_1u) for the Fd3̄m space group.¹⁴ The A_1g Raman mode is associated to the symmetric stretching of the oxygen atom with respect to metal ion in tetrahedral sites. The E_g Raman mode corresponds to the symmetric bending of the oxygen atom with respect to the metal ion at the octahedral site and the T_2g(3) and T_2g(2) Raman modes are due to the symmetric and asymmetric bending of oxygen atom in M–O band at octahedral site. Finally, the T_2g(1) phonon corresponds to the translation movement of the whole MO₄ tetrahedral units.³⁷ So accordingly, all the Raman active bands of NZFAO samples are assigned to the theoretical vibrational mode of Fd3̄m space group and illustrated in Table S3 (ESI).† The observed Raman modes are in good agreement with the literature reports.³⁸ In the Ni600 nanoparticle sample, the peaks centered on 216, 274 and 397 cm⁻¹ could be attributed to A_1g, E_g(1) and E_g(2) vibrational modes of hematite α-Fe₂O₃,³⁹ respectively, which is consistent with the results of the XRD. No additional peak corresponding to any other iron oxide phase is present for the other compounds, thus confirming the monophasic composition throughout. In order to determine lattice effect, the natural frequency, and the positions of the peak and its full width at half maximum (FWHM), Lorentzian line shape was used to fit the Raman spectra (Fig. S4, (ESI)†). In spinel ferrites, the modes above 600 cm⁻¹ are belonged to the vibrations of the oxygen atoms in tetrahedral sites AO₄ groups, whereas the modes below this frequency are related to the motion of the oxygen atoms in octahedral sublattice (O-modes).⁴⁰ Additional shoulder mode are probably related to a breakdown of the momentum conservation rule since the particle diameter are significantly smaller than the wavelength of the exciting radiation.⁴¹ Focusing on the most intense A_1g mode, a clear increase in intensity and blue shift along with the line broadening behavior can be seen with an increase of annealing temperature. The ratio of these signals is directly correlated to the degree of inversion of the spinel.⁴² As in spinel ferrite, the distribution of trivalent and divalent cations can change due to migration of metal ions from octahedral (B) to tetrahedral (A) sites and vice versa. The A_1g splitting suggests the cation migration within both positions and the change in the area and intensity of the band related to the octahedral sites. In other words, the shift in the A_1g modes due to a progressive change in inversion degree of the spinel lattice (see Fig. 5b).⁴² The obtained values of area ratio between the bands associated with the octahedral and tetrahedral sites are depicted in Fig. 5c. It shows that area ratio decreases with the increase in the size of crystallites indicating the decrease of the degree of inversion with increase crystallites size. These changes could be due to cation redistribution and a high degree of cation disorder induced by a crystallite size effect.⁴³

Fig. 5 (a) The Raman spectra of Ni_0.6Zn_0.4Al_0.5Fe_1.5O₄ NPs at different annealing temperature with assigned symmetry types of the Raman active bands, recorded in the region of 100–850 cm⁻¹ at 300 K. (b) An enlarged view of the A_1g modes. (c) The crystallite size D_sc dependence of the area ratio between the bands associated with the octahedral and tetrahedral sites. (d) The relative Raman shifts Δω of the A_1g mode vs. particle size D_SEM, line is the fitted result obtained by the confinement model.

Moreover, this blue shift can be understood quantitatively by estimating the effective force constant of the vibrating cation. Since the vibrational frequency of a species is proportional to its force constant (F), the following equations were used to calculate the force constants of the ions pertaining to tetrahedral (F_T) and octahedral (F_O) positions:³²

F_T = 7.62 × M_T × ν_T × 10⁻³

F_O = 10.62 × M_O × ν_O × 10⁻³

where, M_T and M_O represent the molecular weights of ions in tetrahedral and octahedral positions. The ν_T and ν_O represents the frequencies correspond to A_1g(1) and E_g peaks, respectively. The estimated values of F_T and F_O are given in Table S3.†

The obtained F_O values were found to rise and the F_T values to decrease with an increase in crystallite size. The variation of F_T and F_O values with particle size can be understood as follows. In general, the force constant is inversely related to the bond length (viz., Fe–O, Ni–O, Zn–O and Al–O). Indeed, these bond lengths in ferrites will have an impact on the lattice parameter of the unit cell. Now, the lattice parameter was found to reduce with an increase crystallite size, and hence the Raman peak shifts towards the higher wavenumber side with increasing annealing temperature.

However, we can well understand the overall down shift of Raman bands in terms of size effect, because the size reduction leads to the increase of the micro-deformation and/or the dominance of phonon confinement.⁴⁴ The small size of the crystallites hampers the propagation of phonons and thus induces a folding of the Brillouin zone making all Raman phonons active, leading to a broadening of the Raman spectrum band. The Raman shift and broadening of A_1g peak can be explained by the bond-polarizability model described by Zi et al.⁴⁵ Raman shift due to the confinement can be described by this model using the following relation:

Δω = ω(D) − ω₀ = A(a/D)^δ

where ω(D) is the Raman shift with grain size D. ω₀ is the frequency at the Brillouin zone center, a is the lattice constant of the crystal and the parameters A and δ describes the vibrational confinement in nano-crystallites. Fig. 5d shows the variation of the Raman shift with grain size and the best fit is obtained for A = 32 ± 6 cm⁻¹ with δ = 1.4 reflecting the phonon confinement in the Ni–Zn–Al ferrite NPs due to the finite size in a nanoparticle. Recently, Chandramohan et al. fitted results obtained for CoFe₂O₄ NPs with average particle size in 6 to 500 nm range to the same expression by considering the bond polarization model.⁴⁶ Empirical Raman-versus-size scaling exponent δ is equal to 1.5 for three-dimensional covalent network semiconductors, such as Si and GaAs, to about 1.5 and 1.0 for Si spheres and Si columns.⁴⁵ Considering the fact that the ferrite crystal spans a three-dimensional network and the nanocrystals are spheres, the δ should be 1.5. However, δ is equal to 1.4. The difference may stem from defects, such as oxygen vacancies in Ni–Zn–Al ferrite nanoparticles. Nevertheless, Zn vacancies are formed in the crystal lattice at high annealing temperature and which in turn, increases the presence of Fe²⁺ to compensate for the loss of Zn content, which eventually hop to the Zn site. Other surrounding ions have to move accordingly in order to stabilize the new position of the ions. This hopping process will have a significant impact on the vibrational frequencies of the normal modes of the associated octahedral BO₆ site. The proposed hopping process is also supported via electric studies which will be discussed in the Electric section. Note that this hopping of ions leads to the existence of both Fe²⁺ and Fe³⁺ in the matrix, thus causing a decrease in the resistivity as the annealing temperature increases.

Elastic and thermodynamic properties using FTIR analysis

The Fourier transform infrared spectroscopy spectrum was obtained in the wave number range of 400–4000 cm⁻¹ at room temperature. The spectra of the investigated Ni–Zn–Al ferrite samples are shown in Fig. 6a. The peaks of metal–oxygen bonds at (557–581) cm⁻¹ and (403–410) cm⁻¹ correspond to characteristics of ferrites (see Fig. 6b). According to Waldron,⁴⁷ these peaks are attributed to the stretching vibration of the cation–anion bond M_A–O in tetrahedral sites (A) (ν_A) and the stretching vibration of the cation–anion bond M_B–O in octahedral sites (B) (ν_B), respectively. Hence, the presence of these two peaks (ν_A) and (ν_B) confirms the formation of a spinel ferrite structure in the prepared nanoparticles. The positions of the vibrational bands of the Ni–Zn–Al ferrites are listed in Table S4 (ESI).† As can be seen in Fig. 6b, the peak (ν_A) slightly shifts towards a higher wavenumber with the increase in particle size, this shift is due to change in microstructure with increased annealing temperature, which may be the result of the transformation from the FeO₆ octahedron to the FeO₄ tetrahedron, and this transformation process can be accompanied by the enhanced covalency of Fe–O bonding. This confirms the results discussed in the Raman analysis.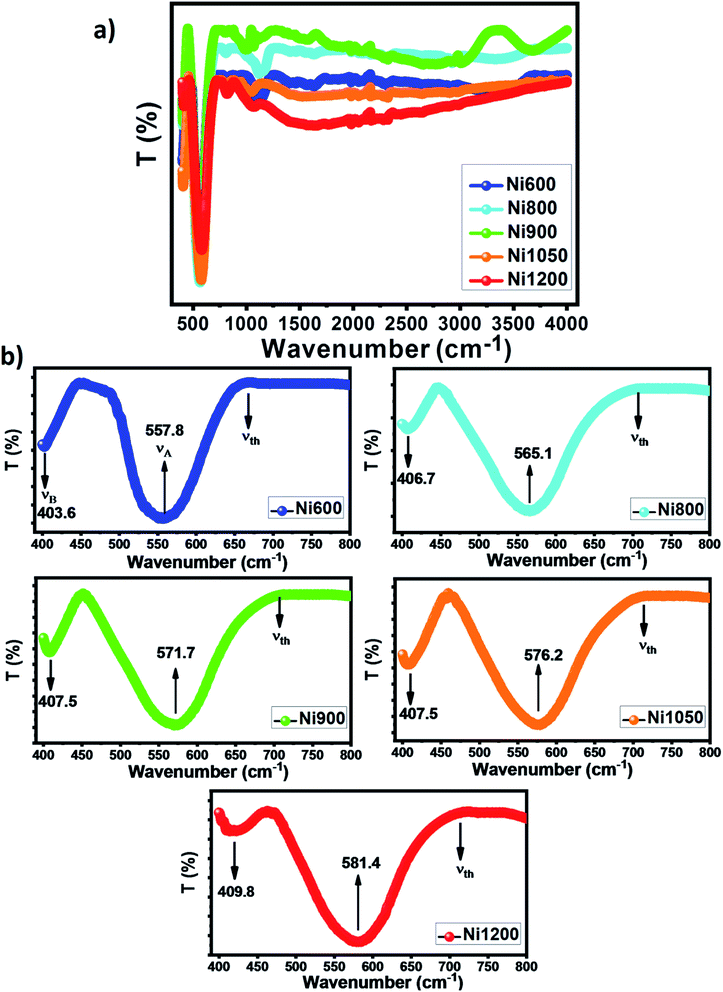

Fig. 6 (a) FT-IR spectra of NZFAO samples. (b) Zoomed views in the wavenumber interval of 400–800 cm⁻¹.

The forces constants of the ions at the tetrahedral site (K_T) and octahedral site (K_O) are connected to the IR band frequencies (ν_A and ν_B) and to the molecular weight of cations on A and B sites which are expressed as:⁴⁸

K_T = 7.62 × M_T × ν_A × 10⁻³

K_O = 10.62 × M_O × ν_B × 10⁻³

The force constant decreases for tetrahedral site while it increases for the octahedral site (Table S4†). The observed variation in the force constant values reflects changes in the Fe–O covalent with lattice contraction upon annealing temperature.⁴⁸

The Debye temperature is an essential parameter to study lattice vibrations in solid-state physics, which is the temperature at which the maximum vibration of the network takes place and simplifies the integration of thermal capacity. The Debye temperature θ_D was determined using the following equation:¹²

where, ℏ is Planck's constant, ν_av is the average value of wavenumbers, K_B is Boltzmann's constant, C is the velocity of light. The value of ℏC/K_B for the ferrite materials is taken as 1.438. It was found that the θ_D increases with the increase of annealing temperature (Table S4†). On the bases of specific heat theory,⁴⁹ the increase of θ_D may be due to a decrease of the conduction electron density N_n (n-type) and to an increase of the density of conduction holes N_p (p-type).

Waldron have evidenced that the FTIR spectroscopy is a useful tool for calculating the threshold energy E_th associated with the electronic transition from the threshold frequency ν_th, which is determined from the maximum point of the absorption spectra, where it reaches a limiting value.⁴⁷ The threshold energy can be calculated using the relation:

E_th = ℏCν_th

The values of ν_th and E_th are shown in Table S4† and are comparable to those previously obtained in mechanically milled spinel ferrite by K. B. Modi et al.¹³ The E_th is found to decrease on increasing annealing temperature. This decrease in threshold energy may be due to the improvement of the electron hopping between the Fe²⁺ and Fe³⁺ ions in the octahedral coordination.

The elastic properties of materials are important for understanding the nature of binding forces in materials and can be used to measure the resistance of a crystal to an externally applied stress. The average force constant (K_av) is a product of lattice constant and stiffness constant (C₁₁). The bulk modulus (B) of solids in terms of stiffness constants is defined as B = 1/3[C₁₁ + 2C₁₂]. According to Waldron,⁴⁷ for the spinel ferrites, C₁₁ = C₁₂, hence B is simply given by C₁₁. The value transverse wave velocity (ν_s), longitudinal wave velocity (ν_l), mean elastic wave velocity (ν_m), Young's modulus (E), rigidity modulus (G), Poisson's ratio (σ), and Debye temperature (θ_E) of the present system were calculated using the standard formulas available in the literature.^12,13

The calculated values of elastic parameters for all the compositions (Table S4†) are in good agreement to those obtained from ultrasonic pulses transmission (UPT) technique.⁵⁰ The values of elastic properties increase with the increase of annealing temperature, which indicates that the size of particles has large impact on elastic properties of spinel ferrite. However, the increase of Young's modulus E can be due to the rise of strength of inter-atomic bonding between the ions with an increase in annealing temperature.⁵¹ In addition, the Poisson's ratio σ (−1 < σ < 0.5) is generally used to quantify the stability of the crystal against shear. The higher the Poisson's ratio, the better the plasticity is. It can be noted that the value of the Poisson's ratio is constant for all the samples (σ = 0.35), which is in accordance with the theory of isotropic elasticity and implies a good elastic behavior. Furthermore, due to the strong effect of the porosity on the elastic properties, the values of elastic moduli have been also corrected to zero porosity using elastic theory and Ledbetter and Datta model⁵² and are listed in Table S5 (ESI).† From Table S5,† it can be observed that the Poisson's ratios increase with a raise of porosity and its existence can improve the plasticity. The elastic constants are similar to the obtained ones for Mn-doped Mg–Cu–Zn ferrites,⁵¹ LiZn₂Fe₃O₈,¹² and Ni_0.5Zn_0.5Fe₂O₄,¹³ which indicates that the elastic properties of our NZFAO samples have a high consistency. According to Pugh criteria,¹² a useful value of bulk modulus to rigidity modulus (B₀/G₀) were used to distinguish if the materials under investigation are ductile or brittle in nature. It can be found that the value of B₀/G₀ is higher than 1.75, which means that the NZFAO compounds are of ductile nature. The high plasticity and ductility make our samples a potential candidate as materials in microelectro-mechanical systems (MEMS).

The lattice energy values (the bond strength values) for nanoparticles Ni–Zn–Al ferrite are estimated by Kadriavtsev's approach. Assuming the additive of internal energy, the velocity of sound wave (ν) in solid and liquid media is given by the standard thermodynamic equation:^13,31,53

where n and m are constants defining the potential energy function, γ is the ratio of specific heat (C_p/C_v), R is the gas constant, T is the temperature, M is the molar mass and U_o is the potential energy. For most of the ionic solids, γ ≈ 1, n = 3 is found suitable to many spinel ferrite materials, ν is replaced by mean sound velocity corrected to zero porosity (ν_m0) and U_o, can be replaced by the lattice energy of the polycrystalline solid U_L. Hence, the lattice energy U_L can be expressed as follow:^13,31

U_L = −3.108 × 10⁻³Mν_m0²

Table S6 (ESI)† lists the U_L values for the different samples. In view of the Table S6,† our calculated values with this approach are close to those obtained by Catlow et al.⁵⁴ from atomistic computer simulation.

Following Waldron's approach⁴⁷ and according to Modi's work,^13,31 the characteristic temperature of Debye θ_J can be defined by:

where ν_max = f_max/C is the approximate mean between the cutoff frequencies of the oxide and metal ion vibrations, f_max = ν_lσ_max is the high frequency cutoff of the elastic waves and σ_max = 2.07 × 10⁻²/a (m⁻¹) is the shortest wave corresponds to 1/2 wave per mean interatomic distance. The values of θ_J thus calculated for all tested samples are shown in Table S6.† The results are in agreement with the previous published results by Modi et al.³¹ However, the θ_J is used to calculate the molar heat capacity at constant volume, C_v. Using Einstein's theory, the C_v value at T = 300 K for all the annealed Ni–Zn–Al spinel ferrite system was calculated.³¹
where p is the number of atoms per chemical formula and R is the gas constant. The values of heat capacity are shown in Table S6.† In the case of spinel ferrite system of the type A²⁺B₂³⁺O₄, according to Dulong and Petit law, the theoretically limiting value of heat capacity at constant volume and at T ≈ θ, C_v = 21, R = 174.5 J K⁻¹ mol⁻¹.^13,31 The C_v values of our samples are in accord with this limiting value as obtained from Dulong and Petit law and to that obtained using Waldron's approach.⁴⁷

The thermal conductivity of a material can be considered a fundamental property of the material. Using the Cahill's model,⁵⁵ we have calculated the minimum lattice thermal conductivity at 300 K of annealed Ni–Zn–Al ferrite by the following relation:

where K_B is the Boltzmann constant, n is number density of atoms, ν_s0 and ν_l0 are the transverse and longitudinal velocities corrected to zero porosity, respectively. The values of minimum lattice thermal conductivity are tabulated in Table S6.† The pronounced increase in Π_min with increasing grain size may be due to the formation of excess vacancies during annealing. As discussed in the Raman analysis, the existence of Fe²⁺ and Fe³⁺ in the matrix leading to an increase in thermal conductivity as the annealing temperature increases. So, the Ni–Zn–Al ferrite samples are useful for various purposes of applications, e.g., as a core material to increase the efficiency of switch-mode power supply (SMPS).⁵⁶

Optical properties

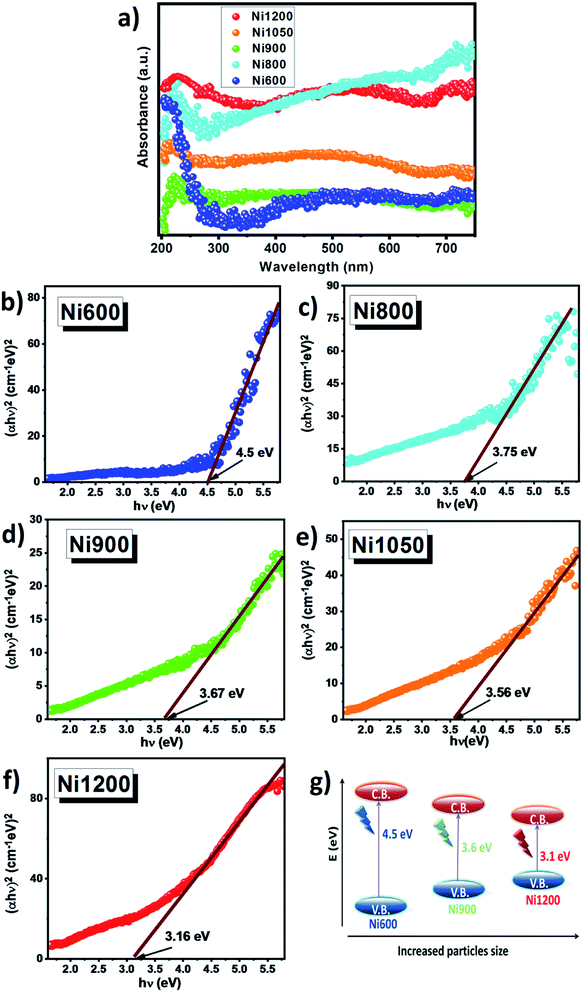
UV-visible absorption spectra were used to understand the optical properties of nickel–zinc ferrite samples. UV-visible absorbance spectra for all samples were recorded in the range 200–800 nm at room temperature and the absorbance spectra are shown in Fig. 7a. It is clear that Ni–Zn–Al ferrite shows high absorption intensity in the UV and visible light region. Absorbance spectra exhibit an absorption peak at around 300 nm. It is well known from past reports on ferrite spinel that, the absorption can be attributed to the photo-excitation of electrons from the valence band to the conduction band (ligand-to-metal (p–d) type charge transition O_2p → Fe_3d) or to the 3d⁵–3d⁴4s¹ transition in Fe³⁺ ions.¹² Interestingly, a slightly redshift in the absorption edge was observed as the size of grain increases. This might be due to changes in their morphologies, particle size, carrier concentrations, surface microstructures, presence of very small amount of impurities, lattice strain and oxygen vacancy.⁵⁷ Furthermore, the optical properties and band gaps of the samples sintered at 600, 800, 900, 1050 and 1200 °C are determined using absorption spectrum. The optical band gap (E_g) is the most important feature of materials that are good candidates for optoelectronic applications. The optical band gap (E_g) of the present Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ nanoparticles can be calculated experimentally from the optical absorption edge using the Tauc's relation as follows:^12,58

αhν = A[hν − E_g]ⁿ

where, the absorption coefficient (α), n = 1/2, 3/2, 2 or 3 depending upon the nature of electronic transition responsible for the absorption and A is a constant.

Fig. 7 (a) UV-vis spectra at room temperature of NZFAO samples annealed at different temperature. (b–f) Variation of (αhν)² versus photon energy hν plot for band gap calculation of annealed Ni_0.6Zn_0.4Al_0.5Fe_1.5O₄ samples. (g) Schematic band structure obtained according to the obtained results.

As ZnFe₂O₄ and NiFe₂O₄ (ref. 59 and 60) have direct gap, the synthesized compound has also a direct gap. So by plotting (αhν)² vs. hν, the optical band gaps (E_g) of the samples were realized as the intercepts with the energy axis, as shown in Fig. 7b–f. The estimated band gap energies values were found to be 4.5, 3.75, 3.67, 3.56 and 3.16 eV for Ni600, Ni800, Ni900, Ni1050 and Ni1200, respectively, denoting redshift as a function of grain size. This might be due to sub-band gap energy level formation and the presence of defects in the nanoparticles as a result of annealing temperature. Similar effect has been observed for other ferrite compounds reported by Singh et al.⁶⁰ (E_g = 4.28–3.80 eV for ZnFe₂O₄ nanoparticles) and Chand et al.⁵⁹ (E_g = 3.54 eV for NiFe₂O₄ nanoparticles). For semiconductor nanoparticles, the quantum confinement effect is expected. In our case, it has been observed that the band gap energy decreases with an increase in the crystallite size. This decrease of band gap between the valence band and conduction band (red shift) with increase particle size can be attributed to weak quantum confinement effect.⁶¹ Additionally, the increase in annealing temperature decreased concentration of oxygen vacancy and may be a source of trapped exciton states that form a series of metastable energy levels within the energy gap, resulting in the red shift of the optical band gap and the absorption band moves to the upper wavelength region.⁶² These values of band gap are greater than the theoretical energy required for water splitting (λ > 1.23 eV) and this prominent red shift may be responsible for enhanced charge separation and increased photocatalytic activity under visible light (absorption capability in the visible range).¹² Fig. 7g shows the change in band gap value and corresponding resultant schematic band structure. Furthermore, the reduction in the wide band gap with increasing particle size and transparency in the visible region makes these Ni–Zn ferrites samples a promising candidate for photodetectors and optoelectronic applications by harvesting more photons of light to excite the electrons from the valence band to the conduction band. In addition, to further investigate the pre-absorption edge, an Urbach tail analysis was also performed. The exponential absorption tails and Urbach energy is given in accordance with the following relation:⁶³

α = A exp[hν/E_U]

where α is absorption coefficient, A constant, hν the photon energy, and E_U the Urbach energy.

Urbach energy of samples is calculated by tacking the reciprocals of the slope of the liner portion in the lower photon energy of this curve by plotting the logarithm of the absorption coefficient, ln(α), against photon energy. The E_U value of this exponential dependence on photon energy may arise due to the random fluctuations associated with the small structural disorder present within the system. It is clear from Table S7 (ESI)† that the band gap energy has a correlation with Urbach energy, and both red shifts with the increase annealing of the temperature. The observed red shift in E_U arises because with increase of structural order variation with growth temperature, short range lattice disorder originates in the samples.⁶³

The refractive index (n₀) of semiconducting materials is very important in determining the optical and electric properties of the crystal. Knowledge of n is essential in the design of hetero-structure lasers in optoelectronic devices as well as in solar cell applications.⁶⁴ The refractive index (n₀) of ferrite nanostructures can be calculated from the value of E_g using Moss empirical relation:^58,59

E_gn₀⁴ = 104 eV

Furthermore, we have calculated the high frequency dielectric constant ε_α with a refractive index by using the following relation:^58,59

ε_α = n₀²

The values of the energy band gap, Urbach energy, refractive index, and high-frequency dielectric constant of Ni–Zn–Al ferrite samples are listed in Table S7.† Evidently, the values of the refractive index n₀ and ε_α were increased with increasing the annealing temperature. The results can be discussed on the basis of the oxygen deficiency with enhanced annealing temperature.

Magnetostrictive properties

Fig. 8 shows the plots of longitudinal magnetostriction λ of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ samples sintered at 800, 900, 1050 and 1200 °C, measured at room temperature along the parallel directions to the applied magnetic field. It has been observed that annealing temperature in Ni–Zn–Al ferrite has a strong influence on the magnetostriction characteristics. The maximum value of magnetostriction increases with increasing grain size. Further, the highest magnitude of magnetostriction, λ_max = −10 ppm, was achieved for sample annealed at 1200 °C. The magnetostrictive properties depends upon the processing parameters such as synthesis method, applied pressure while making pellets, sintering atmosphere, temperature and sintering time.⁶⁵ However, the observed porous nature may be responsible for the decrease of magnetostrictive coefficient in nanoparticle samples. Also, another possibility is that the increase in the magnetostriction with sintering temperature can be due to the minor changes in the degree of inversion in the ferrite, which can be attributed to the increase super-exchange and the direction deflection of the magnetic domain would, therefore, result in a higher magnetostriction.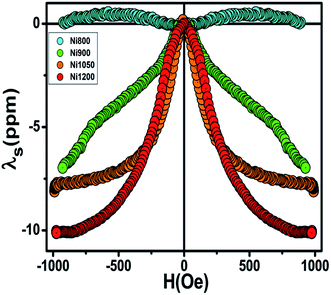

Fig. 8 Magnetostriction of the annealed NZAFO samples at room temperature, as a function of magnetic field, measured along the parallel direction to the applied field.

In the nickel ferrite, the unquenched orbital moment of Ni²⁺ leads to a large anisotropy and magnetostriction value (−26 ppm).⁶⁶ This value of λ_max for our samples are less than that reported for the pure bulk NiFe₂O₄, due to the addition of non-magnetic Zn and Al ions to nickel ferrite and to the difference in the microstructure associated with the different synthetic methods and processing conditions. The λ_max obtained in the bulk sample Ni1200 is relatively larger than the reported values of magnesium and lithium spinel ferrite.⁶⁷ Moreover, this value is similar to the ones of Ni_0.5Zn_0.5Fe₂O₄.⁶⁸ Overall, the reasonable magnetostriction coefficient and the high Curie temperature in Ni1050 and Ni1200 samples makes this material attractive for the use in automotive stress-sensing sensors applications.

Magnetic properties

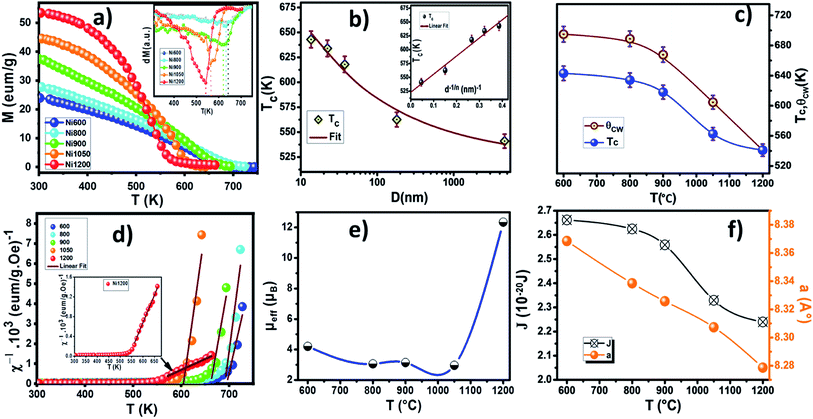
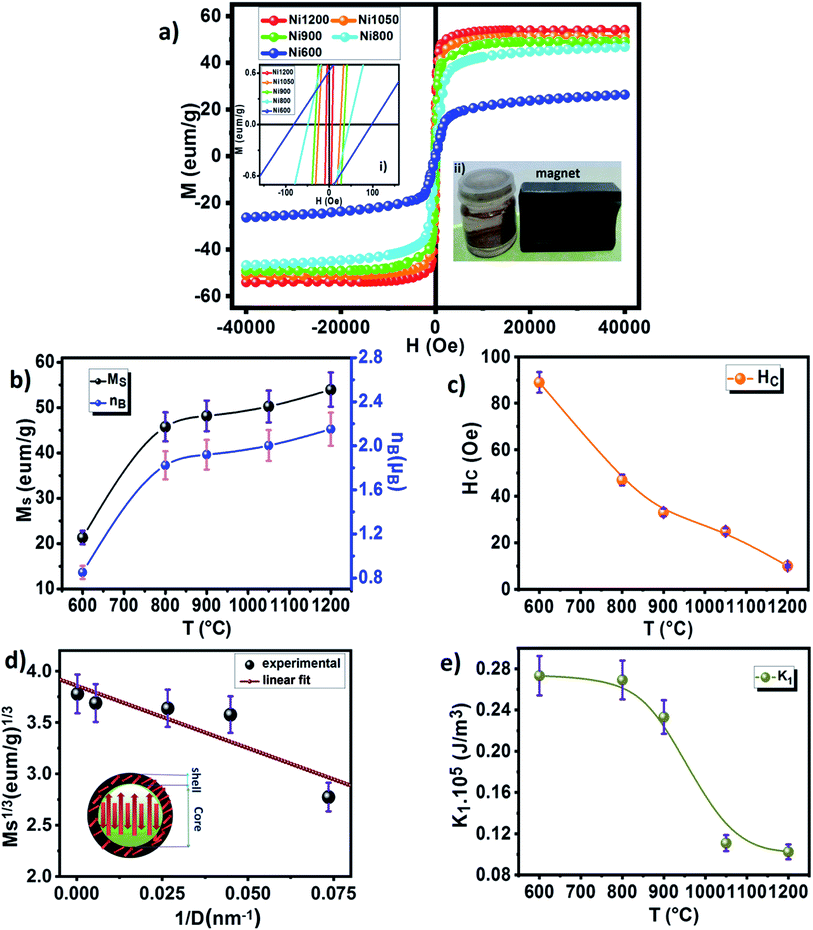
Curie temperature (T_C) is known to be one of the main magnetic parameters of ferrite. So, to determine the Curie temperature of the spinel NZAFO nanoparticles, the temperature dependent magnetization was measured over a temperature range of 300–750 K under an external magnetic field of 1 kOe, as shown in Fig. 9a. All samples exhibit paramagnetic (PM) to ferrimagnetic (FiM) transition at Curie temperature T_C. The T_C was determined from The first point of inflection in the first derivative of the magnetization (inset of Fig. 9a) it appears that the FiM transition in the Ni600 and Ni800 nanoparticles samples are markedly sharper than the transition of the Ni900, Ni1050 and Ni1200 samples. Moreover, the maximum slope of the magnetization curves, i.e. the slope at T_C, systematically decreases from 650 to 540 K with the grain size increases from 17 nm to 4 μm, indicating that a more direct relationship exists between the grain size and the broadening of the Curie transition of the NZFAO system.

Fig. 9 (a) Temperature dependence of magnetization under a magnetic field of 1 kOe of NZFAO samples, inset indicates the plot of dM/dT curve as a function of temperature. (b) The dependences of the T_C on the average particle size D, inset shows the corresponding T_C versus 1/dⁿ curve. (c) Plots of Curie and Curie–Weiss temperature versus annealing temperature. (d) Temperature dependence of the inverse susceptibility for NZFAO samples, the solid line is the fitting result following the Curie–Weiss law. (e) The experimental effective paramagnetic moment as a function of annealing temperature. (f) The lattice parameter (a) and the exchange interaction (J) as a function of annealing temperature.

The obtained Curie temperature value, T_C, of the samples are lower than that of polycrystalline NiFe₂O₄ (T_C = 883 K)³² and NiFe₂O₄ nanoparticles (T_C > 800 K)⁶⁹ as well as Ni_0.6Zn_0.4Fe₂O₄ nanoparticles (T_C = 663 K) reported by Gawas et al.⁷⁰ The difference can be due to the replacement of magnetic Fe³⁺ ions by nonmagnetic Al³⁺ ions. The substitution of nonmagnetic ions reduces active magnetic linkages for magnetic ion per formula unit as a result Curie temperature decreases.

The decrease in Curie temperature can be explained usually on the basis of finite size effects, due to atomic defects at the surface, leading to disorder in nanocrystalline systems.⁷¹ To understand the strong size dependence of the Curie temperature, the finite-size-scaling theory was used to fit the behavior of T_C as seen from Fig. 9b. According to this theory, the shift in the Curie temperature from that of the bulk is given by:⁷²

where, T_C is Curie temperature for given grain size D, T_C (bulk) is the Curie temperature of the bulk sample, d₀ is a constant (should be of the order of the characteristic dimension of the system) and λ = 1/ν is the critical exponent of the correlation length, the system-dependent sign may be either negative or positive. The fit of T_C is shown in Fig. 9b with T_C (bulk) = 522.96 K, d₀ = 0.65 nm, and λ = 0.69. The fit values of λ and d₀ are consistent with the finite size-scaling reported by other groups. The reasonable fit value of d₀ is comparable to the lattice constant. The value λ is an agreement with that for the three-dimensional (3D) Ising critical exponent of the correlation length.⁷³ Thus we conclude our data are consistent with finite size scaling corroborating earlier works.^72,74 In ferrite spinel, according to Neel's two-sublattice model of ferrimagnetism,⁷⁵ three types of magnetic interactions occur between sites A and B, namely A–A, B–B, and the strongest and most dominant A–B sub-lattice exchange. Therefore, the Curie temperature of ferrites is fundamentally determined from the overall strength of A–B exchange interaction. The decrease of Curie temperature with an increasing annealing temperature has been explained by a decrease of the degree of inversion which decreases the A–B strength interaction in the lattice, reducing thereby the T_C. This could be attributed to the decrease in distance between the moment of A and B sites, which is confirmed by the decrease in lattice parameter with the size of particles. The decrease in the value of Curie temperature, with grain size increase, is due to a change in cation distribution between the tetrahedral and octahedral sites of the spinel lattice on the basis of strength of the exchange interactions. The bond angles θ₁ and θ₂ are related to A–B exchange interaction, the bond angles θ₃ and θ₄ are associated to B–B exchange interaction,⁷⁶ the bond angle θ₅ is related to A–A exchange interaction.⁷⁷ As shown in Table S2,† the decrease in lattice parameter, bond angles and bond lengths results in increased A–B exchange interaction. As the exchange interaction is relatively strong, correspondingly higher thermal energy is required to disorient the moments,⁷⁷ thereby resulting in higher T_C values with decreasing particle size.

Further, the values of exchange interaction J can be calculated using the formula:⁷⁸

where z = 8, s = 1/2 and K_B = 1.380 × 10⁻¹⁶ erg K⁻¹. It is clear from Fig. 9f that, as the annealing temperature increases both lattice parameter (a) and the exchange interaction (J) decrease, which further reinforces the fact that the increasing grain size of the nanoparticles Ni–Zn–Al ferrite causes the decrease of the A–B exchange interaction.

In general, a large magnetocaloric effect (MCE) is observed near the transition temperature and is closely related to the order of the corresponding magnetic phase transition. The field cooling (FC) curves show a reversible character of the magnetization around the Curie temperature. Furthermore, the small area of the hysteresis cycle indicates low energy loss during a magnetization–demagnetization process⁷⁹ (see Fig. 10a). Therefore, the Ni–Zn–Al spinel ferrite can be considered as a candidate for magnetic refrigeration in a wide temperature range above room temperature and to transform industrial waste transformed into electrical energy using a thermomagnetic generator.⁸⁰

Fig. 10 (a) Magnetization hysteresis loops at room temperature for different annealing temperatures NZFAO nanoferrites, the inset (i) shows the variation of magnetization at a low applied field, the inset (ii) shows the separation of the MNPs of NZFAO free nanoparticles water dispersion. (b) Annealing temperature T_A dependence of the saturation magnetisation (M_s) and magnetic moments (n_B). (c) The coercive field (H_c) as a function of annealing temperature. (d) M_s^1/3 versus 1/D plot, the inset shows core–shell model. (e) The anisotropy constant (K₁) as a function of annealing temperature.

The inverse magnetic susceptibilities are shown in Fig. 9d. The inverse susceptibility rise sharply when the magnetic state of the ferrite nanoparticles changes from ferrimagnetic to paramagnetic states. In the temperature range, well above T_C, the susceptibility obeys the Curie–Weiss law:⁸¹

where θ_CW is the Curie–Weiss paramagnetic temperature, C denotes the Curie constant and T is the absolute temperature. By using C values obtained from the slope of 1/χ, the experimental effective moment μ_eff has been calculated (in unit of Bohr magneton μ_B) by using the following equation:
where N_A is Avogadro number and K_B is Boltzmann constant. Since the sign of θ_CW is positive (see Fig. 9c), then the ferrimagnetic interaction between spin in these compounds is highly expected. The obtained values of θ_CW are slightly higher than T_C which refers basically to the presence of a magnetic inhomogeneity.⁸² Generally, the difference between T_C and θ_CW is associated with the presence of short-range order slightly above T_C (Fig. 9c). The increase in the experimental effective paramagnetic moment for the bulk sample can be explained by the existence of ferrimagnetic clusters within the paramagnetic phase (Fig. 9e).

The room temperature magnetization M(H) of the nano-Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ varying sizes is shown in Fig. 10a. The inset shows M versus H in a small field range. It could be observed from the hysteresis loop that all composition of nanoparticles shows negligible remanence and coercivity, which confirms the ferrimagnetism of the soft ferrite materials. This soft magnetic nature might be useful for designing multifunctional devices to switch magnetization with a small external magnetic field. The annealing temperature has an enormous impact on the magnetic performance parameters: as the annealing temperature increases (i.e., increasing grain size) the saturated magnetization increases, while the coercivity decreases. The variation of coercivity (H_c) as a function of annealing temperature is summarized in Fig. 10c. The observed decrease in coercivity in the samples has been due to multi-domain nature of particles.⁸³ Recently, Das et al.⁸⁴ reported the variation of coercivity (H_c) with grain size. They found that it increases initially up to 40 nm and then decreases for CoFe₂O₄ nanoparticles. The decreasing trend of H_c with grain size beyond 40 nm gives a hint of transforming single domain into a multidomain particle. In our studied samples, the continuous decrease of coercivity with the increase in grain size indicates that the NZFAO particles do not undergo from single magnetic domain to multi-domain in this range of particle size. Similar variation of H_c with increasing particle size from 10 to 200 nm in NiFe₂O₄ is also reported by Yadav et al.⁸⁵

According to Stoner–Wohlfarth theory, the anisotropy constant value is related to the coercivity by the following relation:⁸⁶

where M_s is the saturation magnetization. We found that the anisotropic constant K₁ increased as the particle size decreased, thereby leading to an increase in coercivity (H_c). According to above relation, H_c is also inversely proportional to M_s, which is consistent with our results.

The increasing of coercivity observed in the Ni600 and Ni800 samples can be related to frustrated magnetic structure developing in the surface layer of nanoparticles.²⁹ Further, the non-zero H_c suggests presence of some blocked particles in the nanoparticles samples and that the samples had both ferrimagnetic and superparamagnetic components together. In addition, the Ni600 sample is magnetically well ordered at 300 K and it displays a substantial amount of coercive field (H_c = 90 Oe) and this has been noticed only in very few nanometric ferrites. The hight coercivity (280 Oe) at room temperature is also reported by S. Dey et al.⁸⁷ in Ni_0.5Zn_0.5Fe₂O₄ nanoparticle with 8–20 nm particle size.

Therefore, further investigation of the observed behavior of H_c is desired. The high saturated magnetization (M_s) values were determined by fitting the high field magnetization data using the saturation approach law given by:⁸⁸

where M_s is the saturation magnetization, A₁ and B₁ are a constant, the term C₁ corresponds to the susceptibility in the high field region, H is applied external magnetic field and K₁ is the first order cubic magnetocrystalline anisotropy coefficient in J m⁻³. This law is valid over the entire field range as shown in Fig. S5 (ESI).† The plot of M_s versus annealing temperature is shown in Fig. 10b. The decreasing of the size of nanoparticles induces more severe surface defects, magnetic responses weaken accordingly, and then saturation magnetization decreases. This behavior was interpreted in terms of the presence of magnetic dead layer on the surface of a nanoparticle. Similar effect has been seen in different types of magnetic nanoparticles previously, including manganite perovskite and ferrite nanoparticles^89,90 and explained in terms of increasing contribution of surface anisotropy for smaller particles. Hence, a large proportion of dislocations and crystal defects can occur within the lattice and this will cause a reduction of the magnetic moment within the particles, as a result of the magnetocrystalline anisotropy distortion.⁹¹

From Table S2,† the cation distribution results clearly indicate that Zn²⁺ has strong preference for the tetrahedral sites, whereas Ni²⁺ ions mainly occupy the octahedral sites and Al³⁺ and Fe³⁺ ions have a preference for both the available A and B sites but the Al³⁺ have strong preference for the octahedral site. As the sintering temperature increases, most of the Fe³⁺ ions occupy the octahedral site and the majority of the Al³⁺ ions occupy the tetrahedral site which increases the net magnetic moment and hence the increase of the saturation magnetization values.

The magnetic moments calculated per the formula unit are chows in Fig. 10b.³²

The magnetic moment of nanoparticles at room temperature increases remarkably with increasing particle size from n_B = 0.85 μ_B (Ni600) to n_B = 2.15 μ_B for Ni1200 sample. This enhancement is attributed to increase in exchange interactions between A and B sites, which resultantly increases net magnetization as well as magnetic moment per formula unit.

The net magnetization of a unit cell in spinel ferrites is considered to be proportional to the difference between magnetic moment of the A and B sites. According to Neel's collinear model, the magnetic moment per formula unit for such a system can be given as:⁹²

n_th = M_B − M_A

where, M_A and M_B are the Bohr magneton on the A and B sites, respectively. The theoretical magnetic moment of Fe (n_Fe) and Ni (n_Ni) are 5 and 2 μ_B. Based on the cation distributions, the n_th values are 3.9, 4.8, 5.6, 6.3 and 6.7 μ_B for Ni600, Ni800, Ni900, Ni1050 and Ni1200, respectively. The variation trends of net magnetic moment (n_th) and observed magnetic moment (n_B) are similar, while the values of observed magnetic moment (n_B) are lower than that of net magnetic moment (n_th). It indicates that the Neel's collinear model is in conformity with our samples, and noncollinear model of Yafet–Kittel (Y–K) model can explain the difference between net magnetic moment (n_th) and observed magnetic moment (n_B). According to the Y–K's noncollinear model, the Yafet–Kittel angle (α_Y–K) can be calculated by the following equation:⁴⁸

The value of α_Y–K angle is in the range 53–65.8°, which confirms the existence of a triangular (canted) spin arrangement in all samples. The estimated values of canting angle are close to the value 53.64° for Ni_0.6Zn_0.4Fe₂O₄.⁹³ It is clear that the non-zero α_Y–K angle suggest that the magnetization behavior for all samples cannot be explained on the basis of Neel two-sublattice model due to non-collinearity of spins on B site. Therefore, we may conclude that our NZFAO samples show Y–K magnetic ordering. Furthermore, the results indicated cation migration as the annealing temperature or the grain size increased. The migration of cation causes strains and it may break the surface exchange bonds to yield a canted spin structure. Thus, the canted spin structure weakens the A–B exchange interactions to reduce the saturation magnetization as the particle size decreases.

For the nanosized materials, the decrease in the saturation magnetization is due to the increasing surface area to volume ratio. It is assumed that a magnetically dead layer is formed at the surface of the particles due to the uncompensated exchange interactions in a surface layer of thickness t which is composed by canted spins that do not contribute to the net magnetic moment of the particle. We can then propose a model of the particles in which the outer part contains defects in the crystallographic structure and oxygen defects which will lead to a magnetically disordered state but the internal part will have the same properties as the bulk compound. Assuming a spherical shape of NZFAO nanoparticles, we will estimate the thickness of the shell (t) using the experimentally determined saturation magnetization (M_s) and particle size (D) values of the samples annealed at various temperatures. The variation of the saturation magnetization versus the diameter of nanoparticles has been fitted according to a core–shell model and shown in Fig. 10d. In this core–shell model, the magnetization of the particles can be expressed as:⁹⁴

M_s^1/3 = M₀^1/3[1 − 2t/D]

where, M₀ is the magnetization that would correspond to the bulk material. Note that the intercept at 1/D = 0 and the slope of the straight line correspond to M₀^1/3 and 2tM₀^1/3, respectively. As can be seen in inset of Fig. 10d, the present experimental data M_s^1/3 and 1/D show a good linear relationship, which confirms the suggestion that the magnetization is actually influenced by the surface of the particle. Thereby, by fitting the data using the above relationship, the saturation magnetization of the bulk material and the thickness of the shell were found to be 57.2 emu g⁻¹ and 1.6 nm, respectively. The shell thickness in NZFAO nanoparticles is comparable to the values estimated for La_1−xSr_xMnO₃ manganite nanocrystalline powders (1–4 nm).⁹⁴ The value of M₀ also is comparable to that expected for the bulk material. However, the existence of the nonmagnetic layer might be caused by the canting of the surface spins or by a high anisotropy layer. The core–shell nanostructure of NZAFO NPs is schematically presented in the inset of Fig. 10d. In general, for non-magnetic nanocrystalline materials, 1 nm is also a typical thickness of grain boundary regions.⁹⁵

Using the saturation approach law, we have determined the anisotropy constant K₁ for different sizes of Ni–Zn–Al ferrite. K₁ values are plotted as a function of the annealing temperature in the Fig. 10e. It is clear that the anisotropy constant decreases with the increase in particle size. This may be due to the finite size effects and the collective fraction of broken lattice symmetry accompanying atoms residing on the surface. These values are slightly greater as compared to the other magnetic nanoparticles, e.g., Fe₂O₃ (ref. 96) and CoFe₂O₄.⁶⁵

In order to check if our material can be useful for high-frequency microwave applications, the microwave frequency (ω_m), of the present NZFAO NPs has been calculated by the following equation:⁹⁷

ω_m = γ₁8π²M_s

where γ₁ is the gyromagnetic ratio (γ₁ = 2.8 MHz Oe⁻¹) and M_s is the saturation magnetization. The calculated values of microwave frequency are 4.7, 10.1, 10.6, 11.1, and 11.9 GHz for Ni600, Ni800, Ni900, Ni1050, and Ni1200, respectively. It can be seen that microwave frequency is increased from C to X band with increasing particle size. However, these values were relatively high, suggesting that the NZFAO samples are strong candidates for high-frequency microwave applications. Further, the ω_m values were comparable to those found in other ferrite systems that are considered potential candidates for the applications in microwave frequency bands.^97,98

Electron spin resonance analysis

Electron spin resonance (ESR) spectra (first derivative of the power absorption curve) were recorded to further investigate the magnetic features and spin related phenomena of the all annealed samples. The X-band ESR spectra of the Ni–Zn–Al ferrite nanoparticles with different crystallite sizes at room temperature are shown in Fig. 11. All main ferrite spectra are well described by a single Lorentz line function in its field-derivative form:
where A is its amplitude factor, H_r is the resonance magnetic field and ΔH_PP is the half width at half maximum of the absorbance line. As can be easily seen from Fig. 11, the ESR spectra are characterized by a broad, single and slightly asymmetric resonance line, which becomes narrower as the annealing temperature increases from 600 to 1200 °C. The broad curves indicate that the existence of dipolar–dipolar interactions among particles and randomly oriented magnetic anisotropy axes, especially for the Ni600, Ni800 and Ni900 nanoparticles samples, which is the characteristic property of superparamagnetic materials. In accordance with this observation, K. Praveena et al.²⁴ have reported a similar behavior in Ni_0.4Zn_0.2Mn_0.4Fe₂O₄ nano powders annealed at different temperatures. In the case of Ni1050 and Ni1200, the reduced value of ΔH_PP can be due to the strong super exchange interaction between magnetic ions through oxygen anions. According to resonance condition of the ESR spectra, we estimated the effective factor g value from ESR spectra by using the formula:
where, υ is the microwave frequency, μ_B is the Bohr magneton, H_r is the resonance field and ℏ is the Planck constant. The resonance line width (ΔH_PP), the resonance filed (H_r), and the effective g-factor are listed in Table S8 (ESI).†

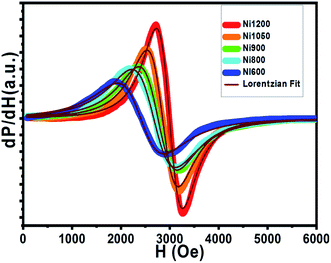Fig. 11 First derivative (dP/dH vs. H) of resonance signals of different annealing temperatures NZFAO nanoferrites.

The g factors for the low temperature annealed samples Ni600, Ni800 and Ni900 are very close to that for polycrystalline Ni–Zn ferrite.⁹⁹ The high value of g and the largest ΔH_PP, indicate the strong interaction between small NZAFO NPs. Increasing the annealing temperature to 1200 °C, the g value decreased to 2.64 accompanied by the smallest value of ΔH_PP of 405 Oe, reflecting the presence of the strong exchange interaction in bulk sample, indicating exchange interaction between Fe³⁺ and Ni²⁺ ions. This decrease can be due to the isotropic alignment of magnetic moments with the increase in particle size. ESR signals show that when the size of particles increases, the resonance field increases, but the peak to peak line width decreases. This means that the net magnetization of the samples increases with the increase of annealing temperature. Therefore, with the increase of grain size, migrate of Ni²⁺ and Fe³⁺ ions from the surface/interface site to bulk one. The octahedral and tetrahedral sites should also alter the interaction of magnetic ions. Moreover, the shell is visualized to be the zone in which created vacancies and the super exchange interaction has been destroyed. The shell has a smaller magnetization compared to the core and the magnetization of this zone decreases with increasing size of grain. Therefore, the decrease in resonance field was observed.

ESR spectroscopy was used to study the relaxation mechanism. The spin relaxation process is a function of static magnetic field and depends on the rate at which microwave energy can be absorbed and dissipated via relaxation processes either by spin–lattice (T₁) or spin–spin relaxation (T₂) process. The spin–spin relaxation process is the energy difference (ΔE) transferred to neighboring electrons and the relaxation time (T₂) can be determined from the ΔH_PP line width according to following equation:⁹⁹

where ΔH is the full-width-at-half-maximum of the absorption curve (ΔH = √3ΔH_PP) and ℏ is the Planck reduced constant. Due to the homogeneous broadening of the ESR signal, the spin–lattice interaction time, T₁, has also been calculated from the relation:¹⁰⁰
where, the spin–lattice relaxation involves the thermal equilibrium of the spin system with the lattice or environment of the spin. Hence, the super-paramagnetic behavior of the samples can be explained on the basis of spin–lattice interaction. Neel superparamagnetic is due to thermally induced fluctuations of the direction of magnetization in single domain particles below a certain critical size. However, the completion of g and ΔH_PP parameters leads to an increase of the relaxation time (T₂) from 2.9 × 10⁻¹¹ s for Ni600 to 6.4 × 10⁻¹¹ s for Ni1200 (Table S8†). It is well know that the specific loss power (SLP) value for hyperthermia treatment depends inversely to the relaxation time; thus, the observed minimum value of T₂ for Ni600, Ni800 and Ni900 makes them a good candidate for use in hyperthermia treatment.¹⁰¹ For these samples, T₁ has a lower magnitude than T₂ showing the dominance of spin–spin interaction. Super-exchange magnetic interaction is dominated in Ni1200 sample where the relaxation rate ratio R₂/R₁ is 1.7 × 10⁻² and dipolar magnetic interactions is dominated in Ni600 sample with highest the relaxation rate ratio R₂/R₁ = 8.6 × 10⁻² (Table S8†).

For magnetic resonance imaging (MRI) T₂-contrast agent, the transverse relaxivity r₂ can be estimated at the magnetic field assuming the magnetic average regime (MAR) to interpret the interaction of nanoparticles with the protons using the following equation:⁷⁸

where, γ_p is the magnetogyric ratio of proton, μ₀ is the magnetic permeability of vacuum, D_F is the water translational diffusion constant at 25 °C,¹⁰² D_SEM is the average particle size obtained from SEM analysis, V_mat is the molar volume of the sample (m³ mol⁻¹) and M_s is the saturation magnetization of sample at 300 K in A m⁻¹. The calculated values of r₂ are reported in Table S9 (ESI),† indicating that the transverse relaxivity increases as the grain size increases. The higher value of transverse relaxivity gives the effective T₂ contrast agent for our Ni–Zn–Al ferrite nanoparticles samples. Also, the broad ESR linewidth of the powders in this study suggests that the ferrite powders may be a good candidate for the radar absorbing materials (RAM) used in microwave applications in broad frequency range.

Electric properties

Let us now turn to the effect of annealing temperature on the electrical properties. Fig. 12a shows the temperature dependence of direct-current resistivity regime (ρ_dc) in the range 220–600 K for the NZFAO nanoparticles (Ni600, Ni900 and Ni1200), the resistivity decreases continuously with increasing temperature for all samples, which reflects a semiconductor behavior. In general, this could be ascribed to the increase in the drift mobility of electric charge carriers which are thermally activated with increasing temperature.¹⁰³ The electrical resistivity of the Ni–Zn nano ferrite decreases from 7 × 10⁶ to 4.7 × 10³ Ω cm at 360 K with the increase in crystallite particles size from 17 to 40 nm. This can be due to the increase of compactness of the specimens assured by increasing the annealing temperature. The observed variations in resistivity with composition can be explained by Verwey's hopping mechanism.¹⁰⁴ The electronic conduction in ferrites is principally due to hopping of electrons between the ions of the same element present in more than one valence state (Fe²⁺ and Fe³⁺ ions), distributed randomly over crystallographically equivalent lattice sites.¹⁰⁵ For the Ni600 and Ni900 nanoparticles with such high resistivity that led to very low eddy current losses are desirable in transformers, electronic inductors, electromagnets and at high frequency application,¹⁰⁶ while the Ni1200 sample having with higher conductivity may be desirable in the use in solid oxide fuel cells.¹⁰³ The relation between resistivity and temperature describes the well-known Arrhenius equation and may be expressed as:
where ρ is the dc electrical resistivity at temperature T, K_B is Boltzmann constant, E_a is activation energy and ρ₀ is the pre-exponential constant. Typical plots of (log ρ_dc) versus 1000/T for the samples sintered at 600, 900 and 1200 °C are shown in Fig. S5 (ESI).† For the Ni600 and Ni900 samples, a change in slope was observed in the resistivity curve that divides the curve into two regions or one break, whereas in the Ni1200 sample, which the studied temperature range was extended to a few degrees upper the Curie temperature, the plot shows three zones, i.e. two breaks. The second break occurs in the vicinity of the Curie temperature (T_C = 540 K) and this has been attributed to the influence of magnetic order on the conduction mechanism.¹⁰⁷ The Curie temperature obtained from the resistivity is in agreement with the T_C obtained by the magnetic measurements. The calculated activation energies (E₁ and E₂) for the three compositions corresponding to the two regions (T_r1 and T_r2) have been estimated and are shown in inset of Fig. S5.† The activations energies in T_r2 region (E₂) were higher than those in T_r1 region (E₁). Increasing activation energy with increasing temperature can be ascribed to the presence of different carriers' traps. For the low temperature process, the dominant conduction mechanism would be an exchange of electrons between nearest neighbor Fe²⁺ ↔ Fe³⁺ pairs, with associated activation energy of the order of 0.1 eV.¹⁰⁸ While for the high-temperature process (T_r2 region), the conduction mechanism is expected via Ni²⁺ or Fe³⁺ neighbors, i.e. Ni²⁺ + Fe³⁺ ↔ Fe²⁺ + Ni³⁺. Similar results to the present study were obtained in the case of a number of mixed ferrites such as Ni–Zn,¹⁰⁷ and Mn–Ni–Zn.¹⁰⁹

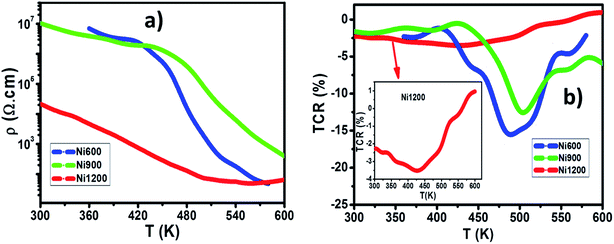Fig. 12 (a) The temperature dependence of direct-current resistivity for Ni600, Ni900 and Ni1200 samples. (b) The TCR as a function of temperature for Ni600, Ni900, and Ni1200.

The value of the temperature coefficient of resistance TCR is very useful for determining the sensitivity of the infrared detectors (IR) for night vision bolometer technologies.¹¹⁰

where T and ρ are the temperature and resistivity, respectively. In this section, the data of the TCR as a function of temperature of Ni600, Ni900, and Ni1200 are investigated and shown in Fig. 12b. As can be seen, the temperature dependence of the TCR for the three samples shows a peak below room temperature. The peak position decreases with the increase of grain size. The TCR values are −14%/K at 550 K, −12%/K at 500 K and −3.4%/K at 400 K for Ni600, Ni900 and Ni1200 sample, respectively. Several factors could affect peak TCR value, including sintering temperature and time. Comparing to other values of TCR collected from other works,^111,112 the Ni–Zn–Al ferrite has a highest TCR. Encouragingly, these results suggest that NZFAO samples could be used for applications in bolometric device.

Conclusion

In this study, we described an investigation on the influence of the particle size in the structural, optical, elastic, thermodynamic, magnetic and electrical properties of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ nanoparticles. The sol–gel technique was successfully used to obtain nano and micro-powders of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄. Heat-treatment in the temperature ranges of 600–1200 °C yields to an average grain size ranging from 17 nm to 4 μm. We arrived at the following conclusion:

(1) Rietveld refinement of the XRD patterns confirmed the high crystalline quality of the particles obtained particles. The grain size and strain were observed to increase with increasing annealing temperature. FTIR and Raman spectroscopy analyses confirmed the presence of tetrahedral and octahedral sites in the prepared samples. The nanometric and micrometric nature of Ni–Zn–Al ferrite was confirmed by SEM microscopy.

(2) The compositional dependence of elastic constants can be explained on the basis of inter-atomic bonding between the ions. The Debye temperature and molar heat capacity values determined from FTIR spectral analysis are in agreement with the reported ones in literature. The increase of size results in an increase of both Debye temperature and thermal conductivity but it decreases of the molar heat capacity. The Ni–Zn–Al ferrite samples can be used for switch-mode power supply.

(3) The optical properties of the synthesized Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ samples were also investigated. The decrease of size results in a decrease of the band gap energy and in an increase of refractive index n₀. Hence, the annealed Ni–Zn–Al ferrite samples display enhanced optical absorption capability in the visible range.

(4) The high temperature magnetic measurements and hysteresis loops at RT indicate that the increase in annealing temperature leads to significant shift in Curie temperature consistent with finite size scaling formula and to an increase of the fraction of the superparamagnetic phase at the expense of the ferrimagnetic one. M_s consistently increases with the increasing of the annealing temperature and this can be explained by an interface/surface region of the nano-spinel ferrite. High values of microwave frequency are calculated (from C to X band) which indicates that it is a promising infrared detector (IR) for night vision bolometer material. Ni–Zn–Al ferrites may have potential in industrial and technological applications e.g. magnetic refrigeration, biomedical applications and microwave frequency (C and X) band applications.

(5) The room temperature ESR spectra reveal that peak width ΔH_PP was reduced and the spin–spin relaxation T₂ increases as the annealing temperature increases due to the increase in the dipole–dipole interaction. Moreover, the high values of the transverse relaxivity r₂ of Ni600, Ni800, and Ni900 make them a potential candidate for use in hyperthermia treatment. In contrast, the reasonable magnetostriction coefficient (λ_max = −10 ppm), which was achieved for bulk sample (Ni1200) makes this material attractive for the use in automotive stress-sensing sensors applications.

(6) The electrical resistivity of the Ni–Zn nanoferrites decrease with the increase in particle size. The temperature coefficient of resistance TCR of three typical samples was calculated. Ni600 (with the highest electrical resistivity) had a highest temperature coefficient of resistance than Ni900 and Ni1200 samples and could reach −14%/K at 550 K, which indicates that it is a promising infrared detector (IR) for night vision bolometer material.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the Tunisian Ministere de l'Enseignement Superieur et de la Recherche Scientifique, the PHCMaghreb 15 MAG07 program.

References

1. Y. Zhang, Z. Yang, D. Yin, Y. Liu, C. Fei, R. Xiong, J. Shi and G. Yan, Composition and magnetic properties of cobalt ferrite nano-particles prepared by the co-precipitation method, J. Magn. Magn. Mater., 2010, 322, 3470–3475.
2. M. Gharibshahian, O. Mirzaee and M. S. Nourbakhsh, Evaluation of superparamagnetic and biocompatible properties of mesoporous silica coated cobalt ferrite nanoparticles synthesized via microwave modified Pechini method, J. Magn. Magn. Mater., 2017, 425, 48–56.
3. B. Rabi, A. Essoumhi, M. Sajieddine, J. M. Greneche, E. K. Hlil, A. Razouk and M. A. Valente, Structural, magnetic and magnetocaloric study of Ni_0.5Zn_0.5Fe₂O₄ spinel, Appl. Phys. A, 2020, 126, 174.
4. A. C. Gandhi, P. M. Reddy, T.-S. Chan, Y.-P. Ho and S. Y. Wu, Memory effect in weakly-interacting Fe₃O₄ nanoparticles, RSC Adv., 2015, 5, 84782–84789.
5. N. Guijarro, P. Bornoz, M. Prévot, X. Yu, X. Zhu, M. Johnson, X. Jeanbourquin, F. Le Formal and K. Sivula, Evaluating spinel ferrites MFe₂O₄ (M = Cu, Mg, Zn) as photoanodes for solar water oxidation: prospects and limitations, Sustainable Energy Fuels, 2018, 2, 103–117.
6. A. M. Popov, T. A. Labutin, A. E. Goldt, O. V. Usovich, S. E. Bozhenko and N. B. Zorov, Determination of lithium in lithium-ionic conductors by laser-enhanced ionization spectrometry with laser ablation, J. Anal. At. Spectrom., 2014, 29, 176–184.
7. M. Colombo, S. Carregal-Romero, M. F. Casula, L. Gutiérrez, M. P. Morales, I. B. Böhm, J. T. Heverhagen, D. Prosperi and W. J. Parak, Biological applications of magnetic nanoparticles, Chem. Soc. Rev., 2012, 41, 4306.
8. A. E. Reddy, T. Anitha, C. V. V. Muralee Gopi, S. S. Rao, B. Naresh and H.-J. Kim, Construction of novel nanocomposite ZnO@CoFe₂O₄ microspheres grown on nickel foam for high performance electrochemical supercapacitors, Anal. Methods, 2018, 10, 223–229.
9. J. Xie, K. Chen, H.-Y. Lee, C. Xu, A. R. Hsu, S. Peng, X. Chen and S. Sun, Ultrasmall c(RGDyK)-Coated Fe₃O₄ Nanoparticles and Their Specific Targeting to Integrin α_vβ₃-Rich Tumor Cells, J. Am. Chem. Soc., 2008, 130, 7542–7543.
10. E. Céspedes, J. M. Byrne, N. Farrow, S. Moise, V. S. Coker, M. Bencsik, J. R. Lloyd and N. D. Telling, Bacterially synthesized ferrite nanoparticles for magnetic hyperthermia applications, Nanoscale, 2014, 6, 12958–12970.
11. Z. Beji, L. S. Smiri, N. Yaacoub, J.-M. Grenèche, N. Menguy, S. Ammar and F. Fiévet, Annealing Effect on the Magnetic Properties of Polyol-made Ni–Zn Ferrite Nanoparticles, Chem. Mater., 2010, 22, 1350–1366.
12. D. Bouokkeze, J. Massoudi, W. Hzez, M. Smari, A. Bougoffa, K. Khirouni, E. Dhahri and L. Bessais, Investigation of the structural, optical, elastic and electrical properties of spinel LiZn₂Fe₃O₈ nanoparticles annealed at two distinct temperatures, RSC Adv., 2019, 9, 40940–40955.
13. K. B. Modi, S. J. Shah, N. B. Pujara, T. K. Pathak, N. H. Vasoya and I. G. Jhala, Infrared spectral evolution, elastic, optical and thermodynamic properties study on mechanically milled Ni_0.5Zn_0.5Fe₂O₄ spinel ferrite, J. Mol. Struct., 2013, 1049, 250–262.
14. G. Datt, M. Sen Bishwas, M. Manivel Raja and A. C. Abhyankar, Observation of magnetic anomalies in one-step solvothermally synthesized nickel–cobalt ferrite nanoparticles, Nanoscale, 2016, 8, 5200–5213.
15. C. J. Brinker and G. W. Scherer, Sol–Gel Science, Academic Press, New York, 1990.
16. M. Tan, Y. Köseoğlu, F. Alan and E. Şentürk, Overlapping large polaron tunneling conductivity and giant dielectric constant in Ni_0.5Zn_0.5Fe_1.5Cr_0.5O₄ nanoparticles (NPs), J. Alloys Compd., 2011, 509, 9399–9405.
17. S. K. Pradhan, S. Bid, M. Gateshki and V. Petkov, Microstructure characterization and cation distribution of nanocrystalline magnesium ferrite prepared by ball milling, Mater. Chem. Phys., 2005, 93, 224–230.
18. P. Dolcet, K. Kirchberg, A. Antonello, C. Suchomski, R. Marschall, S. Diodati, R. Muñoz-Espí, K. Landfester and S. Gross, Exploring wet chemistry approaches to ZnFe₂O₄ spinel ferrite nanoparticles with different inversion degrees: a comparative study, Inorg. Chem. Front., 2019, 6, 1527–1534.
19. S. Atiq, M. Majeed, A. Ahmad, S. K. Abbas, M. Saleem, S. Riaz and S. Naseem, Synthesis and investigation of structural, morphological, magnetic, dielectric and impedance spectroscopic characteristics of Ni-Zn ferrite nanoparticles, Ceram. Int., 2017, 43, 2486–2494.
20. B. R. Babu, K. V. Ramesh, M. S. R. Prasad and Y. Purushotham, Structural, Magnetic, and Dielectric Properties of Ni_0.5Zn_0.5Al_xFe_2−xO₄ Nanoferrites, J. Supercond. Novel Magn., 2016, 29, 939–950.
21. M. Hashim, S. K. Alimuddin, S. Ali, B. H. Koo, H. Chung and R. Kumar, Structural, magnetic and electrical properties of Al³⁺ substituted Ni–Zn ferrite nanoparticles, J. Alloys Compd., 2012, 511, 107–114.
22. L.-Z. Li, X.-X. Zhong, R. Wang, X.-Q. Tu, L. He, R.-D. Guo and Z.-Y. Xu, Structural, magnetic and electrical properties in Al-substituted NiZnCo ferrite prepared via the sol–gel auto-combustion method for LTCC technology, RSC Adv., 2017, 7, 39198–39203.
23. R. Lahouli, J. Massoudi, M. Smari, H. Rahmouni, K. Khirouni, E. Dhahri and L. Bessais, Investigation of annealing effects on the physical properties of Ni_0.6Zn_0.4Fe_1.5Al_0.5O₄ ferrite, RSC Adv., 2019, 9, 19949–19964.
24. K. Praveena, K. Sadhana, S. Matteppanavar and H.-L. Liu, Effect of sintering temperature on the structural, dielectric and magnetic properties of Ni_0.4Zn_0.2Mn_0.4Fe₂O₄ potential for radar absorbing, J. Magn. Magn. Mater., 2017, 423, 343–352.
25. J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192, 55–69.
26. J. Azadmanjiri, S. A. Seyyed Ebrahimi and H. K. Salehani, Magnetic properties of nanosize NiFe₂O₄ particles synthesized by sol–gel auto combustion method, Ceram. Int., 2007, 33, 1623–1625.
27. R. L. Coble, Sintering Crystalline Solids. I. Intermediate and Final State Diffusion Models, J. Appl. Phys., 1961, 32, 787–792.
28. A. Hajalilou, M. Hashim, R. Ebrahimi-Kahrizsangi and H. Mohamed Kamari, Influence of evolving microstructure on electrical and magnetic characteristics in mechanically synthesized polycrystalline Ni-ferrite nanoparticles, J. Alloys Compd., 2015, 633, 306–316.
29. I. S. Lyubutin, S. S. Starchikov, A. O. Baskakov, N. E. Gervits, C.-R. Lin, Y.-T. Tseng, W.-J. Lee and K.-Y. Shih, Exchange-coupling of hard and soft magnetic sublattices and magnetic anomalies in mixed spinel NiFe_0.75Cr_1.25O₄ nanoparticles, J. Magn. Magn. Mater., 2018, 451, 336–343.
30. V. K. Mittal, P. Chandramohan, S. Bera, M. P. Srinivasan, S. Velmurugan and S. V. Narasimhan, Cation distribution in Ni_xMg_1−xFe₂O₄ studied by XPS and Mössbauer spectroscopy, Solid State Commun., 2006, 137, 6–10.
31. K. B. Modi, P. Y. Raval, S. J. Shah, C. R. Kathad, S. V. Dulera, M. V. Popat, K. B. Zankat, K. G. Saija, T. K. Pathak, N. H. Vasoya, V. K. Lakhani, U. Chandra and P. K. Jha, Raman and Mossbauer Spectroscopy and X-ray Diffractometry Studies on Quenched Copper–Ferri–Aluminates, Inorg. Chem., 2015, 54, 1543–1555.
32. K. K. Bestha, J. J. Abraham, J. A. Chelvane and V. Gorige, Influence of cation distribution on magnetic response of polycrystalline Co_1−xNi_xFe₂O₄ (0 ≤ x ≤ 1) ferrites, Phys. Scr., 2020, 95, 085802.
33. E. F. Bertaut, Structures des boroferrites, Acta Crystallogr., 1950, 3, 473–474.
34. A. Hajalilou, H. M. Kamari and K. Shameli, Dielectric and electrical characteristics of mechanically synthesized Ni-Zn ferrite nanoparticles, J. Alloys Compd., 2017, 708, 813–826.
35. S. R. Gawali, A. C. Gandhi, S. S. Gaikwad, J. Pant, T.-S. Chan, C.-L. Cheng, Y.-R. Ma and S. Y. Wu, Role of cobalt cations in short range antiferromagnetic Co₃O₄ nanoparticles: a thermal treatment approach to affecting phonon and magnetic properties, Sci. Rep., 2018, 8, 249.
36. J. P. Singh, R. C. Srivastava, H. M. Agrawal and R. Kumar, Micro-Raman investigation of nanosized zinc ferrite: effect of crystallite size and fluence of irradiation, J. Raman Spectrosc., 2011, 42, 1510–1517.
37. P. Chirawatkul, S. Khoonsap, S. Phumying, C. Kaewhan, S. Pinitsoontorn and S. Maensiri, Cation distribution and magnetic properties of Co_xMg_1−xFe₂O₄ nanoparticles, J. Alloys Compd., 2017, 697, 249–256.
38. S. Aliyeva, S. Babayev and T. Mehdiyev, Raman spectra of Ni_1-XZn_XFe₂O₄ nanopowders, J. Raman Spectrosc., 2018, 49, 271–278.
39. M. I. Dar and S. A. Shivashankar, Single crystalline magnetite, maghemite, and hematite nanoparticles with rich coercivity, RSC Adv., 2014, 4, 4105–4113.
40. D. K. Pradhan, S. Kumari, V. S. Puli, P. T. Das, D. K. Pradhan, A. Kumar, J. F. Scott and R. S. Katiyar, Correlation of dielectric, electrical and magnetic properties near the magnetic phase transition temperature of cobalt zinc ferrite, Phys. Chem. Chem. Phys., 2017, 19, 210–218.
41. B. K. Chatterjee, K. Bhattacharjee, A. Dey, C. K. Ghosh and K. K. Chattopadhyay, Influence of spherical assembly of copper ferrite nanoparticles on magnetic properties: orientation of magnetic easy axis, Dalton Trans., 2014, 43, 7930–7944.
42. J. R. Scheffe, M. D. Allendorf, E. N. Coker, B. W. Jacobs, A. H. McDaniel and A. W. Weimer, Hydrogen Production via Chemical Looping Redox Cycles Using Atomic Layer Deposition-Synthesized Iron Oxide and Cobalt Ferrites, Chem. Mater., 2011, 23, 2030–2038.
43. P. Yaseneva, M. Bowker and G. Hutchings, Structural and magnetic properties of Zn-substituted cobalt ferrites prepared by co-precipitation method, Phys. Chem. Chem. Phys., 2011, 13, 18609–18614.
44. D. Zakutna, I. Matulkova, E. Kentzinger, R. Medlin, Y. Su, K. Nemkovski, S. Disch, J. Vejpravova and D. Niznansky, Dispersible cobalt chromite nanoparticles: facile synthesis and size driven collapse of magnetism, RSC Adv., 2016, 6, 107659–107668.
45. J. Zi, H. Büscher, C. Falter, W. Ludwig, K. Zhang and X. Xie, Raman shifts in Si nanocrystals, Appl. Phys. Lett., 1996, 69, 200–202.
46. P. Chandramohan, M. P. Srinivasan, S. Velmurugan and S. V. Narasimhan, Cation distribution and particle size effect on Raman spectrum of CoFe₂O₄, J. Solid State Chem., 2011, 184, 89–96.
47. R. D. Waldron, Infrared Spectra of Ferrites, Phys. Rev., 1955, 99, 1727–1735.
48. L. Wang, B. K. Rai and S. R. Mishra, Structural and magnetic study of Al³⁺ doped Ni_0.75Zn_0.25Fe_2−xAl_xO₄ nanoferrites, Mater. Res. Bull., 2015, 65, 183–194.
49. S. A. Mazen, S. F. Mansour, E. Dhahri, H. M. Zaki and T. A. Elmosalami, The infrared absorption and dielectric properties of Li–Ga ferrite, J. Alloys Compd., 2009, 470, 294–300.
50. R. A. Pawar, S. S. Desai, S. M. Patange, S. S. Jadhav and K. M. Jadhav, Inter-atomic bonding and dielectric polarization in Gd³⁺ incorporated Co-Zn ferrite nanoparticles, Phys. B, 2017, 510, 74–79.
51. A. Bhaskar and S. R. Murthy, Effect of sintering temperatures on the elastic properties of Mn (1%) added MgCuZn ferrites, J. Magn. Magn. Mater., 2014, 355, 100–103.
52. P. U. Sharma and K. B. Modi, Effect of Fe ³⁺ substitution on elastic properties of yttrium iron garnet, Phys. Scr., 2010, 81, 015601.
53. K. B. Modi, M. C. Chhantbar and H. H. Joshi, Study of elastic behaviour of magnesium ferri aluminates, Ceram. Int., 2006, 32, 111–114.
54. H. Donnerberg and C. R. A. Catlow, Atomistic computer simulations of yttrium iron garnet (YIG) as an approach to materials defect chemistry. I. Intrinsic defects, J. Phys.: Condens. Matter, 1993, 5, 2947–2960.
55. D. G. Cahill, S. K. Watson and R. O. Pohl, Lower limit to the thermal conductivity of disordered crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131–6140.
56. Q. Tariq, A. S. Saleemi, M. Saeed and M. Anis-ur-Rehman, Effect of Sintering on Co-precipitated Nanoparticles of Mn Ferrite, J. Supercond. Novel Magn., 2015, 28, 971–975.
57. T. M. Hammad, J. K. Salem, A. A. Amsha and N. K. Hejazy, Optical and magnetic characterizations of zinc substituted copper ferrite synthesized by a co-precipitation chemical method, J. Alloys Compd., 2018, 741, 123–130.
58. A. O. Turky, M. Mohamed Rashad, A. E.-H. Taha Kandil and M. Bechelany, Tuning the optical, electrical and magnetic properties of Ba_0.5Sr_0.5Ti_xM_1−xO₃ (BST) nanopowders, Phys. Chem. Chem. Phys., 2015, 17, 12553–12560.
59. P. Chand, S. Vaish and P. Kumar, Structural, optical and dielectric properties of transition metal (MFe₂O₄; M = Co, Ni and Zn) nanoferrites, Phys. B, 2017, 524, 53–63.
60. J. P. Singh, R. C. Srivastava, H. M. Agrawal, P. K. Giri, D. K. Goswami, A. Perumal and A. Chattopadhyay, Optical Behaviour of Zinc Ferrite Nanoparticles, AIP Conf. Proc., 2010, 1276, 137.
61. A. Amiri Zarandi, A. A. Sabbagh Alvani, R. Salimi, H. Sameie, S. Moosakhani, D. Poelman and F. Rosei, Self-organization of an optomagnetic CoFe₂O₄–ZnS nanocomposite: preparation and characterization, J. Mater. Chem. C, 2015, 3, 3935–3945.
62. M. Chakraborty, R. Thangavel, A. Biswas and G. Udayabhanu, Facile synthesis, and the optical and electrical properties of nanocrystalline ZnFe₂O₄ thin films, CrystEngComm, 2016, 18, 3095–3103.
63. J. Melsheimer and D. Ziegler, Band gap energy and Urbach tail studies of amorphous, partially crystalline and polycrystalline tin dioxide, Thin Solid Films, 1985, 129, 35–47.
64. L. Hannachi and N. Bouarissa, Band parameters for cadmium and zinc chalcogenide compounds, Phys. B, 2009, 404, 3650–3654.
65. P. N. Anantharamaiah and P. A. Joy, Enhancing the strain sensitivity of CoFe₂O₄ at low magnetic fields without affecting the magnetostriction coefficient by substitution of small amounts of Mg for Fe, Phys. Chem. Chem. Phys., 2016, 18, 10516–10527.
66. K. Kamala Bharathi, K. Balamurugan, P. N. Santhosh, M. Pattabiraman and G. Markandeyulu, Magnetocapacitance in Dy-doped Ni ferrite, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 172401.
67. S. Chikazumi and C. D. Graham, Physics of Ferromagnetism, Oxford University Press, Oxford, New York, 2nd edn, 1997.
68. S. R. Murthy and T. S. Rao, Magnetostriction of Ni-Zn and Co-Zn ferrites, Phys. Status Solidi A, 1985, 90, 631–635.
69. S. M. Patange, S. E. Shirsath, G. S. Jangam, K. S. Lohar, S. S. Jadhav and K. M. Jadhav, Rietveld structure refinement, cation distribution and magnetic properties of Al³⁺ substituted NiFe₂O₄ nanoparticles, J. Appl. Phys., 2011, 109, 053909.
70. U. B. Gawas, V. M. S. Verenkar and S. C. Mojumdar, Synthesis and characterization of Ni_0.6Zn_0.4Fe₂O₄ nano-particles obtained by auto catalytic thermal decomposition of carboxylato-hydrazinate complex, J. Therm. Anal. Calorim., 2011, 104, 879–883.
71. V. M. Andrade, R. J. C. Vivas, S. S. Pedro, J. C. G. Tedesco, A. L. Rossi, A. A. Coelho, D. L. Rocco and M. S. Reis, Magnetic and magnetocaloric properties of La_0.6Ca_0.4MnO₃ tunable by particle size and dimensionality, Acta Mater., 2016, 102, 49–55.
72. C.-b. Rong, D. Li, V. Nandwana, N. Poudyal, Y. Ding, Z. L. Wang, H. Zeng and J. P. Liu, Size-Dependent Chemical and Magnetic Ordering in L1₀-FePt Nanoparticles, Adv. Mater., 2006, 18, 2984–2988.
73. M. Farle, K. Baberschke, U. Stetter, A. Aspelmeier and F. Gerhardter, Thickness-dependent Curie temperature of Gd(0001)/W(110) and its dependence on the growth conditions, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 11571–11574.
74. J. P. Chen, C. M. Sorensen, K. J. Klabunde, G. C. Hadjipanayis, E. Devlin and A. Kostikas, Size-dependent magnetic properties of MnFe₂O₄ fine particles synthesized by coprecipitation, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 9288–9296.
75. B. Barbara, Louis Néel: His multifaceted seminal work in magnetism, C. R. Phys., 2019, 20, 631–649.
76. R. Sharma, P. Thakur, M. Kumar, N. Thakur, N. S. Negi, P. Sharma and V. Sharma, Improvement in magnetic behaviour of cobalt doped magnesium zinc nano-ferrites via co-precipitation route, J. Alloys Compd., 2016, 684, 569–581.
77. M. Mozaffari, J. Amighian and E. Darsheshdar, Magnetic and structural studies of nickel-substituted cobalt ferrite nanoparticles, synthesized by the sol–gel method, J. Magn. Magn. Mater., 2014, 350, 19–22.
78. K. V. Chandekar and K. M. Kant, Relaxation phenomenon and relaxivity of cetrimonium bromide (CTAB) coated CoFe₂O₄ nanoplatelets, Phys. B, 2018, 545, 536–548.
79. M. Wali, R. Skini, M. Khlifi, E. Dhahri and E. K. Hlil, A giant magnetocaloric effect with a tunable temperature transition close to room temperature in Na-deficient La_0.8Na_0.2−x□_xMnO₃ manganites, Dalton Trans., 2015, 44, 12796–12803.
80. S. Dash, A. V. Lukoyanov, Y. V. Knyazev, Y. I. Kuz'min, E. D. Baglasov, B. Weise, P. Kumar, M. Vasundhara and A. K. Patra, Impression of magnetic clusters, critical behavior and magnetocaloric effect in Fe₃Al alloys, Phys. Chem. Chem. Phys., 2019, 21, 10823–10833.
81. M. Jeddi, H. Gharsallah, M. Bejar, M. Bekri, E. Dhahri and E. K. Hlil, Magnetocaloric study, critical behavior and spontaneous magnetization estimation in La_0.6Ca_0.3Sr_0.1MnO₃ perovskite, RSC Adv., 2018, 8, 9430–9439.
82. M. Nasri, M. Triki, E. Dhahri, M. Hussein, P. Lachkar and E. K. Hlil, Investigation of structural, magnetocaloric and electrical properties of La_0.6Ca_0.4−xSr_xMnO₃ compounds, Phys. B, 2013, 408, 104–109.
83. K. Srinivasa Rao, S. V. Ranga Nayakulu, M. Chaitanya Varma, G. S. V. R. K. Choudary and K. H. Rao, Controlled phase evolution and the occurrence of single domain CoFe₂O₄ nanoparticles synthesized by PVA assisted sol-gel method, J. Magn. Magn. Mater., 2018, 451, 602–608.
84. A. Das, K. Kumar Bestha, P. Bongurala and V. Gorige, Correlation between size, shape and magnetic anisotropy of CoFe₂O₄ ferrite nanoparticles, Nanotechnology, 2020, 31, 335716.
85. R. S. Yadav, I. Kuřitka, J. Vilcakova, J. Havlica, J. Masilko, L. Kalina, J. Tkacz, V. Enev and M. Hajdúchová, Structural, magnetic, dielectric, and electrical properties of NiFe₂O₄ spinel ferrite nanoparticles prepared by honey-mediated sol-gel combustion, J. Phys. Chem. Solids, 2017, 107, 150–161.
86. S. E. Shirsath, S. S. Jadhav, B. G. Toksha, S. M. Patange and K. M. Jadhav, Influence of Ce⁴⁺ ions on the structural and magnetic properties of NiFe₂O₄, J. Appl. Phys., 2011, 110, 013914.
87. S. Dey, R. Gomes, R. Mondal, S. K. Dey, P. Dasgupta, A. Poddar, V. R. Reddy, A. Bhaumik and S. Kumar, Stable room temperature magnetic ordering and excellent catalytic activity of mechanically activated high surface area nanosized Ni_0.45Zn_0.55Fe₂O₄, RSC Adv., 2015, 5, 78508–78518.
88. V. Blanco-Gutiérrez, E. Climent-Pascual, R. Sáez-Puche and M. J. Torralvo-Fernández, Temperature dependence of superparamagnetism in CoFe₂O₄ nanoparticles and CoFe₂O₄/SiO₂ nanocomposites, Phys. Chem. Chem. Phys., 2016, 18, 9186–9193.
89. T. Sarkar, A. K. Raychaudhuri, A. K. Bera and S. M. Yusuf, Effect of size reduction on the ferromagnetism of the manganite La_1−xCa_xMnO₃ (x =0.33), New J. Phys., 2010, 12, 123026.
90. V. Šepelák, M. Myndyk, R. Witte, J. Röder, D. Menzel, R. H. Schuster, H. Hahn, P. Heitjans and K.-D. Becker, The mechanically induced structural disorder in barium hexaferrite, BaFe₁₂O₁₉, and its impact on magnetism, Faraday Discuss., 2014, 170, 121–135.
91. L. Hao, Y. Zhao, Q. Jiao and P. Chen, Synthesis of zinc–nickel ferrite nanorods and their magnetic properties, RSC Adv., 2014, 4, 15650–15654.
92. A. B. Nawale, N. S. Kanhe, S. A. Raut, S. V. Bhoraskar, A. K. Das and V. L. Mathe, Investigation of structural, optical and magnetic properties of thermal plasma synthesized Ni-Co spinel ferrite nanoparticles, Ceram. Int., 2017, 43, 6637–6647.
93. T. Slatineanu, A. R. Iordan, M. N. Palamaru, O. F. Caltun, V. Gafton and L. Leontie, Synthesis and characterization of nanocrystalline Zn ferrites substituted with Ni, Mater. Res. Bull., 2011, 46, 1455–1460.
94. S. Daengsakul, C. Thomas, C. Mongkolkachit and S. Maensiri, Effects of crystallite size on magnetic properties of thermal-hydro decomposition prepared La_1−xSr_xMnO₃ nanocrystalline powders, Solid State Sci., 2012, 14, 1306–1314.
95. P. Heitjans, M. Masoud, A. Feldhoff and M. Wilkening, NMR and impedance studies of nanocrystalline and amorphous ion conductors: lithium niobate as a model system, Faraday Discuss., 2007, 134, 67–82.
96. F. Bødker and S. Mørup, Size dependence of the properties of hematite nanoparticles, Europhys. Lett., 2000, 52, 217–223.
97. M. N. Akhtar, M. Saleem and M. A. Khan, Al doped spinel and garnet nanostructured ferrites for microwave frequency C and X-band applications, J. Phys. Chem. Solids, 2018, 123, 260–265.
98. M. N. Akhtar, M. Babar, S. Qamar, Z. ur Rehman and M. A. Khan, Structural Rietveld refinement and magnetic features of prosademium (Pr) doped Cu nanocrystalline spinel ferrites, Ceram. Int., 2019, 45, 10187–10195.
99. K. H. Wu, Y. C. Chang, H. B. Chen, C. C. Yang and D. N. Horng, Variable temperature electron paramagnetic resonance studies of the NiZn ferrite/SiO₂ nanocomposite, J. Magn. Magn. Mater., 2004, 278, 156–163.
100. B. Vigneashwari, S. Dash, A. K. Tyagi and S. A. Suthanthiraraj, Synthesis, Characterization, And Assembly Of CdSe Quantum Dot Array, Int. J. Nanosci., 2008, 7, 9–19.
101. J.-H. Lee, J. Jang, J. Choi, S. H. Moon, S. Noh, J. Kim, J.-G. Kim, I.-S. Kim, K. I. Park and J. Cheon, Exchange-coupled magnetic nanoparticles for efficient heat induction, Nat. Nanotechnol., 2011, 6, 418–422.
102. H. Y. Carr and E. M. Purcell, Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments, Phys. Rev., 1954, 94, 630–638.
103. E. Stefan, P. A. Connor, A. K. Azad and J. T. S. Irvine, Structure and properties of MgM_xCr_2−xO₄ (M = Li, Mg, Ti, Fe, Cu, Ga) spinels for electrode supports in solid oxide fuel cells, J. Mater. Chem. A, 2014, 2, 18106–18114.
104. E. J. W. Verwey and J. H. de Boer, Cation arrangement in a few oxides with crystal structures of the spinel type, Recl. Trav. Chim. Pays-Bas, 2010, 55, 531–540.
105. A. Lakshman, P. S. V. S. Rao, B. P. Rao and K. H. Rao, Electrical properties of In³⁺ and Cr³⁺ substituted magnesium–manganese ferrites, J. Phys. D: Appl. Phys., 2005, 38, 673–678.
106. M. Raghasudha, D. Ravinder, P. Veerasomaiah, K. M. Jadhav, M. Hashim, P. Bhatt and S. S. Meena, Electrical resistivity and Mössbauer studies of Cr substituted Co nano ferrites, J. Alloys Compd., 2017, 694, 366–374.
107. B. P. Rao and K. H. Rao, J. Mater. Sci., 1997, 32, 6049–6054.
108. E. J. W. Verwey and P. W. Haayman, Electronic conductivity and transition point of magnetite (“Fe₃O₄”), Physica, 1941, 8, 979–987.
109. A. A. Sattar, H. M. El-Sayed and M. M. El-Tabey, The effect of Al-substitution on structure and electrical properties of Mn-Ni-Zn ferrites, J. Mater. Sci., 2005, 40, 4873–4879.
110. H. Chouaya, M. Smari, I. Walha, E. Dhahri, M. P. F. Graça and M. A. Valente, The effect of bismuth on the structure, magnetic and electric properties of Co₂MnO₄ spinel multiferroic, J. Magn. Magn. Mater., 2018, 451, 344–350.
111. R. Hamdi, A. Tozri, M. Smari, E. Dhahri and L. Bessais, Structural, magnetic, magnetocaloric and electrical studies of Dy_0.5(Sr_1−xCa_x)_0.5MnO₃ manganites, J. Magn. Magn. Mater., 2017, 444, 270–279.
112. A. J. Miller, A. Rotaru, D. C. Arnold and F. D. Morrison, Effect of local A-site strain on dipole stability in A₆GaNb₉O₃₀ (A = Ba, Sr, Ca) tetragonal tungsten bronze relaxor dielectrics, Dalton Trans., 2015, 44, 10738–10745.

---

Footnote

† Electronic supplementary information (ESI) available: Relations and formulae used to calculate various structural parameters, deconvoluted Raman spectra at 300 K of NZFAO samples annealed at different temperature fitted with the Lorentzian function, representative fitted high field magnetization of annealed Ni–Zn–Al ferrite at room temperature to the saturation approach law, representative fitted resistivity curve of Ni600, Ni900, and Ni1200 samples to Arrhenius equation. See DOI: 10.1039/d0ra05522k

---