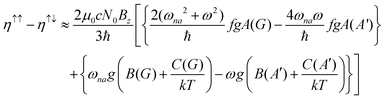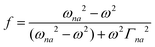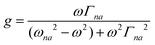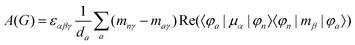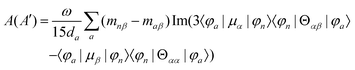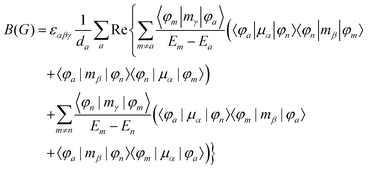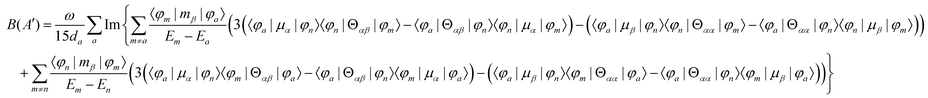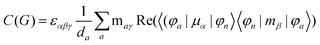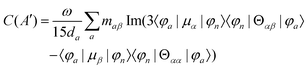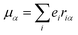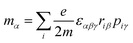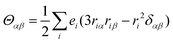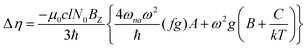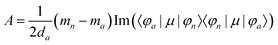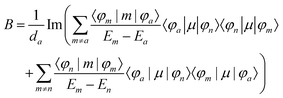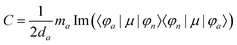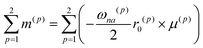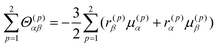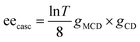Recent advances in studies on the magneto-chiral dichroism of organic compounds
Received
30th September 2019
, Accepted 15th November 2019
First published on 20th November 2019
Abstract
Magneto-chiral dichroism (MChD) is an interesting phenomenon in which the absorbance of a chiral molecule depends on the direction of the magnetic field. As the MChD of two enantiomers is opposite in nature, MChD has received considerable attention for the development of magneto-optical devices and new asymmetric synthetic methods, as well as being an explanation for the origin of the homochirality of life. In this perspective, the theoretical background behind MChD is introduced, and then, the first examples of metal complexes and aromatic π-conjugated systems are discussed. Furthermore, the electronic properties of aromatic π-conjugated systems, such as orbital angular momentum and exciton chirality, are theoretically explained, and the possibility of MChD-based photoresolutions is described.
 Kazuyuki Ishii | Kazuyuki Ishii received his Ph.D. in 1996 from Tohoku University under the supervision of Prof. Seigo Yamauchi, and subsequently worked as a research associate in the laboratory of Prof. Nagao Kobayashi (April 1996–March 2006, Tohoku University). He is currently a full Professor at the Institute of Industrial Science of The University of Tokyo. His interests include homochirality of life, photodynamic therapy, fluorescence bioimaging, time-resolved ESR spectroscopy, and chiroptical spectroscopy. |
 Shingo Hattori | Shingo Hattori earned his Ph.D. in chemistry from The University of Tokyo in 2017 under the direction of Professor Kazuyuki Ishii. He worked as a postdoctoral researcher in the laboratory of Professor Kazuyuki Ishii at The University of Tokyo from 2017 to 2019. Since 2019, he has been an assistant professor at Yokohama City University. His interests include photochemistry of organic chiral compounds and metal complexes. |
 Yuichi Kitagawa | Yuichi Kitagawa obtained his Ph.D. (2012) from the School of Engineering, University of Tokyo. He was a research fellow of the Japan Society for the Promotion of Science (JSPS) (2013) at Ritsumeikan University. He was an assistant professor (2014–2018) at Hokkaido University. Since 2019 he has been a lecturer at Hokkaido University. His interests are molecular photophysics and photochemistry. He is now studying the luminescence, chiroptical, and magneto-optical properties of lanthanide(III) complexes. |
Introduction
Magneto-chiral dichroism (MChD) is a magneto-optical effect in which the absorption coefficient of a chiral molecule in an unpolarised light beam changes depending on whether an externally applied magnetic field is parallel or antiparallel to the direction of light propagation (Fig. 1).1,2 As the MChD of two enantiomers is opposite in nature, this phenomenon is of great interest, receiving considerable attention for the development of novel magneto-optical devices and new asymmetric synthetic methods. MChD is also a possible explanation for the origin of the homochirality of life.3–16
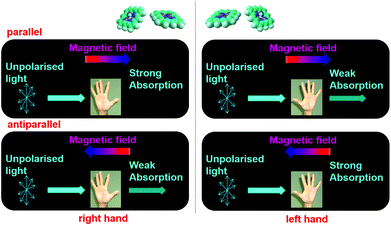 |
| | Fig. 1 Illustration of MChD as a magneto-optical effect. The absorption coefficient of a chiral molecule is different for an unpolarised light beam when an externally applied magnetic field is parallel or antiparallel to the direction of light propagation. The MChD effects of two enantiomers are opposite. | |
Early research on MChD had purely theoretical roots. Wagnière and Meier first calculated the magnetically induced changes for the absorption and emission rates of chiral molecules.1 Based on these results and molecular theory, Barron and Vrbancich later showed that the absorption coefficient of a chiral system exposed to unpolarised light is different when an externally applied magnetic field is parallel or antiparallel to the direction of light propagation, in addition to magneto-chiral birefringence.2,3 This difference occurs even for unpolarised light, and it is opposite for two enantiomers. Compounds that exhibit both strong circular dichroism (CD) and magnetic circular dichroism (MCD) are expected to show MChD. Although CD and MCD effects are seemingly linked, the origins of CD and MCD, which are molecular chirality and orbital angular momentum, respectively, are completely different.
Following these theoretical predictions, MChD was experimentally confirmed for the first time in the 5D0 → 7F1,2 luminescent transition of a europium(III) complex.4 MChD observations have subsequently been reported for inorganic compounds containing transition metal or lanthanide ions, π–π* transitions in organic compounds, and photoresolution based on MChD. Even 20 years after the first observation of MChD, reports on MChD observations have been limited due to both its weak manifestation arising from the cross effect of CD and MCD and the lack of conventional measurement systems. However, despite its challenges, MChD has attracted considerable attention due to the interplay between chirality and magnetism, resulting in the development of not only novel materials but also measurement systems using various electromagnetic waves. The observation of MChD in compounds related to living beings has further led to studies to explore the relationship between MChD and living systems, such as understanding the origin of the homochirality of life.
In this perspective, we describe the recent progress of MChD focusing on organic compounds. In the “Theoretical background” section, the basic theory of MChD is described for readers to understand the principles of MChD. In the “Magneto-chiral dichroism of metal compounds” section, historically representative MChD observations are introduced. In the “Magneto-chiral dichroism of aromatic π-conjugated systems” section, MChD observations of aromatic π-conjugated systems are illustrated, with the origin of the MChD intensity theoretically described in detail. In the “Photoresolution based on magneto-chiral dichroism” section, enantioselective photochemical reactions are introduced in metal complexes and organic polymers. Finally, future directions are described in terms of asymmetric synthesis and provide a clue to the homochirality of life.
Theoretical background
The MChD intensity in isotropic media is expressed as follows.2,3| | 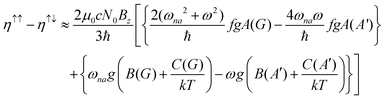 | (1) |
| | 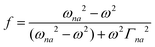 | (2) |
| | 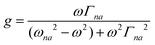 | (3) |
where N0 is the number density, μ0 is the vacuum permeability, and c is the velocity of light in a vacuum. For a transition between the ground state, a, and the excited state, n, the variables f and g represent the dispersion-type and integral-type line shape functions, respectively; ωna and Γna correspond to the angular frequency of the transition energy and the full bandwidth at half maximum, respectively.
MChD effects can be classified into three general terms referred to as the A-term, B-term, and C-term, which depend on the degenerate states and should not be confused with spin sublevel degeneracy. Each general term can be further classified with G or A′, ultimately leading to six possible terms. The magneto-chiral A-terms, A(G) and A(A′), are observed for degenerate electronic states arising from the Zeeman effect, while the magneto-chiral B-terms, B(G) and B(A′), are observed for nondegenerate electronic states that interact with each other via magnetic dipole moments. The magneto-chiral C-terms, C(G) and C(A′), are temperature-dependent due to the change in the Boltzmann distribution. These six terms are expressed by the following equations:
| | 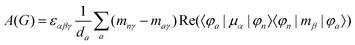 | (4) |
| | 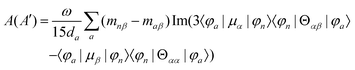 | (5) |
| | 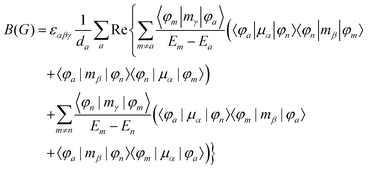 | (6) |
| | 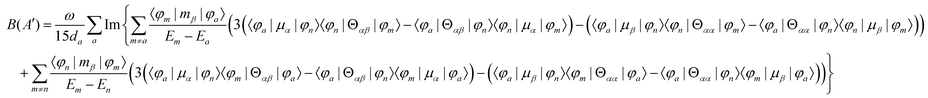 | (7) |
| | 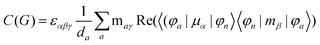 | (8) |
| | 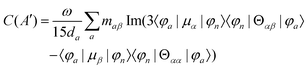 | (9) |
where
ψi and
Ei are the wavefunction and energy of the
i state, respectively (
i =
a,
m, or
n),
da represents the degeneracy of the ground state, and
εαβγ denotes the alternating tensor (Levi-Civita). The electric dipole (
μα), magnetic dipole (
mα), and electric quadrupole (
Θαα) operators are expressed as follows:
| | 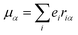 | (10) |
| | 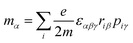 | (11) |
| | 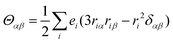 | (12) |
where
e and
m denote the charge and mass of an electron, respectively,
riα is the position operator, and
pir is the momentum operator. When the terms related to 1/(
Em −
Ea) are negligible because of the large excitation energy, the MChD intensity therefore corresponds to the electric dipole, magnetic dipole, and electric quadrupole moments for the transition between the
a and
n (or
m) states in addition to the magnetic dipole moments between
n and
m states.
The matrix elements resulting in CD and MCD intensities are similar to those for the MChD intensity.5,6 The CD intensity corresponds to an imaginary part of the scalar product of the electric dipole and magnetic dipole moments for the transition between the a and n states; only chiral molecules exhibit CD.
| | | R = Im{〈φa|μ|φn〉·〈φn|m|φa〉} | (13) |
Furthermore, the MCD intensity corresponds to the transition electric dipole moment between the a and n states and the magnetic dipole moment between the n and m states; MCD is a property of all matter.
| | 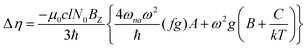 | (14) |
| | 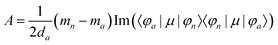 | (15) |
| | 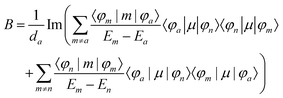 | (16) |
| | 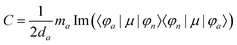 | (17) |
Since the matrix elements for the CD and MCD intensities are similar to those for the MChD intensity,5,6 the following equation can only be used when the MCD spectrum is dominated by the Faraday A-term.5
Here, the g values, gMChD, gCD and gMCD, indicate the ratio of the absorption difference and the total absorption. MChD is a cross effect between the CD and MCD effects, and therefore, the magnitude of gMChD can be roughly estimated from the product of gCD and gMCD.5 Thus, MChD is expected to be experimentally observed for chiral compounds that show both strong CD and MCD, and would be weak.
Magneto-chiral dichroism of metal compounds
After theoretical predictions were made, Rikken and Raupach reported the first experimental MChD observations in the 5D0 → 7F1,2 luminescence of chiral europium(III) tris(3-trifluoroacetyl-±-camphorato), Eu((±)tfc)3.4Fig. 2 shows the MChD spectra for both enantiomers of the Eu3+ complex. The large orbital angular momentum of the f orbitals has a pronounced effect on MChD, with the Eu3+ complex exhibiting considerable MCD in the f–f transitions.17 The unpolarised luminescence intensity changes when an externally applied magnetic field is switched between being parallel and antiparallel to the direction of light propagation. A phase-sensitive detection method and alternating magnetic field directions were employed in order to increase the signal-to-noise ratio. The 5D0 → 7F1 and 5D0 → 7F2 transitions produced MChD signals that were opposite in sign for the two enantiomers. Moreover, the MChD intensity is proportional to the magnetic field strength (inset of Fig. 2). For the 5D0 → 7F1 transition, the experimental gMChD value (5 × 10−3) is ∼10 times greater than the gCD × gMCD cross product (4 × 10−4).5,6
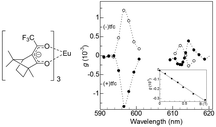 |
| | Fig. 2 A molecular structure of tris(3-trifluoroacetyl-±-camphorato)europium(III) (left) and magneto-chiral luminescence anisotropy of Eu((±)tfc)3 complexes in deuterated dimethyl sulfoxide (right). The inset shows a magnetic field dependence of the magneto-chiral anisotropy (λex = 350 nm, λem = 615.8 nm). Reproduced from ref. 4 with permission from Springer Nature. | |
Rikken and co-workers investigated the MChD effects of chiral uniaxial crystals of α-NiSO4·6H2O,5 which exhibited intense CD and MCD signals.18,19 It was confirmed that MChD was uninfluenced not only by light intensity, but also by reversing the crystals towards the direction of light propagation. The intensity calculated based on the Baranova model is consistent with the observed intensity, but the calculated and observed spectra differ significantly. The possibilities of cascaded MChD were also investigated in this system. When unpolarised light penetrates optically active materials, it becomes circularly polarised light (CPL). Since a magnetic field induces MCD effects in this case, the transmitted light intensity depends on the relationship between the direction of light propagation and the magnetic field direction. This is referred to as cascaded MChD, and it essentially appears as pure MChD. Pure MChD can be distinguished from cascaded MChD by examining concentration dependencies. When the optical path lengths are fixed, pure MChD is linearly proportional to the concentration of MChD-active species. On the other hand, cascaded MChD is proportional to the square of the concentration of the active species because it is proportional to the product of the concentration of CD-active and MCD-active species. By comparing the cascaded MChD spectrum with the MChD spectra of α-NiSO4·6H2O at different concentrations, a pure MChD effect can be identified. Rikken and coworkers also developed a multichannel MChD spectrometer, in which the optical properties of the sample are modulated by an alternating external magnetic field. By using this spectrometer, MChD of α-NiSO4·6H2O crystals was examined.20
Various materials have been investigated in order to enhance MChD. Train et al. reported the first observation of MChD in an enantiopure, chiral ferromagnet using chromium–manganese two-dimensional oxalate layers.8 The MChD intensity was enhanced by a factor of 17 in the ferromagnetic phase. Arima and co-workers reported the very intense MChD effects of CuB2O4, which exhibited magnetically induced chirality.9 The observed MChD was approximately 104 times greater than that observed previously for paramagnetic molecules. They also investigated the MChD of right- and left-handed CsCuCl3 crystals in strong magnetic fields (up to 14.5 T), identifying a change in the absorption coefficient from the d–d transition of intra-atomic Cu2+ ions.21 Rikken and co-workers investigated chiral magnetic nanohelices with critical dimensions comparable to the ferromagnetic domain size.22 A chiral Ni2+ film consisting of an array of nanohelices ∼100 nm in length exhibited a MChD anisotropy factor (gMChD) of ∼10−4 T−1 at room temperature, which is the first report on MChD in a material with structural chirality on the order of the wavelength of light. Taniguchi et al. demonstrated strong MChD for visible light emission using a chiral Tb3+ complex, in which the MChD luminescence signal reaches ∼16% at 14 T.23 They also investigated heterometallic systems with short-range correlations (e.g., cyano-bridged copper(II)–chromium(III) coordination polymers) and demonstrated that MChD in d–d transitions of Cu2+ coordinated to chiral ligands, which is mainly proportional to the magnetisation of the local Cu2+ centre.24 Yannopapas et al. theoretically investigated magnetic nanoparticle helices coiled around plasmonic gold nanorods, calculating very strong MChD for this system.25,26
In addition to the UV-vis-NIR region, MChD effects have also been investigated in the X-ray region. Ceolín investigated the hard X-ray absorption spectra of {Tb[Ni(pro)2]6}3+ (pro = L- or D-prolinate), discovering a large MChD (1%) at room temperature.27 Sessoli and co-workers investigated the element selective hard X-ray MChD of enantiopure crystals of two isostructural molecular helicoidal chains comprising either Co2+ or Mn2+ ions.28 A strong MChD (>3%) was observed in the cobalt chain system, whereas it was practically absent for the manganese derivative.
In the THz and GHz regions, Tokura and co-workers investigated the MChD phenomena based on spin excitation using Ba2CoGe2O7, a square-lattice antiferromagnet that undergoes a magnetic field driven transition to a chiral form.29 Complete MChD (∼100%) in the THz region occurs as a result of spin excitation. They also investigated the MChD of multiferroic materials, such as CuFe1−xGaxO2 (x = 0.035), Ba3NbFe3Si2O14, MnWO4, and Cu2OSeO3. The collective spin excitations active for both electric and magnetic fields are referred to as electromagnons; the electromagnon resonance for the screw spin helimagnet CuFe1−xGaxO2 (x = 0.035) exhibited a very large MChD effect (400%).30–33 Ueda and co-workers investigated the MChD of a metamaterial consisting of a chiral copper structure and ferrite rod, determining the directional differences of X-band microwaves to be 10−3 at 200 mT.34,35 Microwave MChD was observed in the non-centrosymmetric magnet CuB2O4 by Nii et al.36
Magneto-chiral dichroism of aromatic π-conjugated systems
Magneto-chiral dichroism of organic compounds
As described in the previous section, several MChD observations have been reported for inorganic compounds.4–9,20–36 This is a retrospectively reasonable finding, since MCD, a significant contributor to MChD, is intensified by the d (or f) orbital-based degeneracy and angular momentum of metals. This advantage does not exist for organic compounds, making the MChD of organic compounds associated with living beings more difficult to establish; a revelatory research effort identified that the orbital angular momentum of organic aromatic compounds helps overcome this challenge. The magnitude of orbital angular momentum corresponds to the magnetic quantum number, ml. The π molecular orbitals of organic aromatic compounds are quantised by ml (similar to atomic orbitals), and the maximum |ml| values of the π molecular orbitals of organic aromatic compounds increase with an increase in the size of π-conjugated systems, as described in detail in the “Theoretical explanations for magneto-chiral dichroism of aromatic π-conjugated systems” section.37,38
Ishii and co-workers attempted to observe the first MChD of organic compounds associated with living beings.10 To achieve this, the chiral J-aggregates of water-soluble tetraarylporphyrins were employed. Porphyrin molecules possess a large aromatic π-conjugated system with a large orbital angular momentum, resulting in intense MCD signals. Moreover, a very intense CD signal is obtained by exploiting the exciton chirality that exists within the twisted configurations between porphyrin constituents.39,40Fig. 3 shows the UV-vis, CD, and MCD spectra of the protonated forms of meso-tetrakis(4-sulfonatophenyl)porphine (H4TPPS4, Fig. 3a) and the chiral J-aggregates of H4TPPS4 (Fig. 3b). The chiral J-aggregates were prepared by adding chiral tartaric acid, which induces Coulomb interactions between the positively charged protonated pyrroles and the negatively charged sulfonate groups.10,41,42 Formation of the J-aggregates causes a considerable bathochromic shift of the Soret band (π–π* transition) to 490 nm owing to the exciton interactions between the H4TPPS4 constituents (Fig. 3e). In contrast to the unobservable CD signal of the achiral H4TPPS4 monomer, the addition of chiral tartaric acid induces a very intense, reproducible CD signal in the J-band region; positive/negative and negative/positive CD spectral patterns are induced by the addition of L- and D-tartaric acids, respectively (Fig. 3f). Therefore, the enantioselective formation of J-aggregates of H4TPPS4 could be controlled. Density functional theory (DFT) calculations (B3LYP/6-31G*) indicate that the porphyrin units interact to form left-handed helical, planar, or right-handed helical structures (Fig. 3b–d). The right- or left-handed helical structure is preferably formed when the pyrrole protons in the upper and lower porphyrin interact with the sulfonic acid functional groups in the lower and upper porphyrin, respectively. This structure is preferred because the Coulomb interactions between the sulfonic acid groups and the pyrrole protons are more favourable owing to reduced steric hindrance. The planar structure is generated when the pyrrole protons involved in the interaction are located on the right- and left-hand sides of the upper and lower porphyrins, respectively. For a chiral tetramer adopting the optimised helical and planar structures, the experimentally obtained dispersion-type CD spectral pattern can be reproduced by calculations based on the exciton chirality method. The MCD spectrum of the H4TPPS4 monomer shows an intense, dispersion-type signal that corresponds to the Soret band, which is labelled the Faraday A-term (Fig. 3g). This behaviour is a reflection of the orbital angular momentum that derives from the large aromatic π-conjugated system of the porphyrin in addition to the degeneracy of the Soret band. In the case of the chiral J-aggregates of H4TPPS4, an intense, integral-type MCD signal (Faraday B-term) is observed for the J-band (490 nm), indicative of nondegeneracy.
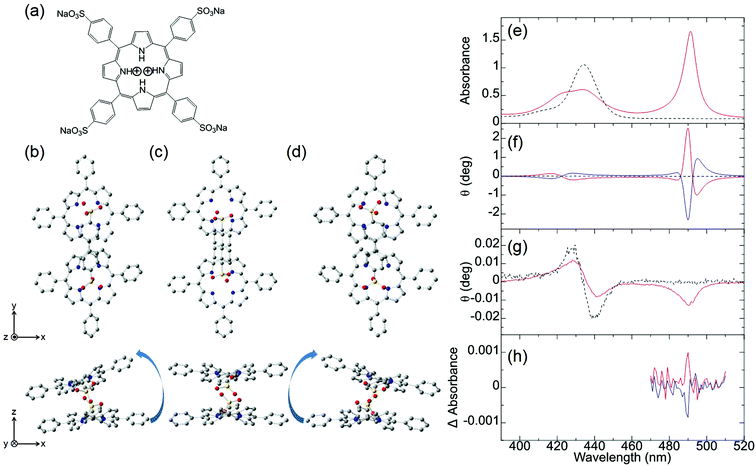 |
| | Fig. 3 H4TPPS4 and chiral J-aggregates of H4TPPS4. (a) The molecular structure of H4TPPS4 and optimised H4TPPS1 dimer configurations as (b) left-handed helical, (c) parallel, and (d) right-handed helical structures. The (e) UV-vis, (f) CD, (g) MCD, and (h) MChD spectra of H4TPPS4 (black broken lines) and the chiral J-aggregates of H4TPPS4 (solid lines). The chiral J-aggregates of H4TPPS4 were prepared by the addition of L-tartaric acid (red solid line) or D-tartaric acid (blue solid line). Reproduced from ref. 10 with permission from John Wiley and Sons. | |
Because the very intense CD signal and the MCD signal are simultaneously observed in the J-band region of the chiral J-aggregates of H4TPPS4, MChD signals were evaluated in the J-band region by measuring the difference in absorbance when the externally applied magnetic field was parallel and antiparallel to the direction of light propagation (Fig. 3h). When the J-aggregates are prepared by adding L-tartaric acid, a sharp, positive MChD signal is observed at 490 nm; the MChD signal of the J-aggregates prepared using D-tartaric acid is observed at the same wavelength, but the sign is negative (Fig. 3h). The peak position (490 nm) of the MChD spectrum is identical to that of the spectrum obtained from the product of the CD and MCD spectra. This finding is consistent with previous reports,1,2,6 and thus, the presence of MChD in organic compounds was demonstrated for the first time.
Magneto-chiral dichroism based on π–π* transitions
In addition to the MChD observed for chiral J-aggregates of water-soluble tetraarylporphyrins, it is important to confirm the presence of MChD for the π–π* transitions by demonstrating its existence in other systems. The observation of MChD is important, not only for clarification of asymmetry observed in biological systems, but also for the development of novel applications, such as asymmetric synthetic methods and magneto-optical devices. Ishii and co-workers demonstrated the second example of MChD for π–π* transitions using chiral J-aggregates of zinc(II) chlorins (ZnChls, Fig. 4a and b).11 This supramolecular system is a model compound for the light-harvesting antennas in green photosynthetic bacteria (i.e., chlorosomes), which are formed through the self-assembly of a large number of bacteriochlorophyll molecules without the assistance of proteins. In this system, the Zn2+ ion was employed as the central metal ion instead of the Mg2+ ion (as found in Nature), because Zn chlorins are more stable than Mg chlorins. In order to acquire an intense CD signal based on exciton chirality, a hydrophilic tetraoxyethylene chain was incorporated into ZnChl. The J-aggregates of ZnChls were prepared by diluting a methanol solution of ZnChl with a 99-fold volume of water.
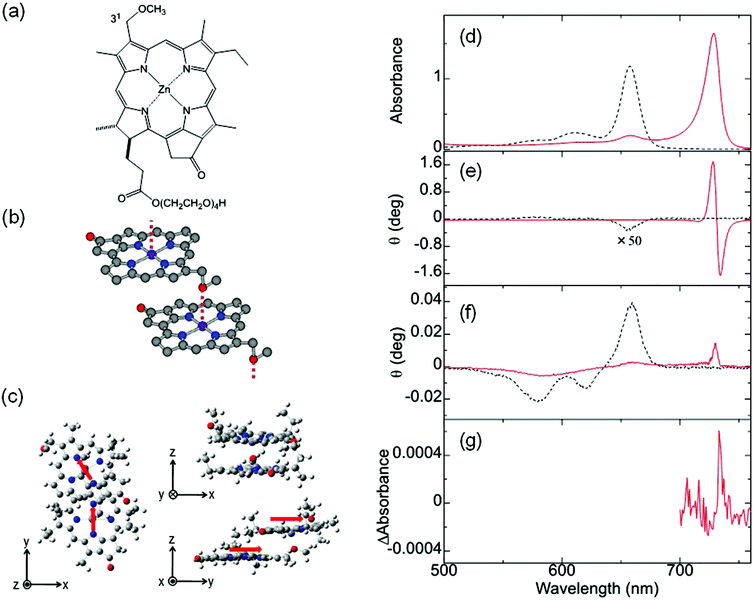 |
| | Fig. 4 ZnChl, a model compound of light-harvesting antenna. Molecular structures of (a) ZnChl, (b) J-aggregates of ZnChls, and (c) the optimised ZnChl dimer. The (d) UV-vis, (e) MCD, (f) CD, and (g) MChD spectra of the chiral J-aggregates of ZnChls. The red arrows indicate the transition electric dipole moments of the ZnChl constituents at the Qy band. Reproduced from ref. 11 with permission from The Royal Society of Chemistry. | |
The UV-vis, MCD, and CD spectra in the Q band region of the ZnChl monomer and chiral J-aggregates of ZnChls are shown in Fig. 4. The UV-vis spectrum of the ZnChl monomer shows typical Q absorption bands for metallochlorins at 658, 611, and 581 nm, which are attributed to the Qy(0,0), Qy(1,0), and Qx(0,0) bands, respectively. In the MCD spectrum of the ZnChl monomer, these bands show intense integral-type MCD signals (the Faraday B-term), which indicate the nondegeneracy of the excited states. In the UV-vis spectrum of the chiral J-aggregates of ZnChls, the Qy band showed a remarkable bathochromic shift to 729 nm due to the exciton interaction between ZnChl constituents, whereas the shift of the Qx band is very small. This indicates that the long axis of the J-aggregates is nearly parallel to the transition dipole moment of the Qy band. Thus, J-aggregation increases the energy separation between the Qy and Qx bands (monomer, 2120 cm−1; J-aggregates, 3510 cm−1). This is consistent with the relatively weak MCD intensity of the Qy band of the J-aggregates (one-third weaker than that of the corresponding monomer) because the Faraday B-term is inversely proportional to the energy separation. The full width at half maximum of the J-band is very narrow (280 cm−1), which indicates that the ZnChl chromophores form highly ordered J-aggregates. DFT calculations (B3LYP/6-31G*) for the ZnChl dimer indicate that the 31-methoxy group of one ZnChl coordinates to the Zn2+ ion of the other ZnChl. In addition, the transition electric dipole moments of the Qy band are calculated to be almost parallel to the long axis of the dimer, which is consistent with the observed J-band. The chiral J-aggregates of ZnChls show an intense, inverse sigmoidal-shaped CD signal in the J-band region (red line in Fig. 4e), whereas the CD signals of the corresponding monomer that are attributed to the chiral centre (Fig. 4a, positions 17 and 18) are very weak (black line in Fig. 4e). The inverse sigmoidal-shaped CD spectral pattern originates from exciton chirality owing to the twisted configuration between the chromophores with a large transition electric dipole moment; this configuration is consistent with the optimised structure (Fig. 4c). A positive MChD signal at 733 nm (Fig. 4g) is identical to that of the spectrum obtained from the product of the CD and MCD spectra of chiral J-aggregates of ZnChls, which is similar to that observed for the chiral J-aggregates of H4TPPS4. Further, the MChD signal for the chiral J-aggregates of ZnChls was observed at 5 T using a MChD measurement with a pulsed electromagnet (Fig. 5).43 From the viewpoint of photosynthesis, observation of MChD in the light-harvesting antenna model indicates the possibility of MChD occurring during the light-harvesting process. This is an intriguing twist to our understanding of photosynthesis, as novel magnetic field effects may play a nuanced yet important role in light-harvesting in Nature.44–51 Jiang and co-workers reported the third example of MChD for π–π* transitions using chiral rare earth triple-decker complexes comprising one phthalocyanine and two porphyrin ligands, which exhibit single-molecule magnet (SMM) behaviour.12 These MChD observations based on the π–π* transition emphasise that on the basis of π electronic properties (e.g., orbital angular momentum and exciton chirality), MChD should be observed in the aggregates of conventional organic aromatic compounds.
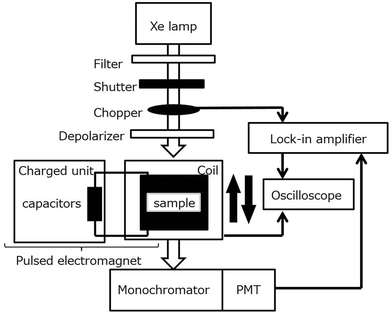 |
| | Fig. 5 Block diagram of a typical pulsed magneto-chiral dichroism measurement system. Reproduced from ref. 43 with permission from Elsevier. | |
Theoretical explanations for the magneto-chiral dichroism of aromatic π-conjugated systems
Based on eqn (1), the MChD intensity is dependent on four matrix elements: (1) the transition electric dipole moments between the a and n (or m) states, (2) the transition magnetic dipole moments between the a and n (or m) states, (3) the transition electric quadrupole moments between the a and n (or m) states, and (4) the magnetic dipole moments between the n and m states.
The MCD intensity is related to the intensity of MChD. The magnetic dipole moments between the n and m states correspond to the orbital angular momentum between the n and m states as evaluated by MCD. Based on the Zeeman effects, both MCD and MChD are intensified by the d (or f) orbital-based degeneracy and angular momentum of metals. In the case of organic aromatic compounds, however, ml, which is related to the orbital angular momentum, increases with increasing π-conjugated systems.37,38 If we consider diamagnetic aromatic compounds, the MCD intensity is proportional to the orbital angular momentum between the excited states. The magnitude of the orbital angular momentum therefore corresponds to the magnetic quantum number, ml. Similar to atomic orbitals, π molecular orbitals of aromatic π-conjugated systems are quantised by ml (Fig. 6a). Although the maximum ml values of d orbitals (ml = 0, ±1, ±2) and f orbitals (ml = 0, ±1, ±2, ±3) are 2 and 3, respectively, those of π molecular orbitals increase as the size of the π-conjugated system increases.37,38 For example, the ml values of the HOMO and LUMO of C16H162−, which is a simple model of a porphyrin analogue, are ±4 and ±5, respectively. In this case, the orbital angular momentum of the excited states corresponds to ML = ±1 or ±9 (Fig. 6b). Thus, in spite of weak absorbance, strong MCD signals are observed for the absorption band with ML = ±9 (Fig. 6c and d). Therefore, large aromatic π-conjugated systems, such as porphyrinic compounds, are appropriate for intensifying not only MCD but also MChD.
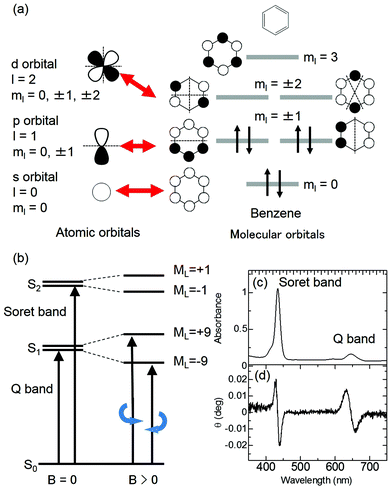 |
| | Fig. 6 Representative explanation for the intensification of MCD by the orbital angular momentum of π-conjugated systems. (a) The relationship between atomic orbitals and molecular orbitals. (b) The energy state diagram of absorption (left) and MCD (right) for π-conjugated systems. (c) UV-vis and (d) MCD spectra of the protonated form of meso-tetrakis(4-sulfonatophenyl)porphine (H4TPPS4). Reproduced from ref. 14 with permission from OSA Publishing. | |
The CD intensity is also correlated with the MChD intensity. The CD intensity is a function of an imaginary part of the cross product of the transition electric dipole moment and the transition magnetic dipole moment.39,40 Because the electric dipole moment and the magnetic dipole moment are associated with linear and rotational electronic motions, respectively, the requisite conditions for coexistence are severe. Therefore, CD transitions should be very weak in conventional systems, yet contrary to the previous explanation, CD transitions can actually be very intense due to exciton chirality; enhancement of CD intensity induced by exciton chirality originates from the approximation from the transition magnetic dipole moment to the transition electric dipole moments of the constituting chromophores. For example, when a dimer is formed by two chromophores (Fig. 7a), low and high exciton states are generated due to the exciton interaction between the chromophores (Fig. 7b). When the transition electric dipole moments of the chromophores are twisted in a chiral dimer, the transition magnetic moment is approximated by the vector products of transition electric dipole moments and position vectors according to:
| | 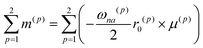 | (19) |
where
r0(p) and
μ(p) are the position vector and the transition electric dipole moment for a
p unit, respectively. In addition, the intrinsic magnetic dipole moment can be neglected since it is sufficiently small for the π–π* transition. Thus, strong CD intensities can be observed for a system such as an aromatic compound with a very intense transition electric dipole moment. This phenomenon is called exciton chirality.
38,39 Because the CD sign of the low and high exciton states is opposite, dispersion-type CD spectra are observed for conventional chiral dimers. Furthermore, the absolute configuration of chromophores in the dimer can be determined from the analysis of the CD spectra. Therefore, when aromatic compounds with large transition electric dipole moments (
e.g., porphyrins and porphyrin analogues) are twisted, as is the case in the chiral J-aggregates of porphyrins, both MChD and CD are strengthened.
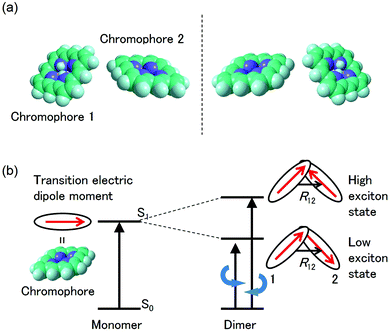 |
| | Fig. 7 Explanation of exciton chirality using a porphyrin dimer. (a) Molecular structures of a pair of enantiomers. (b) The energy state diagram of the CD transitions for one of the enantiomers. | |
Finally, the transition electric quadrupole moments between the a and n (or m) states can also be related to exciton chirality. Based on the exciton chirality, the quadrupole moment can be rewritten using the transition electric dipole moments of the constituting chromophores as follows:3,40
| | 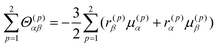 | (20) |
and this is negligible since it is also sufficiently small for the π–π* transition. Using these equations, MChD based on exciton chirality can thus be reproduced from the wavefunctions of the exciton states.
Photoresolution based on magneto-chiral dichroism
It has been well established that circularly polarised light (CPL) can induce enantioselective photochemical reactions (photoresolution) on the basis of CD (i.e., differences in absorption coefficients between two enantiomers from CPL).52–54 The enantiomeric excess (ee) owing to the CPL induced photoresolution is given by gCD/2. The ee value would be small even from pure CPL from synchrotron radiation because the gCD values of organic compounds are small. On the other hand, after the theoretical prediction by Barron,55,56 Rikken and Raupach studied MChD-based photochemistry that results in enantioselective reactions.57 Here, based on the magnetic field effect of the MChD mechanism, an observable photoresolution can be expected even though unpolarised light was used. A thermally racemic mixture of Δ- and Λ-chromium(III) tris(oxalato) ([Cr(ox)3]3−) was employed. The photoresolution of this complex has been extensively studied with CPL;52 one enantiomer should be preferably formed under irradiation with CPL, which is selectively absorbed by the other enantiomer, since ligand dissociation is accelerated by photoexcitation. Thus, this photoresolution is much faster than thermal racemisation. Because one enantiomer selectively absorbs unpolarised light under a magnetic field that is parallel (or antiparallel) to the direction of light propagation, an ee value is obtained for the racemic mixture of Δ- and Λ-[Cr(ox)3]3− complexes owing to magneto-chiral anisotropy.
Similar to photoresolution with CPL, the ee owing to MChD is given by gMChD/2. For the spin-forbidden transition from the ground state (4A2g) to the excited state (2Eg) of [Cr(ox)3]3−, both gCD and gMCD values are very large; therefore, a large gMChD value can be expected. Fig. 8b shows the ee due to MChD, where the 4A2g → 2Eg transition was selectively excited. When the magnetic field direction was parallel to the direction of light propagation, the ee/B value was 1.0 × 10−5 T−1. On the other hand, when the magnetic field direction was perpendicular to the direction of light propagation, no significant ee was observed. These results are in agreement with the properties of MChD, thus demonstrating photoresolution based on MChD.
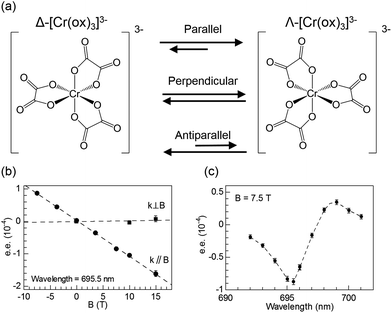 |
| | Fig. 8 (a) Equilibrium between two enantiomers of [Cr(ox)3]3−, (b) enantiomeric excess of [Cr(ox)3]3− obtained after irradiation with unpolarised light (695.5 nm; either parallel (k∥B) or perpendicular (k⊥B) to the magnetic field direction) as a function of the magnetic field, and (c) enantiomeric excess of [Cr(ox)3]3− obtained after irradiation with unpolarised light as a function of the irradiation wavelength (magnetic field of 7.5 T is parallel to the direction of light propagation). Reproduced from ref. 57 with permission from Springer Nature. | |
Fig. 8c shows the excitation wavelength dependence of the ee under 7.5 T, in which a correlation between the dispersion-type spectrum and A-term is observed. Since the ee due to MChD is approximated as (gCD × gMCD)/2 based on eqn (18), the gMCD/B (1.2 × 10−3 T−1) and gCD (2.2 × 10−3) values at 701 nm were used to determine an ee/B value of 1.3 × 10−6 T−1, which is close to the observed ee/B value (1.7 × 10−6 T−1). In addition to pure MChD, cascaded MChD should also be present. The ee due to cascaded MChD is expressed as follows:
| | 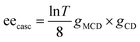 | (21) |
Here,
T denotes the transmittance. Using
eqn (21), the ee
casc/
B value was calculated as 5 × 10
−7 T
−1 at 701 nm, which is an order of magnitude smaller than the observed ee/
B value of 1.7 × 10
−6 T
−1. Thus, the observed ee resulting from the photochemical reactions of [Cr(ox)
3]
3− predominantly originates from pure MChD. The observed ee/
B value is consistent with the
gMChD/2 value, which was determined for pure enantiomers.
Harnessing the effects of MChD, Xu et al. experimentally demonstrated the enantioselective photopolymerisation of a diacetylene (DA) derivative in the liquid crystal (LC) phase, which was previously achieved with irradiation of CPL.58 Photopolymerisation of DA units in the LC phase was performed using linearly polarised light (LPL) under different magnetic field conditions (zero magnetic field, and magnetic field either perpendicular or parallel to the beam of LPL). After polymerisation, a typical intense absorption maximum was observed at ∼640 and 580 nm, indicating the formation of polymeric DA (PDA) chains. When the magnetic field is parallel or antiparallel to the direction of LPL irradiation, an intense Cotton effect of the CD signals corresponding to the absorption bands of the PDA backbone appear at 550 and 670 nm with a crossover at 640 nm, indicating the helical formation of PDA chains. In contrast, when zero magnetic field or a magnetic field perpendicular to the beam of LPL is used, the observed CD signal is weak. Thus, MChD was successfully utilised to realise the enantioselective polymerisation of DA units by the application of LPL and a magnetic field either parallel or antiparallel to the direction of LPL irradiation. Moreover, the prepared helical PDA assemblies could be used to enantioselectively recognise D- or L-lysine.
Homochirality of life
From a chemical viewpoint, three plausible candidates, i.e., (1) the rotational motion of the Earth (the Coriolis force), (2) CPL-induced asymmetric photochemical reactions, and (3) MChD-induced asymmetric photochemical reactions, have been proposed to explain the origins of the homochirality of life (Fig. 9).15,16 Discovery of an excess of L-amino acids in the Murchison meteorite has attracted considerable attention with respect to their relationship with the homochirality of life,59 prompting more questions that require explanations to understand the organic asymmetric reactions that occur in the universe. Asymmetric reactions seem to likely occur in regions relatively close to neutron stars due to the presence of both enormous magnetic fields (108–1012 T) and synchrotron radiation.60,61 Although the pure CPL of synchrotron radiation can induce stereoselectivity in photochemical reactions, the ee value should be small since the gCD values of conventional organic compounds are rather small. On the other hand, the gMChD value is proportional to the magnetic field, thus the ee value due to MChD should be high under the influence of the enormous magnetic fields near neutron stars. For example, MChD-based photochemical reactions of aromatic amino acids may contribute to the asymmetric reactions in the universe because aromatic amino acids exhibit both CD and MCD. Furthermore, intense MChD observed in metal compounds suggests that the MChD of organic compounds may be observed in the X-ray or UV region, which could also potentially contribute to organic asymmetric reactions in the universe. Polyaromatic hydrocarbons (PAHs) are also found in the Murchison meteorite and they are the most abundant organic molecules in the universe (encompassing 20% of total cosmic carbon).62–64 Even in the aggregates of conventional organic aromatic compounds, such as PAHs, MChD can occur based on the previous observations. Furthermore, the MChD-based photoresolution in these systems is highly expected because of the experimental demonstration in the enantioselective photopolymerisation reactions of DA derivatives. Thus, because regions that have a very strong magnetic field exist in the universe, such as those within the vicinity of neutron stars (108 T–1012 T),60 the MChD of PAH aggregates could potentially lead to asymmetric photochemical reactions that introduce a small bias in chirality. Thus, the future development of MChD studies will be concerned not only with the development of magneto-optical devices and asymmetric photochemical reactions, but also for providing insight into the homochirality of life.
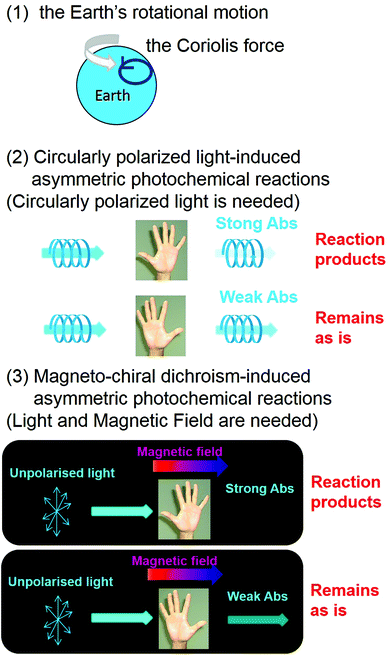 |
| | Fig. 9 Plausible candidates for explaining the homochirality of life:15,16 (1) the rotational motion of the Earth (the Coriolis force), (2) CPL-induced asymmetric photochemical reactions, and (3) MChD-induced asymmetric photochemical reactions. | |
Conclusions
In this perspective, the progress of MChD studies has been reviewed, especially focusing on organic compounds. In addition to the MChD enhancements observed in metal complexes, MChD studies of organic compounds have progressed from aromatic π-conjugated systems to enantioselective photopolymerisation reactions. From the viewpoint of the magnetic field effect, the radical pair mechanism has been investigated in various photochemical reactions,65–70 including photosynthesis.44–51 MChD observations on the artificial model of a photosynthetic light-harvesting antenna are attractive in terms of the novel magnetic field effect in photosynthesis, which may explain unsolved questions related to the magnetic field effects in biological systems. Based on these studies, MChD should not only be useful for asymmetric synthetic methods, but is also currently one of the plausible candidates for explaining the origins of the homochirality of life.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the JSPS KAKENHI JP17H06375. Y. K. acknowledges financial support from the JSPS KAKENHI JP19H04556. S. H. acknowledges financial support from the Yokohama Academic Foundation (1971000033) and the JSPS KAKENHI JP19K23634.
Notes and references
- G. Wagnière and A. Meier, Chem. Phys. Lett., 1982, 93, 78 CrossRef.
- L. D. Barron and J. Vrbancich, Mol. Phys., 1984, 51, 715 CrossRef CAS.
-
L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University press, Cambridge, 2nd edn, 2007 Search PubMed.
- G. L. J. A. Rikken and E. Raupach, Nature, 1997, 390, 493 CrossRef CAS.
- G. L. J. A. Rikken and E. Raupach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 5081 CrossRef CAS.
- N. B. Baranova and B. Ya. Zel'dovich, Mol. Phys., 1979, 38, 1085 CrossRef CAS.
- E. Raupach, G. L. J. A. Rikken, C. Train and B. Malézieux, Chem. Phys., 2000, 261, 373 CrossRef CAS.
- C. Train, R. Gheorghe, V. Krstic, L.-M. Chamoreau, N. S. Ovanesyan, G. L. J. A. Rikken, M. Gruselle and M. Verdaguer, Nat. Mater., 2008, 7, 729 CrossRef CAS PubMed.
- M. Saito, K. Ishikawa, K. Taniguchi and T. Arima, Phys. Rev. Lett., 2008, 101, 117402–117401 CrossRef CAS PubMed.
- Y. Kitagawa, H. Segawa and K. Ishii, Angew. Chem., Int. Ed., 2011, 50, 9133 CrossRef CAS PubMed.
- Y. Kitagawa, T. Miyatake and K. Ishii, Chem. Commun., 2012, 48, 5091 RSC.
- K. Wang, S. Zeng, H. Wang, J. Dou and J. Jiang, Inorg. Chem. Front., 2014, 1, 167 RSC.
-
Y. Kitagawa and K. Ishii, in Advances in Multi-Photon processes and Spectroscopy: Volume 22, ed. S. H. Lin, A. A. Villaeys and Y. Fujimura, World Scientific, Singapore, 2014 Search PubMed.
- S. Hattori and K. Ishii, Opt. Mater. Express, 2014, 4, 2423 CrossRef CAS.
-
G. H. Wagnière, On Chirality and the Universal Asymmetry: Reflections on Image and Mirror, VHCA, Wiley-VCH, Weinheim, 2007 Search PubMed.
-
A. Guijarro and M. Yus, The Origin of Chirality in the Molecules of Life, RSC Publishing, Cambridge, 2009 Search PubMed.
- C. Görller-Walrand and J. Godemont, J. Chem. Phys., 1997, 67, 3655 CrossRef.
- K. Stadnicka, A. M. Glazer and M. Koralewski, Acta Crystallogr., Sect. B: Struct. Sci., 1987, B43, 319 CrossRef CAS.
- A. J. McCaffery, P. J. Stephens and P. N. Schatz, Inorg. Chem., 1967, 6, 1614 CrossRef CAS.
- G. Kopnov and G. L. J. A. Rikken, Rev. Sci. Instrum., 2014, 85, 053106 CrossRef CAS PubMed.
- N. Nakagawa, N. Abe, S. Toyoda, S. Kimura, J. Zaccaro, I. Gautier-Luneau, D. Luneau, Y. Kousaka, A. Sera, M. Sera, K. Inoue, J. Akimitsu, Y. Tokunaga and T. Arima, Phys. Rev. B, 2017, 96, 121102 CrossRef.
- S. Eslami, J. G. Gibbs, Y. Rechkemmer, J. van Slageren, M. Alarcón-Correa, T.-C. Lee, A. G. Mark, G. L. J. A. Rikken and P. Fischer, ACS Photonics, 2014, 1, 1231 CrossRef CAS.
- K. Taniguchi, M. Nishio, S. Kishiue, P.-J. Huang, S. Kimura and H. Miyasaka, Phys. Rev. Mater., 2019, 3, 045202 CrossRef CAS.
- K. Taniguchi, S. Kishiue, S. Kimura and H. Miyasaka, J. Phys. Soc. Jpn., 2019, 88, 093708 CrossRef.
- V. Yannopapas and A. G. Vanakaras, ACS Photonics, 2015, 2, 1030 CrossRef CAS.
- V. Yannopapas, Solid State Commun., 2015, 217, 47 CrossRef CAS.
- M. Ceolín, S. Goberna-Ferrón and J. R. Galán-Mascarós, Adv. Mater., 2012, 24, 3120 CrossRef PubMed.
- R. Sessoli, M.-E. Boulon, A. Caneschi, M. Mannini, L. Poggini, F. Wilhelm and A. Rogalev, Nat. Phys., 2015, 11, 69 Search PubMed.
- S. Bordács, I. Kézsmárki, D. Szaller, L. Demkó, N. Kida, H. Murakawa, Y. Onose, R. Shimano, T. Rõõm, U. Nagel, S. Miyahara, N. Furukawa and Y. Tokura, Nat. Phys., 2012, 8, 734–738 Search PubMed.
- S. Kibayashi, Y. Takahashi, S. Seki and Y. Tokura, Nat. Commun., 2014, 5, 4583 Search PubMed.
- H. Narita, Y. Tokunaga, A. Kikkawa, Y. Taguchi, Y. Tokura and Y. Takahashi, Phys. Rev. B, 2016, 94, 094433 CrossRef.
- Y. Takahashi, S. Kibayashi, Y. Kaneko and Y. Tokura, Phys. Rev. B, 2016, 93, 180404 CrossRef.
- Y. Okamura, F. Kagawa, S. Seki, M. Kubota, M. Kawasaki and Y. Tokura, Phys. Rev. Lett., 2015, 114, 197202 CrossRef CAS PubMed.
- S. Tomita, K. Sawada, A. Porokhnyuk and T. Ueda, Phys. Rev. Lett., 2014, 113, 235501 CrossRef PubMed.
- S. Tomita, H. Kurosawa, K. Sawada and T. Ueda, Phys. Rev. B, 2017, 95, 085402 CrossRef.
- Y. Nii, R. Sasaki, Y. Iguchi and Y. Onose, J. Phys. Soc. Jpn., 2017, 86, 024707 CrossRef.
- K. Ishii, Jasco Rep., 2013, 55, 1 CAS.
- J. Mack, M. J. Stillman and N. Kobayashi, Coord. Chem. Rev., 2007, 251, 429 CrossRef CAS.
-
M. Nakazaki, Introduction to theory of optical rotation, Baifukan, Tokyo, 1973 Search PubMed.
-
N. Harada and K. Nakanishi, Cirucular Dichroic Spectroscopy-Exciton Coupling in Organic Stereochemistry, Tokyo Kagaku Dojin, Tokyo, 1982 Search PubMed.
- O. Ohno, Y. Kaizu and H. Kobayashi, J. Chem. Phys., 1993, 99, 4128 CrossRef CAS.
- J. M. Ribó, J. Crusats, J.-A. Farrera and M. L. Valero, J. Chem. Soc., Chem. Commun., 1994, 681 RSC.
- S. Hattori, Y. Yamamoto, T. Miyatake and K. Ishii, Chem. Phys. Lett., 2017, 674, 38 CrossRef CAS.
- Y. Tanimoto, H. Hayashi, S. Nagakura, H. Sakuragi and K. Tokumaru, Chem. Phys. Lett., 1976, 41, 267 CrossRef CAS.
- K. Schulten, H. Staerk, A. Weller, H.-J. Werner and B. Nickel, Z. Phys. Chem. Neue Folge, 1976, 101, 371 CrossRef CAS.
- N. Hata, Chem. Lett., 1976, 5, 547 CrossRef.
- Y. Sakaguchi, H. Hayashi and S. Nagakura, Bull. Chem. Soc. Jpn., 1980, 53, 39 CrossRef CAS.
- H. Hayashi and S. Nagakura, Bull. Chem. Soc. Jpn., 1984, 57, 322 CrossRef CAS.
- Y. Sakaguchi and H. Hayashi, J. Phys. Chem., 1984, 88, 1437 CrossRef CAS.
- U. E. Steiner and T. Ulrich, Chem. Rev., 1989, 89, 51 CrossRef CAS.
-
J. F. Rabek, Photochemistry and Photophysics vol. I, CRC Press, US, 1990 Search PubMed.
- K. L. Stevenson and J. F. Verdieck, Mol. Photochem., 1969, 1, 271 CAS.
- H. Rau, Chem. Rev., 1983, 83, 535 CrossRef CAS.
- Y. Inoue, Chem. Rev., 1992, 92, 741 CrossRef CAS.
- L. D. Barron, J. Am. Chem. Soc., 1986, 108, 5539 CrossRef CAS.
- L. D. Barron, Rend. Fis. Acc. Lincei, 2013, 24, 179 CrossRef.
- G. L. J. A. Rikken and E. Raupach, Nature, 2000, 405, 932 CrossRef CAS PubMed.
- Y. Xu, G. Yang, H. Xia, G. Zou, Q. Zhang and J. Gao, Nat. Commun., 2014, 5, 5050 CrossRef CAS PubMed.
- M. H. Engel and B. Nagy, Nature, 1982, 296, 837 CrossRef CAS.
- A. G. Lyne, Nature, 1984, 308, 605 CrossRef.
- W. A. Bonner and E. Rubenstein, Biosystems, 1987, 20, 99 CrossRef CAS PubMed.
- E. Dwek, R. G. Arendt, D. J. Fixsen, T. J. Sodroski, N. Odegard, J. L. Weiland, W. T. Reach, M. G. Hauser, T. Kelsall, S. H. Moseley, R. F. Silverberg, R. A. Shafer, J. Ballester, D. Bazell and R. Isaacman, Astrophys. J., 1997, 475, 565 CrossRef CAS.
- J. H. Hahn, R. Zenobi, J. L. Bada and R. N. Zare, Science, 1988, 239, 1523 CrossRef CAS PubMed.
- M. P. Bernstein, S. A. Sandford, L. J. Allamandola, J. S. Gillette, S. J. Clemett and R. N. Zare, Science, 1999, 283, 1135 CrossRef CAS PubMed.
- F. J. Adrian, J. Chem. Phys., 1971, 54, 3918 CrossRef CAS.
- J. B. Pedersen and J. H. Freed, J. Chem. Phys., 1973, 58, 2746 CrossRef.
- J. B. Pedersen and J. H. Freed, J. Chem. Phys., 1973, 59, 2869 CrossRef CAS.
- F. J. Adrian and L. Monchick, J. Chem. Phys., 1979, 71, 2600 CrossRef CAS.
- F. J. Adrian and L. Monchick, J. Chem. Phys., 1980, 72, 5786 CrossRef CAS.
- A. Marais, I. Sinayskiy, F. Petruccione and R. van Grondelle, Sci. Rep., 2015, 5, 8720 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry and Owner Societies 2020 |
 *,
Shingo
Hattori
*,
Shingo
Hattori
 and
Yuichi
Kitagawa
and
Yuichi
Kitagawa