Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A multi-scale perspective of gas transport through soap-film membranes
Gabriele
Falciani†
 a,
Ricardo
Franklin†
b,
Alain
Cagna
c,
Indraneel
Sen
d,
Ali
Hassanali
*b and
Eliodoro
Chiavazzo
a,
Ricardo
Franklin†
b,
Alain
Cagna
c,
Indraneel
Sen
d,
Ali
Hassanali
*b and
Eliodoro
Chiavazzo
 *a
*a
aPolitecnico di Torino, C.so Duca degli Abruzzi 24 - 10129, Torino, Italy. E-mail: eliodoro.chiavazzo@polito.it; Fax: +39 011 090 4499; Tel: +39 011 090 4557
bInternational Centre for Theoretical Physics, Strada Costiera 11 - 34151, Trieste, Italy. E-mail: ahassana@ictp.it; Tel: +39 040 2240 175
cTeclis Scientific, 22 Ch. Des Prés Secs - 69380, Civrieux d'Azergues, France
dUppsala University, Laegerhyddsvaegen 1 - 751 20, Uppsala, Sweden
First published on 16th March 2020
Abstract
Soap films represent unique aqueous systems, whose physical properties can be tuned by acting on their nanoscale structure. Here, we specifically focus on transport properties through membranes realized in the form of soap films. While diffusion phenomena in the water core and surfactant monolayers are described using a continuum model, molecular dynamics is used to compute the static and dynamical properties of water, gases and the surfactant in the monolayers which is hexaethylene glycol monododecyl ether (C12E6). The obtained atomistic details are then incorporated into a drift-diffusion model for consistently extracting a boundary condition for the above continuum model describing transport phenomena at a larger scale. Numerical predictions are validated against experimental data from both properly designed experiments and the literature. Finally, the developed model is used to estimate the characteristic time for disparate gas mixing when initially separated by soap film membranes.
Design, System, ApplicationHere we target the accurate molecular design of thin water layers (whose thickness can be in the range from hundreds down to a few nanometers) realized in the form of soap films, for accurately controlling gas permeation. This is conducted by setting up a comprehensive multi-scale model to elucidate the role of all main design parameters (including the choice of self-assembled surfactant molecules, their concentration and film thickness). Possible future applications that can be envisioned for this work are in the energy sector. In fact, this work is part of a broader multi-disciplinary research project (http://sofiaproject.eu/), recently funded by the European Commission (grant agreement No. 828838), which aims at designing flexible (soap-film based) compartments for oxygen-fuel (mainly CO) generation (by photoreactions) and separation starting from coalescent bubbles initially filled with CO2. In order to accomplish the application above, soap-film membranes should be able to keep separated disparate gases (e.g. O2–CO) generated into separated compartments by photoreactions for dozens of seconds or longer preventing substantial oxygen-fuel mixing. |
1 Introduction
Thin layers of liquid water within a gaseous environment can be generated in the form of soap films, with a range of thickness from hundreds down to a few nanometers (i.e. Newton black films).1–3 Stabilization of soap films is due to the presence of surfactant molecules that self-assemble at the gas–liquid interface, thus lowering surface tension.4 The presence of these intricate assemblies of surfactant molecules makes the transport of species across soap films a non-trivial phenomenon.Gas permeation through soap films has been extensively studied since the seminal work by Princen and co-workers5,6 for a number of common gaseous species. Moreover, due to their high selectivity, soap films and bubbles have been also investigated as possible gas mixture separation membranes.7,8 Despite the several studies reported in the literature, it is fair to say that most of the theoretical models that have been proposed to describe gas transport across soap films still require the evaluation of a number of empirical parameters.9 In this work, we propose a comprehensive multi-scale approach that is capable of consistently coupling molecular dynamics simulation and a continuum model in order to predict soap film permeability, which is a critical parameter affecting gas permeation across soap-film based membranes. In particular, the molecular simulations provide crucial input such as the interfacial thickness and the molecular interactions that both the water molecules and gas molecules (CO2) make with the surfactant. This manuscript is organized in sections as follows. In section 2 the atomistic model is described and validated against experimental data reported in section 3. The continuum model is described in section 4 and validated in section 5, while conclusions are drawn in section 6.
2 Molecular model of the surfactant–water system
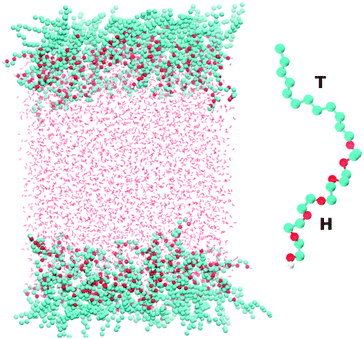
Fig. 1 shows a snapshot of the surfactant–water system that is considered in our atomistic simulations. The surfactant used for these simulations is hexaethylene glycol monododecyl ether (C12E6) which has been the subject of several previous experimental and modelling studies.10–16 C12E6 is a surfactant consisting of a hydrophobic tail made up of 12 alkyl groups and a hydrophilic head which comprises 6 ethylene oxide (EO) groups and 1 hydroxyl (OH) group. The inset of Fig. 1 illustrates an enlarged picture of the surfactant with the head (H) and tail (T) groups.Classical molecular dynamics simulations of C12E6 were performed using the GROMACS package.17 The force-field for the surfactant was adapted from a previous study by Striolo and co-workers. For details on the model, the reader is referred to the original work.18 Briefly, a united atom approach is used for the alkyl groups, while the EO and OH groups are treated explicitly. A combination of the TRaPPE-UA19 and OPLS20,21 force-fields was used for the various bonded and non-bonded interaction potentials.
The system shown in Fig. 1 consists of 96 surfactant molecules, 48 on each surface, and 4055 water molecules. The water molecules were treated using the SPC/E22 potential. The choice of SPC/E was dictated by the fact that it has been already successfully implemented for reproducing the co-existence of liquid H2O and gaseous CO2.23 In addition, the SPC potential accurately reproduces thermodynamic properties such as the second virial coefficient, enthalpy of vaporization and the surface tension of the air–water interface.24 Periodic boundary conditions are applied in the x, y and z directions with a vacuum buffer of 215 Å between the two surfactant layers. The electrostatics were treated with the particle mesh Ewald (PME) method25 using a real-space cutoff of 10 Å. The cutoff for the Lennard-Jones interactions was set to 10 Å. We studied the behavior of the surfactant close to the critical micelle concentration (CMC), which corresponds to 52 Å2 per surfactant (approximately 48 surfactant molecules on each surface). The simulations were equilibrated first within the NVT ensemble for 11 ns using the Nosé–Hoover thermostat26,27 at 298 Kelvin and using a time constant of 2.0 ps. NVT simulations were used to extract the surface tension which will be reported later in the paper. The total simulation time for these runs was 60 ns.
In order to assess the validity of our model, we performed some constant surface-tension simulations, which can be favourably compared with the experimental data reported below. Using the recently developed algorithms in ref. 28, we performed simulations constraining the surface tension under a surface normal pressure of 1 bar. In the latter simulations, the interfacial area fluctuates and allows us to assess the validity of our model.
2.1 Surface tension
From our simulations on the surfactant–water interface, we first determined the surface tension of the C12E6–water interface by examining the difference between the normal and tangential pressures defined as follows: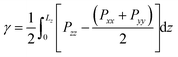 | (1) |
The surface tension extracted from our NVT simulations reaches up to 37.8 ± 0.3 mN m−1, which is in remarkable agreement with the experimental data reported in section 3. We also performed a set of simulations at a constrained surface tension of 41 mN m−1 (experimental value).29 Interestingly, upon monitoring the interfacial surface area, we predict a surface coverage value of 54.4 Å2, which is again consistent with our chosen critical micelle concentration of 52 Å2 in the NVT runs. The above results give us confidence in the accuracy of our molecular model, allowing us to make some important inferences on the structure and dynamics of the surfactant–water interface.
2.2 Surfactant and water density profiles
In the top panel of Fig. 2, the probability density profiles associated with the water and surfactant are shown. For the surfactant, we used the center of mass of the molecules to determine the densities. The bottom panel of Fig. 2 shows a zoom-in of densities, where we separate out the contributions coming from the hydrophobic (shown in green) and hydrophilic (shown in blue) parts of the surfactant. The density profiles reveal some important details regarding the structure of the surfactant and water in the interfacial region. Firstly, we observe that the water density covers a range spanning from the bulk to the vacuum of approximately ∼20 Å. In order to quantify the width of the interfacial region, the water density profile was fitted to the following functional form as done in previous studies (Fig. 3):30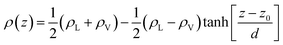 | (2) |
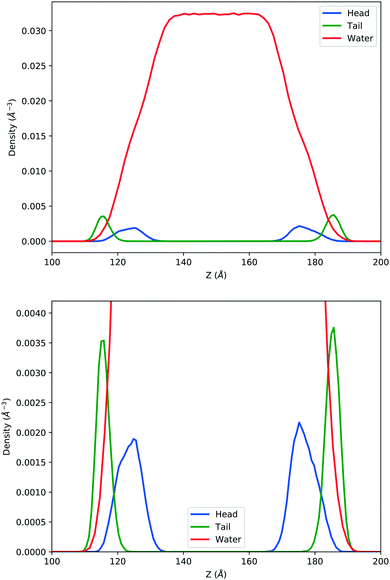 | ||
| Fig. 2 Mass density profile. The red curve corresponds to the water density. The surfactant density was separated into the hydrophobic tail and hydrophilic head. From the figure, the permeation of the water onto the hydrophobic region is shown. Also, the width of the tail/head layer of the surfactant is computed and presented in Table 1 using eqn (3). | ||
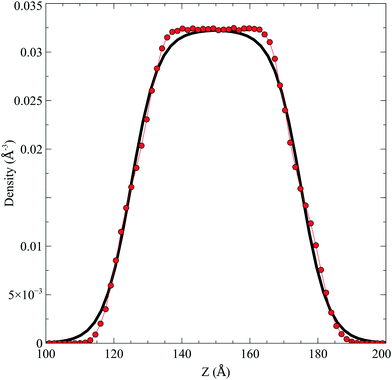 | ||
Fig. 3 The water density profile was fitted to the function presented in eqn (2). With it, an average Gibbs dividing interface is defined at 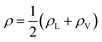 . Also the hydration layer is estimated from the fitted d. . Also the hydration layer is estimated from the fitted d. | ||
In eqn (2), ρL and ρV are the densities corresponding to the liquid and the gas phases, respectively, z0 is the position of the Gibbs dividing surface (where 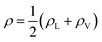 ), and d is the thickness parameter for the interface. As in previous studies,30,31 we computed the “10–90” thickness parameter representing the length-scale over which the density decays from 90 to 10% of the bulk value. This number reported in Table 1 is 2.1972d yielding a value of 17.8 Å.
), and d is the thickness parameter for the interface. As in previous studies,30,31 we computed the “10–90” thickness parameter representing the length-scale over which the density decays from 90 to 10% of the bulk value. This number reported in Table 1 is 2.1972d yielding a value of 17.8 Å.
For the surfactant and its individual head and tail distributions, the densities were fitted to the following Gaussian distribution:
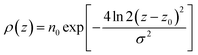 | (3) |
2.3 Surfactant orientation and flexibility
In order to examine the orientation of the surfactant molecules at the surface, we determined the angle θ between the vector formed by the two ends of the molecule and the surface normal reported in the top panel of Fig. 4. The distribution of θ peaks at approximately 31.6° which shows that the surfactant molecules are tilted at the interface. It should be stressed, however, that the distribution is quite broad indicating a rather heterogeneous environment.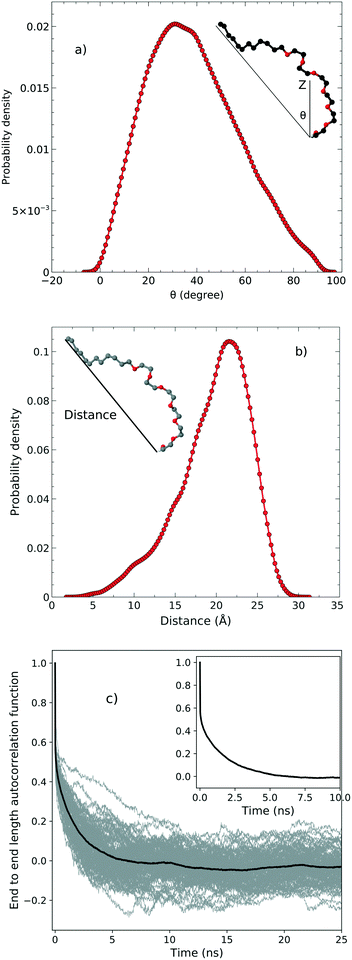 | ||
| Fig. 4 a) The tilt angle distribution, b) the end to end distance and c) the autocorrelation function associated with the end to end distance. | ||
The middle panel of Fig. 4 shows the distribution of the end-to-end distance of the surfactant, which again confirms that the surfactant molecules are quite flexible and characterized by a wide range of different conformations. To assess the timescales associated with these fluctuations, we computed the equilibrium time correlation function associated with the changes in the conformation as probed by the end-to-end distance. The bottom panel of Fig. 4 shows the relaxation dynamics of all the surfactant molecules which features an exponential decay occurring on the timescale of 1.7 ns.
2.4 CO2 concentration in the surfactant monolayer
We performed simulations of a single CO2 molecule that was added to the above surfactant–water system. It is worth noticing here that, under usual operating conditions (i.e. low pressure), the concentration of CO2 in the simulated small system corresponds to one single CO2 molecule. A total of 5 independent trajectories were run each of 10 ns long within the NVT ensemble. The model used for the force field of the CO2 was obtained from the literature.24 Our simulations show that while the CO2 molecule undergoes free diffusion in the gas phase, when it approaches the surfactant it appears to be trapped within the hydrophobic pockets of C12E6 as seen in Fig. 5, which shows a zoom in plot together with the CO2 densities. The CO2 densities are shown in solid black lines for regions that are adequately sampled while the dashed black lines are regions where we did not sample adequately enough the transitions from the hydrophobic part to the hydrophilic part and then into the water.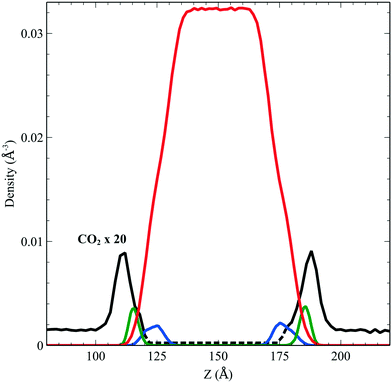 | ||
| Fig. 5 Density profile of C12E6 (head with blue lines and tail in green) and water (red) with the probability to find CO2 (dark line). | ||
Due to the limited statistics involving the CO2 molecule diffusing through the surfactant, we used the CO2 density profiles to infer the local potential that the CO2 experiences in the hydrophobic part of the surfactant. In order to obtain the potential, we computed the potential of the mean force associated with the density: −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(p(r)) which is shown in Fig. 6. The dashed lines correspond to the regions of the potential that are not sampled from the molecular dynamics simulations. We used this potential to infer the minimum activation barrier associated with the transfer of the CO2 across the surfactant monolayer into the liquid. As described below, this potential is a crucial input for a continuum model to be fitted into eqn (12) and (13).
log(p(r)) which is shown in Fig. 6. The dashed lines correspond to the regions of the potential that are not sampled from the molecular dynamics simulations. We used this potential to infer the minimum activation barrier associated with the transfer of the CO2 across the surfactant monolayer into the liquid. As described below, this potential is a crucial input for a continuum model to be fitted into eqn (12) and (13).
3 Surface tension and molecular area measurements
Dynamic surface tension values were measured with a drop tensiometer (Tracker, Teclis) by analyzing the axial symmetric shape (Laplace profile) of a rising air bubble in aqueous solution of C12E6 at different (bulk) concentrations. The air bubble is generated in a thermostated cuvette containing the water phase; the bubble of about 10 μl is delivered from a syringe controlled using a motor drive as shown in Fig. 7.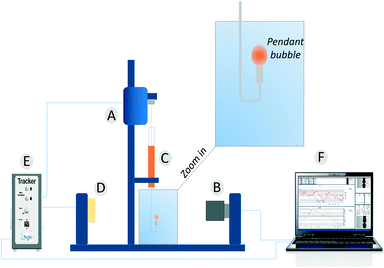 | ||
| Fig. 7 The pendant bubble tensiometer (Tracker). (A) Motor to drive the syringe. (B) Camera and optics. (C) Motor driven syringe. (D) Light source. (E) Electronic box. (F) Software. | ||
All measurements were performed at a controlled temperature of 25 °C. C12E6 with 98% purity from Sigma Aldrich was used without modification and dissolved in distilled water.
Results are reported in Fig. 8, where the surface tension versus time due to adsorption of the surfactant at the air/water interface at several concentrations of C12E6 is reported. For each concentration, the measurements are performed until the equilibrium surface tension is reached. The surfactant concentration is increased until its critical micellar concentration (CMC) is reached; after that point, the equilibrium surface tension is no longer concentration dependent.
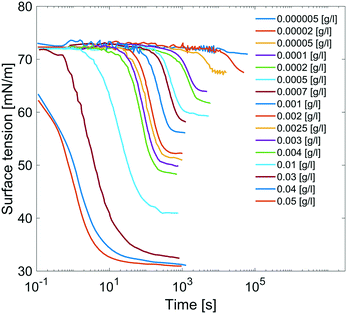 | ||
| Fig. 8 Dynamic surface tensions of clean surface adsorption in C12E6 aqueous solution at different concentrations. | ||
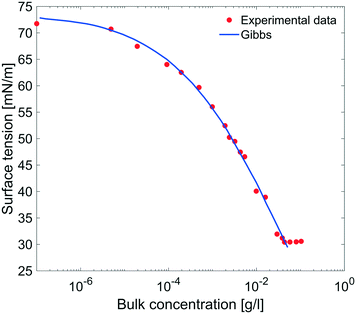 | ||
| Fig. 9 Equilibrium surface tension from Fig. 8 as a function of bulk concentration and compared with the results obtained using the Gibbs adsorption eqn (4). | ||
The equilibrium surface tension versus the concentration of C12E6 (logarithmic scale) is plotted in Fig. 9. The value of the CMC obtained for C12E6 is 0.034 g l−1 (0.075 mM) with a minimum surface tension of 31 mN m−1.
The data in Fig. 9 are compared to the Gibbs adsorption equation. For non-ionic systems, before the CMC, the amount of surfactant adsorbed at the interface at equilibrium (Γeq) is related to the surfactant (bulk) concentration Cb by:
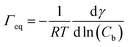 | (4) |
4 Permeation of gaseous species across soap films
Among the various theoretical models for mass transport across a soap film, a widely accepted description in the literature is the one proposed by Princen and co-workers,5,6 who further elaborated this in previous studies.32,33 In this model, permeation of gas molecules through soap films depends on three main resistances due to the liquid water core inside the film and the two surfactant monolayers at the gas–liquid interface. Assuming Fick's diffusion, these authors suggested a linear proportionality between the molar flux of permeating gaseous species and the corresponding concentration difference across the soap film, namely: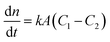 | (5) |
Clearly, the permeability depends on the thickness of the liquid water core. However, k also includes a non-trivial dependence on the surfactants and the involved gas, and it can be more specifically linked to other relevant quantities as follows:
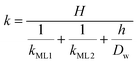 | (6) |
The monolayer permeability kML1 depends on the molecular structure of surfactant molecule (e.g. polarity of the hydrophilic head, length of the hydrophobic tail), on permeating gas, on temperature and surfactant concentration.9 In the case of thick films the permeability is controlled by the liquid core yielding:
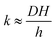 | (7) |
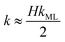 | (8) |
4.1 Monolayer permeability
Focusing specifically on the gas–film interface, the molar rate of a given gas diffusing through a single surfactant monolayer can be estimated by the following equation: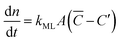 | (9) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) being the actual concentration and the equilibrium concentration of the considered gaseous species in the film liquid core, respectively.6Eqn (9) predicts a net gas flux from the gas to the liquid phase, which only stops when the following equilibrium condition (Henry's law) holds:
being the actual concentration and the equilibrium concentration of the considered gaseous species in the film liquid core, respectively.6Eqn (9) predicts a net gas flux from the gas to the liquid phase, which only stops when the following equilibrium condition (Henry's law) holds: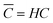 | (10) |
Clearly, in order to have predictive results from eqn (9), there is a need to link the monolayer permeability to more fundamental quantities. In this respect, a rather popular approach is as follows:9
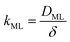 | (11) |
However, it is fair to say that the physical process of gas permeation through surfactant monolayers is not yet completely understood. In fact, as testified in the review by Farajzadeh and co-workers, disparate theoretical models have been suggested so far in the literature, thus also introducing a number of empirical parameters that are often hard to estimate.9
It is interesting to notice that, even when no surfactant molecules are present, classical atomistic simulations suggest that the transport from the gas to the liquid phase occurs within a non-flat potential landscape. In this respect, authors in ref. 34 and 35 report a free energy barrier at the gas–water interface. Hence, based on the above discussion in section 2, we expect an even more complicated picture when also surfactant molecules are present and specifically suggest investigating the perturbation in the free-energy landscape to be linked to eqn (11). Towards this end, here we propose a comprehensive and multi-scale perspective, where a molecular model is utilized for extracting relevant information to be used at a larger scale in a continuum framework.
In particular, throughout the surfactant monolayer, gas molecules are subject to an underlying energy potential. Hence, gas transport can be effectively described by means of the following Smoluchowski model:36
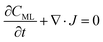 | (12) |
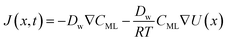 | (13) |
Assuming for simplicity a one-dimensional (1D) stationary process along the coordinate z orthogonal to the monolayer, eqn (12) and (13) yield:
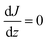 | (14) |
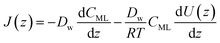 | (15) |
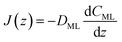 | (16) |
5 Model results and experimental validation
Firstly, we set-up and validated a (COMSOL37 based) continuum model by using the experimental data from Princen and co-workers,5 who accurately characterized the gas diffusion across the soap film of a shrinking bubble (diminishing bubble method). In their experimental setup, a bubble containing a specific gas (i.e. N2, O2, H2, CO2, He, Ne, Ar and air) was formed inside a closed cell filled with the same gas using a 4% solution of CTAB (hexadecyltrimethylammonium bromide). Once the bubble film had reached the equilibrium thickness, they measured the time variation of the following dimensionless parameter β0, defined as: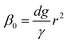 | (17) |
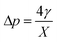 | (18) |
In our continuum model, we focused on the gas transport across the soap film whose thickness is in the order of tens to hundreds of nanometers. A 2D axial-symmetric geometry was chosen as shown in Fig. 10: the lower chamber corresponds to a small section of the bubble's inner gas volume, while the upper chamber represents a small section of the outer gas volume. Fickian diffusion was assumed both in the gas phase and in the soap film. We considered the presence of the surfactants at the air–water interface by implementing eqn (9) in our model. Furthermore, we imposed a fixed pressure difference between the two chambers expressed in terms of concentration difference by the perfect gas law:
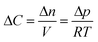 | (19) |
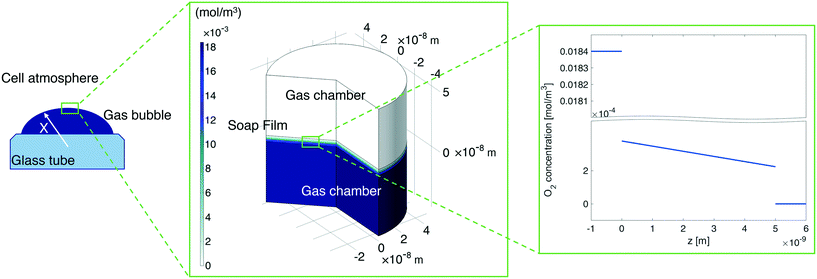 | ||
| Fig. 10 Left-hand side: A sketch of the shrinking bubble in the Princen38 experimental setup. Middle: Continuum model results for oxygen diffusion through the soap film. Right-hand side: O2 concentration distribution across the soap film. | ||
By varying the ΔC, we calculate the molar flux reduction caused by the bubble shrinking with time. In Fig. 11, our simulation results were validated against the experimental data from ref. 5 by using both kML = 0.188 m s−1 and kML = 0.242 m s−1 as suggested in ref. 5.
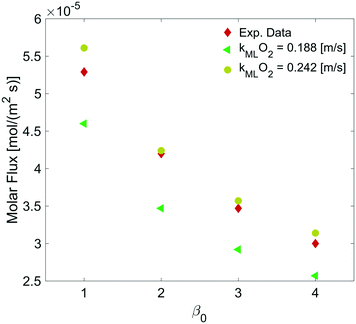 | ||
| Fig. 11 Dependence of the molar flux of oxygen on the permeability for a film thickness of 5 nm against experimental data from ref. 5. | ||
5.1 Monolayer permeability, kML
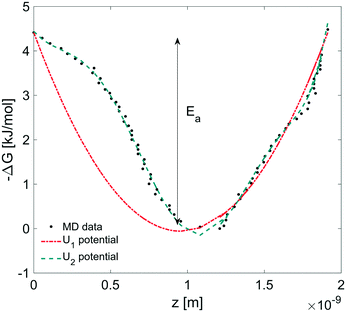
In this section, we coupled the above atomistic description with a continuum model implementing the Smoluchowski diffusion equation. In particular, we solved eqn (12) and (13) in the COMSOL environment under 1D stationary conditions. Firstly, the free-energy landscape from the molecular dynamics simulations reported in Fig. 6 was fitted by using both a harmonic and a higher polynomial model, U1 and U2, as shown in Fig. 12. The main motivation for choosing a harmonic potential can be found in the literature, where gas permeation in the surfactant monolayer is described as a phenomenon mainly dictated by the activation energy (i.e. energy barrier height).39–41 In addition to this, in our work, we decided also to apply a more accurate fitting, U2.The simulation domain length was chosen on the basis of the potential barrier width, 1.9 nm, as shown in Fig. 12. The diffusion coefficient of CO2 in water is assumed to be 1.67 × 10−9 m2 s−1 at T = 20 °C.42 We imposed Dirichlet boundary conditions at the ends of the simulation domain.
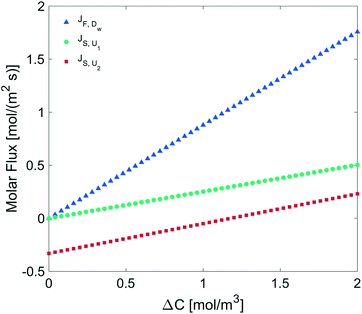
We determined the gas flux as a function of the concentration difference in the case of flat and non-flat potentials. We notice that, as shown in Fig. 13, the presence of asymmetric potentials may lead to a non-vanishing flux (JS,U2) even at ΔC = 0. In contrast, for symmetric potentials, JS,U1 = 0 is found at ΔC = 0.
Finally, we estimated the effective diffusion coefficient in the C12E6 surfactant monolayer by measuring the slope of curves reported in Fig. 13. Here, the diffusion coefficient of a gas within water is denoted as Dw, whereas DML is used as the effective diffusion coefficient in the presence of an underlying potential. By using potential U1 and δ = 1.9 nm, we found a value for 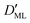 of 0.478 × 10−9 m2 s−1, with the corresponding monolayer permeability being
of 0.478 × 10−9 m2 s−1, with the corresponding monolayer permeability being 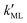 = 0.25 m s−1.
= 0.25 m s−1.
On the other hand, 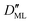 was found to be 0.541 × 10−9 m2 s−1 when implementing potential U2, which led to a slightly higher monolayer permeability of
was found to be 0.541 × 10−9 m2 s−1 when implementing potential U2, which led to a slightly higher monolayer permeability of 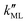 = 0.28 m s−1. Thus, the shape of the potential is found to have a limited influence on the resulting monolayer permeability (as compared to its height).
= 0.28 m s−1. Thus, the shape of the potential is found to have a limited influence on the resulting monolayer permeability (as compared to its height).
As already discussed, due to the possible poor sampling issues in the computation of the energy potential landscape in Fig. 6, we decided to perform additional computations assuming an underlying harmonic potential with a perturbed height and width as compared to the one reported in Fig. 12. More specifically, we assumed a conservative ±10% variation to both the activation energy Ea reported in Fig. 12 and the monolayer thickness δ. The above analysis provided a range of values for the monolayer permeability from 0.12 up to 0.36 m s−1. To the best of our knowledge, values of the monolayer permeability of C12E6 have not been reported yet for CO2 and under the conditions reported in this work.
However, our results appear to be consistent with similar studies in the literature. For instance, Krustev and co-workers43,44 reported the kML from experimental measurements of the permeability for air through SDS (sodium dodecyl sulfate) + electrolyte solutions obtaining values which ranged from 0.063 to 0.278 m s−1 depending on the type of electrolyte and its concentration.
5.2 Sensitivity analysis, film thickness and monolayer permeability
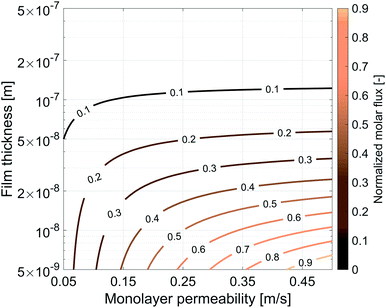
So far we have characterized the CO2 behaviour in the surfactant monolayer. Here, we decided to carry out a wider sensitivity analysis on the monolayer permeability and on the water core thickness to extend our research and investigate the influence of different gases and surfactants on the transport phenomena across soap films.The same simulation setup validated previously was adopted imposing a concentration difference of ΔC = Δp/RT = 0.0184 mol m−3 corresponding to a pressure difference of 45 Pa at the boundaries. We let both the monolayer permeability and the water core thickness vary from 0.05 up to 0.5 m s−1 and from 5 nm up to 500 nm, respectively. We highlight that the film thickness has a major impact on gas diffusion as compared to the monolayer permeability. For instance, for h = 300 nm, a monolayer permeability variation from 0.05 to 0.5 m s−1 reduces the flux by about 18%. Nevertheless, as the water core becomes thinner the effect of the monolayer permeability becomes more significant: e.g. for a film of about 50 nm an increment of the monolayer permeability from 0.05 to 0.5 m s−1 halves the gas flux and this behaviour is even emphasized for thinner films as shown in Fig. 14.
5.3 Estimate of the cross-flow characteristic time through soap-film membranes
In this section, we apply the above models to investigate the characteristic time for gas mixing in two coalescent bubbles with different gas compositions. In particular, we consider the case of a double-bubble configuration which consists of two coalescent spherical shells of soap films (with an equal size and radius of 2 cm) separated by a flat soap film (surface area of 9.425 cm2).45,46 A lower bound for the time needed before 10% of the initial number of moles of gas i inside one of the two bubbles flows to the other was evaluated as: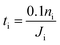 | (20) |
In order to have a conservative estimate, we considered a fixed molar flux constantly driven by the (initial) maximum gas concentration (ΔC(t = 0 s)). Hence, we calculated the time spent to reduce the initial number of moles of the i-th gas inside one of the two bubbles by 10% according to eqn (20). We set the water core thickness to 300 nm and, by applying an uncertainty to the monolayer permeability of ±50%, tO2 was found to vary from 13.7 s up to 14.6 s, whereas tCO was found to vary from 17.9 s up to 19.0 s. It is worth stressing once again that, due to the assumption on the fixed gas concentration, the above mixing times are to be considered as lower bounds.
6 Conclusions
Thin layers of water can be easily realized in the form of soap films. Interestingly, the surfactant nature and the thickness can be easily varied. As a representative example, a thin film pressure balance (TFPB) represents a convenient system where nanoscale properties can be precisely controlled and investigated in a relatively easy manner as shown in numerous studies.47–52 In this work, we have focused on the gas transport across soap films by means of predictive multi-scale numerical models. In particular, we used a combination of molecular and continuum models to characterise and study the transport of gases through soap film membranes. Classical molecular dynamics simulations are used to study the structural and dynamical properties of the surfactant molecules at the air–water interface. The above atomistic model is validated against experimental data from purposely designed experiments in terms of surface tension and molecular area. Simulation results provide crucial insights into the thickness of the hydrophobic and hydrophilic parts of the surfactant as well as the extent of water penetration in the membrane. The molecular simulations of CO2 at the interface reveal that the gas tends to get trapped within the hydrophobic part of the surfactant. These insights provide valuable input for studying the diffusion of CO2 through a soap film using a continuum model. Specifically, the free-energy landscape is incorporated in a Smoluchowski model at a continuum level and utilized to estimate the surfactant monolayer permeability without resorting to empirical parameters. The above procedure is implemented (although it is not limited) to CO2, and it can be easily extended to other gaseous species. Finally, a lower bound for a characteristic mixing time of two different gases initially separated into two coalescent bubbles is provided.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been funded by the European Commission in the framework of the project SoFiA – Soap Film based Artificial Photosynthesis – grant agreement 828838.References
- D. Exerowa and P. M. Kruglyakov, Foam and foam films: theory, experiment, application, Elsevier, 1997, vol. 5 Search PubMed.
- J. Clunie, J. Corkill and J. Goodman, Discuss. Faraday Soc., 1966, 42, 34–41 RSC.
- G. Andreatta, L.-T. Lee, F. K. Lee and J.-J. Benattar, J. Phys. Chem. B, 2006, 110, 19537–19542 CrossRef CAS PubMed.
- I. J. Black and T. M. Herrington, J. Chem. Soc., Faraday Trans., 1995, 91, 4251–4260 RSC.
- H. Princen and S. Mason, J. Colloid Sci., 1965, 20, 353–375 CrossRef CAS.
- H. Princen, J. Overbeek and S. Mason, J. Colloid Interface Sci., 1967, 24, 125–130 CrossRef CAS.
- R. L. Cook and R. W. Tock, Sep. Sci., 1974, 9, 185–193 CAS.
- J. Reznickova, R. Petrychkovych, J. Vejrazka, K. Setnickova and P. Uchytil, Sep. Purif. Technol., 2016, 166, 26–33 CrossRef CAS.
- R. Farajzadeh, R. Krastev and P. L. Zitha, Adv. Colloid Interface Sci., 2008, 137, 27–44 CrossRef CAS PubMed.
- J. R. Lu, Z. X. Li, R. K. Thomas, E. J. Staples, I. Tucker and J. Penfold, J. Phys. Chem., 1993, 97, 8012–8020 CrossRef CAS.
- J. Lu, E. Lee, R. Thomas, J. Penfold and S. Flitsch, Langmuir, 1993, 9, 1352–1360 CrossRef CAS.
- J. R. Lu, T. J. Su, Z. X. Li, R. K. Thomas, E. J. Staples, I. Tucker and J. Penfold, J. Phys. Chem. B, 1997, 101, 10332–10339 CrossRef CAS.
- J. Lu, Z. Li, R. Thomas, B. Binks, D. Crichton, P. Fletcher, J. McNab and J. Penfold, J. Phys. Chem. B, 1998, 102, 5785–5793 CrossRef CAS.
- J. Chanda and S. Bandyopadhyay, J. Chem. Theory Comput., 2005, 1, 963–971 CrossRef CAS PubMed.
- R. Muruganathan, H.-J. Müller, H. Möhwald and R. Krastev, Langmuir, 2005, 21, 12222–12228 CrossRef CAS PubMed.
- L. Shi, N. R. Tummala and A. Striolo, Langmuir, 2010, 26, 5462–5474 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- L. Shi, N. R. Tummala and A. Striolo, Langmuir, 2010, 26, 5462–5474 CrossRef CAS PubMed.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1999, 103, 4508–4517 CrossRef CAS.
- J. M. Briggs, T. Matsui and W. L. Jorgensen, J. Comput. Chem., 1990, 11, 958–971 CrossRef CAS.
- W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276–1284 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- T. Somasundaram, M. In het Panhuis, R. Lynden-Bell and C. Patterson, J. Chem. Phys., 1999, 111, 2190–2199 CrossRef CAS.
- H. Zhang and S. J. Singer, J. Phys. Chem. A, 2011, 115, 6285–6296 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- K. M. Aoki, M. Yoneya and H. Yokoyama, J. Chem. Phys., 2006, 124, 064705 CrossRef PubMed.
- E. Lucassen-Reynders, A. Cagna and J. Lucassen, Colloids Surf., A, 2001, 186, 63–72 CrossRef CAS.
- R. S. Taylor, L. X. Dang and B. C. Garrett, J. Phys. Chem., 1996, 100, 11720–11725 CrossRef CAS.
- A. M. Prpich, Y. Sheng, W. Wang, M. E. Biswas and P. Chen, PLoS One, 2009, 4, 1–6 CrossRef PubMed.
- A. Brown, W. C. Thuman and J. McBain, J. Colloid Sci., 1953, 8, 491–507 CrossRef CAS.
- A. Brown, W. C. Thuman and J. McBain, J. Colloid Sci., 1953, 8, 508–519 CrossRef CAS.
- H. Zhang and S. J. Singer, J. Phys. Chem. A, 2011, 115, 6285–6296 CrossRef CAS PubMed.
- R. Vácha, P. Slavíček, M. Mucha, B. J. Finlayson-Pitts and P. Jungwirth, J. Phys. Chem. A, 2004, 108, 11573–11579 CrossRef.
- P. Ansalone, M. Chinappi, L. Rondoni and F. Cecconi, J. Chem. Phys., 2015, 143, 154109 CrossRef PubMed.
- COMSOL Multiphysics ®v. 5.5 www.comsol.com, COMSOL AB, Stockholm, Sweden.
- H. Princen and S. Mason, J. Colloid Sci., 1965, 20, 156–172 CrossRef CAS.
- I. Langmuir and D. B. Langmuir, J. Phys. Chem., 1927, 31, 1719–1731 CrossRef CAS.
- I. Langmuir and V. J. Schaefer, J. Franklin Inst., 1943, 235, 119–162 CrossRef CAS.
- G. T. Barnes and V. K. La Mer, in Retardation of Evaporation by Monolayers, Elsevier, 1962, pp. 9–33 Search PubMed.
- D. R. Lide, CRC handbook of chemistry and physics, CRC press, 2004, vol. 85 Search PubMed.
- R. Krustev, D. Platikanov and M. Nedyalkov, Colloids Surf., A, 1993, 79, 129–136 CrossRef CAS.
- R. Krustev, D. Platikanov and M. Nedyalkov, Colloids Surf., A, 1997, 123–124, 383–390 CrossRef CAS.
- J. Hass and R. Schlafly, Ann. Math., 2000, 151, 459–515 CrossRef.
- R. Urikovič, Comput. Graph. Forum, 2001, 67–76 CrossRef.
- K. J. Mysels and M. N. Jones, Discuss. Faraday Soc., 1966, 42, 42–50 RSC.
- B. M. Folmer and B. Kronberg, Langmuir, 2000, 16, 5987–5992 CrossRef CAS.
- N. Kristen and R. von Klitzing, Soft Matter, 2010, 6, 849–861 RSC.
- H. Fauser and R. von Klitzing, Soft Matter, 2014, 10, 6903–6916 RSC.
- A. Mamane, E. Chevallier, L. Olanier, F. Lequeux and C. Monteux, Soft Matter, 2017, 13, 1299–1305 RSC.
- D. Langevin, Adv. Colloid Interface Sci., 2019, 102075 Search PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |