Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revisiting the Volmer–Heyrovský mechanism of hydrogen evolution on a nitrogen doped carbon nanotube: constrained molecular dynamics versus the nudged elastic band method†
Rasmus
Kronberg
 ,
Heikki
Lappalainen
and
Kari
Laasonen
,
Heikki
Lappalainen
and
Kari
Laasonen
 *
*
Research Group of Computational Chemistry, Department of Chemistry and Materials Science, Aalto University, P.O. Box 16100, FI-00076 Aalto, Finland. E-mail: kari.laasonen@aalto.fi
First published on 24th January 2020
Abstract
Density functional theory (DFT) based computational electrochemistry has the potential to serve as a tool with predictive power in the rational development and screening of electrocatalysts for renewable energy technologies. It is, however, of paramount importance that simulations are conducted rigorously at a level of theory that is sufficiently accurate in order to obtain physicochemically sensible results. Herein, we present a comparative study of the performance of the static climbing image nudged elastic band method (CI-NEB) vs. DFT based constrained molecular dynamics simulations with thermodynamic integration in estimating activation and reaction (free) energies of the Volmer–Heyrovský mechanism on a nitrogen doped carbon nanotube. Due to cancellation of errors within the CI-NEB calculations, static and dynamic activation barriers are observed to be surprisingly similar, while a substantial decrease in reaction energies is seen upon incorporation of solvent dynamics. This finding is attributed to two competing effects; (1) solvent reorganization that stabilizes the transition and, in particular, the product states with respect to the reactant state and (2) destabilizing entropic contributions due to solvent fluctuations. Our results highlight the importance of explicitly sampling the interfacial solvent dynamics when studying hydrogen evolution at solid–liquid interfaces.
1 Introduction
Accurate simulations of electrochemical interfaces and reactions are becoming increasingly valuable as a complementary method in the rational design of sustainable approaches to energy conversion and storage.1–3 Especially the development of novel electrocatalysts for reactions such as hydrogen evolution/oxidation (HER/HOR) and oxygen evolution/reduction (OER/ORR), important within proton exchange membrane electrolysers and fuel cells, can be augmented by density functional theory (DFT) based methods with the ability to elucidate atomistic details that experiments alone struggle to resolve. The field of computational electrochemistry is, however, still in its infancy and consequently applied methods and levels of theory require careful benchmarking for precise physicochemical predictions.4Computational kinetic modelling of catalytic processes entails the determination of the transition path connecting the initial (reactant, IS) and final (product, FS) states. The most interesting quantities associated with the reaction path are the activation barrier (E‡) and the reaction energy (ΔE), defined by the energy differences between the reactant and transition states (TS) and the reactant and product states, respectively. While the reaction energy quantifies the driving force of the concerned reaction, the rate determining step (RDS) and consequently the reaction kinetics are ultimately dictated by the activation barrier height. Within the framework of DFT simulations, transition path optimizations are frequently conducted using the nudged elastic band (NEB) method,5 especially in conjunction with the climbing image modification (CI-NEB)6 that drives the image with the highest energy up to the saddle point. While the CI-NEB method is successful in describing the transition paths of processes taking place e.g. at vacuum interfaces,7–9 complications arise, however, for reactions lacking well defined initial and final states. Particularly, finite-temperature electrochemical reactions occurring at solid–liquid interfaces are challenging to simulate using static transition search methods such as CI-NEB as the dynamic solvent degrees of freedom may play a decisive part in the reaction coordinate.10 Indeed, ignoring such fluctuations is highly questionable as they constitute a potentially important entropic contribution to the activation barrier.
Consequently, to simulate rare events in dynamic environments appropriate sampling of the fluctuating medium is needed. A rigorous approach for this purpose is the constrained molecular dynamics (MD) method introduced by Sprik and Ciccotti.11 This methodology enables the study of activated processes by enforcing a holonomic constraint on a reaction coordinate along which the reaction is assumed to progress. By performing thermodynamic integration on the average force of constraint unbiased by a geometric correction term, the free energy profile of the reaction can be elegantly computed. The constrained MD method has been consequently applied very successfully to study reactions such as proton transfer,12–16 hydrolysis17,18 and redox reactions of metal ions in solution,19,20 as well as simple interfacial processes.21–26 Nevertheless, to our knowledge DFT based constrained MD simulations have not been applied for the direct simulation of HER/HOR or OER/ORR as of yet. Instead, the kinetics of these within electrochemical energy conversion highly relevant reactions have been investigated atomistically employing only static approaches.27–35
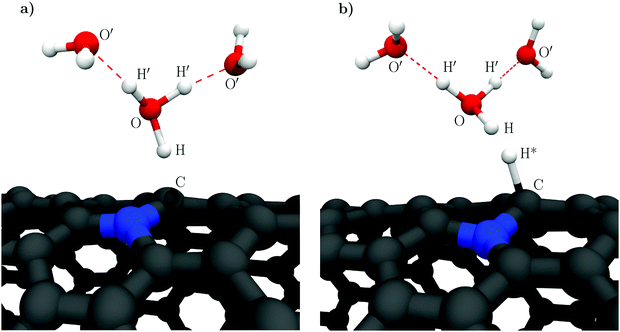
This work presents a comparative study of the CI-NEB and constrained MD methodologies and their ability to describe the transition path and the associated potential energy surface of the Volmer–Heyrovský mechanism of HER. In acidic media, the Volmer–Heyrovský mechanism proceeds via two proton-coupled electron transfer (PCET) steps; (1) electrosorption of a solvated proton, i.e. the Volmer reaction, followed by (2) an Eley–Rideal-type recombination of the adsorbed hydrogen (H*) and another solvated proton to form molecular hydrogen, the Heyrovský reaction.
| [(H2O)n–H]+ + e− ⇌ H* + (H2O)n | (1) |
| [(H2O)n–H]+ + H* + e− ⇌ H2 + (H2O)n | (2) |
In the preceding, the solvated proton complex is denoted by [(H2O)n–H]+, where n = 1, 2 and 4 are recognized as the hydronium (H3O+), Zundel (H5O2+) and Eigen (H9O4+) cations, respectively, often used to model aqueous hydronic species.36
As the model catalyst material we employ a nitrogen doped (14,0) carbon nanotube (NCNT), a noble metal-free electrocatalyst that has received notable experimental and computational attention recently.29,33,37–39 Specifically, we study hydrogen evolution occurring next to a substitutionally doped, graphitic nitrogen site. This site represents evidently only one of the possible dopant configurations and it has in fact recently been proposed that regarding HER and OER catalysis pyridinic moieties may constitute the most active sites.39 Nevertheless, we concentrate on the graphitic nitrogen due to previous research29 on this site which we use as a reference, as well as since the main purpose of the present work is to compare the performances of the aforementioned two computational methodologies and the importance of solvent fluctuations, not to elucidate the catalytic activities of the different dopant sites. Although highly interesting, this topic is beyond the scope of the present research and is consequently left for future efforts.
The remainder of this article is organized as follows. In Section 2.1 we briefly review the central theoretical details of the constrained MD and thermodynamic integration formalisms and motivate the chosen reaction coordinates for the Volmer and Heyrovský steps, respectively. Section 2.2 continues with a discussion of the theoretical aspects of a simple charge-extrapolation scheme that we apply to approximate the constant electrode potential behaviour of the as derived energy profiles. Finally, the theoretical methodology is concluded in Section 2.3 with a summary of the employed computational models and parameters. Next, the obtained results are reported and discussed in Section 3, starting first with the static CI-NEB calculations of the Volmer and Heyrovský reactions in Sections 3.1.1 and 3.1.2, respectively. Secondly, the output of the constrained MD simulations and the thermodynamic integration are presented in Section 3.2 and the results are concluded by a critical discussion of the two methods in Section 3.3, highlighting the key differences, advantages and limitations and their implications on electrochemical modelling. The main conclusions are finally summarized briefly in Section 4.
2 Theoretical methods
2.1 Reaction control by constraints
As introduced by Sprik and Ciccotti,11 the free energy profile related to rare events, such as chemical reactions, can be calculated by introducing a holonomic constraint on a chosen reaction coordinate along which the event under consideration is driven and integrating over the properly unbiased force associated with this constraint. Explicitly, integrating the unbiased, solvent averaged force 〈fs(ξ′)〉ξ′ with respect to the specified reaction coordinate ξ′ yields the relative free energy ΔA(ξ) at some value ξ on the reaction path according to eqn (3),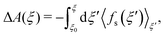 | (3) |
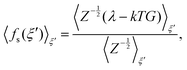 | (4) |
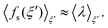 | (5) |
The main challenge of constrained MD with thermodynamic integration is that the, often multidimensional, reaction coordinate is generally not known a priori. Thus, a reasonable choice must be based on chemical intuition and tested properly. Briefly, the constrained reaction coordinate should be sufficiently robust so that a required control of the reaction is maintained throughout the transition path. If the constraint looses control of the reaction, e.g. after passing the transition state the product desorbs from the surface in an uncontrolled manner and diffuses away, a discontinuity will be observed in the force of constraint. This translates to uncertainties in the derived free energy profile and the reaction mechanism itself. On the other hand, the constraint should be indirect enough to allow for as many degrees of freedom as possible for the reaction to explore the phase space and find a realistic reaction path. For example, defining a simple interatomic distance as a constraint would quench the vibrational motion between the involved atoms.
In the present work, we employ the proton transfer coordinate defined by eqn (6) for the Volmer reaction,
| ξV(r) = |rC − rH| − |rO − rH|, | (6) |
For the Heyrovský reaction on the other hand we employ the proton transfer coordinate of eqn (7),
| ξH(r) = |rH − rH*| − |rC − rH*| − |rO − rH|. | (7) |
In practice, however, an apparent issue with simulating proton transfer from an aqueous phase is how to control proton hopping, i.e. the Grotthuss mechanism, so that the proton transfer would truly occur from the solvated complex, not from a water molecule. Two different approaches to mitigate this were tested and the results are detailed in Section 3.2.
2.2 Constant electrode potential via charge extrapolation
Considering electron transfer within the context of electrochemical reactions, the potential dependence of reaction energies and barriers is of considerable interest. While no generally accepted, computationally tractable standard procedure for simulating grand canonical, constant electrode potential processes exists, several approximations and extrapolation schemes have been proposed.40–44According to Chan and Nørskov,43,44 for simple proton transfer reactions in the absence of adsorbates with substantial molecular dipole moments or considerable solvent reorganization, the electrostatic contribution to the change in energy is purely capacitive and can be separated from the chemical energy change component. Following the proposed simple charge extrapolation formalism, the energy change with respect to a chosen reference state along a reaction path E2 − E1 at constant electrode potential U1 is given by eqn (8),
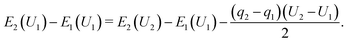 | (8) |
Here, qi denotes the net charge on the electrode surface in state i. Thus, taking for example state 2 as the transition state and state 1 as the initial state, the charge extrapolation scheme yields an estimate of the reaction barrier at the constant electrode potential of the initial state. Analogously, any state along the reaction path can be chosen to obtain estimates of the barrier at different electrode potentials. Conventionally, the absolute electrode potential Uabs is evaluated according to eqn (9),45,46
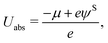 | (9) |
2.3 Computational details
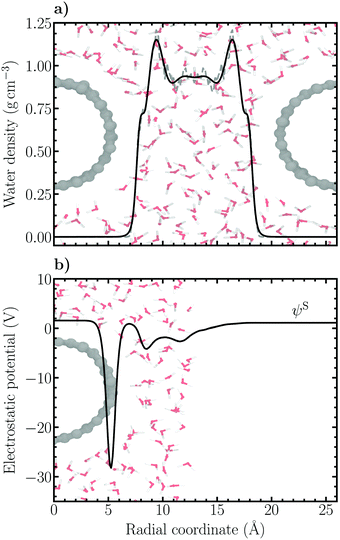
The Volmer–Heyrovský mechanism of HER was studied on a substitutionally nitrogen doped (14,0) single-walled carbon nanotube (C167N) constructed using ASE.47 The model NCNT was solvated using GROMACS48 with 201 classically pre-equilibrated SPC water molecules, resulting in a solvent phase with a minimum thickness of 11 Å between periodic copies of the NCNT. In order to model an acidic solution, one excess hydrogen atom was added to the water contact layer close to the nitrogen dopant. This resulted in a pH-value of 0.6 in accordance with pH = −log[H+] = −log(x/Vm), where x is the proton mole fraction (1/201) and Vm the molar volume of water (ca. 18 cm3 mol−1). The simulation cell size was 26.00 × 26.00 × 12.78 Å3. The water density profile between two periodic copies of the NCNT is presented in Fig. 2a (average density 〈ρ〉 ≈ 0.97 g cm−3). The high-density liquid (HDL) peak of the water contact layer can be seen to be relatively small, indicative of a hydrophobic character as has been inferred for pristine CNTs.49 For calculation of the electrode potential, a vacuum layer of roughly 24 Å was added around solvated NCNT configurations sampled every 100 fs to obtain the vacuum reference level, i.e. the Volta potential. Subsequently, the electrostatic (Hartree) potential of the respective configurations were calculated. An example of the behavior of the average electrostatic potential around the solvated NCNT is shown in Fig. 2b.All DFT calculations presented in this work were conducted using the CP2K/Quickstep quantum chemistry code.50,51 The spin-polarized formulation of the hybrid Gaussian and plane waves (GPW) method52 was used with an auxiliary plane wave basis cutoff of 450 Ry. Unless otherwise stated, the generalized gradient approximation (GGA) was invoked by applying the exchange–correlation functional of Perdew, Burke and Ernzerhof (PBE)53 together with semi-empirical dispersion interaction corrections according to the DFT-D3 scheme of Grimme et al.54,55 The damping function of Becke and Johnson was employed56 and in addition to the pairwise C6R−6 and C8R−8 dispersion correction terms the three-body C9R−9 term was included. The 2s and 2p electrons of carbon, nitrogen and oxygen and the 1s electron of hydrogen were considered as valence states. The Kohn–Sham orbitals corresponding to these states were expanded in molecularly optimized double-ζ plus polarisation quality Gaussian basis sets (MOLOPT-SR-DZVP).57 The remaining ionic cores were represented by norm-conserving scalar relativistic Goedecker–Teter–Hutter (GTH) pseudopotentials.58–60 The orbital transformation (OT) method61 using direct inversion in the iterative subspace (DIIS) was employed for solving the Kohn–Sham equations. Mixing of the electron density between subsequent iterations was performed using the Broyden method with a 30% fraction of new density considered each step. A convergence criterion of 2.7 × 10−5 eV for the energy was employed. In performed geometry optimizations the atomic structures were relaxed using the BFGS algorithm until the force on any atom was less than 2.3 × 10−2 eV Å−1.
Static minimum energy paths (MEP) of the Volmer and Heyrovský reactions were optimized using the CI-NEB method.6 The respective reaction paths were partitioned into 10 and 12 replicas and optimized until the maximum force reached a value less than 0.1 eV Å−1. The initial and final states of the reactions were prepared and optimized as described previously.29,30,33,35 To assess the significance of including exact Hartree–Fock exchange (HFX) and the effect of self-interaction error induced electron overdelocalisation on determined activation energies, the CI-NEB images initially converged at the PBE level were reoptimized by single-point calculations using a modified PBE062 hybrid functional proposed by Guidon et al.63 together with the auxiliary density matrix method (ADMM).64 Here, the standard HFX energy is replaced by a long-range corrected truncated Coulomb operator (PBE0-TC-LRC). A cutoff radius of 6.0 Å was employed.
Constrained Born–Oppenheimer MD simulations were performed in the canonical (NVT) ensemble at a temperature of 348.15 K using a stochastic velocity rescaling thermostat65 with a time constant of 100 fs. A time step of 0.5 fs was applied. The elevated temperature was chosen to reduce overstructuring of PBE water and to mimic proton quantum nuclear effects that are known to affect the structural and dynamical features of liquid water.66–70 We note that the revised PBE (RPBE)71 exchange–correlation functional has also recently been demonstrated as a satisfactory alternative in liquid water simulations when applied in conjunction with the semi-empirical DFT-D3 dispersion correction scheme.72,73 This functional combination overestimates, however, the oxygen–oxygen distances in the aqueous phase, thereby resulting in a considerably underestimated water density of less than 0.90 g cm−3.74 Considering this shortcoming and to allow a better comparison of our results with the ones obtained using the PBE0-D3 hybrid functional as well as the literature, the simulations performed herein were ultimately run using PBE-D3 at the elevated temperature stated above. The SHAKE algorithm75 was applied to integrate the Newtonian equations of motion of the systems subject to the defined constraints enforced using the method of Lagrange multipliers as implemented in the CP2K code. Each constrained MD simulation was run for a minimum of 10 ps, of which the first two picoseconds were considered equilibration and consequently excluded from the analyses. The initial, transition and final states were determined by the constrained MD trajectories which exhibited an average force of constraint of approximately 0.1 eV Å−1 or less.
3 Results and discussion
To compare the CI-NEB and constrained MD methods and to consequently investigate the importance of solvent dynamics in reaction path simulations, reference CI-NEB calculations were first performed for the Volmer–Heyrovský mechanism following computational procedures presented elsewhere.29,30,33,35 Concisely, the initial state of the Volmer reaction was first fully optimized without atomic constraints. Second, the solvent structure excluding the reacting Zundel cation was frozen to ensure a transition between two minima within the same local environment and to prevent the electrode potential from shifting due to changes in the interfacial molecular dipole. The product state was then optimized with the transferring proton placed on the probed adsorption site and finally the CI-NEB calculation was performed. The same solvent structure was also used for the Heyrovský reaction, i.e. only the reactive species in the initial (H5O2+ + H*) and the final (2H2O + H2) states were relaxed. However, in contrast to the previous works wherein a microsolvation (droplet) model was used to model the aqueous phase, we use a fully solvated model for the NCNT–water interface as well as perform further single point calculations at the hybrid PBE0 level of theory to reconverge the electronic structure of the PBE optimized NEB images.In the following, we first present CI-NEB results for the Volmer–Heyrovský mechanism and apply the charge-extrapolation methodology of Chan and Nørskov43,44 to approximate the potential dependence of the activation barriers and reaction energies. Subsequently, the constrained MD results and reaction profiles determined via thermodynamic integration are presented and analysed. Finally, a concluding comparison of the performance of the static and dynamic reaction path simulation methods is performed and the implications are critically discussed.
3.1 CI-NEB
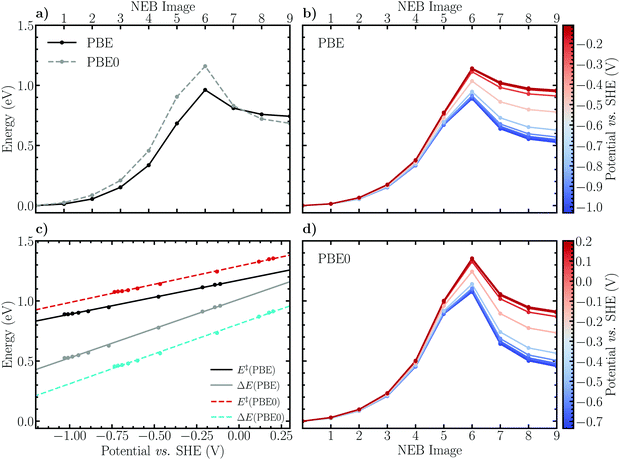
Employing the herein optimized initial and final states of the Volmer reaction, Fig. 3a shows that the CI-NEB method employing the PBE functional converges to a minimum energy path with an apparent activation barrier and reaction energy of 0.96 eV and 0.74 eV, respectively. Although qualitatively similar, the obtained values are somewhat higher than the previous estimates E‡ ≈ 0.5 eV and ΔE ≈ 0.4 eV, respectively.29 This is the first example of the limitations of the static CI-NEB method for studying reactions occurring at a solid–liquid interface. Indeed, the CI-NEB minimum energy path is highly dependent on the converged initial and final states including the selected solvent configuration. Thus, variations in the initial distances between reacting species and orientation of water molecules will yield significantly differing results for energetic and kinetic parameters. In the present case, the inherent ambiguity in defining the initial and final states results in a final state that is more sterically hindered, or equivalently an initial state that is more stable, than in the previous work. Evidently, due the dynamic nature of the solvent phase, a more reliable estimate of the reaction path and the associated energy profile using CI-NEB would require the optimization of multiple alternative paths. Subsequently, an improved description of the reaction kinetics and energetics would be obtained via appropriately weighted averages. This qualitative discussion is in line with the reaction rate theory of Chandler et al.,76–79 who propose that the notion of a single, well-defined minimum energy path should indeed be replaced by the concept of a transition path ensemble. While the formalism of Chandler et al. was not applied in the present work due to its prohibitive computational cost, we note that the constrained MD method of Sprik and Ciccotti is an analogous methodology by which to appropriately sample states along a reaction path. By employing a carefully chosen reaction coordinate, the simulated system is allowed to explore the phase space at each value of the specified constraint. Therefore no single minimum energy path is enforced as in the CI-NEB method, but instead an average constraint force profile and consequently a free energy profile is attained via thermodynamic integration.
Furthermore, Fig. 3a shows that reoptimizing the electronic structures of the converged CI-NEB images using the truncated hybrid PBE0 functional shifts the activation barrier upwards by 0.20 eV and lowers the reaction energy slightly by ca. 0.06 eV. This finding may be interpreted based on the self-interaction error (SIE) inherent in DFT employing (semi-)local functionals. Including exact Hartree–Fock exchange mitigates SIE induced electron overdelocalisation which spuriously stabilizes the reactant and transition states compared to the product state. This conclusion is consistent with earlier studies,80,81 in which electron overdelocalisation effects were alleviated by employing a charge-constrained DFT based configuration interaction approach (CDFT-CI). Specifically, in the CDFT-CI study performed on the Volmer reaction on an open-ended CNT,81 the barrier height was observed to increase by up to 0.2 eV while the reaction energy in the forward direction was lowered by 0.1–0.2 eV.
To obtain a rough estimate of the electrode potential dependence of the minimum energy profile of the Volmer reaction, the charge-extrapolation scheme of Chan and Nørskov43,44 was applied. The electrode potential was calculated according to Trasatti45 and referenced to the SHE scale while the net atomic charges on the electrode surface were approximated using Hirshfeld population analysis. For further details, please see Fig. S1 and S2 and the associated text in the ESI.† The obtained constant electrode potential energy profiles are presented in Fig. 3b and d for the PBE and PBE0 results, respectively. It appears that the behaviour of the energy profile as a function of the electrode potential is qualitatively reasonable. Indeed, decreasing the electrode potential results in decreased activation barriers and reaction energies due to the fact that the activated complex and product (adsorbed) states are stabilized with respect to the initial state as is expected for electrochemical reduction reactions. To more clearly illustrate how the reaction barriers and energies depend on the electrode potential, these values are plotted separately and shown in Fig. 3c. Concisely, using the PBE functional the activation energies are observed to vary between roughly 1.2 eV and 0.9 eV when the potential is decreased from 0.0 V to −1.0 V vs. SHE, while the values for PBE0 are consistently shifted upwards by approximately 0.1 eV. We note that a similar degree of potential dependence has been observed previously29 for the Volmer reaction using an alternative extrapolation scheme in which multiple CI-NEB energy profiles are calculated for several explicitly charged systems. Using this method, a shift in the activation barrier between ca. 0.6 eV and 0.3 eV is observed as the potential decreases from the thermodynamic redox potential of hydrogen, 0.0 V vs. SHE, to −1.0 V. The constant shift in the barrier heights compared to our work is, however, again present, and is due to differences in the employed frozen solvent and initial state configurations.
Considering the reaction energies obtained using PBE, a decrease from ca. 1.0 eV to 0.5 eV within the same electrode potential interval is observed, while the PBE0 results exhibit the same dependence, although shifted downwards by a constant 0.2 eV. Evidently, the above discussed difference between the GGA and hybrid descriptions holds qualitatively also following the charge-extrapolation, although an apparent reversal of the magnitude of the energy shifts is seen; the activation barrier increases and the reaction energy decreases by approximately 0.1 eV and 0.2 eV, respectively. Finally, the absolute difference between the GGA and hybrid results is observed to be largely constant, i.e. independent of the electrode potential.
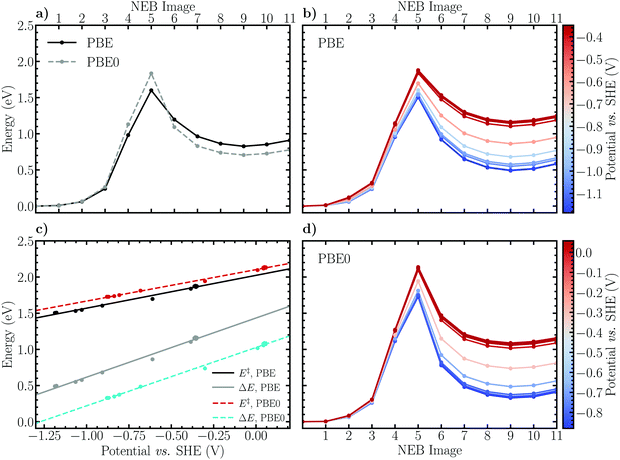
The potential dependence of the Heyrovský reaction was estimated analogously to the Volmer reaction. Expectedly, the results presented in Fig. 4b and d illustrate the same qualitative behaviour, characteristic of reduction reactions. Namely, as the electrode potential decreases (the electrode surface is charged) the transition and product states are stabilized with respect to the reactant state, thus decreasing the activation barrier heights and reaction energies. The potential dependence of the energetics is observed to be slightly more pronounced than for the Volmer reaction. Concretely, the activation and reaction energies determined using the PBE functional decrease from roughly 2.0 eV to 1.5 eV and 1.4 eV to 0.6 eV, respectively, as the electrode potential is decreased from 0.0 V to −1.0 V vs. SHE. For the PBE0 energy profiles the corresponding changes are observed between 2.1 eV and 1.6 eV for the activation barrier and between 1.0 eV and 0.2 eV for the reaction energy. The difference between the GGA and hybrid DFT descriptions of the activation barrier is again seen to hold also for the constant electrode potential energy profiles, namely that the PBE0 functional increases the barrier by ca. 0.1 eV independent of the electrode potential. The trend for the reaction energies is also analogous, although considerably more pronounced, exhibiting a decrease of approximately 0.4 eV compared to the 0.2 eV observed for the Volmer reaction.
Previous results29 obtained using the alternative extrapolation method reveals a somewhat less pronounced potential dependence in which the barrier determined using the PBE functional decreases from ca. 1.4 eV to 1.1 eV as the electrode potential is varied from 0.0 V to −1.0 V. Aside from the constant shift in the barrier height due to differing solvent structures, the potential dependence appears to be nevertheless in a qualitative agreement, providing some support for the computationally lightweight and simple charge-extrapolation scheme of Chan and Nørskov.43,44
3.2 Constrained MD
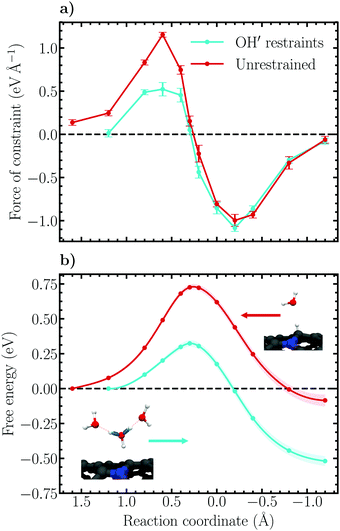
Constrained molecular dynamics simulations employing the introduced reaction coordinates (6) and (7) for the Volmer and Heyrovský reactions, respectively, were performed. The force of constraint associated with each value along the reaction coordinate was sampled and averaged over each trajectory and thermodynamic integration over the force profiles was conducted using the cumulative trapezoidal method to obtain the (Helmholtz) free energy profiles of the respective reactions. In order to elucidate the role of proton diffusion, i.e. the Grotthuss mechanism, the Volmer reaction was simulated both in the forward direction of eqn (1) using harmonic OH restraints to keep the solvated Zundel-like proton complex intact, as well as backward without any additional biasing restraints. For the restrained simulations, a force constant and equilibrium bond length of 19.4 eV Å−2 and 0.99 Å were respectively employed. The applied force constant is roughly 40% of the force constant of OH stretching in water.82Force and free energy profiles in which both approaches have been employed are shown in Fig. 5 together with error estimates. For consistency, the profiles are shown in the direction of the forward reaction, i.e. large values of the reaction coordinate correspond to trajectories which sample the proton in the aqueous phase while small values correspond to the adsorbed state. The forces of constraint in Fig. 5a are observed to increase gradually as the reaction progresses, reaching a maximum at a constraint value of 0.6 Å. Subsequently, the force decreases and passes an inflection point, the transition state, at the value 0.3 Å. Following the transition state, the forces are seen to switch sign (direction) and a minimum is reached at −0.2 Å. Finally, the force diminishes, reaching a value less than 0.1 eV Å−1 at −1.2 Å, which is taken as the final state of the Volmer reaction. The shape of both force profiles are observed to be relatively smooth, exhibiting no significant discontinuous jumps between sampled values of the constraint. This suggests that the Volmer reaction remains well controlled over the whole transition path using the chosen reaction coordinate.
It is noteworthy that the constraint force profiles are practically identical for the restrained and unrestrained simulations for trajectories between the transition and product (adsorbed) states. In contrast, restrained trajectories sampling the initial (solvated) states exhibit average constraint forces that are significantly smaller than in the unrestrained simulations. This difference can be understood considering that no Grotthuss hopping may occur when the proton is close to being, or has been, transferred to the surface, and consequently the imposed restraints on the OH′-bonds become unimportant. On the reactant side, however, the forces decrease substantially compared to the unrestrained ensemble because the proton complex is artificially stabilized.
Integrating the obtained forces yields the free energy profiles presented in Fig. 5b. We observe that the decreased constraint forces associated with the restrained solvated proton states results in a substantially lower activation free energy, 0.32 ± 0.03 eV, and reaction free energy, −0.52 ± 0.04 eV, compared to the unrestrained free energy profile which exhibits the values 0.73 ± 0.02 eV and −0.08 ± 0.05 eV, respectively. The reported error margins correspond to a 95% confidence interval based on standard errors determined using the method of block averaging and the statistical inefficiency test. Additionally, propagation of uncertainty within the thermodynamic integration has been properly accounted for. For further details on the calculation of errors, please see Fig. S3 and S4 including the associated text in the ESI.† Interestingly, inspecting the barrier height in the reverse direction reveals that the two parallel simulations yield nearly identical values, roughly 0.8 eV. This finding illustrates again the role of the imposed OH′ restraints, which play little role on the adsorbed state side of the reaction coordinate, but are decisive for the solvated proton states. Essentially, the initial state is destabilized compared to the transition and final states by ca. 0.4 eV due to the applied restraints.
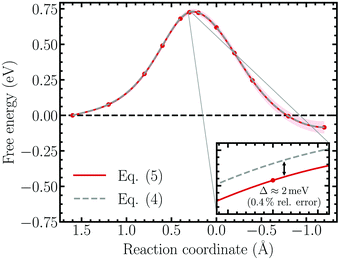
To investigate the importance of correcting the bare forces of constraint using eqn (4) to obtain the properly reweighted, solvent averaged force, the free energy surface of the Volmer reaction simulated within the unrestrained ensemble was re-evaluated using the correction terms derived in the Appendix. The result based on the bare force of constraint is replotted together with the unbiased free energy profile in Fig. 6, which indeed demonstrates that the influence of the correction factors is negligible. Specifically, performing thermodynamic integration on the bare force of constraint results in a relative error of roughly 0.4% (∼2 meV), which is well below the accuracy limit of standard DFT.
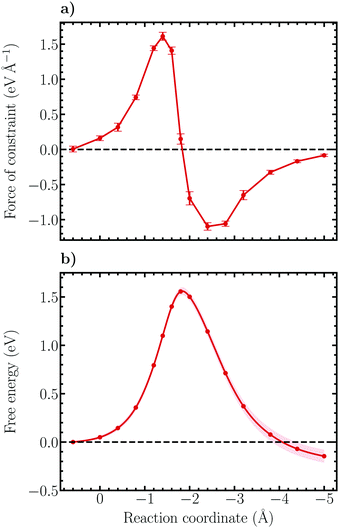
Following thermodynamic integration of the constraint force profile, the free energy surface shown in Fig. 7b is obtained. Due to the larger forces of constraint the free energy profile is observed to be steeper than for the Volmer reaction, exhibiting a free energy barrier of 1.56 ± 0.04 eV and a reaction free energy of −0.15 ± 0.07 eV. While the reaction free energy of the Heyrovský reaction is nearly identical with the one of the Volmer reaction, the activation free energy is a factor of more than two larger, indicating that the Heyrovský reaction corresponds to the RDS of the hydrogen evolution reaction on the investigated NCNT. This result is in qualitative agreement with the CI-NEB results obtained in this work, as well as in previous studies on similar systems.29,33
3.3 Comparison of CI-NEB and constrained MD results
| Method | Reaction | E ‡/A‡ (eV) | ΔE/ΔA (eV) |
|---|---|---|---|
| CI-NEB, PBE | Volmer | 0.96 | 0.74 |
| Heyrovský | 1.60 | 0.83 | |
| CI-NEB, PBE0 | Volmer | 1.16 | 0.68 |
| Heyrovský | 1.83 | 0.71 | |
| Constr. MD, PBE | Volmer (restr.) | 0.32 ± 0.03 | −0.52 ± 0.04 |
| Volmer | 0.73 ± 0.02 | −0.08 ± 0.05 | |
| Heyrovský | 1.56 ± 0.04 | −0.15 ± 0.07 | |
Disregarding the dynamic simulations of the Volmer reaction within the restrained ensemble and the hybrid functional calculations, two main observations separates the CI-NEB and constrained MD results. First, the activation barrier heights are lowered by 0.23 eV and 0.04 eV in the case of the Volmer and Heyrovský reactions, respectively. Secondly, the reaction energies decrease substantially, by roughly 0.82 eV and 0.97 eV, respectively. Comparing to the PBE0 reoptimized CI-NEB results, the difference between activation energies increases further, while a slight decrease is seen for the reaction energies.
Intuitively, one expects an increase in the activation barrier heights and reaction energies when switching from static calculations to dynamic simulations. Indeed, the static approximations provide an estimate of the minimum energy path and consequently neglect important entropic contributions to the potential energy surface. However, the reason for why this is not observed herein can be understood considering the biased, frozen solvent structure in the CI-NEB calculations. The water structure is optimized in the initial state of the reaction, and because solvent reorganization is suppressed the final state of the reaction will consequently be unphysically strained and therefore high in energy. Now, since the initial and final states of the studied reactions are ultimately connected via the respective transition states, solvent reorganization in the constrained MD simulations will appropriately stabilize the final states and subsequently drag the activation barrier heights downward as well. The fact that the net change in the activation barriers and reaction energies is negative upon inclusion of dynamics indicates thus that stabilizing solvent reorganization dominates over the destabilizing entropic contribution. It is furthermore noteworthy that the herein observed significance of solvent dynamics in the proper description of the Volmer–Heyrovský mechanism has been inferred recently for the Volmer step also using a theoretical PCET formalism accounting for vibrational nonadiabaticity and solvent relaxation dynamics.83
Due to the observed considerable influence of solvent reorganization, the Chan–Nørskov charge-extrapolation scheme43,44 applied to the CI-NEB calculations to derive energy profiles at constant electrode potentials is deemed inapplicable for the dynamic results. Indeed, since it appears that solvent relaxation dynamics play an important role also in the case of simple proton transfer reactions, the whole underlying notion of describing the electrostatic contribution to the energy change along a reaction path as purely capacitive is placed in a questionable light. For completeness, we have nevertheless calculated the average electrode potentials and surface charges for the considered constrained MD trajectories (ESI,† Fig. S6 and S7 and the accompanying text). While the estimated surface charges are found to be comparable with the static results, it appears also that the orientational dynamics of interfacial water molecules induce a heavily fluctuating surface dipole moment that strongly influences the electrode potential (0.2 V standard deviation), resulting in a slow convergence of the average quantity which further complicates a reliable employment of the extrapolation scheme. The magnitude of the electrode potential oscillations agrees with previous simulations.29,84 Although the averaged electrode potentials exhibit an increasing trend along the reaction coordinate as expected, the correlation between the surface charge and the electrode potential is weak and the observed slope is significantly lower than in the static calculations. This indicates that solvent fluctuations, reorganization and screening may indeed affect the potential dependence in a decisive manner. Further simulations beyond the scope of this research, such as longer MD runs and application of an alternative constant electrode potential approximation, are however needed for a conclusive say on the matter.
It is nevertheless clear that all obtained activation barriers are irrespective of the applied methodology substantial in magnitude, more than 1.5 eV for the rate-determining Heyrovský step. This suggests in accordance with previous computational studies predicting Heyrovský reaction barriers of 1.3 eV (singly-doped NCNT),29 1.2 eV (doubly-doped NCNT)33 and 1.2 eV (Fe-encapsulating NCNT),85 respectively, that HER catalysis according to the Volmer–Heyrovský mechanism is inefficient on sites adjacent to graphitic nitrogen dopants. Since experimental studies33,39,85 nevertheless observe a moderate HER activity (ca. 250–340 mV overpotential at 10 cm−2), it is evident that another dopant configuration, such as the pyridinic nitrogen moiety, or a combination thereof is responsible for the activity enhancement. We reiterate, however, that the main purpose of the present work was to contrast the performances of the two aforementioned computational methods and highlight the importance of solvent dynamics, not to elucidate the catalytic activities of various dopant sites.
| Reaction | Distance (Å) | CI-NEB | Constr. MD | ||||
|---|---|---|---|---|---|---|---|
| IS | TS | FS | IS | TS | FS | ||
| Volmer | |rC–rH| | 2.59 | 1.39 | 1.12 | 2.58 | 1.48 | 1.12 |
| |rO–rH| | 0.98 | 1.32 | 2.03 | 0.98 | 1.18 | 2.32 | |
| |rO–rH′| | 1.39 | 1.05 | 1.00 | n/a | 1.06 | 0.99 | |
| |rO′–rH′| | 1.10 | 1.50 | 1.75 | n/a | 1.54 | n/a | |
| Heyrovský | |rC–rH*| | 1.11 | 1.67 | 2.96 | 1.11 | 1.45 | 3.02 |
| |rH–rH*| | 1.98 | 0.87 | 0.73 | 2.69 | 0.97 | 0.74 | |
| |rO–rH| | 0.97 | 1.48 | 2.71 | 0.98 | 1.31 | 2.72 | |
| |rO–rH′| | 1.41 | 1.03 | 0.99 | n/a | 1.03 | 0.99 | |
| |rO′–rH′| | 1.08 | 1.58 | 1.84 | n/a | 1.61 | n/a | |
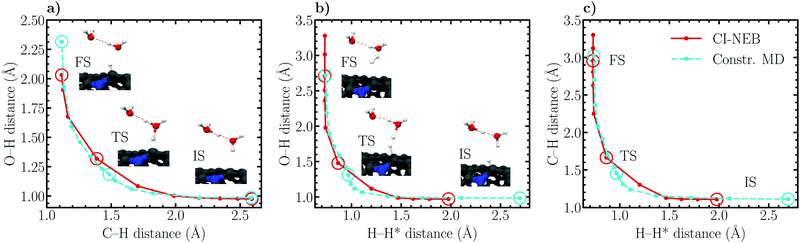
Considering the Volmer reaction (Fig. 8a), a high degree of correspondence between the CI-NEB and constrained MD reaction paths can be observed, although a close inspection reveals a slight “cutting of corners” and sliding of the CI-NEB path. The optimized initial state employed in the CI-NEB calculation exhibits a C–H distance of roughly 2.6 Å, a value identical to the constrained MD initial state trajectory. Also at the final state the C–H bond lengths are identical, ca. 1.1 Å, whereas a larger difference of roughly 0.3 Å is seen in the O–H distance. This difference is due to the fact that the Volmer reaction had to be driven slightly farther in the dynamic simulation to obtain a sufficiently small average force of constraint. At the transition state, the constrained MD C–H and O–H bond lengths are approximately 1.5 Å and 1.2 Å, while the corresponding values optimized using CI-NEB are 1.4 Å and 1.3 Å, respectively. Evidently, the CI-NEB method predicts a transition state structure in which the adsorbing proton is ca. 0.1 Å closer to the surface and farther from the donating oxygen than in the constrained MD simulation. This difference illustrates the effect of entropic contributions on the transition state geometry.
Similar conclusions as for the Volmer reaction can be drawn for the Heyrovský reaction path. Here, the final state geometries are practically identical while the initial state H–H* bond lengths differ by roughly 0.7 Å, the additional distance required to obtain a sufficiently converged reactant state in the dynamic simulation. Importantly, considering the C–H, H–H* and O–H distances, an analogous difference in the static and dynamic transition state geometries of approximately 0.1–0.2 Å is observed. This corresponding behaviour between the Volmer and Heyrovský reactions supports further the above concluded influence of solvent fluctuations, and therefore entropy, on the structural details of the transition state. Again, while the elbow plots in Fig. 8b and c are relatively similar for the CI-NEB and constrained MD approaches, a slight corner cutting is seen in CI-NEB results. Nevertheless, the ability of the static CI-NEB method to predict a reaction path this close to the dynamically sampled path is rather surprising and exemplifies the good performance of CI-NEB for simulating reactions in environments where entropic effects are insignificant.
Lastly, we briefly discuss the structural dynamics of the reactive hydronic species in accordance with the constrained MD results. While in the CI-NEB calculations the solvated proton complex is conventionally described as a Zundel cation, an Eigen configuration is seen to form in the dynamic initial states. However, in neither the Volmer nor Heyrovský steps does the reaction pass through a transition state involving these species. Instead, an intermediate H7O3+ complex, as illustrated in Fig. 1, is observed where the transferring proton is strongly coordinated towards the NCNT. Specifically, the H7O3+ complex is found to persist at the transition states of the Volmer and Heyrovský reactions as well as in the trajectories immediately following the respective transition states (ESI,† Fig. S5). However, moving further towards the reactant side of the transition path makes the Grotthuss mechanism energetically feasible and upon transfer of the acidic excess proton farther from the surface the H7O3+ complex decays and an Eigen cation is formed.
4 Conclusions
We have performed static climbing image nudged elastic band calculations and constrained molecular dynamics simulations with thermodynamic integration to critically assess the importance of incorporating solvent dynamics when investigating the reaction paths of the Volmer–Heyrovský mechanism of hydrogen evolution on a nitrogen doped (14,0) carbon nanotube. Additionally, the exchange–correlation functional dependence of the CI-NEB energy profiles was examined using the PBE and long-range corrected truncated PBE0 functionals and the electrode potential dependence was elucidated via a simple charge-extrapolation scheme.In qualitative agreement with previous research,29 the PBE activation energy of the Heyrovský reaction was observed to be considerably larger than the barrier of the Volmer reaction, by more than 0.6 eV, while the reaction energies were of similar magnitude. Quantitatively, however, the comparison of the reaction energetics is complicated by the employed different static solvent configurations, which in the present work result in a more pronounced stabilization of the initial state. Consequently, the reaction barriers and energies in the forward direction are shifted upwards by roughly 0.3–0.4 eV, while the reverse barriers are similar within 0.1 eV. Reoptimizing the electronic structures of the PBE CI-NEB images using PBE0 was observed to increase the reaction barriers by ca. 0.2 eV, while reaction energies in the forward direction were found to decrease by approximately 0.1 eV. This finding is understood by considering the ability of the hybrid functional to alleviate self-interaction error induced electron overdelocalisation in the initial and transition states and is qualitatively consistent with the results of charge-constrained DFT configuration interaction calculations.80,81 Finally, the electrode potential dependence of the Volmer and Heyrovský energy profiles were found to be qualitatively reasonable and in satisfactory agreement with previous constant potential simulations, taking into account the differences in employed solvent structures resulting in an approximately constant positive shift in the energies of the present work.
The free energy surfaces obtained via thermodynamic integration of the forces of constraint from the constrained MD simulations demonstrated the importance of explicitly sampling the interfacial dynamics when studying hydrogen evolution at a solid–liquid interface. Indeed, the reaction barriers obtained using CI-NEB and the PBE functional were observed to decrease by 0.04–0.23 eV, while even more substantial shifts of up to −1.0 eV were observed for the reaction energies. The differences between the CI-NEB and thermodynamic integration results were attributed to two opposite effects, namely stabilizing solvent reorganization and destabilizing entropic contributions due to solvent fluctuations. Entropic effects were also found to have an influence on the transition state geometries of the respective reaction steps. Our findings indicating the significance of solvent dynamics when studying interfacial proton-coupled electron transfer corroborate recent theoretical results accounting for vibrational nonadiabaticity and solvent relaxation dynamics.83
While a comprehensive computational treatise of electrochemical phenomena is still complicated by the lack of well applicable grand canonical methods, our work exemplifies the importance of incorporating solvent dynamics in the rigorous description of reactions at solid–liquid interfaces and presents an important step towards more accurate electrochemical simulations. The herein applied constrained molecular dynamics simulations employing the proposed reaction coordinates could e.g. be applied to reinvestigate the hydrogen evolution reaction according to the Volmer–Heyrovský mechanism on single-crystal platinum electrodes, a prototypical system where a mismatch between the results of electrochemical experiments and static computational approximations is observed.27,28,86 Indeed, this defines the topic of our ongoing research with the aim to elucidate how electrochemistry and electrocatalysis should be modelled in order to obtain accurate, experimentally meaningful and, ideally, predictive results.
Conflicts of interest
There are no conflicts of interest to declare.Appendix: correction factors to the force of constraint of the Volmer reaction
The general form of the geometric correction factors Z and G for evaluating the properly unbiased solvent averaged force have been proven by Sprik and Ciccotti,11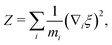 | (A1) |
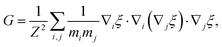 | (A2) |
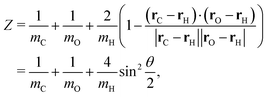 | (A3) |
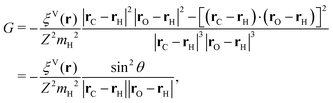 | (A4) |
Acknowledgements
R. K. acknowledges Aalto University School of Chemical Engineering for funding in the form of a doctoral scholarship. Computational resources were provided by the Finnish IT Center for Science (CSC).References
- M. T. M. Koper, J. Electroanal. Chem., 2005, 574, 375–386 CrossRef CAS
.
- M. Nielsen, M. E. Björketun, M. H. Hansen and J. Rossmeisl, Surf. Sci., 2015, 631, 2–7 CrossRef CAS
.
- S. Sakong and A. Groß, ACS Catal., 2016, 6, 5575–5586 CrossRef CAS
.
- R. Jinnouchi, K. Kodama and Y. Morimoto, Curr. Opin. Electrochem., 2018, 8, 103–109 CrossRef CAS
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- J. Greeley and M. Mavrikakis, Nat. Mater., 2004, 3, 810 CrossRef CAS PubMed
.
- A. Krasheninnikov, K. Nordlund, P. O. Lehtinen, A. S. Foster, A. Ayuela and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 073402 CrossRef
.
- B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634 CrossRef CAS PubMed
.
- M. Sprik, Faraday Discuss., 1998, 110, 437–445 RSC
.
- M. Sprik and G. Ciccotti, J. Chem. Phys., 1998, 109, 7737–7744 CrossRef CAS
.
- E. J. Meijer and M. Sprik, J. Am. Chem. Soc., 1998, 120, 6345–6355 CrossRef CAS
.
- M. Sprik, Chem. Phys., 2000, 258, 139–150 CrossRef CAS
.
- N. L. Doltsinis and M. Sprik, Phys. Chem. Chem. Phys., 2003, 5, 2612–2618 RSC
.
- P. R. Markwick, N. L. Doltsinis and D. Marx, J. Chem. Phys., 2005, 122, 054112 CrossRef PubMed
.
- I. Ivanov, B. Chen, S. Raugei and M. L. Klein, J. Phys. Chem. B, 2006, 110, 6365–6371 CrossRef CAS PubMed
.
- P. Carloni, M. Sprik and W. Andreoni, J. Phys. Chem. B, 2000, 104, 823–835 CrossRef CAS
.
- T. Ikeda, M. Hirata and T. Kimura, J. Chem. Phys., 2006, 124, 074503 CrossRef PubMed
.
- J. Blumberger and M. Sprik, J. Phys. Chem. B, 2004, 108, 6529–6535 CrossRef CAS
.
- Y. Tateyama, J. Blumberger, T. Ohno and M. Sprik, J. Chem. Phys., 2007, 126, 204506 CrossRef PubMed
.
- H.-S. Lee and M. E. Tuckerman, J. Phys. Chem. A, 2009, 113, 2144–2151 CrossRef CAS
.
- J. L. Suter, M. Sprik and E. S. Boek, Geochim. Cosmochim. Acta, 2012, 91, 109–119 CrossRef CAS
.
- J.-C. Chen, B. Reischl, P. Spijker, N. Holmberg, K. Laasonen and A. S. Foster, Phys. Chem. Chem. Phys., 2014, 16, 22545–22554 RSC
.
- X. Liu, J. Cheng, M. Sprik, X. Lu and R. Wang, Geochim. Cosmochim. Acta, 2015, 168, 293–301 CrossRef CAS
.
- J. A. Herron, Y. Morikawa and M. Mavrikakis, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E4937–E4945 CrossRef CAS PubMed
.
- C. Zhang, X. Liu, X. Lu, M. He, E. J. Meijer and R. Wang, Geochim. Cosmochim. Acta, 2017, 203, 54–68 CrossRef CAS
.
- E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250 RSC
.
- E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdóttir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 18182–18197 CrossRef
.
- N. Holmberg and K. Laasonen, J. Phys. Chem. C, 2015, 119, 16166–16178 CrossRef CAS
.
- N. Holmberg and K. Laasonen, J. Phys. Chem. Lett., 2015, 6, 3956–3960 CrossRef CAS PubMed
.
- M. Tavakkoli, N. Holmberg, R. Kronberg, H. Jiang, J. Sainio, E. I. Kauppinen, T. Kallio and K. Laasonen, ACS Catal., 2017, 7, 3121–3130 CrossRef CAS
.
- V. Tripkovic and T. Vegge, J. Phys. Chem. C, 2017, 121, 26785–26793 CrossRef CAS
.
- S. Tuomi, O. J. Pakkanen, M. Borghei, R. Kronberg, J. Sainio, E. I. Kauppinen, A. G. Nasibulin, K. Laasonen and T. Kallio, ChemCatChem, 2018, 10, 3872–3882 CrossRef CAS
.
- L. Partanen, G. Murdachaew and K. Laasonen, J. Phys. Chem. C, 2018, 122, 12892–12899 CrossRef CAS PubMed
.
- G. Cilpa-Karhu, O. J. Pakkanen and K. E. Laasonen, J. Phys. Chem. C, 2019, 123, 13569–13577 CrossRef CAS
.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601 CrossRef CAS
.
- Z. Zhang and K. Cho, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 075420 CrossRef
.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed
.
- F. Davodi, M. Tavakkoli, J. Lahtinen and T. Kallio, J. Catal., 2017, 353, 19–27 CrossRef CAS
.
- J.-S. Filhol and M. Neurock, Angew. Chem., Int. Ed., 2006, 45, 402–406 CrossRef CAS PubMed
.
- C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402 CrossRef
.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS
.
- K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2663–2668 CrossRef CAS
.
- K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2016, 7, 1686–1690 CrossRef CAS
.
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CAS
.
- J. Cheng and M. Sprik, Phys. Chem. Chem. Phys., 2012, 14, 11245–11267 RSC
.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus,
et al.
, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef
.
- B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed
.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188 CrossRef CAS
.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS
.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS
.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed
.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed
.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed
.
- C. Hartwigsen, S. Gœdecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS
.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed
.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118, 4365–4369 CrossRef CAS
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2009, 5, 3010–3021 CrossRef CAS
.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- J. C. Grossman, E. Schwegler, E. W. Draeger, F. Gygi and G. Galli, J. Chem. Phys., 2004, 120, 300–311 CrossRef CAS PubMed
.
- J. VandeVondele, F. Mohamed, M. Krack, J. Hutter, M. Sprik and M. Parrinello, J. Chem. Phys., 2005, 122, 014515 CrossRef PubMed
.
- H.-S. Lee and M. E. Tuckerman, J. Chem. Phys., 2006, 125, 154507 CrossRef PubMed
.
- T. Todorova, A. P. Seitsonen, J. Hutter, I.-F. W. Kuo and C. J. Mundy, J. Phys. Chem. B, 2006, 110, 3685–3691 CrossRef CAS PubMed
.
- J. Schmidt, J. VandeVondele, I.-F. W. Kuo, D. Sebastiani, J. I. Siepmann, J. Hutter and C. J. Mundy, J. Phys. Chem. B, 2009, 113, 11959–11964 CrossRef CAS PubMed
.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef
.
- K. Forster-Tonigold and A. Groß, J. Chem. Phys., 2014, 141, 064501 CrossRef PubMed
.
- S. Sakong, K. Forster-Tonigold and A. Groß, J. Chem. Phys., 2016, 144, 194701 CrossRef PubMed
.
- T. Morawietz, A. Singraber, C. Dellago and J. Behler, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8368–8373 CrossRef CAS PubMed
.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS
.
- C. Dellago, P. G. Bolhuis, F. S. Csajka and D. Chandler, J. Chem. Phys., 1998, 108, 1964–1977 CrossRef CAS
.
- C. Dellago, P. G. Bolhuis and D. Chandler, J. Chem. Phys., 1998, 108, 9236–9245 CrossRef CAS
.
- P. G. Bolhuis, C. Dellago and D. Chandler, Faraday Discuss., 1998, 110, 421–436 RSC
.
- C. Dellago, P. G. Bolhuis and D. Chandler, J. Chem. Phys., 1999, 110, 6617–6625 CrossRef CAS
.
- Q. Wu, B. Kaduk and T. Van-Voorhis, J. Chem. Phys., 2009, 130, 034109 CrossRef PubMed
.
- N. Holmberg and K. Laasonen, J. Chem. Phys., 2018, 149, 104702 CrossRef
.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503 CrossRef PubMed
.
- Y.-C. Lam, A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2019, 10, 5312–5317 CrossRef CAS PubMed
.
- S. Sakong and A. Groß, J. Chem. Phys., 2018, 149, 084705 CrossRef PubMed
.
- J. Deng, P. Ren, D. Deng, L. Yu, F. Yang and X. Bao, Energy Environ. Sci., 2014, 7, 1919–1923 RSC
.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06474e |
| This journal is © the Owner Societies 2020 |