Defective crystal plane-oriented induced lattice polarization for the photocatalytic enhancement of ZnO

Abstract

Defects can influence the properties of photocatalysts, and defective ZnO has triggered broad interest and intensive studies for decades. However, the correlation between crystal planes and defects remains unclear. Here, we demonstrate that the (101) plane is superior in producing oxygen vacancies than the (100) plane in rod-like defective ZnO samples. While the optimum intensity of the crystal ratio, (101)/(100), approaches 1, the separation efficiency of electrons–holes is much enhanced. Furthermore, it is found that the (101) plane has stronger spontaneous adsorption and higher dissociation activity of H₂O, which is conducive to the spontaneous formation of oxygen vacancies and eventually enhances the separation efficiency of electrons–holes. The charge difference also shows that the crystal boundary junctions could cause uneven charge distribution, inducing lattice polarization and boosting the charge separation of defective ZnO, which is helpful for improving the photocatalytic activities. As a new proposed mechanism, the relationship between defect engineering and crystal surface could provide inspiration for the design of special nanomaterials for the environment purification and energy fields.

---

1 Introduction

Recently, due to its unique optical, electrical, and physicochemical properties, zinc oxide (ZnO) as an n-type semiconductor (3.3 eV bandgap and 60 meV exciton binding energy) has attracted extensive interest and has been employed in numerous applications.^1–4 Nevertheless, ZnO photocatalysts absorb mainly in the UV region and the recombination rate of photogenerated electron–hole pairs is high, which greatly inhibits their applications.⁵ Defect engineering of ZnO has been one of the methods used to improve photocatalytic efficiency since the fundamental physical and chemical properties of nanomaterials highly rely on their defect structures.^6–10 The absorption of oxides and catalytic activity reportedly can be greatly enhanced by implanting defects. For instance, the decoration of nanomaterials with noble metal nanoparticles (NPs) is a promising method by which to reduce the recombination of the photogenerated electrons–holes and enhance the photodegradation activity.^11–15 In addition, vacuum treatment¹⁶ and temperature-programmed reduction (TPR)^17,18 have been known to be promising and rather facile methods for defect engineering. Lv et al. found that dramatic visible photocatalytic activity and distinct photocurrent were generated due to the introduction of oxygen vacancies on the ZnO surface with vacuum deoxidation.¹⁶ TPR in the hydrogen atmosphere has been used as a good technique for determining the surface structures and properties of reduced and sulfided Mo/Al₂O₃ catalysts.^17,18 Therefore, defective ZnO nanomaterials have been tested as the media for purification, disinfection, removal of heavy metals, degradation of organic compounds and pharmaceuticals.^19–21 Meanwhile, by means of density functional theory (DFT) calculations, the formation energy of surface defects has been calculated.^22–24 Ji et al. systematically investigated the photocatalytic reduction of CO₂ on perfect and defective anatase TiO₂ (101) surfaces following both the fast-hydrogenation and fast-deoxygenation pathways.²² By comparing the properties of the metal-supported ZnO films with those of the free-standing ZnO bilayer, Thang et al. demonstrated the key role of the metal/oxide interface by means of DFT calculations including the adsorption of Au, NO₂, and O₂ atoms on ZnO/X(111) (X = Cu, Ag, Au).²³ Zhou et al. found that the structure alternatives are controlled thermodynamically by nucleation through DFT calculations for the interface structures of two growth orientations, while controlled kinetically by the enhanced Zn adsorption and oxygen diffusion upon the phase transformation.²⁴

However, not enough attention was paid to the relationship between the crystal plane and active substances of defective ZnO, particularly, for the (101) and (100) planes. Therefore, in order to gain a deep understanding of the relationship, the properties and mechanisms of the defects on the (100) and (101) planes need to be carefully identified. The exploration of mechanism and relationship between crystal plane exposure and defects in photocatalysis is essential and urgent. According to previous literature, the term “vacancy” is often used to express a vacant site of atoms while “defective” is employed when modifying specific substance with defect characteristics, these are idiomatic phrases.^9,25,26

In this work, a series of defective ZnO samples were synthesized by vacuum treatment and H₂-TPR with glycerol and CTAB as surfactants. We discovered that the structural features of the hexagonal shape for wurtzite ZnO is favorable for needle tip field formation and the crystal boundary junction of the (101) and (100) planes could generate lattice polarization at the same time. Thus, the synergistic effect of lattice polarization and the needle tip field is conducive to the effective separation of holes and electrons. Meanwhile, the separation efficiency of electrons–holes is much enhanced as the intensity of the crystal ratio approaches 1. Moreover, the (101) plane shows superiority in forming oxygen vacancies and self-adsorption with H₂O in comparison with the (100) plane. Thus, the (101) plane is the most effective active plane, improving the separation efficiency of photogenerated electrons and holes to enhance the photocatalytic activity.

2 Experimental section

2.1 Preparation of ZnO

All chemicals were analytical grade reagents and purchased from Aladdin Chemical Reagent Co., Ltd. In this work, nanometer ZnO samples were prepared by the hydrothermal method using CTAB and different concentrations of glycerol as precursors.^27,28 A batch of CT-ZnO samples were synthesized by dissolving 0.73 g of CTAB in a 50 ml beaker with 40 ml of 0.15 M sodium hydroxide (NaOH) solution and 2 ml of 0.3 M zinc chloride (ZnCl) solution. Then the mixed solution was transferred into 50 ml steel autoclaves and dried at 150 °C for 16 h. The white solid products were treated by centrifuge at 4000 rpm for 20 min, washed with deionized water and ethanol more than three times and finally kept in a dry oven preheated to 60 °C for 8 h. A series of G-ZnO samples were prepared as follows: a total of 53.32 g of NaOH and 7.33 g of zinc acetate dihydrate were mixed in deionized water. Then 26.66 g of NaOH was dissolved into the solution. Then it was transferred into a 200 ml flask. Respectively, 10 ml of the solution was mixed with 15 ml, 20 ml, 25 ml, and 30 ml of glycerol and stirred for 15 min. The mixed solution was transferred into 50 ml steel autoclaves to dry at 150 °C for 24 h. The same method as the preparation of CTAB-ZnO was used. The prepared samples were labeled as 1G-ZnO, 2G-ZnO, 3G-ZnO and 4G-ZnO.

Two defective preparation methods, vacuum treatment and H₂-TPR, were used to study their differences. The vacuum deoxidation process was performed to prepare V-ZnO samples at 250 °C for 4 hours. In order to obtain a sample prepared by TPR with excellent activity, an exploring experiment was carried out. Finally, we found the most appropriate temperature to synthesize defective ZnO during the TPR process was 380 °C (Fig. S1†). The defective samples synthesized by TPR and vacuum treatment were labeled as T-x-ZnO and V-x-ZnO series, respectively, such as T-1G-ZnO (T-G-ZnO), T-CT-ZnO, V-1G-ZnO, V-2G-ZnO, V-3G-ZnO and V-4G-ZnO.

2.2 Characterization

The crystalline structures of the photocatalysts were identified by powder XRD (XRD, Bruker PHI Quantera) in the diffraction angle range 2θ = 3–80°, using Cu Kα radiation. FTIR spectra were performed using a Bruker VERTEX 70 spectrophotometer. The microscopic morphologies of the samples were observed via scanning electron microscopy (SEM, Hitachi SU-8010) and a transmission electron microscope (TEM, Hitachi HT7700). Electron spin resonance (ESR: ESR 300E, Germany) and the capture experiments below analyse the main active species during the photocatalytic reaction. The Brunauer–Emmett–Teller (BET) surface area and pore width of the samples measured by N₂ adsorption–desorption photoelectron spectroscopy (XPS) spectra were obtained via a Thermo VG ESCALAB 250Xi. Photoluminescence (PL) spectra were obtained using a JASCO FP-6500 fluorescence spectrophotometer instrument (ASAP 2460 version 2.01, USA). A 50 W xenon lamp (PLS-SXE300D, Beijing Bofeilai Technology Co. Ltd.) was used as simulated solar irradiation and with a 420 nm cut-off filter (100 mW cm⁻²) was used as the visible light source. The photoelectrochemical measurements were performed via a CHI670E Electrochemical Workstation (CHI Shanghai, Inc.), in which saturated calomel electrodes (SCE) were employed as the reference electrodes. The electrolyte was a 0.1 M Na₂SO₄ aqueous solution.

2.3 Computational methodology

The first-principles calculations were performed using the Vienna ab initio simulation package (VASP)²⁹ based on density functional theory (DFT).^30,31 The projector-augmented plane wave (PAW) method was adopted with the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) to describe the exchange–correlation potential.^32,33 The wave functions were expanded with a plane-wave basis set with a cutoff energy of 500 eV. The Brillouin zone was sampled using 4 × 5 × 1 and 4 × 4 × 1 k-point meshes for the (100) and (101) surfaces, respectively. The self-consistent convergence of total energy was chosen to be as 10⁻⁶ eV, during the calculation, all the atoms positions were optimized with the convergence criterion less than 0.02 eV Å⁻¹.

2.4 Photocatalytic degradation experiment

The photocatalytic degradation of methylene blue (MB) solution was carried out at room temperature in a visible light multi-position photochemical reactor. The specific photocatalytic degradation of methylene blue (MB) solution operations were as follows: the defective ZnO solids (25 mg) were mixed with 50 mL of MB solution (1 × 10⁻⁵ mol L⁻¹). The solution was stirred by an ultrasonic vibration to form a homogeneous composite solution, and then stirred in the dark for 30 minutes to reach adsorption equilibrium, subsequently, the lamp (λ = 420 nm) was turned on to start the photocatalysis reaction. 2 ml samples were taken every 30 min for 3 h. The concentration of supernatant after centrifugation was continuously measured by using an ultraviolet–visible spectrophotometer. Finally, the pollutant removal rate (%) was calculated based on the following equation: contaminants removal rate (%) = ln(C/C₀) × 100%, where C₀ and C refer to the contaminant-concentration of completing dark adsorption and finishing 6 × 30 min photocatalytic separately.

3 Results and discussion

3.1 Crystal structure and morphology of defective ZnO

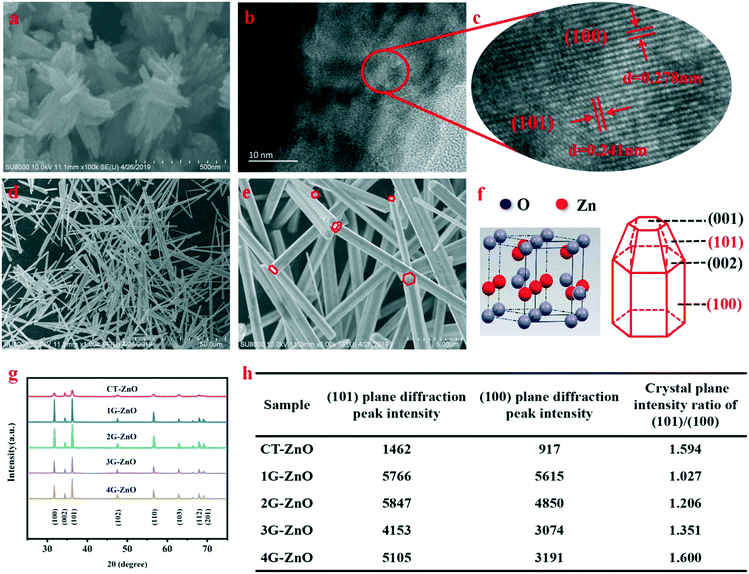
SEM (Fig. 1a) indicates that the V-CT-ZnO samples have a flower-like morphology assembled from nanosheets. The single micro-flower grows radially from the center outward and has a diverse size. The average widths and lengths of ZnO nanosheets are 60–150 nm and 300–500 nm, respectively. This reveals that V-CT-ZnO has a large ratio of length to diameter, a rod-like structure, which is beneficial to form the needle-tip effect. More detailed information on the crystal structure of V-CT-ZnO was gained from the HRTEM image (Fig. 1b and c). Corresponding to lattice spacing, the distances of the (101) and (100) planes are 0.241 nm and 0.278 nm (Fig. 1b and c), respectively. HRTEM confirms that V-CT-ZnO has extraordinary (100) and (101) crystallographic orientation. The morphologies of V-G-ZnO investigated by SEM (Fig. 1d and e) reveal the hexagonal rod-like morphology of V-G-ZnO with around 1 μm in width and 10–50 μm in length. The rod-like structure of defective ZnO with the tip-edge is conducive to the formation of lattice polarization, similar to the electric field needle tip in nature.³⁴

Fig. 1 (a) SEM of CT-ZnO, (b) HRTEM of CT-ZnO, (c) the corresponding HR-TEM images of the marked area in (b), (d) and (e) SEM images of G-ZnO with different magnifications, (f) scheme of G-ZnO wurtzite-type crystals, (g) XRD patterns of ZnO samples and (h) diffraction peak intensity and peak intensity ratio of the dominant crystal plane.

Meanwhile, the XRD diagram (Fig. 1f and g) indicates the potential effect of crystal orientation on the photocatalytic activity: the hexagonal shape of the wurtzite-type crystals (JCPDS no. 36-1451) forming the nanorods allows exposure of both polar planes (001–002) and non-polar planes (100–101).³⁵ The (100) and (101) plane diffraction peaks exhibit much stronger than the others, revealing that the two crystal planes are closely related to the photocatalytic activity. Lv et al. considered that oxygen vacancies are formed on the surface of ZnO photocatalyst and there are no changes in the crystal structure during the process of vacuum treatment.¹⁶ Thus, in our work, defective ZnO can be replaced by bulk ZnO to act as the research object of the lattice structure. In Fig. 1h, the peak intensity ratio of the 1G-ZnO series sample is slightly larger than 1 and its peaks are strongest, suggesting that 1G-ZnO displays a much greater crystallinity. Moreover, the degradation effect increases as the ratio increases, indicating the (101) plane has ascendancy on defect production. Combined with the above analysis, the (101) and (100) crystal boundary junctions and nanorod structural characteristics of defective ZnO are helpful for forming lattice polarization, which is conducive to the separation of photogenerated carriers.

3.2 Microstructure of defective ZnO

To observe the chemical composition of the sample and to elucidate the corresponding chemical states of the elements, XPS analysis is performed for defective ZnO and bulk ZnO. The survey XPS spectra, as shown in Fig. 2a, reveal that the ZnO samples mainly contain Zn, O and C elements. As shown in Fig. 2b, the major C1s XPS peak of the defective ZnO (284.58 eV) is asymmetric, which might be due to the peaks overlapping between contaminant carbon and other carbon species. Whereas, the main peak at 284.68 eV for bulk ZnO is symmetric and can be ascribed to adventitious hydrocarbon.³⁶ In Fig. 2c, the doublet spectral lines of Zn 2p are observed at the binding energies of 1021.18 ± 0.05 eV (Zn 2p_3/2) and 1043.88 ± 0.05 eV (Zn 2p_1/2) with a spin–orbit splitting (Δs) of 23.1 ± 0.05 eV, which coincides with the results for Zn²⁺ in ZnO. The fitted O 1s XPS for both the bulk and defective ZnO samples are presented (Fig. 3d and e). As reported previously, the O 1s peak can be fitted by three Gaussian peaks with different binding energy components.^37–39 The lowest binding energy O1 peak centered at 529.90 ± 0.05 eV can be attributed to the O²⁻ ions in the hexagonal wurtzite structure of ZnO.⁴⁰ The medium binding energy O2 peak located at 530.65 ± 0.05 eV could be related to oxygen vacancies in the oxygen deficient regions of ZnO.³⁹ The intensity of the O2 peak is an indication of the amount of oxygen defects in the samples. The highest peak observed at 531.54 ± 0.05 eV can be assigned to chemisorbed oxygen species such as CO₃ on the surface of ZnO.⁴⁰ It is observed that the intensity of the O1 and O3 peak decreased with defects. Notably, the intensity of the O2 increases, suggesting that oxygen vacancies increased in the defective ZnO system. The analysis suggests that defective ZnO is beneficial to the formation of oxygen vacancies and the rapid separation of electrons and holes.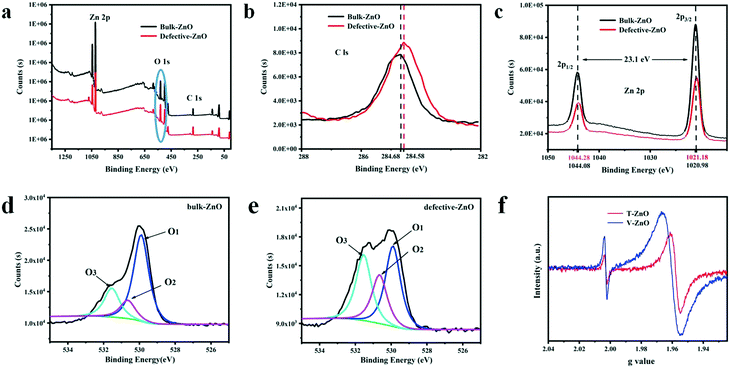

Fig. 2 XPS spectra of (a) survey, (b) C 1s, (c) Zn 2p, and (d and e) O 1s and (f) ESR spectra of defective ZnO in visible light.

Fig. 3 Side views of the surface structures of defective ZnO (a) with O vacancies, (b) adsorption and (c) dissociation H₂O on the (100) plane, side views of the surface structures of defective ZnO (d) with O vacancies and (e) adsorption and (f) dissociation H₂O on the (101) plane.

In addition, the bulk ZnO shows a weak ESR signal at g = 1.960, which was assigned to a shallow donor state due to some impurities or defects and usually assigned to a singly ionized oxygen vacancies defect.⁴¹ From Fig. 2f, an additional signal at g = 2.003 of the defective samples is observed, which may be caused by surface Zn vacancies.^42,43 Such defects have been identified as positively charged oxygen vacancies acting as deep donors.⁴² Meanwhile, the main g values of T-ZnO and V-ZnO, having shifted, are 1.958 and 1.961, respectively. Due to the high sensitivity of ultra high-frequency ESR, we clearly disentangled the overlapping contributions of the small g-factor differences, which indicated that different defect sites are simultaneously present on the surface. These analyses are consistent with the XPS images, revealing that oxygen vacancies exist in defective ZnO. Thus, the existence of oxygen vacancies on the surface of defective ZnO changes the chemical environment and we inferred that the formation of oxygen vacancies may be related to the exposure of planes.

3.3 The relationship between oxygen vacancies formation

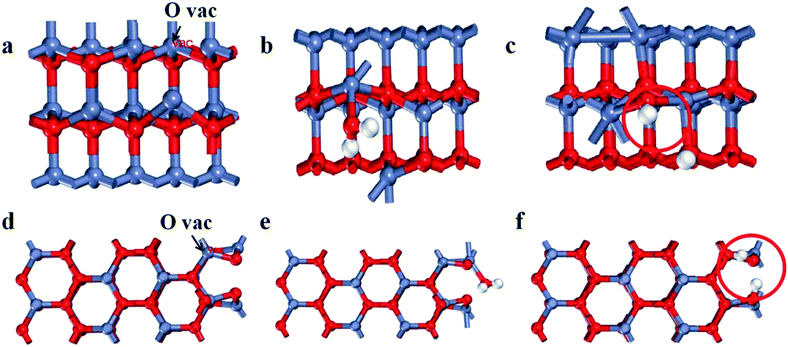
To further determine the relationship between oxygen vacancies formation and crystal surface exposure, we performed DFT calculations of the formation energy activity for oxygen vacancies on the (100) and (101) planes with the most energetically favorable configurations. The (100) and (101) planes are modeled by a supercell with three atomic layers of ZnO, as shown in Fig. 3a–f (Zn, O and H are indicated as red, dark blue and white spheres, particularly, the O of the H₂O molecule is labeled as red). To calculate the formation energy for oxygen vacancies of the ZnO surface, we used the following eqn (1):

E_f = E_N − E_N−n − E_O (1)

where E_f is the formation energy, E_N represents the total energy of the pristine ZnO system with N total atoms, E_N−n represents the energy of the ZnO system with oxygen vacancies, (where n represents the number of missing oxygen atoms), and E_O denotes half the energy of O₂ in the gas phase. From Table 1, the formation energy of the (101) plane is lower than the (100) plane, revealing that the (101) plane is more favorable to form oxygen vacancies on thermodynamics. Meanwhile, to explore the location and features of oxygen vacancies on a molecular level, DFT calculations of the adsorption and dissociation reaction of molecular H₂O were performed. The adsorption energy and dissociation energy were calculated using the following eqn (2) and (3):

E_ads = E_T(surf-mol) − E_T(surf) − E_free(mol) (2)

E_dis = E_T(dis) − E_T(surf-mol) (3)

Table 1 The formation energy for oxygen vacancies of the (100) and (101) planes

Plane	E N−n	E N	E O	E f
100	−174.64	−166.38	−1.68	6.58
101	−220.45	−215.55	−1.68	3.22

---

Here, E_T(surf-mol), E_T(surf) and E_T(dis) stand for the total energy of oxygen vacancies with, without and dissociated from the H₂O molecule, respectively, while E_free(mol) represents the total energy of the free H₂O molecule. As illustrated in Table 2, the adsorption energy of H₂O on the oxygen vacancies of the (100) plane is 0.11 eV. The result suggests that the adsorption of H₂O on the (100) plane is a nonspontaneous reaction which is unstable. Nevertheless, the (101) plane is spontaneous and pretty much stable. Meanwhile, the dissociation energy on the (101) plane increases by 1.24 eV in comparison with that of the (100) plane. Thus, the oxygen vacancies on the (101) plane are more prone to react with H₂O. Thereby, the formation of oxygen vacancies on the (101) plane is spontaneous and the system is very stable, suggesting that the structural features of the (101) plane are helpful for the formation of oxygen vacancies. Whereas, the optimum intensity of the crystal ratio approaches 1, which shows a fast separation efficiency of electrons and holes. Meanwhile, it is found that the (101) plane has stronger spontaneous adsorption and higher dissociation activity of H₂O, indicating the actual behavior of the plane in the process of pollutant degradation.

Table 2 The adsorption and dissociation energy of molecular H₂O

Plane	E (surf)	E T(surf-mol)	E free(mol)	E T(dis)	E ads	E dis
100	−166.38	−180.53	14.26	−181.34	0.11	−0.81
101	−215.55	−230.88	14.26	−232.93	−1.07	−2.05

---

3.4 Features of charge transfer and lattice polarization

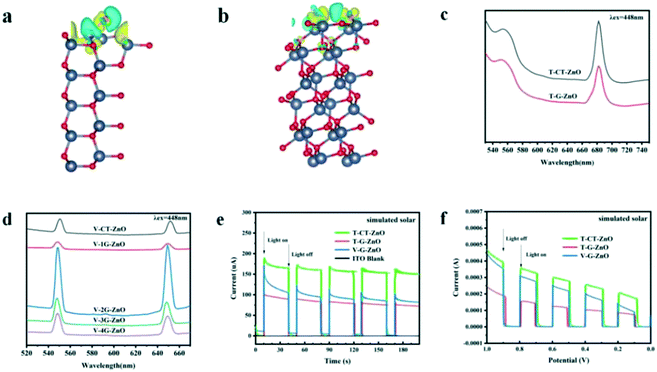
The charge difference of the crystal plane was calculated to analyze the charge transfer behavior (Fig. 4a and b). Enhanced charge accumulation and depletion occur between the O atom and H* from H₂O molecule on the (101) plane remarkably. Meanwhile, charge transfer occurs to OH* absorbed on the oxygen vacancies, in which the charge density is much larger than that of the (100) plane. These verify that the crystal boundary junctions cause an uneven charge distribution inducing lattice polarization and boosting the charge separation of defective ZnO, thus improving the photocatalytic activities. Combined with the needle tip effect caused by wurtzite defective ZnO (Fig. 1f), the synergistic effect makes the (101) plane more able to facilitate carrier separation and defect generation, which is beneficial to promote crystal plane activity.

Fig. 4 Charge difference of (a) the (100) plane and (b) the (101) plane (charge accumulation is in yellow and depletion is in blue), PL of (c) T-ZnO series samples and (d) V-ZnO series samples, (e) transient photocurrents and (f) linear sweep voltammetry.

Photoluminescence (PL) emission spectroscopy is useful for revealing the migration, transfer, and recombination processes of the photogenerated electron–hole pairs. The PL peak of T-CT-ZnO (Fig. 4c) is relatively strong, revealing a higher recombination rate of photogenerated electrons and holes. Meanwhile, as shown in Fig. 4d, V-2G-ZnO also exhibits much stronger peaks, suggesting that the rapid recombination rate induced poor activity.

The carrier migration properties can significantly change with surface modifications.^44,45 Therefore, some effective techniques such as photocurrent tests, electrochemical impedance spectroscopy (EIS) measurements, and linear sweep voltammograms (LSV) are used to study the carrier separation efficiency of defective ZnO samples. The photocurrent response (Fig. 4e) of the T-CT-ZnO was higher than that of the T-G-ZnO and V-G-ZnO under the simulated solar irradiation, which indicated that its electrode has a better separation efficiency of photogenerated carriers than other samples. Furthermore, the photocurrent response could also be enhanced by the applied voltage (Fig. 4f). The EIS (Fig. S2†) shows the low charge transfer resistance (R_ct) for T-ZnO and V-ZnO. The lower R_ct value means that the recombination of carriers (e⁻–h⁺ pairs) at the interface with the electrolyte is decreased. The analysis reveals that the (101) plane is the effective active crystal plane, which is beneficial to form lattice polarization, improving the separation efficiency of photogenerated electrons and holes to enhance the photocatalytic activity.

The Brunauer–Emmett–Teller (BET) method and the Barrett–Joyner–Halenda (BJH) model were used to evaluate the specific surface areas and the pore size, separately.⁴⁶ The specific surface area values were found to be 17.60 and 16.37 m² g⁻¹ (Fig. S3a†) and the pore size (radius) was observed to be 8.20 nm and 12.09 nm for the bulk ZnO and defective-ZnO samples (Fig. S3b†), respectively. The photocatalytic activity of defective ZnO was mainly attributed to rapid carrier transportation induced by the lattice polarization field but not merely as the BET surface increased.

3.5 Proposed photocatalytic mechanism

The photocatalytic activities of the samples were evaluated by the degradation of MB solution under simulated solar irradiation. As Fig. 5a and S4† show, the degradation efficiency of V-1G-ZnO is the highest among all samples. We also found that the degradation efficiency of defective ZnO treated by vacuum with glycerol as the surfactant is higher than that treated by TPR. For instance, the degradation efficiency of V-1G-ZnO is 4 times higher than T-G-ZnO. Lv et al. found that most oxygen atoms were removed from the ZnO surface with vacuum deoxidation, which could generate surface oxygen vacancies.¹⁶ Meanwhile, through H₂-TPR, hydrogen atoms could interact with the surface lattice oxygen of metal oxides, introducing oxygen vacancies and interstitial hydrogen into the ZnO lattice.⁴⁷ However, in this work, combined with the ESR results, V-1G-ZnO shows a better performance, suggesting that V-1G-ZnO has superiority in oxygen vacancies. Besides, Kundu et al. reported that in H₂ atmosphere the oxygen functional groups are less stable and can decompose,⁴⁸ so the oxygen-containing functional groups of the T-G-ZnO system will be reduced and may generate oxygen vacancies in the bulk, which hinders the improvement of photocatalytic activity. Meanwhile, the V-1G-ZnO sample has a rod-like structure, which is conducive to the formation of lattice polarization and oxygen vacancies. These are instrumental in the separation of photogenerated carriers to enhance the photocatalytic activity. The results show that V-1G-ZnO has a better activity than T-G-ZnO.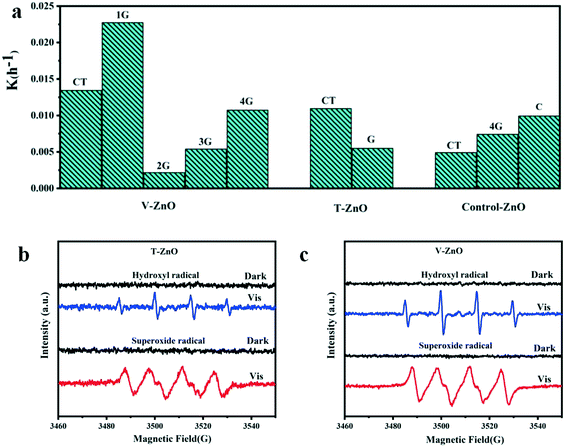

Fig. 5 Histogram of the slope of degradation of MB solution and ESR measurements of (b) T-ZnO and (c) V-ZnO.

The determination of the active substances in the process of photocatalysis was further evaluated by ESR measurements. In order to detect the active substances in the photocatalytic process, the free radical capture detection of singlet oxygen (¹O₂), superoxide radical (˙O₂⁻), hydroxyl (˙OH), holes (h⁺) and electrons (e⁻) by ESR was carried out. In Fig. S5,† the active substances of bulk ZnO samples are ˙O₂⁻ and ˙OH. Obviously, the ESR signals of ˙O₂⁻ and ˙OH of these defective samples are both strong under simulated sunlight (Fig. 5b and c). As shown in Fig. S6,† the active substances of V-ZnO are much stronger than T-ZnO, indicating that V-ZnO has a superiority of active substances and charge carriers, improving the photocatalytic activities, which is in accordance with the conclusions of different defective ZnO prepared by the same surfactants (Fig. 5a). In summary, the active substances of T-ZnO and V-ZnO in photocatalysis are ˙O₂⁻ and ˙OH, respectively.

Based on the above analysis, defective ZnO prepared by vacuum treatment and H₂-TPR with glycerol and CTAB as surfactants could improve photocatalytic performance compared with the bulk ZnO. As shown in Scheme 1, we intuitively analyzed the structural feature of hexagonal shape for wurtzite ZnO which is favorable for needle tip field formation. Meanwhile, the crystal boundary junction of the (101) and (100) planes is beneficial to form lattice polarization. The synergistic effect of lattice polarization and needle tip field provides efficient channels to accelerate the separation of holes and electrons. Besides, the formation of oxygen vacancies on the (101) plane is spontaneous in thermodynamics and the system is very stable, suggesting that the structural feature of the (101) plane is helpful for the formation of oxygen vacancies. The optimum intensity of crystal ratio, (101)/(100), approaches 1 and the separation efficiency of electrons–holes is much enhanced. Meanwhile, it was found that the (101) plane has stronger spontaneous adsorption and higher dissociation activity of H₂O molecules, which is conducive to the spontaneous formation of oxygen vacancies and eventually accelerates the separation efficiency of electrons–holes. Therefore, the experimental and theoretical results highlight the crucial role of the (101) plane that is the effective active crystal plane, which is very favorable for the lattice polarization formation, thus improving photogenerated carrier transfer to enhance the photocatalytic activity.

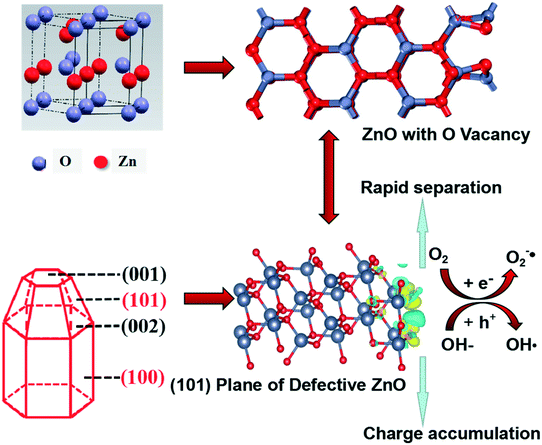Scheme 1 Schematic illustration of the mechanism in the photocatalytic reaction of defective ZnO systems.

4 Conclusions

In conclusion, the relationship of the (101) and (100) planes and oxygen vacancies is revealed by developing a general method for studying surface defects of nanomaterials. All results highlight the crucial role of the (101) plane being superior in producing oxygen vacancies than the (100) plane and exhibiting strong spontaneous adsorption ability on the thermodynamics and high dissociation activity. This demonstrates that the (101) plane is the effective active crystal plane and is very favorable for the lattice polarization formation, thus improving photogenerated carrier transfer to enhance the photocatalytic activity. As a new proposed mechanism, the relationship between defect engineering and crystal surface can provide inspiration and be extended to other nanocomposites with controllable architectures, which may offer more opportunities for their applications in environmental purification.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partly supported by National Natural Science Foundation of China (21607034 and 51978032), Beijing Natural Science Foundation (8192011), Great Wall Scholars Program (CIT&TCD20170313), The Fundamental Research Funds for Beijing Universities (X18173 and X18292).

Notes and references

1. H. Frenzel, A. Lajn, H. von Wenckstern, M. Lorenz, F. Schein, Z. P. Zhang and M. Grundmann, Adv. Mater., 2010, 22, 5332–5349.
2. A. B. Djurisic, X. Y. Chen, Y. H. Leung and A. M. C. Ng, J. Mater. Chem., 2012, 22, 6526–6535.
3. J. L. Yang, S. J. An, W. I. Park, G. C. Yi and W. Choi, Adv. Mater., 2004, 16, 1661–1664.
4. E. Galoppini, J. Rochford, H. Chen, G. Saraf, Y. C. Lu, A. Hagfeldt and G. Boschloo, J. Phys. Chem. B, 2006, 110, 16159–16161.
5. Y. M. Hungea, A. A. Yadavb and V. L. Mathea, Ultrason. Sonochem., 2018, 45, 116–122.
6. J. Jia, C. X. Qian, Y. C. Dong, Y. Li, H. Wang, M. Ghoussoub, K. T. Butler, A. Walsh and G. A. Ozin, Chem. Soc. Rev., 2017, 46, 4631–4644.
7. H. S. Kim, J. B. Cook, H. Lin, J. S. Ko, S. H. Tolbert, V. Ozolins and B. Dunn, Nat. Mater., 2017, 16, 454–460.
8. T. Koketsu, J. W. Ma, B. J. Morgan, M. Body, C. Legein, W. Dachraoui, M. Giannini, A. Demortiere, M. Salanne, F. Dardoize, H. Groult, O. J. Borkiewicz, K. W. Chapman, P. Strasser and D. Dambournet, Nat. Mater., 2017, 16, 1142–1148.
9. S. Das, B. Wang, Y. Cao, M. R. Cho, Y. J. Shin, S. M. Yang, L. F. Wang, M. Kim, S. V. Kalinin, L. Q. Chen and T. W. Noh, Nat. Commun., 2017, 8, 615.
10. G. Ou, Y. S. Xu, B. Wen, R. Lin, B. H. Ge, Y. Tang, Y. W. Liang, C. Yang, K. Huang, D. Zu, R. Yu, W. X. Chen, J. Li, H. Wu, L. M. Liu and Y. D. Li, Nat. Commun., 2018, 9, 1302.
11. Y. F. Xu, C. Zhang, L. X. Zhang, X. H. Zhang, H. L. Yao and J. L. Shi, Energy Environ. Sci., 2016, 9, 2410–2417.
12. Q. B. Sun, D. Cortie, S. Y. Zhang, T. J. Frankcombe, G. W. She, J. Gao, L. R. Sheppard, W. B. Hu, H. Chen, S. J. Zhuo, D. H. Chen, R. L. Withers, G. McIntyre, D. H. Yu, W. S. Shi and Y. Liu, Adv. Mater., 2017, 29, 1605123.
13. S. Kuriakose, K. Sahu, S. A. Khan, A. Tripathi, D. K. Avasthi and S. Mohapatra, Opt. Mater., 2017, 64, 47–52.
14. S. Kuriakose, V. Choudhary, B. Satpati and S. Mohapatra, Phys. Chem. Chem. Phys., 2014, 16, 17560–17568.
15. A. Ziashahabi, M. Prato, Z. Y. Dang, R. Poursalehi and N. Naseri, Sci. Rep., 2019, 9, 11839.
16. Y. H. Lv, C. S. Pan, X. G. Ma, R. L. Zong, X. J. Bai and Y. F. Zhu, Appl. Catal., B, 2013, 138–139, 26–32.
17. B. Muller, A. D. van Langveld, J. A. Moulijin and H. J. Knozinger, J. Phys. Chem., 1993, 97, 9028–9033.
18. P. J. Mangnus, A. Riezebos, A. D. van Langveld and J. A. Moulijin, J. Catal., 1995, 151, 178–191.
19. I. Ali, Chem. Rev., 2012, 112, 5073–5091.
20. J. Gómez-Pastora, E. Bringas and I. Ortiz, Chem. Eng. J., 2014, 256, 187–204.
21. K. Simeonidis, S. Mourdikoudis, E. Kaprara, M. Mitrakasd and L. Polavarapu, Environ. Sci.: Water Res. Technol., 2016, 2, 43–70.
22. Y. F. Ji and Y. Luo, J. Am. Chem. Soc., 2016, 138, 15896–15902.
23. H. V. Thang, S. Tosoni and G. Pacchioni, ACS Catal., 2018, 8, 4110–4119.
24. H. Zhou, L. J. Wu, H. Q. Wang, J. C. Zheng, L. H. Zhang, K. Kisslinger and Y. P. Li, Nat. Commun., 2017, 8, 1474.
25. Y. C. Xu, H. Z. Li, B. J. Sun, P. Z. Qiao, L. P. Ren, G. H. Tian, B. J. Jiang, K. Pan and W. Zhou, Chem. Eng. J., 2020, 379, 122295.
26. P. Camarda, F. Messina, L. Vaccaro, S. Agnello, G. Buscarino, R. Schneider, R. Popescu, D. Gerthsen, R. Lorenzi, F. M. Gelardia and M. Cannas, Phys. Chem. Chem. Phys., 2016, 18, 16237–16244.
27. X. G. Han, H. Z. He, Q. Kuang, X. Zhou, X. H. Zhang, T. Xu, Z. X. Xie and L. S. Zheng, J. Phys. Chem. C, 2009, 113, 584–589.
28. Y. V. Kaneti, J. Yue, X. C. Jian and A. B. Yu, J. Phys. Chem. C, 2013, 117, 13153–13162.
29. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
30. P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, 864–871.
31. W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138.
32. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
34. M. Jeem, L. H. Zhang, J. Y. Ishioka, T. Shibayama, T. Iwasaki, T. Kato and S. Watanabe, Nano Lett., 2017, 17, 2088–2093.
35. A. Ramirez Canon, M. MedinaLlamas, M. Vezzoli and D. Mattia, Phys. Chem. Chem. Phys., 2018, 20, 6648–6656.
36. A. S. Alshammari, L. N. Chi, X. P. Chen, A. Bagabas, D. Kramer, A. Alromaeha and Z. Jiang, RSC Adv., 2015, 5, 27690–27698.
37. S. Bang, S. Lee, Y. Ko, J. Park, S. Shin, H. Seo and H. Jeon, Nanoscale Res. Lett., 2012, 7, 290.
38. P. T. Hsieh, Y. C. Chen, K. S. Kao and C. M. Wang, Appl. Phys. A: Mater. Sci. Process., 2008, 90, 317–321.
39. M. R. Alenezi, A. S. Alshammari, K. D. G. I. Jayawardena, M. J. Beliatis, S. J. Henley and S. R. P. Silva, J. Phys. Chem. C, 2013, 117, 17850–17858.
40. G. H. Mhlongo, D. E. Motaung, S. S. Nkosi, H. C. Swart, G. F. Malgas, K. T. Hillie and B. W. Mwakikunga, Appl. Surf. Sci., 2014, 293, 62–70.
41. B. K. Meyer, H. Alves and D. M. Hofmann, Phys. Status Solidi B, 2004, 241, 231–260.
42. P. Jakes and E. Erdem, Phys. Status Solidi RRL, 2011, 5, 56–58.
43. H. Kaftelen, K. Ocakoglu, S. Tu, R. Thomann, S. Weber and E. Erdem, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014113.
44. G. Spataro, A. Dazzazi, S. Fortuny, Y. Champouret, Y. Coppel, J. Rubio-Garcia, A. Bouhaouss, F. Gauffre and M. L. Kahn, Eur. J. Inorg. Chem., 2016, 2016, 2056–2062.
45. Z. Q. Zheng, M. Mounsamy, N. Lauth-de Viguerie, Y. Coppel, S. Harrisson, M. Destarac, C. Mingotaud, M. L. Kahn and J. D. Marty, Polym. Chem., 2019, 10, 145–154.
46. P. F. Cheng, S. S. Du, Y. X. Cai, F. M. Liu, P. Sun, J. Zheng and G. Y. Lu, J. Phys. Chem. C, 2013, 117, 24150–24156.
47. T. Xia, P. Wallenmeyer, A. Anderson, J. Murowchick, L. Liu and X. B. Chen, RSC Adv., 2014, 4, 41654–41658.
48. S. Kundu, Y. M. Wang, W. Xia and M. Muhler, J. Phys. Chem. C, 2008, 112, 16869–16878.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ce01966a

---