Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Low-order many-body interactions determine the local structure of liquid water†
Marc
Riera
a,
Eleftherios
Lambros
a,
Thuong T.
Nguyen
a,
Andreas W.
Götz
 b and
Francesco
Paesani
b and
Francesco
Paesani
 *abc
*abc
aDepartment of Chemistry and Biochemistry, University of California, San Diego, La Jolla, California 92093, USA
bSan Diego Supercomputer Center, University of California, San Diego, La Jolla, California 92093, USA
cMaterials Science and Engineering, University of California, San Diego, La Jolla, California 92093, USA. E-mail: fpaesani@ucsd.edu
First published on 26th July 2019
Abstract
Despite its apparent simplicity, water displays unique behavior across the phase diagram which is strictly related to the ability of the water molecules to form dense, yet dynamic, hydrogen-bond networks that continually fluctuate in time and space. The competition between different local hydrogen-bonding environments has been hypothesized as a possible origin of the anomalous properties of liquid water. Through a systematic application of the many-body expansion of the total energy, we demonstrate that the local structure of liquid water at room temperature is determined by a delicate balance between two-body and three-body energies, which is further modulated by higher-order many-body effects. Besides providing fundamental insights into the structure of liquid water, this analysis also emphasizes that a correct representation of two-body and three-body energies requires sub-chemical accuracy that is nowadays only achieved by many-body models rigorously derived from the many-body expansion of the total energy, which thus hold great promise for shedding light on the molecular origin of the anomalous behavior of liquid water.
1 Introduction
Covering 71% of the Earth's surface and making up more than two-thirds of the human body weight, water plays an essential role in life which cannot be overemphasized.1 After decades of research, there is now no doubt that the unique properties of water cannot simply be explained in terms of a three-atom, 10-electron molecule, but are rather due to the ability of the water molecules to form a dense, yet flexible, hydrogen-bond (H-bond) network in which both number and strength of H-bonds continually fluctuate. While temperature and pressure variations cause smooth changes in the local properties of simple liquids, this is not the case in liquid water where similar variations modify the equilibrium of different H-bonding environments, resulting in drastic changes in the local structure and, consequently, in both thermodynamic and dynamical properties.2 The competition between two different local H-bonding environments, commonly defined as high-density liquid (HDL) and low-density liquid (LDL) phases, has been suggested as a possible origin of the anomalous properties of liquid water.3As already recognized by Frank and Wen in their picture of liquid water consisting of “flickering clusters of hydrogen-bonded molecules”,4 the relative stability of different H-bonding arrangements in liquid water results from the delicate interplay of many-body effects that may either increase (cooperative effects) or decrease (anticooperative effects) the strength of the overall interaction relative to the sum of all pairwise contributions.5 These many-body interactions are further modulated by nuclear quantum effects.6,7 Many-body interactions in a system containing N water molecules can be rigorously defined through the corresponding many-body expansion (MBE) of the total energy (EN),8
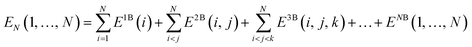 | (1) |
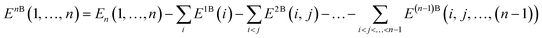 | (2) |
It has been shown that eqn (1) converges rapidly for water, with the 2B and 3B terms contributing, on average, ∼80% and 15–20%, respectively, and all remaining higher-body terms contributing ∼1%.8–10
Besides representing a rigorous theoretical framework for characterizing many-body interactions in liquid water, eqn (1) also provides an efficient computational route for developing analytical potential energy functions (PEFs) that express the total energy of a system composed of N water molecules as a sum of individual many-body terms.11 This has led to the advent of several many-body PEFs for water in which the individual many-body terms in eqn (1) are fitted to large sets of reference data calculated at the coupled cluster level of theory with single, double, and iterative triple excitations, i.e., CCSD(T), the current “gold standard” for molecular interactions.12–17 Among existing many-body PEFs, it has been shown that the MB-pol PEF achieves great accuracy by integrating classical representations of many-body electrostatics, which correctly describe interactions at large molecular separations, with data-driven 2B and 3B terms represented by permutationally invariant polynomials (PIPs) that smoothly turn on as two and three water molecules, respectively, approach each other.15–17 The MB-pol 2B and 3B terms, which were fitted to large sets of CCSD(T) reference data calculated in the complete basis set (CBS) limit, effectively account for non-classical interactions (e.g., Pauli repulsion, charge transfer and charge penetration) arising in regions where the electron densities of individual water molecules overlap.18
Building upon the theoretical framework provided by eqn (1) and the functional form adopted by the MB-pol PEF, we demonstrate that the local structure of liquid water is determined by a delicate balance between 2B and 3B interactions, which requires sub-chemical accuracy for a correct representation of the underlying H-bonding arrangements.
2 Methods
2.1 Electronic structure calculations
All CCSD(T) calculations presented in the main text were carried out using MOLPRO.19 The 2B energies shown in Fig. 1 of the main text were computed by extrapolating the values obtained with aug-cc-pVTZ and aug-cc-pVQZ basis sets supplemented with an additional set of (3s, 3p, 2d, 1f) midbond functions, with exponents equal to (0.9, 0.3, 0.1) for s and p orbitals, (0.6, 0.2) for d orbitals, and 0.3 for f orbitals, placed at the center of mass of each dimer configuration.20–22 The following two-point formula was used to extrapolate the energies to the CBS limit:23,24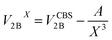 | (3) |
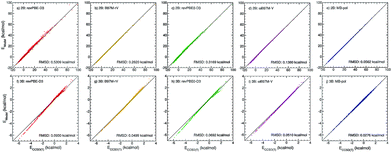 | ||
Fig. 1 Correlation plots for 2B (top panels) and 3B (bottom panels) energies. Plotted on the x axes are CCSD(T)/CBS reference values calculated for 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508 water dimers (ref. 15) and 12 508 water dimers (ref. 15) and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 347 water trimers (ref. 16), respectively. On the y axes are the corresponding energies calculated with revPBE-D3 (red, panels (a) and (f)), B97M-rV (yellow, panels (b) and (g)), revPBE0-D3 (green, panels (c) and (h)), ωB97M-V (magenta, panels (d) and (i)), and MB-pol (blue, panels (e) and (j)). 347 water trimers (ref. 16), respectively. On the y axes are the corresponding energies calculated with revPBE-D3 (red, panels (a) and (f)), B97M-rV (yellow, panels (b) and (g)), revPBE0-D3 (green, panels (c) and (h)), ωB97M-V (magenta, panels (d) and (i)), and MB-pol (blue, panels (e) and (j)). | ||
The reference interaction energies for (H2O)n clusters, with n = 2–6, were obtained using the MBE of the interaction energy8 according to the “stratified approximation many-body approach” (SAMBA) as described in ref. 26. Within SAMBA, the 2B and 3B energies were calculated as described above while all higher (>3B) contributions were computed with the CCSD(T)-F12 method using the VTZ-F12 basis sets.27–29 This method yields results close to the CBS values at lower computational cost than canonical CCSD(T) calculations with large basis sets.30,31 Cluster geometries for n = 2–3 where taken from ref. 32, those for n = 4–5 were taken from ref. 33, and those for n = 6 were taken from ref. 34. All DFT calculations with revPBE-D3,35 B97M-rV,36 revPBE0-D3,37 and ωB97M-V38 functionals were carried with the aug-cc-pVQZ basis set20 using Q-Chem.39
2.2 Path-integral molecular dynamics
Path-integral molecular dynamics (PIMD) simulations40–43 were carried out in the normal-mode representation to calculate both radial distribution functions, RDFs, and distributions of the tetrahedral order parameter, P(qtet). PIMD is based upon Feynman's formulation of statistical mechanics in terms of path integrals44 and exploits the isomorphism between the quantum partition function of a system of N particles and the classical partition function of a system consisting of N flexible ring polymers.40 By construction, PIMD enables the calculation of numerically exact structural and thermodynamic properties of quantum-mechanical systems.45 All PIMD simulations were carried out for a system consisting of 256 H2O molecules in a periodic cubic box in both canonical (NVT: constant number of molecules, volume, and temperature) and isobaric-isothermal (NPT: constant number of molecules, pressure, and temperature) ensembles, with T = 298.15 K and P = 1.0 atm. Each atom was represented by a ring polymer with 32 beads.45 In both ensembles, the equations of motion were propagated for 1 ns using the velocity-Verlet algorithm with a time step Δt = 0.2 fs. The temperature was controlled via Nosé–Hoover chains (NHC) of four thermostats coupled to each degree of freedom.46 The NPT ensemble was generated according to the algorithm described in ref. 47. A radial atom–atom cutoff distance of 9.0 Å was applied to the nonbonded interactions and the Ewald sum was used to treat the long-range electrostatic interactions.482.3 Tetrahedral order parameter
The tetrahedral order parameters qtet was calculated as49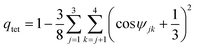 | (4) |
3 Results
3.1 Many-body potential energy functions with ab initio accuracy
To investigate the role played by many-body interactions in determining the structure of liquid water we introduce a series of many-body PEFs that, as MB-pol, are rigorously derived from eqn (1), but, differently from MB-pol, are fitted to reference energies calculated at the density functional theory (DFT) level, using four representative exchange–correlation (XC) functionals belonging to different rungs across the Jacob's ladder of DFT approximations.50 Specifically, considering that the main contributions to the interaction energies between water molecules are associated with the 2B and 3B energies,11 and all many-body terms involving four or more water molecules are quantitatively described by MB-pol,18 we introduce here four families of many-body PEFs in which the original MB-pol 2B and 3B terms, originally fitted to CCSD(T)/CBS reference data, are replaced by analogous terms fitted to 2B and 3B energies calculated with the revPBE-D3 (rung 2),35,51 B97M-rV (rung 3),36 revPBE0-D3 (rung 4),37,51 and ωB97M-V (rung 4)38 functionals, while all other many-body terms of eqn (1) are represented as in MB-pol15,16 (see ESI† for a systematic analysis of many-body contributions to the interaction energies of water clusters).Using the same dimer and trimer training sets adopted in the development of MB-pol,15,16Fig. 1 shows correlation plots between 2B and 3B energies calculated with each of the four XC functionals and the corresponding CCSD(T)/CBS reference values.15,16 Also shown for comparison are the correlation plots for MB-pol. Three general observations can be made with respect to this analysis. First, the overall accuracy of the four XC functionals improves from revPBE-D3 (rung 2) to ωB97M-V (rung 4), with the notable exception of B97M-rV that outperforms revPBE0-D3 despite belonging to a lower rung. Second, all four functionals provide relatively better agreement with the CCSD(T)/CBS reference values for 2B than 3B energies. Third, MB-pol provides the smallest root-mean-square deviation (RMSD) from the CCSD(T)/CBS reference data for both 2B and 3B energies.
3.2 Many-body effects and the energetics of water clusters
To investigate how the interplay between individual many-body effects determines both water structure and energetics, the DFT 2B and 3B energies shown in Fig. 1 are used in eqn (1) to develop three distinct many-body PEFs for each of the four XC functionals. These many-body PEFs, hereafter referred to as (MB)-XC PEFs (with XC = revPBE-D3, B97M-rV, revPBE0-D3, and ωB97M-V) adopt the same functional form as MB-pol but progressively replace the MB-pol 2B and 3B terms, which were fitted to CCSD(T)/CBS data, with analogous fits to the corresponding 2B and 3B energies calculated with the four XC functionals shown in Fig. 1. For each XC functional, the three distinct models are thus labeled as (2B+3B)-XC, (2B)-XC, and (3B)-XC to indicate that both 2B and 3B, only 2B, and only 3B terms are represented by fits to the corresponding data calculated with the specific XC functional, while all other terms are taken from MB-pol. Since the water hexamer exhibits three-dimensional structures reminiscent of the three-dimensional hydrogen-bonding arrangements in liquid water, the ability to reproduce the relative stability of the hexamer isomers is often used to assess the accuracy of water models. Fig. 2 shows that all three many-body PEFs constructed for each XC functional predict relative energies of the low-lying isomers of the water hexamer that are always within 1.0 kcal mol−1, commonly defined as “chemical accuracy”, of the corresponding values calculated fully ab initio with the same XC functional. This analysis thus provides evidence that all MB-XC PEFs are able to correctly reproduce many-body effects as described by the corresponding XC functional.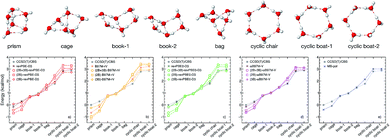 | ||
| Fig. 2 (Top) Geometries of the low-lying isomers of the water hexamer. (Bottom) Comparison of relative interaction energies for the low-lying isomers of the water hexamer calculated using the (2B+3B)-XC PEFs (open circles), (2B)-XC PEFs (open squares), and (3B)-XC PEFs (open diamonds) with XC = revPBE-D3 (red, panel (a)), B97M-rV (yellow, panel (b)), revPBE0-D3 (green, panel (c)), and ωB97M-V (magenta, panel (d)). The isomer geometries were taken from ref. 34. Also shown in each panel are the reference CCSD(T)/CBS values. Analogous comparison between MB-pol and CCSD(T)/CBS reference values taken from ref. 32 are shown in panel (e). | ||
3.3 Many-body effects and the structure of liquid water
To determine how 2B and 3B contributions affect the structure of liquid water at ambient conditions, path-integral molecular dynamics (PIMD) simulations are carried out at 298.15 K in both NVT and NPT ensembles. Fig. 3 shows comparisons between the experimental oxygen–oxygen radial distribution function (RDF)52 and the corresponding RDFs calculated from PIMD simulations in the NVT (top panels) and NPT (bottom panels) ensembles using the three MB-XC PEFs developed for each of the four XC functionals. Also shown for reference are the corresponding MB-pol RDFs.17 Comparisons between the corresponding oxygen-hydrogen and hydrogen–hydrogen RDFs are reported in the ESI.†Fig. 3a demonstrates that, when the simulations are carried out in the NVT ensemble with the density fixed at the experimental value, all (2B+3B)-XC PEFs accurately reproduce the experimental O–O RDF, with only revPBE-D3 predicting a slightly over structured liquid. As discussed in the ESI,† the RDFs calculated with the (2B+3B)-XC PEFs using revPBE-D3, B97M-rV, and revPBE0-D3 are in agreement with those reported in the literature from ab initio PIMD simulations carried out with the corresponding functionals,53,54 which provides evidence for the ability of the present (2B+3B)-XC PEFs to faithfully reproduce the corresponding DFT results at a fraction of the cost associated with fully ab initio simulations. In this context, it should also be noted that small noticeable differences are seen in the comparison between the oxygen–oxygen RDF calculated with the (2B+3B)-revPBE-D3 PEF and the corresponding results from ab initio simulations with the bare revPBE-D3 functional.53 These differences are due to differences in how (2B+3B)-revPBE and revPBE-D3 represent 4B energies. While in (2B+3B)-revPBE the 4B energies are described as in MB-pol which, as shown in Fig. S4–S6 of the ESI,† provides excellent agreement with the CCSD(T)/CBS reference data, significant deviations from the 4B CCSD(T)/CBS reference data are associated with the bare revPBE-D3 functional.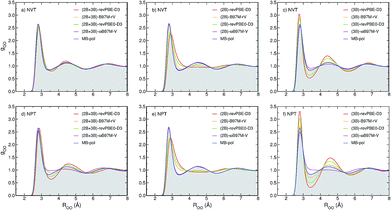 | ||
| Fig. 3 Comparison between oxygen–oxygen radial distribution functions (RDFs) of liquid water at ambient conditions derived from X-ray diffraction measurements (gray area) of ref. 52 and calculated from PIMD simulations carried out at 298.15 K in the NVT (panels a–c) and NPT (panels d–f) ensembles with the (2B+3B)-XC PEFs (panels a and d), (2B)-XC PEFs (panels b and e), and (3B)-XC PEFs (panels c and f) with XC = revPBE-D3 (red), B97M-rV (yellow), revPBE0-D3 (green), and ωB97M-V (magenta). Also shown in each panel are the corresponding RDFs calculated from PIMD simulations with MB-pol. | ||
On the other hand, Fig. 3 shows that noticeable differences are found in the (2B+3B)-XC RDFs calculated from analogous PIMD simulations carried out in the NPT ensemble (Fig. 3d). While the MB-pol RDFs remain in quantitative agreement with the experimental data, all four (2B+3B)-XC RDFs show significant deviations, with both (2B+3B)-revPBE-D3 and (2B+3B)-revPBE0-D3 predicting a slightly overstructured liquid and both (2B+3B)-B97M-rV and (2B+3B)-ωB97M-V predicting a slightly understructured liquid. These differences are directly related to the ability of the four XC functionals to correctly reproduce 2B and 3B energies (Fig. 1), and suggest that the four XC functionals effectively provide a phase diagram of water that is displaced in pressure and temperature compared to experiment, which is in line with previous studies indicating that popular XC functionals tend to predict a freezing point for water that is significantly larger than 273 K.55,56
Fig. 3b and e demonstrate that, when the original MB-pol 2B term is replaced by the corresponding term derived from 2B data calculated with the different XC functionals, with all other many-body terms of eqn (1) being represented as in MB-pol, the agreement between experimental and simulated RDFs deteriorates for all (2B)-XC PEFs, with the exception of (2B)-ωB97M-V. Specifically, both (2B)-revPBE-D3 and (2B)-revPBE0-D3 predict an unstructured liquid characterized by the collapse of the second solvation shell. While (2B)-B97M-rV still predicts a reasonable structure of liquid water when the PIMD simulations are carried out in the NVT ensemble, the agreement with the experimental RDF worsens in the NPT ensemble, with the simulated RDF barely showing a second solvation shell. Nearly quantitative agreement with the experimental RDF is instead predicted by PIMD simulations with the (2B)-ωB97M-V in both NVT and NPT ensembles. The poor performance by both (2B)-revPBE-D3 and (2B)-revPBE0-D3 can be traced back to the relatively large RMSDs associated with 2B energies calculated with these two XC functionals (Fig. 1). On the other hand, the different performance by (2B)-B97M-rV and (2B)-ωB97M-V PEFs suggests that an RMSD lower than ∼0.25 kcal mol−1 relative to the 2B CCSD(T)/CBS reference data adopted in the development of MB-pol and used in the correlation plots of Fig. 1 is required for a correct representation of 2B effects in liquid water.
When only the original MB-pol 3B term is replaced by the corresponding term derived from 3B data calculated with the different XC functionals, keeping all other many-body terms of eqn (1) as in MB-pol, Fig. 3c and f show that none of the (3B)-XC PEFs are able to correctly reproduce the experimental RDFs. In particular, (3B)-revPBE-D3, (3B)-revPBE0-D3 and, to a lesser extent, (3B)-B97M-rV predict an overstructured (i.e., low density) liquid, a feature that is even more emphasized by PIMD simulations in the NPT ensemble. On the other hand, (3B)-ωB97M-V predicts an understructured (i.e., high density) liquid. Combining the results obtained with the (2B)-XC and (3B)-XC PEFs, it is becomes evident that both (2B+3B)-revPBE-D3 and (2B+3B)-revPBE0-D3 achieve apparent agreement with the experimental RDFs through fortuitous error compensation in their representations of 2B and 3B interactions. Although similar conclusions can be drawn from the results obtained with the B97M-rV functional, it should be noted that the errors associated with the B97M-rV representations of 2B and 3B energies are significantly smaller than those associated with revPBE-D3 and revPBE0-D3, indicating that B97M-rV overall provides a more realistic description of liquid water. The case of ωB97M-V is completely different since this XC functional effectively provides CCSD(T)-level accuracy at the 2B level but is affected by nonnegligible errors in the representation of 3B energies. Thus the lack of error compensation in the representation of 2B and 3B interactions is the origin of the deviations between the experimental and (2B+3B)-ωB97M-V RDFs shown in Fig. 3a and d.
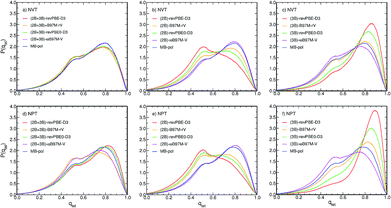
The differences in the RDFs directly translate into differences in the local structure of liquid water as defined by the distribution of the tetrahedral order parameter, P(qtet), calculated from PIMD simulations with the different MB-XC PEFs, which represents an effective metric to determine the local structure of liquid water. Fig. 4a shows that all (2B+3B)-XC PEFs provide similar P(qtet) distributions as MB-pol when the PIMD simulations are carried out at the experimental density in the NVT ensemble. In contrast, the different RDFs obtained from PIMD simulations in the NPT ensemble lead to noticeably different P(qtet) distributions, with both (2B+3B)-B97M-rV and (2B+3B)-ωB97M-V providing a less tetrahedral liquid as indicated by the decrease of the main peak at qtet = 0.8 and the increase of the peak at qtet = 0.5. Instead both (2B+3B)-revPBE-D3 and (2B+3B)-revPBE0-D3 models predict a slightly more tetrahedral liquid, with the main peak shifted to higher qtet values (Fig. 4d), as suggested by their overstructured RDFs.
Larger variations are found in the P(qtet) distributions calculated from PIMD simulations with the (2B)-XC and (3B)-XC PEFs in both NVT and NPT ensembles. Importantly, (2B)-ωB97M-V effectively provides the same P(qtet) distribution as MB-pol while (3B)-ωB97M-V predicts a slightly less tetrahedral liquid, which is a direct consequence of the different ability of ωB97M-V to reproduce 2B and 3B energies, as shown in Fig. 1. Directly following the trends observed in the corresponding RDFs, all other (2B)-XC and (3B)-XC PEFs respectively predict significantly less and more tetrahedral liquids. As already inferred from the analysis of Fig. 1 and 3, the differences in the local hydration structure predicted by the (2B)-XC and (3B)-XC PEFs are largely washed out when the simulations are carried out with the (2B+3B)-XC PEFs due to revPBE-D3, revPBE0-D3 and, to a lesser extent, B97M-rV benefiting from fortuitous error compensation in their representations of 2B and 3B energies.
4 Conclusions
Our study demonstrates that: (1) the local hydration structure of liquid water is primarily determined by the delicate interplay between 2B and 3B energies, which is further modulated by higher order (i.e., larger than 3B) interactions; (2) a correct representation of 2B and 3B energies requires sub-chemical accuracy, which can be achieved by state-of-the-art many-body PEFs, such as MB-pol, rigorously derived from the MBE of eqn (1) where the individual terms are obtained at the CCSD(T)/CBS level of theory but is currently lacking in existing XC functionals that are commonly used in computer simulations of liquid water; (3) most of the XC functionals benefit from fortuitous error compensation in the representation of 2B and 3B energies, which may lead to apparent agreement with experiment for spatially uniform systems (e.g., bulk water) but will likely result in inaccurate descriptions of non-uniform systems (e.g., aqueous interfaces and electrolyte solutions) where error compensation may not be complete. While these results suggest that many-body PEFs, such as MB-pol, hold great promise for shedding light on the molecular origin of the anomalous behavior of liquid water as a function of temperature and pressure, they also warn that a definitive explanation of this behavior might require a level of accuracy in the representation of the underlying molecular interactions which may be out of reach for even the most sophisticated electronic structure methods currently available.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Greg Medders, Volodymyr Babin and Kevin Bao for their key contributions to the development of the theoretical and computational framework employed in this study to disentangle many-body effects in water. This research was supported by the National Science Foundation through grants CHE-1453204 and ACI-1642336, and the U.S. Department of Energy, Office of Science, Office of Basic Energy Science through grant DE-SC0019490. All calculations and simulations used resources of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation through grant ACI-1053575, under allocation TG-CHE110009, and the Triton Shared Computing Cluster (TSCC) at the San Diego Supercomputer Center (SDSC). M. R. was supported by a Software Fellowship from the Molecular Sciences Software Institute, which is funded by the National Science Foundation through grant ACI-1547580.References
- Y. Marèchal, The Hydrogen Bond and the Water Molecule: The Physics and Chemistry of Water, Aqueous and Bio- Media, Elsevier, Amsterdam, 2006 Search PubMed.
- P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. M. Pettersson, Water: A Tale of Two Liquids, Chem. Rev., 2016, 116, 7463–7500 CrossRef CAS PubMed.
- A. Nilsson and L. G. Pettersson, The Structural Origin of Anomalous Properties of Liquid Water, Nat. Commun., 2015, 6, 8998 CrossRef CAS PubMed.
- H. S. Frank and W.-Y. Wen, Ion-solvent Interaction. Structural Aspects of Ion-Solvent Interaction in Aqueous Solutions: A Suggested Picture of Water Structure, Discuss. Faraday Soc., 1957, 24, 133–140 RSC.
- M. J. Elrod and R. J. Saykally, Many-Body Effects in Intermolecular Forces, Chem. Rev., 1994, 94, 1975–1997 CrossRef CAS.
- F. Paesani and G. A. Voth, The Properties of Water: Insights from Quantum Simulations, J. Phys. Chem. B, 2009, 113, 5702–5719 CrossRef CAS PubMed.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Nuclear Quantum Effects in Water and Aqueous Systems: Experiment, Theory, and Current Challenges, Chem. Rev., 2016, 116, 7529–7550 CrossRef CAS PubMed.
- D. Hankins, J. Moskowitz and F. Stillinger, Water Molecule Interactions, J. Chem. Phys., 1970, 53, 4544–4554 CrossRef CAS.
- J. Del Bene and J. Pople, Intermolecular Energies of Small Water Polymers, Chem. Phys. Lett., 1969, 4, 426–428 CrossRef CAS.
- K. Kim, M. Dupuis, G. Lie and E. Clementi, Revisiting Small Clusters of Water Molecules, Chem. Phys. Lett., 1986, 131, 451–456 CrossRef CAS.
- G. A. Cisneros, K. T. Wikfeldt, L. Ojamäe, J. Lu, Y. Xu, H. Torabifard, A. P. Bartók, G. Csányi, V. Molinero and F. Paesani, Modeling Molecular Interactions in Water: From Pairwise to Many-Body Potential Energy Functions, Chem. Rev., 2016, 116, 7501–7528 CrossRef CAS.
- R. Bukowski, K. Szalewicz, G. C. Groenenboom and A. van der Avoird, Predictions of the Properties of Water from First Principles, Science, 2007, 315, 1249–1252 CrossRef CAS PubMed.
- Y. Wang, B. C. Shepler, B. J. Braams and J. M. Bowman, Full-Dimensional, Ab Initio Potential Energy and Dipole Moment Surfaces for Water, J. Chem. Phys., 2009, 131, 054511 CrossRef PubMed.
- Y. Wang, X. Huang, B. C. Shepler, B. J. Braams and J. M. Bowman, Flexible, Ab Initio Potential, and Dipole Moment Surfaces for Water. I. Tests and Applications for Clusters up to the 22-mer, J. Chem. Phys., 2011, 134, 094509 CrossRef.
- V. Babin, C. Leforestier and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers: Dimer Potential Energy Surface, VRT Spectrum, and Second Virial Coefficient, J. Chem. Theory Comput., 2013, 9, 5395–5403 CrossRef CAS PubMed.
- V. Babin, G. R. Medders and F. Paesani, Development of a “First Principles” Water Potential with Flexible Monomers. II: Trimer Potential Energy Surface, Third Virial Coefficient, and Small Clusters, J. Chem. Theory Comput., 2014, 10, 1599–1607 CrossRef CAS PubMed.
- G. R. Medders, V. Babin and F. Paesani, Development of a “First-Principles” Water Potential with Flexible Monomers. III. Liquid Phase Properties, J. Chem. Theory Comput., 2014, 10, 2906–2910 CrossRef CAS.
- F. Paesani, Water: Many-Body Potential from First Principles (From the Gas to the Liquid Phase), Handbook of Materials Modeling: Methods: Theory and Modeling, 2018, pp. 1–25 Search PubMed.
- H.-J. Werner, P. Knowles, G. Knizia, R. Manby, M. Schütz, et al., MOLPRO, Version 2012.1, A Package of Ab Initio Programs, 2012, see http://www.molpro.net Search PubMed.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. Harrison, J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F.-M. Tao and Y.-K. Pan, Møller–Plesset Perturbation Investigation of the He2 Potential and the Role of Midbond Basis Functions, J. Chem. Phys., 1992, 97, 4989 CrossRef CAS.
- A. Halkier, W. Klopper, T. Helgaker, P. Jørgensen and P. R. Taylor, Basis Set Convergence of the Interaction Energy of Hydrogen-Bonded Complexes, J. Chem. Phys., 1999, 111, 9157 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Basis-Set Convergence of the Energy in Molecular Hartree–Fock calculations, Chem. Phys. Lett., 1999, 302, 437–446 CrossRef CAS.
- S. Boys and F. Bernardi, The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- U. Góra, R. Podeszwa, W. Cencek and K. Szalewicz, Interaction Energies of Large Clusters from Many-Body Expansion, J. Chem. Phys., 2011, 135, 224102 CrossRef.
- T. B. Adler, G. Knizia and H. J. Werner, A Simple and Efficient CCSD(T)-F12 Approximation, J. Chem. Phys., 2007, 127, 221106 CrossRef.
- K. A. Peterson, T. B. Adler and H.-J. Werner, Systematically Convergent Basis Sets for Explicitly Correlated Wavefunctions: The Atoms H, He, B–Ne, and Al–Ar, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- G. Knizia, T. B. Adler and H. J. Werner, Simplified CCSD(T)-F12 Methods: Theory and Benchmarks, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- D. P. Tew, W. Klopper, C. Neiss and C. Hättig, Quintuple-Zeta Quality Coupled-Cluster Correlation Energies with Triple-Zeta Basis Sets, Phys. Chem. Chem. Phys., 2007, 9, 1921 RSC.
- F. A. Bischoff, S. Wolfsegger, D. P. Tew and W. Klopper, Assessment of Basis Sets for F12 Explicitly-Correlated Molecular Electronic-Structure Methods, Mol. Phys., 2009, 107, 963 CrossRef CAS.
- S. K. Reddy, S. C. Straight, P. Bajaj, C. Huy Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Götz and F. Paesani, On the Accuracy of the Mb-Pol Many-Body Potential for Water: Interaction Energies, Vibrational Frequencies, and Classical Thermodynamic and Dynamical Properties from Clusters to Liquid Water and Ice, J. Chem. Phys., 2016, 145, 194504 CrossRef.
- B. Temelso, K. A. Archer and G. C. Shields, Benchmark Structures and Binding Energies of Small Water Clusters with Anharmonicity Corrections, J. Phys. Chem. A, 2011, 115, 12034–12046 CrossRef CAS PubMed.
- D. M. Bates and G. S. Tschumper, CCSD(T) Complete Basis Set Limit Relative Energies for Low-Lying Water Hexamer Structures, J. Phys. Chem. A, 2009, 113, 3555–3559 CrossRef CAS PubMed.
- Y. Zhang and W. Yang, Comment on “Generalized Gradient Approximation Made Simple”, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- N. Mardirossian, L. Ruiz Pestana, J. C. Womack, C.-K. Skylaris, T. Head-Gordon and M. Head-Gordon, Use of the rVV10 Nonlocal Correlation Functional in the B97M-V Density Functional: Defining B97M-rV and Related Functionals, J. Phys. Chem. Lett., 2016, 8, 35–40 CrossRef PubMed.
- L. Goerigk and S. Grimme, A Thorough Benchmark of Density Functional Methods for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- N. Mardirossian and M. Head-Gordon, ω B97M-V: A Combinatorially Optimized, Range-Separated Hybrid, Meta-GGA Density Functional with VV10 Nonlocal Correlation, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kús, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr, H. Dop, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, P. A. Pieniazek, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, N. Sergueev, S. M. Sharada, S. Sharmaa, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, V. Vanovschi, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhou, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xua, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in molecular quantum chemistry contained in the Q-Chem 4 program package, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- D. Chandler and P. G. Wolynes, Exploiting the Isomorphism Between Quantum Theory and Classical Statistical Mechanics of Polyatomic Fluids, J. Chem. Phys., 1981, 74, 4078 CrossRef CAS.
- M. Parrinello and A. Rahman, Study of an F Center in Molten KCl, J. Chem. Phys., 1984, 80, 860 CrossRef CAS.
- B. De Raedt, M. Sprik and M. L. Klein, Computer Simulation of Muonium in Water, J. Chem. Phys., 1984, 80, 5719–5724 CrossRef CAS.
- B. J. Berne and D. Thirumalai, On the Simulation of Quantum Systems: Path Integral Methods, Annu. Rev. Phys. Chem., 1986, 37, 401–424 CrossRef CAS.
- R. Feynman, Statistical Mechanics, WA Benjamin, 1972 Search PubMed.
- M. E. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, Oxford University Press, 2010 Search PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover Chains: The Canonical Ensemble Via Continuous Dynamics, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- G. J. Martyna, A. Hughes and M. E. Tuckerman, Molecular Dynamics Algorithms for Path Integrals at Constant Pressure, J. Chem. Phys., 1999, 110, 3275–3290 CrossRef CAS.
- M. Allen and D. Tildesley, Computer Simulations of Liquids, Oxford University Press, 1987 Search PubMed.
- J. R. Errington and P. G. Debenedetti, Relationship Between Structural Order and the Anomalies of Liquid Water, Nature, 2001, 409, 318 CrossRef CAS.
- J. P. Perdew and K. Schmidt, Jacob's Ladder of Density Functional Approximations for the Exchange–Correlation Energy, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- L. B. Skinner, C. Huang, D. Schlesinger, L. G. Pettersson, A. Nilsson and C. J. Benmore, Benchmark Oxygen–Oxygen Pair-Distribution Function of Ambient Water from X-ray Diffraction Measurements with a Wide Q-Range, J. Chem. Phys., 2013, 138, 074506 CrossRef PubMed.
- O. Marsalek and T. E. Markland, Quantum Dynamics and Spectroscopy of Ab Initio Liquid Water: The Interplay of Nuclear and Electronic Quantum Effects, J. Phys. Chem. Lett., 2017, 8, 1545–1551 CrossRef CAS PubMed.
- L. Ruiz Pestana, O. Marsalek, T. E. Markland and T. Head-Gordon, The Quest for Accurate Liquid Water Properties from First Principles, J. Phys. Chem. Lett., 2018, 9, 5009–5016 CrossRef CAS PubMed.
- S. Yoo, X. C. Zeng and S. S. Xantheas, On the phase diagram of water with density functional theory potentials: the melting temperature of ice I h with the Perdew–Burke–Ernzerhof and Becke–Lee–Yang–Parr functionals, J. Chem. Phys., 2009, 130, 221102 CrossRef PubMed.
- S. Yoo and S. S. Xantheas, Communication: The effect of dispersion corrections on the melting temperature of liquid water, J. Chem. Phys., 2011, 134, 121105 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Brief overview of the many-body expansion of the total energy and details about the functional form adopted by MB-pol. Additional analyses of many-body effects in (H2O)n clusters with n = 1–6. Comparisons between radial distribution functions (RDFs) calculated from PIMD simulations with the MB-XC PEFs introduced in this study and the corresponding ab initio XC functionals. See DOI: 10.1039/c9sc03291f |
| This journal is © The Royal Society of Chemistry 2019 |