Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intercomparison measurements of two 33S-enriched sulfur isotope standards
L.
Geng
 *ab,
J.
Savarino
*ab,
J.
Savarino
 *b,
N.
Caillon
b,
E.
Gautier
b,
J.
Farquhar
c,
J. W.
Dottin III
c,
N.
Magalhães
*b,
N.
Caillon
b,
E.
Gautier
b,
J.
Farquhar
c,
J. W.
Dottin III
c,
N.
Magalhães
 c,
S.
Hattori
c,
S.
Hattori
 d,
S.
Ishino
d,
N.
Yoshida
d,
S.
Ishino
d,
N.
Yoshida
 d,
F.
Albarède
e,
E.
Albalat
e,
P.
Cartigny
d,
F.
Albarède
e,
E.
Albalat
e,
P.
Cartigny
 f,
S.
Ono
g and
M. H.
Thiemens
h
f,
S.
Ono
g and
M. H.
Thiemens
h
aAnhui Province Key Laboratory of Polar Environment and Global Change, School of Earth and Space Sciences, University of Science and Technology of China, Hefei, Anhui, China. E-mail: genglei@ustc.edu.cn
bUniv. Grenoble Alpes, CNRS, IRD, G-INP, Institut des Géosciences de l'Environnement, F-38000 Grenoble, France. E-mail: joel.savarino@cnrs.fr
cDepartment of Geology and ESSIC, University of Maryland College Park, College Park, MD 20742, USA
dDepartment of Chemical Science and Engineering, School of Materials and Chemical Technology, Tokyo Institute of Technology, Kanagawa, Japan
eENS de Lyon, CNRS, Université Lyon 1, Université de Lyon, Lyon, France
fLaboratoire de Géochimie des Isotopes Stables, Institut de Physique du Globe de Paris, Sorbonne Paris Cité, Univ. Paris Diderot, UMR 7154, CNRS, 75005 Paris, France
gDepartment of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
hDepartment of Chemistry and Biochemistry, University of California, San Diego, La Jolla, CA 92093, USA
First published on 18th March 2019
Abstract
Despite widespread applications of sulfur isotope mass-independent fractionation (MIF) signals for probing terrestrial and extra-terrestrial environments, there has been no international sulfur isotope reference material available for normalization of Δ33S and Δ36S data. International reference materials to anchor isotope values are useful for interlaboratory data comparisons and are needed to evaluate, e.g., whether issues exist associated with blanks and mass spectrometry when using different analytical approaches. We synthesized two sodium sulfate samples enriched in 33S with different magnitudes, and termed them S-MIF-1 and S-MIF-2, respectively. The sulfur isotopic compositions of these two samples were measured in five different laboratories using two distinct techniques to place them on the V-CDT scale for δ34S and a provisional V-CDT scale for Δ33S and Δ36S. We obtained average δ34S values of S-MIF-1 = 10.26 ± 0.22‰ and S-MIF-2 = 21.53 ± 0.26‰ (1σ, versus V-CDT). The average Δ33S and Δ36S values of S-MIF-1 were determined to be 9.54 ± 0.09‰ and −0.11 ± 0.25‰, respectively, while the average Δ33S and Δ36S values of S-MIF-2 are 11.39 ± 0.08‰ and −0.33 ± 0.13‰ (1σ, versus V-CDT). The lack of variation among the interlaboratory isotopic values suggests sufficient homogeneity of S-MIF-1 and S-MIF-2, especially for Δ33S. Although additional measurements may be needed to ensure the accuracy of the isotopic compositions of S-MIF-1 and S-MIF-2, they can serve as working standards for routine Δ33S analysis to improve data consistency, and have the potential to serve as secondary sulfur isotope reference materials to address issues such as scale contraction/expansion and for normalization and reporting of Δ33S and Δ36S between laboratories. For the same reasons as listed for sulfur isotopes, the same standards were also artificially enriched in 17O. The calibration is still in progress but first estimations gave Δ17O = 3.3 ± 0.3‰ with unassigned δ18O.
1. Introduction
Sulfur has four stable isotopes 32S, 33S, 34S and 36S with approximate abundances of 94.99%, 0.75%, 4.25% and 0.01%, respectively. The relative abundances of these isotopes in geological materials (e.g., rocks, atmospheric aerosols, water, ice, meteorites, etc.) are affected by different geological, atmospheric, biological, and hydrological processes. Therefore, variations in the relative abundances of sulfur isotopes in a variety of terrestrial and extra-terrestrial materials have the potential to serve as useful tracers of the source and transformation of sulfur in different environments, as well as provide information about their physical and/or chemical conditions. The relative abundances of sulfur isotopes are typically measured as the ratios of the rare isotopes (33S, 34S and 36S) to the most abundant isotope, 32S, and expressed as the delta notation which describes a deviation from a primary isotope reference material: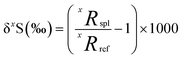 | (1) |
The second historic aspect of sulfur isotope analyses has been on δ34S. This occurred because of the difficulty of measuring 33S and 36S using standard combustion techniques, and a strong mass-dependent correlation between δ33S, δ34S and δ36S that led to the belief that independent information could not be obtained by measuring the two rarest sulfur isotopes. The recognition of mass-independent processes in meteorite samples,3–5 geological samples,6–9 and atmospheric and ice-core samples,10–15 as well as the development of new techniques such as the MC-ICP-MS techniques for 33S measurement16,17 has made it of interest to have better calibrations over the full range of stable sulfur isotopes. In addition, mass-dependent fractionation processes in the biogeochemical sulfur cycle have also been measured and are known to produce small abundance deviations for 33S and 36S from mass-dependent relationships,18–20 and these variations have been shown to be useful in terms of obtaining additional information on the biogeochemical sulfur cycles in, for example, marine environments.21–23 The deviation from mass-dependent trends was commonly termed mass-independent fractionation (MIF), although some were strictly related to mass-dependent processes, and expressed as the capital delta notation as follows:
| Δ33S (‰) = δ33S − [(δ34S/1000 + 1)0.515 − 1] × 1000 | (2) |
| Δ36S (‰) = δ36S − [(δ34S/1000 + 1)1.9 − 1] × 1000 | (3) |
These sulfur isotope anomalous signals, Δ33S and Δ36S, serve as unique proxies to track both mass dependent and mass independent fractionation processes.
Prior community efforts have established a consensual value for the V-CDT scale on the basis of the δ34S for IAEA-S-1 in order to normalize δ34S measurements of different samples in different laboratories, for data comparability and consistency. Other sulfur reference materials, such as IAEA-S-2 and IAEA-S-3, are also routinely used for the same purpose. Provisional assignments of values for Δ33S and Δ36S have been assigned to V-CDT in various studies,24,25 but a full assignment has yet to be made. Other researchers have resorted to normalizations to IAEA-S-1 (ref. 19) or CDT for Δ33S and Δ36S.26–28 The number of studies reporting Δ33S and Δ36S of terrestrial and extra-terrestrial samples29 has increased tremendously in the past two decades due to interest in the geological and/or environmental information embedded in Δ33S and Δ36S signals. Such an increase has resulted in a need for the establishment of working materials and interlaboratory comparisons that will lay the groundwork for establishing a consensus for the normalization of Δ33S and Δ36S of V-CDT.
Appropriate data normalization, aside from precise and accurate measurements, is necessary to ensure proper interlaboratory data comparison and to reach consensual conclusions according to Δ33S and Δ36S values measured from the same or similar types of samples.30 Appropriate data normalization is also important for interpretation of small Δ33S and/or Δ36S values (e.g., 0.03‰). The Δ33S and Δ36S values are not directly measured, but calculated from the measured δ34S, δ33S and δ36S values as shown in the above equations. The δ34S, δ33S and δ36S values are typically measured with respect to a laboratory working reference gas (i.e., SF6), and then need to be anchored to the V-CDT scale in order to ensure consistent comparison of data among different laboratories. Although consensual δ34SV-CDT values of international sulfur isotope reference materials have been established, currently there are no consensual δ33SV-CDT and δ36SV-CDT values. Here we use the provisional Wing and Farquhar24 V-CDT calibration of IAEA-S-1 which assigns Δ33S = 0.094‰ and Δ36S = −0.700‰ as the values for IAEA-S-1 on the V-CDT scale. These values correspond to δ33S and δ36S of −0.061‰ and −1.27‰, respectively. These values along with the community-defined δ34S value of IAEA-S-1 (−0.300‰) are used to normalize multiple sulfur isotope compositions of particular samples to the V-CDT scale, once the working reference gas is calibrated versus IAEA-S-1, or concurrent measurements of IAEA-S-1 are performed.
Given the small Δ33S and Δ36S values measured in, e.g., stratospheric and tropospheric sulfate aerosols, marine S-bearing materials, meteorites and Proterozoic geological samples, small errors, scale contraction, or drift in one-point scale normalization can lead to significant differences in the derived Δ33S and Δ36S values for such samples. In addition, the mechanism behind the origin of S-MIF in atmospheric sulfate is still a subject of debate,31–37 and observations of small negative Δ36S values in atmospheric sulfate possibly associated with combustion processes14,15 raise further questions on the photo-chemical origin of S-MIF. Accurate and precise measurements as well as consistent data normalization are also critical in distinguishing the difference between small non-zero Δ33S and Δ36S values produced by mass-dependent fractionation processes in biogeochemical sulfur cycles and non-zero Δ33S and Δ36S values produced by MIF processes, and in further discerning the contributions of different MIF processes. In principle, data normalization can be considerably improved by using two or more points to provide a normalization spanning a wide delta range. To enable proper data normalization and compatible data reporting from different laboratories, secondary reference materials of Δ33S and Δ36S are necessary in addition to IAEA-S-1. The IAEA-S-1 material is used as a primary reference material to scale or anchor the measured data to the V-CDT scale, rather than a physically real calibration standard.
To date, there is no international sulfur isotope reference material enriched in 33S and/or 36S available for the purpose of global calibration. Individual laboratories generally report Δ33S and Δ36S values normalized using concurrent IAEA-S-1 measurements, but consensus values of Δ33S and Δ36S for IAEA-S-1 on the V-CDT scale have not been assigned. In this study, we report the sulfur isotopic compositions of two synthesized sodium sulfate samples artificially enriched in 33S with different magnitudes. The data we report are from separate analyses performed at five different laboratories. We evaluate the interlaboratory variations in the reported values and use the data to assess the potential for further use of these samples as secondary reference materials for Δ33S data normalization. Concomitantly, these samples are also enriched in 17O for the same reasons as listed for sulfur. The calibration is still in progress and the preliminary result of Δ17O = 3.3 ± 0.3‰ (1σ) is reported only for information purposes. In the following, we will not elaborate more on Δ17O.
2. Experimental
2.1. Synthesis of samples enriched in 33S
Two sodium sulfate (Na2SO4) samples, namely, S-MIF-1 and S-MIF-2, enriched in 33S were prepared in the stable isotope laboratory at the University of California, San Diego. We chose Na2SO4 as it is chemically stable, is nontoxic, does not become hydrated, and is widely available and easy to manufacture. The samples were prepared by chemical conversions of a mixture of sulfur powder and sulfur-33 powder. Reagents used included sulfur powder (99.5%, Fisher ACS, Lot: 897542), sulfur-33 powder (99.8%, Isoflex, Lot: 07111L35969), H2O2 solution (30%, extra pure, Fisher Scientific, Lot: 110251), H2SO4 (95%, extra pure, Fisher Scientific, Lot: 49020), NaOH (99+%, extra pure, Fisher Scientific), and O2 (99.999%, Matheson, USA).For S-MIF-1, 20 g of sulfur powder and 0.00445 g of sulfur-33 powder were weighed and mixed in an agate mortar. For S-MIF-2, 20 g of sulfur powder and 0.0015 g of sulfur-33 powder were weighed and mixed. The composition of the initial mixtures corresponded to Δ33SV-CDT values of ∼30‰ and 10‰, respectively. The powder mixture was transferred into a crucible, and ignited with a flame. The crucible was then placed in a 4 L air-tight glass vessel followed by purging of the glass vessel with a flow of O2 at a rate of 50 mL min−1. As a result, SO2 was produced and carried by O2 into a NaOH solution (made of 33 mL 17O-enriched water (Δ17O = 47‰), 33 mL NaOH (50% w/w) and 133 mL of pure water (18.2 MΩ)), where SO2 was trapped as Na2SO3. The S(IV)-containing the NaOH solution was placed in an ice-water bath during the collection process. After the combustion was complete, we suspended the flow of O2 and slowly added 80 mL 30% H2O2 (due to the exothermicity of the reaction) to the NaOH solution in order to oxidize the trapped SO32− to SO42−. For S-MIF-1, 33 mL H2SO4 was added to dilute Δ33S to ∼10‰, and then a few drops of NaOH were added to adjust to neutral pH. For S-MIF-2, no dilution was made and only a few drops of H2SO4 were added to adjust to neutral pH. The different treatments of S-MIF-1 and S-MIF-2 in this last step were intended to produce Na2SO4 with similar Δ33S but different Δ17O. Both S-MIF-1 and S-MIF-2 were then dried and ground, and the powder was collected and stored. In the end, we recovered ∼136 g and ∼55.6 g Na2SO4 for S-MIF-1 and S-MIF-2, respectively.
2.2. Isotopic analysis
After preparation, S-MIF-1 and S-MIF-2 were circulated to five laboratories, including the stable isotope laboratory at the Ecole Normale Superieure (ENS) de Lyon, the stable isotope laboratory at the Institut de Physique du Globe de Paris (IPGP), the stable isotope laboratory at the University of Maryland, College Park (UMD), the stable isotope Geo-biology laboratory at the Massachusetts Institute of Technology (MIT) and the stable isotope laboratory at the Tokyo Institute of Technology (TIT). In these laboratories, the isotopic compositions of S-MIF-1 and S-MIF-2 were characterized individually.In the laboratories of IPGP, UMD, MIT and TIT, S-MIF-1 and S-MIF-2 were analyzed following the conventional SF6 method. In each laboratory, the Na2SO4 samples were first reduced to silver sulfide (Ag2S) using the STrongly Reducing hydrIodic-hypoPhosphorous-hydrochloric acid (STRIP) method38 or the Kiba reagent39 method following the standard procedure described in Forrest and Newman.40 We note that in practice each laboratory uses slightly different reduction techniques for operational convenience. Briefly, the collected sulfide after sulfate reduction was converted to silver sulfide (Ag2S). After purification, Ag2S was dried, weighed (1–3 mg) and transferred into a small aluminum boat. The aluminum boats were folded and loaded into externally heated nickel reaction tubes. The reaction tubes were evacuated for 0.5–1 hour at ∼100 °C until the desired vacuum was achieved. F2 (in excess) was then introduced into the reaction tubes to produce SF6. The reaction tubes were heated to ∼250 °C and held at this temperature overnight. The produced SF6 gas was purified first using a series of cryogenic techniques and then by gas chromatography using helium as the carrier gas. The purified SF6 was then trapped with liquid nitrogen and transferred under vacuum to a gas-source isotope ratio mass spectrometer (Thermo Fisher MAT 253) where its sulfur isotopic composition was analyzed in dual-inlet mode. Briefly, in each analysis, the sample and reference gas (SF6) were measured one after another for masses of 127 (32SF5+), 128 (33SF5+), 129 (34SF5+) and 131 (36SF5+). In the end, the measured δ34S, δ33S and δ36S values of the sample were expressed in the delta notation with respect to the reference SF6 gas.
In the ENS laboratory, S-MIF-1 and S-MIF-2 were analyzed for sulfur isotopic compositions using multi-collector inductively coupled plasma mass spectrometry (MC-ICP-MS).16 This method allows the measurement of 32S, 33S and 34S at very low sulfur content (180 nmol, but can be as low as 10 nmol sulfur), with a typical reproducibility of ±0.1‰ for δ34S and ±0.15‰ for δ33S (2σ) based on replicate measurements of the in-house Alfa Aesar (AA) standard solution. However, due to the interference of the Ar-36 isotope, 36S cannot be measured by this method. The chemistry procedure requires a first step of isolation and purification of sulfur (sulfate) from the sample matrix. In the ENS lab, after sulfate was isolated with an anion exchange resin (200–400 mesh AG1-X8, in chloride form) and eluted in dilute HNO3 media, the sulfur isotopic compositions were measured on a Neptune Plus MC-ICP-MS with a Cetac Aridus II desolvator in high-resolution mode. The isotopic values of δ33S and δ34S were measured with respect to the AA standard solution using the standard–sample–standard bracketing technique. The δ34SV-CDT value of the AA standard solution, 4.86 ± 0.14‰, was pre-calibrated using the international reference materials IAEA-S-1, IAEA-S-2, IAEA-S-3 and IAEA-S-4. The δ33SV-CDT value of the AA standard solution was calculated using the mass-dependent fractionation law.7 These values were then used to anchor the measured δ33S and δ34S values of S-MIF-1 and S-MIF-2 (with respect to AA) to the V-CDT scale.
In Table 1, we list important technical information about sample preparation and analysis in each laboratory. For the IR-MS method in laboratories other than ENS, IAEA-S-1 was measured repeatedly with S-MIF-1 and S-MIF-2. The measurement uncertainties of δ34S, Δ33S and Δ36S in each laboratory as indicated by repeated measurements of IAEA-S-1 are listed in Table 2. The results of IAEA-S-1 in Table 2 were also used to anchor the sulfur isotopic composition of S-MIF-1 and S-MIF-2 to the V-CDT scale, given its known V-CDT values of δ34S, Δ33S and Δ36S.
| Lab | IPGP | UMD | TIT | MIT | ENS |
|---|---|---|---|---|---|
| a VISC/O: variable ion source conductance (sulfur window) open. | |||||
| Preparation | STRIP/SF6 | STRIP/SF6 | Kiba/SF6 | STRIP/SF6 | Solution/SO42− |
| Purification | GC | GC | GC | GC | Resin |
| Mass spectrometry | MAT-253 DI-IRMS VISC/O | MAT-253 DI-IRMS VISC/O | MAT-253 DI-IRMS VISC/O | MAT-253 DI-IRMS VISC/O | MC-ICP-MS |
| δ33S (‰) | δ34S (‰) | δ36S (‰) | Δ33S (‰) | Δ36S (‰) | |
|---|---|---|---|---|---|
| IPGP | −8.734 | −17.042 | −32.506 | 0.079 | −0.375 |
| −8.727 | −17.004 | −32.079 | 0.066 | −0.019 | |
| −8.764 | −17.096 | −32.643 | 0.077 | −0.411 | |
| Mean | −8.742 | −17.047 | −32.409 | 0.074 | −0.268 |
| σ | 0.020 | 0.046 | 0.294 | 0.007 | 0.217 |
| UMD | −2.581 | −5.177 | −10.701 | 0.088 | −0.888 |
| −2.668 | −5.333 | −10.818 | 0.083 | −0.709 | |
| Mean | −2.624 | −5.255 | −10.760 | 0.086 | −0.799 |
| σ | 0.061 | 0.111 | 0.083 | 0.004 | 0.126 |
| TIT | 3.888 | 7.510 | 14.23 | 0.028 | −0.083 |
| 3.907 | 7.514 | 14.29 | 0.045 | −0.036 | |
| 3.896 | 7.514 | 14.30 | 0.033 | −0.025 | |
| 3.893 | 7.510 | 14.26 | 0.032 | −0.062 | |
| 3.906 | 7.510 | 14.29 | 0.045 | −0.024 | |
| 3.907 | 7.506 | 14.27 | 0.048 | −0.035 | |
| 3.968 | 7.638 | 14.479 | 0.041 | −0.083 | |
| 3.972 | 7.626 | 14.482 | 0.051 | −0.058 | |
| 3.964 | 7.631 | 14.415 | 0.042 | −0.133 | |
| 3.963 | 7.629 | 14.434 | 0.042 | −0.111 | |
| 3.964 | 7.629 | 14.487 | 0.042 | −0.058 | |
| 3.967 | 7.630 | 14.389 | 0.044 | −0.158 | |
| Mean | 3.933 | 7.571 | 14.361 | 0.041 | −0.072 |
| σ | 0.035 | 0.063 | 0.096 | 0.007 | 0.043 |
| MIT | −0.492 | −1.021 | −2.47 | 0.034 | −0.531 |
For information only, Δ17O of these two samples was established based on the Ag2SO4 method,41–43 and preliminary results indicate that the two samples have an identical mean of Δ17O = 3.3 ± 0.3‰ (1σ), despite the efforts taken during sample preparation aiming to produce Na2SO4 with different Δ17O.
3. Results and discussion
3.1. Data reduction
The measured δ34S, δ33S and δ36S values of S-MIF-1 and S-MIF-2 with respect to individual laboratory working reference gas or standard solution are listed in Tables 3 and 4, respectively. These δ34S, δ33S and δ36S values are raw values, and were calculated relative to the measured xS/32S (x = 33, 34 or 36) ratio of the working reference gas (i.e., xS/32S = xRref in eqn (1)). The working reference gas (i.e., SF6) used in each laboratory possesses different sulfur isotopic compositions, i.e., xS/32S values are different. This means the raw δ34S, δ33S and δ36S values of S-MIF-1 and S-MIF-2 from different laboratories are on different scales (xRref is different), and thus they are very different as shown in Tables 3 and 4.| δ33S (‰) | δ34S (‰) | δ36S (‰) | Δ33S (‰) | Δ36S (‰) | |
|---|---|---|---|---|---|
| a Values relative to Alfa Aesar standard solution. | |||||
| IPGP | 6.116 | −6.445 | −12.748 | 9.440 | −0.538 |
| 6.069 | −6.584 | −13.050 | 9.465 | −0.577 | |
| 6.087 | −6.521 | −12.685 | 9.451 | −0.331 | |
| 6.083 | −6.549 | −12.873 | 9.461 | −0.467 | |
| 6.060 | −6.620 | −13.126 | 9.475 | −0.585 | |
| 5.619 | −7.479 | −14.475 | 9.478 | −0.313 | |
| 6.209 | −6.317 | −12.320 | 9.467 | −0.352 | |
| UMD | 12.304 | 5.362 | 9.972 | 9.546 | −0.241 |
| 12.276 | 5.280 | 9.591 | 9.560 | −0.465 | |
| 12.237 | 5.199 | 9.539 | 9.563 | −0.361 | |
| 12.239 | 5.200 | 9.673 | 9.564 | −0.230 | |
| 12.428 | 5.618 | 10.420 | 9.539 | −0.282 | |
| 12.217 | 5.167 | 9.660 | 9.559 | −0.180 | |
| TIT | 18.756 | 18.076 | 35.365 | 9.488 | 0.742 |
| 18.750 | 18.075 | 35.485 | 9.482 | 0.864 | |
| 18.768 | 18.074 | 35.402 | 9.500 | 0.782 | |
| 18.745 | 18.066 | 35.422 | 9.481 | 0.816 | |
| 18.756 | 18.069 | 35.406 | 9.491 | 0.796 | |
| 18.747 | 18.085 | 35.398 | 9.474 | 0.756 | |
| 18.938 | 18.372 | 35.728 | 9.518 | 0.534 | |
| 18.918 | 18.366 | 35.761 | 9.501 | 0.577 | |
| 18.936 | 18.371 | 35.760 | 9.516 | 0.566 | |
| 18.923 | 18.369 | 35.736 | 9.504 | 0.547 | |
| 18.938 | 18.371 | 35.760 | 9.519 | 0.566 | |
| 18.941 | 18.375 | 35.723 | 9.520 | 0.522 | |
| MIT | 14.051 | 9.517 | 17.940 | 9.161 | −0.220 |
| ENSa | 12.322 | 5.139 | 9.679 | ||
| 12.209 | 5.283 | 9.492 | |||
| 12.174 | 5.135 | 9.533 | |||
| 12.330 | 5.370 | 9.569 | |||
| 12.433 | 5.441 | 9.635 | |||
| 12.192 | 5.404 | 9.412 | |||
| Mean | 9.501 | 0.113 | |||
| σ | 0.083 | 0.545 | |||
| δ33S (‰) | δ34S (‰) | δ36S (‰) | Δ33S (‰) | Δ36S (‰) | |
|---|---|---|---|---|---|
| a Values relative to Alfa Aesar standard solution. | |||||
| IPGP | 13.531 | 4.306 | 7.746 | 11.316 | −0.451 |
| 13.529 | 4.260 | 7.662 | 11.337 | −0.448 | |
| 13.506 | 4.236 | 7.498 | 11.327 | −0.566 | |
| 13.790 | 4.860 | 8.720 | 11.290 | −0.534 | |
| 13.666 | 4.644 | 8.391 | 11.277 | −0.451 | |
| UMD | 19.991 | 16.771 | 31.484 | 11.388 | −0.622 |
| 19.924 | 16.640 | 31.283 | 11.389 | −0.571 | |
| 19.786 | 16.432 | 31.097 | 11.357 | −0.355 | |
| 19.726 | 16.280 | 30.745 | 11.375 | −0.413 | |
| 19.770 | 16.358 | 30.984 | 11.379 | −0.324 | |
| TIT | 26.404 | 29.433 | 57.109 | 11.353 | 0.446 |
| 26.422 | 29.434 | 57.016 | 11.370 | 0.351 | |
| 26.412 | 29.445 | 57.004 | 11.354 | 0.317 | |
| 26.404 | 29.447 | 56.942 | 11.346 | 0.253 | |
| 26.409 | 29.450 | 56.985 | 11.349 | 0.289 | |
| 26.417 | 29.448 | 57.035 | 11.357 | 0.342 | |
| 26.316 | 29.256 | 56.751 | 11.354 | 0.433 | |
| 26.315 | 29.262 | 56.809 | 11.350 | 0.480 | |
| 26.305 | 29.265 | 56.710 | 11.339 | 0.376 | |
| 26.307 | 29.269 | 56.790 | 11.339 | 0.449 | |
| 26.300 | 29.261 | 56.788 | 11.336 | 0.461 | |
| 26.298 | 29.259 | 56.795 | 11.335 | 0.472 | |
| MIT | 21.351 | 20.198 | 38.000 | 10.999 | −0.725 |
| ENSa | 20.026 | 16.812 | 11.403 | ||
| 20.165 | 16.886 | 11.504 | |||
| 19.988 | 16.835 | 11.353 | |||
| 20.102 | 16.926 | 11.421 | |||
| 19.990 | 16.782 | 11.382 | |||
| 20.040 | 16.886 | 11.379 | |||
| 20.084 | 16.737 | 11.499 | |||
| 20.015 | 16.903 | 11.345 | |||
| 20.001 | 16.813 | 11.377 | |||
| 19.947 | 16.725 | 11.368 | |||
| 19.871 | 16.575 | 11.369 | |||
| 20.013 | 16.805 | 11.394 | |||
| 19.970 | 16.687 | 11.410 | |||
| Mean | 11.356 | −0.034 | |||
| σ | 0.076 | 0.463 | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
δ33S (‰) | δ34S (‰) | δ36S (‰) | Δ33S (‰) | Δ36S (‰) |
|---|---|---|---|---|---|
| IPGP | 14.907 | 10.458 | 19.419 | 9.535 | −0.545 |
| 14.860 | 10.317 | 19.107 | 9.560 | −0.586 | |
| 14.878 | 10.381 | 19.484 | 9.545 | −0.332 | |
| 14.874 | 10.352 | 19.290 | 9.556 | −0.471 | |
| 14.851 | 10.280 | 19.029 | 9.570 | −0.594 | |
| 14.406 | 9.407 | 17.636 | 9.573 | −0.312 | |
| 15.001 | 10.588 | 19.861 | 9.562 | −0.353 | |
| UMD | 14.906 | 10.370 | 19.661 | 9.579 | −0.134 |
| 14.878 | 10.288 | 19.276 | 9.593 | −0.361 | |
| 14.839 | 10.206 | 19.224 | 9.596 | −0.257 | |
| 14.841 | 10.207 | 19.359 | 9.597 | −0.124 | |
| 15.031 | 10.627 | 20.113 | 9.571 | −0.175 | |
| 14.819 | 10.174 | 19.346 | 9.592 | −0.073 | |
| TIT | 14.704 | 10.123 | 19.410 | 9.503 | 0.089 |
| 14.698 | 10.122 | 19.529 | 9.498 | 0.210 | |
| 14.715 | 10.122 | 19.447 | 9.515 | 0.128 | |
| 14.693 | 10.114 | 19.466 | 9.497 | 0.162 | |
| 14.703 | 10.116 | 19.450 | 9.506 | 0.142 | |
| 14.695 | 10.133 | 19.443 | 9.489 | 0.103 | |
| 14.884 | 10.417 | 19.768 | 9.533 | −0.116 | |
| 14.865 | 10.411 | 19.801 | 9.517 | −0.073 | |
| 14.883 | 10.416 | 19.800 | 9.532 | −0.084 | |
| 14.870 | 10.414 | 19.776 | 9.520 | −0.103 | |
| 14.885 | 10.416 | 19.799 | 9.534 | −0.084 | |
| 14.888 | 10.420 | 19.763 | 9.535 | −0.127 | |
| MIT | 14.393 | 10.246 | 19.879 | 9.130 | 0.323 |
| ENS | 14.869 | 10.054 | 9.703 | ||
| 14.755 | 10.199 | 9.516 | |||
| 14.720 | 10.050 | 9.557 | |||
| 14.877 | 10.286 | 9.593 | |||
| 14.980 | 10.357 | 9.659 | |||
| 14.738 | 10.320 | 9.436 | |||
| Mean | 14.810 | 10.262 | 19.467 | 9.538 | −0.144 |
| σ | 0.141 | 0.215 | 0.457 | 0.090 | 0.250 |
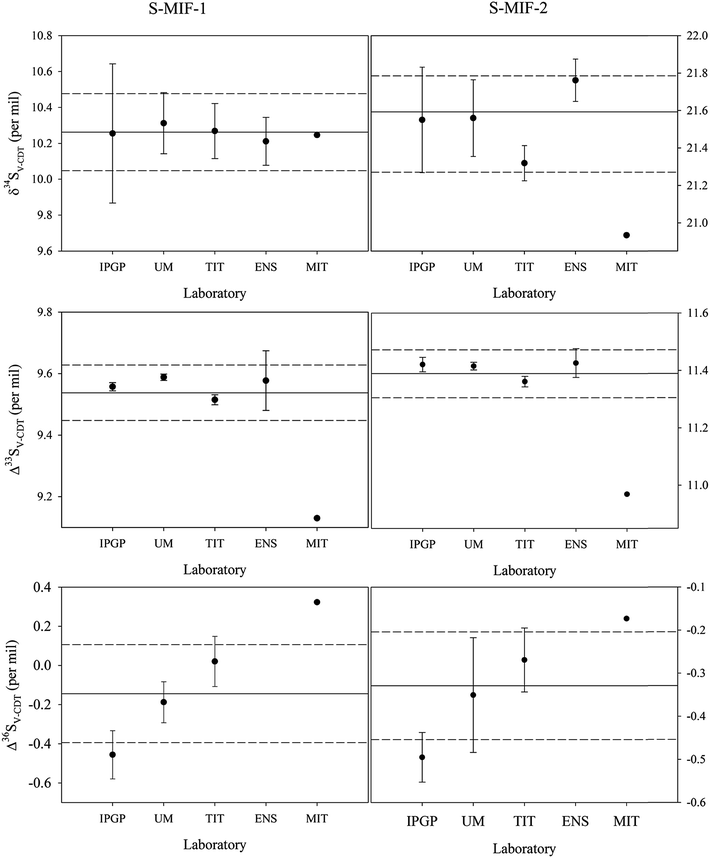
In Tables 3 and 4, the calculated Δ33S and Δ36S values from raw δ34S, δ33S and δ36S data according to eqn (2) and (3) are also listed. Despite the difference in raw δ34S, δ33S and δ36S values among different laboratories, the Δ33S and Δ36S values of the same sample from different laboratories are almost identical. This is because Δ33S and Δ36S are relative values reflecting the deviations from the mass-dependent lines, and are not much affected by the scale differences. But when small differences are focused on, they still need to be on the same scale. The means of Δ33S and Δ36S for S-MIF-1 are 9.50 ± 0.08‰ (1σ, N = 33) and 0.11 ± 0.55‰ (N = 26), respectively, and those for S-MIF-2 are 11.36 ± 0.08‰ (N = 37) and −0.03 ± 0.54‰ (N = 23), respectively.
In order to better compare the data from different laboratories and to evaluate the isotopic variability of S-MIF-1 and S-MIF-2, these values need to be anchored on the same scale (i.e., the V-CDT scale). For measurements done at IPGP, UMD, MIT and TIT, the international reference material IAEA-S-1 was also measured at the same time with S-MIF-1 and S-MIF-2, and the results are reported with respect to laboratory working reference gases and listed in Table 2. IAEA-S-1 has a consensual δ34SV-CDT value of −0.300‰, but its δ33S and δ36S values on the V-CDT scale have not been assigned. Wing and Farquhar24 have compiled Δ33SV-CDT and Δ36SV-CDT data of IAEA-S-1 from the literature, and obtained provisional Δ33SV-CDT and Δ36SV-CDT values of 0.094 ± 0.004‰ and −0.700 ± 0.100‰, respectively. From this the δ33SV-CDT and δ36SV-CDT values of IAES-S-1 were also derived to be −0.061‰ and −1.270‰, respectively. Hereafter, we refer to this scale as the V-CDT scale, but alert the reader to its provisional nature for the rarest isotopes. From the V-CDT values of IAEA-S-1 and its measured mean values with respect to the working gases (Table 2), we obtained the isotopic values of the working reference gas in each laboratory with respect to V-CDT. Finally, the raw δ34S, δ33S and δ36S values of S-MIF-1 and S-MIF-2 with respect to working reference gases were converted into the V-CDT scale.
For measurements done at the ENS, the δ34SV-CDT value of the working standard solution AA was 4.86 ± 0.14‰ as calibrated using international reference materials. According to the mass-dependent fractionation law, its δ33SV-CDT value was calculated to be −2.52‰. These values were then used to convert the raw δ34S and δ33S data of S-MIF-1 and S-MIF-2 to the V-CDT scale.
The above processes placed all δ34S, δ33S and δ36S values on the same scale, i.e., the V-CDT scale with the same xRref. After all raw δ34S, δ33S and δ36S values were anchored on the V-CDT scale, the Δ33S and Δ36S values were re-calculated using eqns (2) and (3).
3.2. Characterization of isotopic variability
The isotopic compositions of S-MIF-1 and S-MIF-2 on the V-CDT scale are listed in Tables 5 and 6, respectively. As shown in these tables, the δ34S, δ33S and δ36S V-CDT values of S-MIF-1 (or S-MIF-2) from different laboratories are identical. This is as expected because now they are all on the same scale (i.e., xRref is the same in eqn (1)), and the small or negligible difference is due to measurement uncertainties. Considering all data from the five laboratories, the uncertainties of δ34SV-CDT for S-MIF-1 and S-MIF-2 are ±0.22 and ±0.26‰ (1σ), respectively, comparable to or better than those of international sulfur reference materials (e.g., ±0.2‰ for IAEA-SO-6 and ±0.4‰ for NBS-127). Regarding the Δ33SV-CDT and Δ36SV-CDT, it can be noted that they are slightly different from those calculated from the raw δ34S, δ33S and δ36S data (Tables 3 and 4). These small differences may be considered to be negligible regardless of the scale when the capital delta values are large, e.g., in the case of Δ33S of S-MIF-1, it is 9.50 ± 0.08‰ and 9.54 ± 0.09‰ before and after anchoring on the V-CDT scale. But when small capital values are the subject of interest, the difference becomes important, e.g., in the case of Δ36S of S-MIF-1, it is 0.11 ± 0.55‰ and −0.14 ± 0.25‰ before and after anchoring on the V-CDT scale. Overall, the uncertainties of Δ33SV-CDT for S-MIF-1 and S-MIF-2 are ±0.09 and ±0.08‰, respectively. For Δ36SV-CDT, the uncertainties are ±0.25 and ±0.13‰ for S-MIF-1 and S-MIF-2, respectively. The relatively large uncertainties in Δ36SV-CDT are in part due to the extremely low abundance of 36S, which makes its accurate measurement more difficult, but maybe more likely come from an isobaric interference on the 131 peak during IRMS measurements probably due to C3F5+.44 In addition, the uncertainties of the small delta values are larger than those of the capital delta values as always observed, and the best precision is obtained for Δ33SV-CDT. This is because the uncertainties of the small delta values are in part from sample preparation and conversion processes, but these processes would only induce mass-dependent fractionation and thus won't significantly affect the capital delta values.| δ33S (‰) | δ34S (‰) | δ36S (‰) | Δ33S (‰) | Δ36S (‰) | |
|---|---|---|---|---|---|
| IPGP | 22.387 | 21.392 | 40.581 | 11.427 | −0.455 |
| 22.385 | 21.345 | 40.494 | 11.449 | −0.451 | |
| 22.362 | 21.321 | 40.325 | 11.438 | −0.573 | |
| 22.649 | 21.956 | 41.587 | 11.401 | −0.541 | |
| 22.523 | 21.736 | 41.247 | 11.388 | −0.455 | |
| UMD | 22.613 | 21.836 | 41.379 | 11.426 | −0.516 |
| 22.546 | 21.704 | 41.176 | 11.426 | −0.464 | |
| 22.407 | 21.495 | 40.989 | 11.395 | −0.247 | |
| 22.347 | 21.343 | 40.633 | 11.412 | −0.307 | |
| 22.391 | 21.421 | 40.874 | 11.416 | −0.217 | |
| TIT | 22.321 | 21.392 | 40.819 | 11.361 | −0.216 |
| 22.339 | 21.393 | 40.728 | 11.378 | −0.310 | |
| 22.329 | 21.404 | 40.716 | 11.363 | −0.343 | |
| 22.321 | 21.405 | 40.655 | 11.354 | −0.406 | |
| 22.326 | 21.409 | 40.697 | 11.357 | −0.371 | |
| 22.334 | 21.407 | 40.746 | 11.366 | −0.319 | |
| 22.234 | 21.216 | 40.467 | 11.363 | −0.229 | |
| 22.232 | 21.222 | 40.524 | 11.359 | −0.183 | |
| 22.223 | 21.225 | 40.427 | 11.348 | −0.285 | |
| 22.225 | 21.228 | 40.506 | 11.348 | −0.213 | |
| 22.217 | 21.221 | 40.503 | 11.344 | −0.201 | |
| 22.215 | 21.219 | 40.510 | 11.343 | −0.191 | |
| 22.381 | 21.406 | 40.832 | 11.413 | −0.232 | |
| MIT | 21.696 | 20.934 | 39.977 | 10.969 | −0.173 |
| ENS | 22.592 | 21.785 | 11.432 | ||
| 22.731 | 21.859 | 11.533 | |||
| 22.553 | 21.808 | 11.381 | |||
| 22.668 | 21.899 | 11.449 | |||
| 22.555 | 21.754 | 11.410 | |||
| 22.606 | 21.858 | 11.407 | |||
| 22.650 | 21.709 | 11.528 | |||
| 22.580 | 21.875 | 11.374 | |||
| 22.567 | 21.786 | 11.406 | |||
| 22.513 | 21.697 | 11.397 | |||
| 22.437 | 21.546 | 11.398 | |||
| 22.579 | 21.777 | 11.422 | |||
| 22.437 | 21.546 | 11.398 | |||
| Mean | 22.418 | 21.528 | 40.725 | 11.389 | −0.329 |
| σ | 0.192 | 0.257 | 0.356 | 0.083 | 0.125 |
It can be noted that the V-CDT values of S-MIF-1 and S-MIF-2 derived from the measurement (one analysis available) done at MIT are slightly different from those done at other labs, i.e., they are at the low end for Δ33SV-CDT but the high end for Δ36SV-CDT among all data derived. However, this is only one measurement and its involvement in the global means did not affect the results (the means and standard deviations) much.
S-MIF-1 was characterized with δ34SV-CDT = 10.26 ± 0.22‰ (1σ, N = 32), Δ33SV-CDT = 9.54 ± 0.09‰ (N = 33) and Δ36SV-CDT = −0.14 ± 0.25‰ (N = 36), and for S-MIF-2, its isotopic compositions were established to be δ34SV-CDT = 21.52 ± 0.26‰ (N = 37), Δ33SV-CDT = 11.39 ± 0.08‰ (N = 37) and Δ36SV-CDT = −0.33 ± 0.13‰ (N = 24).
The mean δ34SV-CDT, Δ33SV-CDT and Δ36SV-CDT values among all the data and those data from each laboratory including their one sigma standard deviations are plotted in Fig. 1. Overall, the derived δ34SV-CDT, Δ33SV-CDT and Δ36SV-CDT values of S-MIF-1 and S-MIF-2 at the laboratories except for MIT are in good agreement, especially for the Δ33SV-CDT values, which are 9.56 ± 0.01‰ (N = 7), 9.59 ± 0.01‰ (N = 6), 9.52 ± 0.02‰ (N = 12) and 9.58 ± 0.09‰ (N = 6) for S-MIF-1, and 11.42 ± 0.03‰ (N = 5), 11.42 ± 0.01‰ (N = 5), 11.36 ± 0.02‰ (N = 12), and 11.43 ± 0.05‰ (N = 13) for S-MIF-2 at IPGP, UMD, TIT and ENS, respectively. In comparison, the Δ33SV-CDT values of S-MIF-1 and S-MIF-2 derived at MIT are 9.13 and 10.97‰, respectively.
4. Summary
There is a compelling need to have international sulfur and oxygen isotope reference materials enriched in 33S, 36S and 17O, respectively, to calibrate the Δ33S, Δ36S and Δ17O values measured from a variety of atmospheric and geological samples. This is important not only in terms of data comparisons within a laboratory and/or among different laboratories, but also regarding the differentiation of small Δ33S and Δ36S values from mass-dependent and mass independent fractionation processes. Currently there is only one international sulfur reference material, IAEA-S-1, with established Δ33S and Δ36S values (0.094 ± 0.004‰, and −0.7 ± 0.1‰, respectively) reported on the V-CDT scale,24 but IAEA-S-1 can be regarded more as a primary reference material. There are no reference materials with apparently large anomalies in Δ33S and Δ36S.In this report, we synthesized two sodium sulfate samples, S-MIF-1 and S-MIF-2, artificially enriched in 33S and 17O. The preliminary assessments of their oxygen isotopic compositions yielded Δ17O = 3.3 ± 0.3‰. The sulfur isotopic compositions of these two samples were characterized at five different laboratories using two distinct methods, the conventional IR-MS method and the newly developed MC-ICP-MS method.16 Except for one data point from the MIT laboratory, results from the other four laboratories are in good consistency. The good precision of these isotopic values indicates isotopic homogeneity of S-MIF-1 and S-MIF-2. Although further calibration efforts may be needed to improve the accuracy of Δ33SV-CDT assessments of S-MIF-1 and S-MIF-2, their current values can be adopted to calibrate Δ33S measurements. In particular, mixing them with other sulfur reference materials with zero Δ33S such as IAEA-SO-5 and IAEA-SO-6 should generate working standards with different Δ33S values, which can be used to establish a calibration curve spanning a large Δ33S range (e.g., 0 to 11‰) for better data normalization. These standards are available for the community and can be requested on demand from Joel Savarino.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Agence Nationale de la Recherche (ANR) via contract NT09-431976-VOLSOL is acknowledged for the financial support for JS. This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska Curie grant agreement No. 700853. This work has also supported by the Japan Society for the Promotion of Science KAKENHI Grant Numbers 16H05884 (S. H.), 25887025, and 17H06105 (N. Y.). S. H. and J. S. appreciate support for this project from JSPS and CNRS under the JSPS–CNRS Joint Research Program. Travel visit support for J. S. was provided by the CNRS/PICS program. JF acknowledges support from NNX16AG39G and the Agouron Foundation. LG acknowledges Marie Curie Individual Fellowship and the University of Science and Technology of China, and additional financial support from the National Key Research and Development Program of China (2016YFA0302200) and National Science Foundation of China (41822605). NM acknowledges the Brazilian Government for a Science without Borders Fellowship (BEX1136-13-5). FA and EA thank Philippe Telouk for help with instrument tuning and INSU and ENS Lyon for support.References
- G. Beaudoin, B. E. Taylor, D. Rumble and M. Thiemens, Geochim. Cosmochim. Acta, 1994, 58, 4253–4255 CrossRef CAS.
- T. B. Coplen and H. R. Krouse, Nature, 1998, 392, 32 CrossRef CAS.
- G. W. Cooper, M. H. Thiemens, T. L. Jackson and S. Chang, Science, 1997, 277, 1072–1074 CrossRef CAS PubMed.
- H. B. Franz, S. T. Kim, J. Farquhar, J. M. D. Day, R. C. Economos, K. D. McKeegan, A. K. Schmitt, A. J. Irving, J. Hoek and J. Dottin, Nature, 2014, 508, 364–368 CrossRef CAS PubMed.
- J. Farquhar, J. Savarino, T. L. Jackson and M. H. Thiemens, Nature, 2000, 404, 50–52 CrossRef CAS PubMed.
- S. Ono, J. L. Eigenbrode, A. A. Pavlov, P. Kharecha, D. Rumble, J. F. Kasting and K. H. Freeman, Earth Planet. Sci. Lett., 2003, 213, 15–30 CrossRef CAS.
- J. Farquhar, H. M. Bao and M. Thiemens, Science, 2000, 289, 756–758 CrossRef CAS PubMed.
- H. Ohmoto, Y. Watanabe, H. Ikemi, S. R. Poulson and B. E. Taylor, Nature, 2006, 442, 908–911 CrossRef CAS PubMed.
- J. Farquhar, M. Peters, D. T. Johnston, H. Strauss, A. Masterson, U. Wiechert and A. J. Kaufman, Nature, 2007, 449, 706–709 CrossRef CAS PubMed.
- M. Baroni, J. Savarino, J. H. Cole-Dai, V. K. Rai and M. H. Thiemens, J. Geophys. Res., 2008, 113, D20112 CrossRef.
- J. Cole-Dai, D. Ferris, A. Lanciki, J. Savarino, M. Baroni and M. H. Thiemens, Geophys. Res. Lett., 2009, 36, L22703 CrossRef.
- J. Savarino, A. Romero, J. Cole-Dai, S. Bekki and M. H. Thiemens, Geophys. Res. Lett., 2003, 30, 2131 CrossRef.
- A. B. Romero and M. H. Thiemens, J. Geophys. Res., 2003, 108, 4524 CrossRef.
- M. Lin, X. L. Zhang, M. H. Li, Y. L. Xu, Z. S. Zhang, J. Tao, B. B. Su, L. Z. Liu, Y. A. Shen and M. H. Thiemens, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8541–8546 CrossRef CAS PubMed.
- R. Shaheen, M. M. Abaunza, T. L. Jackson, J. McCabe, J. Savarino and M. H. Thiemens, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11979–11983 CrossRef CAS PubMed.
- E. Albalat, P. Telouk, V. Balter, T. Fujii, V. P. Bondanese, M. L. Plissonnier, V. Vlaeminck-Guillem, J. Baccheta, N. Thiam, P. Miossec, F. Zoulim, A. Puisieux and F. Albarede, J. Anal. At. Spectrom., 2016, 31, 1002–1011 RSC.
- G. Paris, A. L. Sessions, A. V. Subhas and J. F. Adkins, Chem. Geol., 2013, 345, 50–61 CrossRef CAS.
- S. Ono, Space Sci. Rev., 2008, 135, 203–220 CrossRef CAS.
- S. Ono, B. Wing, D. Johnston, J. Farquhar and D. Rumble, Geochim. Cosmochim. Acta, 2006, 70, 2238–2252 CrossRef CAS.
- D. T. Johnston, J. Farquhar, B. A. Wing, A. Kaufman, D. E. Canfield and K. S. Habicht, Am. J. Sci., 2005, 305, 645–660 CrossRef CAS.
- G. M. Luo, S. Richoz, B. van de Schootbrugge, T. J. Algeo, S. C. Xie, S. Ono and R. E. Summons, Geochim. Cosmochim. Acta, 2018, 231, 73–87 CrossRef CAS.
- D. T. Johnston, S. W. Poulton, P. W. Fralick, B. A. Wing, D. E. Canfield and J. Farquhar, Geochim. Cosmochim. Acta, 2006, 70, 5723–5739 CrossRef CAS.
- Y. A. Shen, J. Farquhar, H. Zhang, A. Masterson, T. G. Zhang and B. A. Wing, Nat. Commun., 2011, 2, 210 CrossRef PubMed.
- B. A. Wing and J. Farquhar, Geochim. Cosmochim. Acta, 2015, 170, 266–280 CrossRef CAS.
- S. Ono, W. C. Shanks, O. J. Rouxel and D. Rumble, Geochim. Cosmochim. Acta, 2007, 71, 1170–1182 CrossRef CAS.
- M. A. Antonelli, S. T. Kim, M. Peters, J. Labidi, P. Cartigny, R. J. Walker, J. R. Lyons, J. Hoek and J. Farquhar, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17749–17754 CrossRef CAS PubMed.
- J. W. Dottin, J. Farquhar and J. Labidi, Geochim. Cosmochim. Acta, 2018, 224, 276–281 CrossRef CAS.
- J. Labidi, P. Cartigny and M. G. Jackson, Earth Planet. Sci. Lett., 2015, 417, 28–39 CrossRef CAS.
- J. M. Eiler, B. Bergquist, I. Bourg, P. Cartigny, J. Farquhar, A. Gagnon, W. F. Guo, I. Halevy, A. Hofmann, T. E. Larson, N. Levin, E. A. Schauble and D. Stolper, Chem. Geol., 2014, 372, 119–143 CrossRef CAS.
- J. Kaiser and T. Röckmann, Rapid Commun. Mass Spectrom., 2008, 22, 3997–4008 CrossRef CAS PubMed.
- S. Hattori, J. A. Schmidt, M. S. Johnson, S. O. Danielache, A. Yamada, Y. Ueno and N. Yoshida, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17656–17661 CrossRef CAS PubMed.
- J. R. Lyons, Geophys. Res. Lett., 2007, 34, L22811 CrossRef.
- A. R. Whitehill, B. Jiang, H. Guo and S. Ono, Atmos. Chem. Phys., 2015, 15, 1843–1864 CrossRef.
- A. R. Whitehill, C. J. Xie, X. X. Hu, D. Q. Xie, H. Guo and S. H. Ono, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17697–17702 CrossRef CAS PubMed.
- A. L. Buchachenko, J. Phys. Chem. B, 2013, 117, 2231–2238 CrossRef CAS PubMed.
- S. Kopf and S. Ono, Geochim. Cosmochim. Acta, 2010, 74, A531 CrossRef.
- J. R. Lyons, Chem. Geol., 2009, 267, 164–167 CrossRef CAS.
- H. G. Thode, J. Monster and H. B. Dunford, Geochim. Cosmochim. Acta, 1961, 25, 159–174 CrossRef CAS.
- T. Kiba, T. Tagaki, Y. Yoshimura and I. Kisha, Bull. Chem. Soc. Jpn., 1955, 28, 641–644 CrossRef CAS.
- J. Forrest and L. Newman, Anal. Chem., 1977, 49, 1579–1584 CrossRef CAS PubMed.
- L. Geng, A. J. Schauer, S. A. Kunasek, E. D. Sofen, J. Erbland, J. Savarino, D. J. Allman, R. S. Sletten and B. Alexander, Rapid Commun. Mass Spectrom., 2013, 27, 2411–2419 CrossRef CAS PubMed.
- J. Savarino, B. Alexander, V. Darmohusodo and M. H. Thiemens, Anal. Chem., 2001, 73, 4457–4462 CrossRef CAS PubMed.
- A. J. Schauer, S. A. Kunasek, E. D. Sofen, J. Erbland, J. Savarino, B. W. Johnson, H. M. Amos, R. Shaheen, M. Abaunza, T. L. Jackson, M. H. Thiemens and B. Alexander, Rapid Commun. Mass Spectrom., 2012, 26, 2151–2157 CrossRef CAS PubMed.
- D. Rumble, T. C. Hoering and J. M. Palin, Geochim. Cosmochim. Acta, 1993, 57, 4499–4512 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |