Single-particle ICP-MS with online microdroplet calibration: toward matrix independent nanoparticle sizing

Abstract

Single-particle inductively coupled plasma mass spectrometry (sp-ICP-MS) has become an effective tool for the detection and quantification of inorganic nanoparticles (NPs). While sizing of NPs suspended in water is relatively straightforward by sp-ICP-MS, accurate mass quantification of NPs in complex media, such as consumer products and natural systems still remains a challenge. When NPs are suspended in a complex medium, the matrix may affect the analyte sensitivity and lead to inaccurate NP sizing. Here, we investigate the use of an online microdroplet calibration system to size NPs in a single step. In this setup, microdroplets—which are used as the calibrant to determine elemental sensitivities—and nebulized NP-containing solutions are introduced concurrently into the ICP via a dual-inlet sample introduction system. Because calibrant microdroplets and analyte NPs experience the same plasma conditions, both the microdroplets and the NPs are subjected to the same matrix-related signal enhancement or suppression. In this way, the microdroplet calibration standards are automatically matrix matched with the NP-containing solution. The online microdroplet calibration system is combined with an ICP-TOFMS instrument for simultaneous measurement of multiple elements in microdroplets and NPs. We investigate the ability of online microdroplet calibration to compensate for matrix effects through a series of experiments, in which Ag and Au NPs are measured with variable plasma-sampling positions, varying concentrations of HCl and HNO₃, varying concentrations of single element solutions, and high concentrations of a salt matrix, i.e. phosphate buffered saline (PBS). Through these experiments, we demonstrate that the online microdroplet calibration strategy provides a matrix-independent mass quantification of analyte NPs in the presence of several established types of matrix effects, including acid effects, space-charge effects, and ionisation suppression. In results presented here, we focus on the size determination of the NPs.

---

1. Introduction

Single-particle inductively coupled plasma mass spectrometry (sp-ICP-MS) is an established method for the determination of metal and metal-oxide nanoparticle (NP) mass distributions and particle number concentrations (PNCs).^1–3 State-of-the-art sp-ICP-MS measurement systems can measure NPs down to ∼6.4 nm in diameter for gold NPs (∼2.2 ag Au, ∼7000 atoms),⁴ though size detection limits vary with NP composition, instrumentation, and how detection limits are defined.^5,6 Additionally, sp-ICP-MS can be used to accurately measure PNCs at environmentally relevant concentrations, from ∼10⁶ to 10⁸ particles per mL.^5,7 Motivation for the development of sp-ICP-MS stems from the expanding use of nanotechnologies in commercial and industrial products as well as the recognized need for measurement tools to characterize NPs released from their product hosts and assess routes of human exposure and environmental impact.^8,9 To this end, many national and international research consortia have been established to develop and evaluate analytical techniques and procedures for NPs analysis (NanoFASE,¹⁰ ACEnano,¹¹ CEINT,¹² SNSF NRP 64,¹³etc.). The research focus of these groups has helped bring sp-ICP-MS from method development^1,5,14–20 to application, such as for the monitoring of engineered TiO₂ NPs in surface waters,²¹ or the capability to distinguish natural NPs from engineered NPs using their elemental fingerprint,²² as well as several interlaboratory comparison studies.^23,24 Research on sp-ICP-MS also led to the introduction of new ISO technical definitions such as ISO/TS 19590:2017, which sets a reference frame for the measurements of size distribution and concentration of inorganic NPs in aqueous media via sp-ICP-MS, as well as ISO/TS 17294-1:2004, which deals with the application of sp-ICP-MS in water quality.

When measuring NPs in real samples (i.e. complex media), sp-ICP-MS can suffer from matrix effects in a way similar to that of conventional ICP-MS. Matrix effects in ICP-MS are well documented and can degrade the accuracy of measurements. In 1987, Tan and Horlick categorized matrix effects in ICP-MS as either matrix-induced spectral overlaps or matrix-induced signal intensity changes.²⁵ Spectral interferences occur when atomic or polyatomic ions are isobaric with analyte isotopes; for example, high concentration of NaCl produces ArNa⁺ and ArCl⁺ species that interfere with ⁶³Cu⁺ and ⁷⁵As⁺, respectively. Common (and potential) spectral interferences in ICP-MS have been extensively catalogued.^26,27 Nonetheless, spectral interferences are persistent and must be considered in ICP-MS measurements. A number of approaches exist to overcome spectral interferences, including prudent choice of quantification isotope, mathematical abundance corrections, separation of isobaric species with mass resolution,²⁸ and chemical reaction or gas-phase collisions in reaction cells.^29,30

The second category of matrix effects—matrix-induced signal intensity changes—lead to different responses of the analyte in the matrix and calibration solutions, and are generally not as predictable as spectral interferences. The magnitude of the suppression or enhancement of analyte signal intensity depends on the properties of the matrix (composition, concentration, ionisation energies, and molecular weights), as well as the operating conditions of the ICP (plasma power and nebulizer gas flow rate) and the mass analyser (lens voltages).^25,31,32 Much research has been done to identify and correct matrix-induced signal-intensity changes,³³ and a complete review is beyond the scope of this report. Here, we discuss two key types of matrix effects that occur post sample introduction—ionisation suppression and space-charge effects—because these matrix effects could influence the recorded NPs signals intensities, and thereby impact the accurate sizing of NPs.

In samples that contain high concentrations of easily ionized elements (EIEs), analyte element signals may be reduced because of ionisation suppression.²⁵ High numbers of EIEs causes an increase in the number of free electrons in the central channel of the plasma, which shifts the thermal ionization equilibrium toward neutral atoms and thus reduces the fraction of ionised analyte atoms extracted into the mass analyser.^34,35 Elements with higher first ionisation potentials are particularly susceptible to this ionisation suppression. Likewise, introduction of any species that cools the plasma, such as excess solvent, can induce shifts in ionisation position and ion-cloud densities of species in the plasma, which in turn causes analyte signals to be enhanced or suppressed dependent on the location of the shifted ion cloud relative to the sampler orifice.^36–38 In addition to changes in ionisation position due to plasma temperature effects, high matrix concentrations can defocus the extracted ion beam in the interface of the mass analyser.³⁹ This type of matrix effect is generically termed a space-charge effect, and is most pronounced with high-mass matrix species. In the extracted ion beam, high-mass-to-charge (m/z) ions tend to stay in the centre of the beam: lighter ions are accelerated more during coulombic repulsion interactions and thus are more diffuse in the extracted ion beam.^40–42 Together, ionisation suppression and space-charge effects indicate that highly ionisable elements with high mass relative to the analyte tend to induce the greatest plasma- and analyser-related matrix effects. For example, Olesik et al.⁴³ reported that the presence of a high-mass element (i.e. Pb) causes temporal broadening and attenuation of signals from a low-mass species (i.e. Li) when these analytes are introduced into the plasma in discrete microdroplets. They attributed this ion-signal broadening to increased size of the Li⁺ ion cloud in the extracted ion beam due to space-charge effects in the mass analyser. As microdroplets may be used as proxy for NPs,⁴⁴ this study has direct implications to accurate NP sizing because NP signals could be attenuated in a similar fashion as microdroplets. However, it is more likely that NP signals will be affected by steady-state matrix effects controlled by the composition of the matrix in which NPs are suspended. Here, we investigate and attempt to correct for steady-state matrix effects, which occur in the plasma and the MS interface—including ionisation suppression and space-charge effects—and influence signal magnitudes from single NPs. Our work is related to the fundamental studies of Lazar and Farnsworth who investigated matrix effects with a dual sample introduction system that they used to introduce matrix via a pneumatic nebulizer and analyte in microdroplets.^45,46

If matrix-induced signal intensity changes are not sufficiently minimized or compensated for, these matrix effects will lead to spurious results that are sometimes difficult to identify. For this reason, care should be taken in ICP-MS analysis to control the impact of matrix effects via thoughtful experimental design. Common approaches applied to account for matrix effects include: sample dilution, matrix separation, flow injection, isotopic dilution, standard addition, use of internal standards, and matrix-matched calibration.³² In sp-ICP-MS, non-matrix-matched element-sensitivity calibrations can lead to incorrect NP size determinations.^47,48 Many of the measurement strategies for conventional solution-based ICP-MS analysis are applicable to sp-ICP-MS, including sample dilution, flow injection analysis,⁴⁹ matrix matching,⁵⁰ and matrix separation.^51–54 However, all of these approaches have drawbacks. For instance, sample dilution can be disadvantageous in sp-ICP-MS for the analysis of real samples because it increases measurement time needed to acquire a statistically relevant number of particle events and could impact the stability of the NPs in natural samples.⁵⁵ Though it is important to note that sample dilutions are sometimes necessary to limit single-particle event frequency to appropriate levels. To correct for matrix effects without sample dilution, one could use matrix-matched calibration standards to determine element sensitivities; however, matrix matching is a challenge for complex samples and quickly becomes impractical for analysis of many sample types. Additionally, NP-containing matrices are often pH neutral and incompatible with dissolved-element calibration standards.^47,56,57 Although theoretically possible, standard addition of NPs is challenging due to the limited availability of reference materials, as well as difficulty to separate signals from spiked NPs and analyte NPs, which is necessary for size distribution measurements.

Here, we investigate the use of an online-microdroplet calibration strategy to compensate for plasma- and MS-related matrix effects in the size determination of Au, SiO₂–Au and Ag NPs. We build off initial studies of the dual sample-introduction system for online microdroplet calibration developed by Ramkorun-Schmidt et al.⁵⁸ and Hendriks et al.⁴⁸ In this system, we introduce microdroplets doped with calibrant elements concurrently with the NP-containing samples, so that the microdroplet standards and analyte NPs experience the same plasma conditions and the same steady-state matrix effects. Our system takes advantage of sparsity of NPs in the sample, which allows us to have “matrix-matched” microdroplet signals without substantially overlapping with NP signals. Additionally, while sp-ICP-MS is usually performed with quadrupole- or sector-field mass analysers that record a single isotope at high time resolution, we use a time-of-flight mass analyser (ICP-TOFMS) to monitor all elements of interest in microdroplets and NPs simultaneously. We investigate the performance of our system with a variety of matrices, including acid matrices, single-element matrices to study space-charge effects, and high salt matrices to study ionisation suppression effects.

2. Experimental

2.1. Materials

Calibration solutions were prepared by diluting commercially available standard solutions in ultra-high purity (UHP) water with 1% sub-boiled HNO₃ or 1% HCl (TraceSelect, Fluka Analytical, Switzerland) for Au if not mentioned otherwise. Dilutions were prepared gravimetrically using a balance (Mettler AE240, Mettler-Toledo, Switzerland). For the acid matrix studies, solutions of HNO₃ and HCl at 0–10% (v/v) concentrations were prepared. Multi-element solutions were prepared from single-element standards (Inorganic Ventures, USA; Merck, Germany; VWR Chemicals, USA). To determine elemental sensitivities (count per g element), we measured calibration solutions injected into the ICP in microdroplets. The solutions for these microdroplets contained 100 ng g⁻¹ of Au or Ag, depending on the NP measured, and 100 ng g⁻¹ caesium, which was used as a tracer element to discriminate between droplet- and NP-induced signals. Matrix elements for the single-element matrix studies, were chosen based on their standard atomic weight (in atomic mass units, u) as well as on their first ionisation potential (IP) to span a range around silver (107.87 u, IP: 7.6 eV), light and heavy elements as well as lower and similar ionisation potential. These include Li (6.9 u, IP: 5.4 eV), Lu (174.97 u, IP. 5.4 eV), Mg (24.3 u, IP. 7.6 eV) and Pb (207.2 u, IP.7.4 eV). Equimolar single-element solutions were prepared from single element standard solutions ranging from 0 to 2.4 mM. For the phosphate buffered saline (PBS) matrix studies, the PBS stock solution (Gibco, pH 7.4) solution contains 1.05 mM KH₂PO₄ (210 mg L⁻¹), 155.17 mM NaCl (9000 mg L⁻¹) and 2.96 mM Na₂HPO₄ (726 mg L⁻¹). For salt-matrix studies, the PBS stock was diluted by factors of 2, 5, 10, and 100 with UHP water.

In this study, two batches of Ag NPs (diameter 79 ± 7 nm and 80 ± 6 nm) and a single stock of Au NPs (diameter 80 ± 9 nm) from NanoComposix (USA) were measured. All NP stocks were delivered as aqueous suspensions stabilized with citrate. Samples were stored in the fridge, and then were allowed to reach room temperature and sonicated for 1 minute prior to dilution in given matrices. For the acid matrix effect studies, a silica (SiO₂) shell of ∼30 nm in thickness was synthesized around the purchased Au NPs (80 nm diameter, NanoComposix). Details of this synthesis procedure are provided in the ESI.† An overview of the different calibrant and matrix solutions used in the different experiments is also presented in the ESI, see Table S1.†

2.2. Instrumentation and data acquisition

To investigate the effect of matrices on accuracy of NP sizing by sp-ICP-MS, as well as to correct for matrix effects via online microdroplet calibration, we combined an ICP-TOFMS instrument (icpTOF, TOFWERK AG, Switzerland) with a dual sample introduction system first described by Ramkorun-Schmidt et al.⁵⁸ A schematic diagram of this setup is provided in Fig. 1. Details of the ICP-TOFMS instrument can be found elsewhere.^59–61 In this setup, NP-containing samples were aspirated by a PFA MicroFlow pneumatic nebulizer (Element Scientific Inc., Omaha, USA) and double-pass cyclonic spray chamber. Microdroplets doped with the analyte of interest and a tracer element were produced by a commercial microdroplet generator (MD-E-3000, Microdrop Technologies GmbH, Germany) equipped with a 50 μm diameter Autodrop Pipette (AD-KH-501-L6). A calibrated video camera was used in all experiments to measure the diameter of the droplets produced by the microdroplet generator.^16,62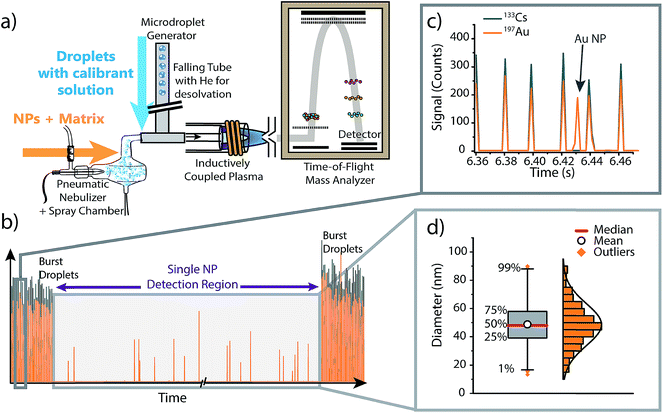

Fig. 1 (a) Schematic diagram of the online microdroplet calibration sp-ICP-TOFMS system. (b) Representative time trace from an online microdroplet sp-ICP-TOFMS experiment. NP-containing solutions are introduced continuously via conventional pneumatic nebulization and microdroplets are introduced in two bursts of 1000 droplets at the start and end of each measurement run. (c) Gold-doped microdroplets can be distinguished from Au NPs based on the multi-element composition of droplets (i.e. Cs is present in signals from microdroplets). (d) The data collected within the “Single NP Detection Region” is treated like a typical sp-ICP-MS experiment: NP signals are identified, the mass of each NP is determined using microdroplet-derived sensitivities (counts per g), then the determined element mass is converted to a diameter and binned into a size distribution (see ESI† for details). Size distributions are plotted as box and whiskers, which simplifies the visualization of the central tendency and spread of the distribution.

Calibrant microdroplets were introduced through a 40 cm long stainless steel falling tube filled with a He/Ar gas mixture, which accelerates evaporation so that microdroplets were reduced to dried droplet residues by the end of the falling tube.^62,63 Dried droplet residues were mixed with nebulized aerosols via a t-piece just in front of the injector base of the ICP torch. With this approach, NPs and matrices from the nebulizer and calibrant droplet residues were introduced simultaneously into the ICP (see Fig. 1). In our online-microdroplet calibration scheme, the nebulized sample was introduced continuously, while bursts of microdroplets were generated at the beginning and end of each sp-ICP-TOFMS dataset. Each burst of microdroplets consisted of 1000 microdroplets at 50 Hz. A tracer element (e.g. Cs) present in microdroplets was used to monitor droplet transmission to the ICP and distinguish microdroplet signals from NP signals. Operating conditions of the online-microdroplet calibration sp-ICP-TOFMS system are provided in Table 1. For single-element matrix studies, the multi-notch mass filter of the ICP-TOFMS instrument was used to attenuate matrix ions prior to TOF analysis and thus prevent detector saturation.

Table 1 Operating parameters. These were optimized daily for each set of experiments in order to achieve highest sensitivity, minimal oxides formation rates and stable microdroplet signals

a From day to day slightly different droplet sizes provided the most reproducible and stable microdroplets. Microdroplets were measured during each set of experiments, so droplet size is accounted for. b During one experiment, the sampling position was varied from optimal conditions, i.e. from a sampling position of 6 mm to 10 mm. c Data presented in Fig. 3 was collected on an earlier version of our ICP-TOFMS instrument, which had a shorter flight path (1 m) and operated with a TOF extraction frequency of 33.333 kHz.
Microdroplet introduction	Droplet diameter^a	55–70 μm
	Droplet frequency	50 Hz
	He gas flow rate in falling tube	0.5–0.7 L min^−1
	Ar gas flow rate in falling tube	0.05–0.15 L min^−1
Matrix and NP introduction via pneumatic nebulizer	Nebulizer gas flow rate (Ar)	0.7–1 L min^−1
	Solution uptake rate	∼600 μL min^−1
ICP conditions	Intermediate gas flow rate (Ar)	0.8 L min^−1
	Outer gas flow rate (Ar)	15 L min^−1
	Power	1550 W
	Sampling position^b	5–6 mm above load coil
TOFMS conditions^c	TOF extraction frequency	21.739 kHz
	Mass spectral acquisition rate	500 Hz

---

For the set of experiments in which Ag is introduced simultaneously as dissolved analyte through the pneumatic nebulizer (PN), in droplets, and as Ag NPs, different operating conditions than the ones outlined above were used. For this dataset, we did not use microdroplet bursts at the start and end of each analysis run or have a tracer element present in the microdroplets. Instead, microdroplets were introduced continuously at a frequency of 10 Hz, and Ag signals from solution and NPs were differentiated based on Ag isotopes. Specifically, we introduced an isotopically-enriched ¹⁰⁹Ag (98.3% ¹⁰⁹Ag, Merck, Germany) sample dissolved in 1% HNO₃ through the PN. The solution introduced as microdroplets and the Ag NPs both have Ag with naturally isotopic abundances (i.e.¹⁰⁷Ag: 51.8% and ¹⁰⁹Ag: 48.2%). Because ¹⁰⁷Ag is depleted in the solution introduced through the PN, signals from ¹⁰⁷Ag were used to identify signals from Ag NPs and Ag-doped microdroplets. Likewise, signal from ¹⁰⁹Ag was used to monitor the response of dissolved Ag as a function of changes in plasma conditions due to nebulizer flow rate and matrix addition (i.e. 100 mg L⁻¹ Li). Separation of ¹⁰⁷Ag attributable to Ag NPs and microdroplets was done by thresholding signal histograms: average ¹⁰⁷Ag signal from microdroplets was ten times higher than that from NPs, so signal origin could be easily assigned. Further details of Ag-species identification procedure are provided in Fig. S4 of the ESI† and a summary of element and matrix composition introduced through the pneumatic nebulizer and in microdroplets is provided in Table S1.† For all measurements, apart from the Ag-analyte study described above, a conserved measurement scheme—as shown in Fig. 1—was used.

2.3. Data evaluation and representation

As illustrated in Fig. 1, each measurement run consisted of three distinct measurement regions: two “burst” regions during which microdroplets are introduced, and a NP detection region in the middle of the ICP-TOFMS signal time traces. Because the size and content of microdroplets is known, average microdroplet signals in each burst region are used to calculate sensitivities (counts per g) of calibrant elements; these sensitivities are used to calibrate mass present in individual NPs from the same measurement run (see ESI† for details). To isolate microdroplet-induced signals, the tracer element time trace is thresholded and signals from all calibrant elements are collected for each identified microdroplet. Single-particle signals from the “Single NP Detection Region”, are processed via a conventional sp-ICP-MS algorithm to identify NP signals.^5,64 In this algorithm, analyte signals were extracted from the raw data and binned into a frequency distribution based on the number of recorded counts per acquisition. Next, a threshold was set to discriminate between the background/dissolved fraction and the particles fraction. In cases where the S/N was sufficient, this threshold was set visually, otherwise, a μ + 5σ criteria was applied, where μ and σ are the mean and standard deviation of the data set, respectively. The μ + 5σ criteria is found iteratively by removing all data points above μ + 5σ, recalculating μ + 5σ, and repeating until no signals remain above the threshold criteria.^65,66 In the case of silver in Fig. 5, signal from both isotopes ¹⁰⁷Ag and ¹⁰⁹Ag were combined to increase S/N.

When reporting NP sizes, it is common to report the average or median value of the size distribution with the standard deviation representing the uncertainty. However, this approach gives limited information about the shape of the measured size distribution. Alternatively, some researchers present NP size distributions as histograms. By using histograms, the general shape of the distribution (e.g. normal, lognormal, bimodal, multimodal…), its tails, and symmetry/skewness, can deliver further insights regarding the state of the NPs (e.g. monodisperse, degraded, aggregates…).⁶⁷ However, data visualization is challenging if many NP-size histograms need to be compared. Here, we report NP-size data as box and whisker plots in order to compare the sizing accuracy of NPs in various matrices. Box and whisker plots allow simple visual comparison of multiple datasets, but also provide important information about size distributions obtained, e.g. the central tendency (median), the mean, and the NPs sizes at the quartiles and the 1% and 99% quantiles (see Fig. S3† in ESI for details). The spread of NP data can provide insight into state of the NPs, such as whether agglomerates are present. Additionally, box plots are less affected by binning bias than histograms.

3. Results and discussion

The research presented here builds off initial studies of the dual sample-introduction system for online microdroplet calibration.^48,58 Specifically, Hendriks et al.⁴⁸ demonstrated that online microdroplet calibration can be used to accurately size Au NPs in fruit juices and milk, even in the presence of matrix-related signal attenuation. Here, we study the ability of the online microdroplet calibration approach to compensate for a range of different matrix effects caused by varying acid concentration and composition, space-charge from single-elements, and high concentrations of easily ionisable elements. For all of these matrices, we measure the attenuation or enhancement of NP-induced signals and quantify NP mass (i.e. size) with online microdroplet calibration. Importantly, the direction and magnitude of signal change due to any matrix effect depends both on the matrix and on the operating conditions of the ICP-MS, such as the nebulizer gas flow rate, plasma power, sampling position, and ion-optics design and settings of the mass analyser.^25,31,32 In this study, we investigate plasma-related matrix effects at set operating conditions (see Table 1). The magnitude and the direction of the matrix effects are measured as the change in normalized analyte-NP signal intensities, where the “no matrix” condition (i.e. optimal ICP operating conditions with UHP water as NP-containing matrix) serves as reference for normalization.

3.1. Proof-of-principle experiments: controlled alteration of plasma operating conditions

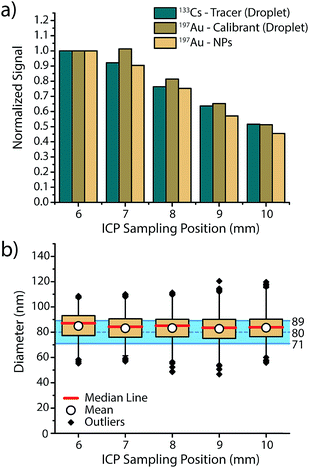
In order to assess if microdroplets can effectively be used to correct for plasma-related matrix effects, we first investigated whether the analyte contained in the microdroplets and the analyte NPs introduced via the nebulizer behave similarly in the plasma and experience the same plasma conditions. In other words: do microdroplet residues atomize and ionize at roughly the same position in the plasma as NPs, and do they also respond to changes in plasma conditions in a similar manner? To answer these questions, we varied sampling position and nebulizer gas flow—these modifications from the normal operating conditions change the relative fraction of ions sampled by the MS interface and help us gauge whether ions from microdroplets and NPs are being generated at similar positions in the plasma.

Sampling position variation. In this experiment, we altered the plasma conditions by increasing the sampling position (here, reported as distance from the end of the ICP torch to the tip of the sampler cone) and evaluated whether the Au-containing microdroplets introduced via the falling tube experienced the same plasma conditions as the Au NPs introduced via the nebulizer. Change in plasma-sampling position can result in ion-signal suppression or enhancement for a number of reasons. First, change in sampling position affects the number of ions sampled by the MS interface because the diffusion of free atoms and ions increases as the sampling position is moved farther from the optimum position. Second, elements may have different optimal sampling positions based on m/z,³⁶ metal-oxide boiling points,⁶⁸ first ionisation energies, or initial particle size entering the plasma.⁶⁹ Finally, because the sampling cone is relatively cool compared to the plasma temperature, changes in sampling position can influence the temperature profile and gas flow patterns of the plasma.⁷⁰

In Fig. 2, we present an overview of the results obtained while changing the sampling position from optimum position (6 mm) to farther from the MS inlet (10 mm). For all three species, namely ¹³³Cs present as tracer in the microdroplets, ¹⁹⁷Au present as calibrant in the microdroplets and ¹⁹⁷Au originating from the Au NPs, a general decrease in signal intensity is observed, which demonstrates that the microdroplets behave almost the same as analyte NPs in the plasma. By increasing the sampling position, ions are sampled further downstream of the point where particle vaporisation occurs, so a decrease in signal intensity due to atom and ion diffusion is expected. The only deviation from expectation comes at sampling position of 7 mm, at which the Au signal from the microdroplets does not decrease to the same extent as Au signal from NPs. This discrepancy could be the result of microdroplet-salt residues vaporising slightly further into the plasma than analyte NPs. A vaporisation position deeper in the plasma would cause slight differences in ion density position of Au for the NPs and the calibrant microdroplets. Moreover, this effect might not be observed with the Cs signal because the low first IP of Cs (3.89 eV) causes near instantaneous ionisation and leads to spatial separation of Cs and Au ion densities in the plasma, with the Au density further along the plasma. Despite minor deviations between analyte NP and microdroplet calibrant signal intensities, Au signal recovered from the NPs and calibrated based on sensitivity recorded from the microdroplet standards results in a correct sizing of the Au NPs at all plasma-sampling positions. This study shows that online microdroplet calibration matches analyte NPs well enough to mimic NP behaviour in different plasma conditions and yield a successful sizing. Likewise, online microdroplet calibration also provides a means to correct for analyte intensity drift (see Fig. S2 in the ESI†).

Fig. 2 (a) Normalised signal intensities of ¹³³Cs in microdroplets and ¹⁹⁷Au in NPs and microdroplets show decrease in signal intensity with increasing sampling position. (b) As both the signal for the Au calibrant in the microdroplets and the recorded Au signals for the NPs follow the same decrease in signal intensity, accurate diameter determination of the 80 nm Au NPs is achieved independent of sampling position. The blue shaded area spans the expected size range provided by the manufacturer.

Nebulizer gas flow variation. In addition to changing sample position, we investigated the influence of varying the nebulizer gas flow rate to assess whether the calibrant microdroplets and NPs of identical elements are affected in a similar way. In this experiment, we introduced dissolved isotopically enriched ¹⁰⁹Ag through the pneumatic nebulizer and spray chamber (PN/SC). Through the use of isotopically enriched ¹⁰⁹Ag, we are able to simultaneously assess matrix effects on a conserved element introduced into the plasma as three different forms, i.e. as solution in small (<∼5 μm diameter) polydisperse aerosols from the PN/SC, in NPs suspended in same small aerosol droplets, and in dried monodisperse droplet residues.

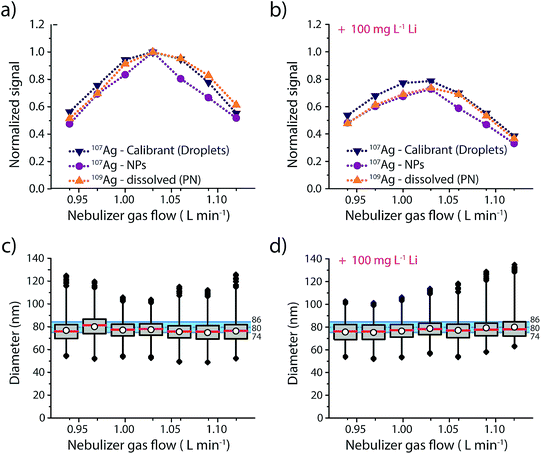
Results of this experiment are provided in Fig. 3 and details regarding the data evaluation are provided in the ESI Fig. S4.† The responses of the three different Ag analytes (Ag in microdroplets, isotopically enriched ¹⁰⁹Ag in solution and Ag NPs) were initially measured in an acid matrix (1% HNO₃), and then in a high matrix concentration of Li (100 mg L⁻¹, 14.4 mM). In both cases the Ag NPs were added right before the sample was aspirated into the nebulizer to make sure that the dissolution of the NPs was kept to a minimum. As seen in Fig. 3, both matrices produce a maximum in signal intensity at a nebulizer gas flow rate of 1.03 L min⁻¹ for all three sample introduction approaches. Furthermore, similar to previous studies,²⁵ we observe a more pronounced effect of the Li-matrix at higher gas flow rates. For example, at a gas flow rate of 0.94 L min⁻¹ both matrices produce a normalized intensity of ∼0.5; however, at gas flow of 1.03 L min⁻¹, the sample with Li matrix is 20% attenuated compared to the no-matrix sample, which would lead to a 20% error in analyte mass quantification. As observed with sampling position studies, we find that online microdroplet calibration accounts for signal attenuation due to both changes in nebulizer gas flow rate and presence of the Li matrix: under all conditions, Ag NPs are sized within the manufacturer-reported size distribution. Because microdroplet calibration accounts for signal attenuation by Li, Ag-NP signals can be collected with a nebulizer gas flow rate that provides maximum sensitivity without suffering quantification error due to matrix effects. Another critical observation from this work is that the sample introduction technique does not have a major impact on the analyte signal: Ag signals introduced via PN/SC liquid-sample introduction, as NPs, and as monodisperse microdroplets all follow similar trends both with PN gas flow change and in the Li matrix. This result supports the use of dissolved standards for sensitivity calibration in sp-ICP-MS and also suggests that the conventional matrix-matched external standards could be used to overcome matrix effects. The advantage of this online droplet calibration approach is that it provides an automatic online matrix matching; droplet composition does not need to be changed to account for varying plasma-related matrix effects caused by different NP-containing samples or instrument operating conditions.

Fig. 3 (a) Normalised signal intensities recorded for Ag analyte in the form of NPs, microdroplets and enriched ¹⁰⁹Ag solution without any additional matrix at nebulizer gas flow rates between 0.94 and 1.12 L min⁻¹. (b) Same experiment as in (a), but with 100 mg L⁻¹ Li matrix. (c) and (d) Corresponding sizing of the 80 nm Ag NPs at different nebulizer gas flow rates. In both (c) and (d), the shaded blue area shows the expected NP diameter from the manufacturer.

3.2. Acid-related matrix effects

In routine ICP-MS analysis, samples are often prepared in 1 or 2% HNO₃; however, the presence and concentration of acids in the analyte solution are not without consequences. Because acid changes the physical properties of the solvent such as density, surface tension, and viscosity, it also changes the aerosol formation, which has a large impact on ICP-MS signals. The size of the droplets that make it through the spray chamber depends on the gas dynamics in the spray chamber, droplet-size distribution from the pneumatic nebulizer, and aerosol density.⁷¹ Solvent droplets of lower densities and smaller diameters will be more likely to exit the spray chamber into the plasma. In previous studies, it was found that the overall transport efficiency of analyte decreases with increasing acid concentration of the sample.⁷² This decrease in transport efficiency is attributed to a reduction of solvent evaporation in the spray chamber and an increase of average droplet size with increasing acid concentrations up to 2%.⁷³ In addition, introduction of acid solutions into the plasma can also cause local cooling of the plasma due to evaporation energy of acidic droplets and dissociation energy of acid solute.⁷⁴ It has been reported that acid-matrix effects could influence the sizing of NPs in sp-ICP-MS because element standards dissolved in acid solutions can have different absolute sensitivities than NPs suspended in water.⁴⁷ Acid-dependent transport efficiencies can also cause a mismatch between the measured transport efficiency of acid solution into the plasma and the true mass flux for a water matrix—this mismatch will lead to inaccurate particle number concentration (PNC) determinations.⁴⁷

Here, we investigated the effect of increasing acid concentrations of HCl and HNO₃ on the size calibration of SiO₂ shelled Au NPs. The SiO₂–Au NPs were introduced in solutions of HNO₃ and HCl at 0–10% (v/v) concentrations. The SiO₂ shell acted as a protective layer around the Au, preventing its dissolution in the acid solution. We were inspired to use SiO₂–Au NPs to study acid-matrix effects based on previous work of Olesik et al.⁴⁷ Due to the presence of agglomerates, an additional upper threshold was set in the data analysis to exclude these NPs clusters from the sizing data analysis (see ESI for details, Fig. S5 and Table S2†).

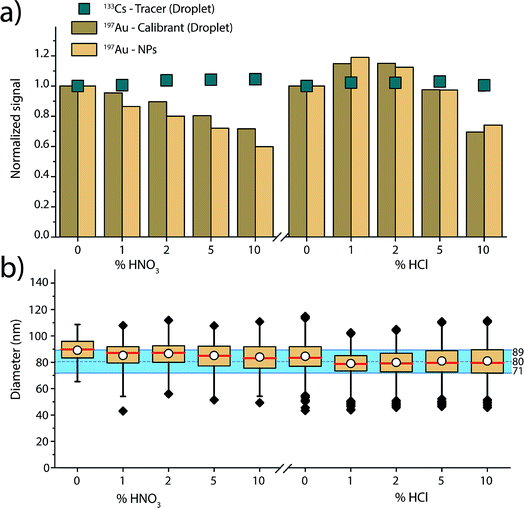
Fig. 4 gives an overview of the recorded signal intensities for the tracer ¹³³Cs present in the microdroplets and for ¹⁹⁷Au present in both NPs and microdroplets as a function of the increasing acid concentrations. These results demonstrate that increasing concentrations of HNO₃ and HCl cause plasma-based matrix effects. In the case of HNO₃, increasing concentration of acid lowers the absolute sensitivity for Au in both the NPs and in the microdroplets. On the other hand, ¹³³Cs shows a steadier signal. These observations are consistent with steady-state acid effects reported by Stewart and Olesik, where they also observed reduced analyte ionisation efficiency with increasing acid concentration.⁷¹ As Au has a higher ionisation potential than Cs (9.23 eV vs. 3.89 eV), it is more affected by the local changes in plasma temperature caused by the acid. The Au-containing microdroplets show sensitivity decrease similar, but not identical, to that of the SiO₂–Au NPs suspended in the acid-containing solution. The cause of the ∼10% difference in change in signal magnitude between SiO₂–Au NPs and Au-containing microdroplets is not certain. But, it is likely that the SiO₂–Au NPs and Au-salt residue particles from the microdroplets vaporise and ionise at different positions in the plasma and this affects the magnitude of matrix effects experienced.

Fig. 4 (a) Overview of the observed trends over different acid concentrations, for ¹⁹⁷Au signal measured from the NPs introduced via the pneumatic nebulizer, and from the microdroplets introduced via the falling tube, as well as for ¹³³Cs used a tracer in the microdroplets. (b) Results of the sizing of the 80 nm SiO₂–Au NPs using the microdroplets for calibration. Independent of the acid type and concentration, a successful sizing is achieved, i.e. each determined median NP diameter is within the expected range established by the manufacturer (blue shaded area).

For the HCl matrix, we observe a slight increase of 15% in both SiO₂–Au NP and Au-microdroplet sensitivities in the presence of 1% (v/v) HCl, and then a significant decrease of 25 to 30% in sensitivities in the presence of 10% HCl. A change in NP signal intensity indicates that plasma-related matrix effects occur: if only sample introduction rate was changing, then the NP intensity should not change because individual NPs have constant mass. Our results contradict previous reports,⁴⁷ which found Au signal enhancement in HCl acid to be caused mostly by increased sample transport efficiency and to only affect dissolved Au solution (i.e. not Au NPs), which would impact the calculated size of the NPs. Here, we mainly observe plasma-related matrix effects. This difference in results can be explained by the many co-dependent parameters in an ICP-MS experiment, from nebulizer and spray chamber design, to various gas flows, to sampling position, to plasma power.

As shown in Fig. 3, when dissolved analyte and NPs are both introduced through the nebulizer and experience the same trend with the matrix (i.e. Li), an external matrix match calibration using dissolved standards should be possible as long as these standards are stable in the given matrix. However, in the case of the increasing nitric acid content, matrix-matched calibration with Au dissolved standard is not possible because Au is not stable in nitric acid. Our results demonstrate that online microdroplet calibration enables accurate mass quantification of the analyte Au NPs in all acid concentrations. Again, the calibrant microdroplets serve as matrix-matched standards that effectively model the behaviour of analyte NPs to produce accurate NP-size information. In addition to signal attenuation or enhancement, change in acid composition can also affect sample transport efficiency into the plasma, which has implications on PNC determination. Online microdroplet calibration does not correct for matrix-related sample transport efficiencies and we do not evaluate PNCs here.

3.3. Single-element matrix effects: accounting for space-charge effects

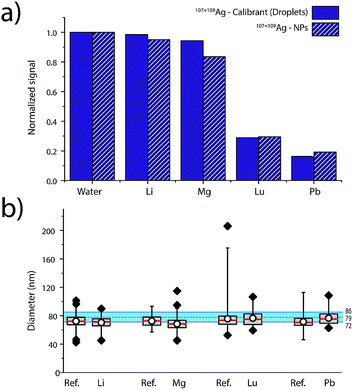
Elemental matrix effects depend upon a wide range of operating conditions, including plasma power, sampling position, nebulizer gas flow, plasma-MS interface design, and MS ion-optics settings. Here, we report results from measurement of 80 nm diameter Ag NPs in four single-element matrix solutions that bracket Ag, based on their standard atomic weights and ionisation potentials: Li (6.9 u, IP: 5.4 eV), Lu (174.97 u, IP. 5.4 eV), Mg (24.3 u, IP. 7.6 eV) and Pb (207.2 u, IP.7.4 eV). Ag NPs were introduced concomitant with single-element solutions and online microdroplet calibration (100 μg L⁻¹ Ag in microdroplets) was performed to calibrate the mass of individual Ag NPs in each of the matrix solutions. Equimolar concentrations of matrix, ranging from 0 to 2.4 mM, were used for each matrix. For all matrix-element solutions, nebulizer gas flows were optimized to provide highest Ag NP signal in the water matrix. Detailed results of the investigation of these four single-element matrices in function of concentration are provided in Fig. S6 in the ESI.†

In Fig. 5, we present a summary of Ag NPs detection in high and low concentrations of Li, Mg, Lu, and Pb. The trends observed here are in agreement with the results published by Tan and Horlick in their comprehensive study of matrix effects.²⁵ When dealing with equimolar concentrations of various matrix elements, the heavy matrix elements (i.e. Pb and Lu) induce more severe analyte signal suppression than light matrix elements (i.e. Li and Mg). Calibrant microdroplet residues experience similar matrix effects to the Ag NPs, which allows for accurate sizing even in the presence of a signal-suppressing single-element solution. As seen in Fig. 5, the median size of the Ag NPs as determined by sp-ICP-TOFMS of the Ag NPs was consistently smaller than expected. This decrease in NP diameter could be due to sample deterioration. Importantly, even a small undersizing of NPs by the online microdroplet calibration approach is minor compared to potential inaccuracies caused by matrix-dependent element sensitivities. For example, the approximate 80% decrease in signal observed for Ag NPs in 2.4 mM Pb would result in an approximately 42% decrease in the determined particle diameter if the mass sensitivity of Ag was not measured in the Pb matrix solution via online microdroplet calibration.

Fig. 5 (a) Normalized signal intensities for Ag measured in the NPs and in the microdroplets in water, as well as in 2.4 mM of the different elemental matrices. (b) Corresponding sizing of the 80 nm Ag NPs using online microdroplet calibration.

The suppression of ion signal from both Ag NPs and Ag in the microdroplets caused by Pb and Lu matrices, as well as the absence of a pronounced suppression from Li and Mg, is best explained as a space-charge effect in the ion-extraction region of the mass spectrometer.^40–42 Because Lu and Pb ions are heavier than Ag ions, they tend to stay in the centre of the extracted ion beam and electrostatically accelerate the Ag ions away from the centre, which makes the Ag ion cloud more diffuse and lowers Ag ion signal intensity. When lighter ions and Ag ions are coulombically repelled, the light ions are accelerated more than the Ag ions. In this case, the light ions tend to get more diffuse and don't cause space-charge dilution of the Ag ion cloud to as great an extent. Space-charge repulsion in the ion-extraction region of the MS interface is relatively constant so long as the number of matrix ions is much greater than the number of analyte ions—in our case, this is achieved for both NPs and microdroplets, so online microdroplet calibration compensates for ion-signal suppression caused by space charge. Apart from space-charge effects, high matrix concentrations can consume the energy typically used to vaporise and ionise analyte species in the ICP, which results in a cooler plasma and in a shift in ionisation position of the analytes. It is possible that some of the ion suppression observed in Fig. 5 is related to plasma effects rather than space-charge. However, we observe no conclusive trend according to first IP of the matrices, which would have required the investigation of elements with higher ionization potentials such as 9.8 and 10.4 eV for As and P, respectively. Indeed, for Li, Mg, Lu and Pb, which predominantly exist as ions, only space charge effects were observable. Suppression seems most correlated to the mass of the matrix-element.

3.4. Application study: phosphate-buffered saline matrix effect

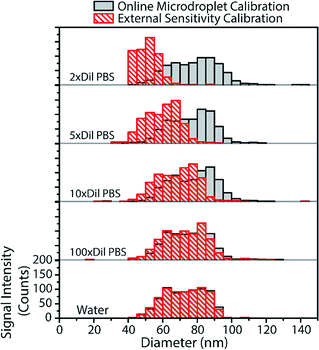
From the above results with online microdroplet calibration and various matrix effects, it is clear that this calibration approach has potential to be used as a matrix-independent system for quantification of element mass in NPs by sp-ICP-MS. The online and automatic matrix matching capabilities of the approach make it ideal for the detection of metal NPs in diverse matrices. Here, we investigate the use of our online microdroplet calibration approach for the quantification of Au NPs in a biologically relevant matrix, i.e. phosphate buffered saline (PBS). PBS is a buffer solution that closely mimics the pH, osmolarity, and ion concentrations of the human body. We were motivated to measure NPs in PBS because there is an increasing use of engineered NPs in medical and biological applications, from NP use as contrast agents and in cancer therapy^75,76 to sustained efforts in nanotoxicology to understand mechanisms of NP uptake and toxicity in living systems.^77,78sp-ICP-MS is a tool that can be used to understand fate and transport of NPs at the single-particle level, with sufficient sensitivity to study the effects of relevant PNCs in biological systems. For these reasons, there is growing interest in sp-ICP-MS in biology,⁷⁹ including recent reports of sp-ICP-MS used for the detection of NPs in blood^50,80 and other body fluids.⁸¹ Especially relevant to our study, Witzler et al.⁵⁰ demonstrated that matrix-matched external calibration can be used to accurately quantify Ag and Au NPs spiked into whole human blood.

In Fig. 6, we present size-distribution histograms for the analysis of 80 nm diameter Au NPs spiked into increasing concentrations of PBS. As the PBS concentration increases, the high concentration of sodium introduced into the plasma causes an ionisation suppression matrix effect that leads to the attenuation of Au signal from both NPs and calibrant microdroplets. In Fig. 6, we also plot the size distributions of Au NPs that would have been measured in the various PBS concentrations without online microdroplet calibration. With twice diluted PBS (77.5 mM NaCl, ∼0.5% [v/v]), Au NP signal is attenuated by 72%, which would lead to a undersizing of the NP diameter by about 35% without correction for signal suppression by PBS. However, with online microdroplet calibration, the NP size histogram and median NP diameter is mostly conserved in all PBS concentrations. In Fig. 6, it is apparent that, at high PBS concentrations (and high signal suppression), the measured histograms of the Au NPs gets broader; this broadening is caused by increased relative standard deviation of suppressed signals due to lower ion counts measured per NP. As mentioned previously, a common approach to reduce matrix effects is to dilute the sample. Indeed, as can be observed in Fig. 6, a 100-fold dilution of PBS would enable accurate NP sizing without signal suppression by PBS. In fact, this dilution strategy has been used before; in 2002, Zhang et al.⁸² measured bulk colloidal Au NP concentrations in a heavily diluted PBS matrix (∼10 mM PBS) without suffering from matrix effects. When possible, dilution is an excellent approach to minimize matrix effects in sp-ICP-MS. However, real samples often contain such low PNCs that dilution cripples the possibility of measuring statistically relevant number of NPs within reasonable measurement times. Also, dilution of concomitant matrix species can destabilize NPs. Online microdroplet calibration allows for accurate quantification of NP mass in both situations that do and do not allow for sample dilution.

Fig. 6 The PBS present in the matrix attenuates the signal of Au NPs to different degrees depending on concentration. From bottom, NP-diameter histograms are provided for water-only matrix, and PBS with dilution factors of 100, 10, 5, and 2 times of the stock PBS concentration. With online microdroplet calibration, the Au NPs are sized correctly in all concentrations of PBS. Plotted in red are the histograms of Au NP diameters determined with non-matrix matched external calibration.

4. Conclusions

Thanks to its capabilities to distinguish dissolved content from particulates as well as to measure NPs at environmentally relevant concentrations, sp-ICP-MS has found its place in the analytical toolbox for NPs analysis. In this work, we show that online microdroplet calibration can be used to account for plasma- and MS-related matrix effects. We demonstrate accurate and matrix-independent mass quantification of Ag and Au NPs with variable sampling positions, and in the presence of acid-matrix effects, space-charge effects caused by single-element matrices, and a high-salt matrix, PBS. Our calibration approach can be used to correct for steady-state matrix effects; however, we have not yet studied the ability of the system to account for matrix effects caused by the composition of the NP itself, i.e. particle-related matrix effects.^83,84 Additionally, the calibration system we presented does not account for sample-introduction related matrix effects that could lead to matrix-dependent PNCs; future work will address online calibration of sample transmission efficiency for PNC measurements. Finally, it has been reported that microdroplets themselves perturb local plasma conditions and could cause a microdroplet-based matrix effect.^85,86 We see no evidence of these effects in our measurements, but it is worth further consideration.

From the set of experiments performed in this work, we can now emphasize some practical benefits of the online microdroplet calibration combined with sp-ICP-TOFMS compared to conventional sp-ICP-MS. Online microdroplet calibration allows for absolute sensitivity (counts per g) determination for all elements in microdroplet calibration standards, which enables quantification of multiple NP types in either a single measurement run, or at least with the same calibration solution. Online microdroplet calibration also eliminates the use NP standards for detection efficiency determination, which reduces measurement steps needed for sp-ICP-MS measurements and the need for hard-to-get certified NP reference materials. With our calibration approach, there is also no need to bracket NP analyses with calibration standard runs because the microdroplet calibration inherently accounts for instrument drift. Matrix-compensation capabilities of online microdroplet calibration increase the general robustness of sp-ICP-MS measurements and improve the reliability of NP quantification in diverse matrices. In principle, our online microdroplet calibration approach can be adapted to conventional quadrupole and sector-field-based ICP-MS instruments. However, the use of ICP-TOFMS extends the benefits of our calibration system because this analyser allows for the simultaneous measurement and quantification of diverse NP types, which will allow for high-throughput measurements that are necessary to understand NP populations in, for example, environmental samples. In the future, we will extend the use of online microdroplet calibration combined with sp-ICP-TOFMS for the simultaneous quantification of multiple NP-types in natural samples.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Roland Mäder from the ETH mechanical workshop for manufacturing custom pieces necessary for the microdroplet introduction system and the dual inlet setup. L. H. acknowledges funding from Swiss National Science Foundation (SNSF) Project no. 200021 162870/1. A. G.-G. acknowledges funding through an Ambizione grant of the SNSF, project no. PZ00P2_174061. Finally, B. R.-S. thanks the School of Analytical Sciences Adlershof (SALSA) together with the Bundesanstalt für Materialforschung und –prüfung for the funding of part of this work.

References

1. C. Degueldre and P. Y. Favarger, Colloids Surf., A, 2003, 217, 137–142.
2. D. M. Mitrano, E. K. Lesher, A. Bednar, J. Monserud, C. P. Higgins and J. F. Ranville, Environ. Toxicol. Chem., 2012, 31, 115–121.
3. F. Laborda, E. Bolea and J. Jiménez-Lamana, Anal. Chem., 2014, 86, 2270–2278.
4. J. Tuoriniemi, G. Cornelis and M. Hassellov, J. Anal. At. Spectrom., 2015, 30, 1723–1729.
5. F. Laborda, J. Jimenez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2013, 28, 1220–1232.
6. S. Lee, X. Bi, R. B. Reed, J. F. Ranville, P. Herckes and P. Westerhoff, Environ. Sci. Technol., 2014, 48, 10291–10300.
7. D. M. Mitrano, J. F. Ranville, A. Bednar, K. Kazor, A. S. Hering and C. P. Higgins, Environ. Sci.: Nano, 2014, 1, 248–259.
8. A. D. Maynard and R. J. Aitken, Nat. Nanotechnol., 2016, 11, 998.
9. B. Nowack, A. Boldrin, A. Caballero, S. F. Hansen, F. Gottschalk, L. Heggelund, M. Hennig, A. Mackevica, H. Maes, J. Navratilova, N. Neubauer, R. Peters, J. Rose, A. Schäffer, L. Scifo, S. v. Leeuwen, F. von der Kammer, W. Wohlleben, A. Wyrwoll and D. Hristozov, Environ. Sci. Technol., 2016, 50, 2747–2753.
10. NanoFASE, http://www.nanofase.eu/, accessed November 2018.
11. ACEnano, http://www.acenano-project.eu/, accessed November 2018.
12. CEINT, https://ceint.duke.edu/about, accessed November 2018.
13. Opportunities and Risks of Nanomaterials, National Research Programme NRP 64, http://www.nrp64.ch/en, accessed November 2018.
14. C. Degueldre, P. Y. Favarger and S. Wold, Anal. Chim. Acta, 2006, 555, 263–268.
15. H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, E. P. Gray, C. P. Higgins and J. F. Ranville, Environ. Sci. Technol., 2012, 46, 12272–12280.
16. S. Gschwind, L. Flamigni, J. Koch, O. Borovinskaya, S. Groh, K. Niemax and D. Gunther, J. Anal. At. Spectrom., 2011, 26, 1166–1174.
17. J. W. Olesik and P. J. Gray, J. Anal. At. Spectrom., 2012, 27, 1143–1155.
18. M. D. Montano, H. R. Badiei, S. Bazargan and J. F. Ranville, Environ. Sci.: Nano, 2014, 1, 338–346.
19. J. Tuoriniemi, G. Cornelis and M. Hassellov, J. Anal. At. Spectrom., 2014, 29, 743–752.
20. I. Strenge and C. Engelhard, J. Anal. At. Spectrom., 2016, 31, 135–144.
21. A. Gondikas, F. von der Kammer, R. Kaegi, O. Borovinskaya, E. Neubauer, J. Navratilova, A. Praetorius, G. Cornelis and T. Hofmann, Environ. Sci.: Nano, 2018, 5, 313–326.
22. A. Praetorius, A. Gundlach-Graham, E. Goldberg, W. Fabienke, J. Navratilova, A. Gondikas, R. Kaegi, D. Günther, T. Hofmann and F. von der Kammer, Environ. Sci.: Nano, 2017, 4, 307–314.
23. A. R. M. Bustos, E. J. Petersen, A. Possolo and M. R. Winchester, Anal. Chem., 2015, 87, 8809–8817.
24. T. P. J. Linsinger, R. Peters and S. Weigel, Anal. Bioanal. Chem., 2014, 406, 3835–3843.
25. S. H. Tan and G. Horlick, J. Anal. At. Spectrom., 1987, 2, 745–763.
26. N. M. Reed, R. O. Cairns, R. C. Hutton and Y. Takaku, J. Anal. At. Spectrom., 1994, 9, 881–896.
27. T. W. May and R. H. Wiedmeyer, At. Spectrosc., 1998, 19, 150–155.
28. N. Jakubowski, L. Moens and F. Vanhaecke, Spectrochim. Acta, Part B, 1998, 53, 1739–1763.
29. J. T. Rowan and R. S. Houk, Appl. Spectrosc., 1989, 43, 976–980.
30. D. W. Koppenaal, G. C. Eiden and C. J. Barinaga, J. Anal. At. Spectrom., 2004, 19, 561–570.
31. J. W. Olesik and S. Jiao, J. Anal. At. Spectrom., 2017, 32, 951–966.
32. C. Agatemor and D. Beauchemin, Anal. Chim. Acta, 2011, 706, 66–83.
33. S. D. Tanner, J. Anal. At. Spectrom., 1995, 10, 905–921.
34. M. H. Ramsey and M. Thompson, J. Anal. At. Spectrom., 1986, 1, 185–193.
35. D. S. Hanselman, N. N. Sesi, M. Huang and G. M. Hieftje, Spectrochim. Acta, Part B, 1994, 49, 495–526.
36. F. Vanhaecke, R. Dams and C. Vandecasteele, J. Anal. At. Spectrom., 1993, 8, 433–438.
37. N. N. Sesi and G. M. Hieftje, Spectrochim. Acta, Part B, 1996, 51, 1601–1628.
38. P. J. Galley, M. Glick and G. M. Hieftje, Spectrochim. Acta, Part B, 1993, 48, 769–788.
39. K. Busch, Spectroscopy, 2004, 19, 35–38.
40. S. D. Tanner, Spectrochim. Acta, Part B, 1992, 47, 809–823.
41. G. Li, Y. Duan and G. M. Hieftje, J. Mass Spectrom., 1995, 30, 841–848.
42. L. A. Allen, J. J. Leach and R. S. Houk, Anal. Chem., 1997, 69, 2384–2391.
43. J. W. Olesik and M. P. Dziewatkoski, J. Am. Soc. Mass Spectrom., 1996, 7, 362–367.
44. J. W. Olesik, Appl. Spectrosc., 1997, 51, A158–A175.
45. A. C. Lazar and P. B. Farnsworth, Appl. Spectrosc., 1999, 53, 457–464.
46. A. C. Lazar and P. B. Farnsworth, Appl. Spectrosc., 1999, 53, 465–470.
47. M. D. Montaño, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Anal. Bioanal. Chem., 2016, 408, 5053–5074.
48. L. Hendriks, A. Gundlach-Graham and D. Günther, CHIMIA International Journal for Chemistry, 2018, 72, 221–226.
49. R. P. Lamsal, G. Jerkiewicz and D. Beauchemin, Anal. Chem., 2016, 88, 10552–10558.
50. M. Witzler, F. Kullmer and K. Gunther, Anal. Lett., 2018, 51, 587–599.
51. D. Rakcheev, A. Philippe and G. E. Schaumann, Anal. Chem., 2013, 85, 10643–10647.
52. M. Hadioui, C. Peyrot and K. J. Wilkinson, Anal. Chem., 2014, 86, 4668–4674.
53. M. Hadioui, V. Merdzan and K. J. Wilkinson, Environ. Sci. Technol., 2015, 49, 6141–6148.
54. M. Mattarozzi, M. Suman, C. Cascio, D. Calestani, S. Weigel, A. Undas and R. Peters, Anal. Bioanal. Chem., 2017, 409, 63–80.
55. I. L. Gunsolus, M. P. S. Mousavi, K. Hussein, P. Buhlmann and C. L. Haynes, Environ. Sci. Technol., 2015, 49, 8078–8086.
56. J. Vidmar, T. Buerki-Thurnherr and K. Loeschner, J. Anal. At. Spectrom., 2018, 33, 752–761.
57. R. Peters, Z. Herrera-Rivera, A. Undas, M. van der Lee, H. Marvin, H. Bouwmeester and S. Weigel, J. Anal. At. Spectrom., 2015, 30, 1274–1285.
58. B. Ramkorun-Schmidt, S. A. Pergantis, D. Esteban-Fernández, N. Jakubowski and D. Günther, Anal. Chem., 2015, 87, 8687–8694.
59. L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2017, 32, 548–561.
60. A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Anal. Chem., 2018, 90, 11847–11855.
61. S. Naasz, S. Weigel, O. Borovinskaya, A. Serva, C. Cascio, A. K. Undas, F. C. Simeone, H. J. P. Marvin and R. J. B. Peters, J. Anal. At. Spectrom., 2018, 33, 835–845.
62. S. Gschwind, H. Hagendorfer, D. A. Frick and D. Günther, Anal. Chem., 2013, 85, 5875–5883.
63. J. Koch, L. Flamigni, S. Gschwind, S. Allner, H. Longerich and D. Günther, J. Anal. At. Spectrom., 2013, 28, 1707–1717.
64. H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Anal. Chem., 2011, 83, 9361–9369.
65. A. R. Poda, A. J. Bednar, A. J. Kennedy, A. Harmon, M. Hull, D. M. Mitrano, J. F. Ranville and J. Steevens, J. Chromatogr. A, 2011, 1218, 4219–4225.
66. J. Tuoriniemi, G. Cornelis and M. Hassellov, Anal. Chem., 2012, 84, 3965–3972.
67. D. Mehn, F. Caputo, M. Rosslein, L. Calzolai, F. Saint-Antonin, T. Courant, P. Wick and D. Gilliland, RSC Adv., 2017, 7, 27747–27754.
68. K.-S. Ho, W.-W. Lee and W.-T. Chan, J. Anal. At. Spectrom., 2015, 30, 2066–2073.
69. K. Niemax, Spectrochim. Acta, Part B, 2012, 76, 65–69.
70. M. A. Vaughan and G. Horlick, Spectrochim. Acta, Part B, 1990, 45, 1289–1299.
71. I. I. Stewart and J. W. Olesik, J. Anal. At. Spectrom., 1998, 13, 1249–1256.
72. A. Canals, V. Hernandis, J. L. Todoli and R. F. Browner, Spectrochim. Acta, Part B, 1995, 50, 305–321.
73. J. L. Todoli and J. M. Mermet, J. Anal. At. Spectrom., 1998, 13, 727–734.
74. I. I. Stewart and J. W. Olesik, J. Anal. At. Spectrom., 1998, 13, 1313–1320.
75. E. H. Chang, J. B. Harford, M. A. W. Eaton, P. M. Boisseau, A. Dube, R. Hayeshi, H. Swai and D. S. Lee, Biochem. Biophys. Res. Commun., 2015, 468, 511–517.
76. L. Zhang, F. X. Gu, J. M. Chan, A. Z. Wang, R. S. Langer and O. C. Farokhzad, Clin. Pharmacol. Ther., 2008, 83, 761–769.
77. K. Savolainen, H. Alenius, H. Norppa, L. Pylkkänen, T. Tuomi and G. Kasper, Toxicology, 2010, 269, 92–104.
78. M. A. Maurer-Jones, I. L. Gunsolus, C. J. Murphy and C. L. Haynes, Anal. Chem., 2013, 85, 3036–3049.
79. A. Malysheva, E. Lombi and N. H. Voelcker, Nat. Nanotechnol., 2015, 10, 835–844.
80. S. V. Jenkins, H. O. Qu, T. Mudalige, T. M. Ingle, R. R. Wang, F. Wang, P. C. Howard, J. Y. Chen and Y. B. Zhang, Biomaterials, 2015, 51, 226–237.
81. K. Loeschner, C. F. Harrington, J. L. Kearney, D. J. Langton and E. H. Larsen, Anal. Bioanal. Chem., 2015, 407, 4541–4554.
82. C. Zhang, Z. Y. Zhang, B. B. Yu, J. J. Shi and X. R. Zhang, Anal. Chem., 2002, 74, 96–99.
83. K.-S. Ho, K.-O. Lui, K.-H. Lee and W.-T. Chan, Spectrochim. Acta, Part B, 2013, 89, 30–39.
84. W.-W. Lee and W.-T. Chan, J. Anal. At. Spectrom., 2015, 30, 1245–1254.
85. G. C. Y. Chan, Z. L. Zhu and G. M. Hieftje, Spectrochim. Acta, Part B, 2012, 76, 87–95.
86. G. C. Y. Chan and G. M. Hieftje, Spectrochim. Acta, Part B, 2016, 121, 55–66.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ja00397a

‡ These authors contributed equally.

---