Open Access Article
Open Access ArticleProbing the structure of giant fullerenes by high resolution trapped ion mobility spectrometry†
Patrick
Weis
 *a,
Frank
Hennrich
b,
Regina
Fischer
a,
Erik K.
Schneider
a,
Marco
Neumaier
b and
Manfred M.
Kappes
*ab
*a,
Frank
Hennrich
b,
Regina
Fischer
a,
Erik K.
Schneider
a,
Marco
Neumaier
b and
Manfred M.
Kappes
*ab
aInstitute of Physical Chemistry, Karlsruhe Institute of Technology (KIT), P.O. Box 6980, 76049 Karlsruhe, Germany. E-mail: patrick.weis@kit.edu
bInstitute of Nanotechnology, Karlsruhe Institute of Technology (KIT), P.O. Box 3640, 76021 Karlsruhe, Germany
First published on 20th August 2019
Abstract
We present high-resolution trapped ion mobility spectrometry (TIMS) measurements for fullerene ions in molecular nitrogen. Three different charge states were studied (monocations, monoanions and dianions) with fullerenes ranging in size from C60 to C150. Ions were prepared by either electrospray ionization (ESI, for mono- and dianions) or by atmospheric pressure chemical ionization (APCI, for monocations) of a preformed fullerene soot extract solution. We demonstrate that TIMS allows to identify (and separate) constituent isomers in favorable cases. Using DFT calculations based on known condensed phase structures and trajectory method (TM) calculations we can reproduce the experimental TIMSCCSN2 for fullerenes up to C108 to within 0.5%. Using candidate structures based on quantum chemical predictions, we have also obtained structural information for fullerenes C110–C150 – a size range not previously accessed in condensed phase studies. We find that soluble fullerenes in this size have near-spherical rather than tubular structures. While the TM programs presently available for CCS modelling do a remarkably good job at describing the ion mobility of high (and even giant) fullerenes we observe a slight but systematic size-dependent deviation between TIMSCCSN2 values and our best computational fits which may reflect systematic bonding changes as the cage size increases.
1. Introduction
The fullerene field dates back to a pioneering molecular beam photoionization mass spectrometry study of carbon clusters generated by laser vaporization. This demonstrated that 60 atom carbon clusters were significantly more abundant than other nearby cluster sizes1 which was rationalized in terms of the particular stability of the now well-known icosahedral symmetry carbon cage structure. C60(Ih) comprises twenty hexagons and twelve isolated pentagons as was subsequently confirmed by preparing and structurally characterizing the molecule in bulk quantities. This is done in three steps: (i) fullerene containing carbon soot is generated by graphite electric arc discharge in argon (“Krätschmer–Huffman” method), (ii) fullerene cages are extracted from this soot by solvent treatment and (iii) specific cages are separated from the extracts by column chromatography.2 Apart from the dominant C60(Ih), C70 as well other “higher” fullerenes can be isolated that way. Higher fullerenes such as C76, C78, C80, C84 (and beyond) are present in the soot extracts in smaller amounts which decrease roughly monotonically with increasing cage size – reflecting low abundances in the raw material and poorer solubility.Molecular structures of chromatographically isolated higher fullerenes have typically been determined by NMR and/or X-ray crystallography. All turn out to have “conventional” structures characterized by isolated pentagon ring (IPR) motifs. Often several isomeric forms of a given cage size are found to be present – also reflecting the kinetics of fullerene growth by graphite arc discharge.3–7 It has been shown mathematically that the number of possible IPR cages for a given conventional fullerene nuclearity increases rapidly with cage size from 1 at C60 to 335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569 for C150. Therefore, in structurally characterizing ever larger solvent extractable fullerenes, the abundance problems already alluded to are also compounded by an increasing number of structurally distinct coexisting isomers that may no longer be separable. As a consequence, NMR spectra eventually become too congested for structure determination. For related reasons, pristine fullerene single crystals suitable for X-ray crystallography can no longer be obtained. As a result, even though mass spectrometry indicates that much larger IPR cages (“giant” fullerenes ranging in size to above C150) are present in Krätschmer–Huffman fullerene soot extracts, structure determination was not feasible for fullerenes much beyond C88.8,9 More recently, it has been shown that adding dopants such as Sc or Sm2O3 to the graphite rods used for arc discharge can shift this limit up a little thus accessing sufficient amounts of C9010 and C9611 for X-ray crystallography. However, C96 presently remains the largest pristine “conventional” fullerene which has been structurally characterized in condensed phase.
569 for C150. Therefore, in structurally characterizing ever larger solvent extractable fullerenes, the abundance problems already alluded to are also compounded by an increasing number of structurally distinct coexisting isomers that may no longer be separable. As a consequence, NMR spectra eventually become too congested for structure determination. For related reasons, pristine fullerene single crystals suitable for X-ray crystallography can no longer be obtained. As a result, even though mass spectrometry indicates that much larger IPR cages (“giant” fullerenes ranging in size to above C150) are present in Krätschmer–Huffman fullerene soot extracts, structure determination was not feasible for fullerenes much beyond C88.8,9 More recently, it has been shown that adding dopants such as Sc or Sm2O3 to the graphite rods used for arc discharge can shift this limit up a little thus accessing sufficient amounts of C9010 and C9611 for X-ray crystallography. However, C96 presently remains the largest pristine “conventional” fullerene which has been structurally characterized in condensed phase.
An alternative approach which has been developed to address the problem of giant fullerenes is the functionalization of HPLC-separated fractions of higher fullerenes by chlorination or trifluoromethylation. This method has proven to be quite powerful and it has been possible to identify and structurally characterize specific IPR isomers for a large number of fullerene cage sizes ranging up to C108.12–26 A drawback is however that such giant fullerene isomers can only be identified if they are functionalized in a well-defined way and if the corresponding derivatives can be crystallized. Furthermore, the reaction conditions for fullerene derivatization are often quite harsh and may be associated with isomerization and/or fragmentation. Consequently, it is unclear how the isomer distributions of empty cages contained in the soot extracts map onto those of the derivatives. Even when disregarding these issues, there are presently no structure determinations of extractable fullerenes beyond C108.
Over the years, ion mobility spectrometry (IMS) coupled with mass spectrometric detection has played a key role as a tool to gain structural information on fullerenes. Soon after the first molecular beam study of fullerenes in gas phase and following the structural characterization of C60(Ih) in condensed phase, von Helden et al. used IMS-MS to confirm that the 60-atom carbon cluster species formed by laser vaporization of graphite in helium has the same closed shell structure – to within experimental error.27 Subsequently, both the Bowers and Jarrold groups applied IMS to show that sufficiently large carbon rings can be annealed into carbon cages thus shedding light onto their growth mechanism.28,29
In IMS, the mobility of an ion is typically measured in an inert collision gas. Its magnitude can be related to the orientationally averaged collision cross section (CCS), which in turn can be related to the molecular structure of the ionic species in question. There are several ways to do this. In the early-day IMS studies alluded to above, experimental cross sections were compared to predicted cross sections obtained by applying the projection approximation (PA)30 to model structures from quantum chemical calculations. PA ignores the details of the fullerene-ion bath gas interaction (beyond the assumption of element-specific hard sphere radii). Nevertheless, PA (coupled with achievable mobility resolution) was accurate enough to allow differentiation of fullerene cages from rings or chains having the same mass-to-charge ratio. This was especially the case since the corresponding studies were conducted in helium – for which the attractive interaction with the drifting ion is small due to the small polarizability of the collision gas. Nevertheless, this interaction is not negligible, as was shown by comparing the mobilities of C60n+ and C70n+versus (positive) charge for n = 1–4: the mobilities grow less than linearly with charge, implying that the interaction potential is more complicated than simple hard sphere.30 More accurate modelling of the experimental CCS can be achieved, e.g., by using a Lennard-Jones (LJ) type potential to describe the fullerene – bath gas interaction. Correspondingly, Wyttenbach et al. measured the temperature dependence of the C60+ mobility in helium and extracted the LJ-parameters for the C–He interaction based on the accurately known molecular structure.31 Using analogous experimental data Mesleh et al. developed the trajectory method,32 in which the (fullerene) ion-bath gas interaction is described by a sum of LJ-type interactions between each atom of the drifting molecular ion and the bath gas (helium) atom. Using this interaction potential (and a structural model of the ion), a series of trajectories are run for randomly oriented ions and the resulting scattering angle distribution is then calculated. Finally, the predicted CCS of the structural model is obtained from the scattering angle distribution by averaging the collision integral. This number is then compared with the experimental value.
Apart from C60, larger carbon clusters ranging in size up to C240 formed upon laser vaporization of graphite in a continuous flow of helium have also been investigated by IMS and results interpreted in terms of closed shell fullerene cage structures.32 Recently Misaizu et al.33 have used IMS to study even larger carbon clusters formed in this way. They showed that apart from single-shelled cages, double-shelled fullerene onion cages begin to be observed starting at roughly C260+. With the availability of bulk quantities of C60 and C70, laser vaporization of fullerene films instead of graphite has opened up another way to create giant carbon clusters in gas phase. C120−, C130−, and C140− have been made with this method and investigated by high-resolution IMS.34 In all cases two isomer families were observed that have been assigned to: “dumbbell” –like [2+2]cycloadducts of (two) C60 and/or C70 cages or giant closed-single-shell fullerenes, respectively. By comparison with quantum-chemically optimized structures, the authors concluded that the giant closed-shell fullerenes formed by high energy laser vaporization/desorption of preformed C60 have preferentially spherical instead of elongated tubular geometries (and that trajectory calculations are necessary to assign the structures correctly).35 In a related IMS study, it was shown that all-carbon coalescence products formed upon laser vaporization of C60O have closer to spherical than tubular structures up to cluster sizes in excess of C240+.36
In all previous IMS studies of carbon clusters in the high (and giant) fullerene size range, the corresponding ions were created in gas phase either by laser vaporization of graphite or of preformed C60/C70. It is unclear whether these high energy, laser-assisted production methods yield the same (fullerene) isomer distributions as are obtained in bulk-scale fullerene synthesis by carbon arc discharge. Such comparisons would require an ion mobility resolution sufficient to resolve individual isomers of a given cage size. Previous IMS studies of large carbon clusters have generally been performed at insufficient resolutions, CCS/ΔCCS, on the order of 30–50. While the Jarrold group in fact pioneered high resolution drift tube IMS and achieved mobility resolutions in excess of 150 in helium, they did not systematically apply their method to this problem (other than to the fullerene dimer study already alluded to above). Meanwhile, there has been a breakthrough in high resolution analytical IMS-MS based on the development of a novel IMS platform: the trapped ion mobility spectrometry (TIMS) method routinely allows for mobility resolutions in excess of 200 in molecular nitrogen collision gas.37 TIMS has recently been commercialized and adapted to various ion sources (including electrospray ionization) as well as to high repetition rate time of flight mass spectrometry. This makes systematic high resolution ion mobility measurements of the components of graphite arc fullerene soot extracts feasible.38 This is the focus of our study in which we explore the structure of such fullerene cages ranging in size from C60 up to C150, which we study in up to three different charge states for a common nuclearity: C2n+, C2n− and C2n2−. For this we use two different (soft) ionisation techniques: electrospray ionisation (ESI) for singly and doubly charged fullerene anions and atmospheric pressure chemical ionisation (APCI) for singly charged fullerene cations. The high trapped ion mobility spectrometry resolution allows us to differentiate between isomers of a given cage size on the basis of their collision cross sections in selected cases. Our measurements are performed in molecular nitrogen instead of helium. This makes the comparison with theory somewhat more challenging (due to the higher polarizability of nitrogen, which leads to an increased attractive interaction with the drifting ion) but offers the opportunity to investigate and improve the CCS modeling procedure by using known structures of the smaller fullerenes (C60, C70, C76,…) as calibrants. On the basis of this calibration procedure we clearly establish that the giant fullerene components of our fullerene extracts consist of near spherical rather than tubular structures.
2. Methods
2.1 Substances and instrumental methods
The mixed fullerene sample used for most of the experiments reported here has been obtained by extraction of pure carbon and lanthanum oxide doped carbon arc-discharge soots with dichlorobenzene.39 It has been column chromatographically enriched in higher fullerenes and contains predominantly C84, but also minor amounts of smaller and larger fullerenes as well as some lanthanum containing endohedral metallofullerenes. It has been stored as a solution in dichlorobenzene for several years prior to this study (without taking particular precautions to exclude, light, oxygen or water). In the following we call this sample “fullerene mix”. Samples of C78 isomers were enriched and separated from the fullerene mix using a two step preparative scale HPLC procedure. First a Cosmosil Buckyprep column (Nacalai Tesque, toluene as mobile phase) was used to fractionate C78 isomers from other high fullerenes (similar to the process reported in ref. 5). In a second HPLC step, the C78 fraction was further separated into constituent isomers by using a Wakosil II 5C18 AR HPLC column (Wako Chemicals, toluene/acetonitrile as mobile phase) similar to the procedure of Kikuchi et al.40 Specifically, we have prepared two different C78 samples enriched in primarily C78(1) (D3) and primarily C78(2) (C2v), respectively. Mass spectra were obtained with an LTQ orbitrap XL and a Bruker timsTOF mass spectrometer. Ion mobility measurements were performed in nitrogen with a Bruker timsTOF mass spectrometer with an electrospray ionisation (ESI) source for the anionic fullerenes and an atmospheric pressure chemical ionisation (APCI) source for the cations. For ESI, the fullerene mix (see above) solution in dichlorobenzene was diluted with toluene (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) and a small amount (ca. 1 part in 10
10) and a small amount (ca. 1 part in 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 parts toluene) of tetrakis(dimethylamino)ethylene (TDAE (Sigma)) was added to the solution as reducing agent. The ESI source was operated in negative mode, with a spray voltage of typically 3.5 kV and a flow rate of 3 μl min−1. For APCI the fullerene mix was diluted (1
000 parts toluene) of tetrakis(dimethylamino)ethylene (TDAE (Sigma)) was added to the solution as reducing agent. The ESI source was operated in negative mode, with a spray voltage of typically 3.5 kV and a flow rate of 3 μl min−1. For APCI the fullerene mix was diluted (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) with toluene/acetonitrile. The source was operated with an ionisation current of 5000 nA and a flow rate of typically 10 μl min−1. The mobilograms were recorded in the high-resolution mode (“custom”) with the longest feasible ramp time (500 ms) and a 1/K0 interval width of typically 0.05 V s cm−2 (in some cases 0.1 or 0.03 V s cm−2). Note, that the resolution increases with the ratio of ramp time to interval width.37 Under these conditions, the resolving power of the timsTOF (determined as CCS/ΔCCS) was typically above 200 in the CCS range of 200 Å2 and 250 in the CCS range of 300 Å2. (Note that the resolving power of a TIMS instrument increases with CCS). A TIMS measurement requires calibration with reference ions of known CCS. We used the low concentration ESI tunemix (Agilent) and the APCI tunemix (Agilent) which is a mixture of phosphazene derivatives with cross sections determined in both negative and positive mode by Stow et al.41 For each measurement run a calibration run was recorded simultaneously (under identical conditions, i.e. identical RF-voltages, ramp speed and width, tunnel pressure and temperature). This procedure results in highly reproducible (within 0.5%, see below) CCS values.
5) with toluene/acetonitrile. The source was operated with an ionisation current of 5000 nA and a flow rate of typically 10 μl min−1. The mobilograms were recorded in the high-resolution mode (“custom”) with the longest feasible ramp time (500 ms) and a 1/K0 interval width of typically 0.05 V s cm−2 (in some cases 0.1 or 0.03 V s cm−2). Note, that the resolution increases with the ratio of ramp time to interval width.37 Under these conditions, the resolving power of the timsTOF (determined as CCS/ΔCCS) was typically above 200 in the CCS range of 200 Å2 and 250 in the CCS range of 300 Å2. (Note that the resolving power of a TIMS instrument increases with CCS). A TIMS measurement requires calibration with reference ions of known CCS. We used the low concentration ESI tunemix (Agilent) and the APCI tunemix (Agilent) which is a mixture of phosphazene derivatives with cross sections determined in both negative and positive mode by Stow et al.41 For each measurement run a calibration run was recorded simultaneously (under identical conditions, i.e. identical RF-voltages, ramp speed and width, tunnel pressure and temperature). This procedure results in highly reproducible (within 0.5%, see below) CCS values.
2.2 Computational methods
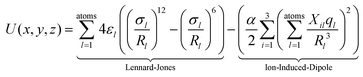
In order to confirm or rule out the presence of specific fullerene isomers in the essentially fragmentation free ion beams resulting from the fullerene mix (and thus to check for their presence in the soot extracts themselves), experimental CCS values were compared with computationally determined cross sections. The corresponding starting geometries (for neutral fullerenes) were obtained as xyz-files with the FULLFUN42–44 software. Beginning with these neutral starting structures, all (di)anion and cation geometries were fully optimized, i.e. without any symmetry restrictions, using the density functional method (DFT) with the BP-86 functional45,46 and the def-SV(P) basis set47 as implemented in the TURBOMOLE48 package. Unless otherwise noted we used the Mulliken population analysis to assign partial charges on each atom. Compared to the starting neutral geometries, the structures of the optimized ions differ only slightly. Therefore we characterize them with the Schoenflies symbol of the corresponding neutral species, and (since that is not distinct for the larger fullerenes) with the isomer numbers assigned to them according to the ring spiral algorithm.49The optimized ion geometries and partial charges (see ESI†) formed the basis of systematic trajectory method (TM) calculations as implemented in the IMoS 1.09 package.50,51 We also obtained very similar results with the TM method as implemented in the Mobcal32,52,53 and Collidoscope54 programs, see ESI.† The interaction of a fullerene ion with the nitrogen buffer gas is modeled with a Lennard-Jones (LJ)-type interaction plus ion-induced dipole potential
 | (1) |
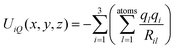 | (2) |
3. Results and discussion
3.1 Mass spectra and TIMS measurements
Mass spectra of the fullerene mix (ESI, negative mode, APCI, positive mode) were obtained with either an Orbitrap LTQ XL (Thermo Scientific) or with the Bruker timsTOF used for the IMS studies reported here. Typical measurements at mass resolutions of respectively 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 20
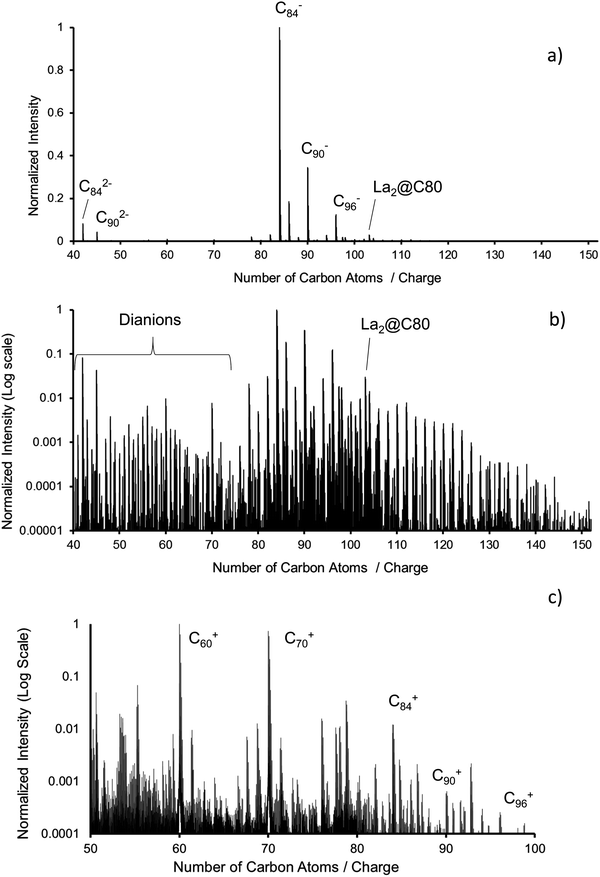
000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for Orbitrap and timsTOF can be found in Fig. 1. Fig. 1a shows ESI mass spectra in negative ion mode obtained with the Orbitrap. The dominant peaks are C84−, C86−, C90− and C96− as well as their dianions. Fig. 1b shows the same spectrum on a logarithmic scale. Higher fullerenes up to C150 can be found with very small but clearly detectable intensities. Note the presence of small but significant amounts of La2C80. The main impurities are oxidation products such as fullerene oxides and hydroxides. Fig. 1c shows the cations as measured using an APCI source with the Bruker timsTOF.
000 for Orbitrap and timsTOF can be found in Fig. 1. Fig. 1a shows ESI mass spectra in negative ion mode obtained with the Orbitrap. The dominant peaks are C84−, C86−, C90− and C96− as well as their dianions. Fig. 1b shows the same spectrum on a logarithmic scale. Higher fullerenes up to C150 can be found with very small but clearly detectable intensities. Note the presence of small but significant amounts of La2C80. The main impurities are oxidation products such as fullerene oxides and hydroxides. Fig. 1c shows the cations as measured using an APCI source with the Bruker timsTOF.
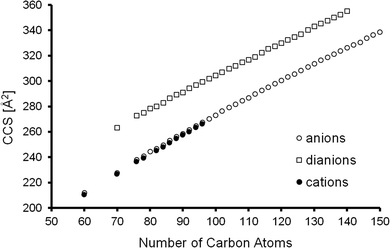
We measured collision cross sections in nitrogen at T = 300 K, for all anionic fullerenes, C2n−, in the range between C60− and C150− (except for C62–C68, C72, and C74 which are either not formed by arc discharge, not extractable from the corresponding fullerene soots with dichlorobenzene or not ionizable by ESI/APCI under the conditions used) as well as for all of the respective dianions, C2n2−, up to C1402−, see Table 1 and Fig. 2. Consistent with previous literature, we could not observe C602− (even when using a pure C60-solution and TDAE in toluene instead of the fullerene mix). It is known that room temperature C602− is not stable with respect to electron loss and decays into C60− on a millisecond time scale.57 Anionic and dianionic signal levels were sufficiently stable and reproducible to allow a rough determination of intensity ratios as a function of cage size. The relative dianion intensity increases dramatically by more than two orders of magnitude from C70 to C142 (see ESI,† Fig. S1), which is in line with previous measurements58 and can be rationalized by the increase of the second electron affinity with the number of carbon atoms (0.02 eV for C70, 0.325 eV for C76, 0.615 eV for C84(D2d)).59,60 Interestingly, we do not observe any triply negatively charged ions. If present after ESI, room temperature thermal activation is sufficient to deplete any such species prior to detection.
| Charge state | Charge state | |||||
|---|---|---|---|---|---|---|
| −1 | −2 | +1 | −1 | −2 | ||
| C60 | 211.8 | 210.0 | C112 | 289.7 | 319.1 | |
| C70 | 227.7 | 263.1 | 226.6 | C114 | 292.6 | 322.4 |
| C76 | 238.1 | 272.6 | 236.2 | C116 | 295.2 | 325.3 |
| C78 | 240.9 | 275.2 | 239.2 | C118 | 297.9 | 327.5 |
| C80 | 244.6 | 278.3 | C120 | 300.7 | 329.9 | |
| C82 | 246.7 | 280.0 | 245.2 | C122 | 303.1 | 332.4 |
| C84 | 249.4 | 282.8 | 247.9 | C124 | 305.5 | 334.7 |
| C86 | 253.1 | 286.3 | 251.1 | C126 | 308.3 | 337.0 |
| C88 | 256.2 | 289.1 | 254.5 | C128 | 311.1 | 340.4 |
| C90 | 258.6 | 291.0 | 257.3 | C130 | 313.7 | 342.8 |
| C92 | 261.7 | 294.2 | 260.1 | C132 | 316.4 | 345.2 |
| C94 | 264.6 | 296.9 | 263.3 | C134 | 318.8 | 347.7 |
| C96 | 267.2 | 299.3 | 266.0 | C136 | 321.1 | 349.9 |
| C98 | 270.3 | 301.9 | C138 | 323.7 | 352.5 | |
| C100 | 273.0 | 304.2 | C140 | 326.2 | 354.9 | |
| C102 | 276.3 | 307.0 | C142 | 328.5 | ||
| C104 | 278.9 | 309.5 | C144 | 330.5 | ||
| C106 | 281.7 | 312.0 | C146 | 333.8 | ||
| C108 | 284.5 | 314.6 | C148 | 336.1 | ||
| C110 | 287.0 | 316.8 | C150 | 338.7 | ||
The cations were ionized by APCI (from a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 solution in dichlorobenzene, toluene, acetonitrile). In this case the largest fullerene cation for which we could determine a CCS value was C96+, due to a poorer signal-to-noise level compared to the ESI ionized (di)anions (from the same fullerene mix). The respective CCS values determined by timsTOF in nitrogen for fullerene cations, anions, and dianions are summarized in Table 1 and Fig. 2.
5 solution in dichlorobenzene, toluene, acetonitrile). In this case the largest fullerene cation for which we could determine a CCS value was C96+, due to a poorer signal-to-noise level compared to the ESI ionized (di)anions (from the same fullerene mix). The respective CCS values determined by timsTOF in nitrogen for fullerene cations, anions, and dianions are summarized in Table 1 and Fig. 2.
As can be seen from Fig. 2 the experimental CCS values of fullerene cations and anions with the same number of atoms agree to within ca. 1% – with the cations being slightly smaller. The dianions on the other hand were found to have CCS values that are 10–15% larger than those of the corresponding monoanions. The results are summarized in Table 1. The standard deviation of the mean value (based on at least 3 measurements) was below 1 Å2 or 0.5% in all cases. Since we always measured a series of fullerenes in one run, under identical conditions (pressure, temperature, RF-voltages in the tunnel, IMS-ramp speed) the relative error, i.e. the uncertainty of the CCS ratio of C60 and C70 for example, was even smaller and typically below 0.3% (see Fig. 3). For C60+ and C70+ Bush et al. have determined CCS values of 213.1 Å2, and 231.4 Å2,53 respectively, within 2% of the results obtained here (note that the data of ref. 53 were recorded with a drift tube IMS instrument; a cross-platform deviation of 2% is typical for IMS studies).
 | ||
| Fig. 3 Typical mobilograms of C60− and C70− recorded in the same measurement runs on three different days. Identical colors indicate identical runs. Within the same run, peak maxima can be determined to a relative accuracy of significantly better than 0.5%.38 | ||
3.2 Modelling CCS values
We model the experimental data using DFT calculations of molecular structures (as well as their charge distributions) and trajectory method simulations of collision integrals with three goals in mind.(i) Examination and improvement of the trajectory method modelling procedure. The experimental data set comprises CCS values also for fullerenes which are well-known from condensed phase studies. Fullerenes up to C96 have been structurally characterized in neutral form and their structures can be used as the basis for high-accuracy DFT calculations of the corresponding ions. In addition, we have determined CCS values for multiple charge states including also fullerene dianions which have not been previously characterized by IMS. Finally, CCS values have been obtained at a significantly higher resolution than previously available (where applicable). As a result an unparalleled reference data set is available with which to check and improve trajectory method modelling procedures for TIMSCCSN2 values.
(ii) Isomer resolution and fractionation. Starting at C76, conventional fullerene cages can have multiple IPR isomers. The number of IPR isomers increases with cage size and multiple IPR isomers of a given cage size have in fact been chromatographically separated in condensed phase (demonstrating that multiple energetically close-lying structures may coexist in appreciable relative amounts in fullerene soots). It seems interesting to establish whether the improved ion mobility resolution associated with timsTOF is sufficient to rapidly resolve or even fractionate these (and other previously unknown) isomers.
(iii) Global structure assignment of giant fullerenes. Beyond the size range for which there are condensed phase structure determinations, CCS values have been obtained with a high enough resolution to allow for a rough structural assignment based on improved modelling procedures.
We begin by assuming that the characteristic neutral isomer distributions present for all cage sizes in the starting fullerene mix solution is mapped onto the three different isolated charge states without significant relative abundance perturbations (e.g., due to isomer-specific differences in ionization and volatilization efficiencies). Then, in order to compare the experimental CCS values with theory for the respective fullerene ions we have performed geometry optimizations at the DFT level with the TURBOMOLE package without symmetry restrictions for charge states +1, −1 and −2 (based on the neutral fullerene starting geometries). In each case we have assigned partial charges to the optimized geometries via a Mulliken population analysis. Finally, we have performed trajectory calculations using the IMoS1.09 package. A crucial point is the parameter choice for these simulations: we always set the temperature to 299 K, since this was the temperature at which the tunemix CCS values used in the calibration procedure were measured (to within 1 K this was also the temperature of our TIMS tunnel). The carbon Lennard-Jones parameters used corresponded to the default values implemented in IMoS, i.e. ρ = 3.5 Å and ε = 4.65 meV, unless otherwise noted. These parameters are based on a least squares fit of calculated and measured CCS values for a set of 16 small molecules55 including the C60+ and C70+ CCS values previously determined by Bush et al.53
| Method 1 | Method 2 | Method 3 | Method 4 | Method 5 | Exp. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| IMoS, Mullik. w/o ion quad. αN2 = 1.74 Å3, ρ = 3.5 Å, ε = 4.65 meV | IMoS, Mullik. w/o ion quad. αN2 = 0 Å3, ρ = 3.5 Å, ε = 4.65 meV | IMoS, Mullik. with ion quad. αN2 = 1.74 Å3, ρ = 3.22 Å, ε = 3.57 meV | IMoS, Mullik. with ion quad. αN2 = 2.00 Å3, ρ = 3.145 Å, ε = 3.57 meV | Method 1 with charge-dependent scaling factors: anions: 0.9815, cations: 0.9743, dianions: 1.0057 | |||||||
| CCS [Å2] | χ [%] | CCS [Å2] | χ [%] | CCS [Å2] | χ [%] | CCS [Å2] | χ [%] | CCS [Å2] | χ [%] | TIMSCCSN2 [Å2] | |
| C60− | 214.8 | 1.4 | 203.9 | −3.7 | 216.1 | 2.0 | 210.9 | −0.4 | 210.8 | −0.5 | 211.8 |
| C70− | 232.0 | 1.9 | 222.3 | −2.4 | 233.0 | 2.3 | 227.0 | −0.3 | 227.7 | 0.0 | 227.7 |
| C76− | 242.3 | 1.8 | 233.5 | −1.9 | 244.0 | 2.5 | 237.9 | −0.1 | 237.8 | −0.1 | 238.1 |
| C84− | 254.1 | 1.9 | 245.7 | −1.5 | 255.4 | 2.4 | 249.1 | −0.1 | 249.4 | 0.0 | 249.4 |
| C96− | 273.9 | 2.5 | 266.5 | −0.2 | 274.7 | 2.8 | 267.5 | 0.1 | 268.8 | 0.6 | 267.2 |
| C702− | 261.8 | −0.5 | 222.5 | −15.4 | 265.3 | 0.9 | 265.0 | 0.7 | 263.3 | 0.1 | 263.1 |
| C762− | 270.7 | −0.7 | 233.6 | −14.3 | 274.8 | 0.8 | 273.9 | 0.5 | 272.3 | −0.1 | 272.6 |
| C842− | 281.0 | −0.6 | 245.8 | −13.1 | 284.4 | 0.6 | 282.8 | 0.0 | 282.6 | −0.1 | 282.8 |
| C962− | 297.9 | −0.5 | 266.6 | −10.9 | 300.3 | 0.4 | 297.4 | −0.6 | 299.6 | 0.1 | 299.3 |
| C60+ | 214.6 | 2.2 | 203.8 | −2.9 | 215.3 | 2.5 | 210.1 | 0.1 | 209.1 | −0.4 | 210.0 |
| C70+ | 231.9 | 2.4 | 222.1 | −2.0 | 233.1 | 2.9 | 227.0 | 0.2 | 226.0 | −0.3 | 226.6 |
| C76+ | 242.4 | 2.6 | 233.3 | −1.2 | 243.5 | 3.1 | 237.4 | 0.5 | 236.2 | 0.0 | 236.2 |
| C84+ | 254.2 | 2.6 | 245.6 | −0.9 | 254.5 | 2.7 | 248.3 | 0.2 | 247.7 | −0.1 | 247.9 |
| C96+ | 274.4 | 3.2 | 266.3 | 0.1 | 275.1 | 3.4 | 267.9 | 0.7 | 267.4 | 0.5 | 266.0 |
| Σχ2 | 53.8 | 772.8 | 74.6 | 2.2 | 1.2 | ||||||
Method 1 uses the default Lennard-Jones parameters and incorporates interactions of Mulliken charges with polarizable N2 (using the IMoS standard average static dipole polarizability of molecular nitrogen of 1.74 Å3). It does not consider charge quadrupole interactions (cf.eqn (2) which is set to zero, i.e. qpol = 0 in IMoS). As can be seen, the agreement between experiment and calculation depends on the charge state. For the cations the calculations predict CCS values that are on average 2.5% larger than experiment, for the anions the deviation is slightly smaller, the predicted CCS values are around 2% larger than experiment. In both cases the deviation increases with fullerene size. Interestingly, the dianions fit much better: for them the calculations predict CCS values that are on average 0.6% smaller than the experimental values with no obvious trend. As a quality parameter we define the sum of the errors squared over all 14 test set ions (C602− cannot be studied, since it is not stable). For method 1 we obtain a score of 53.8. The overall agreement between experiment and calculation with this method is reasonable and within the ±2% interval usually accepted in ion mobility spectrometry, but well outside our experimental uncertainty of 0.5%. More alarming is the fact that the CCS deviations for different charge states show different trends with size. Next we look into the reasons for this (note that with the other TM programs available, Mobcal32,52,53 and Collidoscope54 we obtain similar scores, see ESI†).
The first question one might ask is why is there a 10–15% difference between experimental CCS values for equi-nuclear anions and dianions at all. This is clearly not a geometric effect, as can be easily seen for C84 as an example: The average diameters based on the DFT-optimized geometries of C84+, C84−, C842− are 8.450, 8.457, and 8.464 Å, respectively, i.e. basically the same (all geometries are optimized without symmetry restrictions using the D2-geometry as starting point). The 1 per mil diameter difference between anion and dianion translates into a 2 per mil difference in (geometrical) CCS. This is far smaller than the experimentally observed average difference of 13.3%. Obviously the charge – induced dipole interaction, the second term in eqn (1) is responsible for the observed CCS difference. In order to evaluate its influence on the CCS we performed test trajectory calculations with this interaction switched off by artificially setting the polarizability of N2 to 0. The results are also summarized in Table 2 as method 2. Now all cross sections come out to be too small (except C96+), especially for the dianions, for which basically the same CCS as for the anions is obtained. As a consequence, the mean square error (Σχ2) increases dramatically by more than a factor of 10 to yield a score of 772.8 for method 2. This underlines the importance of the charge-induced dipole interaction in the CCS trajectory calculation with nitrogen as bath gas (note that for helium the effect would be much smaller due to its 8.5 fold smaller polarizability).
The question that remains is why is the experimentally observed cross section increase of 10–15% between anions and dianions only partially reproduced in the calculations when using method 1? The calculations based on Mulliken charges, and the default Lennard-Jones parameters implemented in IMoS apparently systematically underestimate the CCS ratio for dianions and anions, for example: CCS(C842−)/CCS(C84−) = 1.106 (calc.) vs. 1.134 (exp.). A possible explanation lies in the quality of how the partial charges on each carbon atom are assigned. We used Mulliken population analysis, but several other methods such as the natural bond analysis scheme are feasible. However, it turns out that these schemes give basically the same CCS as Mulliken (see ESI,† Tables S2 and S3) and as a consequence we stick with the Mulliken population analysis.
Another reason for the observed difference could be the quadrupole moment of nitrogen that has not been included in trajectory calculations using methods 1 and 2. Besides Lennard-Jones and charge induced dipole interactions the next interaction of importance is ion–quadrupole. The quadrupole moment of nitrogen can be included in IMoS (option qpol = 1), this requires adjustment of the LJ parameters in IMoS, however. The default parameters implemented in IMoS for inclusion of the nitrogen quadrupole moment are ρ = 3.22 Å and ε = 3.57 meV. The corresponding CCS data are summarized in Table 2, method 3. Now all the CCS values calculated with this method turn out to be somewhat too large. Note however, that the predicted CCS ratio of dianions to anions is a little closer to the experimental value, for example CCS(C842−)/CCS(C84−) = 1.113 (calc.) vs. 1.134 (exp.). But the difference is still significant and the Σχ2-score is 74.6, worse than with method 1. Obviously, inclusion of the ion–quadrupole interaction alone does not solve the problem.
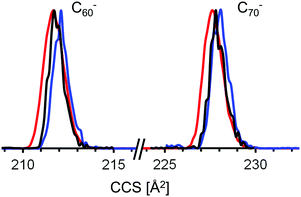
The key is the charge induced dipole interaction, which depends not only on the partial charge distribution of the ion but also on the polarizability of nitrogen, αN2. The calculated CCS ratio of dianions to anions strongly depends on αN2, a parameter which can be set in IMoS. If we increase the value of the average static dipole polarizability of molecular nitrogen in our trajectory calculations from its literature value62 of 1.74 Å3 to 2 Å3 it becomes possible to reproduce the experimental CCS(C842−)/CCS(C84−) ratio. The rationale for treating αN2 as an adjustable parameter in our trajectory calculations (instead of a constant) is the following: the dipole polarizability of N2 is anisotropic, but this anisotropy is neglected in IMoS (and in all other trajectory method programs such as Mobcal or Collidoscope). A small adjustment in the absolute value of αN2 might compensate for this. Unfortunately, the parameters are not completely decoupled: changing αN2 to 2 Å3 fixes the dianion/anion CCS-ratio problem, but the absolute CCS numbers are still off by a few percent. Therefore, in a second step we adjusted the carbon Lennard-Jones parameter ρ from its default value of 3.22 Å to 3.145 Å (while keeping ε at its default value of 3.57 meV) in order bring the calculated CCS of both C84− and C842− into agreement with the experimental CCS value (note, that the default value parameter is the result of a least squares fit to the experimental CCS of only 16 small, cationic molecules55). With these parameters (Mulliken charges, αN2 = 2 Å3, ρ = 3.145 Å, ε = 3.57 meV, with ion–quadrupole interaction on, i.e. qpol = 1), which we name method 4, we are able to reproduce the experimental CCS values of all 14 ions in our test set to within 0.3% on average with a maximum deviation of 0.7% (for C702− and C96+), see Table 2. We obtain a Σχ2-score of 2.2, much better than with the other methods. As a consequence we will use method 4 and its associated parameters in the following for global structure assignment of the giant fullerenes above C96. Note that when applying method 4 to the test set, the errors are smallest for the (mono)anions. The dianions show a somewhat larger variation and it seems that the calculation slightly overestimates the CCS values below C842− and underestimates those above. Therefore, we will focus in the following on the monoanions.
We note in closing this subsection, that an alternative, more pragmatic, but purely empirical procedure is to multiply the CCS values calculated with method 1 with a charge-specific scaling factor based on a least-squares fit to the experimental CCS for our C60–C96 test set. From such a fit we obtain three scaling factors: 0.9815 for the anions, 0.9743 for the cations, and 1.0057 for the dianions. If we scale the method 1-CCS values accordingly, the Σχ2-score (1.2) is of course even smaller than for method 4 but we have to accept three empirical factors. We include this procedure as method 5 in Table 2, but stick in the following with method 4, which can be better rationalized on a theoretical basis.
| Fullerene isomer | Reference (if experimentally confirmed) | Rel. energy (anion) | Calc. CCS | Dev. from exp.% | Exp. TIMSCCSN2 |
|---|---|---|---|---|---|
| C76(1) (D2) | 3 | 0 | 237.9 | −0.1 | 238.1 |
| C76(2) (Td) | 61 | 0.4 | 236.2 | −0.8 | |
| C78(1) (D3) | 4 | 0.50 | 240.8 | −0.5 | 240.9 |
| C78(2) (C2v) | 4 | 0.45 | 239.9 | −0.4 | |
| C78(3) (C2v) | 4 | 0.04 | 239.9 | −0.1 | |
| C80(1) (D5d) | 63 | 0.25 | 246.1 | 0.6 | 244.6 |
| C80(2) (D2) | 5 | 0.37 | 244.9 | 0.1 | |
| C80(5) (C2v) | 61 | 0 | 242.8 | −0.7 | |
| C80(7) (Ih) | 0.56 | 242.9 | −0.7 | ||
| C82(5) (C2) | 61 | 0 | 245.7 | −0.4 | 246.7 |
| C82(7) (C3v) | 4 | 0.46 | 246.5 | −0.1 | |
| C82(9) (C2v) | 4 | 0.06 | 245.9 | −0.3 | |
| C84(22) (D2) | 4 | 0 | 249.1 | −0.1 | 249.4 |
| C84(23) (D2d) | 4 | 0.02 | 248.7 | −0.2 | |
| C86(16) | 7, 12, 65 | 0.46 | 252.2 | −0.3 | 253.1 |
| C86(17) | 7, 12, 65 | 0 | 252.2 | −0.4 | |
| C88(7) | 7 | 0.13 | 257.2 | 0.4 | 256.2 |
| C88(33) | 7, 13 | 0.23 | 256.1 | 0.0 | |
| C88(17) | 7, 13 | 0 | 256.2 | 0.0 | |
| C90(1) | 10 | 1.28 | 264.9 | 2.5 | 258.6 |
| C90(45) | 66 (theory) | 0 | 258.6 | 0.0 | |
| C90(28) | 14 | 0.50 | 259.4 | 0.3 | |
| C90(30) | 14 | 0.40 | 259.0 | 0.2 | |
| C90(32) | 14 | 0.54 | 259.3 | 0.3 | |
| C90(34) | 14 | 1.15 | 259.6 | 0.4 | |
| C90(35) | 14 | 0.27 | 259.1 | 0.2 | |
| C90(46) | 14 | 0.21 | 257.8 | −0.3 | |
| C92(69) | 0 | 261.2 | −0.2 | 261.7 | |
| C92(82) | 13 | 0.20 | 260.8 | −0.3 | |
| C92(38) | 15 | 0.13 | 262.1 | 0.2 | |
| C94(34) | 17 | 0.13 | 265.7 | 0.4 | 264.6 |
| C94(42) | 17 | 0.18 | 265.9 | 0.5 | |
| C94(43) | 17 | 0 | 265.7 | 0.4 | |
| C94(61) | 17, 16 | 0.21 | 265.5 | 0.3 | |
| C94(133) | 17 | 0.14 | 264.7 | 0.0 | |
| C96(183) (D2) | 18 | 0 | 267.5 | 0.1 | 267.2 |
| C96(144) | 18 | 0.16 | 268.0 | 0.3 | |
| C96(145) | 18, 16 | 0.15 | 268.0 | 0.3 | |
| C96(176) | 18 | 0.32 | 267.4 | 0.1 | |
| C96(181) | 11 | 0.07 | 275.8 | 3.2 | |
| C96(3) | 11 | 1.71 | 282.9 | 5.9 | |
| C98(107) | 19 | 0.62 | 272.5 | 0.8 | 270.3 |
| C98(109) | 19 | 0.17 | 271.7 | 0.5 | |
| C98(116) | 26 | 0.30 | 271.3 | 0.4 | |
| C98(120) | 19 | 0 | 271.4 | 0.4 | |
| C98(248) | 26 | 0.06 | 271.1 | 0.3 | |
| C100(1) | 20 | 1.68 | 281.3 | 3.0 | 273.0 |
| C100(18) | 21 | 0.56 | 277.3 | 1.6 | |
| C100(425) | 21 | 0 | 273.4 | 0.1 | |
| C100(449) | 0.05 | 272.6 | −0.2 | ||
| C100(417) | 21 | 0.84 | 275.4 | 0.9 | |
| C102(603) | 22 | 0 | 277.2 | 0.3 | 276.3 |
| C104(234) | 23 | 0 | 280.8 | 0.7 | 278.9 |
| C104(811) | 23 | 0.43 | 280.3 | 0.5 | |
| C104(812) | 23 | 0.43 | 283.0 | 1.4 | |
| C106(1055) | 24 | 0 | 282.5 | 0.3 | 281.7 |
| C108(1771) | 24 | 0 | 286.4 | 0.7 | 284.5 |
 | ||
| Fig. 4 Comparison of calculated (with method 4, see text) and experimental TIMSCCSN2 for the fullerene monoanions shown in Table 3 and discussed in the text. These correspond to all cases for which cage structural information is presently available from condensed phase studies. The numbers correspond to the respective isomer according the ring spiral algorithm (see Table 3). Isomers with CCS that deviate by more than 0.5% from the experimental value can be ruled out. There appears to be a systematic trend from negative to positive deviations with increasing number of carbon atoms, which would imply that method 4 slightly overestimates CCS for smaller cages and underestimates for larger ones. Note however that the fullerene isomers identified crystallographically in condensed phase do not necessarily represent the isomer composition of our fullerene mix. | ||
 | ||
| Fig. 5 (a) Typical mobilograms for selected fullerene monoanions (scan parameters: ramp duration 500 ms, width 0.05 (1/K0)). (b) Mobilograms of HPLC selected C78-isomers (red D3-C78(1) and blue C2v-C78(2)) and of the isomer mixture present in our soot extract (black). The experimental CCS difference between the two isomers is highly reproducible: 0.7 Å2 with a standard deviation of 0.2 Å2. See Fig. S3 (ESI†) for a comparison of three individual runs. | ||
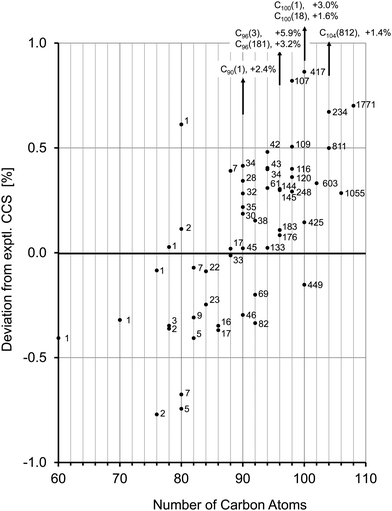
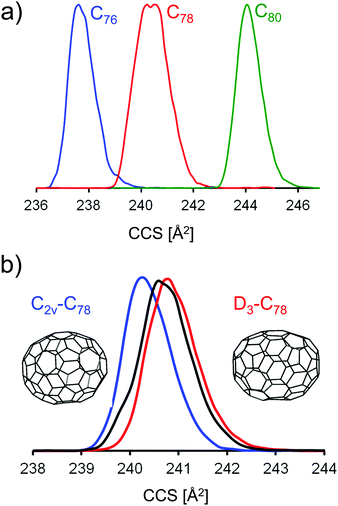
For C78− from the fullerene mix we observe a significantly larger peak width in the mobilogram, see Fig. 5a and Fig. S2 (ESI†). Unlike the position of the peak maximum, the peak width depends somewhat on the instrumental conditions, especially on the ion load (reflecting space charge effects). This effect can be minimized by reducing the accumulation time before the funnel. Nevertheless, widths can still vary a little from run to run. Overall though, the increased peak width for C78 compared to its neighbors C76 and C80 (see below) is highly reproducible. For C78 it is known that several isomers are present in the extract and can be separated by HPLC, namely C78(1) (D3), C78(2) (C2v) and C78(3) (C2v).4 Using literature procedures,40 we prepared fractions of C78(1) and C78(2) from our fullerene mix sample and injected the purified fractions into the timsTOF under identical conditions. Fig. 5b shows a typical run: the fraction containing C78(1) has a slightly larger CCS than C78(2). The difference depends somewhat on the conditions and varies in the range between 0.5 and 1 Å2. This is perfectly in line with the trajectory calculations which predict a difference of 1 Å2, with C78(1) having the larger CCS. This shows that under favorable conditions, TIMS can be used to identify and fractionate IPR fullerene isomers. Although still limited by its resolving power (further improvements may be possible by raising the ramp scan time), TIMS has two important advantages over HPLC: first, it is extremely fast, a TIMS run is performed in less than a second, even averaging over 100 individual runs requires less than a minute. Second, and more importantly, it is possible to directly connect an experimentally obtained CCS value to a DFT candidate structure, as outlined above. This is not possible with HPLC as the interactions between fullerenes and column material as well as fullerenes and solvent are much harder to describe than for fullerene ion/N2 interactions.
The mobilogram for C80 is as narrow as the C76-mobilogram (i.e. instrument limited). The experimental CCS value is 244.6 Å2. Seven IPR-isomers are known to exist for C80, i.e. have been isolated from arc-discharge soot extract, among them the D2 isomer C80(2) and the D5d isomer C80(1).5,63 Another isomer, C80(5) has been isolated directly from the soot with the same methods as used for C76(2),61 but it is insoluble in the solvents used here and therefore should not be present in the extract we have investigated. We calculated the CCS for these C80 isomers and compared them with the experimental value. The D2 isomer, C80(2), agrees with the measurement to within 0.1%, while the tube-like isomer C80(1) with D5d symmetry has a 0.6% larger CCS. The quasi-spherical C80(5) as well as C80(7) isomers are 0.7% smaller than the experimental value and can also be clearly ruled out. Note, that the mobilogram consists of only one narrow peak with a CCS-to-ΔCCS ratio of more than 200 (see Fig. 5a). As for C76, the narrow peak width observed for C80 implies that only one isomer prevails. Interestingly, the DFT calculations do not predict the D2 isomer C80(2) as global minimum. For neutral and cationic C80, isomer C80(1) is lowest in energy. For the anion it is C80(5) and C80(3). However, the D2-isomer based species lies within a few tenths of an eV of these lowest energy forms, independent of charge state. We note in passing that free energy differences at elevated temperatures have been proposed as more relevant for describing detailed fullerene isomer distributions as generated by arc discharge.64 For Cn (82 ≤ n ≤ 108) several isomers have been isolated from soot extracts for each n.4,6,12–25,65 In most cases the lowest energy isomers of these agree within 0.4% with our experimental CCS value. For C82, Achiba4 identified two isomers, C82(7) with C3v symmetry and C82(9) with C2v symmetry. Both agree to within 0.3% with each other and with the experimental value. We cannot distinguish between them. For C84, two isomers, C84(22) with D2d symmetry and D2-C84(23) dominate. Their CCS are almost identical (within 0.2%), an observation which we have already used to justify the choice of C84 as a CCS calibration point for the fullerene test set calculations above. Note that besides C84(22) and C84(23) several other isomers have been identified in much lower abundance.6,25 In the size range above C84 the peak widths tend to increase, i.e. the CCS-to-ΔCCS ratio decreases to values below 200 which is the instrumental resolution in this CCS range (see Fig. S2, ESI†). This indicates that for each fullerene, several isomers must be present in the extract that cannot be resolved by TIMS. For C90 46 IPR isomers exist, among which C90(45) has been predicted to be the most stable,66 which is in line with our calculations. Experimentally, a rather large number of isomers have been reported,10,14 most of them within a few tenths of an eV of the lowest energy form and with CCS values within 0.5% of the experimental value. An interesting exception is C90(1) which is basically a small nanotube, with C60-halves as end caps. This species has a predicted CCS that is more than 2% above our experimental value and is energetically unfavorable relative to C90(45). Nevertheless it has been experimentally observed by using Sm2O3 doped graphite-rods in the arc-discharge.10 We can clearly rule out that it is present in more than 1% relative abundance in our fullerene mix. For C96 the situation is comparable to C84 in as much as the experimentally confirmed isomers have very similar CCS (except C96(3) and C96(181) which can also be ruled out to be present in our fullerene mix, see above). That is the reason why we used it as calibration point as well. For C100, 450 IPR isomers are topologically possible, of which four have been identified experimentally in previous studies (C100(1), C100(18), C100(417), and C100(425)).20,21 Among these, C100(425) is energetically favored, according to our DFT calculations, and its predicted CCS value agrees to within 0.1% with our experimental observation. C100(1) has a nanotube-like structure (similar to C80(1) and C90(1) which we do not observe either), and therefore it has a significantly larger CCS than the almost spherical C100(425). C100(1) is 1.68 eV less stable and its cross section is 3% above the experimental value. We can clearly rule it out as being present in our soot extract. The same holds true for C100(18) with a CCS 1.6% larger than experiment. For C104, three cage isomers have been identified by X-ray diffraction so far.23 For C102, C106 and C108, respectively, there is only one reported structure.22,24 Except for C104(812) which is 1.4% above the experimental value, the calculated CCS of all isomers agree with our experimental values to within 0.7%. However, in all cases the TIMS peak widths imply that several isomers must be present.
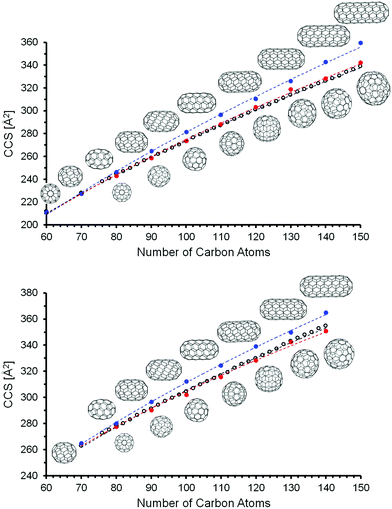
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569 for C150. It was not possible for us to calculate all of the IPR isomers between C110 and C150 at the DFT level. We focused instead on two limiting cases: “Tubes” and “Spheres”. The model tubes were constructed by cutting a C60 molecule into two halves and adding one or more C10 rings in between. This results in a homologous series starting at C70 with a spacing of 10 atoms (see Fig. 6). The next members are C80(1), C90(1), and C100(1) – which have already been discussed above. The structures of the complete series up to C150 were created as xyz-files with the FullFun software and are of D5h or D5d symmetry, respectively. All geometries were optimized at the DFT level without symmetry restrictions. In order to generate model spheres, we used the FullFun software to tabulate all IPR isomers for each cage size of interest. Then we searched for those structures whose xyz-files show the smallest variation in carbon atom distances from the cage centers, i.e. structures that come closest to a sphere. We focused on the same number of carbon atoms (60, 70, 80,…, 150) as was screened for the model tubular structures. For C80, this is isomer C80(7) with Ih symmetry, for C90 it is C90(46) and for C100 it is C100(449). Based on the DFT geometry optimizations, we then performed trajectory calculations (using method 4, see Table 2) to obtain CCS predictions for anions and dianions – in both types of model structure. For a given number of carbon atoms, the tubes are expected to have the larger CCS values. This is confirmed by the results of the DFT and trajectory calculations summarized in Table 4. As a general rule (for both monoanions and dianions), the spherical structures are significantly lower in energy (except for C80). This DFT energy difference between tubes and spheres increases with the number of carbon atoms – from around 1.5 eV for C90 up to more than 6 eV for C140, independent of charge state (as also predicted in earlier calculations67–69). The cross sections of equi-sized tubes between C80 and C150 differ by 6–14 Å2, with the spheres in much better agreement with the experimental CCS values. For fullerenes with more than 100 carbon atoms, the CCS values predicted for tubular structures differ by more than +2% from experiment – see Table 4 and Fig. 6.
569 for C150. It was not possible for us to calculate all of the IPR isomers between C110 and C150 at the DFT level. We focused instead on two limiting cases: “Tubes” and “Spheres”. The model tubes were constructed by cutting a C60 molecule into two halves and adding one or more C10 rings in between. This results in a homologous series starting at C70 with a spacing of 10 atoms (see Fig. 6). The next members are C80(1), C90(1), and C100(1) – which have already been discussed above. The structures of the complete series up to C150 were created as xyz-files with the FullFun software and are of D5h or D5d symmetry, respectively. All geometries were optimized at the DFT level without symmetry restrictions. In order to generate model spheres, we used the FullFun software to tabulate all IPR isomers for each cage size of interest. Then we searched for those structures whose xyz-files show the smallest variation in carbon atom distances from the cage centers, i.e. structures that come closest to a sphere. We focused on the same number of carbon atoms (60, 70, 80,…, 150) as was screened for the model tubular structures. For C80, this is isomer C80(7) with Ih symmetry, for C90 it is C90(46) and for C100 it is C100(449). Based on the DFT geometry optimizations, we then performed trajectory calculations (using method 4, see Table 2) to obtain CCS predictions for anions and dianions – in both types of model structure. For a given number of carbon atoms, the tubes are expected to have the larger CCS values. This is confirmed by the results of the DFT and trajectory calculations summarized in Table 4. As a general rule (for both monoanions and dianions), the spherical structures are significantly lower in energy (except for C80). This DFT energy difference between tubes and spheres increases with the number of carbon atoms – from around 1.5 eV for C90 up to more than 6 eV for C140, independent of charge state (as also predicted in earlier calculations67–69). The cross sections of equi-sized tubes between C80 and C150 differ by 6–14 Å2, with the spheres in much better agreement with the experimental CCS values. For fullerenes with more than 100 carbon atoms, the CCS values predicted for tubular structures differ by more than +2% from experiment – see Table 4 and Fig. 6.
| Fullerene isomer | Anion | Dianion | ||||
|---|---|---|---|---|---|---|
| ΔE, eV | Calc. CCS, Å2 | Exp. TIMSCCSN2, Å2 | ΔE, eV | Calc. CCS, Å2 | Exp. TIMSCCSN2, Å2 | |
| C80(1) (tube) | −0.26 | 246.1 | 244.6 | 0.11 | 280.0 | 278.3 |
| C80(7) (sphere) | 242.9 | 277.6 | ||||
| C90(1) (tube) | 1.28 | 264.9 | 258.6 | 1.82 | 296.5 | 291.0 |
| C90(45) (sphere) | 258.6 | 290.2 | ||||
| C100(1) (tube) | 1.68 | 281.3 | 273.0 | 2.13 | 312.1 | 304.2 |
| C100(449) (sphere) | 272.6 | 302.1 | ||||
| C110(1) (tube) | 2.34 | 296.4 | 287.0 | 2.43 | 324.2 | 316.8 |
| C110(2331) (sphere) | 288.3 | 315.6 | ||||
| C120(1) (tube) | 2.35 | 310.2 | 300.7 | 3.61 | 338.8 | 329.9 |
C120(10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774) (sphere) 774) (sphere) |
303.1 | 328.1 | ||||
| C130(1) (tube) | 3.59 | 325.8 | 313.7 | 4.30 | 349.9 | 342.8 |
C130(39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175) (sphere) 175) (sphere) |
318.7 | 342.4 | ||||
| C140(1) (tube) | 6.30 | 342.5 | 326.2 | 6.57 | 364.9 | 354.9 |
C140(121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 354) (sphere) 354) (sphere) |
328.0 | 350.9 | ||||
| C150(1) (tube) | 7.43 | 359.6 | 338.7 | |||
C150(335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 569) (sphere) 569) (sphere) |
342.3 | |||||
Closer inspection of Fig. 6 indicates that for monoanions, the experimental CCS values tend to fall slightly below the line predicted for the spheres. This, however, is within our uncertainty, since we calibrate the parameters for the trajectory calculations based on smaller fullerenes in the C60–C96 range and by so doing essentially extrapolate to the larger fullerenes. With method 5, i.e. using empirical scaling factors (see above) we obtain the same results, i.e. giant fullerenes from our soot extract have more spherical rather than tubular structures. Without scaling factors (i.e. using method 1, the default parameters of IMoS) even the spheres have CCS slightly larger than experimental values, while the tubes’ CCS are much larger, see ESI.† This shows that the assignment is robust: independent of the method we use, the spheres always fit the experimental data much better. For the dianions the experimental curve is in between spheres and tubes, but much closer to the spheres (calculated with method 4). Method 1 and 5 give even better agreement between spheres and experiment, see Fig. S4 and S5, ESI†. Therefore, we can clearly rule out tubular isomers in our giant fullerene sample. However, this does not mean that we observe only one isomer: even with the highest mobility resolution we can achieve (ca. 250 in the 300 Å2 CCS-range, based on tunemix measurements) and for all fullerenes above C100 we observe peak widths (CCS/ΔCCS) below 200, more typically around 170. This clearly shows, that several isomers must be present for each fullerene. Given that comprehensive DFT calculations of all IPR isomers were not possible in this size range, we cannot say for certain whether the spherical isomers used in our CCS calculations were in fact among the lowest energy isomeric forms of that particular cage size (keeping in mind that there are more than 400 IPR isomers for C100 and literally thousands in the C110–C150 range). Nevertheless, as can be seen in Fig. 7, the mobilograms observed are narrow enough to rule out isomer distributions containing appreciable amounts of isomers with structures deviating significantly from spherical. We conclude, that our fullerene mix contains primarily near-spherical giant fullerenes.
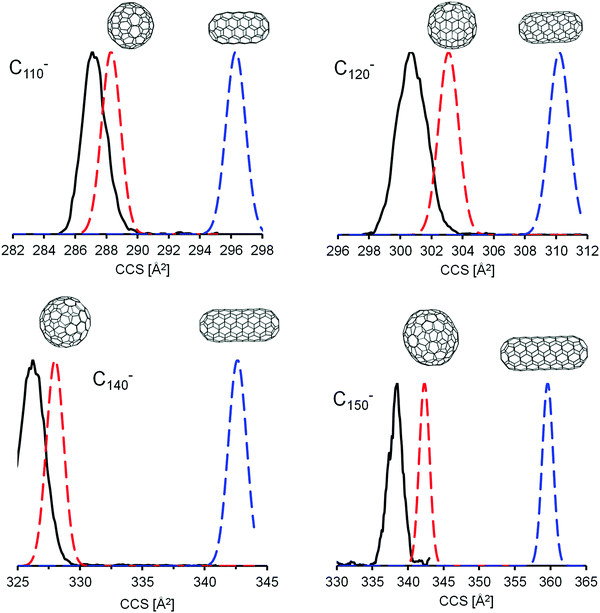 | ||
| Fig. 7 Comparison of simulated (method 4) and measured mobilograms for large monoanionic fullerenes. Black: typical experimental mobilograms; red and blue: simulated (Gaussian mobilograms for sphere and tubular isomers, respectively, based on their calculated CCS (see Table 4) for an instrumental resolution of 200). The distributions for the spherical structures are in much better agreement with the experimental data than the tubular structures and the experimental peak width is only slightly bigger than the instrumental limit implying narrow isomer distributions. Note the small but systematic overestimation of CCS values even for the most spherical fullerene isomers. This deviation increases with cage size. | ||
4. Conclusions and summary
We have used trapped ion mobility spectrometry (TIMS) to obtain both high-precision (<0.5% statistical error) and high-resolution (CCS/ΔCCS > 200) measurements of the ion mobility of fullerene ions (monocations, monoanions and dianions) ranging in size from C60 to C150. The ions were generated by either electrospray ionization (ESI, for mono- and dianions) or by atmospheric pressure chemical ionization (APCI, for monocations) of a fullerene mix solution generated by ortho-dichlorobenzene extraction of fullerene soots produced by (lanthanum oxide doped) graphite-electric arc electric discharge.In favourable cases, TIMS allows to identify (and separate) constituent isomers as demonstrated for C78(1) and C78(2). Apart from more rapid analysis, an important advantage of ion mobility spectrometry over other separation techniques used for fullerenes such as HPLC is its relatively straightforward combination with theory. At least in principle, IMS allows not only separation of isomers but also direct identification via comparison of experimental TIMSCCSN2 values with trajectory calculations using candidate structures based on quantum chemical predictions. We have used this capability here to obtain structural information for fullerenes in the size range C110–C150 – a size range which has not yet been accessed in condensed phase studies.
Fullerene TIMS data also allow to check and advance the DFT+TM based methodology for theoretical description of TIMSCCSN2. Fullerene cages are of particular interest in this context because (i) they do not significantly change their structures over the range of charge states accessed, (ii) they are not polar, i.e. the partial charges on each atom are quite small and their partial charge distribution can be reasonably well described by a Mulliken population analysis and (iii) there is a high-quality data set of condensed phase structures extending over a wide size range which can be used as starting points for DFT-based modelling of the isolated fullerene ions. Therefore, it becomes possible to more carefully look at the various interactions contributing to TIMS “retention” by way of trajectory method calculations. For this we used primarily the IMoS 1.09 package.50,51 We also obtained very similar results with the TM method implementations in Mobcal and Collidoscope programs.
We found that trajectory method calculations using the published Lennard-Jones parameters for carbon can reproduce the experimental CCS within 3%. This is reasonably good, but not good enough to assign isomers, which in the case of fullerenes are expected to differ by less than 0.5%. Furthermore, the predicted CCS ratio between singly and doubly charged fullerene ions turns out to be off by several percent. Measurement and calculation can be reconciled to within 0.5% if we increase the polarizability of nitrogen from 1.74 Å3 to 2 Å3 and decrease the Lennard-Jones parameter σ slightly. The rationale for this is the polarizability anisotropy of nitrogen, that is not taken into account in the calculations. With this adjustment, we find that we can not only reproduce the experimental TIMSCCSN2 values of C60–C96 but also of all other fullerenes that have been characterized by X-ray diffraction, i.e. up to C108, to within 0.5%. This gave us confidence to extend our approach to even larger fullerenes in the range between C110 and C150 whose structures have not yet been determined in condensed phase. We focused on two limiting cases, “tubular” and “spherical” structures, and found that the giant fullerenes present in the soot extract are very close to the spherical limit.
The TM programs presently available for CCS modelling do a remarkably good job at describing the ion mobility of high (and even giant) fullerenes. In turn, fullerenes may be of use as well-behaved calibrants for high-resolution ion mobility studies extending over several different charge states. Isomeric purity is certainly an issue in this context but a further factor of two in TIMS resolution would open up fullerene isomer fractionation significantly beyond C78. Consistent with previous literature on TM modelling, we have assumed the same carbon-atom LJ parameters independent of charge state and fullerene cage size. Under these conditions we observe a slight but systematic size-dependent deviation between TIMSCCSN2 values and our best computational fits. This implies that fullerene LJ parameters are probably slightly dependent on atom count – perhaps reflecting systematic changes in cage curvature, pi-orbital axis vectors and orbital hybridization as the cage size increases. It would be interesting to probe such effects using an atomic collision gas such as argon thus eliminating uncertainties due to anisotropic polarizability and charge quadrupole interactions. This would allow to better investigate the relative contributions of hybridization and partial charges to overall TIMSCCSN2 values.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We gratefully acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) as administered by the Collaborative Research Center TRR 88 “3MET” through project C6. We also thank KIT for funding of the TIMS-TOFMS used in this study and Dr Sergei Lebedkin for providing the fullerene mix solution.References
- H. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, C60: Buckminsterfullerene, Nature, 1985, 318, 162–163 CrossRef CAS.
- W. Krätschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Solid C60: a new form of carbon, Nature, 1990, 347, 354–358 CrossRef.
- R. Ettl, I. Chao, F. Diederich and R. Whetten, Isolation of C76, a chiral D2 allotrope of carbon, Nature, 1991, 353, 149–153 CrossRef CAS.
- K. Kikuchi, N. Nakahara, T. Wakabayashi, S. Suzuki, H. Shiromaru, Y. Miyake, K. Saito, I. Ikemoto, M. Kainosho and Y. Achiba, NMR characterization of isomers of C78, C82 and C84 fullerenes, Nature, 1992, 357, 142–145 CrossRef CAS.
- F. H. Hennrich, R. H. Michel, A. Fischer, S. Richard-Schneider, S. Gilb, M. M. Kappes, D. Fuchs, M. Bürk, K. Kobayashi and S. Nagase, Isolation and Characterization of C80, Angew. Chem., Int. Ed. Engl., 1996, 35, 1732–1734 CrossRef CAS.
- N. Tagmatarchis, A. G. Avent, K. Prassides, T. J. S. Dennis and H. Shinohara, Separation, isolation and characterisation of two minor isomers of the [84]fullerene C84, Chem. Commun., 1999, 1023–1024 RSC.
- Y. Miyake, T. Minami, K. Kikuchi, M. Kainosho and Y. Achiba, Trends in Structure and Growth of Higher Fullerenes Isomer Structure of C86 and C88, Mol. Cryst. Liq. Cryst., 2000, 340, 553–558 CrossRef CAS.
- Y. Achiba, K. Kikuchi, Y. Aihara, T. Wakabayashi, Y. Miyake and M. Kainosho, Mater. Res. Soc. Symp. Proc., 1995, 359, 3–9 CrossRef CAS.
- Y. Achiba; K. Kikuchi; Y. Aihara; T. Wakabayashi; Y. Miyake and M. Kainosho, in The Chemical Physics of Fullerenes 10 (and 5) Years Later, ed. W. Andreoni, Kluwer, Dordrecht, 1996, 139–147 Search PubMed.
- H. Yang, C. M. Beavers, Z. Wang, A. Jiang, Z. Liu, H. Jin, B. Q. Mercado, M. M. Olmstead and A. L. Balch, Isolation of a Small Carbon Nanotube: The Surprising Appearance of D5h(1)-C90, Angew. Chem., Int. Ed., 2010, 49, 886–890 CrossRef CAS PubMed.
- H. Yang, H. Jin, Y. Che, B. Hong, Z. Liu, J. A. Gharamaleki, M. M. Olmstead and A. L. Balch, Isolation of Four Isomers of C96 and Crystallographic Characterization of Nanotubular D3d(3)-C96 and the Somewhat Flat-Sided Sphere C2 (181)-C96, Chem. – Eur. J., 2012, 18, 2792–2796 CrossRef CAS PubMed.
- S. Yang, T. We and S. I. Troyanov, Chlorination of Two Isomers of C86 Fullerene: Molecular Structures of C86(16)Cl6, C86(17)Cl18, C86(17)Cl20, and C86(17)Cl22, Chem. – Eur. J., 2014, 20, 14198–14200 CrossRef CAS PubMed.
- S. I. Troyanov and N. B. Tamm, Cage connectivities of C88(33) and C92(82) fullerenes captured as trifluoromethyl derivatives, C88(CF3)18 and C92(CF3)16, Chem. Commun., 2009, 6035–6037 RSC.
- S. I. Troyanov, S. Yang, C. Chen and E. Kemnitz, Six IPR Isomers of C90 Fullerene Captured as Chlorides: Carbon Cage Connectivities and Chlorination Patterns, Chem. – Eur. J., 2011, 17, 10662–10669 CrossRef CAS.
- N. B. Tamm and S. I. Troyanov, New Isolated-Pentagon-Rule Isomer of C92 Isolated as Trifluoromethyl and Chlorido Derivatives: C92(38)(CF3)14/16 andC92(38)Cl20/22, Inorg. Chem., 2015, 54, 10527–10529 CrossRef CAS PubMed.
- N. B. Tamm, L. N. Sidorov, E. Kemnitz and S. I. Troyanov, Crystal Structures of C94(CF3)20 and C96(C2F5)12 Reveal the Cage Connectivities in C94(61) and C96(145) Fullerenes, Angew. Chem., Int. Ed., 2009, 48, 9102–9104 CrossRef CAS PubMed.
- N. B. Tamm, Y. Shangfeng, T. Wei and S. I. Troyanov, Five Isolated Pentagon Rule Isomers of Higher Fullerene C94 Captured as Chlorides and CF3 Derivatives: C94(34)Cl14, C94(61)Cl20, C94(133)Cl22, C94(42)(CF3)16, and C94(43)(CF3)18, Inorg. Chem., 2015, 54, 2494–2496 CrossRef CAS PubMed.
- S. Yang, T. Wei, E. Kemnitz and S. I. Troyanov, Four Isomers of C96 Fullerene Structurally Proven as C96Cl22 and C96Cl24, Angew. Chem., Int. Ed., 2012, 51, 8239–8242 CrossRef CAS PubMed.
- F. Jin, S. Yang and S. I. Troyanov, New Isolated-Pentagon-Rule Isomers of Fullerene C98 Captured as Chloro Derivatives, Inorg. Chem., 2017, 56, 4780–4783 CrossRef CAS PubMed.
- M. A. Fritz, E. Kemnitz and S. I. Troyanov, Capturing an unstable C100 fullerene as chloride,C100(1)Cl12, with a nanotubular carbon cage, Chem. Commun., 2014, 50, 14577–14580 RSC.
- S. Wang, S. Yang, E. Kemnitz and S. I. Troyanov, New Isolated-Pentagon-Rule and Skeletally Transformed Isomers of C100 Fullerene Identified by Structure Elucidation of their Chloro Derivatives, Angew. Chem., Int. Ed., 2016, 55, 3451–3454 CrossRef CAS PubMed.
- S. Yang, S. Wang and S. I. Troyanov, The Most Stable Isomers of Giant Fullerenes C102 and C104 Captured as Chlorides, C102(603)Cl18/20 and C104(234)Cl16/18/20/22, Chem. – Eur. J., 2014, 20, 6875–6878 CrossRef CAS PubMed.
- F. Jin, S. Yang, M. A. Fritz, E. Kemnitz and S. I. Troyanov, Chloro Derivatives of Isomers of a Giant Fullerene C104: C104(234)Cl16/18, C104(812)Cl12/24, and C104(811)Cl28, Chem. – Eur. J., 2017, 23, 4761–4764 CrossRef CAS PubMed.
- S. Wang, S. Yang, E. Kemnitz and S. I. Troyanov, New Giant Fullerenes Identified as Chloro Derivatives: Isolated-Pentagon-Rule C108(1771)Cl12 and C106(1155)Cl24 as well as Nonclassical C104Cl24, Inorg. Chem., 2016, 55, 5741–5743 CrossRef CAS PubMed.
- N. B. Tamm, L. N. Sidorov and E. Kemnitz, Troyanov S. I. Isolation and Structural X-ray Investigation of Perfluoroalkyl Derivatives of Six Cage Isomers of C84, Chem. – Eur. J., 2009, 15, 10486–10492 CrossRef CAS PubMed.
- So Wang, S. Yang, E. Kemnitz and S. I. Troyanov, The First Experimentally Confirmed lsolated Pentagon Rule (IPR) Isomers of Higher Fullerene C98 Captured as Chlorides, C98(248)Cl22 and C98(116)Cl20, Chem. – Eur. J., 2016, 22, 5138–5141 CrossRef CAS PubMed.
- G. von Helden, M.-T. Hsu, P. R. Kemper and M. T. Bowers, Structures of carbon cluster ions from 3 to 60 atoms: Linears to rings to fullerenes, J. Chem. Phys., 1991, 95, 3835–3837 CrossRef CAS.
- G. von Helden, N. G. Gotts and M. T. Bowers, Experimental evidence for the formation of fullerenes by collisional heating of carbon rings in the gas phase, Nature, 1993, 363, 60–63 CrossRef CAS.
- J. Hunter, J. Fye and M. F. Jarrold, Annealing C60+: Synthesis of Fullerenes and Large Carbon Rings, Science, 1993, 260, 784–786 CrossRef CAS PubMed.
- G. von Helden, M.-T. Hsu, N. Gotts and M. T. Bowers, Carbon cluster cations with up to 84 atoms structures, formation mechanism, and reactivity, J. Phys. Chem., 1993, 97, 8182–8192 CrossRef CAS.
- T. Wyttenbach, G. von Helden, J. J. Batka, D. Carlat and M. T. Bowers, Effect of the Long-Range Potential on Ion Mobility Measurements, J. Am. Soc. Mass Spectrom., 1997, 8, 275–282 CrossRef CAS.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, Structural Information from Ion Mobility Measurements: Effects of the Long-range Potential, J. Phys. Chem., 1996, 100, 16082–16086 CrossRef CAS.
- R. Moriyama, J. W. J. Wu, M. Nakano, K. Ohshimo and F. Misaizu, Small Carbon Nano-Onions: An Ion Mobility Mass Spectrometric Study, J. Phys. Chem. C, 2018, 122, 5195–5200 CrossRef CAS.
- A. A. Shvartsburg, R. R. Hudgins, P. Dugourd and M. F. Jarrold, Structural Elucidation of Fullerene Dimers by High-Resolution Ion Mobility Measurements and Trajectory Calculation Simulations, J. Phys. Chem. A, 1997, 101, 1684–1688 CrossRef CAS.
- A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, Mobilities of carbon cluster ions: Critical importance of the molecular attractive potential, J. Chem. Phys., 1998, 108, 2416–2423 CrossRef CAS.
- P. Weis, S. Gilb, P. Gerhardt and M. M. Kappes, Int. J. Mass Spectrom., 2002, 216, 59–73 CrossRef CAS.
- F. Fernandez-Lima, D. A. Kaplan, J. Suetering and M. A. Park, Gas-phase separation using a trapped ion mobility spectrometer, Int. J. Ion Mobility Spectrom., 2011, 14, 93–98 CrossRef PubMed.
- F. Hennrich, E. Schneider, P. Weis and M. M. Kappes, Comparing empty and filled fullerene cages with high resolution trapped ion mobility spectrometry, J. Am. Soc. Mass Spectrom. DOI:10.1007/s13361-019-02250-2.
- L. D. Fuchs, H. Rietschel, R. H. Michel, M. Benz, A. Fischer and M. M. Kappes Proc. IWEPNM (Kirchberg), 1995.
- K. Kikuchi, N. Nakahara, T. Wakabayashi, S. Suzuki, K. Saito, I. Ikemoto and Y. Achiba, Higher fullerenes; separation and molecular structures, Synth. Met., 1993, 56, 3208–3213 CrossRef CAS.
- S. M. Stow, T. J. Causon, X. Zheng, R. T. Kurulugama, T. Mairinger, J. C. May, E. E. Rennie, E. S. Baker, R. D. Smith, J. A. McLean, S. Hann and J. C. Fjeldsted, An Interlaboratory Evaluation of Drift Tube Ion Mobility−Mass Spectrometry Collision Cross Section Measurements, Anal. Chem., 2017, 89, 9048–9055 CrossRef CAS PubMed.
- Y. Wang, S. Diaz-Tendero, M. Alcami and F. Martin, Cage connectivity and frontier pi orbitals govern the relative stability of charged fullerene isomers, Nat. Chem., 2015, 7, 927–934 CrossRef CAS PubMed.
- Y. Wang, S. Diaz-Tendero, M. Alcami and F. Martin, Relative Stability of Empty Exohedral Fullerenes: pi Delocalization versus Strain and Steric Hindrance, J. Am. Chem. Soc., 2017, 139, 1609–1617 CrossRef CAS PubMed.
- Y. Wang, S. Diaz-Tendero, M. Alcami and F. Martin, Topology-Based Approach to Predict Relative Stabilities of Charged and Functionalized Fullerenes, J. Chem. Theory Comput., 2018, 14, 1791–1810 CrossRef CAS PubMed.
- A. D. Becke, Density-functional Exchange-energy Approximation with Correct Asymptotic-behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Density-functional Approximation for the Correlation-energy of the Inhomogeneous Electron-gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Turbomole, WIREs Comput. Mol. Sci., 2014, 4, 91–100 CrossRef CAS.
- P. W. Fowler and D. E. Manolopoulous, An Atlas of Fullerenes, Clarendon, Oxford, 1995 Search PubMed.
- C. Larriba and C. J. Hogan Jr., Ion Mobilities in Diatomic Gases: Measurement versus Prediction with Non-Specular Scattering Models, J. Phys. Chem. A, 2013, 117, 3887–3901 CrossRef CAS PubMed.
- C. Larriba and C. J. Hogan Jr., Free molecular collision cross section calculation methods for nanoparticles and complex ions with energy accommodation, J. Comput. Phys., 2013, 251, 344–363 CrossRef CAS.
- H. Kim, H. I. Kim, P. V. Johnson, L. W. Beegle, J. L. Beauchamp, W. A. Goddard and I. Kanik, Experimental and theoretical investigation into the correlation between mass and ion mobility for choline and other ammonium cations in N2, Anal. Chem., 2008, 80, 1928–1936 CrossRef CAS PubMed.
- I. D. G. Campuzano, M. F. Bush, C. V. Robinson, C. Beaumont, K. Richardson, H. Kim and H. I. Kim, Structural Characterization of Drug-like Compounds by Ion Mobility Mass Spectrometry: Comparison of Theoretical and Experimentally Derived Nitrogen Collision Cross-sections, Anal. Chem., 2012, 84, 1026–1033 CrossRef CAS PubMed.
- S. A. Ewing, M. T. Donor, J. W. Wilson and J. S. Prell, Collidoscope: An Improved Tool for Computing Collisional Cross-Sections with the Trajectory Method, J. Am. Soc. Mass Spectrom., 2017, 28, 587–596 CrossRef CAS PubMed.
- T. Wu, J. Derrick, M. Nahin, X. Chen and C. Larriba-Andaluz, Optimization of long range potential interaction parameters in ion mobility spectrometry, J. Chem. Phys., 2018, 148, 074102 CrossRef PubMed.
- V. Shrivastav, M. Nahin, C. J. Hogan and C. Larriba-Andaluz, Benchmark Comparison for a Multi-Processing Ion Mobility Calculator in the Free Molecular Regime, J. Am. Soc. Mass Spectrom., 2017, 28, 1540–1551 CrossRef CAS PubMed.
- S. Tomita, J. U. Andersen, H. Cederquist, B. Concina, O. Echt, J. S. Forster, K. Hansen, B. A. Huber, P. Hvelplund, J. Jensen, B. Liu, B. Manil, L. Maunoury, S. Brøndsted Nielsen, J. Rangama, H. T. Schmidt and H. Zettergren, Lifetimes of C602− and C702− dianions in a storage ring, J. Chem. Phys., 2006, 124, 024310 CrossRef CAS.
- A. Lassesson, N. Walsh, F. Martinez, A. Herlert, G. Marx and L. Schweikhard, Formation of fullerene dianions in a Penning trap, Eur. Phys. J. D, 2005, 34, 73–77 CrossRef CAS.
- X.-B. Wang, H.-K. Woo, X. Huang, M. M. Kappes and L.-S. Wang, Direct Experimental Probe of the On-Site Coulomb Repulsion in the Doubly Charged Fullerene Anion C702−, Phys. Rev. Lett., 2006, 96, 143002 CrossRef PubMed.
- X.-B. Wang, H.-K. Woo, J. Jang, M. M. Kappes and L.-S. Wang, Photoelectron Spectroscopy of Singly and Doubly Charged Higher Fullerenes at Low Temperatures: C76−, C78−, C84− and C762−, C782−, C842−, J. Phys. Chem. C, 2007, 111, 17684–17689 CrossRef CAS.
- N. B. Shustova, I. V. Kuvychko, R. D. Bolskar, K. Seppelt, S. H. Strauss, A. A. Popov and O. V. Boltalina, Trifluoromethyl Derivatives of Insoluble Small-HOMO–LUMO-Gap Hollow Higher Fullerenes. NMR and DFT Structure Elucidation of C2-(C74-D3h)(CF3)12, Cs-(C76-Td(2))(CF3)12, C2-(C78-D3h(5))(CF3)12, Cs-(C80-C2v(5))(CF3)12, and C2-(C82-C2(5))(CF3)12, J. Am. Chem. Soc., 2006, 128, 15793–15798 CrossRef CAS PubMed.
- Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, 97th edn, 2016–2017 Search PubMed.
- C.-R. Wang, T. Sugai, T. Kai, T. Tomiyama and H. Shinohara, Production and isolation of an ellipsoidal C80 fullerene, Chem. Commun., 2000, 557–558 RSC.
- M.-L. Sun, Z. Slanina, S.-L. Lee and F. Uhlík, AM1 computations on seven isolated-pentagon-rule isomers of C80, Chem. Phys. Lett., 1995, 246, 66–72 CrossRef CAS.
- G. Sun and M. Kertesz, 13C NMR spectra for IPR isomers of fullerene C86, Chem. Phys., 2002, 276, 107–114 CrossRef CAS.
- G. Y. Sun, Theoretical 13C NMR chemical shifts of the stable isomers of fullerene C90, Chem. Phys., 2003, 289, 371–380 CrossRef CAS.
- X. Zhao, H. Goto and Z. Slanina, C100 IPR fullerenes: temperature-dependent relative stabilities based on the Gibbs function, Chem. Phys., 2004, 306, 93–104 CrossRef CAS.
- G. E. Scuseria, in Buckminsterfullerenes, ed. W. E. Billups and M. A. Ciufolini, VCH Weinheim, 1993 Search PubMed.
- D. Bakowies and W. Thiel, MNDO study of large carbon clusters, J. Am. Chem. Soc., 1991, 113, 3704–3714 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03326b |
| This journal is © the Owner Societies 2019 |