Open Access Article
Open Access ArticleAzobenzene as a photoregulator covalently attached to RNA: a quantum mechanics/molecular mechanics-surface hopping dynamics study†
Padmabati
Mondal
 *a,
Giovanni
Granucci
b,
Dominique
Rastädter
a,
Maurizio
Persico
*b and
Irene
Burghardt
*a,
Giovanni
Granucci
b,
Dominique
Rastädter
a,
Maurizio
Persico
*b and
Irene
Burghardt
 *a
*a
aInstitute of Physical and Theoretical Chemistry, Goethe University Frankfurt, Max-von-Laue-Str. 7, 60438 Frankfurt, Germany. E-mail: padmabati.mondal@gmail.com; burghardt@chemie.uni-frankfurt.de
bDipartimento di Chimica e Chimica Industriale, Università di Pisa, v. Moruzzi 13, I-56124 Pisa, Italy. E-mail: maurizio.persico@unipi.it
First published on 27th April 2018
Abstract
The photoregulation of nucleic acids by azobenzene photoswitches has recently attracted considerable interest in the context of emerging biotechnological applications. To understand the mechanism of photoinduced isomerisation and conformational control in these complex biological environments, we employ a Quantum Mechanics/Molecular Mechanics (QM/MM) approach in conjunction with nonadiabatic Surface Hopping (SH) dynamics. Two representative RNA–azobenzene complexes are investigated, both of which contain the azobenzene chromophore covalently attached to an RNA double strand via a β-deoxyribose linker. Due to the pronounced constraints of the local RNA environment, it is found that trans-to-cis isomerization is slowed down to a time scale of ∼10–15 picoseconds, in contrast to 500 femtoseconds in vacuo, with a quantum yield reduced by a factor of two. By contrast, cis-to-trans isomerization remains in a sub-picosecond regime. A volume-conserving isomerization mechanism is found, similarly to the pedal-like mechanism previously identified for azobenzene in solution phase. Strikingly, the chiral RNA environment induces opposite right-handed and left-handed helicities of the ground-state cis-azobenzene chromophore in the two RNA–azobenzene complexes, along with an almost completely chirality conserving photochemical pathway for these helical enantiomers.
1 Introduction
The light-induced control of conformational changes in nucleic acids by introducing covalently or non-covalently bound photoswitches has proven a promising route towards DNA and RNA functionalization.1–6 Applications range from photoregulation of gene expression7 and functional aptamers,8 to the tailored design of photoresponsive oligonucleotide walkers,9 tweezers,10 and diverse nanoarchitectures.In this context, azobenzene photoswitches play a prominent role,1–6,11,12 besides other photo-switchable chromophores like spiropyrans which have also been employed in DNA control.13 The azobenzene chromophore switches reversibly between the planar trans form and the non-planar cis form, upon absorption of UV light inducing trans-to-cis conversion, or visible light inducing cis-to-trans conversion.14–16 While the planar trans azobenzene isomer intercalates readily between aromatic nucleobases, the non-planar cis form, which is shorter by ∼3 Å, tends to unstack from a DNA or RNA helix.17–20 As a result, preferential destabilization of nucleic acid double helices has been observed after trans-to-cis conversion.5,6,17,18,21 In a paradigm system involving azobenzene covalently linked to DNA or RNA oligomers via a D-threoninol linker,5,17 differences in melting temperatures (Tm) between trans vs. cis azobenzene substituted oligomers of the order of ΔTm = Ttransm − Tcism ∼ 10–20 °C were observed, which can be augmented by inserting multiple azobenzenes into the duplex structure.22
Due to the widely different time scales of azobenzene isomerization (femtoseconds to picoseconds)11 as compared with the much slower DNA or RNA conformational response (microseconds to milliseconds),23 complementary techniques are required to simulate the relevant steps. In particular, Molecular Dynamics (MD) simulations including an effective switching potential19,24 were employed to model the fast isomerization step, while enhanced sampling techniques like Replica Exchange Molecular Dynamics (REMD) were used to explore longer time scales where the effects of DNA and RNA unfolding become manifest.20 Markov State Models (MSM) are the method of choice to provide an embedding of MD and REMD type information into a kinetic description adapted to long-time conformational changes.25
Here, we are concerned with the shortest, ultrafast time scale, in order to investigate whether azobenzene works as an efficient photoswitch in the highly specific nucleic acid environment, and whether azobenzene isomerization proceeds similarly to the gas phase or solution phase. A priori, the DNA or RNA local environment could entail significant modifications of the mechanism and time scales. To this end, we use hybrid Quantum Mechanics/Molecular Mechanics (QM/MM) simulations26–31 in conjunction with Surface Hopping (SH) dynamics27,32,33 in order to obtain a detailed picture of the isomerization process in azobenzene–RNA complexes on a picosecond time scale. In a related approach, QM/MM–SH simulations were recently used to study peptide folding and unfolding driven by azobenzene photoisomerisation.33 The simulations reported in the present work represent an important benchmark for more approximate Molecular Mechanics (MM) based treatments.19,20,34,35
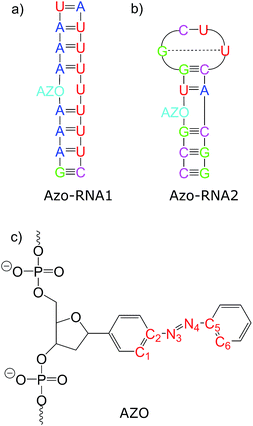
Connecting to our recent work20,34,36 in the context of RNA regulation, we focus on azobenzene-linker–RNA complexes – rather than complexes with DNA – in the present study. To reduce the bias associated with the study of a single system, we carried out parallel investigations of two azobenzene–RNA complexes as depicted in Fig. 1, both of which contain the azobenzene chromophore anchored to one of the RNA strands via a β-deoxyribose linker.34,36 This linker-azobenzene combination has recently been shown to induce a destabilization effect comparable to the widely applied D-threoninol-linked azobenzene,36,37 with excellent efficiencies and high thermal stability. In addition, the β-deoxyribose linker has been shown to impose minimal disturbance on the duplex stability.34,36,37 The two RNAs that were selected correspond to (i) a double-helix structure representing a fragment of a longer double helix that was synthesized and studied both experimentally and theoretically,34,36 and (ii) a 14-mer hairpin structure capped by a tetraloop motif – a frequently occurring RNA motif – which was studied in ref. 20 using REMD simulations. We refer to ref. 1 and 34 for a detailed discussion of the various factors that influence the efficiency of azobenzene photoswitches for nucleic acid functionalization. For the two types of experimentally established linkers mentioned above, i.e., of deoxyribose and threoninol type, different anomeric and enantiomeric forms (i.e., α-, β- and D-, L-, for the deoxyribose and threoninol linkers, respectively) are of critical importance, along with the presence or absence of an opposite base in the duplex structure.
2 Methods
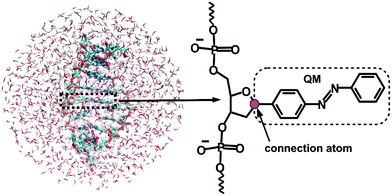
Given that the electronic excitation remains localized on the azobenzene chromophore, a QM/MM treatment is a natural approach to the electronic structure of the azobenzene-linker–RNA complexes. As illustrated in Fig. 2, the QM part corresponds to the azobenzene chromophore, while the MM part combines the β-deoxyribose linker, the RNA duplex, and the surrounding water.For the QM part, we employ a semi-empirical Configuration Interaction (CI) method based upon Floating Occupation Molecular Orbitals (FOMO–CI),38 which has proven successful in the past in the study of azobenzene derivatives.32 Calculations were performed with a development version of the MOPAC program, using a reparametrized AM1 Hamiltonian and additional features as detailed in ref. 38–40.
The linker and the RNA duplex are described by the Amber ff99SB41 force field as implemented in the TINKER 6.1 package,42 and the water molecules are of TIP3P type.43 The connection atom scheme44 is employed to describe the boundary between the covalently linked QM and MM parts. According to this scheme, the C1′ atom of the β-deoxyribose linker is the connection atom which behaves as a hydrogen atom in the QM part and as a normal carbon atom in the MM part (see Fig. 2). The total energy of the system is of additive type and the electrostatic embedding scheme is considered for the calculation of the effective QM/MM Hamiltonian.44
The QM/MM scheme is combined with an approximate representation of the nonadiabatic dynamics using Tully's fewest switches surface hopping algorithm45 including overlap based quantum decoherence corrections (SH–ODC).32,46 Energy gradients and nonadiabatic couplings are calculated using the FOMO–CI method as a function of the time-evolving trajectories. Trajectories are initiated in the S2(π–π*) state, whose squared transition dipole moment averaged over the ensemble is dominant (see ESI Section S1†). In fact, in the photostationary state a much higher fraction of the cis isomer is formed when exciting to the π–π* band than to the n–π* band, so this is the standard experimental situation we aim to simulate. An ensemble of 100 initial conditions is considered, which are sampled from equilibrated ground-state MD simulations for the relevant complexes. Following MD pre-equilibration, a QM/MM equilibration was carried out using Brownian dynamics in the electronic ground state, with an equilibration time of 50 ps at 300 K. To avoid nonequilibrium effects due to heating at the beginning of the QM/MM equilibration, the first 10 ps are excluded from the 50 ps equilibration data for generating initial conditions. During the simulation, the populations of the first six singlet states are monitored.
The QM/MM–FOMO–CI–SH approach has been previously used in various simulations of the photodynamics of azobenzene and its derivatives, often in more or less severely sterically hindered environments.32,47–51 Excited state lifetimes obtained by transient spectroscopies were successfully reproduced.49 Both experiments and simulations highlight the effect of caging, which can be extremely pronounced as in closely packed self-assembled monolayers48 or much milder as in a viscous solvent (ethylene glycol) that hinders overall molecular rotation and, to a lesser extent, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond torsion.49 Quantum yields, when experimentally available, are well reproduced for n–π* excitation49 but tend to be overestimated for π–π* excitation.32 The FOMO–CI method was calibrated specifically to reproduce energetic data for the ground and the first excited states of azobenzene, obtained experimentally and by calculations of the best affordable quality, performed by different authors.39 As a result, the quality of the potential energy surfaces we are using is superior to what might be achieved by any ab initio approach of practical use in simulations of this kind. Furthermore, our surface hopping results compare well with quantum wavepacket calculations for azobenzene photoisomerization.46
N double bond torsion.49 Quantum yields, when experimentally available, are well reproduced for n–π* excitation49 but tend to be overestimated for π–π* excitation.32 The FOMO–CI method was calibrated specifically to reproduce energetic data for the ground and the first excited states of azobenzene, obtained experimentally and by calculations of the best affordable quality, performed by different authors.39 As a result, the quality of the potential energy surfaces we are using is superior to what might be achieved by any ab initio approach of practical use in simulations of this kind. Furthermore, our surface hopping results compare well with quantum wavepacket calculations for azobenzene photoisomerization.46
In the present context, we further carried out selected benchmark calculations using the ab initio second-order Complete Active Space Perturbation Theory (CASPT2)52 method for small fragments involving the azobenzene chromophore and the most important neighboring bases (see Section S3 of the ESI†). These calculations validate the QM/MM–FOMO–CI treatment of azobenzene embedded in the local RNA environment.
For completeness, we point out that triplet states were not included in the present calculations. Even though the azobenzene excited-state lifetimes will turn out to be considerably lengthened as compared with the gas-phase dynamics, intersystem crossing likely does not play an important role, given that the S1 and T1 potential energy surfaces (PESs) are roughly parallel and well separated in energy.53 (Indeed, the latter reference addresses the role of the T1 state in the thermally activated kinetics, not the photochemical pathways).
The ESI† provides further information regarding the simulation set-up, construction of initial conditions, and absorption spectra obtained within the QM/MM set-up (see ESI Section S1 and S2†).
3 Results and discussion
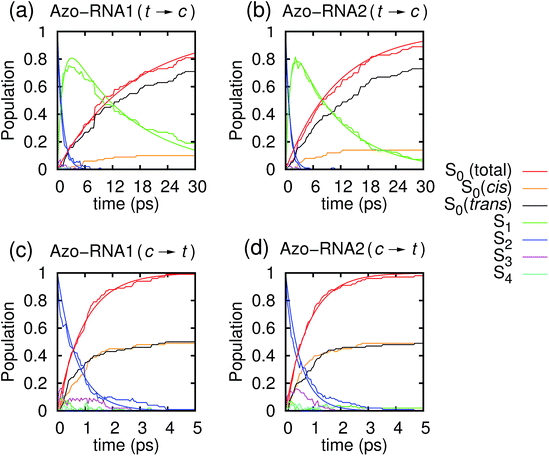
In the following, we first analyze the time-dependent electronic state populations and estimated isomerization quantum yields resulting from the QM/MM–SH simulations. Then, we turn to the isomerization mechanism, with emphasis on the role of the RNA environment, the subtle role of chirality, and the interplay of different dihedral angles whose combined dynamics results in a largely volume-preserving photoreactive path.3.1 Photodynamical time scales and quantum yield
Fig. 3 illustrates one of the key results of this study: trans-to-cis isomerization of azobenzene is slowed down remarkably in the RNA environment, from 500 femtoseconds in the gas phase to ∼10–15 picoseconds in RNA. By contrast, the time scale of cis-to-trans isomerization is almost unaffected and remains less than one picosecond. These findings are very similar for the two RNAs that we investigated. This suggests that the geometric changes accompanying trans-to-cis isomerization are strongly hindered in the RNA environment, for the present azobenzene-linker–RNA combination – pointing towards an important role of stacking interactions that stabilize the intercalated trans form of the chromophore.In further detail, it is seen from Fig. 3a and b for the trans-to-cis dynamics that the decay from the initially excited S2(π–π*) state to the S1(n–π*) state happens within ∼1 picosecond, while the chromophore subsequently remains in the S1 state for ∼10 picoseconds. From the build-up of S0 population, we can infer that most trajectories return to the S0/trans conformation, while a lesser portion isomerizes and yields the S0/cis product.
For the trajectories starting in cis conformation (Fig. 3c and d), a very different scenario is observed: while the S2 state again decays very rapidly, within ∼1 picosecond, the S1 state is only transiently populated – or barely populated at all – while the ground state (S0) population rises within ∼1 picosecond, concomitantly with the S2 decay. This indicates that S1 is at most a transient intermediate rather than a long-lived intermediate as in the trans-to-cis dynamics.
As also shown in Fig. 3, the population decay derived from the trajectory ensemble can be fitted to an approximate set of coupled first-order kinetic equations for the state populations Pn, n = 0, 1, 2, for a three-state system comprising the Sn, n = 0, 1, 2, electronic states (see also ref. 32),
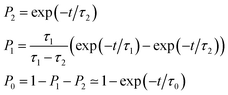 | (1) |
| Isomerisation | Environment | τ 1 (ps) | τ 2 (ps) | τ 0 (ps) |
|---|---|---|---|---|
| trans → cis | In vacuo | 0.525 | 0.191 | |
| Methanol | 0.643 | 0.145 | ||
| Ethylene glycol | 0.534 | 0.091 | ||
| Azo–RNA1 | 14.590 | 1.120 | 16.10 | |
| Azo–RNA2 | 10.233 | 0.952 | 11.30 | |
| cis → trans | In vacuo | 0.085 | 0.446 | |
| Methanol | 0.071 | 0.381 | ||
| Ethylene glycol | 0.082 | 0.352 | ||
| Azo–RNA1 | — | 0.702 | 0.97 | |
| Azo–RNA2 | — | 0.527 | 0.84 |
The nature of the population dynamics is very similar for the Azo–RNA1 and Azo–RNA2 complexes, even though the S1 and S2 lifetimes depend slightly on the environment. Since an analysis with the same FOMO–CI–SH set-up was previously carried out for the azobenzene chromophore in gas phase and in various solvents,32 we compare in Table 1 the results for the relevant lifetimes τn, n = 0, 1, 2. This comparative analysis underscores that (i) S1 lifetimes in the trans-to-cis isomerisation dynamics in an RNA environment differ by a factor of about 20 from previously observed lifetimes in the gas phase and solution phase, and (ii) in the case of cis-to-trans dynamics, S2 lifetimes are slightly augmented, by a factor of two.
The quantum yield for trans-to-cis isomerisation (Φt→c ∼ 0.1) in RNA drops to about half of typical values computed for non-viscous solvents such as methanol. For the cis-to-trans conversion the quantum yield remains high (Φc→t ∼ 0.5) and its decrease with respect to methanol solution is modest. The quantum yields for azobenzene isomerisation in the gas phase, in solution, and in the RNA environment are given in Table 2 for comparison. As in Table 1, all results are obtained by the same simulation method.
| Environment | Φ t→c | Φ c→t |
|---|---|---|
| In vacuo | 0.21 | 0.54 |
| Methanol | 0.24 | 0.57 |
| Ethylene glycol | 0.24 | 0.67 |
| Azo–RNA1 | 0.10 | 0.50 |
| Azo–RNA2 | 0.14 | 0.52 |
| Experiment (methanol) | 0.155 | 0.39 |
These results are in qualitative agreement with recent experimental55,56 and MD-based computational35 studies on the photoisomerisation quantum yield of azobenzene in DNA where the quantum yield for the trans-to-cis conversion was found to depend largely on the local DNA sequence35 as well as on temperature,56 and strongly decreases with decreasing local volume in the nucleic acid environment. Specifically, the experimentally determined quantum yields reported in ref. 56 vary in the range 0.01 < Φt→c < 0.05 for various azobenzene-substituted DNA double strands with a threoninol linker, below the melting temperature Tm. For temperatures above Tm, quantum yields for the different sequences converge towards a temperature-dependent value in the range 0.05 < Φt→c < 0.1, without any sequence specificity. Our QM-based computational study of azobenzene photoisomerisation in an RNA environment points towards a “looser” local environment of azobenzene in RNA, leading to slightly higher quantum yields (Φt→c ∼ 0.1) at room temperature.
The striking lengthening of the S1 lifetime in the trans-to-cis photodynamics and the decrease in the Φt→c quantum yield must clearly be due to steric constraints of the RNA (or DNA) environment that are much less effective in the cis-to-trans case. A slowing down of the azobenzene trans-to-cis photoisomerization and excited state decay in viscous solvents and constrained environments has been previously reported,32,47,49–51,57 even though the effect was by far not as pronounced and typically limited to an increase of the isomerization time by a factor of two to three. Noticeably, though, a full supression of isomerisation,48 mainly due to steric effects,58 has been found for regularly packed self-assembled monolayers of trans-azobiphenyls, with S1 lifetimes of the same order of magnitude as in the present work. In all cases the effect on the cis-to-trans photodynamics was much less important.
The reason why the interactions with the environment affect the trans-to-cis photodynamics much more than the cis-to-trans dynamics is twofold: first, the trans azobenzene isomer preferentially undergoes stacking interactions, which are especially pronounced in the nucleic acid environment. Second, the asymmetry of the PESs comes into play. In particular, the S1 potential energy curve as a function of the CNNC torsional angle is much steeper on the cis side than on the trans side (see Fig. 4), according to various theoretical calculations.39,57,59,60 This is in agreement with the S1 lifetimes, that are much shorter for the cis than for the trans isomer, even in non-viscous solvents.61,62 The S1 Franck–Condon point for the cis isomer is about 0.7 eV higher than for the trans isomer39,60 and the minimum energy pathway in S1 from the trans conformation to the torsional conical intersection is practically flat, perhaps with a very small barrier.39,60,63 Moreover, the S2/S1 conical intersection on the trans side is very close to the Franck–Condon point39,63 whereas in the case of the cis-to-trans photochemical pathway the S2/S1 and S1/S0 conical intersection seams64 are in immediate vicinity, permitting ultrafast S2 → S1→ S0 conversions. Therefore, the driving force that allows the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond to twist even in the presence of steric hindrance is much stronger when starting from the cis conformation than from the trans conformation. Conversely, the shallow PES topology of the trans isomer enhances the susceptibility of the trans isomer to steric effects.
N double bond to twist even in the presence of steric hindrance is much stronger when starting from the cis conformation than from the trans conformation. Conversely, the shallow PES topology of the trans isomer enhances the susceptibility of the trans isomer to steric effects.
3.2 Photochemical pathways
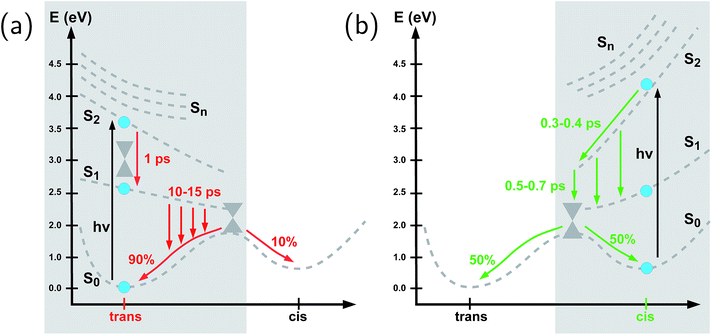
To summarize our observations, Fig. 4 shows a schematic picture of the photodynamics of trans and cis azobenzene in RNA, as obtained from the ensemble of propagated QM/MM–SH trajectories. The effective reaction coordinate is a complex combination of local modes, especially involving a concerted motion of neighboring dihedrals, as further discussed below. In the following, we briefly recapitulate the photochemical pathways delineated in Fig. 4. Detailed information, e.g., regarding the energetic distribution of the trajectory ensemble at the hopping geometries, is provided in the ESI (Section S4†).After the initial excitation from the trans ground state to the S2 state (with an excitation energy of 3.62 eV, averaged over the trajectory ensemble), the close-lying S3, S4 and S5 states are temporarily populated to some extent by nonadiabatic transitions. Within less than a picosecond (i.e., 0.7–1 ps), the population is transferred from S2 and the partially populated upper states to the S1 state, at geometries that remain close to the Franck–Condon region. A majority of trajectories are then found to stay on the S1 surface for an extended time interval, presumably due to existence of a local minimum and shallow barrier preceding the S1/S0 conical intersection at CNNC = 90°. This PES topology, which is modified as compared with the gas phase, is most likely created by the stacking of trans azobenzene with the upper and lower bases, hindering trans-to-cis photoisomerisation (see the discussion below). At this point, a subset of reactive trajectories have high enough energy to proceed to the S1/S0 conical intersection. A trajectory is considered to reach the conical intersection if it meets a threshold criterion for the energy difference between two states, i.e., ΔE < 0.1 eV. The remaining trajectories are unreactive and return to S0, mainly by hopping from the transoid region, where the S1/S0 energy difference is still large. In both reactive and unreactive cases, the dynamics tends to be slow, of the order of 10 picoseconds. Overall, almost 80% of the population is transferred back to the trans ground state via unreactive trajectories. The complementary subset of trajectories which reach the conical intersection are eventually equidistributed between the trans and cis ground-state geometries, rendering the overall quantum yield small, with Φt→c ≃ 0.1.
By contrast, starting in the S2 state of the cis isomer (at an excitation energy of 4.1 eV), trajectories directly reach the three-state conical intersection region between S2, S1, and S0, within <1 ps, promoted by the steep S2 surface. No participation of the S3, S4 and S5 states is noticed when starting from the cis isomer. At the conical intersection, population is transferred either directly to the S0 state or via S1 to S0 almost immediately, such that the S1 lifetime of the cis isomer could not be determined. Since the total population decays through the conical intersection which provides access to the trans and cis channels in a symmetric fashion, the final ground-state populations are found to be equally distributed, such that the cis-to-trans photoisomerisation quantum yield is 50%.
3.3 Isomerisation mechanism
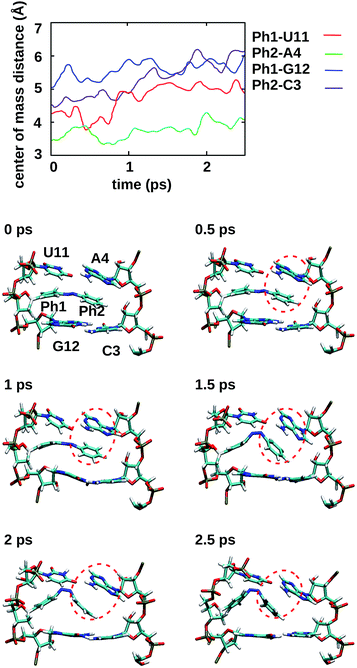
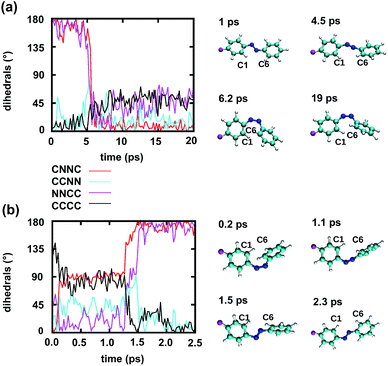
To gain some insight into the effect of the local RNA environment on the isomerisation process, Fig. 5 shows selected snapshots from a reactive trans-to-cis trajectory in the Azo–RNA2 system. This trajectory is among the few realizations that isomerize rapidly, but similar scenarios have been observed for other reactive and unreactive trajectories. The figure illustrates the time-evolving center-of-mass distance between the azobenzene rings and the upper and lower base pairs. Despite the isomerisation event (at ∼1.5 ps), the relative distances evolve smoothly and stacking interactions are preserved to a large extent. This underscores the important role of stacking, and also the flexibility of the chromophore's non-covalent binding interactions within its local RNA environment. As further discussed in the ESI,† the isomerization event indeed does not exert a major disrupting effect on the interaction with the nearest neighbouring RNA bases (see ESI Section S5†).Fig. 5 further suggests that the isomerization event follows a volume-conserving mechanism, to exert as little perturbation on the nearest-neighbor environment as possible. This implies that a cooperative dynamics must be involved, similarly to the related pedal-like mechanism that was found in solution phase.32,57 Fig. S9† shows that substantial changes in the CNN and NNC angles occur very soon after excitation, because in the S1(n–π*) state, the equilibrium CNN/NNC value is larger than in the ground state.39,49,63 Even in the gas phase, an inversion-assisted rotation mechanism of the photoisomerisation is observed.63 To better understand the details of the mechanism, we now analyze the time evolution of several dihedrals – i.e., the CNNC (C2–N3–N4–C5), CCNN (C1–C2–N3–N4), NNCC (N3–N4–C5–C6), and CCCC (C1–C2–C5–C6) dihedral angles – as illustrated in Fig. 6 for two selected trajectories (see Fig. 1c and ESI Section S6† for the atom labels and definition of the relevant dihedral angles).
Fig. 6a illustrates a reactive trans-to-cis trajectory in the Azo–RNA1 complex, where the sudden change in the CNNC dihedral (red trace) is seen to be accompanied by an almost equal change in the NNCC dihedral (black trace). Indeed, the absolute value of the NNCC dihedral changes more – from ≈180° to ≈0° – than the CCNN dihedral (cyan trace), which changes from ≈0° to ≈45° via ≈80° while going from structure 1 to 3 via 2. Note that structure 2 corresponds to a geometry near the conical intersection, preceding the hopping event. From the evolution of the dihedrals, we infer that the N3–N4 twist is immediately followed by a rotation around the N4–C5 single bond. The distant phenyl ring (as seen from the linker position) undergoes partial in-plane rotation around the N4–C5 bond. A very similar scenario is observed for the reactive cis-to-trans trajectory shown in Fig. 6b. The CNNC and NNCC evolution is again found to be closely correlated, even though the NNCC dihedral appears to be delayed until the hopping event occurs. In a complementary fashion to Fig. 6 and S8 of the ESI† shows the signed values of the relevant dihedrals.
Similar observations were made for the Azo–RNA2 complex, even though some details for the individual trajectories differ (see the ESI Section S7.2† for a detailed discussion). In all cases, a concerted mechanism involving several dihedrals is observed, which is consistent with the abovementioned pedal-like mechanism that was found for the azobenzene chromophore in solution.32,57 As can be inferred from Fig. 6 and is further explained below, this mechanism is coupled to a collective rearrangement of the local RNA environment.
3.4 Static vs. dynamic effects of RNA environment
In view of the pronounced effect of the RNA environment on the trans-to-cis isomerization kinetics, the question arises whether the local environment mainly exerts a static or dynamic influence. Therefore, we investigated the equilibrium (static) effects of the RNA environment on the shape of the effective torsional potential energy surface by Boltzmann inversion,65 based on the CNNC dihedral angle distribution from an ensemble of ground state QM/MM equilibration trajectories for azobenzene in different environments (in vacuo, in ethylene glycol and in RNA). As detailed in the ESI (Section S5.3†), the analysis reveals that the shape of the ground state potential energy surface around the cis and trans equilibrium geometry in RNA is very similar to the corresponding potentials in solution and in vacuo. Small shifts in the equilibrium values of the CNNC dihedral are observed – about 5° for trans-azobenzene, and even less for cis-azobenzene – in opposite directions for Azo–RNA1 and Azo–RNA2, which can be related to the effect of the chiral environments (see the discussion below). Perhaps contrary to expectation, the effective torsional potentials in RNA are not steeper – but rather slightly broader – than in solution or in vacuo, showing no evidence of a constraining environment. Therefore, we conclude that the slowing down of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond twisting and of the S1 decay are due to dynamic caging, i.e., to the relatively long time needed for the RNA bases to collectively relax geometrically in order to match the twisting of trans-azobenzene. In this sense, steric hindrance in the context of trans-to-cis isomerization should be thought of as a dynamic effect.
N double bond twisting and of the S1 decay are due to dynamic caging, i.e., to the relatively long time needed for the RNA bases to collectively relax geometrically in order to match the twisting of trans-azobenzene. In this sense, steric hindrance in the context of trans-to-cis isomerization should be thought of as a dynamic effect.
The comparatively slow time scale of collective reorientation can also be inferred from the time evolution of the distance between the azobenzene chromophore and the upper and lower base pairs, see the ESI (Section S5.1†). Here, we analyse the fraction of time spent by the photochemical trajectories in configurations below the sum of van der Waals radii, using a model of interlocking spheres. In line with Fig. 5, the distal phenyl ring (Ph2) is found to be especially close to the upper bases, and spends about 20% of the simulation time at distances below the sum of van der Waals radii (and even up to 70% in the electronic ground state). On average, the distance steadily increases during the simulation time (see Fig. S4†), both for unreactive and reactive trajectories. As also suggested by Fig. 5, the reorientation of the local environment is gradual and leads to an increase in local RNA fluctuations (see Section S5.2†) due to the interaction with the vibronically hot chromophore.
3.5 Chiral selectivity
Finally, we address the role of chirality in the photoisomerization event, which is of particular interest in the present context since the RNA environment as such exhibits right-handed helical chirality. With regard to the chromophore, the trans azobenzene isomer is achiral, while the cis isomer exhibits helical chirality and exists in a P (plus, i.e., right-handed) helical form and an M (minus, i.e., left-handed) helical form (see ESI Section S6† for details). Likewise, the S1/S0 conical intersection exhibits symmetric P and M type precursor structures of the two cis isomers.32,66,67 For the trans-to-cis photochemical pathway, it is therefore of interest to know whether the P or M type cis form is preferentially generated in the reactive trajectories. Conversely, for the cis-to-trans pathway, we will analyze whether a chirality preserving or a chirality inverting pathway is adopted. Even in an achiral environment, it was found that an asymmetry can exist between these pathways.32,66,67 This asymmetry could be enhanced in the chiral RNA–linker environment.Interestingly, a marked preference for M vs. P helicity appears in the cis species of the Azo–RNA1 vs. Azo–RNA2 complexes as a result of the initial equilibration procedure. That is, it turns out that the initial helicity of cis-azobenzene is of M type for Azo–RNA1 and of P type for Azo–RNA2. The reason for this intrinsic difference seems to lie in the preference of cis azobenzene to reside either in the major groove, as is the case for Azo–RNA1, or in the minor groove, as is the case for Azo–RNA2. In earlier MD studies of the Azo–RNA2 complex with a D-threoninol linker,20 we also found a minor groove preference of cis azobenzene.
In the following analysis, we will make use of the fact that the algebraic sign of the CNNC dihedral during the isomerization process informs about the P and M helicity, i.e., a positive sign correlates with P helicity while a negative sign correlates with M helicity.66,68 A complementary analysis can be given in terms of the change of the NNCC and CCNN dihedrals,32 which is especially useful when analyzing the initial chirality preserving or chirality inverting property of the isomerisation pathway (see ESI Section S8†): The pathway is chirality conserving if the CNNC twist is accompanied by a conrotatory torsion of the N–C bonds such that the CCNN and NNCC groups tend to become planar. By contrast, the pathway is chirality inverting if the initial conrotatory torsion of the N–C bonds brings the CCNN and NNCC dihedrals towards 90° and beyond. (Note that disrotatory phenyl torsions cannot be classified in this way).
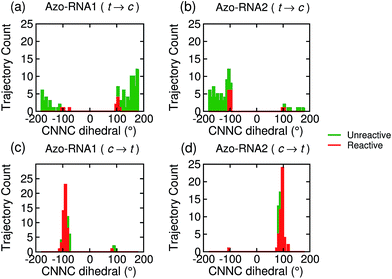
Focusing on the distribution and sign of the CNNC dihedral, Fig. 7 shows the CNNC dihedral at the S1/S0 hopping point in the range [−180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180], for the trajectories starting from the trans (upper panels) and cis (lower panels) isomer, both for reactive (red) and unreactive (green) trajectories.
180], for the trajectories starting from the trans (upper panels) and cis (lower panels) isomer, both for reactive (red) and unreactive (green) trajectories.
For the trans initial conditions (Fig. 7a and b), we focus upon the reactive trajectories (red bars) whose hopping geometries fall into a narrow range around ±90°, where the conical intersection is located. By contrast, for the unreactive trajectories (green bars), the CNNC dihedral at the S1/S0 hopping points is spread over a wide range, i.e., −100° to −180° and 60° to 180°, consistent with the observation that most unreactive trajectories hop far before reaching the conical intersection, and consequently go back to the trans ground state, resulting in a small photoisomerisation quantum yield. As can be seen from Fig. 7a, there is no clear preference for the P-type or M-type cis photoproducts in Azo–RNA1, while a certain preference for the M-type cis photoproduct is found for the Azo–RNA2 complex. However, no definite conclusion can be drawn from the limited set of reactive trajectories. This is confirmed by a complementary analysis based upon the CCNN and NNCC dihedrals, as reported in the ESI (Section S8†).
Conversely, a pronounced chiral selectivity is observed when considering the cis-to-trans photoisomerisation dynamics, as can be inferred from Fig. 7c and d. Starting from the equilibrated M vs. P forms of the cis isomer of Azo–RNA1 and Azo–RNA2, it is seen that the M vs. P forms also prevail at the respective hopping geometries. Indeed, an almost perfectly chirality conserving pathway is found in both cases. This conclusion is confirmed by a detailed analysis of the NNCC and CCNN dihedral angles as described in the ESI (Section S8†): during the initial dynamics (∼200 fs) of the Azo–RNA1 complex, the NNCC dihedral tends to 0° starting from negative values, and its counterpart in the Azo–RNA2 complex also tends to 0° starting from positive values. This confirms that the M-helical form of Azo–RNA1 and the P-helical form of Azo–RNA2 remain conserved on the path towards the S1/S0 conical intersection. Clearly, the chiral RNA environment is the determining factor inducing this pronounced selectivity. For comparison, a ∼75% predominance of the chirality conserving pathway was found for the gas-phase cis-to-trans isomerization in ref. 66 and 67, while the study of ref. 32 did not provide evidence for such a preferential pathway in gas phase or solution. (However, a nearly complete stereospecificity was found for a related arylazopyrazole photoswitch69).
Notably, a narrow, almost normal-type distribution of CNNC dihedrals around ±90° is observed both for the reactive and unreactive cis-to-trans trajectories of Azo–RNA1 and Azo–RNA2 in Fig. 7. All trajectories reach the vicinity of the conical intersection and thereby the quantum yield of photoisomerisation is 50%.
4 Conclusions
To summarize, we have investigated the photoisomerization mechanism of an azobenzene chromophore covalently attached to an RNA double strand using state-of-the-art semiempirical QM/MM–SH methodology that has proven reliable in the treatment of azobenzene in various environments over recent years.32,38–40,48,50 Concerted nonadiabatic dynamics in six singlet electronic states is followed after photoexcitation to the bright S2 state. Our investigation highlights several key features: first, ultrafast internal conversion from the S2 state to the S1 state initiates the photochemical process (apart from minor participation of the S3 and S4 states), very similarly to the photochemistry of the bare azobenzene chromophore in gas phase63,70 or in solution.32,57 Second, the main effect of the extremely constrained RNA environment is felt in the S1 dynamics: the local interactions with the RNA bases lead to an S1 lifetime of ∼15 picoseconds for the trans azobenzene chromophore preceding isomerization, as compared with 500 femtoseconds in vacuo. Further, the trans-to-cis photoisomerization quantum yield is reduced to ∼10%. By contrast, the electronically excited cis isomer remains short-lived, on a time scale of ∼500 femtoseconds, with a 50% cis-to-trans quantum yield. We attribute this pronounced difference to the fact that the upper and lower base pairs exert a highly stabilizing effect on the trans azobenzene isomer – but not on the cis isomer. This picture is confirmed by representative QM/MM trajectories. For the same reasons, the isomerization mechanism is found to be volume-preserving and proceeds by a concerted motion in several dihedral angles, resulting in a pedal-like motion that also prevails in the isomerisation in solution.32,57 This motion is accompanied by a collective rearrangement of the local RNA environment that gives rise to steric constraints which are of dynamical rather than static nature.Even though time-resolved spectroscopic observations for these and related systems are not yet available, our predictions are in line with similar trends observed for azobenzene photoisomerization in constrained environments and adsorbed on surfaces.32,47–51
Finally, we found that RNA chirality plays a subtle role in the process and leads to preferential P type (right-handed) or M type (left-handed) cis-to-trans isomerisation pathways. Strikingly, the equilibrated Azo–RNA1 vs. Azo–RNA2 cis species are of M type vs. P type, respectively, and conserve their helicity during their short-time dynamics such that the preferred M-type vs. P-type forms are also observed at the hopping geometry. While some degree of chiral selectivity has been previously found for cis-to-trans azobenzene isomerization in the gas phase or in less specific environments, the almost full conservation of M-type vs. P-type helicity during the excited-state dynamics of the Azo–RNA complexes is a unique feature of the chiral RNA environment.
Most of these conclusions are remarkably similar for the two types of chromophore-linker–RNA complexes that were investigated in this work, with the exception of the minor vs. major groove preference of the cis azobenzene chromophore, which is opposite for the two complexes, thus entailing opposite preferences for P vs. M helicity. Apart from this difference, the similarity of the mechanism and excited-state lifetimes is striking. Our results underline the crucial role of local stacking interactions in selectively stabilizing the trans form of the chromophore, which should be accounted for as one of the key guiding principles when designing new, optimally tailored RNA–linker-azobenzene combinations. Specific local modifications, using suitable linkers and substituents, could lead to reduced S1 lifetimes and enhanced quantum yields, but possibly at the expense of reduced differences in melting temperatures associated with the trans vs. cis isomers. In view of connecting to longer time scales where RNA unfolding is observed,23 the present benchmark study paves the way for multiscale simulations31 to model light-responsive functional oligonucleotides and nanoassemblies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge support by the DFG via the Research Center SFB 902 (“Molecular Principles of RNA-based Regulation”) and the RTG 1986 “Complex Scenarios of Light Control”, as well as by the Alfried Krupp von Bohlen und Halbach Foundation, associated with the German Scholar Organization (GSO) via grant II-98. M. P. acknowledges the financial support of Pisa University (grant PRA-2016-46). We thank K. Falahati for assistance with the preparation of the figures.Notes and references
- A. S. Lubbe, W. Szymanski and B. L. Feringa, Chem. Soc. Rev., 2017, 46, 1052–1079 RSC.
- G. Mayer and A. Heckel, Angew. Chem., Int. Ed., 2006, 45, 4900–4921 CrossRef CAS PubMed.
- A. Jäschke, FEBS Lett., 2012, 586, 2106–2111 CrossRef PubMed.
- W. Szymański, J. M. Beierle, H. A. V. Kistemaker, W. A. Velema and B. L. Feringa, Chem. Rev., 2013, 113, 6114–6178 CrossRef PubMed.
- H. Ito, X. Liang, H. Nishioka and H. Asanuma, Org. Biomol. Chem., 2010, 8, 5519–5524 CAS.
- J. Li, X. Wang and X. Liang, Chem.–Asian J., 2014, 9, 3344–3358 CrossRef CAS PubMed.
- Y. Kamiya, T. Takagi, H. Ooi, H. Ito, X. Liang and H. Asanuma, ACS Synth. Biol., 2015, 4, 365–370 CrossRef CAS PubMed.
- J. A. Phillips, H. Liu, M. B. O'Donoghue, X. Xiong, R. Wang, M. You, K. Sefah and W. Tan, Bioconjugate Chem., 2011, 22, 282–288 CrossRef CAS PubMed.
- T. Cha, J. Pan, H. Chen, H. N. Robinson, X. Li, C. Mao and J. H. Choi, J. Am. Chem. Soc., 2015, 137, 9429 CrossRef CAS PubMed.
- X. Liang, H. Nishioka, N. Takenaka and H. Asanuma, ChemBioChem, 2008, 9, 702–705 CrossRef CAS PubMed.
- H. M. D. Bandara and S. C. Burdette, Chem. Soc. Rev., 2012, 41, 1809–1825 RSC.
- A. A. Beharry and G. A. Woolley, Chem. Soc. Rev., 2011, 40, 4422–4437 RSC.
- J. Andersson, S. Li, P. Lincoln and J. Andréasson, J. Am. Chem. Soc., 2008, 130, 11836–11837 CrossRef CAS PubMed.
- H. Rau, in Photochemistry and Photophysics, ed. RabekJ. F., CRC Press, Boca Raton, FL, USA, 1990, pp. 119–141 Search PubMed.
- E. Merino and M. Ribagorda, Beilstein J. Org. Chem., 2012, 8, 1071–1090 CrossRef CAS PubMed.
- K. Morgenstern, Acc. Chem. Res., 2009, 42, 213–223 CrossRef CAS PubMed.
- H. Kashida, X. Liang and H. Asanuma, Curr. Org. Chem., 2009, 13, 1065–1084 CrossRef CAS.
- H. Ito, H. Nishioka, X. Liang and H. Asanuma, Nucleic Acids Symp. Ser., 2007, 51, 171–172 CrossRef PubMed.
- M. Biswas and I. Burghardt, Biophys. J., 2014, 107, 932–940 CrossRef CAS PubMed.
- D. Rastädter, M. Biswas and I. Burghardt, J. Phys. Chem. B, 2014, 118, 8478–8488 CrossRef PubMed.
- H. Asanuma, T. Ito, T. Yoshida, X. G. Liang and M. Komiyama, Angew. Chem., Int. Ed., 1999, 38, 2393–2395 CrossRef CAS PubMed.
- H. Asanuma, D. Matsunaga and M. Komiyama, Nucleic Acids Symp. Ser., 2007, 49, 35–36 CrossRef PubMed.
- Y. Nakasone, H. Ooi, Y. Kamiya, H. Asanuma and M. Terazima, J. Am. Chem. Soc., 2016, 138, 9001–9004 CrossRef CAS PubMed.
- M. Böckmann, S. Braun, N. L. Doltsinis and D. Marx, J. Chem. Phys., 2013, 139, 084108 CrossRef PubMed.
- B. G. Keller, A. Kobitski, G. Jäschke, U. Nienhaus and F. Noé, J. Am. Chem. Soc., 2014, 136, 4534–4543 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- O. Weingart, Curr. Org. Chem., 2016, 21, 586–601 CrossRef.
- H. J. Kulik, J. Zhang, J. P. Klinman and T. J. Martínez, J. Phys. Chem. B, 2016, 120, 11381–11394 CrossRef CAS PubMed.
- A. Strambi, B. Durbeej, N. Ferré and M. Olivucci, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21322–21326 CrossRef CAS PubMed.
- V. A. Spata and S. Matsika, J. Phys. Chem. A, 2014, 118, 12021–12030 CrossRef CAS PubMed.
- S. Osella and S. Knippenberg, J. Am. Chem. Soc., 2017, 139, 4418–4428 CrossRef CAS PubMed.
- V. Cantatore, G. Granucci and M. Persico, Comput. Theor. Chem., 2014, 1040–1041, 126–135 CrossRef CAS.
- S.-H. Xia, G. Cui, W.-H. Fang and W. Thiel, Angew. Chem., Int. Ed., 2016, 55, 2067–2072 CrossRef CAS PubMed.
- P. Mondal, M. Biswas, T. Goldau, A. Heckel and I. Burghardt, J. Phys. Chem. B, 2015, 119, 11275–11286 CrossRef CAS PubMed.
- A. Kingsland, S. Samai, Y. Yan, D. S. Ginger and L. Maibaum, J. Phys. Chem. Lett., 2016, 7, 3027–3031 CrossRef CAS PubMed.
- T. Goldau, K. Murayama, C. Brieke, S. Steinwand, P. Mondal, M. Biswas, I. Burghardt, J. Wachtveitl, H. Asanuma and A. Heckel, Chem.–Eur. J., 2015, 21, 2845–2854 CrossRef CAS PubMed.
- T. Goldau, K. Murayama, C. Brieke, H. Asanuma and A. Heckel, Chem.–Eur. J., 2015, 21, 17870–17876 CrossRef CAS PubMed.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615 CrossRef CAS.
- T. Cusati, G. Granucci, E. Martínez-Núñez, F. Martini, M. Persico and S. Vázquez, J. Phys. Chem. A, 2012, 116, 98–110 CrossRef CAS PubMed.
- C. Ciminelli, G. Granucci and M. Persico, Chem.–Eur. J., 2004, 10, 2327–2341 CrossRef CAS PubMed.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725 CrossRef CAS PubMed.
- J. W. Ponder, TINKER 6.1, Washington University School of Medicine, St. Louis, MO, 2012, http://dasher.wustl.edu/tinker Search PubMed.
- W. L. Jorgensen and J. D. Madura, J. Am. Chem. Soc., 1983, 105, 1407–1413 CrossRef CAS.
- I. Antes and W. Thiel, J. Phys. Chem. A, 1999, 103, 9290–9295 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- G. Floss, G. Granucci and P. Saalfrank, J. Chem. Phys., 2012, 137, 234701 CrossRef PubMed.
- V. Cantatore, G. Granucci, G. Rousseau, G. Padula and M. Persico, J. Phys. Chem. Lett., 2016, 7, 4027–4031 CrossRef CAS PubMed.
- T. Cusati, G. Granucci and M. Persico, J. Am. Chem. Soc., 2011, 133, 5109–5123 CrossRef CAS PubMed.
- E. Benassi, G. Granucci, M. Persico and S. Corni, J. Phys. Chem. C, 2015, 119, 5962–5974 CAS.
- L. Creatini, T. Cusati, G. Granucci and M. Persico, Chem. Phys., 2008, 347, 492–502 CrossRef CAS.
- K. Andersson, P.-A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- A. Cembran, F. Bernardi, M. Garavelli, L. Gagliardi and G. Orlandi, J. Am. Chem. Soc., 2004, 126, 3234–3243 CrossRef CAS PubMed.
- V. Ladányi, P. Dvorák, J. Al Anshori, L. Vetráková, J. Wirz and D. Heger, Photochem. Photobiol. Sci., 2017, 16, 1757–1761 Search PubMed.
- Y. Yan, X. Wang, J. I. L. Chen and D. S. Ginger, J. Am. Chem. Soc., 2013, 135, 8382–8387 CrossRef CAS PubMed.
- S. Samal, D. J. Bradley, T. Choi, Y. Yan and D. S. Ginger, J. Phys. Chem. C, 2017, 121, 6997–7004 Search PubMed.
- M. Böckmann, N. L. Doltsinis and D. Marx, J. Phys. Chem. A, 2010, 114, 745–754 CrossRef PubMed.
- E. Titov, G. Granucci, J. P. Gotze, M. Persico and P. Saalfrank, J. Phys. Chem. Lett., 2016, 7, 3591–3596 CrossRef CAS PubMed.
- M. Pederzoli, J. Pittner, M. Barbatti and H. Lischka, J. Phys. Chem. A, 2011, 115, 11136–11143 CrossRef CAS PubMed.
- J. Casellas, M. J. Bearpark and M. Reguero, ChemPhysChem, 2016, 17, 3068–3079 CrossRef CAS PubMed.
- T. Nägele, R. Hoche, W. Zinth and J. Wachtveitl, Chem. Phys. Lett., 1997, 272, 489 CrossRef.
- H. Satzger, S. Spörlein, C. Root, J. Wachtveitl, W. Zinth and P. Gilch, Chem. Phys. Lett., 2003, 372, 216 CrossRef CAS.
- E. Tan, S. Amirjalayer, S. Smolarek, A. Vdovin, F. Zerbetto and W. J. Buma, Nat. Commun., 2015, 6, 5860 CrossRef PubMed.
- Conical Intersections: Theory, Computation, and Experiment, ed. W. Domcke, H. Köppel and D. Yarkony, World Scientific Publishing Company, 2011 Search PubMed.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624 CrossRef CAS PubMed.
- O. Weingart, Z. Lan, A. Koslowski and W. Thiel, J. Phys. Chem. Lett., 2011, 2, 1506–1509 CrossRef CAS.
- Y. Ootani, S. Kiminori, A. Nakayama, T. Noro and T. Taketsugu, J. Chem. Phys., 2009, 131, 194306 CrossRef PubMed.
- J. A. Gámez, O. Weingart, A. Koslowski and W. Thiel, J. Chem. Theory Comput., 2012, 8, 2352–2358 CrossRef PubMed.
- Y. Wang, X. Liu, G. Cui, W. Fang and W. Thiel, Angew. Chem., Int. Ed., 2016, 55, 14009 CrossRef CAS PubMed.
- T. Schultz, J. Quenneville, B. Levine, A. Toniolo, T. J. Martínez, S. Lochbrunner, M. Schmitt, J. P. Shaffer, M. Z. Zgierski and A. Stolow, J. Am. Chem. Soc., 2003, 125, 8098–8099 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00072g |
| This journal is © The Royal Society of Chemistry 2018 |