Open Access Article
Open Access ArticleThermal property improvement of polytetrafluoroethylene nanocomposites with graphene nanoplatelets
Xinzhi
Cai
a,
Zeyi
Jiang
ab,
Xinru
Zhang
 *ac,
Ting
Gao
a,
Kai
Yue
ac and
Xinxin
Zhang
ab
*ac,
Ting
Gao
a,
Kai
Yue
ac and
Xinxin
Zhang
ab
aSchool of Energy and Environmental Engineering, University of Science and Technology Beijing, Beijing, 100083, China. E-mail: xinruzhang@ustb.edu.cn
bBeijing Key Laboratory for Energy Saving and Emission Reduction of Metallurgical Industry, University of Science and Technology Beijing, Beijing, 100083, China
cBeijing Engineering Research Center of Energy Saving and Environmental Protection, University of Science and Technology Beijing, Beijing, 100083, China
First published on 21st March 2018
Abstract
Thermal properties including the crystallization behavior, thermal stability and thermal conductivity for a series of graphene nanoplatelet (GNP)–polytetrafluoroethylene (PTFE) nanocomposites were studied. The GNP–PTFE nanocomposites were fabricated via solvent-assisted blending followed by cold-pressing and sintering. The results indicated that the GNP–PTFE nanocomposites retained the good thermal stability of the PTFE matrix, and possessed better crystallization and much higher thermal conductivity than pure PTFE. The thermal conductivity of PTFE nanocomposites with a GNP mass fraction of 20% could reach 4.02 W (m K)−1, which was increased by 1300% compared with pure PTFE. Additionally, a theoretical model was proposed to analyze the thermal conductivity of GNP–PTFE nanocomposites. It is demonstrated that adding GNPs into PTFE homogeneously can effectively improve the thermal properties of the nanocomposites.
Introduction
Polytetrafluoroethylene (PTFE) is a kind of important fluoropolymer with a low friction coefficient, high chemical resistance, fire-retardant properties and high thermal stability, which is widely used in various high-end applications, such as aerospace, the automotive industry, chemical engineering, biomedicine and heat management.1–3 However, pure PTFE has a low thermal conductivity of ∼0.3 W (m K)−1,4 which limits its application in engineering.5–7 To address this issue, the incorporation of nanofillers with high thermal conductivity into the PTFE matrix has received much attention in the past few years.To date, researchers have investigated the thermal properties of PTFE composites filled with some nanofillers. Using the finite element method, Jin et al. mathematically analyzed the effects of size, volume fraction, and distribution of fillers on the thermal conductivity of graphite particles–PTFE composites and carbon fibers–PTFE composites.8 Chen et al. measured the thermal conductivity of boron nitride (BN)–PTFE, zinc oxide (ZnO)–PTFE, tetra-needle-shaped zinc oxide whiskers (T-ZnO)–PTFE and hybrid filler (ZnO and BN, T-ZnO and BN)-PTFE composites.9 They found that the hybrid filler–PTFE composites had a higher thermal conductivity than those filled with only one kind of filler at the same content, and the thermal conductivity for the hybrid filler–PTFE composites was 1.38 W (m K)−1, when the content of T-ZnO and BN was 3% and 27%, respectively. Recently, Pan et al. reported the thermal conductivity of micro–nano AlN cofilled PTFE composites (mn-AlN–PTFE) and silane coupling agent modified BN filled PTFE composites (scam-BN–PTFE).10,11 The results indicated that when the volume fraction of filler was 30%, the thermal conductivity of mn-AlN–PTFE and scam-BN–PTFE composites was 0.84 W (m K)−1 and 0.722 W (m K)−1, respectively. In addition, Sahli et al. prepared thermally expanded graphite–PTFE composites (TEG–PTFE) and studied the thermal stability and thermal resistance of the composites. They found that with the increase of the TEG content, the glass-transition temperature and the degradation temperature of TEG–PTFE both increased.12 These researches demonstrated that the incorporating of fillers with high thermal conductivity is effective to improve the thermal properties of PTFE matrix.
Graphene is a kind of two-dimensional layered material with an ultrahigh thermal conductivity of ∼5000 W (m K)−1, high Young's modulus of ∼1.0 TPa and high intrinsic mobility of ∼200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm2 (V s)−1,13,14 which shows a great potential to be a filler for the fabrication of nanocomposites with high properties.15–17 Gu fabricated a series of GNPs–polymer nanocomposites, i.e., GNPs–ultrahigh molecular weight polyethylene,18 functionalized GNPs–bisphenol A epoxy resin19 and functionalized GNPs–phenylphosphonate based epoxy resin,20 and found that GNPs have a strong ability to improve the thermal properties of composites. Recently, some researchers have studied the methods of fabricating graphene–PTFE nanocomposite and the effects of graphene filler on the gas barrier behavior, mechanical properties and electrical characteristics for the graphene–PTFE nanocomposites. Van Rooyen et al. investigated the method to prepare graphene–PTFE nanocomposite and evaluated the influence of the powder blending, fabrication method and the graphene concentration on its physical property.21 In addition, van Rooyen et al. studied the gas barrier properties of oxyfluorinated graphene filled PTFE nanocomposites, and found that when the volume fraction of oxyfluorinated graphene was 7%, the helium gas permeability of nanocomposites reduced by 88%.22 Suh and Bae fabricated the graphene–PTFE nanocomposite via high-energy milling of PTFE and graphene powder followed by hot-pressing, and measured its mechanical and electrical properties. The results indicated that, compared to pure PTFE, the yield stress and Young's modulus of graphene (3 vol%)–PTFE nanocomposites increased 60% and 233%, respectively.23 The electrical conductivity of graphene (30 vol%)–PTFE nanocomposites was 7353 S m−1.24 However, to date, little is known about the thermal properties of graphene–PTFE nanocomposites.
000 cm2 (V s)−1,13,14 which shows a great potential to be a filler for the fabrication of nanocomposites with high properties.15–17 Gu fabricated a series of GNPs–polymer nanocomposites, i.e., GNPs–ultrahigh molecular weight polyethylene,18 functionalized GNPs–bisphenol A epoxy resin19 and functionalized GNPs–phenylphosphonate based epoxy resin,20 and found that GNPs have a strong ability to improve the thermal properties of composites. Recently, some researchers have studied the methods of fabricating graphene–PTFE nanocomposite and the effects of graphene filler on the gas barrier behavior, mechanical properties and electrical characteristics for the graphene–PTFE nanocomposites. Van Rooyen et al. investigated the method to prepare graphene–PTFE nanocomposite and evaluated the influence of the powder blending, fabrication method and the graphene concentration on its physical property.21 In addition, van Rooyen et al. studied the gas barrier properties of oxyfluorinated graphene filled PTFE nanocomposites, and found that when the volume fraction of oxyfluorinated graphene was 7%, the helium gas permeability of nanocomposites reduced by 88%.22 Suh and Bae fabricated the graphene–PTFE nanocomposite via high-energy milling of PTFE and graphene powder followed by hot-pressing, and measured its mechanical and electrical properties. The results indicated that, compared to pure PTFE, the yield stress and Young's modulus of graphene (3 vol%)–PTFE nanocomposites increased 60% and 233%, respectively.23 The electrical conductivity of graphene (30 vol%)–PTFE nanocomposites was 7353 S m−1.24 However, to date, little is known about the thermal properties of graphene–PTFE nanocomposites.
In this study, the graphene nanoplatelet (GNP)–PTFE nanocomposites with varied GNP mass fractions of 1%, 5%, 10%, 15% and 20% were fabricated via solvent-assisted blending followed by cold-pressing and sintering. Then, the microstructure, crystallization behavior, thermal stability and thermal conductivity of GNP–PTFE nanocomposites were measured. Finally, based on the Maxwell-Garnett effective medium approach (MGEMA), a mathematical model to analyze and predict the thermal conductivity of GNP–PTFE nanocomposites was developed by incorporating the interface thermal resistance. The findings may have important implications for understanding the thermal properties of GNP–PTFE nanocomposite.
Experimental
Preparation of GNPs
The graphene dispersions with different mass fractions were prepared by liquid phase exfoliation (LPE) of graphite sheets (Supplied by Chengdu Organic Chemicals Co. Ltd. China.) in ethanol using a tip sonicator (Scientz-950E, Scientz Biotechnology Co. Ltd, China) under the power of 300 W for 120 min.25 After that, the morphology, thickness, defects of the produced GNPs were characterized. In detail, the morphology of pristine graphite and the produced GNP was observed by a scanning electron microscopy (SEM) (Nova NanoSEM 430, FEI, USA) operating at a 5 kV acceleration voltage. The thickness of the produced GNP was examined by a transmission electron microscope (TEM) (Tecnai F30, FEI, USA). The defects of the GNPs were measured by Raman spectrometer (LabRAM HR800, Horiba Jobin-Yvon, Japan) with a 514 nm wavelength laser via depositing a GNP film onto a glass slide.Fabrication of GNP–PTFE nanocomposites
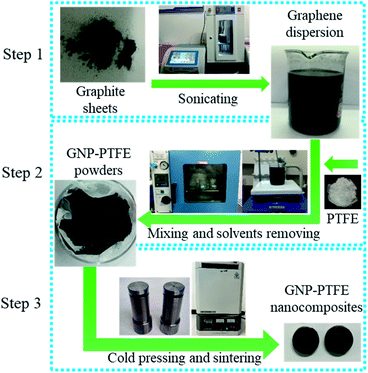
The method to fabricate the GNP–PTFE nanocomposites consisted of three steps, as shown in Fig. 1. Firstly, the graphene dispersions with a series of mass fractions were prepared by exfoliating graphite sheets in ethanol via tip sonicating. Secondly, the PTFE powders (Obtained from DuPont, USA.) were added into the graphene dispersions and then fully mixed with GNPs while removing the ethanol using a heating magnetic stirrer for 6 h at 60 °C. After that, the GNP–PTFE slurry was vacuum dried at 60 °C for 24 h to remove the residual ethanol. Finally, the GNP–PTFE powders were cold pressed into cylindrical samples with a diameter of 15 mm at the pressure of 40 MPa for about 10 min. And then the performed GNP–PTFE samples were put into a muffle oven for sintering. During the sintering, the temperature in the oven was firstly increased to 380 °C in 5 h, and held at 380 °C for 3 h, then decreased slowly to room temperature. In the experiments, the PTFE nanocomposites with the GNP mass fractions of 1%, 5%, 10%, 15% and 20% were fabricated.Characterization of GNP–PTFE nanocomposites
The microstructure, crystallization behavior, thermal stability, thermal conductivity and heat transfer phenomena of GNP–PTFE nanocomposites were characterized. In detail, the microstructure of GNP–PTFE nanocomposites and the homogeneity of GNPs in PTFE matrix were micro-observed by metallographic microscope (Axio Scope A1, Zeiss, Germany) and SEM. It should be noted that, in order to observe the microstructure precisely, the GNP–PTFE nanocomposites were fractured in liquid nitrogen to form a neat cross section. The crystallization behavior and thermal stability of GNP–PTFE nanocomposites were determined with different scanning calorimeter (DSC) and thermogravimetric analysis (TGA) by a thermal analysis platform (Labsys Evo, Setaram, France) at a heating rate of 10 °C min−1 from 25 °C to 900 °C under a nitrogen atmosphere. In addition, the thermal conductivity of GNP–PTFE nanocomposites was measured by the transient plane heat source method using a commercial thermal conductivity meter (2500 s, Hot disc, Sweden). In detail, the measurements were conducted by putting the sensor (diameter: 3 mm) into two similar cylindrical samples (diameter: 15 mm, height: 6 mm). A heat pulse of 0.02 W for 20 seconds was supplied by the sensor. The temperature changes of the samples were recorded and then the thermal conductivity was determined.26 During the measurements, six samples were used. Each measurement was repeated for at least 3 times, and results were shown in mean ± standard deviation. Moreover, to observe the heat transfer phenomena through the GNP–PTFE nanocomposites, the pure PTFE sample and GNP–PTFE nanocomposites samples were placed on a heating plate with a constant temperature of 150 °C. The temperature distribution of the samples was measured with an infrared thermal imaging instrument (E60, FLIR Systems, USA).Predicting the thermal conductivity of GNP–PTFE nanocomposites with a mathematical model
A modified Maxwell-Garnett effective medium approach (MGEMA) is used to predict the thermal conductivity of GNP–PTFE nanocomposites by considering the size and aspect ratio of GNP, the thermal conductivity of GNP in each direction and the interface thermal resistance between the GNPs and PTFE matrix.27,28 Specifically, as shown in Fig. 2, the GNP in nanocomposites was treated as a flat cylinder with a diameter of a1 (or a2, a1 = a2) and a height of a3, where 1 and 2 represented in-plane direction, 3 represented through-plane direction. Considering the interfacial thermal resistance between the GNP and polymer matrix, the GNP and the interfacial thermal barrier were taken as a composite unit cell. The thermal conductivity of the unit Kci can be expressed as,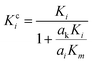 | (1) |
| ak = RkKm | (2) |
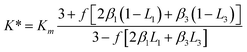 | (3) |
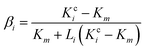 | (4) |
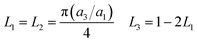 | (5) |
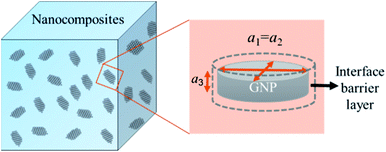 | ||
| Fig. 2 Schematic for a composite unit of a GNP coated with a thin interfacial thermal barrier layer. | ||
Results and discussion
Properties of the produced GNP
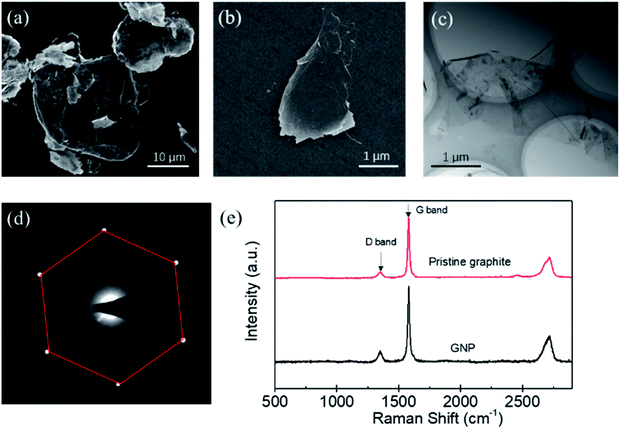
The morphology, thickness, defects of the produced GNPs, were determined by different methods. Fig. 3(a) shows the SEM image of the pristine graphite, which indicates that the graphite sheets are thick and have a size of about 20 μm. Fig. 3(b) is the SEM image of the produced GNP by exfoliating graphite sheets in ethanol via tip sonicating. It can be found that the produced GNP has a size of about 1.5 μm. Fig. 3(c) is the TEM image for the produced GNP, which indicates that the GNPs are few-layered. Fig. 3(d) is the electron diffraction pattern of the produced GNP under the incidence angles of 0°, which provides a six-fold symmetry pattern and shows a typical crystal structure of GNP.29 Evidently, Fig. 3(c) and (d) indicate that, the pristine graphite sheets have been exfoliated into few-layer GNPs.Furthermore, the defects of the produced GNPs were determined by the Raman spectroscopy. Generally, the ratio of intensity of the D band (1350 cm−1) to G band (1580 cm−1) is used to characterize the defects of GNP.30 The less of I (D)/I (G), the lower defect density of GNPs. Fig. 3(e) shows a typical Raman spectroscopy of the pristine graphite sheets and the GNP produced by the exfoliation of graphite via tip sonicating. It can be found that the I (D)/I (G) of the pristine graphite sheets is 0.12, while the I (D)/I (G) of the produced GNP is 0.17. Evidently, the I (D)/I (G) of the produced GNPs is close to that of the pristine graphite sheets, which indicates that comparing with the pristine graphite, the defects of produced GNPs increase little and the GNPs have high quality.
Microstructure of GNP–PTFE composites
As shown in Fig. 4, the microstructure of GNP–PTFE nanocomposites was micro-observed by metallographic microscope and SEM. Fig. 4(a)–(c) show the metallographic microscope images for the surface of pure PTFE, GNP–PTFE nanocomposites with 10% GNP and 20% GNP, respectively. Fig. 4(d)–(f) show the fractured surface morphologies for the pure PTFE, GNP–PTFE nanocomposites with 10% GNP and 20% GNP, respectively. In detail, the Fig. 4(a) and (d) indicate that the pure PTFE has a smooth surface without any impurities. Furthermore, the homogeneity of GNPs in PTFE matrix could be observed in Fig. 4(b) and (c), in which the bright and the dark blocks present the GNPs and PTFE matrix in nanocomposites, respectively. Moreover, the Fig. 4(b) and (e) indicate that, for the GNP (10%)–PTFE nanocomposites, the GNP fillers disperse homogeneously, and are isolated with each other. Meanwhile, when the mass fractions of GNP increased to 20%, as shown in the Fig. 4(c) and (f), more GNPs could be observed in the same range of view, meanwhile, some GNPs are found to contact with each other.Crystalline behavior and thermal stability
PTFE is a kind of semicrystalline polymer with crystalline structure. Generally, the crystalline structure of the polymer matrix is an important factor influencing the thermal properties of nanocomposites.31 In the experiment, to quantitatively analyze the crystalline behavior, the degree of crystallinity (Xc) for the pure PTFE and GNP–PTFE nanocomposites is calculated by,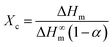 | (6) |
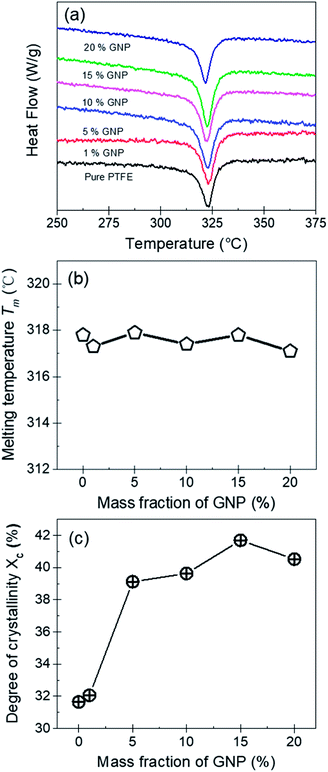
Fig. 5(a), (b) and (c) show the DSC curves, the melting temperature (Tm) and the degree of crystallinity (Xc) for the pure PTFE and GNP–PTFE nanocomposites. It can be found that Tm of all PTFE nanocomposites ranged from 317.1 °C to 317.9 °C, which approximately equal to that of pure PTFE (∼317.8 °C). The results indicate that the presence of GNP induces little change for the Tm of PTFE nanocomposites. Moreover, Fig. 5(c) shows that the Xc of GNP–PTFE nanocomposites are higher than that of the pure PTFE, which indicates that the GNP can improve the crystallization behavior of PTFE nanocomposites. In detail, when the mass fractions of GNP increase from 0% to 15%, the Xc for the pure PTFE and GNP–PTFE nanocomposites increase from 31.65% to 41.69%. The results indicate that GNP has a nucleating effect for the PTFE nanocomposites during the process of crystallization. However, it should be noted that when the mass fraction of GNP increases to 20%, the Xc decreases to 40.52%. It is likely that the increase of GNPs obstructs the mobility of the PTFE chains.33
The thermal stability of nanocomposites is an important parameter in various applications. Fig. 6(a) shows the TGA curves of PTFE nanocomposites, which could be used to evaluate the thermal stability. It can be found that the pure PTFE and the five GNP–PTFE nanocomposites all show a typical one-step decomposition behavior between 500 °C to 615 °C, which indicates that the increase of GNPs can not influence the behavior of thermal decomposition of PTFE matrix. In addition, to analyse the thermal ability quantitatively, the heat-resistance index (THRI) is calculated.34,35 As shown in Table 1, it can be found that the THRI decreases with the increase of GNPs mass fractions. Specifically, THRI for pure PTFE, 10% GNPs–PTFE and 20% GNPs–PTFE nanocomposites are 272.5 °C, 269.8 °C and 269.4 °C, respectively. This indicates that the initial decomposition temperature of PTFE nanocomposites decreases with the addition of GNPs into PTFE matrix. This may be due to two reasons. On one hand, since the thermal conductivity of GNPs is much higher than that of polymer matrix, the enhanced thermal conduction in the presence of GNPs may accelerate the decomposition of matrix, which can reduce the decomposition temperatures.36,37 On the other hand, the difference of surface characteristics between polymer matrix and fillers may induce weak interfacial interactions between them.38,39 Thus, there may be some defects in the composites, which also can decrease the decomposition temperatures of composites. Moreover, Fig. 6(b) shows the residual mass fraction of PTFE nanocomposites as a function of the mass fractions of GNP. Generally, GNPs could be stable at 800 °C in nitrogen. Therefore, the actual mass fraction of GNP can be estimated with the residual mass fraction. It can be found that the actual residual mass fraction of GNP agrees well with the initial designed mass fractions of GNP, which also implies that the GNPs disperse uniformly in PTFE matrix.
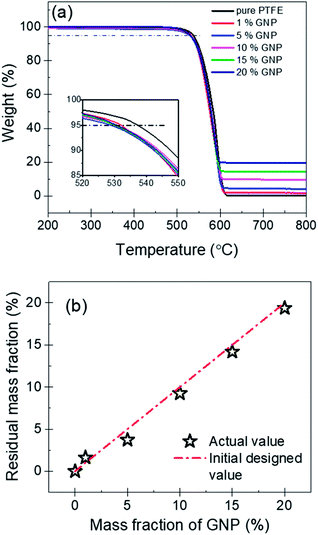 | ||
| Fig. 6 (a) TGA curves of pure PTFE and GNP–PTFE nanocomposites. (b) Actual residual mass fraction of PTFE nanocomposites as a function of the initial designed mass fractions of GNP. | ||
| Samples | Weight loss temperature/°C | The heat resistance index (THRI)a/°C | |
|---|---|---|---|
| T 5 | T 30 | ||
| a The heat resistance index (THRI) = 0.49 [T5 + 0.6(T30 − T5)], T5, T30 is the decomposing temperature at 5%, 30% weight loss, respectively.34 | |||
| Pure PTFE | 537.3 | 568.8 | 272.5 |
| 1% GNPs | 532.1 | 562.6 | 269.7 |
| 5% GNPs | 529.1 | 565.4 | 269.9 |
| 10% GNPs | 530.4 | 564.1 | 269.8 |
| 15% GNPs | 530.1 | 563.9 | 269.7 |
| 20% GNPs | 529.7 | 563.2 | 269.4 |
Thermal conductivity and heat transfer phenomenon
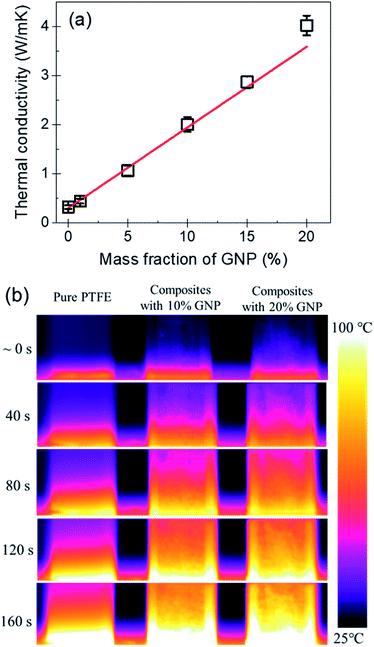
Fig. 7(a) shows the thermal conductivity of the PTFE nanocomposites with the GNP mass fractions of 0%, 1%, 5%, 10%, 15% and 20%. It indicates that the pure PTFE shows a low thermal conductivity of 0.32 W (m K)−1. With the increase of the mass fraction of GNP, the thermal conductivity of GNP–PTFE nanocomposites increases significantly. When the GNP mass fraction is 20%, the effective thermal conductivity of GNP–PTFE nanocomposites reaches 4.02 W (m K)−1, which presents a significant increase of 1300% compared with that of pure PTFE matrix. Additionally, it can be found that the thermal conductivity of GNP–PTFE nanocomposites is much higher than that of BN–PTFE, AlN–PTFE, ZnO–PTFE nanocomposites, when the fillers have the same content. The results indicate that the incorporating of GNP is effective to improve the thermal conductivity of PTFE matrix, and these GNP–PTFE nanocomposites may have important applications in heat management.Furthermore, it should be noted that, the thermal conductivity of GNP–PTFE nanocomposites does not increase linearly with the mass fraction of GNP. Especially, when the mass fraction of GNP reaches 20%, the thermal conductivity of GNP–PTFE nanocomposites increases higher than that of nanocomposites with the mass fraction of GNP lower than 20%. It is likely that, when the mass fraction of GNP is 20%, as shown in the Fig. 4(c) and (f), some GNPs contact with each other, thus, a thermal conductive path may be formed. Unambiguously, these thermal conductive paths contributes to increase the thermal conductivity of GNP–PTFE nanocomposites.
Fig. 7(b) shows the temperature distributions measured with an infrared thermal imaging instrument as a function of heating time for the pure PTFE, GNP–PTFE nanocomposites with GNP content of 10% and 20%. It is clear that the temperatures at the top of the two GNP–PTFE nanocomposites were much higher than that of the pure PTFE. This indicates that, the heat transfer rate of the PTFE nanocomposites with a GNP content of 20% is highest, followed by the PTFE nanocomposites with a GNP content of 10% and the pure PTFE. The results vividly demonstrate that the addition of GNPs into the PTFE can improve the thermal conductivity of matrix and thus enhance the heat transfer through the nanocomposites.
Theoretical analysis for the thermal conductivity of GNP–PTFE nanocomposites with a modified MGEMA
Based on the SEM and TEM observation shown in Fig. 3(b) and (c), the produced GNPs by exfoliation of graphite via tip sonication has a size of ∼1.5 μm and shows few-layered. Therefore, in the MGEMA model, the value of a1 and a2 are set to 1.5 μm and a3 is assumed as 10 nm. It should be noted that, in this study, we characterized the thickness of GNPs by determining the thickness of the folded edges of GNPs based on about 50 SEM images. The results indicate that the average thickness of GNPs produced by exfoliating is about 10 nm. Furthermore, according to our thermal conductivity measurements for pure PTFE, Km is set to 0.32 W (m K)−1. Based on Yu's results about the thermal conductivities of GNP in-plane and through-plane directions, K1 and K2 are set to 3000 W (m K)−1 and K3 is set to 6 W (m K)−1.40 In addition, according to Nan's results about the thermal interfacial resistance between the fillers and matrix,41Rk is set ranging from 4 × 10−8 (m2 K) W−1 to 9 × 10−8 (m2 K) W−1. Moreover, it should be noted that, to predict the thermal conductivity of nanocomposites using MGEMA, the mass fractions of GNP (α) need to be transformed to the volume fractions (![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f
f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) by the followed expression,
) by the followed expression,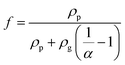 | (7) |
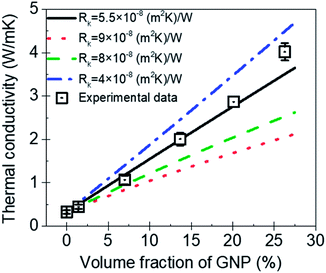
Fig. 8 is the comparison between the thermal conductivity measured in experimental and predicted value by MGEMA. As shown in Fig. 8, it can be found that Rk is a key parameter in the mathematical model, and the thermal conductivity of GNP–PTFE nanocomposites decreased with the increase of Rk. When the Rk equals to 5.5 × 10−8 (m2 K) W−1, the thermal conductivity of nanocomposites predicted by the modified MGEMA is quite correlated with the experimental results. However, it should be noted that, when the volume fraction of GNP reaches to 20%, there is a certain difference between the thermal conductivity of the experimental data and that of the predicted values. This may be due to the fact that when the graphene content is high, the contacts of GNP fillers are not considered in the mathematical model. Nevertheless, the results indicate that the thermal conductivity of nanocomposites can be effectively predicted by the modified MGEMA when the volume fractions of GNP are below 20%.
Conclusions
The PTFE nanocomposites with the GNP mass fractions of 1%, 5%, 10%, 15% and 20% were fabricated via solvent-assisted blending, cold-pressing and sintering. The thermal properties of these nanocomposites, including crystallization behavior, thermal stability and thermal conductivity were studied. The results indicate that the GNP fillers disperse homogeneously in the PTFE matrix. The melting temperature of all PTFE nanocomposites ranges from 317.1 °C to 317.9 °C, which approximately equals to that of pure PTFE (∼317.8 °C). The degree of crystallinity for GNP–PTFE nanocomposites is higher than that of pure PTFE, indicating that the GNPs improve the crystallization behavior of PTFE nanocomposites. Moreover, the GNP–PTFE nanocomposites show a typical one-step decomposition behavior and degrade between 500 °C to 615 °C. Furthermore, the thermal conductivity of PTFE nanocomposites increases with increasing GNP content. When the mass fraction of GNP is 20%, the thermal conductivity of PTFE nanocomposites reaches 4.02 W (m K)−1, which increase by 1300% comparing with the pure PTFE. A modified MGEMA model can analyze and predict the thermal conductivity of GNP–PTFE nanocomposites successfully. The results demonstrated that the addition of GNPs into PTFE can not only maintain the good thermal stability of the PTFE, but also improve the degree of crystallinity and thermal conductivity of nanocomposites significantly. The findings may have important implications to understand the thermal property of GNP–PTFE nanocomposite toward its application in heat management.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (No. 2016YFB0600704), and the Fundamental Research Funds for the Central Universities (No. FRF-TP-16-062A1).Notes and references
- S. Ebnesajjad, Fluoroplastics, Volume 1: Non-Melt Processible Fluoropolymers-The Definitive User's Guide and Data Book, Elsevier, 2014 Search PubMed.
- A. Sarani, N. De Geyter, A. Y. Nikiforov, R. Morent, C. Leys, J. Hubert and F. Reniers, Surf. Coat. Technol., 2012, 206, 2226–2232 CrossRef CAS.
- J. Zhang, X. Yu, H. Li and X. Liu, Appl. Surf. Sci., 2002, 185, 255–261 CrossRef CAS.
- D. M. Price and M. Jarratt, Thermochim. Acta, 2002, 392, 231–236 CrossRef.
- A. L. Moore and L. Shi, Mater. Today, 2014, 17, 163–174 CrossRef CAS.
- H. Chen, V. V. Ginzburg, J. Yang, Y. Yang, W. Liu, Y. Huang, L. Du and B. Chen, Prog. Polym. Sci., 2016, 59, 41–85 CrossRef CAS.
- P. Zhang, J. Zeng, S. Zhai, Y. Xian, D. Yang and Q. Li, Macromol. Mater. Eng., 2017, 302, 1700068 CrossRef.
- Z. Jin, X. Chen, Y. Wang and D. Wang, Comput. Mater. Sci., 2015, 102, 45–50 CrossRef CAS.
- B. Chen, D. Luan, J. Huang and J. Zhang, J. Appl. Polym. Sci., 2015, 132, 42302 Search PubMed.
- C. Pan, K. Kou, Q. Jia, Y. Zhang, Y. Wang, G. Wu and A. Feng, J. Mater. Sci.: Mater. Electron., 2016, 27, 11909–11916 CrossRef CAS.
- C. Pan, K. Kou, Q. Jia, Y. Zhang, G. Wu and T. Ji, Composites, Part B, 2017, 111, 83–90 CrossRef CAS.
- M. Sahli, A. Cablé, K. Chetehouna, S. Hamamda, N. Gascoin and S. Revo, Composites, Part B, 2017, 124, 175–181 CrossRef CAS.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS.
- Y. Zhu, S. Murali, W. Cai, X. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater, 2010, 22, 3906–3924 CrossRef CAS.
- K. M. Shahil and A. A. Balandin, Nano Lett., 2012, 12, 861–867 CrossRef CAS.
- X. Zhang, B. R. S. Rajaraman, H. Liu and S. Ramakrishna, RSC Adv., 2014, 4, 28987–29011 RSC.
- W. K. Chee, H. N. Lim, N. M. Huang and I. Harrison, RSC Adv., 2015, 5, 68014–68051 RSC.
- J. Gu, N. Li, L. Tian, Z. Lv and Q. Zhang, RSC Adv., 2015, 5, 36334–36339 RSC.
- J. Gu, X. Yang, Z. Lv, N. Li, C. Liang and Q. Zhang, Int. J. Heat Mass Transfer, 2016, 92, 15–22 CrossRef CAS.
- J. Gu, C. Liang, X. Zhao, B. Gan, H. Qiu, Y. Guo, X. Yang, Q. Zhang and D.-Y. Wang, Compos. Sci. Technol., 2017, 139, 83–89 CrossRef CAS.
- L. J. van Rooyen, H. Bissett, M. C. Khoathane and J. Karger-Kocsis, J. Appl. Polym. Sci., 2016, 133, 43369 CrossRef.
- L. J. van Rooyen, H. Bissett, M. C. Khoathane and J. Karger-Kocsis, Carbon, 2016, 109, 30–39 CrossRef CAS.
- J. Suh and D. Bae, Composites, Part B, 2016, 95, 317–323 CrossRef CAS.
- J. Y. Suh, S. E. Shin and D. H. Bae, J. Compos. Mater., 2016, 51, 2565–2573 CrossRef.
- Y. Arao and M. Kubouchi, Carbon, 2015, 95, 802–808 CrossRef CAS.
- X. Yang, L. Tang, Y. Guo, C. Liang, Q. Zhang, K. Kou and J. Gu, Composites, Part A, 2017, 101, 237–242 CrossRef CAS.
- C.-W. Nan, R. Birringer, D. R. Clarke and H. Gleiter, J. Appl. Phys., 1997, 81, 6692–6699 CrossRef CAS.
- C. W. Nan, Z. Shi and Y. Lin, Chem. Phys. Lett., 2003, 375, 666–669 CrossRef CAS.
- I. W. P. Chen, Y.-S. Chen, N.-J. Kao, C.-W. Wu, Y.-W. Zhang and H.-T. Li, Carbon, 2015, 90, 16–24 CrossRef CAS.
- H. C. Lee, W.-W. Liu, S.-P. Chai, A. R. Mohamed, A. Aziz, C.-S. Khe, N. M. S. Hidayah and U. Hashim, RSC Adv., 2017, 7, 15644–15693 RSC.
- C. T'Joen, Y. Park, Q. Wang, A. Sommers, X. Han and A. Jacobi, Int. J. Refrig., 2009, 32, 763–779 CrossRef.
- Z. Dong-na, K. Kai-chang, Z. Yu, Z. Qing-xin and Z. Zhen-chao, J. Appl. Polym. Sci., 2013, 130, 3710–3717 CrossRef.
- C. Pan, K. Kou, G. Wu, Y. Zhang and Y. Wang, J. Mater. Sci.: Mater. Electron., 2015, 27, 286–292 CrossRef.
- C. Liang, P. Song, H. Gu, C. Ma, Y. Guo, H. Zhang, X. Xu, Q. Zhang and J. Gu, Composites, Part A, 2017, 102, 126–136 CrossRef CAS.
- J. Gu, W. Dong, Y. Tang, Y. Guo, L. Tang, J. Kong, S. Tadakamalla, B. Wang and Z. Guo, J. Mater. Chem. C, 2017, 5, 6929–6936 RSC.
- Y. R. Lee, A. V. Raghu, H. M. Jeong and B. K. Kim, Macromol. Chem. Phys., 2009, 210, 1247–1254 CrossRef CAS.
- J. Yang, E. Zhang, X. Li, Y. Zhang, J. Qu and Z.-Z. Yu, Carbon, 2016, 98, 50–57 CrossRef CAS.
- H. K. F. Cheng, N. G. Sahoo, Y. P. Tan, Y. Pan, H. Bao, L. Li, S. H. Chan and J. Zhao, ACS Appl. Mater. Interfaces, 2012, 4, 2387–2394 CrossRef CAS.
- H. Feng, X. Wang and D. Wu, Ind. Eng. Chem. Res., 2013, 52, 10160–10171 CrossRef CAS.
- S. Y. Kim, Y. J. Noh and J. Yu, Composites, Part A, 2015, 69, 219–225 CrossRef CAS.
- C.-W. Nan, G. Liu, Y. Lin and M. Li, Appl. Phys. Lett., 2004, 85, 3549–3551 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |