Open Access Article
Open Access ArticleSingle-particle measurements of electrochemical kinetics in NMC and NCA cathodes for Li-ion batteries†
Ping-Chun
Tsai
ab,
Bohua
Wen
 a,
Mark
Wolfman
a,
Mark
Wolfman
 c,
Min-Ju
Choe
c,
Min-Ju
Choe
 d,
Menghsuan Sam
Pan
a,
Liang
Su
a,
Katsuyo
Thornton
d,
Menghsuan Sam
Pan
a,
Liang
Su
a,
Katsuyo
Thornton
 d,
Jordi
Cabana
d,
Jordi
Cabana
 c and
Yet-Ming
Chiang
c and
Yet-Ming
Chiang
 *a
*a
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA. E-mail: ychiang@mit.edu
bDepartment of Materials Science and Engineering, National Cheng Kung University, Tainan, Taiwan
cDepartment of Chemistry, University of Illinois at Chicago, Chicago, Illinois, USA
dDepartment of Materials Science and Engineering, University of Michigan, Ann Arbor, Michigan, USA
First published on 15th March 2018
Abstract
The electrochemical kinetics of battery electrodes at the single-particle scale are measured as a function of state-of-charge, and interpreted with the aid of concurrent transmission X-ray microscopy (TXM) of the evolving particle microstructure. An electrochemical cell operating with near-picoampere current resolution is used to characterize single secondary particles of two widely-used cathode compounds, NMC333 and NCA. Interfacial charge transfer kinetics are found to vary by two orders of magnitude with state-of-charge (SOC) in both materials, but the origin of the SOC dependence differs greatly. NCA behavior is dominated by electrochemically-induced microfracture, although thin binder coatings significantly ameliorate mechanical degradation, while NMC333 demonstrates strongly increasing interfacial reaction rates with SOC for chemical reasons. Micro-PITT is used to separate interfacial and bulk transport rates, and show that for commercially relevant particle sizes, interfacial transport is rate-limiting at low SOC, while mixed-control dominates at higher SOC. These results provide mechanistic insight into the mesoscale kinetics of ion intercalation compounds, which can guide the development of high performance rechargeable batteries.
Broader contextThe performance of high performance Li-ion batteries, central to both electric transportation and grid scale storage, is ultimately reliant on the performance of critical components such as their cathode and anode compounds. For ease of manufacturing, the prevailing technological forms of these materials are secondary particles of nearly spherical morphology containing many nanocrystallites. The electrochemical kinetics at this critical length scale have been difficult to assess; particle-level behavior has primarily been deduced from macroscale cell measurements. Thus the microelectrode technique developed in this work, combined with state-of-the-art TXM imaging, allows for the first time the direct measurement of electrochemical kinetics of particles as they are charged and discharged. Surprising behavior is revealed – interfacial charge transfer kinetics are found to vary greatly with state-of-charge and cycling history, both for intrinsic chemical reasons (in NMC333) and because of massively damaging “electrochemical shock” (in NCA). Moreover, a thin coating of polymer binder is found to ameliorate fracture damage. These results, and the techniques demonstrated, provide a bridge between macroscopic battery function and microscale electrode kinetics as influenced by electrochemomechanical stress and charging history. |
Introduction
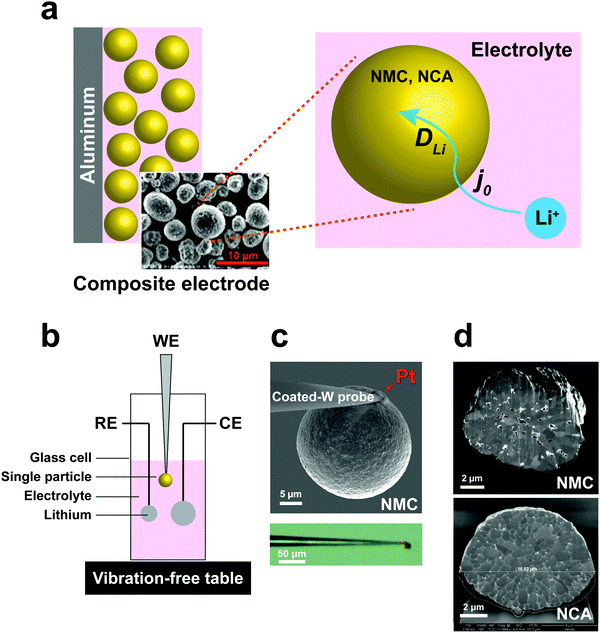
High energy density lithium-ion batteries (LIBs) have emerged as the leading energy storage technology for consumer electronics, electric vehicles, and grid-scale storage. The continuing need for higher rate capability, especially during charge, and higher energy density, by increasing the upper limit of charge voltage, requires detailed understanding of lithium transport kinetics in battery electrodes at multiple length scales.1 In a typical composite electrode, there are many possible rate-limiting transport paths; measurements of macroscopic electrodes can be especially difficult to deconvolute into processes occurring at smaller length scales. There exists a need for techniques that can probe electrochemical kinetics of battery electrode materials in a manner that allows separation of individual transport parameters, including their dependence on state-of-charge (SOC) and cycling.At the particle scale, electrochemical kinetics involve the liquid phase diffusion of Li ions within the electrolyte to each individual cathode particle, the charge-transfer reaction at the cathode–electrolyte interface, and transport of Li ions and electrons (i.e., ambipolar or chemical diffusion) within particles,2,3 as illustrated in Fig. 1a. Understanding of the charge-transfer reaction and bulk ion diffusion is desired to reveal the limiting factors of rate performance. However, in a conventional lithium ion cell, the composite electrodes are composed of active materials, binders, conductive agents, and current collectors. Due to the multicomponent mixture and complex architecture, which includes variations in particle shape and size distribution, it is challenging to extract intrinsic kinetic parameters from cell measurements.4,5 Particle-level characterization of electrochemical kinetics or microstructural changes during cycling have been separately conducted, but not directly correlated with each other.6–10 Moreover, the experimental designs in prior work have involved either “open” electrochemical cells or use of low-vapor pressure ionic liquid electrolytes, which do not represent a realistic Li ion battery environment.
To address these challenges, we developed a sealed single-particle wet cell operating in an argon-filled glovebox to measure the electrochemical kinetics of single cathode particles in a half-cell configuration, and using alkyl carbonate based electrolyte (Fig. 1). To ensure practical relevance of the results, we selected intercalation compounds in the LiNi1−x−yMnxCoyO2 (NMC)11–13 and LiNi1−x−yCoxAlyO2 (NCA)1,14 composition families, which are leading cathodes for current and future LIBs. Specifically, LiNi1/3Mn1/3Co1/3O2 (NMC333) and LiNi0.8Co0.15Al0.05O2 (NCA) were studied, being two model compositions that are in widespread use today. These cathodes are commercially produced as spherical secondary particles (Fig. 1), a morphology that simplifies handling as well as data analysis in this work.
Electrochemical impedance spectroscopy (EIS) and potentiostatic intermittent titration tests (PITT) were carried out using the single-particle cell. In addition, we used ex situ transmission X-ray microscopy (TXM) to characterize fracture at the particle level as a function of state-of-charge. Using these combined techniques, the rate-limiting transport processes at the particle level, their variation across a wide range of state-of-charge, and their dependence on electrochemomechanical stress induced by cycling, are characterized together for the first time.
Results and discussion
Design and fabrication of the single-particle test cell
A three-electrode cell with a single particle as the working electrode (Fig. 1b) was developed to meet critical requirements of sealing against electrolyte loss, thereby permitting long-duration experiments, and ultra-low background vibration and electromagnetic noise. The apparatus was operated in an argon-filled glovebox, and achieved background current noise of <30 pA, compared to measurement currents of 200 pA to 1 nA. The working electrode was assembled by physically isolating and attaching a polycrystalline cathode particle to a tungsten (W) nanoparticle manipulator used in an FIB instrument (Fig. 1c). The tungsten probe was coated with an insulating resin that suppressed the tungsten oxidation side-reaction (see Fig. S1, ESI†). A thin layer of platinum (Pt) was sputter-deposited where the cathode particle contacts the conductive probe, using the sputtering capabilities of the FIB, to ensure a low-resistance, stable electrical contact between the particle and probe. The area of deposited Pt is less than 0.5% of the cathode particle surface area. The reference and counter electrodes are both Li foils with an area of ∼0.2 cm2 and ∼1 cm2, respectively. Fig. 1d shows SEM cross-sections of as-received NMC and NCA particles after ion-beam cross-sectioning in the FIB. It is observed that each of the individual particles is a secondary particle composed of primary crystallites of 0.5–1 μm diameter. The NMC particle contains a few percent internal porosity, generally concentrated towards the center of the particle, while the NCA particles appear to be fully dense.EIS measurements of single-particle interfacial kinetics
The interfacial current density at the electrode–electrolyte in a system with single-electron transfer is described by the Butler–Volmer equation:15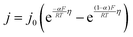 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1); and T is temperature (K). j0 is the relevant materials property that characterizes the charge-transfer reaction at the electrode–electrolyte interface,15 which we seek to quantify and understand. At high overpotentials, bulk diffusion of Li may also contribute to the measured current. Therefore, we limited the measurements of j0 to low overpotentials (<15 mV), where j0 is readily obtained from the simplified Butler–Volmer equation:
485 C mol−1); and T is temperature (K). j0 is the relevant materials property that characterizes the charge-transfer reaction at the electrode–electrolyte interface,15 which we seek to quantify and understand. At high overpotentials, bulk diffusion of Li may also contribute to the measured current. Therefore, we limited the measurements of j0 to low overpotentials (<15 mV), where j0 is readily obtained from the simplified Butler–Volmer equation: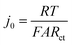 | (2) |
The exchange current density, j0, is a materials-dependent parameter that in principle may vary with cathode type and composition, electrolyte composition, the state of charge (SOC), and sample history.16,19–21 We used 1 M LiPF6 in EC/DMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as a model lithium-ion electrolyte. In order to maximize signal-to-noise ratio during the electrochemical tests, larger particles of ∼25 μm diameter with higher absolute charge/discharge currents were used. For TXM analysis, somewhat smaller particles of ∼10 μm diameter were characterized, as these proved better able to survive shocks experienced during shipping to the instrument facility, which tended to cause fracture or separation of the larger particles from the probe.
1) as a model lithium-ion electrolyte. In order to maximize signal-to-noise ratio during the electrochemical tests, larger particles of ∼25 μm diameter with higher absolute charge/discharge currents were used. For TXM analysis, somewhat smaller particles of ∼10 μm diameter were characterized, as these proved better able to survive shocks experienced during shipping to the instrument facility, which tended to cause fracture or separation of the larger particles from the probe.
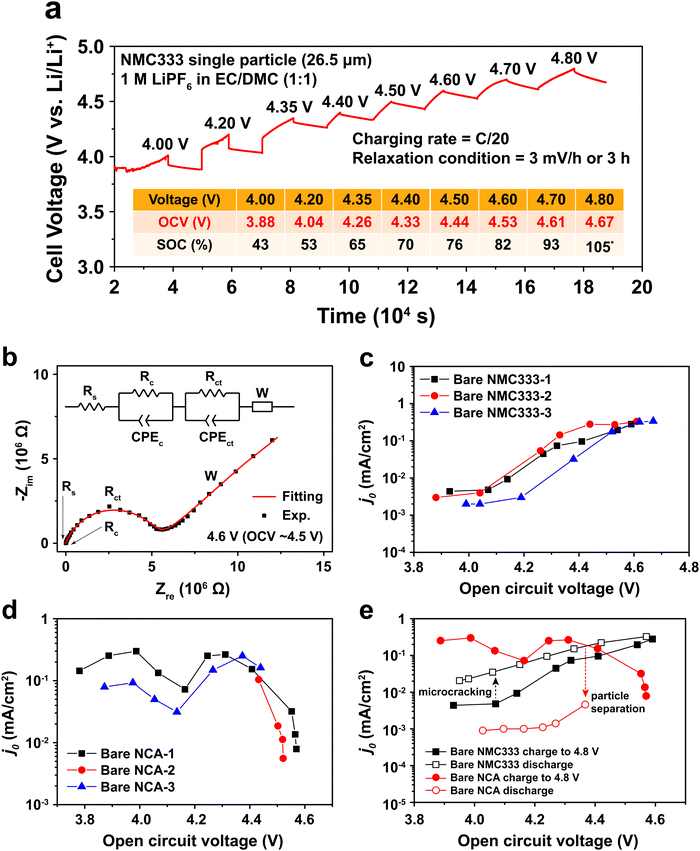
To measure j0 as a function of SOC, a polycrystalline NMC333 or NCA single particle was first charged (electrochemically delithiated) at C/20 rate to a specified voltage, followed by open-circuit relaxation for three hours, or when the rate of voltage change was less than 3 mV hour−1, whichever occurred first. A typical NMC charge voltage profile is shown in Fig. 2a, and a typical NCA profile is shown in Fig. S2 (ESI†). The relaxed OCV and the corresponding SOC at each charge voltage step are summarized in the inset of Fig. 2a. Hereafter, we will use the relaxed OCV as a measure of the SOC of the particle. After relaxation at each voltage step, EIS measurements were performed. Fig. 2b shows the EIS spectrum obtained for an NMC single particle charged to 4.6 V and then relaxed to an OCV of 4.53 V. The equivalent circuit used to fit the EIS data, shown in the inset of Fig. 2b, consists of 5 circuit elements as follows. The high-frequency intercept, Rs, represents the ohmic resistance of the system. A first semicircle corresponds to Rc/CPEc, where Rc is the contact resistance between NMC and Pt and CPEc is the corresponding capacitance. This small feature remained relatively unchanged throughout the measurement of a particle. The second semicircle Rct/CPEct is attributed to the charge-transfer resistance, Rct, at the electrode–electrolyte interface, and its corresponding capacitance, CPEct. j0 associated with each OCV (and SOC) was then calculated from this resistance using eqn (2). The EIS spectra for NMC and NCA as a function of relaxed OCV upon first charging to 4.8 V are shown in Fig. S3a and b (ESI†). The charge voltage, steady OCV, Rct, and j0 values for NMC333 and NCA particles are summarized in Tables S1–S5 (ESI†).
Measurements were made on three single particles for each of NMC333 and NCA, amongst which the results were in good agreement, as Fig. 2c and d show. There are three characteristic features of these results: (1) the j0 values at low SOC (<4.0 V charge voltage) before the onset of any cycling-related effects; (2) the variation in j0 with SOC; and (3) the hysteresis in j0 between the first charge and first discharge. From these results and the TXM observations below, we are able to understand the extent to which interfacial charge transfer rates are determined by composition and SOC, as opposed to microstructure, including microstructure changes due to electrochemically induced stresses.
At low SOC (corresponding to charge voltage 3.8–4.0 V), NCA has more than ten times higher j0 than does NMC333, ∼10−1vs. ∼3 × 10−3 mA cm−2. Literature data for NCA are not available, to our knowledge. For NMC333, a published set of j0 values22 measured on composite electrodes is over an order of magnitude higher than those we obtain here, but since the assumptions about the microstructural geometry were not stated in the previous work (most critically, whether the assumed area is the particle surface area or the electrode area), direct comparison with our results is difficult. Considering next the SOC dependence, we see that for NMC333, j0 increases dramatically, by about a factor of 102, from the lowest to highest OCV tested, ultimately reaching ∼0.3 mA cm−2. The NCA results show a markedly different OCV dependence with two apparent maxima in j0, the first appearing at OCV of 4.0 V, which corresponds to about 50% SOC. Newman15,20 proposed that j0 depends on the concentration of lithium on both sides of the electrode–electrolyte interface through the function:
| j0 = F(kc)α(ka)(1−α)(cs)α(cs,max − cs)(1−α)(cl)α | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), kc and ka are reaction rate constants for the anodic and cathodic reactions, α is the transfer coefficient, cs is the lithium concentration in active materials (mol cm−3), cs,max is the maximum lithium concentration in active materials (mol cm−3), cs,max − cs is the concentration of unoccupied lithium sites in active materials (mol cm−3), and cl is the salt concentration in electrolyte (mol cm−3). According to this model, j0 should exhibit a maximum at some intermediate composition (the exact value depending on the value of α) and tend towards zero as the lithium concentration approaches either 0 or cs,max. It is tempting to interpret the first maximum in Fig. 2d in terms of eqn (3); we return to this point later. However, j0 for NMC333 clearly does not exhibit such a maximum over the measured OCV values, which correspond to the practical SOC range for this cathode.
485 C mol−1), kc and ka are reaction rate constants for the anodic and cathodic reactions, α is the transfer coefficient, cs is the lithium concentration in active materials (mol cm−3), cs,max is the maximum lithium concentration in active materials (mol cm−3), cs,max − cs is the concentration of unoccupied lithium sites in active materials (mol cm−3), and cl is the salt concentration in electrolyte (mol cm−3). According to this model, j0 should exhibit a maximum at some intermediate composition (the exact value depending on the value of α) and tend towards zero as the lithium concentration approaches either 0 or cs,max. It is tempting to interpret the first maximum in Fig. 2d in terms of eqn (3); we return to this point later. However, j0 for NMC333 clearly does not exhibit such a maximum over the measured OCV values, which correspond to the practical SOC range for this cathode.
The j0 for NCA also drops precipitously at OCV above 4.5 V. There is furthermore a large hysteresis in j0, the values measured during charge being over an order of magnitude higher than those measured upon discharge (Fig. 2e). In contrast, the NMC333 exhibits both a much smaller hysteresis and a higher j0 during the first discharge than during the first charge (by a factor of 2–5, depending on the OCV). The results in the following section show that the irreversibility in j0 for NCA is primarily due to electrochemically induced fracture.
TXM observations of 3D microstructural evolution
One potential cause of capacity loss during electrochemical cycling is irreversible mechanical failure.23–27 This phenomenon has been termed “electrochemical shock” in analogy to the thermal shock of brittle materials, which exhibits similar dependences on crystalline properties and microstructure.28–32 Capacity fade and impedance growth in various lithium ion intercalation materials have been correlated to post-cycling observations of mechanical fracture.24,26,27,33 Acoustic emission from electrochemical shock has also been directly recorded during charging and discharging.28–32,34–36 Here, TXM was used to non-destructively generate 3D tomographs of the single particles at different states of charge, which we correlate with the electrochemical measurements. Individual NMC333 and NCA single particles having ∼10 μm diameter were charged at C/3 rate to 3.9 V, 4.1 V, and 4.5 V, respectively. Fig. 3 shows 2D slices at the midpoint of the 3D morphologies of as-received and charged NMC333 and NCA particles as a function of charge voltage. Some internal pores are observed in the starting NMC333 particle (Fig. 3a), while no internal defects were apparent in the starting NCA particle. The TXM slices are consistent with the SEM cross-sectional images of the starting NMC333 and NCA particles in Fig. 1d. It is worth noting that the fine microstructural features due to grain boundaries observed in NCA by SEM are below the spatial resolution of TXM (∼30 nm). Fig. 3a and b show sequentially increasing severity of cracks as charge voltage increases. Visible microcracking starts at about 4.1 V for NMC333 and 3.9 V for NCA. Based on these observations, we conclude that microcracks initiate close to the center of particles and propagate outward. At 4.5 V, dramatic radial cracking and particle separation are observed for NCA; the mechanical damage is considerably less for NMC333. The difference in behavior between the two systems can be correlated with the change in their respective unit cell volumes and c/a ratios as a function of SOC, Fig. 3c.27,37,38 Both show a similar linear decrease in unit cell volume with increasing SOC (increasing delithiation) at low SOC. However, the unit cell volume for NCA decreases sharply at higher SOC. The c/a ratio increases monotonically with SOC for NMC333, while that for NCA first increases and then decreases with SOC. As explained by Woodford et al.,28 an SOC-dependent crystalline anisotropy (c/a ratio) creates misfit stresses between grains that can lead to microfracture; the criteria for fracture include the change in c/a, elastic constants and fracture toughness of the compound, and the crystallite size, but is independent of (dis)charge rate. The present results highlight the different electrochemical shock behaviors of NMC333 and NCA.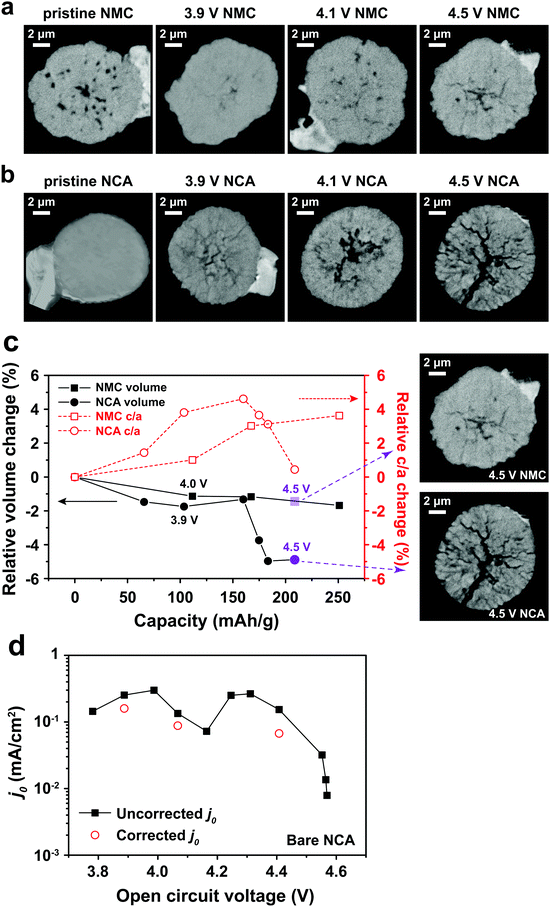 | ||
| Fig. 3 TXM tomograms showing slices at their midpoints of individual particles of (a) NMC333 and (b) NCA, all particles having ∼10 μm diameter. Images are shown for the particles in their pristine state and after charging at C/3 rate to 3.9 V, 4.1 V, and 4.5 V, respectively. The evolution in particle fracture correlates to (c) the percentage change in unit cell volume and c/a ratio of NMC333 and NCA as a function of capacity (i.e., SOC. The data are replotted from ref. 37 and 38.). (d) The measured exchange current density, j0, for an NCA particle vs. SOC, corrected for total surface area obtained from the TXM results after charging to 4.5 V (red points), shows that the fracture surface area correction is small compared to the variation in j0 with OCV (and SOC). | ||
The morphology of the particles as a function of SOC can be used to understand the evolution in j0 in Fig. 2c–e. For NMC333, the TXM images suggest that despite microfracture, electrical continuity is maintained within the particle, which may explain the reasonably reversible j0 between charging and discharging as shown in Fig. 2e. In contrast, NCA shows massive fracture at and above a charge voltage of 4.5 V, which should disrupt electrical continuity, consistent with both the decrease in j0 at high SOC (Fig. 2d) and the large hysteresis between charge (to 4.8 V) and discharge (Fig. 2e). The extreme change in unit cell dimensions that NCA experiences at charge voltage above 4.5 V seems critical to this damage, since we found that an NCA particle charged to only 4.5 V has much more reversible j0, as shown in Fig. S4 (ESI†). We did not image by TXM the NCA particles charged to 4.8 V, since the particles could not be handled and shipped intact. Nonetheless, even for particles charged to 4.5 V, the structural integrity of all particles was greatly compromised, and one out of the three NCA particles tested had separated leaving only a portion attached to the probe.
Particle cracking may allow penetration of the liquid electrolyte into the interior of particles, increasing the active surface area. If so, the observed Rct may decrease and the apparent j0 increase; in Fig. 2 all values have been calculated assuming that the active surface is the outer surface area of the particle. The true j0 should depend on the actual exposed surface area. To estimate the value of the area correction factor, we analyzed the TXM results for the more severely fractured case of NCA. Otsu's method39 was applied to segment the 3D TXM images of the particles. Allen–Cahn dynamics was used to generate a field with diffuse (i.e., not discontinuous) interface from the resulting binary data to obtain smooth isosurface renderings and corresponding surface mesh of the particle.40 The areas of the triangular patches of the surface mesh corresponding to the particle–electrolyte interface were summed to obtain the electrochemically active surface area of each particle. Along with the corresponding solid particle volumes calculated from the segmented image data, the surface/volume ratios for the NCA particles (Table S6, ESI†) were obtained. The surface/volume ratios of fractured NCA particles are normalized to that of the pristine particle (taken to be unity). Since the particle volume does not change, the increase in fracture surface area can be used to correct j0. In Fig. 3d, we show the corrected j0 (red open circles) at three different OCV values, calculated assuming that all of the quantified fracture surface area is exposed to liquid electrolyte and available for charge transfer. The correction factor naturally increases with OCV, and in the most extreme case is about a factor of 3 for charging to 4.5 V (Fig. 3b). Compared to the variation in j0 with OCV, the area correction is modest. For NMC333, the correction factor would be even smaller. We conclude that the monotonic increase in j0 with OCV of a factor of ∼102 for NMC333 cannot be explained by fracture surface area changes, and are most likely due to (electro)chemical changes at the cathode–electrolyte interface occurring with changes in SOC. For NCA, despite extensive fracture, the decrease in j0 by over a factor of 10 above 4.5 V also cannot be explained by the surface area change alone. The large hysteresis in j0 (Fig. 2e) suggests that this is most likely due to a loss of electrical continuity between fractured regions of the particle.
Binder effects on particle separation
Typical LIB electrodes are formulated with polymer binders that promote adhesion of the cathode particles and conductive additives to each other and to the current collector foil. Thus, it is reasonable to ask whether such binders, which are usually soluble in the processing solvent (e.g., N-methyl-2-pyrrolidone, NMP), influence either j0 or the electrochemical shock we observed in the NCA particles. Polyvinylidene fluoride (PVdF), a common binder, was dissolved in NMP, forming a solution into which the attached NCA particles were dipped and then allowed to dry. The coated particles were subjected to the same test protocol as discussed above for the bare NCA. Fig. 4a shows a TXM slice of the PVdF-coated NCA after charging to 4.8 V. Although radial cracks still appear, these are not open cracks, and particle separation is not observed, unlike the bare NCA particles (Fig. 3b). Clearly, a thin surface layer of binder is sufficient to prevent the disintegration that occurs for unconstrained particles. Fig. 4b shows j0 as a function of OCV measured for a PVdF-coated NCA single particle during the first charge and first discharge. The absolute value of j0 on first charge is similar to that measured for the bare NCA (Fig. 2d and e), and again shows a double maximum. This indicates that the PVdF coating does not impose a significant charge transfer barrier between the NCA surface and the electrolyte. However, upon discharge the binder-coated NCA did not exhibit the large hysteresis in j0 seen for the bare NCA (Fig. 2e), and in fact reached a higher peak j0. This supports the interpretation that irreversibility in j0 is due to fracture-induced loss of electrical contact, although a reversible increase in the cathode SEI resistance at high SOC cannot be strictly ruled out. While the PVdF-coated NCA particle exhibits, upon discharge, a j0 curve with a single maximum, further investigation is necessary before it can be concluded that the experimental result corresponds to the theoretical relationship in eqn (3).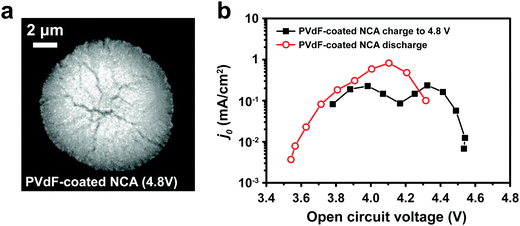 | ||
| Fig. 4 (a) TXM slice of a PVdF-coated NCA particle charged to 4.8 V shows evident radial cracking, but with less crack-opening than observed for the bare NCA particle charged to 4.5 V (Fig. 3b). (b) The PVdF-coated NCA exhibits j0vs. OCV behavior upon charging that is similar to the bare NCA (Fig. 2d and e), but has greatly improved retention of j0 during discharge. | ||
Single-particle PITT of NMC333
In order to understand the relative contributions of interfacial charge transfer and bulk diffusion to electrochemical kinetics at the single-particle level, we performed potentiostatic intermittent titration tests (PITT) as a function of SOC on the NMC333 particles. Corresponding measurements were not made for the NCA particles, due to the uncertainty in interpreting bulk diffusion when particles are heavily cracked. The measurements were performed during discharge, after first charging the particles to 4.8 V. The particles were then galvanostatically discharged to a specified voltage, corresponding to a desired SOC, and allowed to relax under open-circuit conditions for 3 h. The PITT measurement was then performed by stepping up the voltage by 15 mV, and measuring the resulting current as a function of time. The PITT analysis41,42 used here takes into account a finite interfacial reaction rate, allowing j0 and the lithium chemical diffusivity, DLi, to be obtained simultaneously. PITT therefore provides an independent measurement of j0 that can be compared with the EIS measurements presented above. In the current experimental configuration, transport of lithium in the liquid electrolyte is not rate-limiting. Note that due to the sufficiently high electronic conductivity of NMC333 which ranges from ∼10−6 S cm−1 to ∼10−2 S cm−1 over Li concentrations x = 0.00 to 0.75,43 the chemical diffusion coefficient is mainly limited by lithium diffusion rather than electron transport. In addition to j0 and DLi, the PITT analysis also yields the electrochemical Biot number (B), which characterizes the relative rates of interfacial reaction and bulk diffusion, and is given by: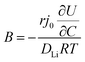 | (4) |
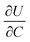 is the slope of the equilibrium potential (U) vs. lithium concentration (C) curve at the given SOC, R is the gas constant, and T is the absolute temperature. The current response under PITT measurement is fitted using eqn (5) to obtain DLi and B:41,42
is the slope of the equilibrium potential (U) vs. lithium concentration (C) curve at the given SOC, R is the gas constant, and T is the absolute temperature. The current response under PITT measurement is fitted using eqn (5) to obtain DLi and B:41,42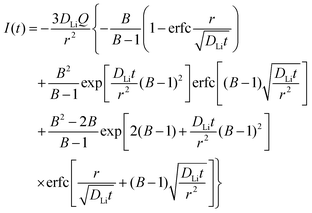 | (5) |
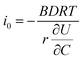 . The term
. The term 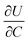 was determined from the slope of the relaxed OCV vs. Li concentration curves for NMC333.
was determined from the slope of the relaxed OCV vs. Li concentration curves for NMC333.
Fig. 5a shows the PITT current response obtained from a 26.5 μm diameter NMC333 particle upon stepping the voltage by +15 mV from an OCV of 4.45 V. Current (i)–time (t−1/2) profiles such as these were fitted to obtain DLi, j0, and B. Raw PITT current vs. time curves for several OCV values are shown in Fig. S5 (ESI†). The measured DLi, j0, and B values are summarized in Table S7 (ESI†). Fig. 5b compares the j0vs. OCV results for NMC333 from the PITT measurements with those from EIS. The good agreement for the two methods is apparent, and further reinforces the observation that for NMC333, j0 increases monotonically with OCV. Fig. 5c shows the voltage dependence of DLi. Amin et al.43 previously measured DLi in single-phase sintered NMC333 at various SOC, and obtained values similar to those obtained here, of order 10−10 cm2 s−1.
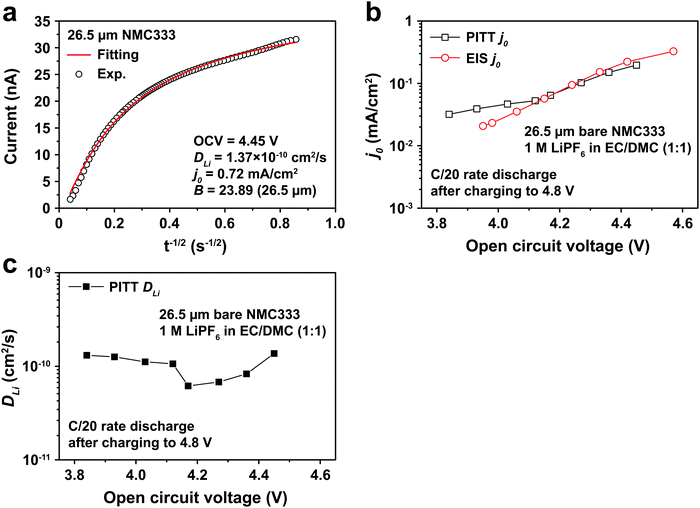 | ||
| Fig. 5 (a) PITT current vs. time data, and corresponding least-squares fit to eqn (5), from which kinetic parameters are obtained, for an NMC333 particle of 26.5 μm diameter, measured for a +15 mV voltage step from a relaxed OCV of 4.45 V. (b) The dependence of j0 on OCV from PITT (black squares) is in good agreement with those obtained from EIS (red circles). (c) Chemical diffusion coefficient DLivs. OCV, based on PITT measurements. | ||
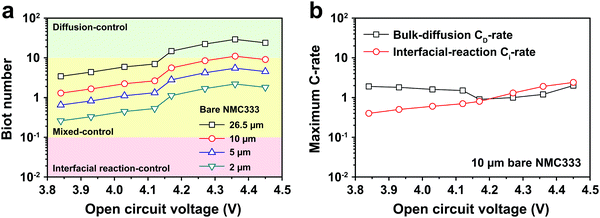
The electrochemical Biot number, B, for the NMC particle in Fig. 5 is plotted vs. OCV as the top curve in Fig. 6a. In general, B < 0.1 corresponds to interfacial reaction-limited kinetics B > 10 corresponds to bulk diffusion-limited kinetics, while 0.1 < B < 10 is considered to represent mixed-control. According to this criterion, the 26.5 μm particle exhibits mixed-control at lower OCV transitioning to diffusion-limited control at higher OCV, due to the steeper increase in j0 than in DLi with OCV. Since B scales linearly with particle radius r (eqn (4)), the top curve in Fig. 6a is readily scaled to various (assumed) particle sizes. For commercially-relevant NMC particle sizes of 5–10 μm, mixed-control kinetics are expected across the OCV range from 3.8 V to 4.5 V. Another useful metric by which the impact of a given j0 and DLi can be viewed is the maximum C-rate that is permitted before the overpotential, η, becomes unacceptably high. For example, a reasonable limit for η in a Li-ion cell may be about 100 mV. The maximum C-rate limited by interfacial kinetics for a particle with volume V, surface area A, and volumetric capacity Cp is:
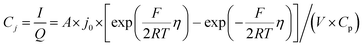 | (6) |
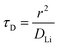 | (7) |
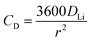 | (8) |
Conclusions
The electrochemical kinetics and concurrent microstructural changes of single secondary cathode particles used in Li-ion batteries are characterized for the first time, using a novel high current resolution wet cell and TXM tomography, respectively. With increasing state-of-charge, both NMC333 and NCA undergo electrochemically induced fracture, but with much greater damage occurring in the latter. Quantification of the 3D TXM images shows that even at high charge voltages (4.5–4.8 V), the increase in surface area cannot account for the observed changes in interfacial charge-transfer kinetics, indicating that the main cause of performance degradation in NCA is loss of electrical contact. NMC333 undergoes a factor of 102 increase in exchange current density with state-of-charge, which also cannot be explained by microstructure change, and is ascribed to (electro)chemical changes at the cathode–electrolyte interface, which may include reversible changes in cathode surface composition or SEI composition with SOC. Micro-PITT measurements show that at commercially relevant particle sizes of ∼10 μm, NMC333 kinetics are interface-limited at low SOC and mixed interfacial/bulk-diffusion limited at higher SOC.Materials and methods
Materials
LiNi1/3Mn1/3Co1/3O2 (NMC333) and LiNi0.8Co0.15Al0.05O2 (NCA) polycrystalline particles were purchased from BASF and TODA America, respectively. Lithium foil, polyvinylidene fluoride (PVdF), and N-methyl-2-pyrrolidone (NMP) were purchased from Alfa Aesar. A conventional electrolyte consisted of 1 M LiPF6 dissolved in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio of ethylene carbonate (EC) and dimethyl carbonate (DMC) was purchased from BASF. Tungsten (W) probes were purchased from Ted Pella. The Amorphous Fluoropolymer CYTOP was purchased from Asahi Glass. Anti-vibration table was purchased from Technical Manufacturing Corporation.
1 weight ratio of ethylene carbonate (EC) and dimethyl carbonate (DMC) was purchased from BASF. Tungsten (W) probes were purchased from Ted Pella. The Amorphous Fluoropolymer CYTOP was purchased from Asahi Glass. Anti-vibration table was purchased from Technical Manufacturing Corporation.
Single-particle electrode cell
The tungsten probe was first coated with an amorphous fluoropolymer, CYTOP, to prevent the tungsten oxidation side reaction (Fig. S1, ESI†). To attach a cathode particle, the coating on the probe tip was removed using a silicon ion source in FIB to allow electrical connection. An individual cathode particle was then manipulated into position in the FIB and attached to the tungsten probe by sputtering platinum. Prior to cell assembly, the microelectrode was dried at 100 °C for ∼8 h under vacuum. To prepared a PVdF-coated NCA microelectrode, PVdF was dissolved in NMP solution at 6 wt%. Afterwards, a bare NCA single-particle microelectrode was dipped into the PVdF/NMP solution and immersed for half an hour. The PVdF-coated NCA single-particle microelectrode was dried at room temperature for ∼8 h, at 60 °C in air for ∼3 h, and then for ∼12 h at 100 °C under vacuum. The single-particle measurement was performed in an argon-filled glovebox at ambient temperature. A conventional electrolyte of 1 M LiPF6 in EC/DMC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio) was used. The reference and counter electrodes were both Li foils with area of ∼0.1 cm2 and ∼1 cm2, respectively. The three-electrode cell was placed on a vibration-free table (Everstill™ K-400) and in a Faraday cage to minimize vibrational and electromagnetic noise. These cells underwent galvanostatic cycling using a Biologic VMP3 potentiostat with low current capability.
1 weight ratio) was used. The reference and counter electrodes were both Li foils with area of ∼0.1 cm2 and ∼1 cm2, respectively. The three-electrode cell was placed on a vibration-free table (Everstill™ K-400) and in a Faraday cage to minimize vibrational and electromagnetic noise. These cells underwent galvanostatic cycling using a Biologic VMP3 potentiostat with low current capability.
EIS and PITT measurements
After charging or discharging a single-particle electrode to selected voltage at a rate of C/20 (11.5 mA g−1), the cell was relaxed under OCV conditions for 3 h until or the voltage changed less than 3 mV hour−1, whichever occurred first. The EIS measurements were performed at each relaxed OCV over the frequency range 200 kHz to 10 mHz. Three oscillation amplitudes (5 mV, 10 mV, and 20 mV) were tested to verify the linearity of the impedance response. The PITT measurements were then performed at each relaxed OCV with 15 mV applied overpotential.TXM measurements
Ex situ TXM was performed on individual NMC333 and NCA particles of ∼10 μm size in the pristine state and after charging to 3.9 V, 4.1 V, and 4.5 V at C/3 rate. Full-field X-ray transmission tomograms were collected at beamline 32-ID-C at the Advanced Photon Source and beamline 6-2c at the Stanford Synchrotron Light Source. Beamline 32-ID-C operates on a 3.30 cm undulator source. Energy selection was accomplished with a liquid-nitrogen-cooled double-crystal monochromator set to 8400 eV in order to achieve strong nickel absorbance contrast. Single particles were mounted in the microscope still attached to the tungsten tip. A series of 2048 × 2048 transmission micrographs were collected at angles between 0° and 180° with a 0.25° angular step and 2 s exposure time. The field-of-view for each projection is 25.90 μm, resulting in a pixel-size of 12.65 nm. Ten white-field and five dark-field images were also collected and used for conversion from transmission to optical-depth contrast. Projections were first down-sampled by a factor of two in each dimension. A three-dimensional optical density volume was then reconstructed using tomopy44 with a combination of simultaneous iteration and filtered back-projection algorithms via the “SIRT-FBP” plugin.45Beamline 6-2c operates on a 56-pole wiggler end-station. Energy selection is acomplished with a liquid-nitrogen-cooled double-crystal monochromator, which was set to 9000 eV in order to be significantly above the nickel K-edge to achieve strong absorbance contrast. Single particles were mounted in the microscope still attached to the tungsten tip and a series of 2048 × 2048 transmission micrographs were collected at angles between 0° and 180° with a 0.5° angular step and 0.5 s exposure time. Reference images were collected both before and after tomogram acquisition to allow for conversion to optical-depth projections. A three-dimensional optical-density volume was reconstructed using “TXM-Wizard” and the iterative algebraic reconstruction technique algorithm.46 In order to account for motor jitter, an iterative alignment technique was used that is built into “TXM-wizard”: the reconstructed volume was forward-projected to calculate a series of projections, which was then compared with the collected projections via image registration techniques. In all cases, segmentation of the internal fractures was done using the scikit-image library:47 morphological opening and black top-hat filters were applied using spherical kernels. Visualization of 3D volumes was done using “ParaView”.48
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of the NorthEast Center for Chemical Energy Storage (NECCES), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award # DE-SC0012583. P.-C. Tsai thanks the Ministry of Science and Technology, Taiwan (MOST 104-2917-I-006-006), for financial support, and Prof. Masahiro Yoshimura and Prof. Shih-kang Lin for helpful guidance. Drs Yijin Liu (Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory) and Vincent De Andrade (Advanced Photon Source, Argonne National Laboratory) are acknowledged for their support of the measurements of transmission X-ray microscopy. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.Notes and references
- M. D. Radin, S. Hy, M. Sina, C. Fang, H. Liu, J. Vinckeviciute, M. Zhang, M. S. Whittingham, Y. S. Meng and A. Van der Ven, Adv. Energy Mater., 2017, 7, 1602888 CrossRef.
- S.-Y. Chung, J. T. Bloking and Y.-M. Chiang, Nat. Mater., 2002, 1, 123–128 CrossRef CAS PubMed.
- N. J. Dudney and J. Li, Science, 2015, 347, 131–132 CrossRef CAS PubMed.
- X. Zeng, G.-L. Xu, Y. Li, X. Luo, F. Maglia, C. Bauer, S. F. Lux, O. Paschos, S.-J. Kim, P. Lamp, J. Lu, K. Amine and Z. Chen, ACS Appl. Mater. Interfaces, 2016, 8, 3446–3451 CAS.
- J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin, Y.-S. Yu, N. J. Salmon, D. A. Shapiro, M. Z. Bazant, T. Tyliszczak and W. C. Chueh, Science, 2016, 353, 566–571 CrossRef CAS PubMed.
- K. Dokko, M. Mohamedi, Y. Fujita, T. Itoh, M. Nishizawa, M. Umeda and I. Uchida, J. Electrochem. Soc., 2001, 148, A422 CrossRef CAS.
- I. Uchida, H. Fujiyoshi and S. Waki, J. Power Sources, 1997, 68, 139–144 CrossRef CAS.
- D. J. Miller, C. Proff, J. G. Wen, D. P. Abraham and J. Bareño, Adv. Energy Mater., 2013, 3, 1098–1103 CrossRef CAS.
- H. Munakata, B. Takemura, T. Saito and K. Kanamura, J. Power Sources, 2012, 217, 444–448 CrossRef CAS.
- J. Y. Huang, L. Zhong, C. M. Wang, J. P. Sullivan, W. Xu, L. Q. Zhang, S. X. Mao, N. S. Hudak, X. H. Liu, A. Subramanian, H. Fan, L. Qi, A. Kushima and J. Li, Science, 2010, 330, 1515–1520 CrossRef CAS PubMed.
- I. Belharouak, Y.-K. Sun, J. Liu and K. Amine, J. Power Sources, 2003, 123, 247–252 CrossRef CAS.
- N. Yabuuchi and T. Ohzuku, J. Power Sources, 2003, 119–121, 171–174 CrossRef CAS.
- J. Choi and A. Manthiram, J. Electrochem. Soc., 2005, 152, A1714–A1718 CrossRef CAS.
- R. Amin, D. B. Ravnsbæk and Y.-M. Chiang, J. Electrochem. Soc., 2015, 162, A1163–A1169 CrossRef CAS.
- J. S. Newman and K. E. Thomas-Alyea, Electrochemical systems, J. Wiley, Hoboken, NJ, 3rd edn, 2004 Search PubMed.
- D. W. Dees, K. G. Gallagher, D. P. Abraham and A. N. Jansen, J. Electrochem. Soc., 2013, 160, A478–A486 CrossRef CAS.
- F. Y. Fan, W. H. Woodford, Z. Li, N. Baram, K. C. Smith, A. Helal, G. H. McKinley, W. C. Carter and Y.-M. Chiang, Nano Lett., 2014, 14, 2210–2218 CrossRef CAS PubMed.
- T. Swamy and Y.-M. Chiang, J. Electrochem. Soc., 2015, 162, A7129–A7134 CrossRef CAS.
- F. Y. Fan, M. S. Pan, K. C. Lau, R. S. Assary, W. H. Woodford, L. A. Curtiss, W. C. Carter and Y.-M. Chiang, J. Electrochem. Soc., 2016, 163, A3111–A3116 CrossRef CAS.
- M. Doyle, J. Electrochem. Soc., 1993, 140, 1526 CrossRef CAS.
- Y. Yamada, Y. Iriyama, T. Abe and Z. Ogumi, Langmuir, 2009, 25, 12766–12770 CrossRef CAS PubMed.
- L. Wang, J. Zhao, X. He, J. Gao, J. Li, C. Wan and C. Jiang, Int. J. Electrochem. Sci., 2012, 7, 345–353 CAS.
- H. Kim, M. G. Kim, H. Y. Jeong, H. Nam and J. Cho, Nano Lett., 2015, 15, 2111–2119 CrossRef CAS PubMed.
- S. Watanabe, M. Kinoshita, T. Hosokawa, K. Morigaki and K. Nakura, J. Power Sources, 2014, 258, 210–217 CrossRef CAS.
- J. G. Swallow, W. H. Woodford, F. P. McGrogan, N. Ferralis, Y.-M. Chiang and K. J. Van Vliet, J. Electrochem. Soc., 2014, 161, F3084–F3090 CrossRef CAS.
- M. Klinsmann, D. Rosato, M. Kamlah and R. M. McMeeking, J. Electrochem. Soc., 2016, 163, A102–A118 CrossRef CAS.
- Y. Itou and Y. Ukyo, J. Power Sources, 2005, 146, 39–44 CrossRef CAS.
- W. H. Woodford, Y.-M. Chiang and W. C. Carter, J. Electrochem. Soc., 2010, 157, A1052 CrossRef CAS.
- W. H. Woodford, W. C. Carter and Y.-M. Chiang, Energy Environ. Sci., 2012, 5, 8014 CAS.
- W. H. Woodford, Y.-M. Chiang and W. C. Carter, J. Electrochem. Soc., 2013, 160, A1286–A1292 CrossRef CAS.
- W. H. Woodford, Y.-M. Chiang and W. C. Carter, J. Mech. Phys. Solids, 2014, 70, 71–83 CrossRef CAS.
- W. H. Woodford, W. C. Carter and Y.-M. Chiang, J. Electrochem. Soc., 2014, 161, F3005–F3009 CrossRef CAS.
- H. Liu, M. Wolf, K. Karki, Y.-S. Yu, E. A. Stach, J. Cabana, K. W. Chapman and P. J. Chupas, Nano Lett., 2017, 17, 3452–3457 CrossRef CAS PubMed.
- J. G. Swallow, W. H. Woodford, Q. Lu, J. J. Kim, D. Chen, Y.-M. Chiang, W. C. Carter, H. L. Tuller and K. J. Van Vliet, J. Electroceram., 2014, 32, 3–27 CrossRef CAS.
- F. P. McGrogan, S. R. Bishop, Y.-M. Chiang and K. J. V. Vliet, J. Electrochem. Soc., 2017, 164, A3709–A3717 CrossRef CAS.
- T. Ohzuku, H. Tomura and K. Sawai, J. Electrochem. Soc., 1997, 144, 3496–3500 CrossRef CAS.
- S. Watanabe, M. Kinoshita, T. Hosokawa, K. Morigaki and K. Nakura, J. Power Sources, 2014, 260, 50–56 CrossRef CAS.
- Y. W. Tsai, B. J. Hwang, G. Ceder, H. S. Sheu, D. G. Liu and J. F. Lee, Chem. Mater., 2005, 17, 3191–3199 CrossRef CAS.
- N. Otsu, IEEE Trans. Syst. Man Cybern., 1979, 9, 62–66 CrossRef.
- D. Fan and L.-Q. Chen, Acta Mater., 1997, 45, 611–622 CrossRef CAS.
- J. Li, X. Xiao, F. Yang, M. W. Verbrugge and Y.-T. Cheng, J. Phys. Chem. C, 2012, 116, 1472–1478 CAS.
- J. Li, F. Yang, X. Xiao, M. W. Verbrugge and Y.-T. Cheng, Electrochim. Acta, 2012, 75, 56–61 CrossRef CAS.
- R. Amin and Y.-M. Chiang, J. Electrochem. Soc., 2016, 163, A1512–A1517 CrossRef CAS.
- D. Gürsoy, F. De Carlo, X. Xiao and C. Jacobsen, J. Synchrotron Radiat., 2014, 21, 1188–1193 CrossRef PubMed.
- D. M. Pelt and K. J. Batenburg, IEEE Trans. Image Process. Publ. IEEE Signal Process. Soc., 2014, 23, 4750–4762 CrossRef PubMed.
- Y. Liu, F. Meirer, P. A. Williams, J. Wang, J. C. Andrews and P. Pianetta, J. Synchrotron Radiat., 2012, 19, 281–287 CrossRef CAS PubMed.
- S. van der Walt, J. L. Schönberger, J. Nunez-Iglesias, F. Boulogne, J. D. Warner, N. Yager, E. Gouillart and T. Yu, PeerJ, 2014, 2, e453 Search PubMed.
- J. Ahrens, B. Geveci and C. Law, in Visualization Handbook, ed. C. D. Hansen and C. R. Johnson, Butterworth-Heinemann, Burlington, 2005, pp. 717–731 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ee00001h |
| This journal is © The Royal Society of Chemistry 2018 |