Elucidation of the inverse trans influence in uranyl and its imido and carbene analogues via quantum chemical simulation

Abstract

The inverse trans influence (ITI) is investigated in uranyl, UO₂²⁺, and its isoelectronic imido (U(NH)₂²⁺) and carbene (U(CH₂)₂²⁺) analogues at the density functional and complete active space self consistent field levels of theory. The quantum theory of atoms in molecules is employed to quantify, for the first time, the effect of the ITI on covalent bond character and its relationship to bond lengths and complex stability.

---

The inverse trans influence (ITI) is manifested in intermediate and high valence f-elements as a shortening of bond lengths of ligands lying trans to highly polarising species. The classic examples of this effect are manifested in [PPh₄][UOCl₅] and [Et₄N]₂[PaOCl₅], where the trans An–Cl bond is some 4.0 and 8.3% shorter than that of equivalent cis interactions, respectively.^1,2 The effect has also been observed in a number of other U(V)/U(VI) mono-oxide and -imide complexes,^3–8 as well as U(IV) and Ce(IV) bis-carbenes.⁹ The interested reader is directed to a comprehensive recent review of the ITI in actinide complexes.³

A qualitative explanation of the ITI, as well as detailed analysis of bonding in the actinyls, has been given by Denning^10,11 in terms of the character of the metal polarisation by the ligand: dipolar in the case of transition metals, which therefore exhibit the trans influence, and quadrupolar in the f-elements, which therefore exhibit the ITI. Both Denning¹¹ and Hoffmann¹² have also highlighted the importance of the pseudocore electronic 6p_σ orbital of the actinide centre in the ITI, and the role of the 6p shell was successfully demonstrated by O’Grady and Kaltosoyannis using quantum chemical simulations, identifying key molecular orbitals associated with the phenomenon.¹³ A quantification of the impact of the ITI on electronic structure has, however, remained elusive. Recently, analysis methods based on the experimentally observable electron density have been shown to be capable of characterising a number of chemical phenomona in the f-elements,¹⁴ and an appealing feature of this approach is that it can also be applied to experimentally derived densities.^15,16 In this contribution, we employ a novel application of the quantum theory of atoms in molecules (QTAIM) to study the ITI in the prototypical U(VI) compound, uranyl (UO₂²⁺), along with its isoelectronic imido and carbene analogues. The imido analogue has been reported by Boncella,¹⁷ who has also reported chalcogenido-substituted uranyl complexes of the form [OUE]²⁺ (E = S, Se),¹⁸ whereas Gibson has shown that linear US₂²⁺ exists 171 kJ mol⁻¹ higher in energy than the η₂-S₂ isomer in the gas phase.¹⁹ To date the carbene analogue is synthetically unrealised, although Liddle and coworkers have reported an [OUCR₂]²⁺ uranyl analogue.²⁰

Since the analogues are expected to be more weakly binding ligands, so the ITI might be expected to be less pronounced. This is the first investigation of the ITI in uranyl via analysis of CASSCF-generated electron densities, although we note Pierloot's authorative CASSCF study of uranyl bonding.²¹ This contribution also represents the first study of the electronic structure of U(CH₂)²⁺. Whilst the ITI is expected to be substantial in uranyl, its effects are not experimentally accessible in their entirety, although Denning has characterised the role of the 6p_σ orbital via O K-edge X-ray absorption and emission (XAS/XES) spectroscopies.²² More recently, Cl K-edge XAS has been used to great effect to probe bond covalency in OUCl₅⁻, as well as chloride complexes of both uranyl and its imido analogue,^23,24 however the lack of equatorial ligands in bare uranyl anologues means that theory is able to provide a unique insight into the phenomenon in this complexes.

In this study, all complexes were assumed to have D_2h symmetry.‡ Density functional theory (DFT) calculations employed the non-empirical PBE0 hybrid-GGA exchange–correlation functional, which we have previously shown to give an accurate description of electronic structure in f-element complexes.^25–29 Complete active space self-consistent field (CASSCF) calculations employed a minimal active space correlating 12 electrons in 12 orbitals, CASSCF(12,12), for uranyl and the imido analogue, and correlating eight electrons in eight orbitals, CASSCF(8,8) for the carbene analogue.§ These active spaces included only those orbitals with bonding or antibonding character between the uranium centre and the coordinating species. All simulations employed the ANO-RCC basis sets of polarised triple-zeta quality and were carried out using version 8.0 of the MOLCAS code.³⁰

Following the approach developed by O’Grady and Kaltsoyannis,¹³ we have focussed on the role played by the pseudocore 6p shell. To achieve this, we have performed a set of simulations in which this shell, along with all those lying lower in energy, are restricted, or frozen, to have atomic character. These simulations are compared to a set in which the entire electronic structure is allowed to relax.

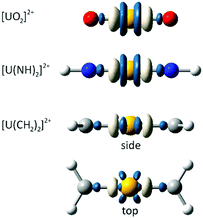
We first consider the variation in the total electron density distribution associated with freezing the 6p shell while maintaining the geometry associated with the fully relaxed electronic structure. These density differences (Fig. 1), obtained at the PBE0 level of theory, immediately demonstrate the validity of Denning's quadrupolar characterisation of the metal polarisation, with a central region of charge accumulation lying between two regions of charge depletion. The density differences of uranyl and its imido analogue exhibit cylindrical symmetry, whereas that of the carbene analogue reflects the sp² hybridisation of the carbon centres.

Fig. 1 PBE0-generated density differences associated with freezing the 6p shell. Blue (white) regions indicate greater (lesser) charge density in the fully-relaxed electronic structure. CASSCF density differences exhibit qualitatively similar features. All isosurfaces rendered at a value of ρ = 0.01 a.u.

Whilst these density differences illustrate the qualitative characteristics of the ITI, they cannot be employed to ascertain its magnitude. To investigate the ITI further, we have therefore analysed the simulated electron densities using the QTAIM. We have focussed on two parameters in particular: the delocalisation index, δ(U,L), and the magnitude of the electron density at the bond critical point, ρ_BCP, between the uranium and coordinating species. δ(U,L) quantifies the number of electrons shared between a pair of atoms, and can, in the absence of polarisation, be considered a measure of bond order, whereas ρ_BCP gives insight into the degree of charge accumulation in the bonding region. The high symmetry of the complexes under consideration here allowed us to employ a novel application of this analysis whereby gerade (g) and ungerade (u) contributions to ρ_BCP and δ(U,L) can be unambiguously identified and, additionally, contributions to δ(U,L) can be further decomposed into contributions from σ- and π-type interactions (note that only σ-type interactions contribute to ρ_BCP). This latter feature is of great value to the present study, since any 6p_σ contributions to metal–ligand interactions will necessarily be of σ_u-character.

To clarify the role of the ITI, we again consider the consequences of freezing the 6p shell when the geometry is held fixed at that obtained with the fully relaxed electronic structure. In Table 1, we report the effect on δ(U,L). In passing, we note that the absolute magnitude of δ(U,L) is largest for the imido analogue (see Table S1 of ESI†). In the case of uranyl, the delocalisation index increases significantly when the 6p shell is frozen. This appears counterintuitive at first, since the effect of freezing this shell is to render it unavailable for chemical interactions. It can, however, be rationalised in the context of the “pushing from below” description of bonding in uranyl, which recognises that the 6p_σ orbital interacts with antibonding character.³¹ Antibonding interactions serve to lower the delocalisation index and so removing 6p contributions therefore leads to the increase found here. The same effect is seen for the imido analogue, although it is reduced in magnitude, particularly when using the CASSCF methodology. In the carbene analogue it is almost entirely absent.

Table 1 Differences in uranium–ligand delocalisation indices, as well as the electron density at the U–L BCP, calculated with a frozen or unfrozen 6p shell, obtained at geometries optimised using a fully relaxed electronic structure

Complex	Method	Δδ(U,L)					ΔρBCP
		Total	σu	σg	πu	πg	Total	u	g
UO2^2+	DFT	0.097	0.065	0.005	0.012	0.014	0.009	0.003	0.006
	CASSCF	0.082	0.044	0.014	0.008	0.016	0.008	0.003	0.005
U(NH)2^2+	DFT	0.081	0.036	0.018	0.010	0.016	0.002	−0.003	0.006
	CASSCF	0.042	0.014	0.016	0.002	0.010	0.005	0.000	0.006
U(CH2)2^2+	DFT	0.008	−0.015	0.015	0.000	0.009	−0.007	−0.011	0.004
	CASSCF	−0.005	−0.015	0.008	0.001	0.003	−0.007	−0.008	0.001

---

The decomposition of δ(U,L) further supports this interpretation, since the σ_u component, in which 6p_σ interactions would manifest themselves, accounts for the majority of the overall variation. This component is positive for uranyl and the imido analogue, but small and negative for the carbene analogue. This trend suggests that the pushing from below mechanism is reduced when the oxo ligand is substituted by a less polarising species and is, perhaps, reversed in the carbene analogue. There is also a small σ_g component which is relatively constant across the different complexes and effectively cancels the σ_u contribution in the carbene complex.

Whilst δ(U,L) characterises the electron sharing between the uranium centre and the coordinating species, it tells us little about the charge accumulation in the bond between the two. Table 1 also reports the differences in ρ_BCP which, as discussed above, provides a direct measure of this accumulation. Absolute values of ρ_BCP can be found in Table S2 of ESI† and, in contrast to the δ(U,L) values, are largest in uranyl. Interestingly, ρ_BCP, like δ(U,L), increases in uranyl when the 6p shell is frozen. Furthermore, the gerade contribution to this increase is approximately twice the magnitude of the ungerade component. Taken as a whole, the data presented in Table 1 suggests that the localisation of the 6p shell is leading to increased shielding of the 6d and 5f shells which therefore become more chemically available. The imido analogue also exhibits this behaviour, although the magnitude of the ungerade contribution is reduced. In the carbene complex, ρ_BCP decreases due to a strong negative ungerade contribution, further supporting the assertion that the 6p_σ interaction in this complex has bonding character.

We now consider the charges and localisation indices in these complexes (see Table 2). The localisation indices, λ(A), complement the delocalisation indices by quantifying the number of electrons localised on each atom. As we have done previously,³² we here consider the charges and localisation indices of the entire ligands, as opposed to just those of the coordinating species. The variation in charges is similar at both the DFT and CASSCF levels of theory, with the freezing of the 6p shell leading, as expected, to a reduction in uranium charge and a (smaller) increase in the uranium localisation index. This reduction is most pronounced in uranyl, and is notably smaller in its carbene analogue, commensurate with our previous assertions of a reduced 6p role in the latter. Ligand localisation indices decrease by a greater amount than ligand charges. The reduction in uranium charge upon substitution by imido ligands is also in agreement with previous Mulliken and NBO analyses.¹⁷ Overall, this data is supportive of a reduction in the magnitude of the ionic interaction due to the greater shielding of the uranium centre provided by the freezing of the 6p shell.

Table 2 Uranium and ligand charges (Q) and localisation indices (λ), obtained at geometries optimised using a fully relaxed electronic structure. Values in parentheses correspond to a frozen electronic 6p shell. Charges are given in a.u

Complex	Method	Q(U)	Q(L)	λ(U)	λ(L)
UO2^2+	DFT	+3.270(+3.101)	−0.635(−0.551)	86.446(86.498)	7.438(7.289)
	CASSCF	+3.328(+3.148)	−0.664(−0.574)	86.857(86.955)	7.724(7.590)
U(NH)2^2+	DFT	+2.934(+2.753)	−0.467(−0.377)	86.634(86.726)	7.197(7.060)
	CASSCF	+3.004(+2.850)	−0.502(−0.425)	87.070(87.270)	7.574(7.430)
U(CH2)2^2+	DFT	+2.303(+2.171)	−0.152(−0.086)	87.517(87.638)	6.978(6.884)
	CASSCF	+2.354(+2.250)	−0.177(−0.125)	88.130(88.230)	7.352(7.310)

---

The energetic stabilisation due to core polarisation can be investigated by comparing total energies obtained with a fully relaxed electronic structure to those obtained with a frozen 6p shell, although we note that it may be exaggerated in electron-deficient systems such as these. The core polarisation stabilisation energy (CPSE) is 2.75 eV at the CASSCF level for uranyl, reducing to 2.46 eV and 1.55 eV for the imido and carbene analogues, respectively. As implied by previous data presented here, the magnitude of the CPSE weakens when the oxo ligands are substituted by less polarising ligands. The reduction in magnitude is more substantial at the DFT level of theory (see Table S3 of ESI†), in broad agreement with the variation in electronic structure data.

The CPSE, while useful to interpret electronic structure data, only gives partial insight into the ITI itself since it would also be expected to be non-zero in other conformations. We therefore evaluated the CASSCF-calculated CPSE in cis conformations, enforcing a L–U–L bond angle of 90° and, for ease of comparison, maintaining the M–L bond lengths found for the trans conformers. The difference in CPSE in the trans and cis conformations would then be expected to provide a first approximation to the magnitude of the ITI. The energetic stabilisation due to the ITI, calculated in this way, was found to be 0.76 for uranyl and 1.08 eV (0.73) eV for the imido (carbene) analogues. The uranyl value therefore represents a substantial fraction of the previously-calculated stability (1.65 eV) of trans uranyl over the cis conformer.³³

While the data presented to this point was obtained using geometries optimised with a fully relaxed electronic structure, an absence of the ITI would be expected to result in an elongation of the uranium–ligand bond and this is reported in Table 3. These data appear somewhat surprising: although the CPSE is strongest in uranyl and weakens upon ligand substitution, this is not reflected in bond length variation: at the DFT level of theory, there is little difference (<0.01 Å) in the elongation exhibited by the three complexes, whereas at the CASSCF level, uranyl actually exhibits the smallest elongation. From the electronic structure data presented here, it would appear that there is an interplay between increased covalent interactions (cf.Table 1) and reduced ionic interactions (cf.Table 2) in the absence of the ITI, resulting in the lack of a simple relationship with structural metrics. It is well-known that the U–O_yl interaction in uranyl is strongly covalent and it appears that this serves to balance out the reduced ionic interaction in the absence of the ITI, thereby resulting in only a moderate bond lengthening.

Table 3 Calculated uranium–ligand bond lengths. Values in parentheses correspond to a frozen electronic 6p shell

Complex	Method	r UL (Å)	ΔrUL (Å)
UO2^2+	DFT	1.684 (1.740)	0.056
	CASSCF	1.709 (1.775)	0.066
U(NH)2^2+	DFT	1.746 (1.801)	0.055
	CASSCF	1.783 (1.874)	0.091
U(CH2)2^2+	DFT	1.905 (1.954)	0.049
	CASSCF	1.970 (2.061)	0.091

---

The CPSE can be reevaluated using geometries optimised in both the presence and absence of core polarisation, see Table S4 of ESI.† As expected, this reduces its magnitude although the obtained trends are very similar. Broadly speaking, the same trends can be found in the electronic structure data, as seen in Tables S1–S7 of ESI.†

In summary, we have, for the first time, characterised the ITI in uranyl and its analogues via analysis of electron densities calculated at the DFT and CASSCF levels of theory, finding that both approaches yield qualitatively similar results. Denning's assertion of the nature of uranium polarisation by strongly coordinating ligands is verified, and the increase in electron sharing and charge accumulation in the metal–ligand bonding region found when the 6p shell is forced to assume localised atomic character can be rationalised as due to an antibonding 6p_σ contribution to the metal–ligand interaction, commensurate with the pushing from below mechanism. Of the complexes considered here, the effect of the ITI on electronic structure is found to be most pronounced in uranyl, consistent with the strong polarising ability of the oxo ligands, and this is reflected in the CPSE energies, where the ITI is found to stabilise the trans U–O_yl bonding interactions by approximately 0.76 eV. Interestingly, the magnitude of the ITI does not correlate with the elongation of the bond found when the ITI is suppressed, and this is interpreted as being due to an interplay of increased covalent and decreased ionic interactions, as previously asserted by La Pierre and Meyer.³

The previously recognised key role of the 6p_σ interactions in the ITI is supported by this study, and the analysis approach taken here is applicable to any systems in which σ-type metal–ligand interactions can be identified via symmetry considerations. Current investigations are focussed on oxohalides of the form AnOX₅, for which structural and spectroscopic data are available.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. K. W. Bagnall, J. du Preez, J. Barry and J. H. Holloway, Dalton Trans., 1975, 1963–1968.
2. B. D. Brown, C. T. Reynolds and P. T. Moseley, Dalton Trans., 1972, 857–859.
3. H. S. La Pierre and K. Meyer, Inorg. Chem., 2013, 52, 529–539.
4. H. S. La Pierre, M. Rosenzweig, B. Kosog, C. Hauser, F. W. Heinemann, S. T. Liddle and K. Meyer, Chem. Commun., 2015, 51, 16671–16674.
5. O. P. Lam, S. M. Franke, H. Nakai, F. W. Heinemann, W. Hieringer and K. Meyer, Inorg. Chem., 2012, 51, 6190–6199.
6. A. J. Lewis, K. C. Mullane, E. Nakamaru-Ogiso, P. J. Carroll and E. J. Schelter, Inorg. Chem., 2014, 53, 6944–6953.
7. A. J. Lewis, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2013, 135, 13185–13192.
8. B. Kosog, H. S. La Pierre, F. W. Heinemann, S. T. Liddle and K. Meyer, J. Am. Chem. Soc., 2012, 134, 5284–5289.
9. M. Gregson, E. Lu, D. Mills, F. Tuna, E. McInnes, C. Hennig, A. Scheinost, J. McMaster, W. Lewis, A. Blake, A. Kerridge and S. T. Liddle, Nat. Commun., 2017, 8, 14137.
10. R. G. Denning, Struct. Bonding, 1992, 79, 215–276.
11. R. G. Denning, J. Phys. Chem. A, 2007, 111, 4125–4143.
12. K. Tatsumi and R. Hoffmann, Inorg. Chem., 1980, 19, 2656–2658.
13. E. O’Grady and N. Kaltsoyannis, J. Chem. Soc., Dalton Trans., 2002, 1233–1239.
14. A. Kerridge, Chem. Commun., 2017, 53, 6685–6695.
15. V. V. Zhurov, E. A. Zhurova, A. I. Stash and A. A. Pinkerton, J. Phys. Chem. A, 2011, 115, 13016–13023.
16. C. G. Gianopoulos, V. V. Zhurov, S. G. Minasian, E. R. Batista, C. Jelsch and A. A. Pinkerton, Inorg. Chem., 2017, 56, 1775–1778.
17. T. W. Hayton, J. M. Boncella, B. L. Scott, P. D. Palmer, E. R. Batista and P. J. Hay, Science, 2005, 310, 1941–1943.
18. J. L. Brown, S. Fortier, G. Wu, N. Kaltsoyannis and T. W. Hayton, J. Am. Chem. Soc., 2013, 135, 5352–5355.
19. Y. Gong, C. L. Pereira, C. Michelini, J. Marc and J. K. Gibson, Inorg. Chem., 2013, 52, 14162–14167.
20. D. P. Mills, O. J. Cooper, F. Tuna, E. J. L. McInnes, E. S. Davies, J. McMaster, F. Moro, W. Lewis, A. J. Blake and S. T. Liddle, J. Am. Chem. Soc., 2012, 134, 10047–10054.
21. K. Pierloot and E. van Besien, J. Chem. Phys., 2005, 123, 204309.
22. R. G. Denning, J. C. Green, T. E. Hutchings, C. Dallera, A. Tagliaferri, K. Giarda, N. B. Brookes and L. Braicovich, J. Chem. Phys., 2002, 117, 8008–8020.
23. S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. D. Conradson, S. A. Kozimor, R. L. Martin, D. E. Schwarz, D. K. Shuh, G. L. Wagner, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2012, 134, 5586–5597.
24. L. P. Spencer, P. Yang, S. G. Minasian, R. E. Jilek, E. R. Batista, K. S. Boland, J. M. Boncella, S. D. Conradson, D. L. Clark, T. W. Hayton, S. A. Kozimor, R. L. Martin, M. M. MacInnes, A. C. Olson, B. L. Scott, D. K. Shuh and M. P. Wilkerson, J. Am. Chem. Soc., 2013, 135, 2279–2290.
25. A. Formanuik, A.-M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. McInnes and D. P. Mills, Nat. Chem., 2017, 9, 578–583.
26. A. Formanuik, F. Ortu, R. Beekmeyer, A. Kerridge, R. W. Adams and D. P. Mills, Dalton Trans., 2016, 45, 2390–2393.
27. A. Formanuik, F. Ortu, J. Liu, L. Nodaraki, F. Tuna, A. Kerridge and D. P. Mills, Chem. – Eur. J., 2017, 23, 2290–2293.
28. A. C. Behrle, A. Kerridge and J. R. Walensky, Inorg. Chem., 2015, 54, 11625–11636.
29. S. D. Woodall, A. N. Swinburne, A. Kerridge, P. Di Pietro, C. Adam, P. Kaden and L. S. Natrajan, Chem. Commun., 2015, 51, 5402–5405.
30. G. Karlström, R. Lindh, P.-Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239.
31. C. K. Jorgensen and R. Reisfeld, Struct. Bonding, 1982, 50, 121.
32. P. Di Pietro and A. Kerridge, Inorg. Chem., 2016, 55, 573–583.
33. G. Schreckenbach, P. J. Hay and R. L. Martin, Inorg. Chem., 1998, 37, 4442–4451.

---

Footnotes

† Electronic supplementary information (ESI) available: Full data tables, structural parameters and natural orbital visualisations. See DOI: 10.1039/c8cc06088f

‡ Both uranyl and its imido analogue were found to be linear, whereas the D_2h-symmetry carbene analogue was found to lie just 3 meV higher in energy than the C_s-symmetry isomer at the DFT level. This energy difference was sufficiently small that the D_2h-symmetry complex was deemed usable for ease of later analysis.

§ Test CASSCF(12,16) uranyl simulations, which included the four non-bonding 5f orbitals, gave structural parameters to within 0.001 Å of those calculated with CASSCF(12,12).

---