Open Access Article
Open Access ArticleThe opposite effects of sodium and potassium cations on water dynamics†
Qiang
Zhang
ab,
Hailong
Chen
c,
Tianmin
Wu
de,
Tan
Jin
a,
Zhijun
Pan
d,
Junrong
Zheng
*cf,
Yiqin
Gao
*f and
Wei
Zhuang
*a
aState Key Laboratory of Structural Chemistry, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou, Fujian 350002, China. E-mail: wzhuang@fjirsm.ac.cn
bDepartment of Chemistry, Bohai University, Jinzhou 121013, China
cDepartment of Chemistry, Rice University, Houston, TX 77005, USA. E-mail: junrong@rice.edu
dDepartment of Chemical Physics, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China
eFujian Provincial Key Laboratory of Theoretical and Computational Chemistry, Xiamen University, Xiamen, Fujian 361005, China
fCollege of Chemistry and Molecular Engineering, Beijing National Laboratory for Molecular Sciences, Peking University, Beijing 100871, China. E-mail: gaoyq@pku.edu.cn
First published on 14th October 2016
Abstract
Water rotational dynamics in NaSCN and KSCN solutions at a series of concentrations are investigated using femtosecond infrared spectroscopy and theory. Femtosecond infrared measurements, consistent with previous NMR observations, detect that sodium slows down while potassium accelerates the water O–H bond rotation. Results of reported neutron scattering measurements, on the other hand, suggested that these two cations have similar structure-breaking effects on water, and therefore should both accelerate water rotation through the presumably dominating large-amplitude angular jump component. To explain this discrepancy, theoretical studies with both classical and ab initio models were carried out, which indicate that both ions indeed accelerate the large-amplitude angular jump rotation of the water molecules, while the observed cation specific effect originates from the non-negligible opposite impact of the sodium and potassium cations on the diffusive rotation of water molecules.
Water dynamics in the hydration shells of ions and charged molecules play a critical role in a plethora of natural phenomena.1–6 The charged amino acids in proteins, for instance, have strong influences on the water dynamics, and therefore play critical roles in various biochemical properties of the proteins including folding as well as enzyme catalysis.7–12 The kinetic energy of water molecules can, as another example, transfer to ionic reactants and drive the chemical reactions.13 Trans-membrane ion transport starts and ends with the reorganization of the ionic hydration shells, which leads to remarkably different behaviors between ions which only have subtle differences such as sodium and potassium.14–17
The rotational dynamics of water in ionic solutions have been extensively studied to reveal the effect of ions on hydrogen bond interactions in water.18–35 Water rotational motions have contributions from both the large-amplitude angular jump during the exchange of hydrogen bond acceptors and the slower diffusive reorientation of the intact hydrogen bond axis.21,23,26,27,36–40 It is proposed, primarily based on studies of anions in water, that only the jump motion is significantly affected by ions, while the diffusive component is rarely changed. This change of jump component is suggested to be caused by ions strengthening or weakening the hydrogen bonding structure of the surrounding water molecules.19,23,26,27,37,38,41
For anions, it has been demonstrated that this perturbation can be understood as replacing the water–water hydrogen bonds with anion–water ones. Anions with stronger (weaker) hydrogen bonds than those in bulk water tend to hinder (accelerate) the angular jump of adjacent water molecules.19,23,26,27,41 For cations, however, this picture is not applicable. Na+ and K+ are two of the most common cations in aqueous solutions in nature, playing critical roles in many important processes. However, the molecular details of these two cations' effect on the surrounding water molecules are yet to be elucidated. Neutron scattering experiments demonstrate that both Na+, a cation considered to enhance the water hydrogen bonding structure (“structure maker”), and K+ which is considered to weaken the water hydrogen bonding structure (“structure breaker”) cause a net disordering of the water structure42 (further discussion on the observations of neutron scattering is given in Section A of the ESI†). The result suggests that both cations should accelerate the angular jump component and, if the diffusive component is negligible as in the anion case, the overall rotation of water. On the other hand, NMR relaxation measurements detect an accelerating effect of potassium while a retarding effect of sodium on the water dynamics (further discussion on this discrepancy between the two types of experiments is given in Section A of the ESI†).28,43,44
To understand these fundamentally important but puzzling observations, we herein investigate, through femtosecond infrared (fsIR) measurements and theoretical studies, how the water rotation is modified by sodium and potassium cations. fsIR focuses specifically on the rotation of water O–H bonds and has a much higher time resolution (further discussion is given in Section A of the ESI†), and therefore can be compared more easily with computer simulations. Due to its excellent time and structure resolution, fsIR has been extensively used to study water dynamics as well as how this is impacted by various ions and charged molecules.19,20,22–26,45,46
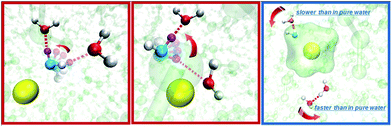
As suggested similarly by the NMR measurements, our fsIR results show opposite effects from Na+ and K+ on water rotation. Further analysis indicates that there are two molecular origins (Fig. 1) that lead to the seemingly contradictory experimental observations of fsIR and neutron scattering experiments: (1) both Na+ and K+, as the functional motifs, accelerate the jump component of the water rotation nearby, which is consistent with the neutron scattering measurement that both ions disrupt the water hydrogen bonding structure. (2) Na+ can significantly slow down the diffusive component in water rotation, while K+ mildly accelerates the diffusive component. The experimental dynamic observations in fsIR are the net effects of these two processes. For Na+, the retarding effect on the diffusive motion overwhelms the accelerating effect on the jump motion, resulting in a net slower molecular reorientation. For K+, it accelerates both components of the rotation and therefore the overall motion is faster.
Methods
A. Experimental setup for fsIR measurements
The rotational dynamics of water molecules were measured using multiple-dimensional vibrational spectroscopy. A similar fsIR experimental set up was used for a group of alkali thiocyanate solutions with a series of concentrations up to 15 M,47 with the discussion focusing on how ion clustering, at high concentrations (>5 M), leads to segregation of the rotational dynamics between water and anions. A ps amplifier and a fs amplifier were synchronized with the same seed pulse from a 82 MHz oscillator. The output of the ps amplifier pumps an OPA to produce ∼0.8 ps mid-IR pulses with tunable frequencies around 2500 cm−1 (close to the OD-stretch central frequency). The bandwidth of the pulse is around 20 cm−1 with an energy ∼40 μJ per pulse at 1 kHz. Light from the fs amplifier is directed to generate a <100 fs ultra-broad band mid-IR and terahertz super-continuum pulse in the frequency range from <10 cm−1 to >3500 cm−1 at 1 kHz. In experiments, the ps IR pulse is the excitation beam, and the fs super-continuum pulse is the detection beam which is frequency resolved using a spectrograph. Two polarizers are added into the detection beam path to selectively measure the parallel or perpendicular polarized signal relative to the excitation beam. Rotational relaxation dynamics of water molecules are acquired from the time dependent anisotropy R(t) = (P∥ − P⊥)/(P∥ + 2 × P⊥), where P∥ and P⊥ are parallel and perpendicular data.To avoid the effect of resonance energy transfer, HOD solutions (1 wt% D2O in H2O) were used to obtain the OD reorientation dynamics in KSCN and NaSCN aqueous solutions, and the excitation and detection OD frequencies were set at the OD central frequency. The signal resulting from the vibrational relaxation induced heat was removed with the model and parameters described previously,48i.e., the energy from the OD-stretch vibration is transferred through an intermediate state to a thermal end level.
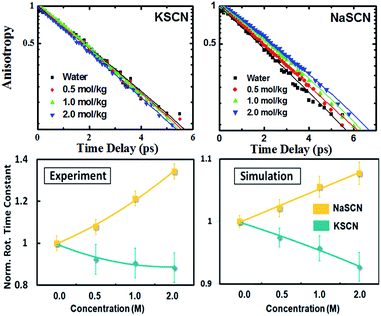
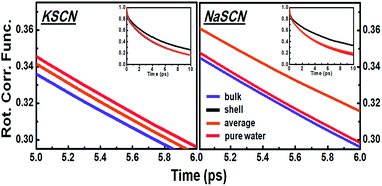
As a result, the time dependent rotation anisotropy of the OD stretch mode in NaSCN and KSCN aqueous solutions at various ion concentrations as well as that in pure water was collected at 295 K, and corresponding rotational time constants were obtained by fitting the rotation anisotropy decays with a single-exponential function (see Fig. 2). FTIR spectra of NaSCN and KSCN aqueous solutions (HOD, 1 wt% D2O in H2O) in the OD stretch region with various concentrations, the waiting time dependent parallel (P∥) and perpendicular (P⊥) data of pure water, KSCN and NaSCN solutions, as well as the transient absorption spectra in the OD frequency region of HOD solution at 0.1 ps, are provided in Fig. S1 (the ESI†). The samples were placed in a Janis cryostat under vacuum. NaSCN and KSCN were purchased from Sigma-Aldrich and used without further purification. D2O was obtained from C/D/N Isotopes Inc.
B. Theoretical modelling
Classical molecular dynamics simulations were carried out for the NaSCN and KSCN aqueous solution systems at a series of concentrations up to 2 M. As a validation of the models used, we also carried out an ab initio simulation in 1 M solutions (simulation setups are discussed in Section B and C of ESI†). The second-order reorientation correlation function Cα(t) of a molecule or ion in a solution along the OH vector α is described as a second-order Legendre polynomial (ESI†).Adopting the Extended Ivanov Jump Model (EJM) we decomposed the difference between the rotational time constants in a solution with concentration c and in pure water into the jump and frame diffusive components of every hydrogen bond switching type:27
τ(c) − τ(0) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δτP + δτJW:W + δτfW:W + δτJW:SCN + δτfW:SCN + δτJSCN:W + δτfSCN:W + δτJSCN:SCN + δτfSCN:SCN δτP + δτJW:W + δτfW:W + δτJW:SCN + δτfW:SCN + δτJSCN:W + δτfSCN:W + δτJSCN:SCN + δτfSCN:SCN | (1) |
To calculate the free energy profiles along the average path of a specific type of hydrogen bond switching, we record all trajectory fragments in which this type of switching happens. The probability P(ΔR, θ) to find the system at a specific configuration (ΔR, θ) is then calculated, in which θ is the angle between the O*H* vector and the bisector plane of OaO*Ob, ΔR is the difference of the distances RO*Oa and RO*Ob. We then choose a common time origin in all these events as the moment that θ = 0, where θ is the angle between the projection of the O*H* vector on the O*OaOb plane and the bisector of the OaO*Ob angle (inset of the left panel of Fig. 4). With this chosen time origin we then calculate the average values of (ΔR(t), θ(t)) at a specific moment t along the hydrogen bond switching path. The probability of the system at that moment is defined as P(ΔR(t), θ(t)). The free energy is calculated with the population free energy function, G = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ΔR(t), θ(t)), and the contributions from the two reaction coordinates are obtained by integration
ln(ΔR(t), θ(t)), and the contributions from the two reaction coordinates are obtained by integration 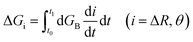 along the reaction path from the reactant to the transition state using a differential approach as described.27
along the reaction path from the reactant to the transition state using a differential approach as described.27
Results and discussion
The opposite cation effects of sodium and potassium on water rotation were measured using fsIR. Using this fsIR technique (details given in the “Methods” section), we measured the rotational time constants τOH of water molecules in KSCN and NaSCN solutions at a series of concentrations up to 2 M (Fig. 2). Opposite effects of Na+ and K+ on the water rotational dynamics are clearly observed: in a more concentrated solution, water rotation in the KSCN solutions speeds up, while in the NaSCN solutions it slows down.Diffusion rather than jumping causes the observed opposite trends in the fsIR experiment. We analyze the underlying molecular mechanism of the opposite cation effect with the assistance of theoretical modelling. Simulations based on the classical interaction model (Fig. 2, details given in Sections B and D of the ESI†) successfully reproduce the opposite trends of the rotational time constants in NaSCN and KSCN solutions. Furthermore, the ab initio simulation of the solutions at a concentration of 1 M (Fig. S4, details of simulation given in Section C of the ESI†) also demonstrates that both Na+ and K+ accelerate the jump rotation, while Na+ slows down the diffusive rotation and K+ slightly accelerates it. The results of the classical model are therefore well validated. Due to the expense of the ab initio calculation, the analysis from this point on is carried out based on the classical interaction model.
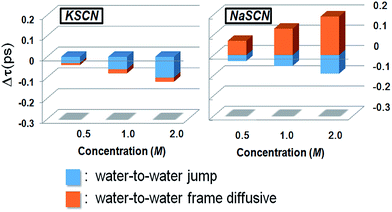
Since the rotation of a water molecule in pure water as well as in ionic solutions is closely related to the hydrogen bond switching,19,23,24,27,35,41 we dissect the trajectory of each water molecule under investigation (the “tagged” water molecule) into a group of successive hydrogen bond switching events. We categorize these trajectory fragments into four groups according to the initial and final hydrogen bond acceptors during the switching: (1) water-to-water; (2) water-to-SCN; (3) SCN-to-water and (4) SCN-to-SCN. A procedure based on the Extended Jump Model (EJM)19,35,41 (details given in Section E of the ESI†) is then used to quantitatively decompose the difference between the overall rotation in solution and that in pure water into the jump and diffusive contributions of all four switching types (details given in Section F of the ESI†). The contributions from the water-to-water hydrogen bond switching are found to be the dominating components which decide the overall ion effect.
Ion effects on the jump (light-blue) and diffusive (brick-red) rotations during the water-to-water hydrogen bond switchings are presented in Fig. 3. The most striking observation here is that the jump rotation is accelerated in both solutions, while the diffusive rotation is accelerated in the KSCN solution and retarded in the NaSCN solution. The theoretical results provide an explanation for the discrepancy between the different experimental observations:42 the water hydrogen bonding structure is disrupted in both solutions as suggested by the neutron scattering experiment, which accelerates the jump rotations. On the other hand, the diffusive rotation is sped up in KSCN while being retarded in NaSCN solution. The sum of the two rotational components results in the observed opposite overall rotations in our fsIR measurements as well as in the reported NMR results.28,43,44 In the following section we discuss the molecular details of how the jump and diffusive rotation during the water-to-water switchings are modified by the cations.
A. Molecular details of the cation effect on the jump rotation
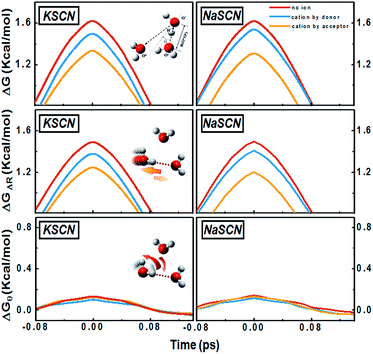
The negative values of the cation effect on the jump component in Fig. 3 suggest that the presence of the ions in the neighbourhood of the tagged water molecule speeds up the jump rotation of water. To study the effects of the cations, we select a dilute solution (0.1 M) and inspect three types of water-to-water hydrogen bond switching, where: (1) no ion is adjacent to either donor or acceptor; (2) one cation is in the first solvation shell of the donor, and (3) one cation is in the first solvation shell of the acceptor. Table S4 in the ESI† gives the jump rotational times of the donor water molecule during these types of hydrogen bond switching.For these three water-to-water switching types, we present the time evolution of the free energy variation (see the “Methods” section for the technique used) along the average jump path in Fig. 4 (see Section G in the ESI† for a further discussion). The time origin is chosen to be the moment that θ = 0, where θ is the angle between the projection of the O*H* vector on the O*OaOb plane and the bisector of the OaO*Ob angle (inset of the left panel of Fig. 4). The transition free energy barriers for the water-to-water jumps with a cation in the vicinity are lower than that with no ion around, which suggests that although the sodium and potassium cations do not form a hydrogen bond with the water molecules like the anions, they can still considerably affect the jump rotation of water.
We further look at the free energy profiles of the cation-bound water-to-water jumps along two coordinates: (1) radial: the difference of the distances RO*Oa and RO*Ob, and (2) angular: the angle θ between the O*H bond and the bisector plane of OaO*Ob (Fig. 4). The free energy differences between the ion-bound and the non-ion configurations are much smaller along the angular dimension than along the radial one. The translational departure of O*Oa and the approach of O*Ob is therefore much more prominently affected by the cations, since the free energy profile is modified more significantly, compared to the reorientational searching-next-hydrogen-bond-acceptor component.
The cation effect on the jump component has two aspects: (1) more commonly (69% in KSCN and 88% in NaSCN solution), a cation is next to the donor water. It breaks the surrounding hydrogen bonding network structure (left panel in Fig. 1) and makes it easier for the donor water to approach or leave the acceptor water molecule. (2) With a much smaller probability (31% in KSCN and 12% in NaSCN solution), a cation is bound to the acceptor water. It occupies part of the space between the donor and acceptor water molecules (center panel in Fig. 1), and directly distorts the H*–Oa hydrogen bond (Fig. 5). The hydrogen bond between the donor water and the cation bound acceptor water becomes easier to break, which lowers the free energy barrier.
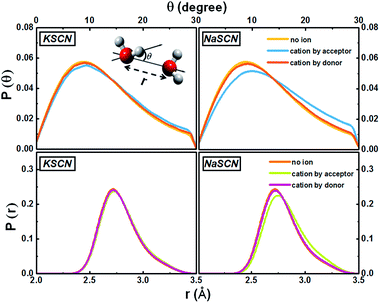 | ||
| Fig. 5 Distributions of the water–water hydrogen bonding angle and distance in the 0.5 M KSCN and NaSCN solutions. The inset of the upper left panel gives the definitions of these two geometrical parameters. When a cation appears next to the acceptor water, both distributions deviate from the non-ion case. In the NaSCN solution, this deviation is much more significant (note that this does not suggest that the Na+ hydration shell is more distorted than that of K+, see Section G of the ESI† for a further discussion). | ||
B. Molecular details of the cation effect on the diffusive rotation
Fig. 3 indicates that the diffusive rotation during the water-to-water switching is accelerated in KSCN but hindered in NaSCN solution. To reveal the molecular origin of this ion specific effect, the average diffusive rotations of all the hydrogen bonding water pairs during the process of hydrogen bond exchange in the 0.5 M NaSCN and KSCN solutions is directly measured from the simulation trajectory (Fig. 6). Consistent with the analytical decomposition results in Fig. 3, we observed acceleration in KSCN and hindrance in NaSCN solutions as well.The water pairs chosen can then be separated into one group with at least one water molecule in the pair staying in the cation first solvation shell and another group with both water molecules in the pair staying out of the first solvation shells of the cations. For NaSCN, the diffusive rotation of the water pairs out of the cation first solvation shells is almost the same as those in pure water, while that of the shell water is slower. This leads to an average diffusive rotation slower than that in pure water. For KSCN, the diffusive rotation of the shell water is slower than that in pure water (Fig. 6), but less significantly so compared to that in NaSCN solution. The average diffusive rotation of the water pairs out of the cation first solvation shell is, however, clearly faster than that in pure water (Fig. 6). The amount of water out of the cation first solvation shell is much larger than that of shell water, which explains the faster overall diffusive rotation than that in pure water.
We next explore the molecular origin of the retardation of shell water and acceleration of water out of the cation first solvation shell in their diffusive rotations. The diffusive rotation of the cation shell water pairs is retarded, and the retardation is more significant for NaSCN. This suggests that they move together with the cations (Fig. 1), with the residence time of water in the cation solvation shell much longer than the rotation time period.49,50 As an example of this long residence time, the simulation of the 0.5 M solutions suggests that the average water rotational time constants are 2.23 ps and 2.46 ps in KSCN and NaSCN solutions, respectively (in pure water it is 2.4 ps), while the corresponding residence times of water in the cation solvation shells are 8.25 ps and 21.61 ps. Furthermore, the sodium-bound water pairs diffuse, interestingly, slower compared with potassium-bound ones despite sodium's smaller size (the radii of bare sodium and potassium ions are 1.06 Å and 1.38 Å, respectively).51 This apparent discrepancy is due to the fact that the ion mobility is related not only to the size of the bare ion but also to the hydration shell structure and lability.49,50,52 A good estimation of the cooperative mobility is the Stokes radius of the ions: R = kBT/6πηD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51–53 in which D is the self diffusion constant of the ions calculated from the root mean square deviation (K+: 1.84 × 10−9 m2 s−1, Na+: 1.27 × 10−9 m2 s−1 in KSCN and NaSCN solutions at 0.5 M). The calculated Stokes radius of sodium is 1.94 Å, larger than that of potassium (1.34 Å), which indicates that sodium can move together with more water molecules, and therefore slows down the diffusive rotations of the shell water molecules more dramatically compared with potassium.
51–53 in which D is the self diffusion constant of the ions calculated from the root mean square deviation (K+: 1.84 × 10−9 m2 s−1, Na+: 1.27 × 10−9 m2 s−1 in KSCN and NaSCN solutions at 0.5 M). The calculated Stokes radius of sodium is 1.94 Å, larger than that of potassium (1.34 Å), which indicates that sodium can move together with more water molecules, and therefore slows down the diffusive rotations of the shell water molecules more dramatically compared with potassium.
To explain the accelerated diffusive rotation of water out of the cation first solvation shell, we adopt a picture based on the well known Eyring viscosity model.53
The Stokes–Einstein–Debye relation suggests that the diffusive rotation of water molecules is proportional to viscosity in dilute solutions.51,52 To examine whether this relation is valid in the systems studied herein, we calculated the viscosities based on simulation trajectories using the Green–Kubo method54,55 (see Section J in the ESI† for the technical details). The calculated viscosities at a series of concentrations are presented in Fig. S5† and compared with the frame rotation time constants τfW–W. A strong correlation is observed.
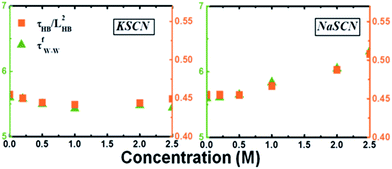
Eyring's model suggests that the amplitude of the viscosity is determined from the ratio ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) /L2 between the time (
/L2 between the time (![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) ) and length (L) of the “excited” hoppings of the molecules. The value of τfW–W should be proportional to the same physical quantity as well. As an identification that these excited hoppings are simply the hydrogen bond switchings in dilute solutions, Fig. 7 shows a good correlation between
) and length (L) of the “excited” hoppings of the molecules. The value of τfW–W should be proportional to the same physical quantity as well. As an identification that these excited hoppings are simply the hydrogen bond switchings in dilute solutions, Fig. 7 shows a good correlation between ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) HB/LHB2 and τfW–W, where LHB is the average hydrogen bond switching length and
HB/LHB2 and τfW–W, where LHB is the average hydrogen bond switching length and ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) HB the average switching time. The diffusive rotation of water out of the cation first solvation shell is therefore controlled by the hydrogen bond switching processes,56 and a higher switching rate leads to faster diffusive rotation. Compared to the switching in pure water, that of water out of the cation first solvation shell in the dilute solutions is accelerated (for instance, the average hydrogen bond switching time is 3.08 ps for water out of the cation first solvation shell in 0.5 M KSCN solution and 3.28 ps in pure water). This speeding-up is due to the spatial correlation of the hydrogen bond switchings in water:57 the acceleration of the switchings in the cation solvation shell (2.77 ps in 0.5 M KSCN solution) leads to acceleration of switching rates nearby. Consequently, the diffusive motion of the water out of the cation first solvation shell becomes faster in the KSCN solution. For NaSCN, this effect is much less significant. The hydrogen bond switching times are 3.21/2.92 ps for water out of/inside the cation first solvation shell, respectively.
HB the average switching time. The diffusive rotation of water out of the cation first solvation shell is therefore controlled by the hydrogen bond switching processes,56 and a higher switching rate leads to faster diffusive rotation. Compared to the switching in pure water, that of water out of the cation first solvation shell in the dilute solutions is accelerated (for instance, the average hydrogen bond switching time is 3.08 ps for water out of the cation first solvation shell in 0.5 M KSCN solution and 3.28 ps in pure water). This speeding-up is due to the spatial correlation of the hydrogen bond switchings in water:57 the acceleration of the switchings in the cation solvation shell (2.77 ps in 0.5 M KSCN solution) leads to acceleration of switching rates nearby. Consequently, the diffusive motion of the water out of the cation first solvation shell becomes faster in the KSCN solution. For NaSCN, this effect is much less significant. The hydrogen bond switching times are 3.21/2.92 ps for water out of/inside the cation first solvation shell, respectively.
Cations do not always accelerate the water jump rotation as in the cases of Na+ and K+. In Mg2+ aqueous solutions (Fig. S2 in ESI†) the water jump rotation is actually retarded. This is due to the high charge density of Mg2+, which leads to a strong interaction between magnesium cations and water oxygens and therefore retards both the jump and diffusive components of water rotation. Such a dual retarding effect leads to slower water rotational dynamics in Mg2+ solutions than in either Na+ or K+ solutions, as experimentally observed.19
In an earlier study on water rotation in dilute KSCN solutions, we demonstrated that the rotation of the “bridge” water adjacent to both ions of a KSCN pair is retarded.58 This effect of ion pairing on water rotation is rather minor since the extent of pairing should have similar small values in dilute KSCN and NaSCN solutions.
The investigations carried out here focus on dilute solutions, and for the more concentrated ones, a general retardation effect is observed for all the ions despite their structure making/breaking characteristics.27 Similar analysis as what has been applied here can be used to understand the underlying physics of this general deceleration.
Conclusions
The modifications of sodium and potassium cations on the rotational motions of the water molecules in their hydration shells are investigated. Contrary to the common view that sodium strengthens the water structure and therefore retards water motion while potassium facilitates the water motion by weakening the water structure, these two cations both speed up the angular jump rotation of the adjacent water molecule because of disruption of the water H-bond by the cations. On the other hand, the two cations have different net impacts on the diffusive rotation of the cation-bound water molecules. Na+ slows down the water diffusive rotation while K+ facilitates the water diffusive rotation. The picture revealed herein explains the apparent contradiction between neutron scattering measurements which suggest that these two cations disrupt the water hydrogen bonding structure and dynamics experiments which suggest that Na+ retards while K+ accelerates the water rotation.Acknowledgements
This material is based upon work supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB20000000 and XDB10040304) and the NSFC Grant (21373201 and 21033008). Y. Q. Gao thanks NSFC for support (21125311 and 91027044). Q. Zhang thanks the Scientific Research Foundation for Returned Scholars, Ministry of Education of China and Liaoning BaiQianWan Talents Program (2015-73) for support. J. Z. gratefully thanks the Welch foundation C-1752, the AFOSR Award FA9550-11-1-0070, the Sloan Foundation and the David and Lucile Packard Foundation for support.Notes and references
- P. Ball, Chem. Rev., 2008, 108, 74 CrossRef CAS PubMed.
- H. Ohtaki and T. Radnai, Chem. Rev., 1993, 93, 1157 CrossRef CAS.
- P. Lo Nostro and B. W. Ninham, Hofmeister phenomena: an update on ion specificity in biology, Chem. Rev., 2012, 112, 2286 CrossRef CAS PubMed.
- Y. Marcus, Chem. Rev., 2009, 109, 1346 CrossRef CAS PubMed.
- J. L. Skinner, Science, 2010, 328, 985 CrossRef CAS PubMed.
- P. Jungwirth and D. J. Tobias, Chem. Rev., 2006, 106, 1259 CrossRef CAS PubMed.
- Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389 CrossRef CAS PubMed.
- B. Halle, Philos. Trans. R. Soc., B, 2004, 359, 1207 CrossRef CAS PubMed.
- A. C. Fogarty, E. Duboué-Dijon, F. Sterpone, J. T. Hynes and D. Laage, Chem. Soc. Rev., 2013, 42, 5672 RSC.
- W. Qiu, Y.-T. T. Kao, L. Zhang, Y. Yang, L. Wang, W. E. Stites, D. Zhong and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13979 CrossRef CAS PubMed.
- B. Born, S. J. Kim, S. Ebbinghaus, M. Gruebele, M. Havenith, D. J. Tobias, G. Zaccai and M. Weik, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18049 CrossRef PubMed.
- D. Russo, J. Ollivier and J. Teixeira, Phys. Chem. Chem. Phys., 2008, 10, 4968 RSC.
- B. J. Gertner, R. M. Whitnell, K. R. Wilson and J. T. Hynes, J. Am. Chem. Soc., 1991, 113, 74 CrossRef CAS PubMed.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular biology of the cell, Garland Science, New York and London, 5th edn, 2007 Search PubMed.
- D. A. Doyle, J. M. Cabral, R. A. Pfuetzner, A. L. Kuo, J. M. Gulbis, S. L. Cohen, B. T. Chait and R. MacKinnon, Science, 1998, 280, 69 CrossRef CAS PubMed.
- C. Maffeo, S. Bhattacharya, J. Yoo, D. Wells and A. Aksimentiev, Chem. Rev., 2012, 112, 6250 CrossRef CAS PubMed.
- L. Vrbka, J. Vondrasek, B. Jagoda-Cwiklik, R. Vacha and P. Jungwirth, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15440 CrossRef CAS PubMed.
- A. W. Omta, M. F. Kropman, S. Woutersen and H. J. Bakker, Science, 2003, 301, 347 CrossRef CAS PubMed.
- K. J. Tielrooij, N. Garcia-Araez, M. Bonn and H. J. Bakker, Science, 2010, 328, 1006 CrossRef CAS PubMed.
- J. Smith, P. Saykally and R. Geissler, J. Am. Chem. Soc., 2007, 129, 13847 CrossRef CAS PubMed.
- M. Ji, M. Odelius and K. J. Gaffney, Science, 2010, 328, 1003 CrossRef CAS PubMed.
- S. Park, M. Odelius and K. J. Gaffney, J. Phys. Chem. B, 2009, 113, 7825 CrossRef CAS PubMed.
- S. Park and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16731 CrossRef CAS PubMed.
- I. A. Heisler, K. Mazur and S. R. Meech, J. Phys. Chem. B, 2011, 115, 1863 CrossRef CAS PubMed.
- S. T. Roberts, K. Ramasesha and A. Tokmakoff, Acc. Chem. Res., 2009, 42, 1239 CrossRef CAS PubMed.
- H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498 CrossRef CAS PubMed.
- G. Stirnemann, E. Wernersson, P. Jungwirth and D. Laage, J. Am. Chem. Soc., 2013, 135, 11824 CrossRef CAS PubMed.
- G. Engel and H. G. Hertz, Ber. Bunsen-Ges. Phys. Chem., 1968, 72, 808 CAS.
- L. Endom, H. G. Hertz, B. Thül and M. D. Zeidler, Ber. Bunsenges. Phys. Chem., 1967, 71, 1008 CAS.
- J. L. Skinner, Theor. Chem. Acc., 2011, 128, 147 CrossRef CAS.
- Y. S. Lin, B. M. Auer and J. L. Skinner, J. Chem. Phys., 2009, 131, 144511 CrossRef PubMed.
- D. A. Turton, J. Hunger, G. Hefter, R. Buchner and K. Wynne, J. Chem. Phys., 2008, 128, 161102 CrossRef PubMed.
- R. Buchner and G. Hefter, Phys. Chem. Chem. Phys., 2009, 11, 8984 RSC.
- A. Chandra and G. N. Patey, J. Chem. Phys., 1994, 100, 8385 CrossRef CAS.
- D. Laage and J. T. Hynes, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11167 CrossRef CAS PubMed.
- D. E. Moilanen, D. B. Spry, N. E. Levinger and M. D. Fayer, J. Am. Chem. Soc., 2007, 129, 14311 CrossRef CAS PubMed.
- M. D. Fayer, Acc. Chem. Res., 2012, 45, 3 CrossRef CAS PubMed.
- D. Laage and J. T. Hynes, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 967 CrossRef CAS PubMed.
- D. Laage, Science, 2006, 311, 832 CrossRef CAS PubMed.
- R. H. Henchman and S. J. Irudayam, J. Phys. Chem. B, 2010, 114, 16792 CrossRef CAS PubMed.
- D. Laage, G. Stirnemann, F. Sterpone, R. Rey and J. T. Hynes, Annu. Rev. Phys. Chem., 2011, 62, 395 CrossRef CAS PubMed.
- (a) R. Mancinelli, A. Botti, M. A. Bruni and A. K. Soper, Phys. Chem. Chem. Phys., 2007, 9, 2959 RSC; (b) R. Mancinelli, A. Botti, M. A. Bruni and A. K. Soper, J. Phys. Chem. B, 2007, 111, 13570 CrossRef CAS PubMed.
- K. Yoshida, K. Ibuki and M. Ueno, J. Solution Chem., 1996, 25, 435 CrossRef CAS.
- K. Fumino, K. Yukiyasu, A. Shimizu and Y. Taniguchi, J. Mol. Liq., 1998, 75, 1 CrossRef CAS.
- J. L. Skinner, P. A. Pieniazek and S. M. Gruenbaum, Acc. Chem. Res., 2011, 45, 93 CrossRef PubMed.
- T. Elsaesser, Acc. Chem. Res., 2009, 42, 1220 CrossRef CAS PubMed.
- H. Bian, H. Chen, Q. Zhang, J. Li, X. Wen, W. Zhuang and J. Zheng, J. Phys. Chem. B, 2013, 117, 7972 CrossRef CAS PubMed.
- K. J. Tielrooij, C. Petersen, Y. L. A. Rezus and H. J. Bakker, Chem. Phys. Lett., 2009, 471, 71 CrossRef CAS.
- S. Koneshan, J. C. Rasaiah, R. M. Lynden-Bell and S. H. Lee, J. Phys. Chem. B, 1998, 102, 4193 CrossRef CAS.
- K. B. Møller, R. Rey, M. Masia and J. T. Hynes, J. Chem. Phys., 2005, 122, 114508 CrossRef PubMed.
- A. Einstein, Investigations on the theory of the Brownian motion, Dover, New York, 1956 Search PubMed.
- P. Debye, Polar molecules, Dover, New York, 1929 Search PubMed.
- J. F. Kincaid, H. Eyring and A. E. Stearn, Chem. Rev., 1941, 28, 301 CrossRef CAS.
- M. S. Green, J. Chem. Phys., 1954, 22, 398 CrossRef CAS.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570 CrossRef.
- J. Qvist, C. Mattea, E. P. Sunde and B. Halleb, J. Chem. Phys., 2012, 136, 204505 CrossRef PubMed.
- C. Liu, W. Li and W. Wang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052309 CrossRef PubMed.
- Q. Zhang, W. Xie, H. Bian, Y. Q. Gao, J. Zheng and W. Zhuang, J. Phys. Chem. B, 2013, 117, 299 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the experiments & simulations, the rotational correlation functions, jump rotations, the free energy profiles along the hydrogen bond switching paths, and viscosity, tables and figures. See DOI: 10.1039/c6sc03320b |
| This journal is © The Royal Society of Chemistry 2017 |