Electronic structure and dynamics of torsion-locked photoactive yellow protein chromophores

Abstract

The photocycle of photoactive yellow protein (PYP) begins with small-scale torsional motions of the chromophore leading to large-scale movements of the protein scaffold triggering a biological response. The role of single-bond torsional molecular motions of the chromophore in the initial steps of the PYP photocycle are not fully understood. Here, we employ anion photoelectron spectroscopy measurements and quantum chemistry calculations to investigate the electronic relaxation dynamics following photoexcitation of four model chromophores, para-coumaric acid, its methyl ester, and two analogues with aliphatic bridges hindering torsional motions around the single bonds adjacent to the alkene group. Following direct photoexcitation of S₁ at 400 nm, we find that both single bond rotations play a role in steering the PYP chromophore through the S₁/S₀ conical intersection but that rotation around the single bond between the alkene moiety and the phenoxide group is particularly important. Following photoexcitation of higher lying electronic states in the range 346–310 nm, we find that rotation around the single bond between the alkene and phenoxide groups also plays a key role in the electronic relaxation from higher lying states to the S₁ state. These results have potential applications in tuning the photoresponse of photoactive proteins and materials with chromophores based on PYP.

---

1 Introduction

Photoreceptor proteins play a vital role in nature facilitating various biological processes, such as ion transport, vision and signal transduction. Following photoexcitation, the small chromophores that are embedded in these proteins undergo fundamental photochemical reactions, such as isomerisation, excited-state proton transfer or excited-state electron transfer.¹ The small-scale structural changes of the chromophore then propagate to large-scale structural changes in the surrounding protein framework that generate longer-lived signalling states to which the host organism may respond. It is important to understand the role the protein plays in orchestrating the photoresponse of the host organism by optimising the efficiency of the process and minimising competing pathways.

Photoactive yellow protein (PYP) is the primary photoreceptor for the negative phototactic response of the Halorhodospira halophila bacterium to blue light that limits its exposure to potentially harmful UV light.³ The chromophore that lies at the centre of PYP is a deprotonated trans-para-coumaric acid anion (pCA⁻) covalently bound to a cysteine residue via a thio-ester linkage and stabilised by nearby residues through a hydrogen bond network (Fig. 1). Upon photoexcitation, PYP undergoes a photocycle that begins with a trans–cis isomerisation of the chromophore and is followed by restructuring of the surrounding hydrogen bond network to accommodate the cis conformation, partial unfolding of the protein and protonation of the chromophore to form the signalling state. Subsequent cis–trans isomerisation of the chromophore, refolding of the protein and deprotonation of the chromophore to form trans-pCA⁻ in its ground electronic state, completes the photocycle. Photoisomerisation is a common initial photoresponse in photoactive proteins; for example, photoisomerisation is the initial step in the photochemistry of rhodopsins, a family of photoreceptor proteins that use the retinal chromophore for light reception.⁴

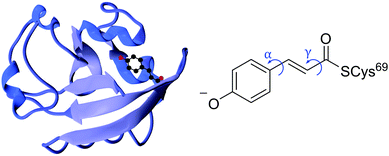Fig. 1 Left: PYP protein structure² with the chromophore enclosed. Right: PYP chromophore as it exists in the protein showing the torsional rotations that are the subject of this paper.

Although the excited state rotation of the double bond is of key importance in the photocycle of PYP, the trans–cis isomerisation couples with other nuclear motions within the chromophore resulting in torsional-motion about the single bonds either side of the double bond (Fig. 1).⁵ However, without the protein environment, it has been suggested that it is single bond, not double bond, rotation that dominates in the first excited state.^6,7 It is well understood that this is the case for the methyl thio-ester analogue of pCA⁻ in an aqueous environment, where rotation about the phenolate-ethene single bond (α rotation, Fig. 1) is the key coordinate in the relaxation pathway following photoexcitation.^8,9 Theoretical studies have suggested that this single bond rotation also dominates when the chromophore is isolated in the gas phase,⁶ or in a mutant protein environment (R52Q).⁷ It was suggested that the global minimum on the excited state surface is a double-bond twisted structure with a dihedral angle across the double bond of 90°. In addition, a local minimum structure was found with a dihedral angle of 90° about the single bond joining the phenoxide and ethene moieties. It was proposed that a role of the protein scaffold is to restrict this competing single bond α rotation (Fig. 1) and hence promote trans–cis isomerisation by stabilising the twisted double bond global minimum structure and lowering the barrier to isomerisation on the excited state potential energy surface. On the other hand, some experimental studies have contradicted this. A time-resolved spectroscopy study probing the photophysics of wild-type PYP and a reconstructed PYP with a chromophore rotation-locked across the phenolate-ethene single bond by an ethane bridge¹⁰ reported that the excited state dynamics of the locked chromophore were accelerated but that the isomerisation yield was reduced by ∼60%, implying that the phenolate rotation is not an alternative to trans–cis isomerisation but that it does help facilitate the isomerisation with some coupled movement. This contrasts with the conclusions of an earlier gas-phase time-resolved photoelectron spectroscopy study of a ketone analogue of the PYP chromophore which did not show any evidence for a single-bond twisted intermediate in the excited state and revealed isomerisation times similar to those in the protein.¹¹

Efforts have also been made to understand the importance of other single bond rotations in the chromophore. Some studies focused on the C_C=O–S_Cys bond, the connection between the chromophore and the protein.^12–14 In a Fourier-transform infrared spectroscopy study it was found that PYP derivatives with locked chromophores were unable to undergo isomerisation but were still able to produce intermediates of the PYP photocycle.¹⁴ Hence, the authors deemed the trans–cis isomerisation process dispensible for photoactivity in PYP and instead suggested that rotation of the carbonyl group is more significant. Thus, it is clear that the roles of the various torsional motions in the early stages of the PYP photocycle are still not completely understood.

Non-radiative electronic relaxation pathways such as internal conversion (IC), intersystem crossing, intramolecular vibrational redistribution and electron detachment can compete with the trans–cis isomerisation process. In order to understand the role of the protein in minimising these competing processes, it is important to understand the intrinsic photochemistry of the isolated chromophores. Following excitation of a ketone analogue of pCA⁻ in the gas-phase at 400 nm (3.1 eV), 20% of the excited state population was found to undergo autodetachment and it was deduced that one of the roles of the protein environment is to funnel excited state population through the conical intersection (CI) seam towards the cis isomer to impede radical formation.¹¹ Electron detachment has also been observed from isolated chromophores in solution¹⁵ and from the protein,¹⁶ and in both cases the spectral signatures were those of solvated electrons, suggesting that the protein pocket provides a water-like environment for the emitted electron.

In recent work, we investigated electron detachment from different structural isomers of pCA⁻. We found that following excitation of high-lying excited states using UV light, the relative contributions from electron detachment and internal conversion to lower lying electronic states was different for ortho-, meta- and para- isomers of pCA⁻.¹⁷ We also investigated the effects of substitution at the tail end of the chromophore.¹⁸ We found that acid and methyl ester moieties had very similar relaxation dynamics but substitution by a thioester appeared to raise the electron detachment threshold and impede internal conversion to lower-lying states.

In this work, we extend our previous studies to structural analogues of pCA⁻ designed to allow us to test the importance of torsional motions on the electronic relaxation dynamics of the PYP chromophore in the gas phase following photoexcitation of the first excited state and higher lying excited states. Specifically, we have employed anion photoelectron spectroscopy and quantum chemistry calculations to investigate the electronic structure and dynamics of four model PYP chromophores (Fig. 2): pCA⁻, its methyl ester pCE⁻, and two analogues of pCE⁻ with aliphatic carbon bridges hindering single-bond torsional motion at either site adjacent to the unsaturated bond, denoted here as PpCE⁻ and NpCE⁻ due to the pyranone and (tetrahydro)napthalene motifs, respectively. We determine the electronic structure and relaxation pathways available to the chromophores and how these are influenced by locking the single bond rotations.

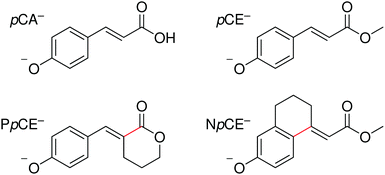Fig. 2 Structures of the deprotonated PYP chromophores used in this study with conformationally-locked bonds shown in red.

2 Experimental and computational methods

2.1 Chromophores

pCA was purchased from Sigma-Aldrich and pCE was purchased from Tokyo Chemical Industry, both were used without further purification. PpCE and NpCE were synthesised by standard chemistry. See ESI† for further details.

2.2 Photoelectron spectroscopy

Anion photoelectron spectra were recorded using our apparatus that has also been described elsewhere.^19–22 In brief, we obtain gas-phase deprotonated anions of pCA, pCE, PpCE and NpCE by electrospray ionisation of ∼1 mM methanol solutions of each chromophore with a few drops of aqueous ammonia added. The anions are mass-selected by a quadrupole and guided into a hexapole ion trap. The anions are released from the ion trap at 20 Hz and focused into the source region of a collinear velocity map imaging spectrometer. Nanosecond laser pulses of wavelength 310–346 nm were generated by frequency-doubling the output of a Nd:YAG pumped dye laser. Femtosecond laser pulses (>50 fs, 250 Hz) of wavelength centred at 400 nm were produced by frequency-doubling the output of a commercial amplified Ti:Sapphire femtosecond laser system. Photoelectrons generated in the interaction region were accelerated towards a position sensitive detector and imaged using a CCD camera. Laser-only images were recorded without the pulsed ion-beam and subtracted from the overall signal to remove background counts from ionisation of residual gas or scattered laser light. Photoelectron velocity distributions were obtained using the pBasex inversion method.²³ Electron kinetic energy (eKE) spectra were obtained by calibrating the radial photoelectron velocity distribution against the photoelectron spectrum of iodide²⁴ (310–346 nm) and p-HBDI⁻²⁵ (400 nm). The energy resolution of the 310–346 nm spectra is <5% and the error in eKE is around 0.05 eV.

2.3 Calculations

The structures of the anionic chromophores and their corresponding neutral radicals were optimised using density functional theory with the B3LYP hybrid functional^26–29 and 6-311++G(3df,3pd) basis set.^30–32 Vibrational analysis was performed to confirm the optimisations resulted in minima.

Vertical excitation energies (VEEs) of the singlet electronic excited states of the chromophores were calculated using time-dependent density functional theory (TD-DFT) and the algebraic diagrammatic construction method to second order (ADC(2)).^33,34 TD-DFT calculations were performed with CAM-B3LYP³⁵/6-311++G(3df,3pd), a method that has been shown to provide qualitative agreement with measured electronic excitation energies of PYP chromophores.¹⁸ ADC(2)/6-31+G** calculations have also been performed and these have shown to calculate the VEEs accurately and reliably with a reasonable computational expense (see Table S1 in ESI† for benchmarking VEE calculations).

Vertical detachment energies (VDEs) were calculated using various methods to compare to the measured values we have obtained. We have used electron propagator theory (EPT)³⁶ with the 6-311++G(3df,3pd) basis set, a method that has proved to agree well with experimental VDEs in earlier work.^18,25 Also, we have used the equation-of-motion coupled cluster method with single and double excitations for the calculation of ionisation potentials (EOM-IP-CCSD),³⁷ performed using the aug-cc-pVDZ basis set³⁸ which has shown previously to calculate detachment energies to higher-lying excited states of similar neutral radicals effectively.^25,39 The VDEs have also been calculated as the anion-neutral radical energy difference using DFT (B3LYP/6-311++G(3df,3pd)) at the optimised geometry of the anion. Calculating the VDEs with this method gives a more direct comparison with the calculated adiabatic detachment energies (ADEs) which are found using energies from DFT (B3LYP/6-311++G(3df,3pd)) calculations. ADEs are determined by the difference in energy between the S₀ minima and D₀ minima (0-0 transition), accounting for zero-point energies.

Geometry optimisations, vibrational frequencies, TD-DFT and EPT calculations were performed using the Gaussian09 software suite,⁴⁰ while EOM-CCSD and ADC(2) calculations were carried out using the Q-Chem software package.⁴¹

3 Results and discussion

3.1 Photoelectron spectra and computational results

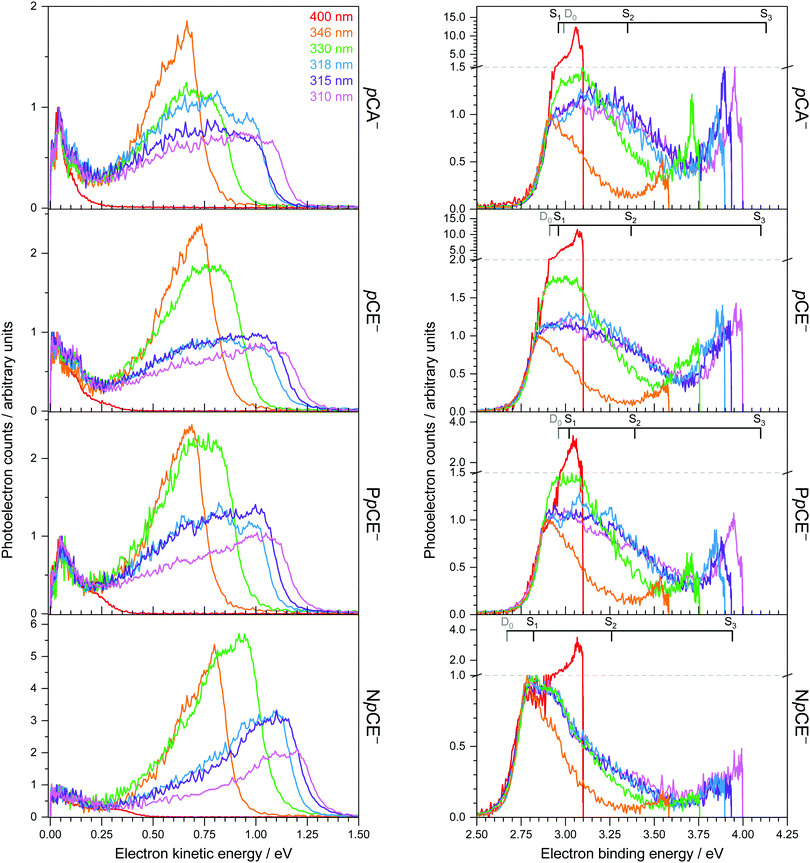
Photoelectron spectra of the deprotonated chromophores (Fig. 2) were recorded as a function of electron kinetic energy (eKE) and are also presented as a function of electron binding energy, eBE = hν − eKE (Fig. 3). Lines on the spectra mark calculated VDEs and VEEs.

Fig. 3 Photoelectron spectra of pCA⁻, pCE⁻, PpCE⁻ and NpCE⁻ recorded at 310 nm (4.00 eV), 315 nm (3.94 eV), 318 nm (3.90 eV), 330 nm (3.76 eV), 346 nm (3.58 eV) and 400 nm (3.10 eV). Intensities of the spectra plotted as a function of eKE (left) have been scaled so that the low eKE features lie on top of one another and are normalised to the maximum of the low eKE feature. Intensities of the spectra plotted as a function of eBE (right) have been scaled to align the rising edges and are normalised to the maximum of the rising edges of the 346 nm spectra. Note the scale changes used to plot the 400 nm data with the shorter wavelength data shown by the grey dashed lines. Combs mark the EPT calculated VDEs (grey) and the first three singlet excited states of the anion calculated using ADC(2)/6-31+G** (black).

Possible direct and indirect photodetachment (PD) processes are illustrated on the Jablonski diagram presented in Fig. 4. The 400 nm spectra are dominated by a strong feature at eKE ≈ 0 (eBE ≈ hν). The eKE profiles are those of structured exponential decays, characteristic of thermionic emission (TE).^42,43 In contrast, the 310–346 nm photoelectron spectra are dominated by broad, unresolved features at low eBEs. The sharp, low eBE edges of these broad features remain at constant eBE for all photon energies, signifying a direct PD process. There is also evidence for direct PD in the 400 nm spectra, although it is particularly weak for pCA⁻ and pCE⁻. For pCA⁻, pCE⁻ and PpCE⁻, the low eBE features broaden on their high eBE edges with increasing photon energy, indicative of an indirect PD process following resonant excitation of an excited electronic state. This broadening is less pronounced for NpCE⁻. The 310–346 nm spectra also have features at eBE ≈ hν (eKE ≈ 0) that increase in intensity with respect to the direct detachment features as the photon energy is increased. These eBE ≈ hν features are less intense in the NpCE⁻ photoelectron spectra compared to those of pCA⁻, pCE⁻ and PpCE⁻.

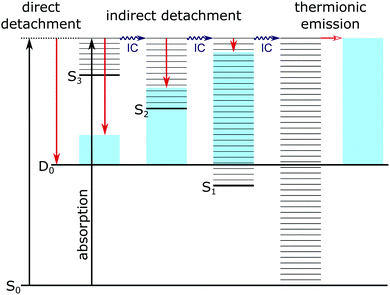Fig. 4 Jablonski diagram illustrating the major photodetachment pathways (red arrows) available for the model PYP chromophores employed in this work (Fig. 2) following UV photoexcitation (346–310 nm) including internal conversion (IC) and thermionic emission (horizontal red arrow). Horizontal black lines represent the vibrational levels of the excited electronic states of the anion and the blue shaded areas represent the vibrational energy left in the neutral radical upon electron detachment as a result of the propensity for conserving vibrational energy.

Approximate VDEs are determined from the maxima of the direct PD features at low eBE in the 346 nm spectra since this wavelength corresponds to a minimum in the action absorption spectra of pCE⁻.⁴⁴ These maxima are presented in Table 1 along with calculated VDEs and ADEs. For D₀, VDEs and ADEs increase in the order NpCE⁻ < pCE⁻ < PpCE⁻ < pCA⁻. The trend in the calculated and experimentally measured detachment thresholds can be explained in terms of the electronic effects of the acyl substituents and structural strain on the resonant stabilisation of the anion. The slight difference between the pCA⁻ and pCE⁻ detachment thresholds can be attributed to the hydroxyl group of pCA⁻ being a slightly weaker electron donor than the OMe group. This is intuitive as the methyl group is electron releasing and in this instance can be shown by the sum of the ChelpG⁴⁵ partial charges on the OH group (−0.296 e) compared to that of the OMe group (−0.275 e). In pCE⁻ the effect of n_O(sp²) → σ*_C=O donation will destabilise the anion. This stereoelectronic effect is not possible with PpCE⁻ so it is surprising that the VDEs of PpCE⁻ and pCE⁻ are similar. The expected greater stabilising effect of the lactone ring in PpCE⁻ may be offset by the conformation induced by the tether compromising the planarity of the system with respect to the simple ester in pCE⁻. The detachment threshold of NpCE⁻ is most likely lowered by the ring strain introduced by the rotation lock (half-chair conformation) inducing a small reduction in the planarity (see Fig. S2 in ESI†) and thus hindering resonant stabilisation of the anion.

Table 1 Vertical detachment energies (VDEs), B3LYP/6-311++G(3df,3pd) D₀−S₀ adiabatic detachment energies (ADEs) (0–0 transition) and maxima of the experimental 346 nm photoelectron spectra in eV for each chromophore. VDEs were calculated using EPT/6-311++G(3df,3pd) (pole strengths in parentheses), EOM-IP-CCSD/aug-cc-pVDZ and B3LYP/6-311++G(3df,3pd) methods. EPT and EOM-IP-CCSD have two values listed corresponding to detachment to the D₀ and D₁ states

	Vertical detachment energy			ADE(0–0)	Expt.
	EPT	EOM-IP-CCSD	DFT
pCA^−	2.99 (0.879)	2.97	3.10	2.99	2.92 ± 0.05
	5.25 (0.872)	5.45
pCE^−	2.91 (0.879)	2.78	3.01	2.91	2.85 ± 0.05
	5.18 (0.873)	4.42
PpCE^−	2.96 (0.878)	2.83	3.03	2.93	2.89 ± 0.05
	5.23 (0.871)	4.48
NpCE^−	2.67 (0.879)	2.71	2.93	2.82	2.78 ± 0.05
	5.02 (0.868)	4.33

---

It is worth noting that pCA can deprotonate at two sites to form either the carboxylate or the phenolate tautomer. The VDE of carboxylate pCA⁻ (4.68 eV)¹⁷ is significantly higher than that of phenolate pCA⁻ and the photon energies used in this work (<4 eV). Additionally, the spectra of pCA⁻ and pCE⁻ are very similar. Hence, although both forms of pCA⁻ could be present in our instrument, we are only sensitive to the phenolate form.

The DFT VDEs are close to the ADEs, suggesting that the geometries of the anions and their corresponding neutral radicals are similar, in agreement with our earlier work on model PYP chromophores.^17,18

In terms of the calculated VDEs for D₀, the EPT method has determined the VDEs of pCA⁻, pCE⁻ and PpCE⁻ to be just slightly higher than the experimental maxima (∼0.05 eV) and slightly lower for NpCE⁻ (0.115 eV). The EPT/6-311++G(3df,3pd) method was employed to calculate the first VDE of the phenoxide anion previously⁴⁶ and it was found to be within 1% of the experimental value of Gunion et al.⁴⁷ Here, we find a 2% difference between the EPT calculated VDE and the experimental maxima for pCA⁻, pCE⁻ and PpCE⁻, and a 4% difference for NpCE⁻. The VDEs calculated using DFT are systematically higher (∼0.15 eV) than the experimental maxima. The EOM-IP-CCSD calculations have predicted the VDEs of the chromophores to within ∼0.06 eV of the experimental maxima, although the deviations are less systematic than with DFT; for example, the EOM-IP-CCSD VDE of pCA⁻ is higher than the experimental maximum whereas the calculated VDE of pCE⁻ is lower than the experimental maximum. It should be noted that the accuracy of our measurement is ±0.05 eV and that the high density of vibrational transitions contributing to these vibrationally unresolved photoelectron spectra can easily shift the maxima away from the true VDE. Thus, we conclude that all the calculated VDEs are in good agreement with experiment and note that the simple, computationally inexpensive DFT method performs just as well as the other methods. Calculated VDEs for D₁ are also listed in Table 1 and are all significantly higher than the photon energies used in this study suggesting that direct PD to D₁ is unlikely.

The first three singlet excited states of the chromophores are 1¹ππ*, 1¹nπ* and 2¹ππ*, as illustrated in Fig. 5. The relevant orbitals of all the chromophores are similar to those of pCA⁻ (shown), as one may expect from a set of structural analogues without any significant changes to functionality (see Tables S2–S5 and Fig. S3–S6, ESI†). The π and orbitals are delocalised across the whole chromophore whereas the n and orbitals are more localised on the phenoxide end of the anion. Hence, the S₃(2¹ππ*) and the S₂(1¹nπ*) transitions have charge transfer character. The delocalised π orbital is the highest occupied molecular orbital and the configuration of the D₀ state of the neutral radical corresponds to the removal of an electron from this orbital.

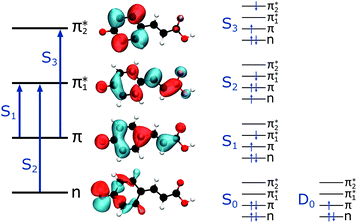Fig. 5 Left: The main molecular orbitals involved in the transitions to the first three singlet excited states of the anion. Although the MOs plotted are calculated for pCA⁻, they are similar for all the chromophores shown in Fig. 2 (see Tables S2–S5 and Fig. S3–S6, ESI†). Right: The electron configurations associated with the ground state of the anion (S₀) and neutral radical (D₀) and the first three singlet excited states of the anion for all the chromophores.

Vertical excitation energies (VEEs) for these first three singlet excited states calculated using CAM-B3LYP/6-311++G(3df,3pd) and ADC(2)/6-31+G** methods are presented in Table 2. They are compared with SA-CASSCF(14,12)-PT2/cc-pVDZ results by Fernández García-Prieto et al.⁴⁸ and experimental values recorded by Rocha-Rinza et al.⁴⁹ as these have been shown to be in excellent agreement with one another and provide a benchmark for our own calculations.

Table 2 Vertical excitation energies (VEEs) calculated using CAM-B3LYP/6-311++G(3df,3pd) and ADC(2)/6-31+G** compared with SA-CASSCF(14,12)-PT2/cc-pVDZ⁴⁸ calculated values and experimental values.⁴⁹ Oscillator strengths are shown in brackets

			pCA^−	pCE^−	PpCE^−	NpCE^−
CAM-B3LYP	1^1ππ*	S1	3.45 (0.910)	3.43 (0.949)	3.49 (0.952)	3.36 (0.812)
6-311++G(3df,3pd)	1^1nπ*	S2	4.10 (0.000)	4.12 (0.000)	4.15 (0.000)	4.10 (0.000)
	2^1ππ*	S3	4.33 (0.071)	4.31 (0.110)	4.34 (0.056)	4.40 (0.026)
ADC(2)	1^1ππ*	S1	2.96 (1.000)	2.96 (1.021)	3.02 (1.032)	2.82 (0.885)
6-31+G**	1^1nπ*	S2	3.35 (0.000)	3.37 (0.000)	3.39 (0.000)	3.26 (0.000)
	2^1ππ*	S3	4.13 (0.091)	4.10 (0.097)	4.10 (0.061)	3.94 (0.065)
SA-CASSCF	1^1ππ*	S1	2.96	2.94	—	—
(14,12)-PT2	1^1nπ*	S2	3.65	3.65	—	—
cc-pVDZ	2^1ππ*	S3	3.82	3.82	—	—
Experiment	1^1ππ*	S1	2.89	2.88	—	—

---

The calculated oscillator strength for the S₁ ← S₀ transition is near unity for each of the chromophores whereas that for the S₂ ← S₀ transition is zero. The S₃ ← S₀ transition has a non-zero oscillator strength for each chromophore of approximately 0.1. From Tables 1 and 2, and the VDEs and VEEs plotted in Fig. 3, it is clear that the D₀ and S₁ states lie close in energy, particularly for pCA⁻, pCE⁻ and PpCE⁻. Due to the good agreement between the literature and ADC(2) methods, the ADC(2) values are plotted on the spectra in Fig. 3. The CAM-B3LYP VEEs are similar to those calculated for PYP chromophores in earlier work using the same method;¹⁸ however, the VEEs for pCA⁻ and pCE⁻ are approximately 0.5 eV higher than those calculated using higher level theory⁴⁸ and obtained from action absorption spectra.⁴⁹ The VEEs calculated using the ADC(2)/6-31+G** method for pCA⁻ and pCE⁻ are in good agreement with those calculated using the SA-CASSCF(14,12)-PT2/cc-pVDZ method⁴⁸ and with the available experimental measurements,⁴⁹ so we use the VEEs calculated with this method to assist with the interpretation of our experimental measurements.

The electron configurations of the accessible electronically excited states of the anions and the corresponding neutral radicals (Fig. 5) are useful in the consideration of coupling strengths of the excited states of the anion to the detachment continua. Indirect PD from the S₁ state to the D₀ continuum involves removing a single electron from the orbital to yield the D₀ electron configuration. Vibrational states of S₁ that lie in the D₀ continuum have shape resonance character and are coupled strongly to the continuum. Indirect PD from S₃ involves removing an electron from the 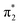orbital. The S₃ state has excited shape resonance character with respect to the D₀ continuum and electron detachment through this channel is expected to be very fast. In contrast, indirect PD from the S₂ state to the D₀ continuum involves removing a 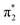electron and making the π ← n electronic transition. Thus S₂ has Feshbach resonance character with respect to the D₀ continuum and indirect detachment from this state is expected to be relatively slow. Although the D₁ VDEs are higher than the photon energies employed in this work, adiabatic detachment to D₁ from the S₂ and S₃ states cannot be ruled out. The D₁ state has electronic configuration 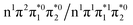so the S₃ state has Feshbach resonance character with respect to the D₁ continuum suggesting that indirect PD to D₁ will not be able to compete with indirect PD to D₀ or ultrafast IC to lower-lying states. The S₂ state is an excited shape resonance with respect to D₁, suggesting that indirect PD from S₂ to D₁ is possible; however, there would still be competition from internal conversion to S₁ or S₀. Overall, it seems most likely that the photoelectron spectra are dominated by direct and indirect electron emission to the D₀ continuum.

3.2 The role of torsional motion

Photoexcitation at 400 nm populates vibrationally excited states of S₁ lying in the D₀ detachment continuum. All the photoelectron spectra are dominated by eKE ≈ 0 (eBE ≈ hν) photoelectrons with an overall exponential decay profile, suggesting that the dominant electronic relaxation mechanism is IC to S₀ followed by TE. However, the ratio of photoelectrons attributed to TE compared with those attributed to direct PD decreases in the order pCA⁻ ≈ pCE⁻ ≫ PpCE⁻ > NpCE⁻. This suggests that torsional motions around both single bonds adjacent to the alkene group are involved in steering the PYP chromophore towards the S₁/S₀ CI but that rotation around the single bond between the alkene moiety and the phenoxide group plays a more important role.

Photoexcitation at 346 nm results predominantly in direct detachment from S₀; however, the observation of eKE ≈ 0 (eBE ≈ hν) photoelectrons with an overall exponential decay profile suggests that there is some contribution from resonant excitation of excited states of the anion followed by IC to S₀ and subsequent TE. We cannot assign the resonant excitation process to any particular excited state of the anion, but the high vibrational levels of S₁, low vibrational levels of S₃ or the S₂ state, through vibronic mixing with the bright S₁ state, are all possibilities. In terms of the role of torsional motions, the ratio of photoelectrons attributed to TE compared with those from direct PD is lower for NpCE⁻ than the other three chromophores, supporting the idea that rotation around the single bond between the alkene moiety and the phenoxide group plays an important role in IC from S₁ to S₀.

Increasing the photon energy to 330–310 nm results in a significant contribution from indirect PD from S₁ and TE from S₀ for pCA⁻, pCE⁻ and PpCE⁻. In contrast, indirect PD from S₁ is far less pronounced for NpCE⁻ and the contribution from TE only increases slightly. The most likely explanation for these observations is that as the photon energy increases, increasing population of S₃ followed by internal conversion to S₁ occurs and subsequent autodetachment to D₀ or IC to S₀ followed by TE. Locking the rotation around the single bond between the alkene moiety and the phenoxide group in NpCE⁻ inhibits these pathways, which suggests that rotation around the single bond between the alkene moiety and the phenoxide group also plays a role in IC from S₃ to S₁.

4 Conclusions

From the combination of photoelectron spectroscopy measurements and computational chemistry calculations, we have improved our understanding of the role of torsional motions around the single bonds either side of the alkene moiety in the electronic relaxation of isolated PYP chromophores in the gas-phase. We have found that single bond rotations are involved in steering the PYP chromophore towards the S₁/S₀ CI and that rotation around the single bond between the alkene moiety and the phenoxide group plays a particularly important role. From measurements at higher photon energies, we also find that rotation around this single bond between the alkene moiety and the phenoxide group plays a key role in IC from S₃ to S₁. This suggests that torsional motions around the single bonds, and particularly around the one between the alkene and phenoxide groups are not restricted in the protein. This supports the conclusion of the earlier time-resolved study by Lee et al. on the ketone analogue of the PYP chromophore in which isomerisation occurred on a similar time scale to the protein, suggesting entry into the photocycle must be unhindered by torsional motion and almost frictionless.¹¹ These results have potential applications in biology and nanotechnology in terms of improving our understanding of how to tune the photoresponse of proteins or materials with a chromophore based on the PYP chromophore.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by EPSRC grant EP/L005646/1. We are grateful to Professor Graham Worth and Dr Mariana Assmann (UCL) for advice on the computational chemistry calculations, to Dr Jörg Saßmannshausen for computational support at UCL, Dr Abil Aliev for NMR and Dr Kersti Karu (UCL) for mass spectra.

References

1. H. Kuramochi, S. Takeuchi, K. Yonezawa, H. Kamikubo, M. Kataoka and T. Tahara, Nat. Chem., 2017, 9, 660–666.
2. Image of 1NWZ: structure of the chromophore in the protein pocket at 0.82 Å resolution (E. D. Getzoff, K. N. Gutwin and U. K. Genick, Nat. Struct. Biol., 2003, 10, 663-668) created with VMD – Visual Molecular Dynamics (W. Humphrey, A. Dalke and K. Schulten, J. Molec. Graphics, 1996, 14, 33-38).
3. K. J. Hellingwerf, J. Hendriks and T. Gensch, J. Phys. Chem. A, 2003, 107, 1082–1094.
4. W. D. Hoff, P. Düx, K. Hård, B. Devreese, I. M. Nugteren-Roodzant, W. Crielaard, R. Boelens, R. Kaptein, J. Van Beeumen and K. J. Hellingwerf, Biochemistry, 1994, 33, 13959–13962.
5. K. Pande, C. D. M. Hutchison, G. Groenhof, A. Aquila, J. S. Robinson, J. Tenboer, S. Basu, S. Boutet, D. P. DePonte, M. Liang, T. A. White, N. A. Zatsepin, O. Yefanov, D. Morozov, D. Oberthuer, C. Gati, G. Subramanian, D. James, Y. Zhao, J. Koralek, J. Brayshaw, C. Kupitz, C. Conrad, S. Roy-Chowdhury, J. D. Coe, M. Metz, P. L. Xavier, T. D. Grant, J. E. Koglin, G. Ketawala, R. Fromme, V. Šrajer, R. Henning, J. C. H. Spence, A. Ourmazd, P. Schwander, U. Weierstall, M. Frank, P. Fromme, A. Barty, H. N. Chapman, K. Moffat, J. J. van Thor and M. Schmidt, Science, 2016, 352, 725–729.
6. G. Groenhof, M. Bouxin-Cademartory, B. Hess, S. P. de Visser, H. J. C. Berendsen, M. Olivucci, A. E. Mark and M. A. Robb, J. Am. Chem. Soc., 2004, 126, 4228–4233.
7. G. Groenhof, L. V. Schäfer, M. Boggio-Pasqua, H. Grubmüller and M. A. Robb, J. Am. Chem. Soc., 2008, 130, 3250–3251.
8. A. Espagne, P. Changenet-Barret, P. Plaza and M. M. Martin, J. Phys. Chem. A, 2006, 110, 3393–3404.
9. A. Baltuška, I. H. M. van Stokkum, A. Kroon, R. Monshouwer, K. J. Hellingwerf and R. van Grondelle, Chem. Phys. Lett., 1997, 270, 263–266.
10. A. D. Stahl, M. Hospes, K. Singhal, I. van Stokkum, R. van Grondelle, M. L. Groot and K. J. Hellingwerf, Biophys. J., 2011, 101, 1184–1192.
11. I.-R. Lee, W. Lee and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 258–262.
12. L. Mendonça, F. Hache, P. Changenet-Barret, P. Plaza, H. Chosrowjan, S. Taniguchi and Y. Imamoto, J. Am. Chem. Soc., 2013, 135, 14637–14643.
13. A. Xie, W. D. Hoff, A. R. Kroon and K. J. Hellingwerf, Biochemistry, 1996, 35, 14671–14678.
14. R. Cordfunke, R. Kort, A. Pierik, B. Gobets, G.-J. Koomen, J. W. Verhoeven and K. J. Hellingwerf, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 7396–7401.
15. D. S. Larsen, M. Vengris, I. H. van Stokkum, M. A. van der Horst, F. L. de Weerd, K. J. Hellingwerf and R. van Grondelle, Biophys. J., 2004, 86, 2538–2550.
16. J. Zhu, L. Paparelli, M. Hospes, J. Arents, J. T. M. Kennis, I. H. M. Van Stokkum, K. J. Hellingwerf and M. L. Groot, J. Phys. Chem. B, 2013, 117, 11042–11048.
17. C. R. S. Mooney, M. A. Parkes, A. Iskra and H. H. Fielding, Angew. Chem., Int. Ed., 2015, 54, 5646–5649.
18. M. A. Parkes, C. Phillips, M. J. Porter and H. H. Fielding, Phys. Chem. Chem. Phys., 2016, 18, 10329–10336.
19. A. R. Mckay, M. E. Sanz, C. R. S. Mooney, R. S. Minns, E. M. Gill and H. H. Fielding, Rev. Sci. Instrum., 2010, 81, 123101.
20. C. R. S. Mooney, M. E. Sanz, A. R. McKay, R. J. Fitzmaurice, A. E. Aliev, S. Caddick and H. H. Fielding, J. Phys. Chem. A, 2012, 116, 7943–7949.
21. J. Tay, M. A. Parkes, K. Addison, Y. Chan, L. Zhang, H. C. Hailes, P. C. Bulman Page, S. R. Meech, L. Blancafort and H. H. Fielding, J. Phys. Chem. Lett., 2017, 8, 765–771.
22. R. Beekmeyer, M. A. Parkes, L. Ridgwell, J. W. Riley, J. Chen, B. L. Feringa, A. Kerridge and H. H. Fielding, Chem. Sci., 2017, 8, 6141–6148.
23. G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996.
24. D. W. Arnold, S. E. Bradforth, E. H. Kim and D. M. Neumark, J. Chem. Phys., 1992, 97, 9468–9471.
25. C. McLaughlin, M. Assmann, M. A. Parkes, J. L. Woodhouse, R. Lewin, H. C. Hailes, G. A. Worth and H. H. Fielding, Chem. Sci., 2017, 8, 1621–1630.
26. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
27. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
28. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
29. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
30. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
31. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
32. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
33. J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416.
34. A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299–2324.
35. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
36. J. Linderberg and Y. Öhrn, Propagators in Quantum Chemistry, John Wiley and Sons, Hoboken, NJ, USA, 2014.
37. A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462.
38. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
39. J. L. Woodhouse, M. Assmann, M. A. Parkes, H. Grounds, S. J. Pacman, J. C. Anderson, G. A. Worth and H. H. Fielding, Phys. Chem. Chem. Phys., 2017, 19, 22711–22720.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, 2009.
41. Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr., H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T. C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215.
42. B. Baguenard, J. C. Pinaré, C. Bordas and M. Broyer, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 63, 023204.
43. C. E. Klots, Z. Phys. D: At., Mol. Clusters, 1991, 20, 105–109.
44. T. Rocha-Rinza, O. Christiansen, D. B. Rahbek, B. Klærke, L. H. Andersen, K. Lincke and M. Brøndsted Nielsen, Chem. – Eur. J., 2010, 16, 11977–11984.
45. C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373.
46. C. R. S. Mooney, M. A. Parkes, L. Zhang, H. C. Hailes, A. Simperler, M. J. Bearpark and H. H. Fielding, J. Chem. Phys., 2014, 140, 205103.
47. R. F. Gunion, M. K. Gilles, M. L. Polak and W. C. Lineberger, Int. J. Mass Spectrom. Ion Processes, 1992, 117, 601–620.
48. F. Fernández García-Prieto, M. A. Aguilar, I. Fdez. Galván, A. Muñoz-Losa, F. J. Olivares del Valle, M. L. Sánchez and M. E. Martín, J. Phys. Chem. A, 2015, 119, 5504–5514.
49. T. Rocha-Rinza, O. Christiansen, J. Rajput, A. Gopalan, D. B. Rahbek, L. H. Andersen, A. V. Bochenkova, A. A. Granovsky, K. B. Bravaya, A. V. Nemukhin, K. L. Christiansen and M. Brøndsted Nielsen, J. Phys. Chem. A, 2009, 113, 9442–9449.

---

Footnote

† Electronic supplementary information (ESI) available: Details of chromophore synthesis and NMR data; VMI images; comparisons of the optimised structures; benchmarking excited state calculations; excited state energies and characters; coordinates of optimised geometries. See DOI: 10.1039/c7cp06950b

---