Open Access Article
Open Access ArticleA look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions†
Lars
Goerigk
 *a,
Andreas
Hansen
*a,
Andreas
Hansen
 b,
Christoph
Bauer
b,
Christoph
Bauer
 b,
Stephan
Ehrlich‡
b,
Asim
Najibi
b,
Stephan
Ehrlich‡
b,
Asim
Najibi
 a and
Stefan
Grimme
a and
Stefan
Grimme
 *b
*b
aSchool of Chemistry, The University of Melbourne, Parkville, Australia. E-mail: lars.goerigk@unimelb.edu.au; Tel: +61-3-83446784
bUniversität Bonn, Mulliken Center for Theoretical Chemistry, Bonn, Germany. E-mail: grimme@thch.uni-bonn.de; Fax: +49-228-739064; Tel: +49-228-732544
First published on 26th October 2017
Abstract
We present the GMTKN55 benchmark database for general main group thermochemistry, kinetics and noncovalent interactions. Compared to its popular predecessor GMTKN30 [Goerigk and Grimme J. Chem. Theory Comput., 2011, 7, 291], it allows assessment across a larger variety of chemical problems—with 13 new benchmark sets being presented for the first time—and it also provides reference values of significantly higher quality for most sets. GMTKN55 comprises 1505 relative energies based on 2462 single-point calculations and it is accessible to the user community via a dedicated website. Herein, we demonstrate the importance of better reference values, and we re-emphasise the need for London-dispersion corrections in density functional theory (DFT) treatments of thermochemical problems, including Minnesota methods. We assessed 217 variations of dispersion-corrected and -uncorrected density functional approximations, and carried out a detailed analysis of 83 of them to identify robust and reliable approaches. Double-hybrid functionals are the most reliable approaches for thermochemistry and noncovalent interactions, and they should be used whenever technically feasible. These are, in particular, DSD-BLYP-D3(BJ), DSD-PBEP86-D3(BJ), and B2GPPLYP-D3(BJ). The best hybrids are ωB97X-V, M052X-D3(0), and ωB97X-D3, but we also recommend PW6B95-D3(BJ) as the best conventional global hybrid. At the meta-generalised-gradient (meta-GGA) level, the SCAN-D3(BJ) method can be recommended. Other meta-GGAs are outperformed by the GGA functionals revPBE-D3(BJ), B97-D3(BJ), and OLYP-D3(BJ). We note that many popular methods, such as B3LYP, are not part of our recommendations. In fact, with our results we hope to inspire a change in the user community's perception of common DFT methods. We also encourage method developers to use GMTKN55 for cross-validation studies of new methodologies.
1 Introduction
Kohn–Sham (KS) density functional theory1 (DFT) has without doubt shaped modern molecular quantum chemistry like no other methodology in recent years, and it is now the by far most frequently applied approach used by computational chemists.2 Its implementation into standard quantum-chemical software packages has also made it easily accessible to the non-expert that may want to support their experimental results with computational insights. While exact in nature, the true exchange–correlation functional in DFT remains elusive, and instead the user has to rely on density functional approximation (DFAs). As a consequence, hundreds of DFAs have been developed, each with their own advantages and disadvantages. This means that despite DFT calculations being technically easy to perform, it is no trivial task to choose the right DFA for a specific problem.Benchmarking—an assessment of DFA results against a set of reference data—has become a vital tool in method development and validation, which provides invaluable information to method users. Early benchmark sets focussed mostly on heat of formations (HoFs), electron affinities (EAs), ionisation potentials (IPs) and proton affinities (PAs) of relatively small molecules with experimental reference values; popular examples are the G2-1,3 G2/97,4 G3/99,5 and G3/056 test sets. Those sets rely heavily on HoFs, which are derived from total atomisation energies (TAEs). While TAEs are without doubt an important test case for any new method, it was also pointed out in 2011 that the results of TAE benchmark studies are not necessarily representative for the treatment of thermochemical problems.7 In 2017, Bartlett and co-workers automatically created 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 247 reaction-energy benchmark values from the 140 TAEs in the W4-11 set8 and they confirmed the aforementioned conclusion from 2011.9 Moreover, they showed that the usually expected error cancellations between the product and reactant species in reaction-energy calculations do not always happen, but that errors can in fact be amplified. This demonstrates the need to specifically design various benchmark sets covering reaction energies.
247 reaction-energy benchmark values from the 140 TAEs in the W4-11 set8 and they confirmed the aforementioned conclusion from 2011.9 Moreover, they showed that the usually expected error cancellations between the product and reactant species in reaction-energy calculations do not always happen, but that errors can in fact be amplified. This demonstrates the need to specifically design various benchmark sets covering reaction energies.
Others also share the latter view, which is why most sets developed after the turn of the millennium introduced chemically more relevant problems, such as reaction energies, barrier heights (BHs) or noncovalent interactions (NCIs). Some sets would still depend on experimental reference data, but gradually, zero-point vibrational-energy (ZPVE) exclusive, non-relativistic high-level ab initio values became the preferred benchmarks. Some popular examples are Truhlar's BH test sets HTBH3810 and NHTBH38,11 the isomerisation set ISO34,12 and Hobza's sets for inter- and intramolecular NCI energies. In particular, we would like to mention the S22 set from 200613 and the Benchmark Energy and Geometry DataBase (BEGDB), which provides online access to Hobza's other seminal contributions to this field.14
Carrying out studies on a single benchmark set may give a biased picture of a DFA's accuracy and applicability, and using a different benchmark set may even give an opposing outcome. One way of introducing an unbiased approach to benchmarking is Korth and Grimme's MB08-165 set15 of randomly generated artificial molecules (AMs), which turned out to be a good indicator for a DFA's robustness.7,15 A different strategy to identify a robust method was first rigorously carried out by Truhlar, who compiled databases that consist of different benchmark sets covering various chemical problems.16–21 The latest of those compilations is the “Database 2015B”, which comprises 471 molecular and atomic data (relative energies).22 A DFA is deemed robust if it performs equally well over different benchmark sets. In that case, there is a higher probability that it can also be safely employed to new problems. Also, two of us developed benchmark databases that focussed on general main-group thermochemistry, kinetics, and noncovalent interactions (GMTKN) that we dubbed GMTKN2423 and GMTKN30.24 Alternative large databases that took parts of GMTKN30 and combined them with other benchmark sets have also been recently promoted by Mardirossian and Head-Gordon.25,26
Our herein presented work focusses entirely on our GMTKN databases. The first version, GMTKN24, contained 24 benchmark sets and was initially used to establish that non-empirically derived DFAs belonging to the generalised-gradient-approximation (GGA) or meta-GGA classes were not necessarily better equipped to describe thermochemistry than (semi-)empirical ones.23 In 2011, GMTKN24 was extended by six additional sets and renamed GMTKN30. While it was initially used to cross-validate the PWPB95 double-hybrid DFA, two of us later used GMTKN30 to test 45 DFAs from all five rungs of Jacob's Ladder, with the lowest rung being the local-density approximation (LDA), followed by GGAs or non-separable gradient approximations (NGAs),27 meta-GGAs/NGAs, hybrid DFAs, and double-hybrid DFAs. Double hybrids are one representative for the fifth rung, as they incorporate information from virtual KS orbitals through a second-order Møller–Plesset-type (MP2) term.28,29 The motivation behind Jacob's Ladder was to be able to classify the chaotic “zoo” of DFAs according to their underlying components, with the expectation that a higher rung would guarantee a more accurate outcome. The 2011 GMTKN30 study showed that this is indeed the case, with double hybrids being the most reliable and accurate functionals, clearly outperforming related MP2-type methods.7 While hybrid functionals followed in this ranking, the difference between meta-GGAs and GGAs was not very pronounced. As no surprise came the finding that LDAs were not competitive at all for molecular chemistry.
The large GMTKN30 study also provided the user community with clear guidelines on which functionals to trust and which to avoid.7 Based on GMTKN30, the best DFAs turned out to be all double hybrids, with the exception of non-empirical double hybrids.29 In particular, Kozuch and Martin's DSD30–32 functionals and the PWPB9524-D333 functional were the clear winners.7,29 The best hybrid DFAs were Truhlar's M062X-D3,34 M052X-D3,35 and PW6B95-D336 DFAs, with the latter showing generally larger robustness and less technical issues, such as occasionally occurring strong quadrature-grid and convergence problems.7 With the exception of ωB97X-D,37 range-separated hybrids showed no better behaviour than global hybrids. Most important was probably the finding that the most popular DFA by far, namely B3LYP,38,39 turned out to be the worst of 23 hybrids for the calculation of reaction energies.7 Some GGAs turned out to be competitive with meta-GGAs, and the revPBE-D340 and B97-D341 approaches were recommended. Furthermore the study demonstrated that London-dispersion effects do also influence reaction energies and BHs, contrary to the common perception that they are weak and, thus, negligible in those cases.7 The large GMTKN30 study also indicated that Minnesota DFAs needed to be long-range dispersion-corrected despite the wide-spread belief that they already incorporate dispersion effects;7 subsequent studies42,43 confirmed these early indications (also see ref. 25 for a related, more recent study).
Shortly after their introduction, GMTKN24 and GMTKN30 became very popular tools in method development and evaluation, with selected examples being ref. 44–51. However, despite this success, some questions became evident to us over time. Are 30 benchmark sets really sufficient to assess a method's robustness? Would the overall picture change if we added new sets? Are the system sizes covered in GMTKN30 still representative of current problems? Is the letter “K” in GMTKN—namely BHs—underrepresented with only two test sets? Are all reference values reliable? Particularly the last question is important. It was inspired by a 2015 study, which showed that the popular CBS-QB352,53 composite approach used to generate reference BHs of pericyclic reactions (BHPERI set) had a surprisingly large mean absolute deviation (MAD) of 2.1 kcal mol−1 with respect to the explicitly-correlated Weizmann protocols W1-F12 and W2-F12.54 This value turned out to be larger than the MADs for double-hybrid DFAs, and thus evaluating DFT methods against CBS-QB3 numbers became questionable.55 Indeed, DFA rankings based on the older reference values changed significantly when the newer ones were used.
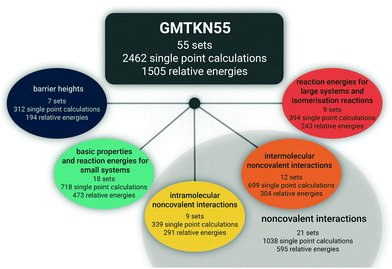
Herein, we intend to answer those questions, and we present the advanced and improved GMTKN55 database, which now covers 55 test sets (Fig. 1). With seven sets for BHs, that category is much better represented than in the two predecessors. We present 13 completely new sets to become part of GMTKN55. In addition, existing sets were modified or the database was further extended by sets (partially) taken from the literature, for which we present new reference values in most cases. For most of the sets that remain identical to GMTKN30, we also present updated reference values. Contrary to related large databases, we tried to increase the accuracy of the reference values substantially by relying on Weizmann composite protocols whenever possible. In GMTKN55, we also provide a higher number of large systems, such as C60 isomers, and we also include more ionic systems. An overview of the new database is given in Table 1. A detailed description of each of the 55 test sets follows in Section 2.
| Set | Description | Changes with respect to GMTKN30 | #a | Ref. method | |
|---|---|---|---|---|---|
| a Number of relative energies and single-point calculations (in parentheses), except for BH76RC, for which the single-point calculations carried out for BH76 are sufficient. b Averaged absolute relative energy (kcal mol−1). c W4.106 d (Theoretically back-corrected) exp. e This work. f W1-F12.54 g W2-F12.54 h CCSD(T)107/CBS. i CCSD(T)-F12108/CBS. j W3.2.106 k DLPNO-CCSD(T)/CBS.109 l Estimated CCSD(T)/CBS. m DLPNO-CCSD(T)/CBS*.104 n W2.2.106 o CP-corrected110 CCSD(T)/CBS. p Estimated CCSD(T)-F12/CBS. q W1h-val.111 | |||||
| Basic properties and reaction energies for small systems | |||||
| W4-118 | Total atomisation energies | Replaces W4-0856 | 140 (152) | 306.91 | |
| G21EA3,23 | Adiabatic electron affinities | None | 25 (50) | 33.62 | |
| G21IP3,23 | Adiabatic ionisation potentials | None | 36 (71) | 257.61 | |
| DIPCS10 | Double-ionisation potentials of closed-shell systems | Newe | 10 (20) | 654.26 | |
| PA26 | Adiabatic proton affinities (incl. of amino acids) | Extension of PA;23,57,58 new ref.e | 26 (52) | 189.05 | , , |
| SIE4x4c | Self-interaction-error related problems | New;e replaces SIE1123 | 16 (23) | 33.72 | |
| ALKBDE1059 | Dissociation energies in group-1 and -2 diatomics | New from lit. | 10 (20) | 100.69 | |
| YBDE1860 | Bond-dissociation energies in ylides | New from lit.; new ref.e | 18 (29) | 49.28 | |
| AL2x6 | Dimerisation energies of AlX3 compounds | Modification of AL2X; new ref.e | 6 (11) | 35.88 | , |
| HEAVYSB11 | Dissociation energies in heavy-element compounds | Newe | 11 (22) | 58.02 | |
| NBPRC23,24,61 | Oligomerisations and H2 fragmentations of NH3/BH3 systems | New ref.62 | 12 (21) | 27.71 | , |
| H2 activation reactions with PH3/BH3 systems | |||||
| ALK8 | Dissociation and other reactions of alkaline compounds | New;e replaces ALK633 | 8 (17) | 62.60 | |
| RC21 | Fragmentations and rearrangements in radical cations | Newe | 21 (41) | 35.70 | |
| G2RC4,23 | Reaction energies of selected G2/97 systems | New ref.e | 25 (47) | 51.26 | |
| BH76RC23 | Reaction energies of the BH7610,11,23 set | New ref.e | 30 | 21.39 | |
| FH5163,64 | Reaction energies in various (in-)organic systems | New from lit. | 51 (87) | 31.01 | |
| TAUT15 | Relative energies in tautomers | Newe | 15 (25) | 3.05 | |
| DC1318,23,28,65–73 | 13 difficult cases for DFT methods | Extension of DC9;23 new ref.e | 13 (30) | 54.98 | , , , , , |
| Reaction energies for large systems and isomerisation reactions | |||||
| MB16-43 | Decomposition energies of artificial molecules | New;e replaces MB08-16515 | 43 (58) | 414.73 | |
| DARC23,74 | Reaction energies of Diels–Alder reactions | New ref.62 | 14 (22) | 32.47 | |
| RSE4375 | Radical-stabilisation energies | New ref.e | 43 (88) | 7.60 | |
| BSR3676,77 | Bond-separation reactions of saturated hydrocarbons | New ref.e | 36 (38) | 16.20 | |
| CDIE2078 | Double-bond isomerisation energies in cyclic systems | New from lit. | 20 (36) | 4.06 | |
| ISO3412 | Isomerisation energies of small and medium-sized organic molecules | New ref.e | 34 (63) | 14.57 | |
| ISOL2479 | Isomerisation energies of large organic molecules | Extension of ISOL22;24 new ref.e | 24 (48) | 21.92 | |
| C60ISO80 | Relative energies between C60 isomers | New from lit. | 9 (10) | 98.25 | |
| PArel | Relative energies in protonated isomers | Newe | 20 (31) | 4.63 | |
| Reaction barrier heights | |||||
| BH7610,11,23 | Barrier heights of hydrogen transfer, heavy atom transfer, nucleophilic substitution, unimolecular and association reactions | New ref.e | 76 (86) | 18.61 | |
| BHPERI23,81–83 | Barrier heights of pericyclic reactions | New ref.55 | 26 (61) | 20.87 | , |
| BHDIV10 | Diverse reaction barrier heights | Newe | 10 (20) | 45.33 | , |
| INV2484 | Inversion/racemisation barrier heights | New from lit. | 24 (48) | 31.85 | , , |
| BHROT27 | Barrier heights for rotation around single bonds | Newe | 27 (40) | 6.27 | , |
| PX1385 | Proton-exchange barriers in H2O, NH3, and HF clusters | Modified set from lit. | 13 (29) | 33.36 | |
| WCPT1886 | Proton-transfer barriers in uncatalysed and water-catalysed reactions | Modified set from lit. | 18 (28) | 34.99 | |
| Intermolecular noncovalent interactions | |||||
| RG18 | Interaction energies in rare-gas complexes | New;e replaces RG633 | 18 (25) | 0.58 | |
| ADIM633 | Interaction energies of n-alkane dimers | New ref.e | 6 (12) | 3.36 | |
| S2213 | Binding energies of noncovalently bound dimers | New ref.87 | 22 (57) | 7.30 | |
| S6688 | Binding energies of noncovalently bound dimers | New from lit. | 66 (198) | 5.47 | |
| HEAVY2833 | Noncovalent interaction energies between heavy element hydrides | New ref.e | 28 (38) | 1.24 | |
| WATER2789 | Binding energies in (H2O)n, H+(H2O)n and OH−(H2O)n | New ref.90 | 27 (30) | 81.14 | |
| CARBHB12 | Hydrogen-bonded complexes between carbene analogues and H2O, NH3, or HCl | Newe | 12 (36) | 6.04 | |
| PNICO2391 | Interaction energies in pnicogen-containing dimers | Modifies set from lit.; new ref.e | 23 (69) | 4.27 | , |
| HAL5992,93 | Binding energies in halogenated dimers (incl. halogen bonds) | Combination of two sets from lit. | 59 (105) | 4.59 | |
| AHB2194 | Interaction energies in anion–neutral dimers | New from lit. | 21 (63) | 22.49 | , |
| CHB694 | Interaction energies in cation–neutral dimers | New from lit. | 6 (18) | 26.79 | , |
| IL1694 | Interaction energies in anion–cation dimers | New from lit. | 16 (48) | 109.04 | |
| Intramolecular noncovalent interactions | |||||
| IDISP12,23,24,95,96 | Intramolecular dispersion interactions | New ref.e | 6 (13) | 14.22 | |
| ICONF | Relative energies in conformers of inorganic systems | Newe | 17 (27) | 3.27 | |
| ACONF97 | Relative energies of alkane conformers | None | 15 (18) | 1.83 | |
| AMINO20x498 | Relative energies in amino acid conformers | Replaces CYCONF99 | 80 (100) | 2.44 | |
| PCONF21100,101 | Relative energies in tri- and tetrapeptide conformers | Extension of PCONF;23,100 new ref.e | 18 (21) | 1.62 | |
| MCONF102 | Relative energies in melatonin conformers | New from lit.; new ref.e | 51 (52) | 4.97 | |
| SCONF23,103 | Relative energies of sugar conformers | New ref.e | 17 (19) | 4.60 | |
| UPU23104 | Relative energies between RNA-backbone conformers | New from lit. | 23 (24) | 5.72 | |
| BUT14DIOL105 | Relative energies in butane-1,4-diol conformers | New from lit.; new ref.e | 64 (65) | 2.80 | |
Having established the new database, we then proceed with a detailed evaluation of DFAs to re-assess whether the old recommendations for GMTKN30 are still valid, and how approaches published since then compare to them as well as methods that were not considered in 2011. As outlined in Section 3, we carefully selected 83 out of 217 DFAs for this task. Contrary to other comprehensive benchmark studies that avoided testing double hybrids,19,22,26 we again include those herein. Moreover, all 83 DFAs are dispersion corrected, which enables us to conduct a more consistent analysis compared to other studies.19,22,26 New DFT-D333,44 dispersion-correction damping parameters are presented for 35 methods for the first time. In Section 4, we suggest how to best analyse GMTKN55, before we proceed with a detailed discussion in Section 5. We will conclude with an update of our previous recommendations for each of the four highest rungs on Jacob's Ladder to guide the DFT user and method developer for future applications.
2 Description of the GMTKN55 database
The new GMTKN55 database covers 55 different test sets and for each tested method, the user has to conduct 2462 single-point calculations to obtain 1505 relative energies for subsequent statistical analysis, as opposed to GMKTKN30 with 1218 systems and 841 relative energies. As shown in Fig. 1, these 55 sets can be distributed amongst four categories. Similarly to the GMTKN24 and GMTKN30 predecessors, the first category comprises what we call “basic properties”, and it includes standard benchmarking problems, such as TAEs, EAs, or IPs. Contrary to its predecessors, though, we also include reactions between smaller systems, as is reflected in the name for this category, which in total comprises 18 test sets. Reactions between larger systems and isomerisations are covered by the second category (nine sets in total). A drawback of GMTKN24 and GMTKN30 is that BHs are underrepresented with only two benchmark sets in the old “basic properties” category. GMTKN55 now features seven different test sets that are collected in a separate category. 21 sets directly allow assessing a method's ability to describe NCIs. This category can be further divided into two subcategories focussing on intermolecular (12 sets) or intramolecular interactions (nine sets), respectively.Table 1 lists all 55 benchmark sets including a short description, the number of data points for each set, the number of single-point calculations that need to be carried out, and the nature of the reference data. For users familiar with the GMTKN30 predecessor, Table 1 also summarises which sets were modified, left unchanged or newly added.
Out of the 55 sets, only three are identical to GMTKN30 (G21EA, G21IP, ACONF). 15 sets have the same geometries as before, but updated reference values, which were either published elsewhere or that were calculated for this work. These are the sets: NBPRC, G2RC, BH76RC, DARC, RSE43, BSR36, ISO34, BH76, BHPERI, ADIM6, S22, HEAVY28, WATER27, IDISP, and SCONF. Five sets are extensions or modifications of existing sets and, in addition, we determined new reference values for these. To reflect these changes, we gave those sets new names. The set formerly known as PA becomes PA26, AL2X becomes AL2X6, ISOL22 was extended to ISOL24, and PCONF is now known as PCONF21. The DC13 set is an extension of DC9 and it also contains parts of the O3ADD6 set, which has become obsolete and will no longer be a part of GMTKN55. Six sets were replaced by new ones: the W4-11 set replaces W4-08, the newly developed SIE4x4 is a replacement for SIE11, the new ALK8 set replaces ALK6, we present the new MB16-43 set as a substitute for MB08-165, the new RG18 set replaces RG6, and AMINO20x4 makes CYCONF obsolete. 26 sets are an addition to GMTKN55. Out of those, 13 were taken from the literature without any or with only minor modifications: ALKBDE10, FH51, CDIE20, C60ISO, INV24, PX13, WCPT18, S66, HAL59, AHB21, CHB6, IL16, and UPU23. Four sets were taken from the literature, but we present new reference values for them: YBDE18, PNICO23, MCONF, and BUT14DIOL. Finally, we add nine entirely new test sets under the names DIPCS10, HEAVYSB11, RC21, TAUT15, PArel, BHDIV10, BHROT27, CARBHB12, and ICONF.
Detailed descriptions of each test set follow below. Similarly to its predecessors, all reference values in GMTKN55 are non-relativistic and ZPVE exclusive, and in the majority of the cases obtained from all-electron treatments. All structures and other information can be obtained from a dedicated website.112
2.1 Basic properties and reaction energies for small systems
In 2016, Manna and Martin carried out a detailed study on C20 isomers and confirmed that those are very challenging systems, as their electronic structures can differ quite strongly, which often prevents error-cancellation effects when calculating the related isomerisation energies.73 Two of those isomers—C20 in its cage and bowl configurations—were already a part of the original DC9 set. Manna and Martin obtained a reliable and accurate isomerisation energy of −8.2 kcal mol−1 based on estimated CCSD(T)/CBS values (MP2/CBS(aug-cc-pVQZ/aug-cc-pV5Z) corrected with the correlation-energy difference between CCSD(T)/cc-pVTZ and MP2/cc-pVTZ). Unfortunately, the authors used geometries that had been obtained at a level of theory different from the structures used in DC9. However, we prefer to keep the original DC9 structures to allow users that have their own local version of GMTKN30 to easily upgrade it to GMTKN55. To solve this dilemma, we estimated the influence of the geometry on the isomerisation energy with the help of DLPNO-CCSD(T)/TightPNO/cc-pVTZ calculations on both sets of geometries. The resulting correction value of 0.5 kcal mol−1 was then added to the reference value proposed by Manna and Martin, thus, yielding a value of −7.7 kcal mol−1, which we will use for the extended DC13 set in GMTKN55.
The changes between the old and new references range from being marginal (0 kcal mol−1 for the tautomeric 2-pyridone/2-hydroxypyridine system) to being sizeable (5 kcal mol−1 for the reaction involving S8 and 5.6 kcal mol−1 for the C20 isomers).
As a tenth system, we include an example from Karton and Martin's study on 45 isomerisation energies in C8H8 systems.71 As GMTKN55 itself already contains a large number of isomerisation energies for hydrocarbons, we decided to include the most difficult reaction from the Karton and Martin study in the DC13 set. This is the 41st reaction in Karton and Martin's set with a W1-F12 reaction energy of 109.92 kcal mol−1. The GMTKN24 and GMTKN30 databases contained the O3ADD6 set that considered the addition of ozone to either ethane or ethyne.72 We decided to leave this set out of GMTKN55, as its analysis is difficult because it involves a mixture of reaction energies, BHs, and association energies. Instead, we took the two reaction energies, re-evaluated them at the W2-F12 level of theory and included them as eleventh and twelfth entries in DC13. The thirteenth and final reaction was taken from a similar test set by Zhao and Truhlar,18 namely the reaction of hexachlorobenzene with hydrogen chloride to dichlorine and benzene. For this reaction, we present new data at the W1-F12 level of theory.
The reaction energies in the extended DC13 set range from −106.0 kcal mol−1 (S8 reaction) to 152.6 kcal mol−1 (reaction 13) with an averaged absolute reaction energy of 54.98 kcal mol−1. A total of 30 single-point calculations need to be carried out for this set.
2.2 Reaction energies for large systems and isomerisation reactions
2.3 Reaction barrier heights
2.4 Intermolecular noncovalent interactions
2.5 Intramolecular noncovalent interactions
3 Computational details
3.1 Selected density functional approximations
We selected the DFAs for the subsequent benchmark study on GMTKN55 based on the following reasoning. DFAs that had performed well for GMTKN30—see, for instance, those mentioned in the introduction—were included again in this study. The same was also true for methods that experience high popularity, such as PBE,137 BP86,138–140 BLYP,138,141,142 B3LYP, PBE0,119,120 BHLYP,143 or TPSSh.144 On the other hand, methods with low accuracy for GMTKN307,29 were excluded from this study, as it was unlikely that their performance relative to other DFAs would significantly improve for GMTKN55. Our previous advice on those functionals will, thus, remain valid; examples are LDA functionals,145–147 PBEsol,148 SSB,149 M06HF,150 “non-empirical” and “one-parameter” double hybrids,29 or the range-separated hybrids CAM-B3LYP151 and LC-ωPBE.152 The well-performing range-separated hybrid ωB97X-D37 with a DFT-D241 dispersion-correction term was replaced by two newer versions that had been reparametrised with the DFT-D333 correction with zero-damping (DFT-D3(0)) or the nonlocal van der Waals (vdW) VV10153 kernel; these versions are called ωB97X-D3154 and ωB97X-V,155 respectively.Additional DFAs are either those that had not been published by the time of the GMTKN30 study—for instance, SCAN156 or Minnesota-type DFAs published since 2011—or older approaches available in Gaussian or ORCA that had never been tested for GMTKN30 before, such as the HCTH family,157 DFAs based on PBE-hole exchange,158 or M08HX.159 In 2011, we reported an incompatibility between dispersion corrections and the VSXC160 meta-GGA functional as well as severe self-consistent-field (SCF) convergence problems for most systems in GMTKN30.7 Unusual problems for NCIs have already been reported for SOGGA11,161 and we additionally observed convergence problems for GMTKN55, which made its routine application unfeasible. The same can be reported for the GLYP141,142,162 GGA functional, which was consequently also excluded from this study.
In this article, we will, thus, investigate the 83 dispersion-corrected DFAs listed in Table 2: 19 GGAs/NGAs, 9 meta-GGAs/NGAs, 48 hybrids, and 7 double hybrids. Note that in some cases different versions of a dispersion correction were applied to the same underlying exchange–correlation functional approximations: ωB97X-D3 and ωB97X-V, VV10 and rPW86PBE-D3(BJ), and B3LYP-D3(BJ) and B3LYP-NL.46 We therefore assess 80 unique exchange–correlation DFAs. In addition, we also analysed the results for dispersion-uncorrected DFAs and for DFAs corrected with the D3(0) variant, even though D3(BJ) should be the preferred one in most cases. This results in a total of 217 DFA variations, whose results are all presented on the GMTKN55 website.112 A recent related study promoted the study of 200 DFAs, however, that number also includes a mixture of dispersion-uncorrected and various dispersion-corrected versions of the same underlying DFA.26 When correcting for this, the 200 DFAs break down to 91 unique exchange–correlation DFAs—10 of which were ruled out from our study, as mentioned above—as well as the HF wave function method.
| Name | Dispersion correctiona | Programb | Name | Dispersion correctiona | Programb |
|---|---|---|---|---|---|
| a Type of dispersion correction. The cited reference presented the respective parameters for the first time. D3(BJ): DFT-D3 with Becke–Johnson damping.33,44 D3(0): DFT-D3 with zero-damping.33 VV10: nonlocal van der Waals kernel, as presented for the VV10 functional.153 APFD: spherical-atom dispersion term.193 b ORCA: ORCA 3.0.3 or ORCA 4.0.0.197,198 TM: TURBOMOLE 7.1.1.199,200 G09: GAUSSIAN09 Revision D.01 or E.02.201 G16: GAUSSIAN16 Revision A.03.202 c Determined for this work. d Local version. e This DFA is called “B3LYP-NL”.46 | |||||
| GGA | PW1PW119,120,163 | D3(0)c | ORCA | ||
| PBE137 | D3(BJ)44 | TM | MPW1KCIS11 | D3(BJ)c | G09 |
| PBEhPBE158 | D3(BJ)c | G09 | MPWKCIS1K11 | D3(BJ)c | G09 |
| revPBE40 | D3(BJ)44 | ORCA | PBE0119,120 | D3(BJ)44 | TM |
| RPBE164 | D3(BJ)c | ORCA | PBEh1PBE119,120,158 | D3(BJ)c | G09 |
| PW91163 | D3(BJ)165 | G09 | PBE1KCIS17 | D3(BJ)c | G09 |
| BLYP138,141,142 | D3(BJ)44 | TM | X3LYP166 | D3(BJ)c | ORCA |
| BP86138–140 | D3(BJ)44 | TM | O3LYP167 | D3(BJ)c | ORCA |
| BPBE137,138 | D3(BJ)7 | ORCA | B97-1168 | D3(BJ)c | G09 |
| OPBE137,169 | D3(BJ)7 | ORCA | B97-2170 | D3(BJ)c | G09 |
| OLYP141,142,169 | D3(BJ)7 | ORCA | B98171 | D3(BJ)c | G09 |
| XLYP141,142,166 | D3(BJ)c | ORCA | HISS172 | D3(BJ)c | G09 |
| mPWLYP141,142,173 | D3(BJ)7 | ORCA | HSE03174 | D3(BJ)c | G09 |
| PW91P86139,140,163 | D3(0)c | ORCA | HSE06174,175 | D3(BJ)176 | G09 |
| mPWPW91163,173 | D3(BJ)c | ORCA | TPSSh144 | D3(BJ)7 | ORCA |
| rPW86PBE137,177 | D3(BJ)44 | ORCA | revTPSSh144,178 | D3(BJ)c | G09 |
| B97-D3(BJ)41 | D3(BJ)44 | TM | TPSS0179 | D3(BJ)44 | ORCA |
| HCTH/407157 | D3(BJ)c | G09 | revTPSS0178,179 | D3(BJ)c | G09 |
| N1227 | D3(0)43 | G09 | TPSS1KCIS180 | D3(BJ)c | G09 |
| VV10153 | VV10153 | ORCA | BMK181 | D3(BJ)7 | G09 |
| τHCTHhyb182 | D3(BJ)c | G09 | |||
| Meta-GGA | M05183 | D3(0)7 | G09 | ||
| PKZB184 | D3(0)c | G09 | M052X35 | D3(0)7 | G09 |
| TPSS113 | D3(BJ)44 | ORCA | M0634 | D3(0)7 | TM |
| revTPSS178 | D3(BJ)c | G09 | M062X34 | D3(0)7 | TM |
| SCAN156 | D3(BJ)185 | TMd | M08HX159 | D3(0)c | G16 |
| τHCTH182 | D3(BJ)c | G09 | M11186 | D3(BJ)43 | G09 |
| M06L187 | D3(0)7 | TM | SOGGA11X188 | D3(BJ)43 | G09 |
| M11L189 | D3(0)43 | G09 | N12SX190 | D3(BJ)43 | G09 |
| MN12L191 | D3(BJ)43 | G09 | MN12SX190 | D3(BJ)43 | G09 |
| MN15L21 | D3(0)c | G16 | MN1522 | D3(BJ)c | G16 |
| LC-ωhPBE192 | D3(BJ)c | G16 | |||
| Hybrid | ωB97X-D3154 | D3(0)154 | ORCA | ||
| B3LYP38,39 | D3(BJ)44/VV10e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 46 |
TM/ORCA | ωB97X-V155 | VV10155 | ORCAd |
| B3PW9138 | D3(BJ)7 | ORCA | APFD193 | APFD193 | G09 |
| B3P8638,138–140 | D3(BJ)c | ORCA | |||
| BHLYP143 | D3(BJ)7 | TM | Double hybrid | ||
| B1P86119,120,138–140 | D3(BJ)c | ORCA | B2PLYP28 | D3(BJ)7 | ORCA |
| B1LYP119,120,138,141,142 | D3(BJ)c | ORCA | B2GPPLYP56 | D3(BJ)7 | ORCA |
| B1B95194 | D3(BJ)7 | ORCA | MPW2PLYP195 | D3(BJ)c | ORCA |
| MPW1B95196 | D3(BJ)7 | ORCA | PWPB9524 | D3(BJ)7 | ORCA |
| PW6B9536 | D3(BJ)44 | TM | DSD-BLYP30 | D3(BJ)7 | ORCA |
| MPWB1K196 | D3(BJ)7 | ORCA | DSD-PBEP8631 | D3(BJ)31 | ORCA |
| mPW1LYP119,120,141,142,173 | D3(0)c | ORCA | DSD-PBEB9532 | D3(BJ)32 | ORCA |
| mPW1PW91119,120,173 | D3(BJ)c | ORCA | |||
3.2 Dispersion corrections
Contrary to other related studies, all 83 methods were consistently assessed with a dispersion-correction term. For the majority of functionals, this was achieved with the DFT-D3(BJ) dispersion correction with Becke–Johnson damping,203,204 which has become the default version due to its physically more correct behaviour for short- and medium-range distances between two interacting non-covalently bound fragments. In some cases—for instance, the majority of older Minnesota functionals—this damping function turned out to be incompatible due to short-range double-counting effects. In those instances, the older zero-damping version was applied. Three functionals were tested with a non-local vdW kernel (VV10, B3LYP-NL, and ωB97X-V), while the APFD functional was developed together with its own correction. The recommended dispersion-correction for each DFA is listed in Table 2 alongside the reference that presented the relevant dispersion-correction parameters for the first time.For 35 DFAs, we had to determine DFT-D3 parameters for the first time. While we did this for both versions, we still recommend DFT-D3(BJ) in most cases, except for PW91P86, PKZB, MN15L, mPW1LYP, PW1PW, and M08HX, for which DFT-D3(0) is recommended. In those cases, no DFT-D3(BJ) parametrisation was achievable because of over-binding tendencies of the functionals and partial coverage of the dispersion interactions due to artificially built-in mid-range correlation effects. In the case of MN15L and MN15, the determined DFT-D3 damping parameters had the smallest influence on their overall performance; whether this is a positive or negative aspect will discussed below in the results section.
For DFT-D3(BJ), three parameters were fitted in a least-squares sense, while for DFT-D3(0) only two parameters had to be determined. The fit was carried out on a training set that contained the S66x8,88 S22x5,205 and NCIBLIND206 sets, which consider noncovalently bound dimers in their equilibrium and non-equilibrium geometries. A total of 718 data points were included in this set which are mostly not overlapping with GMTKN55 sets. This is contrary to the first DFT-D3 parametrisations that relied on sets that were also part of GMTKN30;33 for a third suggested training set for DFT-D3, see ref. 207. The D3(BJ) and D3(0) parameters of all DFAs used in this work are listed in Tables S3 and S4 (ESI†).
3.3 Technical details
Table 2 lists the programs that were used to assess the DFAs. The entire assessment of GMTKN55 and the parametrisations of the DFT-D3 corrections were carried out with the Ahlrichs-type split-valence quadruple-ζ Gaussian atomic-orbital (AO) basis set def2-QZVP. This basis set was chosen not only because it makes results comparable to previous GMTKN30 studies, but also because this basis set provides results close to the CBS limit for most properties; it, thus, provides a picture of a DFA's “true” performance without relying on error-compensation effects, as discussed elsewhere.48 As in the case of the GMTKN24 and GMTKN30 studies,7,23,24 the def2-QZVP set for oxygen was augmented with Dunning's diffuse s and p functions for WATER27.118Diffuse s and p functions were applied to all non-hydrogen atoms in the G21EA, AHB21 and IL16 sets; diffuse s functions were applied to H. The resulting basis set is henceforth called aug'-def2-QZVP. Core-electrons of heavy elements in some systems of HEAVY28, HEAVYSB11, and HAL59 were replaced with the def2-ECP effective-core-potentials.114 Note that herein we do not carry out a basis-set dependence study for smaller AO basis sets. The expected basis-set dependence for conventional and double-hybrid DFAs has already been established for GMTKN30,7,26 and repeating this analysis would not provide any new information.
All TURBOMOLE DFT calculations were carried out with the module RIDFT208 by employing the resolution-of-the-identity method to the Coulomb integrals (RI-J); auxiliary basis functions were taken from the TURBOMOLE library.209,210 TURBOMOLE's multi-grid option “m4” was applied for the numerical integration of the exchange–correlation potentials.209 Note that other studies, including GMTKN30 studies,7 extensively elaborated on the grid-dependence of some DFAs.25,211–214 Herein, we use quadrature grids that are feasible for routine applications to provide more viable guidelines. The SCF convergence criterion was set to 10−7Eh. The SCAN functional may show slow convergence for the radial quadrature grid, and therefore TURBOMOLE's option “radsize” = 40 was used together with a grid size of 4.
All (meta-)GGA functionals in ORCA were also treated with the RI-J approximation, whereas hybrids and the hybrid parts of double hybrids were treated with the chain-of-sphere approximation215 to evaluate exchange integrals (RIJCOSX). ORCA's default settings were used in the latter case. The second-order perturbative treatment for the double hybrids was also carried out with the RI approximation and the appropriate auxiliary basis functions.216 Contrary to previous studies, we also employed the frozen-core approximation for double hybrids to prevent basis-set superposition errors in the treatment of core–core electron correlation.217 All SCF calculations in ORCA were carried out with ORCA's quadrature grid “3”, followed by a non-iterative step with the larger grid “4”. These options are similar to TURBOMOLE's multi-grid strategy. The SCF convergence criterion was set to ORCA's “tightscf” option, which is similar to the option chosen for TURBOMOLE and GAUSSIAN. The nonlocal correction in VV10, B3LYP-NL and ωB97X-V was employed post-SCF and with ORCA's van der Waals grid “vdwgrid2”.
All GAUSSIAN calculations were carried out with the standard quadrature “fine grid”. The SCF convergence criterion was set to 10−7Eh.
MOLPRO2015.1218,219 was used to obtain reference values for the various Weizmann composite schemes mentioned in Section 2. Some W1-F12 calculations were also carried out with TURBOMOLE's CCSDF12220 module for computational efficiency reasons: the hexane and heptane dimers in ADIM6, the hexachlorobenzene reaction in DC13, and all calculations for MB16-43. The same TURBOMOLE module was also used for CCSD(T) calculations to obtain reference values for the HEAVYSB11 and HEAVY28 sets as well as for the tetramethyl-ethene reaction in DC13 (see Section 2 for details).
All DLPNO-CCSD(T)109 calculations were carried out with the sparse-maps version221 implemented in ORCA 4.0.0. Except for the CBS* calculations (see below) and the large systems in IDISP, the “TightPNO” setup128 was used, which corresponds to the following threshold values: TCutPairs = 10−5Eh, TCutPNO = 10−7, TCutDO = 5 × 10−3, and the use of the full MP2 guess. For the extrapolation to the CBS limit, the original scheme with an exponent of 1.63 proposed by Halkier and Helgaker121,122 was employed for HF, while an exponent of 3 was used for the correlation energy. Extrapolations were based on either the def2-TZVPP and def2-QZVPP, or aug-cc-pVTZ and aug-cc-pVQZ basis sets (as indicated above). In the DLPNO-CCSD(T)/CBS* calculations, only the electron pair cut-off was tightened to TCutPairs = 10−5Eh while all other threshold values were kept at their respective defaults. The CBS* basis set extrapolation is based on a multiplicative extrapolation scheme and the def2-TZVP basis set together with the MP2/CBS(cc-pVDZ/cc-pVTZ) energy as well as scaling factor to account for missing diffuse functions (for details, see ref. 104). This protocol was developed specifically for accurate reference calculation of larger systems where a DLPNO-CCSD(T)/TightPNO/CBS calculation is not computationally feasible. The resulting uncertainty of the reference values is, however, slightly larger than for the previous setup.
4 How to analyse GMTKN55
As is common practice, the statistical data that we calculate for each benchmark set and DFA comprise mean deviations (MDs), MADs, root-mean-square deviations (RMSDs), and deviation spans. To be consistent with our previous GMTKN30 studies, we will base the analysis in Section 5 primarily on MADs to determine the best and worst DFAs for each test set. While this analysis could also be carried out with RMSDs, we report those values only in the ESI† alongside the other aforementioned statistical values (Section S7). In fact, the RMSDs reported therein would give a similar overall picture of DFA performance.The average relative absolute energies 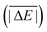 shown in Table 1 can be as small as 0.58 kcal mol−1 (RG18 set) and as large as 414.43 kcal mol−1 (MB16-43) or 654.26 kcal mol−1 (DIPCS10). Consequently, MADs for a benchmark set with a large
shown in Table 1 can be as small as 0.58 kcal mol−1 (RG18 set) and as large as 414.43 kcal mol−1 (MB16-43) or 654.26 kcal mol−1 (DIPCS10). Consequently, MADs for a benchmark set with a large 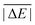 are expected to be larger than for a set with a relatively small
are expected to be larger than for a set with a relatively small 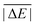 . For instance, MADs for MB16-43 usually exceed 15 kcal mol−1 for most dispersion-corrected hybrid DFAs. When considering the magnitude of the reaction energies—the largest reaction energy is 1290.74 kcal mol−1—such seemingly large MADs are appropriate. To better compare different benchmark sets with each other, we initially tested two strategies. Firstly, we calculated the percentage deviation for each reaction to obtain mean and mean absolute percentage deviations (MPDs and MAPDs) over a benchmark set. While such an analysis had turned out to be very useful in the past for detecting the underbinding tendency of Minnesota functionals for the NCIs in the S66x8 set,42,43 MAPDs for other sets in GMTKN55 turned out to be less robust and very sensitive to outliers. One example is the energy difference between the two lowest-lying tripeptide conformers in PCONF, which is only 0.02 kcal mol−1 according to the reference level of theory. Even the best DFA for this set—DSD-BLYP-D3(BJ) with an MAD of only 0.23 kcal mol−1—predicts an energy difference of 0.16 kcal mol−1. The percentage deviation is, thus, 702.5%. Even though this is the only outlier, this value distorts the MAPD to 56.8%, which does not seem to represent the overall excellent performance of this DFA.
. For instance, MADs for MB16-43 usually exceed 15 kcal mol−1 for most dispersion-corrected hybrid DFAs. When considering the magnitude of the reaction energies—the largest reaction energy is 1290.74 kcal mol−1—such seemingly large MADs are appropriate. To better compare different benchmark sets with each other, we initially tested two strategies. Firstly, we calculated the percentage deviation for each reaction to obtain mean and mean absolute percentage deviations (MPDs and MAPDs) over a benchmark set. While such an analysis had turned out to be very useful in the past for detecting the underbinding tendency of Minnesota functionals for the NCIs in the S66x8 set,42,43 MAPDs for other sets in GMTKN55 turned out to be less robust and very sensitive to outliers. One example is the energy difference between the two lowest-lying tripeptide conformers in PCONF, which is only 0.02 kcal mol−1 according to the reference level of theory. Even the best DFA for this set—DSD-BLYP-D3(BJ) with an MAD of only 0.23 kcal mol−1—predicts an energy difference of 0.16 kcal mol−1. The percentage deviation is, thus, 702.5%. Even though this is the only outlier, this value distorts the MAPD to 56.8%, which does not seem to represent the overall excellent performance of this DFA.
Having ruled out MAPDs, we instead calculated normalised MADs (NMADs) as the ratio of a DFA's MAD and the test set's 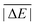 . The NMAD for DSD-BLYP-D3(BJ) for PCONF21, for instance, is only 0.14. The interested reader can find the NMADs for all assessed DFAs and benchmark sets in the ESI† alongside the other statistical values that we introduced above.
. The NMAD for DSD-BLYP-D3(BJ) for PCONF21, for instance, is only 0.14. The interested reader can find the NMADs for all assessed DFAs and benchmark sets in the ESI† alongside the other statistical values that we introduced above.
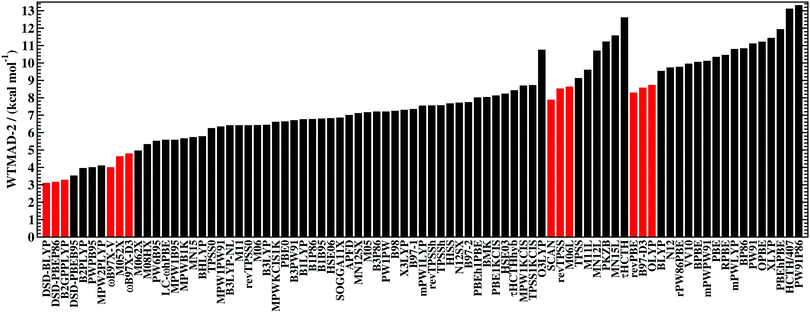
To identify robust DFAs and to enable a ranking of the assessed methods, the so-called weighted total mean absolute deviation (WTMAD) was introduced for GMTKN24 and GMTKN30.23,24 Each benchmark set was assigned a “difficulty factor”, which was calculated as the ratio of the MADs of BLYP and B2PLYP-D2, i.e., between a GGA without dispersion and a very good method with dispersion. The test set's MAD was then multiplied by this difficulty factor and further scaled by the number of data points in the respective set. Finally, the average over all those weighted MADs was taken, resulting in a WTMAD. While this scheme does seem arbitrary, it was also verified that schemes without such weight factors gave similar DFA trends, thus, confirming the validity of the conclusions drawn from WTMADs.23 For instance, the best WTMADs reported for GMTKN30 were for the three DSD methods that we also assess herein (1.3 kcal mol−1).29
Also for GMTKN55, we propose using WTMADs to separate reliable from less accurate methods. In preliminary studies, we tested a total of 11 different schemes, based on MAPDs, NMADs, MADs or RMSDs, and each provided a similar picture. For instance, all schemes correctly reproduced the Jacob's Ladder idea. We narrowed those 11 schemes down to two, which we will use simultaneously to underline the reliability of our DFA recommendations.
In the first scheme, dubbed WTMAD-1, each benchmark set is weighted by a factor w that aims at aligning benchmark sets with largely differing 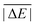 values. The MAD of a test set is scaled up by a factor of w = 10 if the set's average absolute reaction energy is below 7.5 kcal mol−1. The MAD of a test set is scaled down by a factor of w = 0.1 if the set's average absolute reaction energy is larger than 75 kcal mol−1. For the remaining sets, w was set to unity. The WTMAD-1 is then simply calculated as an average value over the 55 sets:
values. The MAD of a test set is scaled up by a factor of w = 10 if the set's average absolute reaction energy is below 7.5 kcal mol−1. The MAD of a test set is scaled down by a factor of w = 0.1 if the set's average absolute reaction energy is larger than 75 kcal mol−1. For the remaining sets, w was set to unity. The WTMAD-1 is then simply calculated as an average value over the 55 sets:
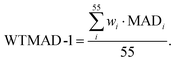 | (1) |
While the weight factors for WTMAD-1 are arbitrarily defined, the alternative WTMAD-2 scheme uses the ratio between average of all 55 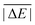 values (56.84 kcal mol−1) and the
values (56.84 kcal mol−1) and the 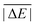 for the respective test set as a weight factor. This value is then scaled by the number of relative energies N in that particular set before it is combined with the MAD. The WTMAD-2 is then calculated as the sum over all 55 weighted MADs and divided by the total number of relative energies in GMTKN55 (1505 data points):
for the respective test set as a weight factor. This value is then scaled by the number of relative energies N in that particular set before it is combined with the MAD. The WTMAD-2 is then calculated as the sum over all 55 weighted MADs and divided by the total number of relative energies in GMTKN55 (1505 data points):
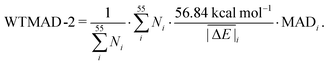 | (2) |
While eqn (1) and (2) allow calculating WTMADs for the entire GMTKN55 database, it is straightforward to apply those schemes to each of GMTKN55's categories (see Fig. 1). To obtain a WTMAD-1, the sum of relevant WTMADs is then simply divided by the number of test sets in that category. Likewise, a WTMAD-2 is obtained by division by the number of data points in the respective category.
The WTMADs for each DFA over the entire GMTKN55 and its categories are listed in the ESI.† While those values formally carry the unit kcal mol−1, they should not be mistaken as an indicator for a method's average error. However, the values can be used as a way to score DFAs and to rank them. Also, we suggest that new DFAs developed in the future can be measured against the DFAs tested herein by comparing their WTMADs. In particular, we challenge developers to beat the best WTMADs presented herein.
5 Benchmark study on GMTKN55
5.1 Example of the benefit of using new reference values
In Section 2, we outlined how we had updated the reference values of most benchmark sets. In some cases, those values only changed marginally, in others we noted significant differences. One example for a significant change had already been given for the BHPERI set in 2015, as also mentioned in the introduction.55 When compared against W2-F12 and W1-F12 numbers, the original CBS-QB3 reference values turned out to be less accurate than double-hybrid DFAs. Moreover, some DFAs that were recommended for BHPERI in previous studies7 turned out to be the least accurate in their respective DFA class when compared with the updated reference values.Herein, we further underline the importance of using new reference values with one additional example. Table S5 in the ESI† shows the MADs for all 83 dispersion-corrected DFAs with respect to the old and the new reference values for the AL2X6 test set. In Section 2, we mentioned that the average absolute change in the reference reaction energies was 1.4 kcal mol−1 when adopting the new benchmark. From the values presented in Table S5 (ESI†), we calculated the average MAD for each rung on Jacob's Ladder. For AL2X6 with the original reference values, it turns out that the average MAD for GGA/NGA functionals is 4.39 kcal mol−1 and that meta-GGAs/NGAs perform on average slightly worse with a value of 4.53 kcal mol−1. When using our new benchmark, the average MADs for both rungs do not only decrease, but meta-GGAs/NGAs become on average slightly better than GGAs/NGAs (3.65 vs. 3.86 kcal mol−1). The average MAD for hybrids drops significantly from 3.66 to 2.83 kcal mol−1 with the new values, and also double hybrids become even more accurate (improvement from 1.71 to 1.18 kcal mol−1).
Most striking, however, is the ranking of the DFAs. For instance, we observe a significant change when analysing the best three DFAs for this set. According to the old reference values, the range-separated Minnesota functional MN12SX-D3(BJ) is the best method with an MAD of 0.72 kcal mol−1. It is followed by BHLYP-D3(BJ) (0.76 kcal mol−1) and B2GPPLYP-D3(BJ) (1.01 kcal mol−1). It comes somewhat as a surprise that the best two DFAs are hybrids and that double hybrids are outperformed. However, this picture changes entirely when the new reference values are applied. The best two performers are the DSD-type double hybrids DSD-PBEP86-D3(BJ) (MAD = 0.31 kcal mol−1) and DSD-BLYP (MAD = 0.54 kcal mol−1). They are followed by the hybrid PW6B95-D3(BJ) with an MAD of 0.61 kcal mol−1. Even more striking is that MN12SX-D3(BJ) is now only the 18th-best DFA with an MAD of 1.35 kcal mol−1; BHLYP is in the 23rd position (MAD = 1.56 kcal mol−1).
The BHPERI example from the literature55 as well as our discussion of AL2X6 demonstrate how recommendations based on DFA rankings can change substantially when more accurate reference values are used. We therefore advocate to use all our new reference values published herein in future studies.
5.2 The need for dispersion corrections
The fact that conventional DFAs need a London-dispersion correction to describe interaction energies in noncovalently bound complexes as well as relative conformational energies is well known; see ref. 222 for a detailed review. An exception to this rule are DFAs that contain a nonlocal vdW kernel, such as VV10 or ωB97X-V.153,155 Over the past years, it has been demonstrated that dispersion corrections also positively influence geometries of organic and biomolecular systems44,223–228 as well as the description of reaction energies and BHs.50,84,222,229 This topic was also discussed for GMTKN30 in 2011.7 These are only some of many examples in the literature, and yet, we still observe the common trend to rely on uncorrected DFAs in many computational organic chemistry applications; for a discussion on the shortcomings of such an approach, see e.g.ref. 48. In light of this discrepancy between theoretical insight and what methods are actually used by some in the user community, it seems necessary to re-emphasise the importance of dispersion corrections for the computational treatment of reactions.Fig. 2 shows the effect of the DFT-D3 correction on the WTMAD-1 values of four DFAs—each is a representative of its corresponding rung on Jacob's Ladder—for the first three categories in GMTKN55 and the entire database. The actual values and results for the NCI categories are shown in the ESI† alongside WTMAD-2 values, which show the same trend. DFT-D3 decreases the WTMAD-1 values even in non-NCI categories with improvements of up to 36% for isomerisations and reactions of large systems (B3LYP). Note that even for smaller systems, where smaller dispersion contributions are expected, we still see sizeable reductions of 25–28% (BLYP and B3LYP).
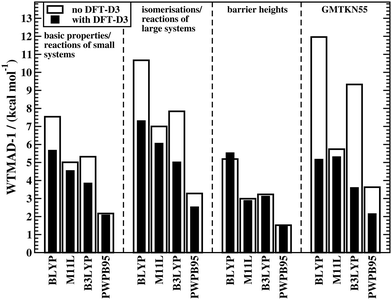 | ||
| Fig. 2 The effect of dispersion corrections on WTMAD-1 values (kcal mol−1) for the thermochemistry and kinetics categories of GMTKN55 and for the entire database. | ||
The results for BHs may indicate that dispersion is less important for those and that dispersion corrections may, in fact, deteriorate the outcome. The latter is seemingly the case for BLYP, for which the WTMAD-1 increases from 5.19 to 5.53 kcal mol−1. This behaviour, however, has a simple explanation. GGAs/NGAs suffer from the SIE to a much larger extent than hybrids. As a consequence, many reaction barriers are underestimated. For instance the MD of BLYP for BH76 is −8.32 kcal mol−1. As the transition state for most reactions in BH76 can be seen as a “complex” of two interacting fragments (the two reactants or products), a dispersion correction stabilises the transition state more than it does the separate reactants (or products). Therefore, a functional that already underestimates a barrier, will do so even more when dispersion energy is added. In fact, the MD for BLYP-D3(BJ) is −9.23 kcal mol−1. The blame for this does not lie with the dispersion correction. The better uncorrected result can be explained with error-compensation effects between the lack of incorporating dispersion and the SIE. A consequence is, therefore, that BLYP is simply not reliable enough to treat such problems. Indeed, dispersion corrections do improve WTMAD-1 values for the other DFAs in Fig. 2 Note that smaller improvements are seen than for the other two categories of GMTKN55. That being said, it was out pointed elsewhere that, for instance, in the INV24 set, dispersion corrections influence inversion barriers of helical and bowl-shaped systems by up to 2 kcal mol−1.84 Indeed, we observe a reduction of the MAD in INV24 for B3LYP from 1.87 to 1.05 kcal mol−1.
It comes as no surprise that the WTMADs for the entire GMTKN55 database also improve when dispersion corrections are employed (Fig. 2), the same was already reported for GMTKN30.7 As a consequence, we will continue our analysis solely with dispersion-corrected methods given in Table 2; the statistics for uncorrected DFAs are shown in the ESI.†
A common strategy in DFT development is to empirically fit a DFA without any nonlocal vdW kernels to a training set of NCI energies. Minnesota DFAs, beginning with M05 and culminating in MN15, are popular examples of this idea. In our GMTKN30 study, we outlined how dispersion corrections can improve the M05 and M06 classes of DFAs; a nonlocal correction for M06L and DFT-D3 parameters for most of the other Minnesota methods were introduced in ref. 43. Herein, we also present DFT-D3 parameters for M08HX and the MN15 class of DFAs (Section 3.2).
The effect of DFT-D3 on all 15 tested Minnesota methods is depicted in Fig. 3, which displays WTMAD-1 values for the intermolecular interaction category (the actual numbers and WTMAD-2 values are shown in the ESI†). In most cases, DFT-D3 does indeed improve the description of the systems in that category, with some improvements being in the 44–71% range (N12, M05, SOGGA11X, N12SX, MN12SX). Note that M06, MN15L, and MN15 are the only Minnesota DFAs that do not seem to benefit from the DFT-D3 correction. This has been explained with the fact that those methods would describe complexes in their equilibrium geometries well, as the regime of overlapping electron clouds of interacting fragments may be partially described by the DFA itself.19 However, for non-equilibrium distances it was conclusively shown that dispersion interactions are severely underestimated by most of the herein assessed Minnesota methods;42,43 also see ref. 25 for another study analysing Minnesota DFAs for NCIs.
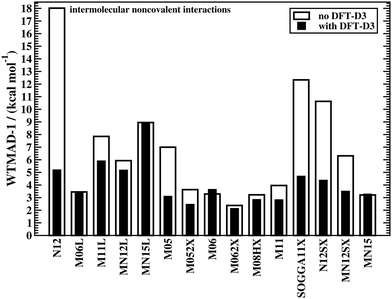 | ||
| Fig. 3 The effect of dispersion corrections on WTMAD-1 values (kcal mol−1) of Minnesota-type DFAs for intermolecular NCIs. | ||
Because of the way Minnesota DFAs had been parametrised, some double-counting effects were reported with the Becke–Johnson version of DFT-D3 for some. These effects may also show up for some conformational energies. WTMADs for the category of intramolecular interactions shown in the ESI† confirm this trend. As such problems are very rare with other DFAs, it indicates that choosing Minnesota DFAs for NCIs is not a generally recommended strategy. However, Fig. 2 also shows how reaction energies and BHs are improved for the M11L method with DFT-D3. To be consistent with our observation and the fact that those methods do not properly describe London dispersion, we will only report dispersion-corrected results for Minnesota DFAs in the following sections, while uncorrected results can be found in the ESI.†
5.3 Discussion of GMTKN55 and its categories
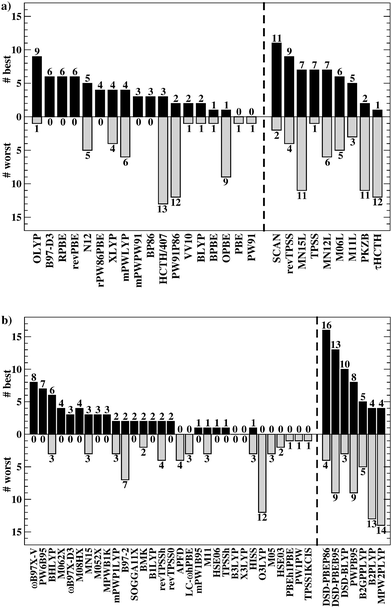
Having established the benefit of our new reference values and the importance of using a London-dispersion correction, we proceed with our analysis of the 83 dispersion-corrected DFAs applied to GMTKN55. We will do so first for the separate categories of GMTKN55 before we conclude with a comprehensive look at the entire database to provide final recommendations to the DFT user. Our main aim in each category will be to identify the most robust DFAs that perform best over a series of benchmark sets. With a few exceptions, we will refrain from giving recommendations for each of the 55 individual test sets. However, the best and worst DFAs for each set are shown in the ESI† (Tables S8–S11).We usually first carry out a “best-worst” analysis by counting how many times a DFA gives the best MAD and how many times the worst. This turned out to be a good estimate of DFA robustness in the past.7 For instance, a method that yields the best and worst MAD an equal number of times should be regarded as less robust and reliable than one that never gives the worst MAD. In a second step, we then analyse the WTMADs as defined in Section 4 to look at our results from a different perspective. A DFA that appears in both analyses will then be recommended as a reliable method for the assessed category. We will give such recommendations for each of the four highest rungs of Jacob's Ladder.
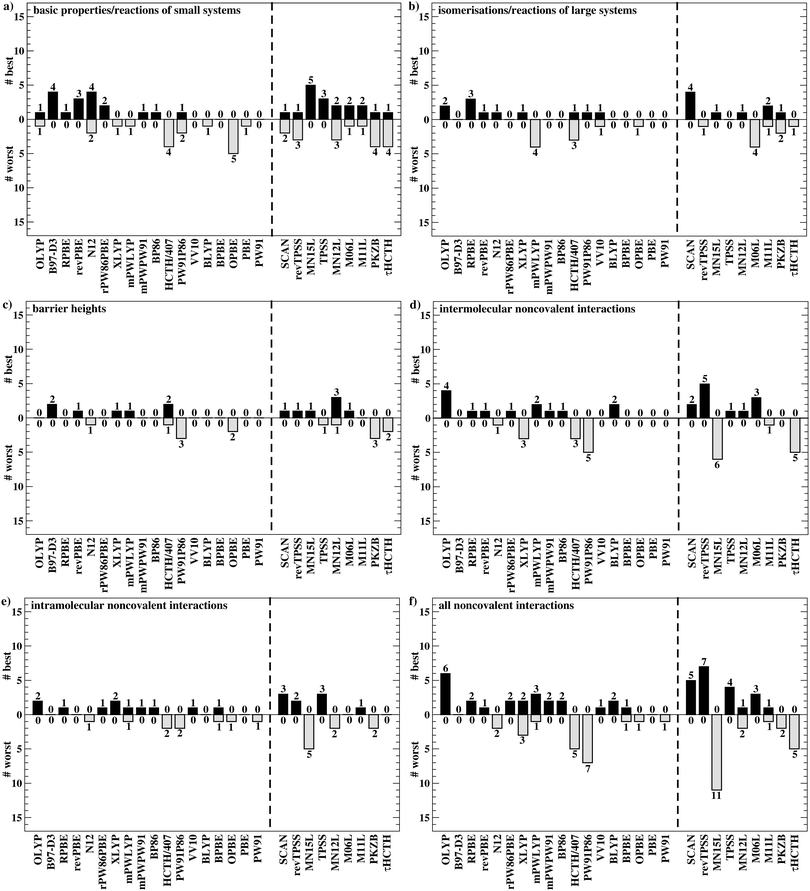
To get a better overview of the large amount of obtained data, we first analyse GGAs and NGAs and identify the best and worst performing representatives (Fig. 4a). While no single method has the best MAD in the absolute majority of cases, we are still able to identify two GGAs that clearly distinguish themselves from others (also see Table S8, ESI†): B97-D3(BJ) yields the best MAD in four cases (W4-11, G21EA, G21IP, and RC21), while revPBE-D3(BJ) does so in three cases (HEAVYSB11, BH76RC, and TAUT15). Both DFAs have in common that they never give the worst MAD. This is in contrast to N12-D3(0), which performs best in four cases (SIE4x4, AL2X6, FH51, and DC13), but also performs worst in two cases (G21IP and TAUT15). Methods that clearly under-perform are HCTH/407-D3(BJ) (4 times) and OPBE-D3(BJ) (5 times). Interestingly, combining OPTX exchange with LYP rather than PBE correlation improves this picture and OLYP-D3(BJ) is the worst GGA in only one case (SIE4x4), while it is the best-performing one for the ALKBDE10 set. The popular PBE-D3(BJ) and BLYP-D3(BJ) are never the best GGAs, and in fact they give the worst MAD in one case each (BH76RC and DIPCS10, respectively). The popular BP86-D3(BJ) method never provides the best nor worst MAD, and for now it is not possible to assess its overall performance without consulting its WTMADs.
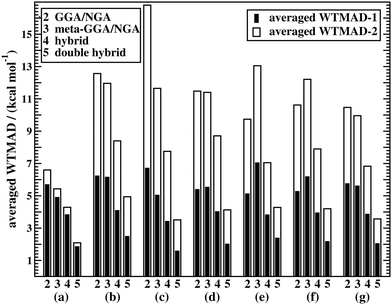
Fig. 5a shows WTMAD averages for each assessed DFA class. The figure confirms the expected trend for Jacob's Ladder, namely that rung-2 DFAs are on average less accurate than higher rungs. It also demonstrates that both our suggested WTMAD schemes predict the same trend, but that WTMAD-2 values are higher for every class than WTMAD-1 ones. The averaged WTMAD-1 for rung 2 for basic properties and reactions of small systems is 5.70 kcal mol−1 and the WTMAD-2 is 6.60 kcal mol−1 (also see Table S12, ESI†). While those numbers are averages, individual WTMAD-1 values for GGAs/NGAs range from 4.70 to 7.77 kcal mol−1, and WTMAD-2 values from 5.54 to 8.23 kcal mol−1 (Tables S20 and S21, ESI†).
The best three GGAs/NGAs according to the WTMAD-1 and WTMAD-2 schemes are shown in Table 3. Both schemes determine revPBE-D3(BJ) to be the best GGA. The BPBE-D3(BJ) method, which neither gives the best nor the worst MAD, performs on average very well and it comes in second place for WTMAD-1, closely followed by BP86-D3(BJ). Based on WTMAD-2, BPBE-D3(BJ) has a slightly lower value than N12-D3(0) and comes in third place. However, the information gathered in Fig. 4 hinted at N12-D3(0) being less robust. Note that B97-D3(BJ) has the seventh-best WTMAD-1 (5.26 kcal mol−1) and the fourth-best WTMAD-2 (5.98 kcal mol−1), while BP86-D3(BJ) has the seventh-best WTMAD-2 with 6.30 kcal mol−1. The two largest WTMADs shown in Table S13 (ESI†) confirm our previous analysis, namely that OPBE-D3(BJ) and HCTH/407-D3(BJ) should be avoided when studying the chemical problems considered in this category. At this stage, we can, thus, conclude that revPBE-D3(BJ) or BPBE-D3(BJ) are most likely the best choices for this category.
| Rung | WTMAD-1 | WTMAD-2 |
|---|---|---|
| GGA/NGA | revPBE-D3(BJ) (4.70) | revPBE-D3(BJ) (5.54) |
| BPBE-D3(BJ) (5.03) | N12-D3(0) (5.76) | |
| BP86-D3(BJ) (5.11) | BPBE-D3(BJ) (5.82) | |
| Meta-GGA/NGA | MN15L-D3(0) (3.42) | MN15L-D3(0) (4.01) |
| M06L-D3(0) (4.42) | MN12L-D3(BJ) (4.44) | |
| M11L-D3(0) (4.54) | M11L-D3(0) (4.89) | |
| Hybrid | M08HX-D3(0) (2.48) | M062X-D3(0) (2.73) |
| ωB97X-V (2.63) | M08HX-D3(0) (2.75) | |
| M062X-D3(0) (2.66) | MN15-D3(BJ) (2.95) | |
| Double hybrid | DSD-PBEP86-D3(BJ) (1.46) | DSD-PBEP86-D3(BJ) (1.69) |
| DSD-BLYP-D3(BJ) (1.63) | DSD-BLYP-D3(BJ) (1.88) | |
| DSD-PBEB95-D3(BJ) (1.70) | DSD-PBEB95-D3(BJ) (1.89) | |
For rung 3 of Jacob's ladder, there are only two DFAs that never give the worst MAD (Fig. 4a). In fact, MN15L-D3(0) gives the best MAD in five cases (W4-11, G21IP, PA26, SIE4x4, and RC21) and TPSS-D3(BJ) in three (DIPCS10, ALKBDE10, and NBPRC). In general, meta-GGAs/NGAs are more accurate than rung-2 methods with averaged WTMADs of 4.91 kcal mol−1 (WTMAD-1) and 5.43 kcal mol−1 (WTMAD-2). That being said, the least accurate meta-GGAs have larger WTMADs than some GGAs/NGAs, with τHCTH-D3(BJ) having the largest WTMAD-1 with 6.82 kcal mol−1 and PKZB-D3(0) the largest WTMAD-2 with 6.71 kcal mol−1 (Table S13, ESI†). Also the results in Fig. 4a indicate that these two methods are among the worst-performing, as they have the largest MADs in four cases each. The best meta-GGAs/NGAs in Table 3 are all Minnesota methods, with MN15L-D3(0) having the lowest WTMADs according to both schemes (WTMAD-1 = 3.42 kcal mol−1, WTMAD-2 = 4.01 kcal mol−1). It is the only DFA for this functional rung that we recommend at this stage, as the other methods occasionally deliver the worst MADs (Fig. 4a).
Given the much larger number of assessed hybrid DFAs, the analysis of best and worst MADs for this category does not allow drawing as clear a picture as before, and there are indeed many approaches that neither give the best nor the worst MAD, but they may still be regarded as reliable. Nevertheless, a figure similarly to Fig. 4 is provided in the ESI.† DFAs that seem to be noteworthy are PW6B95-D3(BJ), M062X-D3(0), M08HX-D3(0), MN15-D3(BJ), SOGGA11X-D3(BJ), and ωB97X-V; they never give the worst MAD, but each of them provides the best in one to four cases. Out of those methods, the WTMAD-1 scheme places M08HX-D3(0), ωB97X-V, and M062X-D3(0) in the top three (Table 3). The WTMAD-2 scheme, confirms that M08HX-D3(0) and M062X-D3(0) do indeed seem to be competitive in this category, as they are predicted to be the best two hybrids. The WTMAD-2 values of the following DFAs are very close together, and while ωB97X-V ranks on seventh place, its WTMAD-2 of 3.34 kcal mol−1 is not too far away from that of MN15-D3(BJ) (2.95 kcal mol−1). Based on their WTMADs shown in Table S13 (ESI†) and the number of times they provide the worst MAD (Fig. S3, ESI†), the worst-performing hybrids are B97-2-D3(BJ), O3LYP-D3(BJ), and the two revTPSS-based hybrids revTPSSh-D3(BJ) and revTPSS0-D3(BJ). In fact, those methods are outperformed by the best (meta-)GGA/NGA approaches. While this indicates that not every hybrid is necessarily better than lower-rung DFAs, we also note that the averaged WTMADs for hybrids are about 1 kcal mol−1 lower than for rung 2 (Fig. 5).
The popular hybrids PBE0-D3(BJ) and B3LYP-D3(BJ) never give the best nor the worst MAD, and they rank in 26th and 29th position with WTMAD-1 values around 3.8 kcal mol−1, which is around the average WTMAD-1 for hybrids. B3LYP-NL is in 27th place with almost the same WTMAD-1 as the D3-corrected version. WTMAD-2 values provide the same picture (ESI†). With an averaged WTMAD-1 of 1.87 kcal mol−1 and an averaged WTMAD-2 of 2.09 kcal mol−1, double hybrids are by far superior than hybrids (Fig. 5). Even the largest WTMADs for double hybrids—for instance MPW2PLYP-D3(BJ) and B2PLYP-D3(BJ) with WTMAD-1 values 2.24 kcal mol−1—are lower than the WTMADs of the best hybrids. In fact, the WTMADs of all seven assessed double hybrids are very close to one another, which makes a best-worst analysis of their MADs less insightful. In fact, any of the assessed double hybrids can safely be applied to the test sets considered so far. That being said, the by far best double hybrids in this category—and also the best DFAs out of all 83—are the three DSD methods (Table 3). We will see next if the DFAs recommended at this stage also perform well in the remaining categories.
As both sets were created independently and without any user bias, this reconfirms the PW6B95's high robustness. While some Minnesota approaches have relatively low MADs close to 12 kcal mol−1 (MN12SX, and SOGGA11X), the two MN15-type DFAs both have nearly identical high MADs above 20 kcal mol−1, thus indicating that the hybrid version is not more robust than the meta-NGA one. Interestingly, the two promising ωB97X-V and ωB97X-D3 methods both have MADs above 32 kcal mol−1. The best second-rung DFA is SCAN-D3(BJ) with an MAD of 17.77 kcal mol−1, while M06L-D3(0) is the worst with an MAD of 63.27 kcal mol−1. The worst DFA of all is HCTH/407-D3(BJ) with an MAD of 76.52 kcal mol−1 (NMAD = 0.18).
While double hybrids are methods that tend to perform better than hybrids,7,29 we like to point out that the new C60ISO set seems to be more challenging for them. In fact, the best double hybrid PWPB95-D3(BJ) has an MAD of 3.48 kcal mol−1, which is double of that of the best hybrid (and the best DFA for this set) PW6B95-D3(BJ) (MAD = 1.65 kcal mol−1). This shows the importance of developing benchmark sets with larger, more realistic (and unsaturated in this case) systems to identify needs for further development. That highly conjugated systems can be challenging for double hybrids was also shown for C20 and C24 isomers in ref. 73.
Due to the nine benchmark sets in this category having larger average absolute reaction energies, the individual weights used in the two WTMAD schemes differ more from one another and WTMAD-2 numbers turn out to be significantly larger than WTMAD-1 ones. That being said, both schemes still provide the same trends. The average WTMADs all reproduce the Jacob's Ladder scheme and double hybrids are the best approaches in this category (Fig. 5). Also, the best three DFAs on each rung are the same in both schemes (Table 4).
| Rung | WTMAD-1 | WTMAD-2 |
|---|---|---|
| GGA/NGA | OLYP-D3(BJ) (4.81) | OLYP-D3(BJ) (9.67) |
| N12-D3(0) (5.10) | RPBE-D3(BJ) (10.02) | |
| RPBE-D3(BJ) (5.17) | N12-D3(0) (10.30) | |
| Meta-GGA/NGA | SCAN-D3(BJ) (4.55) | SCAN-D3(BJ) (7.86) |
| revTPSS-D3(BJ) (5.52) | M11L-D3(0) (10.46) | |
| M11L-D3(0) (6.06) | MN15L-D3(0) (10.58) | |
| Hybrid | M052X-D3(0) (2.62) | M052X-D3(0) (5.20) |
| BMK-D3(BJ) (2.74) | M08HX-D3(0) (5.40) | |
| M08HX-D3(0) (2.82) | BMK-D3(BJ) (5.45) | |
| Double hybrid | DSD-PBEB95-D3(BJ) (1.78) | DSD-PBEB95-D3(BJ) (3.28) |
| DSD-PBEP86-D3(BJ) (1.80) | DSD-PBEP86-D3(BJ) (3.91) | |
| DSD-BLYP-D3(BJ) (2.22) | DSD-BLYP-D3(BJ) (4.32) | |
Fig. 4b points at RPBE-D3(BJ) and OLYP-D3(BJ) as potentially good approaches, as they are the only GGAs that give the best MADs in three and two cases, respectively: RPBE-D3(BJ) is the best for RSE43, BSR36 and ISO34, while OLYP-D3(BJ) performs best for DARC and ISOL24. revPBE-D3(BJ) performs equally well for RSE43, while N12-D3(0) yields the same MAD as RPBE-D3(BJ) for ISO34. In fact, both WTMAD schemes rank OLYP-D3(BJ) as the best GGA followed by N12-D3(0) and RPBE-D3(BJ) for WTMAD-1, whereas the order of the last two is reversed for WTMAD-2 (Table 4). The worst-performing rung-2 DFAs are mPWLYP-D3(BJ), OPBE-D3(BJ), BLYP-D3(BJ), and rPW86PBE-D3(BJ). Again, we see that OPTX exchange combined with PBE correlation does not seem to be a good match, even though this combination is popular in some areas.149
The only meta-GGA that is worth being mentioned according to Fig. 4b is SCAN-D3(BJ), which has the best MAD for four benchmark sets (MB16-43, DARC, ISOL24, and PArel). It outperforms Minnesota DFAs; in fact, M06L-D3(0) has the worst MAD in four cases (MB16-43, DARC, CDIE20, and ISOL24). Also both WTMAD schemes place SCAN-D3(BJ) at the top with a large gap before the second-ranking method. SCAN-D3(BJ) has a WTMAD-1 value of 4.55 kcal mol−1 followed by revTPSS-D3(BJ) with 5.52 kcal mol−1; the WTMAD-2 for SCAN-D3(BJ) is 7.86 kcal mol−1, whereas the next DFA M11L-D3(0) has a value of 10.46 kcal mol−1 (Table 4).
While PW6B95-D3(BJ) and M052X-D3(0) both give the best MADs in two cases (MB16-43 and C60ISO for the first, DARC and CDIE20 for the latter), it is interesting to note that the first does not appear in the list of top three WTMADs, while the latter is ranked as the best hybrid (Table 4). In 2nd and 3rd position follow BMK-D3(BJ) and M08HX-D3(0). The three worst hybrids are M05-D3(0), O3LYP-D3(BJ), and mPW1LYP-D3(0) (see ESI†). B3LYP-D3(BJ)'s WTMAD-1 is with 5.02 kcal mol−1 in 44th place and by nearly 1 kcal mol−1 worse than the average WTMAD-1 of 4.10 kcal mol−1 for this DFA class (Fig. 5). We do note however, that using the nonlocal VV10 kernel improves the WTMAD-1 to 4.00 kcal mol−1 for B3LYP-NL, even though this value still hovers around the average.
Even though their performance may not be the best for C60ISO, double hybrids again feature the lowest WTMADs. This time, however, MPW2PLYP-D3(BJ) and B2PLYP-D3(BJ) are outperformed by the best three hybrids (WTMAD-1 = 3.36 kcal mol−1) (ESI†). The best three double hybrids—and also the best three DFAs in this category—are Martin's DSD methods with both WTMAD schemes ranking them in the same order: DSD-PBEB95-D3(BJ), DSD-PBEP86-D3(BJ), and DSD-BLYP-D3(BJ) (Table 4).
This picture seems to improve for the next rung with the best meta-NGA being MN12L-D3(BJ) (MAD = 2.03), however, this is still not satisfying enough when comparing it with the best hybrid ωB97X-V (MAD = 0.85 kcal mol−1) and the best double hybrid DSD-PBEB95-D3(BJ) (MAD = 0.83 kcal mol−1) (ESI†). Contrary to that, the results for BHROT27 indicate that the best DFAs in each rung show fairly similar accuracy with revPBE-D3(BJ) having an MAD of only 0.37 kcal mol−1, while DSD-PBEP86-D3(BJ) has a value of 0.21 kcal mol−1 (ESI†). Error-compensation effects between the minimum-energy structures and the transition states are the likely reason for the good performance of second-rung methods for this test set. As already reported elsewhere, inversion barriers also show smaller differences between DFAs, however, the Jacob's Ladder picture is still reproduced.84 The best GGA B97-D3(BJ), for instance, has an MAD of 1.80 kcal mol−1, which is reduced to 0.69 kcal mol−1 for B2PLYP-D3(BJ) (see ESI†). As also pointed out before, all double hybrids behave very similarly for this set and all their MADs are below the chemical-accuracy threshold of 1 kcal mol−1.84
The averaged WTMADs in Fig. 5 are significantly higher for (meta-)GGAs/NGAs than for (double-)hybrids. For instance, average WTMAD-2 values are 16.80 kcal mol−1 for the 2nd, 11.64 kcal mol−1 for the 3rd, 7.75 kcal mol−1 for the 4th, and 3.51 kcal mol−1 for the 5th rung. While more detailed results for rungs 2 and 3 are shown in Fig. 4c and Table 5, we do not make specific recommendations for them, as hybrids and double hybrids should be used for BHs to obtain reliable results.
| Rung | WTMAD-1 | WTMAD-2 |
|---|---|---|
| GGA/NGA | B97-D3(BJ) (5.15) | B97-D3(BJ) (13.15) |
| BLYP-D3(BJ) (5.53) | HCTH/407-D3(BJ) (13.76) | |
| rPW86PBE-D3(BJ) (5.56) | rPW86PBE-D3(BJ) (15.17) | |
| Meta-GGA/NGA | M11L-D3(0) (2.88) | M11L-D3(0) (5.47) |
| M06L-D3(0) (3.31) | MN15L-D3(0) (5.49) | |
| MN15L-D3(0) (3.51) | MN12L-D3(BJ) (5.74) | |
| Hybrid | SOGGA11X-D3(BJ) (1.77) | M08HX-D3(0) (3.33) |
| ωB97X-V (1.91) | BMK-D3(BJ) (3.73) | |
| M08HX-D3(0) (1.99) | MN12SX-D3(BJ) (3.74) | |
| Double hybrid | DSD-PBEB95-D3(BJ) (1.02) | DSD-PBEB95-D3(BJ) (2.26) |
| DSD-BLYP-D3(BJ) (1.45) | DSD-BLYP-D3(BJ) (3.04) | |
| PWPB95-D3(BJ) (1.50) | B2GPPLYP-D3(BJ) (3.24) | |
The lowest WTMAD-1 values are observed for SOGGA11X-D3(BJ), ωB97X-V, and M08HX-D3(0), while M08HX-D3(0), BMK-D3(BJ), and MN12SX-D3(BJ) have the lowest WTMAD-2 values (Table 5). The BMK method was originally designed to describe kinetics, as the letter “K” indicates. However, we did not observe it to be the best DFA for any of the seven individual test cases (see ESI†). Instead, the MPWB1K method—also developed for kinetics—gave the best MAD in two cases when dispersion corrected (PX13 and WCPT18). It ranks as the fifth hybrid in the WTMAD-2 scheme, and as seventh in the WTMAD-1 list (see ESI†). Another hybrid specifically designed for the calculation of BHs—MPWKCIS1K-D3(BJ)—does not appear to be of any value and it ranks as 13th (WTMAD-2) and 14th (WTMAD-1). Both schemes evaluate the following three hybrids as the least accurate: O3LYP-D3(BJ), MPW1KCIS-D3(BJ), and TPSSh-D3(BJ).
BHLYP-D3(BJ), which is popular for BHs due to its large fraction of Fock-exchange, cannot be recommend at all for this purpose; it is in 26th position in the WTMAD-1 and in 21st in the WTMAD-2 list. It is almost needless to mention that also B3LYP should not be used (position 34 for B3LYP-D3(BJ) and 40 for B3LYP-NL in the WTMAD-2 picture, see ESI†).
The best double hybrids all deliver MADs that are 1 kcal mol−1 (BH76 set) or lower (all other sets), which means they can provide results with chemical accuracy. The best double hybrid for BHs is DSD-PBEB95-D3(BJ), which yields the best MAD in the majority of cases (BH76, DSD-PBEB95, PX13, and WCPT18). Double hybrids relying on B95 correlation seem to be particularly good in this category, as PWPB95 gives the best MAD for a fifth set, namely BHPERI (also see ref. 55). Both WTMAD schemes place DSD-PBEB95-D3(BJ) in first position with values of 1.02 kcal mol−1 (WTMAD-1) and 2.26 kcal mol−1 (WTMAD-2). These values are significantly lower than the second-best method DSD-BLYP-D3(BJ) with 1.45 and 3.04 kcal mol−1, respectively. DSD-BLYP-D3(BJ) is closely followed by PWPB95-D3(BJ) (WTMAD-1 = 1.50 kcal mol−1) or B2GPPLYP-D3(BJ) (WTMAD-2 = 3.24 kcal mol−1).
| Rung | WTMAD-1 | WTMAD-2 |
|---|---|---|
| GGA/NGA | BLYP-D3(BJ) (3.20) | B97-D3(BJ) (5.95) |
| OLYP-D3(BJ) (3.33) | revPBE-D3(BJ) (6.19) | |
| B97-D3(BJ) (3.42) | OLYP-D3(BJ) (7.03) | |
| Meta-GGA/NGA | M06L-D3(0) (3.41) | revTPSS-D3(BJ) (6.70) |
| revTPSS-D3(BJ) (3.58) | M06L-D3(0) (7.37) | |
| TPSS-D3(BJ) (4.15) | TPSS-D3(BJ) (7.59) | |
| Hybrid | ωB97X-V (1.45) | ωB97X-V (3.03) |
| PW6B95-D3(BJ) (2.01) | PW6B95-D3(BJ) (4.22) | |
| M062X-D3(0) (2.13) | BHLYP-D3(BJ) (4.46) | |
| Double hybrid | PWPB95-D3(BJ) (1.75) | B2PLYP-D3(BJ) (3.78) |
| B2PLYP-D3(BJ) (1.86) | DSD-PBEB95-D3(BJ) (3.90) | |
| DSD-BLYP-D3(BJ) (1.94) | DSD-BLYP-D3(BJ) (3.92) | |
According to Fig. 4d, OLYP-D3(BJ) gives the best MAD for four test sets (ADIM6, HEAVY28, CARBHB12, and HAL59). BLYP-D3(BJ), on the other hand, provides spectacularly low MADs for the popular S22 and S66 sets (0.25 and 0.17 kcal mol−1, respectively), which are commonly used to assess a method's performance to describe NCIs. Among the worst-performing GGAs we find HCTCH/407-D3(BJ), PW91P86-D3(0), PBEhPBE-D3(BJ)—where normal PBE exchange has been replaced by PBE-hole exchange—and XLYP-D3(BJ). The latter will be of importance in the next section.
ωB97X-V (WTMAD-1 = 1.45 kcal mol−1, WTMAD-2 = 3.03 kcal mol−1) is by far the best hybrid for intermolecular NCIs. We report a large gap between this and the second-best hybrid PW6B95-D3(BJ) (WTMAD-1 = 2.01 kcal mol−1, WTMAD-2 = 4.22 kcal mol−1 in Table 6). While M062X-D3(0) follows in third place in the WTMAD-1 ranking, it is very surprising to see BHLYP-D3(BJ) appear as third-best hybrid in the WTMAD-2 list. Unexpectedly, BHLYP-D3(BJ) gives the best MAD in three cases (RG18, ADIM6, and HAL59), while ωB97X-V is the best hybrid in only two instances (S66 and PNICO23). ωB97X-V's MAD for S66 is with 0.12 kcal mol−1 the best of all methods, even outperforming double hybrids—the best double hybrid is DSD-BLYP-D3(BJ) with an MAD of 0.17 kcal mol−1. If a user is unable to apply the nonlocal vdW correction, we recommend ωB97X-D3 as an alternative to ωB97X-V. It also gives the best MAD for two sets (S22 and AHB21). It also ranks fourth among WTMAD-1 results and fifth for WTMAD-2. Also noteworthy is the result for the IL16 set for ion pairs mimicking ionic liquids. B3LYP-NL is—together with HSE06-D3(BJ)—the best hybrid with an MAD of 0.31 kcal mol−1, which is significantly lower than the value of 0.76 kcal mol−1 for B3LYP-D3(BJ). Based on our WTMADs in the ESI,† we discourage from using the following hybrids: O3LYP-D3(BJ), TPSS1KCIS-D3(BJ), HSE03-D3(BJ), and BMK-D3(BJ).
The best three hybrids are competitive with the three double hybrids that have the largest WTMADs: MPW2PLYP-D3(BJ), B2GPPLYP-D3(BJ), and DSD-PBEP86-D3(BJ). That being said, those DFAs are still by far more accurate than the majority of the other DFAs. The best three double hybrids are listed in Table 6, and they are PWPB95-D3(BJ), B2PLYP-D3(BJ), and DSD-BLYP-D3(BJ) according to WTMAD-1 results, and B2PLYP-D3(BJ), DSD-PBEB95-D3(BJ) and DSD-BLYP-D3(BJ) according to the WTMAD-2 scheme.
Next, we investigate if these findings can also be transferred to intramolecular interactions.
The top-3 list of GGAs/NGAs is somewhat surprising, as both WTMAD schemes list XLYP-D3(BJ) as the best GGA, even though it was among the four worst methods for intermolecular interactions (Table 7). revPBE-D3(BJ) and B97-D3(BJ) follow closely, however, and should probably be preferred, as we will discuss in the next section.
| Rung | WTMAD-1 | WTMAD-2 |
|---|---|---|
| GGA/NGA | XLYP-D3(BJ) (4.06) | XLYP-D3(BJ) (7.42) |
| revPBE-D3(BJ) (4.10) | B97-D3(BJ) (7.84) | |
| B97-D3(BJ) (4.20) | revPBE-D3(BJ) (7.99) | |
| Meta-GGA/NGA | SCAN-D3(BJ) (3.61) | SCAN-D3(BJ) (6.61) |
| revTPSS-D3(BJ) (4.43) | revTPSS-D3(BJ) (7.06) | |
| TPSS-D3(BJ) (4.74) | TPSS-D3(BJ) (8.36) | |
| Hybrid | ωB97X-V (2.29) | ωB97X-V (3.62) |
| revTPSS0-D3(BJ) (2.69) | revTPSS0-D3(BJ) (4.77) | |
| B97-1-D3(BJ) (2.77) | B97-1-D3(BJ) (4.82) | |
| Double hybrid | DSD-BLYP-D3(BJ) (1.87) | DSD-BLYP-D3(BJ) (3.15) |
| B2GPPLYP-D3(BJ) (1.90) | B2GPPLYP-D3(BJ) (3.21) | |
| DSD-PBEP86-D3(BJ) (2.08) | DSD-PBEP86-D3(BJ) (3.46) | |
Averaged WTMAD-1 values for rung-3 DFAs are by 2 kcal mol−1 worse than for rung-2 ones. Closer inspection reveals that this is mostly due to the documented problem that double-counting effects of medium-range interactions can occur between a dispersion correction and the Minnesota meta-GGAs/NGAs due to their highly-parametrised nature and the way those parameters had been obtained (also see Fig. S1) (ESI†).7,43 Interestingly, MN15L-D3(0) gives the worst MAD in 5 cases. In Section 3.2, we observed how it was nearly unaffected by the dispersion correction. However, it seems that this does not mean that it is capable of describing dispersion effects accurately, as the errors are relatively high. This means that there seems to be an underlying problem with MN15L for these types of interaction. In fact, the worst two methods among meta-GGAs/NGAs are MN15L-D3(0) and MN12L-D3(0). The only meta-GGA that seems to be competitive with GGAs is SCAN-D3(BJ) with a WTMAD-1 value of 3.61 kcal mol−1, compared to the best GGA XLYP-D3(BJ) with a value of 4.06 kcal mol−1.
Averaged WTMADs demonstrate again that hybrids outperform the lower rungs, but that they are themselves outperformed by double hybrids. The best hybrid for these interactions is ωB97X-V, which gives the best MADs among all 83 tested DFAs for the ACONF and BUT14DIOL test sets with nearly perfect values of 0.03 and 0.04 kcal mol−1, respectively (ESI†). In our ranking of hybrids, this method is followed by two unexpected candidates, namely revTPSS0-D3(BJ) and B97-1-D3(BJ). We note that those methods are by far not common in quantum-chemical software and they do not perform particularly well in any of the previously discussed categories. The first conventional hybrids in the lists of WTMADs are B3LYP-D3(BJ) and BHLYP-D3(BJ). In fact, the WTMAD-2 list places the latter in fourth position together with ωB97X-D3. This comes again as a surprise and we are not aware that BHLYP-D3(BJ) has ever been recommended for, e.g., the calculation of conformational energies.
Among double hybrids, the DSD-type methods DSD-BLYP-D3(BJ) and DSD-PBEP86-D3(BJ) as well as the general-purpose double hybrid B2GPPLYP-D3(BJ) can be recommended, whereas DSD-PBEB95-D3(BJ) is ranked as the worst double hybrid (WTMAD-1 = 3.47 kcal mol−1, WTMAD-2 = 6.70 kcal mol−1) (ESI†).
Repeating the WTMAD analysis without the IDISP set, gives the same top-5 DFAs for each rung, which means that our recommendations above are also valid for the treatment of conformers only. In summary, the discussion of this section has revealed some surprises and differences between intra- and intermolecular noncovalent interactions and we will address these in the following section.
By doing so, we realise that OLYP-D3(BJ) seems to outperform other GGAs/NGAs based on our best-worst analysis; it gives the best MAD in 6 out of the 21 benchmark sets considered herein (Fig. 4f). In fact, it overall ranks as the third-best DFA in this class on the WTMAD-1 list (Table 8), while it is in fourth position in the WTMAD-2 ranking (see ESI†). Ultimately, however, the WTMADs also indicate that BLYP-D3(BJ), B97-D3(BJ), and revPBE-D3(BJ) can be used, which are the GGAs that we recommend for this category. Interestingly, those three methods were also among the best four GGAs that were recommended in the GMTKN30 study meaning that extending GMTKN30 and considering more methods did not alter the recommendations.7
| Rung | WTMAD-1 | WTMAD-2 |
|---|---|---|
| GGA/NGA | BLYP-D3(BJ) (3.70) | B97-D3(BJ) (6.87) |
| B97-D3(BJ) (3.75) | revPBE-D3(BJ) (7.07) | |
| OLYP-D3(BJ) (3.77) | BLYP-D3(BJ) (7.56) | |
| Meta-GGA/NGA | revTPSS-D3(BJ) (3.94) | revTPSS-D3(BJ) (6.88) |
| SCAN-D3(BJ) (4.06) | SCAN-D3(BJ) (7.58) | |
| TPSS-D3(BJ) (4.40) | TPSS-D3(BJ) (7.96) | |
| Hybrid | ωB97X-V (1.81) | ωB97X-V (3.32) |
| ωB97X-D3 (2.56) | BHLYP-D3(BJ) (4.66) | |
| PW6B95-D3(BJ) (2.56) | ωB97X-D3 (4.70) | |
| Double hybrid | DSD-BLYP-D3(BJ) (1.91) | DSD-BLYP-D3(BJ) (3.55) |
| B2PLYP-D3(BJ) (2.00) | B2GPPLYP-D3(BJ) (3.75) | |
| B2GPPLYP-D3(BJ) (2.05) | B2PLYP-D3(BJ) (3.78) | |
Again, the average WTMADs for GGAs/NGAs are smaller than for meta-GGAs/NGAs (Fig. 5). Particularly MN15L-D3(0) under-performs in this class and it gives the worst MAD in 11 out of the 21 cases. revTPSS-D3(BJ), on the other hand, is the best meta-GGA in 7 cases (Fig. 4f), followed by SCAN-D3(BJ) (5 cases). Nevertheless, their WTMADs are higher than those of the best three GGAs (Table 8). Thus, there is no overall advantage in using those for the treatment of NCI energies alone.
Again, we recommend to use DFAs of at least hybrid quality for this category. ωB97X-V clearly outperforms the other hybrids. It is the best hybrid in 5 cases and it also is the best in both WTMAD rankings of hybrids. It is more accurate than ωB97X-D3, which however is a worthwhile alternative. Among the conventional global hybrids we identify PW6B95-D3(BJ) and, surprisingly, BHLYP-D3(BJ) as good methods. The best Minnesota DFA for noncovalent interactions is M052X-D3(0), which ranks in fourth position. None of the newer developments can be recommended; for instance, the best post-2008 Minnesota DFAs are N12SX-D3(BJ) and MN15-D3(BJ), which hover around the 30th place in both WTMAD schemes (ESI†). MN12SX -D3(BJ) is one of the worst-ranking DFAs (see ESI†). We also note that the APFD approach, which had been recommended as an alternative to DFT-D3 and other dispersion corrections, cannot compete with them at all. It ranks 41st on the WTMAD-1 and 27th on the WTMAD-2 list.
Ultimately, double hybrids are to be preferred for the treatment of NCI problems. The average WTMAD-1 value, for instance, improves from 3.95 to 2.18 kcal mol−1 when compared to hybrids (Fig. 5). For this DFA class, we particularly recommend the DSD-BLYP-D3(BJ), B2PLYP-D3(BJ), and B2GPPLYP-D3(BJ) approaches (Table 8).
Fig. 6 shows our best-worst perspective for each of the considered rungs on Jacob's Ladder across all test sets. Among the second rung, OLYP-D3(BJ) gives the best MADs in most of the cases, followed by B97-D3(BJ), revPBE-D3(BJ) and RPBE-D3(BJ). N12-D3(0) gives the best MAD in 5 cases, but also fails for the same number of test sets. Usage of OPBE-D3(BJ), PW91P86-D3(0), and HCTH/407-D3(BJ) should be avoided, as they each provide the worst MADs in 9 to 13 cases. Among the third rung, SCAN-D3(BJ) distinguishes itself from all other DFAs, as it gives the best MAD in 11 cases. MN15L-D3(0) does not seem to be overly robust. While it gives the best MAD 7 times, it also gives the worst in 11 cases. We also discourage from using PKZB-D3(0) and τHCTH-D3(BJ). Among the hybrids, ωB97X-V and PW6B95-D3(BJ) are noteworthy. They never give the worst MAD and instead offer the best outcome in 8 or 7 cases, respectively. While BHLYP-D3(BJ) seems to be surprisingly accurate for NCIs, we also note that it is less robust than the previously mentioned two methods, as it gives the worst MAD in 3 cases. O3LYP-D3(BJ) is the worst of the assessed hybrids, and it gives the highest MAD in 13 cases. Among the double hybrids, DSD-PBEP86-D3(BJ) and DSD-BLYP-D3(BJ) seem to be the most robust, while the statistics for DSD-PBEB95-D3(BJ) suffer from its disappointing performance for NCIs (best MAD in 13 cases, and worst in 9). The first-generation double hybrids B2PLYP-D3(BJ), and MPW2PLYP-D3(BJ) seem to be less accurate than the others, reflecting the progress that has been achieved in this field since their introduction. However, when comparing all 83 DFAs simultaneously, double hybrids never give the worst MAD (Fig. S4) (ESI†).
Next, we will verify if similar conclusions can be drawn from WTMADs. First of all, we confirm again that our results presented herein reproduce the Jacobs's Ladder scheme, indicating that GMTKN55 is indeed a good representative of contemporary chemical problems. The averaged WTMAD-1 for GGAs/NGAs is 5.76 kcal mol−1, which is closely followed by a value of 5.62 kcal mol−1 for meta-GGAs/NGAs (Fig. 5). This is followed by a large reduction to 3.87 kcal mol−1 for hybrids and further improvement to 2.05 kcal mol−1 for double hybrids. The WTMAD-2 data reflect the same trend.
In the previous categories, we saw that, overall, the WTMAD-1 and WTMAD-2 schemes agreed on the best DFAs, but that they differed in functional order. Sometimes a method that was ranked as third best, may have been described as only the fourth or fifth best. However, when carrying out a comprehensive analysis of the entire set, both schemes provide the same top 3 for each DFA rung (Table 9). Fig. 7a shows a histogram for all 83 WTMAD-2 values assigned to bins of 1 kcal mol−1 width that shows an approximate normal-distribution behaviour. Such behaviour is even more pronounced when histograms are separately drawn for hybrid and GGA/NGA DFAs (Fig. 7b). Fig. 8 provides a graphical overview of all WTMAD-2 values, with the red bars indicating the best-performing DFAs for each rung; their actual numbers are shown in Table 9, where they are also compared with WTMAD-1 results. A figure similar to Fig. 8, but based on WTMAD-1, is shown in the ESI.† The overall order of the 83 dispersion-corrected DFAs barely changes when comparing the two different schemes. This indicates the reliability of the WTMADs introduced in this work.
| Rung | WTMAD-1 | WTMAD-2 |
|---|---|---|
| GGA/NGA | revPBE-D3(BJ) (4.66) | revPBE-D3(BJ) (8.27) |
| OLYP-D3(BJ) (4.75) | B97-D3(BJ) (8.55) | |
| B97-D3(BJ) (4.92) | OLYP-D3(BJ) (8.71) | |
| Meta-GGA/NGA | SCAN-D3(BJ) (4.67) | SCAN-D3(BJ) (7.86) |
| revTPSS-D3(BJ) (4.69) | revTPSS-D3(BJ) (8.50) | |
| M06L-D3(0) (4.86) | M06L-D3(0) (8.61) | |
| Hybrid | ωB97X-V (2.32) | ωB97X-V (3.98) |
| ωB97X-D3 (2.71) | M052X-D3(0) (4.61) | |
| M052X-D3(0) (2.73) | ωB97X-D3 (4.77) | |
| Double hybrid | DSD-PBEP86-D3(BJ) (1.80) | DSD-BLYP-D3(BJ) (3.08) |
| DSD-BLYP-D3(BJ) (1.81) | DSD-PBEP86-D3(BJ) (3.14) | |
| B2GPPLYP-D3(BJ) (1.95) | B2GPPLYP-D3(BJ) (3.26) | |
 | ||
| Fig. 7 Histograms (1 kcal mol−1 bins) showing the WTMAD-2 distributions for all 83 dispersion-corrected DFAs (a) and for each rung of Jacob's Ladder (b). | ||
The results presented in Fig. 8 and Table 9 present our final recommendations. The best DFA of the entire study is DSD-BLYP-D3(BJ) (WTMAD-2 = 3.08 kcal mol−1), closely followed by DSD-PBEP86-D3(BJ) (3.14 kcal mol−1), and B2GPPLYP-D3(BJ) (3.26 kcal mol−1). Note that in the case of WTMAD-1, the two DSD methods share the nearly same value (1.80–1.81 kcal mol−1). This recommendation closely resembles the previous result for GMTKN30, with the only difference that DSD-PBEB95-D3(BJ) shared the same WTMAD as the other two DSD methods.29 Overall, any of the tested double hybrids should be preferred over most hybrids, with the only exception being the best hybrid ωB97X-V, which has a slightly better performance than the first-generation MPW2PLYP-D3(BJ) double hybrid (WTMAD-2 = 3.98 vs. 4.08 kcal mol−1) (ESI†).
The second- and third-best hybrids are M052X-D3(0) and ωB97X-D3, but with WTMAD-2 values that are by 0.6–08 kcal mol−1 higher than for ωB97X-V (Table 9). In Fig. 8, it is shown how ωB97X-D3 is followed by M062X-D3(0) and M08HX-D3(0). Next follows the first conventional hybrid PW6B95-D3(BJ), which is neither range-separated nor does it depend on a large number of parameters; even ωB97X-V has 10 empirical parameters, which is 4 more than the PW6B95 exchange-correlation DFA. While the Minnesota DFAs perform very well for thermochemistry, we also have to take into account that the treatment of NCIs with them can be difficult. PW6B95-D3(BJ) may therefore be a more robust alternative with WTMAD-1 = 2.93 kcal mol−1 and WTMAD-2 = 5.50 kcal mol−1.
The results for hybrids so far share resemblance with the recommendations for GMTKN30 made in 2011. Then, M062X-D3(0) was the best hybrid, followed by M052X-D3(0) and PW6B95-D3(0) as the best conventional, global hybrid. The older ωB97X-D, which was based on the DFT-D2 correction, followed. Considering that DFT-D2 has been replaced with DFT-D3 or the VV10 kernel, it is no surprise that ωB97X-V and ωB97X-D3 outperform the other methods, and overall we can reconfirm our initial recommendations from 2011. This is particularly noteworthy, as both the composition of the database and the way we calculate WTMADs have changed. Our results for hybrids are also noteworthy as it seems that none of the developments made on the Minnesota DFAs after 2008 reflect an overall improvement for main-group thermochemistry, when considering a large-enough database. Among those newer methods, MN15-D3(BJ) ranks the highest, however, it is only in tenth position among the hybrids. N12-SX-D3(0) ranks among the ten worst-performing hybrids.
B3LYP-D3(BJ) ranks only as the 18th-best hybrid in the WMTAD-2 scheme, followed closely by PBE0-D3(BJ) (20th). X3LYP-D3(BJ), which has been promoted as one of the best hybrids,166,230 only ranks in 33rd position (WTMAD-2 = 7.28 kcal mol−1). Note that this value increases to 14.07 kcal mol−1 when the dispersion correction is discarded, and we do not see any evidence that supports claims made in favour of X3LYP.166,230 The worst assessed hybrid is O3LYP-D3(BJ); with a WTMAD-2 of 10.72 kcal mol−1 it is worse than the best (meta-)GGAs/NGAs.
For rung 3, we recommend SCAN-D3(BJ) (WTMAD-2 = 7.86) followed by revTPSS-D3(BJ) (WTMAD-2 = 8.50 kcal mol−1) and M06L-D3(0) (WTMAD = 8.61 kcal mol−1). For this rung, we observe the biggest change compared to previous recommendations, but that is mostly because in 2011 the GMTKN30 study only considered three meta-GGAs. The worst method on this rung is τHCTH-D3(BJ) with a WTMAD-2 value of 12.59 kcal mol−1. When comparing the best meta-GGAs with the best GGAs, however, we note that only SCAN-D3(BJ) is noteworthy, as the best GGA revPBE-D3(BJ) has a lower WTMAD-2 result than revTPSS-D3(BJ) (8.27 kcal mol−1). revPBE-D3(BJ) is followed by B97-D3(BJ) and OLYP-D3(BJ) in the list of best GGAs (Fig. 6).
Our final WTMAD-based recommendations are further backed up by the fact that they closely resemble our conclusions drawn earlier based on counting the number of best and worst MADs. We are, therefore, confident about the validity of our conclusions.
6 Summary and conclusions
We have presented the GMTKN55 benchmark database for general main group thermochemistry, kinetics and noncovalent interactions, which is an updated and extended version of its predecessor GMTKN30. Compared to GMTKN30, it allows assessment of a larger variety of chemical problems with 55 test sets in total, 13 of which were presented here for the first time. It involves 2462 single-point calculations that are combined to 1505 relative energies, for most of which we presented new, higher-quality reference values. Indeed, we demonstrated how those newer reference values may change the outcome of a density functional approximation (DFA) ranking when compared with values of lower quality. We therefore recommend adopting the reference values herein. They can be conveniently accessed from a dedicated website that also made all geometries available for download and provides all reported data.112Once again, we were able to demonstrate the importance of London dispersion in thermochemical problems and we re-emphasised the necessity of using (mostly long-range) dispersion corrections in conjunction with DFAs, even in applications that go beyond the determination of noncovalent interaction (NCI) energies. Our work also joins others that disproved the common perception that one can include London-dispersion effects into a DFA lacking nonlocal correlation terms by mere empirical parametrisation. In particular, we showed how the popular Minnesota class of DFAs benefits from dispersion corrections, also for systems in their equilibrium geometries where the electron clouds of two interacting fragments can overlap, contrary to claims in the literature.19 However, those DFAs turned out to be less robust for the treatment of NCIs and ultimately the user fares better with using conventional DFAs corrected either with an additive dispersion correction, such as DFT-D3, or a nonlocal van der Waals kernel, such as in VV10 or ωB97X-V.
To demonstrate the benefits of the new GMTKN55 database, we conducted a comprehensive benchmark study of DFAs belonging to the four highest rungs on Jacob's Ladder. Contrary to other studies on large benchmark databases,19,22 it was particularly important for us to base all assessed DFAs on an equal footing and we discussed only dispersion-corrected results. For this purpose, we determined and presented new parameters for the DFT-D3 dispersion correction for 35 DFAs.
We carried out a detailed study of DFAs, with numerical quadrature grids that are used in common applications and a large basis set to eliminate artificial AO basis-set related error-compensation effects to show a DFA's “true performance”. In total, we assessed 217 variations of dispersion-corrected and -uncorrected DFAs, and then carried out a detailed analysis of 83 of them to identify robust and reliable approaches: 19 GGAs or NGAs (rung 2 of Jacob's Ladder), nine meta-GGAs/NGAs (rung 3), 48 hybrids (rung 4), and seven double hybrids (rung 5).
We divided the test sets of GMTKN55 into four main categories that we first discussed separately to identify DFAs for specific applications: basic properties and reactions of small systems, isomerisation reactions and reactions of large systems, barrier heights, and NCIs. The latter was further divided into a part dealing with intermolecular interactions, and a second part comprising intramolecular interactions.
Subsequently, we carried out a comprehensive analysis of all combined 55 sets, for which we confirmed the Jacob's Ladder scheme with higher-rung methods being more accurate. This comprehensive analysis is valuable for future real-life applications, which may touch more than one of our four categories of GMTKN55. Our final recommendations for robust, reliable and accurate DFAs are:
• Rung 2: revPBE-D3(BJ), followed by B97-D3(BJ), and OLYP-D3(BJ). If NCIs are the main area of interest, BLYP-D3(BJ) can also be used.
• Rung 3: SCAN-D3(BJ), revTPSS-D3(BJ), and M06L-D3(0). However, SCAN-D3(BJ) is the only meta-GGA studied herein that is not outperformed by the best GGAs. Note that our study focussed on energy differences for main-group molecules, and that meta-GGAs may be better than GGAs for bond lengths or main-group solids.
• Rung 4: ωB97X-V, M052X-D3(0), and ωB97X-D3. Note that while thermochemical properties are well described by the Minnesota DFA M052X-D3(0), the treatment of NCIs can pose a problem. For users that cannot apply these three methods for technical reasons, we recommend the global hybrid PW6B95-D3(BJ).
• Rung 5: DSD-BLYP-D3(BJ), DSD-PBEP86-D3(BJ), and B2GPPLYP-D3(BJ). In general, double hybrids should be the method of choice and one should refer to lower DFA rungs only if the application of double hybrids is not feasible. On modern computer architectures and with efficient implementations of the MP2 approach, double-hybrid calculations can be carried out routinely on large systems. Note that if none of the recommended double hybrids are feasible, the PWPB95-D3(BJ) method could be applied in conjunction with a Laplace transform231 approach that brings down the formal scaling behaviour.24 PWPB95-D3(BJ) was previously also shown to provide good results with triple-ζ AO basis sets that are statistically very similar to quadruple-ζ ones.7
Popular approaches, such as B3LYP, PBE0, X3LYP, BP86, PBE, and TPSS, exhibit average performance and we do not see any reasons to recommend them, despite the fact that they are available in every major molecular quantum-chemistry code. In fact, it seems that many DFAs in common programs have become obsolete for the treatment of main-group thermochemistry. Finally, it is particularly noteworthy that the majority of our recommendations are not reflected by the annual “DFT poll”.232 Based on the results of the previous year, the current 2017 poll only features five of the herein recommended DFAs in its list of the 20 most popular methods: revPBE, OLYP, M062X, B97-D2, and B2PLYP, i.e., without or with older dispersion corrections. On the other hand, DFAs made the top-20 that did not perform well for GMTKN55: B3LYP, B3LYP-D2, BP86, HSE06, PBE, PBE0, PW91, and TPSSh.232 When comparing that list with our analysis, one comes to the conclusion that popularity does not imply accuracy. With our study, we would like to inspire a change in the user's perception of DFT-based methods. This can be better achieved if more of the recommended methods are accessible to a broader community, which is why we would like to encourage program developers to implement the recommended approaches.
However, it should also be noted that the DFA assessment problem becomes even more complex when transition-metal containing systems are considered for which in particular rung-2 or rung-3 methods are viable alternatives to the higher-rung methods. The setup of a reliable benchmark of similar quality and extension as GMTKN55 for transition-metal complexes is currently not possible in our opinion, but encouraging steps in this direction were published recently.233,234
We are aware that the “zoo” of DFT-based methods is large and continues to grow. While we could not consider every possible DFA in this study,235–237 we are confident that we have provided a valuable starting point for future studies that would also assess those. Our two newly introduced schemes to represent a DFA's robustness and accuracy with one number (weighted total mean absolute deviation) allowed us to provide a comprehensive ranking of methods and we challenge method developers to identify new approaches that yield lower WTMAD-1/2 values. Work in our groups is also currently pointing into that direction including accuracy-competitive low-cost approaches.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We are in debt to Asst. Prof. Amir Karton for generously providing us with some of his Wn-F12 reference values and for insightful discussions on the Weizmann composite protocols. We thank Prof. Jan Martin for providing us with a reference value for the 27th reaction in the WATER27 set. We are also grateful to Prof. Donald G. Truhlar for providing us with the molecular geometries of the YBDE18 set. We kindly thank Jakob Seibert for creating the TOC graphic of the article, Christoph Bannwarth for fruitful discussions, and Prof. John Perdew for useful feedback on this study. LG acknowledges funding through an Australian Research Council Discovery Early Career Researcher Award (project ID: DE140100550) and allocation of generous computing resources by the Victorian Life Science Computation Initiative/Melbourne Bioinformatics (project ID: RA0005) and by the National Computational Infrastructure (NCI) National Facility within the National Computational Merit Allocation Scheme (project ID: fk5). This work was also funded by the Deutsche Forschungsgemeinschaft in the framework of the “Gottfried Wilhelm Leibniz-Preis” to SG. AN acknowledges an Australian Government Research Training Program Scholarship and a Melbourne Research Scholarship.References
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- A. D. Becke, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- L. A. Curtiss, K. Raghavachari, G. W. Trucks and J. A. Pople, J. Chem. Phys., 1991, 94, 7221–7230 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764–7776 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2005, 123, 124107 CrossRef PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- A. Karton, S. Daon, J. M. L. Martin and B. Ruscic, Chem. Phys. Lett., 2011, 510, 165–178 CrossRef CAS.
- J. T. Margraf, D. S. Ranasinghe and R. J. Bartlett, Phys. Chem. Chem. Phys., 2017, 19, 9798–9805 RSC.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 17, 43–52 RSC.
- Y. Zhao, N. González-García and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 2012–2018 CrossRef CAS PubMed.
- S. Grimme, M. Steinmetz and M. Korth, J. Org. Chem., 2007, 72, 2118–2126 CrossRef CAS PubMed.
- P. Jurečka, J. Sponer, J. Cerny and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- J. Rezac, P. Jurecka, K. E. Riley, J. Cerny, H. Valdes, K. Pluhackova, K. Berka, T. Rezac, M. Pitonak, J. Vondrasek and P. Hobza, Collect. Czech. Chem. Commun., 2008, 73, 1261–1270 CrossRef CAS.
- M. Korth and S. Grimme, J. Chem. Theory Comput., 2009, 5, 993–1003 CrossRef CAS PubMed.
- B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 8996–8999 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 415–432 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- R. Peverati and D. G. Truhlar, Philos. Trans. R. Soc., A, 2014, 372, 20120476 CrossRef PubMed.
- H. S. Yu, W. Zhang, P. Verma, X. He and D. G. Truhlar, Phys. Chem. Chem. Phys., 2015, 17, 12146–12160 RSC.
- H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293 CrossRef CAS PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2010, 6, 107–126 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Theory Comput., 2016, 12, 4303–4325 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef.
- R. Peverati and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 2310–2319 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- L. Goerigk and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 576–600 CrossRef CAS.
- S. Kozuch, D. Gruzman and J. M. L. Martin, J. Phys. Chem. C, 2010, 114, 20801–20808 CAS.
- S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107 RSC.
- S. Kozuch and J. M. L. Martin, J. Comput. Chem., 2013, 34, 2327–2344 CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- L. Goerigk, H. Kruse and S. Grimme, ChemPhysChem, 2011, 12, 3421–3433 CrossRef CAS PubMed.
- L. Goerigk, J. Phys. Chem. Lett., 2015, 6, 3891–3896 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- H. Eshuis and F. Furche, J. Phys. Chem. Lett., 2011, 2, 983–989 CrossRef CAS.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS PubMed.
- M. Korth and W. Thiel, J. Chem. Theory Comput., 2011, 7, 2929–2936 CrossRef CAS PubMed.
- H. Kruse, L. Goerigk and S. Grimme, J. Org. Chem., 2012, 77, 10824–10834 CrossRef CAS PubMed.
- D. Bousquet, E. Bremond, J. C. Sancho-Garcia, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2013, 9, 3444–3452 CrossRef CAS PubMed.
- L. Goerigk, J. Chem. Theory Comput., 2014, 10, 968–980 CrossRef CAS PubMed.
- B. Chan, L. Goerigk and L. Radom, J. Comput. Chem., 2016, 37, 183–193 CrossRef CAS PubMed.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS.
- J. A. Montgomery Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542 CrossRef.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2012, 136, 124114 CrossRef PubMed.
- A. Karton and L. Goerigk, J. Comput. Chem., 2015, 36, 622–632 CrossRef CAS PubMed.
- A. Karton, A. Tarnopolsky, J. F. Lamere, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886 CrossRef CAS PubMed.
- S. Parthiban and J. M. L. Martin, J. Chem. Phys., 2001, 114, 6014–6029 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 10478–10486 CrossRef CAS PubMed.
- H. Yu and D. G. Truhlar, J. Chem. Theory Comput., 2015, 11, 2968–2983 CrossRef CAS PubMed.
- Y. Zhao, H. T. Ng, R. Peverati and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 2824–2834 CrossRef CAS PubMed.
- S. Grimme, H. Kruse, L. Goerigk and G. Erker, Angew. Chem., Int. Ed., 2010, 49, 1402–1405 CrossRef CAS PubMed.
- A. Karton, private communication.
- J. Friedrich and J. Hänchen, J. Chem. Theory Comput., 2013, 9, 5381–5394 CrossRef CAS PubMed.
- J. Friedrich, J. Chem. Theory Comput., 2015, 11, 3596–3609 CrossRef CAS PubMed.
- S. Grimme, C. Mück-Lichtenfeld, E.-U. Würthwein, A. W. Ehlers, T. P. M. Goumans and K. Lammertsma, J. Phys. Chem. A, 2006, 110, 2583–2586 CrossRef CAS PubMed.
- M. Piacenza and S. Grimme, J. Comput. Chem., 2004, 25, 83–99 CrossRef CAS PubMed.
- H. L. Woodcock, H. F. Schaefer III and P. R. Schreiner, J. Phys. Chem. A, 2002, 106, 11923–11931 CrossRef CAS.
- P. R. Schreiner, A. A. Fokin, R. A. Pascal and A. de Meijere, Org. Lett., 2006, 8, 3635–3638 CrossRef CAS PubMed.
- C. Lepetit, H. Chermette, M. Gicquel, J.-L. Heully and R. Chauvin, J. Phys. Chem. A, 2007, 111, 136–149 CrossRef CAS PubMed.
- J. S. Lee, J. Phys. Chem. A, 2005, 109, 11927–11932 CrossRef CAS PubMed.
- A. Karton and J. M. Martin, Mol. Phys., 2012, 110, 2477–2491 CrossRef CAS.
- Y. Zhao, O. Tishchenko, J. R. Gour, W. Li, J. J. Lutz, P. Piecuch and D. Truhlar, J. Phys. Chem. A, 2009, 113, 5786–5799 CrossRef CAS PubMed.
- D. Manna and J. M. L. Martin, J. Phys. Chem. A, 2016, 120, 153–160 CrossRef CAS PubMed.
- E. R. Johnson, P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2008, 129, 204112 CrossRef PubMed.
- F. Neese, T. Schwabe, S. Kossmann, B. Schirmer and S. Grimme, J. Chem. Theory Comput., 2009, 5, 3060–3073 CrossRef CAS PubMed.
- S. N. Steinmann, G. Csonka and C. Carminboeuf, J. Chem. Theory Comput., 2009, 5, 2950–2958 CrossRef CAS PubMed.
- H. Krieg and S. Grimme, Mol. Phys., 2010, 108, 2655–2666 CrossRef CAS.
- L.-J. Yu and A. Karton, Chem. Phys., 2014, 441, 166–177 CrossRef CAS.
- R. Huenerbein, B. Schirmer, J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2010, 12, 6940–6948 RSC.
- R. Sure, A. Hansen, P. Schwerdtfeger and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 14296–14305 RSC.
- V. Guner, K. S. Khuong, A. G. Leach, P. S. Lee, M. D. Bartberger and K. N. Houk, J. Phys. Chem. A, 2003, 107, 11445–11459 CrossRef CAS.
- D. H. Ess and K. N. Houk, J. Phys. Chem. A, 2005, 109, 9542–9553 CrossRef CAS PubMed.
- T. C. Dinadayalane, R. Vijaya, A. Smitha and G. N. Sastry, J. Phys. Chem. A, 2002, 106, 1627–1633 CrossRef CAS.
- L. Goerigk and R. Sharma, Can. J. Chem., 2016, 94, 1133–1143 CrossRef CAS.
- A. Karton, R. J. O'Reilly, B. Chan and L. Radom, J. Chem. Theory Comput., 2012, 8, 3128–3136 CrossRef CAS PubMed.
- A. Karton, R. J. O’Reilly and L. Radom, J. Phys. Chem. A, 2012, 116, 4211–4221 CrossRef CAS PubMed.
- M. S. Marshall, L. A. Burns and C. D. Sherrill, J. Chem. Phys., 2011, 135, 194102 CrossRef PubMed.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef PubMed.
- V. S. Bryantsev, M. S. Diallo, A. C. T. van Duin and W. A. Goddard III, J. Chem. Theory Comput., 2009, 5, 1016–1026 CrossRef CAS PubMed.
- D. Manna, M. K. Kesharwani, N. Sylvetsky and J. M. L. Martin, J. Chem. Theory Comput., 2017, 13, 3136–3152 CrossRef CAS PubMed.
- D. Setiawan, E. Kraka and D. Cremer, J. Phys. Chem. A, 2015, 119, 1642–1656 CrossRef CAS PubMed.
- S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918–1931 CrossRef CAS PubMed.
- J. Rezac, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2012, 8, 4285–4292 CrossRef CAS PubMed.
- K. U. Lao, R. Schäffer, G. Jansen and J. M. Herbert, J. Chem. Theory Comput., 2015, 11, 2473–2486 CrossRef CAS PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406 RSC.
- S. Grimme, Angew. Chem., Int. Ed., 2006, 45, 4460–4464 CrossRef CAS PubMed.
- D. Gruzman, A. Karton and J. M. L. Martin, J. Phys. Chem. A, 2009, 113, 11974–11983 CrossRef CAS PubMed.
- M. K. Kesharwani, A. Karton and J. M. L. Martin, J. Chem. Theory Comput., 2016, 12, 444–454 CrossRef CAS PubMed.
- J. J. Wilke, M. C. Lind, H. F. Schaefer III, A. G. Császár and W. D. Allen, J. Chem. Theory Comput., 2009, 5, 1511–1523 CrossRef CAS PubMed.
- D. Řeha, H. Valdes, J. Vondrasek, P. Hobza, A. Abu-Riziq, B. Crews and M. S. de Vries, Chem. – Eur. J., 2005, 11, 6803–6817 CrossRef PubMed.
- L. Goerigk, A. Karton, J. M. L. Martin and L. Radom, Phys. Chem. Chem. Phys., 2013, 15, 7028–7031 RSC.
- U. R. Fogueri, S. Kozuch, A. Karton and J. M. L. Martin, J. Phys. Chem. A, 2013, 117, 2269–2277 CrossRef CAS PubMed.
- G. I. Csonka, A. D. French, G. P. Johnson and C. A. Stortz, J. Chem. Theory Comput., 2009, 5, 679–692 CrossRef CAS PubMed.
- H. Kruse, A. Mladek, K. Gkionis, A. Hansen, S. Grimme and J. Sponer, J. Chem. Theory Comput., 2015, 11, 4972–4991 CrossRef CAS PubMed.
- S. Kozuch, S. M. Bachrach and J. M. Martin, J. Phys. Chem. A, 2014, 118, 293–303 CrossRef CAS PubMed.
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- J. M. L. Martin and S. Parthiban, in Quantum-Mechanical Prediction of Thermochemical Data, ed. J. Cioslowski, Kluwer, Dordrecht, 2001, pp. 31–65 Search PubMed.
- http://www.thch.uni-bonn.de/GMTKN55 .
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116 CrossRef PubMed.
- B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning, Jr and A. K. Wilson, Theor. Chem. Acc., 2011, 128, 69–82 CrossRef CAS.
- S. Grimme, Angew. Chem., Int. Ed., 2013, 52, 6306–6312 CrossRef CAS PubMed.
- T. Risthaus, M. Steinmetz and S. Grimme, J. Comput. Chem., 2014, 35, 1509–1516 CrossRef CAS PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2003, 24, 1529 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- A. Klamt and G. Schürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- T. Takatani, E. G. Hohenstein, M. Malagoli, M. S. Marshall and C. D. Sherrill, J. Chem. Phys., 2010, 132, 144104 CrossRef PubMed.
- J. M. L. Martin, private communication.
- S. Zahn, D. R. MacFarlane and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2013, 15, 13664–13675 RSC.
- Y. Yuan, M. J. L. Mills, P. L. A. Popelier and F. Jensen, J. Phys. Chem. A, 2014, 118, 7876–7891 CrossRef CAS PubMed.
- J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1951, 81, 385–390 CrossRef CAS.
- S. J. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- M. Swart, M. Solà and F. M. Bickelhaupt, J. Chem. Phys., 2009, 131, 094103 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2007, 110, 13126–13130 CrossRef PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- A. D. Boese and N. C. Handy, J. Chem. Phys., 2001, 114, 5497–5503 CrossRef CAS.
- M. Ernzerhof and J. P. Perdew, J. Chem. Phys., 1998, 109, 3313–3320 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- T. V. Voorhis and G. E. Scuseria, J. Chem. Phys., 1998, 109, 400–410 CrossRef.
- R. Peverati, Y. Zhao and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 1991–1997 CrossRef CAS.
- P. M. W. Gill, Mol. Phys., 1996, 89, 433–445 CrossRef CAS.
- J. P. Perdew, in Proceedings of the 21st Annual International Symposium on the Electronic Structure ofSolids, ed. P. Ziesche and H. Eschrig, Akademie Verlag, Berlin, 1991, p. 11 Search PubMed.
- B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- J. R. Reimers, D. Panduwinata, J. Visser, Y. Chin, C. Tang, L. Goerigk, M. J. Ford, M. Sintic, T.-J. Sum, M. J. J. Coenen, B. L. M. Hendriksen, J. A. A. W. Elemans, N. S. Hush and M. J. Crossley, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E6101–E6110 CrossRef CAS PubMed.
- X. Xu and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677 CrossRef CAS PubMed.
- W.-M. How, A. J. Cohen and N. C. Handy, Chem. Phys. Lett., 2001, 341, 319 CrossRef.
- F. A. Hamprecht, A. J. Cohen, D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 6264–6271 CrossRef CAS.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- P. J. Wilson, T. J. Bradley and D. J. Tozer, J. Chem. Phys., 2001, 115, 9233–9242 CrossRef CAS.
- H. L. Schmider and A. D. Becke, J. Chem. Phys., 1998, 108, 9624–9631 CrossRef CAS.
- T. M. Henderson, A. F. Izmaylov, G. E. Scuseria and A. Savin, J. Chem. Theory Comput., 2008, 4, 1254–1262 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621 CAS.
- E. D. Murray, K. Lee and D. C. Langreth, J. Chem. Theory Comput., 2009, 5, 2754–2762 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403 CrossRef PubMed.
- S. Grimme, J. Phys. Chem. A, 2005, 109, 3067–3077 CrossRef CAS PubMed.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 43–52 RSC.
- A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416 CrossRef CAS PubMed.
- A. D. Boese and N. C. Handy, J. Chem. Phys., 2002, 116, 9559–9569 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Phys., 2005, 123, 161103 CrossRef PubMed.
- J. P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett., 1999, 82, 2544–2547 CrossRef CAS.
- J. G. Brandenburg, J. E. Bates, J. Sun and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 115144 CrossRef.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- R. Peverati and D. G. Truhlar, J. Chem. Phys., 2011, 135, 191102 CrossRef PubMed.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 117–124 CrossRef CAS.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 16187–16191 RSC.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 13171–13174 RSC.
- T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, J. Chem. Phys., 2009, 131, 044108 CrossRef PubMed.
- A. Austin, G. A. Petersson, M. J. Frisch, F. J. Dobek, G. Scalmani and K. Throssell, J. Chem. Theory Comput., 2012, 8, 4989–5007 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046 CrossRef CAS.
- S. Grimme and T. Schwabe, Phys. Chem. Chem. Phys., 2006, 8, 4398–4401 RSC.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- ORCA – an ab initio, density functional and semiempirical program package, V. 4.0.0, F. Neese, MPI für Chemische Energiekonversion, Mülheim A. D. Ruhr, Germany, 2017.
- TURBOMOLE, V7. 1.1, 2016, developed by University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, available from http://www.turbomole.com.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Peterssonet al., Gaussian 09 Revisions D.01 and E.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Peterssonet al., Gaussian 16 Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- L. Gráfová, M. Pitoák, J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2010, 6, 2365–2376 CrossRef PubMed.
- D. E. Taylor, J. G. Ángyán, G. Galli, C. Zhang, F. Gygi, K. Hirao, J. W. Song, K. Rahul, O. A. von Lilienfeld, R. Podeszwa, I. W. Bulik, T. M. Henderson, G. E. Scuseria, J. Toulouse, R. Peverati, D. G. Truhlar and K. Szalewicz, J. Chem. Phys., 2016, 145, 124105 CrossRef PubMed.
- D. G. A. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, J. Phys. Chem. Lett., 2016, 7, 2197–2203 CrossRef CAS PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 CrossRef CAS.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- E. R. Johnson, A. Becke, C. D. Sherrill and G. A. DiLabio, J. Chem. Phys., 2009, 131, 034111 CrossRef PubMed.
- L. Fusti-Molnar, X. He, B. Wang and K. M. Merz Jr., J. Chem. Phys., 2009, 131, 065102 CrossRef PubMed.
- C. A. Jiménez-Hoyos, B. G. Janesko and G. E. Scuseria, Phys. Chem. Chem. Phys., 2008, 10, 6621–6629 RSC.
- S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2010, 6, 395–404 CrossRef CAS PubMed.
- R. Izsak and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- T. Schwabe, J. Phys. Chem. A, 2013, 117, 2879–2883 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schützet al., MOLPRO, version 2015.1, a package of ab initio programs, 2015, see http://www.molpro.net Search PubMed.
- C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102 CrossRef PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- S. Grimme and P. R. S. Schreiner, Angew. Chem., Int. Ed., 2011, 50, 12639–12642 CrossRef CAS PubMed.
- S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031–16042 RSC.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2013, 9, 308–315 CrossRef CAS PubMed.
- L. Goerigk and J. R. Reimers, J. Chem. Theory Comput., 2013, 9, 3240–3251 CrossRef CAS PubMed.
- L. Goerigk, C. A. Collyer and J. R. Reimers, J. Phys. Chem. B, 2014, 118, 14612–14626 CrossRef CAS PubMed.
- S. Rösel, H. Quanz, C. Logemann, J. Becker, E. Mossou, L. Cañadillas-Delgado, E. Caldeweyher, S. Grimme and P. R. Schreiner, J. Am. Chem. Soc., 2017, 139, 7428–7431 CrossRef PubMed.
- S. Grimme, R. Huenerbein and S. Ehrlich, ChemPhysChem, 2011, 12, 1258–1261 CrossRef CAS PubMed.
- S. Zheng, S. Xu, G. Wang, Q. Tang, X. Jiang, Z. Li, Y. Xu, R. Wang and F. Lin, J. Chem. Inf. Model., 2017, 57, 1535–1547 CrossRef CAS PubMed.
- J. Almlöf, Chem. Phys. Lett., 1991, 181, 319–320 CrossRef.
- DFT Poll 2017 organised by M. Swart, M. Bickelhaupt and M. Duran, see http://www.marcelswart.eu/dft-poll/2017.html#start.
- J. Wang, L. Liu and A. K. Wilson, J. Phys. Chem. A, 2016, 120, 737–746 CrossRef CAS PubMed.
- P. Verma, Z. Varga, J. E. M. N. Klein, C. J. Cramer, L. Que and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 13049–13069 RSC.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- The B97M-V and ωB97M-V DFAs were technically not available to us at the time of this study, but results for them will be presented in the near future.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on the new MB16-43 set. Damping parameters for the DFT-D3 dispersion correction. Comparison between the new and old reference values for ALX6. Dispersion-corrected vs. -uncorrected results. Analysis of best and worst MAD/RMSD. Weighted total mean absolute deviations. Statistical results for all test sets and DFAs. See DOI: 10.1039/c7cp04913g |
| ‡ Present address: Schrödinger GmbH, Dynamostr. 13, 68161 Mannheim, Germany. |
| This journal is © the Owner Societies 2017 |