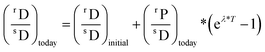Open Access Article
Open Access ArticleIsotopes in cosmochemistry: recipe for a Solar System
Steven
Goderis
*ab,
Ramananda
Chakrabarti
c,
Vinciane
Debaille
d and
János
Kodolányi
e
aVrije Universiteit Brussel, Earth System Sciences, Pleinlaan 2, 1050 Brussels, Belgium. E-mail: Steven.Goderis@vub.ac.be
bGhent University, Department of Analytical Chemistry, Krijgslaan, 281–S12, 9000 Ghent, Belgium
cCenter for Earth Sciences, Indian Institute of Science, Bangalore, India
dLaboratoire G-Time, Université Libre de Bruxelles 50, Av. F.D. Roosevelt CP 160/02, 1050 Brussels, Belgium
eMax Planck Institut für Chemie, Hahn-Meitner-Weg 1, 55128 Mainz, Germany
First published on 18th February 2016
Abstract
Extreme isotopic variations among extraterrestrial materials provide great insights into the origin and evolution of the Solar System. In this tutorial review, we summarize how the measurement of isotope ratios can expand our knowledge of the processes that took place before and during the formation of our Solar System and its subsequent early evolution. The continuous improvement of mass spectrometers with high precision and increased spatial resolution, including secondary ion mass spectrometry (SIMS), thermal ionization mass spectrometry (TIMS) and multi collector-inductively coupled plasma-mass spectrometry (MC-ICP-MS), along with the ever growing amounts of available extraterrestrial samples have significantly increased the temporal and spatial constraints on the sequence of events that took place since and before the formation of the first Solar System condensates (i.e., Ca–Al-rich inclusions). Grains sampling distinct stellar environments with a wide range of isotopic compositions were admixed to, but possibly not fully homogenized in, the Sun's parent molecular cloud or the nascent Solar System. Before, during and after accretion of the nebula, as well as the formation and subsequent evolution of planetesimals and planets, chemical and physical fractionation processes irrevocably changed the chemical and isotopic compositions of all Solar System bodies. Since the formation of the first Solar System minerals and rocks 4.568 Gyr ago, short- and long-lived radioactive decay and cosmic ray interaction also contributed to the modification of the isotopic framework of the Solar System, and permit to trace the formation and evolution of directly accessible and inferred planetary and stellar isotopic reservoirs.
Introduction to the Solar System and Galactic environment
As for any good recipe, the right ingredients and perfect timing are crucial for the preparation of a Solar System capable of sustaining life. At a distance of 8.33 ± 0.35 kiloparsecs from the Galactic Center,1 currently at ∼25 parsecs from the central plane of the Milky Way,2 our Sun and associated planetary bodies formed ∼4.567 Gyr3 to ∼4.568 Gyr4 ago within the Milky Way's Galactic habitable zone. As a younger generation star in a universe of 13.7 ± 0.2 Gyr,5 the Solar System's chemical and isotopic composition is largely the result of nucleosynthesis in multiple generations of Milky Way stars, which enriched the interstellar medium (ISM) with their products of nucleosynthesis, as well as mixing and sampling of Galactic matter, and thus represents several billion years of Galactic chemical evolution.Most of the isotopes making up the baryonic matter in our Universe were produced by complex nuclear processes (nucleosynthesis) in specific astrophysical settings, such as the Big Bang and stars (including supernovae). Big bang (primordial) nucleosynthesis, taking place 10 s to 20 min after the Big Bang, produced most of the universe's 1H, stable helium (in the form of 4He) along with small amounts of deuterium (2H or D), and 3He and stable lithium-7 (primordially produced radioactive 3H and 7Be decayed to 3He and 7Li). Since the late 50s, stellar nucleosynthesis in evolving and exploding stars has been known to be the source of all the elements heavier than Li and Be, and it is considered the main “kitchen stove” preparing the chemical evolution of the Milky Way since its formation.6 Most stars (and their planetary disks), including our Sun, form in groups or clusters of stars in giant molecular clouds, the densest parts of the ISM (e.g., ref. 7). When gravitational contraction of a localized, dense region of a large interstellar molecular cloud leads to the accretion of a central star, the chemical and isotopic compositions of the surrounding rotating disk of gas and fine dust grains will have been influenced by irradiation and influx of matter from older stars.8 For instance, condensates from supernova explosion ejecta and the winds of late-stage red giant branch (RGB) and asymptotic giant branch (AGB) stars have been found admixed to the Sun's molecular cloud (cf. section on presolar grains). In the Solar nebula, dust grains will then be heated up, evaporate, condense and aggregate to form km-size bodies called planetesimals. From that point on accretion progresses, through collisions and gravitational interactions between planetesimals, leading to the formation of a few tens of Moon-to-Mars-sized planetary embryos in a timeframe of roughly 0.1 to 1 Myr.9 Full planets then form by large-scale collisions between these embryos within 10 to 100 Myr, and one of these collisions is thought to have led to the formation of the Earth's Moon.10,11
Isotope cosmochemistry
Cosmochemistry, often defined as a subdivision of geochemistry, studies the chemical and isotopic compositions and history of the Solar System. While astronomical observations as well as robotic and manned orbital and lander probes have contributed significantly to the current understanding of our Galactic and Solar System neighborhoods, the study of extraterrestrial materials in the form of (micro)meteorites, lunar (e.g., Apollo), asteroidal (e.g., 25143 Itokawa through Hayabusa) and cometary (e.g., Wild 2 through Stardust) fragments, interplanetary dust particles (IDPs), and samples of the solar wind (e.g., Genesis) has also provided deep insights into Solar System processes, including accurate and precise time constraints on early Solar System events. The constant growth of meteorite collections worldwide, through systematic hot desert and Antarctic recovery programs, as well as random finds and radar-tracking meteorite falls (e.g., Sutter's Mill)12 combined with continuous innovations and improvements in the capabilities of analytical instruments, aiming at increased precision and spatial resolution (cf. below), have made the last few decades an exciting time to unravel the highly complex processes leading to compositional variability among Solar System objects. Indeed, planetary science has undergone a “supernova explosion” over the last few decades, especially thanks to technological and analytical advances, and this tutorial review summarizes the current state of understanding of the most crucial processes leading to the chemical and isotopic diversity observed among Solar System materials, from fossil stellar dust admixed to the Solar System's precursor gas and dust cloud, thermodynamic fractionation processes, and radioactive decay, to the formation of (accessible as well as hidden) planetary reservoirs.Modern analytical instrumentation
Most analytical instrumentation used to study extraterrestrial materials has seen significant advances over these last few decades. This progress derives from (i) improved user-friendliness due to increased processing power, more robust hard- and software, and more straightforward data handling, (ii) higher spatial resolution and instrument sensitivity facilitating the study of smaller samples, and (iii) perhaps most crucial to the isotopic characterization of Solar System materials, increased precision on the determined isotope ratios, resulting in better constraints on any recorded mass-dependent and mass-independent isotope fractionation effects. Although a wide variety of instruments exists for specific isotope applications, such as infrared laser-assisted fluorination coupled to stable isotope ratio mass spectrometry (IRMS) for high-precision oxygen isotope analysis, static gas mass spectrometry for noble gas isotope ratio determination and resonance ionization mass spectrometry (RIMS) for in situ isotope ratio measurements of isobarically interfered species (e.g., ref. 13), the following sections build on the instrumental progress that has occurred in the more widely utilized thermal ionization mass spectrometers (TIMSs), multi collector-inductively coupled plasma-mass spectrometers (MC-ICP-MSs) and secondary-ion mass spectrometers (SIMSs).In terms of precision, TIMS has long set the standard in the isotopic characterization of bulk extraterrestrial samples. After separation of the elements of interest using ion-exchange chromatography, the sample is loaded on a filament as a salt, which is then heated under vacuum in the source of the mass spectrometer using one, two, or three filament assemblies,14 leading to a stable emission of ions, which are detected on an electron multiplier or Faraday cups. While an electron multiplier records the impact of an individual ion by inducing an electron cascade and is ideally suited for isotope measurements at low count rates at the cost of precision, Faraday cups detect the charges of incoming ions directly and simultaneously, resulting in highly precise isotope ratios. For radiometric dating (e.g., Rb–Sr, U–Pb or Sm–Nd; Table 2) and planetary reservoir studies, excellent precision at the level of a few ppm (2 RSD, relative standard deviation) is critical (cf. section on radioactive decay and chronology of the Solar System). Instrumental mass fractionation is corrected either using internal normalization or by double spiking (e.g., ref. 14–18). In the case of precious or rare samples, however, the lack of sample availability can be an important limiting factor for less abundant elements, for which low ion per atom yields are attained. In addition, the maximum filament temperatures of ∼2500 °C result in the limited ability to ionize elements with high ionization potentials, such as Hf. For those elements, alternative measurement strategies need to be considered, for instance by running the instrument in negative mode (e.g., by measuring Os as OsO3− (ref. 17 and 19)) or by using other, more energetic analytical techniques.
In other cases, the application of MC-ICP-MS with reasonable transmission efficiency for most elements, good analytical precision (15–30 ppm external reproducibility, 2 RSD), and rapid sample-throughput forms a proficient alternative since its introduction in the mid-1990s. Here, a robust and highly efficient Ar-based inductively coupled plasma is operated at atmospheric pressure and used to atomize and ionize the gas-carried sample before extraction, introduction, and separation according to the mass/charge ratio in the mass analyzer under high vacuum. For a variety of elements that includes Ti, Hf, and W, isotope ratio measurement by MC-ICP-MS has proven to be highly valuable (e.g., ref. 20–23). Mass bias can often easily be corrected by doping with an internal standard similar to the element of interest (e.g., Tl for Pb isotope analysis or Ni or Cu for Fe isotope analysis; e.g., ref. 24 and 25), by the usage of the double spike technique (e.g., ref. 26–28 for Cr, Ni, and U), or by sample-standard bracketing (e.g., ref. 29 for Mg isotopes). When mass bias is corrected using sample-standard bracketing, it is essential to ensure that the yield during ion-exchange chromatography for the element of interest is close to 100%. In contrast, the double-spike technique corrects for isotopic fractionation during ion-exchange chromatography. In contrast to TIMS, ionization in a plasma leads to the formation of molecular gaseous species, some of which can cause isobaric interferences with isotopes of certain elements of interest. Such interferences can be avoided by analysis in medium to high resolution (M/ΔM, where M is the (mean) mass and ΔM the mass difference between the 2 species), which however leads to lower sensitivity (e.g., ref. 21 and 25). Due to the high dispersion of energy between the different species, the application of electrostatic filters and zoom optics to focus the ion beam is more important compared to TIMS. Coupling of MC-ICP-MS to nano- and femtosecond laser ablation systems has in recent years also led to highly precise in situ measurements of e.g., Mg and Si isotope ratios (e.g., ref. 30 and 31). The main advantages of MC-ICP-MS include the access to many elements, including those with high ionization potentials, and the relatively high speed of the analyses. On the other hand, even if the TIMS method cannot be applied to every element because of the low ionization energy provided, this low energy also permits a better control of the instrumental mass fractionation, resulting in more precise analyses. The possibility to work in negative (oxide) mode (e.g., ref. 17 and 19) also allows for higher transmission efficiencies for particular elements, which is highly relevant in the case of small samples. Compared to TIMS, MC-ICP-MS is more sensitive to the matrix of the purified samples and hence requires cleaner chemical separation of the element of interest.
Because of their high spatial resolution and sensitivity for many key elements of extraterrestrial materials, ion microprobes have proven to be indispensable for the in situ isotopic characterization of extraterrestrial materials, such as presolar grains (cf. section on presolar grains) or Ca–Al-rich inclusions (CAIs) (cf. sections on presolar grains and isotope anomalies in bulk meteorites as well as on radioactive decay and chronology of the Solar System). In this review, “ion microprobes” refer to instruments that use an ion beam to remove a certain amount of material from the surface of the analyzed sample for elemental and/or isotopic analysis. For precise in situ isotopic analysis of extraterrestrial materials, SIMS instruments with double focusing (DF) mass spectrometers are used most widely and we shall focus on these in the following. In DF-SIMS instruments, a solid sample surface is bombarded with a primary (oxygen or cesium) ion beam of less than 30–40 μm in diameter at 15 to 25 keV. The ion bombardment causes the top layer of the sample to disintegrate (sputtering) and form neutral and charged secondary species. Positively (in the case of an O− or O2− primary beam) or negatively (O+ or Cs+ primary beam) charged secondary ions are extracted and sorted according to their mass/charge ratio in the DF mass spectrometer, which is composed of electrostatic and magnetic analyzers. Also here, electron multipliers or Faraday cups are used for the detection of secondary ions. To improve mass resolving power and thus overcome certain molecular isobaric interferences, some ion probes (e.g., Sensitive High-Resolution Ion Microprobe, or SHRIMP) have been built with a large radius spectrometer. The highest mass resolution achieved by commercially available SIMS instruments is an M/ΔM of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–30
000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The best lateral spatial resolution achievable by SIMS is 0.5–1 μm and the best external reproducibility is <0.5‰ (95% confidence level) for isotope analyses of extraterrestrial materials.32 However, there is always a trade-off between these parameters. For instance, good precision requires larger volumes of sample material, on the order of 100s to 1000s of pg assuming the analyzed isotopes belong to a major element of the analyzed solid, which limits the lateral spatial resolution of high-precision isotope measurements to ≥10–15 μm. With the nanoscale SIMS (NanoSIMS), a lateral spatial resolution of 80–100 nm can be achieved routinely, however at the cost of mass resolution and analytical precision. Routine NanoSIMS stable isotope analyses of major elements with 100 nm lateral spatial resolution have external reproducibilities of a few % at best for objects a few hundred nm in diameter.33 SIMS and NanoSIMS have played a crucial role in the discovery and characterization of presolar silicates, presolar oxides and other presolar grain types. This is not only because of the small size of the grains (e.g., presolar silicates are typically 200–300 nm in diameter; Table 1), but also because they are often accompanied by isotopically non-anomalous materials (e.g., ref. 34), which severely limit (for oxides) or prevent (for silicates) gathering meaningful isotopic information on these grains using bulk analytical methods. Fortunately, presolar grains often exhibit anomalies in the isotopic compositions of one or more major or minor elements on the order of tens to hundreds of % compared to the Solar or terrestrial isotopic composition (cf. section on presolar grains and isotope anomalies in bulk meteorites), so the relatively poor precision of SIMS and NanoSIMS analyses still allows the isotopic and chemical characterization of most presolar grains.
000. The best lateral spatial resolution achievable by SIMS is 0.5–1 μm and the best external reproducibility is <0.5‰ (95% confidence level) for isotope analyses of extraterrestrial materials.32 However, there is always a trade-off between these parameters. For instance, good precision requires larger volumes of sample material, on the order of 100s to 1000s of pg assuming the analyzed isotopes belong to a major element of the analyzed solid, which limits the lateral spatial resolution of high-precision isotope measurements to ≥10–15 μm. With the nanoscale SIMS (NanoSIMS), a lateral spatial resolution of 80–100 nm can be achieved routinely, however at the cost of mass resolution and analytical precision. Routine NanoSIMS stable isotope analyses of major elements with 100 nm lateral spatial resolution have external reproducibilities of a few % at best for objects a few hundred nm in diameter.33 SIMS and NanoSIMS have played a crucial role in the discovery and characterization of presolar silicates, presolar oxides and other presolar grain types. This is not only because of the small size of the grains (e.g., presolar silicates are typically 200–300 nm in diameter; Table 1), but also because they are often accompanied by isotopically non-anomalous materials (e.g., ref. 34), which severely limit (for oxides) or prevent (for silicates) gathering meaningful isotopic information on these grains using bulk analytical methods. Fortunately, presolar grains often exhibit anomalies in the isotopic compositions of one or more major or minor elements on the order of tens to hundreds of % compared to the Solar or terrestrial isotopic composition (cf. section on presolar grains and isotope anomalies in bulk meteorites), so the relatively poor precision of SIMS and NanoSIMS analyses still allows the isotopic and chemical characterization of most presolar grains.
| Mineral/speciesa | Typical size | Typical abundanceb | Parent stars |
|---|---|---|---|
| a There is very limited information about the mineralogy of many grains. Generally, close to stoichiometric major element compositions are taken to indicate a certain phase. Silicates are an exception because they are often amorphous, even if they correspond to a certain mineral compositionally. b Typical matrix-normalized abundance in unaltered and unheated carbonaceous chondrites. c (incl) signifies that the given presolar species has been found only as inclusions in other presolar phase(s). d SNe stands for supernovae. | |||
| Carbonaceous grains | |||
| Diamond | Few nm | ? | SNed, ? |
| Graphite | Few μm | <10 ppm | AGB stars (∼50%), novae (≪1%), SNe (∼30%) |
| SiC (moissanite) | 0.1–3 μm | 10–100 ppm | AGB stars (∼95%), J-type carbon stars (few %), novae (≪1%), SNe (1.3%) |
| Refractory carbides (e.g., TiC) | 20–100 nm | ≪1 ppm (incl)c | AGB stars, SNe |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| O-rich grains | |||
| Silicates | 0.2–0.3 μm | 200–300 ppm | RGB and AGB stars (85–90%), novae (≪1%), SNe (10–15%) |
| Spinel | 0.1–1 μm | Together: 5–30 ppm | RGB and AGB stars (∼90%), novae (≤1%), SNe (<10%) |
| Al2O3 (corundum and amorphous) | 0.1–1 μm | RGB and AGB stars (∼90%), novae (≤1%), SNe (<10%) | |
| Hibonite | 0.1–1 μm | RGB and/or AGB stars (∼90%), SNe (∼10%) | |
| SiO2 | 0.2–0.3 μm | Together: 1–1.5 ppm | AGB stars (∼75%), SNe (∼25%) |
| TiO2 | 0.2–0.3 μm | RGB and/or AGB stars (∼80%), SNe (∼20%) | |
| MgO | 0.2–0.3 μm | ||
| FeO | 0.2–0.3 μm | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Other grain types | |||
| Si3N4 | 0.2–1 μm | ≪1 ppm | SNe |
| TiN | Tens of nm | ≪1 ppm (incl) | SNe |
| AlN | Tens of nm | ≪1 ppm (incl) | AGB stars?, SNe |
| Fe, Ni metal (kamacite) and Fe, Ni silicides | Tens of nm | ≪1 ppm (incl) | AGB stars?, SNe |
| Refractory metal nuggets | Tens of nm | ≪1 ppm (incl) | AGB stars, SNe |
Isotopic variations among Solar System materials
Most of the isotopic variability in the Solar System stems from four distinct processes: (1) stellar inheritance and incomplete (un)mixing in the Solar nebula (including potential late-stage injections), (2) radioactive decay of long-lived and short-lived radionuclides, (3) spallation by cosmic rays (cosmogenic nuclides), and (4) mass-dependent fractionation in equilibrium or kinetic reactions during nebular and planetary processes (e.g., evaporation/condensation, magmatic and metamorphic processes). In contrast to the latter, the former 3 processes lead to mass-independent variations that can be used to constrain the chronology of the Solar System (radiogenic variation), to highlight the effects of exposure, erosion, and impact gardening on asteroidal or planetary surfaces (cosmogenic effects), or to study nucleosynthetic processes in stars. Deviations from terrestrial or bulk Solar isotopic abundances that have resulted from processes other than radioactive decay, cosmic-ray interaction or mass-dependent fractionation are often referred to as isotope anomalies and are generally used to deduce meteorite source regions or to infer genetic relationships between meteorite classes (cf. section on bulk meteorite isotope anomalies).While early studies assumed that planets and other Solar System objects formed from a gaseous nebula with a homogeneous chemical and isotopic composition, evidence for incomplete homogenization in the Solar nebula or its parent molecular cloud was obtained through the study of bulk chondritic meteorites and their components (e.g., refractory inclusions). Over the last few decades, extremely small isotopic anomalies have also been resolved in bulk, often primitive, chondrites for a wide range of elements that includes Ti, Cr, Ni, Zr, Mo, Ru, Ba, Nd, and Sm, as a direct result of the increased performance of TIMS and MC-ICP-MS instruments (e.g., ref. 21, 35–43). Presolar grains, widespread in unequilibrated chondrites, are analyzed individually through the application of (Nano)SIMS and provide highly detailed information on the isotopic variability of some of the dust that went into the making of the Solar System.44 Importantly, some of the isotopic variability observed on the bulk meteorite scale could be linked directly to the presence of variable amounts of certain types of presolar grains (e.g., ref. 45). This highlights the complementary nature of bulk and in situ analytical techniques in cosmochemistry.
Physical and chemical processes, which took place during and shortly after the formation of the Solar System (condensation, evaporation, planetary differentiation, collisional erosion, etc.), can fractionate radioactive parent elements from their daughter elements. Given sufficient amounts of time, this leads to isotopic heterogeneity. This represents the basis of isotope chronology and can be used to identify isotopically distinct planetary reservoirs. The time period from the accretion of the Solar System's molecular cloud to the formation of the first solids (i.e., CAIs) remains the period of the “secret ingredient” and much of our understanding of the origin and evolution of the Solar System depends on how well the timing and the processes that took place during this period can be constrained, which is inescapably linked to the accuracy and precision obtained by modern-day instrumentation (cf. section on radioactive decay and chronology of the Solar System). Although mass-dependent or mass-independent isotopic variations are measured with the same instruments, these types of isotopic variations are essentially different and can be used to answer different questions.
Presolar grains and their isotope anomalies
Primitive meteorites, IDPs, and cometary matter contain minute (usually a few hundred nm in diameter), single or multiphase crystalline or amorphous solids that predate the Solar System, but survived the (partial) chemical and isotopic homogenization, which took place before and during its birth (ref. 34, 46 and 47) and thus represent an “unmodified” fraction of the matter from which the Solar System formed. These components are called presolar grains (Table 1; Fig. 1a). Through their chemical and isotopic analyses, presolar grains have provided a direct route to understanding stellar nucleosynthesis and the isotopic variability in the Solar System's parent molecular cloud. The vast majority of unequivocally presolar material known to date is stellar dust: a direct sample of stellar matter, which condensed from the winds or ejecta of stars, novae and supernovae. As such, “presolar grains” will be used as a synonym for fossil stellar dust in the following sections. The identification of presolar grains is based on their anomalous isotopic compositions relative to the compositional range observed for Solar System matter, indicating formation outside the Solar System. Consequently, grains with no isotope anomalies are not recognized as presolar and remain undiscovered, even if they predate Solar System formation. Thus, a bias towards isotopically anomalous presolar grains exists, influencing our understanding of presolar grains.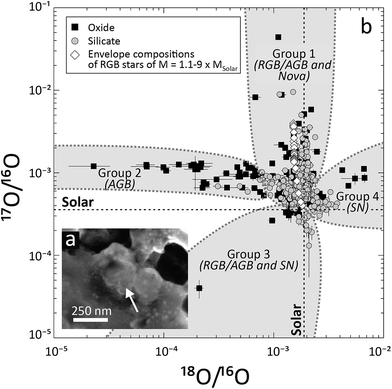 | ||
| Fig. 1 (a) Secondary electron image of a presolar silicate grain from the Acfer 094 ungrouped carbonaceous chondrite (image taken at the Max Planck Institute for Chemistry, Mainz). (b) Oxygen isotope composition of presolar oxide and silicate grains, as determined by SIMS and NanoSIMS (data sources: ref. 60, 66, 69, 76, 77 and 184–191). Grain groups63,192 are identified together with their most likely stellar sources in parenthesis (RGB, AGB = stars on the red giant and asymptotic giant branch, respectively; SN = supernova). The Solar O isotope composition is that estimated by ref. 193. The envelope compositions of ∼Solar metallicity stars of different starting masses after the first dredge-up (during RGB evolution) are taken from Boothroyd and Sackmann.67 Notice the good qualitative agreement between model data and Group 1 grain compositions. | ||
Consequently, it is hardly surprising that the discovery and study of presolar grains is tightly connected to advances in isotope analysis. The small size of the vast majority of presolar grains (Table 1) poses a significant analytical challenge because of the limited amount of material available for chemical and isotopic characterization. Thus, the study of presolar grains is one of the fields of cosmochemistry that benefited the most from the improvements in isotopic analytical techniques over these last few decades.
The existence of presolar components in primitive Solar System materials was first demonstrated through the isotopic analysis of H, O and noble gases of bulk meteorites. Noble gas isotope analyses were especially important in the discovery of actual presolar matter. In particular, the isotopic composition of Ne and Xe released from certain primitive meteorites at temperatures above 600 °C turned out to be isotopically anomalous compared to the meteorites' bulk noble gas signatures and could not be linked to fission, spallation or Solar wind implantation.48–50 Thus, the carrier phases of these “exotic” noble gas components were interpreted to derive from stellar but not Solar lineage and, therefore, to predate Solar System formation. Only the stepwise dissolution of bulk meteorite samples and concomitant isotopic analysis of the chemically separated components could give away these carrier phases, opening the way for multi-elemental and multi-isotopic analyses of bulk presolar grain separates, and, soon after, of individual presolar grains.46,50–53 Because the carrier phases of presolar components were discovered in the way outlined above, the first isotope ratio measurements on individual presolar grains were performed on grain separates of chemically resistant presolar phases, such as graphite and SiC (ref. 52 and 53; cf. below). These analyses could not have been carried out without SIMS, as at that time it was the only instrument with the spatial resolution and sensitivity necessary for precise isotope analysis as small as a μm (actually, SIMS could also measure sub-μm grains, provided that they were not attached to other grains on the sample mount).54 Later, with the advent of the NanoSIMS, the analysis of individual sub-μm presolar grains became more standard (e.g., ref. 55) and presolar silicate grains could be identified for the first time.34 Silicate grains represent the most abundant O-rich presolar grain type (cf. below) but cannot be separated chemically from their host meteorite matrix, unlike the chemically resistant SiC and graphite grains analyzed first. Moreover, the size of individual presolar silicate grains rarely exceeds 300 nm (Table 1; Fig. 1a). Thus, there was no way of detecting and, consequently, isotopically characterizing presolar silicate grains before the advent of NanoSIMS. The impact of NanoSIMS on the isotopic characterization of presolar grains has been exceptional since its introduction, and improvements of the instrument have not stopped. The next decade will continue to see enhancements in spatial resolution through the introduction of new primary ion sources (from 80–100 nm down to 30–40 nm for routine analysis with Cs+ primary ions and from 200–300 nm down to 50 nm with O− primary ions; the new O− source can already be ordered from the instrument manufacturer). In parallel, continuous efforts are being made to improve resonant ionization mass spectrometry, the only technique that has the potential to rival the NanoSIMS in terms of spatial resolution and precision.56
However, the quality of the isotopic data on presolar grains is not only driven by instrumentation improvements. Special measurement and sample preparation protocols have made measurement accuracy and precision better for certain elements and grain types, which were previously inaccessible for unbiased isotope analysis. For example, efforts have been made to obtain accurate Fe isotope composition of presolar silicate grains using two different approaches, which are both innovative but nevertheless differ substantially from each other. Currently, the isotope analysis of typical presolar silicates is possible only using the NanoSIMS (cf. above). The problem with NanoSIMS analysis of elements with low electronegativity, such as Fe, in presolar silicate grains is that the spatial resolution of such isotope measurements is comparable to the size of the grains of interest as a result of the relatively large diameter of the O− primary ion beam (cf. above) used routinely for the analysis of such elements. Because of the relatively poor spatial resolution, a significant contribution from the neighboring Solar System material is likely, which may obscure the grain's native isotopic signatures. In the specific case of Fe, one way to overcome this problem was to measure the Fe isotopes as xFe16O− (accessible when using Cs+ primary ions), instead of as xFe+ (accessible when using O− primary ions).57,58 Using the Cs+ primary ion source of the NanoSIMS allows better spatial resolution and therefore results in less contamination by the neighboring Solar System material. This NanoSIMS method cannot be used for all elements with low electronegativity, because not all of these form complexes with O at high enough rates to result in meaningful isotope ratio measurements. The other, completely different approach to minimize the contamination during Fe isotope analysis was the removal of Solar System materials around the presolar silicate grains using a focused ion beam (FIB) of Ga+ prior to the Fe isotope analyses (the preparation takes place using a separate instrument).59 This method can be applied to other elements, such as Mg, too, but introduces the risk of damaging the grain during the sample preparation with the FIB.60
Chemically, most presolar grains are C- (e.g., graphite) or O-rich (e.g., silicates), although grains with other chemical compositions, such as metals, have also been observed (Table 1). Among the C-rich presolar grains, SiC is likely the most abundant (the abundance of presolar nanodiamonds remains unknown, ref. 44; Table 1). The overwhelming majority of presolar SiC grains (∼93%) belongs to the “mainstream” (MS) type. These grains condensed in the winds of M = 1.5–3 × MSolar stars of close-to-solar metallicity (a measure of the abundance of elements heavier than He) during their evolution along the AGB of the Hertzsprung–Russell diagram.61 Similarly, the majority (∼85%) of the most abundant presolar O-rich grain types (i.e., silicates and oxides), also formed around low mass (M = 1.2–2.2 × MSolar) RGB or, more likely, AGB stars of approximately Solar or slightly lower metallicity (Table 1; Fig. 1b).62,63 The majority of the most abundant presolar grain types thus formed in the winds of low-mass stars (M < ∼4 × MSolar) during the parent stars' evolution along the RGB and/or AGB. This is not surprising as such stars, especially AGB stars, are among the most prolific dust producers of the Galaxy (e.g., ref. 64). The isotopic composition of presolar grains from such stars mostly reflects stellar nucleosynthesis in the CNO cycle during core and shell H burning and nucleosynthesis during He burning (e.g., ref. 54 and 63). The products of nucleosynthesis are brought to the stellar surface by large scale mixing, or “dredge-up”, events within the envelopes of the grains' likely parent stars during RGB and AGB evolution. CNO nucleosynthesis in the grains' potential parent stars with close-to-solar metallicity is reflected by the enrichment of MS SiC grains in 13C (average 12C/13C of ∼60, compared to ∼90 in the Solar System) and 14N (14N/15N of 300–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 compared to ∼440 for the Sun; the Solar composition is taken from ref. 65) and by the enrichment of Group 1 silicates and oxides in 17O (Fig. 1b; 17O/16O of up to 1.5–12× Solar for most grains; even higher enrichments require special formation conditions and are often interpreted to indicate a nova origin; e.g., ref. 66). Enrichment during condensation of MS SiC grains and some Group 1 and 2 presolar oxides and silicates in 26Al, a short-lived radioactive isotope with a half-life of ∼700
000 compared to ∼440 for the Sun; the Solar composition is taken from ref. 65) and by the enrichment of Group 1 silicates and oxides in 17O (Fig. 1b; 17O/16O of up to 1.5–12× Solar for most grains; even higher enrichments require special formation conditions and are often interpreted to indicate a nova origin; e.g., ref. 66). Enrichment during condensation of MS SiC grains and some Group 1 and 2 presolar oxides and silicates in 26Al, a short-lived radioactive isotope with a half-life of ∼700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years (Table 2), attests to the activation of the Mg–Al cycle during H shell burning and/or, especially when paired with depletion in 18O (Group 2 grains; Fig. 1b), may indicate cool bottom processing, an additional mixing process that promotes proton capture in regions directly underlying the envelope of some RGB and AGB stars.60,67–69 In summary, the isotope compositions of the most abundant presolar grain types are in qualitative and, for certain isotopes, quantitative agreement with astrophysical models of stellar nucleosynthesis in low mass stars. Nevertheless, there are still some discrepancies between expected and measured dust compositions. For instance, there are still no models that can account for the lower end of the 14N/15N ratio distribution in MS SiC grains (i.e., 14N/15N < ∼1000) or for the highest 26Al/27Al inferred for AGB-derived presolar oxide grains at their time of formation (i.e., 26Al/27Al > 10−2).70,71
000 years (Table 2), attests to the activation of the Mg–Al cycle during H shell burning and/or, especially when paired with depletion in 18O (Group 2 grains; Fig. 1b), may indicate cool bottom processing, an additional mixing process that promotes proton capture in regions directly underlying the envelope of some RGB and AGB stars.60,67–69 In summary, the isotope compositions of the most abundant presolar grain types are in qualitative and, for certain isotopes, quantitative agreement with astrophysical models of stellar nucleosynthesis in low mass stars. Nevertheless, there are still some discrepancies between expected and measured dust compositions. For instance, there are still no models that can account for the lower end of the 14N/15N ratio distribution in MS SiC grains (i.e., 14N/15N < ∼1000) or for the highest 26Al/27Al inferred for AGB-derived presolar oxide grains at their time of formation (i.e., 26Al/27Al > 10−2).70,71
| Parent isotope | Daughter isotope | Half-life (Gyr) | Decay mode | Comment | Relevant references |
|---|---|---|---|---|---|
| Long-lived isotope systems | |||||
| 40K | 40Ar (11%), 40Ca (89%) | 1.249 | Electron capture, β−-decay | While the majority of 40K (∼89%) decays to 40Ca by β−-disintegration with a half-life of 1.394 Gyr, all remaining 40K decays to 40Ar by electronic capture (t1/2 of 12.044 Gyr), resulting in a combined half-life of 1.249 Gyr. Given K is relatively abundant in a lot of different Solar System materials and the half-life of 40K is sufficiently long to date objects that formed during the earliest stages of the Solar System history, the 40K–40Ar chronometer, often in the form of the 40Ar–39Ar method knows a wide variety of applications in cosmochemistry. Importantly, the initial amount of Ar in the precursor material is often completely degased from the sample, making this system ideal for dating objects that crystallized from a melt or condensed from a gas, including meteorites and samples from the Moon and Mars, but it is also prone to disturbance. | 154, 204 and 205 |
| 87Rb | 87Sr | 48.8 | β−-Decay | This system has widely been used to date metamorphic rocks, because some minerals can be so enriched in Rb compared to Sr that the initial amount of Sr is negligible. Rubidium is moderately volatile while Sr is refractory, so that volatilization related to impact (e.g., the Moon-forming impact) can fractionate Rb from Sr. | 206 |
| 147Sm | 143Nd | 106 | α-Decay | Despite a relatively long half-life and limited fractionation between Sm and Nd, as both are rare earth elements (REEs), this system has proven its use in dating a variety of rocks. Because the REEs are not easily affected by weathering or metamorphism, this system usually behaves fairly robust. Involving lithophile and refractory elements, this system is widely used for defining the chondritic average (CHUR for CHondritic Uniform Reservoir) of the Solar System. | 207 |
| 176Lu | 176Hf | 35.9 | β−-Decay | With a half-life roughly one third of that of the 147Sm–143Nd system and encompassing elements with a similar geochemical behavior, this system is particularly suitable to date metamorphic events and minerals that strongly fractionate Lu from Hf, such as garnet or zircon. | 20 |
| 187Re | 187Os | 41.5 | β−-Decay | Since these elements strongly partition into metal or sulphide phases, this system traces processes that can be quite different from those recorded by the other radiometric systems. As the daughter element Os is compatible, the fractionation between parent and daughter elements can be large. | 208 |
| 190Pt | 186Os | 488 | α-Decay | This system with a very long half-life can only produce detectable 186Os anomaly in objects rich in Pt, such as planetary cores. This system has been used to track mantle–core interaction on Earth. | 209 |
| 232Th | 208Pb | 14.05 | α-Decay, spontaneous fission | With Th being a lithophile and refractory element, while Pb is volatile, lithophile and slightly chalcophile, this system is generally not used for dating, given the two U–Pb decay systems. | |
| 235U | 207Pb | 0.704 | α-Decay, spontaneous fission | In combination with 238U–206Pb, this system has proven to be one the most reliable geochronometers, even though the 238U/235U may not have been constant in the early Solar System. | 27 and 110 |
| 238U | 206Pb | 4.47 | α-Decay, spontaneous fission | cf. above | |
| Parent isotope | Daughter isotope | Half-life (Myr) | Decay mode | Comment | Relevant references |
|---|---|---|---|---|---|
| Short-lived isotope systems | |||||
| 26Al | 26Mg | 0.7 | β+-Decay, electron capture | With Al and Mg both refractory and major elements, this system is very robust for dating very early processes in the early Solar System. Only the most ancient objects, from CAI to ancient achondrites, can be dated using this system. The mechanism that injected 26Al in the Solar System as well as its homogeneous distribution (or not) are still debated. However, it is clear that 26Al was the main source of heat in the earliest Solar System. | 210 |
| 53Mn | 53Cr | 3.7 | Electron capture | Traditionally used to date igneous event and planetary differentiation, the correlation between these two isotopes has also been proposed to relate to mixing between refractory and volatile-rich components in the early Solar System. | 211 |
| 60Fe | 60Ni | 1.5 | β−-Decay | Both siderophile elements, this radioactive couple has traditionally been used to date core formation, even though the mobile behavior of Ni during metamorphic processes may impede the use of this system. | 212 |
| 107Pd | 107Ag | 6.5 | β−-Decay | With Pd a siderophile and Ag a chalcophile element, this system can date objects rich in siderophile elements, such as iron meteorites that fractionate Ag in iron sulfide phases. One issue is the volatile behavior of Ag leading to fractionation during impact-related volatilization. | 213 |
| 129I | 129Xe | 17 | β−-Decay | This system was first used to demonstrate short-lived radioactivity in the early Solar System. | 214 |
| 146Sm | 142Nd | 103 (or 68) | α-Decay | This system has the great advantage of being coupled to a long-lived counterpart. Together, these constrain a very precise timing of silicate differentiation. However, the recently revisited decay constant remains unclear. | 15 and 179 |
| 182Hf | 182W | 9 | β−-Decay | Hafnium is lithophile while W is siderophile. These elements will be strongly fractionated by silicate mantle/metallic core segregation, and to a lesser degree by silicate differentiation. This system is a valuable tool to understand the formation of cores within planets. | 215 |
A few % of presolar SiC, about 30% of presolar graphite, virtually all Si3N4 as well as about 10–15% of presolar oxide and silicate grains are thought to have condensed in the ejecta of core–collapse supernovae (SNe; Table 1; note however that the low abundance of SN grains among presolar silicates may be the result of a sampling bias, as indicated by the results of ref. 72), and thus provide information on nucleosynthesis in massive stars (M > 8–10 MSolar). The significance of the information delivered by SN grains lies in the fact that SNe (in general, i.e., not only core–collapse SNe) are the most important suppliers of stellar nucleosynthetic products to the Galaxy (e.g., ref. 73), thereby greatly influencing its chemical evolution (this is not in contradiction with the fact that most presolar grains derive from AGB stars: SNe recycle material to the ISM with a lower dust/gas ratio than AGB stars).
The majority of SiC grains of SN origin, represented by type X SiCs, have isotopically light Si (i.e., enriched in 28Si relative to Solar and the composition of other SiC types), variable 12C/13C (below and above Solar but mostly supra-Solar) and isotopically heavy N (14N/15N < ∼200). Many X grains have been shown to have contained 1–3 orders of magnitude more 26Al at formation than MS grains (26Al/27Al up to few times 10−1 in X grains) and some of these have provided evidence for the presence of other short-lived radioactive isotopes at the time of their formation, such as 44Ti (t1/2 of 60 years) and 49V (t1/2 of 330 days).74 The inferred presence of the latter two isotopes confirms an SN origin of X grains.75 Furthermore, SiC X grains are enriched in 57Fe (57Fe/56Fe up to ∼2× Solar). SiC grains of type C also originate from SNe. In contrast to X grains, C grains are enriched in the heavy Si isotopes and contain 32S generated by the decay of 32Si. Otherwise, C grains are isotopically similar to X grains. SN-derived presolar graphite is often found enriched in 28Si, but also in 18O, 26Mg (from the decay of 26Al), 49Ti (from the decay of 49V) and 61Ni, similar to SiC X grains. Many SN-graphites are also enriched in 42Ca, 43Ca and 44Ca. Among the O-rich presolar grains, those belonging to Group 4 and some Group 3 grains (with strong depletions in the heavy O isotopes and/or strongly sub-Solar 17O/18O ratios) have been suggested to have a SN origin (Fig. 1b).76,77 Group 4 grains are defined on the basis of their supra-Solar 18O/16O ratios, which are often accompanied by supra-Solar 17O/16O as well. Their 26Mg/24Mg ratios are often higher than Solar but their 25Mg/24Mg ratios are Solar or lower. This 26Mg enrichment is at least partially the result of in situ26Al decay. Isotope data for other elements are scarce, so their statistical significance is difficult to assess. Group 4 oxides may be enriched in 44Ca and slightly depleted in 42Ca and 43Ca, and contained short-lived 41Ca. Group 4 silicates have slightly supra-Solar 30Si/28Si ratios on average but have ∼Solar 29Si/28Si and ∼Solar Fe isotope ratios.58,59 Based on these data, presolar grains of SN origin document hydrostatic burning as well as explosive nucleosynthesis in SNe of most likely 10–25 × MSolar initial mass (e.g., ref. 74, 78 and 79). Importantly, the above isotopic data revealed that not a single SN grain's isotopic composition can be explained by condensation of material from a single zone or layer of a massive star or SN (massive stars develop distinct chemical and isotopic zonation during their pre-SN evolution; cf. for example ref. 80, for details on massive star nucleosynthesis and chemical zonation). Mixing of matter from different zones and chemical/isotopic fractionation within the SN ejecta are invoked to account for the observed isotopic compositions.79,81–83 A lot of recent work focuses on understanding mixing in SN ejecta as well as condensation of SN grains (e.g., ref. 84 and 85). Similar to RGB/AGB grains, a number of isotopic and abundance features of SN grains are not fully understood at present (e.g., the absence of 54Fe enrichment in SiC X and Group 4 silicate grains, the low abundance of 16O-rich SN-derived silicate and oxide grains).
Isotope anomalies in bulk meteorites
Following the first applications of multi-isotope measurements, particular processes, such as cosmic ray spallation effects on sulfur in meteorites,86 were shown to follow mass-independent relationships, linked to nuclear or specific chemical processes. Perhaps the best known and most applied are the oxygen isotope measurements of anhydrous minerals of carbonaceous chondrites showing deviation from mass-dependence.87 The oxygen isotope anomalies in meteorites, generally measured using IRMS or SIMS, were initially interpreted to reflect nucleosynthetic heterogeneities in the Solar nebula, but are now considered to reveal nebular photochemical reactions (e.g., ref. 88) and subsequent mixing between different reservoirs.89 As most planetary bodies show distinct O isotopic compositions that are inherited from a heterogeneous Solar nebula, oxygen isotope variations are often used to infer genetic links among meteorites. For instance, Earth and the Moon have recently been shown to have indistinguishable oxygen isotope ratios, with a difference in Δ′17O of −1 ± 5 ppm (−0.001 ± 0.005‰, 2 SE), with Δ′17O = δ′17O–β δ′18O, δ′17O = 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(17R/17R0), and δ′18O = 103
ln(17R/17R0), and δ′18O = 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(18R/18R0), where 17R is 17O/16O, 18R is 18O/16O, and 17R0 and 18R0 refer to the initial isotope ratios (such as those characterizing bulk Earth).90 These results, combined with planet formation simulations, imply vigorous mixing during the giant impact formation of the Moon, and thus a high-energy, high-angular-momentum collision. Also, as the late veneer impactors must have had an average Δ′17O within approximately 1 per mil of the terrestrial value, this constrains the possible sources for this late addition of mass to the Earth–Moon system, encompassing enstatite chondrites, aqueously altered carbonaceous chondrites, and some ordinary chondrites.90
ln(18R/18R0), where 17R is 17O/16O, 18R is 18O/16O, and 17R0 and 18R0 refer to the initial isotope ratios (such as those characterizing bulk Earth).90 These results, combined with planet formation simulations, imply vigorous mixing during the giant impact formation of the Moon, and thus a high-energy, high-angular-momentum collision. Also, as the late veneer impactors must have had an average Δ′17O within approximately 1 per mil of the terrestrial value, this constrains the possible sources for this late addition of mass to the Earth–Moon system, encompassing enstatite chondrites, aqueously altered carbonaceous chondrites, and some ordinary chondrites.90
Over the last few decades, advances in mass spectrometry have also permitted the determination of tiny but resolvable anomalies in Ti, Cr, Ni, Zr, Mo, Ru, Ba, Nd, and Sm isotopes as well as particular noble gases (using dedicated noble gas mass spectrometers; cf. section on modern analytical instrumentation) in bulk, mostly primitive, meteorites (e.g., ref. 21, 35–43 and 91). At the same time, other elements such as Os and Hf continue to exhibit uniform isotopic compositions (e.g., ref. 17 and 22). Various mechanisms have been invoked to explain (partial) isotope heterogeneity at the planetesimal scale, generally linked to the incorporation of varying proportions of isotopically diverse presolar components (cf. section on presolar grains) into early formed planetary bodies. The observed range of isotope anomalies across different Solar System materials could result from the inheritance from a heterogeneous molecular cloud core, the formation of localized heterogeneities due to differential physical sorting of isotopically distinct dust grains according to size or type or due to varying proportions of CAIs, a late supernova injection, or the selective destruction of thermally labile presolar carrier phases in the nebula (e.g., ref. 36, 38–40, 92 and 93). Secondary processes, such as aqueous alteration, thermal metamorphism, and differential melting, have also been shown to selectively redistribute isotopically distinct components, or their relicts, within parent bodies (e.g., ref. 19 and 94). Despite the remaining questions concerning their origin and nature, isotope anomalies in bulk meteorites, similar to oxygen isotope ratios, have also been used to infer genetic relationships among meteorites and deduce the meteoritic parentage of Earth and its planetary reservoirs (e.g., ref. 36, 40, 41 and 95).
Once highly precise nuclide ratios for bulk meteorite aliquots are obtained, these can be used to constrain the astrophysical origin of the preserved nucleosynthetic anomalies (consistent with s-, p-, or r-process stellar environments), to quantify the degree of homogeneity in the distribution of extinct radionuclides (e.g., 60Fe) and the efficiency of mixing in the early Solar System or to decipher the timing of injection of these extinct radionuclides relative to planetesimal formation.96
Nucleosynthetic Cr isotope anomalies show a rough correlation with Ti isotope anomalies for most Solar System materials (Fig. 2). While chromium is generally run on TIMS with external reproducibilities on the order of ∼15 ppm (2 RSD) for ε54Cr (parts per 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 deviation of the 54Cr/52Cr ratios from the terrestrial standard after fractionation correction by internal normalization), Ti isotope data are commonly obtained by MC-ICP-MS as ε50Ti (parts per 10
000 deviation of the 54Cr/52Cr ratios from the terrestrial standard after fractionation correction by internal normalization), Ti isotope data are commonly obtained by MC-ICP-MS as ε50Ti (parts per 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 deviation of the 50Ti/47Ti ratios from the terrestrial standard after fractionation correction by internal normalization and standard-bracketing), with the typical external reproducibility on the order of ∼20 ppm (2 RSD). Bulk carbonaceous chondrites are distinct from inner Solar System objects, with CR, CM, CO, CV, and CK chondrites plotting away from the inner Solar System correlation line (Fig. 2). This feature has been attributed to the presence of variable amounts of CAI inclusions in these objects.21 Because Ti isotopes of different nucleosynthetic origins (46Ti and 50Ti) also correlate, these isotope signatures suggest that the presolar dust inherited from the protosolar molecular cloud was well mixed when condensation started. Consequently, the observed isotopic heterogeneity must have resulted from the thermal processing of molecular cloud materials and the selective destruction of thermally unstable, isotopically anomalous presolar components.21
000 deviation of the 50Ti/47Ti ratios from the terrestrial standard after fractionation correction by internal normalization and standard-bracketing), with the typical external reproducibility on the order of ∼20 ppm (2 RSD). Bulk carbonaceous chondrites are distinct from inner Solar System objects, with CR, CM, CO, CV, and CK chondrites plotting away from the inner Solar System correlation line (Fig. 2). This feature has been attributed to the presence of variable amounts of CAI inclusions in these objects.21 Because Ti isotopes of different nucleosynthetic origins (46Ti and 50Ti) also correlate, these isotope signatures suggest that the presolar dust inherited from the protosolar molecular cloud was well mixed when condensation started. Consequently, the observed isotopic heterogeneity must have resulted from the thermal processing of molecular cloud materials and the selective destruction of thermally unstable, isotopically anomalous presolar components.21
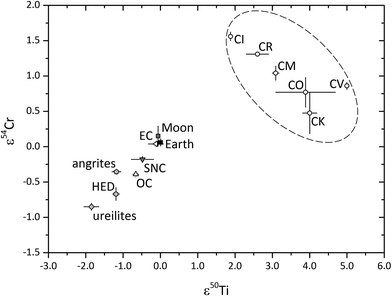 | ||
Fig. 2 Compilation of mass-independent 54Cr/52Cr versus50Ti/47Ti isotope ratios in carbonaceous chondrites, Earth and various other types of meteorites (data from ref. 16, 21, 42 and 194–202). OC = ordinary chondrite; EC = enstatite chondrite; SNC = shergottites, nakhlites, and chassignites from Mars; HED = howardite, eucrite, and diogenites from 4 Vesta or other vestoid asteroids. The ε-notation represents isotopic deviations from a reference value in parts per 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The high-precision isotopic composition of Cr is generally obtained by TIMS, while that of Ti is mostly determined by MC-ICP-MS. Shown values represent compiled meteorite type means, with 2 standard error uncertainties. 000. The high-precision isotopic composition of Cr is generally obtained by TIMS, while that of Ti is mostly determined by MC-ICP-MS. Shown values represent compiled meteorite type means, with 2 standard error uncertainties. | ||
As nucleosynthetic processes cannot fully account for all of the isotopic anomalies for Mg, Si, Ca, Ti, Cr, Sr, Ba, Nd, and Sm in refractory inclusions of chondrites, such as FUN (Fractionated and Unknown Nuclear effects) inclusions,97 mass-independent isotope fractionations induced by nuclear field shift and reflecting evaporation/condensation processes in the Solar nebula have also been considered to explain non-mass dependent fractionation effects.98
Mass-dependent isotope fractionation effects in meteorites
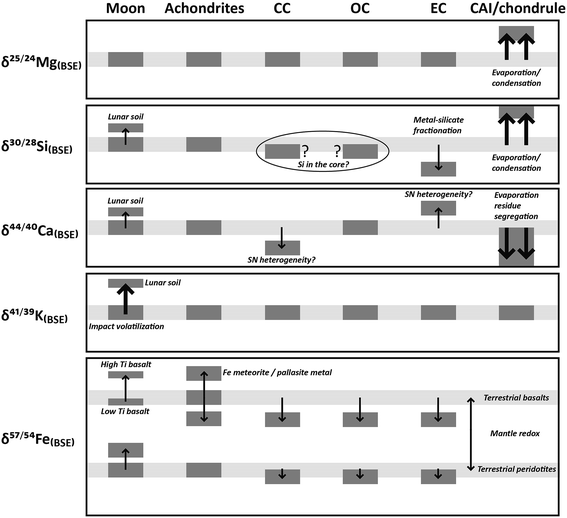
Following conventional models, mass-dependent isotope fractionation occurs because the atomic masses can influence particular thermodynamic properties of mineral phases (e.g., ref. 99). Ignoring potential nuclear field shift effects, the difference is generally made between equilibrium and kinetic fractionation laws. Equilibrium fractionation arises as a quantum mechanical effect because isotopes with heavier atomic masses have lower zero-point energies and lower vibrational frequencies in a molecule. The degree of equilibrium fractionation between phases often depends on temperature, and as such, isotope ratios have been used to calculate temperatures from the distribution of isotopes between phases (i.e., thermometry) or to identify (dis)equilibrium between mineral assemblages using the observed degree of equilibrium.100 On a planetary scale, isotope partitioning has been used to infer the presence of unseen reservoirs (cf. section on tracing planetary differentiation). Kinetic fractionation results from higher velocities for lighter isotopes, to accommodate constant kinetic energy.101 While this concerns all elements and their respective isotopes, elements with low atomic mass show more pronounced isotope fractionation effects, as the relative difference in mass is larger. Depending on an open or closed system, the diffusion rate in the solid, etc., isotope fractionation can occur during both condensation and evaporation.The 50% condensation temperatures of elements (cosmochemical classification)102 provide a first-order indication about their spatial distribution in the early Solar nebula and their condensation sequence (temporal significance) out of a rapidly cooling gas and dust disk. In addition, the geochemical affinity of elements (silicate-loving/lithophile, iron-loving/siderophile, etc.) also controls their distribution in the newly formed solids and their re-distribution during planetary accretion processes (e.g., melting, vaporization upon collision, etc.). These processes not only affected (fractionated) the distribution of elements but also that of the isotopes of these elements, and hence the isotopic composition of elements can be used to trace early Solar System processes. Below is a summary of the variations in the isotopic compositions of different elements observed in Solar System objects that are caused by mass-dependent isotope fractionation. Mass-dependent isotopic variations are generally reported in δ units, as parts per 1000 deviations from a terrestrial standard. By convention, the heavier isotope is the numerator while the lighter isotope makes up the denominator of an isotope ratio. Commonly, corrections for instrumental mass bias or mass fractionation are applied by sample-standard bracketing, doping with an internal isotope standard similar to the element of interest (e.g., Ni or Cu for Fe isotope analysis25), or double spiking.14,18 Isotope ratio variability in bulk rock meteorites is generally on the order of a few ‰, while much larger fractionation effects are commonly found for refractory inclusions, such as CAIs in carbonaceous chondrites, among the first condensed solids in the proto-planetary disk (cf. section on radioactive decay and chronology of the Solar System).
Among the highly refractory elements (1650–1500 K), isotopes of calcium have been studied since the late 70s, mostly using TIMS. Russell et al.103 measured the δ44/40Ca of a suite of primitive and differentiated meteorites and lunar samples and compared these with terrestrial samples. Although a spread of ∼1.2‰ was observed, overall bulk meteorites, the Earth and Moon were homogeneous in δ44/40Ca. A more recent high-precision study showed that the Earth, Moon, Mars and differentiated asteroids have a δ44/40Ca that is indistinguishable (±0.07‰) from ordinary chondrites; carbonaceous chondrites show lower δ44/40Ca (by 0.5‰), while enstatite chondrites show slightly higher δ44/40Ca (by ∼0.5‰)104 (Fig. 3), although a terrestrial calcium isotopic composition was observed for enstatite, O- and CO-chondrites by Valdes et al.105 These fractionations are thought to result from nebular condensation processes. Refractory inclusions (chondrules, solidified molten droplets after which chondrites are named, and CAIs) of chondritic meteorites however show large fractionations in Ca isotopes, with CAIs showing depletion in the lighter isotopes.14,106 In CAIs, δ44/40Ca variations are correlated with the REE patterns, which can be explained by segregation of an ultra-refractive evaporation residue from a chondritic reservoir prior to the formation of the CAIs.14 High temperature Ca stable isotope fractionation is also observed between co-existing clinopyroxene and orthopyroxene from terrestrial mantle peridotites and is thought to be controlled by the strength of the Ca–O bond in the mineral; minerals with a shorter Ca–O bond and a smaller Ca coordination number yield a heavier Ca isotopic ratio.107
The stable isotopic composition of uranium (238U/235U) in meteorites (as well as terrestrial samples) was considered to be constant at 137.88 and is widely used in high-precision Pb–Pb geochronology (cf. section on radioactive decay and chronology of the Solar System). The decay of 247Cm (t1/2 of ∼16 Ma), produced by r-process nucleosynthesis, produces 235U. Studies of bulk carbonaceous chondritic meteorites as well as leachates and mineral separates previously did not show any resolvable differences from the mean chondritic value.108,109 However, a study by Brennecka et al.27 of CAIs of the Allende meteorite showed variable 238U/235U. This variation, measured using MC-ICP-MS, is co-relatable with proxies of the Cm/U ratio (Th/U, Nd/U), but could also be linked to natural fractionation of U isotopes or chemical heterogeneity in the early Solar System.27 Variations in 238U/235U have also been reported for angrites, a rare group of basaltic achondrites that represents the oldest igneous rocks of the Solar System, leading to corrections in the Pb–Pb ages by ∼1 Myr.110 The above findings have implications for absolute dating of CAIs and the chronometry of early Solar System events (cf. section on radioactive decay and chronology of the Solar System).
Among the refractory elements (1500–1360 K), strontium (lithophile) has 4 stable isotopes. A fraction of 87Sr is produced by the decay of long-lived 87Rb (Table 2) and to determine the 87Sr/86Sr ratio, the 88Sr/86Sr ratio is considered to be constant for mass spectrometric measurements. Early work by Patchett et al.,111,112 using Sr double spikes and measured using TIMS, showed that chondrules and CAIs from Allende are enriched in the lighter isotopes such that their 88Sr/86Sr ratio is lower by up to 2.8‰ compared to bulk meteorites and terrestrial mantle-derived samples. More recent studies involving MC-ICP-MS of bulk samples of the terrestrial mantle, martian and lunar meteorites, HED, and most undifferentiated primitive meteorites show a homogeneous Sr stable isotopic composition (up to 50 ppm). However, CV and CO chondrites are isotopically light due to the presence of larger proportions of the light-Sr enriched refractory inclusions.113 The enrichment of the lighter isotopes in the refractory inclusions can be explained by condensation from a material that had been evaporated earlier or by electromagnetic sorting of ionized heavy Sr from neutral Sr in the early Solar System.113
Vanadium, another refractory element, has two stable isotopes with masses 50 and 51. High-energy irradiation of Ti and Cr can produce 50V. Hence, the V isotopic composition of primitive objects could reveal the irradiation history of the early Solar System. Measured using MC-ICP-MS, δ51/50V of chondrites, the HED parent body, and martian meteorites strongly overlap with one another, but are distinctly lower than that of the bulk silicate Earth by ∼1‰.114 While V is siderophile, the extent of fractionation expected during core formation on Earth is much smaller than what is observed in the measured samples. Alternatively, it is possible that the asteroid belt and Mars source region were enriched in high-energy particle irradiated material compared to the Earth-source region resulting in a relatively lower 51V/50V. However, isotopes of Li and B, which are also sensitive to energetic particle reactions, do not show any correlated variations with V isotopes.114
The condensation temperatures of the common elements Mg, Si, and Fe are between 1360 and 1290 K. Isotopic measurements of Mg, Si, and Fe are mostly done using MC-ICP-MS. However, early Mg and Fe isotope ratios were obtained using TIMS, while Si isotopes can also be measured using IRMS. The magnesium stable isotopic composition of the bulk silicate Earth overlaps with that of lunar samples, primitive and differentiated meteorites, indicating that the stable Mg isotopic composition of bulk inner Solar System objects is homogeneous (e.g., ref. 29, 115 and 116). Large mass-dependent fractionation of Mg isotopes has been documented in CAIs117 and laboratory experiments have demonstrated selective enrichment of heavier isotopes of Mg in evaporation residues.118
CAIs also show large (3–4‰) fractionation effects in δ30Si (Fig. 3 and 4).119–121 These large variations in δ30Si have been explained by isotopic exchange reactions between nebular-SiO gas and silicate condensates forming from it, and can be modeled by a Rayleigh process.119 Some inclusions from the carbonaceous chondritic meteorite Allende (e.g., C1, EK 1-4-1, CG-14, HAL, labeled “FUN” – unknown nuclear fractionations) show anomalous compositions for isotopes of many elements, while δ30Si of these FUN inclusions are ∼25‰, which is an order of magnitude higher than most other natural objects that have been measured for their Si isotopic composition.122 The largest fractionation of silicon isotopes (of 100s‰) has been observed in presolar SiC grains, which are thought to have formed in AGB stars123 (cf. section presolar grains and bulk meteorite isotope anomalies). Some studies have argued for a marginally (by ∼0.1‰) lighter δ30Si in bulk ordinary chondrites compared to carbonaceous chondrites.124 Enstatite chondrites, however, clearly show lower δ30Si compared to other chondrite groups and to the Earth (e.g., ref. 124–130) (Fig. 3 and 4). As the light Si is hosted in metals in enstatite chondrites (and also in their differentiated counterparts, aubrites), the metal-free silicate portion of enstatite chondrites shows similar δ30Si compared to other bulk chondrites. This suggests broad homogeneity in the Si isotopic composition of silicates condensing from the Solar nebula. Non-chondritic meteorites, with the exception of angrites,131 do not show much variation in δ30Si, which overlaps with that of bulk carbonaceous and ordinary chondrites (Fig. 3 and 4) (e.g., ref. 125 and 126). The difference in δ30Si of the BSE and chondrites is debated and ranges from 0.2‰ to 0.035 ± 0.035‰ (cf.ref. 125 and 126). The slightly heavier δ30Si of the silicate Earth is explained by Si isotope fractionation between silicates and metal during core formation on Earth. While Si has been long considered as one of the light elements in the Earth's outer core, the amount of Si present in the Earth's core, which in turn would regulate the extent of Si isotopic fractionation, is controlled mainly by the redox conditions of core formation. Intriguingly, the δ30Si of the average Moon is identical to that of the BSE (Fig. 3 and 4) as is the case for the isotopes of most other elements.130 The δ30Si variation range of angrites overlaps with terrestrial and lunar mantle values.131 This deviation from chondritic δ30Si cannot be due to core formation because the conditions (high oxygen fugacity and relatively low pressures) were not favorable for inducing Si isotope fractionation by incorporating Si into the core. Instead, the planetary δ30Si variations are suggested to have been inherited from Solar nebular chemistry through vapor–solid exchange.131
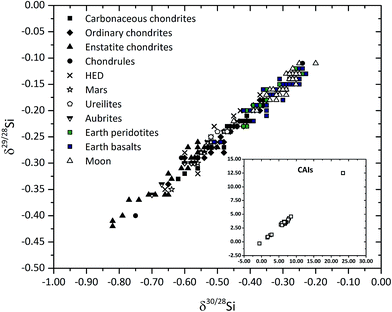 | ||
| Fig. 4 Compilation of the Si isotopic compositions of meteorites and their components as well as terrestrial and lunar rocks show a mass-dependent fractionation. In a plot of δ29/28Si versus δ30/28Si, the slope of the best-fit line for 244 samples is 0.528. Data, mostly acquired by MC-ICP-MS, are compiled from ref. 119, 121, 124–130 and 203. | ||
Initial iron isotopic studies suggested that δ57/54Fe chondrites are identical to differentiated meteorite parent bodies like Vesta and Mars, but lower (by 0.2‰) than that of terrestrial mantle-derived rocks,132,133 although a later study argued that the iron isotopic compositions of Mars, HED, and pallasites were the same as the silicate Earth134 and abyssal peridotites show chondritic Fe isotopic compositions135 (Fig. 3). Positively shifted iron isotope ratios in ureilites track the involvement of iron sulfides during the early stages of core formation.25 Iron meteorites show higher δ57/54Fe than chondrites136 similar to the metal fractions of pallasites relative to the co-existing olivines.134,136 The difference in δ57/54Fe between the metal and co-existing troilite (Fe–Ni alloy with 12 to 45 wt% Ni) in iron meteorites was the highest in slowly cooled meteorites (widest kamacite bands, with kamacite an Fe–Ni alloy with ∼5 to 12 wt% Ni) indicating equilibrium fractionation.137 The Earth's mantle, as represented by peridotites, is lighter than lunar rocks by 0.1‰, although the iron isotopic composition of terrestrial basalts overlaps with lunar basalts (Fig. 3). High-Ti basalts on the Moon show enrichments in heavier isotopes of iron compared to the low-Ti basalts.138 The discrepancy between the terrestrial and lunar iron isotopic composition can be explained by Fe isotope fractionation during terrestrial mantle differentiation (peridotite versus basalt), which is controlled by the redox and structural conditions of the magma.139 Alternatively, based on the enrichment of lighter Fe isotopes in a 4.51 Gyr old lunar dunite, the Fe isotopic composition of the bulk silicate Moon has been suggested to be identical to that of the bulk silicate Earth.140
Based on experimental data, the large mass-dependent fractionations in CAIs were initially suggested to be a result of partial vaporization.141 Hence, large isotopic fractionations were also expected for moderately volatile elements (T = 1290–704 K) like potassium. High precision (0.5‰) K isotopic compositions of bulk chondrites, achondrites, lunar samples, terrestrial samples, as well as chondrules and CAIs, measured using an O− primary source ion microprobe after ion-exchange chromatographic extraction and incorporation into barium borate glass, are however remarkably homogeneous, even though the K concentrations in these planetary bodies vary by a factor of 30 (ref. 142 and 143) (Fig. 3). This suggests that less than 2% of K would have been lost by partial volatilization and the depletion of alkalis and volatiles must have occurred very early, even before the formation of chondrules, during the condensation of the precursor dust in a hot stage in the Solar nebula.143 The only exceptions are lunar soils, which show enrichment in the heavier isotope of K (high δ41K) (Fig. 3). This is explained by fractionation due to micrometeorite bombardment, where the lighter isotopes are lost from the lunar surface to space. Lunar soils are also isotopically fractionated in Si and O.
Lithium has two isotopes with masses 6 and 7. Measured using MC-ICP-MS, the δ7/6Li of the primitive upper mantle is similar to that of carbonaceous chondrites, although ordinary chondrites show distinctly lower values suggesting the presence of distinct Li isotopic reservoirs in the early Solar nebula. Basaltic differentiates from the Earth, Moon, Mars and the achondrites show higher δ7/6Li than carbonaceous chondrites although these compositions partly overlap with those of the mantle olivines and carbonaceous chondrites (ref. 144 and 145 and references therein).
Copper and zinc are also moderately volatile elements with siderophile and dominantly lithophile geochemical affinities, respectively, and isotopic ratios of Zn and Cu are measured using MC-ICP-MS. Large δ65/63Cu variations are found between carbonaceous (CI > CM > CO > CV) and ordinary chondrites (LL > L > H). Between the different groups of carbonaceous chondrites, δ65/63Cu varies with Al/Mn and Ca/Mn. Meteorites with high refractory/volatile element ratios like CV chondrites show the lowest δ65/63Cu.146 On the other hand, δ65/63Cu is positively correlated with Δ17O both for carbonaceous chondrites and ordinary chondrites, suggesting the presence of 2–3 isotopically distinct Cu reservoirs in the early Solar System.146 Also, 63Cu/65Cu is strongly correlated with the Ni/Cu ratios in meteorites suggesting that the excess 63Cu may have been produced from 63Ni (t1/2 of 100 years) by irradiation by electromagnetic flares and particle bursts during the T-Tauri phase of the Sun. All four isotopes of Zn show a mass-dependent relationship, indicating their origin from a single homogeneous source.147 Refractory inclusions are enriched in the light isotopes of Zn. In addition, δ66/64Zn in bulk carbonaceous chondrites is inversely correlated with refractory/volatile element ratios (e.g., Ca/Mn), indicating that the Zn depletion in planetary bodies cannot be explained by simple devolatilization of a CI-like material.147 The observed pattern is an argument in favor of an incomplete accretion origin for the volatile depletion in the Solar System.148
Among the volatile elements (704–371 K), isotopes of cadmium (δ114/110Cd) are homogeneously distributed in terrestrial samples, eucrites, type 1, 2 and some type 3 carbonaceous chondrites and EH4 enstatite chondrites. However, large δ114/110Cd variations, measured using MC-ICP-MS, are observed for the ordinary chondrites, particular enstatite chondrites and type 3 to 5 carbonaceous chondrites, which are explained by open system thermal metamorphism on the meteorite parent bodies. CAIs show enrichment of the light Cd isotopes. Enrichment of the heavy Cd isotopes in lunar soils is correlated with decreasing Cd abundances in lunar soils, which is explained by Raleigh fractionation in response to space weathering.149
Overall, mass-dependent stable isotope fractionation in primitive and differentiated objects in our Solar System is explained by thermal effects (evaporation–condensation), kinetic effects, electromagnetic separation, and possible irradiation effects. The largest fractionations are observed in the refractory inclusions in primitive meteorites. Isotopic variations in bulk planetary objects are mostly explained by accretion from a heterogeneous nebular disk, while planetary differentiation (including core formation) and meteorite impact can also explain some of the observed variations (Fig. 3).
Radioactive decay and chronology of the Solar System
The natural radioactivity of particular isotopes can be used to place constraints on the chronological order of events in the early Solar System. Long-lived radioactive nuclides constrain absolute ages, while the decline in the abundance of short-lived radionuclides (e.g., 26Al–26Mg, 53Mn–53Cr and 182Hf–182W; Table 2) that existed at the beginning of the Solar System, but have since decayed away, can provide relative ages with high temporal resolution based on a highly precise measurement of the daughter's isotopic composition (often at the micrometer-scale). Essential for the application of short-lived radionuclides such as 26Al–26Mg is the assumption that these short-lived radionuclides were homogeneously distributed throughout the Solar nebula, what appears to be valid for this system based on the chronological consistency obtained for multiple short-lived systems150 and the observation that the initial Mg isotopic composition of chondrules is consistent with the 26Al–26Mg evolution of the Solar nebula.151 Nuclide production by cosmic ray irradiation can also be used for particular age determinations. Spallation occurs when a high-energy cosmic ray breaks a target nucleus into two or more pieces. Spallation reactions often release neutrons, which can then be captured by other nuclides. In the outer part of meteorites and lunar surface rocks, these secondary neutrons from spallation reactions in the surface layer can produce measurable changes in the isotopic compositions of the constituent elements (e.g., 3He, 21Ne, 38Ar, 83Kr, and 126Xe) that can be used to determine the so-called exposure ages.152Unfortunately, no method exists that allows constraining the age of all Solar System materials with the required precision. Only U–Pb ages in combination with short-lived systems are sufficiently precise to constrain the first few Myr.153 A combination of methods is thus needed to gain full insight into the timing of events in the Solar System.
Radioactivity is caused by the instability of nuclei. As such, a parent isotope, through various ways, can decay to a daughter isotope at a certain rate, depending on its decay constant λ (Table 2). Radioactive decay is a quantum-mechanical phenomenon, and the number of decays of a radionuclide per unit time is not constant, but decreases exponentially with time. It is the proportion of the radionuclides that decays during one half-life (t1/2 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/λ) that is constant. For most purposes, a radionuclide can be considered to have decayed away after ∼10 half-lives and is no longer detectable after 4–5 half lives. The amount of daughter isotope accumulated through radiogenic decay in a sample is thus a direct function of the age of the dated material and the amount of parent isotope in the material of interest.153 The general equation for radiometric dating is as follows:
2/λ) that is constant. For most purposes, a radionuclide can be considered to have decayed away after ∼10 half-lives and is no longer detectable after 4–5 half lives. The amount of daughter isotope accumulated through radiogenic decay in a sample is thus a direct function of the age of the dated material and the amount of parent isotope in the material of interest.153 The general equation for radiometric dating is as follows:
As such, the age T represents the time at which a fractionation between the parent and daughter elements occurred, as the result of a wide variety of causes that includes partial melting, large-scale planetary differentiation, preferential volatilization induced by impact, etc. For dating to be meaningful, several assumptions need to be made. First, the isotopic compositions of the parent and daughter elements need to have been homogenized, generally through particular nebular or planetary processes, such as condensation, crystallization or partial melting. This homogenous composition of the parent element assures that additions to the amount of daughter isotope only reflect the amount of parent element and the time that has passed. Secondly, the isotopic system (e.g., rock or mineral) needs to remain closed since the event for which the age needs to be constrained. Also, different reservoirs should not be mixed, as this can result in materials with varying parent/daughter ratios forming linear trends that could be interpreted to represent isochrons (cf. below). In other words, losses or gains of the parent or daughter element need to be precluded. The age of the dated material T is thus the timing of a discrete event of which the duration is short compared to the time that passed since this event. Crystallization of a melt is an ideal event to date, as parent/daughter element fractionation will occur because each element has a different affinity between liquid (“melt”) and solid (“mineral”) phases, controlled by their ionic radius and charge. When melting the mantle of a planet generates magma, particular “incompatible” elements will partition into the (liquid) magma while other “compatible” elements will remain in the (solid) depleted residue. As such, after effective fractionation between the parent and daughter of a radioactive couple, the daughter isotope will accumulate at a rate that depends on the amount of parent element in the lava emitted at the surface of the planetary body. Metamorphic episodes are harder to date by radiometric methods, as the time scales are typically longer and cooling from peak temperatures takes place more gradually, leading to differential diffusion for different elements and minerals. As such, the clock in one mineral may start at a different time than that in another mineral. Hypervelocity collisional impacts between planetary bodies, when providing enough energy to reset an entire system, form an example of events that can also be dated.154
While many radioactive parent isotopes are available throughout the Mendeleev table, only isotopes with an ideal half-life are of use in cosmochemistry (Table 2). If the half-life is too short, the entire parent isotope will have decayed too quickly after the formation of the Solar System. If t1/2 is too long, the radioactive decay is too slow to record variations resolvable by present-day mass spectrometers.
As the absolute amount of a particular isotope is difficult to determine because of analytical reasons, isotope ratios can be measured more accurately and precisely (cf. equation above), especially since the advent of multi collector mass spectrometers (cf. section on modern analytical instrumentation). Importantly, at high temperature and for one element considered, isotope ratios will show no isotope fractionation between the source of the magma and the lava emitted at the surface (e.g., liquid–solid interaction). This means that a lava flow will provide a direct insight into the chemical composition of the source. While the present-day concentrations of the daughter D and parent P can be measured, the initial amount of daughter element present in the sample and the time passed since elemental fractionation also need to be constrained. One way to circumvent this is to increase the number of equations for this system by combining several samples affected by the same event or multiple mineral fractions of the same rock showing dissimilar P/D ratios. The unknown T can then be solved graphically, as the slope of the regression line (the so-called “isochron”) determined for the different samples is proportional to the event age, while the intercept gives the initial ratio for the system.
Each isotope system has its own merits and drawbacks and is applicable in the case of particular scientific questions (Table 2). As the details and finesses of each system are beyond the scope of this paper, a few examples of the applicability of particular major systems are presented below. Fig. 5a and b represent Rb–Sr and Sm–Nd isochron diagrams revealing the formation history of low-Ti mare basalt lunar meteorite LaPaz Icefield 02205.155 For further details regarding the various radioactive decay systems, the reader is referred to the relevant literature (e.g., ref. 153, 156 and 157).
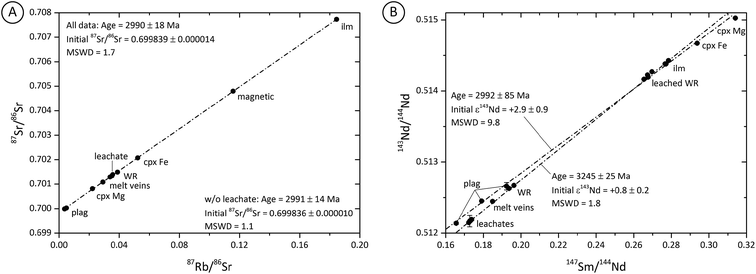 | ||
| Fig. 5 Isochron diagrams revealing the formation history of low-Ti mare basalt lunar meteorite LaPaz Icefield 02205.155 (a) Rb–Sr isochron (error bars smaller than symbols), and (b) Sm–Nd isochron (2σ uncertainties) for mineral separates, leachates, residues and whole rock aliquots (plag = plagioclase; cpx = clinopyroxene; ilm = ilmenite; WR = whole rock). The crystallization age of LAP 02205 is most precisely dated by an internal Rb–Sr isochron of 2991 ± 14 Ma, omitting a combined leachate that does not overlap the isochron with the analytical reproducibility of ±30 ppm. Excluding phases that are dominated by isotopically anomalous phosphates that are likely reset subsequent to crystallization, a Sm–Nd crystallization age of 2992 ± 85 Ma was also obtained, within error of the Rb–Sr age and in general agreement with Ar–Ar and U–Pb ages for LAP 02205. Redrawn from Geochimica et Cosmochimica Acta, Vol 71, Issue 8, K. Rankenburg, A. D. Brandon, M. D. Norman, A Rb–Sr and Sm–Nd isotope geochronology and trace element study of lunar meteorite LaPaz Icefield 02205, 2120-2135, Copyright (2007), with permission from Elsevier. | ||
Ca–Al-rich inclusions (CAIs) are commonly used to define the age of the Solar System, because these represent the oldest dated objects in the Solar System with chemical and isotopic compositions similar to what is expected for the first refractory nebular condensates (e.g., ref. 4; cf. section on mass-dependent isotope fractionation effects in meteorites). These inclusions represent one of two major types of refractory element-rich inclusions next to amoeboid olivine aggregates (AOAs) that occur in most chondrites, but are especially common in carbonaceous chondrites. The largest CAIs are up to 2–3 cm in size, but these occur only in CV3-type carbonaceous chondrites, while most other CAIs are generally less than 1 mm in size.158 First recognized in the late 1960s, CAIs are composed mainly of oxides and silicates of Ca, Al, Mg, and Ti, with their primary minerals clearly lacking any volatile components such as iron, alkalis, and water.158 They show significant enrichments in refractory trace elements, such as Sc, Y, Zr, Hf, rare earth elements (REE), and platinum group elements (PGE), and host isotope anomalies inherited from incorporated presolar grains or from the early nebula (cf. sections on presolar grains and bulk meteorite isotope anomalies). The inferred highest initial 26Al/27Al ratios as well as the ages determined from long-lived isotope chronometers reveal that CAIs are the oldest known components of chondrites, excluding presolar grains.158 The timing of Solar System events is thus commonly given in reference to the time of CAI formation. Accounting for 238U/235U isotopic variations in CAIs (cf. section on chemical and physical fractionation), combined high-precision U and Pb isotope studies constrain absolute ages of 4567.18 ± 0.50 to 4567.38 ± 0.31 Myr before present for Allende CAIs.3,159 This is equivalent to a total age range of only 0.2 Myr, fully consistent with the results obtained from short-lived chronometers (e.g., ref. 150).
Based on 26Al–26Mg chronometry, most chondrules in ordinary chondrites formed ∼2 Myr after CAIs, while chondrules in carbonaceous chondrites appear to have formed over a longer period of time, possibly as late as 4–5 Myr after CAIs (e.g., ref. 160), although other studies suggest a formation contemporaneous to CAI.161 A younger chondrule age poses a significant dynamic complication, known as the storage problem, in that chondrule-sized particles are expected to experience Poynting–Robertson drag and spiral into the Sun (e.g., ref. 162). In contrast, the Hf–W chronology of magmatic iron meteorites, samples from the metallic cores of protoplanets, indicates that accretion and differentiation of their parent bodies must have occurred within ∼1 Ma of CAI formation. Iron meteorites were thus derived from protoplanets or asteroids that were already differentiated before chondrules formed and chondrite parent bodies accreted.23,157,163 Pb–Pb dating of Group IVA iron meteorites confirmed this rapid differentiation of iron meteorite parent bodies.164 This observation has led to the suggestion that chondrules, or at least a fraction of them, could have been generated by impacts on molten bodies that would eject material.165
Tracing planetary differentiation
Radioactive isotopes allow us to constrain the timing when the parent isotope was fractionated from the daughter isotope/element. As stated in the previous paragraphs, this type of fractionation can be reached at small scale, for example in the form of a lava flow, but can also occur at much large scales, for instance when a planet is differentiating into distinct reservoirs. A planetary reservoir is generally considered a part of a planet for which the amount of material contained can be defined.166 Several planetary processes can lead to the formation of such reservoirs, including partial melting or fractional crystallization. The heat present at the beginning of the Solar System, mainly due to the radioactive decay of short-lived nuclide 26Al (Table 2), was sufficient to melt planetary bodies, especially in combination with planetary collisions, the dominant source of heat once planetesimals gained sufficient mass.167 For a chondritic precursor that reached the melting point of all its constituents, the most dramatic change will first be the segregation of metallic liquid from silicate melt (e.g., ref. 168). Subsequently, other differentiation events will take place, including the formation of a crust, depleting a resulting planetary mantle in incompatible elements.Two types of isotopic tools can be combined to understand planetary differentiation. First, traditional long-lived radioactive isotope systems (Table 2), addressed in the previous paragraphs, provide absolute age constraints on planetary processes, but are often associated with relatively large analytical uncertainties. On the other hand, short-lived isotope systems, defined as radioactive systems with half-lives shorter than that of 235U (t1/2 = 704 × 106 year), were only present during the earlier stages of Solar System evolution (Table 2). When the parent isotope is extinct, absolute ages can no longer be obtained, and only the time difference ΔT between two Solar System objects or two events A and B can be determined, resulting in a precisely constrained relative chronology. Consequently, short-lived radioactive systems need to be anchored in absolute chronology. To do this, key samples as CAI or ancient achondrites, such as angrites, need to be studied for both long-lived and short-lived isotope systems (e.g., ref. 169 and 170). These samples can then be used as reference points, by application of short-lived chronometers, to calculate time differences between the selected reference material and sample of interest. A great advantage of short-lived systems over long-lived systems is that these systems shut down at a given point in the planetary body history. While long-lived systems record planetary and geological events taking place anytime during the history of the planetary body, short-lived systems only record what happened during the lifetime of the parent nuclides, generally the first tens to hundreds Myrs after the formation of the Solar System and the accretion of planetary bodies, hence providing a more direct reading of the processes occurring at that time.
The segregation of a metallic core results in a mantle depleted in the (highly) siderophile elements. Crust formation leaves the residual mantle depleted in incompatible lithophile elements. The formation of a metallic core can adequately be addressed using the short-lived 182Hf–182W system (t1/2 of 9 Myr; Table 2), because lithophile Hf partitions into the mantle, while moderately siderophile W becomes depleted in the mantle (e.g., ref. 171). The formation of a core can thus dramatically change the Hf/W ratio of both the core and the silicate mantle, tracking this fractionation event through time. This process was likely not prompt, resulting in an average age for the process rather than an instantaneous age of core formation.172 Another problem to address is that a small amount of W is left behind within the silicate mantle. After core formation, the residual Hf/W in the mantle can subsequently be shifted by silicate differentiation, for example in the presence of garnet.173 Interpreting 182Hf–182W systematics is therefore unfortunately not straightforward and modeling is required to address these issues.174,175 In this context, the long-lived 238,235U–206,207Pb systems have been used as well, as Pb is chalcophile and could have been incorporated in a core composed of Fe, Ni, and S.176
When addressing crust formation, incompatible lithophile elements need to be considered, and this includes the Sm–Nd isotope systems. The uniqueness of these systems resides in the coupling of long-lived 147Sm–143Nd (t1/2 of 106 Gyr) with short-lived 146Sm–142Nd (t1/2 of 103 Myr, recently revised to 68 Myr).177 The combination of these systems during the first 350–500 Myr of Solar System history results in the deconvolution of both the formation age and the Sm/Nd ratio of the source of the studied samples, provided that the considered reservoir evolved in two steps (cf. below). The recent discovery of a resolvable gap between chondrites, the presumed building material of the telluric planets, Earth,178 Moon,179 and possibly Mars and Vesta,180 might imply the possibility of a non-chondritic bulk composition for the terrestrial planets, but could also suggest the existence of isotopic reservoirs hidden deep in the Earth that have not been sampled yet. Alternatively, this difference has been suggested to reflect heterogeneity in the Solar nebula (e.g., ref. 181).
To study planetary interiors, igneous rocks residing at the surface of the planet that are sometimes ejected as meteorites from their parent body can be used. While isotope ratios might not fractionate during partial melting, the parent/daughter nuclide ratios will fractionate according to their different partition coefficients, the mineral composition of the source and the degree of partial melting. As such, the initial parent/daughter composition of the source of melts is complicated to reconstruct. Considering a reservoir that formed directly from a chondritic precursor composition and did not evolve since its formation, the parent/daughter ratio needed to explain the radiogenic ratio observed in that reservoir can be modeled. As such, Fig. 6 can graphically solve the composition and the age of the source reservoir within the planet simultaneously.15 This necessitates the most precise data possible, with external reproducibilities on the order of a few ppm (2 RSD), so far only obtainable by TIMS measurements. To reach this level of precision, considerable analytical efforts are required. In the case of 142Nd, the isobaric interference of 142Ce has to be reduced as much as possible by a strict removal of Ce from the Nd cut (140Ce/146Nd < 0.00006).178 While this removal can never be perfect, optimal results can be achieved either by solvent extraction182 or by 2-methylactic acid column chemistry.178 The technical efforts are also crucial. As only TIMS can reach the required levels of precision for 142Nd, the measurement protocol of the TIMS also needs to be taken into account, for example by considering measurements in static mode (single multi-cups configuration), multi-static mode (simple average of different multi-cups configurations) or multi-dynamic mode (dynamic combination of different multi-cups configurations). In Fig. 6, if a sample is found to plot outside the field of possible compositions, the source of this sample was not characterized by a two-step evolution. If this sample plots within the acceptable ranges of this field, its composition is possibly related to a simple chemical evolution of the source, or alternatively, to a random combination of other arbitrary processes, such as mixing within the planet's interior.15
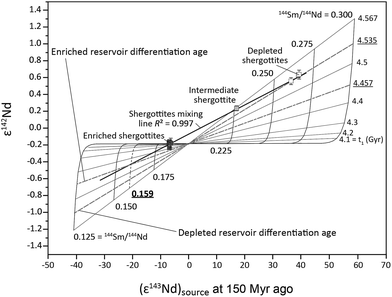 | ||
| Fig. 6 A two-stage coupled 142Nd–143Nd evolution model for a chondritic martian magma ocean projected to 150 Myr ago, determined using TIMS and redrawn after Debaille et al. from Nature.15 The linear arrays observed for Sm–Nd isotope systematics of shergottites are consistent with mixing between two distinct source reservoirs formed at ∼4.535 Gyr and ∼4.457 Gyr ago. The most probable origin for the incompatible-trace-element-enriched reservoir is late-stage quenched residual melt from the Martian magma ocean. For a 147Sm/144Nd ratio between 0.150 and 0.159, the formation time of the depleted and enriched reservoirs record progressive magma ocean crystallization to ∼100 Myr after core formation, in accordance to the survival of shallow magma ocean for 100–200 Myr in the presence of a primitive atmosphere without any heating processes (ref. 15 and references therein). | ||
Combining different isotope systems, short- or long-lived, can help to understand the processes of planetary differentiation. However, one should always keep in mind that short-lived systems do not necessarily have the same closure time. Combining various short-lived systems, such as 182Hf–182W with 146Sm–142Nd should be done with caution, as one system may still be active while the other is already closed.183 Short-lived systems are particularly powerful to investigate planetary differentiation because once the parent element is extinct, no further variation will be recorded, hence preserving a particular recipe of planet formation. The only way to modify the signature from that time on is by reservoir mixing. Mantle convection is a well-known mechanism to do this. On Earth for example, mantle convection is highly efficient, because the planet is geologically active until today and mixing occurs widely within the Earth's mantle, obliterating evidence from its isotopic precursors and evolution. In contrast, on Mars and the Moon, the planetary mantles remained heterogeneous, thus preserving a record of their formation (e.g., ref. 15 and 183).
Summary and outlook
Isotope ratios form a powerful tool to trace nebular and planetary processes. While radioactive nuclides serve as the foundation for isotope chronometers and as the heat source that steered early planetary differentiation (e.g., 26Al), stable nuclide fractionation provides insights into the chemical and physical processes taking place in the Solar System since solid formation (including condensation/evaporation, metal-silicate segregation, magmatic differentiation, etc.). Nuclide abundances can also be used to fingerprint the astrophysical setting of particular Solar nebula contributions (i.e., presolar grains). Our ability to better probe into Solar System processes is linked directly to advancements in mass spectrometry. The improved analytical precision and increased spatial resolution of the latest generation of analytical instrumentation (e.g., SIMS, TIMS, MC-ICP-MS) will continue to unravel the sequence of Solar System events that took place after CAI formation 4568 Myr ago. Sample return mission from planetary bodies will continue to provide key material to complement the already available source of extraterrestrial materials. Also, equipping planetary rovers with compact and improved mass spectrometers could provide critical information on the evolution of the Solar System. While specific processes are now known to have taken place very rapidly (e.g., accretion and differentiation of the first proto-planets in less than ∼1 Ma),23 other processes transpired over more protracted time scales (e.g., progressive magma ocean crystallization ∼100 Myr years after core formation on Mars).15 With growing knowledge on increasingly accessible and precise isotope tools and continued efforts to characterize crucial extraterrestrial samples, a more consistent image of a dynamic Solar System will emerge, with complex interactions between spatial and temporal isotopic reservoirs.Acknowledgements
SG is a Postdoctoral Fellow of the Research Foundation Flanders (FWO). VD acknowledges the FRS-FNRS and ERC StG “ISoSyC” for present support. The writing of this review was also supported by the Interuniversity Attraction Poles Program (IUAP) “Planet Topers”. We gratefully acknowledge the critical reviews by 5 anonymous referees that led to significant improvements of earlier versions of this tutorial.References
- S. Gillessen, F. Eisenhauer, S. Trippe, T. Alexander, R. Genzel, F. Martins and T. Ott, Astrophys. J., 2009, 692, 1075–1109 CrossRef CAS
.
- D. J. Majaess, D. G. Turner and D. J. Lane, Mon. Not. R. Astron. Soc., 2009, 398, 263–270 CrossRef
.
- Y. Amelin, A. Kaltenbach, T. Iizuka, C. H. Stirling, T. R. Ireland, M. Petaev and S. B. Jacobsen, Earth Planet. Sci. Lett., 2010, 300, 343–350 CrossRef CAS
.
- A. Bouvier and M. Wadhwa, Nat. Geosci., 2010, 3, 637–641 CrossRef CAS
.
- D. N. Spergel, L. Verde, H. V. Peiris, E. Komatsu, M. R. Nolta, C. L. Bennett, M. Halpern, G. Hinshaw, N. Jarosik, A. Kogut, M. Limon, S. S. Meyer, L. Page, G. S. Tucker, J. L. Weiland, E. Wollack and E. L. Wright, Astrophys. J., Suppl. Ser., 2003, 148, 175–194 CrossRef
.
- E. M. Burbidge, G. R. Burbidge, W. A. Fowler and F. Hoyle, Rev. Mod. Phys., 1957, 29, 548–654 CrossRef
.
- Y. Fukui and A. Kawamura, Annu. Rev. Astron. Astrophys., 2010, 48, 547–580 CrossRef CAS
.
- A. Vasileiadis, Å. Nordlund and M. Bizzarro, Astrophys. J., 2013, 769, L8 CrossRef
.
- J. E. Chambers, Earth Planet. Sci. Lett., 2004, 223, 241–252 CrossRef CAS
.
- R. M. Canup and E. Asphaugh, Nature, 2001, 412, 708–712 CrossRef CAS PubMed
.
- M. Ćuk and S. T. Stewart, Science, 2012, 338, 1047–1052 CrossRef PubMed
.
- P. Jenniskens, M. D. Fries, Q. Z. Yin, M. Zolensky, A. N. Krot and S. A. Sandford,
et al.
, Science, 2012, 338, 1583–1587 CrossRef CAS PubMed
.
- E. K. Zinner, F. Moynier and R. M. Stroud, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 19135–19141 CrossRef CAS PubMed
.
- S. Huang, J. Farkaš, G. Yu, M. I. Petaev and S. B. Jacobsen, Geochim. Cosmochim. Acta, 2012, 77, 252–265 CrossRef CAS
.
- V. Debaille, A. D. Brandon, Q. Z. Yin and B. Jacobsen, Nature, 2007, 450, 525–528 CrossRef CAS PubMed
.
- L. Qin, C. M. O’D Alexander, R. W. Carlson, M. F. Horan and T. Yokoyama, Geochim. Cosmochim. Acta, 2010, 74, 1122–1145 CrossRef CAS
.
- A. D. Brandon, M. Humayun, I. S. Puchtel, I. Leya and M. Zolensky, Science, 2005, 309, 1233–1236 CrossRef CAS PubMed
.
- A. Heuser, A. Eisenhauer, N. Gussone, B. Bock, B. T. Hansen and Th. F. Nägler, Int. J. Mass Spectrom., 2002, 220, 387–399 Search PubMed
.
- S. Goderis, A. D. Brandon, B. Mayer and M. Humayun, Earth Planet. Sci. Lett., 2015, 431, 110–118 CrossRef CAS
.
- J. Blichert-Toft, C. Chauvel and F. Albarède, Contrib. Mineral. Petrol., 1997, 127, 248–260 CrossRef CAS
.
- A. Trinquier, T. Elliott, D. Ulfbeck, C. Coath, A. N. Krot and M. Bizzarro, Science, 2009, 324, 374–376 CrossRef CAS PubMed
.
- P. Sprung, E. E. Scherer, D. Upadhyay, I. Leya and K. Mezger, Earth Planet. Sci. Lett., 2010, 295, 1–11 CrossRef CAS
.
- T. Kleine, M. Touboul, B. Bourdon, F. Nimmo, K. Mezger, H. Palme, S. B. Jacobsen, Q. Z. Yin and A. N. Halliday, Geochim. Cosmochim. Acta, 2009, 73, 5150–5188 CrossRef CAS
.
- W. M. White, F. Albarède and P. Télouk, Chem. Geol., 2000, 167, 257–270 CrossRef CAS
.
- J. A. Barrat, O. Rouxel, K. Wang, F. Moynier, A. Yamaguchi, A. Bischoff and J. Langlade, Earth Planet. Sci. Lett., 2015, 419, 93–100 CrossRef CAS
.
- B. Gueguen, O. Rouxel, E. Ponzevera, A. Bekker and Y. Fouquet, Geostand. Geoanal. Res., 2013, 37, 297–317 CrossRef CAS
.
- G. A. Brennecka, S. Weyer, M. Wadhwa, P. E. Janney, J. Zipfel and A. D. Anbar, Science, 2010, 327, 449–451 CrossRef CAS PubMed
.
- J. Farkaš, V. Chrastný, M. Novák, E. Ćadkova, J. Pašava, R. Chakrabarti, S. B. Jacobsen, L. Ackerman and T. D. Bullen, Geochim. Cosmochim. Acta, 2013, 123, 74–92 CrossRef
.
- R. Chakrabarti and S. B. Jacobsen, Earth Planet. Sci. Lett., 2010, 293, 349–358 CrossRef CAS
.
- E. D. Young, R. D. Ash, A. Galy and N. S. Belshaw, Geochim. Cosmochim. Acta, 2002, 66, 683–698 CrossRef CAS
.
- A. Shahar and E. D. Young, Earth Planet. Sci. Lett., 2007, 257, 497–510 CrossRef CAS
.
- P. Hoppe, S. Cohen and A. Meibom, Geostand. Geoanal. Res., 2013, 37, 111–154 CrossRef CAS
.
- A. Besmehn and P. Hoppe, Geochim. Cosmochim. Acta, 2003, 67, 4693–4703 CrossRef CAS
.
- S. Messenger, E. P. Keller, F. J. Stadermann, R. M. Walker and E. Zinner, Science, 2003, 300, 105–108 CrossRef CAS PubMed
.
- W. Akram, M. Schönbächler, S. Bisterzo and R. Gallino, Geochim. Cosmochim. Acta, 2015, 165, 484–500 CrossRef CAS
.
- C. Burkhardt, T. Kleine, F. Oberli, A. Pack, B. Bourdon and R. Wieler, Earth Planet. Sci. Lett., 2011, 312, 390–400 CrossRef CAS
.
- C. Burkhardt, T. Kleine, N. Dauphas and W. Wieler, Earth Planet. Sci. Lett., 2012, 357, 298–307 CrossRef
.
- R. W. Carlson, M. Boyet and M. Horan, Science, 2007, 316, 1175–1178 CrossRef CAS PubMed
.
- J. H. Chen, D. A. Papanastassiou and G. J. Wasserburg, Geochim. Cosmochim. Acta, 2010, 74, 3851–3862 CrossRef CAS
.
- N. Dauphas, B. Marty and L. Reisberg, Astrophys. J., 2002, 569, L139–L142 CrossRef CAS
.
- M. Regelous, T. Elliott and C. D. Coath, Earth Planet. Sci. Lett., 2008, 272, 330–338 CrossRef CAS
.
- A. Trinquier, J.-L. Birck and C. J. Allègre, Astrophys. J., 2007, 655, 1179–1185 CrossRef CAS
.
- Q. Yin, S. B. Jacobsen and K. Yamashita, Nature, 2002, 415, 881–883 CrossRef CAS PubMed
.
- E. Zinner, Annu. Rev. Earth Planet. Sci., 1998, 26, 147–188 CrossRef CAS
.
- N. Dauphas, L. Remusat, J. H. Chen, M. Roskosz, D. A. Papanastassiou, J. Stodolna, Y. Guan, C. Ma and J. M. Eiler, Astrophys. J., 2010, 720, 1577–1591 CrossRef CAS
.
- T. Bernatowicz, G. Fraundorf, T. Ming, E. Anders, B. Wopenka, E. Zinner and P. Fraundorf, Nature, 1987, 330, 728–730 CrossRef CAS
.
- K. D. McKeegan, J. Aléon, J. Bradley, D. Brownlee, H. Busemann, A. Butterworth, M. Chaussidon, S. Fallon, C. Floss, J. Gilmour, M. Gounelle, G. Graham, Y. Guan, P. R. Heck, P. Hoppe, I. D. Hutcheon, J. Huth, H. Ishii, M. Ito, S. B. Jacobsen, A. Kearsley, L. A. Leshin, M.-C. Liu, I. Lyon, K. Marhas, B. Marty, G. Matrajt, A. Meibom, S. Messenger, S. Mostefaoui, S. Mukhopadhyay, K. Nakamura-Messenger, L. R. Nittler, R. Palma, R. O. Pepin, D. A. Papanastassiou, F. Robert, D. Schlutter, C. J. Snead, F. J. Stadermann, R. Stroud, P. Tsou, A. Westphal, E. D. Young, K. Ziegler, L. Zimmermann and E. Zinner, Science, 2006, 314, 1724–1728 CrossRef CAS PubMed
.
- J. H. Reynolds and G. Turner, J. Geophys. Res., 1964, 69, 3263–3281 CrossRef CAS
.
- D. C. Black, Geochim. Cosmochim. Acta, 1972, 36, 377–394 CrossRef CAS
.
- R. S. Lewis, B. Srinivasan and E. Anders, Science, 1975, 190, 1251–1262 CrossRef CAS
.
- R. S. Lewis, M. Tang, J. F. Wacker, E. Anders and E. Steel, Nature, 1987, 326, 160–162 CrossRef CAS
.
- E. Zinner, M. Tang and E. Anders, Nature, 1987, 330, 730–732 CrossRef CAS
.
- S. Amari, E. Anders, A. Virag and E. Zinner, Nature, 1990, 345, 238–240 CrossRef CAS
.
- P. Hoppe, J. Geiss, F. Bühler, J. Neuenschwander, S. Amari and R. S. Lewis, Geochim. Cosmochim. Acta, 1993, 57, 4059–4068 CrossRef CAS
.
- E. Zinner, S. Amari, R. Guinness, A. Nguyen, F. J. Stermann, R. M. Walker and R. S. Lewis, Geochim. Cosmochim. Acta, 2003, 67, 5083–5095 CrossRef CAS
.
- A. M. Davis, T. Stephan, M. J. Pellin, D. Rost, M. R. Savina, R. Trappitsch and N. Liu, Mineral. Mag., 2013, 77, 951 Search PubMed
.
- S. Mostefaoui and P. Hoppe, Astrophys. J., Lett., 2004, 613, 149–152 CrossRef
.
- W. J. Ong and C. Floss, Meteorit. Planet. Sci., 2015, 50, 1392–1407 CrossRef CAS
.
-
A. N. Nguyen, S. Messenger, M. Ito and Z. Rahman, Lun. Planet. Sci. Conf. XLII, 2011, Abstr. 2711 Search PubMed
.
- J. Kodolányi, P. Hoppe, E. Gröner, C. Pauly and F. Mücklich, Geochim. Cosmochim. Acta, 2014, 140, 577–605 CrossRef
.
- M. Lugaro, A. M. Davis, R. Gallino, M. J. Pellin, O. Straniero and F. Käppeler, Astrophys. J., 2003, 593, 486–508 CrossRef CAS
.
- L. R. Nittler, Publ. Astron. Soc. Aust., 2009, 26, 271–277 CrossRef
.
- L. R. Nittler, C. M. O. 'D. Alexander, X. Gao, R. M. Walker and E. Zinner, Astrophys. J., 1997, 483, 475–495 CrossRef CAS
.
- A. S. Ferrarotti and H.-P. Gail, Astron. Astrophys., 2006, 447, 553–576 CrossRef CAS
.
- B. Marty, L. Zimmermann, P. G. Burnard, R. Wieler, V. S. Heber, D. L. Burnett, R. C. Wiens and P. Bochsler, Geochim. Cosmochim. Acta, 2012, 74, 340–355 CrossRef
.
- F. Gyngard, E. Zinner, L. R. Nittler, A. Morgand, F. J. Stadermann and K. M. Hynes, Astrophys. J., 2010, 717, 107–120 CrossRef CAS
.
- A. I. Boothroyd and I.-J. Sackmann, Astrophys. J., 1999, 510, 232–250 CrossRef CAS
.
- K. M. Nollett, M. Busso and G. J. Wasserburg, Astrophys. J., 2003, 582, 1036–1058 CrossRef CAS
.
- E. Zinner, L. R. Nittler, P. Hoppe, R. Gallino, O. Straniero and C. M. O. 'D. Alexander, Geochim. Cosmochim. Acta, 2005, 69, 4149–4165 CrossRef CAS
.
- S. Palmerini, M. L. Sergi, M. La Cognata, L. Lamia, R. G. Pizzone and C. Spitaleri, Astrophys. J., 2013, 764, 128, DOI:10.1088/0004-637x/764/2/128
.
- O. Straniero, G. Imbriani, F. Strieder, D. Bemmerer, C. Broggini, A. Caciolli, P. Corvisiero, H. Costantini, S. Cristallo, A. DiLeva, A. Formicola, Z. Elekes, Zs. Fülöp, G. Gervino, A. Guglielmetti, C. Gustavino, Gy. Gyürky, M. Junker, A. Lemut, B. Limata, M. Marta, C. Mazzocchi, R. Menegazzo, L. Piersanti, P. Prati, V. Roca, C. Rolfs, C. Rossi Alvarez, E. Somorjai, F. Terrasi and H.-P. Trautvetter, Astrophys. J., 2013, 763, 100, DOI:10.1088/0004-637x/763/2/100
.
- P. Hoppe, J. Leitner and J. Kodolányi, Astrophys. J., Lett., 2015, 808, L9 CrossRef
.
- C. Kobayashi, A. I. Karakas and H. Umeda, Mon. Not. R. Astron. Soc., 2011, 414, 3231–3250 CrossRef CAS
.
- P. Hoppe, R. Strebel, P. Eberhardt, S. Amari and R. S. Lewis, Meteorit. Planet. Sci., 2000, 35, 1157–1176 CrossRef CAS
.
- S. Amari, P. Hoppe, E. Zinner and R. S. Lewis, Astrophys. J., Lett., 1992, 394, L43–L46 CrossRef CAS
.
- L. R. Nittler, C. M. O. 'D. Alexander, R. Gallino, P. Hoppe, A. N. Nguyen, F. J. Stadermann and E. K. Zinner, Astrophys. J., 2008, 682, 1450–1478 CrossRef CAS
.
- A. N. Nguyen, L. R. Nittler, F. J. Stadermann, R. M. Stroud and C. M. O. 'D. Alexander, Astrophys. J., 2010, 719, 166–189 CrossRef CAS
.
- T. Yoshida, Astrophys. J., 2007, 666, 1048–1068 CrossRef CAS
.
- M. Pignatari, M. Wiescher, F. X. Timmes, R. J. De Boer, F.-K. Thielemann, C. Fryer, A. Heger, F. Herwig and R. Hirschi, Astrophys. J., Lett., 2013, 767, L22, DOI:10.1088/2041-8205/767/2/l22
.
- B. S. Meyer, T. A. Weaver and S. E. Woosley, Meteoritics, 1995, 30, 325–334 CrossRef CAS
.
- K. K. Marhas, S. Amari, F. Gyngard, E. Zinner and R. Gallino, Astrophys. J., 2008, 689, 622–645 CrossRef CAS
.
- A. V. Fedkin, B. S. Meyer and L. Grossman, Geochim. Cosmochim. Acta, 2010, 74, 3642–3658 CrossRef CAS
.
- A. N. Nguyen and S. Messenger, Astrophys. J., 2014, 784, 149, DOI:10.1088/0004-637x/784/2/14
.
-
T. K. Croat, M. Jadhav, E. Lebsack and T. J. Bernatowicz, 42nd Lunar. Planet. Sci. Conf., 2011, abstr. 1533 Search PubMed
.
- Y. Xu, E. Zinner, R. Gallino, A. Heger, M. Pignatari and Y. Lin, Astrophys. J., 2015, 799, 156 CrossRef CAS
.
- J. R. Hulston and H. G. Thode, J. Geophys. Res., 1965, 70, 3475–3484 CrossRef CAS
.
- R. N. Clayton, L. Grossman and T. K. Mayeda, Science, 1973, 182, 485–488 CrossRef CAS PubMed
.
-
R. N. Clayton in Treatise on Geochemistry, ed. H. D. Holland, Pergamon, Oxford, 2003, pp. 129–142 Search PubMed
.
- K. D. McKeegan, A. P. A. Kallio, V. S. Heber, G. Jarzebinski, P. H. Mao, C. D. Coath, T. Kunihiro, R. C. Wiens, J. E. Nordholt, R. W. Moses Jr, D. B. Reisenfeld, A. J. G. Jurewicz and D. S. Burnett, Science, 2001, 332, 1528–1532 CrossRef PubMed
.
- E. D. Young, I. E. Kohl, P. H. Warren, D. C. Rubie, S. E. Jacobsen and A. Morbidelli, Science, 2016, 351, 493–496 CrossRef CAS PubMed
.
- E. Zinner, M. Tang and E. Anders, Geochim. Cosmochim. Acta, 1989, 53, 3273–3290 CrossRef CAS
.
- R. Andreasen and M. Sharma, Astrophys. J., 2007, 665, 874–883 CrossRef CAS
.
- L. Qin, N. Dauphas, M. Wadhwa, A. Markowski, R. Gallino, P. E. Janney and C. Bouman, Astrophys. J., 2008, 674, 1234–1241 CrossRef CAS
.
- T. Yokoyama, D. Walker and R. J. Walker, Earth Planet. Sci. Lett., 2009, 279, 165–173 CrossRef CAS
.
- M. Fischer-Gödde, C. Burkhardt, T. S. Kruijer and T. Kleine, Geochim. Cosmochim. Acta, 2015, 168, 151–171 CrossRef
.
- N. Dauphas, D. L. Cook, A. Sacarabany, C. Fröhlich, A. M. Davis, M. Wadhwa, A. Pourmand, T. Rauscher and R. Gallino, Astrophys. J., 2008, 686, 560–569 CrossRef CAS
.
- J. L. Birck, Rev. Mineral. Geochem., 2004, 55, 25–64 CrossRef CAS
.
- T. Fuiji, F. Moynier and F. Albarède, Earth Planet. Sci. Lett., 2006, 247, 1–9 CrossRef
.
- H. C. Urey, J. Chem. Soc., 1947, 562–581 RSC
.
- E. D. Young, C. E. Manning, E. A. Schauble, A. Shahar, C. A. Macris, C. Lazar and M. Jordan, Chem. Geol., 2015, 395, 176–195 CrossRef CAS
.
- E. D. Young, A. Galy and H. Nagahara, Geochim. Cosmochim. Acta, 2002, 66, 1095–1104 CrossRef CAS
.
- K. Lodders, Astrophys. J., 2003, 591, 1220–1247 CrossRef CAS
.
- W. A. Russell, D. A. Papanastassiou and T. A. Tombrello, Geochim. Cosmochim. Acta, 1978, 42, 1075–1090 CrossRef CAS
.
- J. I. Simon and D. J. DePaolo, Earth Planet. Sci. Lett., 2010, 289, 457–466 CrossRef CAS
.
- M. C. Valdes, M. Moreira, J. Foriel and F. Moynier, Earth Planet. Sci. Lett., 2014, 394, 135–145 CrossRef CAS
.
- F. R. Niederer and D. A. Papanastassiou, Geochim. Cosmochim. Acta, 1984, 48, 1279–1293 CrossRef CAS
.
- S. Huang, J. Farkaš and S. B. Jacobsen, Earth Planet. Sci. Lett., 2010, 292, 337–344 CrossRef CAS
.
- C. H. Stirling, D. Porcelli and A. N. Halliday, Geochim. Cosmochim. Acta, 2005, 69, 1059–1071 CrossRef CAS
.
- C. H. Stirling, A. N. Halliday, E.-K. Potter, M. B. Andersen and B. Zanda, Earth Planet. Sci. Lett., 2006, 251, 386–397 CrossRef CAS
.
- G. A. Brennecka and M. Wadhwa, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9299–9303 CrossRef CAS PubMed
.
- P. J. Patchett, Earth Planet. Sci. Lett., 1980, 50, 181–188 CrossRef CAS
.
- P. J. Patchett, Nature, 1980, 281, 438–441 CrossRef
.
- F. Moynier, A. Agranier and D. Hezel, Earth Planet. Sci. Lett., 2010, 300, 359–366 CrossRef CAS
.
- S. G. Nielsen, J. Prytulak, B. J. Wood and A. N. Halliday, Earth Planet. Sci. Lett., 2014, 389, 167–175 CrossRef CAS
.
- B. Bourdon, E. T. Tipper, C. Fitoussi and A. Stracke, Geochim. Cosmochim. Acta, 2010, 74, 5069–5083 CrossRef CAS
.
- F.-Z. Teng, W.-Y. Li, S. Ke, B. Marty, N. Dauphas, S. Huang, F.-Y. Wu and A. Pourmand, Geochim. Cosmochim. Acta, 2010, 74, 4150–4166 CrossRef CAS
.
- G. J. Wasserburg, T. Lee and D. A. Papanastassiou, Geophys. Res. Lett., 1977, 4, 299–302 CrossRef CAS
.
- A. M. Davis, A. Hashimoto, R. N. Clayton and T. K. Mayeda, Nature, 1990, 347, 655–658 CrossRef CAS
.
-
R. N. Clayton, T. K. Mayeda and S. Epstein, in Proceedings of the Lunar Planetary Science Conference, 1978, pp. 1267–1278 Search PubMed
.
- K. B. Knight, N. T. Kita, R. A. Mendybaev, F. M. Richter, A. M. Davis and J. W. Valley, Geochim. Cosmochim. Acta, 2009, 73, 6390–6401 CrossRef CAS
.
- A. Shahar and E. D. Young, Geochim. Cosmochim. Acta, 2007, 257, 497–510 CAS
.
- R. N. Clayton, G. J. MacPherson, I. D. Hutcheon, A. M. Davis, L. Grossman, T. K. Mayeda, C. Molini-Velsko and J. M. Allen, Geochim. Cosmochim. Acta, 1984, 48, 535–548 CrossRef CAS
.
- L. R. Nittler, R. Gallino, M. Lugaro, O. Straniero, I. Domínguez and E. Zinner, Nucl. Phys. A, 2005, 758, 348c–351c CrossRef
.
- C. Fitoussi, B. Bourdon, T. Kleine, F. Oberli and B. C. Reynolds, Earth Planet. Sci. Lett., 2009, 287, 77–85 CrossRef CAS
.
- R. Chakrabarti and S. B. Jacobsen, Geochim. Cosmochim. Acta, 2010, 74, 6921–6933 CrossRef CAS
.
- R. B. Georg, A. N. Halliday, E. A. Schauble and B. C. Reynolds, Nature, 2007, 447, 1102–1106 CrossRef CAS PubMed
.
- C. Fitoussi and B. Bourdon, Science, 2012, 335, 1477–1480 CrossRef CAS PubMed
.
- P. S. Savage, R. B. Georg, R. M. G. Armytage, H. M. Williams and A. N. Halliday, Earth Planet. Sci. Lett., 2010, 295, 139–146 CrossRef CAS
.
- P. S. Savage and F. Moynier, Earth Planet. Sci. Lett., 2013, 361, 487–496 CrossRef CAS
.
- R. M. G. Armytage, R. B. Georg, H. M. Williams and A. N. Halliday, Geochim. Cosmochim. Acta, 2012, 77, 504–514 CrossRef CAS
.
- N. Dauphas, F. Poitrasson, C. Burkhardt, H. Kobayashi and K. Kurasawa, Earth Planet. Sci. Lett., 2015, 427, 236–248 CrossRef CAS
.
- F. Poitrasson, A. N. Halliday, D. C. Lee, S. Levasseur and N. Teutsch, Earth Planet. Sci. Lett., 2004, 223, 253–266 CrossRef CAS
.
- R. Schoenberg and F. von Blanckenburg, Earth Planet. Sci. Lett., 2006, 252, 342–359 CrossRef CAS
.
- S. Weyer, A. D. Anbar, G. P. Brey, C. Münker, K. Mezger and A. B. Woodland, Earth Planet. Sci. Lett., 2005, 240, 251–264 CrossRef CAS
.
- P. R. Craddock, J. M. Warren and N. Dauphas, Earth Planet. Sci. Lett., 2013, 365, 63–76 CrossRef CAS
.
- F. Poitrasson, S. Levasseur and N. Teutsch, Earth Planet. Sci. Lett., 2005, 234, 151–164 CrossRef CAS
.
- H. M. Williams, A. Markowski, G. Quitté, A. N. Halliday, N. Teutsch and S. Levasseur, Earth Planet. Sci. Lett., 2006, 250, 486–500 CrossRef CAS
.
- Y. Liu, M. J. Spicuzza, P. R. Craddock, J. M. D. Day, J. W. Valley, N. Dauphas and L. A. Taylor, Geochim. Cosmochim. Acta, 2010, 74, 6249–6262 CrossRef CAS
.
- N. Dauphas, M. Roskosz, E. E. Alp, D. R. Neuville, M. Y. Hu, C. K. Sio, F. L. H. Tissot, J. Zhao, L. Tissandier, E. Médard and C. Cordier, Earth Planet. Sci. Lett., 2014, 398, 127–140 CrossRef CAS
.
- K. Wang, S. B. Jacobsen, F. Sedaghatpour, H. Chen and R. L. Korotev, Earth Planet. Sci. Lett., 2015, 430, 202–208 CrossRef CAS
.
- J. Wang, A. M. Davis, R. N. Clayton and T. K. Mayeda, Lunar Planet. Sci., 1994, XXV, 1457–1458 Search PubMed
.
- M. Humayun and R. N. Clayton, Geochim. Cosmochim. Acta, 1995, 59, 2115–2130 CrossRef CAS
.
- M. Humayun and R. N. Clayton, Geochim. Cosmochim. Acta, 1995, 59, 2131–2148 CrossRef CAS
.
- H. M. Seitz, G. P. Brey, J. Zipfel, U. Ott, S. Weyer, S. Durali and S. Weinbruch, Earth Planet. Sci. Lett., 2007, 260, 582–596 CrossRef CAS
.
- T. Magna, U. Wiechert and A. N. Halliday, Earth Planet. Sci. Lett., 2006, 243, 336–353 CrossRef CAS
.
- J. M. Luck, D. B. Othman, J. A. Barrat and F. Albarède, Geochim. Cosmochim. Acta, 2003, 67, 143–151 CrossRef CAS
.
- J. M. Luck, D. B. Othman and F. Albarède, Geochim. Cosmochim. Acta, 2005, 69, 5351–5363 CrossRef CAS
.
- F. Albarède, Nature, 2009, 461, 1227–1233 CrossRef PubMed
.
- F. Wombacher, M. Rehkämper, K. Mezger, A. Bischoff and C. Münker, Geochim. Cosmochim. Acta, 2008, 72, 646–667 CrossRef CAS
.
- L. E. Nyquist, T. Kleine, C.-Y. Shih and Y. D. Reese, Geochim. Cosmochim. Acta, 2009, 73, 5115–5136 CrossRef CAS
.
- J. Villeneuve, M. Chaussidon and G. Libourel, Science, 2009, 325, 985–988 CrossRef CAS PubMed
.
- O. Eugster, Chemie der Erde - Geochemistry, 2003, 63, 3–30 CrossRef CAS
.
- Y. Amelin and T. R. Ireland, Elements, 2013, 9, 39–44 CrossRef
.
- D. D. Bogard, Meteoritics, 1995, 30, 244–268 CrossRef CAS
.
- K. Rankenburg, A. D. Brandon and M. D. Norman, Geochim. Cosmochim. Acta, 2007, 71, 2120–2135 CrossRef CAS
.
-
M. Wadhwa, in Treatise on Geochemistry, ed. H. D. Holland and K. K. Turekian, Pergamon, Oxford, 2007, pp. 1–25 Search PubMed
.
- T. Kleine and J. F. Rudge, Elements, 2011, 7, 41–46 CrossRef CAS
.
-
G. J. Macpherson, S. B. Simon, A. M. Davis, L. Grossman and A. N. Krot, Astronomical Society of the Pacific Conference Series, in Chondrites and the Protoplanetary Disk, ed. A. N. Krot, E. R. D. Scott and B. Reipurth, 2005, vol. 341, pp. 225–250 Search PubMed
.
- J. N. Connelly, M. Bizzarro, A. N. Krot, A. Nordlund, D. Wielandt and M. A. Ivanova, Science, 2012, 338, 651–655 CrossRef CAS PubMed
.
- A. N. Krot, Y. Amelin, P. Bland, F. J. Ciesla, J. Connelly, A. M. Davis, G. R. Huss, I. D. Hutcheon, K. Makide, K. Nagashima, L. E. Nyquist, S. S. Russell, E. R. D. Scott, K. Thrane, H. Yurimoto and Q.-Z. Yin, Geochim. Cosmochim. Acta, 2009, 73, 4963–4997 CrossRef CAS
.
- M. Bizzarro, J. A. Baker and H. Haack, Nature, 2004, 431, 275–278 CrossRef CAS PubMed
.
- A. G. W. Cameron, Meteoritics, 1995, 30, 133–161 CrossRef CAS
.
- T. S. Kruijer, M. Touboul, M. Fischer-Godde, K. R. Bermingham, R. J. Walker and T. Kleine, Science, 2014, 344, 1150–1154 CrossRef CAS PubMed
.
- J. Blichert-Toft and F. Albarède, Earth Planet. Sci. Lett., 1997, 148, 243–258 CrossRef CAS
.
- E. Asphaug, M. Jutzi and N. Movshovitz, Earth Planet. Sci. Lett., 2011, 308, 369–379 CrossRef CAS
.
-
H. R. Rollinson, Early Earth Systems - a Geochemical Approach, Blackwell Publishing, Oxford, 2007, p. 296 Search PubMed
.
- L. T. Elkins-Tanton, E. M. Parmentier and P. C. Hess, Meteorit. Planet. Sci., 2003, 38, 1753–1771 CrossRef CAS
.
- K. Righter and M. J. Drake, Icarus, 1996, 124, 513–529 CrossRef CAS
.
- M. Wadhwa, Y. Amelin, O. Bogdanovski, A. Shukolyukov, G. W. Lugmair and P. Janney, Geochim. Cosmochim. Acta, 2009, 73, 5189–5201 CrossRef CAS
.
-
A. M. Davis, in Treatise on Geochemistry, ed. H. D. Holland and K. K. Turekian, Elsevier-Pergamon, Oxford, 2004, p. 737 Search PubMed
.
- D. C. Lee and A. N. Halliday, Nature, 1995, 378, 771–774 CrossRef CAS
.
- C. L. Harper and S. B. Jacobsen, Geochim. Cosmochim. Acta, 1996, 60, 1131–1153 CrossRef CAS
.
- K. Righter and C. K. Shearer, Geochim. Cosmochim. Acta, 2003, 67, 2497–2507 CrossRef CAS
.
- F. Nimmo and T. Kleine, Icarus, 2007, 191, 497–504 CrossRef
.
- S. B. Jacobsen, M. C. Ranen, M. I. Petaev, J. L. Remo, R. J. O'Connell and D. D. Sasselov, Philos. Trans. R. Soc., A, 2008, 366, 4129–4162 CrossRef CAS PubMed
.
- C. J. Allègre, G. Manhès and C. Göpel, Geochim. Cosmochim. Acta, 1995, 59, 1445–1456 CrossRef
.
- N. Kinoshita, M. Paul, Y. Kashiv, P. Collon, C. M. Deibel, B. DiGiovine, J. P. Greene, D. J. Henderson, C. L. Jiang, S. T. Marley, T. Nakanishi, R. C. Pardo, K. E. Rehm, D. Robertson, R. Scott, C. Schmitt, X. D. Tang, R. Vondrasek and A. Yokoyama, Science, 2012, 335, 1614–1617 CrossRef CAS PubMed
.
- M. Boyet and R. W. Carlson, Science, 2005, 309, 576–581 CrossRef CAS PubMed
.
- A. D. Brandon, T. J. Lapen, V. Debaille, B. L. Beard, K. Rankenburg and C. R. Neal, Geochim. Cosmochim. Acta, 2009, 73, 6421–6445 CrossRef CAS
.
- G. Caro, B. Bourdon, A. N. Halliday and G. Quitté, Nature, 2008, 452, 336–339 CrossRef CAS PubMed
.
- M. C. Ranen and S. B. Jacobsen, Science, 2006, 314, 809–812 CrossRef CAS PubMed
.
- M. Rehkämper, M. Gärtner, S. J. G. Galer and S. L. Goldstein, Chem. Geol., 1996, 129, 201–208 CrossRef
.
- V. Debaille, A. D. Brandon, C. O'Neill, Q. Z. Yin and B. Jacobsen, Nat. Geosci., 2009, 2, 548–552 CrossRef CAS
.
- A. N. Nguyen, F. J. Stadermann, E. Zinner, R. M. Stroud, C. M. O. 'D. Alexander and L. R. Nittler, Astrophys. J., 2007, 656, 1223–1240 CrossRef CAS
.
- C. Floss and F. J. Stadermann, Geochim. Cosmochim. Acta, 2009, 73, 2415–2440 CrossRef CAS
.
- C. Floss and F. J. Stadermann, Meteorit. Planet. Sci., 2012, 47, 992–1009 CrossRef CAS
.
- C. Vollmer, P. Hoppe, F. J. Stadermann, C. Floss and F. E. Brenker, Geochim. Cosmochim. Acta, 2009, 73, 7127–7149 CrossRef CAS
.
- M. Bose, C. Floss and F. J. Stadermann, Astrophys. J., 2010, 714, 1624–1636 CrossRef CAS
.
- M. Bose, C. Floss, F. J. Stadermann, R. M. Stroud and A. K. Speck, Geochim. Cosmochim. Acta, 2012, 93, 77–101 CrossRef CAS
.
- J. Leitner, C. Vollmer, P. Hoppe and J. Zipfel, Astrophys. J., 2012, 745, 38, DOI:10.1088/0004-637x/745/1/38
.
- X. Zhao, C. Floss, Y. Lin and M. Bose, Astrophys. J., 2013, 769, 49, DOI:10.1088/0004-637x/769/1/49
.
- L. R. Nittler, C. M. O. 'D. Alexander, X. Gao, R. M. Walker and E. K. Zinner, Nature, 1994, 370, 443–446 CrossRef CAS
.
- K. D. McKeegan, A. P. A. Kallio, V. S. Heber, G. Jarzebinski, P. H. Mao, C. D. Coath, T. Kunihiro, R. C. Wiens, J. E. Nordholt, R. W. Moses Jr, D. B. Reisenfeld, A. J. G. Jurewicz and D. S. Burnett, Science, 2011, 332, 1528–1532 CrossRef CAS PubMed
.
- L. Qin, D. Rumble, C. M. O. 'D. Alexander, R. W. Carlson, P. Jenniskens and M. H. Shaddad, Meteorit. Planet. Sci., 2010, 45, 1771–1777 CrossRef CAS
.
- A. Trinquier, J.-L. Birck and C. J. Allègre, Earth Planet. Sci. Lett., 2006, 241, 780–788 CrossRef CAS
.
- A. Trinquier, J.-L. Birck, C. J. Allègre, C. Göpel and D. Ulfbeck, Geochim. Cosmochim. Acta, 2008, 72, 5146–5163 CrossRef CAS
.
-
A. Shukolyukov and G. W. Lugmair, 37th Lunar. Planet. Sci. Conf., 2006, abstr. 1478 Search PubMed
.
- A. Shukolyukov and G. W. Lugmair, Earth Planet. Sci. Lett., 2006, 250, 200–213 CrossRef CAS
.
-
A. Shukolyukov and G. W. Lugmair and A. J. Irving, 40th Lunar. Planet. Sci. Conf., 2009, abstr. 1381 Search PubMed
.
- A. Yamakawa, K. Yamashita, A. Makishima and E. Nakamura, Anal. Chem., 2009, 81, 9787–9794 CrossRef CAS PubMed
.
- A. Yamakawa, K. Yamashita, A. Makishima and E. Nakamura, Astrophys. J., 2010, 720, 150–154 CrossRef CAS
.
-
K. Yamashita, T. Ueda, N. Nakamura, N. Kita and L. M. Heaman, 29th NIPR Symposium on Antarctic Meteorites, 2005, pp. 100–101 (abstr.) Search PubMed
.
- R. M. G. Armytage, R. B. Georg, P. S. Savage, H. M. Williams and A. N. Halliday, Geochim. Cosmochim. Acta, 2011, 75, 3662–3676 CrossRef CAS
.
- D. D. Bogard, Meteorit. Planet. Sci., 2009, 44, 3–14 CrossRef CAS
.
- K. H. Joy, M. E. Zolensky, K. Nagashima, G. R. Huss, D. K. Ross, D. S. McKay and D. A. Kring, Science, 2012, 336, 1426–1429 CrossRef CAS PubMed
.
- A. N. Halliday, Nature, 2004, 427, 505–509 CrossRef CAS PubMed
.
- S. B. Jacobsen and G. J. Wasserburg, Earth Planet. Sci. Lett., 1980, 50, 139–155 CrossRef CAS
.
- R. J. Walker, Chemie der Erde - Geochemistry, 2009, 69, 101–125 CrossRef CAS
.
- A. D. Brandon, R. J. Walker, J. W. Morgan, M. D. Norman and H. M. Prichard, Science, 1998, 280, 1570–1573 CrossRef CAS PubMed
.
- M. Gounelle and G. Meynet, Astron. Astrophys., 2012, 545, A4, DOI:10.1051/0004-6361/201219031
.
- E. R. D. Scott and I. S. Sanders, Geochim. Cosmochim. Acta, 2009, 73, 5137–5149 CrossRef CAS
.
- G. Quitté, C. Latkoczy, M. Schönbächler, A. N. Halliday and D. Günther, Geochim. Cosmochim. Acta, 2011, 75, 7698–7706 CrossRef
.
- M. Schönbächler, R. W. Carlson, M. F. Horan, T. D. Mock and E. H. Hauri, Geochim. Cosmochim. Acta, 2008, 72, 5330–5341 CrossRef
.
- J. H. Reynolds, Phys. Rev. Lett., 1960, 4, 8–9 CrossRef CAS
.
- Q.-Z. Yin, S. B. Jacobsen, K. Yamashita, J. Blichert-Toft, P. Télouk and F. Albarède, Nature, 2002, 418, 949–952 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2016 |