Open Access Article
Open Access ArticleCapabilities of fast data acquisition with microsecond time resolution in inductively coupled plasma mass spectrometry and identification of signal artifacts from millisecond dwell times during detection of single gold nanoparticles†
I.
Strenge
and
C.
Engelhard
 *
*
University of Siegen, Department of Chemistry and Biology, Adolf-Reichwein-Str. 2, 57068 Siegen, Germany. E-mail: engelhard@chemie.uni-siegen.de
First published on 3rd August 2015
Abstract
In inductively coupled plasma mass spectrometry (ICP-MS), short transient signals originating from individual nanoparticles are typically recorded in a time-resolved measurement with reduced dwell times in the millisecond time regime. This approach was termed single-particle ICP-MS in the past and used for particle counting and sizing but is not without limitations. In this work, a home-built data acquisition unit (DAQ) specifically tailored to the needs of single-particle ICP-MS applications was developed to study and alleviate some of these limitations. For best comparison, data were acquired simultaneously with both techniques. Each experiment was carried out as a conventional time-resolved measurement, while the DAQ directly probed the instrument's detection circuitry. Our DAQ features dwell times as low as 5 μs during continuous data acquisition and can be operated for virtually unlimited measurement time. Using a time resolution much higher than the typical duration of a particle-related ion cloud, the probability of measurement artifacts due to particle coincidence could be significantly reduced and the occurrence of split-particle events in fact was almost eliminated. Moreover, a duty cycle of 100% of the counting electronics improves the method's accuracy compared to the acquisition system of currently available ICP-Q-MS instruments. Fully time-resolved temporal profiles of transient signals originating from single gold nanoparticles as small as 10 nm are presented. The advantages and disadvantages of millisecond versus microsecond dwell times are critically discussed including measurement artifacts due to particle coincidence, split-particle events, and particle number concentration.
Introduction
Engineered nanomaterial (ENM) production and use are steadily increasing, which, in turn, lead to environmental release of ENMs.1 In the past, their widespread use raised concerns that call for risk assessment and toxicity studies.2 Clearly, powerful analytical instruments and procedures are required to identify, quantify, and characterize ENMs in terms of shape, size, and elemental composition.3One promising approach for the rapid detection of ENMs (even at environmentally relevant concentrations) is the analysis of single particles by means of inductively coupled plasma mass spectrometry (ICP-MS). The idea dates back to 1986, when Kawaguchi et al. demonstrated the detection of emission signals from single airborne particles using inductively coupled plasma optical emission spectrometry (ICP-OES).4 Three years later, Bochert and Dannecker presented the first continuous acquisition of millisecond time-resolved emission signals from particles in combination with a computer-assisted data processing solution.5 At this time, Nomizu et al. adopted the analysis of single airborne particles using ICP-MS.6 Olesik and Hobbs demonstrated in an early investigation the influence of single vaporizing particles and incompletely vaporized droplets on signals in ICP-MS. They sampled the detector's analog signal and were able to record temporal profiles of individual transients with a time resolution of tens of microseconds.7 It is important to note that outstanding time resolution for both emission and mass spectrometric signals was achieved quite early, but sophisticated (and costly) equipment and modifications to the instruments were required. Ultimately, Degueldre and Favarger showed the feasibility of analyzing sub-micrometer sized colloids using an unmodified, commercial ICP-MS.8 They analyzed highly diluted aqueous suspensions with a low particle number concentration, allowing analysis of single particles even at lower time resolution, a concept nowadays termed single particle ICP-MS (spICP-MS). Later, nano-sized airborne particles were studied using the same instrument and approach but in combination with an aerosol particle mass analyzer as a complementary technique for particle size determination by Suzuki et al.9 Recently, additional advantages due to the combination of spICP-MS with separation techniques were demonstrated, for example, by Pergantis et al.10 using hydrodynamic chromatography, and Loeschner et al.11 using asymmetrical flow field flow fractionation for characterization of nanoparticles in more complex samples.
To determine the particle size distribution, particle number concentration, and chemical composition of single nanoparticles on a particle-by-particle basis solely by means of ICP-MS one would need an ICP-MS instrument that provides truly simultaneous multi-element detection capabilities combined with sufficient sensitivity, linear range, and suitable time resolution. Apart from very specialized and expensive multi-collector ICP-MS instrumentation, however, only very few instruments were recently developed (i.e., time-of-flight ICP-MS instruments developed by Bandura et al.12 and Borovinskaya et al.,13 respectively) that are aiming to achieve these goals for the detection of individual biological cells and micro-/nanoparticles. The majority of ICP-MS instruments, however, apply quadrupole (ICP-Q-MS) or magnetic sector field (ICP-SF-MS) mass analyzers and most of the published work on spICP-MS was carried out using these scanning-type instruments. In the case of spICP-Q-MS, the settling time of the quadrupole is currently a fundamental limitation; a fully time-resolved analysis of more than only a few different isotopes throughout the transient ion signal originating from a single particle event cannot be performed today. In addition, currently available ICP-Q-MS instruments are considered to be not very well suited for the acquisition of fast transient signals and over long periods of measurement time. Typically, the minimal dwell time that can be selected ranges from 0.1 ms to 10 ms, the recorded data may contain dead times between individual dwells,14 and the total measurement time is restricted by a maximum number of acquisitions per run. Clearly, accurate and time-resolved detection of single particles by ICP-Q-MS remains challenging. It is noteworthy that particle analysis today is typically carried out by undersampling transient signals with rather long dwell times of 5–10 ms. If one considers the fact that particles will reach the ICP in a rather unpredictable manner (i.e., varying frequencies) when conventional sample introduction systems are used, shorter dwell times will result in a higher probability of splitting up signals originating from single particles into two adjacent dwell time intervals (“split-particle events”). In contrast, longer dwell times will increase the probability of more than one particle reaching the ICP in one dwell time/integration window (“particle coincidence”) and result in decreased signal-to-noise ratios. To tackle the limitations mentioned above and to make higher particle number concentrations accessible to spICP-MS, a fully time-resolved acquisition of every single particle by oversampling its transient signals using a much shorter dwell time would be required.
In recent years, several attempts have been made to improve the time resolution in spICP-MS. In 2002, Nomizu et al. developed a high-speed digital signal processing system capable of sampling the detector's pulse signal with a time resolution of 20 μs continuously for up to 5 s.15 Liu et al. investigated artifacts of particle coincidence and split-particle events by using a conventional, unmodified ICP-Q-MS operating at 100 μs dwell time for up to 6.5 s.16 Gschwind et al. used a combination of ICP-Q-MS software plus a digital storage oscilloscope for shorter dwell time acquisitions. Here, a time resolution of 10 μs was achieved during discontinuous introduction of monodisperse droplets. Data were stored and processed using a custom LabView program.17,18 Shigeta et al. reported temporal profiles of ion events with 100 μs time resolution using an ICP-SF-MS instrument in fast E-scanning mode.19 Recently, Montaño et al. demonstrated the feasibility to detect silver and gold in a core–shell particle using spICP-Q-MS with a dwell time of 100 μs and a fixed settling time of 100 μs. Per single particle event, one to three data points were obtained for 107Ag and 197Au, respectively.20 Clearly, very interesting approaches to improve the time resolution in spICP-Q-MS have been reported in recent years. However, previous studies were either severely limited in the total measurement time, required specialized (and costly) instrumentation or were restricted to a certain instrumental setup.
In this work, a home-built data acquisition unit (DAQ) is presented that features dwell times as short as 5 μs during truly continuous acquisition over any length of measurement. It was successfully tested on three different ICP-Q-MS systems (Perkin-Elmer Elan 6000, Agilent Technologies 7500, and Thermo iCap Qc). The performance is critically discussed in direct comparison to data obtained from simultaneous detection of ion events using the vendor DAQ system on the same ICP-Q-MS (iCap Qc). Gold nanoparticles were investigated as model particles and fully time-resolved temporal profiles of transient signals originating from single gold nanoparticles as small as 10 nm are presented. The capabilities of millisecond versus microsecond dwell times are critically discussed including measurement artifacts due to particle coincidence, split-particle events, and particle number concentration.
Experimental
Sample preparation
Monodisperse AuNPs with a spherical shape and nominal sizes of 10 (9.1 ± 0.8) nm, 20 (20.0 ± 1.8) nm, 30 (28.8 ± 3.3) nm, 40 (39.5 ± 3.8) nm and 60 (58.7 ± 6.8) nm were purchased from nanoComposix (San Diego, CA, USA). All samples were stored in darkness at 2 °C prior to analysis. The suspensions were shaken for 30 s before dilution to the desired concentration with double-distilled water. Sample analysis was performed immediately after dilution.Aqueous solutions for instrument tuning were prepared by diluting standard stock solutions of 1000 μg L−1 Li, In, Ba, Ce, Au, Tl, and U (Inorganic Ventures, Christiansburg, VA, USA) in 2–3% HNO3 (CertiPUR, Merck KGaA, Darmstadt, Germany) with double-distilled water to the desired final concentration.
Experimental setup
A model DS-5 micro-flow nebulizer (Teledyne CETAC Technologies, Omaha, NE, USA) with a low-volume spray chamber was coupled to different ICP-Q-MS instruments and operated in self-aspiration mode. The sample uptake rate at a nebulizer gas flow rate of 0.58 L min−1 (cf.Table 1) was found to be 2.60 ± 0.1 μL min−1.| RF power | 1400 W |
| Sampling depth | 0.5 mm |
| Cooling gas flow | 14 L min−1 |
| Auxiliary gas flow | 0.8 L min−1 |
| Nebulizer gas flow | 0.58 L min−1 |
| Torch injector ID | 1.0 mm (quartz) |
| Skimmer type | Ni (insert version) |
| Insert type | Cone insert 2.8 |
| Interface pressure | 1.25 ± 0.01 mbar |
All work presented in the following section was performed on a model iCap Qc (Thermo Fisher Scientific, Bremen, Germany) ICP-Q-MS instrument. To increase the overall sensitivity, the original skimmer cone insert was replaced by a high-sensitivity insert (insert “2.8”, Glass Expansion, Melbourne, Australia). In addition, a second roughing pump (UNO 030 B, Pfeiffer Vacuum, Asslar, Germany) was added to the first vacuum stage to further reduce the interface pressure (p = 1.25 ± 0.01 mbar throughout all measurements).
Previous development of the home-built DAQ was carried out on a model ELAN 6000 (PerkinElmer, Toronto, Canada) instrument (cf. Fig. SI-1† for exemplary data) as well as on a model 7500 (Agilent Technologies, Santa Clara, CA, USA) instrument (data not shown) under similar operating conditions.
Data acquisition
All data shown in this work were simultaneously acquired using two different techniques, while each experiment was carried out as a conventional time-resolved measurement using vendor software, and the home-built DAQ directly probed the instrument's detection circuitry as described in the following. In doing so, the vendor software retained control over all important operation parameters (i.e., measurement runtime, SEM and lens voltages, and quadrupole settings). At the same time, software-defined threshold conditions of the detection circuitry are valid for both the instrument and the home-built DAQ.Data acquisition with vendor software
To achieve suitable conditions when using the instrument and vendor software (QTegra ISDS 2.4, Thermo Fisher Scientific), measurements of only one isotope (197Au, resolution “normal”, no interference correction) were carried out with the dwell time set to 10 ms or 0.5 ms, respectively. Because only raw data were of interest for subsequent data processing steps, a simple acquisition mode (“tQuant”) was selected in the vendor software. Data were exported as a text file containing character-separated values (.csv-file).Data acquisition with the home-built DAQ
In this work, a custom DAQ specifically tailored to the needs of spICP-Q-MS applications was developed. It enables continuous ICP-Q-MS data acquisition with microsecond time resolution and 100% duty cycle. Fully time-resolved temporal profiles of each single particle event can be obtained. Most importantly, data can be acquired continuously for any length of measurement time (only limited by the capacity of the data storage device). The DAQ presented here currently features a shortest integration time (i.e., highest time resolution) of 5 μs during continuous acquisition.Data processing and evaluation
Ideally, the transient signal from a single AuNP (i.e., the number of pulses detected per particle event) is directly proportional to the number of gold ions that are sampled after complete particle vaporization/ionization in the ICP. In turn, the number of gold ions should be proportional to the number of atoms present in the corresponding particle. For a dispersion of NPs with known morphology and chemical composition, the observed transient signals can then be analyzed to obtain information about the particle size distribution in the sample. Fundamentals and considerations required to use spICP-MS for the characterization of the nanoparticle size and number concentration were discussed, for example, by Olesik and Gray,21 Laborda et al.22 and Pace et al.,23 and shall not be repeated here.According to the manufacturer's specification, characteristic size distributions of solid, spherical NPs with a certain mean size are to be expected for all AuNP dispersions used in this work. To a first approximation, the particle size therefore should relate to the cubic root of the observed signal intensity. Because the focus of this work is on the accurate counting of pulses from transient signals rather than on the precise sizing of particles, only histograms illustrating the intensity distributions will be used below. Simple Gaussian fits providing mean intensity xc and standard deviation σ are considered to sufficiently describe any obtained intensity distribution, while still providing direct access to the absolute count values for better comparison. It is important to note that accurate size determination of particles by ICP-MS is still a challenging task and several aspects have to be carefully considered including size-dependent vaporization of nanoparticles,7,24 possible variations in the diffusion of ion clouds from microdroplets,25 and non-ideal aerosol trajectories26 in the plasma.21
Processing of data acquired with vendor software
When using the export plugins provided by the vendor software to export time-resolved measurements, data are obtained in counts per second (CPS), regardless of the actual dwell time used at the time of data acquisition. Clearly, this is not suitable for the description of discrete signal spikes resulting from individual particles. In this work, the exported data were manually corrected by multiplying the reported intensity with the set dwell time to give the absolute number of pulses registered in a specific integration window (counts per dwell time, cpd).After conversion to cpd, data were processed in either of the two following ways, depending on the particle number concentration (CNP) of the sample. For CNP ≤ 5 × 105 NP mL−1, intensity histograms were obtained by directly binning the data, since not more than one particle was expected to reach the ICP per dwell time of 10 ms. The bin size was chosen to be approximately one tenth of the lowest mean count rate in the corresponding distribution. For CNP > 5 × 105 NP mL−1, where data were acquired at a dwell time of 0.5 ms, a series of five, ten, and twenty data points of the transient signal were summed up prior to binning the data. This resulted in calculated integration times of 0.5, 2.5, 5, and 10 ms, respectively.
Processing of data acquired with the home-built DAQ
Data obtained from the DAQ are a sequence of truly continuous dwells with a period of 5 μs each. With a time base significantly shorter than the shortest expectable single-particle event, an individual ion cloud from a particle event typically appears as a series of signal pulses in quick succession. Therefore, additional data processing is necessary to obtain information on a per-particle basis. Particle-related information was extracted from the raw data using a command-line tool (written in “C”) specifically tailored for this task. After extraction, a reduced dataset only containing time-resolved data from transient events matching user-defined extraction conditions (threshold conditions) is provided. By summing up all signal pulses per particle event, a further simplified dataset is generated that provides only the number of counts per event (cpe) for a given period of time. These data can then be handled similarly to the data acquired with vendor software, as described above.Signal artifacts
It is important to note that signal artifacts due to dead time effects are intrinsically associated with strong transient signals. They are observed regardless of the acquisition system, and especially for short signal bursts an appropriate correction still remains challenging. Thankfully, typically only a small part of the particles' ion clouds is affected by these count losses. Ion counting at the rising and falling edges of each ion cloud, where much lower count rates are observed, is considered to be almost unaffected. Nevertheless, all data presented in this work were carefully evaluated and only samples containing particles, which are small enough that their maximum count rates at least did not exceed ≈ 35 counts/5 μs, are presented in the following (cf. Fig. SI-3,† depicting <7% total count losses supposed to occur for a typical transient signal of 30 nm AuNPs). Hence, all given data represent the actual count values registered by the electronics and no correction for possible count losses was performed.
Results and discussion
In total, three different samples (30 nm AuNPs with CNP = 2.5 × 105 NP mL−1, 30 nm AuNPs with CNP = 2.5 × 106 NP mL−1, and 10 nm AuNPs with CNP = 5 × 105 NP mL−1) were analyzed in the following. The corresponding results will be discussed from different perspectives. Prior to each measurement, experimental conditions (cf.Table 1) were thoroughly optimized with respect to a stable and homogeneous sample aerosol, highest sensitivity for 197Au, and low background. Therefore, the overall detection efficiencies might slightly differ between these experiments.Capabilities of microsecond vs. millisecond time-resolved data acquisition at different particle number concentrations
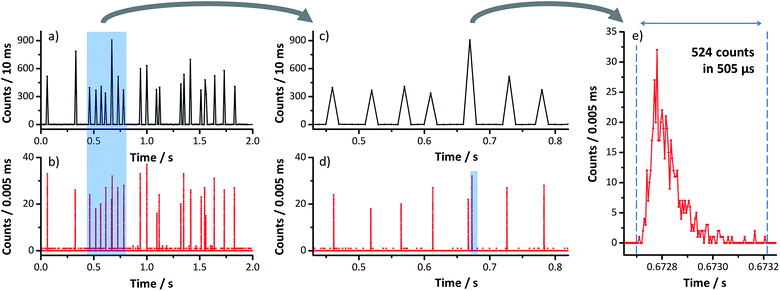
Typically, very dilute samples are used in proof-of-principle spICP-MS studies to avoid unwanted measurement artifacts from particle coincidence. However, it is unlikely that the particle concentration can always be controlled, for example, during analyses of unknown environmental samples or when coupling separation techniques to ICP-MS. Thus, the following two experiments were performed to study the influence of the particle number concentration on the data quality from conventional (ms time scale) versus fast data acquisition with increased time resolution (μs time scale).In Fig. 1, a selection of the recorded detector response acquired simultaneously with both techniques during the introduction of a single 30 nm AuNP into the ICP-Q-MS is presented. Individual signal spikes that were detected over the course of two seconds (cf.Fig. 1a and b) match fairly well on both detection channels. However, by taking a closer look (cf.Fig. 1c and d), a first discrepancy of data from micro- vs. millisecond time-resolved DAQ can be observed at 0.67 s. Here, ion signals originating from two individual particles occurred during a single 10 ms dwell but were not adequately resolved by the vendor software. Fig. 1e exemplarily shows the temporal profile of an ion cloud from a 30 nm sized AuNP (zoom-in, Fig. 1d at 0.67 s). In this example of a coincidence of two particles, the vendor DAQ (10 ms dwell time) registered one particle event with approximately 900 counts, whereas the home-built DAQ was able to detect two particles with, for example, one NP featuring 524 counts in 505 μs.
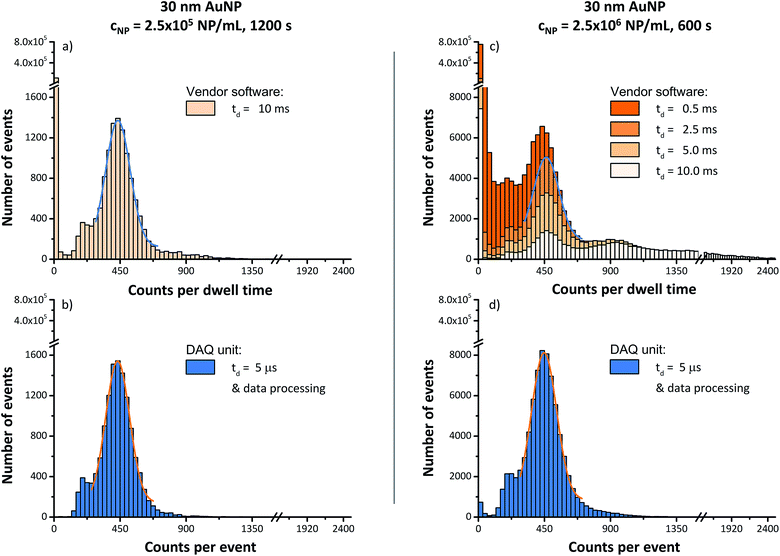
In Fig. 2a and b, the corresponding intensity histograms after binning raw data (cf.Fig. 1) with a bin size of 30 counts (per dwell time or per event) are presented. Here, both histograms show similar patterns. Gaussian fits were used (with limited applicability to the actual intensity distribution) and result in almost identical mean count rates of xc = 435 cpd and xc = 433 cpe, respectively. Nevertheless, two significant peculiarities can be observed. On the one hand, the distribution acquired with vendor software shows a very high number of events in the first bin (0–30 cpd) due to the continuous background signal. On the other hand, a slightly broader distribution is obtained from data acquired with vendor software, including a number of events that show significantly higher count rates when compared to acquisition with the home-built DAQ. In most cases, transient data with microsecond time resolution can give evidence that this is due to aforementioned measurement artifacts of particle coincidence. In a total measurement time of 1200 s, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 551 events were observed with the vendor software that show an intensity >30 cpd. In comparison with the home-built DAQ, a slightly higher number of 12
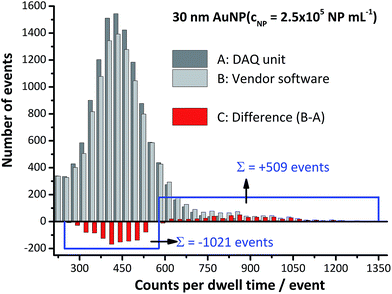
551 events were observed with the vendor software that show an intensity >30 cpd. In comparison with the home-built DAQ, a slightly higher number of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 events was observed. In the signal range from 240 cpd to 600 cpd, acquisition with vendor software resulted in the detection of 1021 fewer events compared to results obtained with the home-built DAQ (cf.Fig 3). In the range from 601 cpd to 1350 cpd, however, 509 events more compared to acquisition with the home-built DAQ were found. If one assumes that these events are solely due to particle coincidences (two particles per dwell time), 509 × 2 = 1018 of the missing 1021 events can be recovered. Clearly, this is a simplification of the situation, but this data evaluation already leads to a percentage of 3.9% of all events (acquired with vendor software) that are likely to be affected by particle coincidence. This is in good agreement with the theoretically calculated value of 5% (cf. Table SI-1†). It should be noted that except from conditions applied to extract particle-related data (signal pulses have to occur in a successive manner rather than randomly distributed over a certain timeframe) no cut-off at lower count values was applied to the data acquired with the home-built DAQ. In total, only eleven events were observed in the first four bins (0–120 cpe).
928 events was observed. In the signal range from 240 cpd to 600 cpd, acquisition with vendor software resulted in the detection of 1021 fewer events compared to results obtained with the home-built DAQ (cf.Fig 3). In the range from 601 cpd to 1350 cpd, however, 509 events more compared to acquisition with the home-built DAQ were found. If one assumes that these events are solely due to particle coincidences (two particles per dwell time), 509 × 2 = 1018 of the missing 1021 events can be recovered. Clearly, this is a simplification of the situation, but this data evaluation already leads to a percentage of 3.9% of all events (acquired with vendor software) that are likely to be affected by particle coincidence. This is in good agreement with the theoretically calculated value of 5% (cf. Table SI-1†). It should be noted that except from conditions applied to extract particle-related data (signal pulses have to occur in a successive manner rather than randomly distributed over a certain timeframe) no cut-off at lower count values was applied to the data acquired with the home-built DAQ. In total, only eleven events were observed in the first four bins (0–120 cpe).
When qualitatively comparing the intensity histograms from vendor software (cf.Fig. 2c) with the previously obtained histogram at CNP = 2.5 × 105 NP mL−1 and tdwell = 10 ms (cf.Fig. 2a), a dwell time of 2.5 ms reflects the expected intensity distribution best. However, the mean count value shifted from xc = 435 cpd to xc = 462 cpd. Also, coincidence of multiple particles per dwell time occurred significantly more often. 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575 events could be observed in total (2.5 ms dwell time, first bin at 0–30 cpd considered background) with 6654 events (10.3%) that exhibited count values ≥2xc. In comparison, around 12% of the observed events are expected to be affected by particle coincidence from a Poisson distribution (cf. Table SI-1†).
575 events could be observed in total (2.5 ms dwell time, first bin at 0–30 cpd considered background) with 6654 events (10.3%) that exhibited count values ≥2xc. In comparison, around 12% of the observed events are expected to be affected by particle coincidence from a Poisson distribution (cf. Table SI-1†).
In contrast, the DAQ unit intensity distribution (cf.Fig. 2d) remained virtually unaffected at a higher particle number concentration and even slightly asymmetric characteristics in the histogram (e.g., bins 180–240 cpe) were reported in a similar manner. The mean count value (xc = 448 cpe) as well as the upper and lower limits of count values did not change significantly. In total, 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 events were detected, whereof only 1320 events (1.7%) showed count values ≥2xc. From Poisson statistics, not more than 3% of the obtained particle events are supposed to be affected by particle coincidence.
912 events were detected, whereof only 1320 events (1.7%) showed count values ≥2xc. From Poisson statistics, not more than 3% of the obtained particle events are supposed to be affected by particle coincidence.
Identification of signal artifacts from millisecond dwell times during detection of single gold nanoparticles
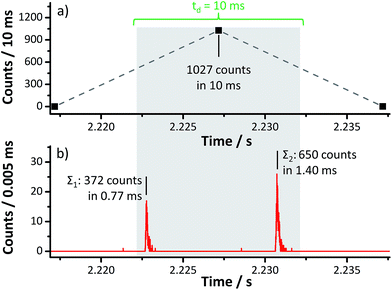
In the following, microsecond time-resolved transient data are used to investigate signal artifacts that can likely occur in conventional spICP-MS. In Fig. 4 and 5, 197Au signals are exemplarily depicted that belong to the same measurement of 30 nm sized AuNPs (dwell time of 10 ms, 1200 s) that was discussed above. Two artifacts that were observed (and will be discussed in detail below) in fact entered the intensity distribution, shown in Fig. 2a.In the first example, two nanoparticles were introduced into the ICP shortly after each other (7 ms) and were individually detected successfully with the home-built DAQ (cf.Fig. 4b, tdwell = 5 μs). Count rates were 372 counts in 0.77 ms and 650 counts in 1.40 ms, respectively (sum 1022 counts). A potential pitfall in spICP-MS (and when selecting dwell times on the millisecond time scale) is evident from Fig. 4a. Here, the vendor software detected 1027 counts in a single 10 ms dwell. One would think to just have recorded one single particle of a bigger size.
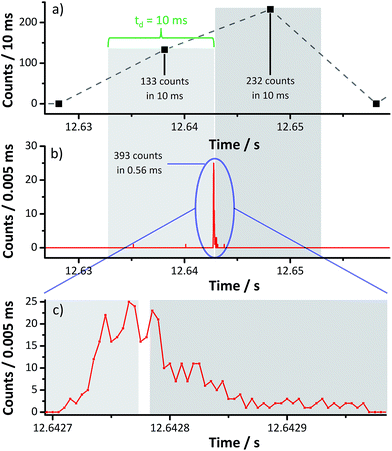
In contrast, another artifact may lead to a complete opposite conclusion. In Fig. 5a, two adjacent dwells recorded with vendor software show a count value different from zero (133 cpd and 232 cpd, respectively). In turn, one would assume to have registered two small but individual particles reaching the ICP shortly one after each other. Time-resolved data from the acquisition with our DAQ, however, reveal that only one particle was present but was detected at the very end of the first dwell (cf.Fig. 5b). In the vendor software, the corresponding signal is being split up and counts are partly assigned to the dwell that follows. Based on the examples discussed above, split-particle events have to be carefully considered in spICP-MS because they will distort the results. Specifically, at least three artifacts may emerge at the same time: underestimation of the corresponding particle size, overestimation of the overall particle number concentration and potential underestimation of the total count rate of the affected transient signal.
In addition, another artifact was uncovered using microsecond time resolved data acquisition. It seems to be the case that the conventional acquisition system is blind in between two sequential dwells for a short period of time. To render this artifact visible more easily, an example was chosen in which the transient event is being split up just at the moment where the highest count rate should occur (cf.Fig. 5c). In this case, the observed deviation is more significant compared to a short counting gap occurring at the rising or falling edge of the transient signal. In particular, with vendor software only 133 + 232 = 365 cpd instead of 393 cpe were detected. In other words, acquisition with the conventional DAQ results in a duty-cycle <100% even when operated at a dwell time as long as 10 ms.
Detection efficiency and analyte mass detection limits
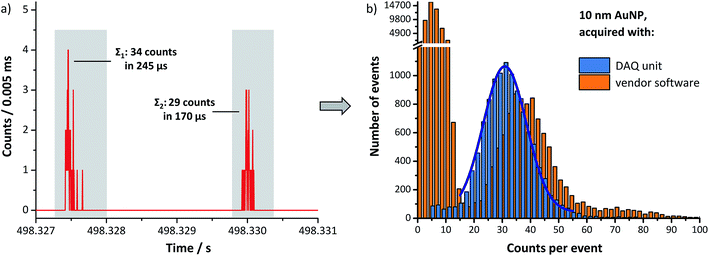
After careful ICP-MS optimization, a diluted suspension of 10 nm sized AuNPs (CNP = 5 × 105 NP mL−1, ttotal = 600 s) was analyzed. Single ion events originating from 10 nm AuNPs were successfully detected with microsecond time resolution using the home-built DAQ (cf.Fig. 6a) but also with the vendor software (transient data not shown here).For acquisition with vendor software, a continuous background signal from dissolved gold was observed for the particle suspension used in this experiment. This is reflected in the corresponding intensity histogram (cf.Fig. 5b), which shows a bimodal intensity distribution from signals of dissolved analytes (xc,BG = 5.7 cpd, background) and particles (xc,NP = 38.1 cpd, no background correction), respectively. The total number of particles that were detected in 600 s was found to be 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118 particles, assuming the first eight bins (0–16 cpd) to be only non-particle-related background. In the histogram, however, also the intensity distribution >17 cpd, supposedly representing mainly particle-related data, clearly deviates from a distribution expected for a sample containing a monodisperse particle suspension. This is assumed to be due to the artifacts discussed above including particle coincidence (probability of a dwell time of 10 ms approximately 5%, cf. Table SI-1†) and split-particle events.
118 particles, assuming the first eight bins (0–16 cpd) to be only non-particle-related background. In the histogram, however, also the intensity distribution >17 cpd, supposedly representing mainly particle-related data, clearly deviates from a distribution expected for a sample containing a monodisperse particle suspension. This is assumed to be due to the artifacts discussed above including particle coincidence (probability of a dwell time of 10 ms approximately 5%, cf. Table SI-1†) and split-particle events.
In contrast, data acquired with the home-built DAQ reveal only one relatively narrow intensity distribution at xc = 30.9 cpe. Transient signals from AuNPs as small as 10 nm can be identified and handled independently, even when they occur very closely one after each other (cf.Fig. 6a, events are separated by only 2.3 ms). As a result, noticeably fewer events for count rates significantly lower or higher than the mean count rate were observed. Clearly, it cannot be excluded that single non-particle-related pulses from the continuous background signal are buried under the two pulse sequences. With a continuous background of 5.7 counts in 10 ms, in fact 2.28 counts are expected to occur on average even in the depicted section of 4 ms. Events are neither lost due to particle coincidence (probability of CNP = 5 × 105 NP mL−1 and average temporal duration of 400 μs per particle is assumed to be <1%, cf. Table SI-1†), nor because any part of a split-particle event is falsely counted as continuous background. Therefore, the slightly higher number of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 particles obtained for acquisition with the DAQ is assumed to be more accurate. Further experiments on this finding are planned for the future.
120 particles obtained for acquisition with the DAQ is assumed to be more accurate. Further experiments on this finding are planned for the future.
Acquisition with the DAQ resulted in a mean count value of 30.9 cpe for AuNPs with an average size of 9.1 nm. This corresponds to approximately 2.3 × 104 atoms if one assumes a perfect spherical shape and bulk density of gold. Thus, the instrument's detection efficiency for 197Au under given conditions can be calculated to be 1.3 × 10−3 counts per atom.
The analyte mass detection limit typically is determined by calculating three times the standard deviation of the blank divided by the instrument's sensitivity. In spICP-MS, instead of a true blank measurement, the continuous background signal of every sample should be taken into account but cannot be measured independently of any particle-related signal. In addition, counting statistics have to be considered. With short dwell times, the background signal often may be at or near zero counts, resulting in a finite uncertainty of at least 0.25 ag for the given sensitivity. Therefore, all values in the following are adjusted upward to the next integer.
When using the vendor software, it was found that at least 3σBG = 9 cpd have to be registered to be able to flag the detection of a single gold particle. Acquisition with the home-built system (using a short integration time of 5 μs) resulted in a slightly improved limit of detection (LOD) of 3 cpe because σBG was observed to be below 1 count in any time span between two particle events occurring. Here, a minimum count rate of 3 ± 1 cpe corresponds to a calculated lower LOD of approximately 2200 ± 750 gold atoms, which corresponds to a spherical and solid AuNP with a diameter of 3.9 to 4.6 nm. When using the vendor software for acquisition, a limit of detection of approximately 4500 ± 750 gold atoms (AuNP particle diameter of 5.3 to 5.6 nm) was obtained.
However, it should be noted that AuNPs with a nominal size of 5 nm were not used in the study. Also, a low ionic background is an ideal (and not always realistic) case for the determination of the analytical performance. In real samples, the particle size detection limit will degrade, for example, when dissolved analytes are present.
Conclusions
In this study, the influence of the data acquisition system on the data quality in single nanoparticle ICP-MS is critically discussed. Samples containing AuNPs with nominal sizes of 10 nm and 30 nm at different particle number concentrations were analyzed simultaneously using two different acquisition techniques, one of them being a home-built DAQ. Measurements with a time resolution of 5 μs were performed continuously for up to 1200 s.It could be demonstrated that providing microsecond time resolution to conventional ICP-Q-MS is a very effective method to increase both the quality and validity of the obtained data when using a single-particle based approach for nanoparticle analysis. Simultaneous acquisition allows precise identification of measurement artifacts due to insufficient time resolution and confirms that Poisson statistics can appropriately describe the probability of these artifacts to occur. Temporal profiles of individual ion clouds can give evidence of a detected signal specifically originating from a single particle. In addition, proper recognition of all transmitted ions due to a 100% duty cycle of the counting electronics can improve the method accuracy, especially with respect to small particles and short transient signals. A time resolution much higher than the typical duration of a particle-related ion cloud can help to estimate the impact of potential count losses due to the occurrence of intense signals from larger particles. Furthermore, the probability of particle coincidence is significantly reduced. At the same time, split-particle events are unlikely to occur due to the absence of a fixed integration time window. This, in turn, helps to use spICP-MS in a wider particle number concentration range than that reported before.
Acknowledgements
Support by the glassblower and the machine shop services at the Department of Chemistry and Biology, University of Siegen, is gratefully acknowledged.Notes and references
- F. Gottschalk and B. Nowack, J. Environ. Monit., 2011, 13, 1145–1155 RSC.
- M. A. Maurer-Jones, I. L. Gunsolus, C. J. Murphy and C. L. Haynes, Anal. Chem., 2013, 85, 3036–3049 CrossRef CAS PubMed.
- A. G. Howard, J. Environ. Monit., 2010, 12, 135–142 RSC.
- H. Kawaguchi, N. Fukasawa and A. Mizuike, Spectrochim. Acta, Part B, 1986, 41, 1277–1286 CrossRef.
- U. K. Bochert and W. Dannecker, J. Aerosol Sci., 1989, 20, 1525–1528 CrossRef CAS.
- T. Nomizu, S. Kaneco, T. Tanaka, T. Yamamoto and H. Kawaguchi, Anal. Sci., 1993, 9, 843–846 CrossRef CAS.
- S. E. Hobbs and J. W. Olesik, Anal. Chem., 1992, 64, 274–283 CrossRef CAS PubMed.
- C. Degueldre and P. Y. Favarger, Colloids Surf., A, 2003, 217, 137–142 CrossRef.
- Y. Suzuki, H. Sato, S. Hikida, K. Nishiguchi and N. Furuta, J. Anal. At. Spectrom., 2010, 25, 947–949 RSC.
- S. A. Pergantis, T. L. Jones-Lepp and E. M. Heithmar, Anal. Chem., 2012, 84, 6454–6462 CrossRef CAS PubMed.
- K. Loeschner, J. Navratilova, C. Kobler, K. Molhave, S. Wagner, F. von der Kammer and E. H. Larsen, Anal. Bioanal. Chem., 2013, 405, 8185–8195 CrossRef CAS PubMed.
- D. R. Bandura, V. I. Baranov, O. I. Ornatsky, A. Antonov, R. Kinach, X. Lou, S. Pavlov, S. Vorobiev, J. E. Dick and S. D. Tanner, Anal. Chem., 2009, 81, 6813–6822 CrossRef PubMed.
- O. Borovinskaya, B. Hattendorf, M. Tanner, S. Gschwind and D. Günther, J. Anal. At. Spectrom., 2013, 28, 226–233 RSC.
- C. Degueldre and P. Y. Favarger, Talanta, 2004, 62, 1051–1054 CrossRef CAS PubMed.
- T. Nomizu, H. Hayashi, N. Hoshino, T. Tanaka, K. Kitagawa and S. Kaneco, J. Anal. At. Spectrom., 2002, 17, 592–595 RSC.
- J. Liu, K. E. Murphy, R. I. Maccuspie and M. R. Winchester, Anal. Chem., 2014, 86, 3405–3414 CrossRef CAS PubMed.
- S. Gschwind, L. Flamigni, J. Koch, O. Borovinskaya, S. Groh, K. Niemax and D. Günther, J. Anal. At. Spectrom., 2011, 26, 1166–1174 RSC.
- J. Koch, L. Flamigni, S. Gschwind, S. Allner, H. Longerich and D. Günther, J. Anal. At. Spectrom., 2013, 28, 1707–1717 RSC.
- K. Shigeta, H. Traub, U. Panne, A. Okino, L. Rottmann and N. Jakubowski, J. Anal. At. Spectrom., 2013, 28, 646–656 RSC.
- M. D. Montaño, H. R. Badiei, S. Bazargan and J. F. Ranville, Environ. Sci.: Nano, 2014, 1, 338–346 RSC.
- J. W. Olesik and P. J. Gray, J. Anal. At. Spectrom., 2012, 27, 1143–1155 RSC.
- F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2011, 26, 1362–1371 RSC.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, C. P. Higgins and J. F. Ranville, Anal. Chem., 2011, 83, 9361–9369 CrossRef CAS PubMed.
- K. Niemax, Spectrochim. Acta, Part B, 2012, 76, 65–69 CrossRef CAS.
- C. C. Garcia, A. Murtazin, S. Groh, V. Horvativ and K. Niemax, J. Anal. At. Spectrom., 2010, 25, 645–653 RSC.
- O. Borovinskaya, M. Aghaei, L. Flamigni, B. Hattendorf, M. Tanner, A. Bogaerts and D. Günther, J. Anal. At. Spectrom., 2014, 29, 262–271 RSC.
- H. E. Pace, N. J. Rogers, C. Jarolimek, V. A. Coleman, E. P. Gray, C. P. Higgins and J. F. Ranville, Environ. Sci. Technol., 2012, 46, 12272–12280 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ja00177c |
| This journal is © The Royal Society of Chemistry 2016 |