Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing of molecular replication and accumulation in shallow heat gradients through numerical simulations†
Lorenz
Keil
,
Michael
Hartmann
,
Simon
Lanzmich
and
Dieter
Braun
*
Systems Biophysics, Physics Department, Nanosystems Initiative Munich and Center for NanoScience, Ludwig-Maximilians-Universität München, Amalienstraße 54, 80799 München, Germany. E-mail: dieter.braun@lmu.de
First published on 6th May 2016
Abstract
How can living matter arise from dead matter? All known living systems are built around information stored in RNA and DNA. To protect this information against molecular degradation and diffusion, the second law of thermodynamics imposes the need for a non-equilibrium driving force. Following a series of successful experiments using thermal gradients, we have shown that heat gradients across sub-millimetre pores can drive accumulation, replication, and selection of ever longer molecules, implementing all the necessary parts for Darwinian evolution. For these lab experiments to proceed with ample speed, however, the temperature gradients have to be quite steep, reaching up to 30 K per 100 μm. Here we use computer simulations based on experimental data to show that 2000-fold shallower temperature gradients – down to 100 K over one metre – can still drive the accumulation of protobiomolecules. This finding opens the door for various environments to potentially host the origins of life: volcanic, water-vapour, or hydrothermal settings. Following the trajectories of single molecules in simulation, we also find that they are subjected to frequent temperature oscillations inside these pores, facilitating e.g. template-directed replication mechanisms. The tilting of the pore configuration is the central strategy to achieve replication in a shallow temperature gradient. Our results suggest that shallow thermal gradients across porous rocks could have facilitated the formation of evolutionary machines, significantly increasing the number of potential sites for the origin of life on young rocky planets.
Introduction
The formation of RNA-like biopolymers that exhibit both catalytic functions and information storage capabilities is central to the origin of life. However, geochemical evidence points towards very low molecular concentrations in prebiotic oceans. Therefore, the formation of complex informational molecules that require a number of molecular precursors is severely hindered.1–3 The problem can be approached by searching for geological non-equilibrium conditions that make an origin of life possible, if not highly likely or even imperative under certain boundary conditions. Such a search will focus on experimentally testable conditions that create an evolutionary machine for protobiomolecules, achieving the first steps of Darwinian evolution naturally by a combination of physico-chemical effects. Here, we discuss such a machine, one driven solely by a natural temperature gradient in porous rocks.One of the first problems to solve is the so-called “concentration problem of the origin of life”.1–3 All approaches to generate molecules such as amino acids,4 purines,5–7 pyrimidines, and oligonucleotides, as well as alternative early replicators, are limited to high initial concentrations of precursor molecules.8–13 While present-day cells run elaborate systems to maintain spatial compartmentalization, and feed their interiors by complex protein-based transport machineries,14,15 only a few settings on the primordial Earth are predicted to have featured comparable segmentation and accumulation of molecules from aqueous solutions. If periodic changes in the environment do not cause the degradation of the protobiological molecules, evaporated terrestrial ponds,16 self-assembled lipid bilayers, or coacervates as precursors of protocells and catalysing inorganic surfaces can offer favourable conditions for the synthesis or preservation of protobiomolecules.17–21
On the other hand, porous rocks emitting geothermally heated water into the ocean were an abundant setting on the early Earth.22,23 The dissipation of heat forms a temperature gradient across sub-millimetre sized pores inside these rocks. This type of heat fluxes drive a highly efficient accumulation mechanism which is based on the interplay of thermal convection and thermophoresis. Temperature gradients across artificial pores lead to the accumulation of dilute lipids and nucleotides,24–26 enable the polymerization of long DNA/RNA strands,27 and select, feed, and replicate nucleic acids towards increasing length.28 Previous numerical approaches and experiments have shown that the mechanism is robust with respect to a large variety of geometries and works within artificial pores of different sizes.26,29
This work demonstrates in silico that shallow temperature gradients of 100 K per metre in prebiotically abundant volcanic settings are sufficient to accumulate a variety of molecules at least a million-fold. Previously conducted studies used temperature gradients at least 2000-times higher,26–28 which we show is not necessary to achieve high accumulation ratios. Here, we extend the concept of narrow, vertical pores to pores with variable orientation, proving their versatility to achieve extreme accumulations under all spatial orientations of the pore. We thereby expand the range of thermal gradients capable of driving prebiotic molecular evolution to various environments such as steam-, volcanic-, and hydrothermal settings (Fig. 1). The heat dissipated from these sites creates a temperature gradient across adjacent pore systems, irrespective of their being filled with water. The accumulation mechanism, however, occurs solely in water-filled parts of the pore. Our new theoretical findings provide an abundant, simple, and universally applicable scenario of accumulation and a possible solution to the concentration problem of the origin of life.
 | ||
| Fig. 1 Possible microthermal habitats for the origins of life. (a) Heat dissipation across submerged porous rocks and the cold ocean form steep temperature gradients which drive an efficient accumulation mechanism.22,23 (b and c) Shallow temperature gradients, approximately 100–2000-fold weaker than previously assumed, still enable an efficient accumulation, extending the range of possible microthermal habitats from previously discussed hydrothermal settings to volcanic and steam settings. These surface-based microhabitats provide wet–dry cycles and UV illumination for trapped molecules, facilitating the generation and polymerization of nucleotides.9 (d) Numerical approaches show that elongated pore systems within shallow temperature gradients efficiently accumulate molecules such as DNA and RNA (1) and enable a heat-driven replication reaction due to cyclic temperature changes induced by the laminar thermal convection (2). (a) Adapted from MARUM, University of Bremen/Germany. | ||
In addition, we have simulated a large number of single, stochastic particles following unique trajectories that mimic the behaviour of nucleic acid strands inside the pores. The statistics derived from these numerical simulations suggest that particles frequently shuttle between hot and cold parts of the pore. The accumulated molecules are therefore subjected to temperature oscillations in a laminar convective flow, allowing for e.g. template-directed replication mechanisms.13,30–33 Such mechanisms are central to the origin of life since they offer a pathway to the long-term storage, propagation, and mutation of information.
The concentration mechanism could also assist in the formation and selection of the first self-replicating molecules. The RNA-world hypothesis for example posits that RNA played a crucial role in the origin of life due to its catalytic function and information storage capabilities. The question remains of how a self-replicating ribozyme, containing at least 200 nt, could have emerged. Previous numerical and experimental studies have shown that the thermally driven accumulation mechanism concentrates oligonucleotides and thereby shifts a polymerization reaction towards longer polymers.27 These polymers could then be selected for function and sequence, e.g. through a gelation process, providing an essential requirement for Darwinian evolution.34 The numerical findings presented here suggest that pore systems subjected to shallow temperature gradients achieve comparable accumulation efficiencies and therefore have similar effects on the polymerization reaction. As a result, the number of potential sites for the formation of ribozymes vastly increases, assuming that enough feedstock molecules are available.
A supply of protobiomolecules inside such pores, however, is not only limited to e.g. diffusive coupling with the ocean and Fischer–Tropsch-type synthesis.35 Porous rocks near the surface could have also been supplied with feedstock molecules synthesized by surface chemistry.9,36 In such a regime, molecules such as precursors of ribonucleotides, lipids, or amino acids are synthesized on the surface and subsequently leached into the pores e.g. by downhill streams from rainfall. This makes reaction products particularly those of wet/dry and UV-reactions available in the pores. Surface directed ends of the pores can also be directly struck by sunlight and include the case of partially dried pores, e.g. based on moisture changes in steamy environments.
This work specifically studies the thermally driven accumulation mechanism inside porous rocks from the physical perspective, thereby neglecting chemical reactions.
Experimental
The accumulation of molecules can be described by Debye's approach, originally used to characterize separation columns.37 The basic principle of molecular accumulation is given by the superposition of gravitational convection and thermophoresis. Both mechanisms result from heat fluxes across water-filled compartments. The thermophoretic effect moves molecules along the thermal gradient, resulting in a net movement of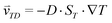 . Hereby, D and ST denote the diffusion and Soret coefficients and ∇T the temperature gradient, respectively. Thermophoresis is still subject to active research;38,39 however, it has been found that the effect on charged molecules, e.g. short oligonucleotides, is dominated by ion shielding and Seebeck effects.40 The latter is induced by the fact that each ionic species has a different Soret coefficient, generating a global electrical field that moves charged molecules. Thereby, the Seebeck effect highly depends on the ionic composition of the solution. In conjunction with convection, molecules erratically move within the temperature gradient while slowly accumulating at the bottom of the compartment. This effect has emerged to be highly potent in gaining extreme concentrations in distinct regions.
. Hereby, D and ST denote the diffusion and Soret coefficients and ∇T the temperature gradient, respectively. Thermophoresis is still subject to active research;38,39 however, it has been found that the effect on charged molecules, e.g. short oligonucleotides, is dominated by ion shielding and Seebeck effects.40 The latter is induced by the fact that each ionic species has a different Soret coefficient, generating a global electrical field that moves charged molecules. Thereby, the Seebeck effect highly depends on the ionic composition of the solution. In conjunction with convection, molecules erratically move within the temperature gradient while slowly accumulating at the bottom of the compartment. This effect has emerged to be highly potent in gaining extreme concentrations in distinct regions.
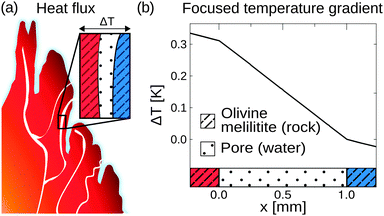
On the prebiotic Earth, such compartments could be found in volcanic rocks, highly porous minerals that exhibit micrometre sized pores. In this work, we approach molecular traps in silico, using a commercial finite-element solver (COMSOL Multiphysics 4.4). For calculating the temperature profile, rectangular compartments of 1 mm in width serve as pores, surrounded by 1 m of volcanic rock. Temperatures of 104 °C and 4 °C are applied to the left and right boundaries of the rock, respectively, spanning a temperature gradient of 0.1 K mm−1. The linear temperature profile is calculated along a water filled pore for various minerals of hydrothermal-, steam-, and volcanic settings such as gabbro, peridotite, olivine-melilitite, and clay (see Fig. S1 in the ESI†).41–44
These minerals cover hydrothermal vent settings such as the Lost City (gabbro, peridotite), volcanic settings (olivine-melilitite), and the common material clay for comparison. Ancient versions of hydrothermal fields such as the Lost City existed on the early Earth; however, the exact composition is assumed to differ. The shape of the temperature profile for a mineral is mainly defined by its thermal conductivity, holding for different materials with equal thermal conductivity. Thermal conductivities may be even higher because of sediments within the rocks, e.g. sulfide sediments in black smokers.45 The simulation, however, does not take into account interactions at the mineral/water boundary layers such as catalytic effects or surface induced polymerization reactions.20,21
The accumulation efficiencies are based on three consecutive steady state calculations of two-dimensional pore models:
(i) Partial differential equations (PDE) for transient heat transfer are employed to calculate the temperature profile within the pore. Here, a low temperature of Tlow = 55 °C and a high temperature of Thigh = Tlow + ΔT on the right and left side are applied, respectively, while insulating the top and bottom. The temperature difference ΔT is calculated by assuming a temperature gradient of 0.1 K mm−1 across the porous rock.
(ii) The temperature profile is used to calculate a convectional flow profile by numerically solving the incompressible Navier–Stokes equations. Reciprocal effects upon the temperature profile are ignored since the laminar convection negligibly alters the heat-transfer of (i). The porous rock material is assumed to have a combined thermal conductivity of κ = 3 W mK−1, a combination of quartz (κ = 6.6 W mK−1) and olivine-melilitite (κ = 1.7–2.5 W mK−1).41,46
(iii) The resulting flow profile is superimposed by thermophoretic and diffusive movement of the molecules, using PDEs (see eqn (1)). The top of the pores are assumed to have a constant molecule concentration c = c0 (i.e. connected to a reservoir with the initial molecule concentration) and a closed bottom, resulting in a concentration distribution over the pore. The molecular flux is given by:
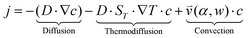 | (1) |
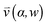 , pore width w, and the angle α between the pore and the direction of gravity. The tilting angle α and pore width w affect the gravitationally induced convective flow
, pore width w, and the angle α between the pore and the direction of gravity. The tilting angle α and pore width w affect the gravitationally induced convective flow 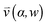 , which is solved in the preceding step of the simulation. Here, 90° and 0° denote a vertically and horizontally aligned pore, respectively. The Soret coefficients for oligonucleotides were experimentally measured by Reineck et al.47 Our simulation follows Debye's approach by neglecting perturbations at the ends of the pore
, which is solved in the preceding step of the simulation. Here, 90° and 0° denote a vertically and horizontally aligned pore, respectively. The Soret coefficients for oligonucleotides were experimentally measured by Reineck et al.47 Our simulation follows Debye's approach by neglecting perturbations at the ends of the pore 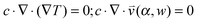 . Those assumptions have previously been shown to be in good agreement with experimental data, e.g. Duhr and Braun,48 Mast et al.,27 Reichl et al.,40 and Kreysing et al.28 A change in molecular concentration over time (eqn (2) and (3)) is derived from the molecular flux eqn (1) by using the continuity equation:
. Those assumptions have previously been shown to be in good agreement with experimental data, e.g. Duhr and Braun,48 Mast et al.,27 Reichl et al.,40 and Kreysing et al.28 A change in molecular concentration over time (eqn (2) and (3)) is derived from the molecular flux eqn (1) by using the continuity equation: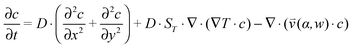 | (2) |
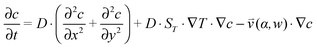 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, resulting in a maximum pore length of 50 mm given a width of 1 mm. The results from these simulations are then scaled according to Baaske et al.26 to obtain concentrations for pore lengths of 1 m. Those pores are formed by a stacking of shorter pores that are connected by mass diffusion. They behave analogously to a single, elongated pore, thereby increasing the effective pore length. The large length allows both the accumulation and the thermal cycling of the molecules.
1, resulting in a maximum pore length of 50 mm given a width of 1 mm. The results from these simulations are then scaled according to Baaske et al.26 to obtain concentrations for pore lengths of 1 m. Those pores are formed by a stacking of shorter pores that are connected by mass diffusion. They behave analogously to a single, elongated pore, thereby increasing the effective pore length. The large length allows both the accumulation and the thermal cycling of the molecules.
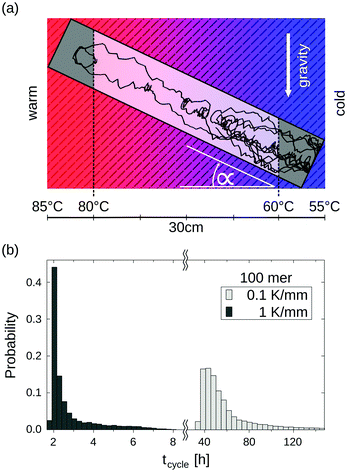
Random walk simulations investigate thermal cycling statistics of 100-mer oligonucleotides in shallow temperature gradients. The molecules are placed within an inclined, rectangular pore embedded in volcanic rock composed of olivine-melilitite. The volcanic rock serves solely as a heat-conducting material, since surface chemistry is not included in the model. It is exposed to thermal gradients of 0.1 K mm−1 and 1 K mm−1, applying a temperature difference of ΔT = 30 K over 30 cm and 3 cm, respectively. A temperature gradient in the range of 55 °C to 85 °C, as chosen here, enables e.g. replication reactions by allowing elongation and denaturation processes. In the steady state scenario, trapped molecules still shuttle between hot and cold areas, continuously undergoing temperature cycles. A temperature cycle is defined using two threshold temperatures for elongation and denaturation. Molecules complete a temperature cycle by first moving into a cold temperature region below 60 °C for elongation, followed by a high temperature region above 80 °C for denaturation, and finally back to the low temperature region. The thermal cycling statistics are inferred from 100 particle trajectories. These particles are randomly distributed along the pore and simulated for 3 × 105 h, corresponding to the steady-state reached after approximately 4.2 × 105 h, derived from L2/D, where L denotes the pore length. The random walk model accounts for the superposition of laminar flow, thermophoresis, and Brownian motion for 100-mer oligonucleotides. The diffusion and Soret coefficients are given by D = 127 μm2 s−1 and ST = 0.07 K−1 for 100-mer RNA/DNA at a Debye length of λD = 2.1 nm at 70 °C, both measured experimentally.40,47 Thermophoresis contributes with a net movement 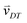 along the gradient, resulting in a thermophoretic velocity of
along the gradient, resulting in a thermophoretic velocity of 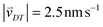 for a 100-mer oligonucleotide. A convectional flow profile with a maximum of vmax ≈ 8 μm s−1 shuttles molecules between warm and cold areas. The displacement Δs(x,y) of these particles is given by:
for a 100-mer oligonucleotide. A convectional flow profile with a maximum of vmax ≈ 8 μm s−1 shuttles molecules between warm and cold areas. The displacement Δs(x,y) of these particles is given by:
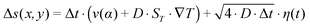 | (4) |
Results and discussion
Heat dissipation across submerged porous rocks,22,23 an abundant setting on the early Earth, has been advocated as a possible source for the origin of life (Fig. 1a).26 Porous rocks comprise multiple branched pore systems which serve as water channels. We have proposed that a major temperature difference between the hot rock, generated by volcanic activity and the cold ocean, forms a temperature gradient, which drives a highly robust and efficient accumulation mechanism within the pore system. We have previously argued that these systems can thermophoretically accumulate, thermally cycle, and continuously feed the first prebiotic molecules for evolution, employing a temperature gradient of 400 K mm−1 and 200 K mm−1 in theory and experiment respectively.27,28,49 Steep gradients of 10–400 K mm−1, however, limit the scope of the approach to hydrothermal orifices and vapour heating with high flow rates. Here we show in simulations that 100–2000 fold shallower temperature gradients (0.1 K mm−1) still achieve at least a million-fold accumulation within elongated pore systems. Such gradients can be found in near-surface volcanic and steam settings (Fig. 1b and c). Here, we further investigate the accumulation behaviour of tilted elongated pores in shallow gradients for oligonucleotides and small molecules. In addition, random walk simulations are performed to derive thermal cycling behaviour of single molecules within micro-thermal pores (Fig. 1d).A minor difference in temperature between both heat reservoirs, e.g. volcanic rock and water/air, suffices to enable highly efficient accumulation of molecules (Fig. 2a). This is facilitated by a difference in heat conductivity between the rock (2 W mK−1 for olivine-melilite) and the water (0.6 W mK−1), which results in a local increase of the temperature gradient across the water-filled pore by a factor of 3 (Fig. 2b). Steeper temperature gradients arise from different minerals, all naturally occurring in hydrothermal vents. The temperature gradient increases by a factor of 6.6, 20, or 33 for materials such as quartz, pyrite–silica, and pyrite,46,50 respectively. A porous rock consisting of pyrite–silica is therefore able to locally create a temperature gradient of 2 K mm−1 across a single pore, despite having an average temperature gradient of 0.1 K mm−1 across the porous rock. Clay represents the worst case scenario for rock materials. Its heat conductivity of 0.9 W mK−1 increases the temperature gradient only by a factor of 1.5. Subsequent simulations are performed assuming a geological realistic temperature gradient of 0.1 K mm−1 along the porous rock.
The exact geometry of the pore system within rocks – be it e.g. triangular, rectangular, or curved – barely affects the accumulation efficiency, i.e. the maximum concentration (Fig. 3a). Based on these findings, subsequent simulations are carried out in rectangular pores only, assuming that the difference in amplification is insignificant for our main statement. However, extreme accumulation for 100-mer oligonucleotides up to 106-fold – concentrating molecules from pM to μM – is possible even for 10 cm pore systems (Fig. 3b). Typical pore lengths are significantly larger.51 The accumulation efficiencies of longer pore systems can be determined since the concentrated material of a short pore, located at the bottom of the pore, serves as the starting concentration for an adjacent pore. For example, when stacking two triangularly shaped pores of 10 cm each, the concentration increases by a factor of 1012, which is the product of both accumulations.
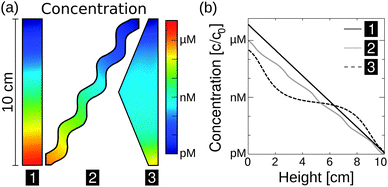 | ||
| Fig. 3 Extreme accumulations of 100-mer oligonucleotides for various pore geometries via finite-element analysis, assuming shallow temperature gradients of 0.1 K mm−1. Diffusion and Soret coefficients are based on experimental data.40,47 (a) The accumulation mechanism is found to be highly robust with respect to the shape of the pore system. Pore systems of 10 cm in length achieve accumulations in concentration from pM to near μM. (b) The shape has only a minor impact on the magnitude of accumulation. The exact distribution of concentration is shown for the geometries in (a). A rectangular geometry shows the highest efficiency, accumulating molecules by a factor of 7 × 106. All pore geometries achieve at least a 105-fold accumulation. | ||
Besides its robustness with respect to the geometry of the pore, the mechanism also accumulates a large variety of molecules. Here, we extend previous simulations focused solely on oligonucleotides to a large pool of molecules (Fig. 4a), including monovalent ions like Li+ (D = 1029 μm2 s−1, ST = 0.0007 K−1) and divalent ions such as Mg2+ (D = 706 μm2 s−1, ST = 0.012 K−1) and Ca2+ (D = 792 μm2 s−1, ST = 0.013 K−1).40 To calculate the particle's accumulation efficiency, only its diffusion and Soret coefficients D and ST, respectively, are necessary. Both parameters are strongly affected by salt concentration and ambient temperature, which is shown for 1- to 200-mer oligonucleotides (Fig. 4a and b). The diffusion and Soret coefficients were experimentally measured for Debye lengths of 0.79–5.6 nm, corresponding to salt concentrations in physiological solutions and more diluted solutions, respectively.40 High salt concentrations (Debye length λD = 0.79 nm) and cold ambient temperatures (30 °C) result in relatively low accumulation efficiencies of c/c0 = 1014 for 200-mer oligonucleotides due to a drastic decrease in ST. High ambient temperatures of 70 °C and medium salt conditions (λD = 2.1 nm) achieve a considerably higher accumulation of 1039 for a 200-mer. Still, even in the worst case scenario, the overall accumulation is high enough to provide a possible solution to the concentration problem of the origin of life, thereby affecting the outcome of chemical reactions considerably.1,52 While the length of the pore exponentially increases the accumulation efficiency, the optimal width of the pore varies for each molecule (Fig. 4c).
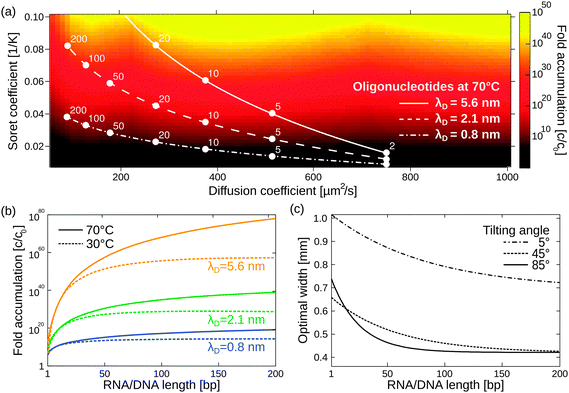 | ||
| Fig. 4 Simulating exponential molecular accumulation. (a) Highly efficient accumulation of various molecules with a given diffusion coefficient and Soret coefficient. This allows the prediction of the accumulation for a very large range of molecules, including monovalent or divalent ions or single nucleotides. The curves show scenarios for the accumulation of 1- to 200-mer oligonucleotides at various salt concentrations. Diffusion and Soret coefficients were measured experimentally.40,47 (b) The accumulation for RNA and DNA is shown as a line plot for better readability. DNA and RNA show very similar accumulation and are not distinguished. Debye lengths of 0.79 nm, 2.1 nm, and 5.6 nm denote high, medium, and low salt concentrations, respectively. (c) Optimal accumulation is achieved at a unique pore width. For example, short oligonucleotides accumulate best in a pore width above 500 μm, while longer oligonucleotides typically require pore widths below 500 μm. Tilting the pore from the vertical case (90°) to almost horizontal case (5°) results in an increase in optimal pore width. | ||
The largest accumulation for short oligonucleotides can be found for pores wider than 0.5 mm, while longer oligonucleotides typically require pore widths below 0.5 mm. Artificial molecular traps with a predefined pore width can therefore be used to accumulate a specific length regime of oligonucleotides, which has previously been shown for oligonucleotides of 20–200 bp.28 This concept can be further extended to small molecules, such as mono- and divalent ions. The simulation also covers the case of geologically realistic, randomly aligned pores by adding a tilting angle for rectangular pores. Previous simulations focused on vertically aligned pores. Tilting the pore from a vertical case (90°) to an almost horizontal case (5°) results in a decrease in optimal pore width. Therefore, a certain pore width is able to accumulate various molecules depending on the arrangement of the pore.
Long-term storage and propagation of information, which is encoded in precursors of DNA – quite possibly RNA – at the origins of life, require environments that feature reliable replication mechanisms. The laminar convection within microthermal pores offers cyclic temperature changes and enables Watson–Crick-type replication mechanisms.49,53,54 Random walk simulations derive temperature cycle statistics of 100-mer nucleotides. The oligonucleotides are placed inside a 0.75 mm thin, water-filled pore, which is embedded in a square of volcanic rock with a side length of 30 cm (Fig. 5a). The pore is tilted at α = 45° and exposed to a shallow temperature gradient of 0.1 K mm−1, which results in a slightly steeper gradient of 0.3 K mm−1 within the pore due to thermal conductivity differences of olivine-melilitite and water (see Fig. 2).
The particles perform temperature cycles within the pore by shuttling between the different temperature regions. 100-mer oligonucleotides take on average 60 h to complete a temperature cycle (Fig. 5b). For comparison, we evaluated the cycle statistics of 100-mer nucleotides assuming a ten fold steeper gradient (1 K mm−1). Particles subjected to steeper gradients achieve considerably faster temperature cycles, requiring 3 h on average for completion. The molecules undergo thermal cycling comparable to regular polymerase chain reaction (PCR) protocols, comprising of long elongation and short denaturation times. Given that melting temperatures for random 100 mer oligonucleotides at a Debye length of λD = 2.1 nm are in the range of ∼80 °C, the induced temperature cycles enable the denaturation of oligonucleotides and thus replication reactions.
Conclusion
The new theoretical findings suggest an abundance of potential sites on prebiotic Earth that would have been capable of solving the concentration problem of the origin of life. While previous studies were limited to large temperature gradients across hydrothermal porous rocks, we showed that shallow temperature gradients are sufficient to drive highly efficient molecular accumulation processes. As a result, various environments, such as steam- and volcanic settings, become available as potential sites for the origins of life. These sites, if located near the surface, also enable a supply to the pores of feedstock molecules that are synthesized on the surface. The results may prompt experiments with actual rock samples in more shallow gradients and longer time frames than used before, e.g. to probe the formation of long polynucleotides from low starting concentrations inside porous rocks.Acknowledgements
Financial support from the Simons Collaboration on the Origin of Life, the NanoSystems Initiative Munich, the Ludwig-Maximilians-Universität Munich Initiative Functional Nanosystems, and the SFB 1032 Project A4 is acknowledged.References
- K. Dose, BioSystems, 1975, 6, 224–228 CrossRef CAS PubMed.
- S. J. Mojzsis, T. M. Harrison and R. T. Pidgeon, Nature, 2001, 409, 178–181 CrossRef CAS PubMed.
- N. Lane, Life ascending: the ten great inventions of evolution, Profile books, London, 2010 Search PubMed.
- S. L. Miller, Science, 1953, 117, 528–529 CAS.
- J. Oró, Biochem. Biophys. Res. Commun., 1960, 2, 407–412 CrossRef.
- J. Oró and A. P. Kimball, Arch. Biochem. Biophys., 1961, 94, 217–227 CrossRef.
- J. Oró and A. P. Kimball, Arch. Biochem. Biophys., 1962, 96, 293–313 CrossRef.
- B. T. Burcar, L. M. Barge, D. Trail, E. B. Watson, M. J. Russell and L. B. McGown, Astrobiology, 2015, 15, 509–522 CrossRef CAS PubMed.
- M. W. Powner, B. Gerland and J. D. Sutherland, Nature, 2009, 459, 239–242 CrossRef CAS PubMed.
- H. Kuhn and J. Waser, Nature, 1982, 298, 585–586 CrossRef CAS PubMed.
- M. Eigen, Naturwissenschaften, 1971, 58, 465–523 CrossRef CAS PubMed.
- G. F. Joyce, Nature, 1989, 338, 217–224 CrossRef CAS PubMed.
- D. Sievers and G. von Kiedrowski, Nature, 1994, 369, 221–224 CrossRef CAS PubMed.
- R. Pascal, A. Pross and J. D. Sutherland, Open Biol., 2013, 3, 130156 CrossRef PubMed.
- E. Schrödinger, What is life?, Cambridge University Press, Cambridge, 1944 Search PubMed.
- K. E. Nelson, M. P. Robertson, M. Levy and S. L. Miller, Origins Life Evol. Biospheres, 2001, 31, 221–229 CrossRef CAS.
- J. Oro and A. Lazcano, Adv. Space Res., 1984, 4, 167–176 CrossRef CAS PubMed.
- T. Oberholzer and P. L. Luisi, J. Biol. Phys., 2002, 28, 733–744 CrossRef CAS PubMed.
- S. Koga, D. S. Williams, A. W. Perriman and S. Mann, Nat. Chem., 2011, 3, 720–724 CrossRef CAS PubMed.
- J. P. Ferris, A. R. Hill, Jr, R. Liu and L. E. Orgel, Nature, 1996, 381, 59–61 CrossRef CAS PubMed.
- C. Huber, Science, 1998, 281, 670–672 CrossRef CAS PubMed.
- M. J. Russell, A. J. Hall, A. J. Boyce and A. E. Fallick, Econ. Geol., 2005, 100, 419–438 CAS.
- D. S. Kelley, J. A. Karson, G. L. Früh-Green, D. R. Yoerger, T. M. Shank, D. A. Butterfield, J. M. Hayes, M. O. Schrenk, E. J. Olson, G. Proskurowski, M. Jakuba, A. Bradley, B. Larson, K. Ludwig, D. Glickson, K. Buckman, A. S. Bradley, W. J. Brazelton, K. Roe, M. J. Elend, A. Delacour, S. M. Bernasconi, M. D. Lilley, J. A. Baross, R. E. Summons and S. P. Sylva, Science, 2005, 307, 1428–1434 CrossRef CAS PubMed.
- I. Budin, R. J. Bruckner and J. W. Szostak, J. Am. Chem. Soc., 2009, 131, 9628–9629 CrossRef CAS PubMed.
- D. Braun and A. Libchaber, Phys. Rev. Lett., 2002, 89, 188103 CrossRef PubMed.
- P. Baaske, F. M. Weinert, S. Duhr, K. H. Lemke, M. J. Russell and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9346–9351 CrossRef CAS PubMed.
- C. B. Mast, S. Schink, U. Gerland and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8030–8035 CrossRef CAS PubMed.
- M. Kreysing, L. Keil, S. Lanzmich and D. Braun, Nat. Chem., 2015, 7, 203–208 CrossRef CAS PubMed.
- B. Herschy, A. Whicher, E. Camprubi, C. Watson, L. Dartnell, J. Ward, J. R. G. Evans and N. Lane, J. Mol. Evol., 2014, 79, 213–227 CrossRef CAS PubMed.
- S. S. Mansy, J. P. Schrum, M. Krishnamurthy, S. Tobe, D. A. Treco and J. W. Szostak, Nature, 2008, 454, 122–125 CrossRef CAS PubMed.
- A. Wochner, J. Attwater, A. Coulson and P. Holliger, Science, 2011, 332, 209–212 CrossRef CAS PubMed.
- N. Paul and G. F. Joyce, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12733–12740 CrossRef CAS PubMed.
- Z. Yang, F. Chen, J. B. Alvarado and S. A. Benner, J. Am. Chem. Soc., 2011, 133, 15105–15112 CrossRef CAS PubMed.
- M. Morasch, D. Braun and C. B. Mast, Angew. Chem., 2016 DOI:10.1002/ange.201601886.
- T. M. McCollom, G. Ritter and B. R. Simoneit, Origins Life Evol. Biospheres, 1999, 29, 153–166 CrossRef CAS.
- B. H. Patel, C. Percivalle, D. J. Ritson, C. D. Duffy and J. D. Sutherland, Nat. Chem., 2015, 7, 301–307 CrossRef CAS PubMed.
- K. Clusius and G. Dickel, Naturwissenschaften, 1938, 26, 546 CrossRef CAS.
- A. Würger, Phys. Rev. Lett., 2016, 116, 138302 CrossRef PubMed.
- J. K. G. Dhont, S. Wiegand, S. Duhr and D. Braun, Langmuir, 2007, 23, 1674–1683 CrossRef CAS PubMed.
- M. Reichl, M. Herzog, A. Götz and D. Braun, Phys. Rev. Lett., 2014, 112, 198101 CrossRef PubMed.
- R. Büttner, B. Zimanowski, J. Blumm and L. Hagemann, J. Volcanol. Geotherm. Res., 1998, 80, 293–302 CrossRef.
- P. B. Kelemen, E. Kikawa and D. J. Miller, Proc. Ocean Drill. Program, Initial Rep., Ocean Drilling Program, 2004, vol. 209.
- K. Midttømme, E. Roaldset and P. Aagaard, Clay Miner., 1998, 33, 131–145 CrossRef.
- A. Geptner, H. Kristmannsdóttir, J. Kristjansson and V. Marteinsson, Clays Clay Miner., 2002, 50, 174–185 CrossRef CAS.
- P. M. Herzig and M. D. Hannington, Ore Geol. Rev., 1995, 10, 95–115 CrossRef.
- P. A. Rona, E. E. Davis and R. J. Ludwig, Proc. Ocean Drill. Program: Sci. Results, 1998, 158, 329–336 CAS.
- P. Reineck, C. J. Wienken and D. Braun, Electrophoresis, 2010, 31, 279–286 CrossRef CAS PubMed.
- S. Duhr and D. Braun, Phys. Rev. Lett., 2006, 96, 168301 CrossRef PubMed.
- C. B. Mast and D. Braun, Phys. Rev. Lett., 2010, 104, 188102 CrossRef PubMed.
- C. Clauser, Landolt-Börnstein - Numerical Data and Functional Relationships in Science and Technologies, Group VIII: Advanced Materials and Technologies, 2006, vol. 3, pp. 493–604 Search PubMed.
- M. J. Russell, A. J. Hall, A. J. Boyce and A. E. Fallick, Econ. Geol., 2005, 100, 419–438 CAS.
- C. de Duve, Blueprint for a cell—the nature and origin of life, N. Patterson, Burlington, N.C., 1991 Search PubMed.
- M. Krishnan, Science, 2002, 298, 793 CrossRef PubMed.
- S. Rajamani, J. K. Ichida, T. Antal, D. A. Treco, K. Leu, M. A. Nowak, J. W. Szostak and I. A. Chen, J. Am. Chem. Soc., 2010, 132, 5880–5885 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp00577b |
| This journal is © the Owner Societies 2016 |