Molecular motion of donor–acceptor catenanes in water

Abstract

In this article, we use ¹H NMR spectroscopy to study the spontaneous molecular motion of donor–acceptor [2]catenanes in water. Our data supports the hypothesis that conformational motion dominantly occurs through a pirouetting mechanism, which involves less exposure of hydrophobic surfaces than in a rotation mechanism. Motion is controlled by the size of the catenane rings and the arrangement of the electron-deficient and electron-rich aromatic units.

---

Water-soluble catenanes are emerging as a class of molecules that have the potential to perform programmable tasks in aqueous media.¹ Our knowledge of their behaviour, however, is limited to just a few examples,^1–7 and establishing general trends that could help chemists to design water-soluble catenanes with specific properties would be invaluable.

While Fujita et al. had reported in 1994 the assembly of the first water-soluble catenanes based on the platinum(II)–pyridine coordination bond,² it is only recently that fully organic water-soluble [2] and [3]catenanes have been synthesized by the Sanders and the Stoddart groups.^1,3–7 Initial studies have shown that these structures can be used for molecular recognition in water.^1–3 The aqueous environment is also likely to confer unique mechanical properties on catenanes. Conformational motion spontaneously occurring in water has, however, not yet been the subject of a complete study.

In this article, we propose to use ¹H NMR spectroscopy to rationalise the conformational motion of the [2]catenanes that can be constructed from macrocycles 1 to 6. These macrocycles are composed of electron-deficient (naphthalenediimide, or acceptor A) and electron-rich (dialkoxynaphthalene, or donor D) units linked via flexible peptide-derived and/or aliphatic side-chains. They are shown in Fig. 1 in order of increasing ring size from the smallest (1) to the largest (6).

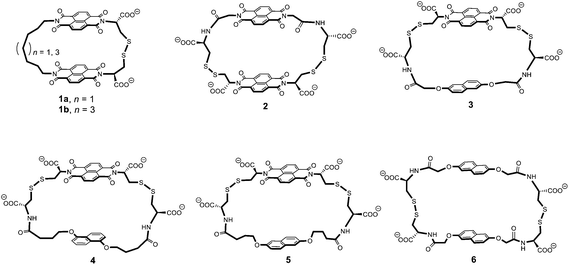Fig. 1 Chemical structure of the macrocycles 1 to 6 in order of increasing ring size. Ring size was evaluated from the linker length and we also considered the fact that the 1,5-dialkoxynaphthalene is slightly smaller than the 2,6-dialkoxynaphthalene.^3c A rough evaluation of ring size is given by the minimum number of atoms necessary to close the ring – 29 (1a), 31 (1b), 34 (2), 34 (3), 36 (4), 38 (5), and 40 (6) atoms, as counted by following the bonds highlighted in bold.

The NMR spectra of eight of these catenanes, previously reported simply as a means of characterization (1a·6,^3a1b·6,^3a2·5,⁵2·4,⁵2·6,⁵3·6,⁶4·4 ⁴ and 5·5,⁷ using a notation that specifies the identity of the two interlocked rings), provided the starting point of this study. The data gathered from these [2]catenanes suggest that conformational motion in water occurs through a pirouetting mechanism, which is primarily governed by three factors: (a) minimal exposure of hydrophobic surfaces during motion, (b) the size of the catenane rings, and (c) the arrangement of donor–acceptor electronic stacks.

Ring rotation or ring pirouetting? The case of catenanes 1a·6 and 1b·6

Conformational motions commonly observed in [2]catenanes in organic solvents^8,9 occur either through mechanisms of ring rotation or ring pirouetting (Fig. 2). In the first mechanism (ring rotation), motion of one of the macrocycles allows the yellow unit to move from the outside to the inside of the catenane. In the second mechanism (ring pirouetting), a rocking motion of the yellow unit around the core of the catenane (in red) maintains it on the outside.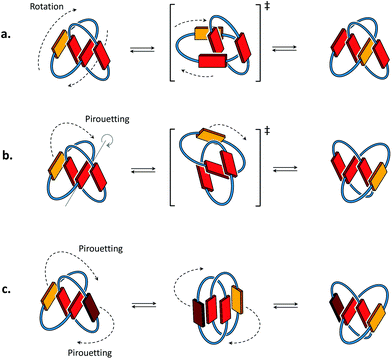

Fig. 2 Cartoon representation of the two types of motion commonly observed in [2]catenanes: (a) ring rotation and (b) ring pirouetting. (c) Other types of motion, such as the simultaneous pirouetting of the two outer units of the catenane may be considered. A previous communication⁷ suggests that the intermediate illustrated in the centre can be found as a stable conformation.

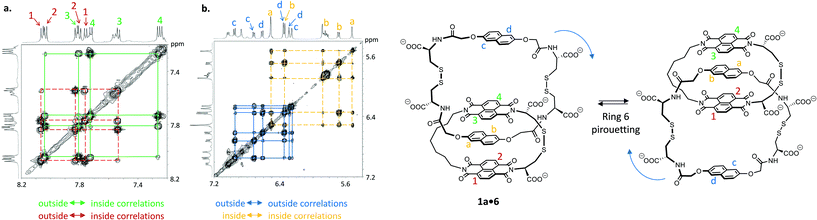
Catenane 1a·6 is fully asymmetric and each of the aromatic protons is inequivalent (Fig. 3) in ¹H NMR (500 MHz, 298 K, D₂O). The spectrum displays eight doublets in the acceptor region (7.2 to 8.2 ppm) corresponding to each naphthalenediimide proton: four upfield-shifted (inner acceptor: pair of signals 3 and 4) and four downfield-shifted (outer acceptor: pair of signals 1 and 2). The donor region (5.5 to 7.1 ppm) displays a similar pattern (inner donor: a and b; outer donor: c and d). In 2D NOESY this catenane exhibits exchange cross-peaks that can be explained either by a rotation of the acceptor ring or a pirouetting of the outer donor unit. Either motions result in the exchange between the inner and outer acceptor protons, and in the exchange between the right and the left donor protons. The two mechanisms of exchange are not differentiable by NMR. We propose that the larger and more flexible ring (6) is more likely to undergo motion than the tighter ring (1a). Rotation of 1a would involve a highly unfavourable transition state associated with the rupture of all the donor–acceptor stacks and the exposure of most hydrophobic surfaces to water. Pirouetting of the outer donor unit of 6, on the other hand, is favoured both on entropic and enthalpic grounds, because the transition state is associated with a higher degree of freedom and it involves the disruption of fewer donor–acceptor hydrophobic stacks. Along the same lines, more bonds in the linker units have to become rigid in the transition state of the rotation mechanism compared to that of the pirouetting mechanism. These considerations lead us to rationalise that a pirouetting of the outer donor unit is the most likely mechanism that produces the exchange correlations observed by NOESY. A similar behaviour was observed for 1b·6 (see ESI†).

Fig. 3 Partial NOESY spectrum of 1a·6 (a) in the acceptor region, between 7.2 ppm and 8.20 ppm and (b) in the donor region, between 5.40 ppm and 7.20 ppm (D₂O, 298 K, 500 MHz, mixing time d₈ = 800 ms).

The energy barriers (ΔG^‡) of these two catenanes were calculated by 2D exchange spectroscopy¹⁰ (EXSY, Table 1) by monitoring the relative intensity of NOE cross-peaks with change in temperature. The activation enthalpy (ΔH^‡) and entropy (ΔS^‡) were determined to be 69 kJ mol⁻¹ and −29 J mol⁻¹ K⁻¹, respectively, for 1a·6. Upon increasing the acceptor ring size (catenane 1b·6), the enthalpy of activation remains unaffected (70 J mol⁻¹ K⁻¹) while a more favourable entropy of activation (2 J mol⁻¹ K⁻¹) is observed. These values reflect an increase in the overall catenane flexibility from 1a·6 to 1b·6, and shows that the pirouetting of 6 can be affected, albeit to a small extent, by the size of ring 1 (a or b).

Table 1 Kinetic parameters of the motion observed for catenanes 1a·6, 1b·6 and 2·5 obtained from 2D EXSY in D₂O

Catenane	1a·6 (n = 1)	1b·6 (n = 3)	2·5
ΔH^‡(kJ mol^−1)	69	70	88
ΔS^‡(J mol^−1 K^−1)	−29	2	57
ΔG^‡ at 298 K (kJ mol^−1)	77	69	71
k at 298 K (s^−1)	0.2	5	2

---

What structural features affect ring pirouetting? A comparison of catenanes 2·5 and 2·4

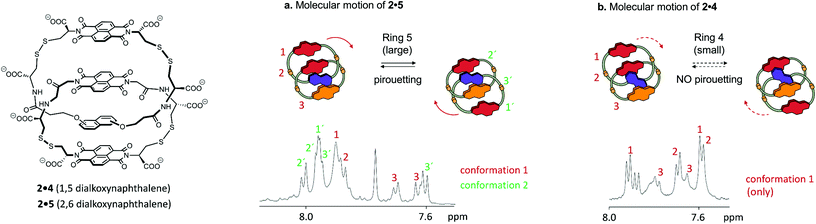
For each of the catenanes described above (1a·6 and 1b·6) the two exchanging conformations were strictly identical, and therefore equally populated and undistinguishable by 1D ¹H NMR. In contrast, the side-chains of each ring of catenane 2·5 are asymmetric, and motion can generate up to four conformations, inequivalent in terms of NMR environments and of Gibbs free energy. Hence, these conformations are directly observable in 1D ¹H NMR, and differently populated.

Out of four conformations, only two were identified in the 1D ¹H spectrum, in a 1 : 2 molar ratio (Fig. 4a). Indeed, the nature of the arrangement of the electron-donor and acceptor units considerably restricts the conformational motion of 2·5, as the resulting conformations may display either ADAA or DAAA stacked structures. All these conformations have, in terms of hydrophobicity, a nearly identical solvent-exposed surface, but the relative strength of electrostatic interactions, in the order D–A > A–A > D–D,¹¹ induces a dramatic difference between the free energy between the DAAA and ADAA structures, in favour of the latter.

Fig. 4 Effect of ring size: replacing ring 5 (catenane 2·5) by the slightly smaller ring 4 (catenane 2·4) restricts the pirouetting motion. (a) ¹H NMR of the acceptor region of 2·5 highlighting the presence of two distinct conformations, and (b) ¹H NMR of the acceptor region of 2·4 highlighting the presence of one single conformation. The yellow cartoon dots represent sulfur atoms. In each case, only the naphthalenediimide protons are labelled.

The two ADAA conformations can be generated by either pirouetting of the outer unit of 5 or rotation of 2. The above discussion on ring size, similarly applicable to 2·5, suggests that pirouetting of the outer unit of the larger ring, now ring 5, is still the dominant mechanism of exchange. The overall higher flexibility of catenane 2·5, compared to 1a·6 or 1b·6, is reflected in the entropically more favoured (56 J mol⁻¹ K⁻¹) transition state, while the activation enthalpy is slightly less favoured (88 kJ mol⁻¹). All our catenanes were assembled following a dynamic combinatorial approach¹² that necessitates the catenanes rings to be in relatively narrow range of size.⁵ Consequently, it is not surprising that the ΔG^‡ is of similar magnitude for all these catenanes.

Small differences in ΔG^‡ result, however, in variations of one order of magnitude in the rate constants k of pirouetting motion. The rate constant increases with the overall flexibility of the catenanes, suggesting that kinetics of pirouetting depend mostly on entropic factors. The linker bonds become more rigid in the transition state associated with the pirouetting motion, an effect that could contribute to the observed change in ΔS^‡ as the connector length increases. Importantly, conformational exchange is prevented when the pirouetting ring 5 is replaced by the slightly smaller ring 4 (Fig. 4b), thereby allowing us to refine our qualitative statement on the effect of ring size, and to propose that the minimum ring size necessary for pirouetting is situated between the size of rings 4 and 5.

Ring pirouetting – a general mechanism of exchange in water?

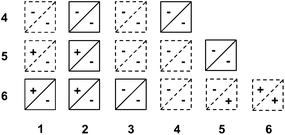
We hypothesized that pirouetting may be a general mechanism of exchange in water. In the previous parts, we concluded that pirouetting only occurs for rings larger than 4, providing that the resulting conformations maintain an identical arrangement of the electron-donor and acceptor units. We then tentatively applied these conclusions to other catenanes that can be constructed from macrocycles 1 to 6.

The results are partially summarized in Table 2: rings that cannot undergo pirouetting are marked with a negative sign (−), while rings that can undergo pirouetting are marked with a positive sign (+). The occurrence – or not – of pirouetting, reflected in the number of observable conformations, was successfully verified for three other isolated catenanes: 2·6,⁵3·6,⁶ and 4·4⁴ (see ESI†).

Table 2 The motion for each ring of the catenanes constructed from macrocycles 1 (a or b) to 6 (absence (−) or presence (+) of pirouetting) can be tentatively predicted from the conclusions drawn from this work. The boxes drawn in solid lines were experimentally verified, while the boxes drawn in dashed lines were not verified

---

It is noteworthy to mention that Table 2 only describes the motion of one ring while the second ring remains motionless on the NMR timescale. We should not, however, exclude the occurrence of more complex types of motion.

For example, simultaneous pirouetting of the two rings may also be envisaged (Fig. 2c). In the case of 5·5, both rings are large enough to undergo motion. The two rings composing this catenane are identical, and the kinetics of pirouetting should therefore be equal, producing two equivalent DAAD conformations. Such motion may explain the formation of the previously proposed gemini-like conformation of 5·5,⁷ which could be an intermediate conformation between two fully stacked DAAD conformations.

Conclusions

This study suggests that pirouetting is a general mechanism of conformational exchange for this type of donor–acceptor [2]catenanes in water. The occurrence of a pirouetting motion correlates to minimized exposure of hydrophobic surfaces, and is controlled both by the size of the rings and the arrangement of donor and acceptor units. These observations could provide a tool to design new types of molecular machines in water.

Acknowledgements

We are grateful to EPSRC (F.B.L.C., J.K.M.S.), Gates Cambridge (N.P.) and the University of Bath (G.D.P.) for financial support.

Notes and references

1. (a) S. Grunder, P. L. McGrier, A. C. Whalley, M. M. Boyle, C. Stern and J. F. Stoddart, J. Am. Chem. Soc., 2013, 135, 17691; (b) R. S. Forgan, J. J. Gassensmith, D. B. Cordes, M. M. Boyle, K. J. Hartlieb, D. C. Friedman, A. M. Z. Slawin and J. F. Stoddart, J. Am. Chem. Soc., 2012, 134, 17007; (c) L. Fang, C. Wang, A. C. Fahrenbach, A. Trabolsi, Y. Y. Botros and J. F. Stoddart, Angew. Chem., Int. Ed., 2011, 50, 1805; (d) L. Fang, S. Basu, C.-H. Sue, A. C. Fahrenbach and J. F. Stoddart, J. Am. Chem. Soc., 2011, 133, 396.
2. (a) M. Fujita, F. Ibukuro, H. Hagihara and K. Ogura, Nature, 1994, 367, 720; (b) M. Fujita, F. Ibukuro and K. Ogura, J. Am. Chem. Soc., 1995, 117, 4175; (c) A. Hori, K. Kumazawa, T. Kusukawa, D. K. Chand, M. Fujita, S. Sakamoto and K. Yamaguchi, Chem. – Eur. J., 2001, 7, 4142.
3. (a) F. B. L. Cougnon, N. Ponnuswamy, N. A. Jenkins, G. D. Pantoş and J. K. M. Sanders, J. Am. Chem. Soc., 2012, 134, 19129; (b) F. B. L. Cougnon, N. A. Jenkins, G. D. Pantoş and J. K. M. Sanders, Angew. Chem., Int. Ed., 2012, 51, 1443; (c) H. Y. Au-Yeung, G. D. Pantoş and J. K. M. Sanders, J. Org. Chem., 2011, 76, 1257.
4. H. Y. Au-Yeung, G. D. Pantoş and J. K. M. Sanders, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10466.
5. F. B. L. Cougnon, H. Y. Au-Yeung, G. D. Pantoş and J. K. M. Sanders, J. Am. Chem. Soc., 2011, 133, 3198.
6. H. Y. Au-Yeung, G. D. Pantoş and J. K. M. Sanders, J. Am. Chem. Soc., 2009, 131, 16030.
7. H. Y. Au-Yeung, G. D. Pantoş and J. K. M. Sanders, Angew. Chem., Int. Ed., 2010, 49, 5331.
8. O. Š. Miljanić, W. R. Dichtel, S. I. Khan, S. Mortezaei, J. R. Heath and J. F. Stoddart, J. Am. Chem. Soc., 2007, 129, 8236.
9. (a) D. A. Leigh, A. Troisi and F. Zerbetto, Chem. – Eur. J., 2011, 7, 1450; (b) M. S. Deleuze, D. A. Leigh and F. Zerbetto, J. Am. Chem. Soc., 1999, 121, 2364.
10. M. Pons and O. Millet, Prog. Nucl. Magn. Reson. Spectrosc., 2001, 38, 267.
11. M. S. Cubberley and B. L. Iverson, J. Am. Chem. Soc., 2001, 123, 7560.
12. For reviews of dynamic combinatorial chemistry, see: F. B. L. Cougnon and J. K. M. Sanders, Acc. Chem. Res., 2012, 45, 2211; A. Herrmann, Org. Biomol. Chem., 2009, 7, 3195; S. Ladame, Org. Biomol. Chem., 2008, 6, 219; J.-M. Lehn, Chem. Soc. Rev., 2007, 36, 151; M. M. Rozenman, B. R. McNaughton and D. R. Liu, Curr. Opin. Chem. Biol., 2007, 11, 259; P. T. Corbett, J. Leclaire, L. Vial, K. R. West, J.-L. Wietor, J. K. M. Sanders and S. Otto, Chem. Rev., 2006, 106, 3652; B. de Bruin, P. Hauwert and J. N. H. Reek, Angew. Chem., Int. Ed., 2006, 45, 2660.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ob02457e

‡ Current address: Department of Chemistry, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA; E-mail: cougnon@mit.edu.

§ Current address: Dana-Farber Cancer Institute, Harvard University, Cambridge, Massachusetts 02138, USA; E-mail: nandhini_ponnuswamy@dfci.harvard.edu

---