Open Access Article
Open Access ArticlePrediction of microalgae hydrothermal liquefaction products from feedstock biochemical composition†
Shijie
Leow
a,
John R.
Witter
a,
Derek R.
Vardon
ab,
Brajendra K.
Sharma
c,
Jeremy S.
Guest
a and
Timothy J.
Strathmann‡
*a
aDepartment of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, 205 N. Mathews Ave., Urbana, IL 61801, USA. E-mail: strthmnn@mines.edu
bNational Bioenergy Center, National Renewable Energy Laboratory, Golden, CO 80401, USA
cIllinois Sustainable Technology Center, University of Illinois at Urbana-Champaign, 1 Hazelwood Dr., Champaign, IL 61820, USA
First published on 11th May 2015
Abstract
Hydrothermal liquefaction (HTL) uses water under elevated temperatures and pressures (200–350 °C, 5–20 MPa) to convert biomass into liquid “biocrude” oil. Despite extensive reports on factors influencing microalgae cell composition during cultivation and separate reports on HTL products linked to cell composition, the field still lacks a quantitative model to predict HTL conversion product yield and qualities from feedstock biochemical composition; the tailoring of microalgae feedstock for downstream conversion is a unique and critical aspect of microalgae biofuels that must be leveraged upon for optimization of the whole process. This study developed predictive relationships for HTL biocrude yield and other conversion product characteristics based on HTL of Nannochloropsis oculata batches harvested with a wide range of compositions (23–59% dw lipids, 58–17% dw proteins, 12–22% dw carbohydrates) and a defatted batch (0% dw lipids, 75% dw proteins, 19% dw carbohydrates). HTL biocrude yield (33–68% dw) and carbon distribution (49–83%) increased in proportion to the fatty acid (FA) content. A component additivity model (predicting biocrude yield from lipid, protein, and carbohydrates) was more accurate predicting literature yields for diverse microalgae species than previous additivity models derived from model compounds. FA profiling of the biocrude product showed strong links to the initial feedstock FA profile of the lipid component, demonstrating that HTL acts as a water-based extraction process for FAs; the remainder non-FA structural components could be represented using the defatted batch. These findings were used to introduce a new FA-based model that predicts biocrude oil yields along with other critical parameters, and is capable of adjusting for the wide variations in HTL methodology and microalgae species through the defatted batch. The FA model was linked to an upstream cultivation model (Phototrophic Process Model), providing for the first time an integrated modeling framework to overcome a critical barrier to microalgae-derived HTL biofuels and enable predictive analysis of the overall microalgal-to-biofuel process.
1. Introduction
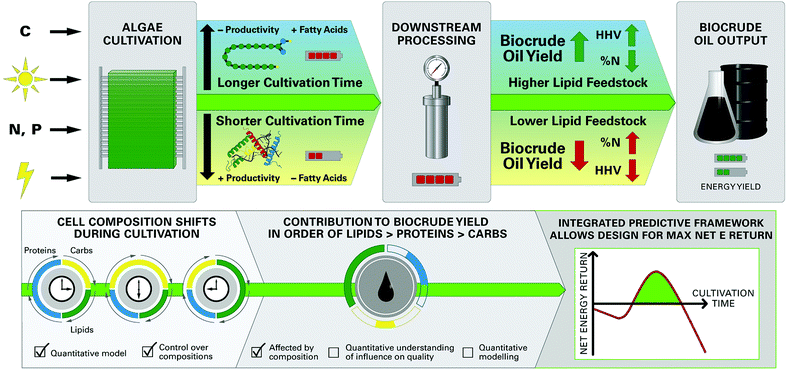
The growing scarcity of fossil fuel resources combined with transportation systems and infrastructure that rely heavily on low-cost liquid fuels has created a critical need for the development of economical and sustainable pathways for production of bio-renewable liquid fuels.1,2 Algal biofuels have attracted growing attention based on the documented advantages of microalgae feedstocks, including relatively low nutritional requirements and use of non-arable land for cultivation.1,3–6 There is growing interest in converting whole wet biomass like microalgae to liquid “biocrude” oil via hydrothermal liquefaction (HTL§) processes that use subcritical water at elevated temperatures (200–350 °C) and pressures (5–15 MPa) as the reaction medium,7,8 conveniently eliminating energy intensive drying steps.9 A unique facet of microalgae feedstocks pertinent to HTL is the high degree of control over biochemical composition during cultivation,10,11 such as the accumulation of energy-dense lipids or fatty acids (FA) in cells under depletion of nitrogen in culture media.11,12 Since HTL is directly affected by cell composition,13–15 it follows that the composition of feedstocks can be tailored to achieve optimized HTL product yields, biocrude oil quality, and net energy recovery of the biofuel production system (Fig. 1).Such synergy unique to microalgae-HTL processing is achievable only through a detailed understanding of the relationships between feedstock biochemical composition and HTL product characteristics which, to date, remains poorly understood. This knowledge gap results in a lack of predictive models quantitatively linking HTL product yield and quality to feedstock characteristics. Development of robust prediction models allows for integration with upstream microalgae cultivation models such as the Phototrophic Process Model (PPM),11 forming an integrated modeling framework (Fig. 1) that can predict important outcomes of the overall microalgae-HTL process using cultivation inputs (e.g., energy demand, nutrients, irradiance) to yield biocrude conversion outputs (e.g., biocrude yield, energy density). This framework would, for the first time, allow a comprehensive system-scale modeling of broad interest to microalgae HTL research areas, and to address a long-standing critical barrier to the integration of hydrothermal processing into microalgae biofuel production systems.1,3,4
Previous work focusing on microalgae HTL has shown that product yield, chemical properties of the biocrude, and the carbon and nitrogen distributions between the different HTL product fractions (i.e., biocrude, aqueous, solid, gas) are intrinsically tied to all or some portion of the biomass composition.13,16 To this end, initial predictive model development by Biller and Ross13 sought to estimate biocrude yield by linear summation of the yields obtained from HTL of individual model lipid, protein, and carbohydrate compounds (termed here as component additivity). The component additivity model was more recently revised by Teri et al.17 utilizing various mixtures of the same model compounds as Biller and Ross. Valdez and co-workers18 introduced an alternative kinetics-based reaction network model which accounts for how the biochemical components and product distribution shift with respect to reaction time and temperature. Component additivity models, while useful for estimating biocrude yield with proximate composition analysis, are unable to account for neutral and polar lipid fractions or FA profiles of biomass, which are known to affect biocrude elemental composition, higher heating values (HHV), and molecular weight distribution.19,20 Developing a model to predict additional parameters (e.g., %C and %N of the biocrude, C and N distribution to the product fractions, net energy recovery) is further critical to enable incorporation into overall algal biofuel system process models, techno-economic analyses (TEAs), and life-cycle assessments (LCAs).21,22
Attempts to develop a broadly applicable additivity model that accurately characterizes the influence of biochemical composition on microalgae HTL product quality have been limited in part because past efforts used non-algal based model compounds (e.g., sunflower oil, soy protein, corn starch), or focused on comparing HTL of different algae species, each with a single biochemical composition.13,17,18 Differences in species-specific factors such as cell wall thickness and ash compositions might affect the HTL process,23 introducing variability that obscures the true relationships between biochemical composition and HTL products; these limitations may be overcome by comparing HTL products obtained from a single microalgae species grown to variable cell compositions. Moving beyond the limitations of additivity models to enable prediction of biocrude quality, a new model structure is needed that incorporates more detailed feedstock characterization (i.e., beyond crude proximate composition), especially the energy dense lipid fraction, which may reveal important effects from components that makeup these proximate classes (e.g., FAs). The use of FAs as the main variable would also allow seamless integration with the PPM, which outputs biomass productivity in terms of functional cell biomass and accumulation products (i.e., FAs).11 The model would ideally also be capable of adjusting for the variability in microalgae-HTL processing methodology (e.g., reaction time, temperature, microalgae species, recovery methods).14,24
The objective of this contribution is to quantitatively assess the influence of variable microalgae biochemical compositions on the yields and characteristics of HTL products, and use this information to develop quantitative predictive models for microalgae HTL processing including: (1) an improved component additivity model; and, if supported by analytical evidence from the in-depth analytical suite employed in this study, (2) a new predictive model formulation that can be more easily applied to diverse microalgae species and HTL conditions. This was accomplished by HTL of a single microalgae species, Nannochloropsis oculata, cultivated under conditions designed to systematically vary cell composition. Nannochloropsis was selected as a model microalgae species because of the wide range of achievable lipid contents10,12 and extensive reports on HTL of commercially available Nannochloropsis.18,25,26 Distribution of mass yields and biomass carbon and nitrogen between the HTL products were compared for different harvested batches. Biocrude bulk and chemical properties were also extensively characterized. Data was used to develop and calibrate models linking HTL products to feedstock composition, and model predictions were validated by comparison with HTL measurements of diverse microalgae feedstocks reported in literature. Robust HTL conversion models can potentially be used in conjunction with the PPM11 to predict key outcomes of the overall microalgae biofuel process, linking once-separate upstream cultivation and downstream conversion steps through a unified modeling framework.
2. Experimental
2.1. Acquisition of algae biomass
A flat-panel, acrylic photobioreactor (PBR) with a working volume of 3.5 L and 1 in. light path was constructed as previously described.11 Detailed operational methods and conditions of the PBR are provided in the ESI (ESI-1†). Starter cultures of Nannochloropsis oculata (strain CCMP525) obtained from the National Center for Marine Algae and Microbiota (East Boothbay, ME) were used to inoculate the PBRs immediately upon arrival of cultures. Six batches of biomass with varying compositions were obtained by harvesting after varying periods of growth between 3–14 days. Batches harvested at longer cultivation times were expected to have larger lipid contents (and thus smaller protein and carbohydrate contents) as cultures typically transitioned from N-replete to N-deplete conditions after six days of growth. In order to demonstrate that the composition of a harvested batch and its subsequent HTL conversion were reproducible, two additional batches were harvested under conditions identical to the batch with the lowest lipid content. A defatted batch of Nannochloropsis was also prepared by extracting the lipids from harvested biomass using a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chloroform–methanol mix (Folch method described in Section 2.2) and freeze-drying the residual biomass solids after filtration and removal of extraction solvents.15 To supplement the cultivated batches, a slurry of Nannochloropsis (>70 wt% moisture) was purchased from Reed Mariculture (Campbell, CA) similar to previous HTL studies,20,25 and was processed as described above (two repetitions of rinsing and centrifugation followed by lyophilization) prior to use. Supplier documentation indicated the biomass was grown from the same strain used in batch cultivations here.
1 chloroform–methanol mix (Folch method described in Section 2.2) and freeze-drying the residual biomass solids after filtration and removal of extraction solvents.15 To supplement the cultivated batches, a slurry of Nannochloropsis (>70 wt% moisture) was purchased from Reed Mariculture (Campbell, CA) similar to previous HTL studies,20,25 and was processed as described above (two repetitions of rinsing and centrifugation followed by lyophilization) prior to use. Supplier documentation indicated the biomass was grown from the same strain used in batch cultivations here.
2.2. Biomass composition analysis
All biomass composition analyses were conducted on freeze-dried biomass samples. Moisture content was determined gravimetrically after drying samples at 105 °C for 1 h and desiccating for 30 min before weighing, and ash content was measured after heating the dried biomass at 550 °C for 30 min and desiccating for 30 min.11 C, H and N content was measured at the University of Illinois Microanalysis Laboratory (Urbana, IL) using an Exeter CE-440 Elemental Analyzer. Oxygen content was estimated by difference (%O = 100% − %C − %H − %N − %Ash) assuming sulfur was insignificant based on previous reports and analysis conducted here on representative batches (see ESI-2†).20,27 HHV was estimated from the elemental composition using the method of Dulong.13,20 Crude protein content was estimated by multiplying %N by 6.25.27 Crude carbohydrate content was analyzed with the DuBois method.28 Crude lipid content was analyzed according to the Folch method.29 To further characterize the lipid content, neutral lipid (NL) and polar lipid (PL) fractions of the crude lipid extract were separated by solid phase extraction (SPE) and determined gravimetrically after evaporation of eluents.30,31 Details of the SPE method and classification of NL and PL are provided in the ESI (ESI-3†). Fatty acid profiles of the biomass were determined by in situ transesterification fatty acid methyl esters (FAMEs) analysis according to Laurens et al. (see ESI for details; ESI-4†).32Raw results from the proximate biochemical analyses are provided in the ESI (Table S2†). Summation of crude lipids, proteins, and carbohydrates together with the ash and moisture contents ranged from 94.6–106.7 wt%, indicating that the methods used provided good mass balance closure, albeit with slight overestimations given that some of the proximate methods count the same components within biomass twice (e.g., glycoproteins contain both protein and carbohydrate).33 For subsequent analysis and model development, the proximate analyses of lipid, protein, carbohydrate, and ash contents of the Nannochloropsis batches were corrected to a summation of 100% dw (% dry weight, by dividing by the summed total of all components and then adjusting for moisture) as shown in Table 1.
| Proximate analysis | Elemental composition (%) | Lipid fractionationb | Fatty acid profile (% dw as FAMEs)c | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Batchd | Lipids | Protein | Carbs | Ash | %C | %H | %N | %O | HHV (MJ kg−1) | NL | PL | NL/PL | PL/Prot | Total FAMEs | 14:0 | 16:0 | 16:1 | 18:1 | 20:3n3 | 20:5n3 | SAFAse | MUFAs | PUFAs |
| a All values (unless otherwise stated) reported in % dw as the mean of duplicate analysis with min/max values (±) shown only if >±0.5% dw. b NL/PL = ratio of neutral lipids to polar lipids; PL/Prot = ratio of polar lipids to proteins. c Individual FAME only shown if >1.0% dw for majority of batches. d Batch 1 – defatted batch prepared from cultivated biomass; Batch 2 – biomass purchased from Reed Mariculture, and Batches 3–8 – biomass grown in PBRs in exponential phase through increasingly prolonged periods of N-starvation to vary biochemical compositions. e Saturated (SA); mono-unsaturated (MU); and poly-unsaturated (PU) fatty acids (FAs). f n.d. means not detected based on limits of corresponding method. | |||||||||||||||||||||||
| 1 | n.d.f | 74.7 | 19.4 | 5.9 | 46.3 | 6.4 | 11.2 | 30.4 | 19.3 | N/A; trace lipids | 0.59 ± 0.0 | n.d. | 0.1 | 0.1 | n.d. | 0.1 | 0.3 | 0.1 | 0.1 | 0.4 | |||
| 2 | 23.0 ± 0.3 | 58.1 | 13.2 | 5.7 | 53.7 | 7.5 | 9.6 | 23.5 | 24.7 | 7.0 | 16.0 | 0.4 | 0.3 | 13.6 ± 0.1 | 0.4 | 3.0 | 1.7 | 0.4 | 0.3 | 2.3 | 3.5 | 2.5 | 7.1 |
| 3 | 30.7 ± 0.3 | 51.4 | 12.3 | 5.6 | 54.6 | 7.8 | 8.7 | 23.5 | 25.3 | 12.2 | 18.5 | 0.7 | 0.4 | 19.8 ± 1.7 | 1.0 | 4.7 | 4.7 | 1.1 | 1.1 | 5.8 | 6.2 | 5.9 | 7.5 |
| 4 | 46.8 ± 0.0 | 28.0 | 22.0 | 3.2 | 59.2 | 8.8 | 4.6 | 24.3 | 28.2 | 31.0 | 15.9 | 2.0 | 0.6 | 38.6 ± 0.1 | 2.2 | 9.8 | 11.5 | 2.8 | 2.8 | 7.7 | 12.5 | 14.6 | 11.3 |
| 5 | 48.8 ± 0.2 | 32.1 | 16.7 | 2.4 | 60.1 | 8.8 | 5.4 | 23.4 | 28.7 | 29.3 | 19.6 | 1.5 | 0.6 | 39.9 ± 0.2 | 2.4 | 11.2 | 9.9 | 1.7 | 2.5 | 9.6 | 14.2 | 12.2 | 13.1 |
| 6 | 51.0 ± 1.0 | 26.5 | 19.0 | 3.5 | 60.3 | 9.2 | 4.3 | 22.8 | 29.4 | 36.1 | 14.9 | 2.4 | 0.6 | 42.4 ± 0.3 | 2.4 | 12.9 | 12.8 | 2.5 | 1.8 | 7.5 | 15.9 | 16.1 | 10.3 |
| 7 | 56.1 ± 0.6 | 23.4 | 18.4 | 2.1 | 62.9 | 9.3 | 3.9 | 21.8 | 30.6 | 43.3 | 12.8 | 3.4 | 0.6 | 50.3 ± 0.0 | 3.2 | 16.3 | 14.7 | 2.9 | 2.1 | 8.4 | 20.2 | 18.4 | 11.5 |
| 8 | 58.7 ± 0.8 | 17.1 | 22.2 | 2.0 | 62.3 | 9.3 | 2.8 | 23.5 | 30.1 | 50.0 | 8.6 | 5.8 | 0.5 | 52.0 ± 0.3 | 4.0 | 14.6 | 16.7 | 4.8 | 2.3 | 6.7 | 19.5 | 22.3 | 10.2 |
2.3. HTL of biomass
HTL of the harvested batches were conducted in duplicate using 6 mL 316-stainless steel tube batch reactors.18,20,25,34 Full details of the procedure can be found in the ESI (ESI-5†). Briefly, de-ionized water was added to freeze-dried biomass samples to achieve an 80 wt% moisture slurry, approximately 4 g of which was loaded into the tube reactor under ambient air. Reactors were sealed and placed in a preheated muffle furnace (Type 30400, Thermolyne) at 300 °C for 30 min, followed by quenching the reaction by submerging in cold water. Biocrude oil, aqueous phase-dissolved solids, filtered solids and gas products were recovered and separated (ESI-5†), and then measured gravimetrically and mass yields of the four product phases were reported as % dw of the input feedstock. A single set of HTL conditions was used here to enable greater focus on establishing the influence of microalgae cell composition on HTL products. The test conditions were selected based on optimal conditions in terms of yield and net energy efficiency widely reported to be within 300–350 °C and 30–60 min for both algal and lignocellulosic biomass feedstocks.14,25,35,362.4. Product analysis and energy, C, and N distribution
The biocrude product was analyzed for elemental composition and HHV via similar methods described for the biomass samples, except the ash content of biocrude was assumed to be negligible (%C + %H + %N + %O = 100%).37 C and N content was used to calculate the distribution of biomass carbon and nitrogen to the biocrude product. Size Exclusion Chromatography (SEC; molecular weight distribution) and Simulated Distillation (SimDist; approximate boiling point distribution) were performed on biocrude products according to methods described previously.15,16 Fatty acid reference standards (Sigma-Aldrich) were also analyzed via SimDist to identify individual peaks observed in the biocrude boiling point profile. The FA profile of the biocrude was also quantified via the same FAMEs analysis procedure described for biomass samples.32 The Energy Consumption Ratio (ECR), defined as the ratio of input energy required for reactor heating to the output combustion energy available in the biocrude oil product,13,15 and the Energy Recovery Percentage (ER%), defined as the fraction of energy in the dry biomass feedstock recovered as energy in the biocrude oil,13,25 were also calculated; detailed descriptions of the mathematical expressions, assumptions and parameters are provided in the ESI (ESI-6†).Total Kjeldahl nitrogen (TKN), ammonia (NH3), nitrate and nitrite (NO3− + NO2−) and orthophosphate (PO43−) concentrations in the aqueous phase were analyzed by Midwest Laboratories (Omaha, NE). The fraction of microalgae-derived carbon distributing to the HTL aqueous phase product was determined by analysis of total organic carbon (TOC; Shimadzu TOC-V CPN TOC analyzer), which has been reported as the dominant type of carbon (i.e., minimal inorganic carbon production).38 The fraction of nitrogen distributing to the aqueous phase product was determined by total nitrogen (TN), defined as the sum of TKN and NO3−/NO2−. Headspace gas was assumed to be 100% CO2 for the purpose of estimating biomass carbon distribution, based on past reports that the gas phase product from HTL of Nannochloropsis is predominantly CO2 (91.5 mol% for HTL at 300 °C for 1 h and >93 mol% under alternative HTL conditions).20,25 C, H, and N contents of the solid phase products were analyzed via similar methods described for the biomass samples, except that composite samples were required for some batches (solid products were combined for Batches 4 and 5, and another for Batches 6–8) due to the low yield of solids generated during HTL reactions of these batches (results and details in ESI Table S4†). The measured C and N values were used to estimate the biomass carbon and nitrogen distribution to the solid phase products.
2.5. Predictive modeling
Calibration of a linear component additivity model for predicting biocrude yield was performed by multiple linear regression of biomass composition parameters (i.e., lipid, protein, and carbohydrates) against corresponding HTL biocrude product yields using the regression function available in the Microsoft Excel 2010 Data Analysis package (Analysis ToolPak). Regression confidence level was 95% and intercept was set to zero. Calibration of an FA-based model was dependent on experimental observations and is described in greater detail in Section 3.4.Model validation was accomplished by comparing predictions with measurements reported in microalgae HTL literature. Batch composition data and corresponding yields were obtained from 14 peer-reviewed journal papers for a total of 21 marine and freshwater microalgae species, and more than one composition for the same species was included if unique data were reported.13,15,18,20,23,25,26,38–44 The entire list of studies is provided in the ESI (Table S1†) along with species, proximate compositions, and biocrude yields. Results for HTL conducted at 300 °C, regardless of reaction time, were used to validate the component additivity model calibrated in this paper.15,18,20,25,26,38–44 Model accuracy was compared against the component additivity models previously calibrated with model compounds13,17 and the reaction network model18 by calculating the coefficient of determination (r2) values. Residuals were also analyzed to identify patterns, if any. Validation of the FA model was done using experimental data from the ten harvested batches, since FAMEs analysis has not typically been conducted in prior reports on microalgae HTL.
To conceptually demonstrate an integrated modeling approach predicting overall system outputs and product characteristics from upstream cultivation inputs, the FA model developed in this paper was combined with a lumped pathway metabolic model (the Phototrophic Process Model, PPM).11 Parameters used for the PPM modeling are described in the ESI (ESI-7†). The execution of the integrated framework was meant as a demonstration of the potential of coordinated modeling of upstream cultivation and downstream conversion, and thus no further calibration was performed beyond that as described in Guest et al.11
3. Results and discussion
3.1. Composition of Nannochloropsis feedstocks
Batches 1–8 were organized in order of increasing lipid content (Table 1). Batch 1 was obtained after solvent extraction of lipids (defatting), and Batch 2 was obtained from a commercial source (Reed Mariculture). Batches 3–8 were cultivated biomass samples harvested during exponential growth and after increasingly prolonged periods of N-starvation, resulting in batches with increasing lipid content (23.0–58.7% dw, including Batch 2) and correspondingly decreasing protein content (58.1–17.1% dw). Carbohydrate content varied to a lesser degree (12.3–22.2% dw). The defatted Batch 1 was primarily made up of proteins (74.7% dw) and carbohydrates (19.4% dw), which extended the range of compositions beyond those that could be achieved through cultivation alone. Elemental analysis (Table 1) showed that %C and %H increased while %N decreased with increasing lipid fraction, whereas %O remained fairly constant. As a result, estimated HHV values of the HTL feedstocks increased from 19.3 to 30.1 MJ kg−1, reflecting the growing content of energy dense lipids in the HTL feedstocks. Reproducibility of harvested cell compositions was demonstrated (see ESI, Table S3†).The range of proximate compositions of Nannochloropsis batches used in this study overlapped with both marine and freshwater microalgae species that have been previously studied as HTL feedstocks (Fig. 2). The limited range of carbohydrates of harvested batches (15–25% afdw) is not expected to appreciably affect model development given that carbohydrates are considered to be the least significant contributor to HTL biocrude yields by a large margin.13,17 Apart from that, the harvested batches extended well beyond the general range of compositions previously investigated, suggesting that conclusions drawn from conversions of Nannochloropsis (a marine microalgae) in this study may be applicable to other marine and freshwater microalgae species as biofuel feedstocks.10
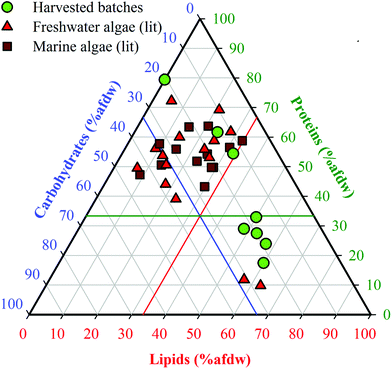 | ||
| Fig. 2 Ternary plot of biomass compositions of Nannochloropsis from this study compared to reported microalgae HTL feedstock compositions in the literature. The complete list of references is available in ESI Table S1†. Ash-free dry weight (% afdw) is used only in reference to data shown in this figure; all other results in this study are presented as % dw. The colored intersecting lines are located at reference fractions of 33.3% afdw for lipids (red), proteins (green) and carbohydrates (blue), respectively. | ||
Analysis of lipid speciation was conducted to determine if fatty acid (FA) content could be used as a key determinant for modeling purposes. Results (Table 1) revealed that the differences in lipid content were strongly attributable to the accumulation of neutral lipids (NL, 7.0–50.0% dw; NL/protein ratio of 0.1–2.9), while retaining a fairly constant polar lipid (PL) content as indicated by the comparatively stable PL/protein ratio (0.3–0.6). Previous studies on the cultivation of Nannochloropsis have shown that increases in the NL fraction can be primarily attributed to the accumulation of triacylglycerides (TAGs).12,45 FAMEs analysis of the batches showed a trend similar to the NL content (13.6–52.0% dw), consistent with the fact that the NLs are predominantly TAGs, which are the main source of FAs in microalgae biomass (noting that polar lipids do include FA-containing phospholipids).46 In all batches, palmitic (C16:0) and palmitoleic (C16:1) acids were the predominant FAs, along with comparatively smaller portions of myristic (C14:0), oleic (C18:1), eicosatrienoic (C20:3n3), and eicosapentaenoic (C20:3n5) acids. The predominance of these FAs is consistent with previous reports of FA content of Nannochloropsis species,12,27,45 though their exact distribution among these FAs can vary widely with cultivation methods and across growth phases.47
3.2. Influence of biochemical composition on product yields
Product yield distribution results from the HTL conversion of Nannochloropsis batches are shown in Fig. 3A, arranged in order of increasing lipid content of the HTL feedstock batches. Biocrude oil yield increased from 33.2 to 68.3% dw as feedstock lipid content increased, while aqueous phase yield decreased from 36.2 to 13.1% dw. Replicate HTL of Batch 3 produced near-identical product distributions (see ESI Table S3†), demonstrating minimal variance of HTL products resulting from batches of near-identical biochemical compositions. Biocrude yield from HTL of commercial Nannochloropsis (Batch 2–51.3% dw at 23% dw lipids) agreed with results reported by Valdez et al. (39% dw yield at 9% dw lipids)18 in that the smaller lipid content (likely due to the rinsing done here which removed salt as ash content) resulted in a corresponding decrease in biocrude yield as expected from the linear trend (r2 of 0.969) to lipid content shown in Fig. 3A (i.e., ∼40% dw biocrude yield is expected at 10% dw lipid content). Batches 1–3 produced similar biocrude yields to other microalgae species with comparable compositions such as Chlorella and Dunaliella (43% dw and 42% dw yields, respectively).23,39 Results similar to lipid-rich Batches 4–8 (with lipid content >46.8% dw) have also been observed for lipid-rich Chlorella (63% dw yield for feedstock with 60% dw lipids)44 under identical HTL conditions.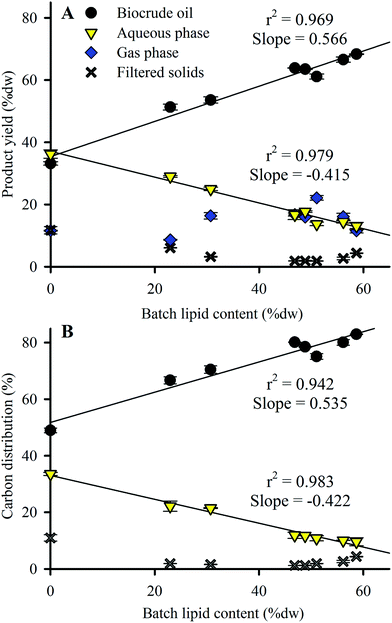 | ||
| Fig. 3 (A) HTL product yield and (B) carbon distribution as a function of Nannochloropsis feedstock lipid content. Symbols indicate the mean of duplicate analysis with error bars showing min/max values. Total product recovery for all batches ranged from 93.1–99.7% dw of loaded biomass. Total carbon recovery for all batches was 95.2–102% of loaded biomass carbon (see ESI Table S4† for complete data including estimated gas phase carbon distribution results). Linear fit r2 values shown only for biocrude oil and aqueous phase products. | ||
Larger amounts of biomass carbon partitioned to the biocrude product (increasing from 49.0 to 83.0%; Fig. 3B and ESI Table S4†) as feedstock lipid content increased, which was largely matched by reduced carbon partitioning to the aqueous phase (decreasing from 33.6 to 9.6%; Table S4†). The trends observed in Fig. 3 indicate that the lipid content or some component thereof (likely the FAs as shown in Section 3.1) heavily influences the yield and carbon distributions of HTL biocrude and aqueous products. Additional analysis of the biocrude product would pinpoint the responsible component to be used as a baseline for predictive model calibration.
In comparison to biocrude and aqueous yields, solid and gas phase yields from HTL are much lower (sum of both phases <25% dw for all batches; Fig. 3A). Solid phase yields decreased from 11.7% dw with the defatted Nannochloropsis batch to 1.8–4.4% dw for Batches 3–8. Gas phase yields were fairly static and showed no discernable trend with varying lipid content. Subsequent analysis and discussion will therefore focus on the biocrude and aqueous phase products because of their predominance in the observed mass balances.
3.3. Influence of biochemical composition on elemental distribution and energy balance
The elemental composition and HHV of biocrude products and energy recovery analysis (ECR and ER%) of the varying batches are shown in Table 2. Slight increases for the %C and %H and decreases in %O of the biocrude were observed with increasing feedstock lipid content. Feedstocks produced HTL biocrude with lower %N (decreasing from 9.1 to 2.0% N) as protein contents decreased, in agreement with previous reports that nitrogen-rich biomass produces HTL biocrude containing larger quantities of nitrogenous compounds.13,16 If the biocrude is not subjected to hydrodenitrogenation or other upgrading techniques to remove nitrogen, the %N is undesirable as a source for higher NOx emissions during combustion.16,48 Significantly lower %N in the biocrude could therefore be an important advantage that lipid-accumulated biomass offers over protein-rich feedstock. Interestingly, as the decreasing %N of biocrude would otherwise suggest, a larger percentage of feedstock N is actually transferred to the biocrude product as feedstock protein content decreased (ESI Table S4†), in part due to the much higher yield of biocrude for low protein feedstocks (i.e., there is relatively more biocrude volume to which partitioning of N-containing products can occur).| Batch | %C | %H | %N | %O | HHV (MJ kg−1) | ECRb (−) | ER%c |
|---|---|---|---|---|---|---|---|
| a All values (unless otherwise stated) reported in % as the mean of duplicate analysis with min/max values (±) shown only if >±0.5%. b Energy consumption ratio. c Energy recovery percent. | |||||||
| 1 | 68.3 | 8.5 | 9.1 | 14.1 | 32.7 | 0.325 | 56.3 |
| 2 | 69.8 | 9.5 | 6.1 | 14.6 | 34.5 | 0.199 | 71.7 |
| 3 | 71.8 | 10.2 | 5.5 | 12.5 | 36.5 | 0.180 | 77.3 |
| 4 | 74.3 | 11.1 | 3.4 | 11.2 | 38.9 | 0.142 | 88.0 |
| 5 | 74.2 | 11.1 | 3.7 | 11.0 | 38.9 | 0.143 | 86.0 |
| 6 | 74.0 | 11.1 | 3.4 | 11.4 | 38.8 | 0.149 | 80.8 |
| 7 | 75.7 | 11.5 | 2.7 | 10.1 | 40.2 | 0.132 | 87.5 |
| 8 | 75.6 | 11.8 | 2.0 | 10.5 | 40.6 | 0.127 | 92.0 |
Variation in the estimated HHVs of the biocrudes was found to be comparatively smaller (32.7–40.6 MJ kg−1, Table 2), relative to the breadth of biocrude yields observed (33.2–68.3% dw, Fig. 3A). Thus, the marked improvement in ER% and ECR observed with increasing lipid content of the feedstocks (increase in ER% from 56.3 to 92.0% and decrease in ECR from 0.325 to 0.127, respectively) was attributable disproportionately to the improvements in biocrude yield. ECR is highly dependent on moisture content of the HTL feedstock slurry, becoming more favorable at lower water contents.15 Given that the energy demand for dewatering steps during the harvesting of microalgae biomass has been identified as a major hurdle to the successful implementation of microalgae biofuels,1,3 lipid-rich microalgae feedstocks exhibiting higher HTL yields and HHV may be more amenable to processing with higher moisture contents (i.e., favorable ECR with less dewatering).16 Similarly, higher ER% values reflect a greater recovery of embedded feedstock energy in the biocrude product, suggesting that a batch with more lipids would be advantageous if maximizing energy recovery in the form of biocrude oil is the primary goal. However, it must be noted that both the ER% and ECR only consider the HTL processing step and do not account for the energy inputs during upstream cultivation, harvesting or dewatering. Thus, economic and life cycle optimization of the overall microalgae HTL biofuel process may involve trade-offs that lead to an optimum harvested cell composition that is not simply targeting maximum lipid content.
Recycling of the nutrient-rich aqueous phase product to upstream microalgae cultivation processes has been proposed as a key feature of microalgae HTL,8,39,42 insofar as suggesting it is essential for the microalgae HTL process to be feasible.1 The aqueous phase products from HTL conversion of the varying biomass batches in this study were analyzed for typical phototrophic nutrients (ESI Table S5†). TOC and TKN generally decreased as batch lipid content increased. Ammonia concentrations were roughly 50% of TKN for all batches, similar to previous reports for HTL of Nannochloropsis at comparable HTL conditions.24 Collective information from the literature reporting the successful cultivation of different species of microalgae from recycled HTL aqueous phases suggest that concentrations of 200–400 mg L−1 TOC, 50–150 mg L−1 TKN and 10–60 mg L−1 PO43− allow algae to thrive in the aqueous phase-derived media.39,42,49 Decreasing dilution factors (estimated at 150 for Batch 1 to 40 for Batch 8, data not shown) to meet these concentrations indicate that HTL produces aqueous phase products that require smaller amounts of valuable water resources for dilution as biomass lipid content increases (Table S5†).39
3.4. Influence of biochemical composition on biocrude oil characteristics
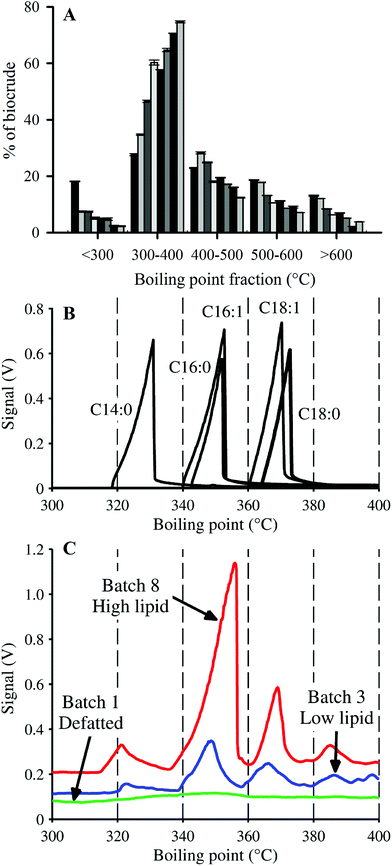
In addition to yield and elemental content, HTL biocrudes were characterized through the determination of molecular weight (MW) and boiling point (BP) distributions, and FAMEs analysis. The MW distributions of the biocrude products displayed a similar pattern across the cultivated batches (ESI Fig. SI1†). The profiles converged towards the 200–300 Da range as biomass lipid content increased from Batch 2 to Batch 8, as indicated by the major peak centered around 250 Da. SEC analysis of HTL biocrude from other microalgae species have shown distinctive MW distributions.15,50 The consistent profile patterns in ESI Fig. SI1† therefore suggest that the biocrudes contained mostly similar compounds, with the major difference attributed to variations in quantity of a certain group of lipid-type molecules with MWs in the 200–300 Da region (e.g., FAs such as C16:0–256 Da and C18:1–282 Da).Simulated distillation (SimDist) analysis (Fig. 4) showed that regardless of composition, the largest fraction of each biocrude fell in the 300–400 °C BP range, and the second largest in the 400–500 °C range, consistent with the boiling point fractions reported for other microalgae-derived HTL biocrudes.8,15,16 These two BP ranges make up the majority fraction of heavy vacuum gas oil (343–538 °C),16 which is typically catalytically upgraded in petroleum refineries into more valuable transportation fuels (e.g., gasoline, kerosene).51 Vardon et al.15 observed minimal differences in the BP profiles of biocrudes from Spirulina and Scenedesmus species (e.g., ∼31% in the 300–400 °C BP fraction for both microalgae) despite significant differences in biomass compositions. In contrast, there was a significant difference in the 300–400 °C fractions of the harvested batches in this study, increasing from 27.6 to 74.7% of the biocrude with increasing lipid content (0–58.7% dw lipids), a trend that was compensated for by decreasing amounts of biocrude in the other BP ranges.
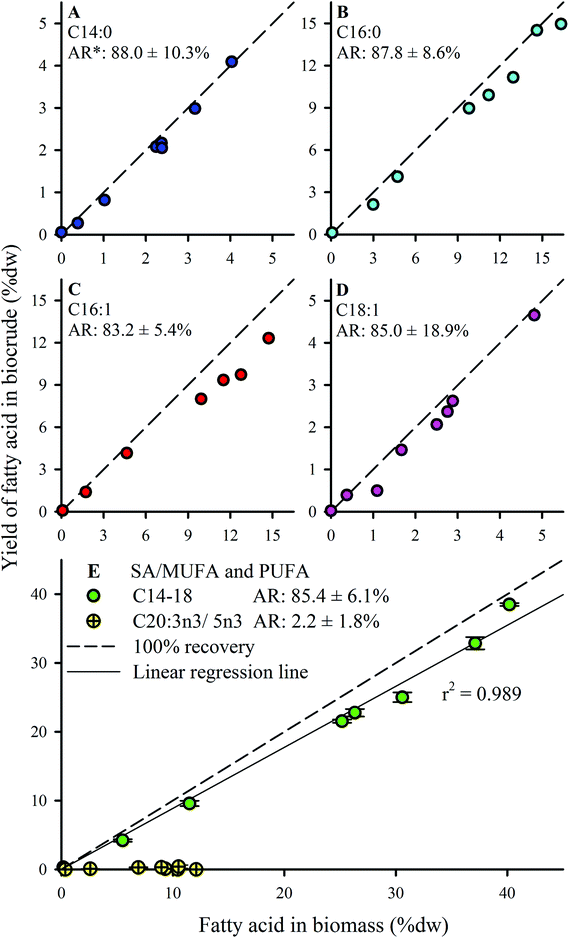
FA profiles of the biocrude products were analyzed to explore the fate and recovery of the six major FAs identified in the Nannochloropsis feedstock (Section 3.1) during HTL conversion. The % dw yields as biocrude (i.e., % FA content × % dw yield) of the FAs were quantified and shown in Fig. 5. Only four significant FAs (>1 wt% of biocrude; Fig. 5A–D) were observed in the biocrude products regardless of batch, with good recovery from the feedstocks being observed for the saturated FAs (SAFAs – C14:0 and C16:0; >87.8% average recovery) and mono-unsaturated FAs (MUFAs – C16:1 and C18:1; >83.2% average recovery). These four FAs became the dominant lipid component as batch lipid content increased, such as Batch 8 biocrude where the FAs constituted 62.0% of the biocrude, with C16:0 and C16:1 making up 21% and 22% of the biocrude, respectively (data not shown; cross-referenced from Fig. 3).
Conversely, almost no recovery of the poly-unsaturated FAs (PUFAs; C20:3n3 and C20:5n3) was observed in any biocrude (<2.5% average recovery). Brown et al.20 reported similar observations for HTL biocrude oil derived from Nannochloropsis, even where C20:5n3 was the predominant FA detected in the feedstock biomass.20 The susceptibility of PUFAs to reformation mechanisms under hydrothermal conditions is commonly attributed to the greater degrees of unsaturation.52–54 In particular, PUFAs have been shown to undergo polymerization in subcritical water,55 forming dimeric fatty acids that likely still partition to the biocrude phase despite being transformed. The poor PUFA recovery could also suggest that pre-treatment to convert the PUFAs into MUFAs or SAFAs (e.g., hydrogenation at lower temperature regimes where PUFAs are not susceptible to subcritical water hydrolysis) prior to HTL might be a viable strategy to improve the recovery of linear chain FAs, which are more amenable for upgrading into liquid fuel-type compounds.48
Given that the dominant FAs (2 SAFAs and 2 MUFAs) all displayed good recovery in HTL biocrude compared to PUFAs, these 4 dominant FAs were lumped together as a single parameter (C14–18) to determine a collective average recovery of 85.4% for SA/MUFAs (Fig. 5E). The good recovery observed for all feedstock batches (i.e., linear fit with r2 of 0.989) strongly suggests that C14–18 SA/MUFAs, and by extension any other SAFA or MUFA present in microalgal biomass, transfer largely intact to the biocrude after liberation from their respective TAGs and other FA-containing polar phospholipids. This general mechanism for the fate of FA-containing cell components explains the observed SEC and SimDist results as discussed above. The growing peak in the 200–300 Da region of the molecular weight distribution profiles observed for feedstocks with increasing lipid content (ESI Fig. SI1†) can thus be attributed to an increasing contribution of C14–18 FAs (MWs of 256–282 Da). SimDist analysis of individual model C14–18 SAFAs and MUFAs revealed peaks that aligned with those observed in HTL biocrude samples derived from different Nannochloropsis batches (Fig. 4B and C). Together, this provides further confirmation that as the cell structure is broken down in subcritical water, the TAGs and phospholipids are hydrolyzed to free FAs that subsequently partition with other hydrophobic conversion products to form the biocrude phase.20,53,56 The near quantitative recovery of SAFAs and MUFAs in biocrude also affirm that the collective SA/MUFA content of the feedstock biomass would be a promising predictor variable when developing models for HTL conversion of microalgae feedstocks.
3.5. Predictive modeling of biocrude yield and quality from algal biomass
| Biocrude yield (% dw) = x × L + y × P + z × C | (1) |
| (Biller and Ross): Biocrude yield (% dw) = 0.80 × L + 0.18 × P + 0.06 × C | (2) |
More recently, Teri et al.17 calibrated eqn (1) using the same approach and identical model compounds but at a HTL condition (300 °C, 20 min) more similar to the one in this study. It is noted that additional attempts to address cross-interactions between components by using mixtures of model compounds (e.g., a batch consisting of 33.3% of each component) provided a model with poorer accuracy,17 and therefore the model using single model compounds was selected here:
| (Teri et al.): Biocrude yield (% dw) = 0.95 × L + 0.33 × P + 0.06 × C | (3) |
As a comparison, eqn (1) was calibrated by multiple linear regression with experimental data derived from the HTL of 10 batches of Nannochloropsis with varying proximate compositions (as % dw; Table 1 and ESI Table S3†). This analysis resulted in an alternative set of model coefficients (eqn (4))
| (This study): Biocrude yield (% dw) = 0.97 (±0.10) × L + 0.42 (±0.07) × P + 0.17 (±0.35) × C | (4) |
Errors of coefficients (95% confidence levels) are shown in parentheses. Detailed results from the regression analysis including ANOVA, residuals, and Cook's Distance (D) values, are provided in the ESI (Table S6†), but the multiple R (0.999) and Significance F (6.142 × 10−10) values were highlighted to affirm the goodness of fit to Nannochloropsis batch data. Calibrated coefficients were insensitive to the compositions of individual batches given that Cook's D values were <0.5 for all data points except the defatted batch (Cook's D of 12.5), which was expected since it was an artificially created batch with a composition of ∼0% dw lipids.
The coefficients derived from HTL of Nannochloropsis (eqn (4)) agreed with the principle of the biochemical components’ relative contribution to yield given the coefficients have relative magnitudes of lipids > proteins > carbohydrates.13,17 However, all three coefficients were larger than previous studies obtained from model compounds (eqn (2) and (3)). Yield predictions for all three component additivity models (eqn (2)–(4)) were obtained by using compositions from all known microalgae HTL studies conducted at 300 °C, regardless of reaction time (Section 2.5) and compared to published experimental results (Fig. 6A–C); recent work by Valdez et al. showed little effect of reaction time on HTL product yields at t > 20 min.18 Predictions by eqn (2) (Fig. 6B) and (3) (Fig. 6C) generally underestimated the experimental results, which could suggest that the cross-interaction mechanisms between the biochemical components during HTL of microalgae biomass could have had constructive effects on biocrude yields36 which were not sufficiently represented by the HTL of model compound mixtures.17 Alternatively, the selected model compounds were not representative of the component class within microalgae or were unable to account for conversion of the same components when initially encapsulated within the microalgal cell (i.e., complications such as cellular compartmentalization, protein matrix, and lipid bodies). In any case, due to the higher coefficients obtained using the Nannochloropsis data set, predictions with eqn (4) (Fig. 6A) were generally more accurate and balanced in distribution (r2 of 0.463), with similar patterns in the residuals among the additivity models (see ESI Fig. SI2†).
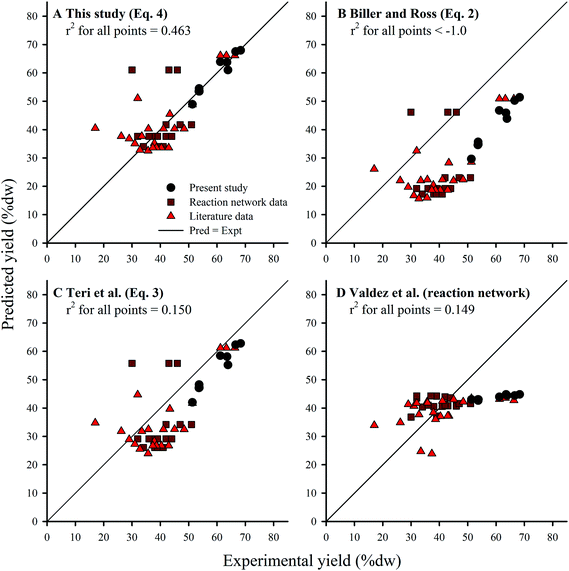 | ||
Fig. 6 Comparison of yield predictions obtained by component additivity models from: (A) this study (eqn (4)); (B) Biller and Ross (eqn (2)); and (C) Teri et al. (eqn (3)). Kinetic-based reaction network model by Valdez et al. shown in (D). All points are results of HTL of microalgae biomass at 300 °C only; reaction times range 5–90 min. 53 Points were demarcated to show: (●) 9 calibration points for eqn (4); ( ) 22 calibration points for the kinetic-based model; and ( ) 22 calibration points for the kinetic-based model; and ( ) 22 other literature data points. The complete list of literature data is available in the ESI (Table S1†). The r2 values were calculated from all 53 points. ) 22 other literature data points. The complete list of literature data is available in the ESI (Table S1†). The r2 values were calculated from all 53 points. | ||
As an alternative to the linear component additivity approach, Valdez et al.18 proposed a reaction network model which attempted to account for the kinetics of various transformation pathways that individual biochemical components and the resultant HTL product fractions undertake during treatment in sub-critical water. Model formulation includes a set of first-order differential equations that define the evolution of each component (obtained via proximate analysis) and product fraction with respect to reaction time, and thus requires computational solvers to make predictions. One unique aspect of the reaction network model is that it seeks to predict the effects of both reaction time and temperature (e.g., HTL has been studied in the range of 5–90 min, 200–375 °C).18 Although the reaction network model was designed to apply to a wider set of conditions, here we compared predictions with the same validation data set (HTL at 300 °C, all reaction times) as eqn (2)–(4) (Fig. 6D). The reaction network model predictions were generally more accurate than eqn (4) for experimental results within 35–45% dw lipids (which constitute a significant portion of the calibration data), but over-estimated and largely under-predicted the yields for feedstocks with <35% dw and >45% dw lipids, respectively. Visual inspection of the residuals underscores this bias (see ESI Fig. SI2†), suggesting that the structure of the reaction network model requires refinement to better characterize biocrude yield across a wider range of feedstock compositions. Thus, the model trades a decrease in average accuracy across a wide range of compositions (and hence biocrude yields) for increased accuracy within a small band of results (in this case, 35–45% dw lipids). It is conceivable that future work to improve the component additivity model presented here (eqn (4)) can adopt the approach used for the reaction network model,18 using varying biomass compositions tested at a wider range of HTL conditions in order to develop even more robust prediction models.
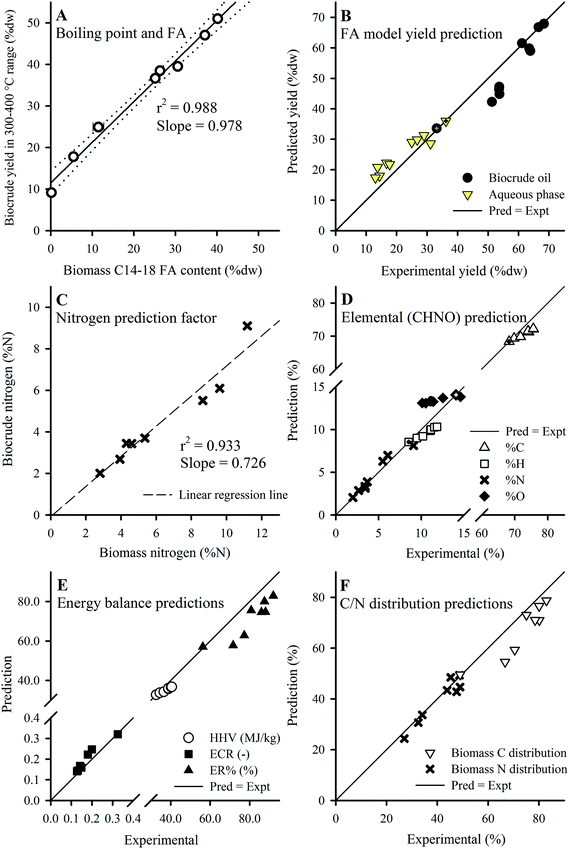 | ||
| Fig. 7 (A) Plot of biocrude yield in the 300–400 °C range and biomass C14–18 FA content. (B) Predicted vs. experimental yields using the FA model (eqn (5) and (6)). Application of the N predictor (C; eqn (8)) and FA model (as eqn (7)) predicts elemental composition (D), from which the energy balances (E) and C/N distributions (F; calculated using yields shown in B and values from D) were obtained. Defatted batch results used for calibration are marked with a cross, and Batches 2–8 were used for validation except in (B) which included 3b and 3c (ESI Table S3†). Error bars in (A) show min/max values of the FA content (smaller than symbol if not shown). | ||
The strong correlation served as the basis for an alternative “FA model” for microalgae that considers the behavior of FA and defatted biomass components separately. Compositional analysis (Table 1) suggested that for a single species cultivated for lipid accumulation, each harvested batch contained a baseline composition of structural compounds (e.g., PL/prot ratio 0.3–0.6) along with varying degrees of FA accumulation as TAGs (0.59–52.0% dw FAMEs). Thus, in the context of HTL conversion, lipid accumulation in microalgae biomass could be approximated as increasing FA content on top of a baseline structural composition as represented by the defatted Batch 1 (noting that this is an approximation given that the defatting process via a Folch method29 solvent mixture removes all lipids, some of which may be structural or functional). Although the recovery of the SA/MUFAs was ∼85% (Section 3.4), HTL of model lipids have shown that the hydrolysis products of these FAs would be incorporated into the biocrude phase (e.g., yield of ∼95% biocrude from HTL of sunflower oil, after accounting for losses as glycerol).17 Despite the poor recovery of intact PUFAs (Section 3.4), their content was also included together with the SA/MUFAs since the hydrolysis products of PUFAs under subcritical water conditions, and therefore the PUFAs themselves, are also expected to partition quantitatively to the biocrude phase as earlier discussed.54,55 The FA model is introduced here for both biocrude yield and aqueous phase yield which considers the contribution of FA and non-FA biomass components to HTL biocrude yield:
| Biocrude yield (% dw) = FAs + (defat BC yield) × (100% − FAs) | (5) |
| Aqueous phase yield (% dw) = (defat AQ yield) × (100% − FAs) | (6) |
Eqn (5) predicts biocrude yield as the summation of biomass FA content (FAs = % dw total FAMEs) and the yield from the non-FA fraction (100% – FAs) as determined by the HTL of defatted biomass of identical species (prepared according to the method in Section 2.1). The model entails a straightforward and principally sound method to embrace the numerous degrees of freedom (e.g., conversion conditions, microalgae species) using the defatted batch product yield, which directly accounts for the species-specific structural content of the target species and variations in HTL processing methods. The model also assumes that any accumulated carbohydrates would not markedly affect predictions given their low contribution to biocrude yield (i.e., coefficient of 0.17 from eqn (4)). Eqn (6) predicts the aqueous phase yield based on the yield obtained by the defatted batch through the same principles for biocrude yield as described, and assumes insignificant contributions from FA components of the feedstock algae.
The FA model predicted biocrude yields for batches with higher FA content (Batches 4–8; >38.6% dw as FAMEs) accurately (Fig. 7B), while predictions slightly underestimated yield for lower FA content batches (<21.0% dw FAMEs) at 82–88% accuracy (data not shown). The underestimations for lower FA content batches can be attributed, in part, to the significant portion of non-FA type lipid compounds (e.g. plant waxes, pigments; PL content 14.9–18.5% dw) contained in these feedstocks, which end up being lumped together with the (100% – FA) parameter and multiplied by the low yield for defatted biomass (0.332). Presumably, a much larger coefficient should be applied to this portion of biomass (e.g., 0.97 as shown in Section 3.5.1, eqn (4)) given their larger contribution to biocrude yields. A possible future improvement would be developing a method to extract only FA-containing compounds (e.g., TAGs and phospholipids) from biomass in preparation of the defatted batch, thereby better preserving the non-FA lipids in biomass for enhanced model calibration. The aqueous phase predictions were opposite in terms of accuracy to the biocrude yields, where predictions were fairly accurate for low FA content batches (92–116%; data not shown) but overestimated for high FA content batches (125–152%; data not shown), suggesting more complex mechanisms involved in the prediction of aqueous phase yields that were not explored in this study.
The FA modeling approach can be extended to predict other important HTL parameters (e.g., %CHNO, HHV, C/N distribution), as expressed in the general form:
| X = (FAs) × (X of FAs) + (100% − FAs) × (X of defat batch) | (7) |
Prediction of nitrogen content in biocrude precludes the use of the FA model given that FAs have no %N content. Instead, for this parameter a strong linear correlation (r2 of 0.933, Fig. 7C) between both %N of biomass and biocrude indicates that a pre-determined fraction of protein-derived N partitions to the biocrude phase regardless of protein content in the feedstock, thereby dictating the actual N distribution to the biocrude product, explaining the increase of biocrude phase distribution of N earlier (Section 3.3). The %N content of biocrude can thus be predicted as:
| Biocrude %N = 0.726 (±0.194) × Biomass %N | (8) |
Errors of coefficients (95% confidence levels) are shown in parenthesis. This served as a preliminary suggestion in predicting the %N content of biocrude based on the biochemical composition, and therefore the exact causes or mechanisms were not further explored.
4. Conclusions and technological applications
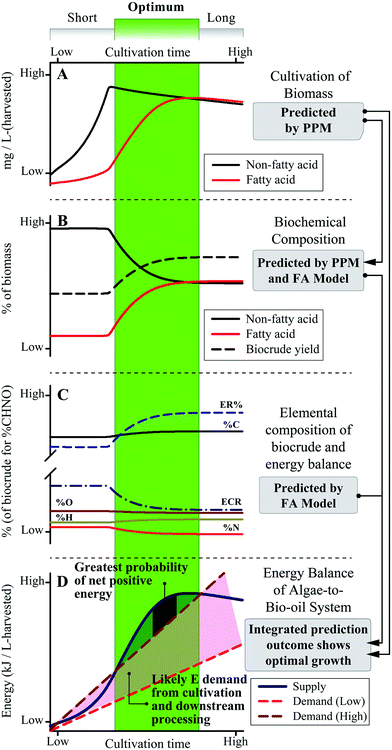
A systems-scale modeling approach of the complete microalgae cultivation to HTL conversion process by integrating a dynamic biological cultivation model (PPM)11 and thermochemical conversion model (the FA model introduced here) is demonstrated conceptually in Fig. 8. The PPM uses a lumped pathway metabolic model of microalgae metabolism to predict the FA and non-FA content of cultivated biomass as a function of cultivation time and conditions (including light intensity, nutrient content, etc.),11 which can be directly linked to the FA model to predict downstream biocrude yield and energetic content (as HHV) of the biocrude product, in order to predict systems-level metrics (e.g., net energy return, NER) by comparing net energy yield to energy demand across all processes. For example, the qualitative representation in Fig. 8 suggests that for shorter periods of cultivation there is a high probability for poor to negative net energy returns depending on the amount of energy required for cultivation and harvesting of biomass (Fig. 8D). Conversely, over-extending the cultivation period does not appear to result in significant improvements to biocrude yield and quality or potential recoverable energy despite increasing cultivation energy demand. The integrated prediction framework instead suggests an optimal growth period which balances cultivation and FA accumulation (Fig. 8, green region), translating to improved biocrude yield and quality over the short period and a positive NER of the overall system compared to longer periods of cultivation. The model further implies an optimal cultivation period which provides the highest NER that systems would seek to achieve in order to maximize energy production.Ultimately, system optimization would be dependent upon microalgae growth and FA accumulation rates, HTL conversion conditions, and all other process parameters which would vary from system to system,10,14 which is where the PPM-FA-model approach would excel given that it can be tailored to each end-user for a wide variety of predictive and system design applications (such as that shown in Fig. 8),3,57 providing opportunities to tackle complex and interdependent questions in microalgae-HTL research such as the balance of energy-consuming cultivation for FA accumulation and energy return in the form of increased biocrude yield and quality.7,22 This section and Fig. 8 demonstrates how overall process predictions that were previously unavailable to the microalgae-biofuel research community can now be utilized to address a multitude of key research questions moving forward.1,3,22
In conclusion, the analyses of HTL products derived from Nannochloropsis batches cultivated with systematically varying compositions were used to inform the development of two predictive models for HTL biocrude yield, with the FA model able to predict other important outputs of the process (e.g., aqueous phase product yield, %CHNO, HHV). The FA model does not render the additivity model obsolete; it is expected that the additivity model would have lower barriers-to-entries of use given that the proximate analytical suite (i.e., lipid, carbohydrate, protein) is generally less complex compared to FAMEs analysis and calibration via HTL of a defatted batch. However, it bears repeating that the FA model is highly customizable for target HTL conditions and microalgae species of interest, allowing seamless integration with upstream cultivation models that predict composition of harvested biomass, as demonstrated with the PPM-FA-model in Section 4, to enable quantitative analysis of whole-system biofuel production operational costs, environmental sustainability such as the fate of gases produced from HTL reactions, and net energy return on investments.3,4 The integrated modeling framework, together with future research, will unlock the promised synergy in tailoring cell composition of biomass for optimizing biofuel production systems,7 presenting a new trajectory towards the realization of sustainable microalgal biofuel production. Finally, the integrated models would support more accurate techno-economic and life cycle assessments (TEA/LCA) of microalgae biofuel production systems that incorporate HTL downstream processes, or vice versa, bringing considerable advancement in dealing with the multi-faceted, interdependent multiple-technology challenges of microalgal-biofuel research.1
Acknowledgements
This material is based upon work supported by the National Science Foundation under grant no. 1438667 and 1438218. SL is supported by the National Research Foundation Singapore under its National Research Foundation (NRF) Environmental and Water Technologies (EWT) PhD Scholarship Programme and administered by the Environment and Water Industry Programme Office (EWI). We thank Ian Bradley (CEE, UIUC) and Dheeptha Murali (ISTC) for help with microalgae cultivation and biocrude characterization, respectively. We thank John Scott and Susan Barta at ISTC for help with TOC analysis. The authors thank Kelly Pisanko (College of Fine and Applied Arts, UIUC) for assistance in graphic design (Fig. 1, 8 and the TOC figure).References
-
U.S. D.O.E., National Algal Biofuels Technology Roadmap, Office of Energy Efficiency and Renewable Energy Report DOE/EE-0332, U.S. D.O.E., Washington, D.C., 2010
.
- A. A. Koutinas, A. Vlysidis, D. Pleissner, N. Kopsahelis, I. L. Garcia, I. K. Kookos, S. Papanikolaou, T. H. Kwan and C. S. K. Lin, Chem. Soc. Rev., 2014, 43, 2587–2627 RSC
.
-
National Research Council (U.S.) and National Academies Press (U.S.), Sustainable development of algal biofuels in the United States, National Academies Press, Washington, D.C., 2012 Search PubMed
.
- P. M. Foley, E. S. Beach and J. B. Zimmerman, Green Chem., 2011, 13, 1399–1405 RSC
.
- L. M. L. Laurens, N. Nagle, R. Davis, N. Sweeney, S. V. Wychen, A. Lowell and P. T. Pienkos, Green Chem., 2015, 17, 1145–1158 RSC
.
- L. Brennan and P. Owende, Renewable Sustainable Energy Rev., 2010, 14, 557–577 CrossRef CAS
.
- P. E. Savage, Science, 2012, 338, 1039–1040 CrossRef CAS PubMed
.
- G. W. Roberts, B. S. M. Sturm, U. Hamdeh, G. E. Stanton, A. Rocha, T. L. Kinsella, M.-O. P. Fortier, S. Sazdar, M. S. Detamore and S. M. Stagg-Williams, Green Chem., 2015, 17, 2560–2569 RSC
.
- D. C. Elliott, T. R. Hart, A. J. Schmidt, G. G. Neuenschwander, L. J. Rotness, M. V. Olarte, A. H. Zacher, K. O. Albrecht, R. T. Hallen and J. E. Holladay, Algal Res., 2013, 2, 445–454 CrossRef
.
- L. Rodolfi, G. Chini Zittelli, N. Bassi, G. Padovani, N. Biondi, G. Bonini and M. R. Tredici, Biotechnol. Bioeng., 2009, 102, 100–112 CrossRef CAS PubMed
.
- J. S. Guest, M. C. M. van Loosdrecht, S. J. Skerlos and N. G. Love, Environ. Sci. Technol., 2013, 47, 3258–3267 CAS
.
- P. A. Hodgson, R. J. Henderson, J. R. Sargent and J. W. Leftley, J. Appl. Phycol., 1991, 3, 169–181 CrossRef CAS
.
- P. Biller and A. B. Ross, Bioresour. Technol., 2011, 102, 215–225 CrossRef CAS PubMed
.
- D. López Barreiro, W. Prins, F. Ronsse and W. Brilman, Biomass Bioenergy, 2013, 53, 113–127 CrossRef
.
- D. R. Vardon, B. K. Sharma, G. V. Blazina, K. Rajagopalan and T. J. Strathmann, Bioresour. Technol., 2012, 109, 178–187 CrossRef CAS PubMed
.
- D. R. Vardon, B. K. Sharma, J. Scott, G. Yu, Z. Wang, L. Schideman, Y. Zhang and T. J. Strathmann, Bioresour. Technol., 2011, 102, 8295–8303 CrossRef CAS PubMed
.
- G. Teri, L. Luo and P. E. Savage, Energy Fuels, 2014, 28, 7501–7509 CrossRef CAS
.
- P. J. Valdez, V. J. Tocco and P. E. Savage, Bioresour. Technol., 2014, 163, 123–127 CrossRef CAS PubMed
.
- P. Biller, R. Riley and A. B. Ross, Bioresour. Technol., 2011, 102, 4841–4848 CrossRef CAS PubMed
.
- T. M. Brown, P. Duan and P. E. Savage, Energy Fuels, 2010, 24, 3639–3646 CrossRef CAS
.
- A. F. Clarens, E. P. Resurreccion, M. A. White and L. M. Colosi, Environ. Sci. Technol., 2010, 44, 1813–1819 CrossRef CAS PubMed
.
-
S. Jones, Y. Zhu, D. Anderson, R. Hallen, D. Elliott, A. Schmidt, K. Albrecht, T. Hart, M. Butcher, C. Drennan, L. Snowden-Swan, R. Davis and C. Kinchin, Process Design and Economics for the Conversion of Algal Biomass to Hydrocarbons: Whole Algae Hydrothermal Liquefaction and Upgrading, Pacific Northwest National Laboratory (PNNL), Richland, WA (US), 2014 Search PubMed
.
- D. López Barreiro, C. Zamalloa, N. Boon, W. Vyverman, F. Ronsse, W. Brilman and W. Prins, Bioresour. Technol., 2013, 146, 463–471 CrossRef PubMed
.
- P. J. Valdez, J. G. Dickinson and P. E. Savage, Energy Fuels, 2011, 25, 3235–3243 CrossRef CAS
.
- P. J. Valdez, M. C. Nelson, H. Y. Wang, X. N. Lin and P. E. Savage, Biomass Bioenergy, 2012, 46, 317–331 CrossRef CAS
.
- P. J. Valdez and P. E. Savage, Algal Res., 2013, 2, 416–425 CrossRef
.
- M. M. Rebolloso-Fuentes, A. Navarro-Pérez, F. García-Camacho, J. J. Ramos-Miras and J. L. Guil-Guerrero, J. Agric. Food Chem., 2001, 49, 2966–2972 CrossRef CAS PubMed
.
- M. DuBois, K. A. Gilles, J. K. Hamilton, P. A. Rebers and F. Smith, Anal. Chem., 1956, 28, 350–356 CrossRef CAS
.
- J. Folch, M. Lees and G. H. S. Stanley, J. Biol. Chem., 1957, 226, 497–509 CAS
.
- H. C. Pinkart, R. Devereux and P. J. Chapman, J. Microbiol. Methods, 1998, 34, 9–15 CrossRef CAS
.
- J. G. Hamilton and K. Comai, Lipids, 1988, 23, 1146–1149 CrossRef CAS PubMed
.
- L. M. L. Laurens, M. Quinn, S. V. Wychen, D. W. Templeton and E. J. Wolfrum, Anal. Bioanal. Chem., 2012, 403, 167–178 CrossRef CAS PubMed
.
- L. M. L. Laurens, T. A. Dempster, H. D. T. Jones, E. J. Wolfrum, S. Van Wychen, J. S. P. McAllister, M. Rencenberger, K. J. Parchert and L. M. Gloe, Anal. Chem., 2012, 84, 1879–1887 CrossRef CAS PubMed
.
- P. Duan and P. E. Savage, Ind. Eng. Chem. Res., 2011, 50, 52–61 CrossRef CAS
.
- J. Akhtar and N. A. S. Amin, Renewable Sustainable Energy Rev., 2011, 15, 1615–1624 CrossRef CAS
.
- S. S. Toor, L. Rosendahl and A. Rudolf, Energy, 2011, 36, 2328–2342 CrossRef CAS
.
- G. Yu, Y. Zhang, L. Schideman, T. Funk and Z. Wang, Energy Environ. Sci., 2011, 4, 4587–4595 CAS
.
- T. Minowa, S. Yokoyama, M. Kishimoto and T. Okakura, Fuel, 1995, 74, 1735–1738 CrossRef CAS
.
- P. Biller, A. B. Ross, S. C. Skill, A. Lea-Langton, B. Balasundaram, C. Hall, R. Riley and C. A. Llewellyn, Algal Res., 2012, 1, 70–76 CrossRef CAS
.
- L. Garcia Alba, C. Torri, C. Samorì, J. van der Spek, D. Fabbri, S. R. A. Kersten and D. W. F. Brilman, Energy Fuels, 2012, 26, 642–657 CrossRef CAS
.
- U. Jena, K. C. Das and J. R. Kastner, Bioresour. Technol., 2011, 102, 6221–6229 CrossRef CAS PubMed
.
- Y. Zhou, L. Schideman, G. Yu and Y. Zhang, Energy Environ. Sci., 2013, 6, 3765–3779 CAS
.
- S. Zou, Y. Wu, M. Yang, C. Li and J. Tong, Energy Environ. Sci., 2010, 3, 1073–1078 CAS
.
- H. Li, Z. Liu, Y. Zhang, B. Li, H. Lu, N. Duan, M. Liu, Z. Zhu and B. Si, Bioresour. Technol., 2014, 154, 322–329 CrossRef CAS PubMed
.
- G. A. Dunstan, J. K. Volkman, S. M. Barrett and C. D. Garland, J. Appl. Phycol., 1993, 5, 71–83 CrossRef CAS
.
- T. Tonon, D. Harvey, T. R. Larson and I. A. Graham, Phytochemistry, 2002, 61, 15–24 CrossRef CAS PubMed
.
- M. Y. Roleda, S. P. Slocombe, R. J. G. Leakey, J. G. Day, E. M. Bell and M. S. Stanley, Bioresour. Technol., 2013, 129, 439–449 CrossRef CAS PubMed
.
- P. Duan and P. E. Savage, Energy Environ. Sci., 2011, 4, 1447–1456 CAS
.
- U. Jena, N. Vaidyanathan, S. Chinnasamy and K. C. Das, Bioresour. Technol., 2011, 102, 3380–3387 CrossRef CAS PubMed
.
- C. Torri, L. Garcia Alba, C. Samorì, D. Fabbri and D. W. F. Brilman, Energy Fuels, 2012, 26, 658–671 CrossRef CAS
.
- G. W. Huber, P. O'Connor and A. Corma, Appl. Catal., A, 2007, 329, 120–129 CrossRef CAS
.
- O. Tavakoli and H. Yoshida, Ind. Eng. Chem. Res., 2006, 45, 5675–5680 CrossRef CAS
.
- R. L. Holliday, J. W. King and G. R. List, Ind. Eng. Chem. Res., 1997, 36, 932–935 CrossRef CAS
.
- H.-Y. Shin, J.-H. Ryu, S.-Y. Park and S.-Y. Bae, J. Anal. Appl. Pyrolysis, 2012, 98, 250–253 CrossRef CAS
.
- T. Kocsisová, J. Juhasz and J. Cvengroš, Eur. J. Lipid Sci. Technol., 2006, 108, 652–658 CrossRef
.
- J. W. King, R. L. Holliday and G. R. List, Green Chem., 1999, 1, 261–264 RSC
.
- B. D. Shoener, I. M. Bradley, R. D. Cusick and J. S. Guest, Environ. Sci.: Processes Impacts, 2014, 16, 1204–1222 CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5gc00574d |
| ‡ Present location: Department of Civil and Environmental Engineering, Colorado School of Mines, Golden, CO 80401, USA. |
| § Table of abbreviations is available in the ESI.† |
| This journal is © The Royal Society of Chemistry 2015 |