Artificial multiferroic heterostructures

Abstract

The electric field control of magnetism in the solid state has become a very active topic of research recently, made possible by the advances in the synthesis and fabrication of new materials and artificial heterostructures. Key strategies include structural manipulation through epitaxial growth to create single crystalline multiferroic materials with enhanced properties, and exploring proximity effects between magnetic and ferroelectric materials to create strong magnetoelectric couplings. The current state-of-the-art shows that tremendous progress has been achieved in this field and that functionalisation of this class of materials is within reach.

---

Carlos António Fernandes Vaz

Carlos A. F. Vaz graduated from Lisbon University and received his Ph.D. degree from Cambridge University. After a spell at Yale University as a Postdoctoral Associate, he joined the Paul Scherrer Institut, where he currently works as a staff scientist. His research interests include magnetism, spintronics, multiferroics, X-ray and electron spectroscopy, and epitaxial growth and characterization of multifunctional materials, with a focus on thin films, heterostructures, and patterned elements of transition metal ferromagnets and complex oxides.

Urs Staub

Urs Staub received his Ph.D. degree in physics from the Eidgenössiche Technische Hochschule (ETH) Zürich in 1993. After a Postdoctoral Fellowship of the Swiss National Science foundation at Argonne National Laboratory, he joined the Paul Scherrer Institut in 1995, where he is currently Leader of the Magnetism and Microscopy Group. His research interests are in condensed matter, including metal–insulator transitions, colossal magnetoresistance, multiferroics, electronic ordering phenomena, and ultrafast science, with the focus on using large facilities such as neutron, synchrotron X-ray sources, and X-ray free electron lasers.

---

Long-range ordering in condensed matter is at the origin of the many functional properties of materials that underpin science and technology. Hence, not surprisingly, a large fraction of the research effort to date has been devoted to discovering new states of matter and to enhancing the properties of ordered materials. One example is provided by the renewed interest in a special class of materials systems characterised by the simultaneous presence of magnetic and ferroelectric order, called magnetoelectric multiferroics.^1,2 These are systems that fulfill both requirements for the presence of magnetism (break in time-reversal symmetry) and ferroelectricity (break in space-inversion symmetry), representing therefore a much smaller subset of the magnetic and ferroelectric systems. Examples of naturally occurring multiferroics include Fe₃O₄ (magnetite)^3,4 and CuO (tenorite).⁵ The motivation for studying multiferroic systems is twofold: at a basic science level, they provide model systems for the investigation of electron correlation effects and their role on the material properties, both at the experimental and theoretical levels.^6,7 From an applied physics perspective, the electrostatic control of magnetism and the direct magnetic generation of electromotive forces in the solid state have potential for the development of disruptive technologies, including novel electronic devices in which both charge and spin carry information (spintronics), non-volatile random-access memories, ultra-sensitive detectors and actuators, and solid state transformers.^8–10

A feature common to all intrinsic (single phase) multiferroics is the presence of strong electron correlations, which renders a full understanding of the microscopic mechanisms of magnetoelectric coupling challenging.^6,7 They can be divided into type I and II depending on whether the magnetic and ferroelectric order are uncorrelated or derived from one another, respectively.¹¹ Type I multiferroics are characterised by large polarisations, an independent onset of magnetic and ferroelectric order (as reflected in very different magnetic and ferroelectric critical temperatures) and by small magnetoelectric couplings. Type II multiferroic behaviour occurs in spiral magnets (induced by spin–orbit coupling in the form of a Dzyaloshinskii-Moriya exchange interaction) or in spin frustrated collinear systems (arising from exchange striction, where atomic displacements of the magnetic ions set in at the critical temperature to minimize the magnetic exchange energy), where the onset of magnetic order triggers a ferroelectric state.^11–13 Hence, they are characterised by strong magnetoelectric couplings, but have typically small polarisations and low critical temperatures. For practical applications both the presence of a strong coupling between the two order parameters and room temperature operation are required, conditions that are not met for most known single phase multiferroics—the best known exceptions to date being BiFeO₃ and the hexaferrites.^14–17 Additionally, single phase multiferroics have complex crystal structures, which renders the growth of high quality crystals challenging.

One way to circumvent the difficulties associated with intrinsic multiferroics is to explore proximity effects that arise at the interface between magnetic and ferroelectric systems. This results in artificial multiferroics, composed of heterogeneous systems where an interfacial magnetoelectric coupling is created between the two order parameters.^18,19 One key advantage of this approach is that one can draw from the much larger magnetic and ferroelectric group of materials to optimise the magnetoelectric strength with large polarisations and operation at ambient temperatures. This approach to multiferroic behaviour relies on high quality, sharp, interfaces between the different phases of the composite; hence, particular attention must be given to the chemical stability of the interface to prevent intermixing that may lead to a dulling of the interaction mechanism between the different order parameters. In this context, the recent developments in nanoscale characterisation tools, such as scanning transmission electron microscopy,^20,21 X-ray synchrotron spectroscopy techniques,^22–29 and scanning probe microscopy,^30,31 have been instrumental for the recent advances in our understanding of the physics and chemistry of interfaces. In the time domain, X-ray based ultrafast time-resolved techniques have recently become available^32,33 that have a large potential for addressing the fundamentals of electron dynamical processes that govern the physical, chemical, and functional behaviour of surfaces and interfaces.

In this Highlight, we present a brief overview of recent developments in the field of artificial multiferroics, with particular focus on the electric field control of the magnetic state and on the fast dynamics associated with multiferroic systems. The latter aspect is critical for the understanding of the physical mechanisms underlying the magnetoelectric coupling and is also of primary importance for electronic device applications, where fast switching is essential.

I. Proximity effects and artificial multiferroics

One approach to multiferroic behaviour is that of combining ferroelectric and ferromagnetic materials to define composite heterostructures with an interfacial coupling between the two order parameters, with a strength that is dependent on the electronic mechanisms linking the order parameters.^34,35 The challenge is to engineer a strong coupling across the interface to achieve large magnetoelectric effects.

Compared with the case of single phase multiferroics, the origin of the magnetoelectric coupling in artificial multiferroics is much simpler to address since the origin of the ferroelectric and magnetic order can be dissociated from the coupling mechanism between them, which itself is limited to a few number of possibilities: (i) strain, (ii) direct (spin) exchange, and (iii) charge coupling,¹⁸ as illustrated diagrammatically in Fig. 1. Further, the control of magnetism is done through modification of one of the three fundamental parameters in magnetism: (a) the exchange constant (which drives the magnetic order), (b) the magnetisation (local spin amplitude), and (c) the magnetic anisotropy (originating from spin-orbit coupling).¹⁹

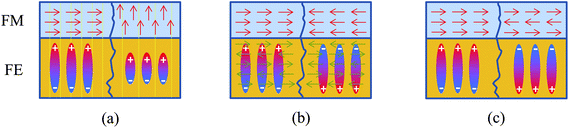Fig. 1 Diagrammatic illustration of the different types of interfacial coupling in ferromagnetic/ferroelectric artificial multiferroic structures: (a) strain, where electro-strain in the ferroelectric propagates to the ferromagnet to induce a magnetoelastic anisotropy; (b) spin exchange, where the exchange bias direction is controlled by the orientation of the antiferromagnetic spin alignment of a multiferroic layer; and (c) charge mediated, where charge modulation through screening of the ferroelectric polarisation induces changes in the magnetic interaction of the ferromagnet. Arrows represent magnetic moments, ellipses the ferroelectric polarisation.

The figure of merit that characterizes the coupling between the electric and magnetic order parameters is the magnetoelectric susceptibility, corresponding to the change in magnetic (electric) polarisation for a given applied electric (magnetic) field, α_r = cμ₀ΔM/ΔE or α_r = cμ₀ΔP/ΔB, in general a tensor and defined here as a dimensionless quantity (in c.g.s. units, c = μ₀ = 1).^18,36,37 While for intrinsic multiferroics the magnetoelectric constant is an extensive quantity, for artificial multiferroics the coupling is interfacial in nature and the magnetoelectric coupling mostly scales with the area. For comparison, however, we consider here the effective coupling averaged over the magnetic volume of the system and representative values for a selected number of multiferroic systems are given in Table 1, illustrating that the macroscopic magnetoelectric coupling can be made much larger in artificial multiferroic systems. We consider in the following some recent developments in the three approaches that have been used to controlling magnetism electrostatically.

Table 1 Effective magnetoelectric coupling coefficient for selected multiferroic systems (PMN-PT stands for Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ and PZT for Pb(Zr,Ti)O₃)

System	Structure	Coupling	αr	Temperature (K)	Ref.
a Linear variation at high magnetic fields (above 15 T).b Absolute peak value.c μ0ΔM is taken as the change in exchange bias field, μ0ΔHex.
CuO	Tenorite	Intrinsic	<5 × 10^−5	200	38
BiFeO3	Perovskite	Intrinsic	−1.3 × 10^−4^a	300	39
Ba0.52Sr2.48Co2Fe24O41	Hexaferrite	Intrinsic	0.9^b	300	40
La0.67Sr0.33MnO3/BaTiO3	Composite	Strain	69	200	41
Ni/PMN-PT	Composite	Strain	660	300	42
La0.7Sr0.3MnO3/BiFeO3	Composite	Spin exchange	0.015^c	5.5	43
NiFe/LuMnO3	Composite	Spin exchange	∼1.1^c	5	44
BaTiO3/La0.67Sr0.33MnO3	Composite	Charge	∼0.04	300	45
PZT/La0.8Sr0.2MnO3	Composite	Charge	−49	180	46

---

(i) In strain-mediated magnetoelectric coupling, the piezoelectric or electrostrictive effect of the ferroelectric component is used to modulate the magnetic anisotropy of the magnetic subsystem through the magnetoelastic interaction;^8,9,18,47,48 in some instances, such as in the manganites, direct modifications in the electronic structure give rise to changes in the exchange interaction.^41,49–54 Several approaches to strain-mediated coupling have been considered, from bulk particulate composites formed by sintering ferroelectric and ferromagnetic nanoparticles,^8,18,48 laminate structures composed of ferroelectric and ferromagnetic slabs bonded together,^8,9 and the corresponding nanoscale equivalents consisting of self-assembled ferromagnetic nanostructures embedded in a ferroelectric matrix,^55–59 epitaxial ferromagnetic films grown on ferroelectric substrates,^60–66 to lithographically defined magnetic structures on ferroelectric layers.^42,67 This approach to magnetoelectric coupling has been extensively explored and well discussed in recent reviews.^{8,9,18,47,48,68} In particular, strain-mediated coupling has been used successfully to control the magnetic configuration of ferromagnetic elements by using the strain induced by the ferroelectric to modify the magnetic anisotropy, including the magnetic easy axis.^69–72 One example is the recent demonstration of reversible electric field switching of the magnetisation direction by 90° in single domain Ni dots deposited on out of plane ferroelectric domains of PMN-PT(011).⁴² The measurements were carried out by X-ray magnetic microspectroscopy as a function of the applied electric field and show that the magnetisation direction follows the strain amplitude applied through the ferroelectric as shown in Fig. 2(c): on increasing the field from 0 to 0.15 MV m⁻¹, the magnetisation direction of the dots inside circles and triangles (which lie on out of plane ferroelectric domains) changes by 90°, and upon further increasing the field (which results in a reduction of the applied strain), the magnetisation of the dots inside triangles reorients back to 0°, showing that the switching process is reversible. On the other hand, dots grown on in-plane ferroelectric domains see their original anisotropy reinforced by the applied strain and do not change the magnetisation direction (dots inside squares), a point that illustrates the need for a good control of the ferroelectric polarisation state. Since the magnetisation of the whole dot changes orientation, a correspondingly very large magnetoelectric constant of about α_r = 660 is obtained.

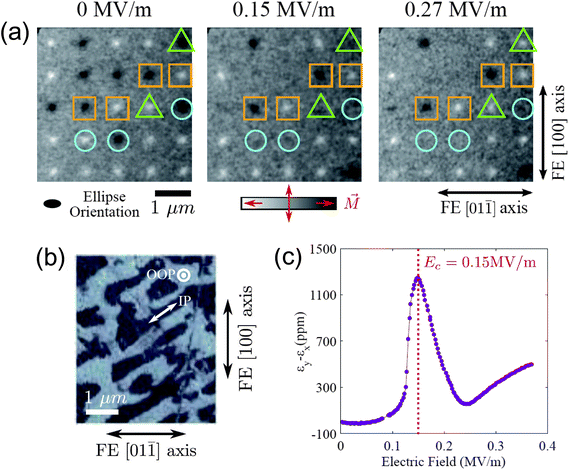Fig. 2 (a) X-ray magnetic microscopy images of the magnetisation of Ni dots deposited on PMN-PT(110) versus applied electric field showing a 90° orientation of the magnetisation (dots inside circles and triangles); the strain relaxation at a larger electric field (0.27 MV m⁻¹) leads to a reorientation back to 0° for the dots in the triangles. Squared dots do not change the magnetisation direction, corresponding to dots initially deposited on in-plane ferroelectric domains. (b) Piezoelectric force microscopy image of the ferroelectric domain structure of PMN-PT; control of the magnetisation orientation is achieved only for Ni dots grown on out of plane domains. (c) The anisotropic in-plane piezoresponse of PMN-PT against the electric field, applied out of plane. Reprinted with permission from ref. 42. Copyright (2013) by the American Physical Society.

(ii) In spin exchange magnetoelectric coupling, one explores the exchange coupling between the spins of a ferromagnet and the uncompensated spins at the interface of an antiferromagnetic multiferroic.^{35,44,73–75} This gives rise to a so-called exchange bias effect^76,77 characteristic of ferromagnetic/antiferromagnetic interfaces, with the added function that the antiferromagnetic spin orientation (and as a consequence, the uncompensated interfacial spins and the direction of the exchange bias field) can be controlled by an applied electric field. The exchange bias effect is extensively used in read heads of hard disk drives (HDD) to bias the hard layer of the spin-valve sensors.⁷⁸ Electric field control of exchange bias has been demonstrated in multiferroic heterostructures using BiFeO₃,^43,74,79,80 and in hexagonal YMnO₃ (ref. 73 and 81) and LuMnO₃ (ref. 44) as ferroelectric antiferromagnets. The most extensively studied systems to date employ BiFeO₃. Traditionally, the exchange bias field is set by cooling down the system from above the antiferromagnetic critical temperature under an applied magnetic field, which poses some difficulties in BiFeO₃ due to the elevated Néel temperature (643 K). However, full electric control of the exchange bias without the need for temperature cycling has been recently demonstrated in La_0.7Sr_0.3MnO₃/BiFeO₃ (up to about 30 K) for the particular case when the magnetic field is applied along the [110] direction with respect to the SrTiO₃ (001) substrate.⁴³ These results are displayed in Fig. 3, showing that the sign and amplitude of the exchange bias are reversibly controlled by the gate voltage and also that the direction of the exchange bias can be reversed, depending on whether the electric field pulse is applied at the negative or positive remanent magnetisation state. These findings are interpreted in terms of a model that takes into account the relative ionic displacements in BiFeO₃ upon ferroelectric switching and the consequent change in the interatomic distance between the Fe and Mn cations at the interface that leads to a modification in the exchange interaction, acting in combination with the expected exchange bias effect.⁴³ This is a telling example where physical phenomena in artificial multiferroics can shed new light on an effect that, despite our improved understanding gained over the last decades, is still far from being fully understood.^82–88 Room temperature control of exchange bias has been demonstrated in BiFeO₃/Fe₃O₄ nanocomposite structures⁵⁹ and in heterostructures using the magnetoelectric antiferromagnet Cr₂O₃,⁸⁹ indicating that robust electric field control of exchange bias in functional devices can be achieved.

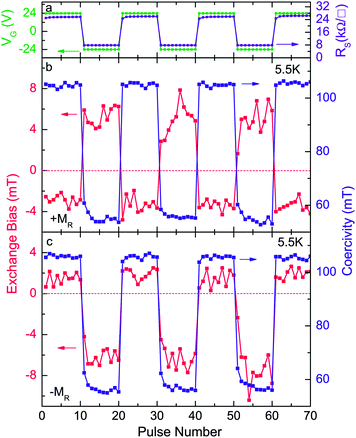Fig. 3 Variation of the exchange bias field and coercivity after the gate pulse voltage sequence shown on the top panel, demonstrating electric field control of exchange bias. Middle and bottom panels show the results of applying the gate voltage at positive and negative remanent magnetisation states, respectively. Reprinted with permission from ref. 43. Copyright (2013) by the American Physical Society.

(iii) In charge-mediated artificial multiferroics, the bound charge at the ferroelectric interface is used to modulate the charge carrier density in the ferromagnetic layer of device structures through charge screening in a field effect geometry (ferroelectric field effect).^90–94 This approach enables large modulations in the carrier density (charge doping), which are required in strongly correlated oxides, where typical carrier densities are of the order of 10²¹ cm⁻³.⁹⁵ In addition, the charge modulation is both reversible and non-volatile, which is advantageous for device applications. This approach also avoids the structural distortions in the system that occurs with chemical doping.⁹⁶ More generally, since the charge density is a fundamental quantity in the solid state,^97–99 one may expect important modifications in the electronic and magnetic properties of the system by using electrostatic doping, including control of magnetism, electron transport, orbital state, electron correlations, etc.

Charge screening in metallic ferromagnetic systems results in a change of the spin imbalance at the Fermi level with respect to the equilibrium state,¹⁰⁰ hence one can infer the presence of an intrinsic interfacial magnetoelectric effect in such systems. For example, in bcc Fe(001), Ni(001), and hcp Co(0001), an effective surface magnetoelectric response of ∼2–3 × 10⁻¹⁴ Oe cm² V⁻¹ (α_r ∼ 6 × 10⁻⁴) has been estimated.³⁶ For half-metallic systems, the charge carrier density determines also the magnetic moment, and a simple argument shows that an effective universal surface magnetoelectric constant due to charge screening, α_s = μ_B/ec² ≈ 6.44 × 10⁻¹⁴ Oe cm² V⁻¹, is expected.^101,102 When the electric field is applied across a dielectric instead of through a vacuum barrier, the magnetoelectric effect is enhanced due to the larger dielectric constant of the former.^103,104 Additionally, chemical bonding (or hybridisation) occurring at the interface will also play a role. For instance, density functional theory (DFT) calculations for Fe/BaTiO₃ (001) show a large surface magnetoelectric response whose origin is largely attributed to changes in the chemical bonding at the interface, i.e., to modulations in the Ti 3d, Fe 3d and O 2p orbital overlap upon reversal of the ferroelectric polarization direction due to the displacement of the Ti atoms, which additionally become magnetically polarised.^105–110 The latter effect has been observed experimentally in Fe/BaTiO₃ (001) by soft X-ray resonant magnetic scattering,¹¹¹ which shows that the Ti cations become ferromagnetic by proximity with the Fe film, turning the interface region of BaTiO₃ both ferroelectric and ferromagnetic, i.e., multiferroic, at room temperature.

The modulation of the charge carrier density at the interface can also modify strongly the surface magnetic anisotropy of a ferromagnetic material via spin–orbit coupling through a change in the relative electron occupancy of the different d orbitals.^{36,104,112–117} The effect can be very strong in 3d transition metal ferromagnets, where the surface magnetocrystalline anisotropy is often the dominant term of the magnetic energy of ultrathin films.¹¹⁸ Recently, the control of the surface magnetic anisotropy through charge screening has been demonstrated in a number of systems, including Fe,¹¹³ FePt,¹¹⁹ Co₄₀Fe₄₀B₂₀,^120–122 Co,¹²³ Ni,¹²⁴ Fe_0.5Pd_0.5,¹²⁵ Fe₈₀Co₂₀,^126–128 and in Fe₈₀Co₂₀/MgO/Fe (ref. 129 and 130) and Fe₄₀Co₄₀B₂₀/MgO/Fe₄₀Co₄₀B₂₀ tunnel junctions.^131,132 One motivation for such studies is the control of the relative magnetisation alignment of ferromagnetic layers in spin-valve device structures by means of electric fields, aiming at enabling the electric field control of the resistive states through the giant (GMR) or tunneling magnetoresistance (TMR) effects for applications in non-volatile magnetic random access memories (MRAM) and logic switches.^133,134

Changes in the charge carrier density can lead to more profound modifications in the magnetic interactions by directly perturbing the relative weight of the kinetic and Coulomb energy terms. In this context, the sensitivity of the electronic and magnetic properties of complex oxide materials to the charge density¹³⁵ offers a promising venue for the electrostatic control of the magnetic and electronic responses.^{92,95,136,137} One materials system of interest is the doped manganites, such as La_1−xA_xMnO₃ (A = Ca, Sr, Ba), which are characterized by rich magnetic and electronic phase diagrams as a function of chemical doping, including the coexistence of competing ground states.^138,139 The sensitivity to charge carrier density suggests that large susceptibilities to external electric fields can be attained when the system lies at the boundary separating two different ground states by driving it across the phase boundary using charge doping. We illustrate this approach to magnetoelectric coupling by considering the case of La_1−xSr_xMnO₃ (LSMO) films in contact with a ferroelectric (Fig. 4). The first direct demonstration of electric field control of magnetism in LSMO was carried out for a Sr doping of 0.2, which lies near the boundary separating insulating and metallic ferromagnetic ground states in the phase diagram of this compound.¹⁴⁰ Measurements of the temperature response of magnetisation for the two states of ferroelectric polarisation (Fig. 4(b)) show that switching from the accumulation to the depletion state leads to a large increase in the saturation magnetisation and a decrease in the magnetic critical temperature (by about 20 K),¹⁴¹ resulting in a large magnetoelectric response with a non-linear temperature behaviour (Fig. 4(b), inset).⁴⁶ In addition, a modulation in the Mn valency as a function of the ferroelectric polarisation direction was determined directly by X-ray absorption near edge spectroscopy (XANES), demonstrating that the effect is electronic in origin and results from a direct change in carrier density at the LSMO/PZT interface.^142,143 One important conclusion from these studies was that the change in magnetic moment could not be explained solely by a change in the spin state due to the change in cation valency, thus implying that a change in the interfacial spin configuration must occur, from ferromagnetic in the depletion state to antiferromagnetic in the accumulation state.¹⁴² This mechanism gives rise to a dramatic change in the average magnetic moment and explains the large magnetoelectric coupling observed in this system. Independent studies support these findings, including the measurement of a similarly large change in the magnetic moment of an LSMO film at 0.13 Sr doping with SQUID magnetometry (Fig. 4(a)).¹⁴⁴ The presence of an interfacial magnetic reconstruction at the interface, from a ferromagnetic coupling in the depletion state to an antiferromagnetic coupling in the accumulation state, agrees with the results of first principles calculations, as arising from a change in the relative weights of the superexchange and double exchange energy terms as a function of the 3dz² orbital occupancy induced by screening.^145–148 One direct consequence of these findings is that one can control electrostatically both the spin state and magnetic spin configuration of the interfacial LSMO layer. A different behaviour has been reported at the 0.3 Sr doping in LSMO/BaTiO₃ heterostructures,⁴⁵ where the magnetisation is found to increase when going from the depletion to the accumulation state while only a small modulation in the critical temperature of the system is observed (Fig. 4(c)).^149,150 In addition, the same study finds that the magnetic moment changes mostly for the depletion state, with a depletion layer that extends well beyond the interface. The results are explained in terms of a phase separation picture whereby magnetism is suppressed over a layer thickness up to 2.9 nm due to charge depletion (which favours an antiferromagnetic insulating state), in qualitative agreement with the behaviour expected from the bulk phase diagram.

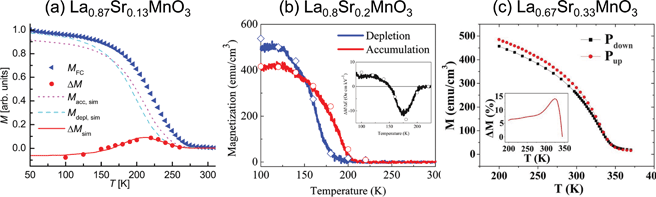Fig. 4 Magnetic response versus temperature of La_1−x Sr_xMnO₃/ferroelectric heterostructures at different chemical dopings, (a) x = 0.13,144 (b) x = 0.2,46 and (c) x = 0.33,45 for the two directions of the ferroelectric polarisation (accumulation and depletion states). Insets in (b) and (c) show the variation of the magnetoelectric coupling and of the change in magnetisation, respectively, as a function of temperature. (a) Reprinted with permission from ref. 144. Copyright (2013) by the American Physical Society. (b) Reprinted with permission from ref. 46. Copyright 2010, American Institute of Physics. (c) Reprinted with permission from ref. 45. Copyright 2012, American Institute of Physics.

A related topic which has seen tremendous progress is that of charge transport phenomena in multiferroics and multiferroic heterostructures.^19,151–155 In common with ferroelectrics, the ferroelectric domain walls in single phase multiferroics form a region in the material with significantly distinct structural and electronic properties,^156,157 which manifest in strongly modified electron transport, including enhanced or depressed conductivity in BiFeO₃ and YMnO₃, respectively.^158–165 Multiferroic heterostructures often consist of a ferroelectric layer sandwiched between ferromagnetic electrodes, and for sufficiently thin ferroelectric barrier layers, magnetic quantum tunneling phenomena are expected. Indeed, the magnetotransport properties of tunnel junctions composed of metallic ferromagnetic electrodes and ferroelectric or single-phase multiferroic tunnel barriers have been intensively investigated. Such structures are found to display large changes in resistance when switching both the ferroelectric and ferromagnetic polarisation directions, demonstrating both electric and magnetic control of charge transport.^{81,111,166,167,167–177}

II. Ultrafast dynamic response

Understanding ultrafast dynamical responses in complex oxides has recently attracted significant interest, an area of research made possible by the recent developments in experimental methods capable of probing dynamic processes down to the fs time scale, such as fs X-ray spectroscopy and scattering using X-ray free electron lasers³² or electron-beam “slicing” in synchrotrons.³³ Indeed, fundamental questions such as how the magnetic, electronic, and crystal structure respond to external stimuli on the ultrafast timescales have now begun to be addressed.^178,179 For example, recent experiments in the doped manganites have studied quantitatively how fast the system can transform from an insulating charge ordered state into a disordered metallic regime¹⁸⁰ and through which structural coherent motions the transition takes place.^181–183 In particular, ultrafast optical pump, X-ray probe experiments allow one to extract direct and quantitative information on the crystal and electronic structure at ultra-short times after excitation. Optical pump-probe experiments are now able to induce an ultrafast phase transition in a manganite system lying close to the antiferromagnetic/ferromagnetic phase boundary and to probe the fs transition regime between the different phases.¹⁸⁴ Such ultrafast time resolutions are necessary to resolve the electronic processes responsible for the magnetic and electric properties. Table 2 illustrates the different velocities and timescales relevant for multiferroic systems.

Table 2 Velocities and time scales relevant to magnetic and ferroelectric systems

Process	Time/velocity
Ferromagnetic domain wall velocity	≤10^3 m s^−1
Ferroelectric domain wall velocity	≤10^3 m s^−1
Speed of sound in solids	10^3–10^4 m s^−1
Fermi velocity	∼10^6 m s^−1
Ferromagnetic spin-wave period	∼ns
Antiferromagnetic spin-wave period	∼0.1 ns
Optical phonon period	∼ps
Electron tunnelling	∼10 fs
Electron hopping	∼fs

---

In single phase multiferroics, ultrafast magnetic processes have been studied in cupric oxide, CuO, in which the ferroelectric polarization sets in at a relatively high temperature for a type II multiferroic (230 K) and where the multiferroic state persists in an incommensurate antiferromagnetic state down to 213 K, below which the system reverts to a paraelectric, commensurate antiferromagnetic state, as illustrated in Fig. 5 (top).⁵ Optical pump, resonant soft X-ray diffraction probe experiments show that a strong optical excitation of a CuO crystal held at 207 K results in an ultrafast transition from an antiferromagnetic ordered state to the incommensurate multiferroic state, as shown in Fig. 5 (bottom).¹⁸⁵ The transition takes place after a short time delay, which varies with laser fluence: increasing the fluence excites the system more strongly and the time delay decreases, as shown in Fig. 5 (bottom, inset). This time delay does however level off at higher fluences, indicating that there is a minimum time delay that is necessary before the phase transition sets it. This minimum time delay is related to the lowest lying magnetic excitations (spin-gap) available to the system. Therefore, even shorter delays for the onset of such phase transitions can be anticipated in systems with suitable magnetic excitation spectra. Although the phase to which the system is driven to by the optical excitation is multiferroic, little is known on how the polarisation is built up in time. Such questions remain to be explored. The future of these developments clearly rely on the exploitation of selective excitations, such as specific magnon or phonon modes, with the potential of enabling us to control the magnetic and polarization properties at will. The required excitation energies that directly relate to the energy of these physical excitations in the material lie in the mid-IR and THz regimes. One exciting proposal for such a manipulation has been proposed theoretically for TbMnO₃ by Michozuki and Nagaosa,¹⁸⁶ who predict that the electric polarization can be switched in the picosecond time domain by strong, single cycle, THz pulses by directly exciting an electromagnon. The latter are collective spin excitations with electric dipole activity,^187–193 in which the electric field of the photon couples directly to the magnon. Such coupling makes the previous concept particularly appealing for controlling the ferroic state in multiferroics. Although the experimental confirmation remains challenging, the creation of short and intense THz pulses has recently made significant progress.¹⁹⁴ The implications of such excitations to artificial multiferroics might be stronger than anticipated at first, since for such systems large electric field gradients in the material might be achieved more easily.

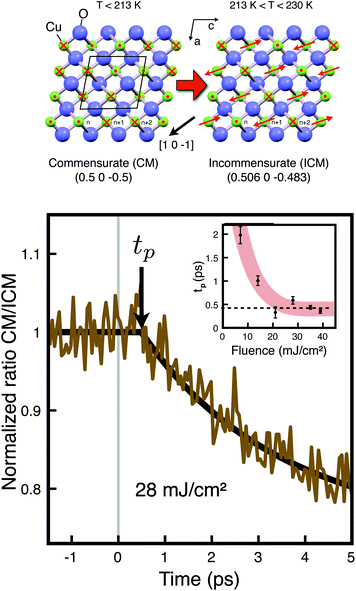Fig. 5 Top: Magnetic structure of CuO in the commensurate antiferromagnetic phase (CM) and in the incommensurate antiferromagnetic phase (ICM); arrows on the Cu ions indicate the spin direction. Bottom: Relative ICM/CM phase population following optical excitation, showing an increase in the ICM phase population. The inset shows the variation of the time delay t_p as a function of optical light fluence. Reprinted with permission from ref. 185. Copyright (2012) by the American Physical Society.

The study of the dynamic response of artificial multiferroics to external stimuli is also important both at fundamental and practical levels, because it elucidates the interaction mechanisms underlying the magnetoelectric coupling in both composite and single phase ferroic materials and because fast responses are required for device applications. While in intrinsic multiferroics one may expect a complex interaction mechanism between the magnetic and electric order parameters (for example, through electromagnons), in composite multiferroics the dynamics of the system is expected to be much simpler and can, in general terms, be separated into three components, namely: the time response of the ferroelectric,^195,196 the ferromagnet,^197,198 and the coupling mechanism linking the two order parameters. In particular, we may expect the magnetoelectric time response to depend strongly on the mechanisms responsible for the coupling, e.g., strain versus exchange interactions. The dynamics of ferromagnets and of ferroelectrics are now mature fields of research, although several outstanding issues still remain to be addressed, particularly in thin films and nanostructures, and at time scales associated with the various (electronic, lattice, and spin) relaxation processes.

Electric field control of the spin-wave spectrum of strain-coupled ferromagnet/ferroelectric layered systems has been investigated by means of ferromagnetic resonance (FMR).^199–217 Here, a modulation in the strain-induced magnetic anisotropy of the ferromagnetic component generated by the ferroelectric via the inverse piezoelectric effect or electrostriction leads to a change in the ferromagnetic resonance frequency, typically in the range from 1–100 GHz. Electric field modulation of the spin wave spectra has also been demonstrated in single phase multiferroics, such as in bulk BiFeO₃,²¹⁸ arising from a direct linear magnetoelectric coupling of the system. Such effects could be exploited for electrostatically tunable microwave devices, such as resonators, phase shifters, and band-pass filters.^9,10,199,216 However, while the magnetic response is measured at fast time scales, the dynamics of the magnetoelectric coupling as such is not addressed in these studies. The use of THz pulses might offer a direct way to couple to the strain of a ferroelectric and influence the magnetic properties. One way of achieving the large electric fields required to overcome the electrostatic energy is that of embedding the multiferroic structure within a nanoslit or nanosplit resonator, where very large field enhancements of up to 10⁴ can be achieved.^219,220

III. Conclusions

In summary, we have illustrated how novel functionalities can be generated by exploring the new phenomena that arise at the interface between dissimilar materials and how such an approach can be used to achieve electrostatic control of magnetism in multiferroic heterostructures. Electrostatic control of magnetism has been achieved as a proof of principle in a range of materials. The field of artificial multiferroics has expanded tremendously in the past few years, and trends in the type of approaches for magnetoelectric coupling are emerging. These approaches rely on strain, spin exchange, and charge interactions to achieve effective couplings between the magnetic and ferroelectric polarisations. They give rise to magnetoelectric couplings that are much larger than those typical of intrinsic multiferroics and with functionalities that can in principle be optimized for device applications. In addition, new physics is being unveiled at the ultrafast dynamic scale and new exciting results are expected on this front in the near future. While much remains to be investigated in terms of materials optimization, development and characterization of new systems, and understanding of the interfacial processes mediating the magnetoelectric coupling, the work achieved thus far illustrates how novel device structures enabling electric field control of the magnetic spin state can be tailored to provide the requisite characteristics that will make them excellent candidates for next-generation electronic devices.

References

1. H. Schmid, Ferroelectrics, 1994, 162, 317.
2. N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694.
3. M. Alexe, M. Ziese, D. Hesse, P. Esquinazi, K. Yamauchi, T. Fukushima, S. Picozzi and U. Gösele, Adv. Mater., 2009, 21, 4452.
4. K. Yamauchi and S. Picozzi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085131.
5. T. Kimura, Y. Sekio, H. Nakamura, T. Siegrist and A. P. Ramirez, Nat. Mater., 2008, 7, 291.
6. S. Picozzi and C. Ederer, J. Phys.: Condens. Matter, 2009, 21, 303201.
7. J. M. Rondinelli and N. A. Spaldin, Adv. Mater., 2011, 23, 3363.
8. C.-W. Nan, M. I. Bichurin, S. Dong, D. Viehland and G. Srinivasan, J. Appl. Phys., 2008, 103, 031101.
9. G. Srinivasan, Annu. Rev. Mater. Res., 2010, 40, 153.
10. J. F. Scott, J. Mater. Chem., 2012, 22, 4567.
11. D. I. Khomskii, Physics, 2009, 2, 20.
12. S.-W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13.
13. T. Kimura, Annu. Rev. Mater. Res., 2007, 37, 387.
14. G. Catalan and J. F. Scott, Adv. Mater., 2009, 21, 2463.
15. A. N. Kalinkin and V. M. Skorikov, Russ. J. Inorg. Chem., 2010, 55, 1794.
16. T. Kimura, Annu. Rev. Condens. Matter Phys., 2012, 3, 93.
17. L. Wang, D. Wang, Q. Cao, Y. Zheng, H. Xuan, J. Gao and Y. Du, Sci. Rep., 2013, 2, 223.
18. C. A. F. Vaz, J. Hoffman, C. H. Ahn and R. Ramesh, Adv. Mater., 2010, 22, 2900.
19. C. A. F. Vaz, J. Phys.: Condens. Matter, 2012, 24, 333201.
20. D. A. Muller, Nat. Mater., 2009, 8, 263.
21. H. Tan, S. Turner, E. Yücelen, J. Verbeeck and G. V. Tendeloo, Phys. Rev. Lett., 2011, 107, 107602.
22. A. Damascelli, Z. Hussain and Z.-X. Shen, Rev. Mod. Phys., 2003, 75, 473.
23. S. Eisebitt, J. Lüning, W. F. Schlotter, M. Lörgen, O. Hellwig, W. Eberhardt and J. Stöhr, Nature, 2004, 432, 885.
24. S. W. Lovesey, E. Balcar, K. S. Knight and J. F. Rodríguez, Phys. Rep., 2005, 411, 233.
25. B. Kaulich, P. Thibault, A. Gianoncelli and M. Kiskinova, J. Phys.: Condens. Matter, 2011, 23, 083002.
26. C. A. F. Vaz, C. Moutafis, C. Quitmann and J. Raabe, Appl. Phys. Lett., 2012, 101, 083114.
27. X. M. Cheng and D. J. Keavney, Rep. Prog. Phys., 2012, 75, 026501.
28. M. B. Holcomb, S. Polisetty, A. F. Rodríguez, V. Gopalan and R. Ramesh, Int. J. Mod. Phys. B, 2012, 26, 1230004.
29. Q. He, E. Arenholz, A. Scholl, Y.-H. Chu and R. Ramesh, Curr. Opin. Solid State Mater. Sci., 2012, 16, 216.
30. Magnetic microscopy of nanostructures, Nanoscience and Nanotechnology, ed. H. Hopster and H. P. Oepen, Springer-Verlag, Berlin, 2005.
31. D. A. Bonnell and J. Garra, Rep. Prog. Phys., 2008, 71, 044501.
32. H. N. Chapman, A. Barty, M. J. Bogan, S. Boutet, M. Frank, S. P. Hau-Riege, S. Marchesini, B. W. Woods, S. Bajt, W. H. Benner, R. A. London, E. Plönjes, M. Kuhlmann, R. Treusch, S. Düsterer, T. Tschentscher, J. R. Schneider, E. Spiller, T. Möller, C. Bostedt, M. Hoener, D. A. Shapiro, K. O. Hodgson, D. van der Spoel, F. Burmeister, M. Bergh, C. Caleman, G. Huldt, M. M. Seibert, F. R. N. C. Maia, R. W. Lee, A. Szöke, N. Timneanu and J. Hajdu, Nat. Phys., 2006, 2, 839.
33. P. Beaud, S. L. Johnson, R. A. A. Streun, D. Abramsohn, D. Grolimund, F. Krasniqi, T. Schmidt, V. Schlott and G. Ingold, Phys. Rev. Lett., 2007, 99, 174801.
34. R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6, 21.
35. C. Binek, Physics, 2013, 6, 13.
36. C.-G. Duan, J. P. Velev, R. F. Sabirianov, Z. Zhu, J. Chu, S. S. Jaswal and E. Tsymbal, Phys. Rev. Lett., 2008, 101, 137201.
37. F. W. Hehl, Y. N. Obukhov, J.-P. Rivera and H. Schmid, Phys. Rev. A, 2008, 77, 022106.
38. F. Wang, T. Zao, L.-Q. Yan and Y. Sun, J. Appl. Phys., 2011, 110, 054106.
39. M. Tokunaga, M. Azuma and Y. Shimakawa, J. Phys. Soc. Jpn., 2010, 79, 064713.
40. S. H. Chun, Y. S. Chai, B.-G. Jeon, H. J. Kim, Y. S. Oh, I. Kim, H. Kim, B. J. Jeon, S. Y. Haam, J.-Y. Park, S. H. Lee, J.-H. Chung, J.-H. Park and K. H. Kim, Phys. Rev. Lett., 2012, 108, 177201.
41. W. Eerenstein, M. Wiora, J. L. Prieto, J. F. Scott and N. D. Mathur, Nat. Mater., 2007, 6, 348.
42. M. Buzzi, R. V. Chopdekar, J. L. Hockel, A. Bur, T. Wu, N. Pilet, P. Warnicke, G. P. Carman, L. J. Heyderman and F. Nolting, Phys. Rev. Lett., 2013, 111, 027204.
43. S. M. Wu, S. A. Cybart, D. Yi, J. M. Parker, R. Ramesh and R. C. Dynes, Phys. Rev. Lett., 2013, 110, 067202.
44. V. Skumryev, V. Laukhin, I. Fina, X. Martí, F. Sánchez, M. Gospodinov and J. Fontcuberta, Phys. Rev. Lett., 2011, 106, 057206.
45. H. Lu, T. A. George, Y. Wang, I. Ketsman, J. D. Burton, C.-W. Bark, S. Ryu, D. J. Kim, J. Wang, C. Binek, P. A. Dowben, A. Sokolov, C.-B. Eom, E. Y. Tsymbal and A. Gruverman, Appl. Phys. Lett., 2012, 100, 232904.
46. C. A. F. Vaz, Y. Segal, J. Hoffman, R. D. Grober, F. J. Walker and C. H. Ahn, Appl. Phys. Lett., 2010b, 97, 042506.
47. K. F. Wang, J. M. Liu and Z. F. Ren, Adv. Phys., 2009, 58, 321.
48. R. C. Kambale, D.-Y. Jeong and J. Ryu, Adv. Condens. Matter Phys., 2012, 2012, 824643.
49. Y. P. Lee, S. Y. Park, Y. H. Hyun, J. B. Kim, V. G. Prokhorov, V. A. Komashko and V. L. Svetchnikov, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224413.
50. G. E. Sterbinsky, B. W. Wessels, J.-W. Kim, E. Karapetrova, P. J. Ryan and D. J. Keavney, Appl. Phys. Lett., 2010, 96, 092510.
51. Z. X. Cheng, X. L. Wang, S. X. Dou, M. Osada and H. Kimura, Appl. Phys. Lett., 2011, 99, 092103.
52. A. Alberca, N. M. Nemes, F. J. Mompean, N. Biskup, A. de Andres, C. Munuera, J. Tornos, C. Leon, A. Hernando, P. Ferrer, G. R. Castro, J. Santamaria and M. Garcia-Hernandez, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 134402.
53. S. Chen, H. Zhang, F. Liu, Q. Ye, L. Tang, Z. Huang and D. Wang, J. Appl. Phys., 2013, 113, 17C712.
54. T. Zhang, Q. Wei, R. K. Zheng, X. P. Wang and Q. F. Fang, J. Appl. Phys., 2013, 113, 013705.
55. H. Zheng, J. Wang, S. E. Lofland, Z. Ma, L. Mohaddes-Ardabili, T. Zhao, L. Salamanca-Riba, S. R. Shinde, S. B. Ogale, F. Bai, D. Viehland, Y. Jia, D. G. Schlom, M. Wuttig, A. Roytburd and R. Ramesh, Science, 2004, 303, 661.
56. Y. S. Oh, S. Crane, H. Zheng, Y. H. Chu, R. Ramesh and K. H. Kim, Appl. Phys. Lett., 2010, 97, 052902.
57. N. M. Aimon, D. H. Kim, H. K. Choi and C. A. Ross, Appl. Phys. Lett., 2012, 100, 092901.
58. C. Schmitz-Antoniak, D. Schmitz, P. Borisov, F. M. F. de Groot, S. Stienen, A. Warland, B. Krumme, R. Feyerherm, E. Dudzik, W. Kleemann and H. Wende, Nat. Commun., 2013, 4, 2051.
59. E.-M. Choi, E. Weal, Z. Bi, H. Wang, A. Kursumovic, T. Fix, M. G. Blamire and J. L. MacManus-Driscoll, Appl. Phys. Lett., 2013, 102, 012905.
60. C. Thiele, K. Dörr, O. Bilani, J. Rödel and L. Schultz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 054408.
61. C. A. F. Vaz, J. Hoffman, A.-B. Posadas and C. H. Ahn, Appl. Phys. Lett., 2009, 94, 022504.
62. J. Chakhalian, A. J. Millis and J. Rondinelli, Nat. Mater., 2012, 11, 92.
63. S. Geprägs, M. Opel, S. T. B. Goennenwein and R. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134432.
64. G. Zhu, K. L. Wong, J. Zhao, P. K. Amiri, J. Zhu, I. Krivorotov and K. L. Wang, Appl. Phys. Lett., 2012, 101, 202404.
65. S. Geprägs, D. Mannix, M. Opel, S. T. B. Goennenwein and R. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 057712.
66. M. Liu, J. Hoffman, J. Wang, J. Zhang, B. Nelson-Cheeseman and A. Bhattacharya, Sci. Rep., 2013, 3, 1876.
67. H. Kojima, T. Naito, H. Muraoka, E. Wada, I. Suzuki, Y. Shirahata, M. Itoh and T. Taniyama, J. Appl. Phys., 2013, 113, 17C713.
68. J. Ma, J. Hu, Z. Li and C.-W. Nan, Adv. Mater., 2011, 23, 1062.
69. N. A. Pertsev, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 212102.
70. J.-M. Hu and C. W. Nan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 224416.
71. M. Liu, J. Lou, S. Li and N. X. Sun, Adv. Funct. Mater., 2011, 21, 2593.
72. J.-M. Hu, T. N. Yang, L. Q. Chen and C. W. Nan, J. Appl. Phys., 2013, 113, 194301.
73. V. Laukhin, V. Skumryev, X. Martí, D. Hrabovsky, F. Sánchez, M. V. García-Cuenca, C. Ferrater, M. Varela, U. Lüders, J. F. Bobo and J. Fontcuberta, Phys. Rev. Lett., 2006, 97, 227201.
74. S. M. Wu, S. A. Cybart, P. Yu, M. D. Rossell, J. X. Zhang, R. Ramesh and R. C. Dynes, Nat. Mater., 2010, 9, 756.
75. J. T. Heron, M. Trassin, K. Ashraf, M. Gajek, Q. He, S. Yang, D. E. Nikonov, Y.-H. Chu, S. Salahuddin and R. Ramesh, Phys. Rev. Lett., 2011, 107, 217202.
76. W. H. Meiklejohn and C. P. Bean, Phys. Rev., 1956, 102, 1413.
77. W. H. Meiklejohn, J. Appl. Phys., 1962, 33, 1328.
78. E. Hirota, H. Sakakima and K. Inomata, Giant Magneto-Resistance Devices, Springer Series in Surface Science No. 40, Springer-Verlag, Berlin, 2002.
79. Y.-H. Chu, L. W. Martin, M. B. Holcomb, M. Gajek, S.-J. Han, Q. He, N. Balke, C.-H. Yang, D. Lee, W. Hu, Q. Zhan, P.-L. Yang, A. Fraile-Rodríguez, A. Scholl, S. X. Wang and R. Ramesh, Nat. Mater., 2008, 7, 478.
80. D. Lebeugle, A. Mougin, M. Viret, D. Colson and L. Ranno, Phys. Rev. Lett., 2009, 103, 257601.
81. V. Laukhin, X. Martí, V. Skumryev, D. Hrabovsky, F. Sánchez, M. V. García-Cuenca, C. Ferrater, M. Varela, U. Lüders, J. F. Bobo and J. Fontcuberta, Philos. Mag. Lett., 2007, 87, 183.
82. J. Nogués, J. Sort, V. Langlais, V. Skumryev, S. Suriñach, J. S. Muñoz and M. D. Baró, Phys. Rep., 2005, 422, 65.
83. F. Radu and H. Zabel, in Magnetic Heterostructures, STMP No. 227, ed. H. Zabel and S. D. Bader, Springer-Verlag, Berlin Heidelberg, 2007p. 97.
84. O. Iglesias, A. Labarta and X. Batlle, J. Nanosci. Nanotechnol., 2008, 8, 2761 , preprint: arXiv:cond-mat/0607716v2 [cond-mat.mtrl-sci].
85. I. Schmid, P. Kappenberger, O. Hellwig, M. J. Carey, E. E. Fullerton and H. J. Hug, Europhys. Lett., 2008, 81, 17001.
86. S. Dong, K. Yamauchi, S. Yunoki, R. Yu, S. Liang, A. Moreo, J.-M. Liu, S. Picozzi and E. Dagotto, Phys. Rev. Lett., 2009, 103, 127201.
87. C. A. F. Vaz, E. I. Altman and V. E. Henrich, Phys. Rev. B: Condens. Matter Mater. Phys., 2010c, 81, 104428.
88. S. Dong, Q. Zhang, S. Yunoki, J.-M. Liu and E. Dagotto, Phys. Rev. B: Condens. Matter Mater. Phys., 2011a, 84, 224437.
89. X. He, Y. Wang, N. Wu, A. N. Caruso, E. Vescovo, K. D. Belashchenko, P. A. Dowben and C. Binek, Nat. Mater., 2010, 9, 579.
90. S. Mathews, R. Ramesh, T. Venkatesan and J. Benedetto, Science, 1997, 276, 238.
91. M. Dawber, K. M. Rabe and J. F. Scott, Rev. Mod. Phys., 2005, 77, 1083.
92. C. H. Ahn, A. Bhattacharya, M. D. Ventra, J. N. Eckstein, C. D. Frisbie, M. E. Gershenson, A. M. Goldman, I. H. Inoue, J. Mannhart, A. J. Millis, A. F. Morpurgo, D. Natelson and J.-M. Triscone, Rev. Mod. Phys., 2006, 78, 1185.
93. N. Setter, D. Damjanovic, L. Eng, G. Fox, S. Gevorgian, S. Hong, A. Kingon, H. Kohlstedt, N. Y. Park, G. B. Stephenson, I. Stolitchnov, A. K. Taganstev, D. V. Taylor, T. Yamada and S. Streiffer, J. Appl. Phys., 2006, 100, 051606.
94. T. Venkatesan, D. C. Kundaliya, T. Wu and S. B. Ogale, Philos. Mag. Lett., 2007, 87, 279.
95. C. H. Ahn, J.-M. Triscone and J. Mannhart, Nature, 2003, 424, 1015.
96. X. Hong, J. Yau, J. D. Hoffman, C. H. Ahn, Y. Bason and L. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 174406.
97. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
98. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
99. A. J. Freeman and E. Wimmer, Annu. Rev. Mater. Sci., 1995, 25, 7.
100. S. Zhang, Phys. Rev. Lett., 1999, 83, 640.
101. C.-G. Duan, C.-W. Nan, S. S. Jaswal and E. Y. Tsymbal, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 140403.
102. T. Cai, S. Ju, J. Lee, N. Sai, A. A. Demkov, Q. Niu, Z. Li, J. Shi and E. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 140415.
103. J. M. Rondinelli, M. Stengel and N. A. Spaldin, Nat. Nanotechnol., 2008, 3, 46.
104. M. K. Niranjan, C.-G. Duan, S. S. Jaswal and E. Y. Tsymbal, Appl. Phys. Lett., 2010, 96, 222504.
105. C.-G. Duan, S. S. Jaswal and E. Tsymbal, Phys. Rev. Lett., 2006, 97, 047201.
106. M. Fechner, I. V. Maznichenko, S. Ostanin, A. Ernst, J. Henk, P. Bruno and I. Mertig, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 212406.
107. H. L. Meyerheim, F. Klimenta, A. Ernst, K. Mohseni, S. Ostanin, M. Fechner, S. Parihar, I. Maznichenko, I. Mertig and J. Kirschner, Phys. Rev. Lett., 2011, 106, 087203.
108. J.-Q. Dai, Y.-M. Song and H. Zhang, J. Appl. Phys., 2012, 111, 114301.
109. L. Bocher, A. Gloter, A. Crassous, V. Garcia, K. March, A. Zobelli, S. Valencia, S. Enouz-Vedrenne, X. Moya, N. D. Marthur, C. Deranlot, S. Fusil, K. Bouzehouane, M. Bibes, A. Barthélémy, C. Colliex and O. Stéphan, Nano Lett., 2012, 12, 376.
110. S. Borek, I. Maznichenko, G. Fischer, W. Hergert, I. Mertig, A. Ernst, S. Ostanin and A. Chassé, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134432.
111. S. Valencia, A. Crassous, L. Bocher, V. Garcia, X. Moya, R. O. Cherifi, C. Deranlot, K. Bouzehouane, S. Fusil, A. Zobelli, A. Gloter, N. D. Mathur, A. Gaupp, R. Abrudan, F. Radu, A. Barthélémy and M. Bibes, Nat. Mater., 2011, 10, 753.
112. K. Nakamura, R. Shimabukuro, Y. Fujiwara, T. Akiyama, T. Ito and A. J. Freeman, Phys. Rev. Lett., 2009, 102, 187201.
113. T. Maruyama, Y. Shiota, T. Nozaki, K. Ohta, N. Toda, M. Mizuguchi, A. A. Tulapurkar, T. Shinjo, M. Shiraishi, S. Mizukami, Y. Ando and Y. Suzuki, Nat. Nanotechnol., 2009, 4, 158.
114. M. Tsujikawa and T. Oda, Phys. Rev. Lett., 2009, 102, 247203.
115. K. Nakamura, T. Akiyama, T. Ito, M. Weinert and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 220409.
116. R. Shimabukuro, K. Nakamura, T. Akiyama and T. Ito, Physica E, 2010, 42, 1014.
117. S. Haraguchi, M. Tsujikawa, J. Gotou and T. Oda, J. Phys. D: Appl. Phys., 2011, 44, 064005.
118. C. A. F. Vaz, J. A. C. Bland and G. Lauhoff, Rep. Prog. Phys., 2008, 71, 056501.
119. T. Seki, M. Kohda, J. Nitta and K. Takanashi, Appl. Phys. Lett., 2011, 98, 212505.
120. M. Endo, S. Kanai, S. Ikeda, F. Matsukura and H. Ohno, Appl. Phys. Lett., 2010, 96, 212503.
121. C. Fowley, N. Decorde, K. Oguz, K. Rode, H. Kurt and J. M. D. Coey, IEEE Trans. Magn., 2010, 46, 2116.
122. C. Fowley, K. Rode, K. Oguz, H. Kurt and J. M. D. Coey, J. Phys. D: Appl. Phys., 2011, 44, 305001.
123. A. Mardana, S. Ducharme and S. Adenwalla, Nano Lett., 2011, 11, 3862.
124. L. Shu, Z. Li, J. Ma, Y. Gao, L. Gu, Y. Shen, Y. Lin and C. W. Nan, Appl. Phys. Lett., 2012, 100, 022405.
125. F. Bonell, S. Murakami, Y. Shiota, T. Nozaki, T. Shinjo and Y. Suzuki, Appl. Phys. Lett., 2011, 98, 232510.
126. Y. Shiota, T. Maruyama, T. Nozaki, T. Shinjo, M. Shiraishi and Y. Suzuki, Appl. Phys. Express, 2009, 2, 063001.
127. S.-S. Ha, N.-H. Kim, S. Lee, C.-Y. You, Y. Shiota, T. Maruyama, T. Nozaki and Y. Suzuki, Appl. Phys. Lett., 2010, 96, 142512.
128. K. H. He, J. S. Chen and Y. P. Feng, Appl. Phys. Lett., 2011, 99, 072503.
129. T. Nozaki, Y. Shiota, M. Shiraishi, T. Shinjo and Y. Suzuki, Appl. Phys. Lett., 2010, 96, 022506.
130. Y. Shiota, S. Murakami, F. Bonell, T. Nozaki, T. Shinjo and Y. Suzuki, Appl. Phys. Express, 2011, 4, 043005.
131. W.-G. Wang, M. Li, S. Hageman and C. L. Chien, Nat. Mater., 2012, 11, 64.
132. H. Meng, R. Sbiaa, M. A. K. Akhtar, R. S. Liu, V. B. Naik and C. C. Wang, Appl. Phys. Lett., 2012, 100, 122405.
133. M. Bibes and A. Barthélémy, Nat. Mater., 2008, 7, 425.
134. T. Zhou, S. H. Leong, Z. M. Yuan, S. B. Hu, C. L. Ong and B. Liu, Appl. Phys. Lett., 2010, 96, 012506.
135. E. Dagotto, Science, 2005, 309, 257.
136. E. Mikheev, I. Stolichnov, E. D. Ranieri, J. Wunderlich, H. J. Trodahl, A. W. Rushforth, S. W. E. Riester, R. P. Campion, K. W. Edmonds, B. L. Gallagher and N. Setter, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235130.
137. S. Cao, P. Liu, J. Tang, H. Lu, C.-W. Bark, S. Ryu, C. B. Eom, A. Gruverman and P. A. Dowben, Appl. Phys. Lett., 2013, 102, 172402.
138. A. Moreo, S. Yunoki and E. Dagotto, Science, 1999, 283, 2034.
139. Y. Tokura and Y. Tomioka, J. Magn. Magn. Mater., 1999, 200, 1.
140. E. Dagotto, T. Hotta and A. Moreo, Phys. Rep., 2001, 344, 1.
141. H. J. A. Molegraaf, J. Hoffman, C. A. F. Vaz, S. Gariglio, D. van der Marel, C. H. Ahn and J.-M. Triscone, Adv. Mater., 2009, 21, 3470.
142. C. A. F. Vaz, J. Hoffman, Y. Segal, J. W. Reiner, R. D. Grober, Z. Zhang, C. H. Ahn and F. J. Walker, Phys. Rev. Lett., 2010, 104, 127202.
143. C. A. F. Vaz, J. Hoffman, Y. Segal, M. S. J. Marshall, J. W. Reiner, Z. Zhang, R. D. Grober, F. J. Walker and C. H. Ahn, J. Appl. Phys., 2011, 109, 07D905.
144. M. Leufke, R. Kruk, R. A. Brand and H. Hahn, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094416.
145. J. D. Burton and E. Y. Tsymbal, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 174406.
146. S. Dong, X. Zhang, R. Yu, J.-M. Liu and E. Dagotto, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155117.
147. N. C. Bristowe, M. Stegel, P. B. Littlewood, J. M. Pruneda and E. Artacho, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 024106.
148. H. Chen and S. Ismail-Beigi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 024433.
149. T. Kanki, H. Tanaka and T. Kawai, Appl. Phys. Lett., 2006, 89, 242506.
150. S. Brivio, M. Cantoni, D. Petti and R. Bertacco, J. Appl. Phys., 2010, 108, 113906.
151. T. Wu, S. B. Ogale, J. E. Garrison, B. Nagaraj, A. Biswas, Z. Chen, R. L. Greene, R. Ramesh, T. Venkatesan and A. J. Millis, Phys. Rev. Lett., 2001, 86, 5998.
152. T. Zhao, S. B. Ogale, S. R. Shinde, R. Ramesh, R. Droopad, J. Yu, K. Eisenbeiser and J. Misewich, Appl. Phys. Lett., 2004, 84, 750.
153. M. Bibes, J. E. Villegas and A. Barthélémy, Adv. Phys., 2011, 60, 5.
154. J. D. Burton and E. Y. Tsymbal, Phys. Rev. Lett., 2011, 106, 157203.
155. Y. Segal, K. F. Garrity, C. A. F. Vaz, J. D. Hoffman, F. J. Walker, S. Ismail-Beigi and C. H. Ahn, Phys. Rev. Lett., 2011, 107, 105501.
156. E. K. H. Salje, ChemPhysChem, 2010, 11, 940.
157. G. Catalan, J. Seidel, R. Ramesh and J. F. Scott, Rev. Mod. Phys., 2012, 84, 119.
158. J. Seidel, L. W. Martin, Q. He, Q. Zhan, Y.-H. Chu, A. Rother, M. E. Hawkridge, P. Maksymovych, P. Yu, M. Gajek, N. Balke, S. V. Kalinin, S. Gemming, F. Wang, G. Catalan, J. F. Scott, N. A. Spaldin, J. Orenstein and R. Ramesh, Nat. Mater., 2009, 8, 229.
159. A. Lubk, S. Gemming and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 104110.
160. J. Seidel, P. Maksymovych, Y. Batra, A. Katan, S.-Y. Yang, Q. He, A. P. Baddorf, S. Kalinin, C.-H. Yang, J.-C. Yang, Y.-H. Chu, E. K. H. Salje, H. Wormeester, M. Salmeron and R. Ramesh, Phys. Rev. Lett., 2010, 105, 197603.
161. P. Maksymovych, J. Seidel, Y. H. Chu, P. Wu, A. P. Baddorf, L.-Q. Chen, S. V. Kalinin and R. Ramesh, Nano Lett., 2011, 11, 1906.
162. S. Farokhipoor and B. Noheda, Phys. Rev. Lett., 2011, 107, 127601.
163. T. Choi, Y. Horibe, H. T. Yi, Y. J. Choi, W. Wu and S.-W. Cheong, Nat. Mater., 2010, 9, 253.
164. O. Diéguez, P. Aguado-Puente, J. Junquera and J. I. niguez, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024102.
165. W. Ren, Y. Yang, O. Diéguez, J. Íñiguez, N. Choudhury and L. Bellaiche, Phys. Rev. Lett., 2013, 110, 187601.
166. C. Binek and B. Doudin, J. Phys.: Condens. Matter, 2005, 17, L39.
167. M. Gajek, M. Bibes, A. Barthélémy, K. Bouzehouane, S. Fusil, M. Varela, J. Fontcuberta and A. Fert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 020406.
168. M. Gajek, M. Bibes, S. Fusil, K. Bouzehouane, J. Fontcuberta, A. Barthélémy and A. Fert, Nat. Mater., 2007, 6, 296.
169. H. Béa, M. Gajek, M. Bibes and A. Barthélémy, J. Phys.: Condens. Matter, 2008, 20, 434221.
170. J. P. Velev, C.-G. Duan, K. D. Belashchenko, S. S. Jaswal and E. Tsymbal, J. Appl. Phys., 2008, 103, 07A701.
171. J. P. Velev, C.-G. Duan, J. D. Burton, A. Smogunov, M. K. Niranjan, E. Tosatti, S. S. Jaswal and E. Tsymbal, Nano Lett., 2009, 9, 427.
172. F. Yang, Y. C. Zhou, M. H. Tang, F. Liu, Y. Ma, X. J. Zheng, W. F. Zhao, H. Y. Xu and Z. H. Sun, J. Phys. D: Appl. Phys., 2009, 42, 072004.
173. M. Hambe, A. Petraru, N. A. Pertsev, P. Munroe, V. Nagarajan and H. Kohlstedt, Adv. Funct. Mater., 2010, 20, 2436.
174. V. Garcia, M. Bibes, L. Bocher, S. Valencia, F. Kronast, A. Crassous, X. Moya, S. Enouz-Vedrenne, A. Gloter, D. Imhoff, C. Deranlot, N. D. Mathur, S. Fusil, K. Bouzehouane and A. Barthélémy, Science, 2010, 327, 1106.
175. J. M. López-Encarnación, J. D. Burton, E. Y. Tsymbal and J. P. Velev, Nano Lett., 2011, 11, 599.
176. D. Pantel, S. Goetze, D. Hesse and M. Alexe, Nat. Mater., 2012, 11, 289.
177. Y. W. Yin, J. D. Burton, Y.-M. Kim, A. Y. Borisevich, S. J. Pennycook, S. M. Yang, T. W. Noh, A. Gruverman, X. G. Li, E. Y. Tsymbal and Q. Li, Nat. Mater., 2013, 12, 397.
178. H. Ehrke, R. I. Tobey, S. Wall, S. A. Cavill, F. örst, V. Khanna, T. Garl, N. Stojanovic, D. Prabhakaran, A. T. Boothroyd, M. Gensch, A. Mirone, P. Reutler, A. Revcolevschi, S. S. Dhesi and A. Cavalleri, Phys. Rev. Lett., 2011, 106, 217401.
179. A. D. Caviglia, R. Scherwitzl, P. Popovich, W. Hu, H. Bromberger, R. Singla, M. Mitrano, M. C. Hoffmann, S. Kaiser, P. Zubko, S. Gariglio, J.-M. Triscone, M. Först and A. Cavalleri, Phys. Rev. Lett., 2012, 108, 136801.
180. P. Beaud, S. L. Johnson, E. Vorobeva, U. Staub, R. A. D. Souza, C. J. Milne, Q. X. Jia and G. Ingold, Phys. Rev. Lett., 2009, 103, 155702.
181. H. Matsuzaki, H. Uemura, M. Matsubara, T. Kimura, Y. Tokura and H. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235131.
182. A. Caviezel, U. Staub, S. L. Johnson, S. O. Mariager, E. Möhr-Vorobeva, G. Ingold, C. J. Milne, M. Garganourakis, V. Scagnoli, S. W. Huang, Q. X. Jia, S.-W. Cheong and P. Beaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 174105.
183. A. Caviezel, S. O. Mariager, S. L. Johnson, E. Möhr-Vorobeva, S. W. Huang, G. Ingold, U. Staub, C. J. Milne, S.-W. Cheong and P. Beaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205104.
184. T. Li, A. Patz, L. Mouchliadis, J. Yan, T. A. Lograsso, I. E. Perakis and J. Wang, Nature, 2013, 496, 69.
185. S. L. Johnson, R. A. de Souza, U. Staub, P. Beaud, E. Möhr-Vorobeva, G. Ingold, A. Caviezel, V. Scagnoli, W. F. Schlotter, J. J. Turner, O. Krupin, W.-S. Lee, Y.-D. Chuang, L. Patthey, R. G. Moore, D. Lu, M. Yi, P. S. Kirchmann, M. Trigo, P. Denes, D. Doering, Z. Hussain, Z.-X. Shen, D. Prabhakaran and A. T. Boothroyd, Phys. Rev. Lett., 2012, 108, 037203.
186. M. Mochizuki and N. Nagaosa, Phys. Rev. Lett., 2010, 105, 147202.
187. G. A. Smolenskiǐ and I. E. Chupis, Sov. Phys. Usp., 1982, 25, 475.
188. A. Pimenov, A. A. Mukhin, V. Y. Ivanov, V. D. Travkin, A. M. Balbashov and A. Loidl, Nat. Phys., 2006, 2, 97.
189. B. Sushkov, R. V. Aguilar, S. Park, S.-W. Cheong and H. D. Drew, Phys. Rev. Lett., 2007, 98, 027202.
190. H. Katsura, A. V. Balatsky and N. Nagaosa, Phys. Rev. Lett., 2007, 98, 027203.
191. A. Pimenov, A. M. Shuvaev, A. A. Mukhin and A. Loidl, J. Phys.: Condens. Matter, 2008, 20, 434209.
192. A. M. Shuvaev, A. A. Mukhin and A. Pimenov, J. Phys.: Condens. Matter, 2011, 23, 113201.
193. Y. Takahashi, R. Shimano, Y. Kaneko, H. Murakawa and Y. Tokura, Nat. Phys., 2012, 8, 121.
194. M. C. Hoffmann and J. A. Fülöp, J. Phys. D: Appl. Phys., 2011, 44, 083001.
195. J. Li, B. Nagaraj, W. Cao, C. H. Lee and R. Ramesh, Appl. Phys. Lett., 2004, 84, 1174.
196. J. F. Scott, Adv. Mater., 2010, 22, 5315.
197. J. Ferré, in Spin Dynamics in Confined Magnetic Structures I, Topics Appl. Physics No. 83, Springer-Verlag, Berlin, 2002, p. 127.
198. A. Kirilyuk, A. V. Kimel and T. Rasing, Rev. Mod. Phys., 2010, 82, 2731.
199. M. I. Bichurin, R. V. Petrov and Y. V. Kiliba, Ferroelectrics, 1997, 204, 311.
200. S. Shastry, G. Srinivasan, M. I. Bichurin, V. M. Petrov and A. S. Tatarenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 064416.
201. Y. K. Fetisov and G. Srinivasan, Appl. Phys. Lett., 2006, 88, 143503.
202. A. S. Tatarenko, V. Gheevarughese and G. Srinivasan, Electron. Lett., 2006, 42, 540.
203. A. Semenov, S. F. Karmanenko, V. E. Demidov, B. A. Kalinikos, G. Srinivasan, A. N. Slavin and J. V. Mantese, Appl. Phys. Lett., 2006, 88, 033503.
204. R. Heindl, H. Srikanth, S. Witanachchi, P. Mukherjee, T. Weller, A. S. Tatarenko and G. Srinivasan, J. Appl. Phys., 2007, 101, 09M503.
205. C. Pettiford, J. Lou, L. Russell and N. X. Sun, Appl. Phys. Lett., 2008, 92, 122506.
206. A. B. Ustinov and G. Srinivasan, Appl. Phys. Lett., 2008, 93, 142503.
207. Y. Chen, J. Wang, M. Liu, J. Lou, N. X. Sun, C. Vittoria and V. G. Harris, Appl. Phys. Lett., 2008, 93, 112502.
208. J. Lou, D. Rheed, C. Pettiford, M. Liu, P. Han, S. Dong and N. X. Sun, Appl. Phys. Lett., 2008, 92, 262502.
209. M. Liu, O. Obi, J. Lou, Y. Chen, Z. Cai, S. Stoute, M. Espanol, M. Lew, X. Situ, K. S. Ziemer, V. G. Harris and N. X. Sun, Adv. Funct. Mater., 2009, 19, 1826.
210. Y.-Y. Song, J. Das, P. Krivosik, N. Mo and C. E. Patton, Appl. Phys. Lett., 2009, 94, 182505.
211. J. Das, Y.-Y. Song, N. Mo, P. Krivosik and C. E. Patton, Adv. Mater., 2009, 21, 2045.
212. N. Benatmane, S. P. Crane, F. Zavaliche, R. Ramesh and T. W. Clinton, Appl. Phys. Lett., 2010, 96, 082503.
213. M. Liu, O. Obi, Z. Cai, J. Lou, G. Yang, K. S. Ziemer and N. X. Sun, J. Appl. Phys., 2010, 107, 073916.
214. Y. Wang, J. Hu, Y. Lin and C.-W. Nan, NPG Asia Mater., 2010, 2, 61.
215. A. L. Geiler, S. M. Gillette, Y. Chen, J. Wang, Z. Chen, S. D. Yoon, P. He, J. Gao, C. Vittoria and V. G. Harris, Appl. Phys. Lett., 2010, 96, 053508.
216. A. S. Tatarenko, V. Gheevarughese, G. Srinivasan, O. V. Antonenkov and M. I. Bichurin, J. Electroceram., 2011, 24, 5.
217. S. Li, M. Liu, J. Lou, S. Beguhn, J. Wu, J. Qiu, J. Lin, Z. Cai, Y. Hu, F. Xu, J. Duh and N. X. Sun, J. Appl. Phys., 2012, 111, 07C705.
218. P. Rovillain, R. de Sousa, Y. Gallais, A. Sacuto, M. A. Méasson, D. Colson, A. Forget, M. Bibes, A. Barthélémy and M. Cazayous, Nat. Mater., 2010, 9, 975.
219. M. A. Seo, H. R. Park, S. M. Koo, D. J. Park, J. H. Kang, O. K. Suwal, S. S. Choi, P. C. M. Planken, G. S. Park, N. K. Park, Q. H. Park and D. S. Kim, Nat. Photonics, 2009, 3, 152.
220. H. Merbold, A. Bitzer and T. Feurer, Opt. Express, 2011, 19, 7262.

---